The Influence of Shell-Sand Mixing on the Dynamic Response of the Seabed Foundation in Front of a Slope Breakwater

Abstract

Shell-sand mixing, as a novel technique for coastal protection and seabed improvement, holds broad application prospects. However, the underlying mechanism of its influence on the wave-induced dynamic response of the seabed beneath slope breakwaters remains unclear. In this study, physical model experiments were conducted in a wave flume to analyze the effects of shell-sand mixing on the amplitude of pore water pressure in front of the breakwater and the vertical attenuation coefficient of the seabed. The results indicate that the amplitude of pore water pressure decreased by up to 46.5% after the application of shell-sand mixing. As the mixing ratio of shell-sand increased, the vertical attenuation coefficient of pore pressure initially rose and then stabilized. When the shell-sand mixing ratio reached 15%, the average vertical attenuation coefficient of pore pressure had already stabilized. Furthermore, this paper established an empirical formula for the pore pressure response of shell-sand mixed seabed in front of slope breakwaters, applicable to sandy seabeds. The correlation coefficient $R^2$ between the predicted values from the formula and the measured data reached 0.881. This research provides a scientific basis for the engineering application and improvement evaluation of shell-sand mixing. The study also assessed the application of shell-sand mixing technology along the West African coast, with results indicating that the Western Sahara region is the most suitable area for implementing this technique.

1. Introduction

With the growing demand for shipping in Africa, the scale of port construction is continuously expanding. As a crucial structure for wave protection, the slope breakwater provides safe berthing conditions and operational waters for vessels within port facilities and is also widely used in coastal protection and other marine engineering projects. The seabed response is critical to the foundation stability of the breakwater and significantly influences its overall safety. Shell-sand mixing, as a novel method for seabed protection, alters the original composition and physical properties of the seabed by incorporating large-sized shell fragments. This technique can enhance the liquefaction resistance of the seabed, holding significant engineering importance for the foundational stability of breakwaters.

Previous research on the stability of breakwater foundations has primarily focused on the influence of hydrodynamic conditions on wave-structure-seabed interactions, such as the wave transmission characteristics of breakwaters and the stability of armor blocks, as well as wave-induced liquefaction around breakwaters. The wave transmission characteristics of a breakwater affect the forces on the breakwater body and armor blocks; optimizing the armor layer design helps improve the overall safety of the structure. Pilar et al. [1] investigated the energy transformation process during the interaction of normal waves with a breakwater using numerical and physical experiments, exploring the influence of two key factors: relative water depth $h/\lambda$ and incident wave steepness $H/\lambda$. Yuksel et al. [2] compared different placement methods for breakwater armor blocks and proposed a “double-layer pyramidal placement” rule for blocks at the slope bottom and on the breakwater face. This method demonstrated superior stability in experimental tests. María et al. [3] studied the energy dissipation process of the armor layer in slope breakwaters, analyzing the interaction between incident waves and the breakwater. They evaluated the impact of using different types of armor blocks on structural performance and established a functional relationship between the stability parameter and the total energy dissipation through dimensional analysis.

Wave-induced liquefaction around breakwaters can lead to a loss of bearing capacity in the foundation seabed, severely impacting the overall safety of the structure. Liao et al. [4] used numerical simulations to study the wave-structure-uniform seabed interactions around the head of a slope breakwater. They found that the wave-induced flow field near the breakwater head is significantly disturbed by the structure, and the maximum wave-induced pore water pressure in front of the head is often greater than that on the front and rear sides, leading to more severe seabed liquefaction. Cui et al. [5] analyzed the long-term cyclic load response and liquefaction risk of a loose sandy seabed around an offshore detached breakwater using a three-dimensional model. Their findings indicated that alongshore currents can intensify the wave field and increase the risk of seabed liquefaction, particularly in the surface soil layer. Chen et al. [6] experimentally investigated the effects of wave loads on the pore water pressure in the seabed near a slope breakwater and the potential for soil liquefaction. They observed that the excess pore water pressure around the slope breakwater increases with wave height and period but decreases with water depth. The aforementioned studies are limited to wave-structure-seabed interactions under uniform seabed conditions, with little consideration given to non-uniform seabed conditions, including shell-sand mixed seabeds.

Building upon prior research, the theory of non-homogeneous seabeds has undergone continuous advancement, evolving from simple layered models [7,8] to complex anisotropic analyses [9], and from linear approximations [10,11,12,13] to nonlinear coupling [14,15,16]. This progressive development has laid a critical foundation for the study of special non-homogeneous seabeds, such as those involving shell-sand mixing. Seabeds containing shell-sand possess unique characteristics distinct from conventional non-homogeneous seabeds.

Sui et al. [17] investigated the liquefaction of mixed seabed soils containing silt and two particle sizes of shells. They found that the susceptibility of the mixed seabed to wave-induced liquefaction decreases with an increasing shell-sand mixing ratio, and the maximum shell mixing ratio at which liquefaction can occur is 30%. This study thoroughly investigated wave-non-uniform seabed interactions without structures but was limited to the mechanism of shell-sand mixing’s influence on a silty seabed, with little consideration given to seabed types with structures. Luijendijk et al. [18] studied the distribution of coastlines worldwide and found that the coastal types along the African coastline are predominantly sandy.

In summary, while existing research has addressed issues related to breakwater foundation stability and has established a relatively comprehensive theoretical framework for non-homogeneous seabed response, a significant gap remains regarding the stability of breakwater foundations on shell-sand seabeds—particularly concerning the influence of the shell content ratio on pore water pressure response characteristics and liquefaction risk. Different shell contents can substantially alter seabed properties, such as the permeability coefficient and porosity. Given that the African coastline predominantly consists of sandy shores, investigating the mechanism by which shell-sand mixing affects sandy seabeds holds considerable engineering significance for coastal protection and the safety of marine structures in Africa. This study examines the influence mechanism of shell-sand mixing on the pore water pressure response characteristics of sandy seabeds surrounding sloping breakwaters, aiming to provide a scientific basis for the design of such breakwaters and the assessment of seabed stability in the African region.

2. Physical Model Experimental Setup

A physical model of a slope breakwater and its foundation seabed was designed and tested in a wave flume. The model scale and seabed composition were determined based on flume dimensions, wavemaker capacity, and representative wave climate and seabed conditions along the African coastline.

2.1. Flume and Model Setup

The physical model used in this experiment represents a slope breakwater, a common structure in marine engineering. The overall configuration of the model within the wave flume is illustrated in Figure 1. The structure on the left side of the figure is the wave maker, and the structure on the right side is the breakwater. A sand trench was excavated in front of the dike, equipped with pore water pressure transducers (PPTs) to measure pore water pressure changes. Wave gauges were installed directly above the PPTs at corresponding positions to record wave height variations.

The instrumentation was categorized into two systems: wave measurement and pore water pressure measurement. The pore water pressure transducers (PPTs) and wave gauges were deployed along four distinct cross-sections, labeled #1 through #4. Cross-section #1 was positioned immediately adjacent to the dike toe, with its location set 0.05 m from the front edge of the toe. The subsequent cross-sections (#2, #3, and #4) were spaced at equal intervals of 0.6 m. Within each cross-section, four PPT probes were installed vertically. The shallowest probe was positioned flush with the seabed surface, with the remaining probes spaced at 0.06 m intervals vertically below it. A wave gauge was installed directly above the PPT array at each cross-section. In total, the experimental setup comprised 16 PPT probes and 4 wave gauge rods.

The wave flume used in this study has total dimensions of 50.0 m in length, 1.0 m in width, and 1.5 m in height. Both sidewalls of the flume are constructed of transparent glass, facilitating clear observation of wave profiles during testing. The slope breakwater model was constructed with a crest elevation of 0.48 m and a seaside slope of 1:1.5. To focus the investigation on the foundation seabed in front of the structure and to make optimal use of the flume length, the dike cross-section was simplified to a right-trapezoidal shape. The model was positioned near the end of the flume, approximately 37 m from the wavemaker. The sand trench was excavated starting from the toe of the dike, extending over two glass panel bays for a length of approximately 2.3 m. The trench had a depth of 0.3 m, representing the full thickness from the flume bed to the concrete foundation, and spanned the entire 1.0 m width of the flume.

This experiment adopts the Froude similarity criterion, which is widely recognized as an effective scaling method for studying wave–seabed structure interaction problems. Based on typical wave conditions in the African region and the wave-generating capacity of the laboratory equipment, a scaling ratio of 1:25 was selected. Regarding the selection of quartz sand: the reference area for this study is primarily characterized by sandy coastlines, with sediment particle sizes ranging from 0.063 mm to 2 mm. Since the core objective of this research is to investigate the influence mechanism of shell-sand mixtures on the dynamic response of the seabed, it is essential to ensure that the observed dynamic response mechanisms of the seabed in the laboratory are as consistent as possible with real-world conditions. Therefore, the seabed was scaled at a 1:1 ratio.

For the experiments, standard quartz sand with a median grain size ($d_{50}$) of 0.18 mm was selected as the base seabed material to represent the particle size characteristics of a typical sandy coast. As shown in Figure 2, the shell fragments used for mixing had a notably larger median grain size ($d_{50}$) of 5 mm. This size is typically the most common among shells of bivalve mollusks. Throughout the testing program, the mixing ratio of quartz sand to shell fragments was systematically varied between test stages according to the predefined experimental matrix.

The shell-sand mixing ratio (SC) was set with reference to the study by Sui et al. [17]. The $SC$ was adjusted by adding shell sand to the sand pile using the following method: thorough stirring to ensure uniform distribution of the shell sand; after mixing, the mixture was backfilled into the sand tank, leveled, and left to settle.

As shown in Figure 3, the left panel presents a schematic diagram of the constant-head apparatus for measuring soil permeability coefficient. The numbered components are as follows: 1 indicates piezometer inlets (upper, middle, and lower positions), 2 and 3 represent overflow outlets, 4 denotes the drainage outlet, 5, 6, and 7 correspond to glass tube supports, while 8 and 9 identify graduated glass tubes. A perforated metal plate is installed at the bottom of the instrument cylinder to ensure effective drainage through the specimen base. The right panel displays a photograph of the actual measuring apparatus.

The permeability coefficient is calculated using a modified form of Darcy’s law:

$$K={\displaystyle \frac{qL}{A\Delta h}}$$

(1)

where, q represents the flow rate, A denotes the cross-sectional area of the soil specimen, L indicates the distance between measurement points, and $\Delta h$ represents the hydraulic head difference.

In seabed soils, the void ratio is another physical parameter closely related to the hydraulic conductivity. As illustrated in Figure 4, blue represents free water, and yellow represents saturated sand. Compared to the measurement of hydraulic conductivity, determining the void ratio is relatively straightforward, with the equation and specific operation as follows:

$$e={\displaystyle \frac{V_1^{\prime }}{V_2}}$$

(2)

First, use a graduated cylinder to measure an appropriate amount of water and an appropriate amount of seabed soil sample. The volume of water should be slightly greater than that of the seabed soil sample. Record the volume of water as $V_1$. Pour the water into the seabed soil sample and mix thoroughly. Allow the mixture to stand until it reaches a saturated state. Read the liquid level scale of the mixture as $V_1+V_2$ and the scale of the seabed’s upper surface as $V_1^{\prime }+V_2$. Here, the volume of free water after mixing is obtained by subtracting the seabed scale from the liquid level scale, while the volume of pore water in the saturated seabed is the total volume of water minus the volume of free water, which is $V_1^{\prime }$. The total volume of the soil skeleton in the seabed is obtained by subtracting the volume of pore water in the seabed from the upper surface scale of the saturated seabed, which is $V_2$. The void ratio of the seabed soil can then be calculated using the Formula (2).

Following measurement, the resulting permeability coefficient (k) and void ratio (e) of the experimental seabed are presented in

Table 1. Permeability of shell-sand mixture seabed.

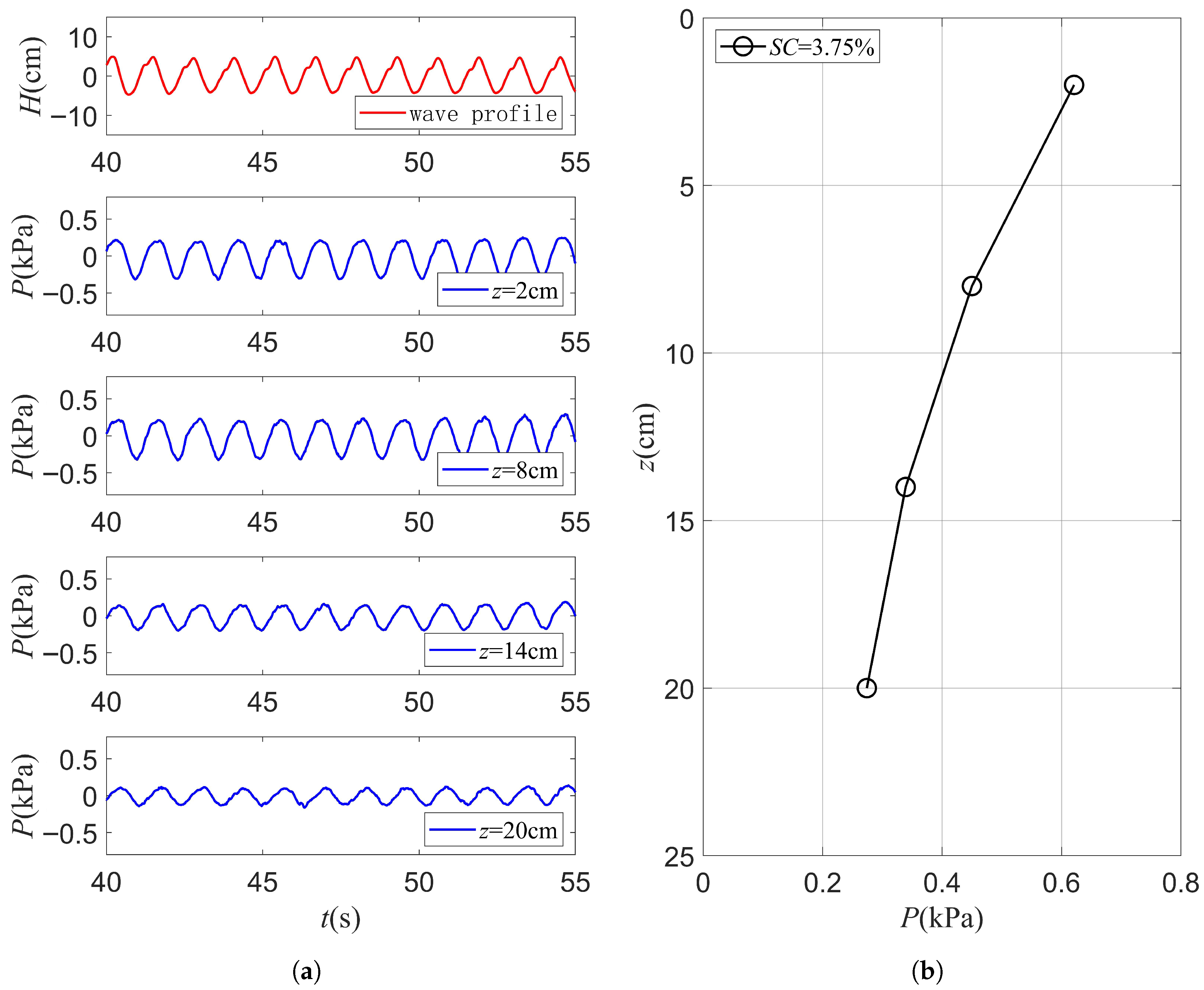
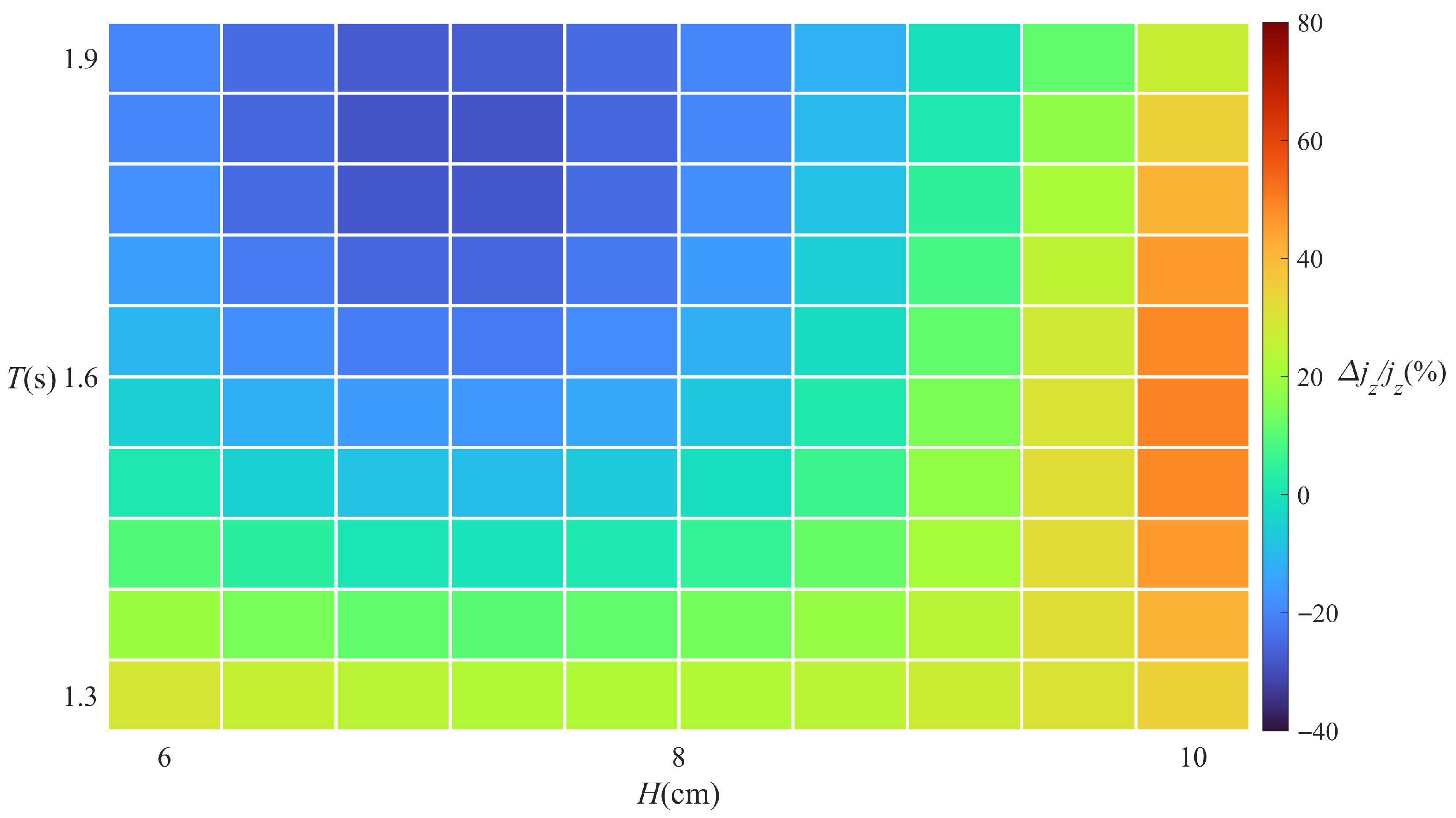
No.	Shell-Sand Mixing Ratios SC (%)	Void Ratio e	Permeability Coefficient K
1	3.75	0.76	4.41
2	7.5	0.69	4.16
3	15	0.59	3.15
4	30	0.57	3.11

. In the table, shell-sand mixing ratio $SC$ is the shell content by weight. That is, it represents the proportion of shell weight to the total weight of the mixed sand.

2.2. Experimental Group Arrangement

A comprehensive experimental matrix was designed for the uniform seabed study. The test program included four wave heights (H = 0.06 m, 0.08 m, 0.10 m, 0.12 m), five wave periods (T = 1.0 s, 1.3 s, 1.6 s, 1.9 s, 2.2 s), and two water depths (d = 0.228 m, 0.292 m). This resulted in a total of 40 test combinations, the specific arrangement of which is detailed in

Table 2. Text wave parameter conditions of experiments.

No.	Water Depth d (m)	Wave Height H (m)	Wave Period T (s)	Wavelength $\mathit{\lambda }$ (m)
1–5	0.228	0.06	1.0/1.3/1.6/1.9/2.2	1.27/1.77/2.24/2.72/3.19
6–10	0.228	0.08	1.0/1.3/1.6/1.9/2.2	1.27/1.77/2.24/2.72/3.19
11–15	0.228	0.10	1.0/1.3/1.6/1.9/2.2	1.27/1.77/2.24/2.72/3.19
16–20	0.228	0.12	1.0/1.3/1.6/1.9/2.2	1.27/1.77/2.24/2.72/3.19
21–25	0.292	0.06	1.0/1.3/1.6/1.9/2.2	1.36/1.94/2.50/3.04/3.57
26–30	0.292	0.08	1.0/1.3/1.6/1.9/2.2	1.36/1.94/2.50/3.04/3.57
31–35	0.292	0.10	1.0/1.3/1.6/1.9/2.2	1.36/1.94/2.50/3.04/3.57
36–40	0.292	0.12	1.0/1.3/1.6/1.9/2.2	1.36/1.94/2.50/3.04/3.57

. Among these, the groups of experimental data that did not experience wave breaking and are of practical application value were selected as the experimental wave conditions.

For the comparative study on shell-sand mixing, this experimental program selected a subset of conditions from the uniform seabed tests, maintaining a constant water depth of d = 0.292 m. The selected parameters included three wave heights (H = 0.06 m, 0.08 m, 0.10 m) and three wave periods (T = 1.3 s, 1.6 s, 1.9 s), resulting in a total of 36 test combinations. The specific arrangement of these tests is detailed in

Table 3. Wave parameters of shell-sand mixture seabed experiments.

No.	Shell-sand Mixing Ratio SC (%)	Wave Height H (m)	Wave Period T (s)	Wavelength $\mathit{\lambda }$ (m)
41–43	3.75	0.06	1.3/1.6/1.9	1.94/2.50/3.04
44–46	3.75	0.08	1.3/1.6/1.9	1.94/2.50/3.04
47–49	3.75	0.10	1.3/1.6/1.9	1.94/2.50/3.04
50–52	7.5	0.06	1.3/1.6/1.9	1.94/2.50/3.04
53–55	7.5	0.08	1.3/1.6/1.9	1.94/2.50/3.04
56–58	7.5	0.10	1.3/1.6/1.9	1.94/2.50/3.04
59–61	15	0.06	1.3/1.6/1.9	1.94/2.50/3.04
62–64	15	0.08	1.3/1.6/1.9	1.94/2.50/3.04
65–67	15	0.10	1.3/1.6/1.9	1.94/2.50/3.04
68–70	30	0.06	1.3/1.6/1.9	1.94/2.50/3.04
71–73	30	0.08	1.3/1.6/1.9	1.94/2.50/3.04
74–76	30	0.10	1.3/1.6/1.9	1.94/2.50/3.04

.

2.3. Experimental Phenomena

The experimental observations in this study primarily encompass two distinct phenomena: the cross-sectional variation in pore water pressure response within the seabed in front of the slope breakwater, and the vertical attenuation of the seabed pore water pressure response.

The cross-sectional variation in pore water pressure response in the seabed fronting the slope breakwater is governed by the local hydrodynamic characteristics. Wave interaction with the dike’s slope results in partial reflection, and the superposition of the reflected and incident waves generates a “partial standing wave” system. This system establishes alternating nodes and antinodes before the dike, where the spacing between these features is predominantly controlled by the incident wavelength, while their magnitude is primarily determined by the reflection coefficient of the dike’s slope. Variations in the incident wave period cause the nodal and antinodal bands to shift along the flume. Consequently, the wave conditions corresponding to the four instrumented sections change, leading to the observed sectional differences in the pore water pressure response amplitude within the seabed.

The vertical attenuation of the pore water pressure response in the seabed fronting the slope breakwater is intrinsically related to the composition of the seabed itself. According to the foundational studies by Yamamoto [19] and Jeng [20], the vertical distribution of wave-induced pore water pressure follows a logarithmic relationship. Consequently, its specific form can be expressed as:

$$p_z(z,t)=p_z(0,t)e^{-za}$$

(3)

where $p_z(0,t)$ represents the pore water pressure at the seabed surface at time t. a is the vertical attenuation coefficient of the pore water pressure. The value of a is dependent on the seabed material properties, and the equation describes the exponential decay of the pore water pressure amplitude with increasing depth beneath the seabed surface. The vertical attenuation coefficient of pore water pressure is a key parameter that quantifies how rapidly pore water pressure (induced by external loads such as waves) attenuates with depth into the seabed.

Of these two observed phenomena, the cross-sectional variation in seabed pore water pressure response is primarily induced by the “partial standing wave” system in front of the slope breakwater and exhibits low correlation with the physical properties of the seabed material. In contrast, the vertical attenuation of the pore water pressure response is highly dependent on these properties. Consequently, this study focuses on examining the effects of shell-sand mixing on the vertical attenuation phenomenon and elucidating the underlying mechanisms.

3. Results

3.1. Influence of Shell-Sand Mixing Ratio on the Vertical Attenuation Coefficient

In the present experiments, four distinct shell-sand mixing ratios were investigated, with the vertical attenuation of pore water pressure observed across all cases. Taking the condition with a shell-sand mixing ratios ($SC$) of 3.75%, as an example, Figure 5 presents the data from the four measurement points at cross-section #1, located immediately in front of the dike toe. The figure clearly demonstrates a decrease in pore water pressure amplitude with increasing depth.

By performing curve fitting on the data from the four measurement points, the vertical attenuation coefficient of the pore water pressure a, for the seabed under this specific condition can be determined. To analyze the influence of the shell-sand mixing ratio and conduct a more in-depth quantitative investigation, it is necessary to compare the vertical attenuation coefficients obtained from the four different mixing ratios. As shown in Figure 6, it can be observed that as $SC$ increases from 3.75% to 15%, the vertical attenuation of pore water pressure within the seabed becomes more pronounced. However, when $SC$ increases further from 15% to 30%, the attenuation phenomenon does not intensify but instead shows a reduction.

To further quantify the influence of $SC$ on a, a parametric analysis was conducted on the relationship between $SC$ and a across all nine test conditions. As shown in Figure 7, the differently colored lines represent results for different wave periods, while distinct data point shapes correspond to different wave heights. A comparison of the data for H = 6 cm, 8 cm, 10 cm and T = 1.3 s, 1.6 s, 1.9 s reveals how $SC$ affects the vertical attenuation coefficient a of the pore water pressure response. Qualitatively, lines of the same color exhibit similar trends, indicating that the wave period exerts a decisive influence on the vertical attenuation characteristics of the seabed pore water pressure response. Changes in the wave period significantly alter the vertical attenuation coefficient. Considering the impact of the “partial standing wave” phenomenon on the seabed pore water pressure response, the values of a under various wave parameters were averaged to isolate and highlight the effect of shell-sand mixing on the vertical attenuation.

As shown in Figure 8, it depicts the relationship between $SC$ and the mean vertical attenuation coefficient $a_{\mathrm{mean}}$, which is defined as the average value of a across all parameter study cases under a given $SC$. When the $SC$ increases from 3.75% to 15%, $a_{\mathrm{mean}}$ increases by 205%, whereas from 15% to 30%, it only changes by 2%, remaining essentially unchanged. This indicates that with the increase in the shell-sand mixing ratio, $a_{\mathrm{mean}}$ initially rises and eventually stabilizes.

Shell sand exhibits abundant lamellar structures and interlaced notches. When $SC$ increases moderately, the lamellar structures and notches of the experimental sand and shells form a tight interlock, which reduces pores, hinders the flow of pore fluids, and causes the permeability coefficient and void ratio to decrease rapidly, thereby enhancing the vertical attenuation of pore water pressure. When the $SC$ exceeds the critical value, the proportion of coarse-grained components increases excessively. The experimental sand between shells is insufficient to fill all the gaps and notches, leading to weakened intergranular bonding and no further reduction in the permeability of pore fluids. This is reflected in the trend that the permeability coefficient and void ratio of the seabed soil first decrease and then stabilize, and the vertical attenuation of pore water pressure inside the seabed intensifies initially and then tends to be stable.

This trend reflects the influence of coarse shell particles on seabed properties. A comparison with the measured permeability coefficient K and void ratio e for the four seabed types, presented in Table 1, shows that as $SC$ increases, the permeability coefficient K decreases rapidly and then stabilizes, while the void ratio e also exhibits a marked decrease. These observations are consistent with the analysis of the vertical attenuation coefficient a presented in this chapter.

3.2. Empirical Formula for Pore Water Pressure Response in Shell-Sand Mixed Seabeds Fronting Slope Breakwater

Based on the analysis in the preceding section, the pore water pressure response within the seabed is governed by both wave parameters and seabed properties. The seabed properties exhibit a strong correlation with $SC$, while the relevant wave parameters primarily include wave height, water depth, and period. Consequently, the functional relationship can be generalized as follows:

$$p_z=f(p_o,H,T,d,z,SC)$$

(4)

On the left-hand side, $p_z$ is normalized by $p_0$. The $p_0$ is the pore water pressure on seabed surface. On the right-hand side, after removing $p_0$, five parameters remain. Among these, H, d, and z all share the dimension of length $\left[L\right]$, and $SC$ is inherently dimensionless. Since T possesses a different dimension, it can be incorporated using the wavelength $\lambda$. The resulting decomposed empirical formula is as follows:

$${\displaystyle \frac{p_z}{p_0}}=f({\displaystyle \frac{H}{\lambda }},{\displaystyle \frac{d}{\lambda }},{\displaystyle \frac{z}{\lambda }},SC)$$

(5)

It can be expressed in polynomial form as follows:

$${\displaystyle \frac{p_z}{p_0}}=b_{0}S{C}^{b_1}{\left({\displaystyle \frac{H}{\lambda }}\right)}^{b_2}{\left({\displaystyle \frac{d}{\lambda }}\right)}^{b_3}{\left({\displaystyle \frac{z}{\lambda }}\right)}^{b_4}$$

(6)

Through dimensional analysis, the empirical formula for the pore water pressure response in a shell-sand mixed seabed fronting a slope breakwater was formulated with the objective of determining five coefficients: a, $b_1$, $b_2$, $b_3$, and $b_4$. In this experimental study, where the shell-sand mixing ratios ($SC$) ranged from 3.75% to 15%, the pore water pressure response exhibited a monotonic relationship with variations in $SC$. Consequently, 27 datasets from the pore water pressure response measurements in front of the slope breakwater were selected for analysis. As each test configuration included 4 measurement points at different burial depths, this yielded a total of 108 valid data points. These points were utilized for function fitting to solve for the five coefficients (a, $b_1$, $b_2$, $b_3$, $b_4$), thereby obtaining the final empirical formula.

By applying logarithms to both sides of the equation, the complex problem of solving for multiple exponents can be reduced to a multivariate linear regression problem, as shown:

$$lg({\displaystyle \frac{p_z}{p_0}})=lg(b_{0}S{C}^{b_1}{({\displaystyle \frac{H}{\lambda }})}^{b_2}{({\displaystyle \frac{d}{\lambda }})}^{b_3}{({\displaystyle \frac{z}{\lambda }})}^{b_4})$$

(7)

$$lg({\displaystyle \frac{p_z}{p_0}})=lg{b}_0+lgS{C}^{b_1}+lg{({\displaystyle \frac{H}{\lambda }})}^{b_2}+lg{({\displaystyle \frac{d}{\lambda }})}^{b_3}+lg{({\displaystyle \frac{z}{\lambda }})}^{b_4}$$

(8)

$$lg({\displaystyle \frac{p_z}{p_0}})=lg{b}_0+b_{1}lgSC+b_{2}lg({\displaystyle \frac{H}{\lambda }})+b_{3}lg({\displaystyle \frac{d}{\lambda }})+b_{4}lg({\displaystyle \frac{z}{\lambda }})$$

(9)

Substituting the experimental data into Equation (9), a linear regression analysis was performed. The results of the linear regression computation are presented in

Table 4. Result of linear regression.

Term	Unstandardized Coefficient	Std. Error	Standardized Coefficient	t	Sig.
(Constant)	0.927	0.127		7.328	0.001
lgSC	−0.413	0.037	−0.385	−11.299	0.001
lgH_L	−0.205	0.099	−0.094	−2.079	0.040
lgd_L	2.852	0.152	0.861	18.786	0.001
lgz_L	−0.342	0.024	−0.504	−14.491	0.001

. In the table, t represents the t-statistic, which is used to measure the difference between the estimated regression coefficient and zero (i.e., “no effect”) and Sig. denotes significance.

The resulting empirical formula is obtained as:

$${\displaystyle \frac{p_z}{p_0}}=8.5S{C}^{-0.4}{\left({\displaystyle \frac{H}{\lambda }}\right)}^{-0.2}{\left({\displaystyle \frac{d}{\lambda }}\right)}^{2.9}{\left({\displaystyle \frac{z}{\lambda }}\right)}^{-0.34}$$

(10)

As shown in

Table 5. Correlation coefficient.

Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	0.938	0.881	0.876	0.0932397

, the coefficient of determination ($R^2$) between the empirical formula’s predictions and the measured values reaches 0.881.

The empirical formula derived in the preceding section was used to calculate the corresponding data points from the present experiments. A comparison between these calculated values and the measured data is presented in Figure 9.

In the figure, the abscissa of each point represents the measured value of the seabed pore water pressure response amplitude, while the ordinate represents the corresponding estimated value from the empirical formula. The proximity of a data point to the $y=x$ line indicates the agreement between the estimated and measured values. The predictions generated by the empirical formula reveal a strong positive correlation between the pore water pressure response amplitude in the shell-sand mixed seabed fronting the slope breakwater and the water depth (d). In contrast, weak negative correlations are observed with the shell-sand mixing ratios ($SC$), wave height (H), and burial depth (z). The scatter of data points is consistently tight across all tested shell-sand mixing ratios, with no significant outliers. Furthermore, as the wave height and the resulting dynamic pressure on the seabed surface increase, the predictions for the internal pore water pressure response show no systematic bias, maintaining stable accuracy. This demonstrates that the formulated structure of the empirical formula effectively captures the underlying physical mechanisms governing the pore water pressure response in shell-sand mixed seabeds.

3.3. Parametric Analysis of Shell-Sand Mixing Effectiveness

To further elucidate the application potential of shell-sand mixing as a seabed protection method, a parametric analysis can be conducted. This analysis would quantitatively compare the rate of change in key seabed indicators before and after the application of shell-sand mixing across various operational conditions, thereby establishing the practicality of this technique for different seabed types. The pore water pressure response amplitude and liquefaction potential were selected as key indicators for evaluating seabed protection effectiveness. A parametric analysis was conducted to compare the alteration rates of these two indicators due to shell-sand mixing under different wave heights and periods. Regarding the pore water pressure response amplitude, Figure 10a compares the amplitudes under a wave period of 1.3 s and wave heights of 6 cm, 8 cm, and 10 cm. The two polygonal lines correspond to the left vertical axis, representing the pore water pressure response amplitude itself. The bar chart corresponds to the right vertical axis, indicating the rate of change in this amplitude before versus after mixing. A vertical comparison (comparing before and after mixing for the same wave condition) reveals that the pore water pressure in the seabed after shell-sand mixing is evidently lower than that before mixing, with a reduction of approximately 40%. This demonstrates the significant effectiveness of shell-sand mixing in reducing seabed pore water pressure. A horizontal comparison (across different wave heights for the same seabed condition) shows that for both the untreated and treated seabed, the pore water pressure amplitude increases with increasing wave height. Furthermore, the rate of change in the amplitude (the improvement due to mixing) also increases with wave height, indicating that the effectiveness of shell-sand mixing is more pronounced in regions with larger waves.

Figure 10b compares the results for a wave height of 8 cm and periods of 1.3 s, 1.6 s, and 1.9 s. The vertical comparison confirms that shell-sand mixing significantly reduces seabed pore water pressure across all tested periods. Horizontally, as the wave period increases, both the absolute pore water pressure amplitude and its rate of change show a decreasing trend. This suggests that the effectiveness of shell-sand mixing is more significant in areas with shorter wave periods.

As shown in Figure 10c, the horizontal axis represents different wave height parameters, the vertical axis denotes different wave period parameters, and the color gradient illustrates the rate of change in the pore water pressure amplitude before and after shell-sand mixing. It can be observed that the most significant alteration in the seabed pore water pressure response due to shell-sand mixing occurs in regions characterized by high wave heights and short periods. In this experimental study, the maximum observed change rate reached 46.5%.

Regarding the seabed liquefaction potential, it serves as a critical parameter for assessing the susceptibility of seabed soil to liquefaction. Physically, the liquefaction potential represents the ratio of the seepage force acting on the soil to the effective overburden stress. It can be calculated using the following formula:

$$I_z={\displaystyle \frac{j_z}{\frac{1+2k_t}{3}{\gamma }^{\prime }}}$$

(11)

where $j_z$ can be calculated by $\Delta p/\Delta z$, $k_t$ is the coefficient of lateral earth pressure, which can be derived from Poisson’s ratio, and ${\gamma }^{\prime }$ is the submerged buoyant unit weight of the sand, determinable from the soil particle density, porosity, and degree of saturation.

In this experimental study, for a given seabed type subjected to various wave conditions, the denominator of the liquefaction potential $I_z$ remains constant. In contrast, the numerator is computed from experimentally measured pore water pressure data. Consequently, the seepage force is directly proportional to the liquefaction potential.

For seabeds before and after shell-sand mixing, the alteration in soil composition changes the denominator of the liquefaction potential $I_z$. As shown in Figure 11, assuming constant values for the coefficient of lateral earth pressure and the submerged buoyant unit weight (i.e., ignoring changes in these properties due to mixing), the rate of change in the seabed seepage force is quantitatively compared. However, in reality, the denominators differ between the two seabeds, necessitating consideration of their actual coefficients of lateral earth pressure and submerged buoyant unit weights. Qualitatively, the incorporation of shell fragments is expected to decrease the Poisson’s ratio of the seabed soil and reduce its void ratio (n). Consequently, the denominator in the liquefaction potential formula increases. Furthermore, as indicated by Figure 10, the inclusion of shell fragments also reduces the numerator of the liquefaction potential. Therefore, it is reasonable to conclude that the overall liquefaction potential will decrease. Based on this, it can be inferred that after shell-sand mixing, the pore water pressure response amplitude in the seabed is less likely to reach the critical excess pore water pressure threshold required for liquefaction of that specific soil, thereby reducing the liquefaction risk.

Based on the analysis of variation rates in pore water pressure amplitude before and after mixing under different wave parameters, nine working conditions corresponding to specific sea states were established. The experimental model was designed at a scale of 1:25. According to Froude similarity criteria, the time scale is 1:5 and the spatial scale is 1:25. Thus, the corresponding prototype wave conditions consist of wave heights of 1.5 m, 2.0 m, and 2.5 m, with wave periods of 6.5 s, 8.0 s, and 9.5 s. The analysis results are presented in

Table 6. Effect of shell sand mixing with different wave parameters (PPA is the pore water pressure amplitude).

Wave Parameters	H = 1.5 m	H = 2.0 m	H = 2.5 m
T = 6.5 s	PPA Change: 37.6%	PPA Change: 44.6%	PPA Change: 46.5%
T = 8.0 s	PPA Change: 38.1%	PPA Change: 39.3%	PPA Change: 40.7%
T = 9.5 s	PPA Change: 30.8%	PPA Change: 31.4%	PPA Change: 31.0%

. The results demonstrate that the most effective prototype wave condition for shell-sand mixing in this experiment is a wave height of 2.5 m with a wave period of 6.5 s.

4. Application of Shell-Sand Mixing in the West Coast of Africa and Discussion

Based on the parametric analysis of pore water pressure response amplitude, it can be inferred that the effectiveness of shell-sand mixing is more pronounced in regions characterized by larger wave heights and shorter wave periods. Incorporating findings from previous studies—Perez et al. [21] analyzed the global distribution of significant wave height (details available in Figure 11 of Perez’s paper), while Gao et al. [22] examined the global mean wave period distribution (details provided in Figure 4 of Gao’s paper)—it is concluded that along the African coast, the wave conditions off Western Sahara are the most suitable for the application of shell-sand mixing.

Regarding the application of shell-sand mixing technology along the Western Sahara coast, two aspects can be considered: (1) port distribution, which reflects the local demand for seabed improvement and protection; and (2) shellfish populations, which reflect the source of shell-sand materials.

In terms of port distribution, according to statistical data from the port data website SEARATES [23], the global distribution of container ports is summarized, as shown in subplot (a) of Figure 12. There are seven container ports along the Western Sahara coast, among which the port marked with a red dot is Tanger Med in Morocco. This port ranked among the top 100 container ports in terms of throughput in 2022, with a total throughput of 7.597 million twenty-foot equivalent units (TEUs), ranking 24th globally [24]. The other six ports marked in blue points are also significant maritime gateways and transportation hubs for their respective countries.

In terms of shellfish populations, shell-sand materials can be sourced from various types of shelled mollusks. According to research by José Antonio Caballero-Herrera et al. [25], bivalve species are widely distributed along the Atlantic coast west of the Sahara. As shown in subplot (b) of Figure 12, the dots represent the distribution areas of bivalve populations along the coast, with the color and size of the dots indicating the number of bivalve species in each area, as labeled on the right side of the dots. The figure reveals that there are at least 231 bivalve species near Tanger Med port in Morocco, indicating abundant shell-sand materials in the local seabed. This ensures a sufficient supply of raw materials for shell-sand mixing operations and low transportation costs. Therefore, the sea area near the Western Sahara of Africa are suitable for the application of the shell-sand mixing technology.

5. Conclusions

This study investigates the pore water pressure response characteristics and engineering application potential of shell-sand mixed seabeds through physical model tests. The main conclusions are as follows:

(1) With the increase in the shell-sand mixing ratio ($SC$), the vertical attenuation coefficient (a) of pore water pressure in the seabed at the front of the sloping breakwater gradually increases within the range of $SC=3.75\%$ to $SC=15\%$, and then tends to stabilize. In engineering practice, the protective effect of seabed can be optimized by controlling the $SC$ at approximately $15\%$.

(2) An empirical formula for the pore water pressure response of shell-sand mixed seabeds was established. The coefficient of determination ($R^2$) between the calculated values from this formula and the measured data reaches $0.881$, providing a feasible method for rapidly determining the pore water pressure of shell-sand mixed seabeds in engineering projects.

(3) Parameter analysis indicates that the incorporation of shell sand can reduce the liquefaction risk of the seabed. Under the test conditions, the protective effect is most significant under the wave condition with a wave height of $2.5\mathrm{m}$ and a wave period of $6.5\mathrm{s}$. Based on a comprehensive assessment of the local marine environment, the coastal areas of Western Sahara have favorable technical applicability and promotion feasibility for this technology.