Parametrization of Seabed Liquefaction for Nonlinear Waves

Abstract

In actual marine environments, significant nonlinear changes occur during wave propagation toward the nearshore, resulting in noticeable wave asymmetry. This leads to substantial differences in seabed response and liquefaction compared to conditions under linear waves. This study employs numerical simulations to investigate the liquefaction depth of the seabed under nonlinear wave loading. Building upon existing liquefaction prediction formulas, a more widely applicable seabed liquefaction prediction formula is derived through dimensional analysis and the least squares method. The proposed formula provides a better fit to the numerically simulated values and significantly reduces prediction errors. Based on waveform analysis, a parametric method is established. By integrating the liquefaction prediction formula, this method allows rapid estimation of the maximum seabed liquefaction depth on a sloped beach under random wave action. The calculated results show that the prediction formula closely matches the numerical simulation results.

1. Introduction

The rapid development of the global economy and ongoing ocean exploration have fueled significant advances in marine engineering in recent years. However, foundation failure in seabeds has become a central challenge in the design and construction of offshore structures, often leading to their instability. Extensive studies have shown that wave-induced seabed liquefaction is a primary cause of such structural failures [1]. Wave action can eliminate effective stress between soil grains, triggering liquefaction that causes the water–sediment matrix to behave as a fluid [2]. This phenomenon may result in the floatation or sinking of submarine pipelines, the overturning of offshore platforms, and major marine geohazards such as submarine landslides, thereby posing substantial threats to coastal economies and public safety.

Due to limitations in early cognitive understanding and research methods, initial studies often treated waves as linear phenomena without fully considering their nonlinear characteristics, and established corresponding mechanical models by regarding waves as deterministic loads. However, during actual wave propagation, as waves approach the nearshore area, changes in water depth and topography lead to pronounced nonlinear transformations in wave characteristics [1]. This phenomenon is primarily characterized by wave crests becoming steeper and higher with shortened duration, while wave troughs become flatter with prolonged duration. The wave surface generally maintains symmetry about the crest point, as exemplified by cnoidal waves. As waves continue to propagate shoreward, their velocity gradually decreases; however, this reduction often lags behind the wave propagation itself. The resistance encountered by the front wave face causes its propagation speed to drop significantly, while the rear waves continue to advance, resulting in a pronounced forward-leaning wave profile and loss of the original symmetry, forming what is known as a sawtooth wave. These waveform alterations directly modify the wave-induced dynamic pressure acting on the seabed, thereby triggering changes in the seabed’s dynamic response. Consequently, the characteristics of seabed liquefaction under these conditions differ significantly from those observed under linear wave action.

For more accurate simulation of nonlinear waves in real ocean conditions, many studies have developed adaptive theories and methods focusing on wave construction. Abreu et al. [3] proposed a simple analytical formula to reproduce the orbital velocities of skewed nonlinear waves. The results demonstrated that this method is sufficiently versatile for application in coastal engineering under various nonlinear wave conditions. Chen et al. [4] derived an analytical solution for the pore water pressure response based on second-order nonlinear wave theory. Compared to linear random wave theory, this method further incorporates the correction second-order transfer terms for nonlinear waves. Wang et al. [5] conducted a parametric study on the influence of nonlinear variations in wave loading on seabed response and liquefaction, defining a liquefaction depth attenuation coefficient and a width growth coefficient to quantitatively characterize the nonlinear effects of waves on seabed liquefaction.

Regarding the seabed response under nonlinear wave action, scholars have proposed various theoretical models and numerical methods for analysis. Among them, Yamamoto et al. [6] treated both the pore water and the seabed as compressible deformable media and derived an analytical solution for an isotropic, poro-elastic seabed of infinite thickness. Subsequently, Hsu and Jeng [7] extended this framework to a finite-thickness, unsaturated, isotropic seabed and considered the loading effects of three-dimensional short-crested waves. These studies were based on the quasi-static Biot consolidation equations. Later, Jeng et al. [8] and Jeng and Cha [9] proposed analytical solutions for the dynamic response of an isotropic poro-elastic seabed under wave loading, based on the u–p approximation and the fully dynamic approximation, respectively. In terms of numerical simulation, Biot [10] and Zienkiewicz et al. [11] developed semi-dynamic and fully dynamic models to study the dynamic response of the seabed. The semi-dynamic model, also known as the u–p model, introduces the acceleration term of the soil skeleton into the traditional static formulation. Sakai et al. [12] adopted a finite difference method (FDM) numerical model to study the effects of soil inertia and gravity terms on the dynamic response of the seabed under nonlinear wave action. They concluded that the gravity term has a minor influence on the seabed’s dynamic response and that the soil inertia term can be neglected outside the wave-breaking zone. Their model was also applied to simulate the dynamic response of the seabed around an embedded elastic submarine pipeline. Ye and Jeng [13] employed the u–p approximation combined with a poro-elastic model and used the finite element method to investigate the influence of ocean currents—which commonly coexist with waves—on the seabed response under third-order nonlinear waves and currents. Ye at al. [14] further proposed a numerical model based on an elasto-plastic formulation to simulate wave–seabed–structure interaction.

In summary, previous researchers have conducted extensive studies on the dynamic response of seabeds under wave action. However, certain limitations remain. On one hand, regarding the issue of seabed liquefaction under nonlinear waves, the existing predictive formulas for liquefaction depth under nonlinear wave conditions were proposed based on specific wave and seabed parameters. Their reliability under varying wave and seabed conditions has not been systematically analyzed. Furthermore, existing studies lack quantitative analysis of the maximum seabed liquefaction depth under random waves. Based on current research, it is impossible to quickly predict the maximum seabed liquefaction depth that may occur under a random wave sequence using analytical solutions. In light of this, the present study will build upon previous work by separately analyzing the applicability of existing seabed liquefaction depth predictive formulas under changing wave and seabed parameters. It will further derive a more widely applicable predictive formula for the maximum seabed liquefaction depth. Subsequently, by analyzing the wave profiles within random wave sequences, a parametrization method will be established. Combined with the liquefaction depth predictive formula, this parametrization method will be applied to analyze the seabed liquefaction depth under random waves on a sloped beach.

2. Formulation and Verification

2.1. Formulation of Nonlinear Wave Pressure

Most existing nonlinear wave theories, such as second-order Stokes wave theory and cnoidal wave theory, can only describe one of the aforementioned patterns of wave pressure variation and fail to simultaneously capture both nonlinear trends. Abreu et al. [3] proposed a formula to characterize the time series of nonlinear wave oscillatory velocity at a specific location, thereby describing the time series of nonlinear wave pressure loading. By introducing the nonlinear parameters $\varphi$ (wave form coefficient) and r (asymmetry coefficient), a complete description of the nonlinear wave pressure field is achieved. This formula can individually or simultaneously characterize the wave pressure $p_w\left(t\right)$ as follows:

$$p_w\left(t\right)=p_{0}f{\displaystyle \frac{sin\left(\omega t\right)+\frac{r}{1+f}\sin \varphi }{\left[1-r\cos (\omega t+\varphi )\right]}}$$

(1)

where $p_0$ is the reference amplitude of wave pressure; $\varphi$ is the wave form coefficient with a value range of $0\le \varphi \le -\pi /2$; r is the asymmetry coefficient with a value range of $0\le r<1$; f depends only on r, $f=\sqrt{1-r^2}$; and $\omega$ is the frequency, with $\omega =2\pi /T$, where T is the wave period.

$$p_0={\rho }_{f}g{\displaystyle \frac{H}{2cosh\left(Kd\right)}}$$

(2)

where ${\rho }_f$ is the water density; g is the gravitational acceleration; H is the wave height; K is the number of waves; d is the water depth; and L is the wavelength, which can be approximately calculated according to linear wave theory.

$$L={\displaystyle \frac{g{T}^2}{2\pi }}tanh\left(Kd\right)$$

(3)

Regarding the waveform coefficient $\varphi$ and the asymmetry coefficient r, they respectively represent the type and degree of asymmetry in the wave pressure field. When the waveform coefficient is fixed, the magnitude of the asymmetry coefficient determines the degree of asymmetry in the wave pressure field; the larger its value, the higher the degree of asymmetry. When r = 0, it indicates that the wave pressure field corresponds to a linear wave pressure field. Figure 1 shows the time series plots of wave pressure under different $\varphi$ values.

2.2. Seabed Response Model

In this study, the WSSI (Wave-Structure-Seabed Interaction) toolbox [15] was employed to analyze the seabed response induced by waves. The investigation was based on the partially dynamic response model of Biot’s equations, specifically utilizing the u–p approximation formulation.

$$\nabla ·\left[C:{\displaystyle \frac{1}{2}}\left(\nabla U+{(\nabla U)}^T\right)\right]-\nabla p-\rho {\displaystyle \frac{{\partial }^{2}U}{\partial t^2}}=0$$

(4)

$${\displaystyle \frac{n}{K^{\prime }}}{\displaystyle \frac{\partial p}{\partial t}}-{\displaystyle \frac{1}{{\gamma }_{\omega }}}\nabla (\mathrm{k}\nabla p)+{\displaystyle \frac{1}{g}}\nabla ·\left(\mathrm{k}·{\displaystyle \frac{{\partial }^2\mathrm{U}}{\partial t^2}}\right)+{\displaystyle \frac{\partial }{\partial t}}(\nabla ·\mathrm{U})=0$$

(5)

where C is the fourth-order elastic stiffness tensor; U is the soil skeleton displacement vector; p is the pore water pressure; g is the gravitational acceleration, with its components being (0, 0, g); n is the porosity; k is the permeability tensor, with its principal diagonal components being $k_x$, $k_y$ and $k_z$; $\rho$ is the density of the soil mixture, with $\rho =n{\rho }_f+(1-n){\rho }_s$, where ${\rho }_s$ is the density of the soil, and ${\rho }_f$ is the density of fluid; and $K^{\prime }$ is the bulk modulus of the compressible pore fluid, which can be approximated by the following expression:

$${\displaystyle \frac{1}{K^{\prime }}}={\displaystyle \frac{1}{K_{\omega }}}+{\displaystyle \frac{1-S_r}{p_a}}$$

(6)

where $S_r$ is the degree of saturation of the soil; $K_{\omega }$ is the bulk modulus of water (approximately 2 GPa); and $p_a={\rho }_{f}g{h}_{\omega }$, which is the pore water pressure within the seabed.

2.3. Boundary Condition

Since this study does not involve structural elements and neglects air flow, focusing solely on the wave–seabed interaction, the model only considers the seabed’s lateral and bottom boundary conditions, along with the wave–seabed interface boundary conditions.

2.3.1. Seabed Lateral and Bottom Boundary Conditions

The lateral and bottom boundaries of the seabed are assumed to be rigid boundaries with zero permeability. At these boundaries, the displacements of both the soil skeleton ${\overrightarrow{u}}_{\mathrm{soil}}$ and the pore fluid ${\overrightarrow{u}}_{\mathrm{f}}$ are zero, and the normal gradient of the pore water pressure is also zero.

$${\overrightarrow{u}}_{\mathrm{soil}}=0,{\overrightarrow{u}}_{\mathrm{f}}=0,{\displaystyle \frac{\partial p}{\partial n}}=0$$

(7)

2.3.2. Wave–Seabed Interface Boundary Conditions

At the wave–seabed interface, the boundary condition is specified as a Dirichlet type, where the instantaneous pore water pressure at the seabed surface equals the wave-induced pressure, and both the normal and shear stresses at the seabed surface are equal to the corresponding wave-induced normal and shear stresses.

$$p=p_w,{\sigma }_{\mathrm{soil}}^{\prime }={\sigma }_{\mathrm{soil}},{\tau }_{\mathrm{soil}}^{\prime }={\tau }_{\mathrm{soil}}$$

(8)

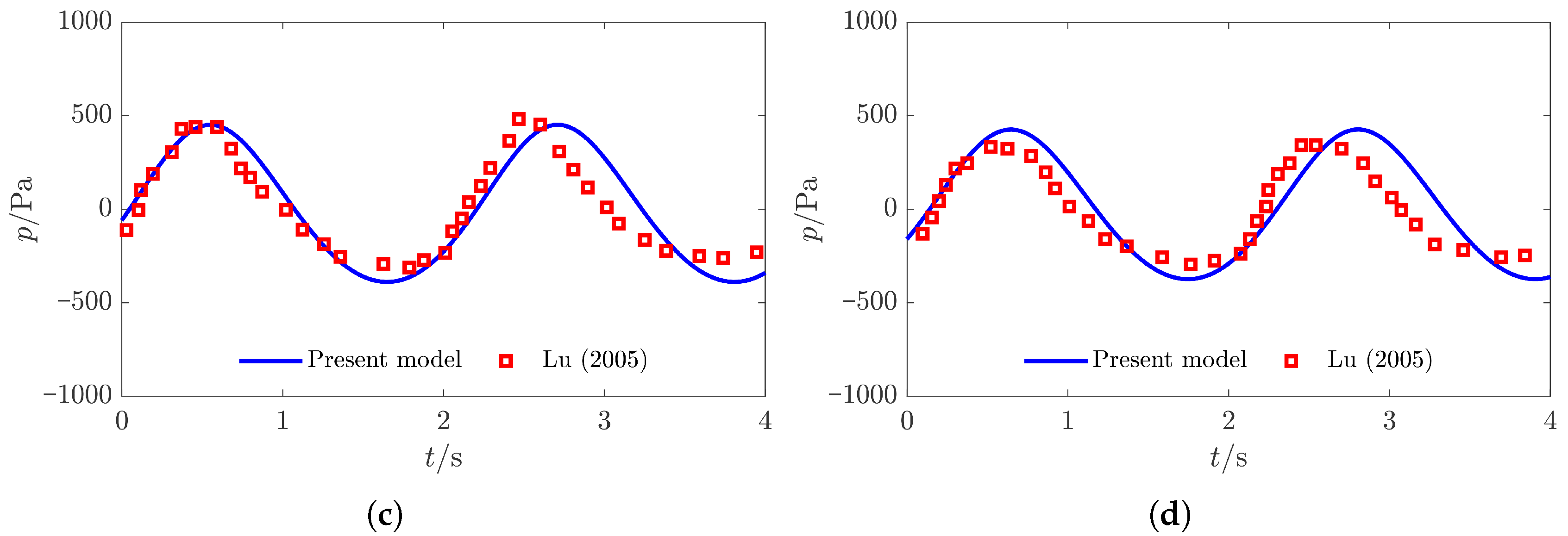
2.4. Model Verification

2.4.1. Parameter Setting

The model requires thorough validation prior to its practical application. In this section, the proposed model is evaluated by comparing its predictions with existing analytical solutions and experimental data. Three validation cases with different hydraulic conductivity conditions are established, with the corresponding parameters summarized in

Table 1. Parameter Settings for Verification Conditions.

Parameter	Symbol	Verification 1	Verification 2	Verification 3	Unit
Water Depth	d	0.488	0.3	10	m
Wave Height	H	0.02	0.14	0.1	m
Wave Period	T	1.5	1.4	12	s
Waveform Coefficient	$\varphi$	0	0.44	0	-
Asymmetry Coefficient	r	0	0.48	0	-
Seabed density	$\rho$	2.65 × ${10}^3$	2.65 × ${10}^3$	2.65 × ${10}^3$	kg/${\mathrm{m}}^3$
permeability coefficient	k	5 × ${10}^{-4}$∼1 × ${10}^{-3}$	1.4 × ${10}^{-3}$	1.0 × ${10}^{-2}$	m/s
Pore Fluid Density	${\rho }_f$	1.0 × ${10}^3$	1.0 × ${10}^3$	1.0 × ${10}^3$	kg/${\mathrm{m}}^3$
Young’s Modulus	$E_v$	1.3 × ${10}^7$	1.4 × ${10}^7$	2.67 × ${10}^7$	Pa
Poisson’s Ratio	$\mu$	0.33	0.33	0.3333	-
Degree of Saturation	$S_r$	0.985, 0.988	0.98	0.975	-
Porosity	n	0.3	0.39	0.3	-

: Case 1 validates the pore water pressure under linear waves; Case 2 examines the pore water pressure under nonlinear waves; and Case 3 assesses both the soil stress and pore pressure under linear waves.

2.4.2. Vertical Distribution of Pore Water Pressure in a Sandy Seabed Under Progressive Waves

Under wave action, the pore water pressure within the seabed exhibits significant amplitude attenuation along the depth direction. Tsui and Helfrich [16] experimentally observed the vertical attenuation process of internal pore water pressure in two types of sandy seabeds (dense sand/loose sand) under linear waves and compared the results with the analytical solution proposed by Hsu and Jeng [17] for verification. The wave pressure at the seabed surface can be simply calculated using Equation (1).

As shown in Figure 2, the numerical model used in this study is compared with physical model test data and analytical solution data, respectively. The root-mean-square error (RMSE) between the numerical results and the experimental data is 0.091, with a normalized RMSE (nRMSE) of 8.48% relative to the range of the experimental values. Compared with the theoretical analytical solution, the RMSE is 0.0544, corresponding to an nRMSE of 9.1% relative to the range of the analytical solution. The numerical simulation results show reasonable agreement with both the experimental data and the analytical solution. This indicates that the model can accurately capture the attenuation trend of pore water pressure with depth within the seabed, verifying its effectiveness under the studied conditions.

2.4.3. Spatiotemporal Distribution of Pore Water Pressure Under Cnoidal Wave Action

To validate the mathematical model used in this study for simulating the instantaneous seabed response under nonlinear wave loading, a comparative analysis was conducted with the physical model test by Lu et al. [18]. Their experiment measured the temporal variation of pore water pressure in a seabed under cnoidal wave action. The wave pressure at the seabed surface is determined according to Equation (1).

Figure 3 presents a comparison between simulated and measured pore water pressures under cnoidal wave conditions. The pore pressure distribution shows a strong correlation with the variation in wave pressure at the seabed surface. Specifically, under cnoidal wave action, the pore pressure time history exhibits a steep, asymmetric profile: the positive pressure phase is shorter in duration but higher in amplitude compared to the negative pressure phase. The RMSE between the numerical model and the experimental data is 195.52, and the normalized RMSE (nRMSE), calculated as the ratio of RMSE to the data range, is 19.1%. These results indicate strong agreement between the numerical model and the experimental data, validating the model’s accuracy in capturing these nonlinear characteristics.

2.4.4. Vertical Distribution of Pore Pressure and Soil Stress Under Linear Wave Action

To validate the accuracy of the numerical model in this study for seabed response under linear waves with high hydraulic conductivity, the analytical solution for short wave-induced pore pressure variations proposed by Jeng [17] is adopted for comparison.

Figure 4 shows the distributions of simulated (blue solid line) and analytical (red dash-dot line) pore pressure and seabed stress. The results indicate that the soil stress near the seabed surface is generally small, whereas the pore water pressure reaches its maximum there and gradually decreases with increasing seabed depth. The simulation results show good consistency with the analytical solution, demonstrating that the numerical model can accurately reproduce the vertical distribution of soil stress.

3. Results and Discussion

3.1. Study on Seabed Response and Instantaneous Liquefaction Under Asymmetric Wave Pressure Acceleration

Given that wave skewness ($\varphi$) and asymmetry (r) are the principal control parameters for nonlinear waves, a comparative analysis of seabed response under linear versus nonlinear wave loading was performed. This analysis simulated the internal pore water pressure distribution and seabed liquefaction for different values of $\varphi$ and r. The corresponding simulation parameters are provided in

Table 2. Wave and Seabed Parameters for Seabed Response under Nonlinear Waves.

Parameter	Symbol	Value	Unit
Water Depth	d	10	m
Wave Height	H	4	m
Wave Period	T	10	s
Wavelength	L	92.32	m
Benchmark amplitude of wave pressure	$P_0$	15,810	Pa
Waveform Coefficient	$\varphi$	0, $-\pi /4$, $-\pi /2$	-
Asymmetry Coefficient	r	0, 0.25, 0.5, 0.75	-
Soil Density	$\rho$	2.0 × ${10}^3$	kg/${\mathrm{m}}^3$
Pore Fluid Density	${\rho }_f$	1.0 × ${10}^3$	kg/${\mathrm{m}}^3$
Young’s Modulus	$E_v$	1.0 × ${10}^7$	Pa
Poisson’s Ratio	$\mu$	0.3	-
Bulk Modulus of Pore Fluid	$K_{\omega }$	2.0 × ${10}^9$	Pa
Degree of Saturation	$S_r$	0.99	-
Porosity	n	0.476	-

.

As shown in Figure 5, when the asymmetry coefficient r increases, the positive pore pressure magnitude rises noticeably, its distribution becomes more concentrated, and the propagation depth into the seabed increases. In contrast, under wave amplitude asymmetry ($\varphi$ = $-\pi$/2), as r increases, the magnitude of the negative pressure zone decreases significantly, and the concentration of the negative pressure distribution is substantially reduced compared to the case of wave acceleration asymmetry ($\varphi$ = 0).

The liquefaction criterion proposed by Zen and Yamazaki [19] was adopted. According to this criterion, liquefaction occurs at a specific point in the seabed when the upward seepage force exceeds the total weight of the overlying soil. For a two-dimensional plane problem, the criterion can be expressed as follows:

$$-[p_b(x,0,t)-p(x,z,t)]\ge -({\gamma }_s-{\gamma }_{\omega })z$$

(9)

where $p_b$ is the wave pressure on the seabed surface; p is the wave pressure at a certain position inside the seabed; ${\gamma }_s$ is the unit weight of seabed soil; ${\gamma }_{\omega }$ is unit weight of water; and z is the depth below the seabed surface.

As shown in Figure 6, under a constant wave skewness, an increase in the asymmetry coefficient r results in a noticeable decrease in both the depth and width of seabed liquefaction. Concurrently, the location of maximum liquefaction shifts consistently forward along the horizontal direction of the seabed. This behavior can be explained by two primary mechanisms. First, as derived from the liquefaction criterion, liquefaction initiates only when the expression $-[p_b(x,0,t)-p(x,z,t)]$ reaches a sufficiently high value. An increase in r shifts the position of the negative pressure amplitude, thereby raising the threshold for liquefaction and reducing its depth. Second, under high-saturation conditions, a larger r concentrates the negative pressure zone, leading to a sharper and more localized pressure distribution. This concentration weakens the downward propagation of pore pressure, resulting in lower pore pressure values at the same depth and a consequent reduction in liquefaction depth. In the specific case where $\varphi =-\pi /2$ and r = 0.75, no liquefaction occurs. This is attributed to a significant decrease in the negative wave-induced pressure amplitude at the seabed surface, which becomes insufficient to trigger liquefaction. More generally, under combined acceleration and amplitude asymmetry, the vertical pore pressure distribution reflects the interplay of both effects, leading to a further suppression of liquefaction depth. For $r\ge$ 0.5 in this study, the negative pore pressure decreases with increasing nonlinear asymmetry, preventing liquefaction entirely.

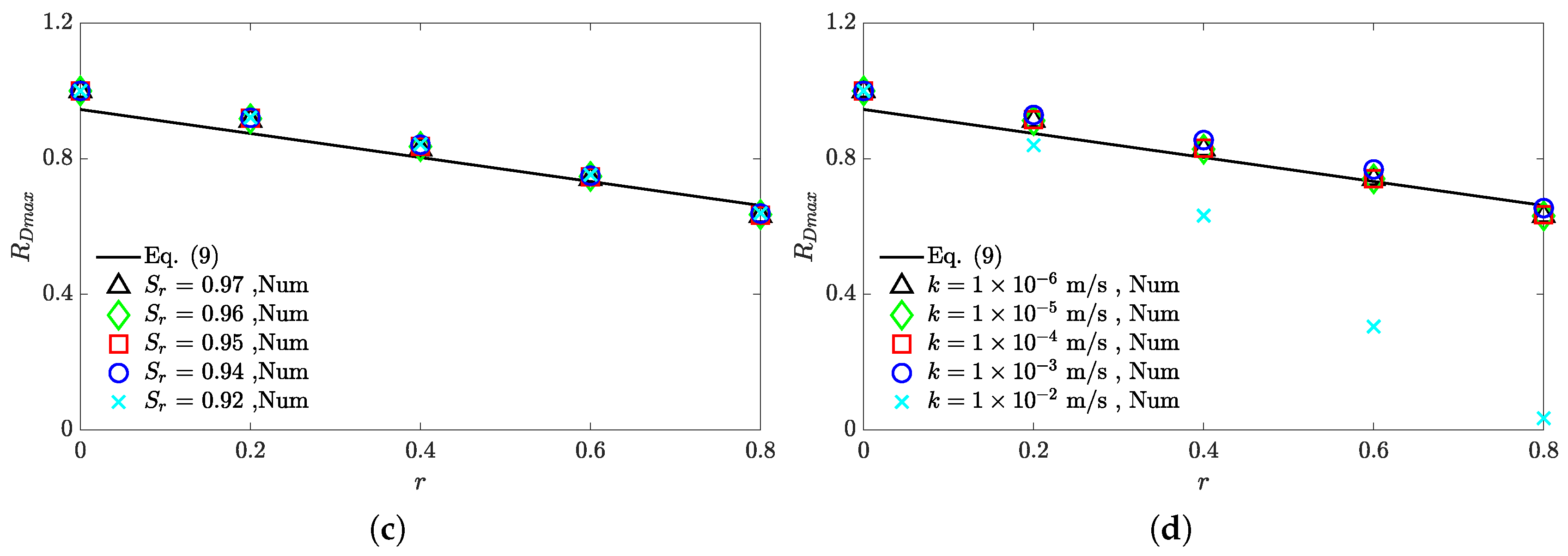
3.2. Analysis of Liquefaction Prediction Formula Applicability

Wang et al. [5] proposed a predictive formula for the maximum seabed liquefaction depth under specific wave and seabed parameters, as expressed in Equation (10).

$$R_{Dmax}={\displaystyle \frac{D_{max}}{D_{max0}}}=0.913-0.354r-0.041\varphi$$

(10)

where $R_{Dmax}$ is the ratio of the maximum liquefaction depth under nonlinear waves to that under linear waves. $D_{max}$ is the maximum liquefaction depth under nonlinear waves, $D_{max0}$ is the maximum liquefaction depth under linear waves. The formula was applied to multiple sets of conditions with varying wave heights, water depths, degrees of saturation, and permeability coefficients. Its applicability was verified through comparative analysis with numerical simulation results. The parameters for the numerical simulations in this section are set as shown in

Table 3. Parameter Settings for Case Studies on the Applicability Analysis of Liquefaction Prediction Formulas.

Parameter	Symbol	Value	Unit
Water Depth	d	5∼9	m
Wave Height	H	$0.6$∼$1.4$	m
Wave Period	T	4	s
Wave Form Coefficient	$\varphi$	$-\pi$/4	-
Asymmetry Coefficient	r	0, 0.2, 0.4, 0.6, 0.8	-
Soil Density	$\rho$	$2.0\times {10}^3$	kg/${\mathrm{m}}^3$
Pore Fluid Density	${\rho }_f$	$1.0\times {10}^3$	kg/${\mathrm{m}}^3$
Young’s Modulus	$E_v$	$1.0\times {10}^7$	Pa
Poisson’s Ratio	$\mu$	0.3	-
Soil Permeability Coefficient	k	$1.0\times {10}^{-6}$∼$1.0\times {10}^{-2}$	m/s
Bulk Modulus of Pore Fluid	$K_{\omega }$	$2.0\times {10}^9$	Pa
Degree of Saturation	$S_r$	0.97	-
Porosity	n	0.4	-

. The water depth ranges from 5.0 m to 9.0 m with intervals of 1.0 m; for each depth group, the asymmetry coefficient is set to 0, 0.2, 0.4, 0.6, and 0.8 respectively. The wave height ranges from 0.6∼1.4 m with intervals of 0.2 m; the degree of saturation is set to 0.97, 0.96, 0.95, 0.94, and 0.92; and the permeability coefficient ranges from $1.0\times {10}^{-6}$ m/s to $1.0\times {10}^{-2}$ m/s. A total of 100 numerical simulation cases are configured.

A comparison between the numerical simulation results and the liquefaction formula predictions was conducted under various parameter combinations, as illustrated in Figure 5.

As shown in Figure 7, the previously proposed prediction formula demonstrates good agreement with numerical simulations under conditions of varying wave heights, water depths, degrees of saturation, and lower permeability coefficients. However, under higher permeability coefficients, significant discrepancies emerge between predicted and simulated values. Furthermore, Figure 7d indicates that the prediction error increases with rising values of the asymmetry coefficient r.

Development of a Parametric Formula for Seabed Liquefaction Under Nonlinear Wave Action

Based on the aforementioned numerical simulation results, additional simulation cases were conducted specifically for scenarios with higher permeability coefficients. In these cases, the seabed permeability coefficients were set to k = $6\times {10}^{-3}$ m/s, k = $3\times {10}^{-3}$ m/s, respectively, while the remaining wave and seabed parameters were configured as specified in Table 3.

The functional relationship between the comparison results of numerical simulation and original predicted values with the asymmetry coefficient r and permeability coefficient k is defined as F. As indicated in the previous section, within the permeability coefficient range of $1.0\times {10}^{-6}$∼$1.0\times {10}^{-3}$ m/s the original prediction formula demonstrates good agreement with the simulated values; thus F can be taken as within this range. According to the study by Wang et al. [5], the waveform coefficient $\varphi$ has negligible effects on seabed liquefaction depth and is therefore excluded from the parametric formula analysis.

The expression for F is given as follows:

$$F=f(r,k)$$

(11)

The permeability coefficient k is non-dimensionalized and introducing a dimensionless parameter S, whose expression is given below:

$$S={\displaystyle \frac{(Gk/\gamma )T}{L^2}}$$

(12)

where G is the shear modulus; k is the permeability coefficient; $\gamma$ is the unit weight of water; T is the wave period; and L is the wavelength.

Through least squares fitting of the liquefaction depth values obtained from the above cases with respect to the dimensionless parameter S and the asymmetry coefficient r, a parametric formula $F(r,S)$ was derived for the permeability coefficient range of $1.0\times {10}^{-3}$∼$1.0\times {10}^{-2}$ m/s, corresponding to S = $2.9\times {10}^{-3}$∼$2.9\times {10}^{-2}$. The expression of this formula is shown in Equation (13).

$$F=-0.0464-631.1051·r^{37.6257}+1.2715·S^{0.0201}-39.6059(r·S)$$

(13)

Based on the function $F(r,S)$, a new predictive formula for the maximum seabed liquefaction depth can be derived, with its specific expression given below.

$$R_{D_{max}}={\displaystyle \frac{D_{max}}{D_{max,0}}}·F(r,S)=\left(0.913-0.354r-0.041\varphi \right)·F(r,S)$$

(14)

$$F(r,\mathrm{S})=\left\{\begin{array}{cc}1& ,S<2.9\times {10}^{-3}\hfill \\ \\ -0.0464-631.1051·r^{37.6257}+1.2715·{\mathrm{S}}^{0.0201}-39.6059(r·\mathrm{S})& ,S=2.9\times {10}^{-3}\sim 2.9\times {10}^{-2}\hfill \end{array}\right.$$

(15)

The calculation yielded a coefficient of determination of $R^2=0.9283$ for the numerical formula, indicating a strong fit.

Based on the new liquefaction depth prediction formula, a comparison between simulated and predicted values of seabed liquefaction depth is shown in Figure 8, for the permeability coefficient range of $1.0\times {10}^{-3}\sim 1.0\times {10}^{-2}$ m/s, corresponding to the dimensionless parameter S = $2.9\times {10}^{-3}\sim 2.9\times {10}^{-2}$.

As evidenced in Figure 8, the prediction error between liquefaction depth values obtained from the proposed formula and numerical simulations shows significant reduction compared to the original formula, particularly under high-permeability conditions (e.g., k = $1.0\times {10}^{-2}$ m/s) where the error decreases from $27\%$ to $7\%$ at r = 0.4, from $140\%$ to $47\%$ at r = 0.6, and dramatically from $1814\%$ to $120\%$ at r = 0.8, demonstrating that the new formula accounting for seabed permeability variations achieves substantially improved accuracy in predicting liquefaction depth. Under the four tested conditions, the overall normalized root mean square error (nRMSE)—calculated as RMSE divided by the average of the maximum liquefaction depths from all numerical simulations, then multiplied by 100%—is 19.95%, which is below 20%. Across the four permeability coefficients considered, the nRMSE of the formula ranges from 17% to 21%. These results demonstrate that the modified formula offers reasonably accurate predictions of the maximum liquefaction depth for permeability coefficients $k={10}^{-3}$ to ${10}^{-2}$.

3.3. Method for Computing Nonlinear Wave Parameters via Waveform Analysis

After generating a random wave sequence using the JONSWAP spectrum through waves2Foam, the Lower span zero point method is employed to identify individual waveforms within the sequence. This process yields the wave height and period data corresponding to each waveform, enabling the calculation of the Ursell number for each wave profile using the standard Ursell number formula.

$$U_r={\displaystyle \frac{3}{4}}{\displaystyle \frac{a_{w}K}{{\left(Kh\right)}^3}}$$

(16)

where the wave amplitude is related to the significant wave height by $a_w=0.5H_s$, and the wave number K obtained from the linear wave dispersion relation is based on the wave period T.

Further referencing Ruessink et al. [20], who analyzed large-scale observational data from gentle-slope beaches using empirical orthogonal function analysis, the skewness $S_u$ for each time series was derived from the oscillatory velocity time series $u_w\left(t\right)$ of wave propagation, along with its functional relationship to the Ursell number.

$$S_u={\displaystyle \frac{\overline{u_w^3\left(t\right)}}{{\sigma }_{u_w}^3}}$$

(17)

where ${\sigma }_{u_w}$ is the standard deviation of $u_w\left(t\right)$; by replacing $u_w\left(t\right)$ with its Hilbert transform, the asymmetry degree $A_u$ can be obtained.

The nonlinearity degree B is calculated from the skewness $S_u$ and the asymmetry degree $A_u$ using the following formula:

$$B=\sqrt{S_u^2+A_u^2}$$

(18)

The functional relationship between the nonlinearity degree B and the Ursell number $U_r$ is expressed as follows:

$$B=p_1+{\displaystyle \frac{p_2-p_1}{1+exp\frac{p_3-logUr}{p_4}}}$$

(19)

where $p_1$ and $p_2$ represent the values of B when Ursell number $U_r\to 0$ and $U_r\to \infty$; $p_3$ is associated with the inflection point; $p_4$ is the slope measurement. Nonlinear least-squares fitting with $p_1=0$ yielded $p_2=0.857\pm 0.016$, $p_3=-0.471\pm 0.025$, and $p_4=0.297\pm 0.021$, with the ± values representing the 95% confidence bounds.

The expression for calculating the phase $\psi$ is given by:

$$\psi ={tan}^{-1}(A_u/S_u)$$

(20)

It can be derived that $S_u=Bcos\psi$ and $A_u=Bsin\psi$.

To describe the relationship between $\psi$ and $U_r$, the following equation can be used for fitting:

$$\psi =-{90}^{\circ }+{90}^{\circ }tanh(p_5/U{r}^{p_6})$$

(21)

where the best-fit estimates for parameters $p_5$ and $p_6$ obtained through fitting are $0.815\pm 0.005$ and $0.672\pm 0.073$, respectively.

Subsequently, the waveform coefficient $\varphi$ and asymmetry coefficient r will be calculated from B and $\psi$, where B is correlated with r [21].

$$B=3b/\sqrt{2(1-b^2)}$$

(22)

$$b=r/\left(1+\sqrt{1-r^2}\right)$$

(23)

The relationship between $\psi$ and $\varphi$ is given by the following expression:

$$\varphi =-{tan}^{-1}(A_u/S_u)-\pi /2=-\psi -\pi /2$$

(24)

Thus, the nonlinear parameters and asymmetry coefficient corresponding to each waveform can be calculated using the above equations.

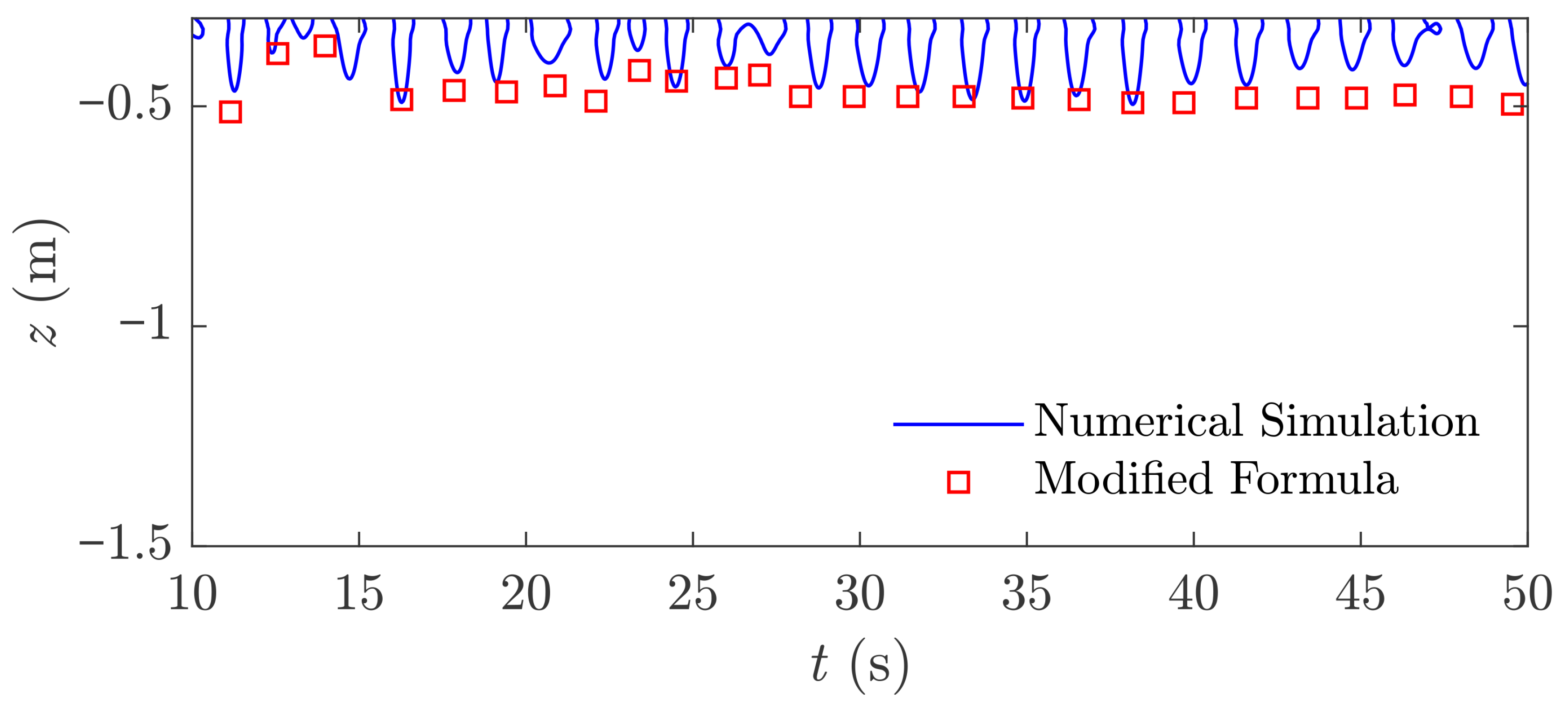
3.4. Application of the Parametrization Method to Seabed Liquefaction Problems

The schematic diagram of the sloped beach model used in this study is shown in Figure 9, the upper portion represents the wave module, while the lower portion represents the seabed module. The total length of the seabed section is 17.5 m, consisting of a 5.0 m long horizontal section at the front and a 12.5 m long sloping section at the rear, with a beach slope of 1:25.

For the wave parameter settings, the characteristic wave height $H_s$ to 0.145 m; the spectrum peak period $T_p$ to 1.6 s; $\gamma$ to 3.3, the seabed computational thickness to 1.0 m; and the simulation duration t to 60 s. The specific parameter configuration is detailed in

Table 4. Parameter Settings for the Verification of the Parameterization Method on Submarine Slopes.

Parameter	Symbol	Value	Unit
Spectrum Peak Period	$T_p$	1.6	s
Characteristic Wave Height	$H_S$	0.145	m
Soil Density	$\rho$	$2.65\times {10}^3$	kg/${\mathrm{m}}^3$
Pore Fluid Density	${\rho }_f$	$1.0\times {10}^3$	kg/${\mathrm{m}}^3$
Young’s Modulus	$E_v$	$1.0\times {10}^7$	Pa
Poisson’s Ratio	$\mu$	0.3	-
Compression Modulus of Pore Fluid	$K_{\omega }$	$2.0\times {10}^9$	m
Soil Permeability Coefficient	k	$1.0\times {10}^{-6}$	m/s
Bulk Modulus of Pore Fluid	$K_{\omega }$	$2.0\times {10}^9$	Pa
Degree of Saturation	$S_r$	0.99	-
Porosity	n	0.4	-

.

A comparative analysis was conducted between the predicted values from the formula and the numerical simulation results at two distinct locations along the sloping section of the beach. The selected positions, aligned with the direction of random wave propagation, are at x = 7.0 m and x = 10.0 m respectively.

At the location of x = 7.0 m on the beach slope section, a comparative analysis was conducted between the predictions obtained using the parametrization method and the numerical simulation results, following the methodology described previously. The comparison is illustrated in Figure 8.

As shown in Figure 10, at section A (x = 7.0 m) on the slope seabed, a comparison between the predicted values from the modified formula and the numerical simulation results indicates that the modified formula effectively captures the maximum liquefaction depth under different wave forms and at various time steps, with the overall trend being largely consistent. The maximum liquefaction depth obtained by the parametric method is 0.195 m, while the numerical simulation yields a value of 0.190 m, resulting in a relative error of 2.63%. This demonstrates that the modified formula meets the engineering requirements for rapid estimation at this site.

Similarly, at the location of x = 10.0 m on the beach slope section, a comparative analysis was conducted between the predictions obtained using the parametrization method and the numerical simulation results. The comparison is illustrated in Figure 11.

As shown in Figure 11, at section B (x = 10.0 m) on the slope seabed, a comparison between the predicted results from the modified formula and the numerical simulation values reveals that the formula can reasonably capture the maximum liquefaction depth under different waveforms and at various time steps, with the predicted trend aligning reasonably well with the simulation results. The maximum liquefaction depth given by the parametric method is 0.192 m, while the numerical simulation result is 0.181 m, yielding a relative error of 6.08%. This indicates that the modified formula maintains good simulation accuracy at different locations along the sloped seabed.

Based on the numerical simulation results and the outcomes calculated from the predictive formula, a comparison of the maximum liquefaction depths at different locations on the sloped beach is shown in Figure 12.

As evidenced in Figure 12, the relative errors between the predicted liquefaction depths and the numerical simulation results at different locations on the sloped beach (x = 7.0 m and x = 10.0 m) are 2.63% and 6.08%, respectively, indicating a generally small margin of error. This demonstrates that the liquefaction depth prediction formula proposed in this study exhibits good reliability in predicting liquefaction depths under random wave action on a sloped seabed.

4. Conclusions

Based on the nonlinear numerical method proposed by Abreu [3] et al. and the seabed response model of the WSSI toolbox [15], this study conducts numerical simulations to investigate the seabed liquefaction formula under nonlinear waves and analyzes wave profiles. By comparison with numerical results, the following conclusions are drawn:

• Analysis based on the formula by Wang et al. [5] reveals that the predictive accuracy of their nonlinear wave-induced liquefaction formula significantly decreases when the permeability coefficient k falls within the range of ${10}^{-2}$∼${10}^{-3}$ m/s. By introducing a dimensionless parameter S, the formula is modified, which substantially improves the prediction accuracy of seabed liquefaction depth under specific permeability conditions.
• Through waveform analysis, nonlinear wave parameters are obtained, and a parametric method is established by integrating the liquefaction depth prediction formula. This method allows for rapid determination of the maximum liquefaction depth at each time step based on wave decomposition. Applied to a sloping seabed under practical engineering conditions, comparison with numerical results demonstrates that the modified formula performs effectively in real-world scenarios.

Limitation: This paper proposes a liquefaction prediction formula applicable to flat or mildly sloping, non-cohesive sandy seabeds with a permeability coefficient of $k\le {10}^{-2}$. It should be noted that, for random wave conditions, the formula has so far been validated only against the JONSWAP spectrum. Its applicability to other wave spectra and seabed types requires further investigation.