Singularity-Free Fixed-Time Cooperative Tracking Control of Unmanned Surface Vehicles with Model Uncertainties
Abstract
1. Introduction
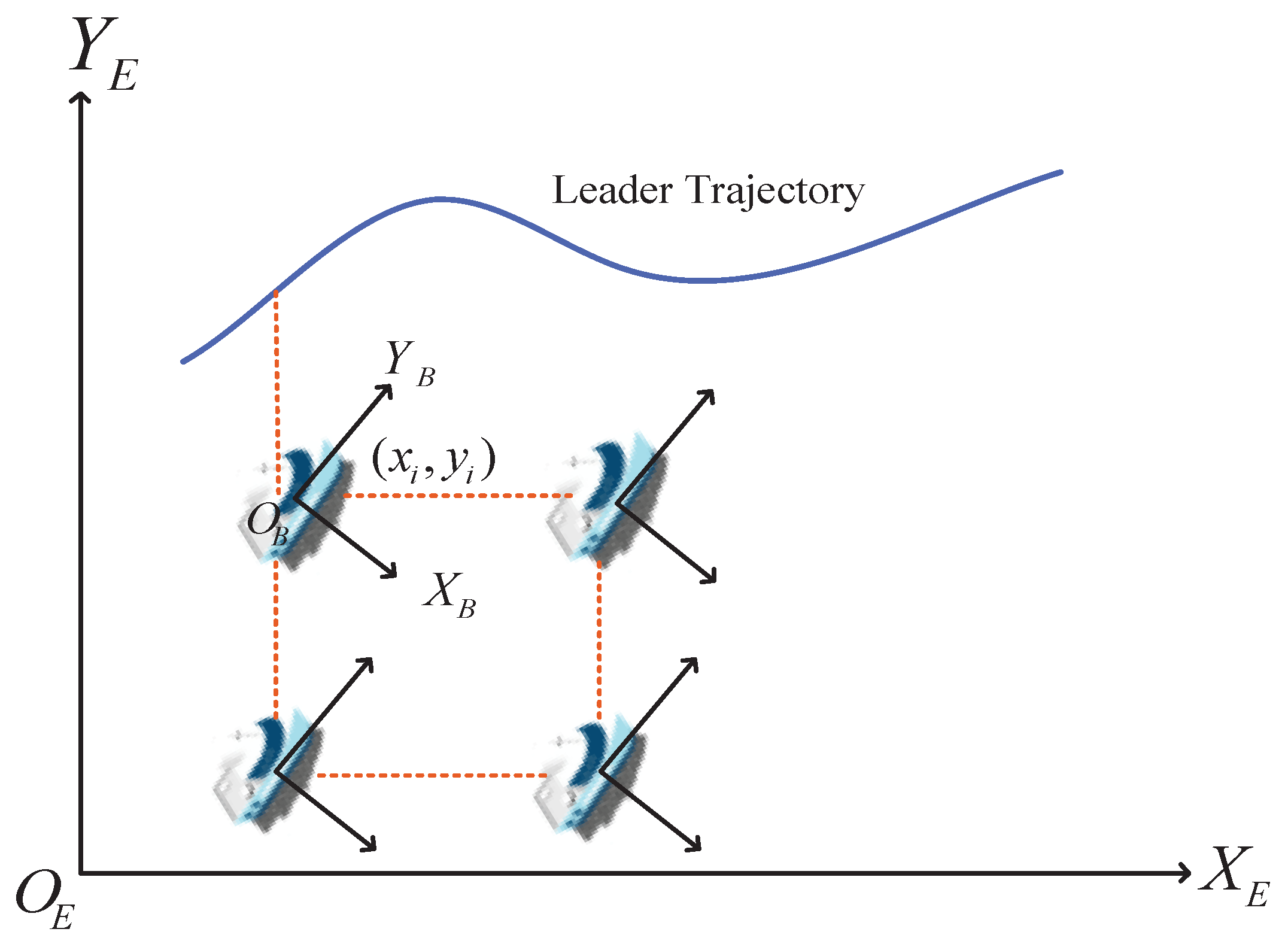
2. Modeling and Problem Statement
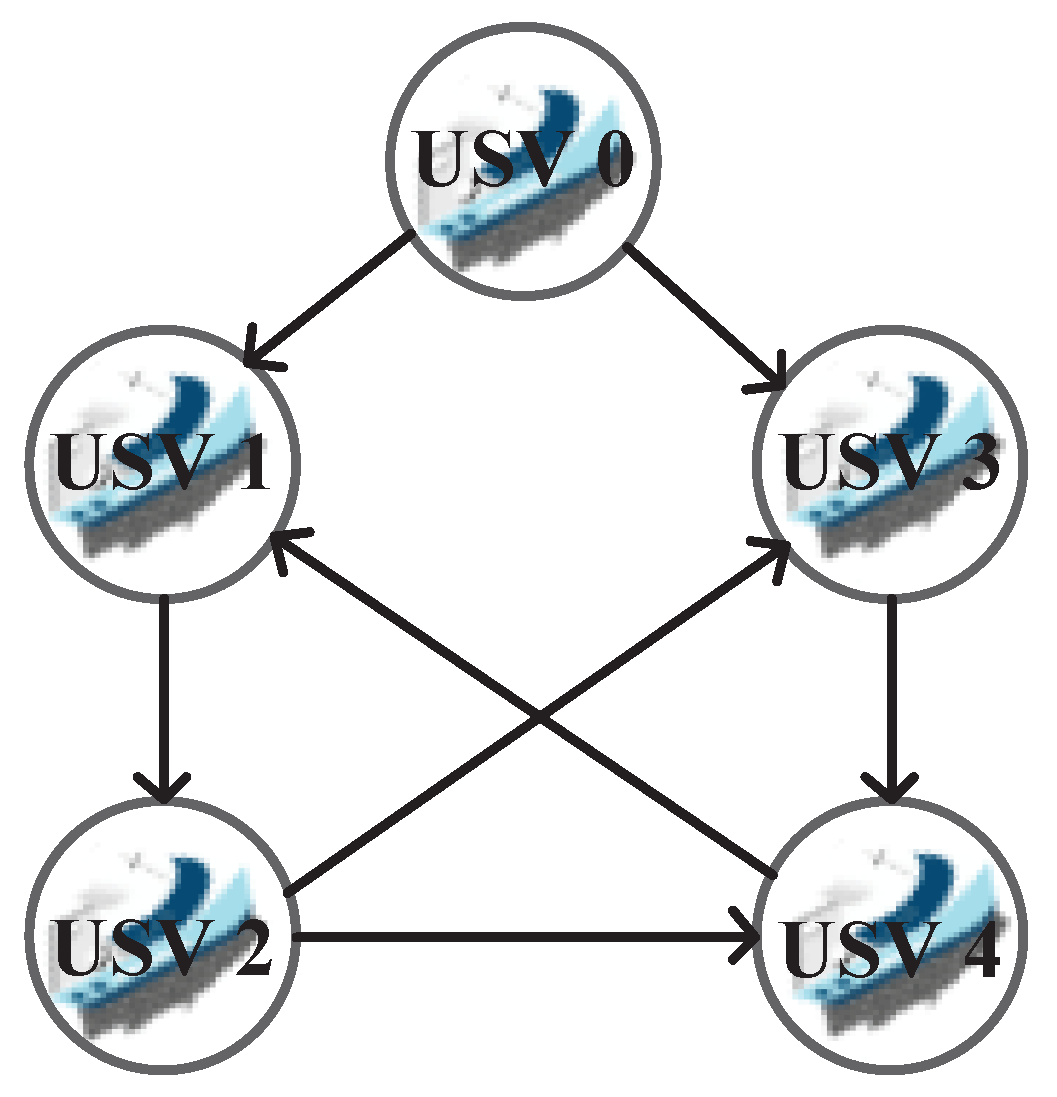
2.1. Communication Network
2.2. System Formulation
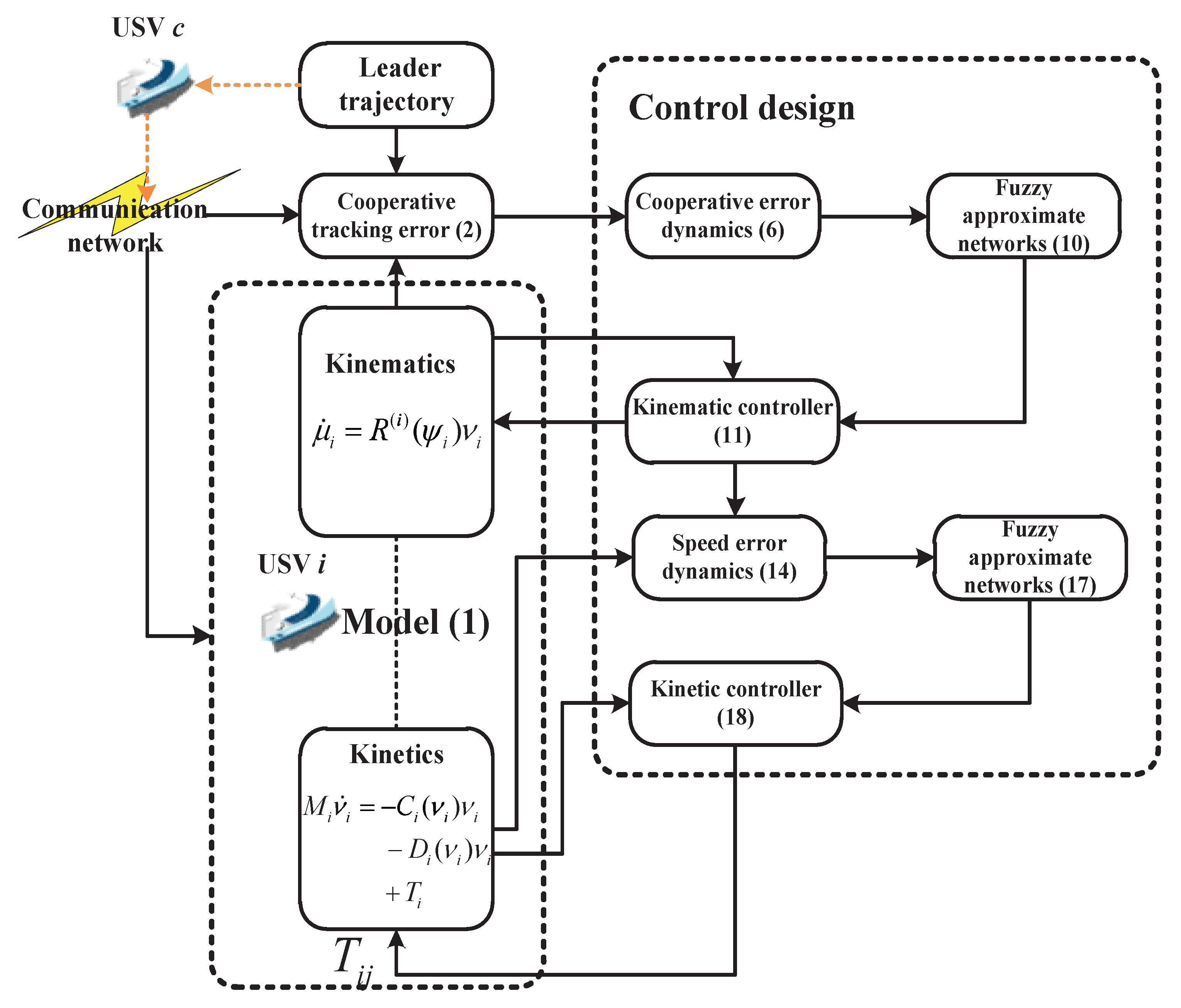
3. Control Design
3.1. Distributed Fixed-Time Kinematics and Kinetics Controller Design
3.2. Stability Analysis
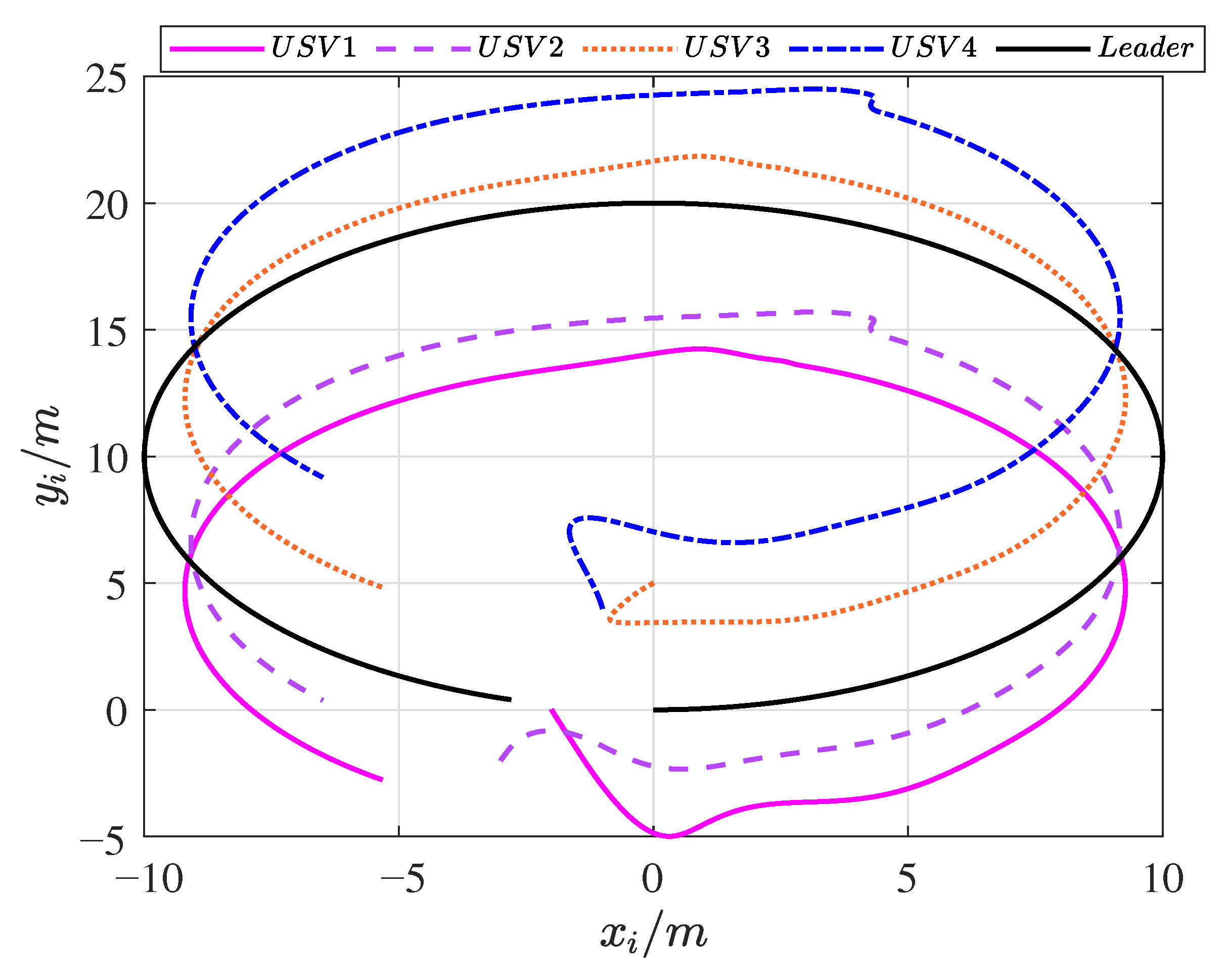
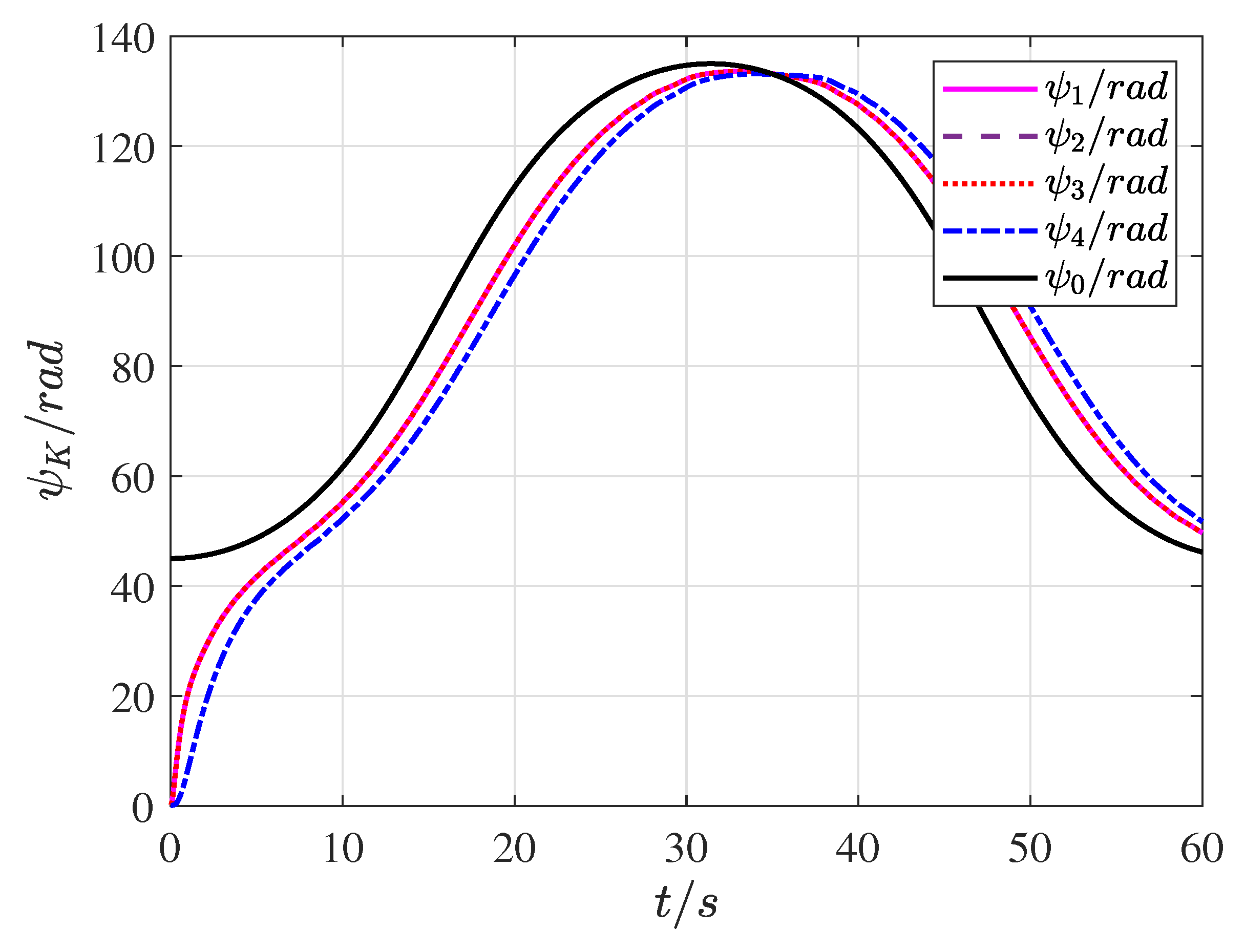
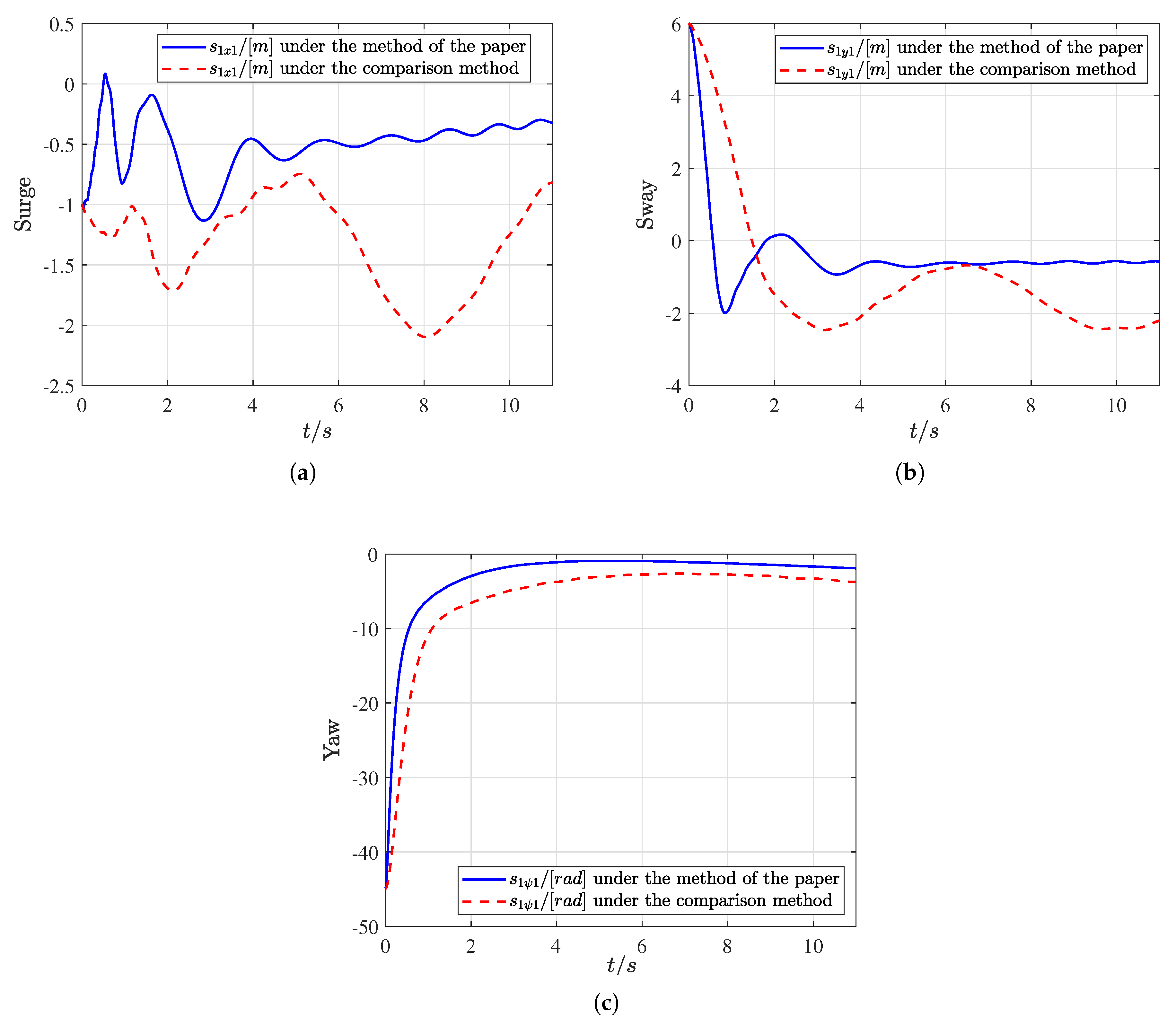
4. Simulation Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shan, Q.; Liu, W.; Li, T.; Zhang, H. A topology reconfiguration strategy for containment control of the multi-USV system based on algebraic connectivity. IEEE Trans. Ind. Electron. 2025, 72, 5322–5332. [Google Scholar] [CrossRef]
- Chang, Z.; Zong, G.; Wang, W.; Yue, M.; Zhao, X. Formation control and obstacle avoidance design for networked USV swarm with exogenous disturbance under intermittent communication. IEEE Trans. Netw. Sci. Eng. 2025, 12, 3234–3243. [Google Scholar] [CrossRef]
- Wang, W.; Shan, Q.; Li, T.; Chen, C.L.P.; Wang, Y. Finite-time-prescribed performance-based platoon formation control for unmanned surface vehicles using event-triggered extended state observer. IEEE Trans. Veh. Technol. 2024, 73, 18460–18471. [Google Scholar]
- Xue, J.; Song, Y.; Hu, H. Formation control of a multi-unmanned surface vessel system: A bibliometric analysis. J. Mar. Sci. Eng. 2024, 12, 1484. [Google Scholar]
- Wang, S.; Wen, G.; Shen, H.; Wang, L. A LOS-based path-following control of underactuated autonomous surface vessels for time-varying formations: Theory and experiment. IEEE Trans. Ind. Electron. 2025, 72, 10804–10813. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Zhang, W.; Shan, Q.; Zhang, W. Cooperative path following control of USV-UAVs considering low design complexity and command transmission requirements. IEEE Trans. Intell. Veh. 2024, 9, 715–724. [Google Scholar]
- Yuan, P.; Zhang, Z.; Li, Y.; Cui, J. Leader-follower control and APF for Multi-USV coordination and obstacle avoidance. Ocean Eng. 2024, 313, 119487. [Google Scholar]
- Sun, X.; Wang, G.; Fan, Y.; Mu, D.; Qiu, B. A formation collision avoidance system for unmanned surface vehicles with leader-follower structure. IEEE Access 2019, 7, 24691–24702. [Google Scholar] [CrossRef]
- Xue, K.; Wu, T. Distributed Consensus of USVs under Heterogeneous UAV-USV multi-agent systems cooperative control scheme. J. Mar. Sci. Eng. 2021, 9, 1314. [Google Scholar]
- Liu, C.; Xia, Z.; Tian, Y.; Patton, R. Defense and tolerance technique against attacks and faults on leader-following multi-USVs. IEEE Trans. Intell. Transp. Syst. 2021, 25, 5450–5461. [Google Scholar] [CrossRef]
- Chen, L.; Dai, S.; Dong, C. Adaptive optimal tracking control of an underactuated surface vessel using actor–critic reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 7520–7533. [Google Scholar] [CrossRef]
- Song, W.; Zuo, Y.; Tong, S. Fuzzy optimal event-triggered control for dynamic positioning of unmanned surface vehicle. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 2302–2311. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.; Luo, F. Leader–follower formation control of USVs with prescribed performance and collision avoidance. IEEE Trans. Ind. Inform. 2019, 15, 572–581. [Google Scholar] [CrossRef]
- He, S.; Wang, M.; Dai, S.; Luo, F. Distributed formation maneuvering quantized control of underactuated unmanned surface vehicles with collision and velocity constraints. J. Mar. Sci. Eng. 2024, 12, 848. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, Y.; Ahn, C.; Cheng, J.; Chen, C. Adaptive fuzzy backstepping-based formation control of unmanned surface vehicles with unknown model nonlinearity and actuator saturation. IEEE Trans. Veh. Technol. 2020, 69, 14749–14764. [Google Scholar] [CrossRef]
- Ghommam, J.; Saad, M.; Mnif, F.; Zhu, Q. Guaranteed performance design for formation tracking and collision avoidance of multiple USVs with disturbances and unmodeled dynamics. IEEE Syst. J. 2021, 15, 4346–4357. [Google Scholar] [CrossRef]
- Wu, T.; Xue, K.; Wang, P. Leader-follower formation control of USVs using APF-based adaptive fuzzy logic nonsingular terminal sliding mode control method. J. Mech. Sci. Technol. 2022, 36, 2007–2018. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Lu, R.; Zuo, Z.; Li, X. An overview of finite/fixed-time control and its application in engineering systems. IEEE/CAA J. Autom. Sin. 2022, 9, 2106–2120. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control. 2011, 57, 2106–2110. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. A new class of finite-time nonlinear consensus protocols for multi-agent systems. Int. Control. 2014, 87, 363–370. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems. Int. Syst. Sci. 2016, 47, 1366–1375. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Chen, G.; Li, Z. A fixed-time convergent algorithm for distributed convex optimization in multi-agent systems. Automatica 2018, 95, 539–543. [Google Scholar] [CrossRef]
- Shen, H.; Yin, Y.; Qian, X. Fixed-time formation control for unmanned surface vehicles with parametric uncertainties and complex disturbance. J. Mar. Sci. Eng. 2022, 10, 1246. [Google Scholar] [CrossRef]
- Li, J.; Fan, Y. Fixed-time event-triggered fault-tolerant formation-containment control for underactuated USVs with uncertain dynamics. Nonlinear Dyn. 2025, 113, 21435–21454. [Google Scholar] [CrossRef]
- Pan, Y.; Du, P.; Xue, H.; Lam, H.K. Singularity-free fixed-time fuzzy control for robotic systems with user-defined performance. IEEE Trans. Fuzzy Syst. 2021, 29, 2388–2398. [Google Scholar] [CrossRef]
- Liu, G.; Liang, H.; Wang, R.; Sun, Z.; Sui, Q. Adaptive event-triggered output feedback control for nonlinear multiagent systems using output information only. IEEE Trans. Syst. Man, Cybern. Syst. 2025, 1–12. [Google Scholar] [CrossRef]
- He, S.; Dai, S.; Zhao, Z.; Zou, T. UDE-based distributed formation control for MSVs with collision avoidance and connectivity preservation. IEEE Trans. Ind. Inform. 2024, 20, 1476–1487. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.; Qu, Z. Lyapunov, adaptive, and optimal design techniques for cooperative systems on directed communication graphs. IEEE Trans. Ind. Electron. 2012, 59, 3026–3041. [Google Scholar] [CrossRef]
- Wang, F.; Lai, G. Fixed-time control design for nonlinear uncertain systems via adaptive method. Syst. Control. Lett. 2020, 140, 104704. [Google Scholar] [CrossRef]
- Wu, W.; Tong, S. Adaptive fuzzy distributed optimal FTC for nonlinear multiagent systems based multiplayer differential game. IEEE Trans. Fuzzy Syst. 2025, 33, 657–668. [Google Scholar] [CrossRef]
- Su, Y.; Teng, F.; Li, T.; Liang, H. Fuzzy-based optimal control for an underactuated surface vessel with user-specified performance. IEEE Trans. Intell. Transp. Syst. 2025, 26, 7036–7050. [Google Scholar]
- Chen, G.; Zhou, Q.; Ren, H.; Li, H. Sensor-fusion-based event-triggered following control for nonlinear autonomous vehicles under sensor attacks. IEEE Trans. Autom. Sci. Eng. 2025, 22, 17411–17420. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, Q.; Li, H.; Yao, D.; Ahn, C.K. Event-triggered state estimation and control for networked nonlinear systems under dynamic sparse attacks. IEEE Trans. Netw. Sci. Eng. 2024, 11, 1947–1958. [Google Scholar] [CrossRef]
- Yang, W.; Jiang, Y.; Zhu, Y.; Wang, S.; Rubio, J. Fuzzy adaptive prescribed-time secure control for constrained human–robot cotransportation: A novel self-triggered quantized control strategy. IEEE Trans. Fuzzy Syst. 2024, 32, 4724–4734. [Google Scholar] [CrossRef]
- Ni, J.; Wu, Z.; Liu, L.; Liu, C. Fixed-time adaptive neural network control for nonstrict-feedback nonlinear systems with deadzone and output constraint. ISA Trans. 2020, 97, 458–473. [Google Scholar]
- Su, Y.; Xue, H.; Liang, H.; Chen, D. Singularity avoidance adaptive output-feedback fixed-time consensus control for multiple autonomous underwater vehicles subject to nonlinearities. Int. J. Robust Nonlinear Control. 2022, 32, 4401–4421. [Google Scholar]
- Liang, H.; Du, Z.; Huang, T.; Pan, Y. Neuroadaptive performance guaranteed control for multiagent systems with power integrators and unknown measurement sensitivity. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 9771–9782. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G. Fault-tolerant leader-follower formation control of marine surface vessels with unknown dynamics and actuator faults. Int. J. Robust Nonlinear Control 2018, 28, 4188–4208. [Google Scholar] [CrossRef]
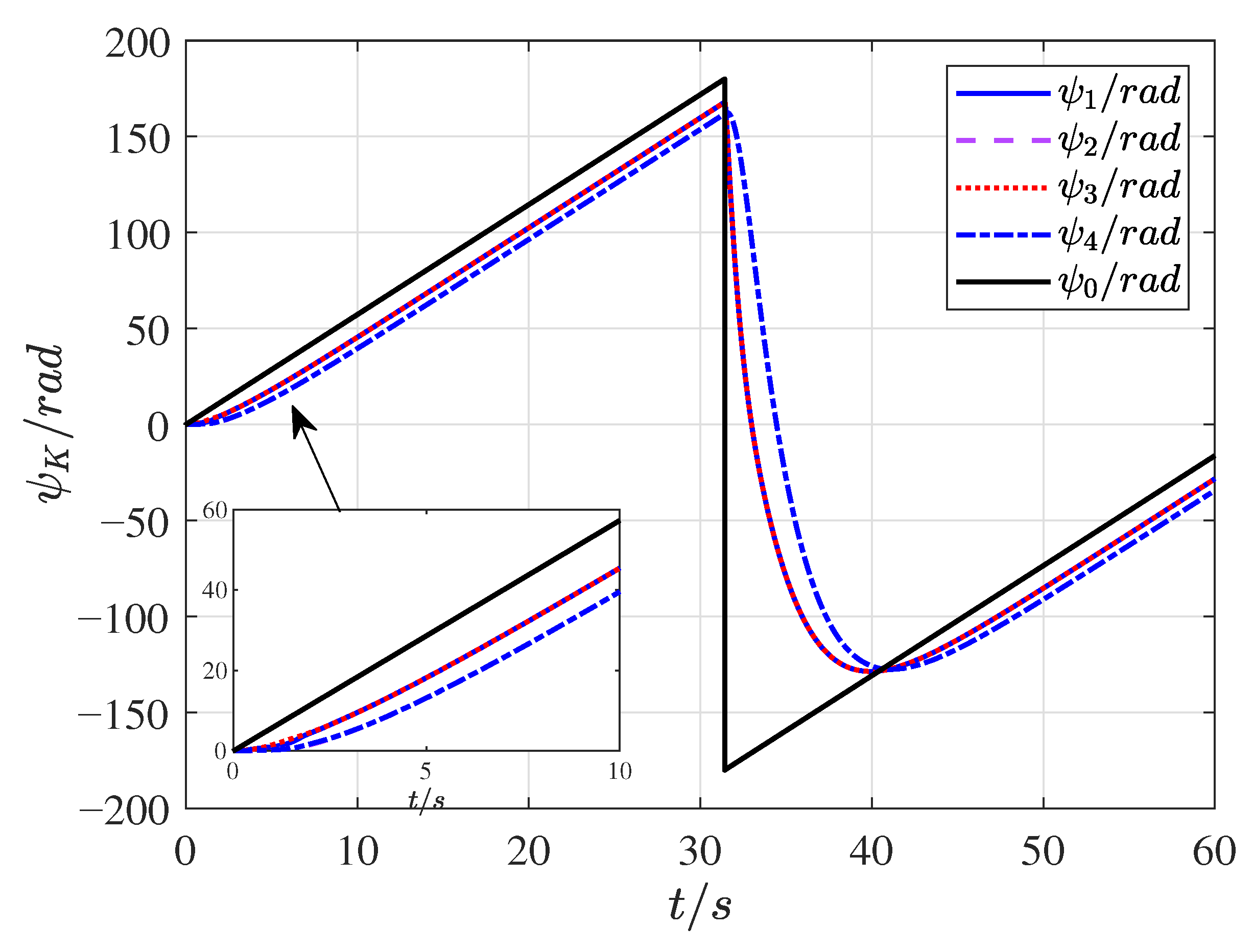
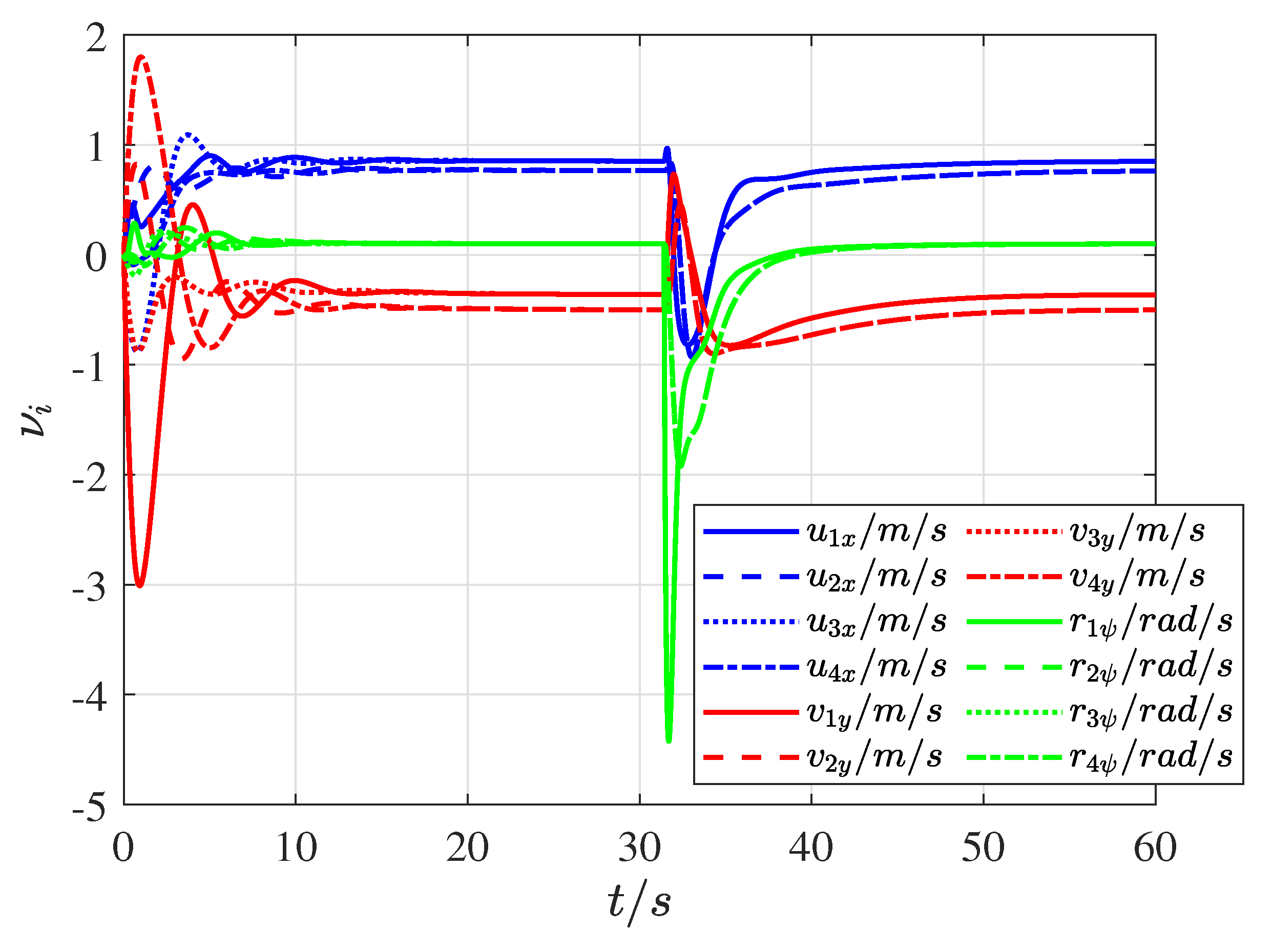
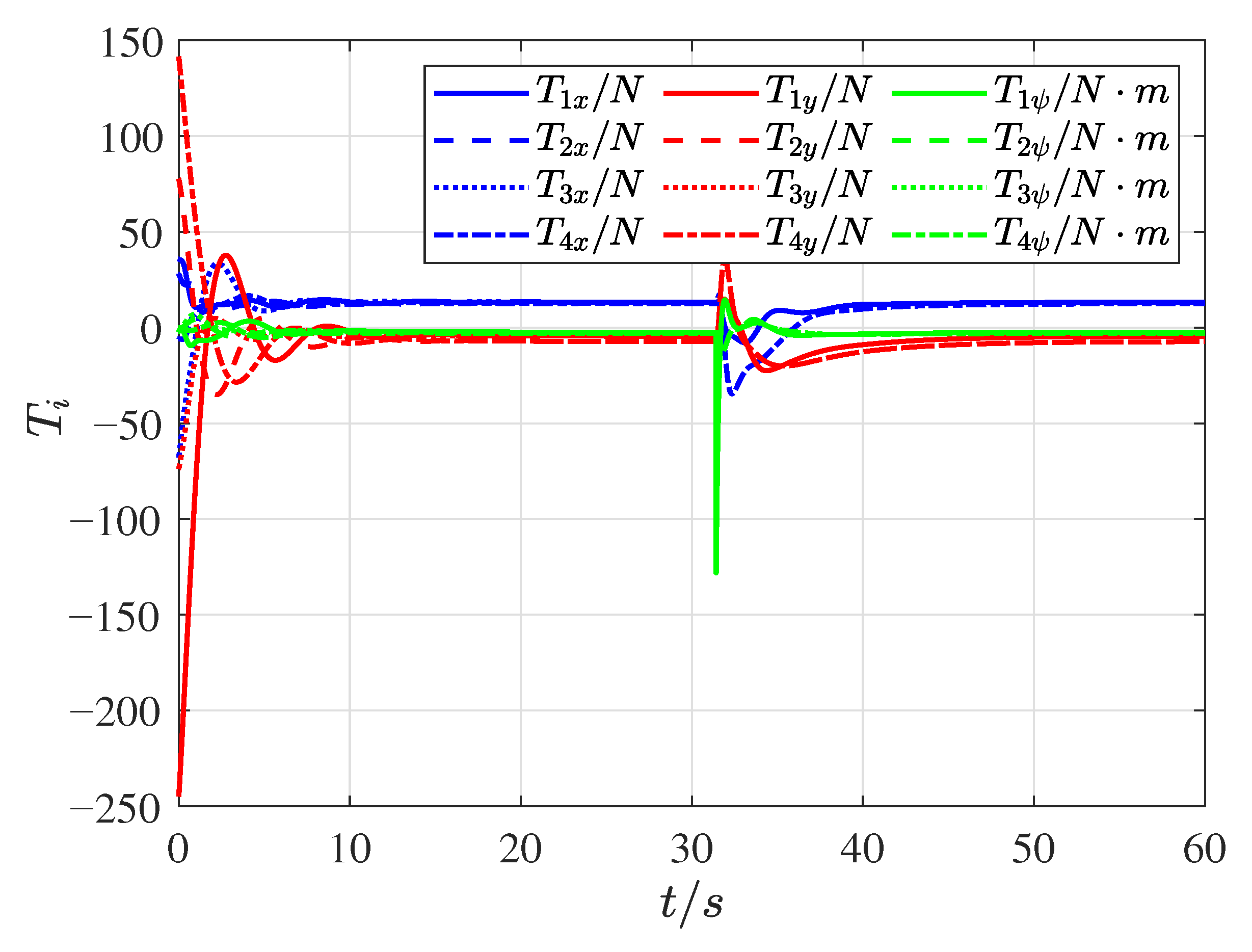
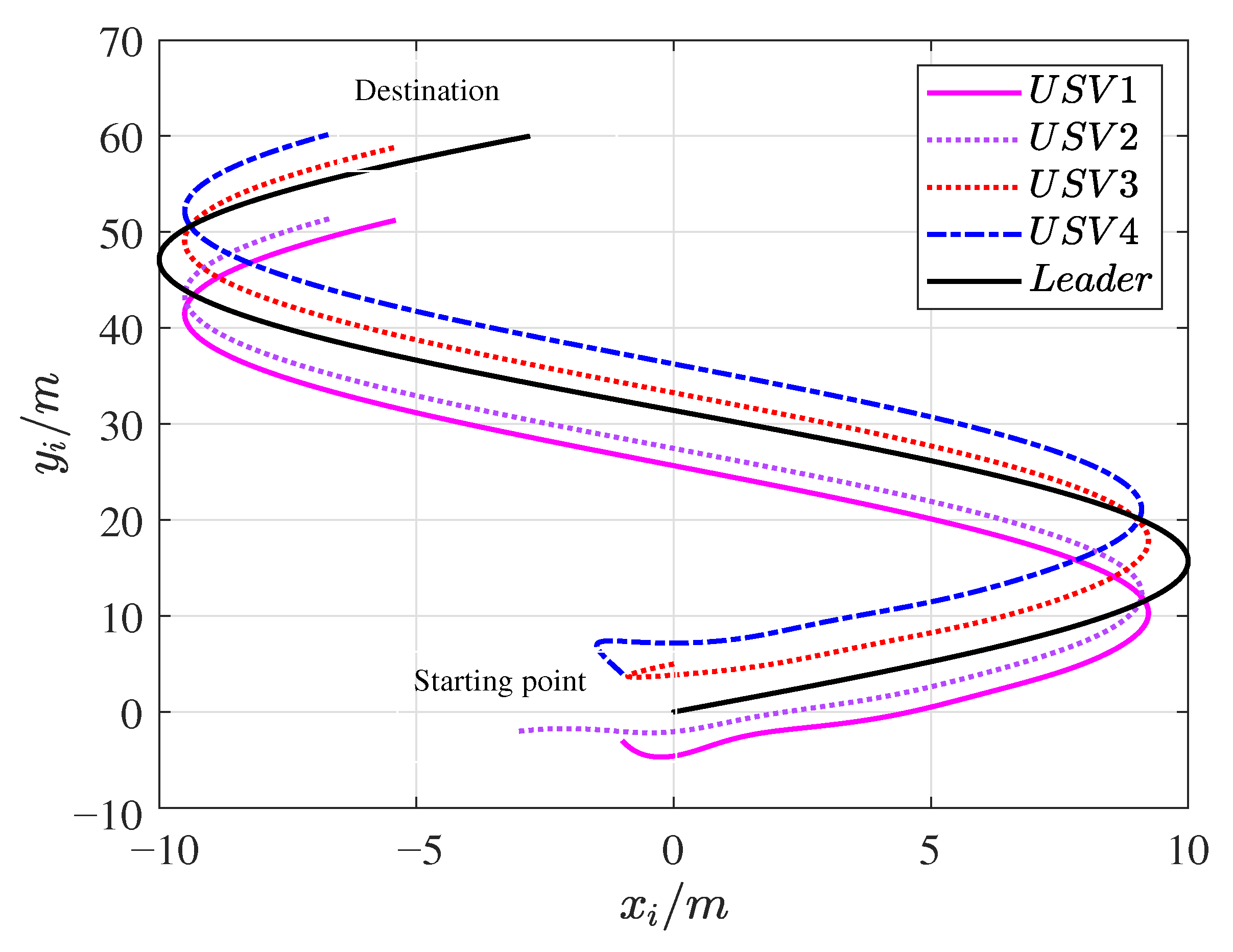
| Symbol | Interpretation |
|---|---|
| , , , | 2, 2.5, 15, 13, 5, 34 |
| , , , , , | 0.5, 0.3, 1.3, 4, 0.15, 3.4 |
| q, p | 197/101, 97/99 |
| , | 0.4, 0.4 |
| , | 3, 3 |
| Symbol | Interpretation |
|---|---|
| , , , | − 2, −3, 0, −1 |
| , , , | 0, −2, 0.1, 0.1 |
| , , , | 0.1, 0.1, 0.1, 0.1 |
| , , | 0, 0, 0 |
| Metric | Under Our Control Method | Under the Control Method [15] |
|---|---|---|
| Average consensus error of USV 1 in surge | −0.0124/m | −0.0925/m |
| Average consensus error of USV 1 in sway | −0.3206/m | −1.0781/m |
| Average consensus error of USV 1 in yaw | −0.320/rad | −3.8166/rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Yu, R.; Ye, P.; Li, T. Singularity-Free Fixed-Time Cooperative Tracking Control of Unmanned Surface Vehicles with Model Uncertainties. J. Mar. Sci. Eng. 2025, 13, 1791. https://doi.org/10.3390/jmse13091791
Su Y, Yu R, Ye P, Li T. Singularity-Free Fixed-Time Cooperative Tracking Control of Unmanned Surface Vehicles with Model Uncertainties. Journal of Marine Science and Engineering. 2025; 13(9):1791. https://doi.org/10.3390/jmse13091791
Chicago/Turabian StyleSu, Yuanbo, Renhai Yu, Peiyun Ye, and Tieshan Li. 2025. "Singularity-Free Fixed-Time Cooperative Tracking Control of Unmanned Surface Vehicles with Model Uncertainties" Journal of Marine Science and Engineering 13, no. 9: 1791. https://doi.org/10.3390/jmse13091791
APA StyleSu, Y., Yu, R., Ye, P., & Li, T. (2025). Singularity-Free Fixed-Time Cooperative Tracking Control of Unmanned Surface Vehicles with Model Uncertainties. Journal of Marine Science and Engineering, 13(9), 1791. https://doi.org/10.3390/jmse13091791







