Deep Learning-Based Wind Speed Retrieval from Sentinel-1 SAR Wave Mode Data
Abstract
1. Introduction
2. Data and Methods
2.1. S-1 SAR Data
2.2. ERA5 Winds
2.3. In Situ Buoy Observations
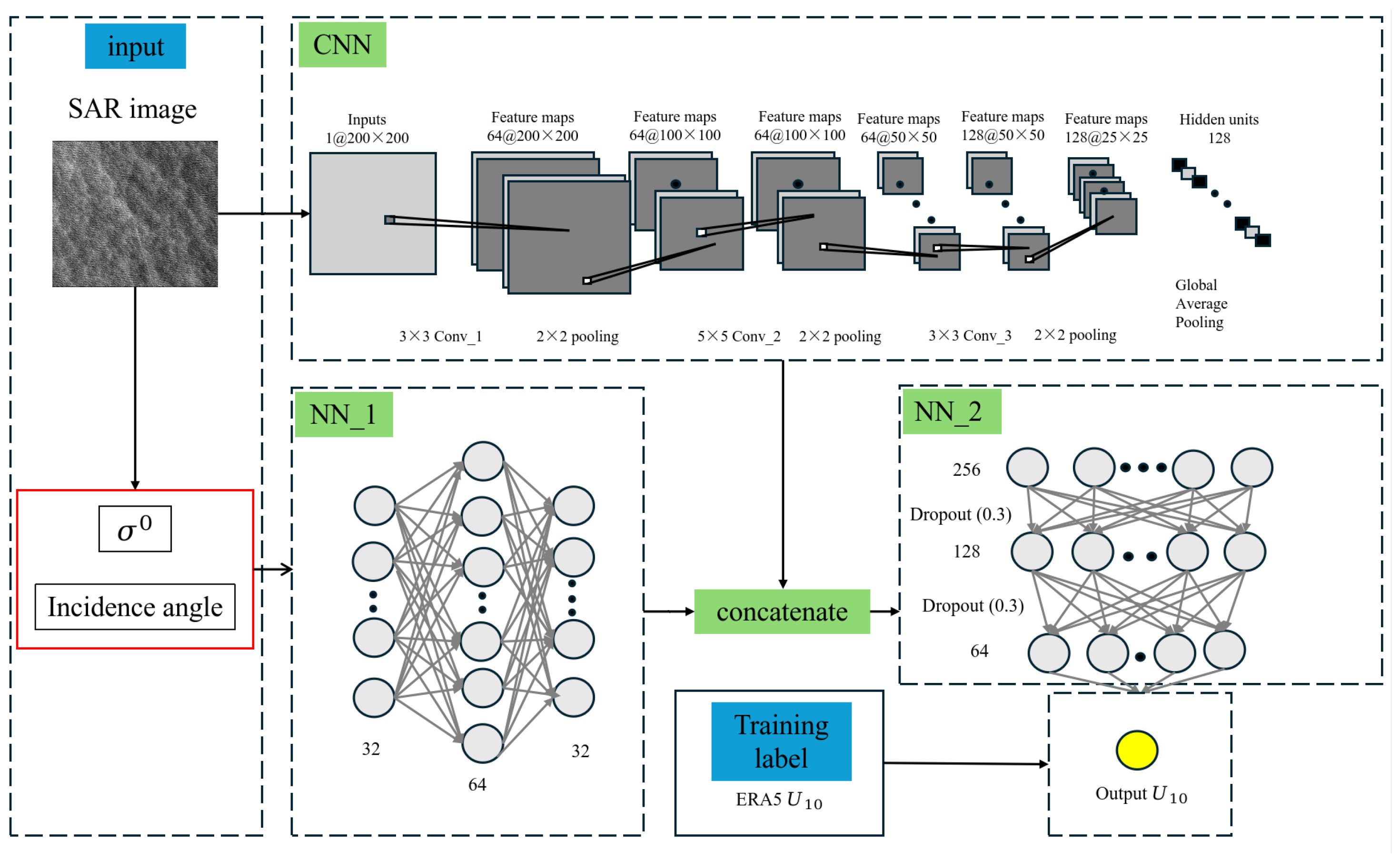
2.4. Model Architecture
3. Model Training
3.1. Sensitivity Test
3.2. Unimodel for Two Incidence Angle
3.3. Respective Model for Each Incidence
4. Results Validation
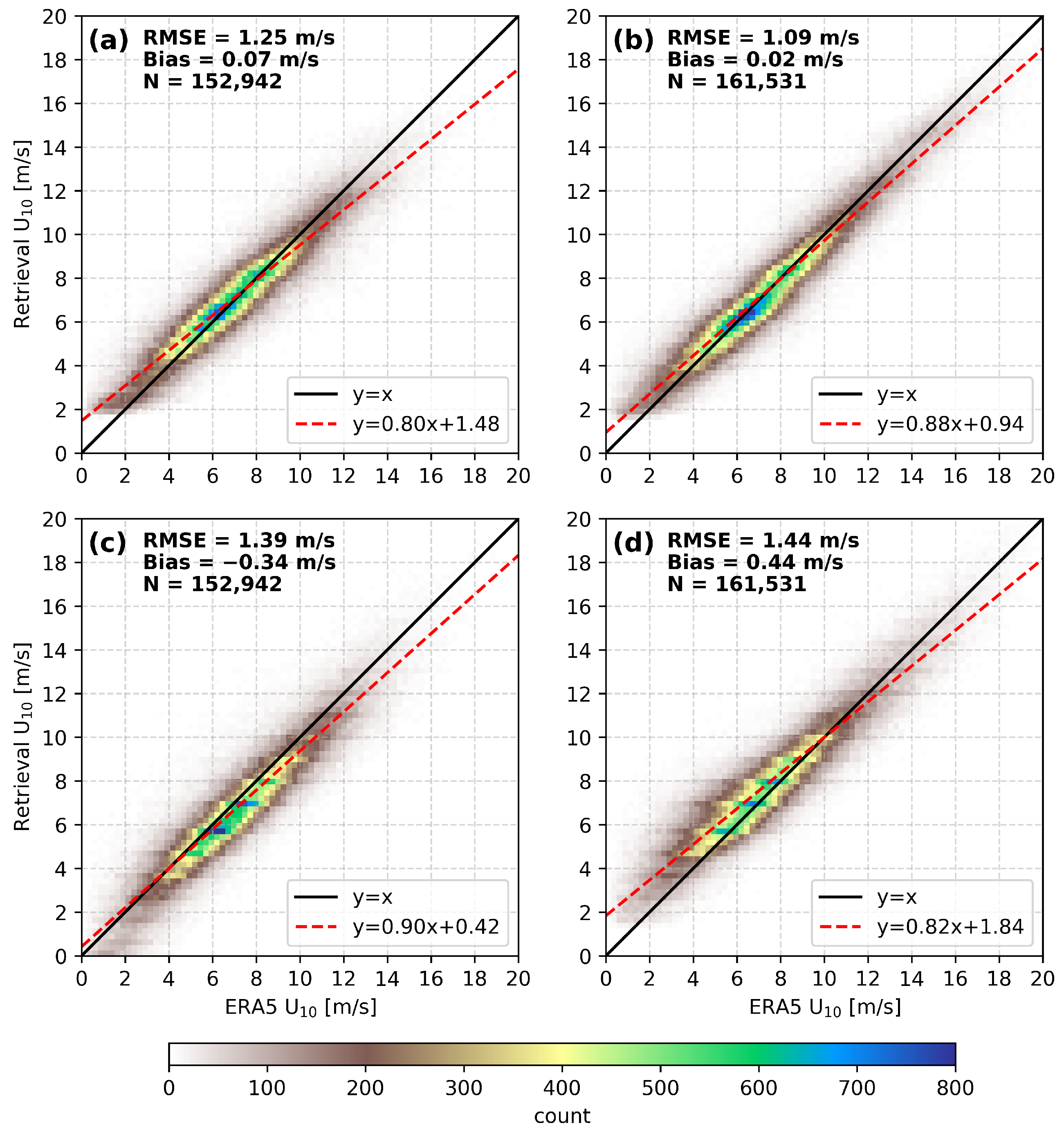
4.1. Independent Validation with ERA5 Wind Speed
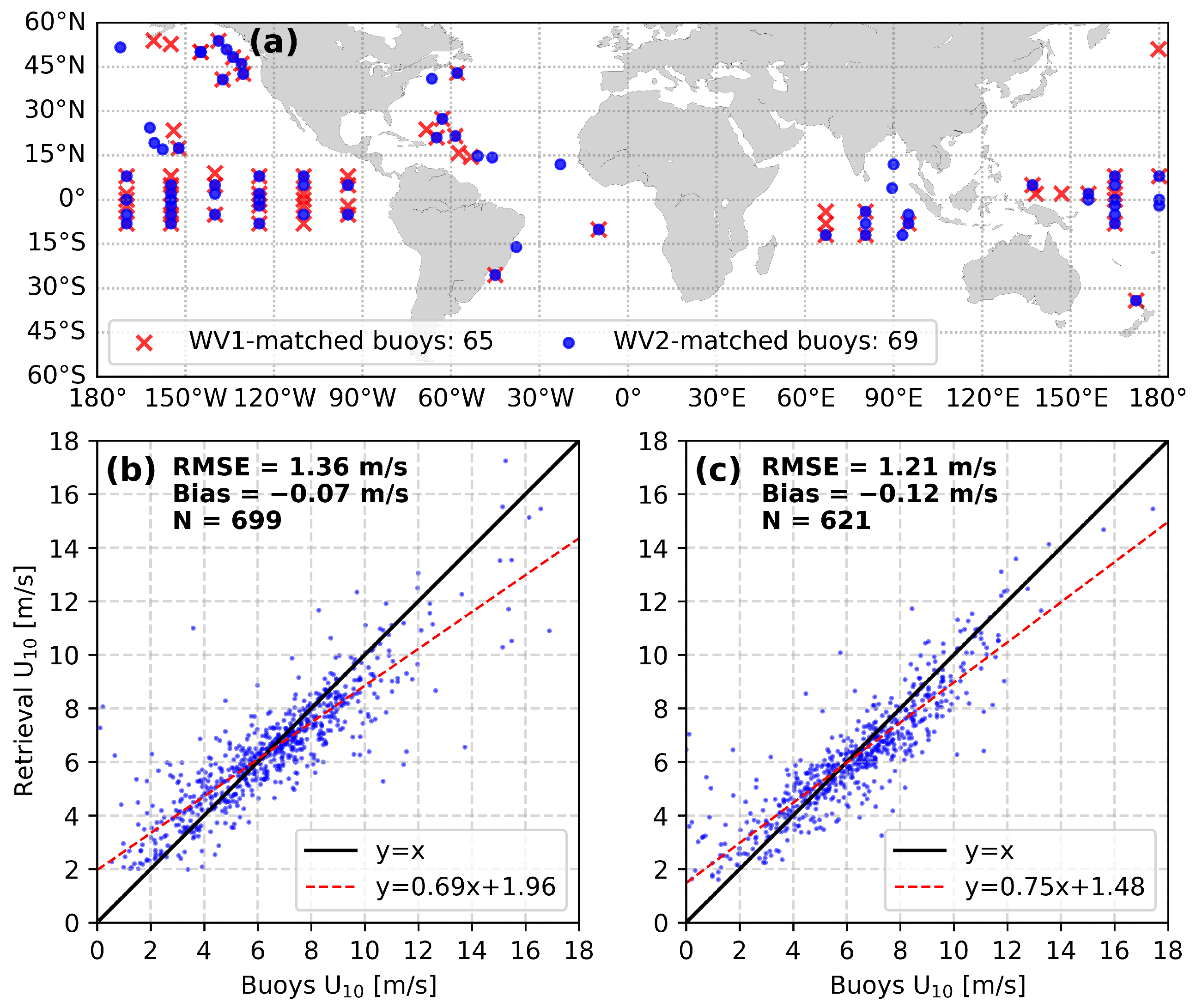
4.2. Comparison with Buoys
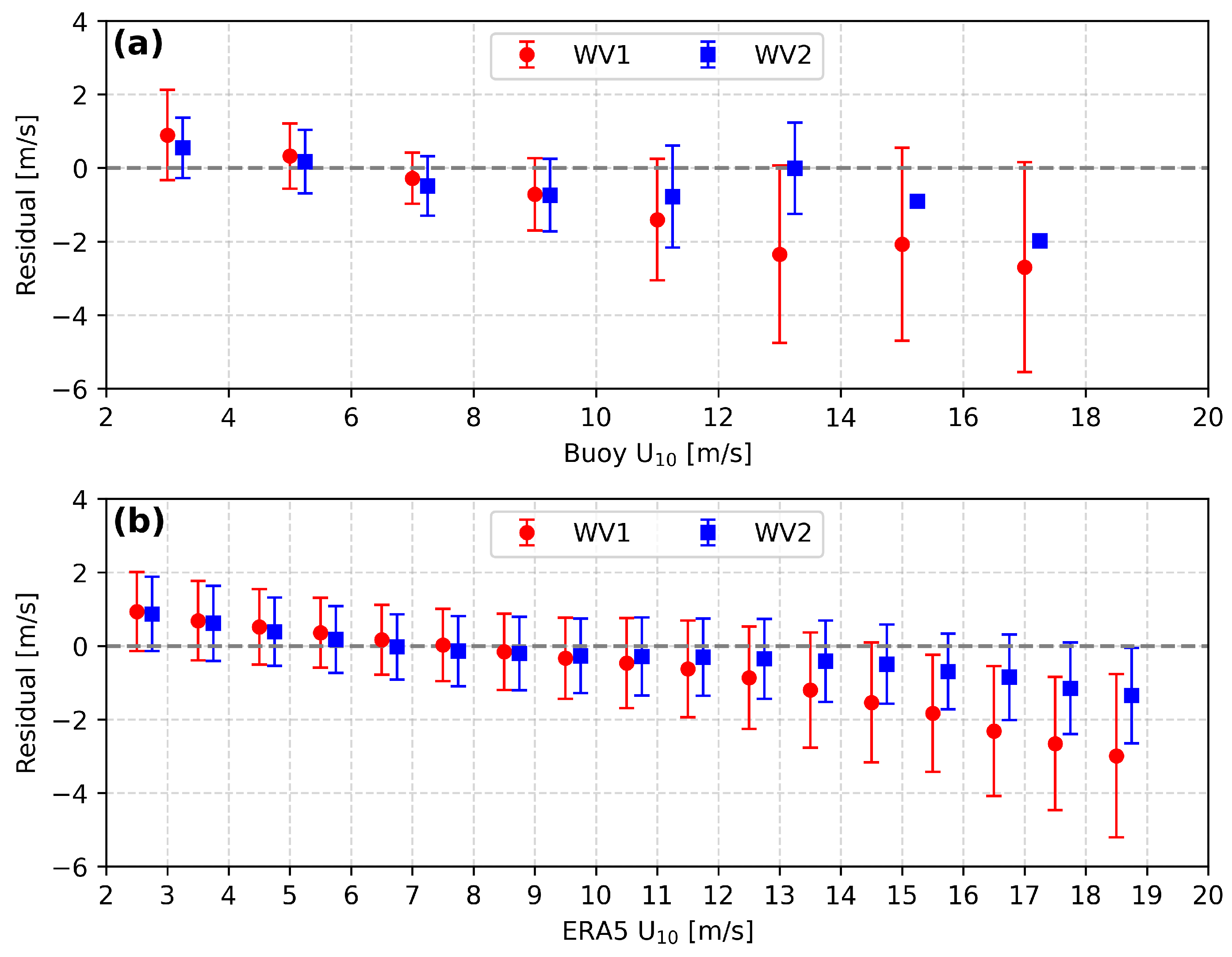
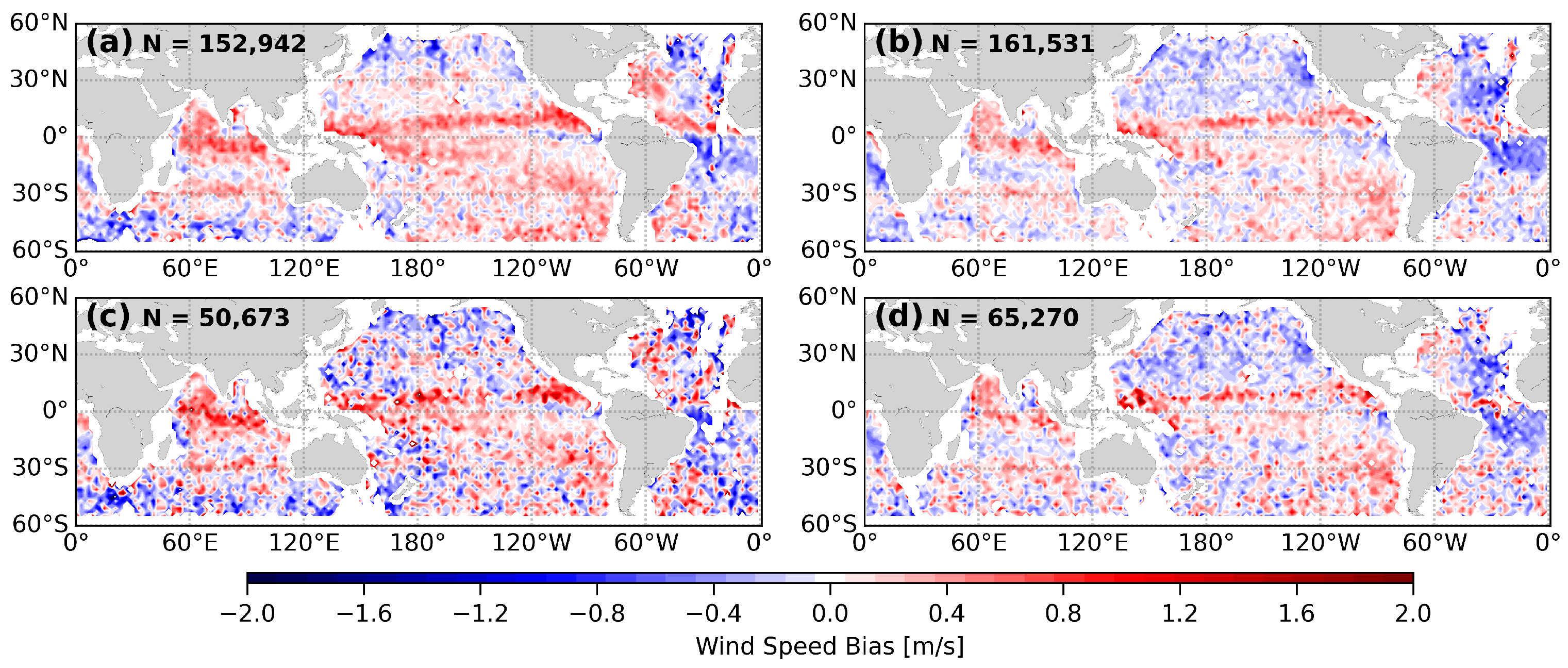
4.3. Performance Diagnostics
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, S.D. Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature. J. Geophys. Res. Ocean. 1988, 93, 15467–15472. [Google Scholar] [CrossRef]
- Yu, L. Global air–sea fluxes of heat, fresh water, and momentum: Energy budget closure and unanswered questions. Annu. Rev. Mar. Sci. 2019, 11, 227–248. [Google Scholar] [CrossRef]
- Cronin, M.F.; Gentemann, C.L.; Edson, J.; Ueki, I.; Bourassa, M.; Brown, S.; Clayson, C.A.; Fairall, C.W.; Farrar, J.T.; Gille, S.T.; et al. Air-sea fluxes with a focus on heat and momentum. Front. Mar. Sci. 2019, 6, 430. [Google Scholar] [CrossRef]
- Villas Bôas, A.B.; Ardhuin, F.; Ayet, A.; Bourassa, M.A.; Brandt, P.; Chapron, B.; Cornuelle, B.D.; Farrar, J.T.; Fewings, M.R.; Fox-Kemper, B.; et al. Integrated observations of global surface winds, currents, and waves: Requirements and challenges for the next decade. Front. Mar. Sci. 2019, 6, 434339. [Google Scholar] [CrossRef]
- Hong, B.; Zhang, J. Long-term trends of sea surface wind in the northern South China Sea under the background of climate change. J. Mar. Sci. Eng. 2021, 9, 752. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Meissner, T.; Cerovecki, I.; Chang, P.S.; Dong, X.; De Chiara, G.; Donlon, C.; Dukhovskoy, D.S.; Elya, J.; Fore, A.; et al. Remotely sensed winds and wind stresses for marine forecasting and ocean modeling. Front. Mar. Sci. 2019, 6, 443. [Google Scholar] [CrossRef]
- Sempreviva, A.M.; Barthelmie, R.J.; Pryor, S. Review of methodologies for offshore wind resource assessment in European seas. Surv. Geophys. 2008, 29, 471–497. [Google Scholar] [CrossRef]
- Doubrawa, P.; Barthelmie, R.J.; Pryor, S.C.; Hasager, C.B.; Badger, M.; Karagali, I. Satellite winds as a tool for offshore wind resource assessment: The Great Lakes Wind Atlas. Remote Sens. Environ. 2015, 168, 349–359. [Google Scholar] [CrossRef]
- Ricciardulli, L.; Manaster, A.; Lindsley, R. Investigation of a calibration change in the ocean surface wind measurements from the TAO buoy array. Bull. Am. Meteorol. Soc. 2025, 106, E242–E260. [Google Scholar] [CrossRef]
- Yueh, S.H.; Dinardo, S.J.; Fore, A.G.; Li, F.K. Passive and active L-band microwave observations and modeling of ocean surface winds. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3087–3100. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing techniques for studying coastal ecosystems: An overview. J. Coast. Res. 2011, 27, 2–17. [Google Scholar]
- Chelton, D.B.; Schlax, M.G.; Freilich, M.H.; Milliff, R.F. Satellite Measurements Reveal Persistent Small-Scale Features in Ocean Winds. Science 2004, 303, 978–983. [Google Scholar] [CrossRef]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. Covariability of Surface Wind and Stress Responses to Sea Surface Temperature Fronts. J. Clim. 2012, 25, 5916–5942. [Google Scholar] [CrossRef]
- Figa-Saldaña, J.; Wilson, J.J.; Gelsthorpe, R.; Stoffelen, A. The advanced scatterometer (ASCAT) on the meteorological operational (MetOp) platform: A follow on for European wind scatterometers. Can. J. Remote Sens. 2002, 28, 404–412. [Google Scholar] [CrossRef]
- Sun, J.; Li, H.; Lin, W.; He, Y. Joint inversion of sea surface wind and current velocity based on Sentinel-1 synthetic aperture radar observations. J. Mar. Sci. Eng. 2024, 12, 450. [Google Scholar] [CrossRef]
- Montuori, A.; Portabella, M.; Guimbard, S.; Gabarró, C.; Migliaccio, M. Assessment of the SMOS inversion scheme for salinity and wind speed retrieval purposes. Eur. J. Remote Sens. 2013, 46, 855–873. [Google Scholar] [CrossRef]
- Mourad, P.D.; Thompson, D.R.; Vandemark, D.C. Extracting fine-scale wind fields from synthetic aperture radar images of the ocean surface. Johns Hopkins APL Tech. Dig. 2000, 21, 108–115. [Google Scholar]
- Lin, H.; Xu, Q.; Zheng, Q. An overview on SAR measurements of sea surface wind. Prog. Nat. Sci. 2008, 18, 913–919. [Google Scholar] [CrossRef]
- Wang, C.; Vandemark, D.; Mouche, A.; Chapron, B.; Li, H.; Foster, R.C. An assessment of marine atmospheric boundary layer roll detection using Sentinel-1 SAR data. Remote Sens. Environ. 2020, 250, 112031. [Google Scholar] [CrossRef]
- Mouche, A.A.; Collard, F.; Chapron, B.; Dagestad, K.F.; Guitton, G.; Johannessen, J.A.; Kerbaol, V.; Hansen, M.W. On the use of Doppler shift for sea surface wind retrieval from SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2901–2909. [Google Scholar] [CrossRef]
- Li, H.; Chapron, B.; Mouche, A.; Wang, C.; Lin, W.; He, Y. Ocean Surface Wind Wave Signatures in Single-Look Complex SAR Data. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4203111. [Google Scholar] [CrossRef]
- Yu, P.; Xu, W.; Zhong, X.; Johannessen, J.A.; Yan, X.H.; Geng, X.; He, Y.; Lu, W. A neural network method for retrieving sea surface wind speed for C-Band SAR. Remote Sens. 2022, 14, 2269. [Google Scholar] [CrossRef]
- Li, X.M. Retrieval of Sea Surface Wind Speed by Spaceborne SAR Based on Machine Learning. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 4011–4014. [Google Scholar]
- Zanchetta, A.; Zecchetto, S. Wind direction retrieval from Sentinel-1 SAR images using ResNet. Remote Sens. Environ. 2021, 253, 112178. [Google Scholar] [CrossRef]
- Li, H.; Mouche, A.; Stopa, J.E. Impact of sea state on wind retrieval from Sentinel-1 wave mode data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 559–566. [Google Scholar] [CrossRef]
- Eyre, J.R.; English, S.J.; Forsythe, M. Assimilation of satellite data in numerical weather prediction. Part I: The early years. Q. J. R. Meteorol. Soc. 2020, 146, 49–68. [Google Scholar] [CrossRef]
- Ramon, J.; Lledó, L.; Torralba, V.; Soret, A.; Doblas-Reyes, F.J. What global reanalysis best represents near-surface winds? Q. J. R. Meteorol. Soc. 2019, 145, 3236–3251. [Google Scholar] [CrossRef]
- Wang, C.; Mouche, A.; Tandeo, P.; Stopa, J.E.; Longépé, N.; Erhard, G.; Foster, R.C.; Vandemark, D.; Chapron, B. A labelled ocean SAR imagery dataset of ten geophysical phenomena from Sentinel-1 wave mode. Geosci. Data J. 2019, 6, 105–115. [Google Scholar] [CrossRef]
- Young, I.R. Seasonal variability of the global ocean wind and wave climate. Int. J. Climatol. A J. R. Meteorol. Soc. 1999, 19, 931–950. [Google Scholar] [CrossRef]
- Wang, C.; Tandeo, P.; Mouche, A.; Stopa, J.E.; Gressani, V.; Longepe, N.; Vandemark, D.; Foster, R.C.; Chapron, B. Classification of the global Sentinel-1 SAR vignettes for ocean surface process studies. Remote Sens. Environ. 2019, 234, 111457. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Wang, C.; Jiang, Z.; Kong, X. Deep Learning-Based Wind Speed Retrieval from Sentinel-1 SAR Wave Mode Data. J. Mar. Sci. Eng. 2025, 13, 1751. https://doi.org/10.3390/jmse13091751
Sun R, Wang C, Jiang Z, Kong X. Deep Learning-Based Wind Speed Retrieval from Sentinel-1 SAR Wave Mode Data. Journal of Marine Science and Engineering. 2025; 13(9):1751. https://doi.org/10.3390/jmse13091751
Chicago/Turabian StyleSun, Ruixuan, Chen Wang, Zhuhui Jiang, and Xiaojuan Kong. 2025. "Deep Learning-Based Wind Speed Retrieval from Sentinel-1 SAR Wave Mode Data" Journal of Marine Science and Engineering 13, no. 9: 1751. https://doi.org/10.3390/jmse13091751
APA StyleSun, R., Wang, C., Jiang, Z., & Kong, X. (2025). Deep Learning-Based Wind Speed Retrieval from Sentinel-1 SAR Wave Mode Data. Journal of Marine Science and Engineering, 13(9), 1751. https://doi.org/10.3390/jmse13091751






