Stability Analysis of Coastal Sheet Pile Wall Considering Soil Weakening Induced by Earthquake Loading
Abstract
1. Introduction
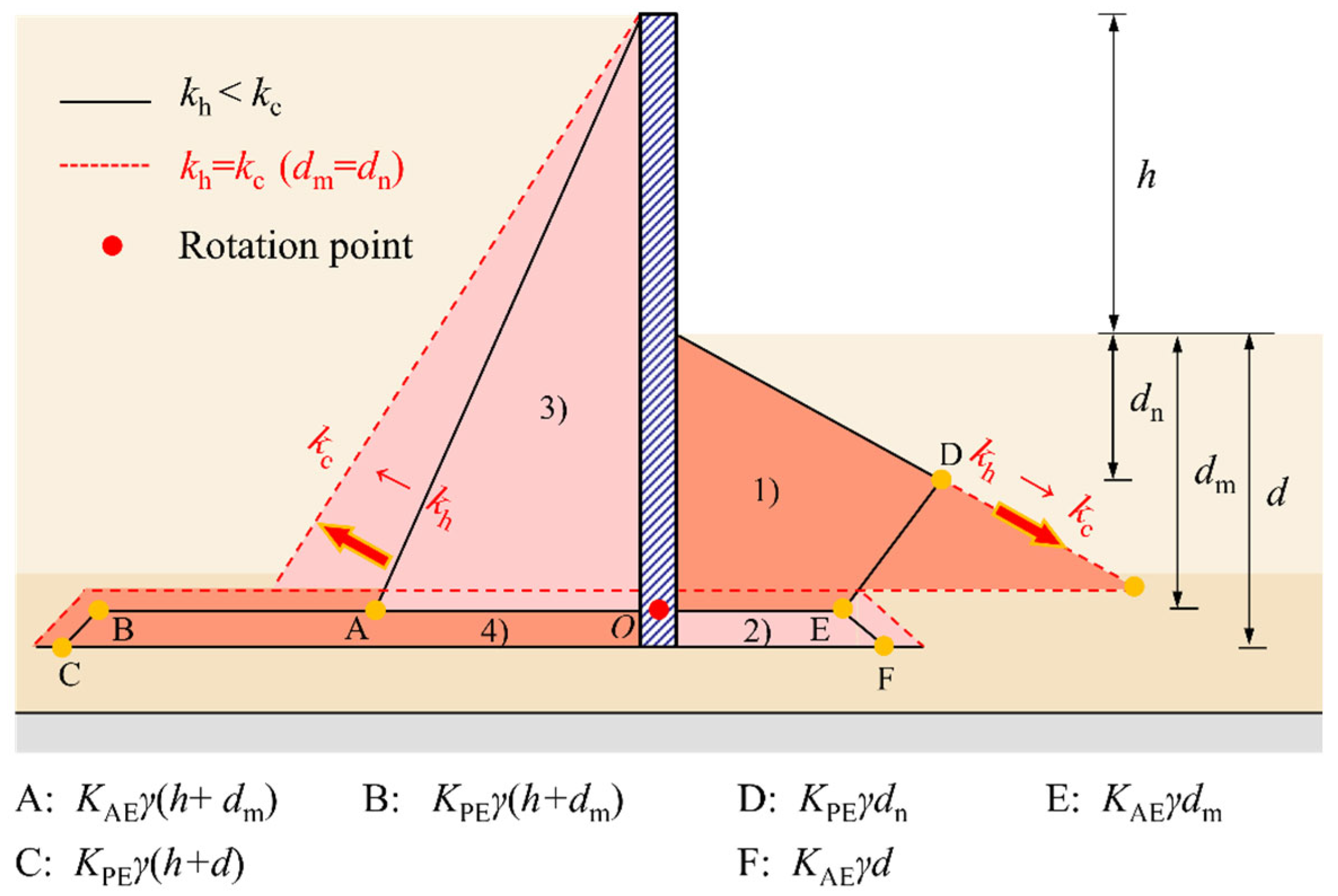
2. Calculation Method of Conti and Viggiani (Hereafter, the C–V Method)
3. Proposed Method
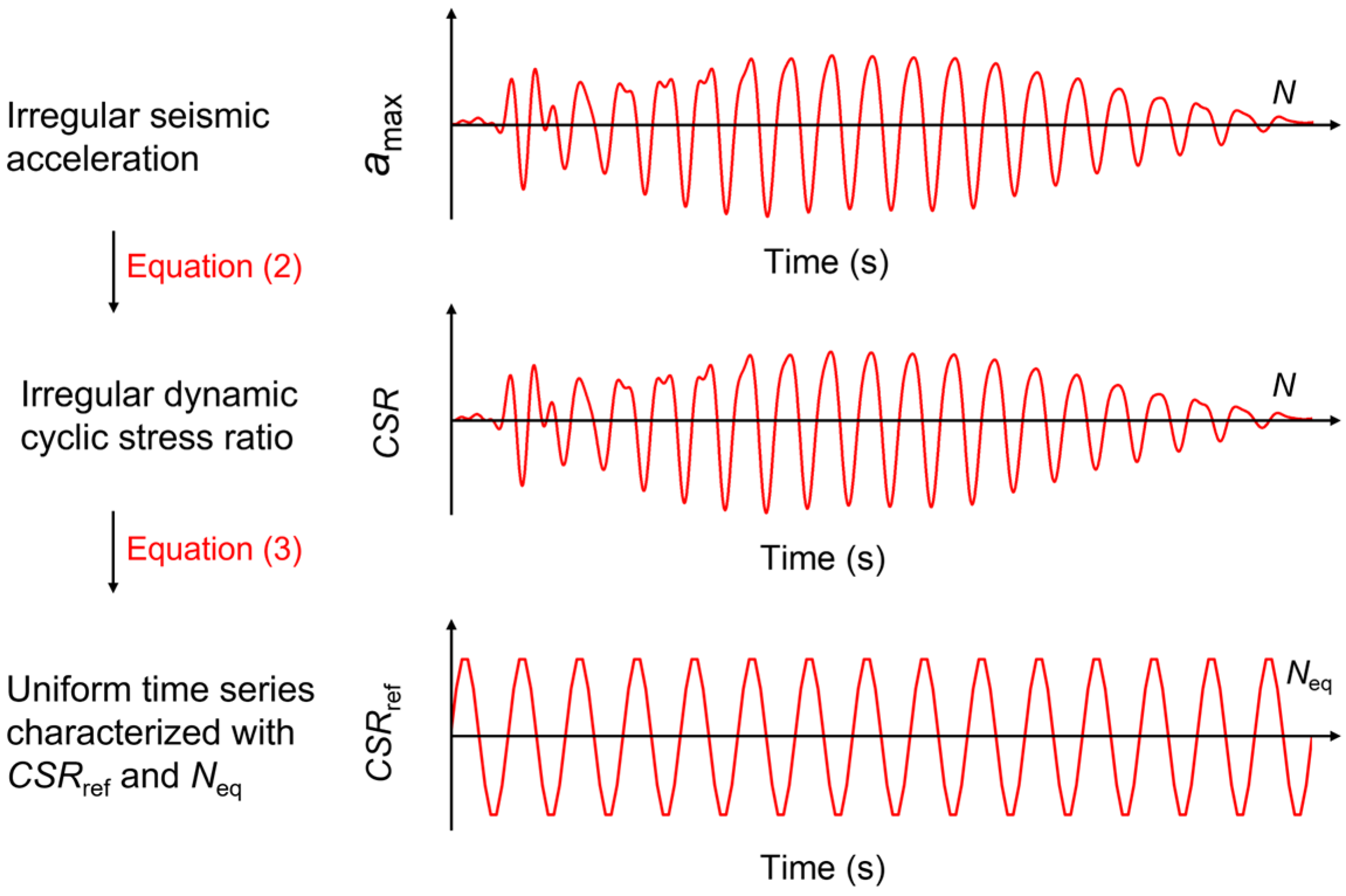
3.1. Equivalent Number of Cycles Principle
3.2. Stability Analysis of Sheet Pile Wall with Pore Pressure Generation
4. Centrifuge Model Test
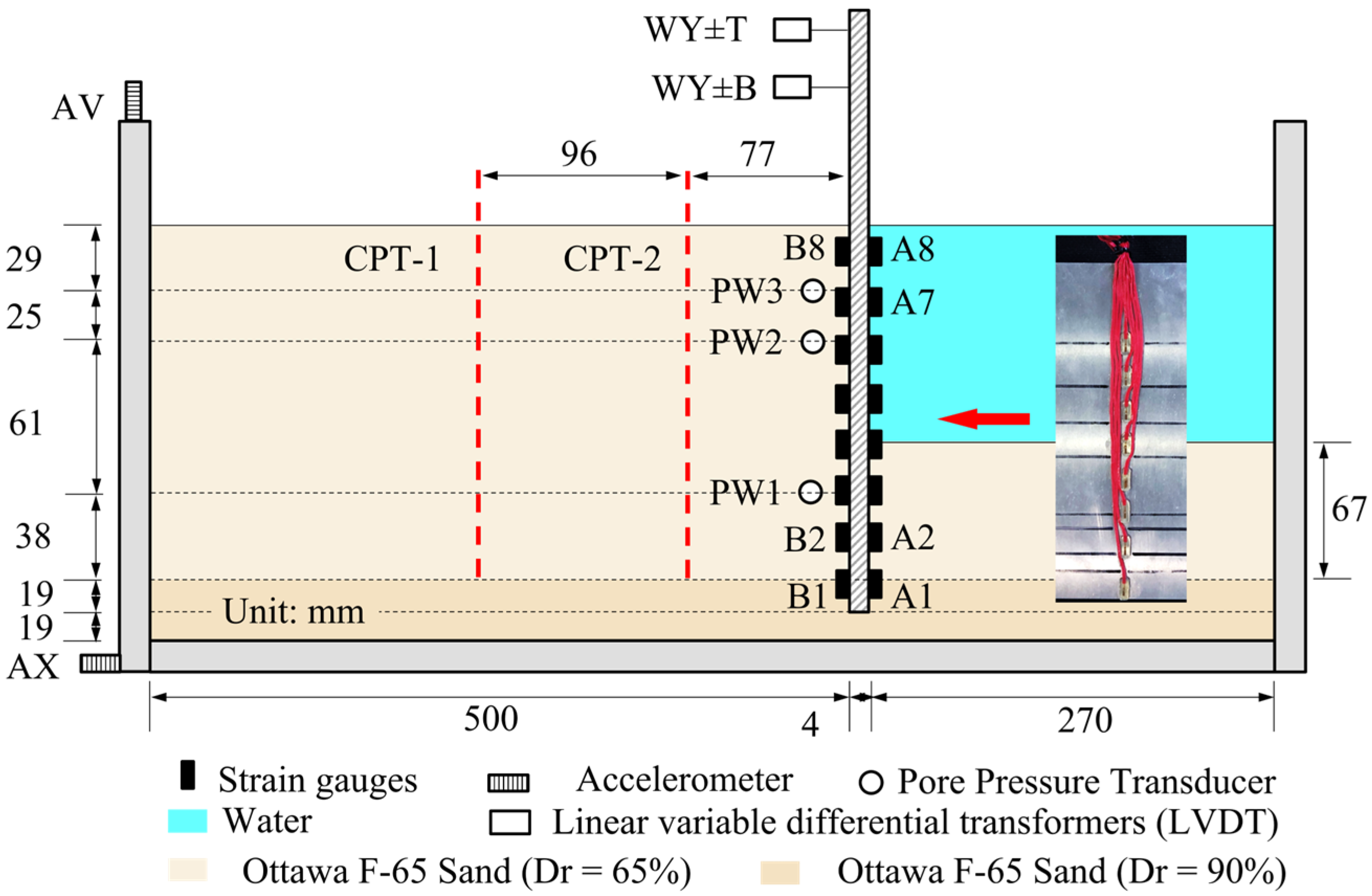
4.1. Model Design
4.2. Model Geometry and Sensors
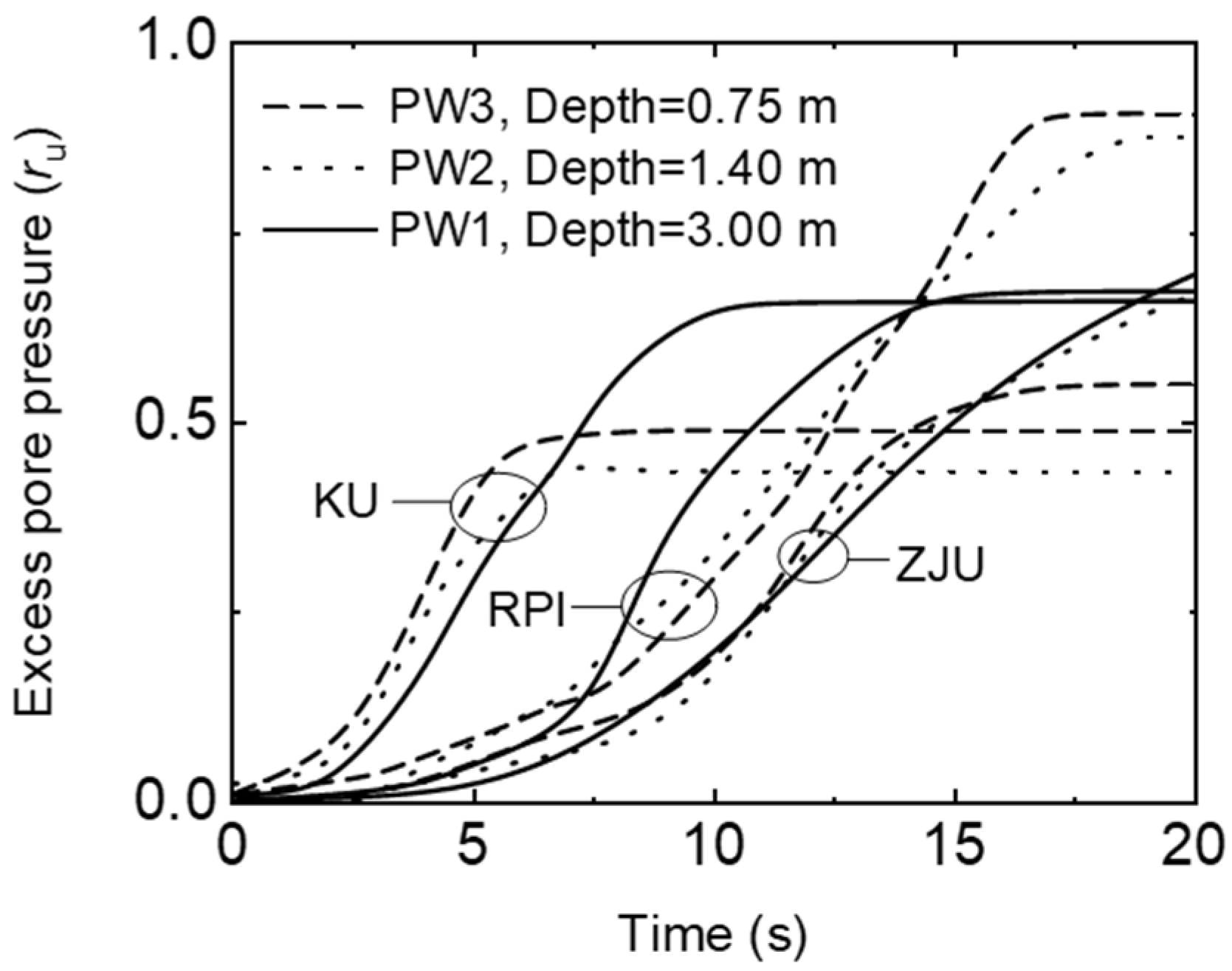
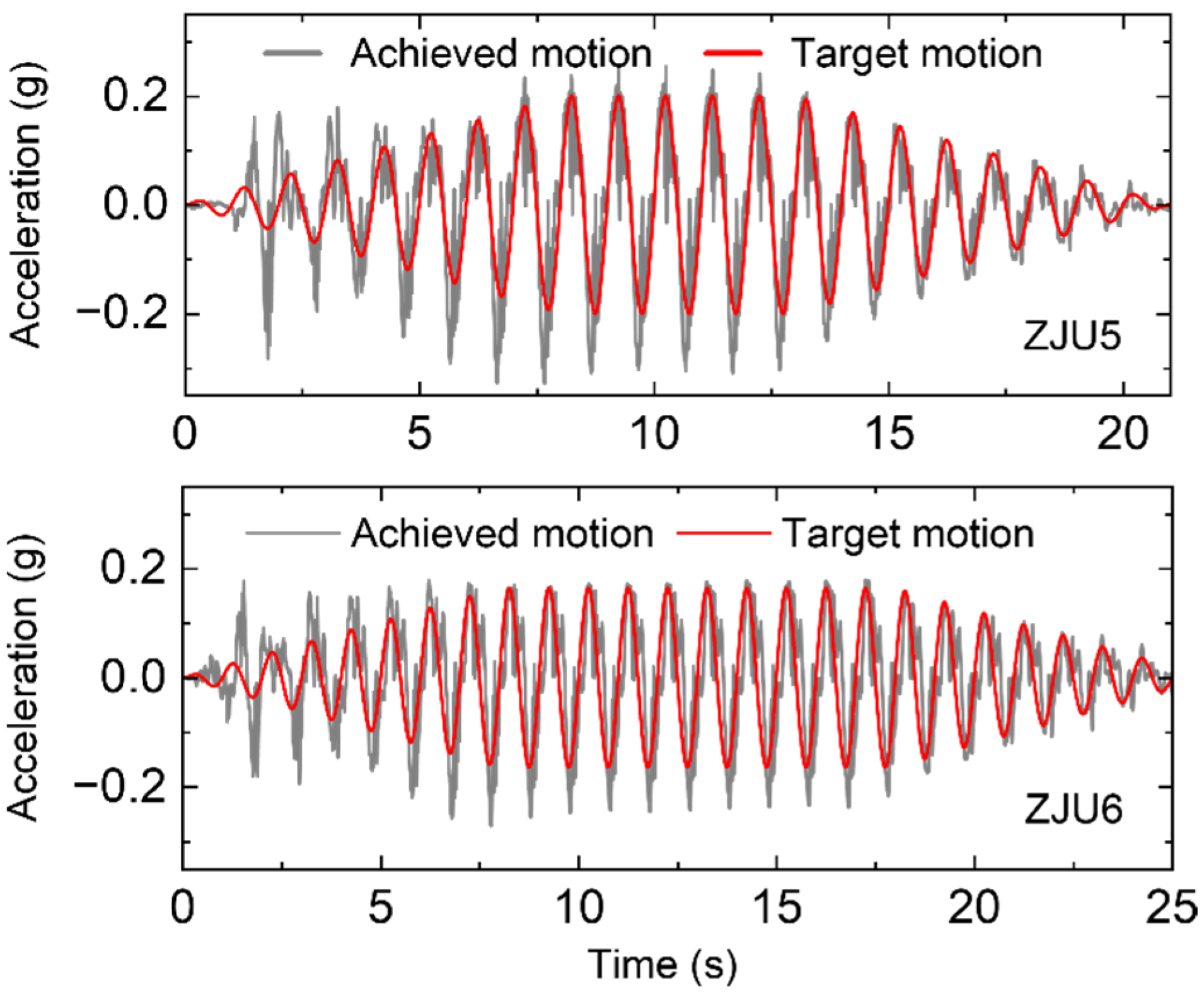
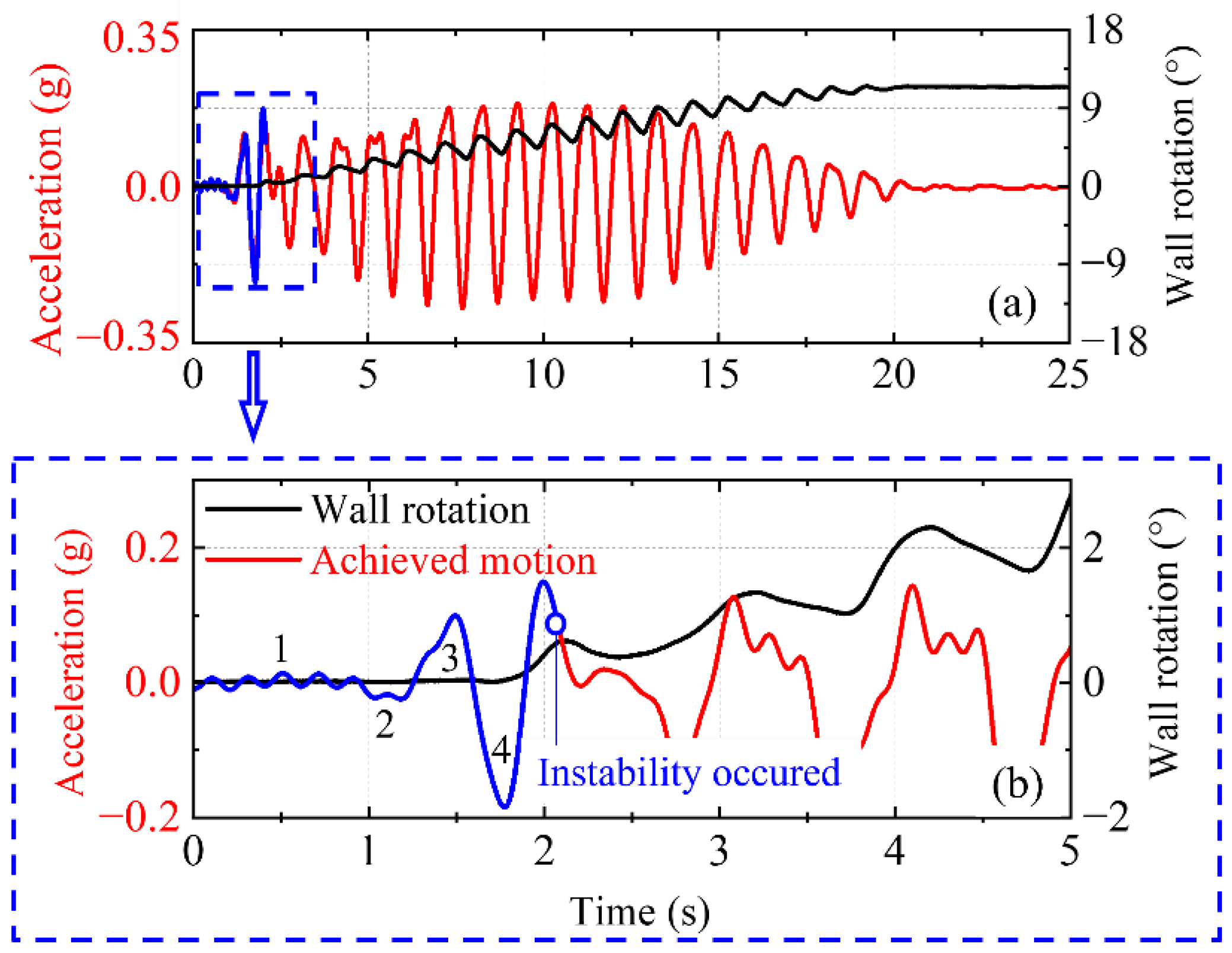
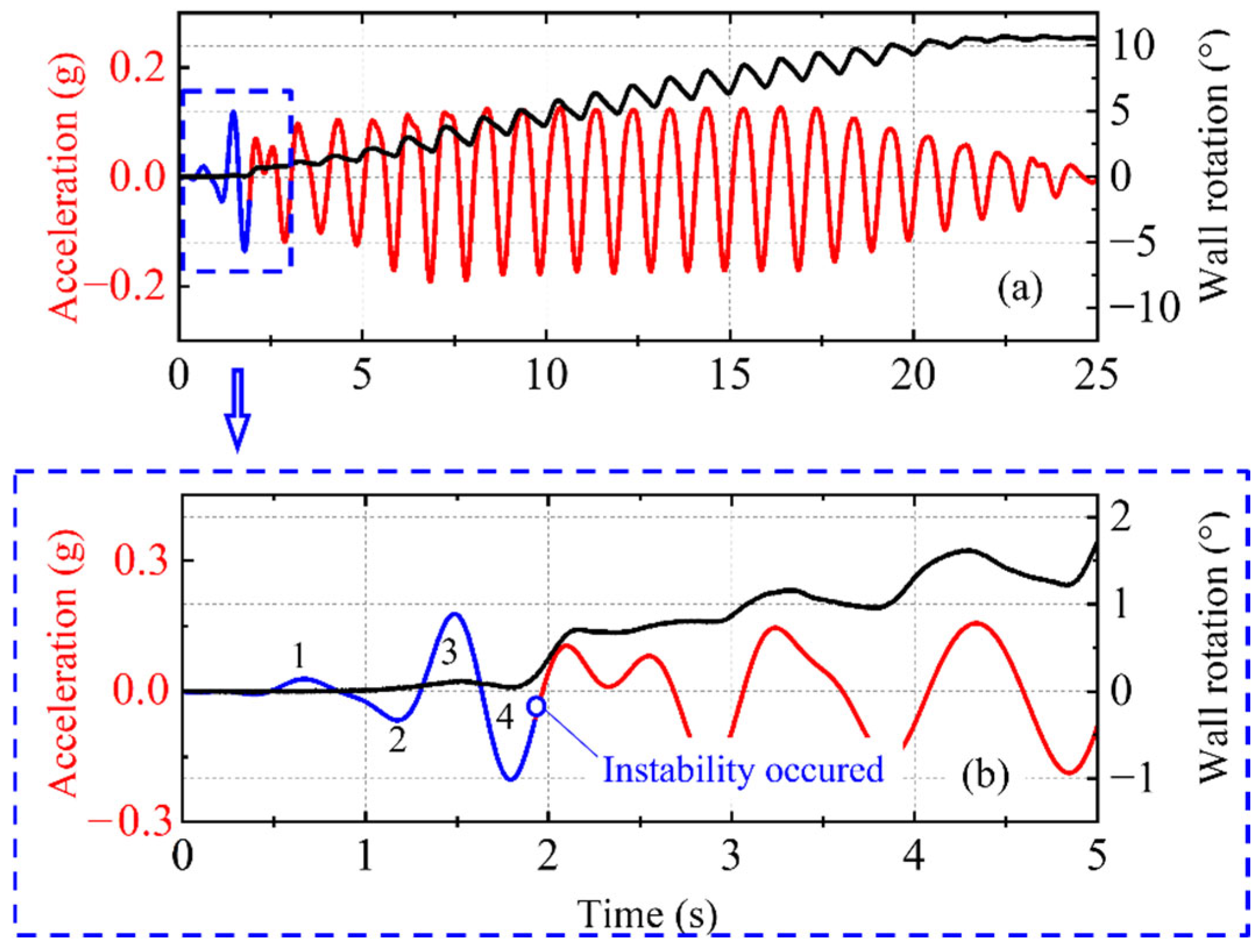
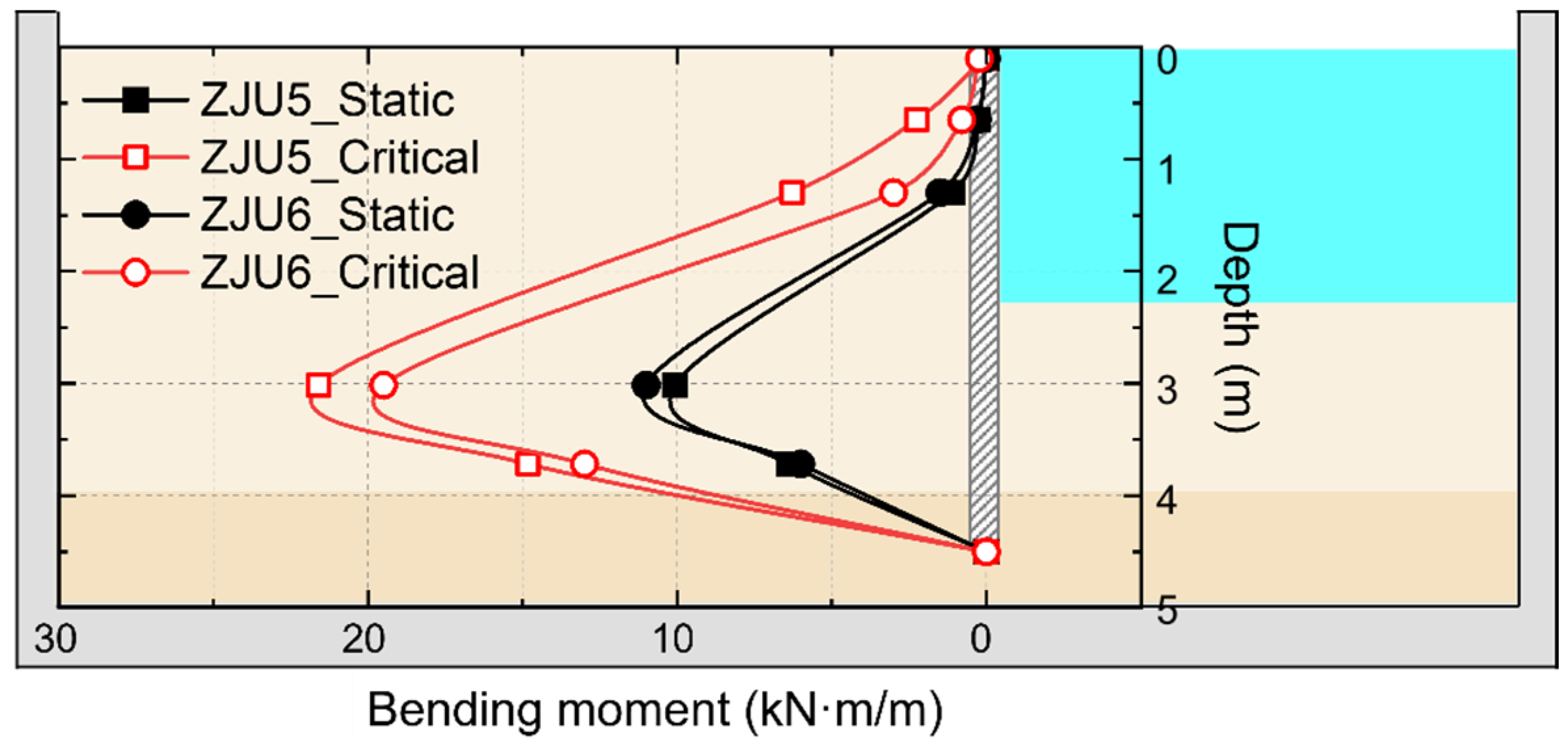
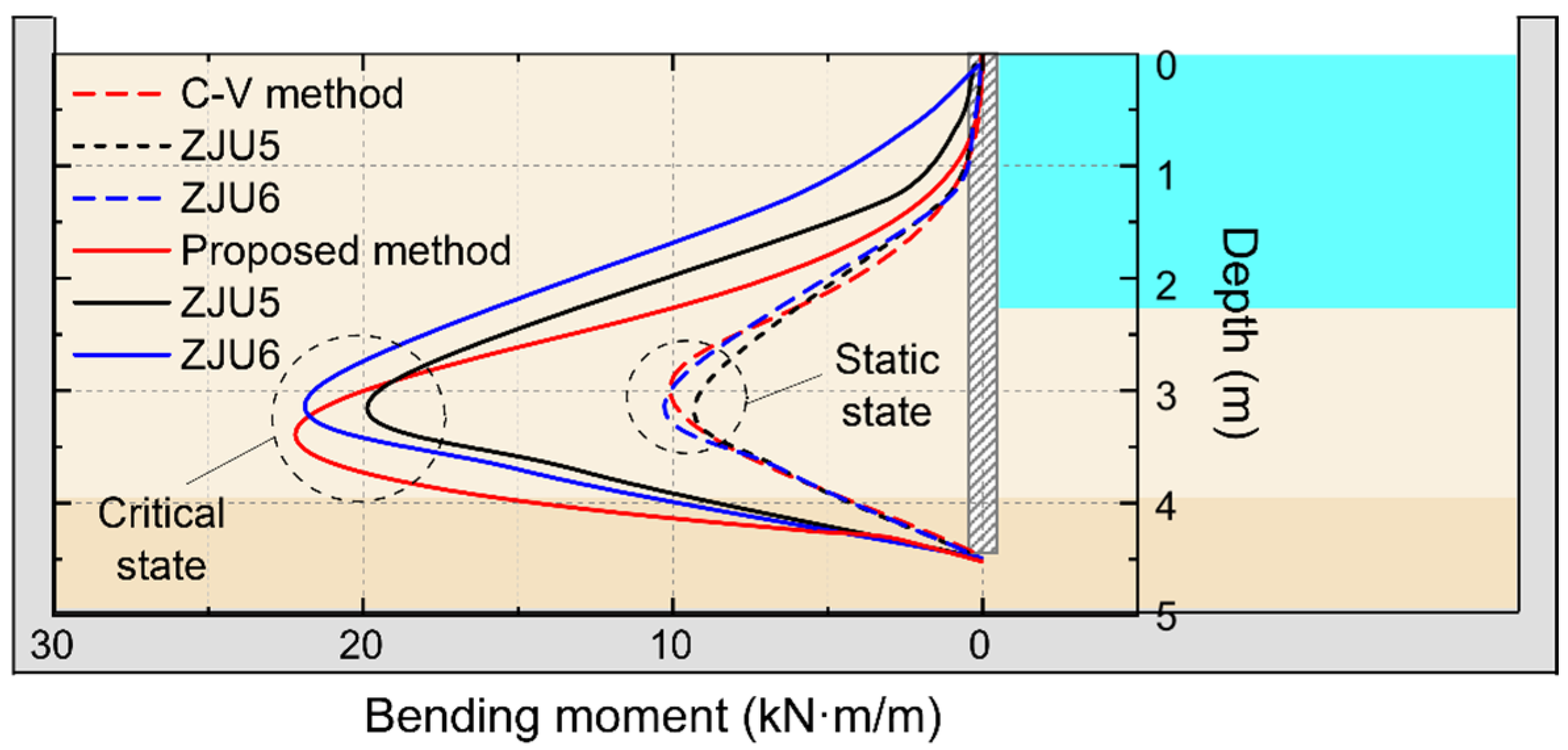
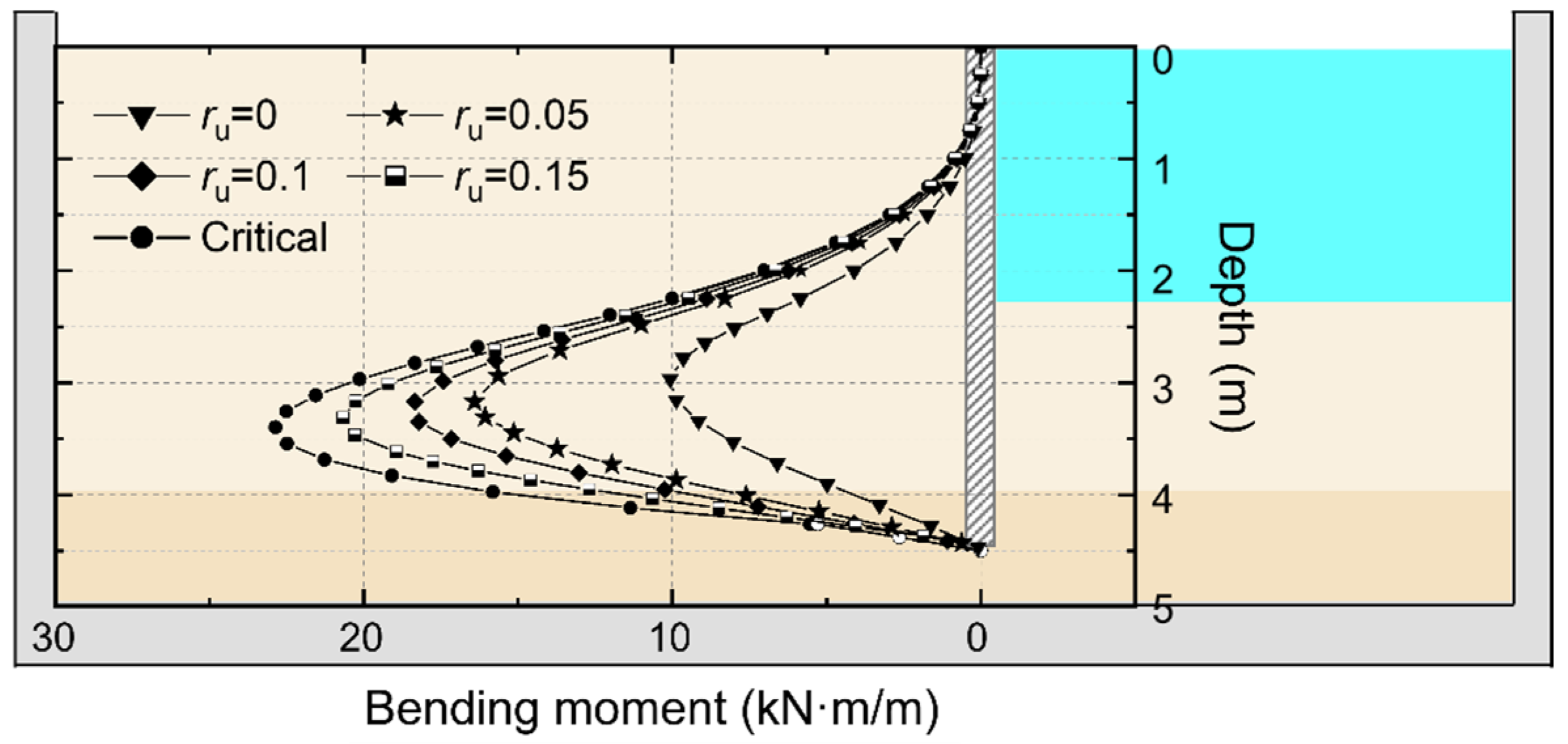
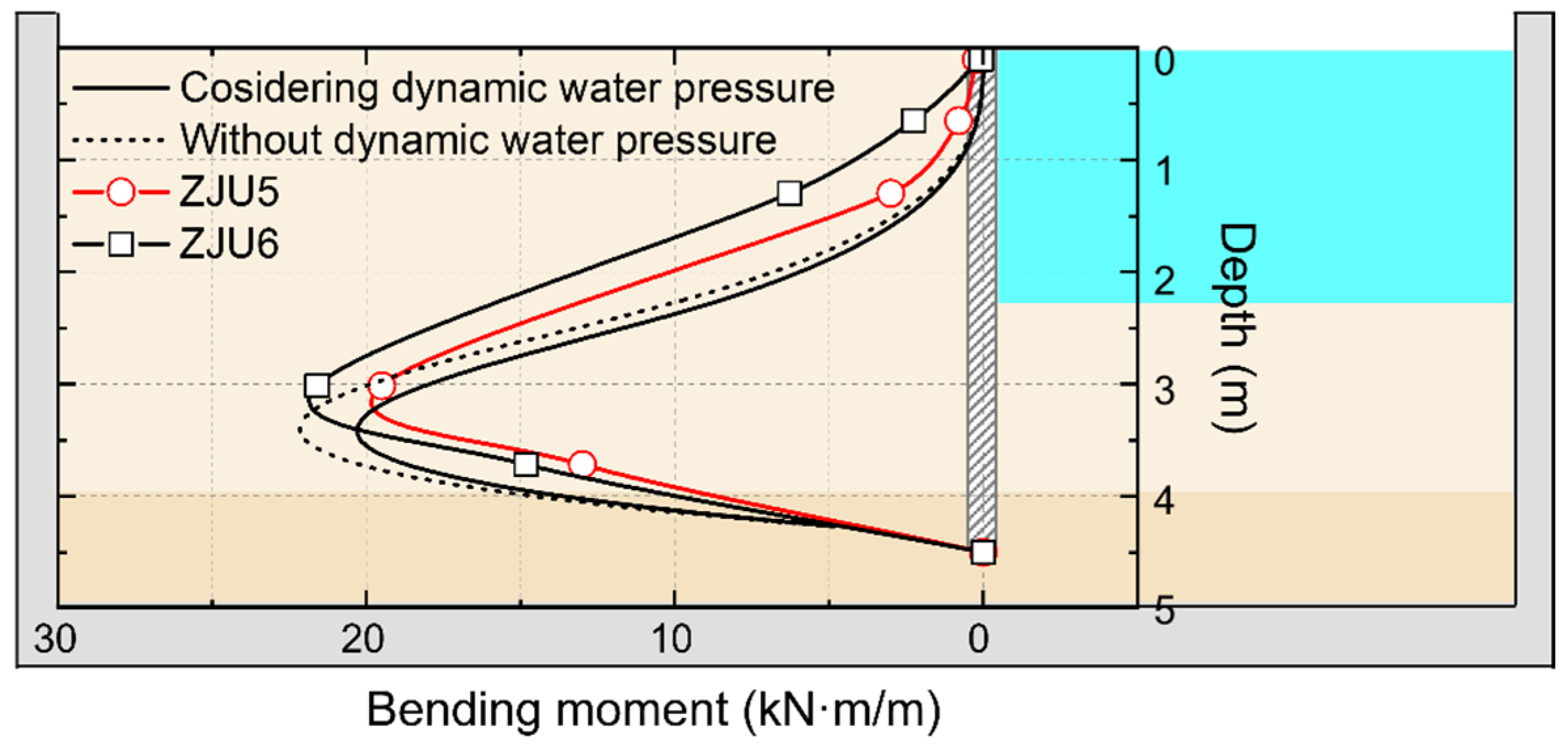
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, Z. Innovation and development of earth pressure theories for sheet-pile structures. Chin. J. Geotech. Eng. 2020, 42, 201–220. (In Chinese) [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, Y.G.; Ma, Q.; Zhou, X.H.; Chen, Y.M. Liquefaction and fluidization responses of level ground retained by sheet-pile wall through centrifuge model tests. Soil Dyn. Earthq. Eng. 2024, 178, 108517. [Google Scholar] [CrossRef]
- Soga, K. Soil Liquefaction Effects Observed in the Kobe Earthquake of 1995. Proc. Inst. Civ. Eng.-Geotech. Eng. 1998, 131, 34–51. [Google Scholar] [CrossRef]
- Inagaki, H.; Iai, S.; Sugano, T.; Yamazaki, H.; Inatomi, T. Performance of caisson type quay walls at Kobe port. Soils Found. 1996, 36, 119–136. [Google Scholar] [CrossRef]
- Allen, J.; Bradley, B.; Green, R.A.; Ashford, S.; Wotherspoon, L. Geotechnical reconnaissance of the 2010 Darfield (Canterbury) earthquake. Bull. N. Z. Soc. Earthq. Eng. 2010, 43, 243–320. [Google Scholar] [CrossRef]
- Yasuda, S.K.; Harada; Ishikawa, K.; Kanemaru, Y. Characteristics of liquefaction in Tokyo Bay area by the 2011 Great East Japan Earthquake. Soils Found. 2012, 52, 793–810. [Google Scholar] [CrossRef]
- Cubrinovski, M. Liquefaction-Induced Damage in the 2010–2011 Christchurch (New Zealand) Earthquakes. In Proceedings of the 7th Conference of the International Conference on Case Histories in Geotechnical Engineering, Chicago, IL, USA, 29 April–4 May 2013; Available online: https://scholarsmine.mst.edu/icchge/7icchge/session12/1 (accessed on 15 July 2025).
- Henderson, D.R.K. The Performance of House Foundations in the Canterbury Earthquakes. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2013. [Google Scholar]
- Cao, Y.; Zhou, Y.G.; Ishikawa, A.; Kurimoto, K.; Chen, Y.M. Initial cyclic shear strain-based pore pressure generation model of saturated sands under cyclic stress loading. Soil Dyn. Earthq. Eng. 2025, 190, 109167. [Google Scholar] [CrossRef]
- Okabe, S. General theory on earth pressure and seismic stability of retaining wall and dam. J. Jpn. Civil Eng. Soc. 1924, 10, 1277–1323. [Google Scholar]
- Mononobe, N.; Matsuo, M. On the determination of earth pressures during earthquakes. In Proceedings of the World Engineering Congress, Tokyo, Japan, 29 October–7 November 1929. [Google Scholar]
- Steedman, R.S.; Zeng, X. The influence of phase on the calculation of pseudo-static earth pressure on retaining wall. Geotechnique 1990, 40, 103–112. [Google Scholar] [CrossRef]
- Yang, J.; Wang, R.W.; Shen, Y.; Peng, X.J. Analytical solution of seismic passive earth pressure for negative friction angle of wall-soil interface. Chin. J. Geotech. Eng. 2011, 33, 785–791. (In Chinese) [Google Scholar]
- Conti, R.; Viggiani, G.M. A new limit equilibrium method for the pseudo-static design of embedded cantilevered retaining walls. Soil Dyn. Earthq. Eng. 2013, 50, 143–150. [Google Scholar] [CrossRef]
- Singh, A.P.; Chatterjee, K. The influence of strip load on the seismic design of cantilever sheet pile walls: A simplified analytical solution. Bull. Earthq. Eng. 2022, 20, 5301–5322. [Google Scholar] [CrossRef]
- Fusco, A.; Conti, R.; Viggiani, G.M.B.; Madabhushi, G.S.P.; Prüm, C. Centrifuge and theoretical study of the seismic response of anchored steel sheet pile walls in dry sand. Geotechnique 2023, 73, 1561–1576. [Google Scholar] [CrossRef]
- Atik, L.A.; Sitar, N. Seismic earth pressures on cantilever retaining structures. J. Geotech. Geoenviron. Eng. 2010, 136, 1324–1333. [Google Scholar] [CrossRef]
- Zheng, G.; Liu, C.; Liu, Y.; Hu, Q.; Wang, C.; Kang, G.; Liu, Y. Experimental study on horizontal bearing behaviors of different types of full-scale piles under reciprocating horizontal loads. Chin. J. Geotech. Eng. 2019, 41, 32–40. (In Chinese) [Google Scholar] [CrossRef]
- Zeng, X.; Steedman, R.S. On the behaviour of quay walls in earthquakes. Geotechnique 1933, 43, 417–431. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, F. Dynamic active earth pressure on rigid retaining walls with submerged soils. Rock Soil Mech. 2006, 27, 566–570. (In Chinese) [Google Scholar]
- Balkema. Seismic Design Guidelines for Port Structures; International Navigation Association: Brussels, Belgium, 2001. [Google Scholar]
- Iai, S. Seismic actions for designing geotechnical works-ISO23469. J. Jpn. Assoc. Earthq. Eng. 2004, 4, 483–485. [Google Scholar] [CrossRef]
- Kramer, S.L.; Stewart, J.P. Geotechnical Earthquake Engineering; CRC Press: Oxford, UK, 2024. [Google Scholar]
- Yang, X.T.; Zhou, Y.G.; Cao, Y.; Ishikawa, A.; Chen, Y.M. On the determination of cyclic shear stress for soil liquefaction triggering in centrifuge model test. Soil Dyn. Earthq. Eng. 2023, 173, 108137. [Google Scholar] [CrossRef]
- Zhou, X.H.; Zhou, Y.G.; Ma, Q.; Chen, Y.M. Shear wave velocity-based evaluation of cyclic mobility type of liquefaction and validation by centrifuge model tests in LEAP. Soil Dyn. Earthq. Eng. 2024, 183, 108787. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of liquefaction potential using field performance data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Wilkins, E.W.C. Cumulative Damage in Fatigue; Springer: Berlin/Heidelberg, Germany, 1956. [Google Scholar] [CrossRef]
- Green, R.A.; Terri, G.A. Number of equivalent cycles concept for liquefaction evaluations–Revisited. J. Geotech. Geoenviron. Eng. 2005, 131, 477–488. [Google Scholar] [CrossRef]
- Seed, H.B.; Martin, P.P.; Lysmer, J. Pore-Water Pressure Changes during Soil Liquefaction. J. Geotech. Eng. Div. 1976, 102, 323–346. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H. Study of Seismic Active Earth Pressure Acted on Gravity Wall in Backfill Sand. China J. Highway. Transp. 2009, 22, 26–33. (In Chinese) [Google Scholar]
- Zhou, Y.; Ma, Q.; Liu, K.; Cao, Y.; Chen, Y. Centrifugal shaking table tests on soil liquefaction and progress of LEAP projects. Chin. J. Geotech. Eng. 2023, 46, 54–62. (In Chinese) [Google Scholar] [CrossRef]
- Kutter, B.L.; Manzari, M.T.; Zeghal, M. Model Tests and Numerical Simulations of Liquefaction and Lateral Spreading LEAP-UCD-2017; Springer Nature: London, UK, 2020. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, S.R.; Manzari, M.T.; Cho, G.C. Seismic performance of sheet pile walls in liquefiable soil using centrifuge tests and an assessment of nonlinear effective stress analysis using PM4Sand. Soil Dyn. Earthq. Eng. 2024, 183, 108777. [Google Scholar] [CrossRef]
- Ono, K.; Okamura, M. Stability of sheet-pile wall in liquefiable soil: LEAP-2020 and LEAP-2022 centrifuge tests at Ehime University. Soil Dyn. Earthq. Eng. 2024, 182, 108743. [Google Scholar] [CrossRef]
- Korre, E.; Zeghal, M.; Abdoun, T. Liquefaction in the presence of soil-structure interaction: Centrifuge tests of a sheet-pile quay wall in LEAP-2020. Soil Dyn. Earthq. Eng. 2024, 181, 108650. [Google Scholar] [CrossRef]
- Guan, X.; Fusco, A.; Haigh, S.K.; Madabhushi, G.S.P. LEAP centrifuge tests on retaining walls at Cambridge University. Soil Dyn. Earthq. Eng. 2024, 180, 108610. [Google Scholar] [CrossRef]
- Westergaard, H.M. Water pressures on dams during earthquakes. Trans. Am. Soc. Civ. Eng. 1933, 98, 418–433. [Google Scholar] [CrossRef]




| Parameter | Model/Prototype | Parameter | Model/Prototype |
|---|---|---|---|
| Acceleration | N | Unit weight | N |
| Length | 1/N | Force | 1/N2 |
| Frequency | N | Bending moment | 1/N3 |
| Strain | 1 | Viscosity | N |
| Density | 1 | Velocity | 1 |
| Stress | 1 | Time | 1/N |
| Material | Thickness t (mm) | Density ρ (kg/m3) | Elastic Modulus E (Gpa) | Poisson Ratio |
|---|---|---|---|---|
| 6063 aluminum alloy | 4 | 2800 | 69 | 0.31 |
| Test | Location | Relative Density (%) | |||
|---|---|---|---|---|---|
| 1.5 m | 2.0 m | 2.5 m | 3.0 m | ||
| ZJU5 | CPT-1 | 58 | 60 | 62 | 64 |
| CPT-2 | 60 | 62 | 60 | 65 | |
| ZJU6 | CPT-1 | 65 | 70 | 64 | 65 |
| CPT-2 | 63 | 62 | 64 | 65 | |
| i | α | CSRi | Ni | 0.5/Ni | SUM |
|---|---|---|---|---|---|
| 1 | 0.005 | 0.00625 | 1.50 × 107 | 3.32 × 10−8 | 0 |
| 2 | −0.05 | 0.06251 | 1024.7 | 0.0005 | 0.0005 |
| 3 | 0.16 | 0.20004 | 8.0 | 0.062 | 0.063 |
| 4 | −0.18 | 0.22505 | 4.9 | 0.101 | 0.164 |
| 5 | 0.17 | 0.21255 | 6.3 | 0.080 | 0.244 |
| 6 | −0.195 | 0.24380 | 3.5 | 0.142 | 0.386 |
| 7 | 0.165 | 0.20630 | 7.1 | 0.071 | 0.457 |
| i | α | CSRi | Ni | 0.5/Ni | SUM |
|---|---|---|---|---|---|
| 1 | 0.03 | 0.03751 | 8609 | 5.81 × 10−5 | 0 |
| 2 | −0.06 | 0.07502 | 479 | 0.001 | 0.001 |
| 3 | 0.18 | 0.22505 | 4.9 | 0.101 | 0.102 |
| 4 | −0.2 | 0.25006 | 3.2 | 0.157 | 0.259 |
| 5 | 0.105 | 0.13128 | 46.6 | 0.011 | 0.270 |
| 6 | −0.09 | 0.11252 | 88.5 | 0.006 | 0.276 |
| 7 | 0.075 | 0.09377 | 189.2 | 0.003 | 0.279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, S.; Ma, Q.; Cao, Y. Stability Analysis of Coastal Sheet Pile Wall Considering Soil Weakening Induced by Earthquake Loading. J. Mar. Sci. Eng. 2025, 13, 1752. https://doi.org/10.3390/jmse13091752
Ning S, Ma Q, Cao Y. Stability Analysis of Coastal Sheet Pile Wall Considering Soil Weakening Induced by Earthquake Loading. Journal of Marine Science and Engineering. 2025; 13(9):1752. https://doi.org/10.3390/jmse13091752
Chicago/Turabian StyleNing, Shuai, Qiang Ma, and Yuan Cao. 2025. "Stability Analysis of Coastal Sheet Pile Wall Considering Soil Weakening Induced by Earthquake Loading" Journal of Marine Science and Engineering 13, no. 9: 1752. https://doi.org/10.3390/jmse13091752
APA StyleNing, S., Ma, Q., & Cao, Y. (2025). Stability Analysis of Coastal Sheet Pile Wall Considering Soil Weakening Induced by Earthquake Loading. Journal of Marine Science and Engineering, 13(9), 1752. https://doi.org/10.3390/jmse13091752





