Break-Out Resistance of Offshore Pipelines Buried in Inclined Sandy Seabed
Abstract
1. Introduction
2. Methodology
2.1. Finite Element Limit Analysis
2.2. Numerical Details
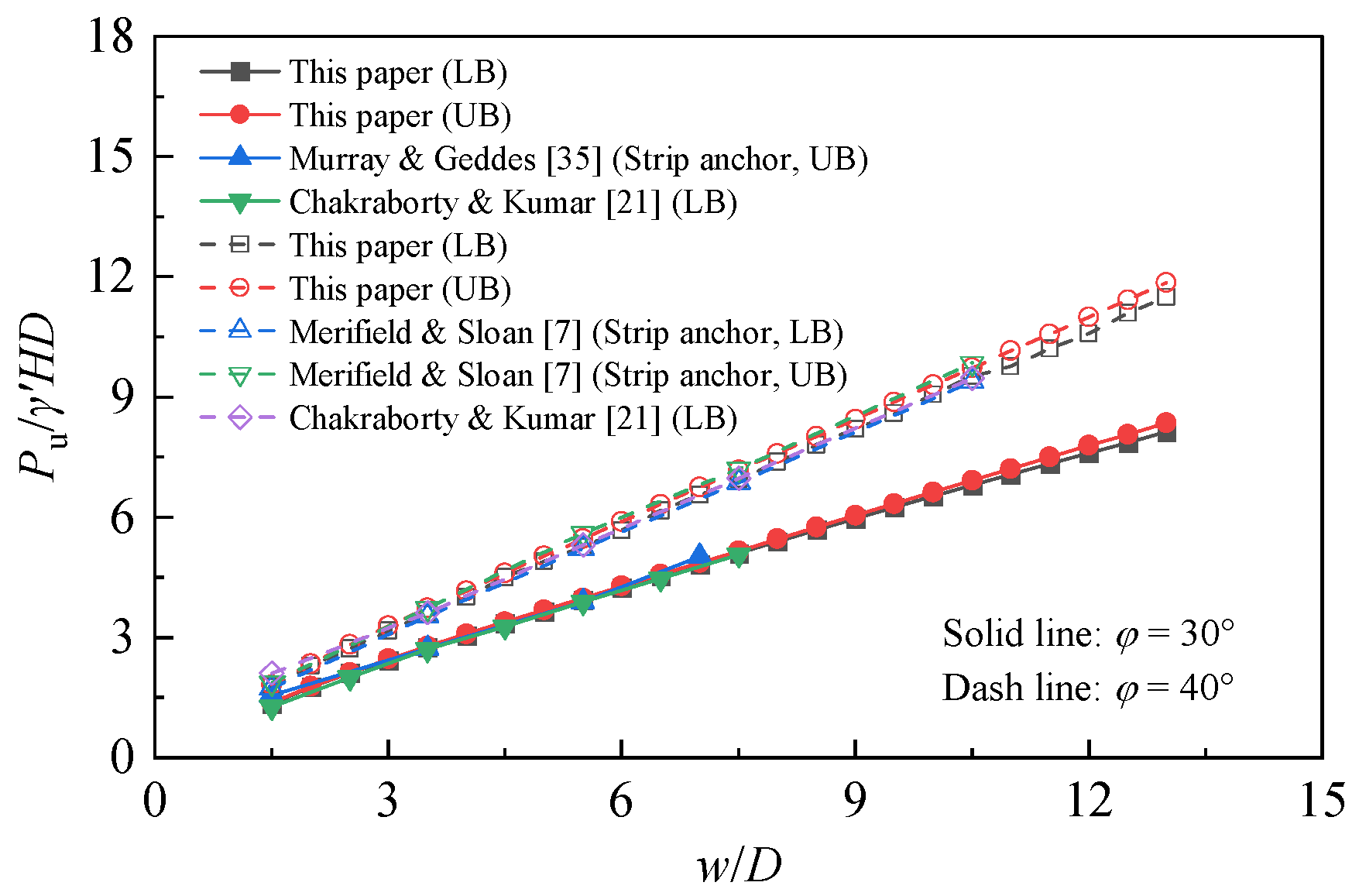
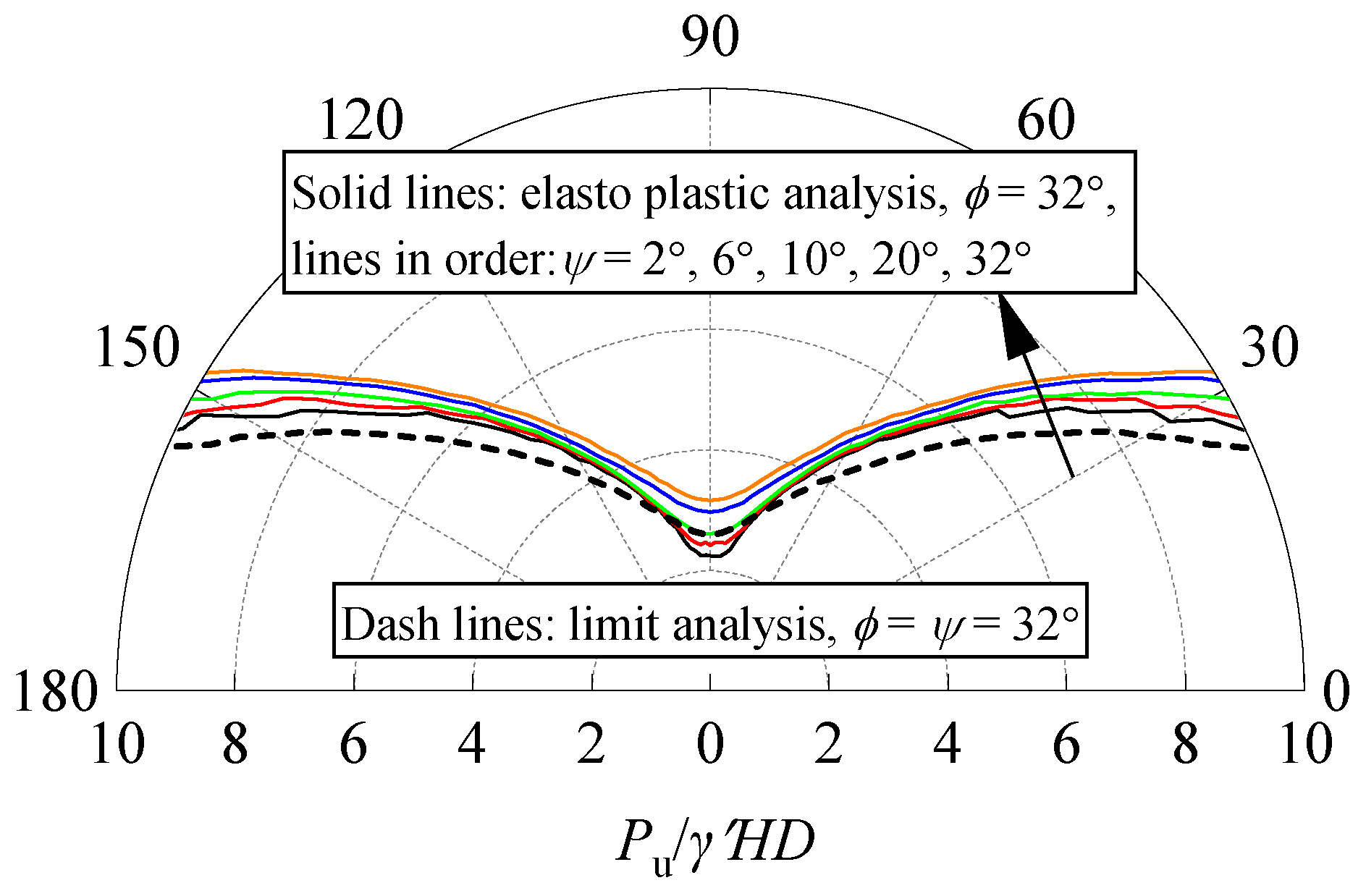
2.3. Model Verification
3. Results and Discussions
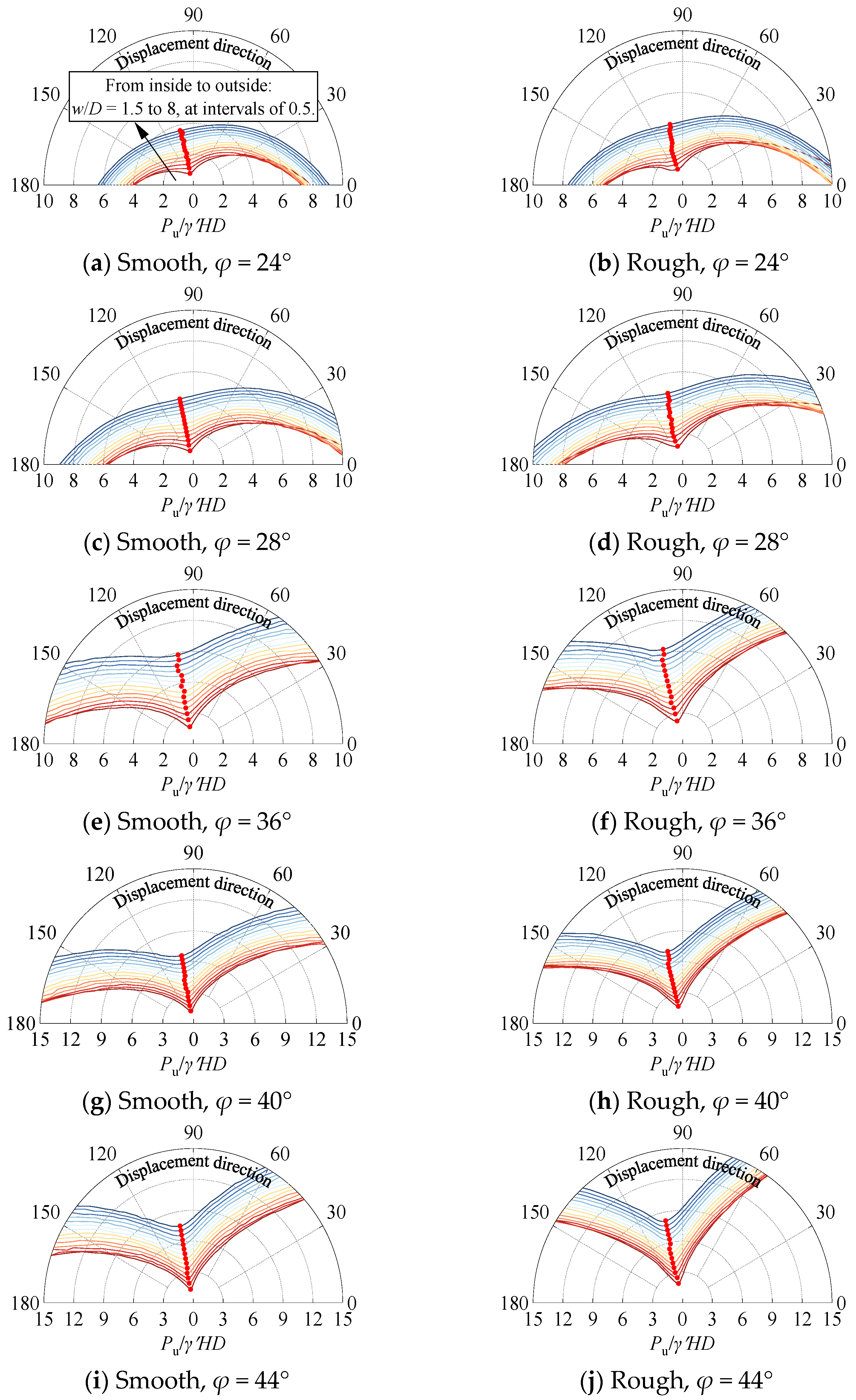
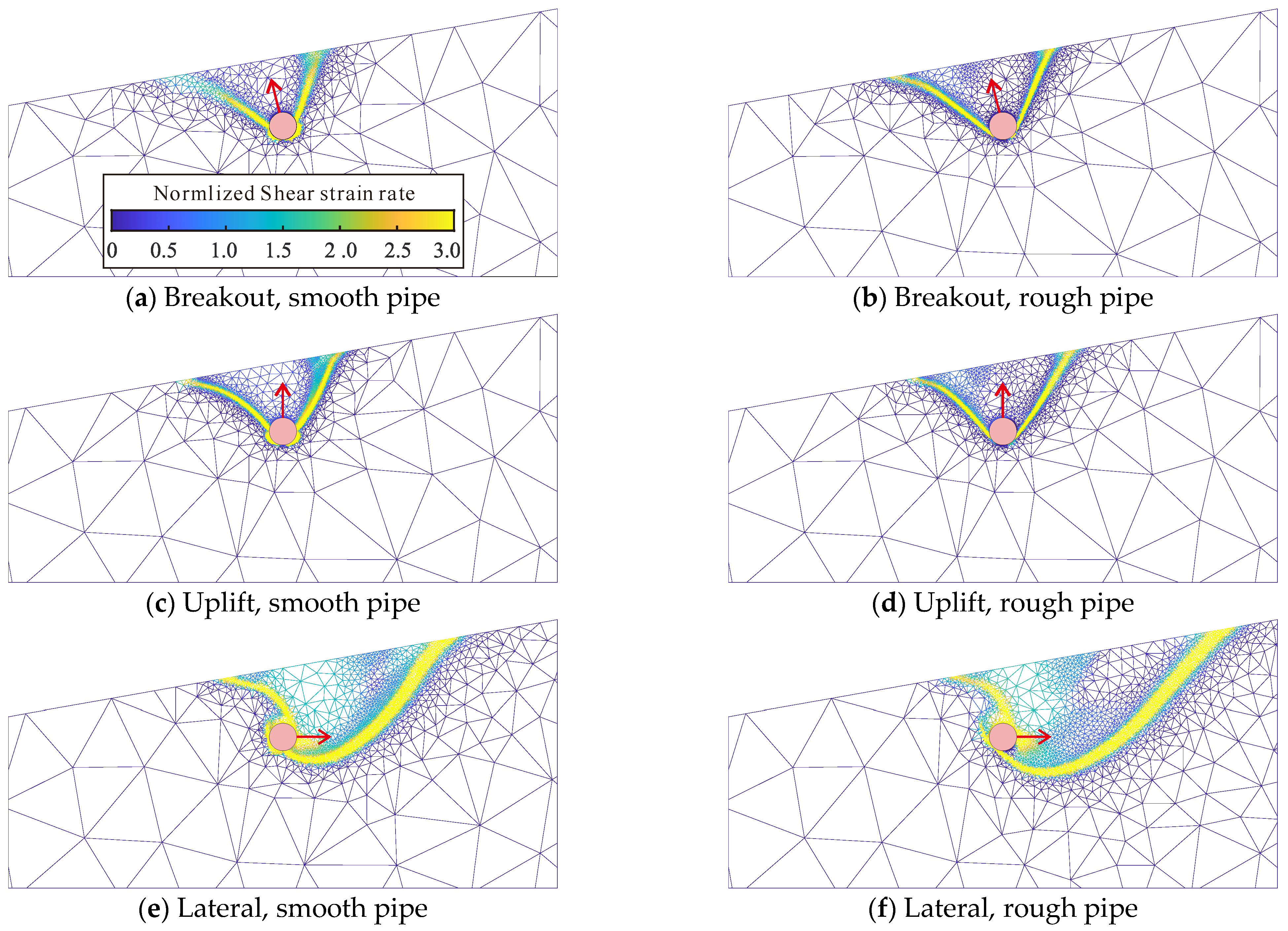
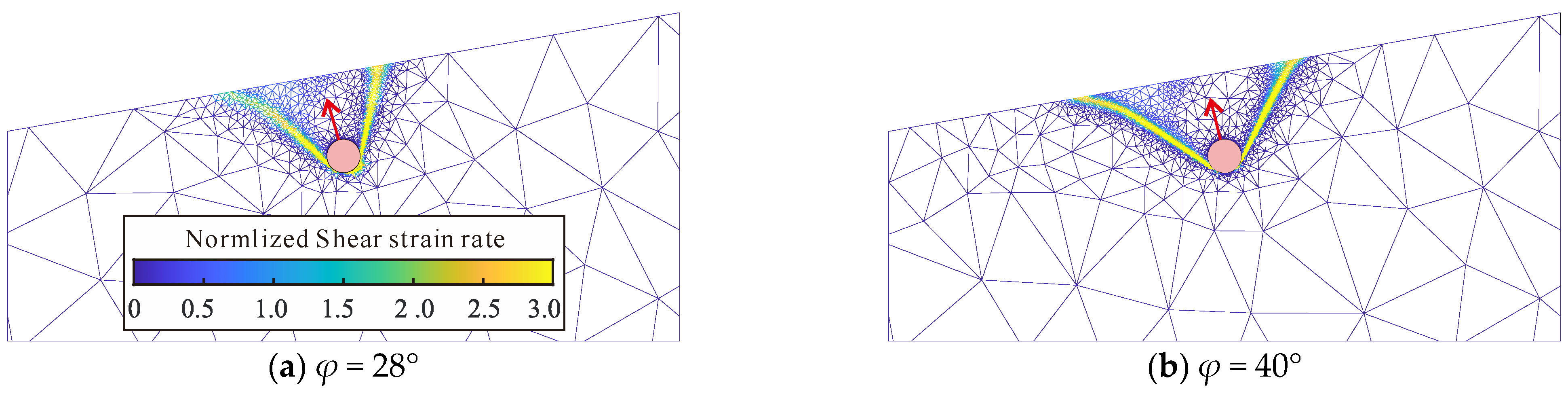
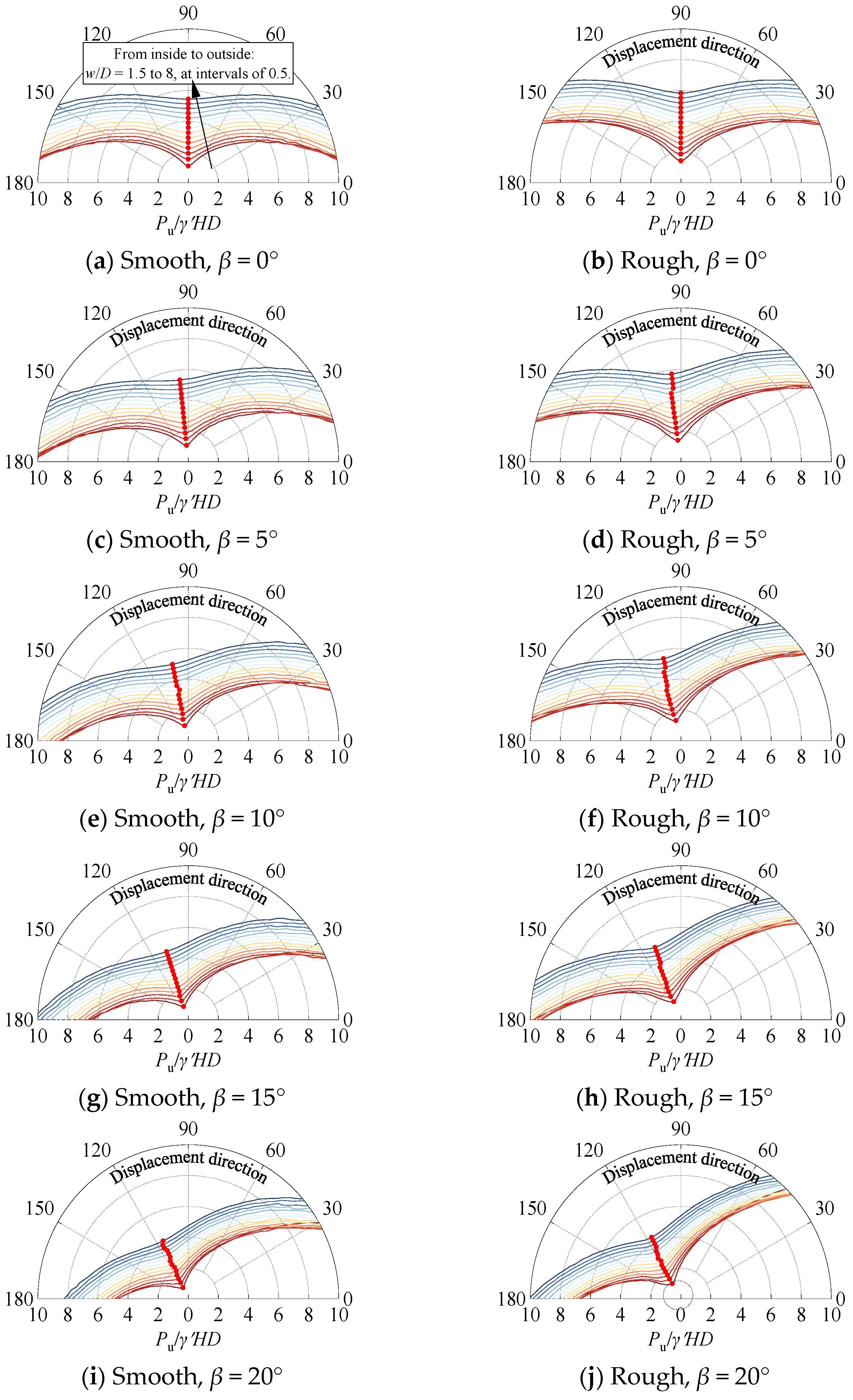
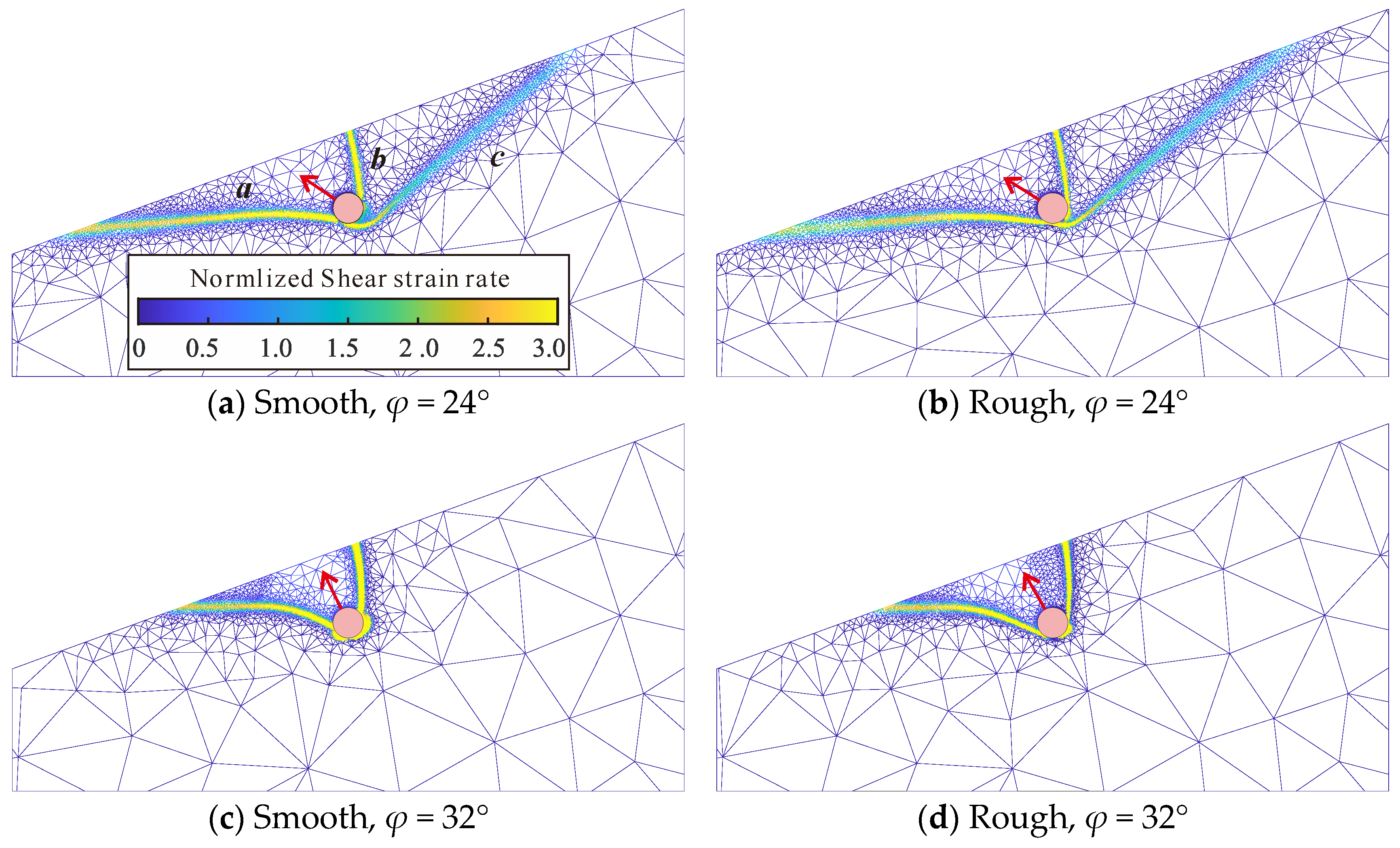
3.1. Breakout Resistances at Differing Probing Directions
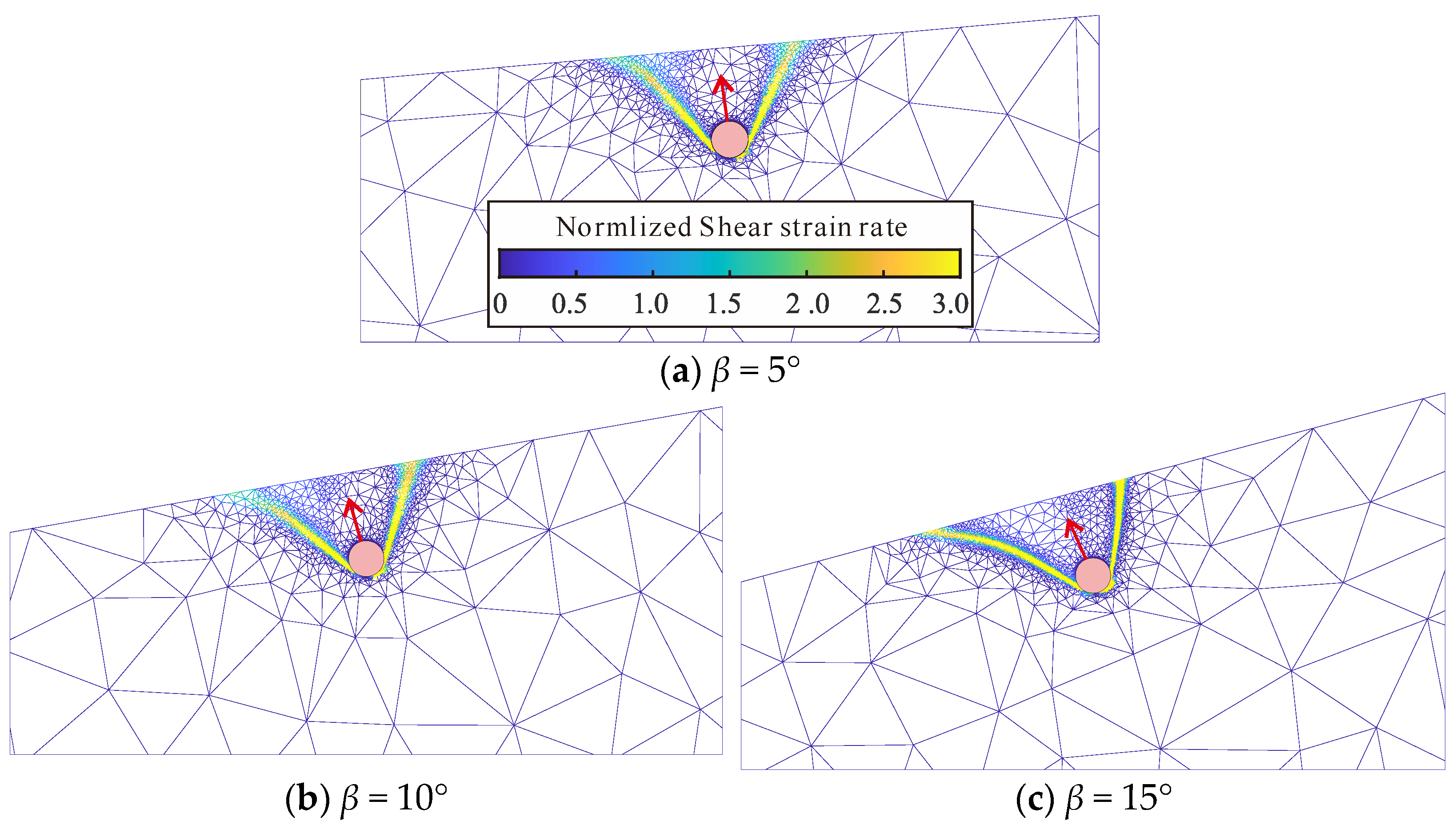
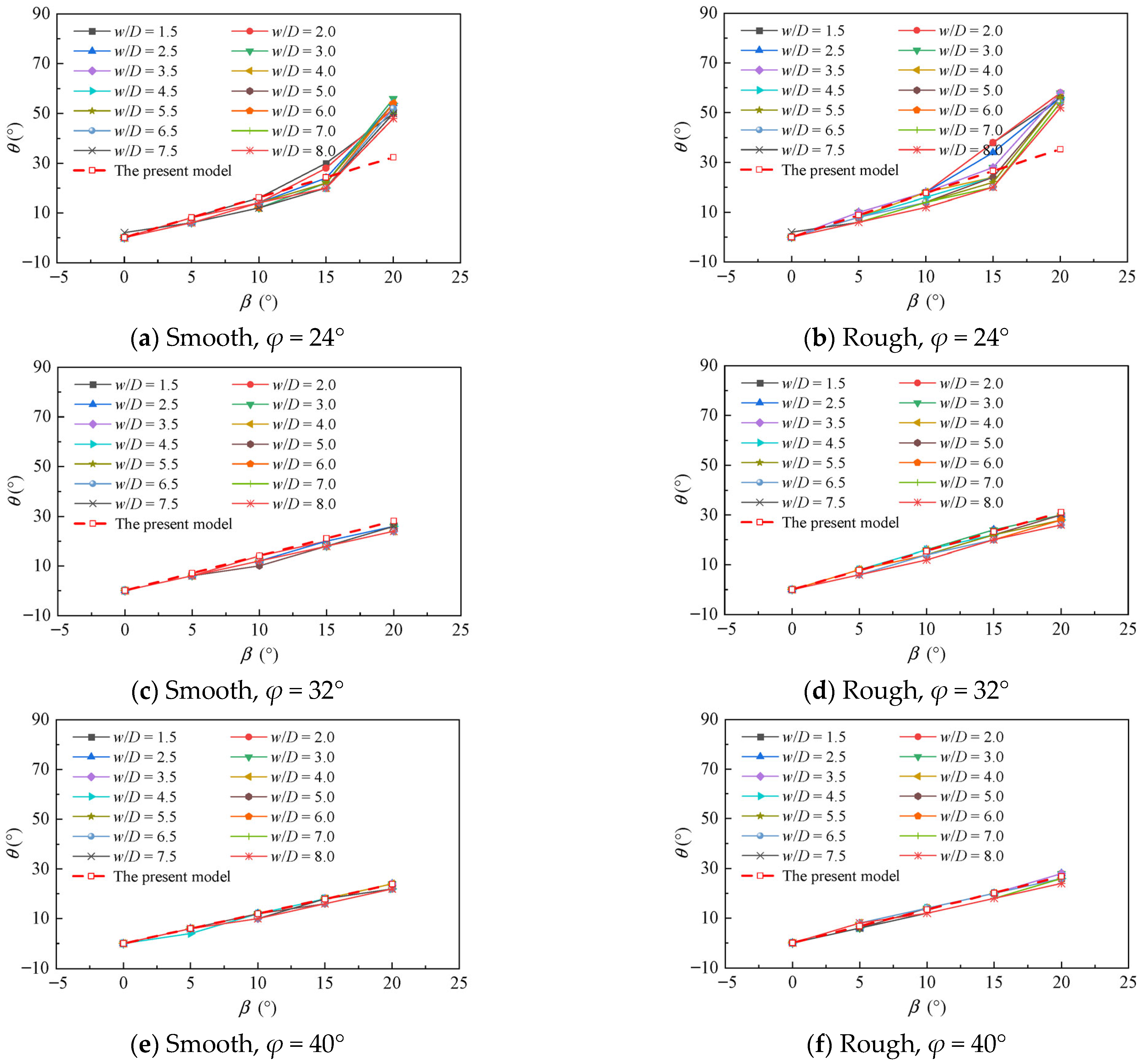
3.2. MVPs Prediction Model
3.3. Breakout Resistances Along MVPs
4. Conclusions
- (1)
- Failure mechanisms are significantly influenced by the direction of applied displacement load, resulting in considerable variations in ultimate bearing capacity. To ensure accurate calculations, the influence of loading direction must be explicitly accounted for when determining the minimum bearing capacity.
- (2)
- The seabed inclination was found to have a significant effect on the deflection of the most vulnerable plane (MVP). As the inclination approaches the seabed friction angle, the failure mechanism transitions to landslide-type failure, shifting the weakest plane to the slope toe and causing a considerable reduction in the ultimate bearing capacity. When the inclination is considerably smaller than the friction angle, the MVPs were observed to align closely with the outer normal planes of the seabed. A predictive model for the MVP under wedge-type failure mode was successfully developed in this study.
- (3)
- The inclined seabed angle (β) was observed to significantly reduce the minimal ultimate bearing capacity associated with the most vulnerable plane. For shallow burial depths, β increases the uplift bearing capacity, which does not accurately reflect the minimum bearing capacity. Consequently, relying on uplift resistance as the minimum ultimate bearing capacity poses significant safety risks.
- (4)
- The ultimate bearing capacity calculated by DNV [19] is frequently overestimated, even for low estimates, particularly in cases of shallow burial depth. To mitigate this discrepancy, a reduction factor model based on the best estimates from DNV [19] was proposed in this study to improve accuracy and safety.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | model coefficient |
| B | model coefficient |
| D | pipe diameter, m |
| Fuplift | uplift resistance |
| FBE | best estimate uplift resistance of DNV code |
| F | uplift resistance factor |
| fLE | low estimate uplift resistance factor |
| fBE | best estimate uplift resistance factor |
| fHE | high estimate uplift resistance factor |
| H | vertical distance from pipeline center to the seabed surface, m |
| Pu | ultimate breakout resistance |
| Pu,b | ultimate breakout resistance |
| Pu,u | ultimate uplift resistance |
| Pu,l | ultimate lateral resistance |
| W | vertical distance from pipeline bottom to the seabed surface, m |
| H | horizontal load |
| V | vertical load |
| Β | inclined angle of seabed, in degrees |
| γ′ | submerged unit weight, kN/m3 |
| θ | angle between the most vulnerable plane and the upright plane |
| Φ | friction angle of seabed, in degrees |
| Ψ | dilation angle of sand, in degrees |
References
- Trautmann, C.H.; O’Rourfce, T.D.; Kulhawy, F.H. Uplift Force-Displacement Response of Buried Pipe. J. Geotech. Eng. 1985, 111, 1061–1076. [Google Scholar] [CrossRef]
- White, D.J.; Barefoot, A.J.; Bolton, M.D. Centrifuge modelling of upheaval buckling in sand. Int. J. Phys. Model. Geotech. 2001, 1, 19–28. [Google Scholar] [CrossRef]
- White, D.J.; Cheuk, C.Y.; Bolton, M.D. The uplift resistance of pipes and plate anchors buried in sand. Géotechnique 2008, 58, 771–779. [Google Scholar] [CrossRef]
- Rowe, R.K.; Davis, E.H. The behaviour of anchor plates in sand. Géotechnique 1982, 32, 25–41. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Drescher, A.; Detournay, E. Limit load in translational failure mechanisms for associative and non-associative materials. Géotechnique 1993, 43, 443–456. [Google Scholar] [CrossRef]
- Merifield, R.S.; Sloan, S.W. The ultimate pullout capacity of anchors in frictional soils. Can. Geotech. J. 2006, 43, 852–868. [Google Scholar] [CrossRef]
- Zhuang, P.-Z.; Yue, H.-Y.; Song, X.-G.; Yang, H.; Yu, H.-S. Uplift Behavior of Pipes and Strip Plate Anchors in Sand. J. Geotech. Geoenviron. Eng. 2021, 147, 04021126. [Google Scholar] [CrossRef]
- Ansari, Y.; Kouretzis, G.; Sloan, S.W. Development of a prototype for modelling soil–pipe interaction and its application for predicting uplift resistance to buried pipe movements in sand. Can. Geotech. J. 2018, 55, 1451–1474. [Google Scholar] [CrossRef]
- Roy, K.; Hawlader, B.; Kenny, S.; Moore, I. Finite element modeling of lateral pipeline–soil interactions in dense sand. Can. Geotech. J. 2016, 53, 490–504. [Google Scholar] [CrossRef]
- Wu, J.; Kouretzis, G.; Suwal, L.; Ansari, Y.; Sloan, S.W. Shallow and deep failure mechanisms during uplift and lateral dragging of buried pipes in sand. Can. Geotech. J. 2020, 57, 10. [Google Scholar] [CrossRef]
- Mukherjee, S.; Sivakumar Babu, G.L. The Behavior of Horizontal Anchor Foundations Embedded in Sand under Uplift and Lateral Loads. Int. J. Geomech. 2024, 24, 06024007. [Google Scholar] [CrossRef]
- Yang, H.; Wang, L.; Lei, Z.; Rui, S.; Liu, Z.; Guo, Z. Numerical study of lateral soil resistance to pipe movement in sandy slopes. Appl. Ocean Res. 2025, 155, 104419. [Google Scholar] [CrossRef]
- Coleman, J.M.; Bouma, A.H.; Prior, D.B.; Roberts, H.H. Nearsurface Geology of the Gulf of Mexico Continental Slope. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1 May 1989. [Google Scholar] [CrossRef]
- Costello, M.J.; Cheung, A.; De Hauwere, N. Surface Area and the Seabed Area, Volume, Depth, Slope, and Topographic Variation for the World’s Seas, Oceans, and Countries. Environ. Sci. Technol. 2010, 44, 8821–8828. [Google Scholar] [CrossRef]
- Gao, F.-P.; Han, X.-T.; Cao, J.; Sha, Y.; Cui, J.-S. Submarine pipeline lateral instability on a sloping sandy seabed. Ocean Eng. 2012, 50, 44–52. [Google Scholar] [CrossRef]
- Kumar, J. Upper bound solution for pullout capacity of anchors on sandy slopes. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 477–484. [Google Scholar] [CrossRef]
- Bazán-Zurita, E.; Williams, D.M.; Bledsoe, J.K.; Pugh, A.D.; Newman, F.B. AEP 765 kV transmission line: Uplift capacity of shallow foundations on sloping ground. In Electrical Transmission Line and Substation Structures: Structural Reliability in a Changing World; Amer Society of Civil Engineers: Reston, VA, USA, 2006; pp. 215–226. [Google Scholar]
- DNVGL-RP-F114; Pipe-Soil Interaction for Submarine Pipelines. DNV: Oslo, Norway, 2017.
- Martin, C.M.; White, D.J. Limit analysis of the undrained bearing capacity of offshore pipelines. Géotechnique 2012, 62, 847–863. [Google Scholar] [CrossRef]
- Chakraborty, D.; Kumar, J. Vertical Uplift Resistance of Pipes Buried in Sand. J. Pipeline Syst. Eng. Pract. 2014, 5, 04013009. [Google Scholar] [CrossRef]
- Kong, D.; Feng, L.; Zhu, B. Assessment model of pipe–soil interaction during large-amplitude lateral displacements for deep-water pipelines. Comput. Geotech. 2020, 117, 103220. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Lyamin, A.V.; Sloan, S.W. Formulation and solution of some plasticity problems as conic programs. Int. J. Solids Struct. 2007, 44, 1533–1549. [Google Scholar] [CrossRef]
- Makrodimopoulos, A.; Martin, C.M. Lower bound limit analysis of cohesive-frictional materials using second-order cone programming. Int. J. Numer. Methods Eng. 2006, 66, 604–634. [Google Scholar] [CrossRef]
- Makrodimopoulos, A.; Martin, C.M. Upper bound limit analysis using simplex strain elements and second-order cone programming. Int. J. Numer. Anal. Methods Geomech. 2007, 31, 835–865. [Google Scholar] [CrossRef]
- Chakraborty, D.; Kumar, J. Uplift Resistance of Interfering Pipelines Buried in Sand. J. Pipeline Syst. Eng. Pract. 2016, 7, 06015002. [Google Scholar] [CrossRef]
- Kouretzis, G.P.; Krabbenhøft, K.; Daichao, S.; Scott, W. Sloan. Soil-buried pipeline interaction for vertical downwards relative offset. Can. Geotech. J. 2014, 51, 1087–1094. [Google Scholar] [CrossRef]
- Tom, J.G.; White, D.J. Drained Bearing Capacity of Shallowly Embedded Pipelines. J. Geotech. Geoenviron. Eng. 2019, 145, 04019097. [Google Scholar] [CrossRef]
- Davis, E.H. Theories of Plasticity and Failure of Soil Masses. In Soil Mechanics: Selected Topics; Lee, I.K., Ed.; Elsevier: New York, NY, USA, 1968; pp. 341–354. [Google Scholar]
- Wang, B.; Yuan, M.; Yan, Y.; Yang, K.; Zhang, H.; Liang, Y. Optimal design of an oil pipeline with a large-slope section. Eng. Optim. 2019, 51, 1480–1494. [Google Scholar] [CrossRef]
- Zhang, W.; Askarinejad, A. Behaviour of buried pipes in unstable sandy slopes. Landslides 2019, 16, 283–293. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Puzrin, A.M. The bearing capacity of a strip footing on clay under combined loading. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 893–916. [Google Scholar] [CrossRef]
- Merifield, R.; White, D.J.; Randolph, M.F. The ultimate undrained resistance of partially embedded pipelines. Géotechnique 2008, 58, 461–470. [Google Scholar] [CrossRef]
- Cheuk, C.Y.; White, D.J.; Bolton, M. D Uplift Mechanisms of Pipes Buried in Sand. J. Geotech. Geoenvironmental Eng. 2008, 134, 154–163. [Google Scholar] [CrossRef]
- Murray, E.J.; Geddes, J.D. Uplift of Anchor Plates in Sand. J. Geotech. Eng. 1987, 113, 202–215. [Google Scholar] [CrossRef]
- Kumar, J. Uplift response of buried pipes in sands using FEM. Indian Geotech. J. 2002, 32, 146–160. [Google Scholar]
- Dickin, E.A. Uplift Resistance of Buried Pipelines in Sand. Soils Found. 1994, 34, 41–48. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Karim, M.R.; Lyamin, A.V.; Sloan, S.W. Associated computational plasticity schemes for nonassociated frictional materials. Int. J. Numer. Methods Eng. 2012, 90, 1089–1117. [Google Scholar] [CrossRef]
- Katebi, M.; Wijewickreme, D.; Maghoul, P.; Roy, K. Lateral force–displacement response of buried pipes in slopes. Géotechnique 2023, 73, 375–387. [Google Scholar] [CrossRef]
- Cocchetti, G.; di Prisco, C.; Galli, A.; Nova, R. Soil–pipeline interaction along unstable slopes: A coupled three-dimensional approach. Part 1: Theoretical formulation. Can. Geotech. J. 2009, 46, 1289–1304. [Google Scholar] [CrossRef]
- Matyas, E.L.; Davis, J.B. Prediction of Vertical Earth Loads on Rigid Pipes. J. Geotech. Eng. 1983, 109, 190–201. [Google Scholar] [CrossRef]
- Kong, D.; Zhu, J.; Wu, L.; Zhu, B. Break-out resistance of offshore pipelines buried in inclined clayey seabed. Appl. Ocean Res. 2020, 94, 102007. [Google Scholar] [CrossRef]
- Kong, D. Quantifying Residual Resistance of Light Pipelines during Large-Amplitude Lateral Displacement Using Sequential Limit Analysis. J. Geotech. Geoenvironmental Eng. 2022, 148, 04022054. [Google Scholar] [CrossRef]
- Miyamoto, J.; Sassa, S.; Tsurugasaki, K.; Sumida, H. Wave-Induced Liquefaction and Floatation of a Pipeline in a Drum Centrifuge. J. Waterw. Port Coast. Ocean Eng. 2020, 146, 04019039. [Google Scholar] [CrossRef]
- Su, S.; Zhu, J.; Kong, D.; Li, Z.; Zhu, B.; Chen, Y. Modelling wave-seabed-pipe interaction through centrifuge experiment and a double-layered fluid model. Ocean Eng. 2025, 322, 120506. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Submerged unit weight (γ′) | 10 kN/m3 |
| Friction angle (φ) | 24°~44°, interval of 4° |
| Inclined seabed angle (β) | 0°~20°, interval of 5° |
| Roughness of pipe–soil interface | Rough, smooth |
| Tension of pipe–soil interface | No tension |
| Pipe embedment depth (w) | 1.5~8.0 D, at interval of 0.5 D |
| φ = 24° | φ = 28° | φ = 32° | |||||||||||||
| w/D | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° |
| 1.5 | 0.48 | 0.47 | 0.43 | 0.37 | 0.23 | 0.54 | 0.53 | 0.50 | 0.45 | 0.37 | 0.56 | 0.55 | 0.52 | 0.47 | 0.41 |
| 2.0 | 0.70 | 0.68 | 0.64 | 0.57 | 0.39 | 0.78 | 0.77 | 0.72 | 0.65 | 0.56 | 0.80 | 0.79 | 0.75 | 0.68 | 0.60 |
| 2.5 | 0.82 | 0.80 | 0.76 | 0.68 | 0.49 | 0.93 | 0.91 | 0.86 | 0.78 | 0.67 | 0.94 | 0.93 | 0.88 | 0.81 | 0.71 |
| 3.0 | 0.91 | 0.89 | 0.84 | 0.75 | 0.56 | 1.03 | 1.01 | 0.96 | 0.87 | 0.75 | 1.04 | 1.03 | 0.97 | 0.89 | 0.78 |
| 3.5 | 0.97 | 0.95 | 0.90 | 0.81 | 0.61 | 1.11 | 1.09 | 1.03 | 0.94 | 0.81 | 1.12 | 1.10 | 1.04 | 0.96 | 0.84 |
| 4.0 | 1.02 | 1.00 | 0.94 | 0.85 | 0.66 | 1.17 | 1.15 | 1.09 | 0.99 | 0.86 | 1.18 | 1.16 | 1.10 | 1.01 | 0.89 |
| 4.5 | 1.06 | 1.04 | 0.98 | 0.88 | 0.70 | 1.22 | 1.20 | 1.13 | 1.03 | 0.90 | 1.22 | 1.20 | 1.14 | 1.05 | 0.93 |
| 5.0 | 1.09 | 1.07 | 1.01 | 0.91 | 0.73 | 1.26 | 1.24 | 1.17 | 1.07 | 0.93 | 1.26 | 1.24 | 1.18 | 1.08 | 0.96 |
| 5.5 | 1.12 | 1.09 | 1.03 | 0.93 | 0.75 | 1.29 | 1.27 | 1.20 | 1.10 | 0.96 | 1.30 | 1.28 | 1.21 | 1.11 | 0.98 |
| 6.0 | 1.13 | 1.11 | 1.05 | 0.95 | 0.78 | 1.32 | 1.30 | 1.23 | 1.12 | 0.98 | 1.32 | 1.30 | 1.24 | 1.13 | 1.00 |
| φ = 36° | φ = 40° | φ = 44° | |||||||||||||
| w/D | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° |
| 1.5 | 0.54 | 0.53 | 0.51 | 0.46 | 0.41 | 0.53 | 0.52 | 0.50 | 0.46 | 0.41 | 0.52 | 0.51 | 0.49 | 0.46 | 0.41 |
| 2.0 | 0.76 | 0.75 | 0.71 | 0.66 | 0.58 | 0.74 | 0.73 | 0.69 | 0.64 | 0.57 | 0.73 | 0.72 | 0.68 | 0.64 | 0.57 |
| 2.5 | 0.89 | 0.88 | 0.83 | 0.77 | 0.68 | 0.86 | 0.84 | 0.81 | 0.74 | 0.67 | 0.84 | 0.82 | 0.79 | 0.74 | 0.66 |
| 3.0 | 0.97 | 0.96 | 0.91 | 0.84 | 0.75 | 0.93 | 0.92 | 0.88 | 0.81 | 0.73 | 0.91 | 0.90 | 0.86 | 0.80 | 0.72 |
| 3.5 | 1.04 | 1.02 | 0.97 | 0.90 | 0.80 | 0.98 | 0.97 | 0.93 | 0.86 | 0.77 | 0.96 | 0.95 | 0.91 | 0.84 | 0.76 |
| 4.0 | 1.08 | 1.07 | 1.02 | 0.94 | 0.83 | 1.03 | 1.01 | 0.97 | 0.90 | 0.80 | 1.00 | 0.98 | 0.94 | 0.88 | 0.79 |
| 4.5 | 1.12 | 1.10 | 1.05 | 0.97 | 0.86 | 1.06 | 1.04 | 1.00 | 0.92 | 0.83 | 1.03 | 1.01 | 0.97 | 0.90 | 0.81 |
| 5.0 | 1.15 | 1.13 | 1.08 | 1.00 | 0.89 | 1.09 | 1.07 | 1.02 | 0.95 | 0.85 | 1.05 | 1.04 | 0.99 | 0.92 | 0.83 |
| 5.5 | 1.18 | 1.16 | 1.10 | 1.02 | 0.91 | 1.11 | 1.09 | 1.04 | 0.96 | 0.86 | 1.07 | 1.05 | 1.01 | 0.94 | 0.84 |
| 6.0 | 1.20 | 1.18 | 1.12 | 1.04 | 0.92 | 1.13 | 1.11 | 1.06 | 0.98 | 0.88 | 1.09 | 1.07 | 1.02 | 0.95 | 0.86 |
| φ = 24° | φ = 28° | φ = 32° | |||||||||||||
| w/D | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° |
| 1.5 | 0.64 | 0.63 | 0.59 | 0.52 | 0.36 | 0.71 | 0.70 | 0.67 | 0.62 | 0.53 | 0.74 | 0.73 | 0.70 | 0.65 | 0.58 |
| 2.0 | 0.85 | 0.84 | 0.80 | 0.71 | 0.51 | 0.95 | 0.94 | 0.90 | 0.83 | 0.71 | 0.98 | 0.96 | 0.92 | 0.86 | 0.77 |
| 2.5 | 0.97 | 0.95 | 0.90 | 0.82 | 0.60 | 1.09 | 1.07 | 1.02 | 0.94 | 0.82 | 1.11 | 1.09 | 1.05 | 0.97 | 0.87 |
| 3.0 | 1.04 | 1.03 | 0.98 | 0.88 | 0.66 | 1.18 | 1.16 | 1.11 | 1.02 | 0.89 | 1.20 | 1.18 | 1.13 | 1.05 | 0.93 |
| 3.5 | 1.10 | 1.08 | 1.03 | 0.93 | 0.71 | 1.25 | 1.23 | 1.17 | 1.07 | 0.94 | 1.26 | 1.24 | 1.19 | 1.10 | 0.98 |
| 4.0 | 1.14 | 1.12 | 1.06 | 0.96 | 0.75 | 1.30 | 1.28 | 1.22 | 1.12 | 0.98 | 1.31 | 1.29 | 1.23 | 1.14 | 1.01 |
| 4.5 | 1.17 | 1.16 | 1.09 | 0.99 | 0.78 | 1.34 | 1.32 | 1.26 | 1.15 | 1.01 | 1.35 | 1.33 | 1.27 | 1.17 | 1.04 |
| 5.0 | 1.20 | 1.18 | 1.12 | 1.01 | 0.80 | 1.38 | 1.36 | 1.29 | 1.18 | 1.04 | 1.38 | 1.36 | 1.30 | 1.20 | 1.06 |
| 5.5 | 1.23 | 1.20 | 1.14 | 1.03 | 0.83 | 1.41 | 1.39 | 1.32 | 1.20 | 1.06 | 1.41 | 1.39 | 1.32 | 1.22 | 1.08 |
| 6.0 | 1.25 | 1.22 | 1.15 | 1.04 | 0.84 | 1.43 | 1.41 | 1.34 | 1.22 | 1.07 | 1.43 | 1.41 | 1.34 | 1.24 | 1.10 |
| φ = 36° | φ = 40° | φ = 44° | |||||||||||||
| w/D | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° | β = 0° | β = 5° | β = 10° | β = 15° | β = 20° |
| 1.5 | 0.73 | 0.72 | 0.69 | 0.64 | 0.58 | 0.73 | 0.72 | 0.69 | 0.65 | 0.59 | 0.74 | 0.73 | 0.70 | 0.66 | 0.60 |
| 2.0 | 0.94 | 0.93 | 0.89 | 0.84 | 0.75 | 0.93 | 0.91 | 0.88 | 0.83 | 0.75 | 0.93 | 0.92 | 0.89 | 0.83 | 0.76 |
| 2.5 | 1.05 | 1.04 | 1.00 | 0.93 | 0.84 | 1.03 | 1.01 | 0.97 | 0.91 | 0.83 | 1.02 | 1.01 | 0.97 | 0.91 | 0.83 |
| 3.0 | 1.12 | 1.11 | 1.06 | 0.99 | 0.89 | 1.09 | 1.07 | 1.03 | 0.97 | 0.88 | 1.07 | 1.06 | 1.02 | 0.96 | 0.87 |
| 3.5 | 1.17 | 1.16 | 1.11 | 1.03 | 0.93 | 1.13 | 1.11 | 1.07 | 1.00 | 0.91 | 1.11 | 1.09 | 1.05 | 0.99 | 0.90 |
| 4.0 | 1.21 | 1.20 | 1.15 | 1.07 | 0.95 | 1.16 | 1.14 | 1.10 | 1.03 | 0.93 | 1.13 | 1.12 | 1.08 | 1.01 | 0.92 |
| 4.5 | 1.24 | 1.22 | 1.17 | 1.09 | 0.98 | 1.18 | 1.16 | 1.12 | 1.04 | 0.94 | 1.15 | 1.14 | 1.09 | 1.02 | 0.93 |
| 5.0 | 1.26 | 1.25 | 1.19 | 1.11 | 0.99 | 1.19 | 1.18 | 1.13 | 1.06 | 0.95 | 1.16 | 1.15 | 1.11 | 1.04 | 0.94 |
| 5.5 | 1.28 | 1.26 | 1.21 | 1.12 | 1.00 | 1.21 | 1.20 | 1.15 | 1.07 | 0.96 | 1.18 | 1.16 | 1.12 | 1.05 | 0.95 |
| 6.0 | 1.30 | 1.28 | 1.22 | 1.13 | 1.01 | 1.22 | 1.21 | 1.16 | 1.08 | 0.97 | 1.19 | 1.17 | 1.13 | 1.05 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Su, S.; Chen, F. Break-Out Resistance of Offshore Pipelines Buried in Inclined Sandy Seabed. J. Mar. Sci. Eng. 2025, 13, 1669. https://doi.org/10.3390/jmse13091669
Zhu J, Su S, Chen F. Break-Out Resistance of Offshore Pipelines Buried in Inclined Sandy Seabed. Journal of Marine Science and Engineering. 2025; 13(9):1669. https://doi.org/10.3390/jmse13091669
Chicago/Turabian StyleZhu, Jingshan, Siyang Su, and Fuquan Chen. 2025. "Break-Out Resistance of Offshore Pipelines Buried in Inclined Sandy Seabed" Journal of Marine Science and Engineering 13, no. 9: 1669. https://doi.org/10.3390/jmse13091669
APA StyleZhu, J., Su, S., & Chen, F. (2025). Break-Out Resistance of Offshore Pipelines Buried in Inclined Sandy Seabed. Journal of Marine Science and Engineering, 13(9), 1669. https://doi.org/10.3390/jmse13091669






