Numerical Study on High-Speed Icebreaking of a Hemispherically Capped Cylinder Based on the Smoothed Particle Hydrodynamics Method
Abstract
1. Introduction
2. Theory and Numerical Methods
2.1. Principles of the SPH Method
2.2. Governing Equations of the SPH Method
2.2.1. Spatial Discretization of the Deformation Tensor
2.2.2. Decomposition of Stress Tensor
2.2.3. Governing Equations for Solids Under ULSPH Form
2.3. Numerical Processing Techniques
2.4. Material Model and Damage Criterion of Ice
2.4.1. Elastoplastic Constitutive Model
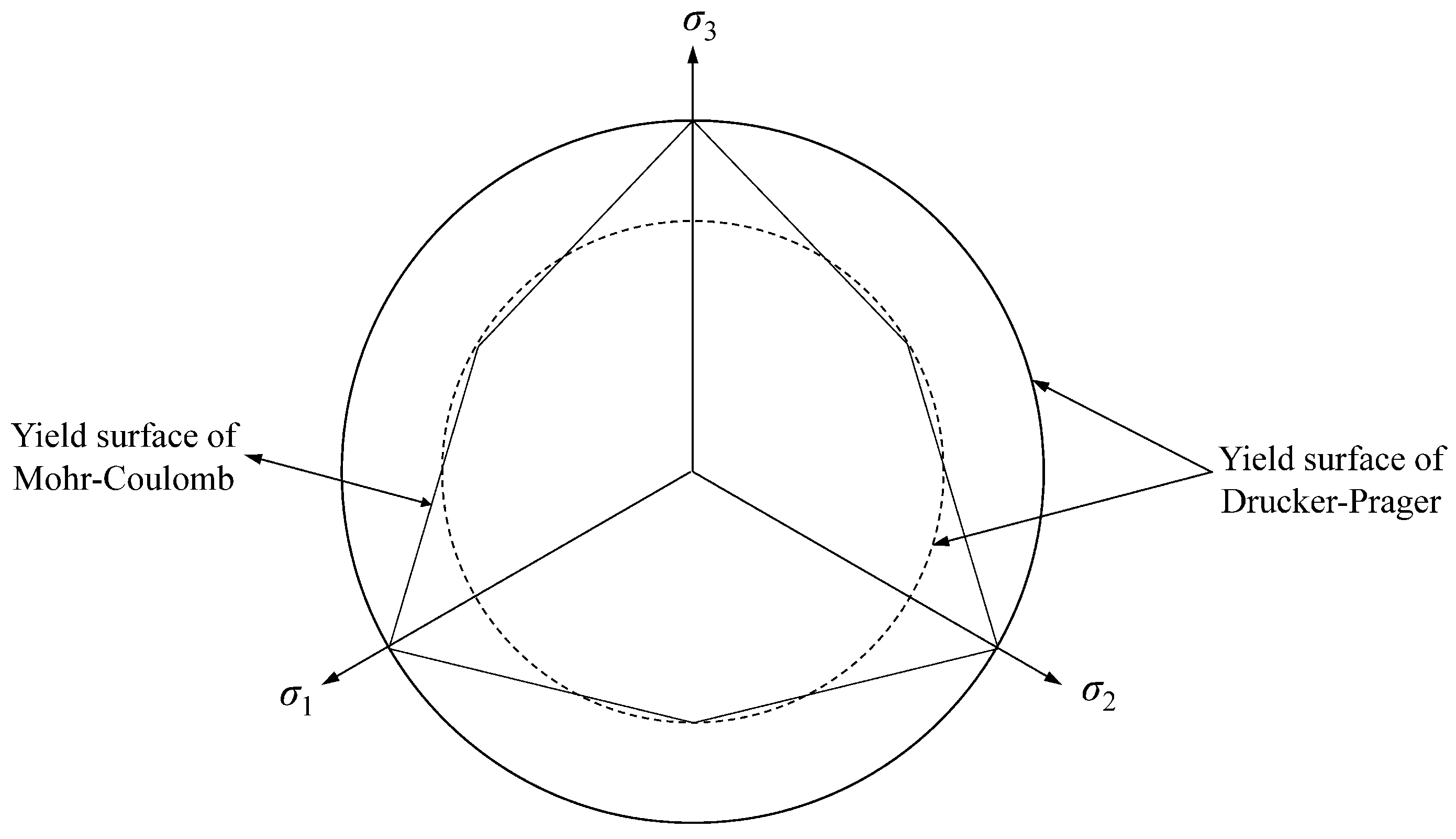
2.4.2. Drucker–Prager Criterion
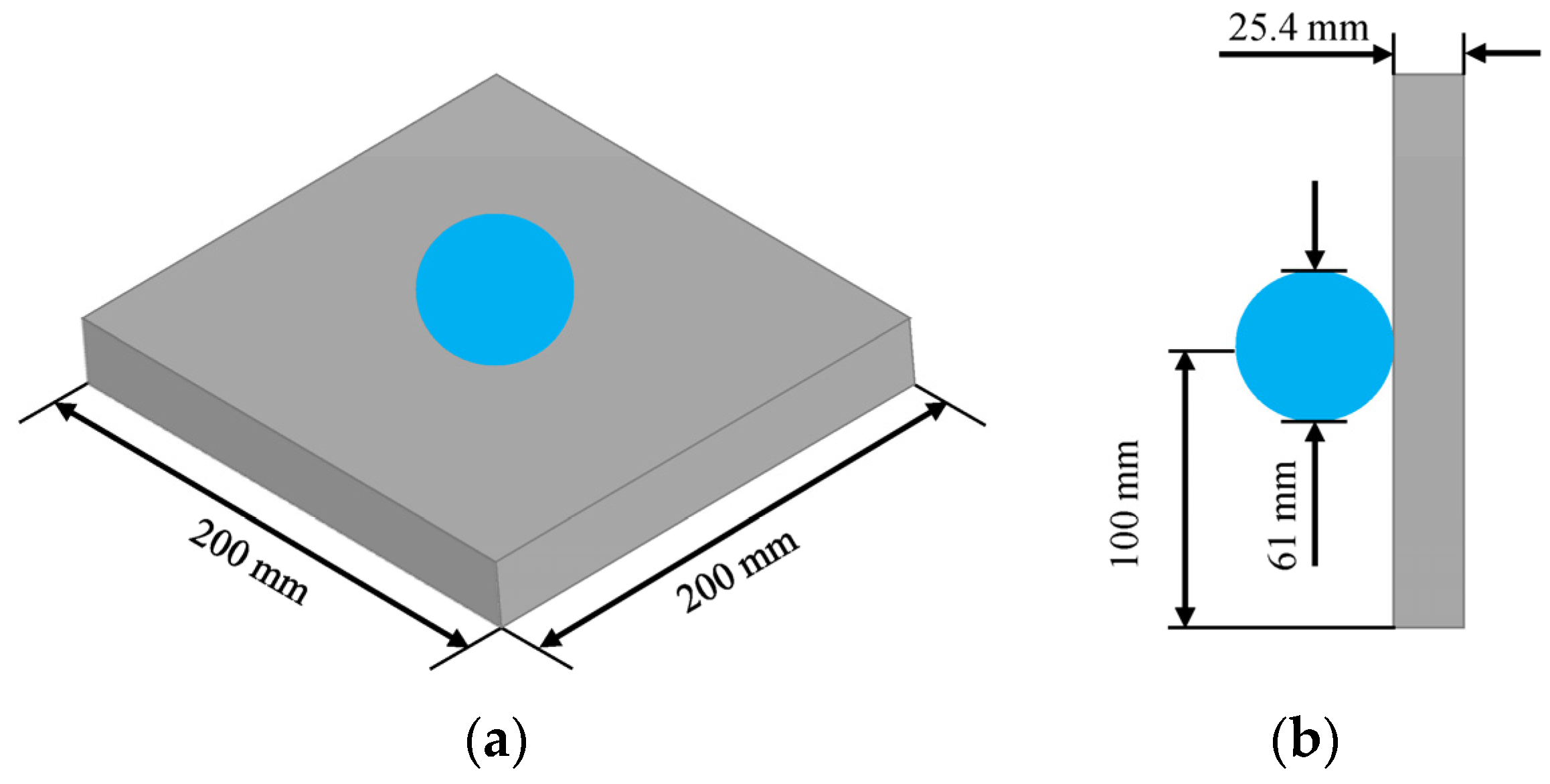
3. Numerical Model Validation
4. Results and Discussion
4.1. Initial and Boundary Conditions
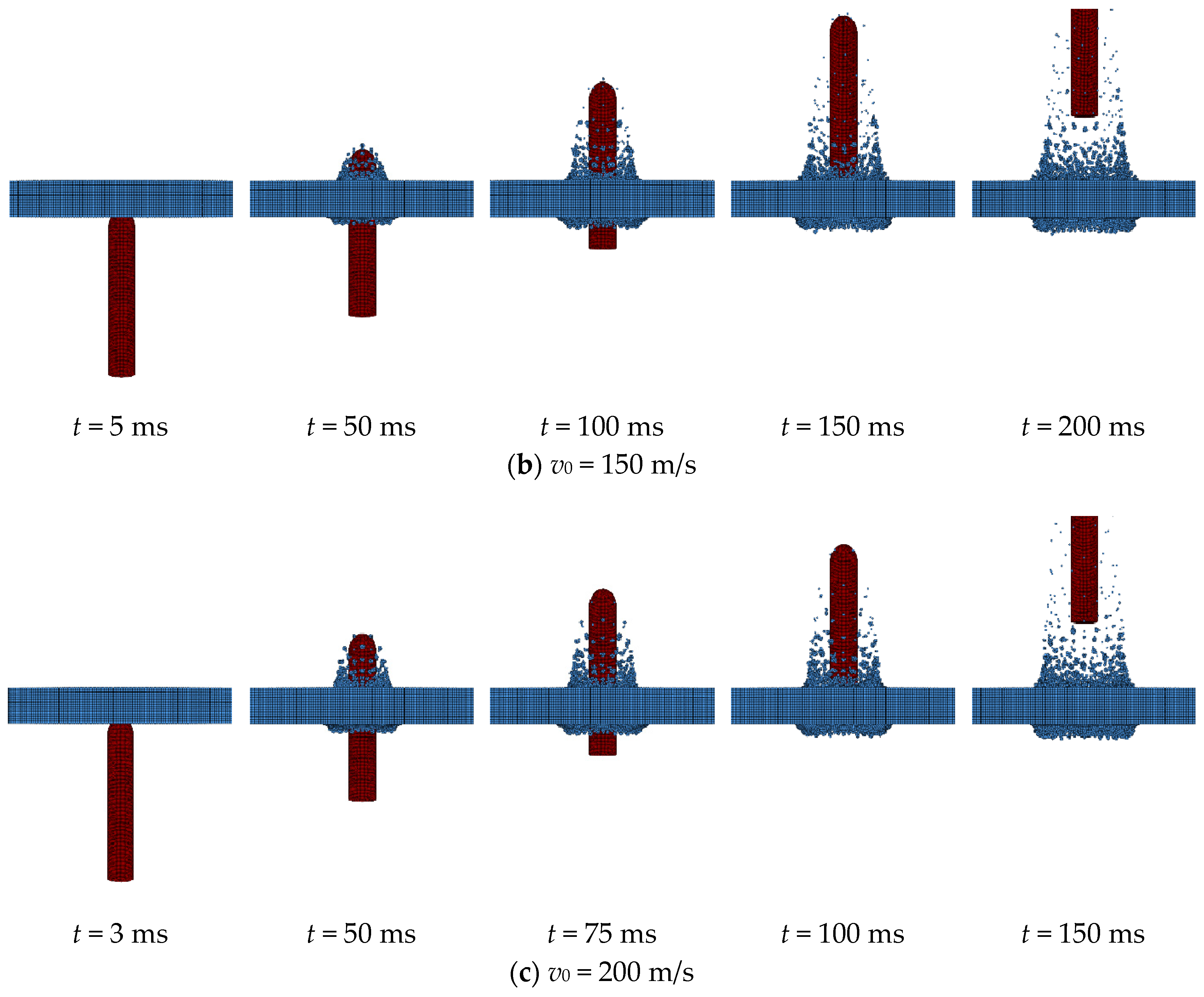
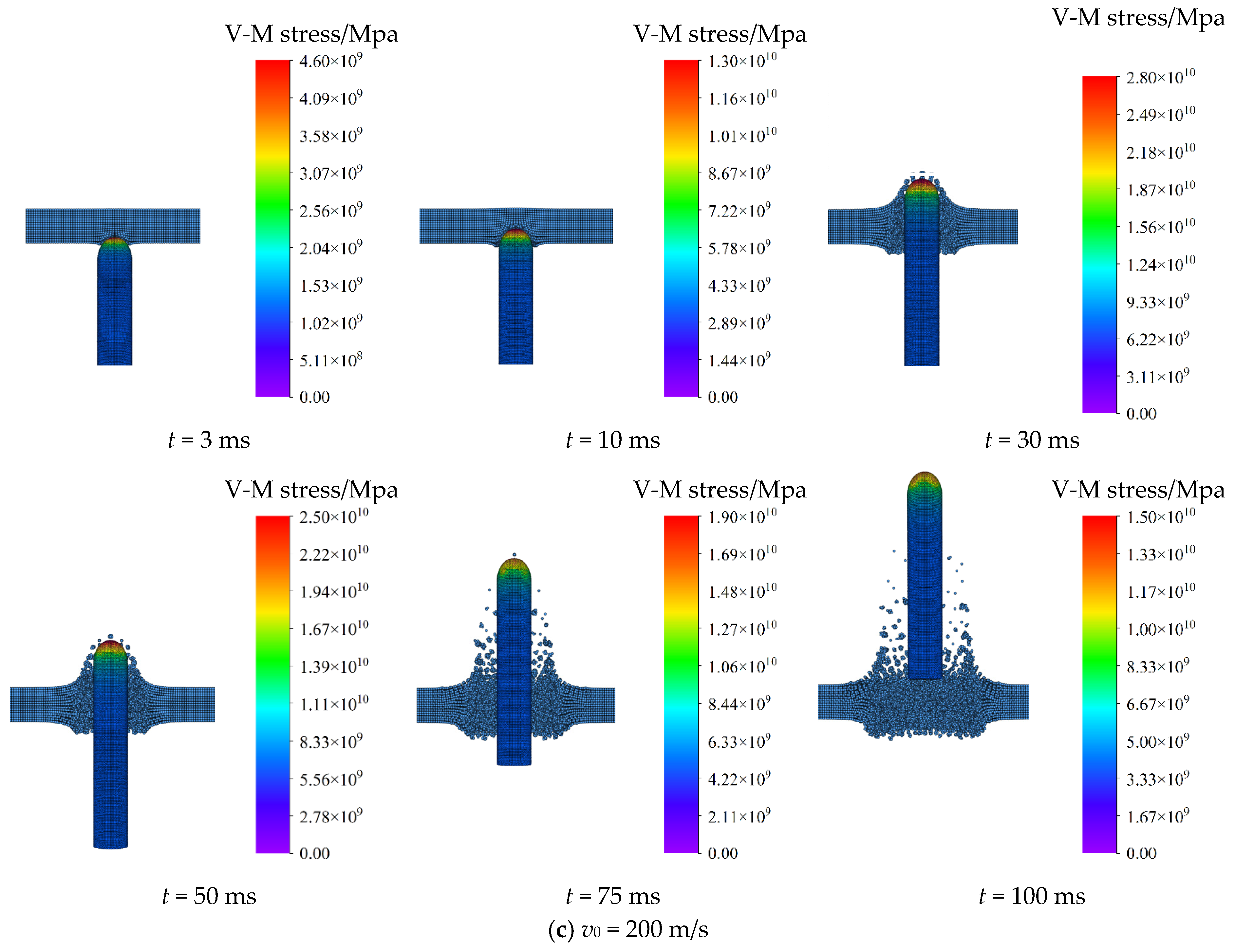
4.2. Effect of Initial Velocity
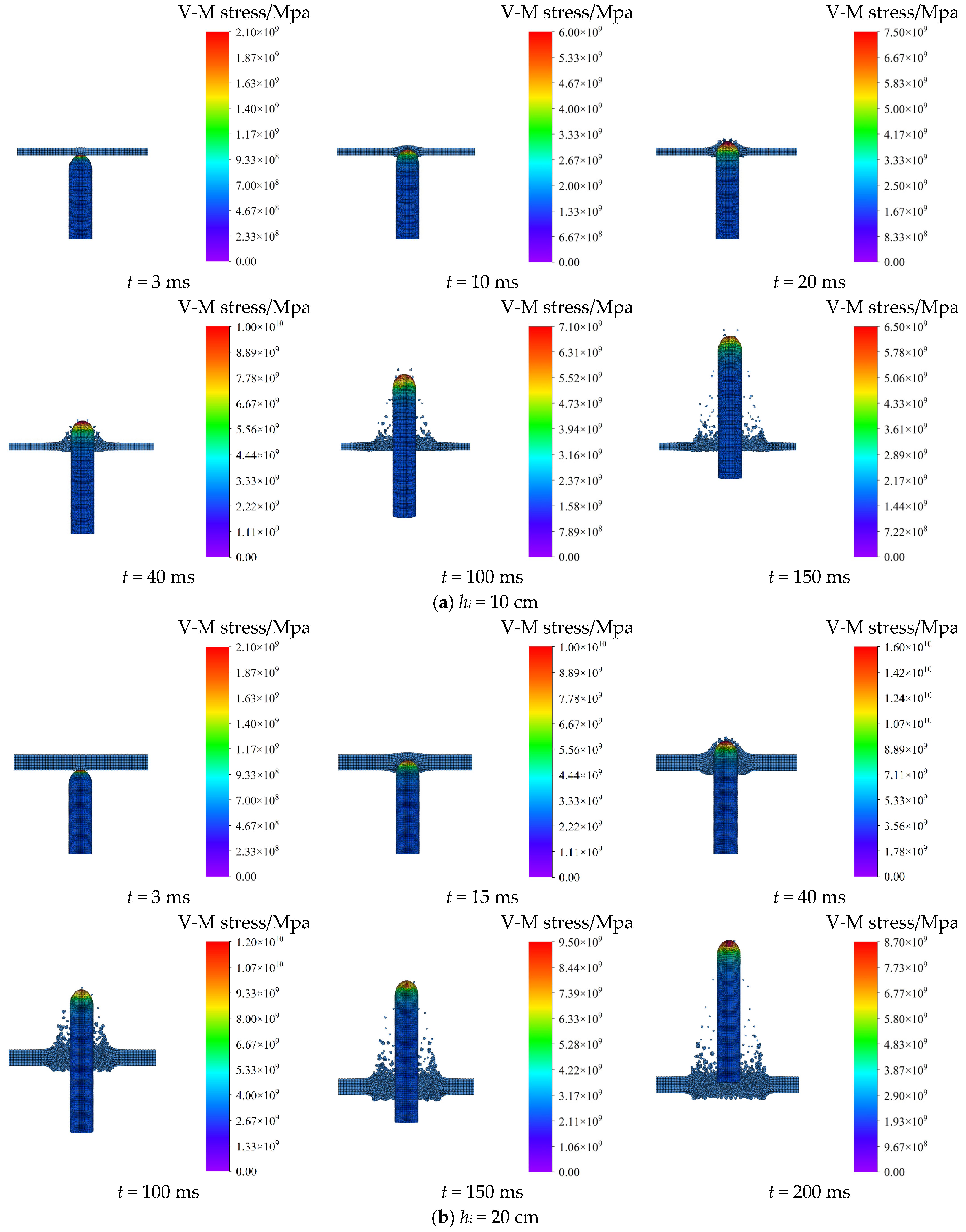
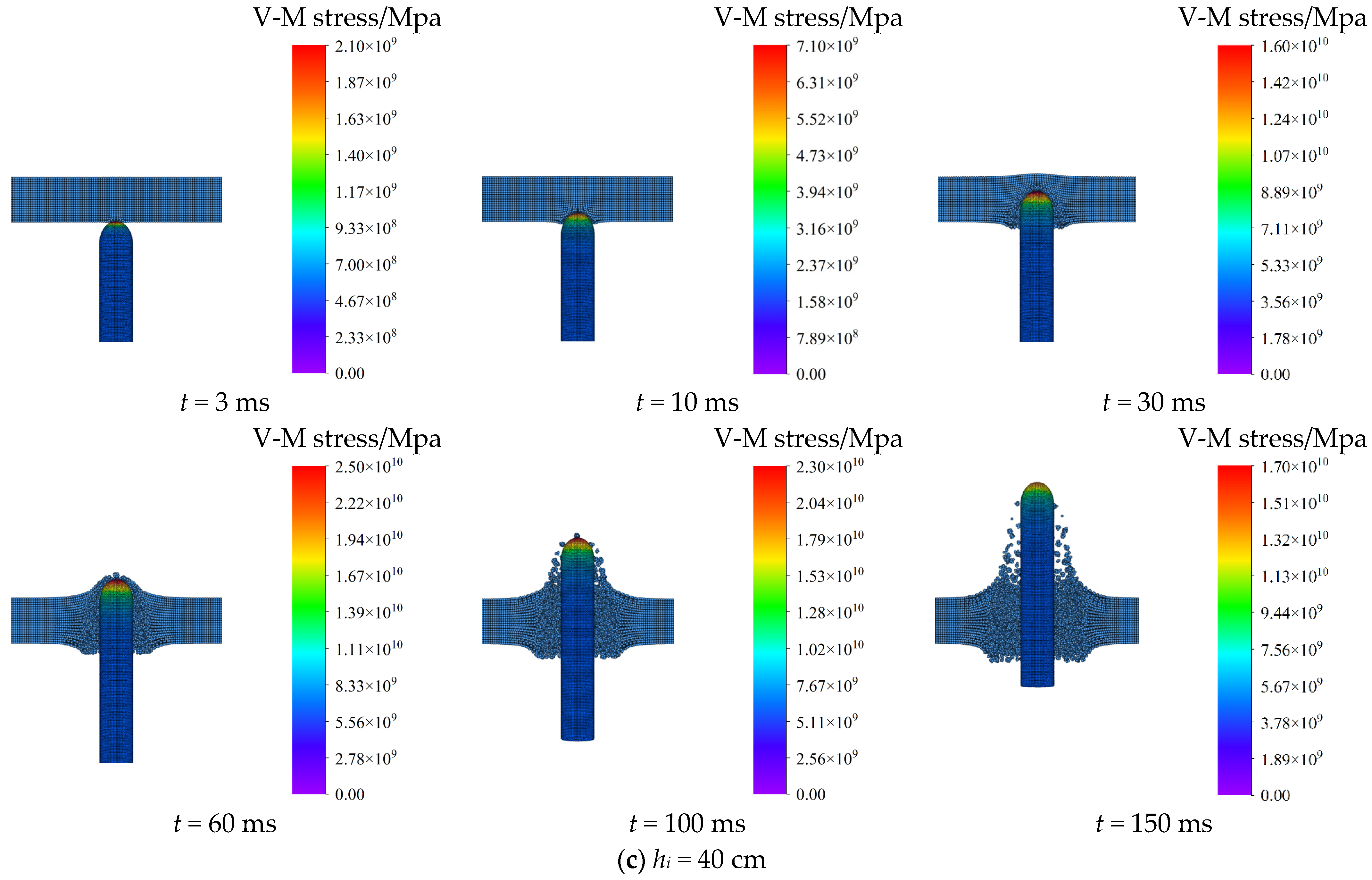
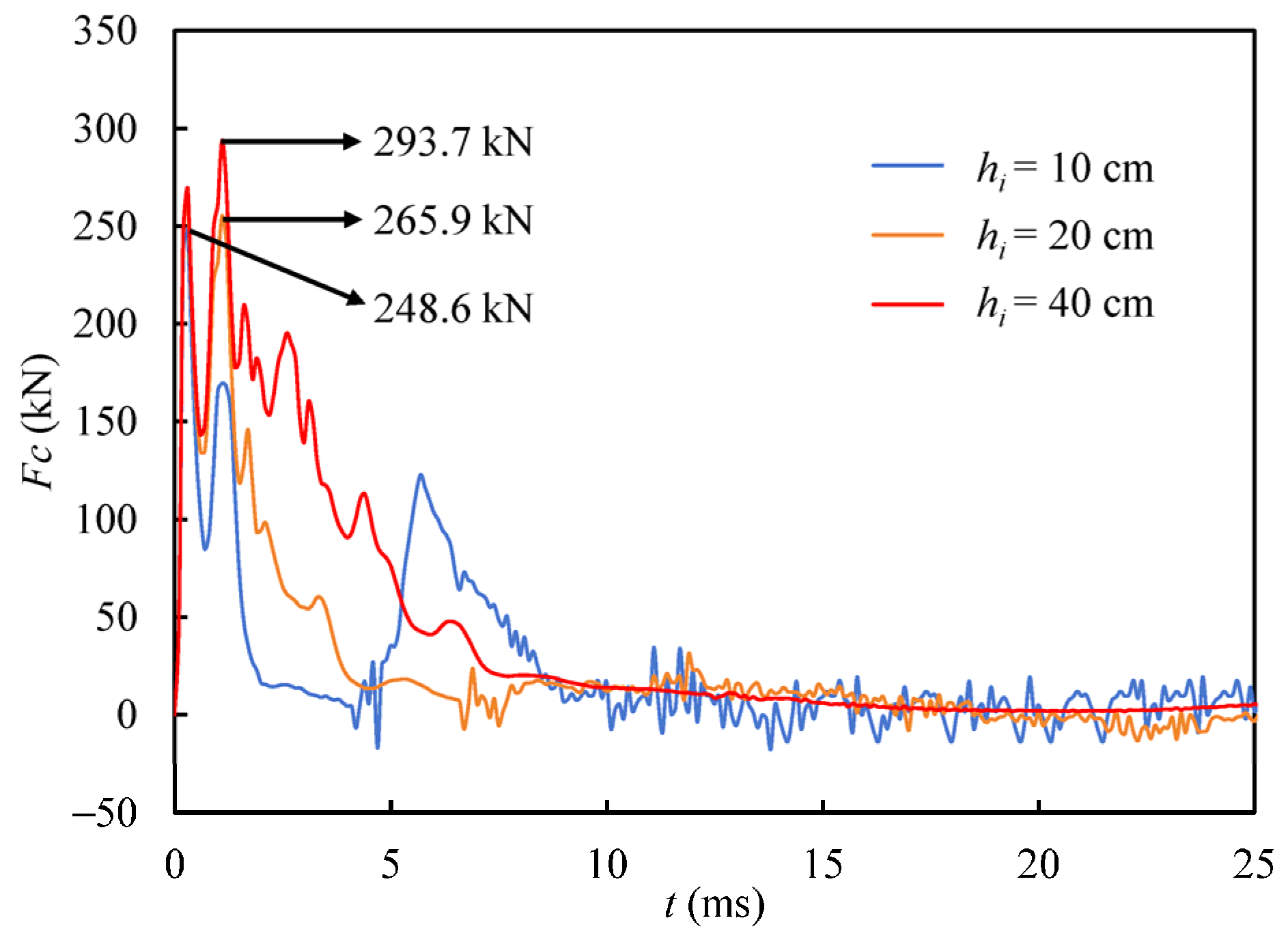
4.3. Effect of Thickness of Ice Layer
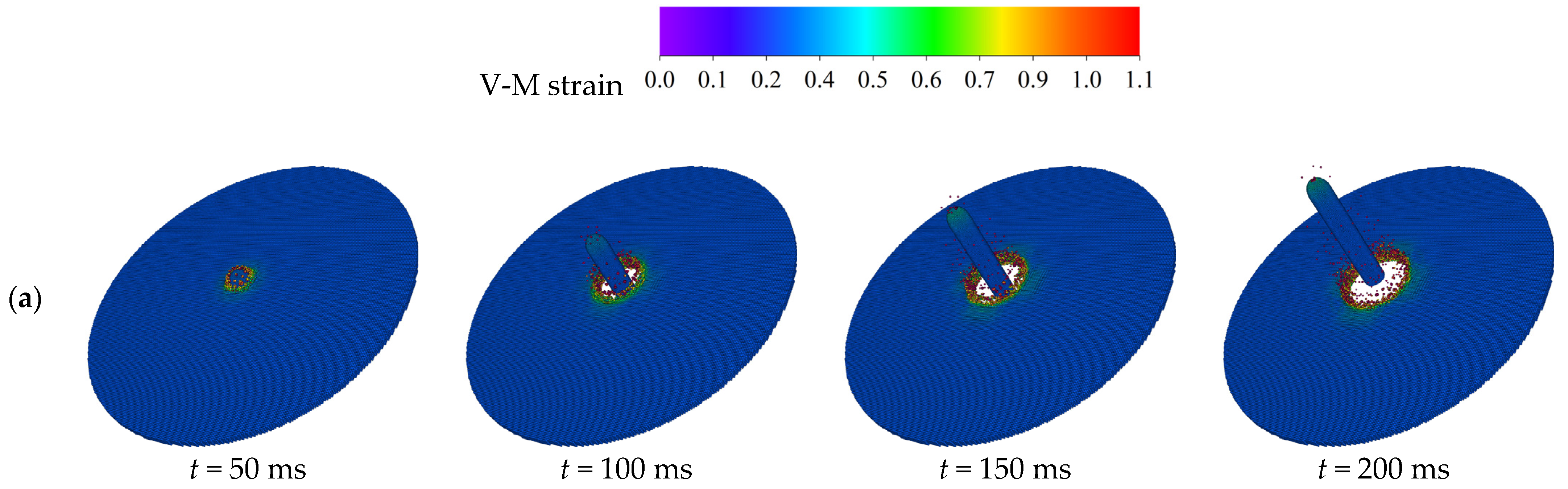
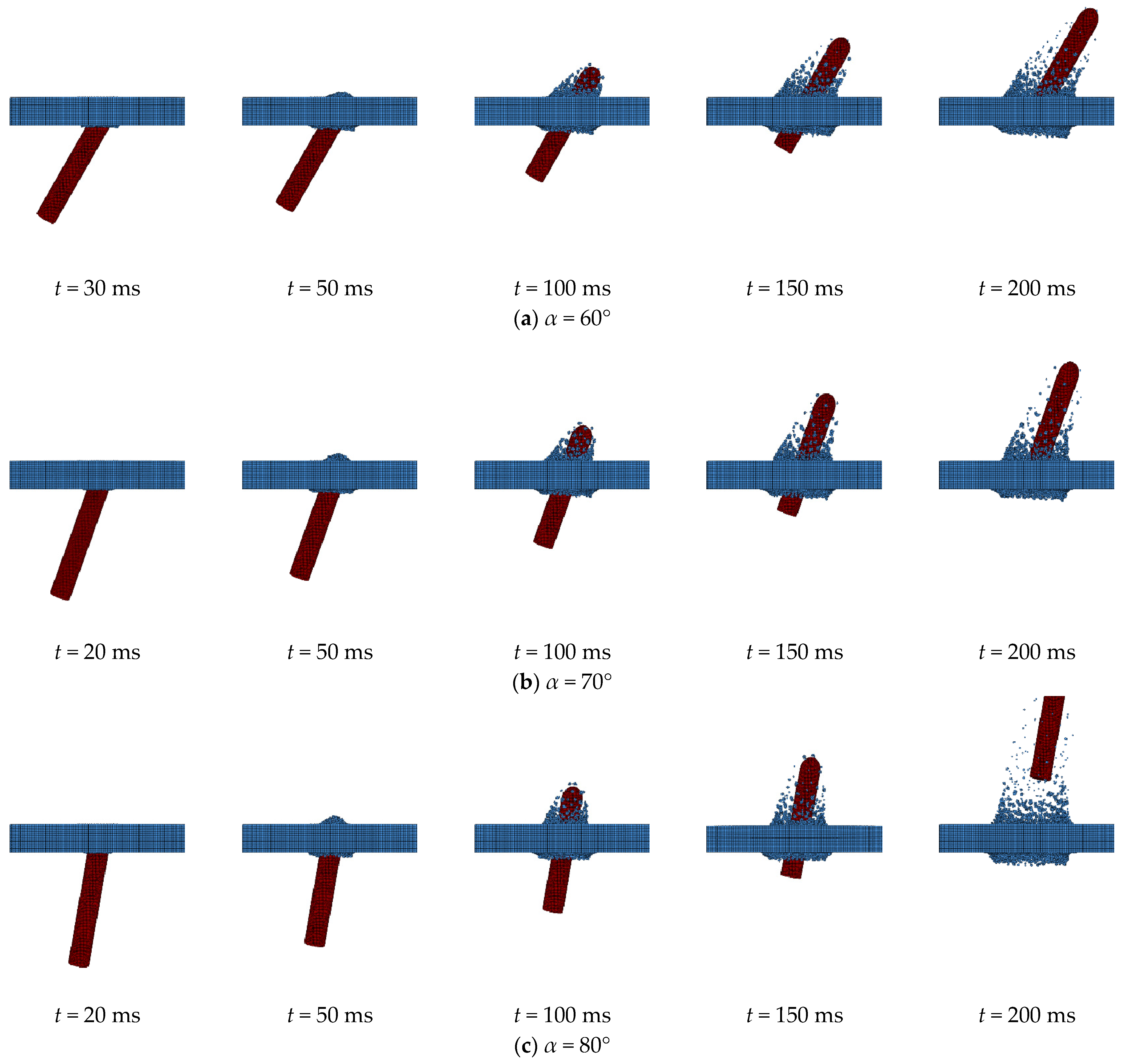
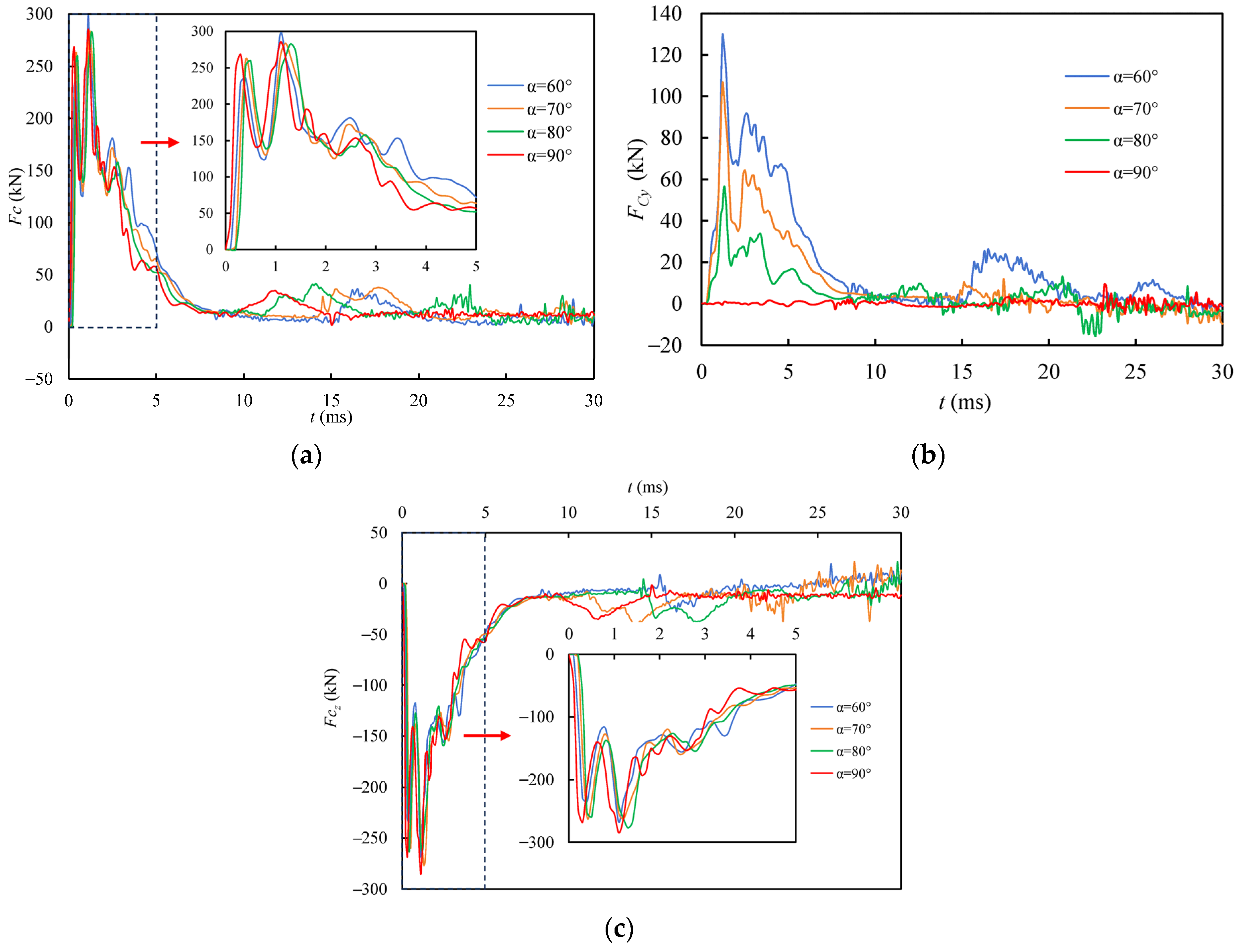
4.4. Effect of Initial Impact Angle
5. Conclusions
- (1)
- Under the initial impact angle of 90° and ice thickness of 30 cm, as the impact velocity increases from 100 m/s to 200 m/s, the peak impact force experienced by the HCC increases from 285.31 kN to 917.51 kN, indicating a power-law scaling of . The stress and strain generated by the HCC and the ice exhibit symmetrical distributions. The deformation and damage of the ice are generally consistent, and the ice strain mainly propagates radially.
- (2)
- Under the initial impact angle of 90° and initial velocity of 100 m/s, as the ice thickness increases from 10 cm to 40 cm, the peak impact force on the HCC increases from 248.6 kN to 293.7 kN, indicating a power-law scaling of . The corresponding deformation and damage caused by impact on the ice become more severe, and the radial propagation of ice strain becomes more pronounced.
- (3)
- When the thickness of the ice layer is 30 cm and the initial velocity is 100 m/s, as the initial impact angles decrease from 90° to 60°, the component of the impact force in the y direction becomes larger, while the impact force and the component of impact force in the z direction change little. Additionally, except for the impact angle 90°, the strains produced in the ice under other impact angles exhibit asymmetric distribution.
- (4)
- The high-speed icebreaking process of the HCC is primarily characterized by the collision between the HCC’s head and the ice layer. The head of the HCC experiences significant impact forces, resulting in obvious stress concentration. Therefore, protective design of the front structure is essential during structural design of the HCC.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALE | Arbitrary Lagrangian–Eulerian |
| CEL | Coupled Eulerian–Lagrangian |
| CFL | Courant–Friedrichs–Lewy |
| FEM | Finite Element Method |
| HCC | Hemispherically capped cylinder |
| SPH | Smoothed Particle Hydrodynamics |
| ULSPH | Update Lagrange Smoothed Particle Hydrodynamics |
| V-M | von Mises |
References
- Zhang, J.J.; Guo, P.Q. The Direction and lmpact of Geopolitical Games in the Arctic Againstthe Background of the Russia-Ukraine Conflict. Russ. East Eur. Cent. Asian Stud. 2024, 6, 91–113+161–162. [Google Scholar]
- Jin, Y.Q.; Zhang, Y.; Chen, C.S.; Xu, D.Y. Comparison and Assessment of Data on Multi-Source Satellite Remote Sensing Arctic Sea Ice Thickness. Chin. J. Polar Res. 2023, 35, 238–250. [Google Scholar]
- Yu, T.Q.; Liu, K.; Liu, J.J.; Wang, Z.L. Constitutive Model of Ice Material in Ship-Ice Collision Considering Temperature Effect. J. Ship Mech. 2023, 27, 250–259. [Google Scholar]
- Timco, G.W.; Weeks, W.F. A Review of the Engineering Properties of Sea Ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Thomas, D.N.; Dieckmann, G.S. Sea Ice: An Introduction to Its Physics, Chemistry, Biology and Geology; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Drucker, D.C.; Prager, W. Soil Mechanics and Plastic Analysis or Limit Design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Carney, K.S.; Benson, D.J.; DuBois, P.; Lee, R. A Phenomenological High Strain Rate Model with Failure for Ice. Int. J. Solids Struct. 2006, 43, 7820–7839. [Google Scholar] [CrossRef]
- Tsai, S.W.; Wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Yu, B.; Low, Y.M. A Phenomenological Model for Simulating Ice Loads on Vertical Structures Incorporating Strain Rate-Dependent Stress-Strain Characteristics. Appl. Math. Model. 2022, 101, 132–156. [Google Scholar] [CrossRef]
- Zong, R. Finite Element Analysis of Ship-Ice Collision Using LS-Dyna. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2012. [Google Scholar]
- Xu, Y.; Wu, J.; Li, P.; Kujala, P.; Hu, Z.; Chen, G. Investigation of the Fracture Mechanism of Level Ice with Extended Finite Element Method. Ocean Eng. 2022, 260, 112048. [Google Scholar] [CrossRef]
- Wang, G.; Ji, S.; Lv, H.; Yue, Q. Drucker–Prager Yield Criteria in Viscoelastic-Plastic Constitutive Model for the Study of Sea Ice Dynamics. J. Hydrodyn. 2006, 18, 714–722. [Google Scholar] [CrossRef]
- Shi, C.; Hu, Z.; Ringsberg, J.; Luo, Y. Validation of a Temperature-Gradient-Dependent Elastic-Plastic Material Model of Ice with Finite Element Simulations. Cold Reg. Sci. Technol. 2017, 133, 15–25. [Google Scholar] [CrossRef]
- Jeon, S.; Kim, Y. Numerical Simulation of Level Ice–Structure Interaction Using Damage-Based Erosion Model. Ocean Eng. 2021, 220, 108485. [Google Scholar] [CrossRef]
- Long, X.; Liu, S.; Ji, S. Discrete Element Modelling of Relationship Between Ice Breaking Length and Ice Load on Conical Structure. Ocean Eng. 2020, 201, 107152. [Google Scholar] [CrossRef]
- Marnix, V.D.B.; Raed, L.; Sveinung, L. An Implicit Time-Stepping Scheme and an Improved Contact Model for Ice-Structure Interaction Simulations. Cold Reg. Sci. Technol. 2018, 155, 193–213. [Google Scholar]
- Liu, M.; Wang, Q.; Lu, W. Peridynamic Simulation of Brittle-Ice Crushed by a Vertical Structure. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 209–218. [Google Scholar] [CrossRef]
- Shi, H.T.; Yuan, G.Y.; Ni, B.Y.; Zhang, L.W. Quasi-Brittle Ice Breaking Mechanisms by High-Velocity Water Jet Impacts: An Investigation Based on PD-SPH Coupling Model and Experiments. J. Mech. Phys. Solids 2024, 191, 105783. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, W.; Xu, H.; Sun, T. Dynamic Characteristics of an Underwater Ventilated Vehicle Exiting Water in an Environment with Scattered Ice Floes. J. Mar. Sci. Eng. 2023, 11, 2046. [Google Scholar] [CrossRef]
- Zhao, W.H. Simulation Research on Ice loading of Typical Floating Vertical Icebreaking. Master’s Thesis, China Ship Research and Development Academy, Wuxi, China, 2023. [Google Scholar]
- Yue, J.Z.; Wu, X.Q.; Huang, C.G. Multi-Field Coupling Effect and Similarity Law of Floatingice Break by Vehicle Launched Underwater. Chin. J. Theor. Appl. Mech. 2021, 53, 1930–1939. [Google Scholar]
- Zhang, G.Y.; You, C.; Wei, H.P.; Sun, T.; Yang, B. Experimental Study on the Effects of Brash Ice on the Water-Exit Dynamics of an Underwater Vehicle. Appl. Ocean Res. 2021, 117, 102948. [Google Scholar] [CrossRef]
- Cui, W.Z.; Kong, D.C.; Sun, T.Z.; Yan, G. Coupling Dynamic Characteristics of High-Speed Water-Entry Projectile and Ice Sheet. Ocean Eng. 2023, 275, 114090. [Google Scholar] [CrossRef]
- Qian, Y. Study on the Calculation Method for the Ice-Load of Vertical Ice-Breaking. Master’s Thesis, Harbin Engineering University, Harbin, China, 2020. [Google Scholar]
- You, C.; Sun, T.Z.; Zhang, G.Y.; Wei, Y.; Zong, Z. Numerical Study on Effect of Brash Ice on Water Exit Dynamics of Ventilated Cavitation Cylinder. Ocean Eng. 2022, 245, 110443. [Google Scholar] [CrossRef]
- Wang, H.; Luo, Y.H.; Chen, Z.H.; Huang, Z. Influences of Ice-Water Mixture on the Vertical Water-Entry of a Cylinder at a Low Velocity. Ocean Eng. 2022, 256, 111464. [Google Scholar] [CrossRef]
- Sun, T.Z.; Zhang, J.Y.; Wei, H.P.; Zhang, D.; Zhang, G. Experimental Investigation of the Influence of Floating Ices Constraint on the Cavity Dynamics of an Axisymmetric Body During the Water Exit Process. Ocean Eng. 2022, 244, 110383. [Google Scholar] [CrossRef]
- Wang, C.H.; Wang, J.A.; Wang, C.; Guo, C.; Zhu, G. Research on Vertical Movement of Cylindrical Structure Out of Water and Breaking Through Ice Layer Based on S-Ale Method. Chin. J. Theor. Appl. Mech. 2021, 53, 3110–3123. [Google Scholar]
- Khabakhpasheva, T.; Chen, Y.; Korobkin, A. Impact onto an Ice Floe. J. Adv. Res. Ocean Eng. 2018, 4, 146–162. [Google Scholar]
- Ghandehari, M.A.; Masoodi, A.R.; Hosseininia, E.S. Temperature-Dependency and Boundary Condition Impacts on the Multiscale Vibrational Behavior of Laminated Nested Dual Conical Shell Structure Semi-AUV Applications. Appl. Ocean Res. 2025, 154, 104425. [Google Scholar] [CrossRef]
- Ghandehari, M.A.; Masoodi, A.R.; Hosseininia, S.E.S. Multiscale Dynamic Behavior of Imperfect Hybrid Matrix/Fiber Nanocomposite Nested Conical Shells with Elastic Interlayer. Thin-Walled Struct. 2024, 205, 112494. [Google Scholar] [CrossRef]
- Masoodi, A.R.; Arabi, E. Geometrically Nonlinear Thermomechanical Analysis of Shell-Like Structures. J. Therm. Stress. 2018, 41, 37–53. [Google Scholar] [CrossRef]
- Lee, C.H.; Refachinho de Campos, P.R.; Gil, A.J.; Giacomini, M.; Bonet, J. An Entropy-Stable Updated Reference Lagrangian Smoothed Particle Hydrodynamics Algorithm for Thermo-Elasticity and Thermo-Visco-Plasticity. Comput. Part. Mech. 2023, 10, 1493–1531. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, C.; Tang, X.; Hu, X. An Essentially Non-Hourglass Formulation for Total Lagrangian Smoothed Particle Hydrodynamics. Comput. Methods Appl. Mech. Eng. 2023, 407, 115915. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Q.; Liu, Y.; Liu, X. Improved Mesh-Free SPH Approach for Loose Top Coal Caving Modeling. Particuology 2024, 95, 1–27. [Google Scholar] [CrossRef]
- Wiragunarsa, M.; Zuhal, L.R.; Dirgantara, T.; Putra, I.S. SPH Method for Crack Growth Modelling Using Particle Deletion and Interaction Pair-based Framework. Procedia Struct. Integr. 2024, 52, 583–593. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Libersky, L.D.; Randles, P.W.; Carney, T.C.; Dickinson, D.L. Recent Improvements in SPH Modeling of Hypervelocity Impact. Int. J. Impact Eng. 1997, 20, 525–532. [Google Scholar] [CrossRef]
- Gray, J.P.; Monaghan, J.J.; Swift, R.P. SPH Elastic Dynamics. Comput. Methods Appl. Mech. Eng. 2001, 190, 6641–6662. [Google Scholar] [CrossRef]
- Kupchella, R.; Stowe, D.; Weiss, M.; Pan, H.; Cogar, J. SPH Modeling Improvements for Hypervelocity Impacts. Procedia Eng. 2015, 103, 326–333. [Google Scholar] [CrossRef]
- Wang, L.; Xu, F.; Yang, Y. An Improved Total Lagrangian SPH Method for Modeling Solid Deformation and Damage. Eng. Anal. Bound. Elem. 2021, 133, 286–302. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Hu, X.; Lourenço, S.D. A Riemann-Based SPH Method for Modelling Large Deformation of Granular Materials. Comput. Geotech. 2024, 167, 106052. [Google Scholar] [CrossRef]
- Das, J.; Ehlers, S. Numerical Simulation of Crushing and Bending Failure of Ice Using SPH. International Conference on Offshore Mechanics and Arctic Engineering. Am. Soc. Mech. Eng. 2015, 56567, V008T07A019. [Google Scholar]
- Anghileri, M.; Castelletti, L.L.; Invernizzi, F.; Mascheroni, M. A Survey of Numerical Models for Hail Impact Analysis Using Explicit Finite Element Codes. Int. J. Impact Eng. 2005, 31, 929–944. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, X.; Ma, Q.; Hu, Z. A Numerical Study on Ice Failure Process and Ice-Ship Interactions by Smoothed Particle Hydrodynamics. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 796–808. [Google Scholar] [CrossRef]
- Chen, Z.; He, Y.; Gu, Y.; Su, B.; Ren, Y.; Liu, Y. A Novel Method for Numerical Simulation of the Interaction Between Level Ice and Marine Structures. J. Mar. Sci. Technol. 2021, 26, 1170–1183. [Google Scholar] [CrossRef]
- Mokhtari, M.; Kim, E.; Amdahl, J. A Non-Linear Viscoelastic Material Model with Progressive Damage Based on Microstructural Evolution and Phase Transition in Polycrystalline Ice for Design Against Ice Impact. Int. J. Impact Eng. 2023, 176, 104563. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, G.; Qian, L.; Ma, J. HLFEMP: A Coupled MPM-FEM Method Under a Hybrid Updated and Total Lagrangian Framework. Appl. Math. Model. 2024, 136, 115644. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar]
- Khayyer, A.; Shimizu, Y.; Lee, C.H.; Gil, A.; Gotoh, H.; Bonet, J. An Improved Updated Lagrangian SPH Method for Structural Modelling. Comput. Part. Mech. 2024, 11, 1055–1086. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Monaghan, J.J. SPH Without a Tensile Instability. J. Comput. Phys. 2000, 159, 290–311. [Google Scholar] [CrossRef]
- Zhang, C.; Rezavand, M.; Hu, X. A Multi-Resolution SPH Method for Fluid-Structure Interactions. J. Comput. Phys. 2021, 429, 110028. [Google Scholar] [CrossRef]
- Adami, s.; Hu, X.Y.; Adams, N.A. A Generalized Wall Boundary Condition for Smoothed Particle Hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Wu, D.; Tang, X.; Zhang, S.; Hu, X. Unified Non-Hourglass Formulation for Total Lagrangian SPH Solid Dynamics. Comput. Mech. 2024, 75, 1081–1113. [Google Scholar] [CrossRef]
- Fan, J.; Yuan, Q.H.; Jing, F.L.; Bai, G.; Shen, X. Macro-Phenomenological High-Strain-Rate Elastic Fracture Model for Ice-Impact Simulations. Chin. J. Aeronaut. 2023, 36, 146–160. [Google Scholar] [CrossRef]










| Object | Item | Value/Description |
|---|---|---|
| Ice | Density | 900 kg/m3 |
| Elastic modulus | 9.38 GPa | |
| Poisson’s ratio | 0.33 | |
| Friction angle | 36° | |
| Cohesion | 0.58 MPa | |
| Shear dilation angle | 12° | |
| Material model | Elastoplastic material model | |
| Target plate | Damage criterion | Drucker–Prager criterion |
| Density | 2700 kg/m3 | |
| Elastic modulus | 0.67 GPa | |
| Poisson’s ratio | 0.33 | |
| Material model | Elastic continuum |
| Scheme 1 | Scheme 2 | Scheme 3 | |
|---|---|---|---|
| ht/∆x | 12 | 16 | 20 |
| Dt/∆x | 45 | 60 | 75 |
| Particles of the target plate | 115,248 | 260,400 | 524,800 |
| Particles of the ice ball | 44,388 | 105,216 | 205,304 |
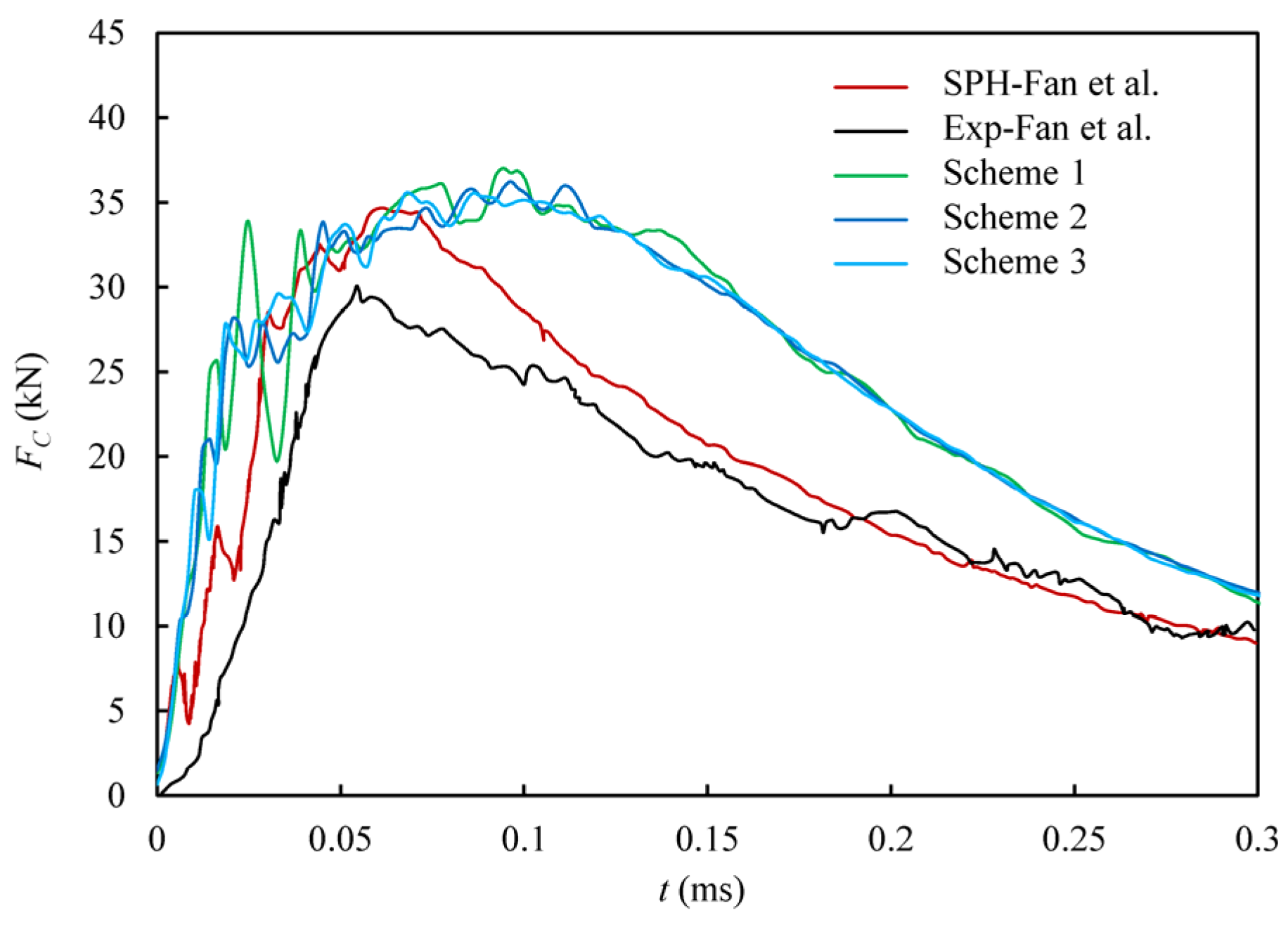
| Maximum impact force FCmax | 36.86 kN | 36.25 kN | 35.56 kN |
| Error between numerical results obtained from this work and Ref. [56] | 6.3% | 4.5% | 5.4% |
| Error between numerical and experimental results obtained from this work and Ref. [56], respectively | 16.7% | 14.8% | 15.3% |
| Item | Value/Description |
|---|---|
| Density | 1500 kg/m3 |
| Elastic modulus | 2.10 GPa |
| Poisson’s ratio | 0.33 |
| Material model | Elastic continuum |
| Item | FCmax (kN) | FCymax (kN) | FCzmax (kN) |
|---|---|---|---|
| 60° | 297.8 | 129.3 | −268.3 |
| 70° | 283.6 | 106.3 | −262.9 |
| 80° | 282.9 | 56.5 | −277.2 |
| 90° | 285.3 | −5.4 | −285.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, X.; Li, Z.; Zhang, J.; Zhao, J.; Jiao, Y. Numerical Study on High-Speed Icebreaking of a Hemispherically Capped Cylinder Based on the Smoothed Particle Hydrodynamics Method. J. Mar. Sci. Eng. 2025, 13, 1637. https://doi.org/10.3390/jmse13091637
Cai X, Li Z, Zhang J, Zhao J, Jiao Y. Numerical Study on High-Speed Icebreaking of a Hemispherically Capped Cylinder Based on the Smoothed Particle Hydrodynamics Method. Journal of Marine Science and Engineering. 2025; 13(9):1637. https://doi.org/10.3390/jmse13091637
Chicago/Turabian StyleCai, Xiaowei, Zhenwang Li, Jun Zhang, Jie Zhao, and Yanmei Jiao. 2025. "Numerical Study on High-Speed Icebreaking of a Hemispherically Capped Cylinder Based on the Smoothed Particle Hydrodynamics Method" Journal of Marine Science and Engineering 13, no. 9: 1637. https://doi.org/10.3390/jmse13091637
APA StyleCai, X., Li, Z., Zhang, J., Zhao, J., & Jiao, Y. (2025). Numerical Study on High-Speed Icebreaking of a Hemispherically Capped Cylinder Based on the Smoothed Particle Hydrodynamics Method. Journal of Marine Science and Engineering, 13(9), 1637. https://doi.org/10.3390/jmse13091637







