Predefined-Time Formation Tracking Control for Underactuated AUVs with Input Saturation and Output Constraints
Abstract
1. Introduction
- In contrast to work [42,43,44], the formation control method for underactuated AUVs proposed in our work provides the user with the freedom to adjust the maximum convergence time of formation error. Furthermore, considering the effect of actuator saturation on the predefined time formation control of the AUV, a new auxiliary dynamic system (ADS) is constructed to ensure the system stability within the predefined time.
- Different from the methods proposed in the work [45,46,47,48]. In this work, a universal time-varying asymmetric barrier function (UTABF) is introduced to achieve formation output constraint control of AUVs. The BLF can be applied to address more general dynamic constraint issues and can deal with both constrained and unconstrained cases without changing the control law.
- In this work, the active disturbance rejection control (ADRC) framework is utilized to design the predefined-time output constraint control method for AUV formation. The method eliminates dependence on exact AUV modeling and provides stronger anti-disturbance abilities.
2. Problem Formulation
2.1. AUV Dynamics and Assumptions
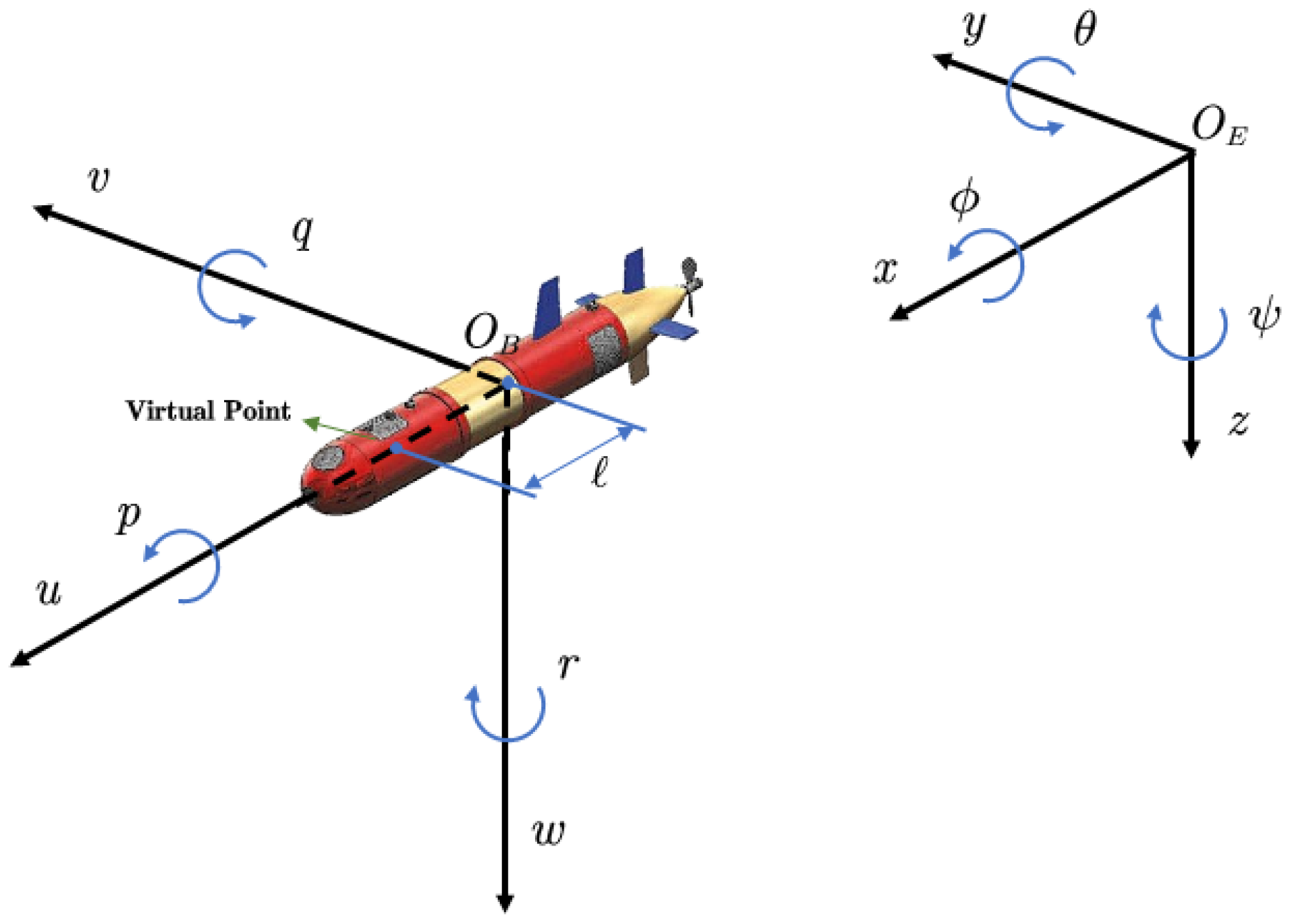
2.1.1. AUV Dynamics and Coordinate Transformation
2.1.2. Assumptions
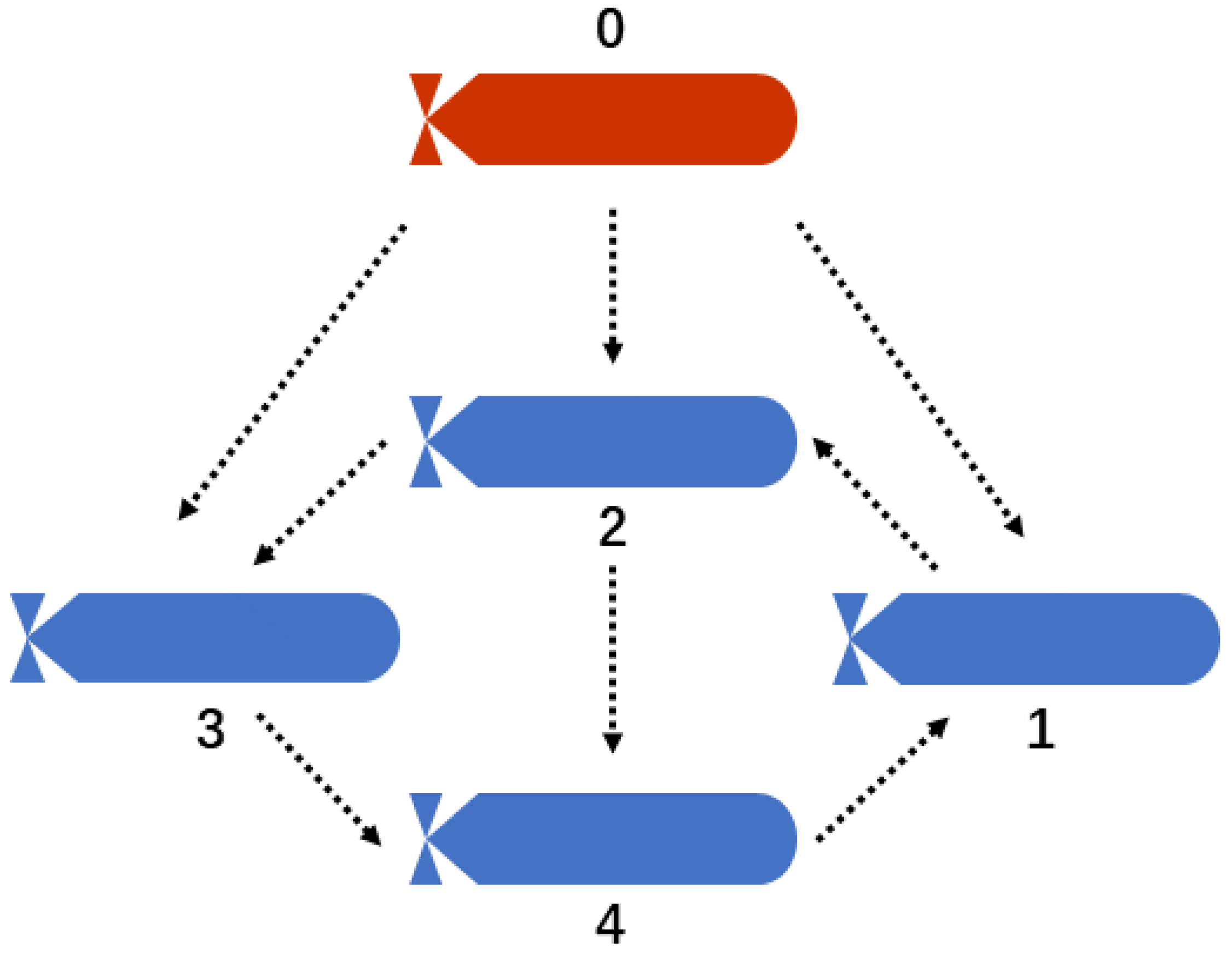
2.2. Graph Theory
2.3. Lemmas
3. Main Results
3.1. Nonlinear Transformation Function
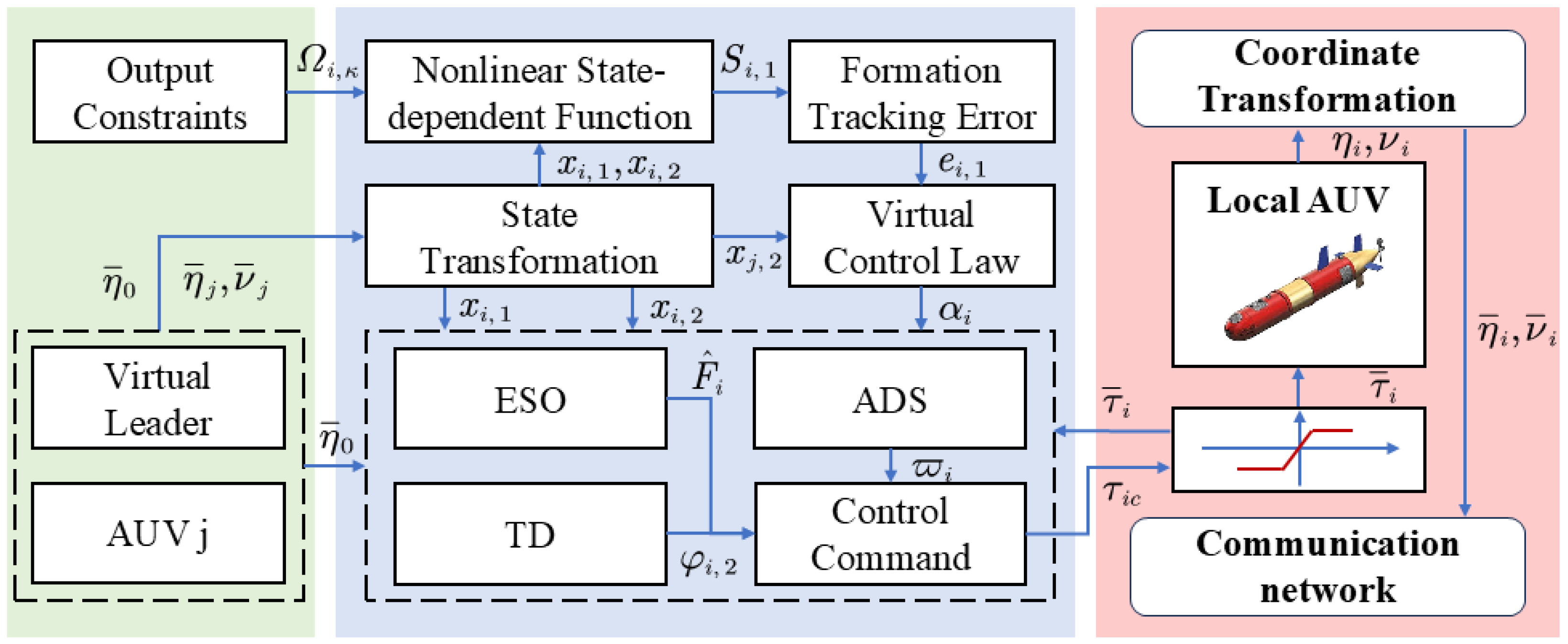
3.2. Distributed Predefined-Time Active Disturbance Rejection Formation Control Law Design
3.3. Stability Analysis
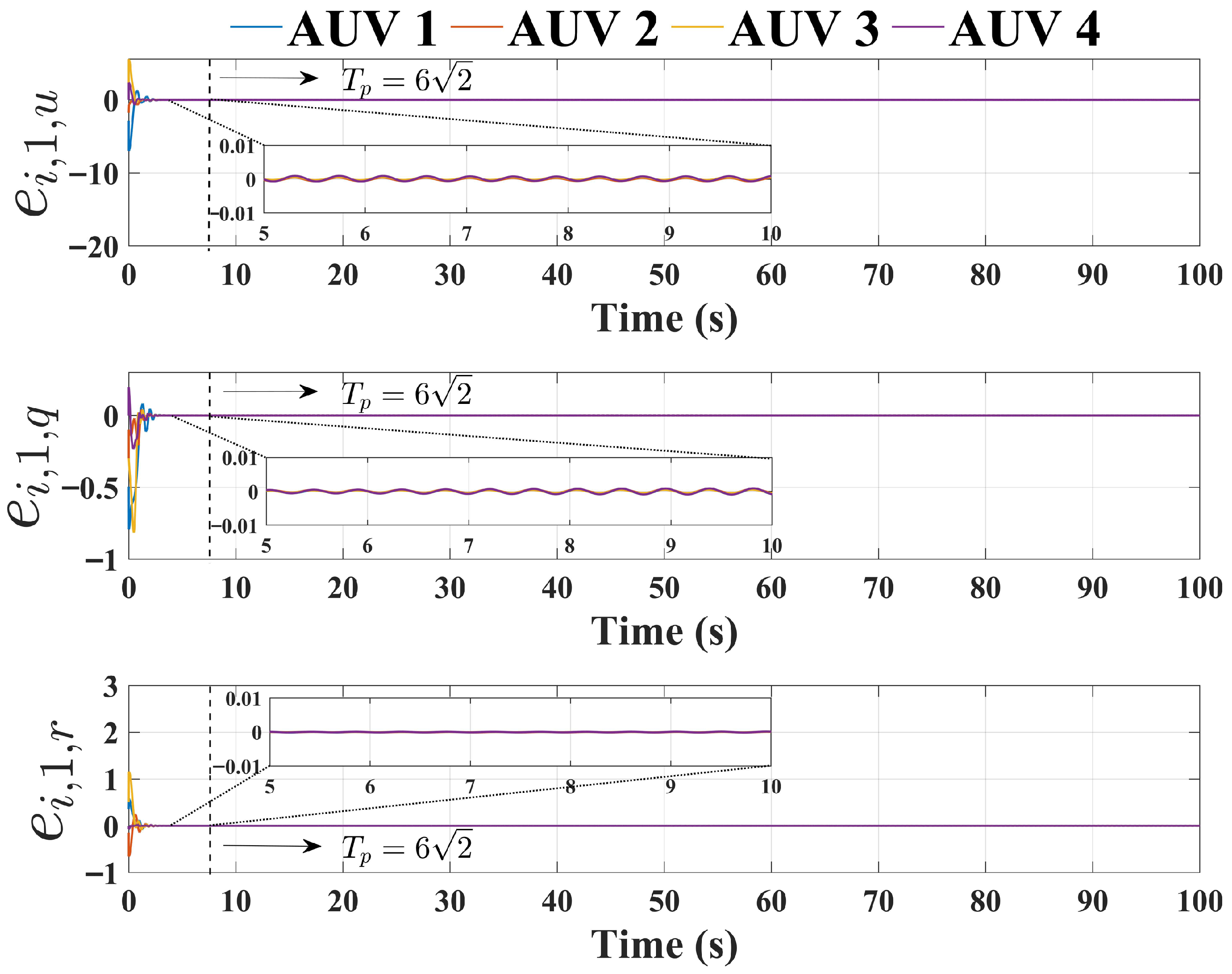
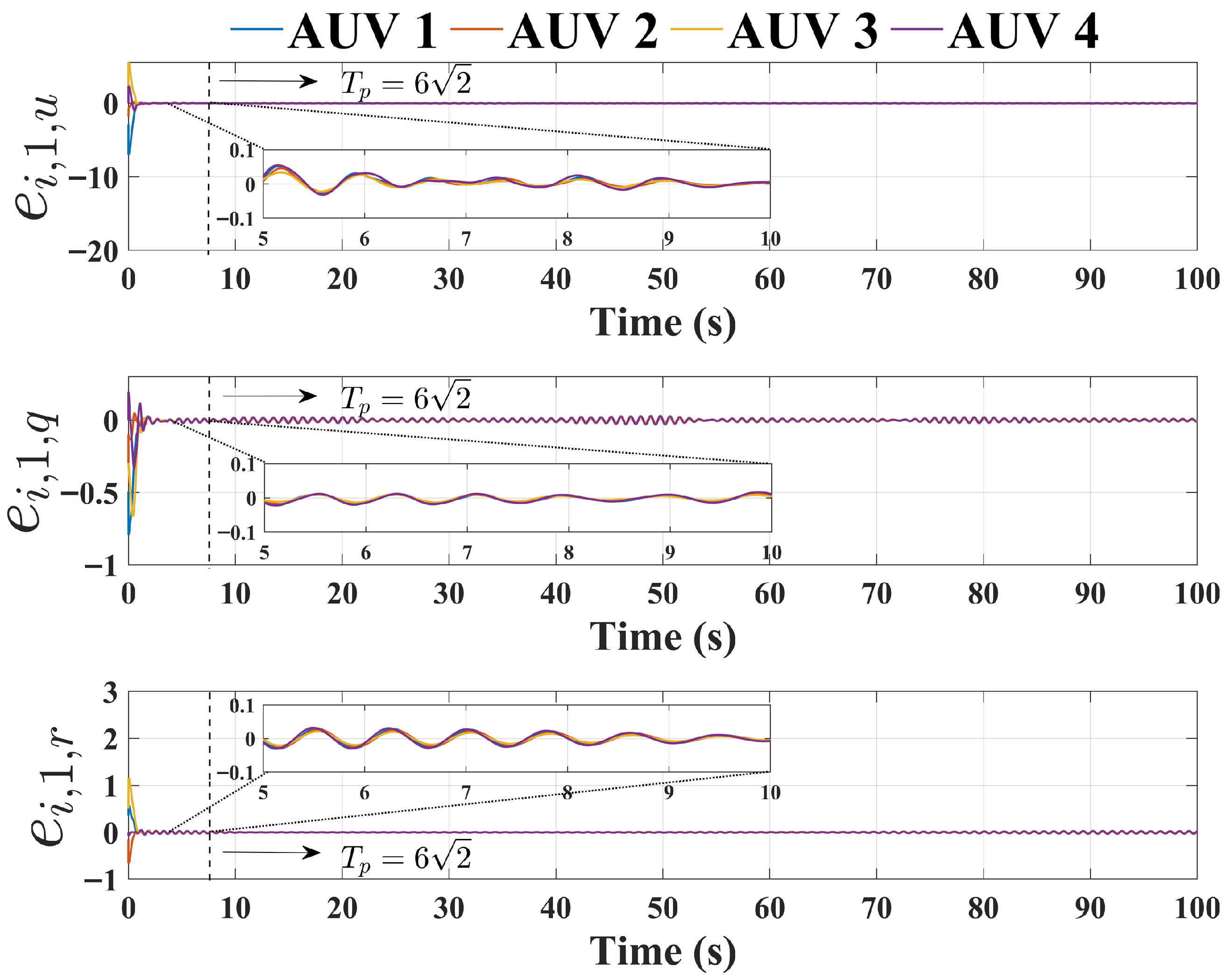
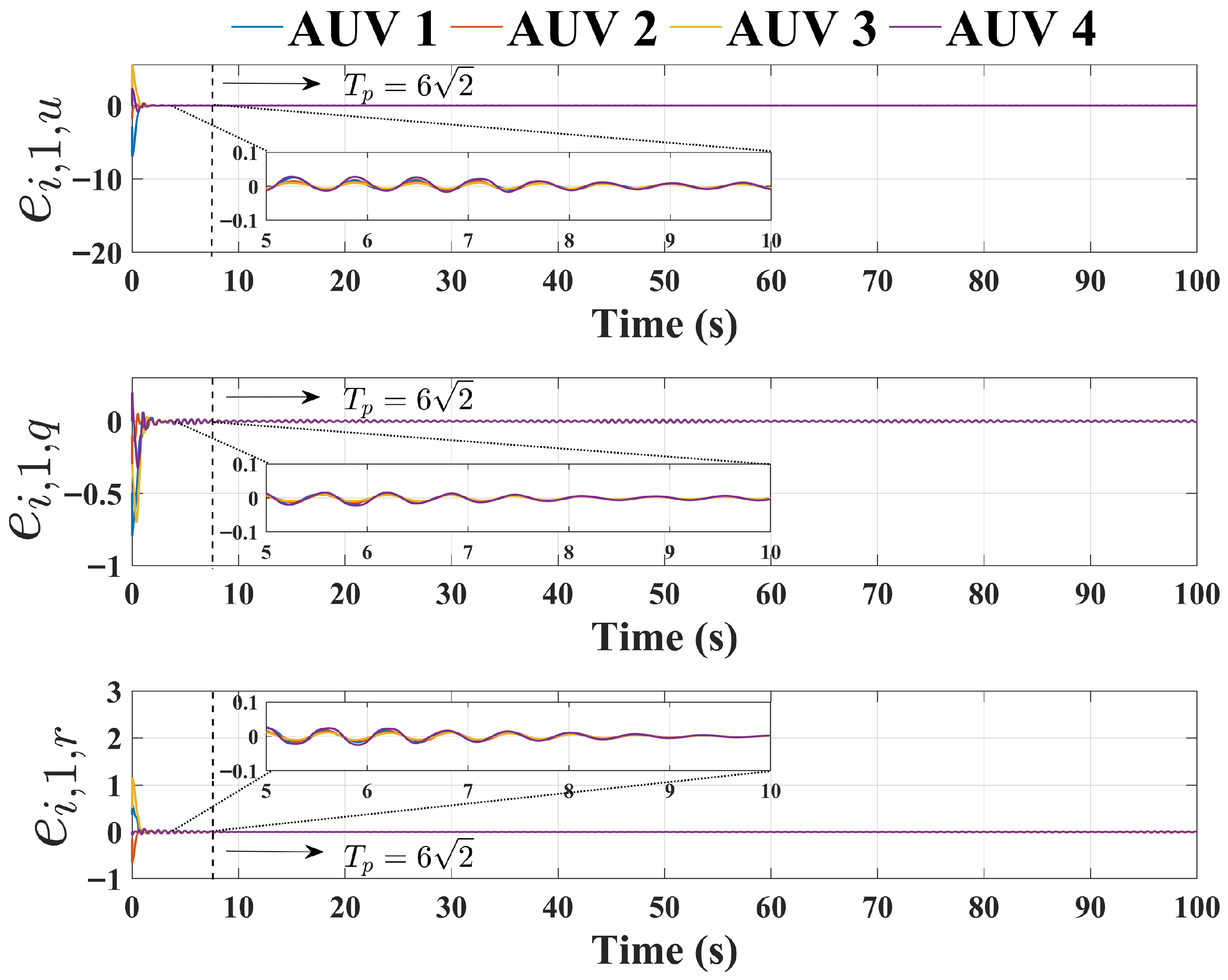
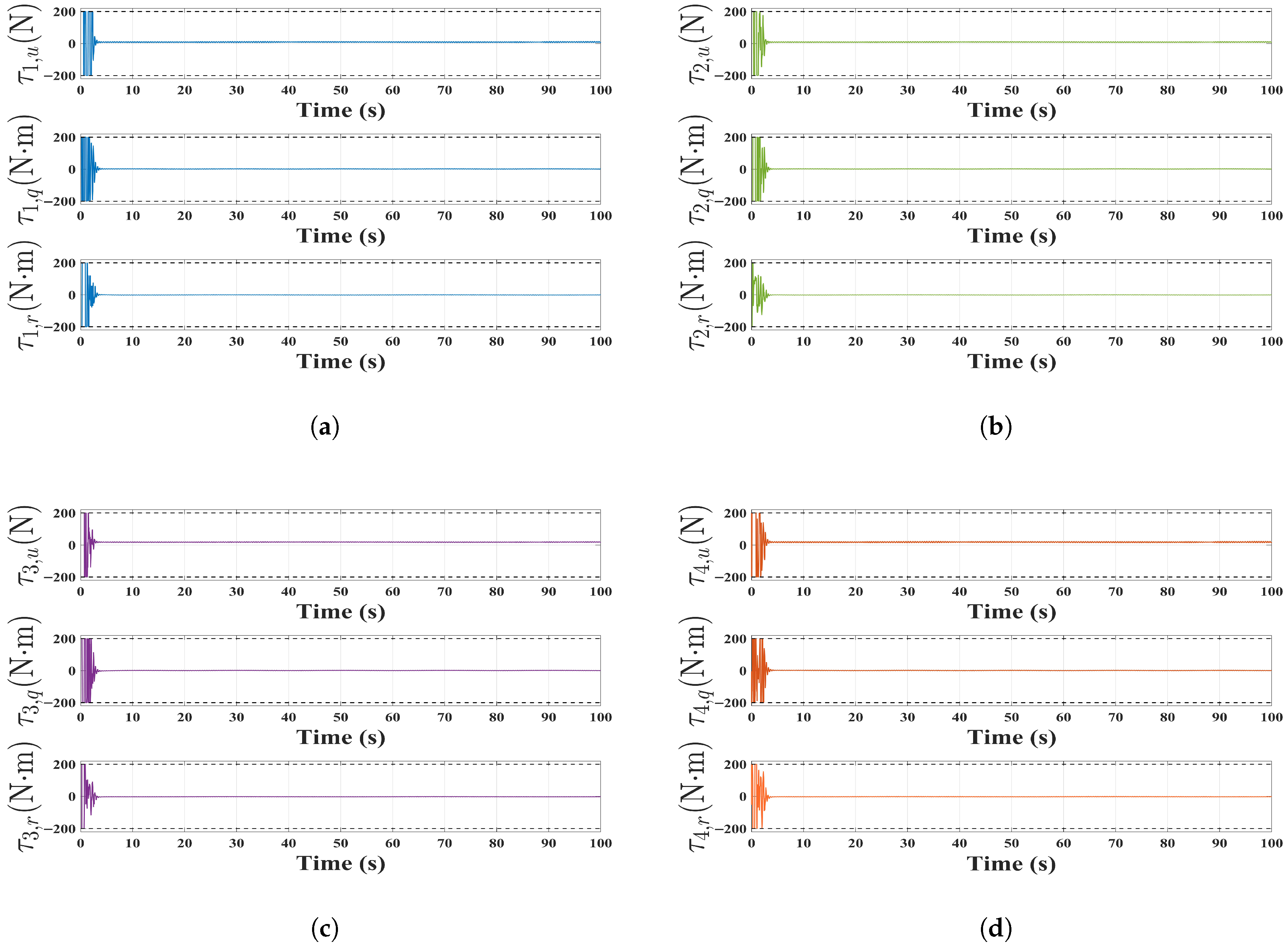
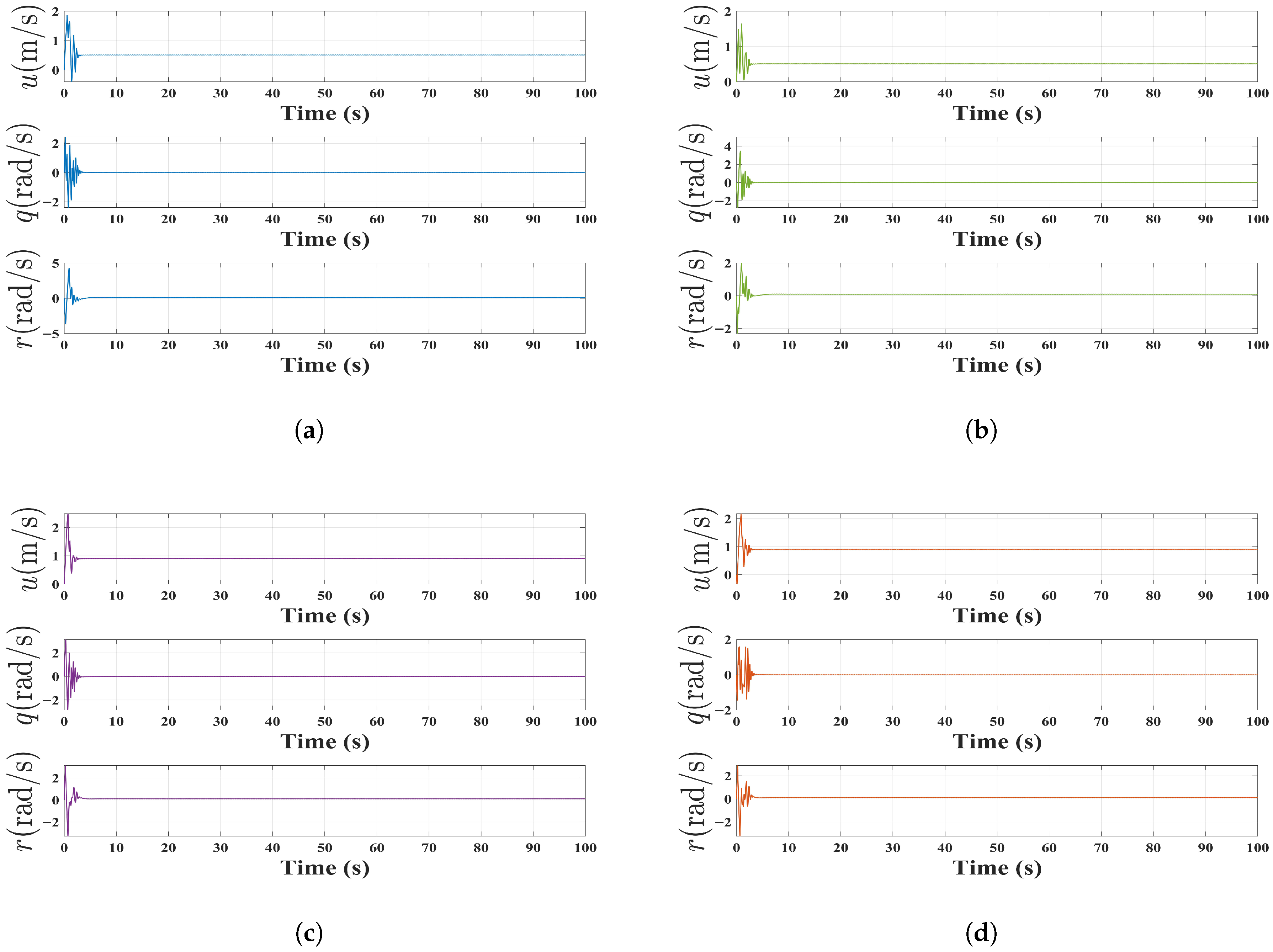
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Li, X.; Zhu, D. An adaptive SOM neural network method for distributed formation control of a group of AUVs. IEEE Trans. Ind. Electron. 2018, 65, 8260–8270. [Google Scholar] [CrossRef]
- Refsnes, J.E.; Sorensen, A.J.; Pettersen, K.Y. Model-based output feedback control of slender-body underactuated AUVs: Theory and experiments. IEEE Trans. Control Syst. Technol. 2008, 16, 930–946. [Google Scholar] [CrossRef]
- Er, M.J.; Gong, H.; Liu, Y.; Liu, T. Intelligent trajectory tracking and formation control of underactuated autonomous underwater vehicles: A critical review. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 543–555. [Google Scholar] [CrossRef]
- Zhang, J.; Xiang, X.; Li, W.; Zhang, Q. Adaptive saturated path following control of underactuated AUV with unmodeled dynamics and unknown actuator hysteresis. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6018–6030. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Nikou, A.; Dimarogonas, D.V. Robust trajectory tracking control for underactuated autonomous underwater vehicles in uncertain environments. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1288–1301. [Google Scholar] [CrossRef]
- Bhat, S.; Panteli, C.; Stenius, I.; Dimarogonas, D.V. Nonlinear model predictive control for hydrobatics: Experiments with an underactuated AUV. J. Field Robot. 2023, 40, 1840–1859. [Google Scholar] [CrossRef]
- Rout, R.; Subudhi, B. Design of line-of-sight guidance law and a constrained optimal controller for an autonomous underwater vehicle. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 416–420. [Google Scholar] [CrossRef]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Gravdahl, J.T.; Sørensen, A.J.; Milovanović, M.; Bruzzone, G. Integral line-of-sight guidance and control of underactuated marine vehicles: Theory, simulations, and experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Zhao, Y.; Ghosh, B.K. Finite-time velocity-free rendezvous control of multiple AUV systems with intermittent communication. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6618–6629. [Google Scholar] [CrossRef]
- Sedghi, F.; Arefi, M.M.; Abooee, A.; Kaynak, O. Adaptive robust finite-time nonlinear control of a typical autonomous underwater vehicle with saturated inputs and uncertainties. IEEE/ASME Trans. Mechatron. 2020, 26, 2517–2527. [Google Scholar] [CrossRef]
- Qin, J.; Du, J.; Li, J. Adaptive finite-time trajectory tracking event-triggered control scheme for underactuated surface vessels subject to input saturation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8809–8819. [Google Scholar] [CrossRef]
- Hu, J.; Chen, B.; Ghosh, B.K. Formation–circumnavigation switching control of multiple ODIN systems via finite-time intermittent control strategies. IEEE Trans. Control Netw. Syst. 2024, 11, 1986–1997. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Fixed-time sliding mode formation control of AUVs based on a disturbance observer. IEEE/CAA J. Autom. Sin. 2020, 7, 539–545. [Google Scholar] [CrossRef]
- Wang, P.; Yu, C.; Lv, M. Optimized Formation Control of Nonlinear Systems With Full-State Constraints Using Adaptive Fixed-Time Techniques. IEEE Trans. Autom. Sci. Eng. 2025, 22, 3331–3344. [Google Scholar] [CrossRef]
- Ju, X.; Jiang, Y.; Jing, L.; Liu, P. Quantized predefined-time control for heavy-lift launch vehicles under actuator faults and rate gyro malfunctions. ISA Trans. 2023, 138, 133–150. [Google Scholar] [CrossRef]
- Guo, C.; Hu, J. Time base generator-based practical predefined-time stabilization of high-order systems with unknown disturbance. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2670–2674. [Google Scholar] [CrossRef]
- Yu, C.; Xiang, X.; Wilson, P.A.; Zhang, Q. Guidance-error-based robust fuzzy adaptive control for bottom following of a flight-style AUV with saturated actuator dynamics. IEEE Trans. Cybern. 2019, 50, 1887–1899. [Google Scholar] [CrossRef]
- Zong, G.; Sun, H.; Nguang, S.K. Decentralized adaptive neuro-output feedback saturated control for INS and its application to AUV. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5492–5501. [Google Scholar] [CrossRef]
- Van, M.; Sun, Y.; Mcllvanna, S.; Nguyen, M.N.; Zocco, F.; Liu, Z. Control of multiple AUV systems with input saturations using distributed fixed-time consensus fuzzy control. IEEE Trans. Fuzzy Syst. 2024, 32, 3142–3153. [Google Scholar] [CrossRef]
- Ebrahimpour, M.; Lungu, M. Fault-Tolerant Robust Fast Finite-Time Path-Following Control for Underactuated AUVs With Actuator Dynamics and Saturation. J. Field Robot. 2025. [Google Scholar] [CrossRef]
- Alattas, K.A.; Vu, M.T.; Mofid, O.; El-Sousy, F.F.; Alanazi, A.K.; Awrejcewicz, J.; Mobayen, S. Adaptive nonsingular terminal sliding mode control for performance improvement of perturbed nonlinear systems. Mathematics 2022, 10, 1064. [Google Scholar] [CrossRef]
- Liu, H.; Zhen, S.; Liu, X.; Zheng, H.; Gao, L.; Chen, Y.H. Robust approximate constraint following control design for collaborative robots system and experimental validation. Robotica 2024, 42, 3957–3975. [Google Scholar] [CrossRef]
- Wang, J.; Dong, H.; Chen, F.; Vu, M.T.; Shakibjoo, A.D.; Mohammadzadeh, A. Formation control of non-holonomic mobile robots: Predictive data-driven fuzzy compensator. Mathematics 2023, 11, 1804. [Google Scholar] [CrossRef]
- Qian, Y.; Hu, D.; Chen, Y.; Fang, Y.; Hu, Y. Adaptive neural network-based tracking control of underactuated offshore ship-to-ship crane systems subject to unknown wave motions disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3626–3637. [Google Scholar] [CrossRef]
- Shen, Z.; Zhou, L.; Yang, Y.; Liu, Y.; Yu, H. Dynamic event-triggered ADP optimized tracking control of marine surface vessels with asymmetric time-varying full-state constraint. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7352–7362. [Google Scholar] [CrossRef]
- Xu, L.X.; Ma, H.J.; Guo, D.; Xie, A.H.; Song, D.L. Backstepping sliding-mode and cascade active disturbance rejection control for a quadrotor UAV. IEEE/ASME Trans. Mechatron. 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Liu, C.; Yue, X.; Zhang, J.; Shi, K. Active disturbance rejection control for delayed electromagnetic docking of spacecraft in elliptical orbits. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2257–2268. [Google Scholar] [CrossRef]
- Liu, Y.; Li, W.; Dong, X.; Ren, Z. Resilient formation tracking for networked swarm systems under malicious data deception attacks. Int. J. Robust Nonlinear Control 2025, 35, 2043–2052. [Google Scholar] [CrossRef]
- Chen, J.; Li, M.; Marcantoni, M.; Jayawardhana, B.; Wang, Y. Range-only Distributed Safety-Critical Formation Control based on Contracting Bearing Estimators and Control Barrier Functions. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [PubMed]
- Liu, Z.; Lai, G.; Zhang, Y.; Chen, C.L.P. Adaptive neural output feedback control of output-constrained nonlinear systems with unknown output nonlinearity. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1789–1802. [Google Scholar] [PubMed]
- Li, B.; Wen, S.; Yan, Z.; Wen, G.; Huang, T. A survey on the control lyapunov function and control barrier function for nonlinear-affine control systems. IEEE/CAA J. Autom. Sin. 2023, 10, 584–602. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Chairez, I.; Poznyak, A. Sliding-mode control of full-state constraint nonlinear systems: A barrier Lyapunov function approach. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6593–6606. [Google Scholar] [CrossRef]
- Fuentes-Aguilar, R.Q.; Chairez, I. Adaptive tracking control of state constraint systems based on differential neural networks: A barrier Lyapunov function approach. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5390–5401. [Google Scholar] [CrossRef]
- Liang, X.; Ge, S.S. Zone barrier Lyapunov functions for state constrained systems. IEEE Trans. Instrum. Meas. 2023, 72, 3001911. [Google Scholar] [CrossRef]
- Sun, W.; Su, S.F.; Wu, Y.; Xia, J.; Nguyen, V.T. Adaptive fuzzy control with high-order barrier Lyapunov functions for high-order uncertain nonlinear systems with full-state constraints. IEEE Trans. Cybern. 2019, 50, 3424–3432. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.J.; Tong, S.; Chen, C.P.; Li, D.J. Adaptive NN control using integral barrier Lyapunov functionals for uncertain nonlinear block-triangular constraint systems. IEEE Trans. Cybern. 2016, 47, 3747–3757. [Google Scholar] [CrossRef]
- Yuan, F.; Liu, Y.J.; Liu, L.; Lan, J.; Li, D.; Tong, S.; Chen, C.P. Adaptive neural consensus tracking control for nonlinear multiagent systems using integral barrier Lyapunov functionals. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4544–4554. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y. Neuroadaptive robotic control under time-varying asymmetric motion constraints: A feasibility-condition-free approach. IEEE Trans. Autom. Control 2020, 50, 15–24. [Google Scholar] [CrossRef]
- Feng, Z.; Li, R.B.; Zhang, W.; Qiu, J.; Jiang, Z. Neuroadaptive output-feedback tracking control for stochastic nonlower triangular nonlinear systems with dead-zone input. IEEE Trans. Cybern. 2024, 54, 7839–7850. [Google Scholar] [CrossRef]
- Long, H.; Zhang, P.; Guo, T.; Zhao, J. Saturated Adaptive Fuzzy Fixed-Time Nonsingular Integral Terminal Sliding-Mode Control of AUVs. IEEE Trans. Cybern. 2025, 55, 1634–1647. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, D.; Pang, W.; Luo, C. A novel obstacle avoidance consensus control for multi-AUV formation system. IEEE/CAA J. Autom. Sin. 2023, 10, 1304–1318. [Google Scholar] [CrossRef]
- Feng, Z.; Yao, S. Dynamic event-triggered active disturbance rejection formation control for constrained underactuated AUVs. IEEE/CAA J. Autom. Sin. 2025, 12, 460–462. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y. Adaptive fuzzy tracking control of autonomous underwater vehicles with output constraints. IEEE Trans. Fuzzy Syst. 2020, 29, 1311–1319. [Google Scholar] [CrossRef]
- Dai, S.L.; He, S.; Wang, M.; Yuan, C. Adaptive neural control of underactuated surface vessels with prescribed performance guarantees. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3686–3698. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hua, C.; Sun, Z.; Zhang, B.; Luo, X.; Chen, J. Hemispherical Space Constrained Velocity Free Control of UUVs via a Coupled Funnel Scheme. IEEE Trans. Ind. Electron. 2024, 72, 7452–7461. [Google Scholar] [CrossRef]
- Zhu, Z.; Ma, J.; Sun, H.; Wang, W.; Zhao, H.; Lee, T.H. Game-theoretic optimization toward diffeomorphism-based robust control of fuzzy dynamical systems with state and input constraints. IEEE Trans. Fuzzy Syst. 2023, 32, 373–387. [Google Scholar] [CrossRef]
- Xu, J.; Cui, Y.; Xing, W.; Huang, F.; Du, X.; Yan, Z.; Wu, D. Distributed active disturbance rejection formation containment control for multiple autonomous underwater vehicles with prescribed performance. Ocean Eng. 2022, 259, 112057. [Google Scholar] [CrossRef]
- Du, J.; Li, J.; Lewis, F.L. Distributed 3-D time-varying formation control of underactuated AUVs with communication delays based on data-driven state predictor. IEEE Trans. Ind. Inform. 2022, 19, 6963–6971. [Google Scholar] [CrossRef]
- Gao, Z.; Guo, G. Command-filtered fixed-time trajectory tracking control of surface vehicles based on a disturbance observer. Int. J. Robust Nonlinear Control 2019, 29, 4348–4365. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time extended state observer-based trajectory tracking and point stabilization control for marine surface vessels with uncertainties and disturbances. Ocean Eng. 2019, 186, 106109. [Google Scholar] [CrossRef]
- Xu, H.; Cui, G.; Ma, Q.; Li, Z.; Hao, W. Fixed-time disturbance observer-based distributed formation control for multiple QUAVs. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2181–2185. [Google Scholar] [CrossRef]



| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 45 | 45 | ||
| −2.5 | 194.8 | ||
| −49 | 44.7 | ||
| −49 | 41.7 | ||
| 6.75 | 23.8 | ||
| −6.75 | 3.9 | ||
| 6.75 | 2.72 | ||
| −6.75 | 4.9 | ||
| 13.5 | 6.4 |
| Values | |
|---|---|
| Values | |
|---|---|
| Components | Parameters |
|---|---|
| Virtual control law (14) | , , , , , |
| TD (20) | , , , , , , , |
| ADS (21) | , |
| ESO (24) | , , , , |
| Command control law (25) | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, S.; Wang, Y.; Feng, Z. Predefined-Time Formation Tracking Control for Underactuated AUVs with Input Saturation and Output Constraints. J. Mar. Sci. Eng. 2025, 13, 1607. https://doi.org/10.3390/jmse13091607
Yao S, Wang Y, Feng Z. Predefined-Time Formation Tracking Control for Underactuated AUVs with Input Saturation and Output Constraints. Journal of Marine Science and Engineering. 2025; 13(9):1607. https://doi.org/10.3390/jmse13091607
Chicago/Turabian StyleYao, Sibo, Yiqi Wang, and Zhiguang Feng. 2025. "Predefined-Time Formation Tracking Control for Underactuated AUVs with Input Saturation and Output Constraints" Journal of Marine Science and Engineering 13, no. 9: 1607. https://doi.org/10.3390/jmse13091607
APA StyleYao, S., Wang, Y., & Feng, Z. (2025). Predefined-Time Formation Tracking Control for Underactuated AUVs with Input Saturation and Output Constraints. Journal of Marine Science and Engineering, 13(9), 1607. https://doi.org/10.3390/jmse13091607






