Weak Fault Feature Extraction for AUV Thrusters with Multi-Input Signals

Abstract

This paper investigates weak fault feature extraction in AUV thrusters under multi-input signal conditions. Conventional methods often rely on insufficient input signals, leading to a non-monotonic mapping between fault features and fault severity. This, in turn, makes accurate fault severity identification infeasible. To overcome this limitation, this paper increases the number of input signals by utilizing all available measurable signals. To address the problems arising from the expanded signal set, a signal denoising method that combines Feature Mode Decomposition and wavelet denoising is proposed. Furthermore, a signal enhancement technique that integrates energy operators and the Modified Bayes method. Additionally, distinct technical approaches for noise reduction and enhancement are specifically designed for different input signals. Unlike conventional methods that extract features directly from raw input signals, for fault feature extraction and fusion, this study transforms the signals into the time, frequency, and time–frequency domains, extracting diverse fault features across these domains. A sensitivity factor selection method is then employed to identify the sensitive features. These selected features are subsequently fused using Dempster–Shafer evidence theory to construct the final fault feature. Finally, fault severity identification is carried out using the classical grey relational analysis. Pool experiments using the “Beaver II” AUV prototype validate the effectiveness of the proposed method.

1. Introduction

With the ongoing depletion of non-renewable terrestrial resources, the development of marine resources has accelerated [1,2,3]. Advanced equipment is essential in this process, and autonomous underwater vehicles (AUVs) play a pivotal role due to their high maneuverability and wide operational range, making them indispensable tools for marine exploration and exploitation [4,5,6].

AUVs operate autonomously and without cables in complex marine environments, making real-time human monitoring and control difficult. Consequently, safety has become a critical focus in both AUV development and practical deployment [7,8]. Fault diagnosis is a key technology for ensuring AUV safety. Among various components, thrusters are both essential and common sources of failure, with their malfunction having a significant impact on overall system reliability [9,10]. Early-stage faults in thrusters are typically weak faults, often characterized by a power loss of less than 10% [11,12]. Detecting these faults at an early stage and enabling timely decision-making is essential for preventing more severe damage and system failure [12,13]. Therefore, research on weak fault diagnosis for thrusters holds substantial practical significance for enhancing the operational safety of AUVs [11,14].

The thruster fault diagnosis process typically involves several key stages: signal denoising, signal enhancement, fault feature extraction, feature fusion, and fault severity identification [11,15]. This paper focuses on the stages of signal denoising, signal enhancement, and fault feature fusion, aiming to establish a robust technical foundation for subsequent fault severity identification.

This section provides a brief review of traditional methods used for AUV thruster fault signal denoising, signal enhancement, and feature fusion. For signal denoising, conventional techniques include wavelet denoising, sparse decomposition, etc. For example, Zhang et al. [15] employed wavelet denoising to reduce noise in AUV thruster signals, while Jiang et al. [16] applied sparse decomposition to isolate fault signals from background noise. In terms of signal enhancement, commonly used methods include the Modified Bayesian (MB) approach and neural networks. Cui et al. [11] utilized the MB method to enhance thruster signals, and Shi et al. [17] adopted neural networks for the same purpose. Regarding fault feature fusion, traditional methods often rely on Dempster–Shafer (D–S) evidence theory and neural networks. Fan et al. [18] used D–S evidence theory to fuse fault features, whereas Liu et al. [19] applied neural networks for feature fusion. While these approaches have shown satisfactory performance in diagnosing strong faults (with thrust loss greater than 10%), they are generally inadequate for detecting weak faults (with thrust loss less than 10%) [11,12,15]. Currently, there is no mature theoretical framework or universally accepted methodology for effective weak fault feature extraction in AUV thrusters [11,12,15].

The conventional technical approach for signal denoising and enhancement typically combines wavelet denoising with MB enhancement [11,15]. However, when applied to fault feature extraction in AUV thrusters, the mapping between fault features and fault severity is non-monotonic. To address this issue, [15] proposed the peak region energy method. Building on this foundation, the study integrated wavelet denoising, MB enhancement, evidence theory, and the wavelet peak region energy method into a unified feature fusion framework—hereinafter referred to as the “conventional method.” This approach effectively resolved the non-monotonic mapping between fused fault features and fault severity in cases of strong faults [15]. However, when applied to weak faults, the problem of non-monotonicity in the mapping relationship remains unresolved. An analysis of the root causes reveals that the conventional method relies on only two homogeneous input signals: the surge velocity signal and the main thruster voltage signal. Homogeneous signals are defined as signals that exhibit strong mutual correlation. In this case, surge velocity is directly controlled by the main thruster voltage, resulting in a high degree of correlation between the two signals. This limited input restricts the available fault-related information, making it difficult to effectively extract weak fault features.

Based on the above analysis, effectively extracting weak fault features requires incorporating additional heterogeneous input signals, such as the yaw angle signal and lateral thruster voltage signal. However, experimental results in this study reveal that when new input signals are added, the conventional method fails to maintain a monotonic mapping between the extracted fault features and fault severity. This non-monotonic relationship hinders the accurate identification of fault severity, rendering the conventional method ineffective under multi-input conditions for weak faults. Further research in this study reveals that, under weak fault conditions, the conventional method exhibits limited effectiveness in noise reduction and signal enhancement across multiple input signals. Moreover, the denoising and enhancement effects vary considerably among different input signals, leading to inconsistent fault feature extraction. These findings highlight the need for novel approaches to signal denoising and enhancement. In addition, due to the distinct characteristics of each input signal, it is essential to design signal-specific approaches for denoising, enhancement, and fault feature fusion.

Key contributions of this paper are as follows:

• Conventional methods are constrained by an insufficient number of input signals, leading to a non-monotonic mapping between extracted fault features and fault severity in the context of weak faults. Consequently, subsequent fault severity identification becomes infeasible. To overcome this limitation, this study expands the input set by incorporating all available measurable signals.
• Increasing the number of input signals introduces challenges in signal denoising and enhancement. Specifically, the conventional method demonstrates limited effectiveness in reducing noise and enhancing features across multi-input signals, with substantial variability in performance across different signal types. This inconsistency adversely affects the results of subsequent feature fusion. To address this issue, this paper proposes a denoising method that integrates Feature Mode Decomposition (FMD) with wavelets, along with a signal enhancement approach that combines energy operators with the Modified Bayesian (MB) method. Moreover, the study adopts signal-specific strategies for denoising, enhancement, and fault feature fusion, tailored to the specific characteristics of each input signal.
• The expansion of input signal quantity introduces a challenge in fault feature extraction and fusion: the mapping between extracted fault features and fault severity becomes non-monotonic, thereby preventing accurate fault severity identification. To overcome this issue, this study proposes a multi-domain fault feature extraction and fusion method based on sensitive feature selection and evidence theory. Unlike conventional approaches that extract features solely from the raw input signals, the proposed method derives multiple fault features from the time, frequency, and time–frequency domains. A sensitivity analysis method is introduced to select the most relevant fault features, and multi-feature fusion is performed using evidence theory to obtain the final weak fault features of the thruster. Finally, weak fault severity is identified using grey relational theory.

2. General Ideas of the Proposed Method

In this section, three problems existing in the conventional method are briefly described. And the solutions, the overall structure of the proposed method, and its differences from the conventional method, are explained.

2.1. Problems with Conventional Methods and Corresponding Solutions of the Proposed Method

This subsection describes the problems encountered when the conventional fault feature extraction method is applied to weak faults in AUV thrusters, as well as the solutions proposed in this paper.

Problem 1: The conventional method involves a limited number of input signals, comprising merely two homogeneous input signals, namely the surge velocity and main thruster voltage. This results in a non-monotonic mapping relationship between fault features and fault severity during the extraction of weak fault features, subsequently impeding the subsequent identification of fault severity.

Solution to Problem 1: The proposed method increases the number of heterogeneous input signals. By incorporating the lateral thruster voltage signal and yaw angle signal into the original inputs, namely the surge velocity signal and main thruster voltage signal, the problem of insufficient input information for weak fault feature extraction is resolved.

Problem 2: After increasing the number of input signals, the conventional method exhibits poor denoising and enhancement performance across multi-input signals—specifically the surge velocity signal, yaw angle signal, lateral thruster voltage signal, and main thruster voltage signal. The denoising and enhancement effects vary significantly among different input signals, which negatively impacts subsequent feature fusion. Subsequently, this impacts the identification of the severity of subsequent faults.

Solution to Problem 2: This paper proposes a novel method for signal denoising and enhancement, and devises distinct technical approaches for signal denoising and enhancement tailored to various input signals. For signal denoising, a denoising method combining FMD and wavelets is proposed. The introduction of FMD aims to address the problem of frequency band aliasing between fault signals and external interferences under weak fault conditions. For signal enhancement, an enhancement method combining the energy operator and MB is proposed. The incorporation of the energy operator aims to tackle the problem of weak transient variations under weak fault conditions. Additionally, distinct denoising and enhancement technical routes are designed for different input signals, resolving the inconsistent performance of the conventional method across multiple input signals.

Problem 3: After increasing the number of input signals, the conventional method still suffers from a non-monotonic mapping between fault features and fault severity during feature extraction and fusion, which prevents subsequent fault severity identification.

Solution to Problem 3: The proposed method extracts multiple fault features from the time, frequency, and time–frequency domains of input signals. A sensitivity factor selection method is then introduced to select sensitive features from these multiple features. Finally, multi-sensitive fusion based on D-S evidence theory is applied to obtain the final thruster weak fault features, thereby resolving the non-monotonic mapping problem between fault features and severity.

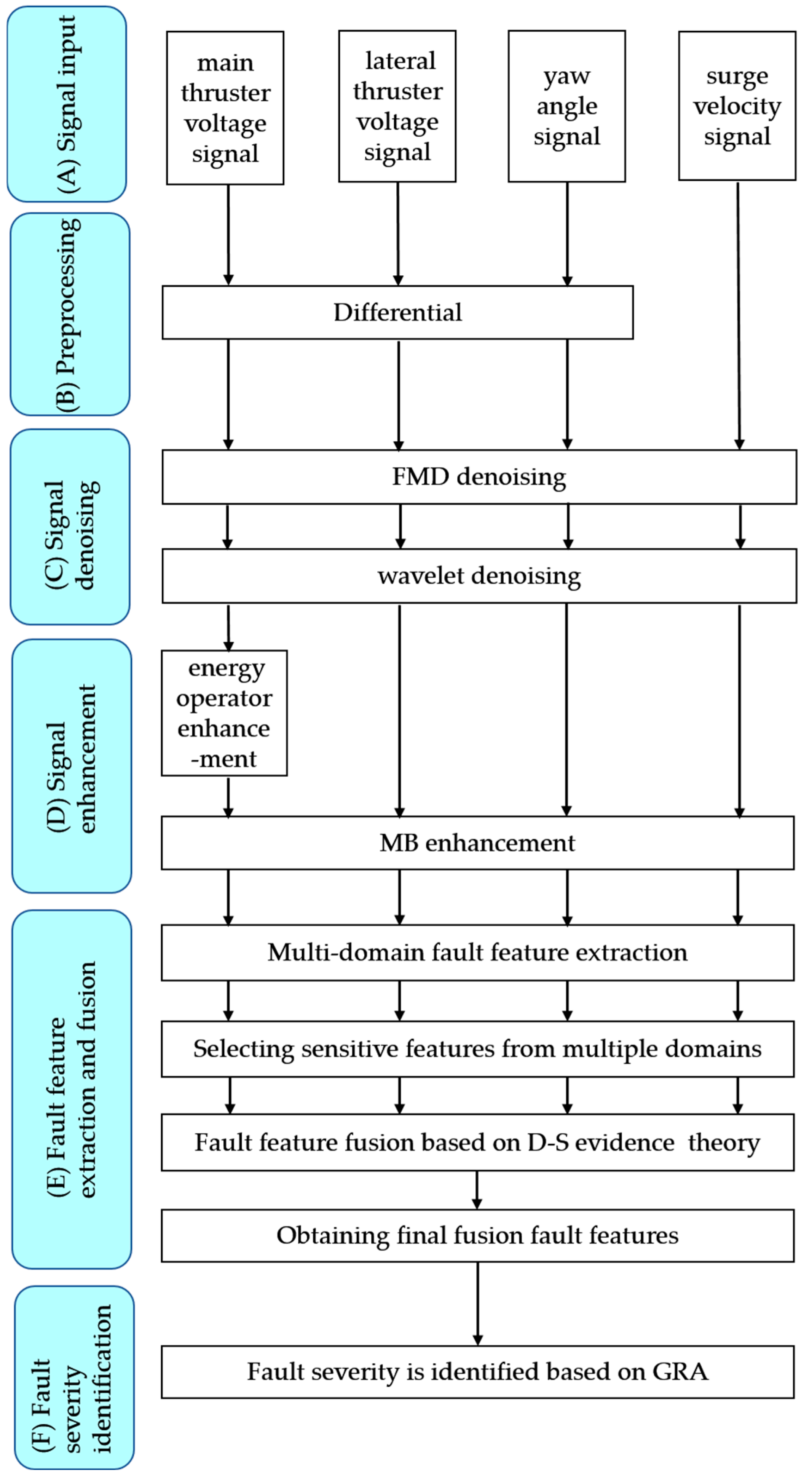
2.2. Overall Structure of the Proposed Method

Based on the solution of the proposed method presented in Section 2.1, the overall structure of the proposed method is illustrated in Figure 1.

Combined with Figure 1, the overall structure of the proposed method is described as follows:

(A)

Signal input

The input signals include the surge velocity signal, yaw angle signal, lateral thruster voltage signal, and main thruster voltage signal.

(B)

Preprocessing

Differential preprocessing is applied to the yaw angle, lateral thruster voltage, and main thruster voltage signal. Differentiation amplifies the rapidly changing components caused by faults. However, the surge velocity signal has measurement noise, and differential preprocessing is not effective; therefore, it is not differentiated.

(C)

Signal denoising

FMD and wavelets are applied to denoise all the input signals. Introduce FMD onto the traditional wavelet denoising to address the frequency band aliasing problem of weak fault signals and external interference, thereby enhancing the denoising effect on weak fault signals.

(D)

Signal enhancement

For the surge velocity, yaw angle, and lateral thruster voltage signal, signal enhancement is achieved using MB; for the main thruster voltage signal, enhancement is performed using an energy operator combined with MB. The energy operator is introduced to address the problem of weak transient variations in the main thruster voltage signal under weak fault conditions, thereby improving the enhancement effect on weak fault signals.

(E)

Fault feature extraction and fusion

This paper extracts a large number of fault features from the time domain, frequency domain, and time–frequency domain. The sensitivity factor selection method is employed to select sensitive features from these multi-domain features. Subsequently, fault feature fusion is conducted using D-S evidence theory to obtain the final fused fault features. This process resolves the non-monotonic mapping problem between the final fused fault features and fault severity under multi-input signal conditions during weak faults.

(F)

Fault severity identification

Fault severity is identified based on grey relational analysis (GRA).

2.3. Differences Between the Proposed Method and the Conventional Method

To illustrate the distinctions between the proposed method and the conventional method, the overall structure of the conventional method is presented in Figure 2.

Based on Figure 1 and Figure 2, the differences between the proposed method and the conventional method are described as follows:

(1)

Differences in input signals

The conventional method uses two input signals: the main thruster voltage signal and the surge velocity signal, which are fewer in number and homogeneous. The surge velocity signal is controlled by the main thruster voltage signal, indicating a strong correlation between the surge velocity signal and the main thruster voltage signal. In contrast, this paper introduces two additional signals: the lateral thruster voltage signal and the yaw angle signal. These signals are heterogeneous to the main thruster voltage signal and surge velocity signal. They are less controlled by the main thruster voltage signal and surge velocity signal, and their correlation with the latter is weaker.

(2)

Differences in signal denoising method

The conventional method employs wavelet denoising for signal denoising. In contrast, this paper introduces FMD and applies a method that combines FMD denoising and wavelet denoising to denoise all input signals.

(3)

Differences in signal enhancement method

The conventional method employs MB for signal enhancement. In contrast, for the main thruster voltage signal, this paper introduces an energy operator and proposes a hybrid methodology that integrates the energy operator with MB to enhance the main thruster voltage signal. Other input signals are enhanced using the traditional MB method.

(4)

Differences in fault feature extraction and fusion method

The conventional method only extracts fault features from the input signals themselves and fuses them. In contrast, this paper extracts multiple fault features from the time domain, frequency domain, and time–frequency domain of the input signals. Subsequently, a sensitivity factor selection method is applied to select sensitive features from these multi-domain features. Fault feature fusion is then performed using D-S evidence theory to obtain the final fused fault features. Finally, fault severity identification is conducted based on the classical GRA.

3. Implementation Process of the Proposed Method

In this section, the implementation processes of the three contributions are elaborated in detail.

3.1. Adding New Input Signals

(1) 

Problem and causal analysis

Problem 1: The conventional method involves only two homogeneous signals: the surge velocity signal and the main thruster voltage. This results in a non-monotonic mapping relationship between fault features and fault severity during the extraction of weak fault features, subsequently impeding the subsequent identification of fault severity.

To address Problem 1, the causes are analyzed as follows:

For strong faults, due to the strong fault features and high signal-to-noise ratio (SNR), the denoising and enhancement effects of the conventional method, combined with wavelet denoising and MB enhancement, are remarkable. However, for weak faults, the number of input signals is insufficient, with only a homogeneous surge velocity signal and the main thruster voltage signal utilized. With only two homogeneous signals available for weak faults, it becomes challenging to effectively extract their fault features. Hence, multi-type input signals are necessary for weak faults.

(2) 

Idea of the proposed method

Based on the above analysis, this paper incorporates all measurable signals as input signals. The original input signal includes the surge velocity signal and the main thruster voltage signal. Heterogeneous input signals—including the lateral thruster voltage signal and yaw angle signal—are introduced in addition to this original input signal. This resolves the problem of insufficient input information during weak fault feature extraction.

3.2. Signal Denoising and Enhancement Method

(1) 

Problem and causal analysis

Problem 2: The conventional denoising and enhancement method combines wavelet denoising and MB enhancement, demonstrating notable denoising and enhancement effects when dealing with strong faults and two homogeneous input signals. However, when it comes to weak faults and multiple heterogeneous input signals, the overall performance in denoising and enhancement is less than ideal, with considerable variations observed in the effects across different input signals.

To address Problem 2, the causes are analyzed as follows:

(A)

The intensity of weak fault signals is weaker than that of interference noise signals.

(B)

Frequency band aliasing occurs between weak fault signals and external interference, rendering their effective separation challenging. Wavelet denoising reduces noise by thresholding high-frequency coefficients (which typically contain noise). However, due to the low intensity of weak fault features, although wavelet denoising is effective in noise reduction, its effectiveness remains suboptimal. This, in turn, leads to inadequate performance of subsequent traditional MB enhancement.

(C)

For multiple heterogeneous input signals, each with distinct characteristics, the same denoising and enhancement method should not be uniformly applied. Instead, technical approaches for denoising and enhancement tailored to the specific characteristics of each signal type should be designed.

(2) 

Idea of the proposed method

Based on the above analysis, the methodology proposed in this paper is outlined as follows.

(A)

To resolve the problem of separating weak fault signals from interfering noise due to frequency band aliasing, this paper introduces FMD. FMD separates noise from fault information by adaptively adjusting bandwidth and excels in addressing overlaps between fault features and interference [20]. Thus, a denoising method for AUV thruster fault signals that combines wavelet denoising with FMD denoising is proposed.

(B)

To resolve the problem of weak fault signals relative to interference, this paper introduces the energy operator. Characterized by its capability to enhance the transient features of signals, the energy operator can amplify the transient variations in the main thruster voltage signal caused by faults [21,22]. Consequently, an enhancement method for AUV thruster fault signals that combines an energy operator with MB is proposed.

(C)

We design distinct denoising and enhancement technical routes for different input signals. The results of this study indicate that, across all input signal scenarios, the traditional processing workflow failed to achieve optimal processing performance for all signals. This workflow comprises two steps: first, applying a denoising method, followed by signal enhancement. Among these, the denoising method integrates the wavelet transform with FMD, while the enhancement method is based on the energy operator and MB. While incorporating the energy operator notably enhances the main thruster voltage signal, it yields insignificant improvements or even detrimental effects for the surge velocity signal, yaw angle signal, and lateral thruster voltage signal. Consequently, it is imperative to devise specific noise reduction and enhancement strategies for different input signals. Specifically, for the main thruster voltage signal, wavelet and FMD are employed for noise reduction, followed by energy operator and MB for enhancement; for the remaining three input signals, wavelet and FMD are used for noise reduction, with MB then applied for enhancement.

(3) 

Implementation of the proposed signal denoising and enhancement method

The implementation process and detailed steps of the proposed signal denoising and enhancement method are outlined as follows.

(A)

Signal preprocessing

Perform differential preprocessing on the three input signals: yaw angle signal, lateral thruster voltage signal, and main thruster voltage signal. The differential formula is as follows [15]:

$$\widehat{y}\left(n\right)={\displaystyle \frac{y\left(n+1\right)-y\left(n-1\right)}{2\mathsf{\Delta }t}}$$

(1)

where $y\left(n\right)$ represents the input signal, $y\left(n+1\right)$ denotes the signal at the $\left(n+1\right)$-th beat, and $y\left(n-1\right)$ signifies the signal at the $\left(n-1\right)$-th beat. The dimensions of $y\left(n\right)$ corresponding to the three input signals are as follows: the main thruster voltage and the lateral thruster voltage are in volts (V); the yaw angle is in degrees (°). $∆t$ stands for the sampling time interval. The experiment utilized a sampling frequency of 5 Hz (i.e., 5 samples per second). According to the sampling theorem, the theoretical time interval should be 0.2 s. To simplify subsequent data processing and analysis, this paper normalizes the time and uniformly maps the actual time interval to 1 beat (i.e., $∆t$ = 1 beat). Additionally, $\widehat{y}\left(n\right)$ signifies the differential at the nth beat, and its dimension is the same as that of $y\left(n\right)$.

(B)

FMD-based denoising

FMD-based denoising is applied to four preprocessed input signals, with the specific steps outlined as follows:

(a)

Mode decomposition

First, construct the FMD model. FMD seeks the solution to the following constrained problem [20]:

$$\underset{f_k\left(l\right)}{arg max} \left\{C{K}_M\left({\mathit{u}}_k\right)={\displaystyle \sum _{i=1}^N} {\left({\displaystyle \prod _{m=0}^M} u_k\left(i-m{T}_s\right)\right)}^2\right.\left./{\left({\displaystyle \sum _{i=1}^N} u_k(i{)}^2\right)}^{M+1}\right\}$$

(2)

$$s.t.u_k\left(n\right)={\displaystyle \sum _{l=1}^L} f_k\left(l\right) x\left(n-l+1\right)$$

(3)

where $x$ represents the preprocessed input signal, and the dimensions corresponding to the four input signals are as follows: the main thruster voltage and lateral thruster voltage are in volts (V), the yaw angle is in degrees (°), and the surge velocity is in meters per second (m/s). N denotes the length of the signal. $u_k$ signifies the $k$-th mode, where $k=2$ in this paper; $f_k$ stands for the $k$-th FIR filter, with a length of $L$, where $L=20$ in this paper; ${CK}_M$ indicates the correlation kurtosis of the mode; $M$ denotes the order of the shift; and $T_S$ represents the signal period in seconds (s), which corresponds to the first local maximum of the autocorrelation spectrum following the zero crossing point.

Next, solve the FMD model.

The iterative feature decomposition algorithm [23] is employed to address the constraint problem in Equation (2), resulting in $k$ modes.

(b)

Retain the modality with a low noise level

The specific steps are as follows:

(I)

Calculate the information entropy of each mode

The steps for information entropy are as follows [24]:

First, calculate the probability of each value occurring in each mode.

The complete set of values for the $k$-th mode $u_k$ is denoted as $W_k=\left\{w_k\left(1\right),w_k\left(2\right),\dots ,w_k\left({\theta }_k\right)\right\}$, where ${\theta }_k$ represents the total number of elements in the set $W_k$. The number of occurrences of each value within $W_k$ is given by $C_k=\left\{c_k\left(1\right),c_k\left(2\right),\dots ,c_k\left({\theta }_k\right)\right\}$. Then, the probability of each value occurring is calculated as follows:

$$p_k\left(i_k\right)={\displaystyle \frac{c_k\left(i_k\right)}{N}}$$

(4)

where $k$ denotes the number of modes and $i_k=\mathrm{1,2},\dots ,{\theta }_k$. The meanings of other symbols are consistent with those defined in the preceding equations.

Next, calculate the information entropy of each mode.

$$H_k=-{\displaystyle \sum _{i_k=1}^{{\theta }_k}}{p}_k\left(i_k\right)\ln p_k\left(i_k\right)$$

(5)

where $H_k$ denotes the information entropy of the $k$-th mode. The meanings of other symbols are consistent with those defined in the preceding equations.

(II)

Evaluating the noise content of each mode

Information entropy is a common method for quantifying information uncertainty. A smaller information entropy indicates lower noise content in the mode. Therefore, the noise content of each mode is evaluated based on information entropy, and the modes are sorted from highest to lowest noise content.

(III)

Obtain the FMD-denoised signal

Remove modes with high noise content and retain modes with low noise content as the FMD-denoised signal.

(C)

Wavelet denoising

Wavelet denoising is applied to perform secondary denoising on the four input signals after FMD denoising.

The specific steps are as follows [25]:

(a)

Wavelet decomposition

The FMD-denoised input signal $x_{\mathrm{F}\mathrm{d}}\left(n\right)$ is decomposed into approximation coefficients and detail coefficients by the discrete wavelet transform:

The approximation coefficients are given as follows:

$$c{A}_j\left(\tau \right)=\sum _n{x}_{\mathrm{F}\mathrm{d}}\left(n\right)\cdot {\varphi }_{j,\tau }\left(n\right)$$

(6)

The detail coefficients are given as follows:

$$c{D}_j\left(\tau \right)=\sum _n{x}_{\mathrm{F}\mathrm{d}}\left(n\right)\cdot {\psi }_{j,\tau }\left(n\right)$$

(7)

where $x_{\mathrm{F}\mathrm{d}}\left(n\right)$ denotes the input signal denoised using FMD. The dimensions of $x_{\mathrm{F}\mathrm{d}}\left(n\right)$ corresponding to the four input signals are as follows: the main thrust voltage and lateral thrust voltage are in volts (V), the yaw angle is in degrees (°), and the surge velocity is in meters per second (m/s). $n=\mathrm{1,2},\dots ,N$,${\varphi }_{j,\tau }\left(n\right)$ is the Daubechies4 discrete scaling function; ${\psi }_{j,\tau }\left(n\right)$ is the Daubechies4 discrete wavelet function; $j$ denotes the decomposition level, with $j=5$ in this paper, and $\tau$ is the translation parameter. The meanings of other symbols are consistent with those defined in preceding equations.

(b)

Threshold processing

This study applies soft-thresholding wavelet denoising and selects the optimal threshold using Stein’s Unbiased Risk Estimate (SURE) method [26,27].

First, calculate the SURE values corresponding to different thresholds $\lambda$ for the high-frequency coefficients at each decomposition scale (excluding the approximation coefficients at the coarsest scale). The definition of SURE is as follows:

$$SURE(\lambda )=p-2{\displaystyle \sum _{i=1}^p} I(|W_i|\le \lambda )+{\displaystyle \sum _{i=1}^p} (|W_i|\wedge \lambda {)}^2$$

(8)

where $\left|W_i\right|\wedge \lambda =\mathrm{m}\mathrm{i}\mathrm{n}(\left|W_i\right|,\lambda )$, $\lambda$ is the candidate threshold, $W_i$ is the wavelet coefficient, $p$ is the data size, and $I(\cdot )$ is an indicator function. The meanings of other symbols are consistent with those defined in preceding equations.

Next, for the high-frequency coefficients at each scale, the optimal threshold $\tilde{\lambda }$ for these coefficients is determined as the value of $\lambda$ that minimizes the SURE.

Finally, the soft thresholding method is applied to process the high-frequency coefficients at each scale. The soft-threshold formula is as follows:

$$\mathrm{c}{\tilde{D}}_j\left(\tau \right)=\left\{\begin{array}{c}\mathrm{sign}\left(c{D}_j\left(\tau \right)\right)\left(\left|c{D}_j\left(\tau \right)\right|-\tilde{\lambda }\right), \left|c{D}_j\left(\tau \right)\right|\ge \tilde{\lambda }\\ 0, \left|c{D}_j\left(\tau \right)\right|<\tilde{\lambda }\end{array}\right.$$

(9)

where $\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(·)$ is the sign function.

(c)

Wavelet reconstruction

The threshold-processed detail coefficients $c{\tilde{D}}_j\left(k\right)$ and the original approximation coefficients $c{A}_J\left(k\right)$ are used to reconstruct the signal via inverse discrete wavelet transform, resulting in the wavelet-denoised signal $x_{wd}\left(n\right)$. The dimensions of $x_{wd}\left(n\right)$ is the same as that of $x_{\mathrm{F}\mathrm{d}}\left(n\right)$. The calculation formula is as follows:

$$x_{wd}\left(n\right)=\sum _j \left(\sum _k {\widetilde{cD}}_j\left(k\right)\cdot {\psi }_{j,k}\left(n\right)+\sum _k c{A}_J\left(k\right)\cdot {\phi }_{J,k}\left(n\right)\right)$$

(10)

where $J$ denotes the coarsest scale. The meanings of other symbols are consistent with those defined in preceding equations.

(D)

Signal enhancement

To address different input signals, this paper designs distinct technical approaches for noise reduction and enhancement, as illustrated in Figure 1. For the surge velocity signal, yaw angle signal, and lateral thruster voltage signal, the MB enhancement method is adopted; for the main thruster voltage signal, the enhancement method combined energy operator and MB is employed. The specific implementations of MB enhancement and energy operator enhancement are detailed below.

(a)

Energy operator enhancement

The energy operator formula is given as follows [21,22]:

$$\Psi \left[g\left(n\right)\right]={\left[g\left(n\right)\right]}^2-g\left(n+1\right)\cdot g\left(n-1\right)$$

(11)

where $g\left(n\right)$ denotes the wavelet denoised signal of the main thruster voltage signal, with a unit of volts (V); $\Psi \left[g\left(n\right)\right]$ represents the energy operator signal, with a unit of volts squared (V²). The meanings of other symbols are consistent with those in the preceding formula.

(b)

MB enhancement

The specific formula for MB is as follows [15]:

$$d\left(n\right)={\displaystyle \frac{{\widehat{\sigma }}_1^2\left(n\right)}{{\widehat{\sigma }}_0^2}}-ln{\displaystyle \frac{{\widehat{\sigma }}_2^2\left(n\right)}{{\widehat{\sigma }}_0^2}}-1$$

(12)

where the calculation formulas for ${\widehat{\sigma }}_0^2$, ${\widehat{\sigma }}_1^2\left(n\right)$, and ${\widehat{\sigma }}_2^2\left(n\right)$ are as follows.

$${\widehat{\sigma }}_0^2={\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N}{\left[h_0\left(n\right)-{\widehat{h}}_0\right]}^2$$

$${\widehat{\sigma }}_1^2\left(n\right)={\displaystyle \frac{1}{N_t-1}}{\displaystyle \sum _{j=1}^{N_t}}{\left[h\left(n-j\right)-{\widehat{h}}_0\right]}^2$$

$${\widehat{\sigma }}_2^2\left(n\right)={\displaystyle \frac{1}{N_t-1}}{\displaystyle \sum _{j=1}^{N_t}}{\left[h\left(n-j\right)-\widehat{h}\left(n\right)\right]}^2$$

$${\widehat{h}}_0={\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N}{h}_0\left(n\right)$$

$$\widehat{h}\left(n\right)={\displaystyle \frac{1}{N_t}}{\displaystyle \sum _{j=1}^{N_t}}h\left(n-j\right)$$

In the above equations, $h\left(n\right)$ and $h_0\left(n\right)$, respectively, represent the wavelet denoised signal $x_{wd}\left(n\right)$ or the energy operator signal $x_{wd}\left(n\right)$ under the fault occurrence state and the normal operation state. Their specific expressions are dictated by the input signals, with the units of $h\left(n\right)$ and $h_0\left(n\right)$ corresponding to the four input signals as follows: main thruster voltage is in volts squared (V²), lateral thruster voltage in volts (V), yaw angle is in degrees (°), and surge velocity is in meters per second (m/s). ${\widehat{h}}_0$ is the expected value of the signal under normal operation of AUVs, and its unit is the same as that of the input signal; $N$ is the signal length; $N_t$ is the time window length, with $N_t=25$.

3.3. Fault Feature Extraction and Fusion Method

(1) 

Problem and causal analysis

Problem 1: After increasing the number of input signals, the conventional method encounters a problem where the mapping relationship between fault features and fault severity becomes non-monotonic, making subsequent fault severity identification infeasible.

To address Problem 1, the causes are analyzed as follows:

The conventional method performs signal-level fusion on denoised and enhanced signals, then extracts the maximum peak value as a single time-domain fault feature. However, for weak faults in thrusters, the intensity of this fault feature is relatively weak. After increasing the number of input signals, different input signals exhibit varying response times to the same fault, leading to discrepancies in the timing of maximum peaks. This weakens the fusion effect and results in minimal improvement in the maximum peak value after fusion. Consequently, the method fails to ensure that the fused fault feature value for a higher fault severity is greater than that for a lower severity, ultimately causing a non-monotonic mapping relationship between fault features and fault severity.

(2) 

Idea of the proposed method

Based on the analysis of the root causes of the above problems, the methodology proposed in this paper is outlined as follows. The conventional method extracts only a single feature within the time domain for various input signals and fuses them at the signal level. First, in contrast, this paper extracts multiple fault features from the time, frequency, and time–frequency domains of the input signals. Second, the proposed methodology fuses these features at the fault feature level. Finally, this approach avoids the drawbacks of fusion at the signal level. The process of the proposed method is as follows: Initially, this paper broadens the scope of fault feature extraction beyond the time domain to encompass the frequency and time–frequency domains. Then, sensitive features are selected from these multi-domain fault features based on the sensitivity factor selection method. Ultimately, fault features are fused using evidence theory to obtain definitive fault features, thereby addressing the non-monotonic mapping problem between fault features and fault severity.

(3) 

Implementation of the proposed fault feature extraction and fusion method

The implementation process and detailed steps of the proposed fault feature extraction and fusion method are outlined as follows.

(A)

Multi-domain fault feature extraction

Multi-domain fault feature extraction is performed on the enhanced signals. Fault features are extracted from the time domain, frequency domain, and time–frequency domain, respectively, with specific implementations as follows:

(a)

Determination of fault features in time, frequency, and time–frequency domains

Time-domain fault features include (12 features): maximum value, minimum value, peak-to-peak value, mean value, variance, root mean square (RMS), skewness, kurtosis, waveform factor, crest factor, impulse factor, and margin factor.

Frequency-domain features include (4 features): mean frequency, RMS frequency, centroid frequency, and standard deviation frequency.

Time–frequency-domain features include (4 features): approximate entropy, fuzzy entropy, negentropy, and sample entropy.

(b)

Calculation of fault features in time, frequency, and time–frequency domains

For each input signal, the above 20 features need to be calculated, resulting in a total of 80 feature values to be computed. The specific calculation method for these features can be found in the literature [28,29,30,31]. To maintain the focus and logical clarity of this paper, detailed descriptions are omitted here.

(B)

Selecting sensitive features from multiple domains

Based on the method of multi-domain fault feature extraction outlined in step (A), we conducted the extraction process on four signals from the AUV, resulting in 20 fault features for each signal and a total of 80 fault features across the four signals. Upon further analysis of these fault features, it was discovered that not all fault features could be utilized for subsequent fault feature fusion. Consequently, this paper performs sensitive feature selection on the fault features obtained in step (A), with the specific steps outlined as follows:

(a)

Identification of fault features with monotonicity

Upon analyzing all fault features of the four signals, fault features exhibiting monotonicity were identified.

(b)

Processing for consistency of monotonic trends in fault features

Inconsistent monotonic trends among fault features can weaken the fused feature values. Thus, this paper performs processing to ensure consistency in the monotonic trends of fault features, while preserving the order of magnitude, length of the variation interval, and degree of variation of the feature values.

The monotonic fault features identified in Step (a) are transformed to achieve consistency in monotonic trends, i.e., converting monotonically decreasing fault features into monotonically increasing ones. The formula for this monotonic trend consistency transformation is as follows:

$$f^{\prime }=\left\{\begin{array}{cc}100-f& \mathsf{\Delta }f\ge 10\\ 10-f& 1\le \mathsf{\Delta }f<10\\ 1-f& 0.1\le \mathsf{\Delta }f<1\\ 0.1-f& \mathsf{\Delta }f<0.1\end{array}\right.$$

(13)

where $\mathsf{\Delta }f$ denotes the variation interval length of the fault feature, $f$ represents the original fault feature value, and $f^{\prime }$ denotes the transformed fault feature value.

(c)

Selection of sensitive features

Different fault features exhibit varying sensitivities to changes in fault severity. Therefore, a subset of sensitive features is selected from multiple fault features for fault severity identification.

Distance metric is a common method for evaluating sensitive features [32]. This paper employs this method to identify sensitive features, with specific steps outlined as follows:

(I)

Definition of feature set

Assuming there are $C$ types of AUV thruster faults with varying severity levels, and each severity level has $J$ types of fault features (in this paper, $C=4$ and $J=21$), the feature set of AUV thruster faults can be defined as follows:

$$f_{c,j}, c=\mathrm{1,2},\cdots C;j=\mathrm{1,2},\cdots J$$

(14)

where $f_{c,j}$ denotes the $j$-th feature value under the $c$-th severity level of faults.

(II)

Calculation of the mean value of the j-th type of feature

$$f_j={\displaystyle \frac{1}{C}}{\displaystyle \sum _{c=1}^c}{f}_{c,j}$$

(15)

where $f_j$ represents the mean value of the $j$-th type of feature.

(III)

Calculation of the inter-class average distance of the j-th type of feature

$$d_j={\displaystyle \frac{1}{C\left(C-1\right)}}{\displaystyle \sum _{\begin{array}{c}c,j=1\\ c\ne j\end{array}}^C} {\left|f_{c,j}-f_{l,j}\right|}^2$$

(16)

where $d_j$ denotes the inter-class average distance of the $j$-th type of feature.

(IV)

Calculation of the sensitivity factor of the j-th type of feature

$${\alpha }_j={\displaystyle \frac{d_j}{f_j}}$$

(17)

where ${\alpha }_j$ is the sensitivity factor of the $j$-th type of feature.

The magnitude of ${\alpha }_j$ reflects the sensitivity of the $j$-th type of feature for AUV thruster fault severity identification. A larger ${\alpha }_j$ indicates higher sensitivity of the $j$-th type of feature, enabling better distinction and identification of different fault severity levels. In this paper, indicators with a sensitivity factor ${\alpha }_j\ge 0.5$ are selected as sensitive features for weak faults in AUV thrusters.

(C)

Fault feature fusion based on D-S evidence theory

The fusion of all sensitive features obtained by selecting sensitive features from multiple domains in Step (A) is performed based on the D-S evidence theory. The specific steps are as follows:

(a)

Construction of the frame of discernment Θ

Using the $n$ sensitive features obtained in Step (2) as $n$ focal elements, the frame of discernment is constructed [33]:

$$\mathsf{\Theta }=\left\{A_1,A_2,\cdots ,A_n\right\}$$

(18)

(b)

Construction of two mass functions m₁ and m₂

The mass function of the frame of discernment is critical for fusing weak fault-sensitive features of AUV thrusters. This subsection proposes a mass function $m_1$ based on sensitivity factors and a mass function $m_2$ based on Pearson correlation coefficients.

(I)

Mass function m₁ based on sensitivity factors

The mass function $m_1$ is constructed using the percentage of sensitivity factors, with the specific calculation method as follows:

$$m_{1i}={\displaystyle \frac{{\alpha }_i}{{\displaystyle {\sum }_{i=1}^n}{\alpha }_i}}$$

(19)

where $m_{1i}$ denotes the value of the mass function $m_1$ for the $i$-th feature in the frame of discernment; ${\alpha }_i$ represents the sensitivity factor of the $i$-th feature in the frame of discernment.

(II)

Mass m₂ based on Pearson correlation coefficients

The mass function $m_2$ is constructed using the percentage of Pearson correlation coefficients, with the specific calculation method as follows [34]:

$$r={\displaystyle \frac{\sum \left(X-\bar{X}\right)\left(Y-\bar{Y}\right)}{\sqrt{\sum {\left(X-\bar{X}\right)}^2{\left(Y-\bar{Y}\right)}^2}}}$$

(20)

where $r$ is the Pearson correlation coefficient between the feature vector $X$ and the fault degree vector $Y$.

$$m_{2i}={\displaystyle \frac{r_i}{{\displaystyle {\sum }_{i=1}^n}{r}_i}}$$

(21)

where $m_{2i}$ denotes the value of the mass function $m_2$ for the $i$-th feature in the frame of discernment; $r_i$ represents the Pearson correlation coefficient between the $i$-th feature vector and the fault severity vector.

(c)

Fusion based on Dempster’s rule

Dempster’s rule for two mass functions is defined as follows:

For $\forall A,B,C\subseteq \mathsf{\Theta }$, the Dempster’s rule for two mass functions $m_1$ and $m_2$ on Θ is as follows [35]:

$$m_1\oplus m_2\left(A\right)={\displaystyle \frac{1}{K}}\sum _{B\cap C=A} m_1\left(B\right)\cdot m_2\left(C\right)$$

(22)

where $K$ is the normalization constant, calculated as follows:

$$K=\sum _{B\cap C\ne \mathsf{\Theta }} m_1\left(B\right)\cdot m_2\left(C\right)=1-\sum _{B\cap C=\mathsf{\Theta }} m_1\left(B\right)\cdot m_2\left(C\right)$$

(23)

(d)

Obtaining final fusion fault features

For the four input signals, the fault fusion feature $f_r$ for each fault degree is calculated. The formula for $f_r$ is as follows:

$$f_r=⟨F,M⟩$$

(24)

where $F$ denotes the pre-fusion feature vector; $M$ denotes the mass function vector $m$; $⟨·⟩$ represents the dot product operation.

4. Experimental Validation

After briefly introducing the experimental setup of this study, comparative experiments between the proposed method and the conventional method are conducted in this section to verify the effectiveness of the proposed approach.

4.1. Experimental Setup

(1)

Experimental Equipment and Environment

This study employs an AUV prototype named “Beaver II” (as shown in Figure 3) to conduct flow environment experiments in a pool [15]. To simulate water flow, a self-developed current generation device and its operational process are illustrated in Figure 4 [15]. The measured flow field and flow velocity conditions are presented in Figure 5.

The sensor system of Beaver II comprises three key components: a digital compass, a Doppler velocity log, and a depth meter (Figure 3). Its propulsion system incorporates six brush thrusters (Figure 6). Specifically, surge speed regulation is managed by thrusters HT3 and HT4; heading control is executed by thrusters HT1 and HT2; and depth adjustment is achieved through thrusters VT1 and VT2. The overall control architecture is grounded in a proportional-integral-derivative (PID) controller framework.

(2)

Experimental Process

The AUV conducted a constant-velocity straight-line experiment at 0.3 m/s in a flowing environment. The experimental process and key parameters are as follows: In the flowing environment (the main direction of the AUV traversing the flow field is indicated by line B in Figure 5), the AUV’s target velocity was 0.3 m/s. Starting from rest, it accelerated to the target velocity and then performed steady-state straight-line motion with a control cycle of 0.2 s. A left main thruster fault was simulated using a soft fault simulation method [15]. From the 250th time step (i.e., 50 s), the left main thruster experienced a thrust loss fault, which persisted until the end of the experiment. Weak fault experiments with left main thrust losses of 2%, 5%, 8%, and 10% were conducted [15].

Since this study focuses on the diagnosis of weak thruster faults during the AUV’s steady-state operation, the startup phase was excluded, and experimental data from time steps 200 to 400 were analyzed.

4.2. Experimental Verification of Signal Denoising and Enhancement Effects for the Proposed Method and the Conventional Method

To address the problems encountered when applying the conventional signal denoising and enhancement method (wavelet denoising combined with MB enhancement) to multi-input signals for AUV thruster fault feature extraction, this paper proposes a signal denoising method combining FMD and wavelet denoising, as well as a signal enhancement method combining energy operators and MB.

Previous literature has predominantly utilized two evaluation parameters: fault feature values and fault eigenvalues to noise eigenvalues ratio (FNR) [11,12,15]. Fault feature values reflect the intensity of the fault from an absolute perspective, while the FNR indicates the difference between the fault and noise from a relative perspective. The simultaneous application of both can effectively circumvent the limitations of a single evaluation parameter. Therefore, this paper adopts fault feature values and FNR as the evaluation metrics for signal denoising and enhancement effects.

4.2.1. Enhancement Effect of the Main Voltage Signal

Experiments were conducted on AUV thrusters with fault severities of 2%, 5%, 8%, and 10%. The case with 8% fault severity is used for illustration.

The original signal diagram of the main thruster voltage signal with 8% fault severity is shown in Figure 7. This study focuses on the weak fault diagnosis of thrusters under steady-state operational conditions of AUVs. It is important to note that the first 200 beats correspond to the AUV start-up phase, which is generally not included in thruster fault diagnosis research. Based on these considerations, the signal data from the 200th beat (marked by a blue dot-dashed line) to the 400th beat are selected for analysis. Among them, the 250th beat marked by the red dashed line is the moment when the fault occurs. By applying the proposed method (FMD + wavelet + MB) and the conventional method (wavelet + MB) to denoise and enhance the original signal, the enhancement results of the main thruster voltage signal obtained using different methods are shown in Figure 8.

There is a discrepancy in the x-axis range between Figure 7 and Figure 8, primarily due to the following reasons: the starting beat of Figure 8 (labeled as 0) corresponds to the 200-beat position in Figure 7, as explained in Section 4.1; additionally, the x-axis of Figure 8 ends at 175 beats because the fixed length of the time window used in this study is 25 beats. The x-axis settings of subsequent relevant figures follow the same pattern.

By following the same procedure, signal enhancement effects for different methods with fault severities of 2%, 5%, and 10% can be obtained. Based on these signal enhancement effects, the fault feature values and FNR after signal enhancement using different methods are derived, as shown in

Table 1. Signal enhancement effects for weak faults in main thruster voltage signals.

Fault Severity	Conventional Method		Proposed Method		Enhancement Ratio of Fault Feature Values	Enhancement Ratio of FNR
	Fault Feature Values	FNR	Fault Feature Values	FNR
2%	3.37	1.19	3.44	2.10	2.11%	76.43%
5%	2.43	1.12	6.05	8.77	148.79%	680.26%
8%	9.66	1.65	11.55	11.08	19.56%	570.47%
10%	3.57	4.28	5.28	6.27	47.97%	46.38%

.

Based on Table 1, a comparative analysis of the noise reduction and enhancement effects of different methods is conducted using the evaluation metrics of fault feature values and FNR.

(A)

Comparative analysis of fault thruster values

Analysis of Table 1 reveals that, for different AUV thruster fault severities (2%, 5%, 8%, 10%), the fault feature values of the proposed method increase by proportions of 2.11%, 148.79%, 19.56%, and 47.97% compared to the conventional method. For the conventional method, fault feature values remain below 4.00 for fault severities of 2%, 5%, and 10%. In contrast, the proposed method only has a fault feature value below 4.00 at the 2% fault severity, with values exceeding 5.00 for all other severities, reflecting its enhanced effectiveness for weak faults. These experimental results validate the proposed method’s efficacy in enhancing fault feature values of main thruster voltage signals, laying a solid foundation for subsequent identification of weak fault severities.

(B)

Comparative analysis of FNR

For different AUV thruster fault severities (2%, 5%, 8%, 10%), the FNR of the proposed method increases by proportions of 76.43%, 680.26%, 570.47%, and 46.38% compared to the conventional method. For the conventional method, FNRs remain very low (slightly greater than 1) for fault severities of 2%, 5%, and 8%. In contrast, the minimum FNR of the proposed method is 2.10, reflecting its enhanced effectiveness for weak faults. These experimental results validate the proposed method’s efficacy in enhancing the FNR of main thruster voltage signals.

In summary, the experimental results demonstrate that for AUV thruster weak faults with fault severities of 2%, 5%, 8%, and 10%, the proposed method exhibits significantly higher fault feature values and FNRs than the conventional method, further validating its effectiveness in enhancing the main thruster voltage signal under weak faults.

4.2.2. Enhancement Effects of Other Input Signals

This section summarizes the experimental results of signal denoising and enhancement for other input signals: yaw angle signal, lateral thruster voltage signal, and surge velocity signal.

To validate the proposed method’s effectiveness, comparative experiments on signal enhancement were conducted using both the conventional method and the proposed method for yaw angle, lateral thruster voltage, and surge velocity signal. Experiments were performed under AUV thruster fault severities of 2%, 5%, 8%, and 10%, taking a fault severity of 8% as an example for illustration.

Original signal diagrams of yaw angle, lateral thruster voltage, and surge velocity signal with 8% fault severity are presented in Figure 9a–c, respectively. Their analysis time window is consistent with that in Figure 7: data from the 200th beat (blue dot–dash line) to the 400th beat are selected, with the fault initiating at the 250th beat (marked by the red dashed line). After denoising and enhancement using the proposed method and the conventional method, the enhancement effects for yaw angle, lateral thruster voltage, and surge velocity signal are presented in Figure 10.

Following the same procedure, signal enhancement effect diagrams for yaw angle, lateral thruster voltage, and surge velocity signal using different methods under other fault severities (2%, 5%, and 10%) can be obtained.

Based on the signal enhancement effect diagrams, the fault feature values and FNRs of enhanced yaw angle signal, lateral thruster voltage signal, and surge velocity signal using different methods are derived, as shown in

Table 2. The enhancement effects for weak faults in the yaw angle signal, lateral thruster voltage signal, and surge velocity signal.

Input Signal	Fault Severity	Conventional Method		Proposed Method		Enhancement Ratio of Fault Feature Values	Enhancement Ratio of FNR
		Fault Feature Values	FNR	Fault Feature Values	FNR
Yaw angle signal	2%	3.32	1.17	4.34	1.19	30.72%	1.71%
	5%	2.73	1.15	5.03	3.8	84.25%	230.43%
	8%	2.15	1.16	2.53	1.54	17.67%	32.44%
	10%	2.24	1.82	2.46	2.68	9.82%	47.25%
Lateral thruster voltage signal	2%	1.14	1.64	1.88	1.88	64.91%	14.63%
	5%	0.63	1.02	7.04	7.04	1017.46%	590.20%
	8%	2.06	1.40	4.14	4.14	100.97%	195.71%
	10%	0.92	1.11	4.93	4.93	435.87%	344.14%
Surge velocity signal	2%	1.15	1.79	54.98	55.53	4680.87%	3002.23%
	5%	2.54	1.28	23.71	18.96	833.46%	1378.88%
	8%	1.57	1.67	31.22	36.30	1888.54%	2073.65%
	10%	2.78	1.03	46.63	47.58	1577.34%	4515.26%

.

Based on Table 2, a comparative analysis of the noise reduction and enhancement effects of different methods is conducted using the evaluation metrics of fault feature values and FNRs.

(A)

Comparative analysis of fault feature values

For the yaw angle signal, under different AUV thruster fault severities (2%, 5%, 8%, 10%), the fault feature values of the proposed method increase by 30.72%, 84.25%, 17.67%, and 9.82%, respectively, compared to the conventional method. For all fault severities, the fault feature values of the conventional method remain below 4.00. In contrast, the proposed method yields fault feature values greater than 4.00 at 2% and 5% severities.

For the lateral thruster voltage signal, under different AUV thruster fault severities (2%, 5%, 8%, 10%), the fault feature values of the proposed method increase by 64.91%, 1017.46%, 100.97%, and 435.87%, respectively, compared to the conventional method. For 2%, 5%, and 10% severities, the fault feature values of the conventional method are very small (all less than 1.14). In contrast, the minimum fault feature value of the proposed method is 1.18.

For the surge velocity signal, under different AUV thruster fault severities (2%, 5%, 8%, 10%), the fault feature values of the proposed method increase by 4680.87%, 833.46%, 1888.54%, and 1577.34%, respectively, compared to the conventional method. For all fault severities, the fault feature values of the conventional method remain below 3. In contrast, the minimum fault feature value of the proposed method is 13.71.

(B)

Comparative analysis of FNR

For the yaw angle signal, under different AUV thruster fault severities (2%, 5%, 8%, 10%), the SNRs of the proposed method improve by 1.71%, 230.43%, 32.44%, and 47.25%, respectively, compared to the conventional method. For 2%, 5%, and 8% severities, the FNRs of the conventional method are very small (all less than 1.17). In contrast, the minimum FNR of the proposed method is 1.19.

For the lateral thruster voltage signal, under different AUV thruster fault severities (2%, 5%, 8%, 10%), the FNRs of the proposed method improve by 14.63%, 590.20%, 195.71%, and 344.14%, respectively, compared to the conventional method. For all fault severities, the FNRs of the conventional method are very small (all less than 1.79). In contrast, the minimum FNR of the proposed method is 1.88.

For the surge velocity signal, under different AUV thruster fault severities (2%, 5%, 8%, 10%), the FNRs of the proposed method improve by 3002.23%, 1378.88%, 2073.65%, and 4515.26%, respectively, compared to the conventional method. For all fault severities, the FNRs of the conventional method are very small (all less than 1.64). In contrast, the minimum FNR of the proposed method is 18.96.

Summary of Section 4.2. Aiming at the problems of the conventional method of fault feature extraction and fusion (wavelet denoising combined with MB enhancement) under multi-input signal conditions, this paper proposes a signal denoising method combining FMD and wavelet denoising, as well as a signal enhancement method combining energy operators and MB. For fault severities of 2%, 5%, 8%, and 10% for the AUV thruster, comparative experiments on four input signals (main thruster voltage signal, yaw angle signal, lateral thruster voltage signal, and surge velocity signal) demonstrate that the proposed method achieves higher fault feature values and FNRs than the conventional method. Additionally, this method exhibits notable noise reduction and signal enhancement effects across all four input signals, with the most significant improvements observed in surge velocity signals. These experimental results validate the effectiveness and superiority of the proposed method compared to the conventional method.

4.3. Experimental Verification of Fault Feature Extraction and Fusion Effects for the Proposed Method and the Conventional Method

Aiming at the problems of the conventional method of fault feature extraction and fusion under multi-input signal conditions, this paper proposes a fault feature extraction and fusion method based on multi-domain sensitive feature selection and D-S evidence theory.

4.3.1. Experimental Results of Multi-Domain Sensitive Feature Selection

Aiming at the problems of the conventional method of fault feature extraction and fusion under multi-input signal conditions, this paper proposes a fault feature extraction and fusion method based on multi-domain sensitive feature selection and D-S evidence theory. This section presents the experimental results of multi-domain sensitive feature selection to support subsequent fault feature fusion and fault severity identification.

(1)

Extraction of multi-domain monotonic fault features

Following the multi-domain fault feature extraction method in Section 3.3, time-domain, frequency-domain, and time–frequency-domain fault features were extracted for four types of input signals (main thruster voltage signal, yaw angle signal, lateral thruster voltage signal, and surge velocity signal). A total of 80 fault features were obtained. After removing 59 non-monotonic fault features, 21 monotonic fault features were retained, as shown in

Table 3. All Monotonic fault features.

Input Signal	Fault Feature	Fault Severity
		2%	5%	8%	10%
Surge velocity signal	Mean value	3.21	3.25	3.89	5.87
	Variance	50.31	65.25	77.85	79.65
	Skewness	0.33	0.28	0.2	0.1
	Margin factor	78.29	63.54	46.14	36.14
	Mean frequency	0.0009	0.00093	0.0017	0.0018
	Approximate entropy	1.092	1.194	1.324	1.647
	Sample entropy	0.154	0.173	0.191	0.193
Yaw angle signal	Mean value	1.36	2.46	2.56	3.59
	RMS	5.39	5.66	8.63	9.81
	Mean frequency	0.00058	0.00059	0.0024	0.0034
	Approximate entropy	0.48	0.85	0.89	1.75
	Fuzzy entropy	0.98	1.44	1.47	1.71
Main thruster voltage signal	Variance	13.17	14.64	15.88	19.09
	RMS	5.25	6.97	7.446	9.49
	Margin factor	12.915	13.23	23.99	24.6
	Standard deviation frequency	1.465	1.434	1.158	1.155
	Centroid frequency	99.593	101.675	101.383	102.317
	Negentropy	0.23	0.35	0.66	1.178
Lateral thruster voltage signal	Rms	5.258	5.584	9.627	10.584
	Kurtosis	2.32	2.99	3.483	3.83
	Fuzzy entropy	0.96	0.52	0.34	0.11

.

(2)

Monotonic trend consistency processing of fault features

Among the 21 monotonic fault features selected in Step (1) above, 17 exhibit a monotonic increasing trend, while 4 exhibit a monotonic decreasing trend. The monotonic decreasing fault features are skewness and margin factor of surge velocity signal, standard deviation frequency of main thruster voltage signal, and fuzzy entropy of lateral thruster voltage signal.

Based on the monotonic trend consistency processing method for fault features described in Section 3.2, the monotonically decreasing fault feature values undergo monotonic trend transformation, yielding 4 monotonically increasing fault features. The results are shown in

Table 4. Monotonically increasing fault features after monotonic trend transformation.

Input Signal	Fault Feature	2%	5%	8%	10%
Surge velocity signal	Skewness	0.67	0.72	0.8	0.9
	Margin factor	21.71	36.46	53.86	63.86
Main thruster voltage signal	Standard deviation frequency	8.535	8.566	8.842	8.845
Lateral thruster voltage signal	Fuzzy entropy	0.04	0.48	0.66	0.89

.

(3)

Selection of sensitive features

Using the sensitive feature selection method in Section 3.2, sensitive feature selection was conducted on the 21 monotonically increasing features obtained after the monotonic trend consistency processing of fault features. This process resulted in 13 sensitive features, as shown in

Table 5. Sensitive features.

Input Signal	Fault Feature	2%	5%	8%	10%	Sensitive Factor
Surge velocity signal	Mean value	3.21	3.25	3.89	5.87	0.770
	Variance	50.31	65.25	77.85	79.65	5.400
	Margin factor	21.71	36.46	53.86	63.86	15.848
Yaw angle signal	Mean value	1.36	2.46	2.56	3.59	0.667
	RMS	5.39	5.66	8.63	9.81	1.301
	Approximate entropy	0.48	0.85	0.89	1.75	0.583
Main thruster voltage signal	Variance,	13.17	14.64	15.88	19.09	0.809
	RMS	5.25	6.97	7.446	9.49	0.835
	Margin factor	12.915	13.23	23.99	24.60	4.502
	Negentropy	0.23	0.35	0.66	1.178	0.592
Lateral thruster voltage signal	Rms	5.258	5.584	9.627	10.584	1.928
	Kurtosis	1.32	2.99	3.483	3.83	0.851
	Fuzzy entropy	0.31	0.48	0.66	0.72	0.500

.

4.3.2. Experimental Verification of the Effect of Adding Sensitive Feature Selection on Monotonicity in the Proposed Method

The previous method of fault feature extraction and fusion typically follows a workflow: first, perform multi-domain fault feature extraction, then conduct fusion based on D-S evidence theory. In contrast, the proposed method involves three steps: multi-domain fault feature extraction, sensitive feature selection, and finally, fusion based on D-S evidence theory. To verify the effectiveness of adding the sensitive feature selection step in the proposed method, comparative experiments between the previous method and the proposed method are conducted in this section.

Based on the data from Section 4.3.1, the fault feature fusion results of the previous method and the proposed method are shown in

Table 6. Final fusion fault features of the previous and proposed methods.

Fault Severity	Previous Method	Proposed Method
2%	0.098	0.142
5%	0.094	0.258
8%	0.110	0.289
10%	0.082	0.387

.

To qualitatively illustrate the effectiveness of the proposed method, the mapping relationship diagrams of final fusion fault feature values versus fault severity for both the previous method and the proposed method are plotted based on Table 6, shown as Figure 11.

Based on Figure 11, the monotonic relationships between the final fusion fault feature values and fault severity of each method are analyzed as follows:

Monotonicity analysis of fault features for the previous method. As indicated by the red dashed line in Figure 11a, a final fusion fault feature value of 0.10 obtained using the previous method corresponds to two distinct fault severities. This demonstrates an absence of a monotonic relationship between the final fusion fault feature values generated by previous methods and the fault severities. Such a deficiency fails to satisfy the fundamental requirements for fused fault features.

Monotonicity analysis of fault features for the proposed method. As shown in Figure 11b, the final fused fault feature values obtained by the proposed method exhibit a clear monotonic relationship with the fault severity. That is, any fault feature value uniquely corresponds to a single fault severity value, satisfying the essential requirement for fused fault features.

These experimental results and analyses indicate that the sensitive feature selection method effectively addresses the problem of non-monotonic mapping relationships between fault features and fault severity in the previous method, thereby validating the effectiveness and superiority of the added sensitive feature selection in the proposed method.

4.3.3. Experimental Comparison of Fusion Fault Features Between the Proposed Method and the Conventional Method

The conventional method for extracting and integrating fault features involves a combination of D-S evidence theory and the peak region energy method. However, when processing multi-input signals, this conventional method encounters a problem, specifically the non-monotonic mapping relationship between fault features and fault severity. To address this, the proposed method integrates multi-domain sensitive feature selection with D-S evidence theory for fault feature extraction and fusion, followed by fault severity identification based on the classical GRA. Therefore, to verify the effectiveness of the proposed fault feature extraction and fusion method, comparative experiments are conducted from two perspectives: the monotonicity of fault features and the results of fault severity identification, comparing the conventional method with the proposed method.

(1)

Comparison of fault feature monotonicity

Based on the data from Section 4.3.1, the fault feature fusion results of the conventional method and the proposed method are shown in

Table 7. Final fusion fault features of the conventional and proposed methods.

Fault Severity	Conventional Method	Proposed Method
2%	0.598	0.142
5%	0.794	0.258
8%	0.793	0.289
10%	0.429	0.387

.

To qualitatively illustrate the effectiveness of the proposed method, the mapping relationship diagrams of final fault feature values versus fault severity for both the conventional method and the proposed method are plotted based on Table 7, as shown in Figure 12.

Based on Figure 12, the monotonic relationships between the final fused fault feature values and fault severity for each method are analyzed as follows:

Monotonicity analysis of fault features for the conventional method. As denoted by the red dashed line in Figure 12a, the final fusion fault feature value of 0.70 obtained by the conventional method corresponds to two distinct fault severities. This reveals an absence of a monotonic relationship between the final fused fault feature values derived from conventional methods and the fault severities, which deviates from the indispensable criteria for fused fault features.

Monotonicity analysis of fault features for the proposed method. As shown in Figure 12b, the final fused fault feature values obtained by the proposed method exhibit a clear monotonic relationship with the fault severity. That is, any fault feature value uniquely corresponds to a single fault severity value, satisfying the essential requirement for fused fault features.

These experimental results and analyses indicate that the sensitive feature selection method effectively addresses the problem of non-monotonic mapping relationships between fault features and fault severity in the conventional method, thereby validating the effectiveness and superiority of the proposed method.

(2)

Comparison of fault severity identification results

Based on GRA, the fault severity identification results of both the conventional method and the proposed method were obtained, as presented in

Table 8. Fault severity identification results for various methods.

Fault Severity	Conventional Method		Proposed Method
	Identification Results	Relative Error	Identification Results	Relative Error
2%	3.52%	76.00%	1.56%	22.00%
5%	5.34%	6.80%	5.26%	5.20%
8%	7.26%	9.25%	7.85%	1.88%
10%	2.56%	74.40%	9.12%	8.80%

.

Analysis of fault severity identification results based on Table 8.

Analysis of fault severity identification results for the conventional method. As shown in Table 8, when identifying a 10% fault, the conventional method exhibits a relative error of 74.40%, incorrectly classifying the 10% fault as a fault close to 2%. This result deviates significantly from the actual scenario. These experimental results indicate that the conventional method fails to provide effective fault feature values for subsequent fault severity identification, thereby confirming its inability to resolve the problem of non-monotonic relationships between final fused fault feature values and fault severity under weak fault conditions.

Analysis of fault severity identification results for the proposed method. As shown in Table 8, for different AUV thruster fault severities (2%, 5%, 8%, and 10%), the relative errors of the proposed method are reduced by 54.00%, 1.60%, 7.37%, and 65.60%, respectively, compared to the conventional method. At a 2% fault severity of the proposed method, the relative error reaches 22%, which is significantly higher than the relative errors under other fault severities. This is attributed to the fact that a small denominator amplifies the relative error. From the perspective of absolute error, the absolute error at 2% fault severity is 0.44%, which falls within the allowable error range, indicating that the proposed method can accurately identify a 2% fault. These experimental results demonstrate that the proposed method provides effective fault feature values for subsequent fault severity identification, thereby resolving the non-monotonic relationship problem between final fused fault feature values and fault severity. However, to address the problem of large relative error at 2% fault degree, a new method needs to be investigated more thoroughly in the future to further enhance the effectiveness of feature fusion and severity recognition.

4.3.4. Discussion on the Real-Time Applicability of the Proposed Method

The application background of the proposed method is the online monitoring of weak faults in thrusters during the operation of AUVs. The main parameters of the computer used for the proposed method are as follows: CPU: Intel i7-7700 (base frequency: 3.6 GHz, maximum single-core turbo frequency: 4.2 GHz, L3 cache: 8 MB); Memory: 16 GB DDR4 (frequency: 2400 MHz); Storage: 512 GB NVMe SSD (read speed: 5000 MB/s). The single-execution runtime of this method is approximately 3 s. In the context of weak fault diagnosis, a 3 s processing latency fully satisfies the real-time requirements for online monitoring applications. Furthermore, in practical experimental contexts involving AUVs, the computing devices deployed on the experimental platform demonstrate superior comprehensive performance relative to those employed in this method. Consequently, the single-execution runtime is shorter. Based on the above comparative analysis, it can be proved that this method demonstrates good real-time applicability.

Summary of Section 4.3. Aiming at the problems of the conventional method in fault feature extraction and fusion under multi-input signal conditions, this paper proposes a fault feature extraction and fusion method based on multi-domain sensitive feature selection and D-S evidence theory. Comparative experiments on four input signals (main thruster voltage signal, yaw angle signal, lateral thruster voltage signal, and surge velocity signal) under thruster fault severities of 2%, 5%, 8%, and 10% demonstrate that the proposed method achieves monotonic relationships between fault feature values and fault severity, with significantly lower fault severity identification errors compared to the conventional method. These results validate the effectiveness of the proposed method in addressing the monotonicity problem of final fused fault feature values and fault severity, thereby confirming the validity and superiority of its weak fault feature extraction capability for AUV thrusters.

5. Conclusions

This paper investigates the challenge of weak fault feature extraction for AUV thrusters under multi-input signal conditions. Conventional methods are limited by the use of insufficient input signals and suffer from non-monotonic mapping relationships between fault features and fault severity, impeding accurate fault severity identification. To overcome these limitations, this study expands the input set by incorporating all measurable signals. To address the challenges introduced by the increased number of input signals, an improved approach is proposed, focusing on two key aspects: signal denoising and enhancement, and fault feature extraction and fusion.

In terms of signal denoising and enhancement, the conventional method performs badly when applied to multi-input signals. To address this limitation, this paper proposes a denoising approach by combining FMD with wavelet denoising. Additionally, we also propose a signal enhancement method that integrates energy operators with MB. Pool experiments demonstrate the effectiveness of the proposed methods.

In terms of fault feature extraction and fusion, a key limitation of the conventional method under multi-input signal conditions is the non-monotonic relationship between fault features and fault severity. To address this issue, this paper proposes a fault feature extraction and fusion approach based on multi-domain sensitive feature selection and D-S evidence theory. Pool experiments demonstrate that the proposed method establishes a monotonic mapping between fault feature values and fault severity. Additionally, compared to the conventional method, the proposed approach reduces fault severity identification errors by 54.00%, 1.60%, 7.37%, and 65.60% under 2%, 5%, 8%, and 10% fault severity conditions, respectively. These results validate the effectiveness of the proposed signal denoising and enhancement method.

Collectively, these experimental results validate the effectiveness and superiority of the proposed weak fault feature extraction method for AUV thrusters. By providing a robust foundation for subsequent fault severity identification, the method enables accurate detection of early weak faults and contributes significantly to enhancing the operational safety of AUV systems.

The experimental results reported in this study were acquired under consistent flow conditions or noise levels. Future research will focus on further evaluating the adaptability of the proposed method to different flow conditions and noise levels, along with developing corresponding optimization strategies. These efforts aim to enhance the method’s applicability in complex marine environments.