Maritime Rescue Task Allocation and Sequencing Using MOEA/D with Adaptive Operators and Idle-Time-Aware Decoding Strategy
Abstract
1. Introduction
2. Literature Review
2.1. Multi-Objective Optimization Algorithms for Maritime Rescue Task Allocation and Sequencing
2.2. Efficiency Enhancement Methods for Solution Generation
2.3. Efficiency Enhancement Methods for Mission Execution
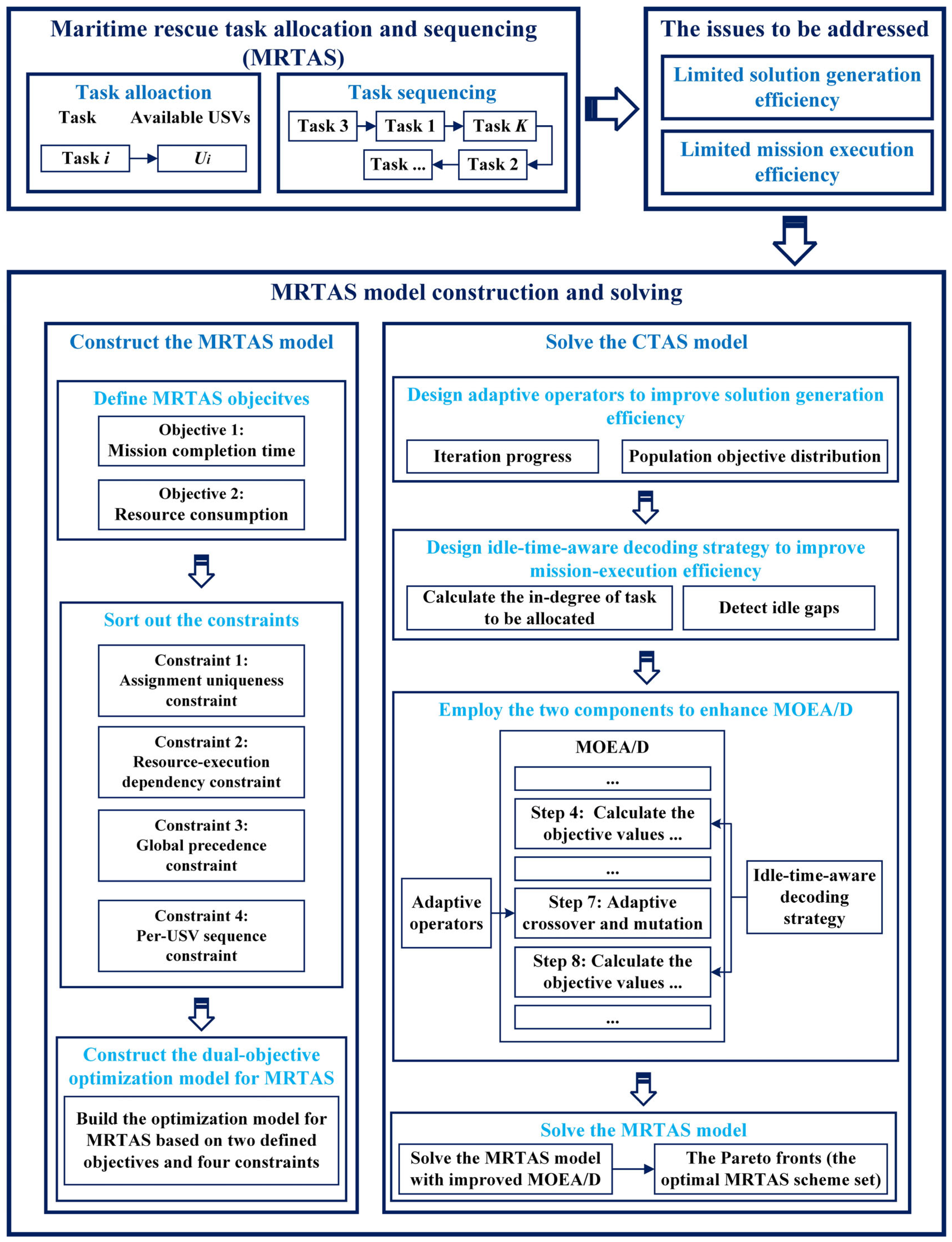
3. Maritime Rescue Task Allocation and Sequencing Model Construction and Solving
3.1. Maritime Rescue Task Allocation and Sequencing Model Construction
3.2. Maritime Rescue Task Allocation and Sequencing Model Solving Using Enhanced MOEA/D
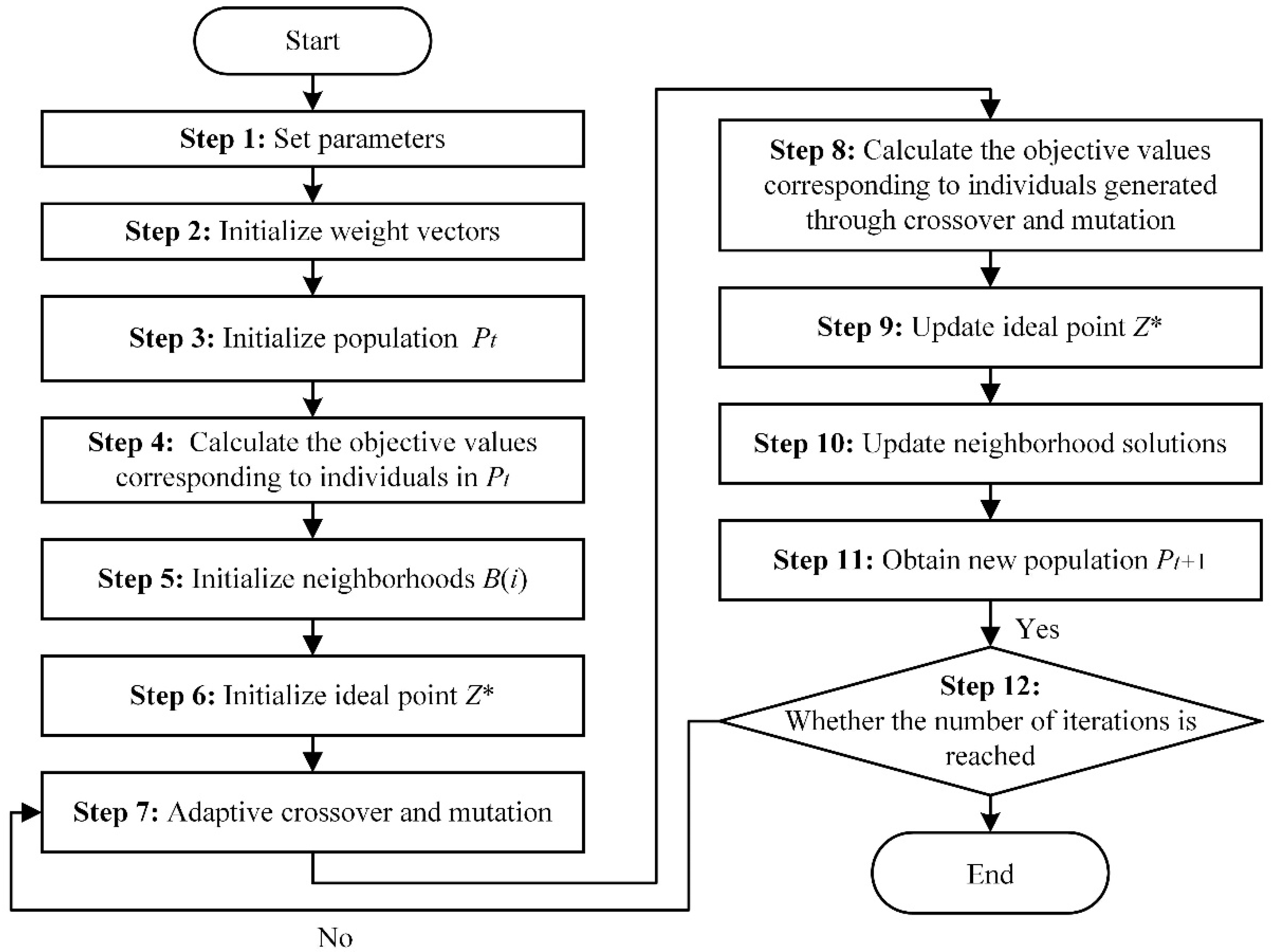
3.2.1. Process of the Enhanced MOEA/D
3.2.2. Adaptive Operators
3.2.3. Idle-Time-Aware Decoding Strategy
| Algorithm 1. Idle-Time-Aware Decoding Strategy | |
| Input: the sequence chromosome, the USV chromosome, the number of tasks matrix of tasks | |
| Output: the execution time lists of USVs | |
| Initialize: Let EXEC_LIST be a collection of execution time lists, one for each USV For each USV: initialize its execution time list as empty Let denote the j-th task object, with attributes duration . Let be a scalar variable representing the earliest start time allowed by the current USV sequence. Let EXEC_LIST[usv_id] be a chronologically ordered list of non-overlapping time intervals already allocated to USV usv_id. | |
| 1. | fordo |
| 2. | the task number of xth task in // x is the task serial number and j is the task number |
| 3. | USV chromosome’s allocation for task j // Get assigned USV for this task |
| 4. | |
| 5. | Calculate the in-degree using Equation (8) |
| 6. | ifthen |
| 7. | // Earliest start time considering global precedence constraint in Equation (4) |
| 8. | else |
| 9. | the maximum end time of pre-tasks of |
| 10. | endif |
| 11. | If is the first task allocated to the usv_id then |
| 12. | // Earliest start time considering per-USV sequence constraint in Equation (5) |
| 13. | else |
| 14. | the end time of the last task executed by usv_id |
| 15. | endif |
| 16. | ifthen |
| 17. | // Start time determined by global constraints |
| 18. | |
| 19. | Update execution time list for usv_id |
| 20. | else // in EXEC_LIST[usv_id] |
| 21. | false |
| 22. | for in EXEC_LIST[usv_id] (earliest first) do |
| 23. | |
| 24. | ifthen |
| 25. | candidate_start |
| 26. | Schedule task to USV usv_id in this idle gap at time |
| 27. | Update idle gaps in EXEC_LIST[usv_id] |
| 28. | true |
| 29. | break // Stop searching after the first valid idle gap |
| 30. | endif |
| 31. | endfor |
| 32. | if not found_idle then |
| 33. | // // No suitable idle gap, schedule sequentially |
| 34. | |
| 35. | Update execution time list for usv_id |
| 36. | endif |
| 37. | endif |
| 38. | endfor |
| 39. | Return EXEC_LIST // Execution time lists for all USVs |
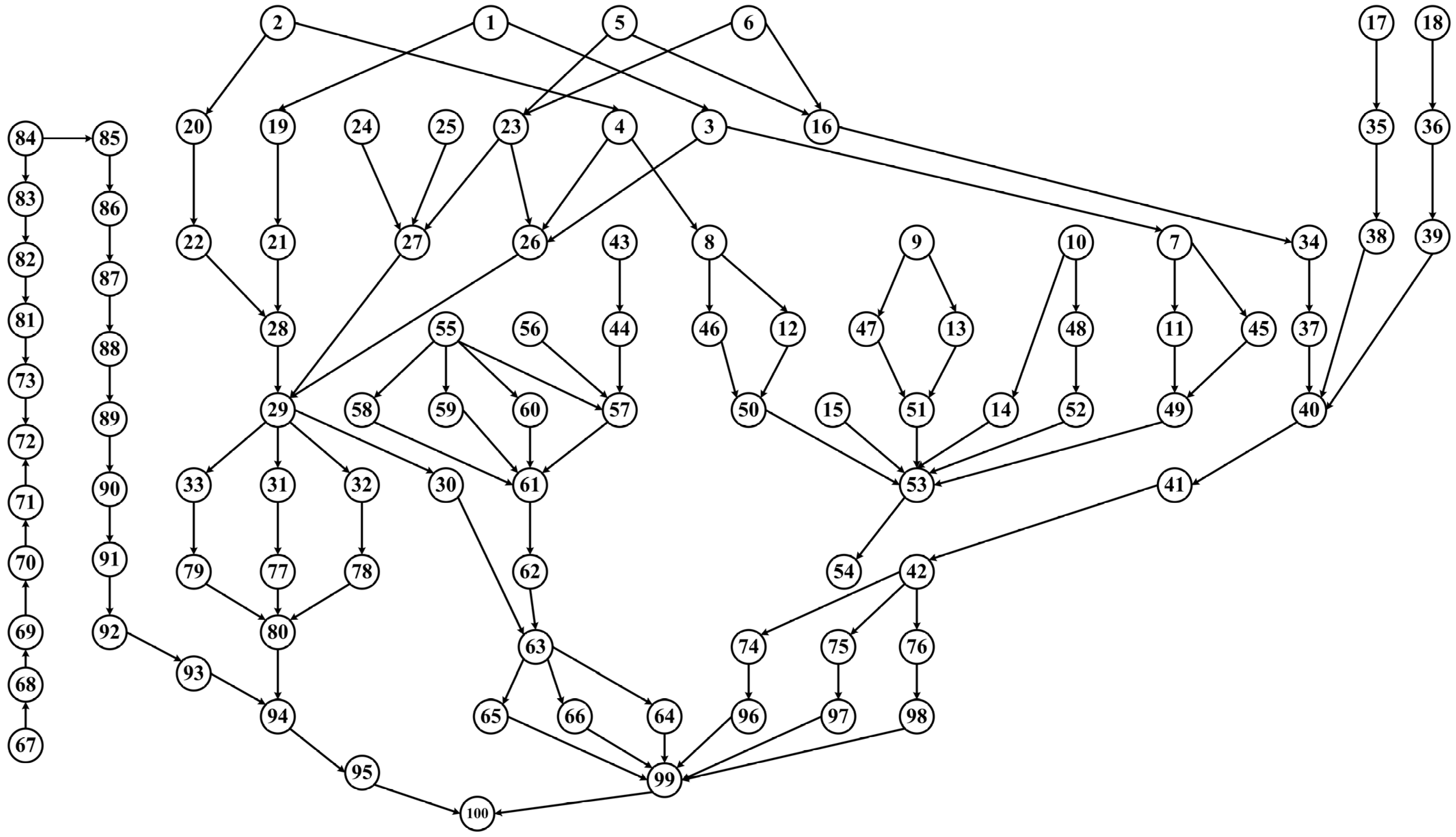
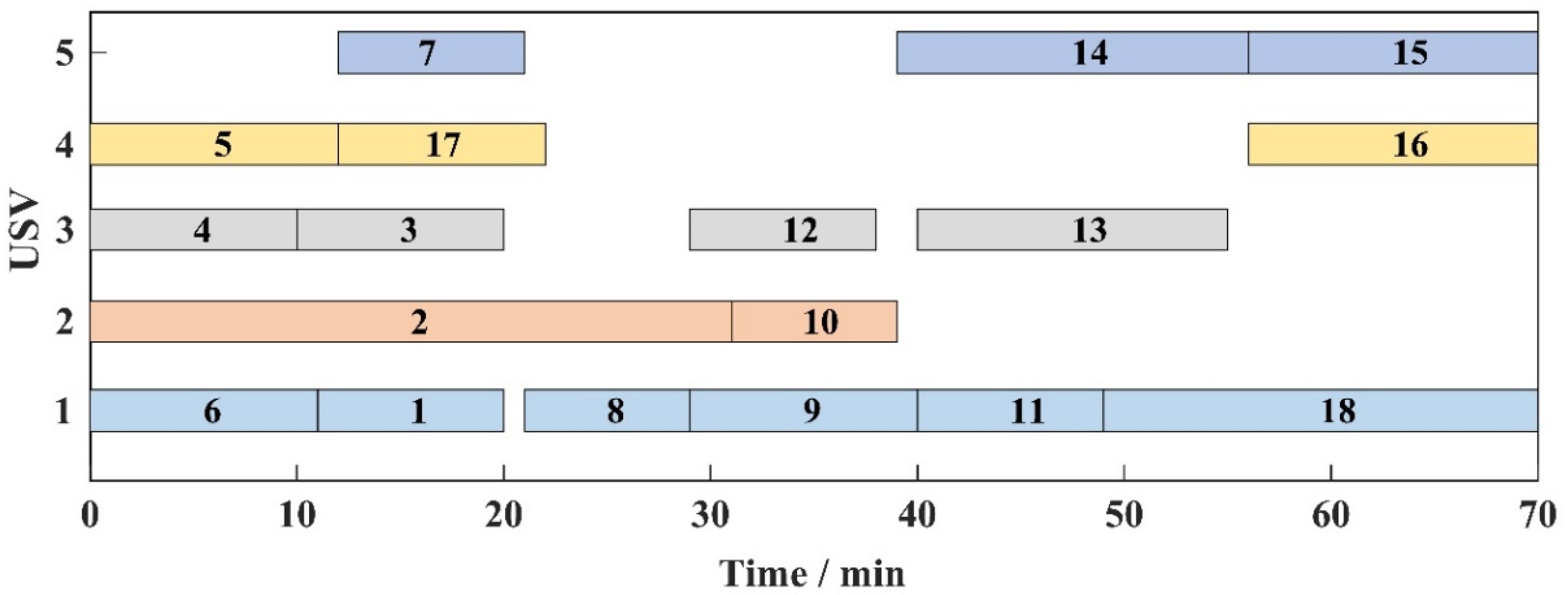
4. Case Studies
5. Comparison and Discussion
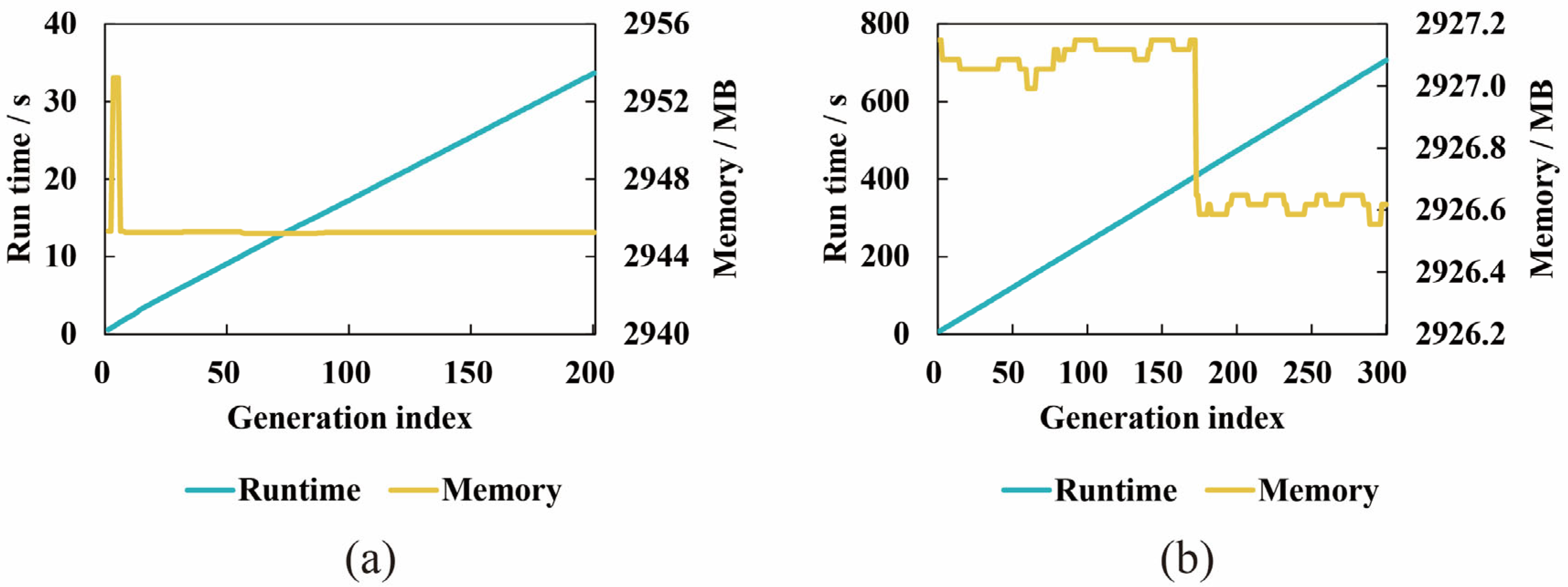
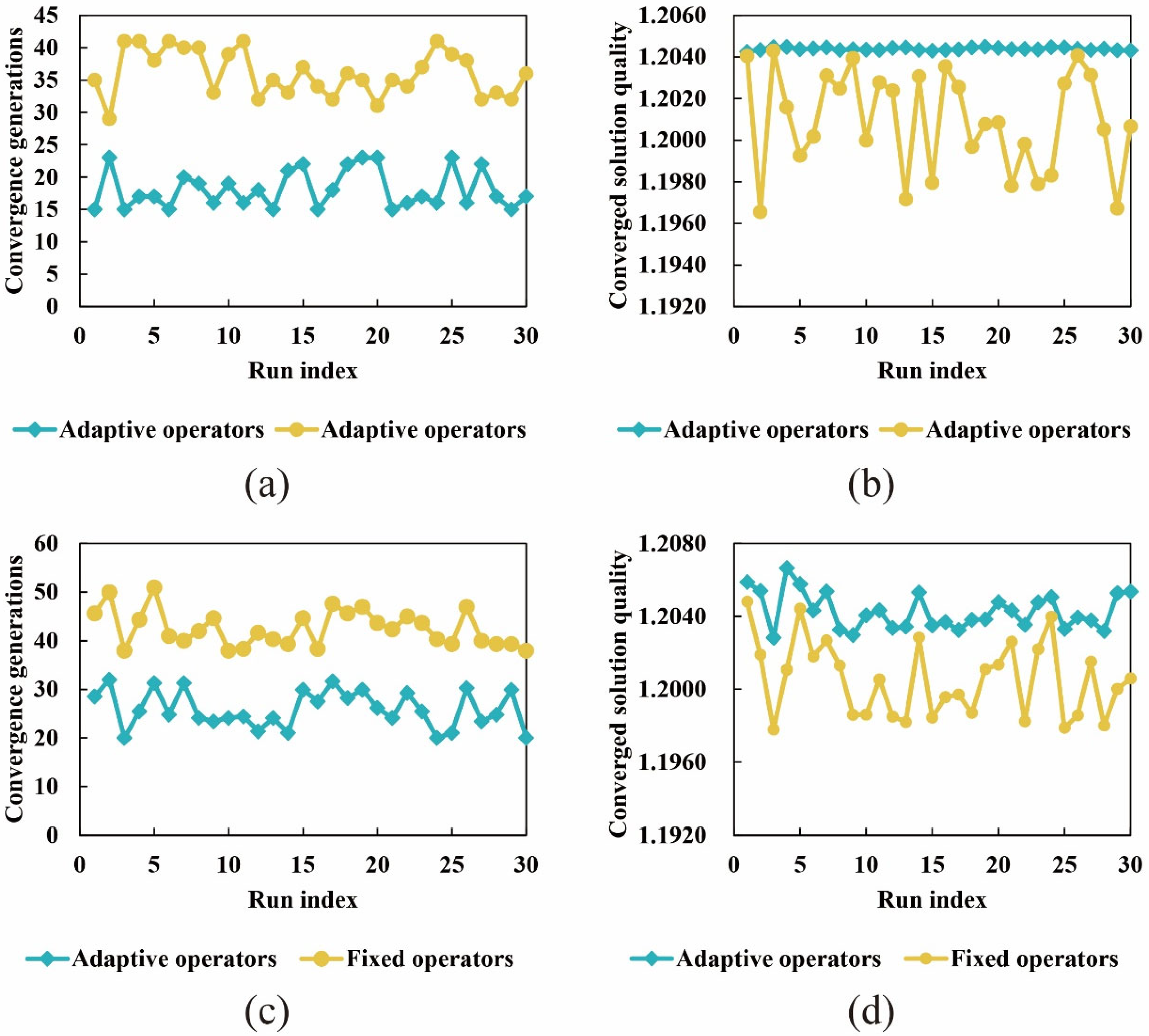
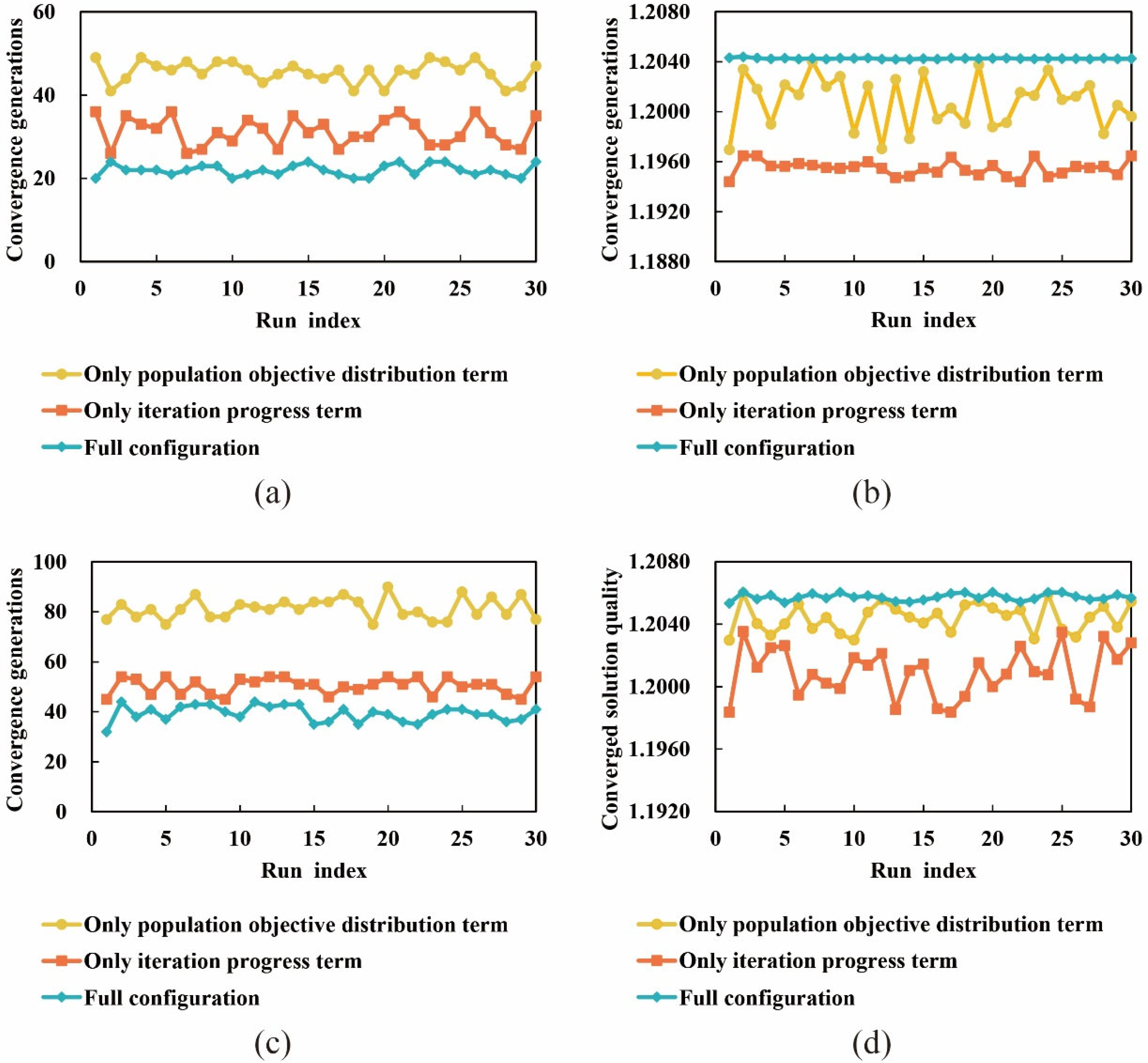
5.1. Ablation Studies
5.1.1. Comparison with Fixed Operators
5.1.2. Ablation Study on Adaptive Terms
5.2. Comparison with State-of-the-Art Algorithms
5.3. Sensitivity Analysis
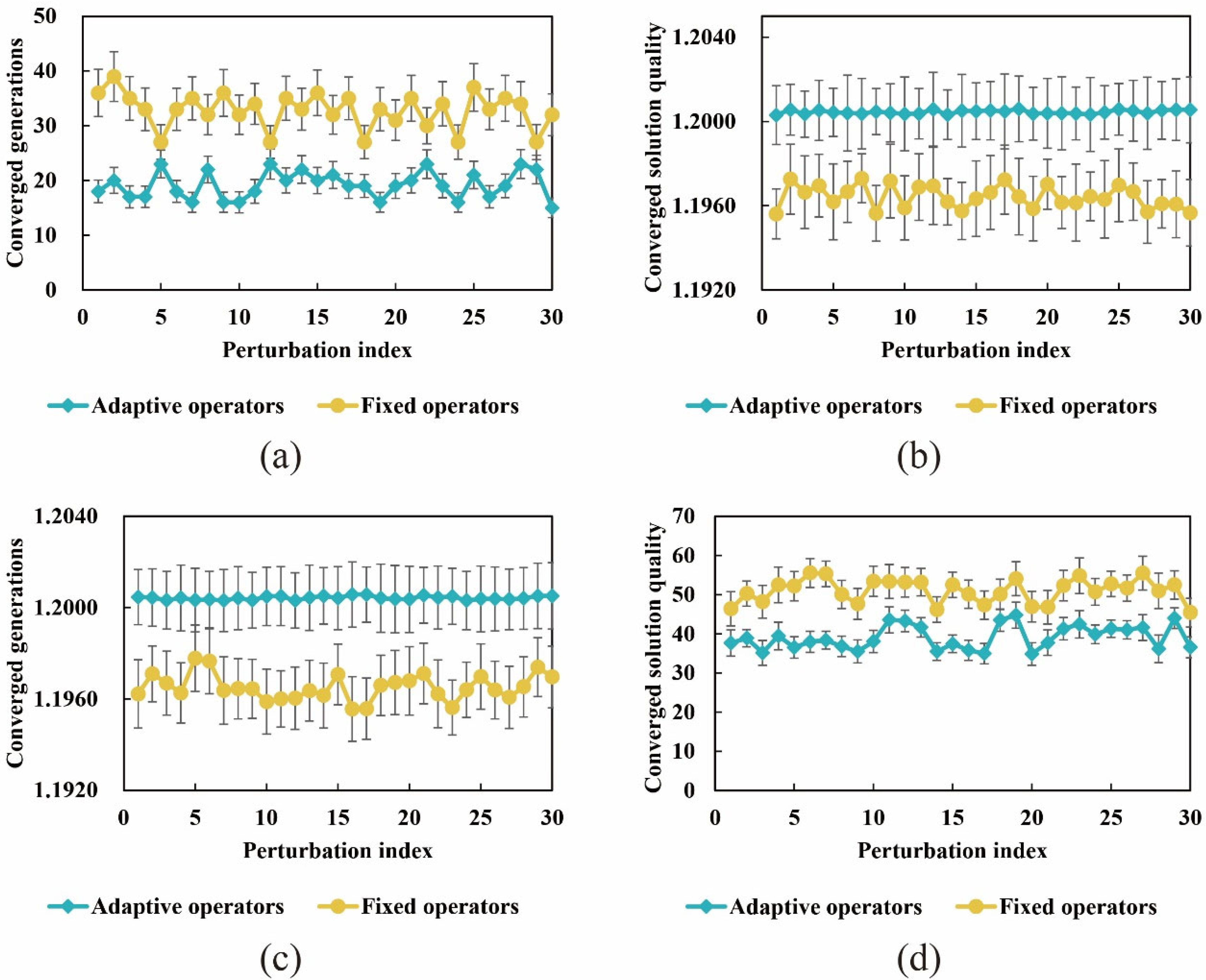
5.3.1. Sensitivity Analysis on Algorithm Coefficients
5.3.2. Sensitivity Analysis to Input Perturbations
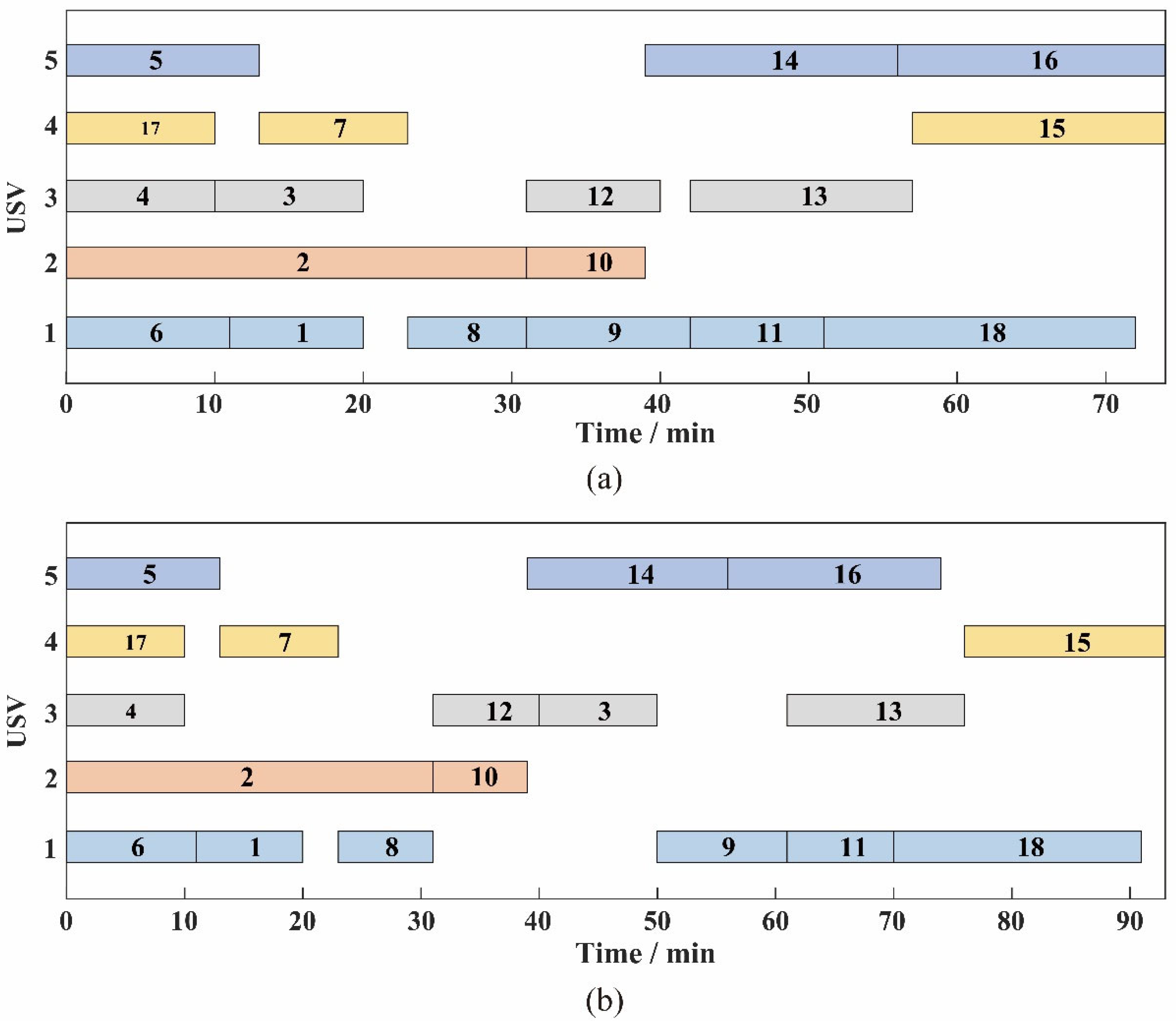
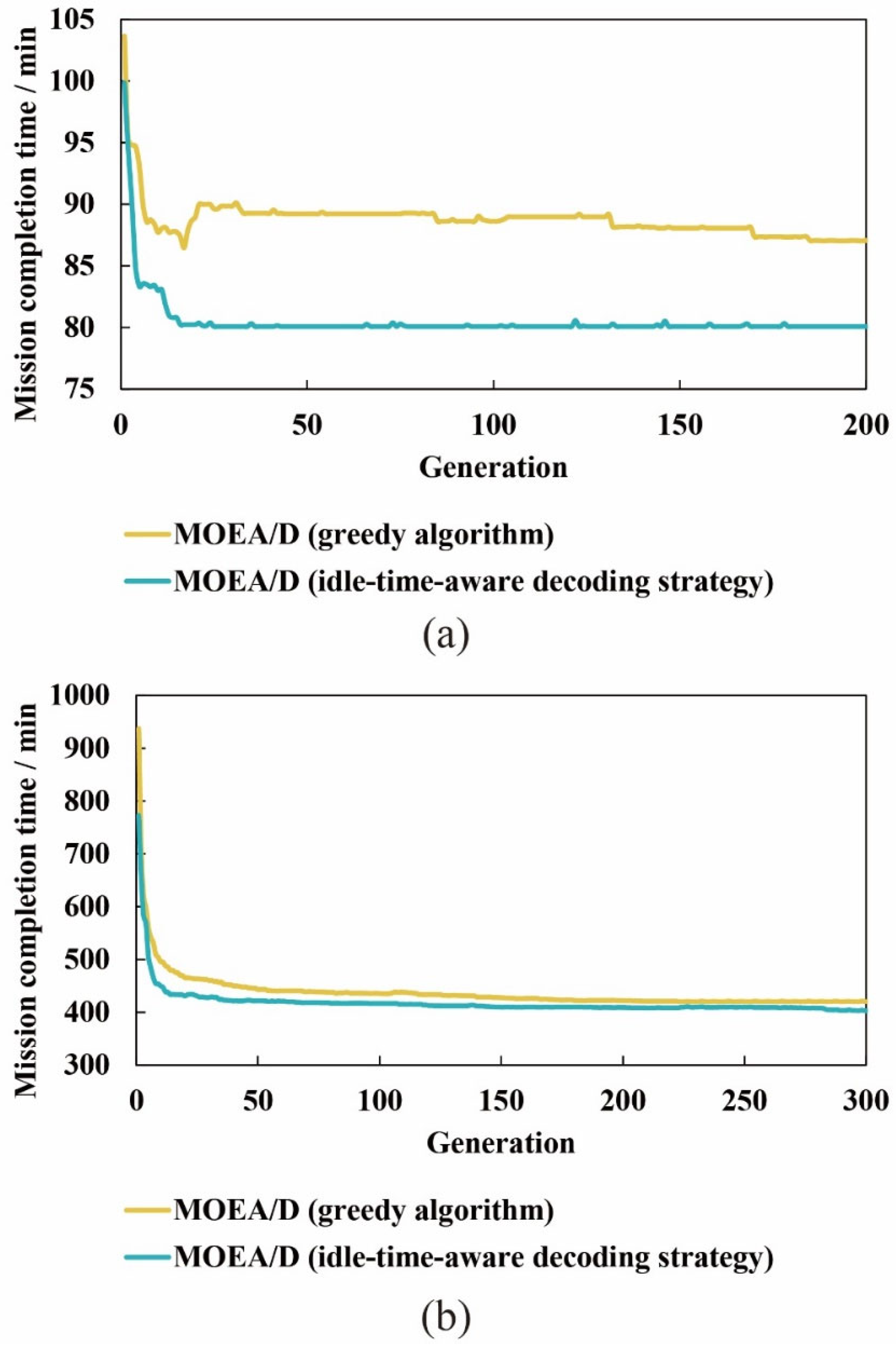
5.4. Comparison with Traditional Greedy Algorithm
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MRTAS | Maritime rescue task allocation and sequencing |
| MOEA/D | Multi-objective evolutionary algorithm based on decomposition |
| USV | Unmanned surface vehicle |
| MOEA/D-DE | Multi-objective evolutionary algorithms based on decomposition with differential evolution variants |
| SPEAs | Strength Pareto evolutionary algorithms |
| NSGAs | Non-dominated sorting genetic algorithms |
| ENS-MOEA/D | Ensemble neighborhood search based multi objective evolutionary algorithm based on decomposition |
| MOEA/D-QL | Multi objective evolutionary algorithm based on decomposition with Q learning based adaptive operator selection |
| MOEA/D-CTAOS | Multi objective evolutionary algorithm based on decomposition with classification tree based adaptive operator selection |
| DAG | Task directed acyclic graph |
| MOEA/DD | multi-objective evolutionary algorithm based on decomposition with dynamic resource allocation |
| SAO-MOEA/D | Stable-state adaptive optimization multi-objective evolutionary algorithm based on decomposition |
| SparseEA-AGDS | Sparse evolutionary algorithm with adaptive gradient descent strategy |
References
- Ai, B.; Li, B.; Gao, S.; Xu, J.; Shang, H. An Intelligent Decision Algorithm for the Generation of Maritime Search and Rescue Emergency Response Plans. IEEE Access 2019, 7, 155835–155850. [Google Scholar] [CrossRef]
- Xiong, W.; van Gelder, P.H.A.J.M.; Yang, K. A Decision Support Method for Design and Operationalization of Search and Rescue in Maritime Emergency. Ocean Eng. 2020, 207, 107399. [Google Scholar] [CrossRef]
- Yan, L.; Jinsong, B.; Xiaofeng, H.; Ye, J. A Heuristic Project Scheduling Approach for Quick Response to Maritime Disaster Rescue. Int. J. Proj. Manag. 2009, 27, 620–628. [Google Scholar] [CrossRef]
- Ai, B.; Jia, M.; Xu, H.; Xu, J.; Wen, Z.; Li, B.; Zhang, D. Coverage Path Planning for Maritime Search and Rescue Using Reinforcement Learning. Ocean Eng. 2021, 241, 110098. [Google Scholar] [CrossRef]
- Rani, S.; Babbar, H.; Kaur, P.; Alshehri, M.; Shah, S. An Optimized Approach of Dynamic Target Nodes in Wireless Sensor Network Using Bio Inspired Algorithms for Maritime Rescue. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2548–2555. [Google Scholar] [CrossRef]
- Xu, S.; Bi, W.; Zhang, A.; Mao, Z. Optimization of Flight Test Tasks Allocation and Sequencing Using Genetic Algorithm. Appl. Soft Comput. 2022, 115, 108241. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, X.; Song, Y.; Wang, H.; Wu, J. Recent Advances in Maritime Security Risk Detection and Rescue. Acad. J. Manag. Soc. Sci. 2025, 11, 13–22. [Google Scholar] [CrossRef]
- Chutima, P.; Arayikanon, K. Many-Objective Low-Cost Airline Cockpit Crew Rostering Optimisation. Comput. Ind. Eng. 2020, 150, 106844. [Google Scholar] [CrossRef]
- Zhan, H.; Zhang, Y.; Huang, J.; Song, Y.; Xing, L.; Wu, J.; Gao, Z. A Reinforcement Learning-Based Evolutionary Algorithm for the Unmanned Aerial Vehicles Maritime Search and Rescue Path Planning Problem Considering Multiple Rescue Centers. Memet. Comput. 2024, 16, 373–386. [Google Scholar] [CrossRef]
- Tanimu, M. Leveraging moea/d and echo state networks for solving complex optimization problems in time series prediction. Int. J. Digit. Innov. Built Environ. 2025, 1, 85–92. [Google Scholar]
- Wang, W.; Li, K.; Tao, X.; Gu, F. An Improved MOEA/D Algorithm with an Adaptive Evolutionary Strategy. Inf. Sci. 2020, 539, 1–15. [Google Scholar] [CrossRef]
- Tanabe, R.; Ishibuchi, H. Review and Analysis of Three Components of the Differential Evolution Mutation Operator in MOEA/D-DE. Soft Comput. 2019, 23, 12843–12857. [Google Scholar] [CrossRef]
- Zhou, H.; Qiao, J. Multiobjective Optimal Control for Wastewater Treatment Process Using Adaptive MOEA/D. Appl. Intell. 2019, 49, 1098–1126. [Google Scholar] [CrossRef]
- Konstantinidis, A.; Yang, K. Multi-Objective Energy-Efficient Dense Deployment in Wireless Sensor Networks Using a Hybrid Problem-Specific MOEA/D. Appl. Soft Comput. 2011, 11, 4117–4134. [Google Scholar] [CrossRef]
- Dong, Z.; Wang, X.; Tang, L. MOEA/D with a Self-Adaptive Weight Vector Adjustment Strategy Based on Chain Segmentation. Inf. Sci. 2020, 521, 209–230. [Google Scholar] [CrossRef]
- Xiang, D.; Lin, H.; Ouyang, J.; Huang, D. Combined Improved A* and Greedy Algorithm for Path Planning of Multi-Objective Mobile Robot. Sci. Rep. 2022, 12, 13273. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, N.; Song, Y.; Gao, Z. Optimization Model and Algorithm to Locate Rescue Bases and Allocate Rescue Vessels in Remote Oceans. Soft Comput. 2021, 25, 3317–3334. [Google Scholar] [CrossRef]
- Yousefi, M.H.N.; Goudarzi, M. A Task-Based Greedy Scheduling Algorithm for Minimizing Energy of MapReduce Jobs. J. Grid Comput. 2018, 16, 535–551. [Google Scholar] [CrossRef]
- Xue, F.; Chen, Y.; Dong, T.; Wang, P.; Fan, W. MOEA/D with Adaptive Weight Vector Adjustment and Parameter Selection Based on Q-Learning. Appl. Intell. 2025, 55, 399. [Google Scholar] [CrossRef]
- Tan, Y.-Y.; Jiao, Y.-C.; Li, H.; Wang, X.-K. A Modification to MOEA/D-DE for Multiobjective Optimization Problems with Complicated Pareto Sets. Inf. Sci. 2012, 213, 14–38. [Google Scholar] [CrossRef]
- Yu, J. Intelligent Construction Scheduling Based on MOEA/D-DE, SPEA2+SDE, and NSGA-III by Integrating Safety Assessment with Resource Efficiency. Informatica 2025, 49, 17–28. [Google Scholar] [CrossRef]
- Chen, X.; Yan, R.; Wu, S.; Liu, Z.; Haoyu, M.; Wang, S. A Fleet Deployment Model to Minimize the Covering Time of Maritime Rescue Missions. Marit. Policy Manag. 2021, 50, 724–749. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Mirjalili, S.; Chakrabortty, R.; Ryan, M. An Efficient Marine Predators Algorithm for Solving Multi-Objective Optimization Problems: Analysis and Validations. IEEE Access 2021, 9, 42817–42844. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Bai, J.; Ma, L.; Shi, C.; Zhang, G.; Shi, J. Multi-Objective Optimization of Marine Nuclear Power Secondary Circuit System Based on Improved Multi-Objective Particle Swarm Optimization Algorithm. Prog. Nucl. Energy 2023, 161, 104740. [Google Scholar] [CrossRef]
- Maurya, V.K.; Nanda, S.J. Time-Varying Multi-Objective Smart Home Appliances Scheduling Using Fuzzy Adaptive Dynamic SPEA2 Algorithm. Eng. Appl. Artif. Intell. 2023, 121, 105944. [Google Scholar] [CrossRef]
- Zeng, S.; Wu, Y.; Yu, Y. Multi-Skilled Worker Assignment in Production System for the Trade-off between Production Efficiency and Workload Fairness. Kybernetes 2023, 52, 3495–3518. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, X.; Qiao, J. A Multi-Objective Particle Swarm Optimization Algorithm Based on Two-Archive Mechanism. Appl. Soft Comput. 2022, 119, 108532. [Google Scholar] [CrossRef]
- Falcón-Cardona, J.; Coello, C. Indicator-Based Multi-Objective Evolutionary Algorithms: A Comprehensive Survey. ACM Comput. Surv. 2020, 53, 1–35. [Google Scholar] [CrossRef]
- Li, K.; Du, T.; Zhou, R.; Fan, Q. Multi-Objective Optimization of Material Properties for Enhanced Battery Performance Using Artificial Intelligence. Expert Syst. Appl. 2025, 288, 128179. [Google Scholar] [CrossRef]
- Zhang, C.; Dai, Z.; Liang, X.; Xu, G.; Zhang, C.; Zhang, B. An Evolutionary Generation Method of Deep Neural Network Sets Combined with Gaussian Random Field. Wirel. Netw. 2021, 7553, 1–10. [Google Scholar] [CrossRef]
- Schryen, G. Parallel Computational Optimization in Operations Research: A New Integrative Framework, Literature Review and Research Directions. Eur. J. Oper. Res. 2020, 287, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.-G.; Li, K.; Yeh, W.-C.; Jian, M.; Dong, J. Enhancing MOEA/D with Information Feedback Models for Large-Scale Many-Objective Optimization. Inf. Sci. 2020, 522, 1–16. [Google Scholar] [CrossRef]
- Xue, Y.; Zhu, H.; Liang, J.; Słowik, A. Adaptive Crossover Operator Based Multi-Objective Binary Genetic Algorithm for Feature Selection in Classification. Knowl. Based Syst. 2021, 227, 107218. [Google Scholar] [CrossRef]
- Das, P.K.; Jena, P.K. Multi-Robot Path Planning Using Improved Particle Swarm Optimization Algorithm through Novel Evolutionary Operators. Appl. Soft Comput. 2020, 92, 106312. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, L.; Shao, S.; Zhang, Y.; Zhang, X. Deep Reinforcement Learning Based Adaptive Environmental Selection for Evolutionary Multi-Objective Optimization. In Proceedings of the 2024 IEEE Congress on Evolutionary Computation (CEC), Yokohama, Japan, 30 June–5 July 2024. [Google Scholar]
- Cheng, H.; Li, L.; You, L. Dynamic Neighborhood Adjustment Strategy for Multi-Objective Evolutionary Algorithm Based on Decomposition. IEEE Access 2023, 11, 6574–6583. [Google Scholar] [CrossRef]
- Brambila-Hernández, J.A.; García-Morales, M.Á.; Fraire-Huacuja, H.J.; Cruz-Reyes, L.; Frausto-Solís, J. Novel Decomposition-Based Multi-Objective Evolutionary Algorithm Using Reinforcement Learning Adaptive Operator Selection (MOEA/D-QL). In New Horizons for Fuzzy Logic, Neural Networks and Metaheuristics; Castillo, O., Melin, P., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 149–165. ISBN 978-3-031-55684-5. [Google Scholar]
- Geng, H.; Xu, K.; Zhang, Y.; Zhou, Z. A Classification Tree and Decomposition Based Multi-Objective Evolutionary Algorithm with Adaptive Operator Selection. Complex Intell. Syst. 2023, 9, 579–596. [Google Scholar] [CrossRef]
- Wang, Y.; Zuo, X. An Effective Cloud Workflow Scheduling Approach Combining PSO and Idle Time Slot-Aware Rules. IEEE/CAA J. Autom. Sin. 2021, 8, 1079–1094. [Google Scholar] [CrossRef]
- Yang, S.; Meng, L.; Ullah, S.; Zhang, C.; Sang, H.; Zhang, B. MILP Modeling and Optimization of Three-Stage Flexible Job Shop Scheduling Problem with Assembly and AGV Transportation. Chin. J. Mech. Eng. 2025, 38, 115. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.; Zhang, Y.; Xu, G. Energy-Saving Distributed Flexible Job Shop Scheduling Optimization with Dual Resource Constraints Based on Integrated Q-Learning Multi-Objective Grey Wolf Optimizer. CMES—Comput. Model. Eng. Sci. 2024, 140, 1459–1483. [Google Scholar] [CrossRef]
- Afshar-Nadjafi, B. Multi-Skilling in Scheduling Problems: A Review on Models, Methods and Applications. Comput. Ind. Eng. 2021, 151, 107004. [Google Scholar] [CrossRef]
- Yannibelli, V.; Amandi, A. Project Scheduling: A Multi-Objective Evolutionary Algorithm That Optimizes the Effectiveness of Human Resources and the Project Makespan. Eng. Optim. 2013, 45, 45–65. [Google Scholar] [CrossRef]
- Wu, B.; Xiao, Y.; Ren, H.; Yang, L.; Lu, R. Design and Application of Workshop Production Scheduling Strategy Based on Manufacturing Big Data. In Proceedings of the 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 7 July 2023; pp. 1182–1189. [Google Scholar]
- Singh, K.; Sundar, S. Artificial Bee Colony Algorithm Using Permutation Encoding for the Bounded Diameter Minimum Spanning Tree Problem. Soft Comput. 2021, 25, 11289–11305. [Google Scholar] [CrossRef]
- Xing, H.; Zhou, X.; Wang, X.; Luo, S.; Dai, P.; Li, K.; Yang, H. An Integer Encoding Grey Wolf Optimizer for Virtual Network Function Placement. Appl. Soft Comput. 2019, 76, 575–594. [Google Scholar] [CrossRef]
- Sun, J.; Yu, S.; Chu, J.; Cun, W.; Wang, H.; Chen, C.; Li, F.; Huang, Y. A Crew Task Allocation and Sequencing Method Considering Workload Distribution and Minimum Task Completion Time. Kybernetes 2024, 1–29, ahead-of-print. [Google Scholar] [CrossRef]
- Naresh, R.; Sayeekumar, M.; Karthick, G.M.; Supraja, P. Attribute-Based Hierarchical File Encryption for Efficient Retrieval of Files by DV Index Tree from Cloud Using Crossover Genetic Algorithm. Soft Comput. 2019, 23, 2561–2574. [Google Scholar] [CrossRef]
- Barbulescu, A.; Șerban, C.; Indrecan, M.-L. Computing the Beta Parameter in IDW Interpolation by Using a Genetic Algorithm. Water 2021, 13, 863. [Google Scholar] [CrossRef]
- Zainuddin, F.; Abd Samad, M.F. A Review of Crossover Methods and Problem Representation of Genetic Algorithm in Recent Engineering Applications. Int. J. Adv. Sci. Technol. 2020, 29, 759–769. [Google Scholar]
- Chen, C.; Xu, Y.; Cheng, G.; Wang, H.; Zhang, Y. Task-Resource Matching Modeling and Optimization Algorithm. In Methods for Modelling and Optimizing Military Mission Plans; National Defense Industry Press: Beijing, China, 2019; pp. 89–92. [Google Scholar]
- Danacı, M.; Yıldırım, U. Comprehensive Analysis of Lifeboat Accidents Using the Fuzzy Delphi Method. Ocean Eng. 2023, 278, 114371. [Google Scholar] [CrossRef]
- Pescaroli, G.; Velazquez, O.; Alcántara-Ayala, I.; Galasso, C.; Kostkova, P.; Alexander, D. A Likert Scale-Based Model for Benchmarking Operational Capacity, Organizational Resilience, and Disaster Risk Reduction. Int. J. Disaster Risk Sci. 2020, 11, 404–409. [Google Scholar] [CrossRef]
- Guerreiro, A.; Fonseca, C.; Paquete, L. The Hypervolume Indicator: Problems and Algorithms. ACM Comput. Surv. 2020, 54, 1–42. [Google Scholar] [CrossRef]
- Bringmann, K.; Friedrich, T. Approximation Quality of the Hypervolume Indicator. Artif. Intell. 2013, 195, 265–290. [Google Scholar] [CrossRef]
- Meng, F.; Liu, J.; Tong, G.; Zhao, H.; Wen, C.; Zhou, Y.; Rasouli, V.; Rabiei, M. Multiobjective Optimization of CO2 Injection under Geomechanical Risk in High Water Cut Oil Reservoirs Using Artificial Intelligence Approaches. Sci. Rep. 2025, 15, 25643. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Zhu, Q. Intelligent Optimization Method for Hazardous Materials Transportation Routing with Multi-Mode and Multi-Criterion Collaborative Constraints. Sci. Rep. 2025, 15, 7804. [Google Scholar] [CrossRef]
- Kalita, K.; Jangir, P.; Pandya, S.B.; Alzahrani, A.I.; Alblehai, F.; Abualigah, L.; Ezugwu, A.E. MORKO: A Multi-Objective Runge–Kutta Optimizer for Multi-Domain Optimization Problems. Int. J. Comput. Intell. Syst. 2025, 18, 3. [Google Scholar] [CrossRef]
- Böðvarsdóttir, E.B.; Stidsen, T. A Review of Multi-Objective Optimization Methods for Personnel Rostering Problems. J. Sched. 2025, 1–19. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, A.; Sun, C.; Ye, Q. An Evolutionary Algorithm for Multi-Objective Workflow Scheduling with Adaptive Dynamic Grouping. Electronics 2025, 14, 2586. [Google Scholar] [CrossRef]
- Castro, O.R.; Santana, R.; Lozano, J.A.; Pozo, A. Combining CMA-ES and MOEA/DD for Many-Objective Optimization. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 1451–1458. [Google Scholar]
- Yang, Z.; Qiu, H.; Gao, L.; Chen, L.; Liu, J. Surrogate-Assisted MOEA/D for Expensive Constrained Multi-Objective Optimization. Inf. Sci. 2023, 639, 119016. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, W.; Tang, J.-N.; Dai, Z.-B.; Feng, Y.-N. Evolution Algorithm with Adaptive Genetic Operator and Dynamic Scoring Mechanism for Large-Scale Sparse Many-Objective Optimization. Sci. Rep. 2025, 15, 9267. [Google Scholar] [CrossRef]







| Core Characteristics | ENS-MOEA/D | MOEA/D-QL | MOEA/D-CTAOS | This Paper |
|---|---|---|---|---|
| Adaptive mechanism | Linear combination of neighborhood operator weights | Q-learning discrete decision | Classification tree threshold-based piecewise control | Dual-dimensional composite response: temporal dimension (linear decay of iteration progress) and spatial dimension (nonlinear adjustment of objective distribution) |
| Exploration–exploitation balance | Fixed intensity operator switching | ε-greedy random exploration | Rule-constrained perturbation | Dynamic dual-mode adjustment: high perturbation in the early stage and linear plus distribution-sensitive decay in the later stage |
| Computational efficiency | Requires maintenance of multiple operator instances | Q-table training overhead | Decision tree inference overhead | Analytical computation without iterative training, only requiring the calculation of objective value statistics |
| Engineering adaptability | General optimization requiring a preset operator library | Dynamic environment adaptation | Strong rule interpretability | Ensures convergence efficiency and precisely adapts to disaster relief scenarios |
| Category | Symbol | Description |
|---|---|---|
| Decision Variables | Binary (0 or 1); 1 if task i is assigned to USV m | |
| Start time of task i | ||
| Binary (0 or 1); 1 if USV m executes task j next after task i, not necessarily immediately, but with no other task in between | ||
| Derived Variables | Actual execution duration of task i | |
| Actual resource consumption of task i | ||
| Objective Functions | Mission completion time | |
| Resource consumption | ||
| Parameters | The required duration for USV m to execute task i | |
| The required resource consumption for USV m to execute task i | ||
| Set of USVs capable of executing task i | ||
| Task precedence relationship, 1 if task i must finish before task j starts | ||
| Indices | i, j | Task indices |
| m | USV index | |
| K | Number of tasks |
| Task | Task Content | Resource Demands | |||
|---|---|---|---|---|---|
| Communication | Navigation Energy | Sensor Payload | Battery Consumption | ||
| 1 | Coastal hazard mapping (north) | 7 | 8 | 9 | 2 |
| 2 | Coastal hazard mapping (south) | 7 | 8 | 9 | 2 |
| 3 | Medical supply delivery (north) | 8 | 7 | 2 | 10 |
| 4 | Medical supply delivery (south) | 8 | 7 | 2 | 10 |
| 5 | Submerged debris scanning | 4 | 11 | 3 | 6 |
| 6 | Surface obstacle neutralization | 3 | 6 | 15 | 3 |
| 7 | Northern logistics hub setup | 3 | 6 | 9 | 11 |
| 8 | Southern beach assessment | 3 | 5 | 10 | 10 |
| 9 | Coastal surveillance (north) | 6 | 8 | 9 | 2 |
| 10 | Coastal surveillance (south) | 6 | 8 | 9 | 2 |
| 11 | Evac route recon (north) | 2 | 8 | 6 | 10 |
| 12 | Evac route recon (south) | 4 | 9 | 5 | 11 |
| 13 | Maritime threat clearance (south) | 4 | 9 | 5 | 11 |
| 14 | Maritime threat clearance (north) | 7 | 6 | 4 | 12 |
| 15 | Port access coordination | 5 | 7 | 9 | 8 |
| 16 | Airfield access coordination | 4 | 7 | 8 | 9 |
| 17 | Refugee encampment setup | 6 | 6 | 8 | 9 |
| 18 | Aid route blockade | 5 | 9 | 10 | 3 |
| USV | Lower/Upper Limit | Resource Capacity | |||
|---|---|---|---|---|---|
| Communication | Navigation Energy | Sensor Payload | Battery Consumption | ||
| 1 | Lower limit | 2 | 5 | 6 | 2 |
| Upper limit | 7 | 9 | 15 | 10 | |
| 2 | Lower limit | 2 | 5 | 6 | 2 |
| Upper limit | 7 | 9 | 15 | 10 | |
| 3 | Lower limit | 3 | 6 | 2 | 10 |
| Upper limit | 8 | 9 | 12 | 11 | |
| 4 | Lower limit | 3 | 6 | 3 | 6 |
| Upper limit | 7 | 11 | 12 | 12 | |
| 5 | Lower limit | 3 | 6 | 3 | 6 |
| Upper limit | 7 | 11 | 12 | 12 | |
| Task | Available USVs | Execution Duration/Min | Communication | Navigation Energy | Sensor Payload | Battery Consumption | Resource Consumption |
|---|---|---|---|---|---|---|---|
| 1 | 1, 2 | 9, 11 | 7, 7 | 9, 9 | 12, 15 | 2, 2 | 30, 33 |
| 2 | 1, 2 | 29, 31 | 7, 7 | 8, 8 | 15, 13 | 2, 3 | 32, 31 |
| 3 | 3 | 10 | 8 | 9 | 3 | 10 | 30 |
| 4 | 3 | 10 | 8 | 9 | 3 | 10 | 30 |
| 5 | 4, 5 | 12, 13 | 7, 4 | 11, 11 | 4, 4 | 6, 6 | 28, 25 |
| 6 | 1, 2 | 11, 14 | 3, 3 | 6, 9 | 15, 15 | 4, 5 | 28, 32 |
| 7 | 3, 4, 5 | 8, 10, 9 | 3, 3, 3 | 6, 6, 6 | 12, 9, 10 | 11, 11, 11 | 32, 29, 30 |
| 8 | 1, 2 | 8, 10 | 7, 4 | 5, 5 | 10, 10 | 10, 10 | 32, 29 |
| 9 | 1, 2 | 11, 8 | 6, 7 | 9, 9 | 11, 14 | 2, 2 | 28, 32 |
| 10 | 1, 2 | 11, 8 | 6, 7 | 9, 9 | 11, 14 | 2, 2 | 28, 32 |
| 11 | 1, 2 | 9, 8 | 6, 7 | 8, 9 | 6, 7 | 10, 10 | 30, 33 |
| 12 | 3 | 9 | 4 | 9 | 6 | 11 | 30 |
| 13 | 3 | 15 | 4 | 9 | 6 | 11 | 30 |
| 14 | 4, 5 | 20, 17 | 7, 7 | 6, 10 | 5, 4 | 12, 12 | 30, 33 |
| 15 | 4, 5 | 17, 14 | 5, 7 | 7, 7 | 9, 11 | 9, 8 | 30, 33 |
| 16 | 4, 5 | 14, 18 | 7, 4 | 7, 7 | 9, 8 | 10, 10 | 33, 29 |
| 17 | 4, 5 | 10, 9 | 6, 7 | 6, 7 | 8, 10 | 10, 9 | 30, 33 |
| 18 | 1, 2 | 21, 17 | 5, 5 | 9, 9 | 10, 15 | 4, 3 | 28, 32 |
| Task | Task Content | Available USVs | Execution Duration/Min | Resource Consumption |
|---|---|---|---|---|
| 1 | Harbor entrance recon (north) | 1, 2, 3 | 7, 8, 9 | 33, 34, 35 |
| 2 | Harbor entrance recon (south) | 1, 2, 3 | 8, 9, 10 | 34, 35, 36 |
| 3 | Coastal hazard map (north) | 1, 2, 3 | 10, 11, 12 | 35, 36, 37 |
| 4 | Coastal hazard map (south) | 1, 2, 3 | 11, 12, 13 | 36, 37, 38 |
| 5 | Aerial drone launch | 4, 5 | 5, 6 | 25, 24 |
| 6 | Aerial drone recovery | 4, 5 | 5, 6 | 24, 25 |
| 100 | Mission debrief and return to base | 1, 10 | 8, 12 | 30, 35 |
| Solution | MRTAS Scheme | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sequence | 5 | 2 | 6 | 17 | 4 | 7 | 8 | 3 | 12 | 1 | 10 | 9 | 11 | 13 | 14 | 18 | 15 | 16 |
| USV | 4 | 2 | 1 | 4 | 3 | 5 | 1 | 3 | 3 | 1 | 2 | 1 | 1 | 3 | 5 | 1 | 5 | 4 | |
| 2 | Sequence | 2 | 3 | 6 | 5 | 4 | 17 | 7 | 8 | 12 | 1 | 9 | 13 | 10 | 14 | 11 | 18 | 15 | 16 |
| USV | 2 | 3 | 1 | 5 | 3 | 4 | 5 | 1 | 3 | 1 | 1 | 3 | 2 | 5 | 1 | 1 | 5 | 4 | |
| 3 | Sequence | 6 | 5 | 2 | 3 | 7 | 8 | 4 | 12 | 1 | 10 | 14 | 9 | 13 | 11 | 17 | 18 | 16 | 15 |
| USV | 1 | 5 | 2 | 3 | 4 | 1 | 3 | 3 | 1 | 2 | 5 | 1 | 3 | 1 | 4 | 1 | 4 | 5 | |
| 4 | Sequence | 5 | 6 | 17 | 2 | 7 | 8 | 4 | 12 | 3 | 10 | 1 | 9 | 13 | 11 | 18 | 14 | 15 | 16 |
| USV | 5 | 1 | 4 | 2 | 4 | 1 | 3 | 3 | 3 | 2 | 1 | 1 | 3 | 1 | 1 | 4 | 5 | 4 | |
| 5 | Sequence | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 12 | 9 | 13 | 10 | 17 | 14 | 11 | 18 | 15 | 16 |
| USV | 2 | 3 | 3 | 5 | 1 | 4 | 1 | 1 | 3 | 1 | 3 | 2 | 4 | 5 | 1 | 1 | 4 | 5 | |
| 6 | Sequence | 6 | 2 | 5 | 3 | 7 | 8 | 4 | 12 | 1 | 9 | 10 | 14 | 13 | 17 | 11 | 18 | 15 | 16 |
| USV | 1 | 2 | 5 | 3 | 4 | 1 | 3 | 3 | 1 | 1 | 2 | 4 | 3 | 4 | 1 | 1 | 4 | 5 | |
| 7 | Sequence | 5 | 3 | 6 | 2 | 17 | 7 | 8 | 4 | 12 | 1 | 10 | 9 | 13 | 11 | 18 | 14 | 15 | 16 |
| USV | 5 | 3 | 1 | 2 | 4 | 4 | 1 | 3 | 3 | 1 | 1 | 1 | 3 | 1 | 1 | 4 | 4 | 5 | |
| 8 | Sequence | 2 | 17 | 6 | 4 | 1 | 3 | 5 | 7 | 8 | 12 | 9 | 10 | 13 | 14 | 11 | 18 | 15 | 16 |
| USV | 2 | 4 | 1 | 3 | 1 | 3 | 5 | 4 | 2 | 3 | 1 | 1 | 3 | 4 | 1 | 1 | 4 | 5 | |
| Solution | MRTAS Scheme | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Sequence | 67 | 68 | 69 | 70 | 2 | 4 | 25 | 71 | 20 | 24 | 6 | 56 | 5 | 23 | 55 | 60 | … | 100 |
| USV | 4 | 4 | 1 | 2 | 2 | 1 | 4 | 1 | 1 | 5 | 4 | 5 | 5 | 5 | 6 | 1 | … | 1 | |
| 2 | Sequence | 67 | 55 | 68 | 59 | 2 | 69 | 58 | 4 | 5 | 60 | 24 | 1 | 70 | 25 | 71 | 56 | … | 100 |
| USV | 4 | 6 | 4 | 1 | 2 | 1 | 1 | 1 | 5 | 1 | 5 | 1 | 2 | 4 | 1 | 5 | … | 1 | |
| 3 | Sequence | 55 | 67 | 68 | 59 | 69 | 2 | 24 | 6 | 25 | 58 | 70 | 60 | 4 | 71 | 56 | 1 | … | 54 |
| USV | 6 | 4 | 4 | 1 | 1 | 2 | 5 | 4 | 4 | 1 | 2 | 1 | 1 | 1 | 5 | 1 | … | 7 | |
| 4 | Sequence | 55 | 67 | 68 | 59 | 69 | 2 | 5 | 24 | 4 | 25 | 58 | 70 | 60 | 6 | 71 | 56 | … | 54 |
| USV | 6 | 4 | 4 | 1 | 1 | 2 | 5 | 5 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 5 | … | 7 | |
| 5 | Sequence | 67 | 55 | 68 | 6 | 5 | 24 | 2 | 69 | 59 | 58 | 56 | 23 | 1 | 70 | 71 | 43 | … | 100 |
| USV | 4 | 4 | 4 | 4 | 4 | 5 | 1 | 1 | 1 | 1 | 4 | 5 | 1 | 1 | 1 | 1 | … | 1 | |
| 6 | Sequence | 67 | 55 | 68 | 6 | 5 | 24 | 2 | 69 | 59 | 58 | 16 | 43 | 56 | 23 | 1 | 70 | … | 100 |
| USV | 4 | 4 | 4 | 4 | 4 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 4 | 5 | 1 | 1 | … | 1 | |
| 7 | Sequence | 67 | 55 | 25 | 6 | 5 | 24 | 2 | 16 | 68 | 69 | 59 | 58 | 56 | 23 | 1 | 70 | … | 100 |
| USV | 4 | 4 | 5 | 4 | 4 | 5 | 1 | 5 | 4 | 1 | 1 | 1 | 4 | 5 | 1 | 1 | … | 1 | |
| 8 | Sequence | 5 | 6 | 16 | 25 | 55 | 67 | 24 | 2 | 58 | 59 | 56 | 23 | 1 | 19 | 43 | 20 | 100 | |
| USV | 4 | 4 | 5 | 5 | 4 | 4 | 5 | 1 | 1 | 1 | 4 | 5 | 1 | 1 | 1 | 1 | 1 | ||
| 9 | Sequence | 5 | 6 | 16 | 25 | 55 | 67 | 24 | 2 | 58 | 59 | 56 | 23 | 1 | 19 | 43 | 20 | 100 | |
| USV | 4 | 4 | 5 | 5 | 4 | 4 | 5 | 1 | 1 | 1 | 4 | 5 | 1 | 1 | 1 | 1 | 1 | ||
| 10 | Sequence | 5 | 6 | 25 | 55 | 67 | 16 | 24 | 2 | 58 | 59 | 56 | 23 | 1 | 43 | 19 | 20 | 100 | |
| USV | 4 | 4 | 5 | 4 | 4 | 5 | 5 | 1 | 1 | 1 | 4 | 5 | 1 | 1 | 1 | 1 | 1 | ||
| Score | Anchor Description | Quantitative Threshold Example |
|---|---|---|
| 5—Excellent | Fully meets or exceeds expert benchmarks; no improvement needed. | Time deviation ≤ ±2%; resource deviation ≤ ±2%; and zero conflicts. |
| 4—Good | Generally within expert range; minor deviations acceptable. | Time deviation ≤ ±5%; resource deviation ≤ ±5%; and ≤1 minor conflict. |
| 3—Fair | Partially meets criteria; small adjustments required. | Time deviation ≤ ±10%; resource deviation ≤ ±10%; and ≤2 adjustable conflicts. |
| 2—Poor | Noticeably outside range; major revisions necessary. | Deviation or conflicts exceed the “Fair” thresholds. |
| 1—Unacceptable | Severely violates benchmarks; not implementable. | Significant deviations or conflicts that lead to outright rejection. |
| Case 1 | Case 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| Expert 1 | Expert 2 | Expert 3 | Mean | Expert 1 | Expert 2 | Expert 3 | Mean | |
| Scenario Fit | 5 | 4 | 5 | 4.67 | 5 | 5 | 5 | 5 |
| Time Reasonableness | 4 | 5 | 4 | 4.67 | 4 | 5 | 4 | 4.67 |
| Resource Reasonableness | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Operational Feasibility | 5 | 5 | 5 | 5 | 5 | 4 | 5 | 4.67 |
| Baseline Value | Lower Limit | Upper Limit | |
|---|---|---|---|
| 1 | 0.85 | 1.00 | |
| 0.07 | 0.06 | 0.08 | |
| 0.3 | 0.26 | 0.36 | |
| 0.015 | 0.01 | 0.02 |
| 1 | 0.85 | 0.06 | 0.26 | 0.01 |
| 2 | 0.85 | 0.06 | 0.3 | 0.015 |
| 3 | 0.85 | 0.06 | 0.36 | 0.02 |
| 4 | 0.85 | 0.07 | 0.26 | 0.015 |
| 5 | 0.85 | 0.07 | 0.3 | 0.02 |
| 6 | 0.85 | 0.07 | 0.36 | 0.01 |
| 7 | 1 | 0.06 | 0.26 | 0.015 |
| 8 | 1 | 0.06 | 0.3 | 0.02 |
| 9 | 1 | 0.06 | 0.36 | 0.01 |
| 10 | 1 | 0.07 | 0.26 | 0.02 |
| 11 | 1 | 0.07 | 0.3 | 0.01 |
| 12 | 1 | 0.07 | 0.36 | 0.015 |
| 13 | 1 | 0.07 | 0.26 | 0.01 |
| 14 | 1 | 0.07 | 0.3 | 0.015 |
| 15 | 1 | 0.07 | 0.36 | 0.02 |
| 16 | 1 | 0.07 | 0.26 | 0.01 |
| 17 | 1 | 0.07 | 0.3 | 0.015 |
| 18 | 1 | 0.07 | 0.36 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Yu, S.; Chu, J.; Liu, R. Maritime Rescue Task Allocation and Sequencing Using MOEA/D with Adaptive Operators and Idle-Time-Aware Decoding Strategy. J. Mar. Sci. Eng. 2025, 13, 1518. https://doi.org/10.3390/jmse13081518
Sun J, Yu S, Chu J, Liu R. Maritime Rescue Task Allocation and Sequencing Using MOEA/D with Adaptive Operators and Idle-Time-Aware Decoding Strategy. Journal of Marine Science and Engineering. 2025; 13(8):1518. https://doi.org/10.3390/jmse13081518
Chicago/Turabian StyleSun, Jianhua, Suihuai Yu, Jianjie Chu, and Ruisi Liu. 2025. "Maritime Rescue Task Allocation and Sequencing Using MOEA/D with Adaptive Operators and Idle-Time-Aware Decoding Strategy" Journal of Marine Science and Engineering 13, no. 8: 1518. https://doi.org/10.3390/jmse13081518
APA StyleSun, J., Yu, S., Chu, J., & Liu, R. (2025). Maritime Rescue Task Allocation and Sequencing Using MOEA/D with Adaptive Operators and Idle-Time-Aware Decoding Strategy. Journal of Marine Science and Engineering, 13(8), 1518. https://doi.org/10.3390/jmse13081518






