Wave-Induced Seabed Stability in an Infinite Porous Seabed: Effects of Phase-Lags

Abstract

The evaluation of the wave-induced seabed stability such as liquefaction and shear failure is one of the factors that must be considered in the design of marine infrastructures. Due to the transformation within the porous medium, the wave-induced soil response manifests itself as a phase delay in the dynamic wave pressure on the seabed surface, which is referred to as “phase-lag”. In this study, the analytical solutions of wave-induced soil response in an infinite porous seabed are further examined to clarify the effects of phase-lags. Based on the coefficient of relative rigidity of the soil skeleton to the pore fluid ($R_k$), a simplified approximation is derived. The expressions of the phase-lags for wave-induced soil response are presented for various cases. Moreover, the phase-lag effects on instantaneous liquefaction and shear failure are analysed. Based on the parametric study, it is concluded the extreme phase-lag for wave-induced pore pressure increases with increasing $R_k$, the extreme phase-lag for horizontal effective stress and shear stress decrease with increasing $R_k$. Furthermore, the liquefaction zone and shear failure zone increase with increasing $R_k$.

1. Introduction

The phenomenon of wave-induced seabed stability in the vicinity of marine infrastructures has been recognised as one of the key factors in the design of marine infrastructures, as several events have been reported in the literature [1,2,3]. In general, as shown in Figure 1a, when ocean waves propagate over the seafloor, wave-induced dynamic wave pressures at the surface of a seabed will further induce pore pressures and effective stresses within a porous seabed and result in seabed instability around marine infrastructures, such as liquefaction, shear failure, scour, etc. [2].

Based on laboratory experiments and field measurements [4,5,6], two mechanisms of wave-induced soil response have been observed, as shown in Figure 1b, depending on the way the pore pressure is generated. In the figure, $P_t$ represents the total pore pressure, P is oscillatory pore pressure and $P_r$ denotes the residual pore pressure and $P_t=P_r+P$. One is caused by the progressive nature of excess pore pressure, which appears in the initial stage of the cyclic loading, which requires a poroelastoplastic soil model. The other is generated by the oscillatory pore pressure, which is accompanied by the amplitude damping and phase-lag in the pore pressure. This type of soil response appears periodically during a storm sequence and can be described by a poroelastic soil model. The phase-lag is relative to the dynamic wave pressure at the surface of the seabed. In this study, only the oscillatory mechanism is considered.

Figure 1. (a) Sketch of the interaction between wave and seabed; and (b) mechanism of wave-induced pore pressure (re-produced from [7]).

Figure 1. (a) Sketch of the interaction between wave and seabed; and (b) mechanism of wave-induced pore pressure (re-produced from [7]).

Due to transformation within a porous medium, the wave-induced soil response, including pore pressures, stresses, and displacements, will appear as a phase delay from the dynamic wave pressures acting on the seabed surface. This phenomenon was named “phase-lag” [8,9]. Figure 2 illustrates a schematic diagram of the phase-lag for wave-induced pore pressures. In this study, phase-lag is defined within the range of $\pm 180$ degrees. It should be noted that the signs “+” and “−” in Figure 2 only indicate the direction of the phase delay. Note that Figure 2 is a conceptual diagram of phase-lag, based on the summary of the experimental results available in the literature.

The phenomenon of phase-lag was first reported by Sleath [8]. In his wave-flume experiments, the phase-lag was reported to be less than 10 degrees. However, these experimental results were inconsistent with his theoretical results because his theoretical model was based on the assumption of a rigid porous medium. Later, Tsui and Helfrich [10] reported a phase-lag about 30% of a wave period in a series of wave flume experiments. Okusa [9] further investigated the phase-lag between dynamic wave pressures and pore water pressures in unsaturated marine sediments. Recently, Liu et al. [11] further confirmed the existence of phase-lags based on one-dimensional compressive tests.

Recently, based on the analytical solution for wave-induced pore pressures in an infinite seabed [12], Li and Gao [13] examined the characteristics of amplitude attenuation and phase-lag for pore pressures in a silt bed. With the framework work, Li et al. [14] further adopted an explicit approximation of the depth of liquefaction to reflect the presence of phase delay in wave-induced pore pressures and conducted a parametric analysis to explore the influence of phase delay on instantaneous liquefaction. However, existing investigations focused only on the impact of phase-lag on pore pressure, rather than other soil response variables such as stresses and displacements.

Two types of seabed instability around marine infrastructures have been recognised by offshore geotechnical engineers. In general, when the excess pore pressure is greater than the upward seepage, liquefaction of the seabed will occur [4]. Another type of seabed instability is shear failure, which is based on the Mohr–Coulomb criterion. Shear failure in soil usually occurs when the shear stress exceeds its shear bearing capacity at the given point and instance [15].

The phenomenon of the phase-lags of the wave-induced soil response in a porous seabed has been observed in the experiments available in the literature. However, theoretical investigations of phase lag were rare [13,14] and focused only on pore pressures. The main objective is to fill this research gap and provides simplified approximations for all response variables on the seabed. In addition, this study will further examine the effects of phase lag on wave-induced liquefaction and shear failure.

In this study, the analytical solution of the wave-induced soil response in an infinite porous seabed [16] is further examined to obtain the explicit expressions of phase-lag. This paper is organised as follows. In Section 2, the analytical solution for the wave-induced soil response in an infinite seabed proposed by Hsu et al. [16] is outlined. Then, a detailed derivation of phase-lags for all soil response variables will be provided in Section 3. In the section, a parameter ($R_k$) representing the relative rigidity of the soil skeleton to the pore fluid is adopted and simplified approximations are obtained. Based on the analytical solution, in Section 5, the wave-induced liquefaction and shear failure with phase-lags are discussed. Finally, the key findings are summarised in Section 6.

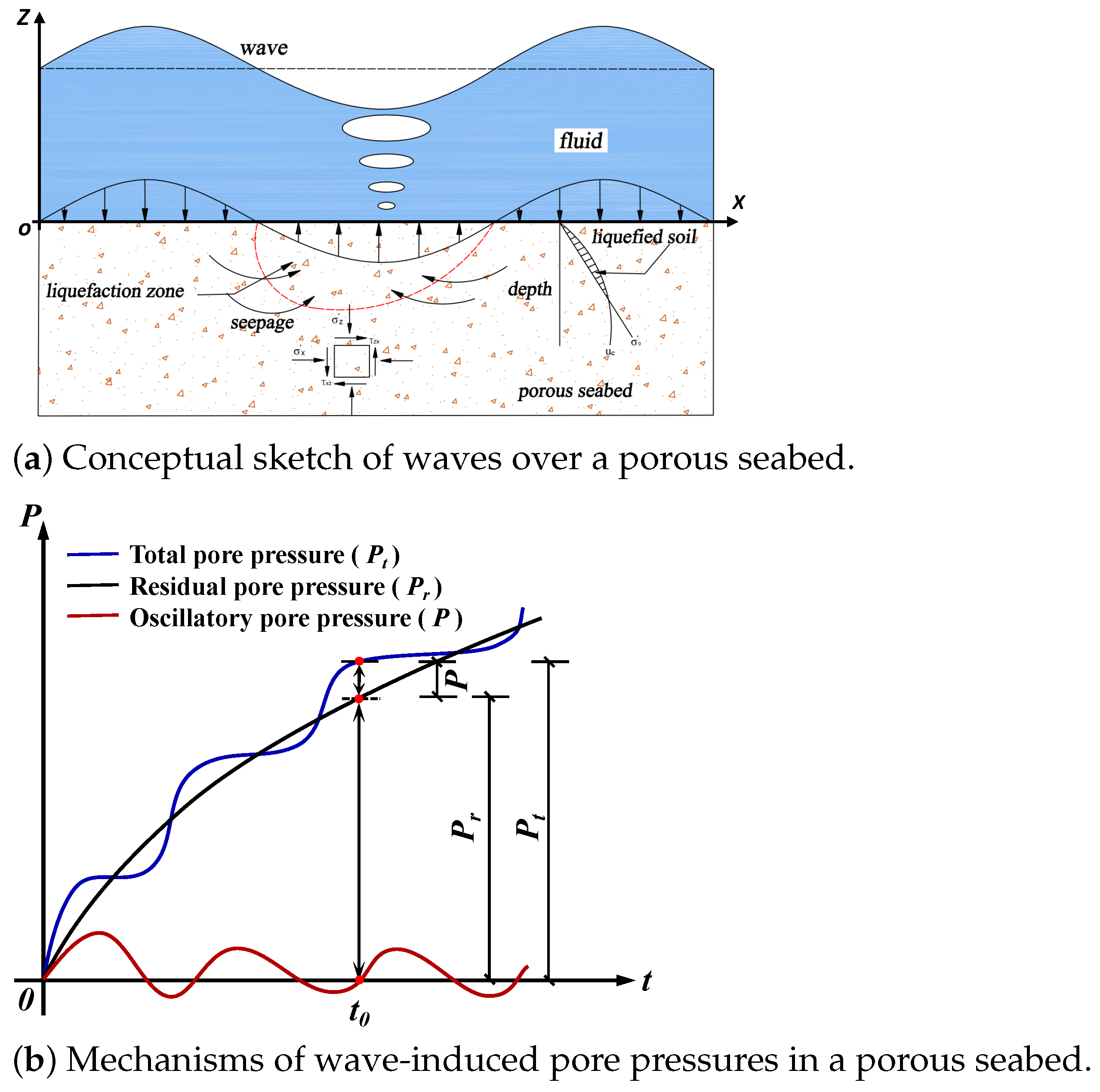
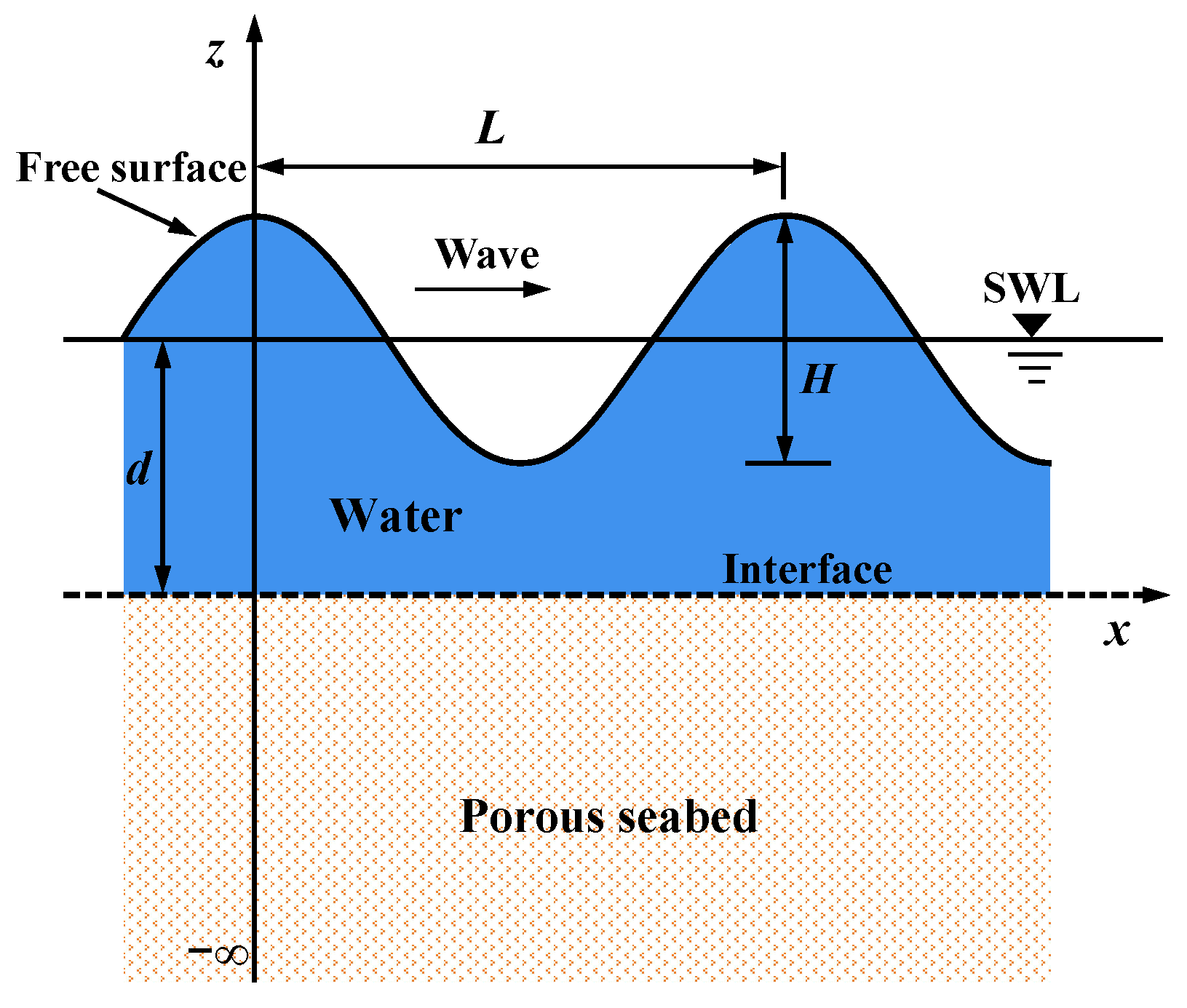
2. Analytical Solution for Wave-Induced Soil Response

Based on linear pore-elastic theory, numerous analytical solutions have been proposed for the wave-induced soil response in an infinite seabed. Among these, Yamamoto et al. [12] considered an isotropic seabed, while Hsu et al. [16] considered a hydraulically anisotropic seabed. In this study, the analytical solution proposed by Hsu et al. [16] is used.

In this study, a progressive wave is considered. The wave system has a free surface that periodically fluctuates in the direction of propagation (in the x direction). The z-axis is an upward from the surface of the seabed (see Figure 3). Several assumptions about soil properties are adopted in the analytical solutions [16]: (1) The porous seabed is homogeneous, unsaturated, hydraulically anisotropic and of infinite thickness. (2) The soil skeleton and the pore fluid are compressible. (3) The soil skeleton obeys Hooke’s law, implying linear, reversible, and non-retarded mechanical properties. (4) The flow in the porous seabed is governed by Darcy’s law [17].

As shown in Figure 3, on the seabed surface (z = 0), based on the linear wave theory, the dynamic wave pressure can be expressed as follows [18].

$$P_w={\displaystyle \frac{{\gamma }_{w}H}{2\cosh \left(kd\right)}}\cos (kx-\omega t)=p_0\cos (kx-\omega t),$$

(1)

in which $p_0$ is the amplitude of dynamic wave pressure at the surface of a seabed; ${\gamma }_w$ is the unit weight of water; d is water depth; t is time; $k$ (=2π/L, L is the wavelength) is the wave number; $\omega$ (=2$\pi$/T, in which T is the wave period) is the wave angular frequency. The wave angular frequency ($\omega$) and the wave number (k) satisfy the wave dispersion relation [18]

$${\omega }^2=gk\tanh \left(kd\right).$$

(2)

The analytical solution of the wave-induced soil response in an infinite porous seabed is summarised as follows [16].

$$P={\displaystyle \frac{p_0}{1-2\mu }}\mathrm{Re}\left\{\left[(1-2\mu -\lambda )C_1{e}^{kz}+{\displaystyle \frac{{\delta }^2-k^2}{k}}(1-\mu )C_2{e}^{\delta z}\right]e^{i(kx-\omega t)}\right\},$$

(3)

$${\sigma }_x^{\prime }=-p_0\mathrm{Re}\left\{\left[k(C_0+C_{1}z)e^{kz}+{\displaystyle \frac{2\mu \lambda }{1-2\mu }}{C}_1{e}^{kz}+\left(k-{\displaystyle \frac{\mu ({\delta }^2-k^2)}{k(1-2\mu )}}\right)C_2{e}^{\delta z}\right]e^{i(kx-\omega t)}\right\},$$

(4)

$$\begin{array}{cc}\hfill {\sigma }_z^{\prime }=p_0\mathrm{Re}\left\{\right[k(C_0+C_{1}z)e^{kz}& -{\displaystyle \frac{2\lambda (1-\mu )}{1-2\mu }}{C}_1{e}^{kz}\hfill \\ \hfill & +\left({\displaystyle \frac{\mu ({\delta }^2(1-\mu )-k^2\mu )}{k(1-2\mu )}}\right)C_2{e}^{\delta z}\left]e^{i(kx-\omega t)}\right\},\hfill \end{array}$$

(5)

$${\tau }_{xz}=p_0\mathrm{Re}\left\{i\left[\left(k(C_0+C_{1}z)-\lambda C_1\right)e^{kz}+\delta C_2{e}^{\delta z}\right]e^{i(kx-\omega t)}\right\},$$

(6)

$$u={\displaystyle \frac{p_0}{2G}}\mathrm{Re}\left\{i\left[(C_0+C_{1}z)e^{kz}+C_2{e}^{\delta z}\right]e^{i(kx-\omega t)}\right\},$$

(7)

$$w={\displaystyle \frac{p_0}{2G}}\mathrm{Re}\left\{\left[\left(C_0-{\displaystyle \frac{1+2\lambda }{k}}{C}_1+C_{1}z\right)e^{kz}+{\displaystyle \frac{\delta }{k}}{C}_2{e}^{\delta z}\right]e^{i(kx-\omega t)}\right\},$$

(8)

where P is wave-induced pore pressure; ${\sigma }_x^{\prime }$ and ${\sigma }_z^{\prime }$ are effective stresses in the x- and z-direction, respectively; ${\tau }_{xz}$ is shear stress; u and w are soil displacements in the x- and z-direction, respectively; $\mu$ is the Poisson’s ratio; G is the shear modulus of the soil; “Re” is the real part of a complex number; $i=\sqrt{-1}$ denotes the imaginary part of a complex number; and the complex coefficients, $C_j(j=0,1,2)$, are given here.

$$C_0={\displaystyle \frac{-\lambda \left[\mu {(\delta -k)}^2-\delta (\delta -2k)\right]}{k(\delta -k)(\delta -\delta \mu +k\mu +k\lambda )}},$$

(9)

$$C_1={\displaystyle \frac{\delta -\delta \mu +k\mu }{\delta +\delta \mu +k\mu +k\lambda }},$$

(10)

$$C_2={\displaystyle \frac{k\lambda }{(\delta -k)(\delta +\delta \mu +k\mu +k\lambda )}},$$

(11)

in which the variables $\lambda$ and $\delta$ can be expressed as

$$\lambda ={\displaystyle \frac{(1-2\mu )\left[{\displaystyle k^2\left({\displaystyle 1-\frac{K_x}{K_z}}\right)+\frac{i\omega {\gamma }_{w}n\beta }{K_z}}\right]}{{\displaystyle k^2\left({\displaystyle 1-\frac{K_x}{K_z}}\right)+\frac{i\omega {\gamma }_w}{K_z}\left({\displaystyle n\beta +\frac{1-2\mu }{G}}\right)}}},$$

(12)

$${\delta }^2=k^2{\displaystyle \frac{K_x}{K_z}}-{\displaystyle \frac{i\omega {\gamma }_w}{K_z}}\left[n\beta +{\displaystyle \frac{1-2\mu }{2G(1-\mu )}}\right],$$

(13)

where $K_x$ and $K_z$ are the coefficients of soil permeability in the x- and z-directions, respectively; n is the soil porosity; G is the shear modulus of soil; $\beta$ is the compressibility of the pore fluid, which is defined as

$$\beta ={\displaystyle \frac{1}{K_w}}+{\displaystyle \frac{1-S_r}{P_{w0}}}.$$

(14)

in which $K_w$ (≈$2\times {10}^9$ N/m²) represents the true bulk modulus of water, $S_r$ denotes the degree of saturation of the soil, $P_{w0}$ represents the absolute pore pressure. It is noted that a different definition of the compressibility of the pore pore fluid can be found by considering the bulk modulus of air in Cui and Jeng [19].

In this study, the effective stress analysis is used. In (4) and (5), ${\sigma }_x^{\prime }$ and ${\sigma }_z^{\prime }$ are effective normal stresses. The relationship between total stress and effective stress is defined as follows.

$${\sigma }_x={\sigma }_x^{\prime }+P,{\sigma }_z={\sigma }_z^{\prime }+P,$$

(15)

where ${\sigma }_x$ and ${\sigma }_z$ are the total stress in the x- and z-direction, respectively.

3. Phase-Lag for Soil Response Variables

In this section, the above analytical solution is re-examined to further derive the phase-lag for all wave-induced soil response variables. To achieve it, the real and imaginary parts of all complex variables, such as $C_0$, $C_1$, $C_2$ and soil response variables, are introduced into the solution and then the real part is chosen.

The parameters $\lambda$ and $\delta$ in (12) and (13) can be expressed as

$$\lambda ={\eta }_1+i·{\eta }_2,$$

(16)

$$\delta ={\xi }_1+i·{\xi }_2,$$

(17)

in which ${\eta }_1$, ${\eta }_2$, ${\xi }_1$ and ${\xi }_2$ are real numbers. Substituting (16) and (17) into (12) and (13), we have

$${\eta }_1={\displaystyle \frac{(1-2\mu )\left[k^4{\left({\displaystyle 1-\frac{K_x}{K_z}}\right)}^2+n\beta {\left({\displaystyle \frac{\omega {\gamma }_w}{K_z}}\right)}^2\left({\displaystyle n\beta +\frac{1-2\mu }{G}}\right)\right]}{{\displaystyle k^4{\left({\displaystyle 1-\frac{K_x}{K_z}}\right)}^2+{\left(\frac{\omega {\gamma }_w}{K_z}\right)}^2{\left({\displaystyle n\beta +\frac{1-2\mu }{G}}\right)}^2}}},$$

(18)

$${\eta }_2={\displaystyle \frac{{\displaystyle -k^2\left({\displaystyle 1-\frac{K_x}{K_z}}\right)\frac{\omega {\gamma }_w}{K_z}\frac{{(1-2\mu )}^2}{G}}}{{\displaystyle k^4{\left({\displaystyle 1-\frac{K_x}{K_z}}\right)}^2+{\left(\frac{\omega {\gamma }_w}{K_z}\right)}^2{\left({\displaystyle n\beta +\frac{1-2\mu }{G}}\right)}^2}}},$$

(19)

$${\xi }_1={\displaystyle \frac{\sqrt{2}}{2}}\sqrt{k^2{\displaystyle \frac{K_x}{K_z}}+\sqrt{{\left(k^2{\displaystyle \frac{K_x}{K_z}}\right)}^2+{\left({\displaystyle \frac{\omega {\gamma }_w}{K_z}}\right)}^2{\left[n\beta +{\displaystyle \frac{1-2\mu }{2G(1-\mu )}}\right]}^2}},$$

(20)

$${\xi }_2=-{\displaystyle \frac{\sqrt{2}}{2}}\sqrt{-k^2{\displaystyle \frac{K_x}{K_z}}+\sqrt{{\left(k^2{\displaystyle \frac{K_x}{K_z}}\right)}^2+{\left({\displaystyle \frac{\omega {\gamma }_w}{K_z}}\right)}^2{\left[n\beta +{\displaystyle \frac{1-2\mu }{2G(1-\mu )}}\right]}^2}}.$$

(21)

Similarly, substituting (16) and (17) into (9)–(11), the real and imaginary parts of the $C_i$ (i = 0, 1, 2) coefficients can be obtained, respectively, that is,

$$\mathrm{Re}\left(C_0\right)=-{\displaystyle \frac{(a_1{a}_3+a_2{a}_4)({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)+(a_1{a}_4-a_2{a}_3)({\eta }_1{\xi }_2-{\eta }_2{\xi }_1+k{\eta }_2)}{k\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(22)

$$\mathrm{Im}\left(C_0\right)={\displaystyle \frac{(a_1{a}_3+a_2{a}_4)({\eta }_1{\xi }_2-{\eta }_2{\xi }_1+k{\eta }_2)-(a_1{a}_4-a_2{a}_3)({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)}{k\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(23)

$$\mathrm{Re}\left(C_1\right)={\displaystyle \frac{a_1^2+a_2^2-k({\eta }_1{a}_1+{\eta }_2{a}_2)}{a_1^2+a_2^2}},$$

(24)

$$\mathrm{Im}\left(C_1\right)={\displaystyle \frac{k({\eta }_1{a}_2-{\eta }_2{a}_1)}{a_1^2+a_2^2}},$$

(25)

$$\mathrm{Re}\left(C_2\right)={\displaystyle \frac{k[{\eta }_1(({\xi }_1-k)a_1-{\xi }_2{a}_2)+{\eta }_2({\xi }_2{a}_1+({\xi }_1-k)a_2)]}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(26)

$$\mathrm{Im}\left(C_2\right)={\displaystyle \frac{k[{\eta }_2(({\xi }_1-k)a_1-{\xi }_2{a}_2)-{\eta }_1({\xi }_2{a}_1+({\xi }_1-k)a_2)]}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(27)

where the parameters $a_i$ (i = 1–4) can be expressed as

$$a_1=(1-\mu ){\xi }_1+k{\eta }_1+k\mu ,a_2=(1-\mu ){\xi }_2+k{\eta }_2,$$

(28)

$$a_3=(1-\mu )({\xi }_2^2-{\xi }_1^2+2k{\xi }_1)+k^2\mu ,a_4=2{\xi }_2(1-\mu )(k-{\xi }_1).$$

(29)

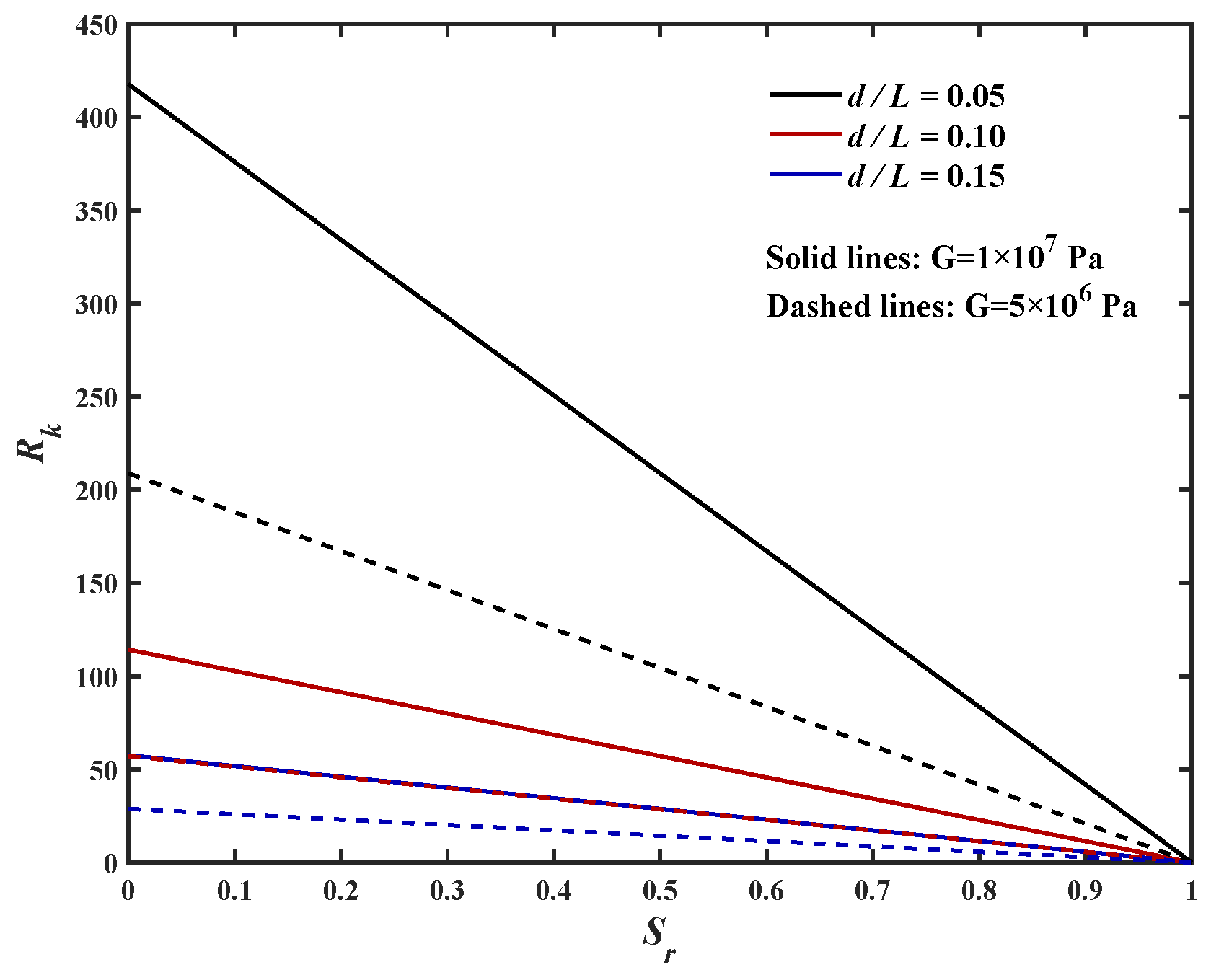
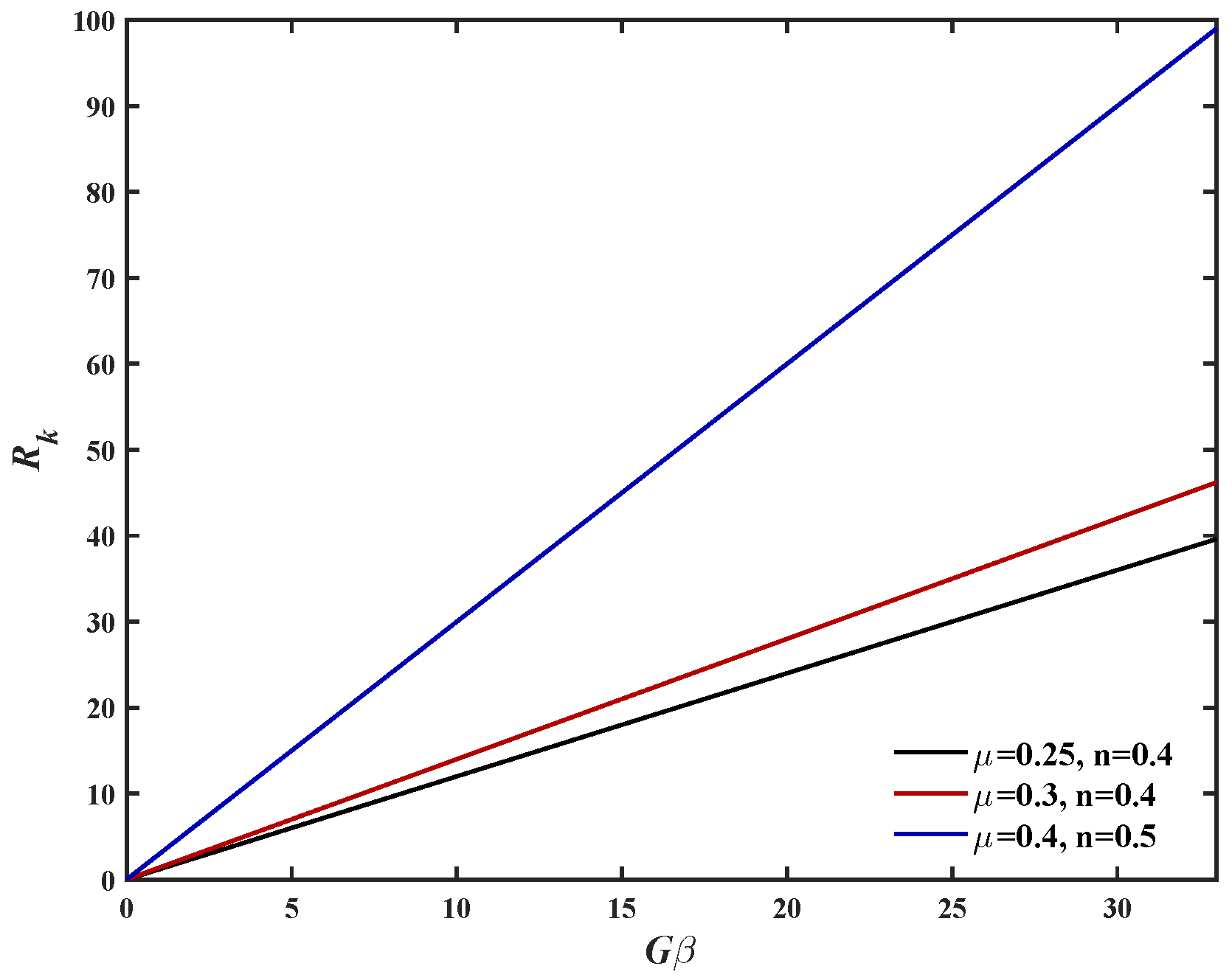
3.1. Relative Rigidity Parameter ($R_k$)

Base on $\lambda$ and $\delta$, to quantitatively characterise the relative rigidity of soil skeleton to pore fluid, the parameter $R_k$ is introduced [13], that is,

$$R_k={\displaystyle \frac{2n(1-\mu )G\beta }{1-2\mu }}.$$

(30)

Herein, $R_k$ is related to the thickness of the boundary layer ($1/R_k$) in the problem of fluid-seabed interactions [20]. Outside the boundary layer, the effects of the porous medium can be ignored and are more dominated by the wave damping. To examine the relationship between $R_k$ and $S_r$ and $G\beta$, the input data for the numerical examples are tabulated in

Table 1. Wave parameters and soil properties in this study.

Wave Parameters	Value
Wave period (T) [s]	9.0
Water depth (d) [m]	15.0
Wave height (H) [m]	3.0
Wave length (L) [m]	95.5
Soil properties	Coarse sand	Fine sand	Silt
Permeability ($K_x$, $K_z$) [m/s]	${10}^{-2}$	${10}^{-4}$	${10}^{-5}$
Shear modulus (G) [Pa]	${10}^7$	${10}^7$	$5\times {10}^6$
Poisson’s ratio ($\mu$) [-]	0.3
Porosity (n) [-]	0.4

.

It is noted that $R_k$ = 1.0 indicates that the rigidity of the soil skeleton is equal to that of the pore fluid. When $R_k\ll 1.0$, it is a fully saturated soil with $S_r$ = 1.0, and when $R_k\gg 1.0$, it is a dry soil with $S_r$ = 0 (see Figure 4). According to (14), the depth of the water will affect the value of $P_{w0}={\gamma }_{w}d$ and then indirectly affect $\beta$. As shown in Figure 4, $R_k$ increases with increasing relative depth of water ($d/L$). Similarly, as seen in Figure 5, $R_k$ increases with increasing $G\beta$, and increases with increasing combinations of n and $\mu$. In marine environments, the seabed will never have the case with $S_r$ = 0. Two limiting cases of $R_k$ (that is, $R_k\ll 1.0$, $R_k\gg 1.0$) are only used to obtain simplified expressions of the wave-induced soil response. In the following analysis, $R_k$ = 1, 5, 10 (in coarse and fine sand, $S_r$ = 0.990, 0.948, 0.895; in silt, $S_r$ = 0.979, 0.896, 0.790) are taken.

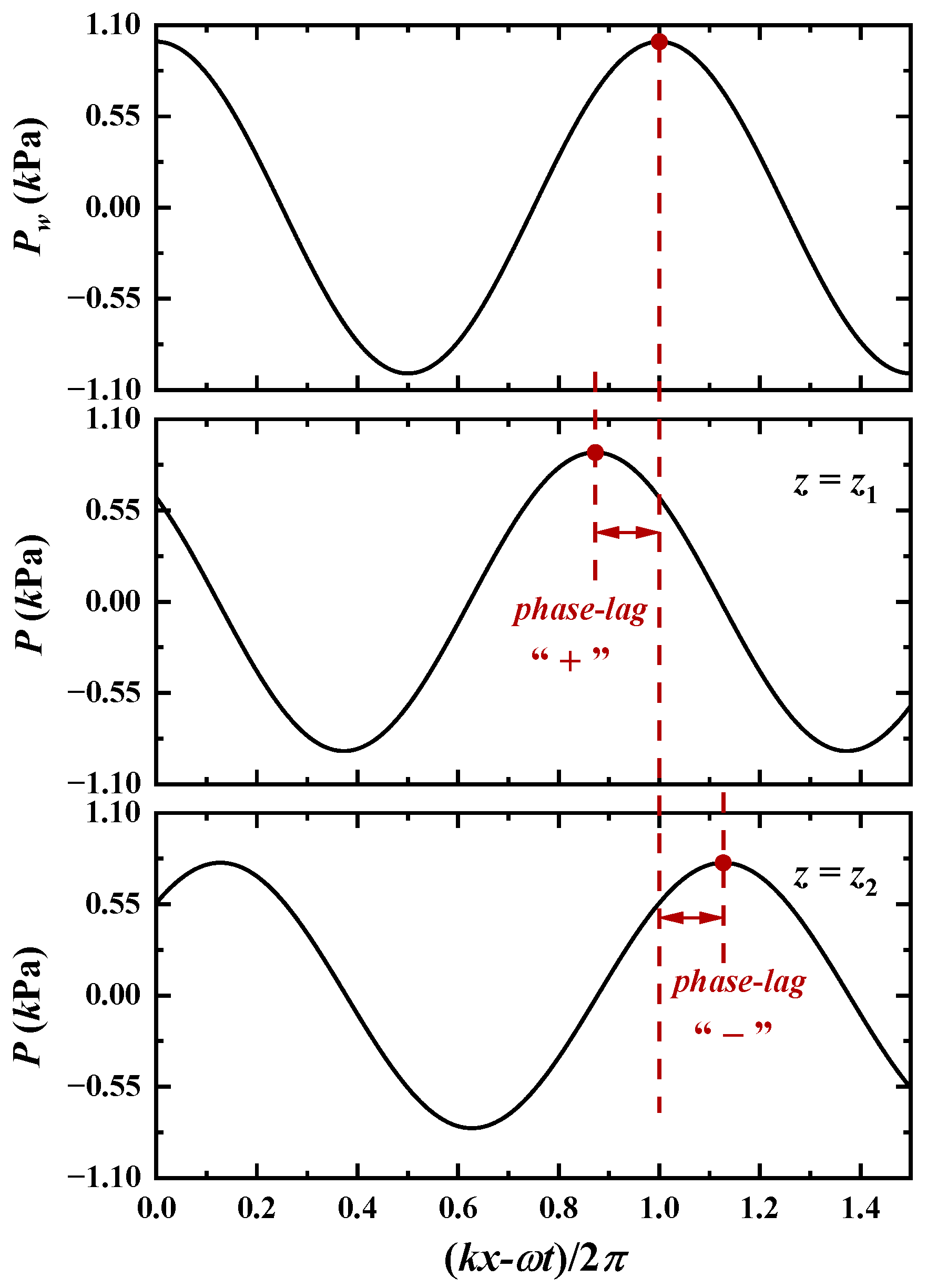
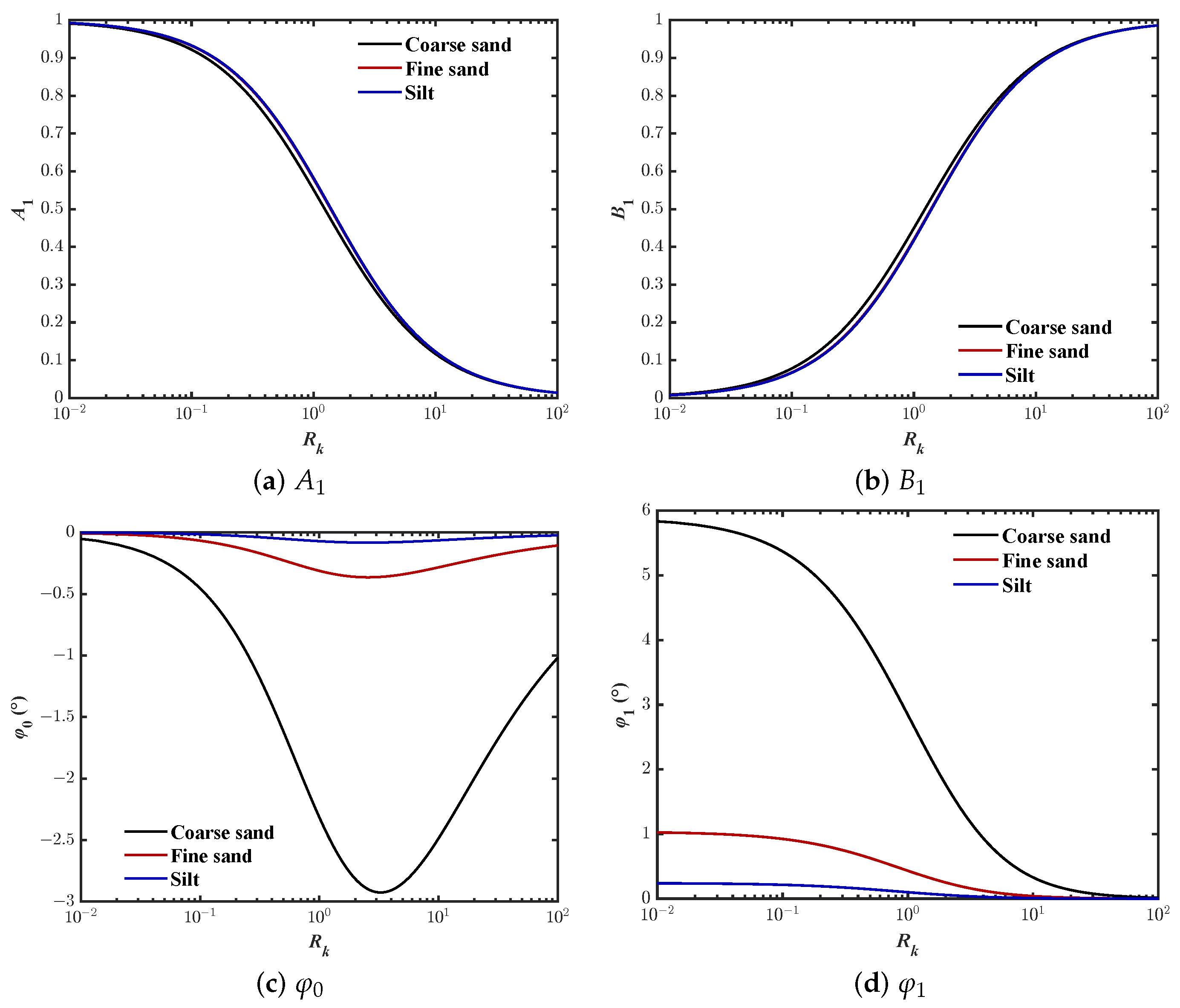
3.2. Phase-Lag for Pore Pressure (P)

Substituting (16)–(19), (24)–(27) into (3), the wave-induced pore pressure (P) can be rewritten as

$$\begin{array}{cc}\hfill P=& p_0\left[A_1\cos (kx-\omega t+{\phi }_0)e^{kz}+B_1\cos (kx-\omega t+{\phi }_1+{\xi }_{2}z)e^{{\xi }_{1}z}\right]\hfill \\ \hfill =& p_0\left(\sqrt{A_1^2{e}^{2kz}+B_1^2{e}^{2{\xi }_{1}z}+2A_1{B}_1{e}^{(k+{\xi }_1)z}\cos ({\phi }_1+{\xi }_{2}z-{\phi }_0)}\right)\cos (kx-\omega t+\Delta {\theta }_1),\hfill \end{array}$$

(31)

where the phase-lag can be expressed as

$$\Delta {\theta }_1=\arctan \left({\displaystyle \frac{A_1{e}^{kz}\sin {\phi }_0+B_1{e}^{{\xi }_{1}z}\sin ({\phi }_1+{\xi }_{2}z)}{A_1{e}^{kz}\cos {\phi }_0+B_1{e}^{{\xi }_{1}z}\cos ({\phi }_1+{\xi }_{2}z)}}\right).$$

(32)

It is noted that the positive or negative values of the numerator and denominator in a phase expression can be used to determine the quadrant where the phases are located, thereby obtaining the correct value of phases.

In (31), the coefficients $A_1$, $B_1$, ${\phi }_0$ and ${\phi }_1$ can be determined from

$$A_1=\sqrt{D_0^2+D_1^2},B_1=\sqrt{D_2^2+D_3^2},$$

(33)

$${\phi }_0=\arctan \left({\displaystyle \frac{D_1}{D_0}}\right),{\phi }_1=\arctan \left({\displaystyle \frac{D_3}{D_2}}\right),$$

(34)

where the parameters $D_i$ (i = 0–3) are

$$D_0={\displaystyle \frac{(1-2\mu -{\eta }_1)\left[a_1^2+a_2^2-k({\eta }_1{a}_1+{\eta }_2{a}_2)\right]+k{\eta }_2({\eta }_1{a}_2-{\eta }_2{a}_1)}{(1-2\mu )\left(a_1^2+a_2^2\right)}},$$

(35)

$$D_1={\displaystyle \frac{k(1-2\mu -{\eta }_1)({\eta }_1{a}_2-{\eta }_2{a}_1)-{\eta }_2\left[a_1^2+a_2^2-k({\eta }_1{a}_1+{\eta }_2{a}_2)\right]}{(1-2\mu )\left(a_1^2+a_2^2\right)}},$$

(36)

$$D_2={\displaystyle \frac{(1-\mu )[a_1({\eta }_1{\xi }_1-{\eta }_2{\xi }_2+k{\eta }_1)+a_2({\eta }_1{\xi }_2+{\eta }_2{\xi }_1+k{\eta }_2)]}{(1-2\mu )\left(a_1^2+a_2^2\right)}},$$

(37)

$$D_3={\displaystyle \frac{(1-\mu )[a_1({\eta }_1{\xi }_2+{\eta }_2{\xi }_1+k{\eta }_2)-a_2({\eta }_1{\xi }_1-{\eta }_2{\xi }_2+k{\eta }_1)]}{(1-2\mu )\left(a_1^2+a_2^2\right)}}.$$

(38)

As shown in (31), ${\phi }_0$ and (${\phi }_1+{\xi }_2$) represent the phase delay in both items. It is necessary to examine the effect of $R_k$ on the coefficients $A_1$, $B_1$, ${\phi }_0$ and ${\phi }_1$ before establishing the simplified approximation. Figure 6 illustrates the variations in the amplitude coefficients ($A_1$, $B_1$) and the phase (${\phi }_0$, ${\phi }_1$) versus $R_k$ with the input data listed in Table 1. As shown in Figure 6a, $A_1$ approaches one when $R_k$ approaches zero, while it approaches zero when $R_k$ approaches infinity. On the other hand, $B_1$ approaches one when $R_k$ approaches zero, while it approaches zero when $R_k$ approaches infinity (see Figure 6b). Regarding the phase (${\phi }_0$), it approaches zero when $R_k$ approaches zero, as shown in Figure 6c. It is noted that although ${\phi }_0$ in coarse sand is not zero when $R_k=0.01$ in the figure, the trend of ${\phi }_0$ approaches zero with $R_k$ approaching zero. On the other hand, the phase (${\phi }_1$) approaches zero when $R_k$ approaches infinity.

Based on the above discussion, the wave-induced pore pressure for the two limiting cases of $R_k$ can be summarised as follows.

(1)

Case-I: $R_k\ll 1.0$

For $R_k\ll 1.0$, the coefficients $A_1$ approaches 1.0, $B_1$ approaches zero, and the phase ${\phi }_0$ approach zero, as shown in Figure 6. Therefore, (31) can be simplified to

$$P=p_0\cos (kx-\omega t)e^{kz}.$$

(39)

As indicated by (39), when the seabed is fully saturated, there is no phase delay. This confirms the conclusion obtained from previous studies [12,16].

(2)

Case-II: $R_k\gg 1.0$

As shown in Figure 6, for $R_k\gg 1.0$, the coefficients $A_1$ approaches zero, $B_1$ approaches 1.0, and ${\phi }_1$ approaches zero when $R_k\gg 1.0$. That is,

$$P=p_0\cos (kx-\omega t+{\xi }_{2}z)e^{{\xi }_{1}z}=p_0\cos \left(kx-\omega t+\Delta {\theta }_{01}\right)e^{{\xi }_{1}z},$$

(40)

where the phase-lag for the wave-induced pore pressure can be expressed as

$$\Delta {\theta }_{01}(={\xi }_{2}z)=-{\displaystyle \frac{z}{\sqrt{2}}}\sqrt{-k^2{\displaystyle \frac{K_x}{K_z}}+\sqrt{{\left(k^2{\displaystyle \frac{K_x}{K_z}}\right)}^2+{\left({\displaystyle \frac{\omega {\gamma }_w}{K_z}}\right)}^2{\left[n\beta +{\displaystyle \frac{1-2\mu }{2G(1-\mu )}}\right]}^2}}.$$

(41)

which is a function of soil depth (z).

From (32), the same conclusion as previously stated can be drawn: when $R_k\ll 1.0$, no phase-lag occurs (see Figure 7), and when $R_k\gg 1.0$, according to Figure 6, the coefficient $A_1$ approaches zero, $B_1$ approaches 1.0, and the phases ${\phi }_0$ cannot be ignored, ${\phi }_1$ approaches zero for $R_k\gg 1.0$. (32) can be simplified to (41).

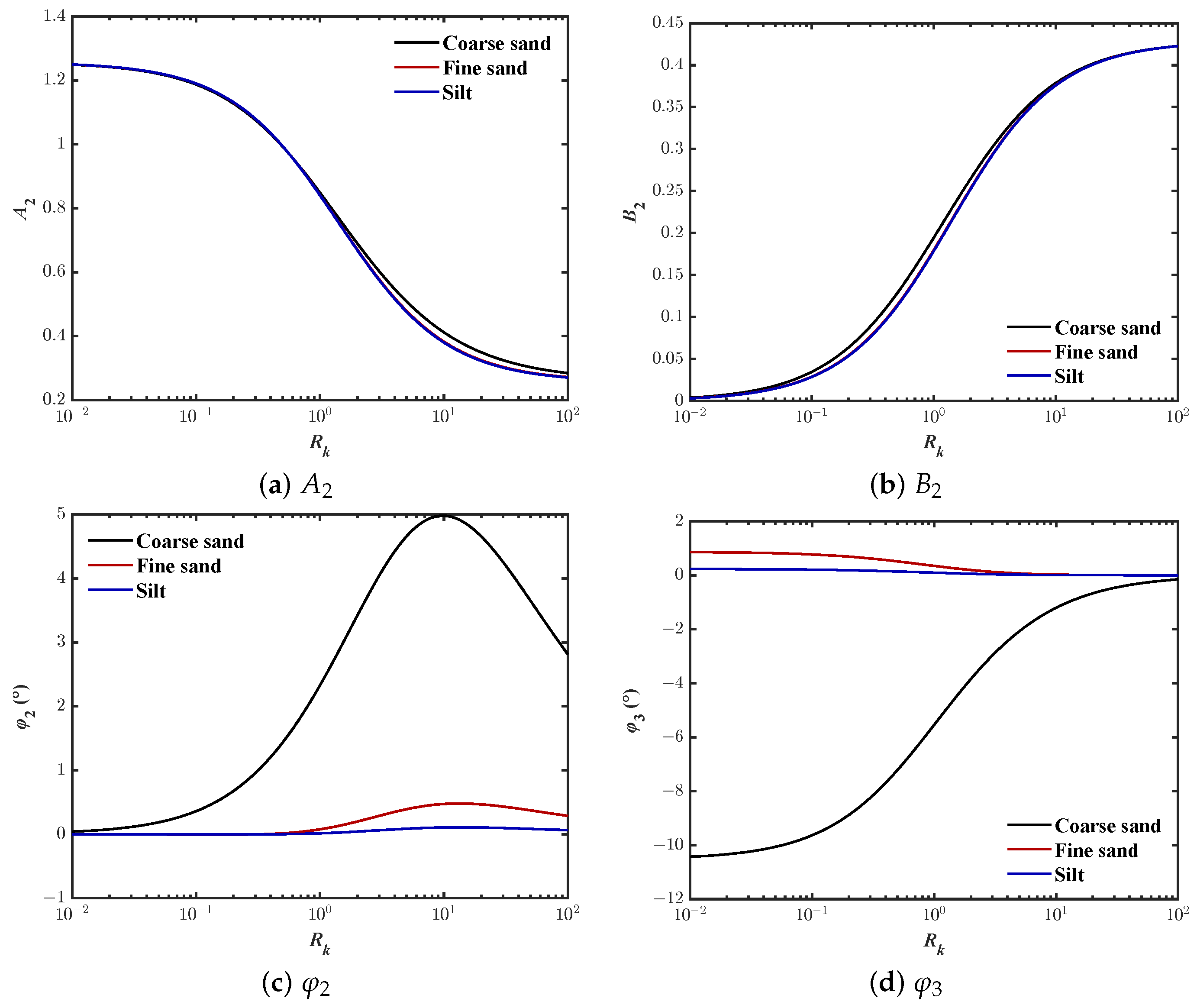
3.3. Phase-Lag for Effective Normal Stresses (${\sigma }_x^{\prime }$, ${\sigma }_z^{\prime }$)

Substituting (16)–(27) into (4), the horizontal effective stress (${\sigma }_x^{\prime }$) can be represented as

$$\begin{array}{cc}\hfill {\sigma }_x^{\prime }=& p_0\left[A_2\cos (kx-\omega t+{\phi }_2)e^{kz}+B_2\cos (kx-\omega t+{\xi }_{2}z)e^{{\xi }_{1}z}\right]\hfill \\ \hfill =& p_0\left(\sqrt{A_2^2{e}^{2kz}+B_2^2{e}^{2{\xi }_{1}z}+2A_2{B}_2{e}^{(k+{\xi }_1)z}\cos ({\phi }_3+{\xi }_{2}z-{\phi }_2)}\right)\cos (kx-\omega t+\Delta {\theta }_2),\hfill \end{array}$$

(42)

where the phase-lag ($\Delta {\theta }_2$) is,

$$\Delta {\theta }_2=\arctan \left({\displaystyle \frac{A_2{e}^{kz}\sin {\phi }_2+B_2{e}^{{\xi }_{1}z}\sin ({\phi }_3+{\xi }_{2}z)}{A_2{e}^{kz}\cos {\phi }_2+B_2{e}^{{\xi }_{1}z}\cos ({\phi }_3+{\xi }_{2}z)}}\right).$$

(43)

In (42), the coefficients $A_i$, $B_i$ (i = 2, 3) and phases ${\phi }_i$ (i = 2–5) are given here.

$$A_2=\sqrt{{(D_4-k{D}_{6}z+D_8)}^2+{(D_5-k{D}_{7}z+D_9)}^2},$$

(44)

$$B_2=\sqrt{{(D_{10}+D_{12})}^2+{(D_{11}+D_{13})}^2},$$

(45)

$${\phi }_2=\arctan \left({\displaystyle \frac{D_5-k{D}_{7}z+D_9}{D_4-k{D}_{6}z+D_8}}\right),$$

(46)

$${\phi }_3=\arctan \left({\displaystyle \frac{D_{11}+D_{13}}{D_{10}+D_{12}}}\right),$$

(47)

where the parameters $D_i$ (i = 4–13) are

$$D_4={\displaystyle \frac{(a_1{a}_3+a_2{a}_4)({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)+(a_1{a}_4-a_2{a}_3)({\eta }_1{\xi }_2-{\eta }_2{\xi }_1+k{\eta }_2)}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(48)

$$D_5={\displaystyle \frac{(a_1{a}_4-a_2{a}_3)({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)-(a_1{a}_3+a_2{a}_4)({\eta }_1{\xi }_2-{\eta }_2{\xi }_1+k{\eta }_2)}{k\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(49)

$$D_6=1-{\displaystyle \frac{k({\eta }_1{a}_1+{\eta }_2{a}_2)}{a_1^2+a_2^2}},D_7={\displaystyle \frac{k({\eta }_1{a}_2-{\eta }_2{a}_1)}{a_1^2+a_2^2}},$$

(50)

$$D_8={\displaystyle \frac{2\mu }{1-2\mu }}({\eta }_2{D}_7-{\eta }_1{D}_6),D_9=-{\displaystyle \frac{2\mu }{1-2\mu }}({\eta }_1{D}_7+{\eta }_2{D}_6),$$

(51)

$$D_{10}={\displaystyle \frac{\mu }{1-2\mu }}{D}_2,D_{11}={\displaystyle \frac{\mu }{1-2\mu }}{D}_3,$$

(52)

$$D_{12}={\displaystyle \frac{-k^2[a_1({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)+a_2({\eta }_2{\xi }_1-{\eta }_1{\xi }_2-k{\eta }_2)]}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(53)

$$D_{13}={\displaystyle \frac{-k^2[a_1({\eta }_2{\xi }_1-{\eta }_1{\xi }_2-k{\eta }_2)-a_2({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)]}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}}.$$

(54)

Figure 8 illustrates the variations in coefficients ($A_2$, $B_2$) and phases (${\phi }_2$, ${\phi }_3$) versus $R_k$. As shown in Figure 8a, $A_2$ approaches a constant when $R_k$ approaches zero, and the constant can vary with the wave and soil properties. When $R_k$ approaches infinity, $A_2$ also approaches a constant. Similar to $A_2$, it can be seen from Figure 8b that $B_2$ approaches a constant when $R_k$ approaches infinity, but when $R_k$ approaches zero, $B_2$ approaches zero. Regarding the phase (${\phi }_2$), it approaches zero when $R_k$ approaches zero, as shown in Figure 8c. On the contrary, the phase (${\phi }_3$) approaches zero when $R_k$ approaches infinity (see Figure 8d). It is noted that although ${\phi }_3$ in coarse sand is not zero when $R_k=100$ in the figure, the trend of ${\phi }_3$ approaches zero with $R_k$ approaching infinity.

The effective horizontal stresses for two limiting cases of $R_k$ are outlined here.

(1)

Case-I: $R_k\ll 1.0$

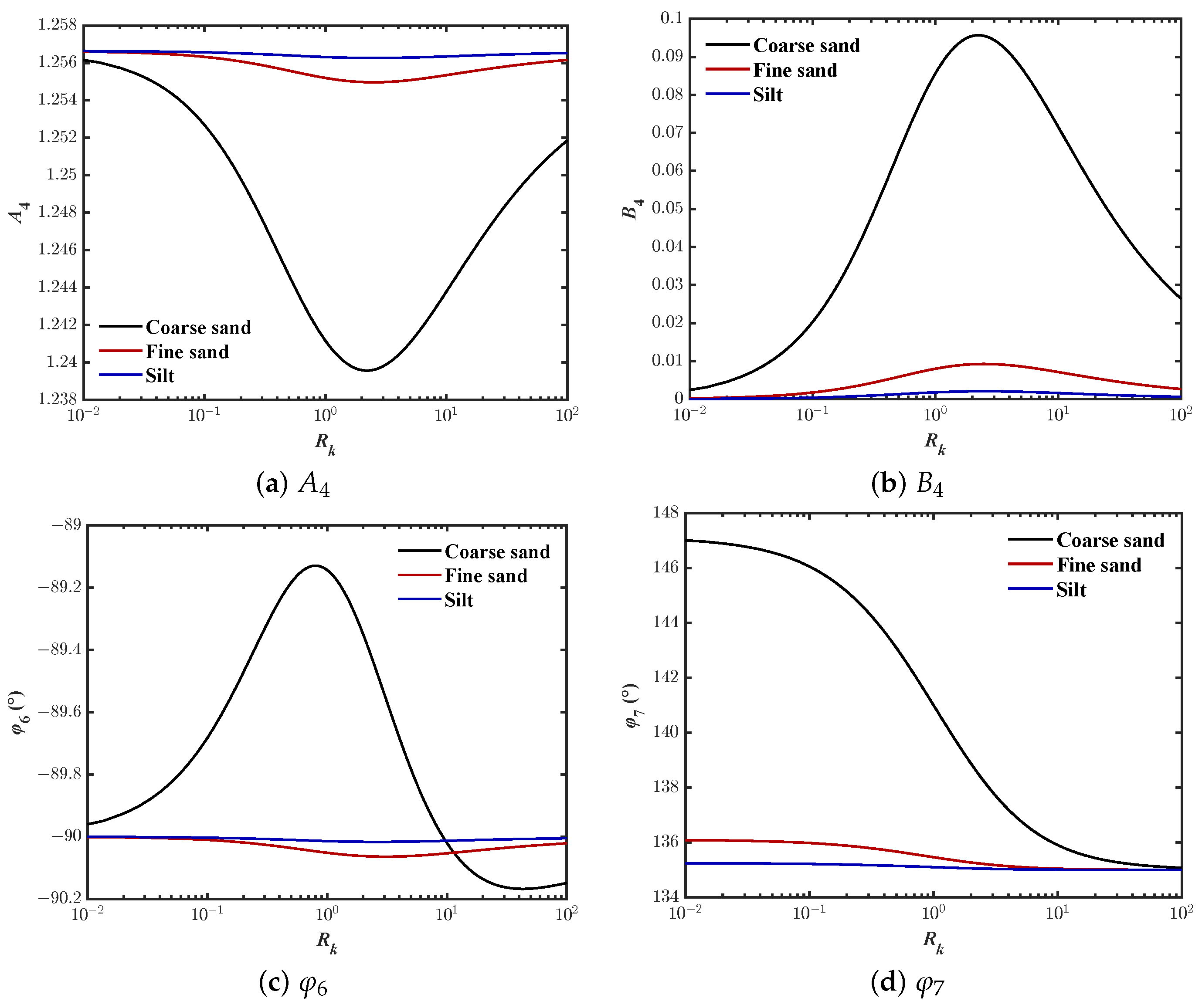
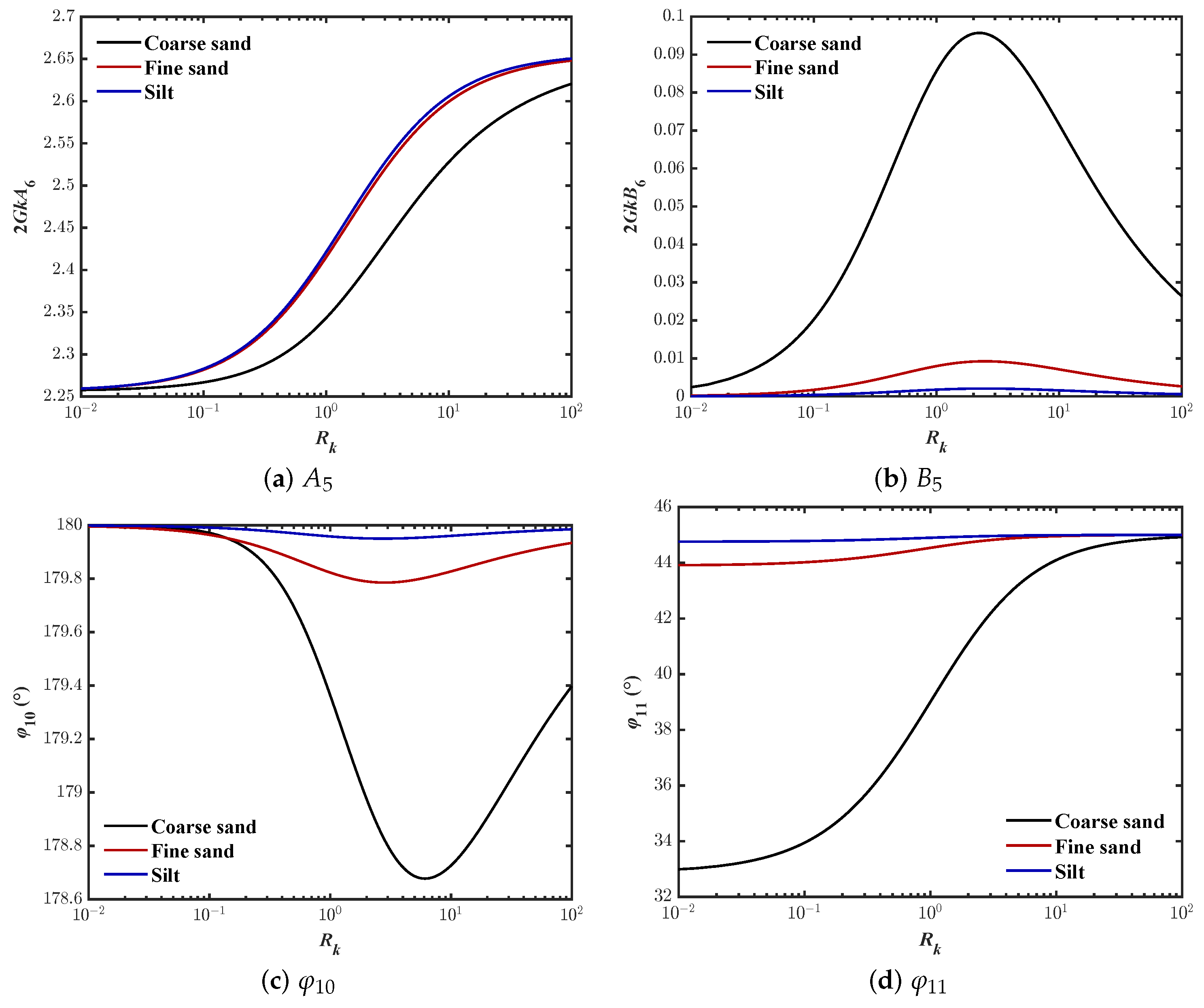
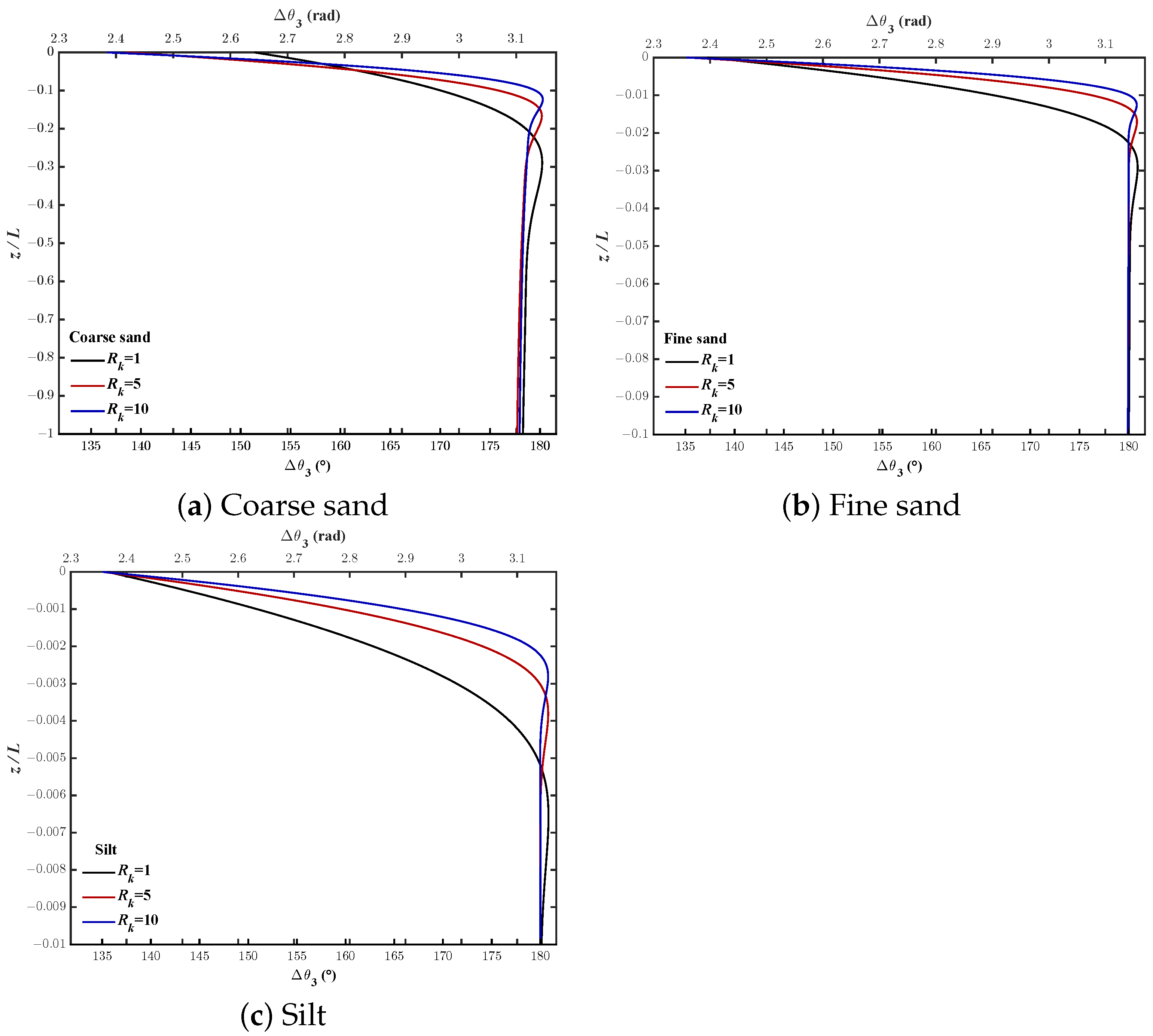
As shown in Figure 8, if $R_k\ll 1.0$, the coefficient $A_2$ approaches a constant, but the constant varies with the different parameters and $B_2$ approaches zero. Therefore,

$${\sigma }_x^{\prime }=p_0{A}_2\cos (kx-\omega t)e^{kz}.$$

(55)

According to (55), the effective horizontal stress does not have phase delay in a fully saturated seabed.

(2)

Case-II: $R_k\gg 1.0$

When $R_k\gg 1.0$, as shown in Figure 8, both $A_2$ and $B_2$ approach constants, they also vary with the parameters. Phase ${\phi }_2$ cannot be ignored, while phase ${\phi }_3$ approaches 0 degrees. Therefore, (42) can be simplified to

$$\begin{array}{cc}\hfill {\sigma }_x^{\prime }=& p_0\left[A_2\cos (kx-\omega t+{\phi }_2)e^{kz}+B_2\cos (kx-\omega t+{\xi }_{2}z)e^{{\xi }_{1}z}\right]\hfill \\ \hfill =& p_0\left(\sqrt{A_2^2{e}^{2kz}+B_2^2{e}^{2{\xi }_{1}z}+2A_2{B}_2{e}^{(k+{\xi }_1)z}\cos ({\xi }_{2}z-{\phi }_2)}\right)\cos (kx-\omega t+\Delta {\theta }_{02}),\hfill \end{array}$$

(56)

where the phase-lag for horizontal effective stress can be expressed as

$$\Delta {\theta }_{02}=\arctan \left({\displaystyle \frac{A_2{e}^{kz}\sin {\phi }_2+B_2{e}^{{\xi }_{1}z}\sin \left({\xi }_{2}z\right)}{A_2{e}^{kz}\cos {\phi }_2+B_2{e}^{{\xi }_{1}z}\cos \left({\xi }_{2}z\right)}}\right).$$

(57)

As shown in Figure 9, if $R_k\ll 1.0$, the phase-lag $\Delta {\theta }_2$ approaches zero. When $R_k\gg 1.0$, according to Figure 8, (43) can also be simplified to (57). This is consistent with the previous discussion.

Regarding vertical effective stress (${\sigma }_z^{\prime }$), substituting (16)–(27) into (5), yields the following.

$$\begin{array}{cc}\hfill {\sigma }_z^{\prime }=& p_0[A_3\cos (kx-\omega t+{\phi }_4)e^{kz}+B_3\cos (kx-\omega t+{\phi }_5+{\xi }_{2}z)e^{{\xi }_{1}z}]\hfill \\ \hfill =& p_0\left(\sqrt{A_3^2{e}^{2kz}+B_3^2{e}^{2{\xi }_{1}z}+2A_3{B}_3{e}^{(k+{\xi }_1)z}\cos ({\phi }_5+{\xi }_{2}z-{\phi }_4)}\right)\cos (kx-\omega t+\Delta {\theta }_3),\hfill \end{array}$$

(58)

where the phase-lag for vertical effective stress is given as,

$$\Delta {\theta }_3=\arctan \left({\displaystyle \frac{A_3{e}^{kz}\sin {\phi }_4+B_3{e}^{{\xi }_{1}z}\sin ({\phi }_5+{\xi }_{2}z)}{A_3{e}^{kz}\cos {\phi }_4+B_3{e}^{{\xi }_{1}z}\cos ({\phi }_5+{\xi }_{2}z)}}\right).$$

(59)

In (58), the coefficients $A_i$, $B_i$ (i = 2, 3) and phases ${\phi }_i$ (i = 2–5) can be determined from

$$A_3=\sqrt{{(D_{14}-k{D}_{16}z-D_{18})}^2+{(D_{15}-k{D}_{17}z-D_{19})}^2},$$

(60)

$$B_3=\sqrt{D_{20}^2+D_{21}^2},$$

(61)

$${\phi }_4=\arctan \left({\displaystyle \frac{D_{15}-k{D}_{17}z+D_{19}}{D_{14}-k{D}_{16}z+D_{18}}}\right),$$

(62)

$${\phi }_5=\arctan \left({\displaystyle \frac{D_{21}}{D_{20}}}\right),$$

(63)

where the parameters $D_i$ (i = 4–21) are

$$D_{14}=-D_4,D_{15}=-D_5,D_{16}=D_6,D_{17}=D_7$$

(64)

$$D_{18}={\displaystyle \frac{2(1-\mu )}{1-2\mu }}({\eta }_1{D}_6-{\eta }_2{D}_7),D_{19}={\displaystyle \frac{2(1-\mu )}{1-2\mu }}({\eta }_2{D}_6+{\eta }_1{D}_7),$$

(65)

$$D_{20}={\displaystyle \frac{(a_1{a}_5+a_2{a}_6)({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)+(a_1{a}_6+a_2{a}_5)({\eta }_1{\xi }_2-{\eta }_2{\xi }_1+k{\eta }_2)}{(1-2\mu )\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(66)

$$D_{21}={\displaystyle \frac{(a_1{a}_6-a_2{a}_5)({\eta }_1{\xi }_1+{\eta }_2{\xi }_2-k{\eta }_1)-(a_1{a}_5+a_2{a}_6)({\eta }_1{\xi }_2-{\eta }_2{\xi }_1+k{\eta }_2)}{(1-2\mu )\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(67)

in which the parameters $a_5$ and $a_6$ are given as follows.

$$a_5=(1-\mu )\left({\xi }_1^2-{\xi }_2^2\right)-k^2\mu ,a_6=2{\xi }_1{\xi }_2(1-\mu ).$$

(68)

Figure 10 illustrates the variations in coefficients ($A_3$, $B_3$) and phases (${\phi }_4$, ${\phi }_5$) versus $R_k$. As shown in Figure 10a, $A_3$ approaches a constant when $R_k$ approaches zero, and it varies with wave and soil properties. When $R_k$ approaches infinity, $A_3$ approaches different constants for various soil types. It is seen from Figure 10b that $B_3$ approaches zero when $R_k$ approaches zero, while it approaches one when $R_k$ approaches infinity. It is noted that although it is not one when $R_k$ = 100 in the figure, the trend of $B_3$ approaches one with $R_k$ approaching infinity. Regarding the phase (${\phi }_4$), it approaches 180 degrees (see Figure 10c). It is noted that although it in coarse sand is not 180 degrees when $R_k$ = 0.01 in the figure, the trend of ${\phi }_4$ approaches 180 degrees with $R_k$ approaches zero. On the other hand, the phase (${\phi }_5$) approaches zero when $R_k$ approaches infinity, as shown in Figure 10d.

The effective vertical stress (58) is examined for the limiting cases of $R_k$:

(1)

Case-I: $R_k\ll 1.0$

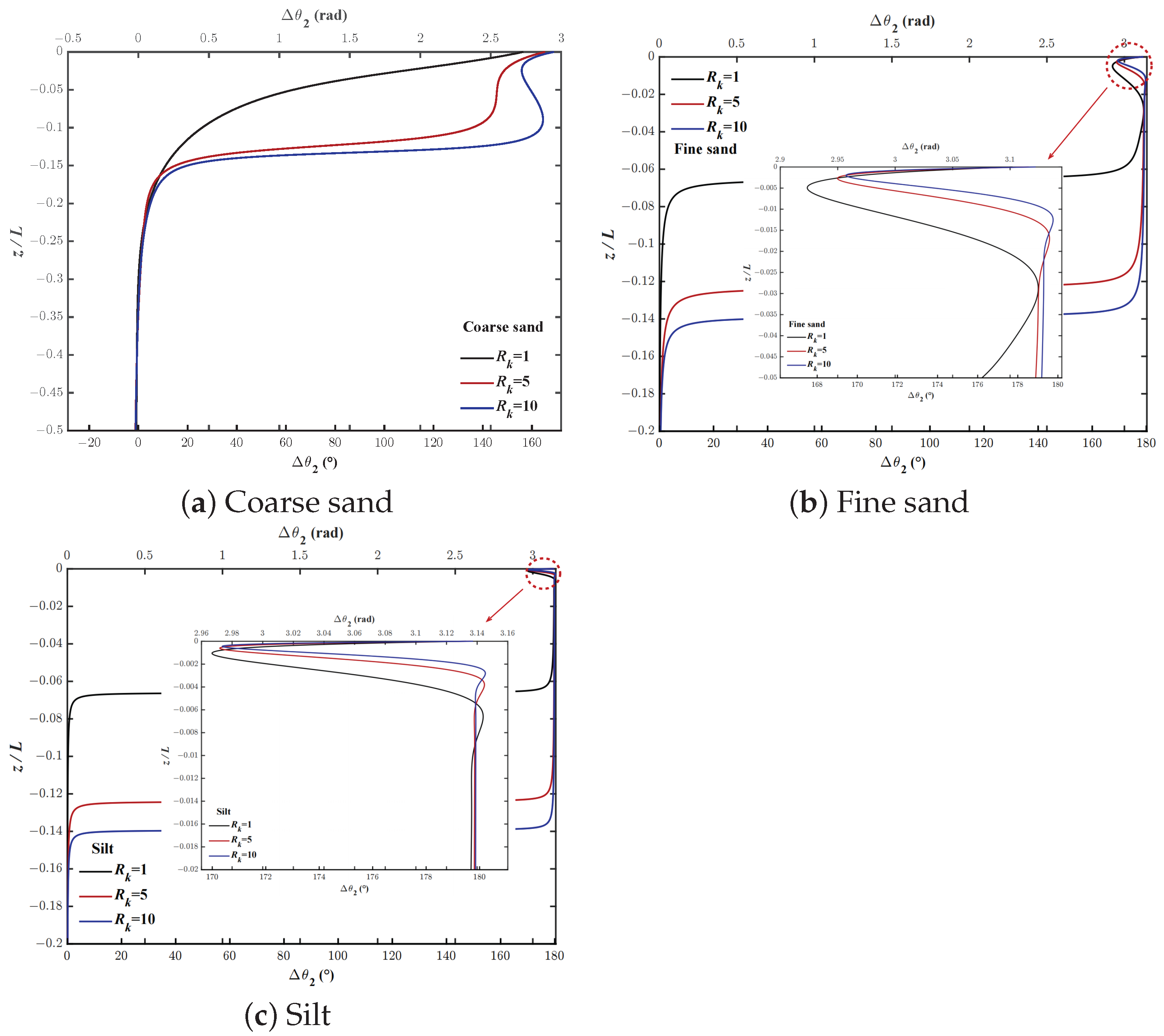
As shown in Figure 10, if $R_k\ll 1.0$, $A_3$ approaches a constant, while $B_3$ approaches zero and ${\phi }_4$ approaches 180 degrees. Therefore, (58) can be simplified to

$${\sigma }_z^{\prime }=p_0{A}_3\cos (kx-\omega t+\pi )e^{kz}.$$

(69)

According to (69), when the seabed is fully saturated, the phase-lag for the effective vertical stress is 180 degrees.

(2)

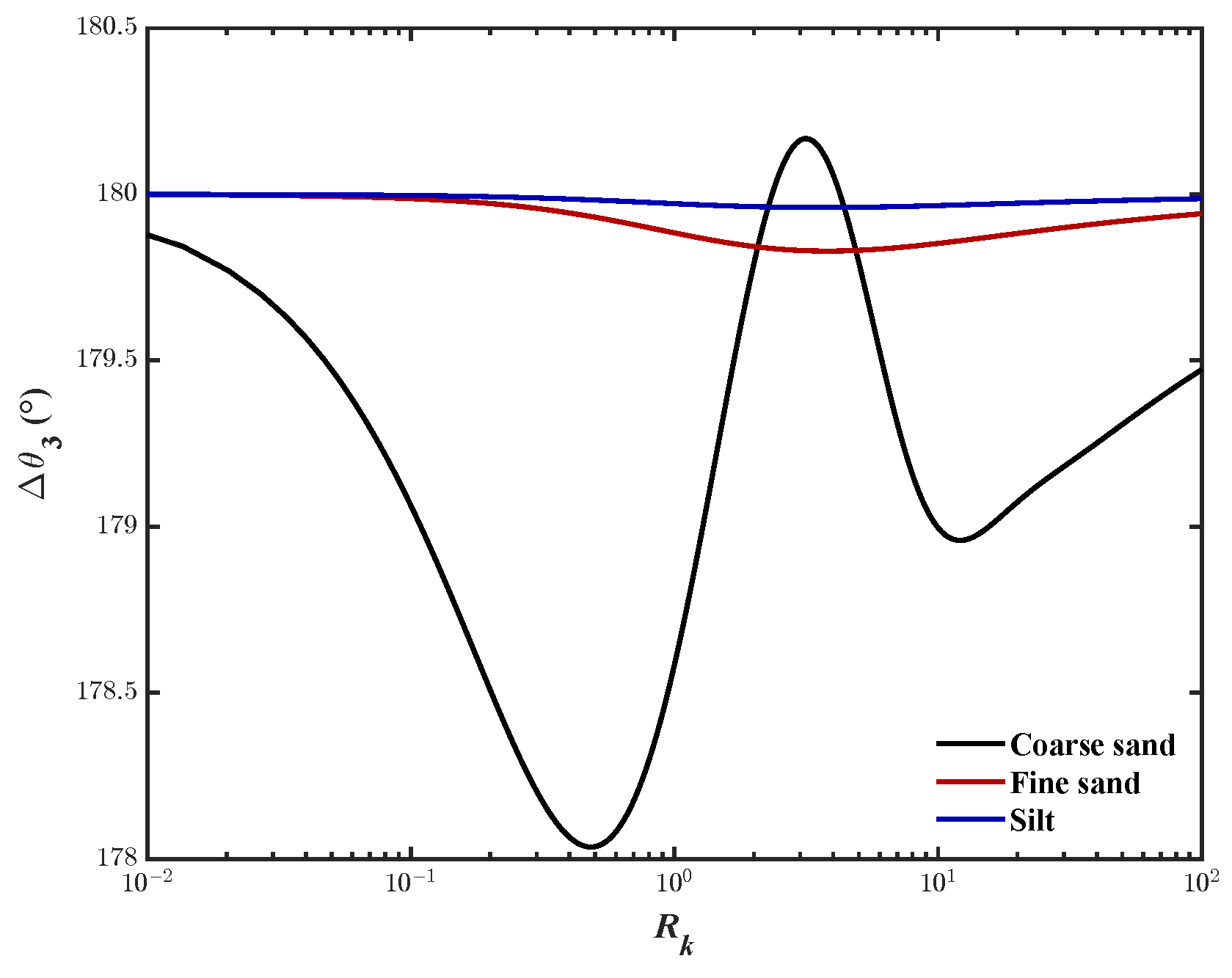
Case-II: $R_k\gg 1.0$

As shown in Figure 10, when $R_k\gg 1.0$, $A_3$ approaches a constant, $B_3$ approaches 1.0, and ${\phi }_5$ approaches 0 degrees. That is

$$\begin{array}{cc}\hfill {\sigma }_z^{\prime }=& p_0[A_3\cos (kx-\omega t+{\phi }_4)e^{kz}+\cos (kx-\omega t+{\xi }_{2}z)e^{{\xi }_{1}z}]\hfill \\ \hfill =& p_0\left(\sqrt{A_3^2{e}^{2kz}+e^{2{\xi }_{1}z}+2A_3{e}^{(k+{\xi }_1)z}\cos ({\xi }_{2}z-{\phi }_4)}\right)\cos (kx-\omega t+\Delta {\theta }_{03}),\hfill \end{array}$$

(70)

where the phase-lag for the effective vertical stress can be expressed as

$$\Delta {\theta }_{03}=\arctan \left({\displaystyle \frac{A_3{e}^{kz}\sin {\phi }_4+e^{{\xi }_{1}z}\sin \left({\xi }_{2}z\right)}{A_3{e}^{kz}\cos {\phi }_4+e^{{\xi }_{1}z}\cos \left({\xi }_{2}z\right)}}\right).$$

(71)

As shown in Figure 11, when $R_k\ll 1.0$, the phase-lag $\Delta {\theta }_3$ approaches 180 degrees. When $R_k\gg 1.0$, (59) can be simplified to (71). This is consistent with the preceding discussion.

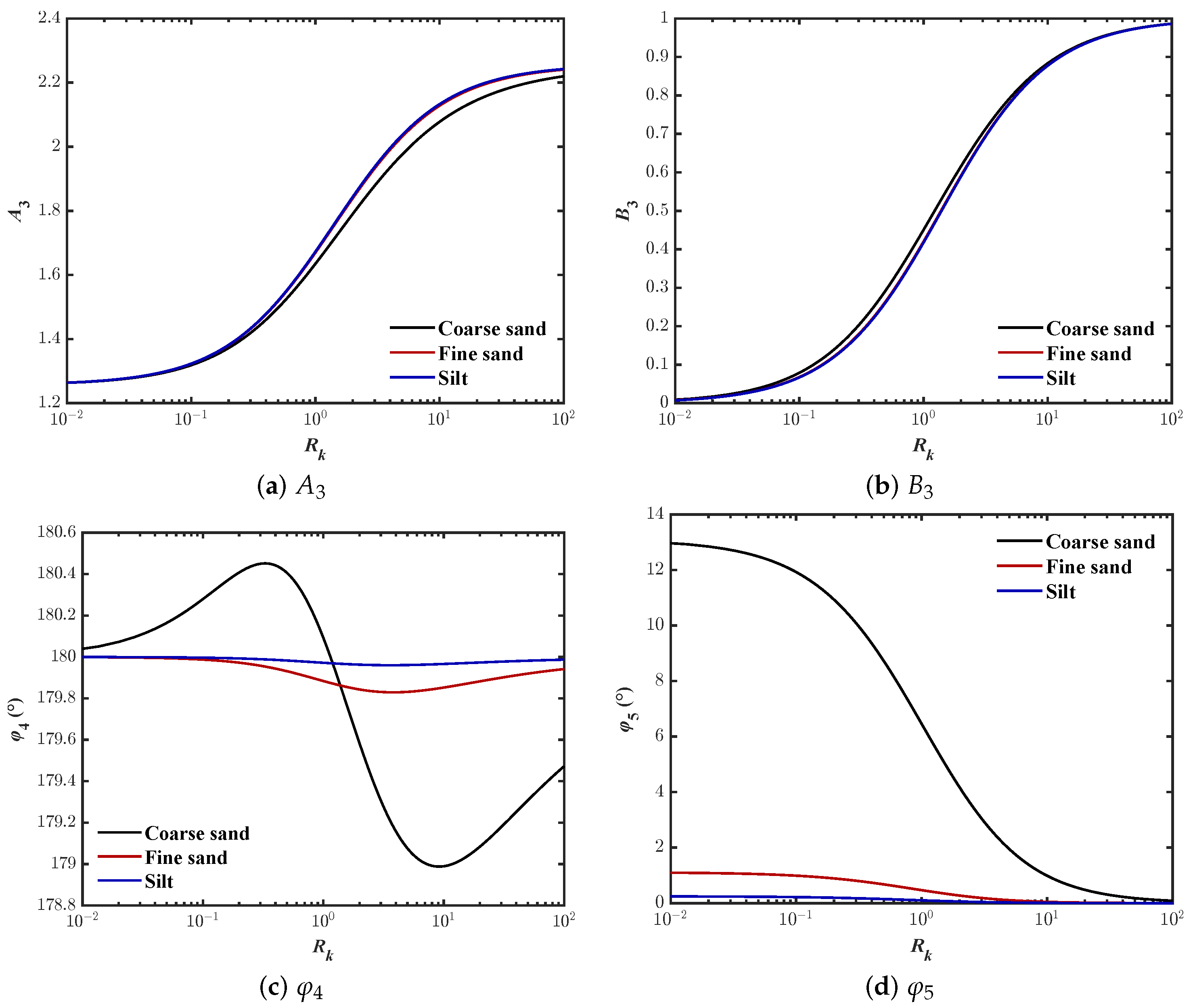
3.4. Phase-Lag for Shear Stress (${\tau }_{xz}$)

Substituting (16)–(27) into (6), the analytical solution of shear stress (${\tau }_{xz}$) can be rewritten as

$$\begin{array}{cc}\hfill {\tau }_{xz}=& p_0[A_4\cos (kx-\omega t+{\phi }_6)e^{kz}+B_4\cos (kx-\omega t+{\phi }_7+{\xi }_{2}z)e^{{\xi }_{1}z}]\hfill \\ \hfill =& p_0\left(\sqrt{A_4^2{e}^{2kz}+B_4^2{e}^{2{\xi }_{1}z}+2A_4{B}_4{e}^{(k+{\xi }_1)z}\cos ({\phi }_7+{\xi }_{2}z-{\phi }_6)}\right)\cos (kx-\omega t+\Delta {\theta }_4),\hfill \end{array}$$

(72)

and the phase-lag for shear stress can be expressed as

$$\Delta {\theta }_4=\arctan \left({\displaystyle \frac{A_4{e}^{kz}\sin {\phi }_6+B_4{e}^{{\xi }_{1}z}\sin ({\phi }_7+{\xi }_{2}z)}{A_4{e}^{kz}\cos {\phi }_6+B_4{e}^{{\xi }_{1}z}\cos ({\phi }_7+{\xi }_{2}z)}}\right).$$

(73)

In (72), the coefficients $A_4$, $B_4$ and the phases ${\phi }_6$, ${\phi }_7$ are obtained from

$$A_4=\sqrt{{(D_{22}+k{D}_{24}z+D_{26})}^2+{(D_{23}+k{D}_{25}z+D_{27})}^2},$$

(74)

$$B_4=\sqrt{D_{28}^2+D_{29}^2},$$

(75)

$${\phi }_6=\arctan \left({\displaystyle \frac{D_{23}+k{D}_{25}z+D_{27}}{D_{22}+k{D}_{24}z+D_{26}}}\right),$$

(76)

$${\phi }_7=\arctan \left({\displaystyle \frac{D_{29}}{D_{28}}}\right),$$

(77)

where the parameters $D_i$ (i = 22–29) are

$$D_{22}=D_5,D_{23}=-D_4,D_{24}=-D_7,D_{25}=D_6,$$

(78)

$$D_{26}={\eta }_2{D}_6+{\eta }_1{D}_7,D_{27}={\eta }_2{D}_7-{\eta }_1{D}_6,$$

(79)

$$D_{28}={\displaystyle \frac{k{a}_2\left[{\eta }_1\left({\xi }_1^2+{\xi }_2^2\right)+k({\eta }_2{\xi }_2-{\eta }_1{\xi }_2)\right]-k{a}_1\left[{\eta }_2\left({\xi }_1^2+{\xi }_2^2\right)-k({\eta }_1{\xi }_2+{\eta }_2{\xi }_1)\right]}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(80)

$$D_{29}={\displaystyle \frac{k{a}_1\left[{\eta }_1\left({\xi }_1^2+{\xi }_2^2\right)+k({\eta }_2{\xi }_2-{\eta }_1{\xi }_2)\right]+k{a}_2\left[{\eta }_2\left({\xi }_1^2+{\xi }_2^2\right)-k({\eta }_1{\xi }_2+{\eta }_2{\xi }_1)]\right]}{\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}}.$$

(81)

Figure 10 illustrates the variations in coefficients ($A_3$, $B_3$) and phases (${\phi }_4$, ${\phi }_5$) versus $R_k$. As shown as Figure 12a, $A_4$ approaches a constant when $R_k$ approaches zero. On the other hand, $B_4$ approaches zero when $R_k$ approaches zero, as shown in Figure 12b. It is noted that although $B_4$ in coarse sand is not zero when $R_k$ = 0.01 in the figure, the trend of $B_4$ approaches zero with $R_k$ approaching zero. Regarding the phase (${\phi }_6$), it approaches −90 degrees when $R_k$ approaches zero. It is noted that although it in coarse sand is not −90 degrees when $R_k$ = 0.01 in the figure, the tend of ${\phi }_6$ approaches −90 degrees with $R_k$ approaching zero, as shown in Figure 12c on the other hand, when $R_k$ approaches infinity, the phase (${\phi }_7$) approaches 135 degrees (see Figure 12d).

For two extreme cases of $R_k$, the shear stress is discussed:

(1)

Case-I: $R_k\ll 1.0$

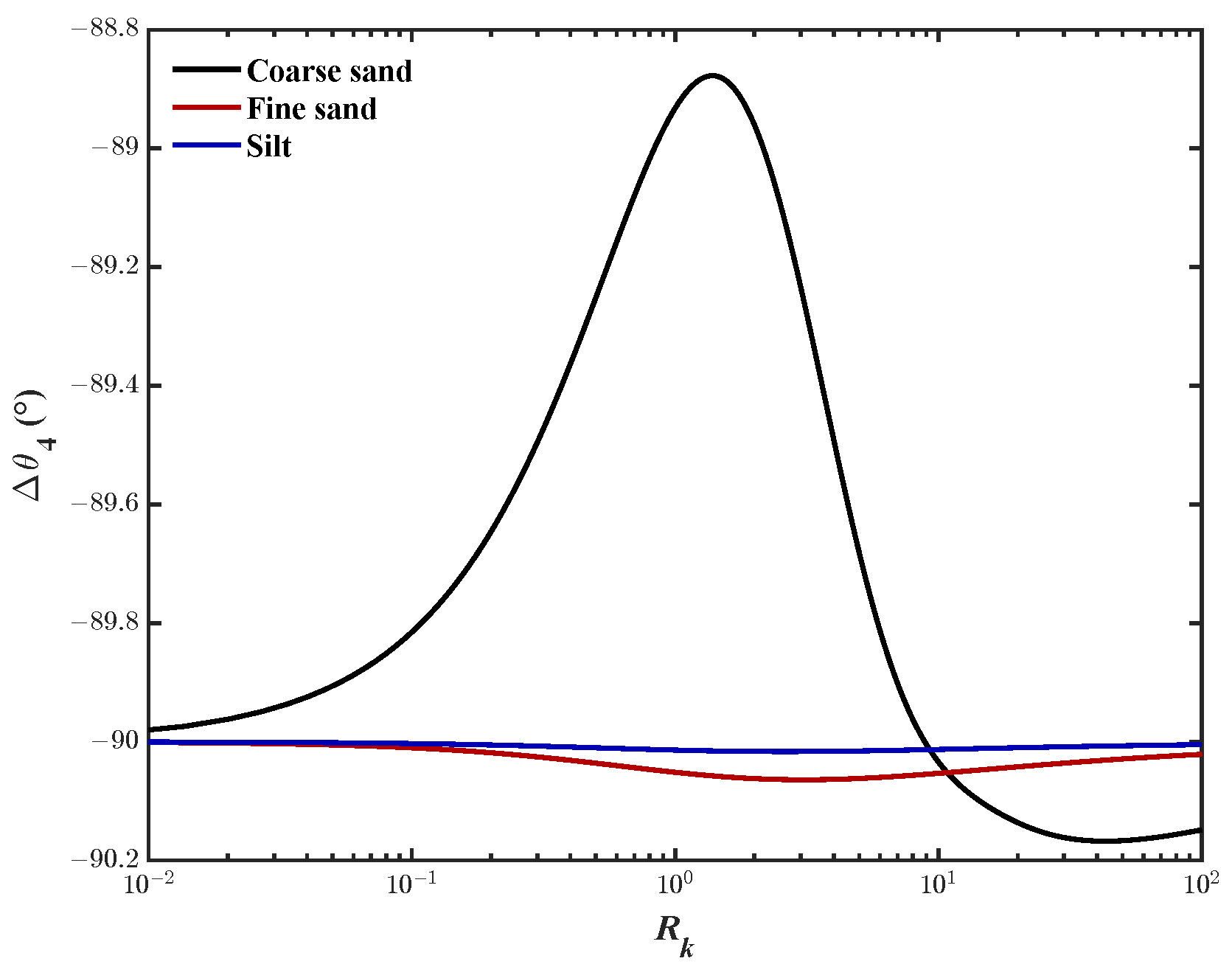
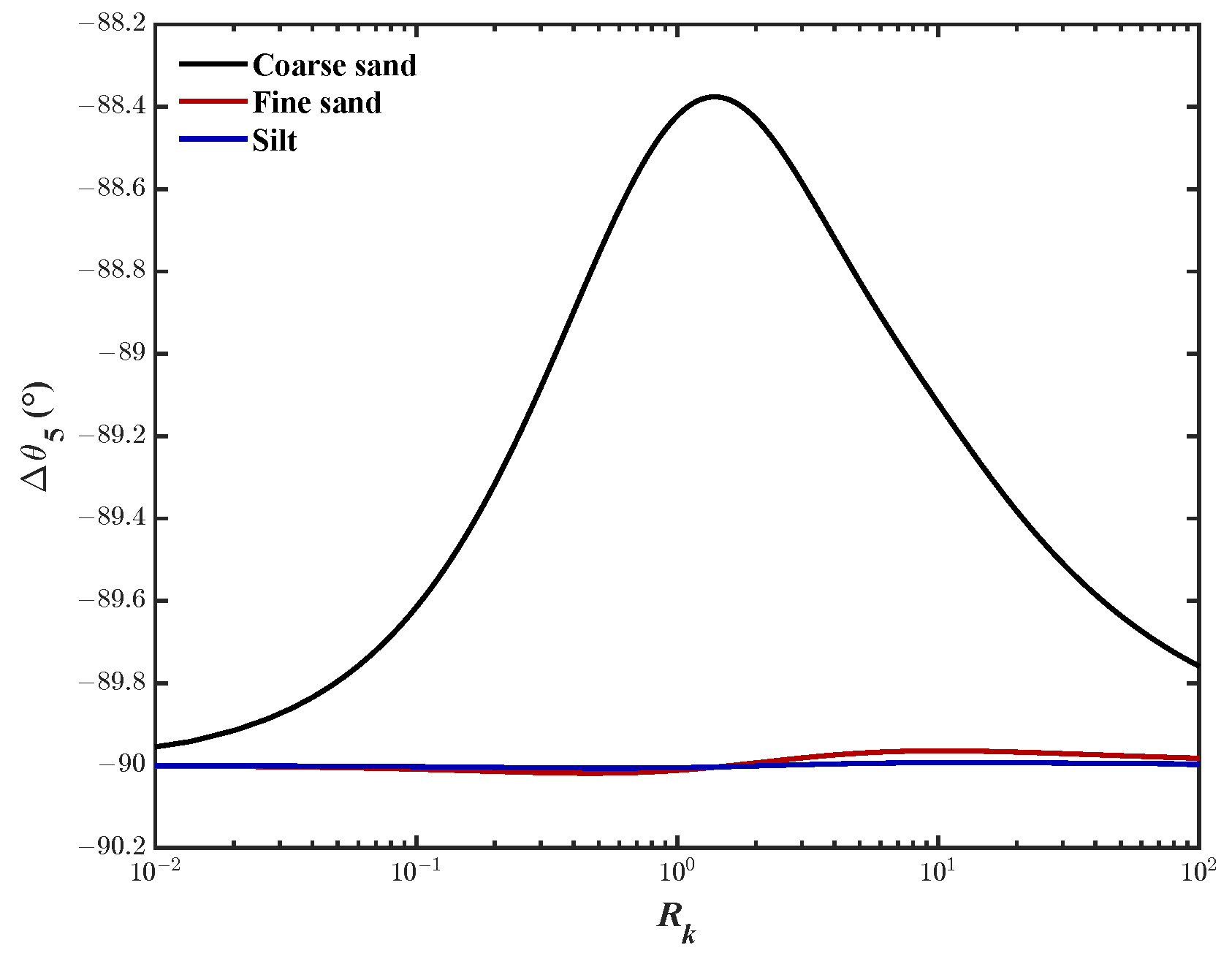
As shown in Figure 12, for this case, $A_4$ cannot be ignored, $B_4$ approaches zero, and ${\phi }_6$ approaches −90 degrees. Then, (72) can be simplified to

$${\tau }_{xz}=p_0{A}_4\cos (kx-\omega t-{\displaystyle \frac{\pi }{2}})e^{kz}.$$

(82)

From (82), when $R_k\ll 1.0$, the phase-lag for shear stress is −90 degrees.

(2)

Case-II: $R_k\gg 1.0$

When $R_k\gg 1.0$, $B_4$ is much smaller than $A_4$, so the second term can be neglected. Then, (72) can be simplified to

$${\tau }_{xz}=p_0{A}_4\cos (kx-\omega t+{\phi }_6)e^{kz},$$

(83)

and the phase-lag for shear stress can be calculated by

$$\Delta {\theta }_{04}(={\phi }_6)=\arctan \left({\displaystyle \frac{D_{23}+k{D}_{25}z+D_{27}}{D_{22}+k{D}_{24}z+D_{26}}}\right).$$

(84)

As seen in Figure 12, if $R_k\gg 1.0$, $B_4\ll A_4$, then the phase-lag can be simplified to (76). This is consistent with the preceding discussion. As shown in Figure 13, when $R_k\ll 1.0$, the phase-lag $\Delta {\theta }_4$ approaches −90 degrees. It is noted that although $\Delta {\theta }_4$ in coarse sand is not −90 degrees when $R_k$ = 0.01 in the figure, the trend of $\Delta {\theta }_4$ approaches −90 degrees with $R_k$ approaching zero. This is similar to the variation in ${\phi }_6$ versus $R_k$.

3.5. Phase-Lag for Soil Displacements (u, w)

Substituting (16)–(27) into (7), the analytical solutions for soil displacements in the x-directions (u) can be further expressed as:

$$\begin{array}{cc}\hfill u=& p_0[A_5\cos (kx-\omega t+{\phi }_8)e^{kz}+B_5\cos (kx-\omega t+{\phi }_9+{\xi }_{2}z)e^{{\xi }_{1}z}]\hfill \\ \hfill =& p_0\left(\sqrt{A_5^2{e}^{2kz}+B_5^2{e}^{2{\xi }_{1}z}+2A_5{B}_5{e}^{(k+{\xi }_1)z}\cos ({\phi }_9+{\xi }_{2}z-{\phi }_8)}\right)\cos (kx-\omega t+\Delta {\theta }_5),\hfill \end{array}$$

(85)

and the phase-lag for horizontal displacement can be calculated by

$$\Delta {\theta }_5=\arctan \left({\displaystyle \frac{A_5{e}^{kz}\sin {\phi }_8+B_5{e}^{{\xi }_{1}z}\sin ({\phi }_9+{\xi }_{2}z)}{A_5{e}^{kz}\cos {\phi }_8+B_5{e}^{{\xi }_{1}z}\cos ({\phi }_9+{\xi }_{2}z)}}\right).$$

(86)

In (85), the coefficients ($A_5$, $B_5$), and the phases (${\phi }_8$, ${\phi }_9$) are given by

$$A_5=\sqrt{{(D_{30}+D_{32}z)}^2+{(D_{31}+D_{33}z)}^2},$$

(87)

$$B_5=\sqrt{D_{34}^2+D_{35}^2},$$

(88)

$${\phi }_8=\arctan \left({\displaystyle \frac{D_{31}+D_{33}z}{D_{30}+D_{32}z}}\right),$$

(89)

$${\phi }_9=\arctan \left({\displaystyle \frac{D_{35}}{D_{34}}}\right),$$

(90)

where the variables $D_i$ (i = 30–35) are

$$D_{30}={\displaystyle \frac{D_5}{2Gk}},D_{31}={\displaystyle \frac{-D_4}{2Gk}},D_{32}={\displaystyle \frac{-D_7}{2G}},D_{33}={\displaystyle \frac{D_6}{2G}},$$

(91)

$$D_{34}={\displaystyle \frac{k{\eta }_1[{\xi }_2{a}_1+({\xi }_1-k)a_2]-k{\eta }_2[({\xi }_1-k)a_1-{\xi }_2{a}_2]}{2G\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}},$$

(92)

$$D_{35}={\displaystyle \frac{k{\eta }_1[({\xi }_1-k)a_1-{\xi }_2{a}_2]+k{\eta }_2[{\xi }_2{a}_1+({\xi }_1-k)a_2]}{2G\left[{({\xi }_1-k)}^2+{\xi }_2^2\right]\left(a_1^2+a_2^2\right)}}.$$

(93)

Figure 14 illustrates the variations in coefficients ($A_5$, $B_5$) and phases (${\phi }_8$, ${\phi }_9$) versus $R_k$. As shown in Figure 14a, $A_5$ approaches a constant when $R_k$ approaches zero, and when $R_k$ approaches infinity, $A_5$ also approaches constant. The constants vary with wave and soil properties. On the other hand, $B_5$ approaches zero when $R_k$ is from 0.01 to 100, as shown in Figure 14b. It is noted that although $B_5$ in coarse sand is not zero in the figure, it is so small that it can be regarded as approximately zero. Regarding the phase (${\phi }_8$), it approaches −90 degrees when $R_k$ approaches zero, as shown in Figure 14c. Although ${\phi }_8$ in coarse sand is not −90 degrees when $R_k$ = 0.01 in the figure, it is very close to zero. On the other hand, when $R_k$ approaches infinity, the phase (${\phi }_9$) approaches −180 degrees (see Figure 14d).

In the two limiting cases of $R_k$, the horizontal displacement is discussed:

(1)

Case-I: $R_k\ll 1.0$

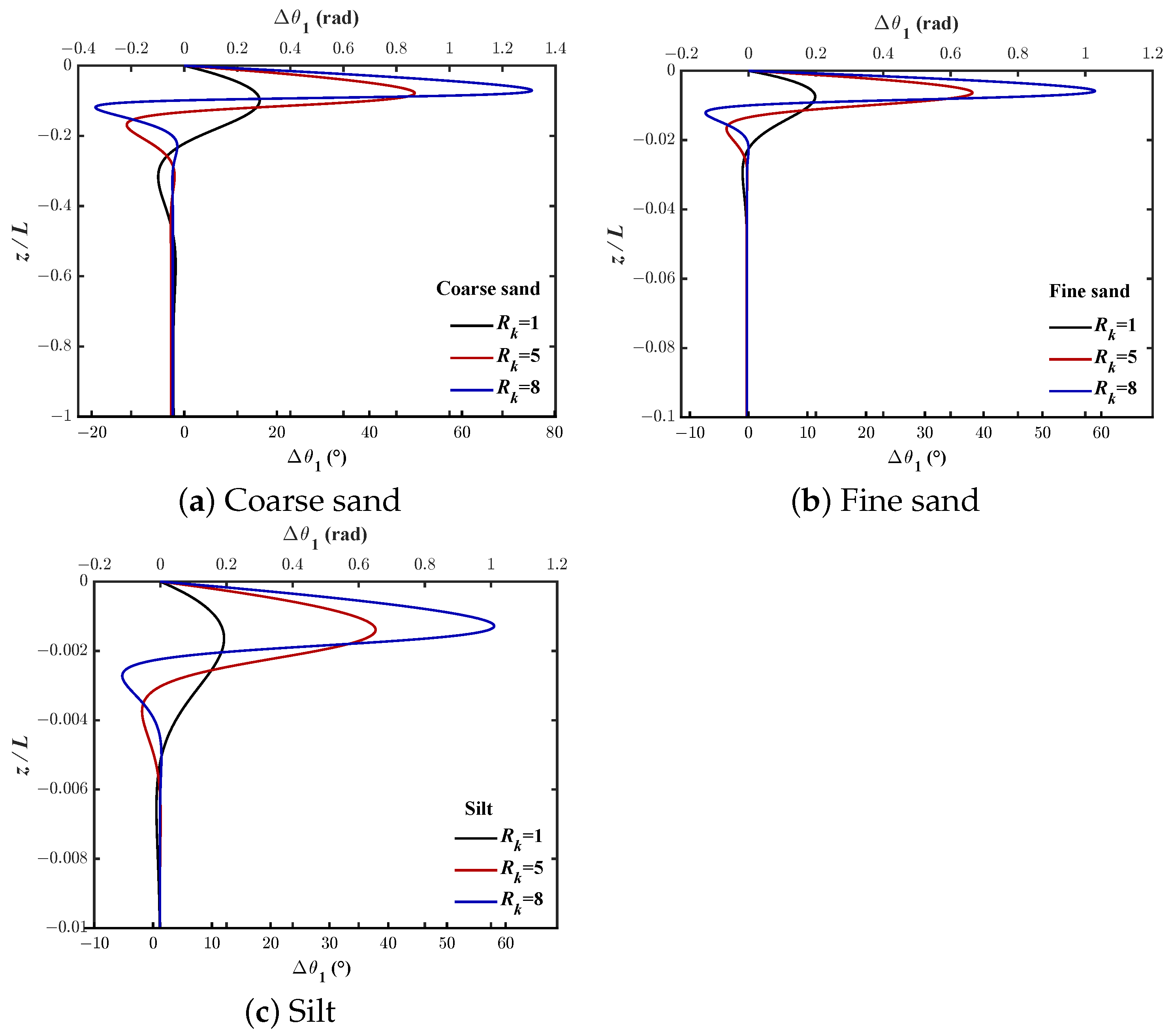
As illustrated in Figure 14, when $R_k\ll 1.0$, $A_5$ approaches the constant, $B_5$ approaches zero, and ${\phi }_8$ approaches $-{90}^{\circ }$. (85) can be simplified to

$$u=p_0{A}_5\cos (kx-\omega t-{\displaystyle \frac{\pi }{2}})e^{kz}.$$

(94)

From (94), when $R_k\ll 1.0$, the phase-lag for x-displacement is −90 degrees.

(2)

Case-II: $R_k\gg 1.0$

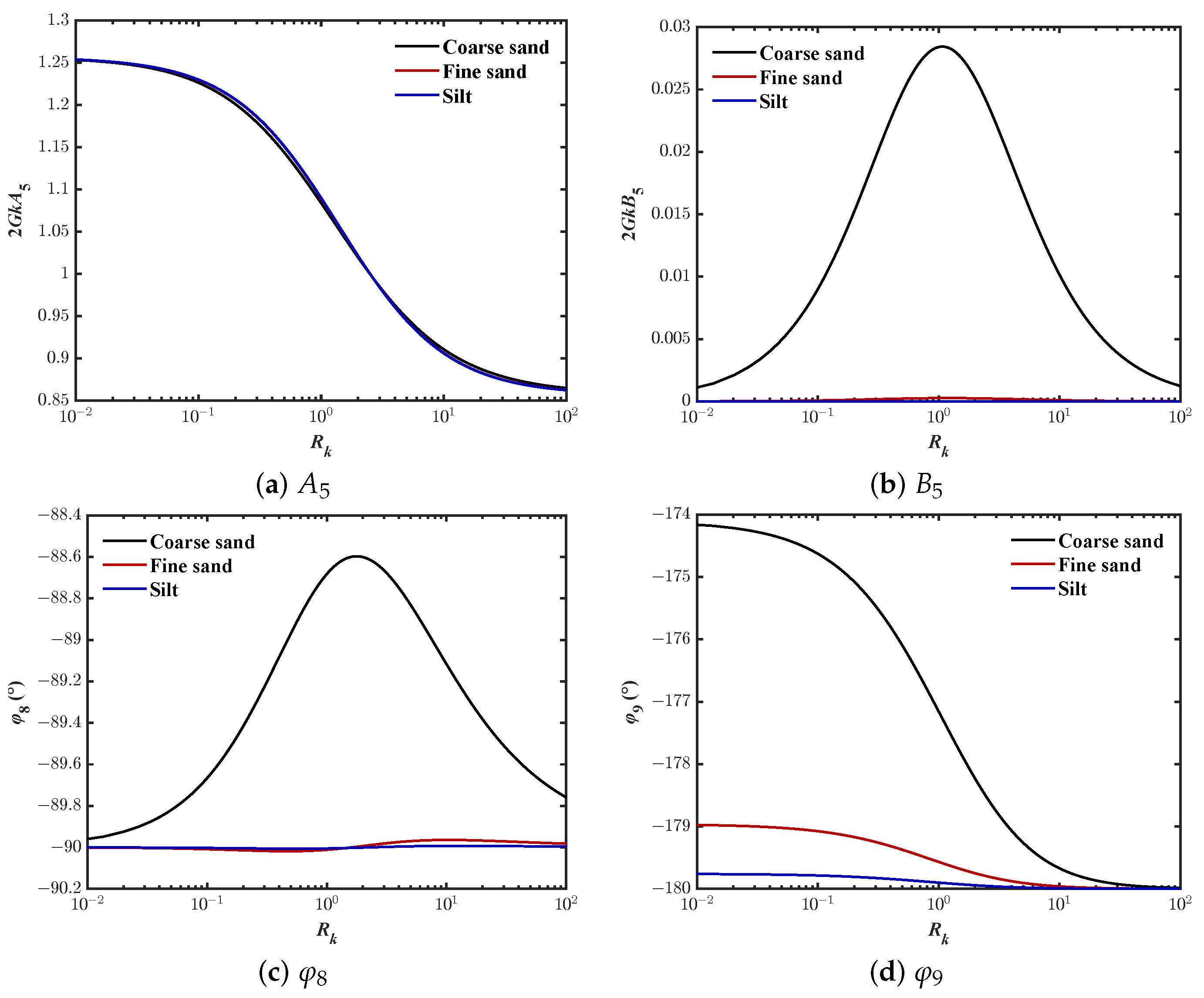
If $R_k\gg 1.0$, $B_5$ is also much smaller than $A_5$, and ${\phi }_9$ approaches zero (see Figure 14). That is

$$u=p_0{A}_5\cos (kx-\omega t+{\phi }_8)e^{kz},$$

(95)

and the phase-lag for soil displacement in x-direction can be expressed as

$$\Delta {\theta }_{05}(={\phi }_8)=\arctan \left({\displaystyle \frac{D_{31}+D_{33}z}{D_{30}+D_{32}z}}\right).$$

(96)

When $R_k\gg 1.0$, as discussed above, $B_5\ll A_5$. Therefore, the phase-lag (86) also can be simplified to (89). This is consistent with the conclusion obtained above. As shown in Figure 15, when $R_k$ approaches zero, the phase-lag ($\Delta {\theta }_5$) approaches −90 degrees. And the variations in it versus $R_k$ is similar to the variations in ${\phi }_8$ versus $R_k$ at $z/L$ = −0.2.

Substituting (16)–(27) into (8), the analytical solutions for soil displacements in the z-directions (w) can be further expressed as:

$$\begin{array}{cc}\hfill w=& p_0\left[A_6\cos (kx-\omega t+{\phi }_{10})e^{kz}+B_6\cos (kx-\omega t+{\phi }_{11}+{\xi }_{2}z)e^{{\xi }_{1}z}\right]\hfill \\ \hfill =& p_0\left(\sqrt{A_6^2{e}^{2kz}+B_6^2{e}^{2{\xi }_{1}z}+2A_6{B}_6{e}^{(k+{\xi }_1)z}\cos ({\phi }_{11}+{\xi }_{2}z-{\phi }_{10})}\right)\cos (kx-\omega t+\Delta {\theta }_6),\hfill \end{array}$$

(97)

and the expression of the phase-lag can be obtained

$$\Delta {\theta }_6=\arctan \left({\displaystyle \frac{A_6{e}^{kz}\sin {\phi }_{10}+B_6{e}^{{\xi }_{1}z}\sin ({\phi }_{11}+{\xi }_{2}z)}{A_6{e}^{kz}\cos {\phi }_{10}+B_6{e}^{{\xi }_{1}z}\cos ({\phi }_{11}+{\xi }_{2}z)}}\right).$$

(98)

In (97), the coefficients ($A_6$, $B_6$), and the phases (${\phi }_{10}$, ${\phi }_{11}$) are given by

$$A_6=\sqrt{{(D_{36}-D_{38}+D_{40}z)}^2+{(D_{37}-D_{39}+D_{41}z)}^2},$$

(99)

$$B_6=\sqrt{D_{42}^2+D_{43}^2},$$

(100)

$${\phi }_{10}=\arctan \left({\displaystyle \frac{D_{37}-D_{39}+D_{41}z}{D_{36}-D_{38}+D_{40}z}}\right),$$

(101)

$${\phi }_{11}=\arctan \left({\displaystyle \frac{D_{43}}{D_{42}}}\right),$$

(102)

where the variables $D_i$ (i = 36–43) are

$$D_{36}={\displaystyle \frac{-D_4}{2Gk}},D_{37}={\displaystyle \frac{-D_5}{2Gk}},$$

(103)

$$D_{38}={\displaystyle \frac{(1+2{\eta }_1)D_6-2{\eta }_2{D}_7}{2Gk}},D_{39}={\displaystyle \frac{(1+2{\eta }_1)D_7+2{\eta }_2{D}_6}{2Gk}},$$

(104)

$$D_{40}={\displaystyle \frac{D_6}{2G}},D_{41}={\displaystyle \frac{D_7}{2G}},D_{42}={\displaystyle \frac{D_{29}}{2Gk}},D_{43}={\displaystyle \frac{-D_{28}}{2Gk}}.$$

(105)

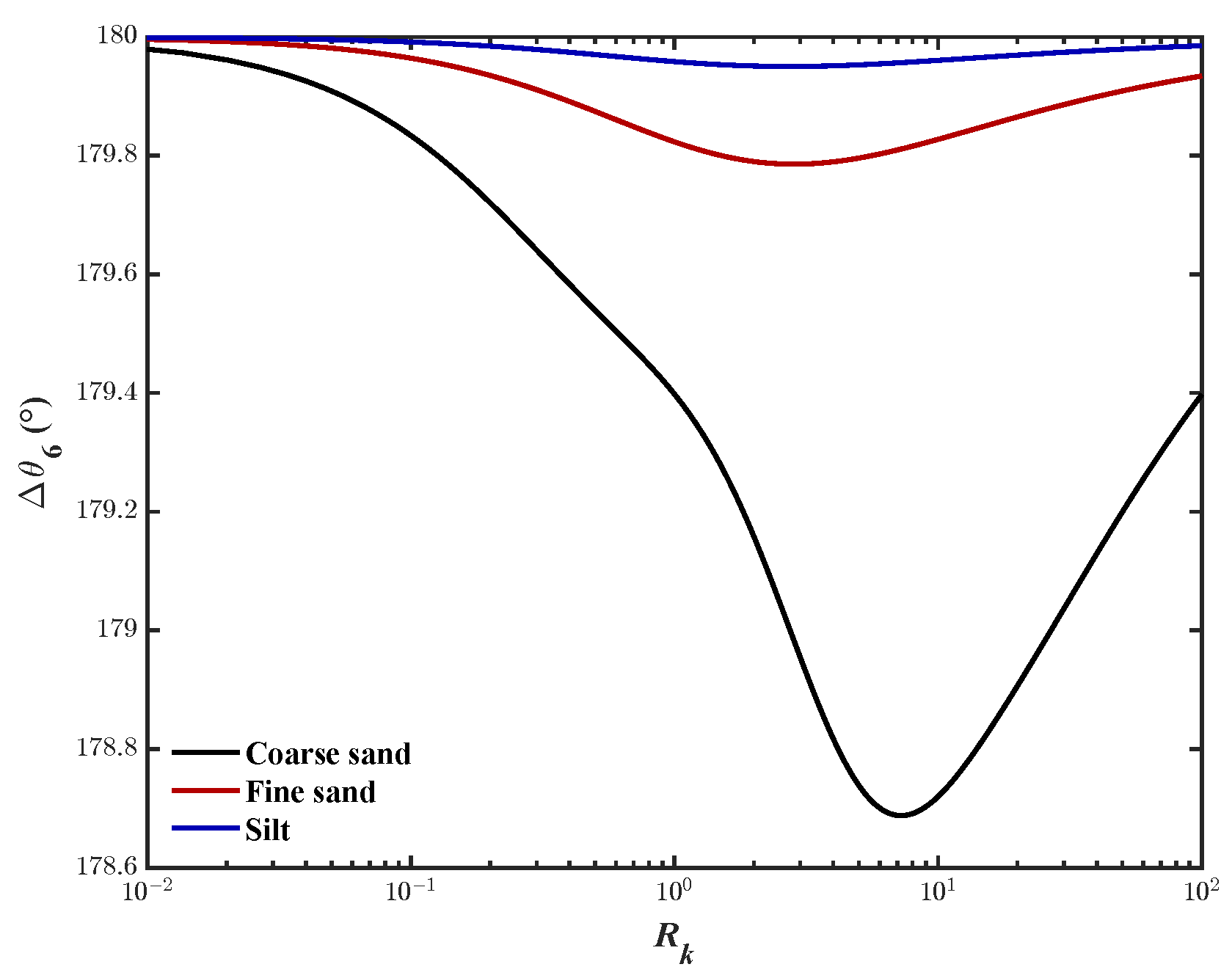
Figure 16 illustrates the variations in coefficients ($A_6$, $B_6$) and phases (${\phi }_{10}$, ${\phi }_{11}$) versus $R_k$. As shown in Figure 16a, $A_6$ approaches a constant when $R_k$ approaches zero. And at this time, $B_6$ approaches zero (see Figure 16b). It is noted that $B_6$ in coarse sand is not zero when $R_k$ = 0.01 in the figure, it is so small that can be regarded approximately as zero. Regarding the phase (${\phi }_{10}$), it approaches 180 degrees when $R_k$ approaches zero, as shown in Figure 16c. On the other hand, when $R_k$ approaches infinity, the phase (${\phi }_{11}$) approaches 45 degrees (see Figure 16d).

The analytical solution of soil displacement in the z-direction (w) for two limiting cases of $R_k$ is examined:

(1)

Case-I: $R_k\ll 1.0$

When $R_k\ll 1.0$, $A_6$ approaches a constant, $B_6$ approaches zero, and ${\phi }_{10}$ approaches $0^{\circ }$ as seen in Figure 16. Then, (97) can be simplified to

$$w=p_0{A}_6\cos (kx-\omega t+\pi )e^{kz}.$$

(106)

From (106), in this case, the phase-lag is 180 degrees.

(2)

Case-II: $R_k\gg 1.0$

If $R_k\gg 1.0$, $B_6$ is much smaller than $A_6$, so the second term can be ignored (see Figure 16). That is

$$w=p_0{A}_6\cos (kx-\omega t+{\phi }_{10})e^{kz},$$

(107)

and the phase-lag for vertical displacement can be expressed as

$$\Delta {\theta }_{06}(={\phi }_{10})=\arctan \left({\displaystyle \frac{D_{37}-D_{39}+D_{41}z}{D_{36}-D_{38}+D_{40}z}}\right).$$

(108)

According to Figure 17, when $R_k\ll 1.0$, the phase-lag $\Delta {\theta }_6$ approaches 180 degrees. For $R_k\gg 1.0$, since $B_6\ll A_6$, (98) also can be simplified to (101). This is consistent with the conclusion obtained above.

4. Parametric Study for Phase-Lags

Based on the phase-lags derived in the previous section, in this section, a parametric study is performed to examine the effects of wave and seabed characteristics on the phase-lag for the wave-induced pore pressures and stresses in a porous seabed. It is noted that only phase-lag for wave-induced pore pressures was discussed in previous studies available in the literature [9,13,14]. The input data for the numerical examples are listed in Table 1.

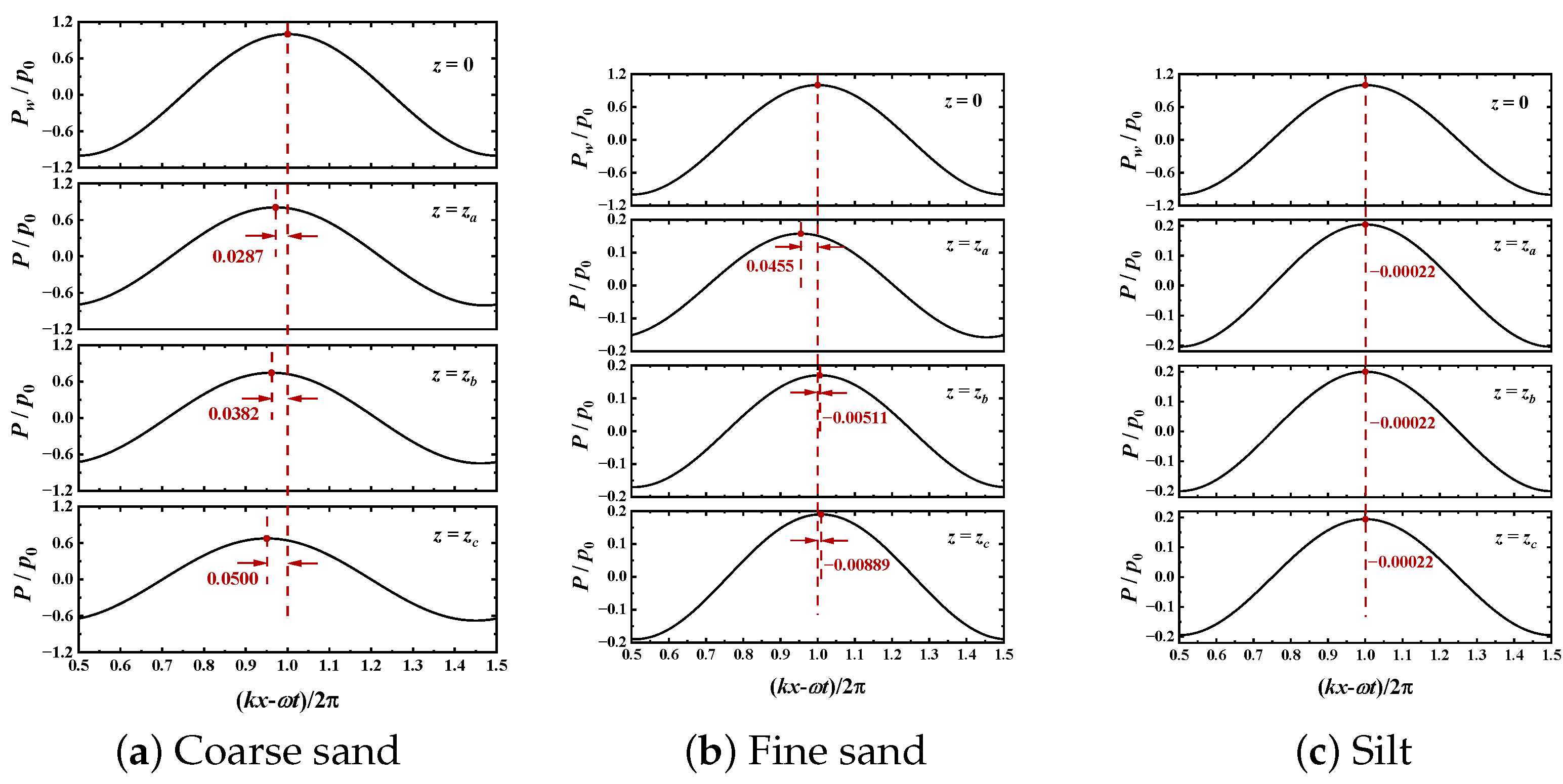
4.1. Wave-Induced Pore Pressures (P)

Figure 18 presents the vertical distribution in the phase-lag for wave-induced pore pressure ($\Delta {\theta }_1$) versus $z/L$ for various $R_k$. It can be seen in Figure 18a, the phase-lag for wave-induced pore pressure is obvious between $z/L$ = 0 and $z/L=-0.2$ in coarse sand, while it is obvious in the zone $z/L$ = [−0.04, 0] in fine sand (see Figure 18b). Furthermore, the phase-lag in silt occurs only in the shallower layer ($z/L$ = [−0.0006, 0], see Figure 18c). In deeper soil layers, the phase-lag would no longer exist despite of soil types. Moreover, the larger $R_k$ is, the change of $\Delta {\theta }_1$ is more obvious.

Hydraulic anisotropy ($K_x/K_z$) is one of the important factors affecting the distribution of the wave-induced pore pressures. Therefore, it is necessary to examine the effects of hydraulic anisotropy on the phase-lag for pore pressures. Figure 19 illustrates the vertical distribution in the phase-lag for wave-induced pore pressure ($\Delta {\theta }_1$) versus $z/L$ for various $K_x/K_z$. As shown in the figure, the extreme phase-lag decreases with increasing $K_x/K_z$ in coarse sand. However, in fine sand and silt, $K_x/K_z$ has almost no effect on phase-lag.

In the literature, wave characteristics have been reported to significantly affect wave-induced soil response [16]. Herein, effect of wave period on phase-lag for pore pressure is further examined. As shown in Figure 20, the phase-lag decreases with increasing T, which is most obvious in coarse sand, followed by fine sand, and least obvious in silt. The shorter the wave period (T), the deeper the zone affected by phase-lag.

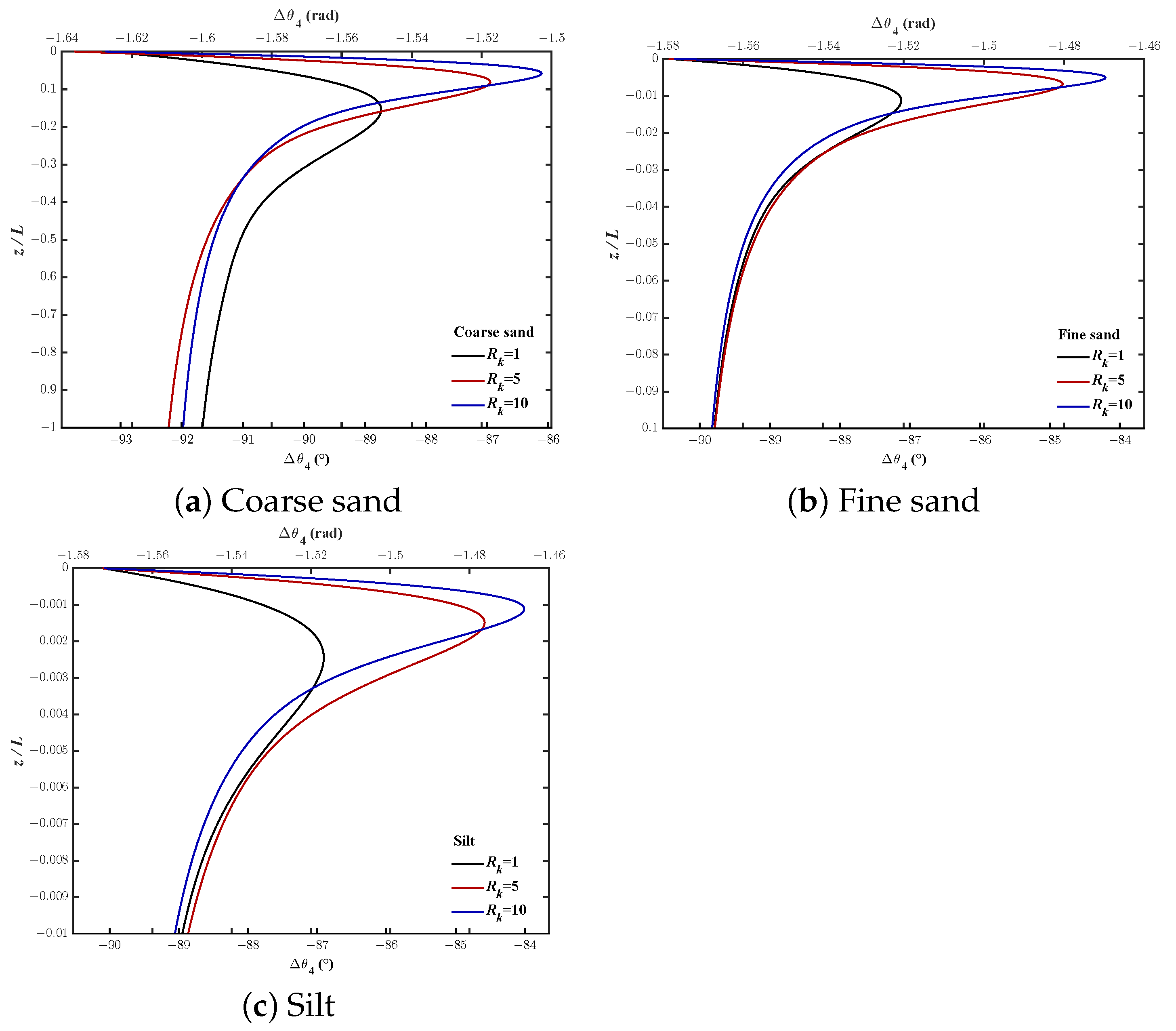
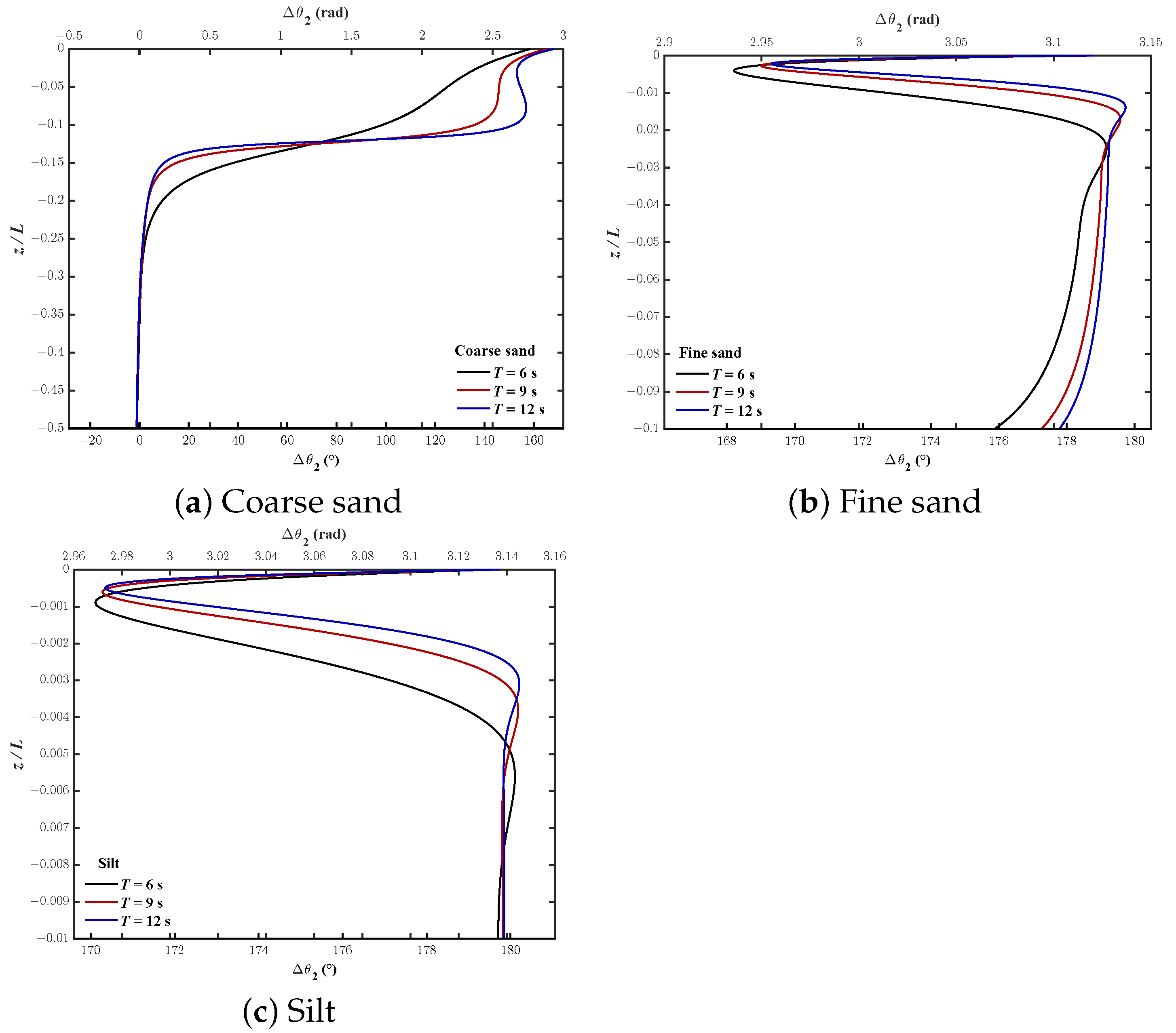
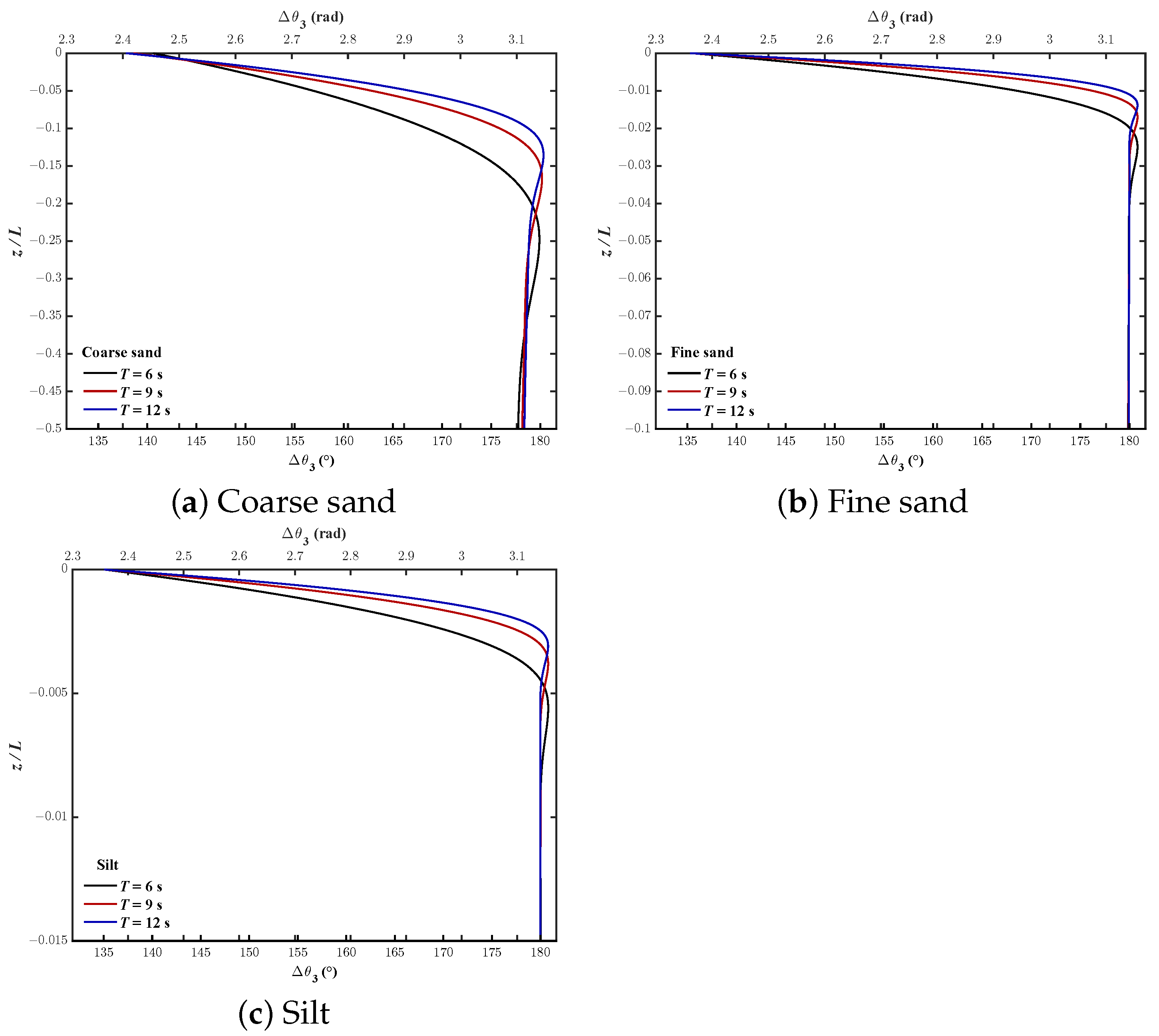
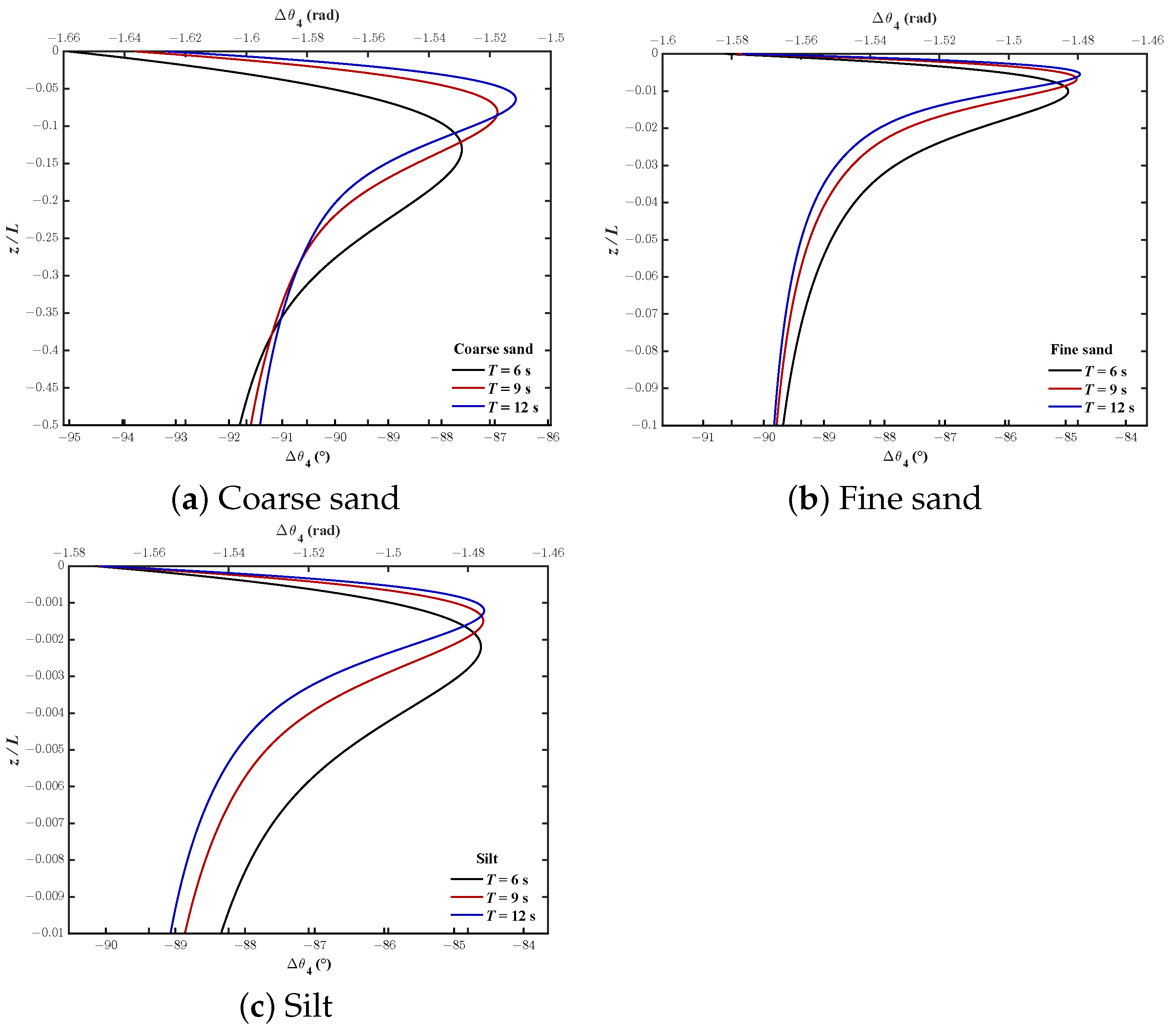
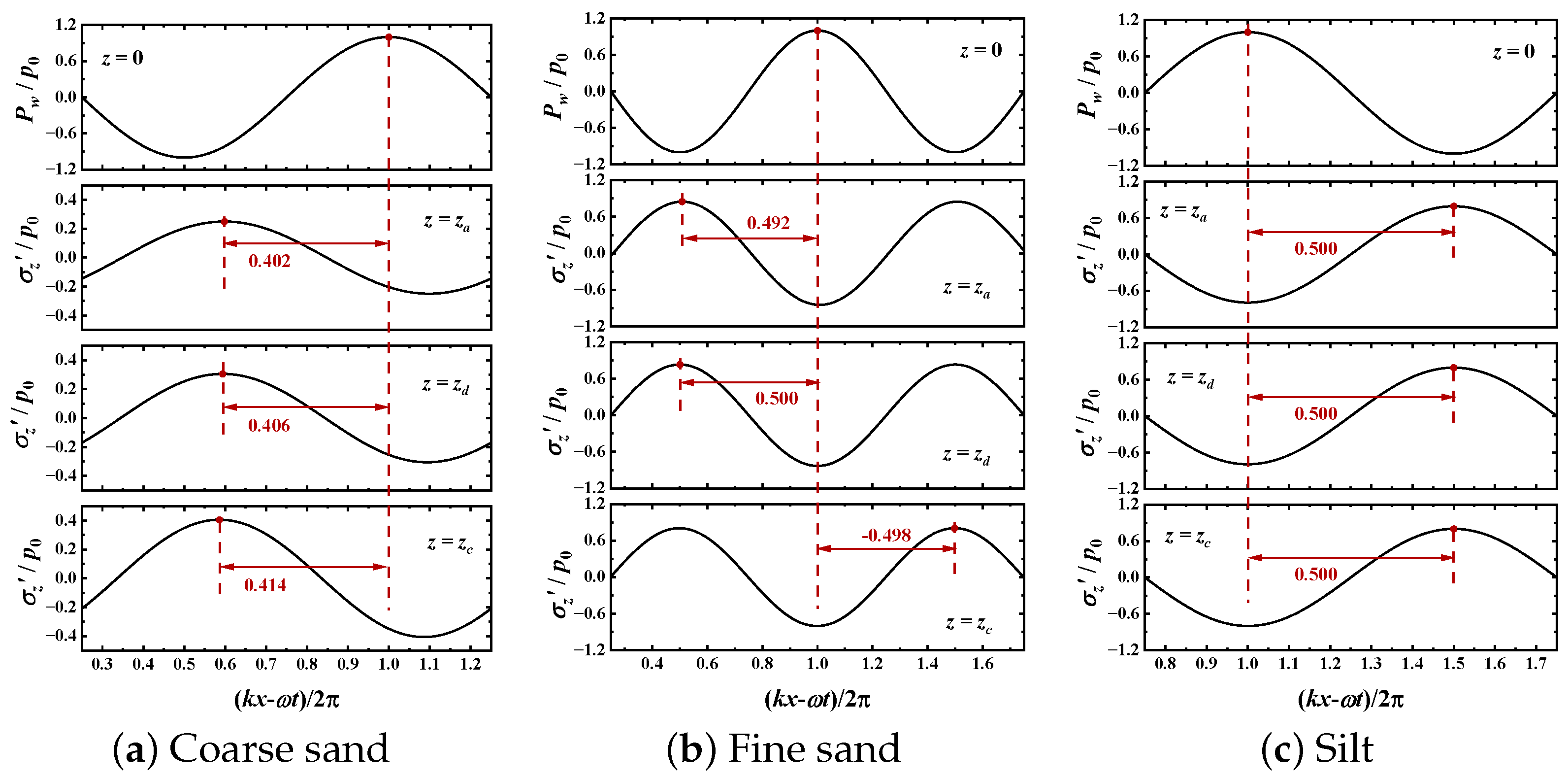
4.2. Wave-Induced Stress (${\sigma }_x^{\prime }$, ${\sigma }_z^{\prime }$ and ${\tau }_{xz}$)

In this section, phase-lags for the wave-induced effective normal stresses (${\sigma }_x^{\prime }$ and ${\sigma }_z^{\prime }$) with various parameters are examined. Figure 21 provides a more detailed illustration of phase-lag $\Delta {\theta }_2$ (referring to (43)) versus $z/L$ for various $R_k$. In coarse sand, the phase-lag in shallow soil layers increases with increasing $R_k$, but for deeper soil depths, there is no phase-lag. For fine sand and silt, phase-lag can be found in shallow soil layers, increases with increasing $R_k$ and then continues to be close to 180 degrees. However, no phase-lag can be found in a deeper soil zone.

Figure 22 provides a more detailed illustration of phase-lag $\Delta {\theta }_3$ (referring to (59)) versus $z/L$ for various $R_k$. In the shallow soil layers, the phase-lag increases with increasing $R_k$ and then continues to be close to 180 degrees in fine sand and silt. In coarse sand, the phase-lag in deeper soil layers is close to 178 degrees. Moreover, the larger $R_k$ is, the shallower soil layers the phase-lag tends to 180 degrees.

Figure 23 provides a more detailed illustration of phase-lag $\Delta {\theta }_4$ (referring (73)) versus $z/L$ for various $R_k$. It can be seen that in shallow soil layers the phase-lag decreases with increasing $R_k$. Then, in fine sand and silt it tends to the degrees which near −90 degrees. Additionally, the larger $R_k$ is, the change of $\Delta {\theta }_4$ is more obvious.

Again, Figure 24 illustrates the variations in phase-lag for stresses versus soil depth ($z/L$) under different permeability coefficient ratios $K_x/K_z$. Because the phase-lag for wave-induced pore pressure is nearly unaffected by variations in $K_x/K_z$ in fine sand and silt; therefore, only the results for coarse sand are presented. For the phase delay of horizontal effective stress, in shallow soil layers, the phase-lag increases with higher $K_x/K_z$, and in deeper layers, the phase-lag gradually decreases, with an earlier disappearance observed for larger ratios. The phase-lag for vertical effective stress increases with increasing $K_x/K_z$, and the higher the ratios, the closer the phase-lag approaches 180 degrees. In contrast, the extreme phase-lag for shear stress decreases slightly with increasing $K_x/K_z$.

Furthermore, the wave period (T) also has an impact on phase-lag. Figure 25, Figure 26 and Figure 27 illustrate vertical distribution in the phase-lag for stresses versus $z/L$ for various T. The phase-lag for horizontal effective stress ($\Delta {\theta }_2$) increases with increasing T in coarse sand, for deeper soil layers, the phase-lag gradually disappear, with earlier disappearance occurring for longer wave periods. In fine sand and silt, the extreme phase-lag increases with increasing T. The phase-lag for the vertical effective stress ($\Delta {\theta }_3$) increases with increasing T. The longer T lead to phase-lag earlier tends to 180 degrees. The extreme phase-lag for shear stress ($\Delta {\theta }_4$) decreases with increasing T, and the larger T, the faster the phase-lag decreases with increasing soil depth.

5. Wave-Induced Seabed Stability

In this section, two types of wave-induced seabed instability will be discussed, namely liquefaction and shear failure. Liquefaction and shear failure are critical issues for marine foundations, pipelines, and breakwaters. The instantaneous liquefaction caused by the oscillatory pore pressure is mainly studied in this section. When the seabed soil is fine sand or silt, due to extreme wave loading, the effective stress within the seabed soil decreases or even disappears, causing the seabed liquefaction and subsequently leading to marine structures are damaged. Meanwhile, shear failure occurs when the soil is subjected to stresses exceeding its shear resistance, leading to bearing capacity failure in offshore structures.

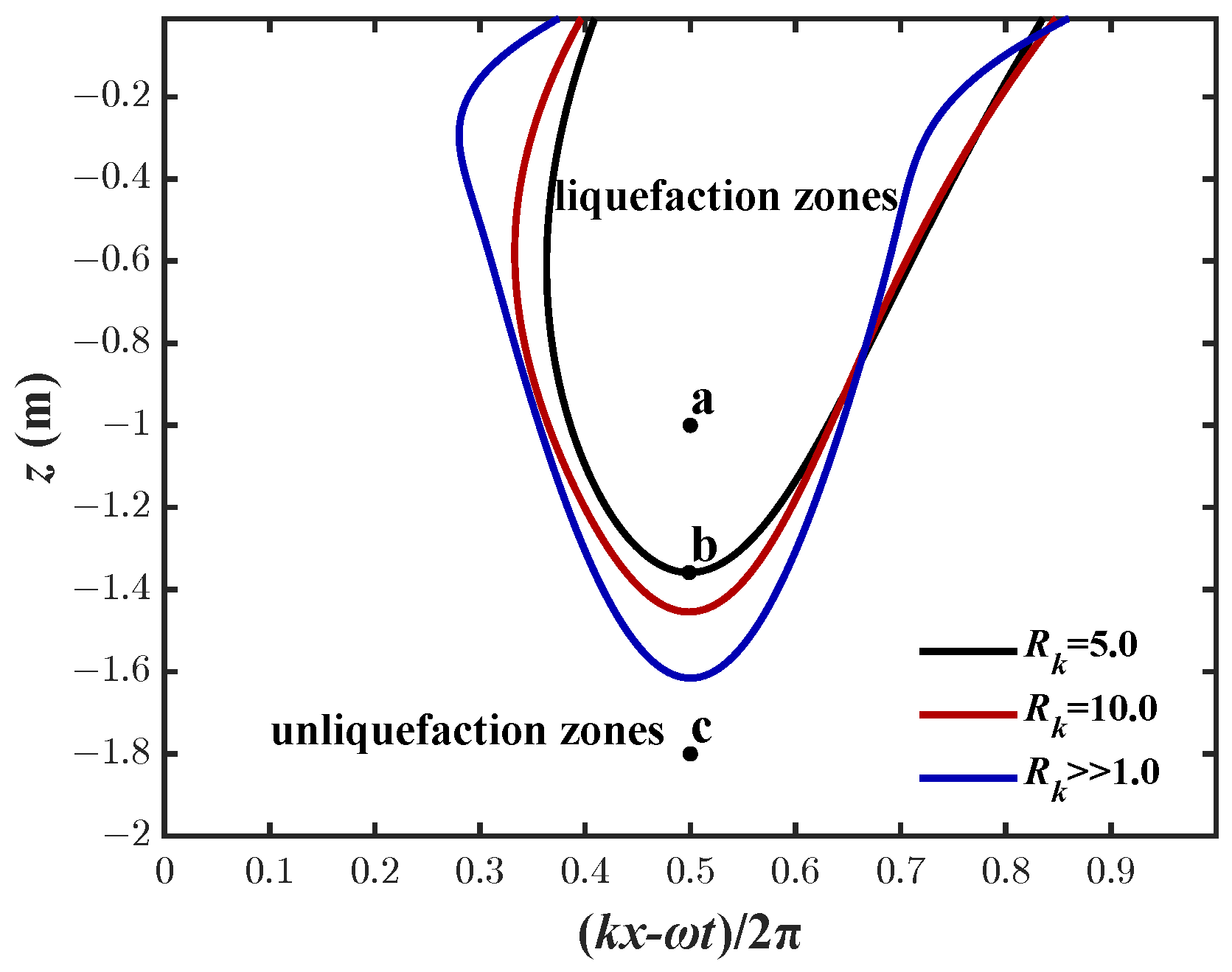
5.1. Liquefaction

In general, when excess pore pressure and the associated upward seepage is greater than the self-weight of the soil column, the seabed will liquefy [6,15]. The instantaneous liquefaction criterion proposed by Zen and Yamazaki [4] is used to evaluate wave-induced liquefaction, that is,

$$-{\displaystyle \frac{1}{3}}({\gamma }_s-{\gamma }_w)(1+2K_0)z\le P-P_w.$$

(109)

where ${\gamma }_s$ is the unit weights of the soil, and is taken as ${\gamma }_s=1.9{\gamma }_w$. $K_0$ is the coefficient of soil pressure at rest. The $K_0$ = 0.5 is commonly used for marine sediments [21].

Then, substituting (31) into (109), we can obtained

$$\begin{array}{cc}\hfill -{\displaystyle \frac{1}{3}}({\gamma }_s-{\gamma }_w)& (1+2K_0)z\le p_0[A_1\cos (kx-\omega t+{\phi }_0)e^{kz}\hfill \\ \hfill & +B_1\cos (kx-\omega t+{\phi }_1+{\xi }_{2}z)e^{{\xi }_{1}z}-\cos (kx-\omega t)].\hfill \end{array}$$

(110)

Figure 28 shows the liquefaction zone in fine sand with different $R_k$. It can be seen that the liquefaction zone presents an asymmetric distribution. Furthermore, the maximum depth of liquefaction increases with increasing $R_k$. Using $R_k=5$ as an example, three different soil depths are taken as follows: $z_a$ = −1.0 m ($z_a/L$ = −0.010), $z_b$ = −1.36 m ($z_b/L$ = −0.014), $z_c$ = −1.8 m ($z_c/L$ = −0.019), as shown in Figure 28. Here, $z_a$ is the depth within the liquefied zone, $z_b$ is at the maximum liquefaction depth, and $z_c$ is a depth in the non-liquefied zone. In the following example, we further examine the phase-lag at these three locations.

Figure 29 illustrates the distribution of wave-induced pore pressure ($P/p_0$) versus wave phase ($(kx-\omega t)/2\pi$) for three depths of the soil ($z_a$, $z_b$ and $z_c$). As shown in Figure 29a, the phase-lag for pore pressure ($\Delta {\theta }_1$) in coarse sand increases with increasing three soil depths. It can be seen from Figure 18a that $\Delta {\theta }_1$ increases with increasing soil depths before $z_c/L$ = −0.019. In fine sand, the phase-lag ($\Delta {\theta }_1$) decreases with increasing three soil depths (see Figure 29b). As shown in Figure 29b, the rang of $z/L$ = −0.006 to −0.013, $\Delta {\theta }_1$ decreases with increasing soil depths when $R_k$ = 5.0. It can be seen from Figure 29b that in the liquefaction zone the phase-lag is positive degrees, while in the unliquefaction zone the phase-lag direction is opposite and the value is smaller than that in the liquefaction zone. After $z/L$ = −0.006, the phase-lag in silt is close to zero, as shown in Figure 18c and Figure 29c.

The wave height has been reported to directly affect the wave-induced liquefaction zone [15]. Figure 30a plots the distribution of the liquefaction zone with various wave height for $R_k=5$, the higher the wave height (H), the larger the liquefaction zone and the greater the maximum liquefaction depth. According to $p_0={\gamma }_{w}H/\left(2\cosh \left(kd\right)\right)$, $p_0$ shows a linear and positive correlation with H. The right of (110) linearly increases with increasing $p_0$, so the zone where the left of (110) is smaller than the right linearly increase. Therefore, the liquefaction zone increases with increasing H. And the liquefaction depth also linearly increases with increasing H.

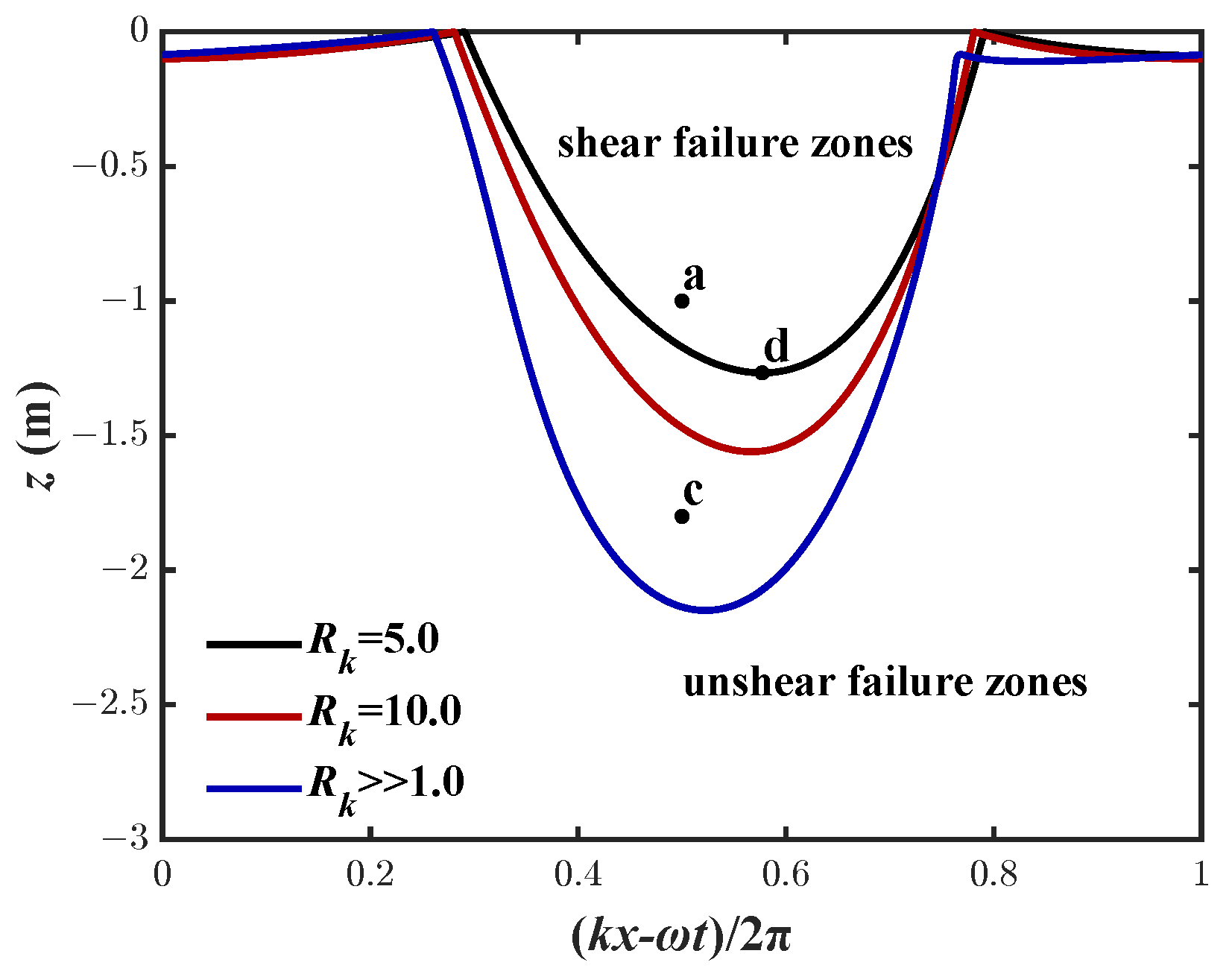
5.2. Shear Failure

For the wave-induced shear failure, Mohr–Coulomb theory has been commonly used [15]. Based on Mohr–Coulomb’s failure criterion, the shear failure criterion proposed by Zen et al. [15] is adopted.

$${\varphi }^{\prime }=\arcsin {\displaystyle \frac{\sqrt{{({\overline{\sigma }}_z^{\prime }-{\overline{\sigma }}_x^{\prime })}^2+4\left({\tau }_{xz}\right)}}{{\overline{\sigma }}_z^{\prime }+{\overline{\sigma }}_x^{\prime }}}\ge {\varphi }_f^{\prime },$$

(111)

where ${\varphi }^{\prime }$ is the stress angle, ${\varphi }_f^{\prime }$ is the internal friction angle of the soil (30–35 degrees for sand), ${\overline{\sigma }}_z^{\prime }$ and ${\overline{\sigma }}_x^{\prime }$ are the total effective stresses in the z- and x- directions, respectively.

$${\overline{\sigma }}_z^{\prime }={\sigma }_{z0}^{\prime }+{\sigma }_z^{\prime },{\overline{\sigma }}_x^{\prime }={\sigma }_{x0}^{\prime }+{\sigma }_x^{\prime },$$

(112)

in which ${\sigma }_{z0}^{\prime }$ and ${\sigma }_{x0}^{\prime }$ are the initial stresses for calm sea conditions without wave action in the z- and x- directions, respectively.

$${\sigma }_{z0}^{\prime }=-({\gamma }_s-{\gamma }_w)z,{\sigma }_{x0}^{\prime }=-K_0({\gamma }_s-{\gamma }_w)z.$$

(113)

Figure 31 presents the shear failure zone for various $R_k$ in coarse sand with ${\varphi }_f^{\prime }$ = 35 degrees. The shear failure zone increases with increasing $R_k$. The maximum shear failure depth $z_d$ = −1.27 m ($z_d/L$ = −0.013) is taken at the shear failure limit at $R_k$ = 5.0. Similarly to the previous analysis, two points $z_a$ and $z_c$ (referring to Figure 28) are selected to represent within and outside the shear failure zones. In addition, $z_d$ represents the point on the shear failure curve. In the following example, the wave-induced stresses at these three points are further examined.

Figure 32 shows the distribution of horizontal effective stress (${\sigma }_x^{\prime }/p_0$) versus wave phase $(kx-\omega t)/2\pi$ for different soils at three points ($z_a$, $z_d$ and $z_c$). It can be observed that when $R_k$ = 5.0, the phase-lag for horizontal effective stresses exhibits a simple pattern of variation at different depths. As shown in Figure 32a, the phase-lag ($\Delta {\theta }_2$) in coarse sand decreases with increasing three soil depths. It can be seen form Figure 21a that $\Delta {\theta }_2$ gradually decreases along the soil depth direction before $z_c/L$ = −0.019. In fine sand, $\Delta {\theta }_2$ increases with increasing three soil depths, as shown in Figure 32b. It can be seen from Figure 21b that $\Delta {\theta }_2$ increases with increasing soil depths after $z/L$ = −0.003. As shown in Figure 21c, $\Delta {\theta }_2$ is close to 180 degrees after $z/L$ = −0.007. Therefore, $\Delta {\theta }_2$ remains constant at 0.5 ($\times 2\pi$) with increasing three soil depth.

Combining Figure 33 and Figure 22, the phase-lag ($\Delta {\theta }_3$) in coarse sand increases with increasing z before $z/L$ = −0.17, so $\Delta {\theta }_3$ increases with increasing three soil depths (see Figure 33a). In fine sand, $\Delta {\theta }_3$ increases with increasing z before $z/L$ = −0.017, and when $z_c/L$ = −0.019, the direction of $\Delta {\theta }_3$ changes and it is close to 180 degrees (see Figure 22b). Therefore, as shown in Figure 33b, the phase-lag ($\Delta {\theta }_3$) is −0.498 ($\times 2\pi$) when $z=z_c$. In silt, it can be seen from Figure 33c that $\Delta {\theta }_3$ is close to 180 degrees after $z/L$ = −0.006. Therefore, the phase-lag ($\Delta {\theta }_3$) is 0.5 ($\times 2\pi$) at three soil depths.

Combining Figure 34 and Figure 23, the phase-lag ($\Delta {\theta }_4$) in coarse sand decreases with increasing z before $z/L$ = −0.08, so $\Delta {\theta }_4$ decreases with increasing three soil depths (see Figure 34a). While $\Delta {\theta }_4$ in fine sand increases with increasing z after $z/L$ = −0.0067 (see Figure 22b). Therefore, as shown in Figure 34b, $\Delta {\theta }_4$ increases with increasing three soil depths. In silt, it can be seen from Figure 23 that the change of $\Delta {\theta }_4$ is slow after $z/L$ = −0.01. So it at the three soil depths is approximately consistent (see Figure 34c).

As shown in Figure 35, the shear failure zone increases with increasing wave height H. And the maximum shear failure soil depth also increases with increasing H. It is noted that the maximum shear failure depth no longer occurs near the wave trough with increasing H, while it shifts to the right.

6. Conclusions

In this paper, the previous analytical solution for the wave-induced soil response in an infinite seabed [16] was re-examined. The explicit forms of the phase-lags for each soil response were derived. Based on the analytical solution, influences of the phase-lag effects of $R_k$ (relative stiffness of the soil skeleton and pore fluid) on wave-induced soil response are examined through a parametric study. The wave-induced liquefaction and shear failure are further clarified with phase-lag effects. Based on numerical examples, the following conclusions can be drawn.

• When the seabed is completely saturated, there are no phase-lags for wave-induced pore pressure and horizontal effective stress. However, the phase-lags for vertical effective stress and z-displacement are 180 degrees, and the phase-lags for shear stress and x-displacement are −90 degrees.
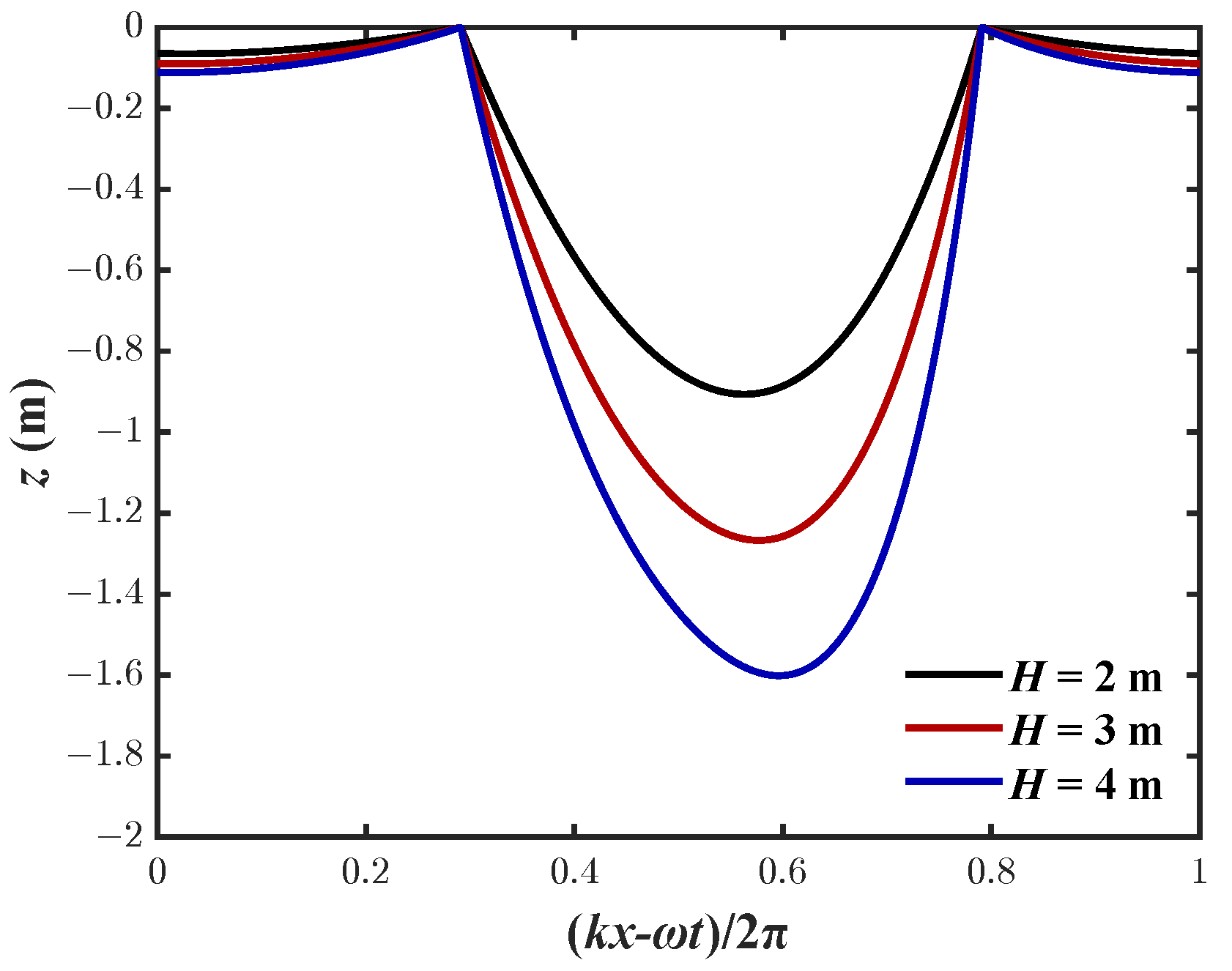
• The instantaneous liquefaction zone and shear failure zone increase with increasing $R_k$. In addition, the liquefaction zone and the maximum liquefaction depth, as well as the shear failure zone and the maximum shear failure depth. Both increase with increasing wave height H.
• The phase-lag for wave-induced pore pressure increases with increasing $R_k$. In contrast, the extreme phase delay for horizontal effective stress and shear stress decreases with increasing $R_k$.
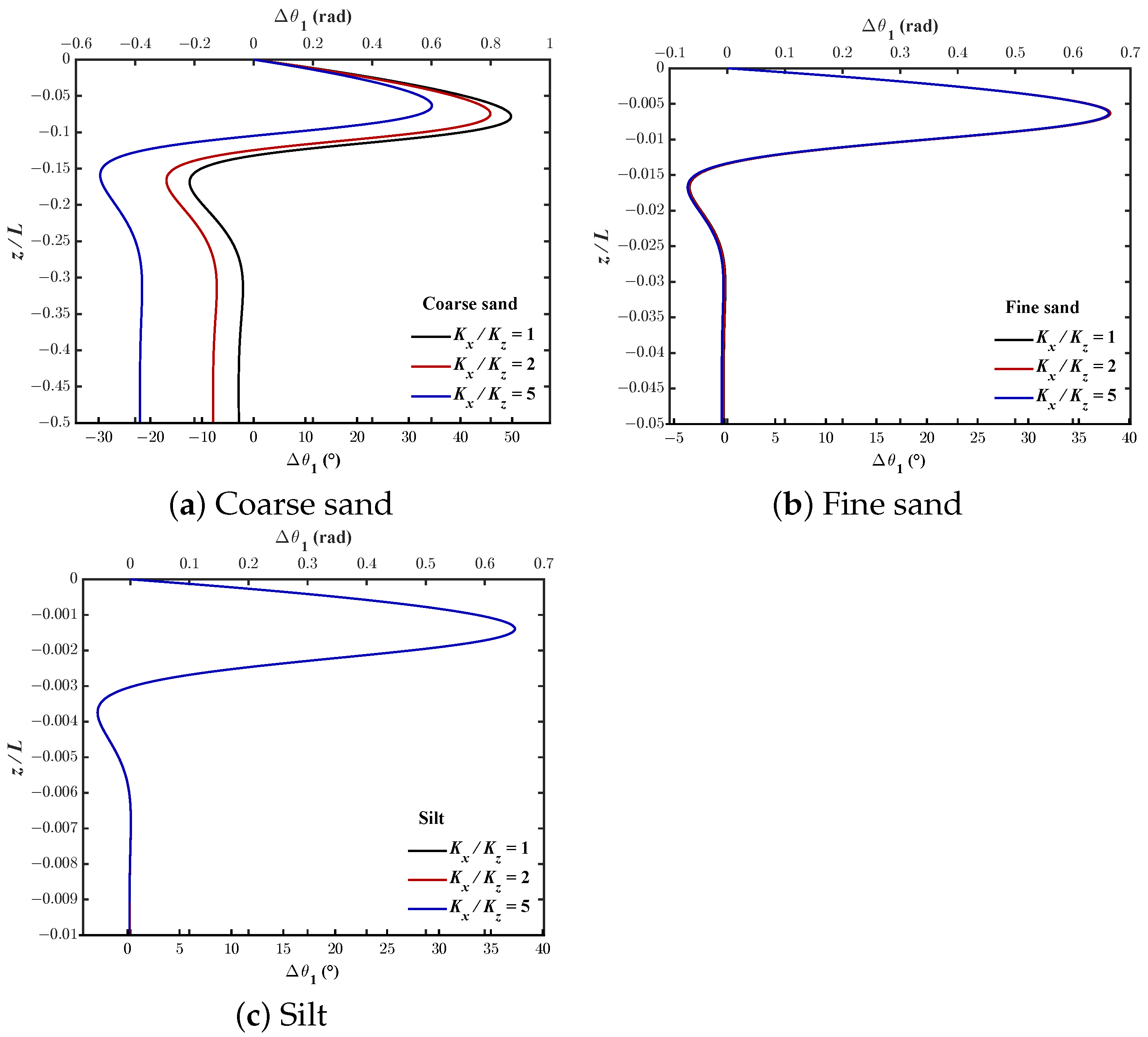
• When $K_x\ne K_Z$, in fine sand and silt, $K_x/K_z$ has almost no influence on phase-lag. In coarse sand, the phase-lag for wave-induced pore pressure and shear stress decreases with increasing $K_x/K_z$, while the phase-lag for effective normal stresses is opposite.
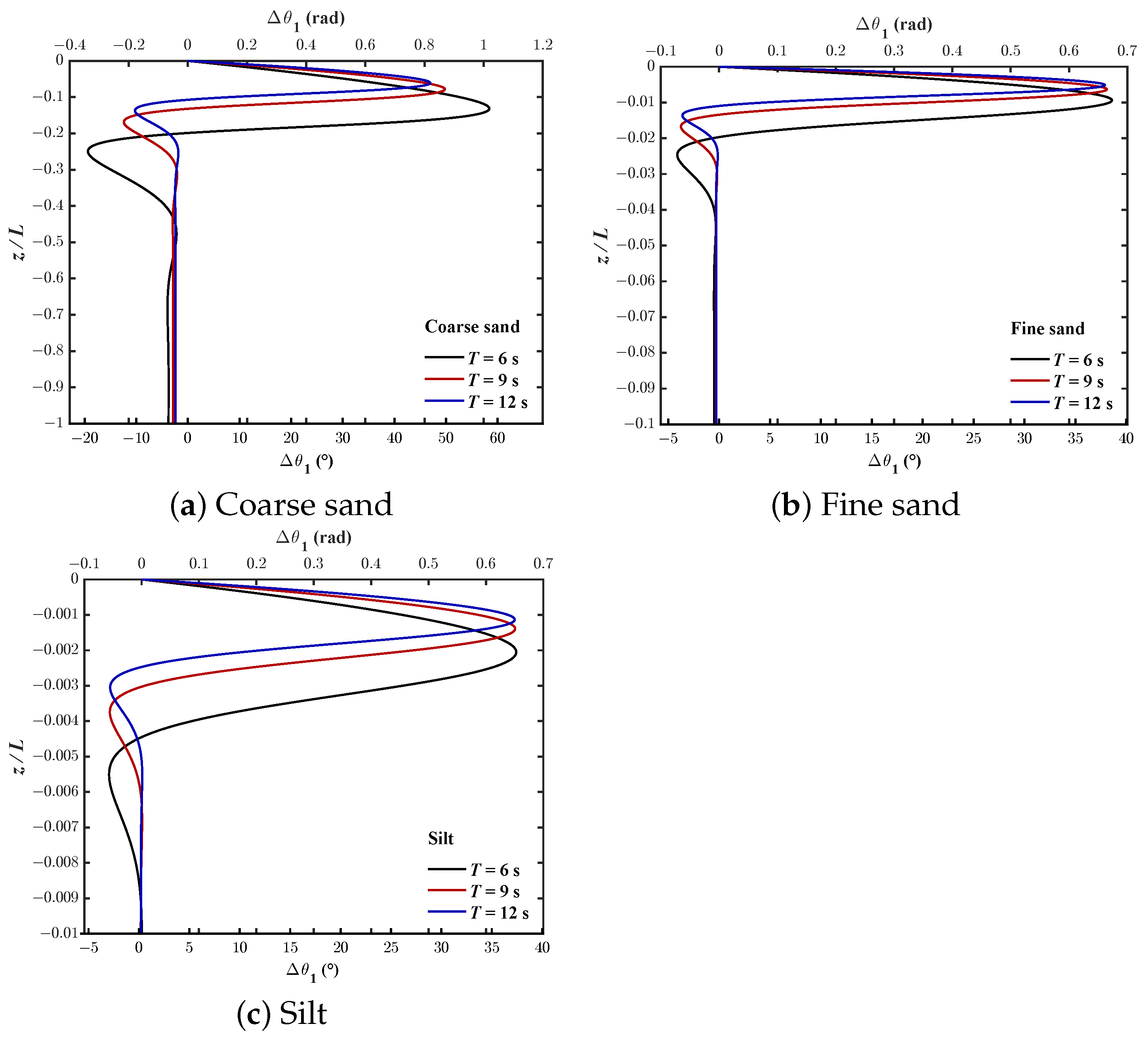
• The phase-lag for wave-induced pore pressure and shear stress decreases with increasing T, while the phase-lag for effective normal stresses is opposite. Moreover, the shorter the wave period, the deeper the soil depth affected by the phase-lag.

In this paper, only ocean waves propagating over an infinite seabed was considered, based on linear poroelastic theory. For a seabed of finite thickness and under different environmental loading such as combined wave and current loading, the framework can be extended further in the future.