Effects of Different Solid–Liquid Parameters on Flow Characteristics and Performance Output of Mineral Extraction Pumps: Analysis and Experimental Validation
Abstract
1. Introduction
2. Basis for Numerical Calculations
2.1. Model Construction
2.2. Numerical Calculation Method
2.2.1. Mesh Generation
2.2.2. Numerical Method
2.2.3. Boundary Conditions
2.2.4. Wear Model Selection
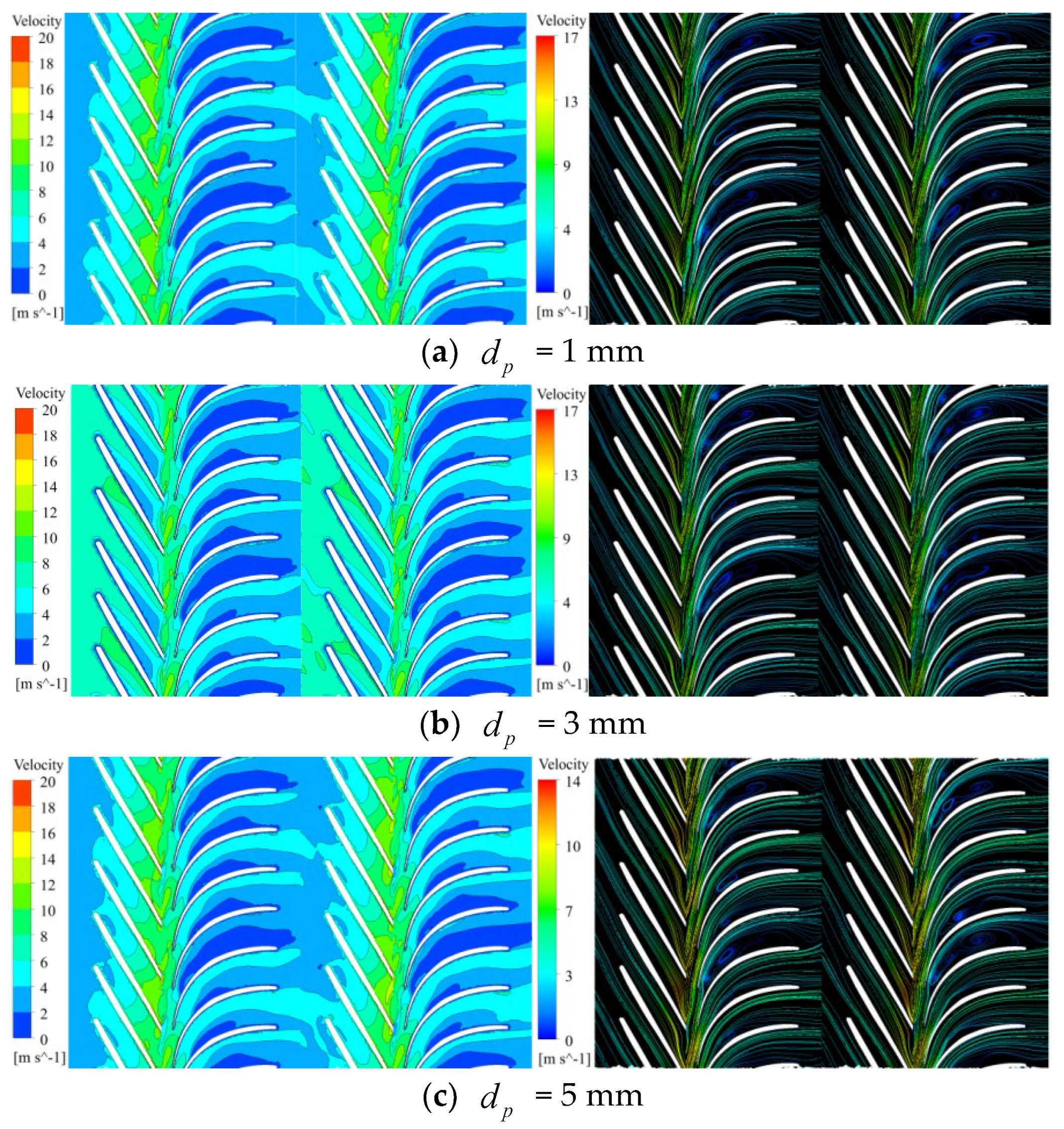
3. Analysis of Internal Flow Characteristics
3.1. Low Flow Rate
3.2. Rated Flow Condition
3.3. High Flow Rate
4. Performance Analysis
4.1. Definition of Head and Efficiency Drop Rates
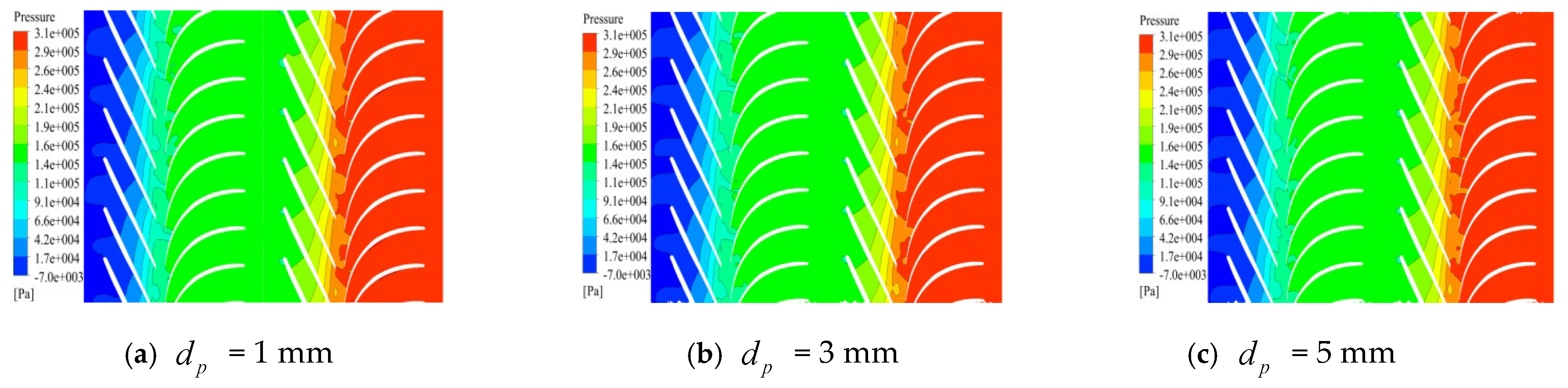
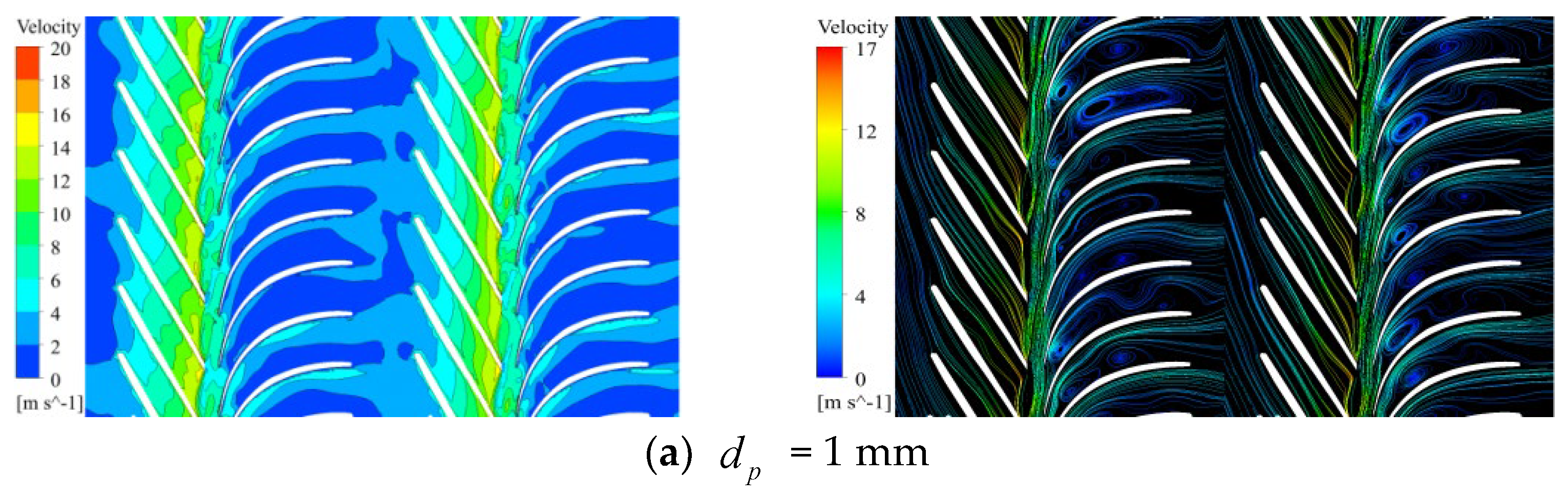
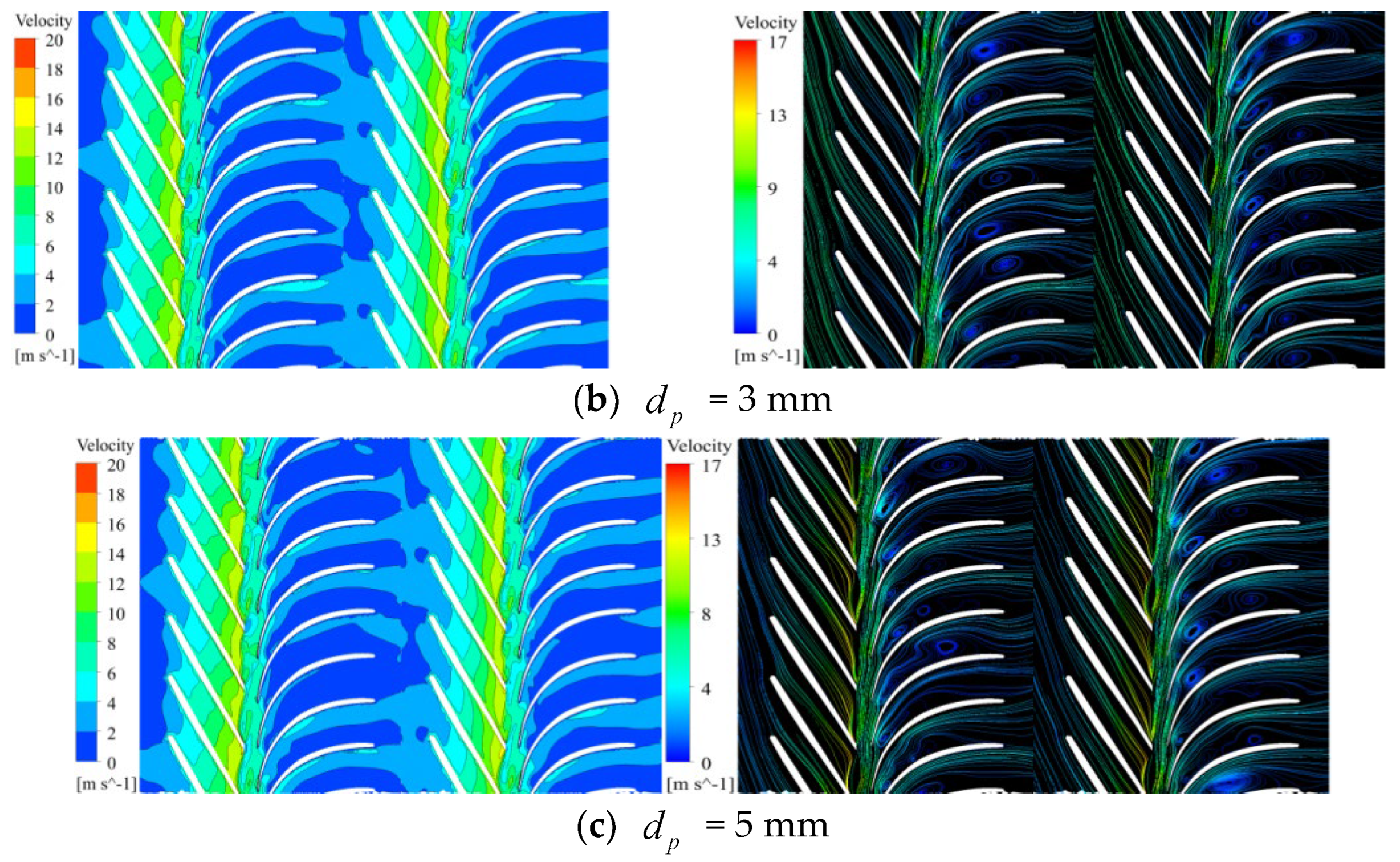
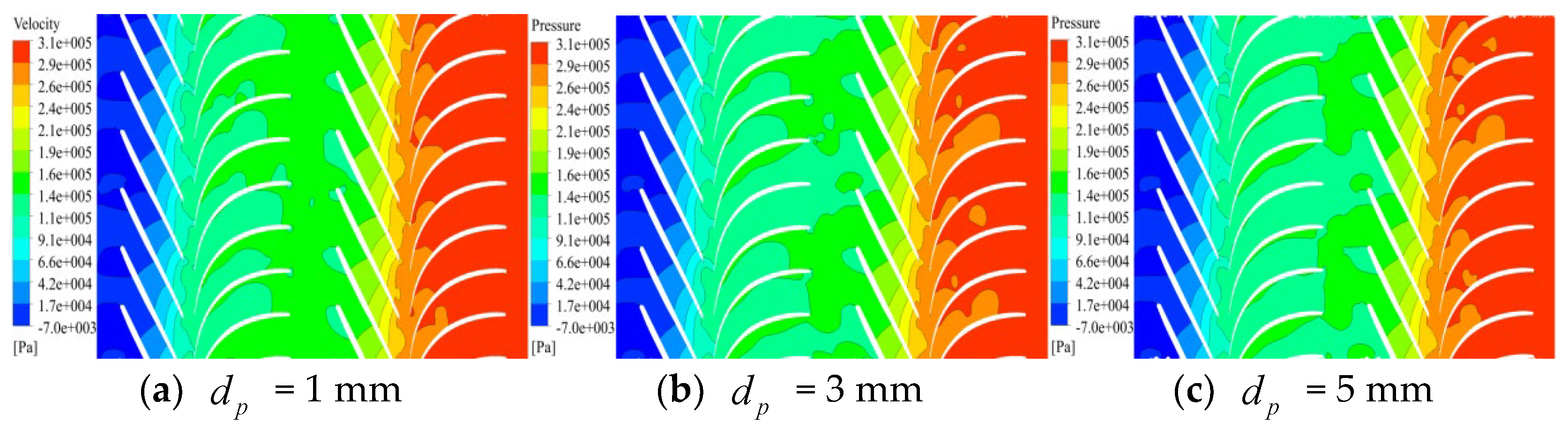
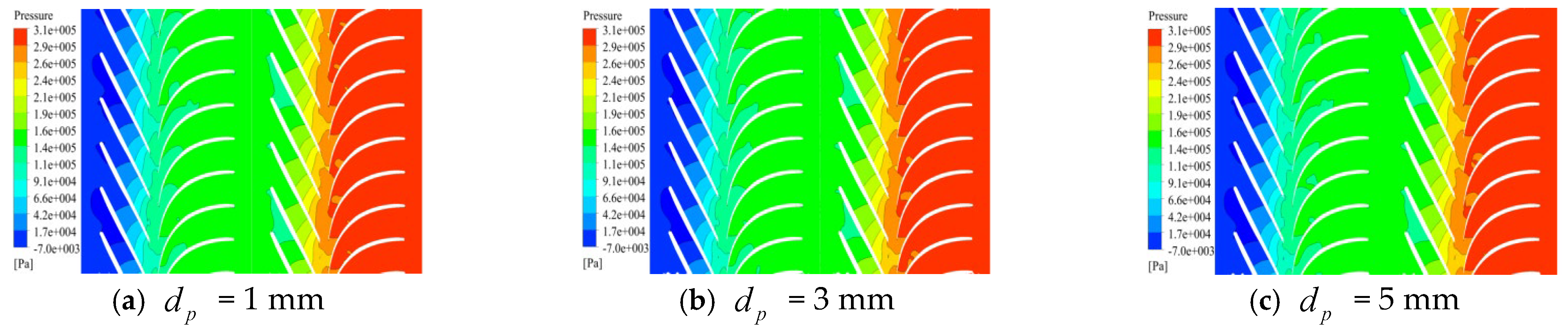
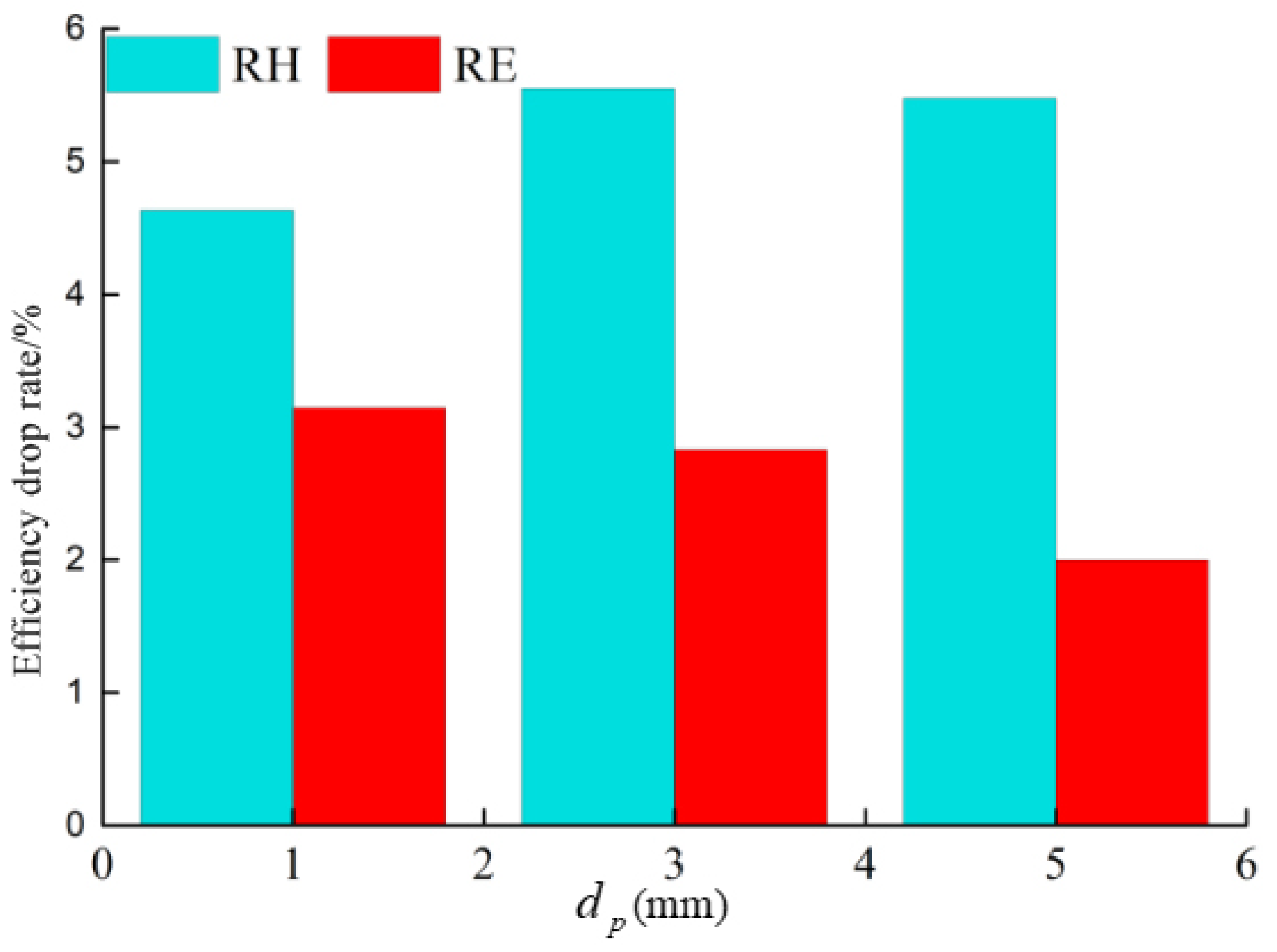
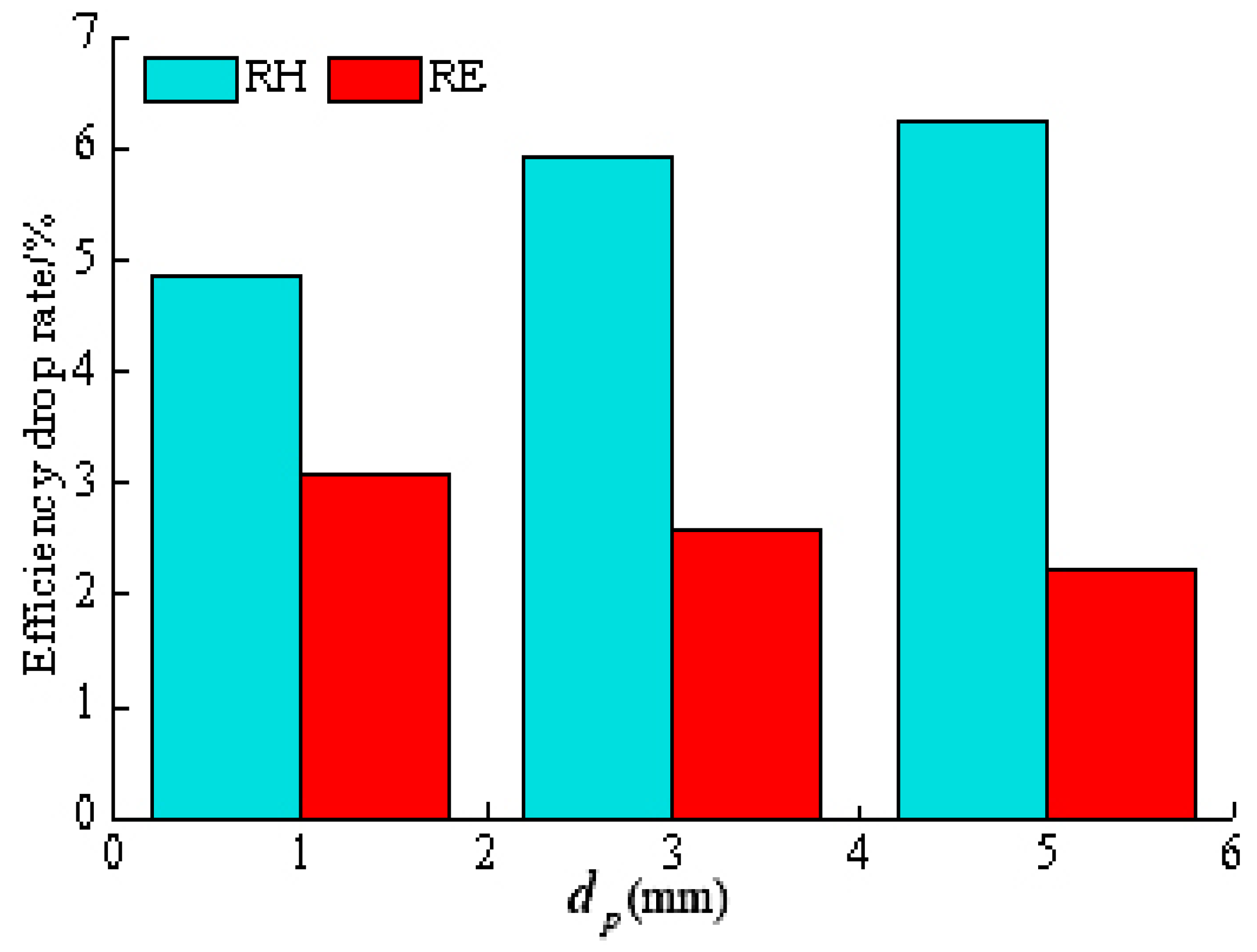
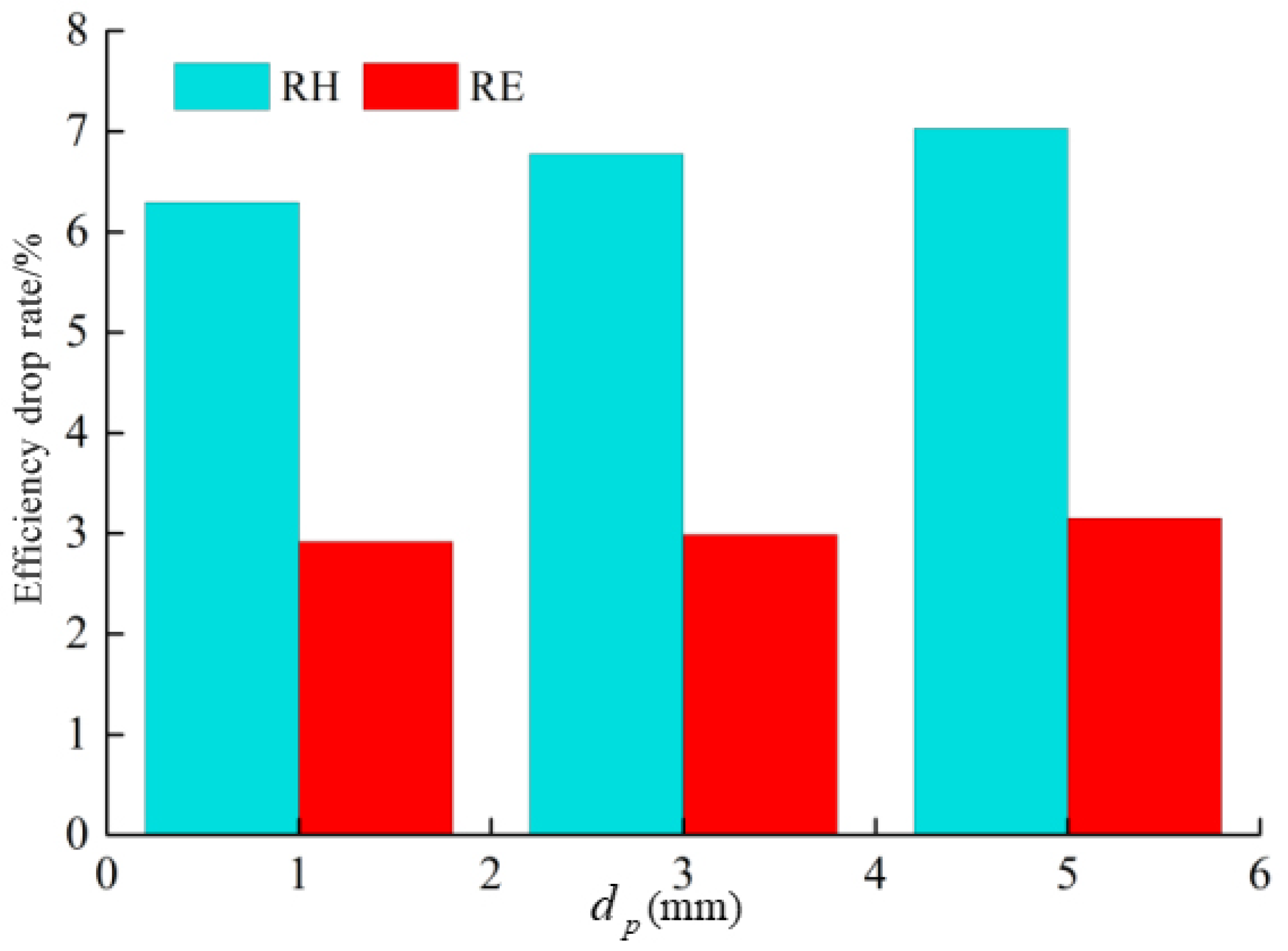
4.2. Effect of Particle Size Under Different Flow Conditions
4.2.1. Low Flow Rate
4.2.2. Rated Flow Condition
4.2.3. High Flow Rate
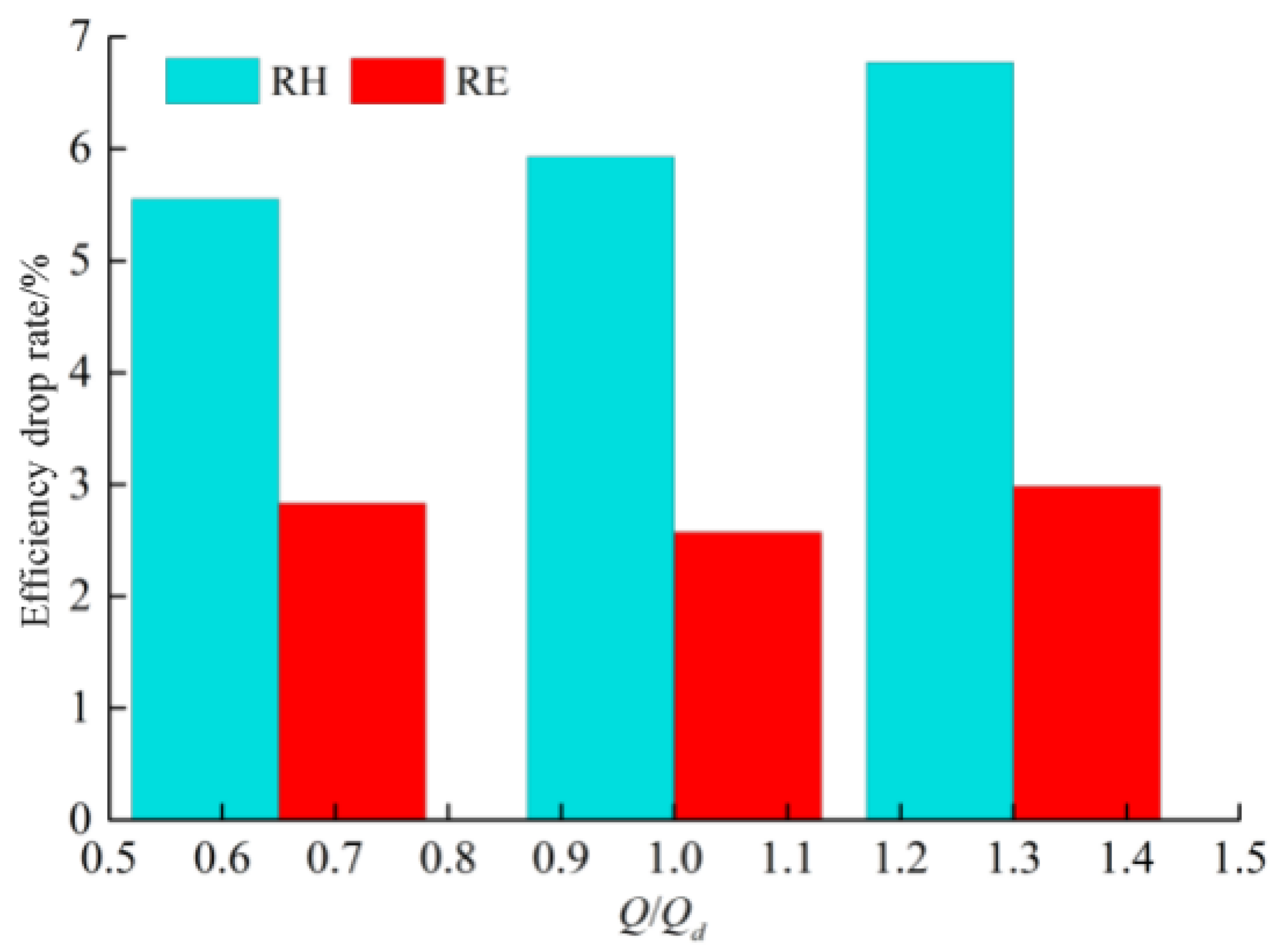
4.2.4. Effects of 3 mm Particles on Pump Wear and Performance Output
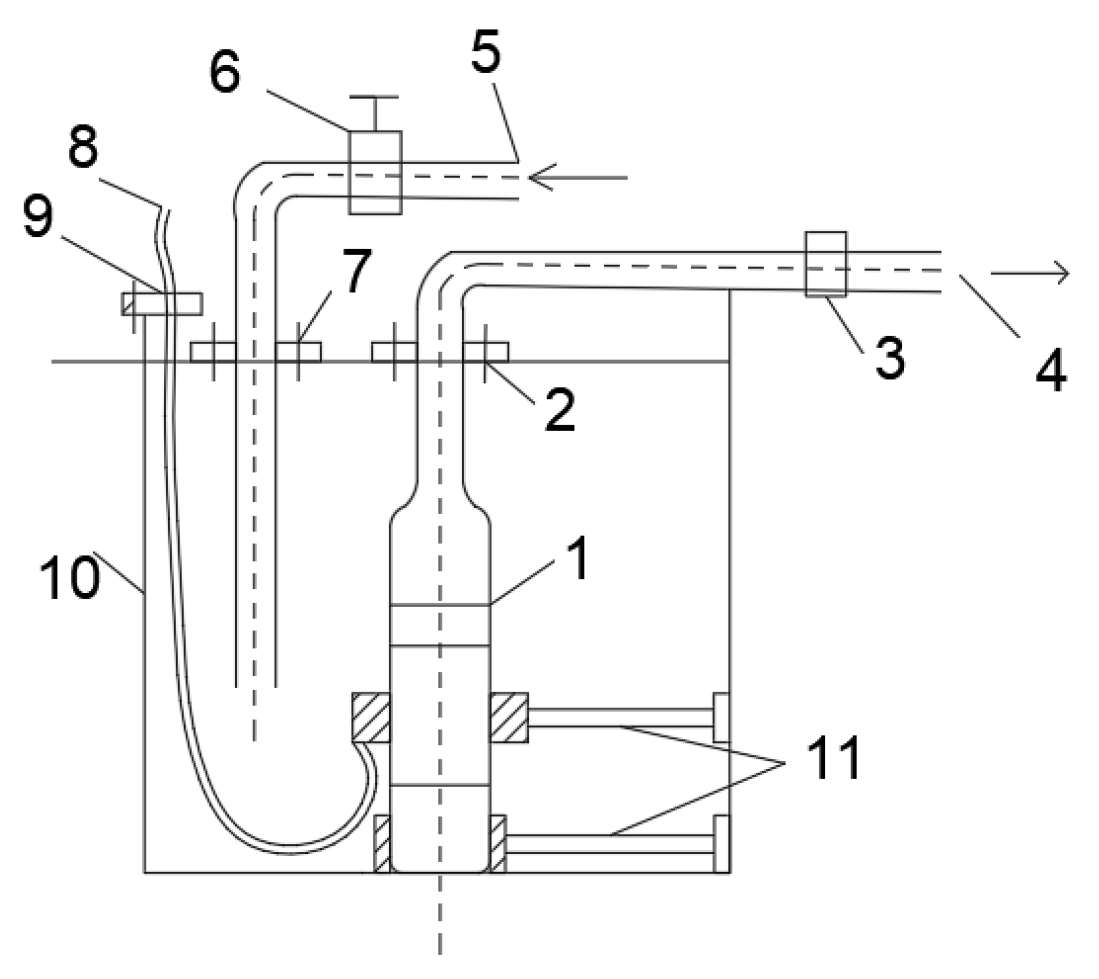
5. Experimental Validation
Experimental Principles
6. Conclusions
- (1)
- According to the numerical calculation results, under the same flow condition, larger particle sizes result in a more pronounced disturbance effect on the liquid phase, leading to an expansion of the vortex region within the mining pump.
- (2)
- According to the numerical calculation results, under the low flow rate condition, an increase in particle size leads to varying degrees of performance degradation in the mining pump. Under the rated flow condition, the particle size is positively correlated with the pump head drop rate and negatively correlated with the efficiency drop rate. Under the high flow rate condition, the particle size is positively correlated with the head drop rate but has a small impact on efficiency.
- (3)
- According to the experimental validation results, the numerical calculation method employed in this study for analyzing the flow characteristics, performance output, and wear characteristics of small-scale pumps is reasonable and effective. The small-scale pump was developed as a scaled-down model based on a prototype deep-sea mining pump. This method can be applied to the prototype deep-sea mining pump, thus further expanding the methodologies for the numerical analysis of deep-sea mineral extraction pumps.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ji, L.L.; He, X.R.; Li, W.; Tian, F.; Shi, W.D.; Zhou, L.; Liu, Z.B.; Yang, Y.; Xiao, C.; Agarwal, R. Research progress of advanced design method, numerical simulation, and experimental technology of pumps in deep-sea resource exploitation. Water 2024, 16, 1881. [Google Scholar] [CrossRef]
- Liu, S.J.; Liu, C.; Dai, Y. Status and progress on researches and developments of deep ocean mining equipments. J. Mech. Eng. 2014, 50, 8–18. [Google Scholar] [CrossRef]
- Yu, H.Y.; Liu, S.J. Dynamics of vertical pipe in deep-ocean mining system. J. Cent. South Univ. Technol. 2007, 14, 552–556. [Google Scholar] [CrossRef]
- Kumar, D.; Amudha, K.; Gopakumar, K.; Ramadass, G.A. Air-lift pump systems for vertical solid particle transport: A comprehensive review and deep sea mining potential. Ocean Eng. 2024, 297, 116928. [Google Scholar] [CrossRef]
- Wang, R.K.; Zhu, Z.C.; Su, X.H.; Tang, D.S.; Jin, X.; Gruszczynski, M. Influence on the solid-liquid two-phase flow from cross-section area of slurry pumps for deep-sea mining. China Ocean Eng. 2022, 36, 439–450. [Google Scholar] [CrossRef]
- Zhu, Z.; Lv, Y.; Su, X.; Zhang, J.; Wang, R.; Lu, W.; Sun, J. Balance of Efficiency and Security-influence on Slurry Transport from the Diffusion of Flow Passages of a Deep-sea Mining Pump. J. Appl. Fluid Mech. 2023, 16, 1690–1703. [Google Scholar]
- Li, Y.W. CFD-DEM analysis of internal flow characteristics in multistage deep-sea mining pumps. Ships Offshore Struct. 2024, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Liu, D.X.; Cui, B.L.; Lin, Z.; Zheng, Y.H.; Ishnazarov, O. Studying particle transport characteristics in centrifugal pumps under external vibration using CFD-DEM simulation. Ocean Eng. 2024, 301, 117538. [Google Scholar] [CrossRef]
- Zhu, Z.C.; Sun, J.B.; Lin, Z.; Jin, Y.J.; Li, Y. Characterization of the ellipsoidal particle motion in a two-stage lifting pump using CFD-DEM method. Comput. Part. Mech. 2024, 1–16. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Tan, M.G.; Wu, X.F.; Liu, H.L.; Shao, C.; Qu, B. The effect of particle size on the reflux performance of the lifting pumps. Comput. Part. Mech. 2024, 11, 1837–1847. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J.C.; Lin, Z.; Zhang, G.; Gao, Z.J.; Ishnazarov, O. Liquid-solid two-phase flow and wear characteristics in a two-stage mixed-transport pump. J. Mech. Sci. Technol. 2024, 38, 4187–4197. [Google Scholar] [CrossRef]
- Chen, J.L.; Chen, X.; Li, W.J.; Zheng, Y.H.; Li, Y. Research on two-phase flow and wear of inlet pipe induced by fluid prewhirl in a centrifugal pump. J. Mar. Sci. Eng. 2024, 12, 950. [Google Scholar] [CrossRef]
- Deng, L.W.; Lu, H.N.; Liu, S.J.; Hu, Q.; Yang, J.M.; Kang, Y.J.; Sun, P.F. Particle anti-accumulation design at impeller suction of deep-sea mining pump and evaluation by CFD-DEM simulation. Ocean Eng. 2023, 279, 114598. [Google Scholar] [CrossRef]
- Lv, Y.; Su, X.; Yang, H.; Zhang, J.; Wang, R.; Zhu, Z. Velocity slip in a deep-sea slurry pump and its effect on particle transportation. J. Appl. Fluid Mech. 2023, 16, 1654–1665. [Google Scholar]
- Hu, Q.; Chen, J.; Deng, L.W.; Kang, Y.J.; Liu, S.J. CFD-DEM simulation of backflow blockage of deep-sea multistage pump. J. Mar. Sci. Eng. 2021, 9, 987. [Google Scholar] [CrossRef]
- Wang, P.K.; Guan, Y.J.; Jin, X.; Tang, Z.J.; Zhu, Z.C.; Su, X.H. Impact of particle sizes on flow characteristics of slurry pump for deep-sea mining. Shock Vib. 2021, 2021, 6684944. [Google Scholar] [CrossRef]
- Deng, L.W.; Hu, Q.; Chen, J.; Kang, Y.J.; Liu, S.J. Particle distribution and motion in six-stage centrifugal pump by means of slurry experiment and CFD-DEM simulation. J. Mar. Sci. Eng. 2021, 9, 716. [Google Scholar] [CrossRef]
- Hu, Q.; Zou, L.; Lv, T.; Guan, Y.J.; Sun, T.Z. Experimental and numerical investigation on the transport characteristics of Particle-Fluid Mixture in Y-Shaped Elbow. J. Mar. Sci. Eng. 2020, 8, 675. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Hu, X. Research on reflux in deep-sea mining pump based on DEM-CFD. Mar. Georesour. Geotechnol. 2019, 38, 744–752. [Google Scholar]
- Cheng, Z.M.; Liu, H.L.; Zhang, R.J.; Kim, H.B.; Dong, L.; Wang, X.L.; Zhou, R.Z. Energy characteristics of a deep-sea mining pump under solid-phase interaction. Ocean Eng. 2024, 311, 118835. [Google Scholar] [CrossRef]
- Xie, B.Q.; Cheng, Y.R.; Tang, P.; Wang, T.; Ma, W.B. Energy loss of deep-sea mining pump for polymetallic nodule particles transport based on entropy production method. Powder Technol. 2024, 445, 120080. [Google Scholar] [CrossRef]
- Hu, J.; Jin, G.Q.; Zou, L.; Yu, Z.B.; Dong, X.L.; Qian, H.Y. Solid-liquid two-phase flow characteristics considering nonspherical mineral particles in deep-sea mining systems. Ocean Eng. 2025, 320, 120323. [Google Scholar] [CrossRef]
- Jin, Y.Z.; Cai, Z.X.; Cui, J.Y. The characteristics of coarse particle solid-liquid two-phase flow and wear properties in deep-sea multistage mining pumps. Phys. Fluids 2025, 37, 013339. [Google Scholar] [CrossRef]
- Hu, Q.; Zhai, X.Y.; Li, Z.F. Multi-objective optimization of deep-sea mining pump based on CFD, GABP Neural Network and NSGA-III algorithm. J. Mar. Sci. Eng. 2022, 10, 1063. [Google Scholar] [CrossRef]
- Xu, H.L.; Chen, W.; Li, L.; Yang, F.Q. Morphology of deep-sea mining hydraulic conveying pipeline and its influencing laws in marine dynamic environment. J. Cent. South Univ. 2023, 30, 3790–3807. [Google Scholar] [CrossRef]
- Zhu, X.M.; Sun, L.P.; Li, B. Dynamic analysis of vessel/riser/equipment system for deep-sea mining with RBF neural network approximations. Mar. Georesour. Geotechnol. 2020, 38, 174–192. [Google Scholar] [CrossRef]
- Chen, Y.X.; Xiong, H.; Cheng, H.; Yu, C.L.; Xie, J.H. Effect of particle motion on the hydraulic collection of coarse spherical particles. Acta Mech. Sin. 2020, 36, 72–81. [Google Scholar] [CrossRef]
- Adam, N.M.; Attia, O.H.; AI-Sulttani, A.O.; Mahmood, H.A.; As’arry, A.; Rezali, K.A.M. Numerical analysis for solar panel subjected with an external force to overcome adhesive force in desert areas. CFD Lett. 2020, 12, 60–75. [Google Scholar] [CrossRef]
- Zhao, R.J.; Zhao, Y.L.; Zhang, D.S.; Li, Y.; Geng, L.L. Numerical investigation of the characteristics of erosion in a centrifugal pump for transporting dilute particle-laden flows. J. Mar. Sci. Eng. 2021, 9, 961. [Google Scholar] [CrossRef]

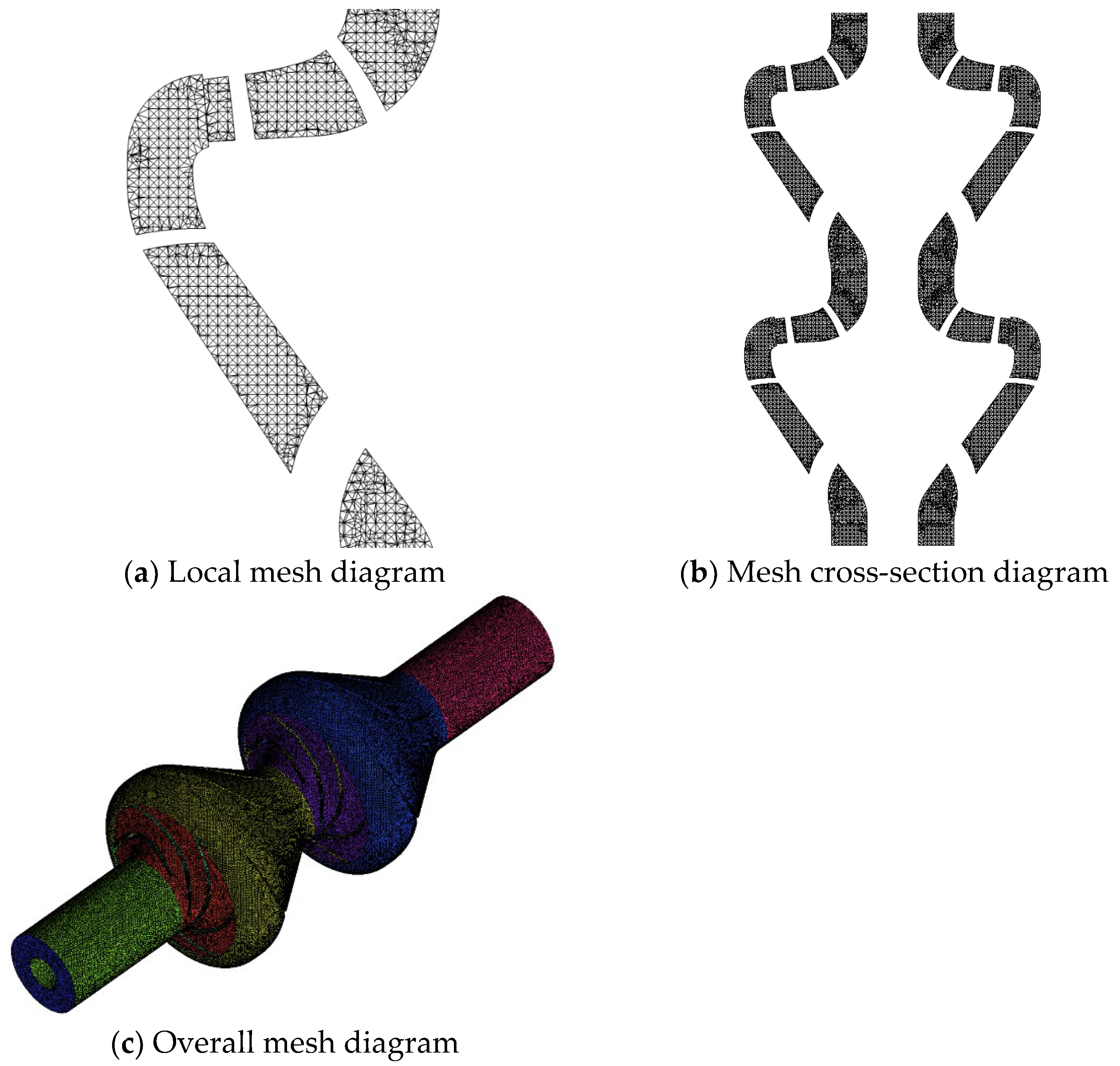




| Mesh Plan | Impeller (Ten Thousand) | Guide Vane (Ten Thousand) | Inlet/Outlet (Ten Thousand) | Total Number (Ten Thousand) | Head (m) |
|---|---|---|---|---|---|
| 1 | 9.1 | 24.9 | 13.2 | 94 | 31.71 |
| 2 | 15.2 | 42.0 | 22.8 | 160 | 30.84 |
| 3 | 20.0 | 55.1 | 29.9 | 210 | 31.22 |
| 4 | 29.1 | 80.2 | 42.9 | 300 | 30.35 |
| 5 | 51.5 | 142 | 76.0 | 530 | 30.36 |
| 6 | 66.0 | 184 | 101 | 700 | 30.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.; Li, Y.; Hu, X.; Yang, Z.; Lei, S.; Wei, P.; Hu, J.; Wang, X. Effects of Different Solid–Liquid Parameters on Flow Characteristics and Performance Output of Mineral Extraction Pumps: Analysis and Experimental Validation. J. Mar. Sci. Eng. 2025, 13, 1218. https://doi.org/10.3390/jmse13071218
Hong S, Li Y, Hu X, Yang Z, Lei S, Wei P, Hu J, Wang X. Effects of Different Solid–Liquid Parameters on Flow Characteristics and Performance Output of Mineral Extraction Pumps: Analysis and Experimental Validation. Journal of Marine Science and Engineering. 2025; 13(7):1218. https://doi.org/10.3390/jmse13071218
Chicago/Turabian StyleHong, Shunjun, Yuanwen Li, Xiaozhou Hu, Zihai Yang, Shaowei Lei, Pengyun Wei, Junhong Hu, and Xingpeng Wang. 2025. "Effects of Different Solid–Liquid Parameters on Flow Characteristics and Performance Output of Mineral Extraction Pumps: Analysis and Experimental Validation" Journal of Marine Science and Engineering 13, no. 7: 1218. https://doi.org/10.3390/jmse13071218
APA StyleHong, S., Li, Y., Hu, X., Yang, Z., Lei, S., Wei, P., Hu, J., & Wang, X. (2025). Effects of Different Solid–Liquid Parameters on Flow Characteristics and Performance Output of Mineral Extraction Pumps: Analysis and Experimental Validation. Journal of Marine Science and Engineering, 13(7), 1218. https://doi.org/10.3390/jmse13071218






