Abstract
Enhancing the safety standards of autonomous ships is a shared objective of all stakeholders involved in the maritime industry. Since the existing hazard analysis work for autonomous ships often exhibits a degree of subjectivity, in the absence of data support, the verification of hazard analysis results has become increasingly challenging. In this study, a formal verification method in a risk-based assessment framework is proposed to verify the hazard analysis results for autonomous ships. To satisfy the characteristics of high time sensitivity, time automata are adopted as a formal language while model checking based on the formal verification tool UPPAAL is used to complete the automatic verification of the liveness of system modeling and correctness of hazard analysis results derived from extended System-Theoretic Process Analysis (STPA) by traversing the finite state space of the system. The effectiveness of the proposed method is demonstrated through a case study involving a remotely controlled ship. The results indicate that the timed automata network model for remotely controlled ships, based on the control structure, has no deadlocks and operates correctly, which demonstrates its practicability and effectiveness. By leveraging the verification of risk analysis results based on model checking, the framework enhances the precision and traceability of these inputs into RBAT. The results disclose the significance of the collaborative work between safety and system engineering in the development of autonomous systems under the definition of human–computer interaction mode transformation. These findings also hold reference value for other intelligent systems with potential hazards.
1. Introduction
In recent years, digitalization and autonomy have become significant topics of discussion within the maritime industry, and they currently exhibit unstoppable rapid growth trends. In the context of new developmental paradigms in shipping safety and global maritime governance, autonomous ships, which are grounded in digitalization and aim at achieving autonomy, have become symbols of the industry’s digital transformation and revolutionary innovation. These vessels are transforming traditional ship design and operations [1,2,3,4]. Despite their advantages in enhancing operational efficiency, reducing human involvement in hazardous and repetitive tasks, and promoting a green shipping infrastructure, there remains a prevalent concern within the industry regarding whether autonomous ships can maintain safety levels comparable to conventional ships.
From the operational perspective, some new operational states and state transition paths of autonomous ships are identified and highlighted in the Draft International Code of Safety for Maritime Autonomous Surface Ships (MASS Code—MSC 109/WP.8) [5]. In order to prevent deviations from the operational envelope (OE), specifically, to address hazards associated with the intended OE and to ensure that autonomous ships can perform various tasks effectively and reliably, the preliminary framework of risk assessment and regulation for autonomous ships has been generated. Risk assessment should include a comprehensive description of the autonomous and remote-control function’s utilization, effectiveness, and reliability by performing a thorough hazard analysis, conducting a mitigation analysis, evaluating the identified risks, and implementing effective risk control measures.
A growing number of studies on the hazard analysis and risk influence factor (RIF) identification of autonomous ships have been published, where the literature and expert scoring are widely used data sources in these research studies [6,7,8]. Due to the variations in researchers’ academic backgrounds and experiences, the outputs of their research focus and RIF identification results are different. In the absence of sufficient autonomous ship navigation data and public accidents, the process of hazard analysis and RIF identification is inevitably influenced by subjectivity. The accuracy of hazard analysis and the priority of RIF have not been addressed. To reduce the influence of subjectivity on risk assessment, it is necessary to verify the conclusions drawn from hazard analysis and RIF identification, thereby improving the accuracy and reliability of risk assessment. Furthermore, verification can find the shortcomings and mistakes in the process of risk assessment and provide feedback for the continuous improvement in risk assessment methods. Although the current research field has achieved certain progress in the area of autonomous ship hazard analysis, so far, the relevant literature and empirical research have failed to demonstrate that the existing results of hazard analysis have been verified.
For this purpose, this study endeavors to pioneer a novel approach to ensure a more objective and efficient hazard analysis process and to produce more reliable hazard analysis results. Through exhaustively searching the system state space, the correctness of the hazard analysis process and results can be verified from a structural point of view. Additionally, given that autonomous ships are large real-time embedded systems with stringent safety requirements, they must not only maintain high safety characteristics but also exercise precise control over time constraints. Timed automata constitute a theoretical framework for the modeling and verification of real-time systems [9,10], which can accurately describe time constraints, effectively handle concurrent behaviors, and support the automated verification process. Therefore, a formal verification approach based on timed automata is proposed to extend the process of modeling, reducing, and verifying autonomous ships. This extended process establishes a timed automata network model through rigorous semantics. The available UPPAAL model checker is used to automatically traverse the finite state space of the system model, checking the satisfaction relation between the semantic model and its property abstractions, thereby filling the gap of automatic verification of hazard analysis results.
As a result, time automata are adopted as a formal language to model the behavior of the system components, while model checking based on UPPAAL is used to verify the unsafe control actions (UCAs) obtained from STPA through the system liveness and reachability of semantics. Compared to existing hazard analysis work, this new method makes it possible to perform automatic verification of the results of hazard analysis and reduces the need for human intervention and supervision simultaneously. Risk-Based Assessment Tool (RBAT) [11], as recommended in the latest draft MASS Code, is designed to support risk assessment in the absence of statistical data and enables the evaluation of safety equivalence in the introduction of technologies with autonomous functionalities. This approach aligns with this principle by systematically identifying unsafe conditions associated with control actions and causal factors that can trigger unsafe conditions in autonomous ship operations [12,13]. Additionally, our study addresses key challenges associated with MASS, in line with the objectives of RBAT, by refining hazard identification and improving risk differentiation across scenarios. Even though the application in this study is focused on autonomous ships, it is expected that the methodology will be relevant to other intelligent systems with inherent potential hazards. The contributions and originalities of this study are evident from four perspectives.
- To propose a three-phase methodological framework to verify hazard analysis results and support risk assessment for autonomous ships.
- To provide a verification technology that satisfies the characteristics of high time sensitivity by introducing model checking based on time automata.
- To model formalism based on the UPPAAL model checker that can automatically verify the results of hazard analysis.
- The implementation of this study achieves the closed-loop hazard analysis of STPA in the risk-based assessment framework. Results disclose the significance of the collaborative work between safety and system engineering in the development of autonomous systems under the definition of human–computer interaction mode transformation.
The remainder of this paper is organized as follows. Section 2 leads through the relevant literature. Section 3 presents the proposed methodological framework, which introduces model checking based on time automata into the hazard analysis process to facilitate the automatic verification of compliance with the property specifications of the constructed system model and hazard analysis results. Section 4 presents an illustrative example of a remotely controlled ship to demonstrate the effectiveness of the model. Section 5 includes the discussion. Section 6 presents the conclusions drawn from this study.
2. Literature Review
Compared to the rapid progress in autonomous technologies, a consistent hazard analysis conclusion in the field of autonomous ships failed to be generated. In order to promote the process in this area, RIF identification is presented from multiple perspectives according to researchers’ respective academic backgrounds. Due to the varying concerns across professional fields, there is notable heterogeneity in RIF identification results. In the field of hazard analysis and risk identification of autonomous ships, Tao et al. [8] utilized a systematic approach to conduct a bibliometric analysis of the autonomous ship studies from January 2010 to November 2022. There are 62 papers retained for a detailed discussion through a manual screening process in terms of the research methods, research subjects, and scope of application. This study retrieves papers additionally from December 2022 to December 2024, yielding 356 results using the same keywords, and 41 papers are retained through the aforementioned screening. Out of 103 papers, 32 representative papers clearly presented the number of identified risk-influencing factors (RIFs) (Appendix A), and the number of RIFs (including the results presented in the form of cases) is visualized, as shown in Figure 1.
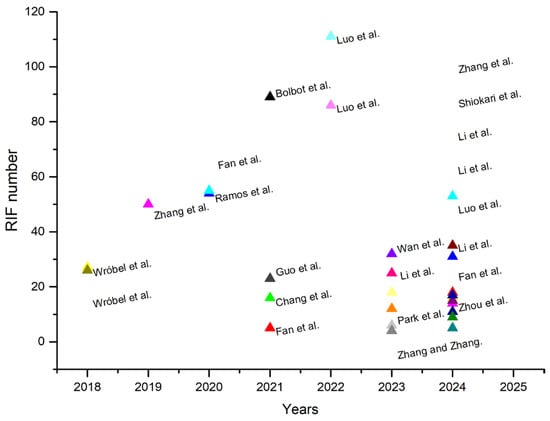
Figure 1.
Representative publications that identified RIFs for autonomous ships.
Fan et al. [14] identified 55 RIFs affecting remote-controlled ships based on the selected literature and on experts’ judgment; similarly, the description of hazards is presented from the same data source [15,16]. Ramos et al. [17] pointed out that a set of performance-influencing factors, which served to either enhance or degrade human performance relative to a baseline, can be obtained from the discussion on the factors from the relevant literature in the shipping industry. Zhang et al. [18] identified 50 RIFs related to shipping safety according to the literature. As the historical data that could be used were limited, expert knowledge was utilized to predict the shipping safety risk probability based on the Bayesian network. Chang et al. [19] identified the main operational hazards of autonomous ships based on a thorough literature review and further ranked them using the Likert scale by a group of experts. Inspired by the literature, expert knowledge and expert scoring have been widely used in hazard analysis research studies of autonomous ships [20,21,22]. However, the expert’s academic background, years of experience, and education can affect the accuracy of the results. There still remains a gap in the study of hazard analysis as insights from multiple perspectives are solely obtained using expert questionnaires.
Bolbot et al. [23] pointed out that considerable uncertainty was observed during expert scoring, and more detailed analyses are required to verify these cost results. Some studies have addressed automatic verification in other domains to reduce the dependence on subjectivity. A hazard identification method based on hierarchical Colored Petri Nets (CPNs) can achieve higher comprehensiveness and effectiveness in hazard identification for complex systems, reduce dependence on expert experience, and standardize the hazard identification process [24,25]. In order to reduce the influence of subjectivity, some automation methods are applied in combination with System-Theoretic Process Analysis (STPA). Yan et al. [26] proposed an automated accident causal scenario identification method for Fully Automatic Operation (FAO) systems based on STPA, which systematically identifies and analyzes potential accident causal scenarios within FAO systems. Causal scenario search rules have been developed to ensure the automatic identification of accident causal scenarios. This method mitigates the subjectivity and inconsistency inherent to manual analysis, thereby enhancing the efficiency and accuracy of accident causal scenario identification. Zhu et al. [27] integrated System-Theoretic Accident Modeling and Process (STAMP) with Control Logical Petri Net (CLPN) to obtain a comprehensive framework for eliciting component-interaction-related safety requirements, particularly focusing on interactions within the control process. This framework offers a standardized and systematic approach for safety requirement elicitation in complex systems, such as automotive systems and train control systems. Inspired by the above, the research needs to focus on the automation and standardization of the hazard analysis approach across the maritime community.
In order to identify or quantify risk factors, researchers sometimes use traditional ship accident reports. Valdez Banda et al. [28] created the existing frameworks for autonomous ship risk analysis by utilizing accident statistics in the European maritime context. Hwang and Youn [29] developed a methodology for the systematic verification of autonomous ship collision avoidance systems by analyzing collision risk situations extracted from the AIS data. Aiding to achieve the human-centered risk analysis for autonomous ships, Fan et al. [30] extracted the frequency and impact of RIFs from historical accident data into a graph-based model. The accident data were obtained from the Marine Accident Investigation Branch (MAIB), the Transportation Safety Board of Canada (TSB), and the Global Integrated Shipping Information System (GISIS). However, no accident data of autonomous ships has been made public so far, and they may not always conform with the actual situation as the traditional ship accident data are transformed into accident data that match autonomous ships [31]. Therefore, a novel approach should be urgently deployed to verify the results of the hazard analysis of autonomous ships.
Currently, autonomous ships are still in the stages of design, testing, and validation. There has not been any accident with autonomous ships disclosed so far; thus, there is a lack of statistical data for risk modeling. Accident information and monitoring data from conventional ships are difficult to directly apply to autonomous ships, which is one of the main challenges in autonomous ship safety and risk research. On the other hand, the introduction of complex software and algorithms, along with the changes in human–system role allocation, has altered the human–machine interaction patterns, thereby changing the composition of risks in autonomous ships. New risks are more related to software control and human–machine interactions, making traditional methods focused on hardware failure analysis less effective. Against this backdrop, a structured approach to risk assessment that goes beyond traditional hardware failure analysis is essential to deepen the understanding of autonomous ship safety. Specifically, performing hazard analysis in conjunction with evaluating the severity of worst-case outcomes from unexpected events and the effectiveness of mitigation measures aimed at loss prevention offers a more robust framework for assessing the safety of autonomous ships.
Although System-Theoretic Process Analysis (STPA) is a recommended hazard analysis method in the draft MASS Code, current research and practice show that the hazard analysis work for autonomous ships has not yet developed an effective verification mechanism to ensure the accuracy and reliability of the analysis results. Moreover, based on the literature review, the existing hazard analysis work for autonomous ships often exhibits a degree of subjectivity, which can result in obvious limitations of manual verification. The subjective judgments of experts may further introduce biases, and the manual verification process is time-consuming and costly, making it difficult to adapt to the reality of the rapid development and increasing complexity of autonomous ships. Therefore, to ensure a more scientific and rigorous hazard analysis process and generate more objective and reliable hazard analysis results, the foremost problem is that it is necessary to develop a verification method for hazard analysis results applicable to autonomous ships.
Verification technology mostly focuses on hardware acceleration, dynamic simulation, and virtual prototype platforms; however, they are difficult to apply directly to autonomous ships. To deal with the complexity resulting from the large number of functionalities under consideration, formal methods have been proven to be more effective means [32,33]. Formal methods refer to software and system development approaches that are based on strict mathematical foundations, supporting activities such as the specification, design, verification, and evolution of software and systems, including model-oriented formal methods and property-oriented formal methods. Incorporating them into the hazard analysis process can be regarded as a way to address this challenge. Johansen et al. [33] systematically tested and verified the performance of autonomous ship control systems under different environmental conditions by using a formal verification method based on temporal logic and Gaussian processes. Wang et al. [34] proposed a verification approach by using the NuSMV to verify the results of STPA. The proposed method based on model checking can automatically evaluate whether the IMA model meets safety requirements, and the drawn conclusions have been proven to be more accurate and complete than those obtained with traditional methods.
Model checking emerged as a popular automated formal verification technique [35] that is used to verify critical properties such as security [36], fairness [37], and reachability [32]. The core of model checking is the traversal strategy and algorithm for the finite state space, that is, through an explicit or implicit exhaustive search of all reachable states and behaviors in a given system or model. The automated verification of hazard analysis results can be achieved through the verification of safety, liveness, and reachability properties [38]. Therefore, the formal verification method based on model checking can effectively fill the knowledge gap. At present, although the technology has not been widely used in maritime research, especially for autonomous ships, its potential value and application prospects cannot be ignored.
3. Methodology
3.1. STPA-Based Analysis Method That Synthesizes Safety and Security (STPA-SynSS)
STPA is a novel hazard analysis tool based on STAMP, and it can be used at any stage of the system lifecycle to ensure safety by enforcing constraints on system behavior. According to Leveson [39,40], who developed this method, system safety is considered an emergent property of the system, controlled by imposing constraints on the behavior of individual components and their interactions. In this approach, system safety is preserved or strengthened by applying safety constraints to the behavior of components and their interactions. Once safety constraints are met, system safety can be ensured. Compared to traditional hazard analysis tools, STPA shifts its focus from preventing failures or malfunctions to constraining unsafe control actions in the system.
Existing research indicates that STPA has gained popularity and has become one of the most promising and forward-looking hazard analysis methods currently applicable to autonomous ships [8,28,41,42,43]. However, compared to conventional ships, autonomous ships, as representatives of complex, safety-critical cyber–physical systems (CPSs), exhibit significantly increased interactive complexity, dynamic complexity, decomposition complexity, and nonlinear complexity. The dynamic shifts in autonomy levels and changes in ship control modalities have triggered new safety requirements. Where cybersecurity threats and intentional disruptions can pose significant risks, their safety and security are receiving considerable attention in the industry.
Consequently, in our preliminary research [44], a new STPA-based analysis method was proposed that synthesizes safety and security (STPA-SynSS) to address the interdependencies between safety and security, thereby reducing the number of iterations that could be triggered by conflicts in requirements within parallel approaches. Relative to the original STPA method, STPA-SynSS encompasses the full hazard analysis process and introduces six enhancements, focusing on key issues for preventing system losses in aspects of system design that may cause vulnerability and unacceptable losses.
Although STPA-SynSS has been somewhat validated in terms of feasibility and effectiveness [45,46,47], its modeling and analysis still rely largely on manual deduction, and the accuracy and completeness of the hazard analysis results are greatly reliant on the experience and skills of the analysts. Therefore, verifying the correctness of hazard analysis results is crucial, and the challenges associated with the rationality of outputs from STPA and its expanded methods must be overcome.
3.2. Model Checking Based on Timed Automata
In formal methods, model checking is an automated verification technique that involves automatically traversing the finite state space of the system model under verification to check if the system’s behavior possesses the anticipated properties [48,49]. In complex transition systems, it can quickly produce testing results and identify and correct minor errors. The core of model checking is the traversal strategies and algorithms over a finite state space, involving an explicit or implicit exhaustive search of all reachable states and behaviors reflected in the given system or model. The model-checking method can generally be divided into the following three basic steps.
- Modeling: Initially, a formalized description method is chosen to transform the actual system to be verified into a format compatible with model-checking tools. Typically, finite state models, such as transition systems, finite automata, and Petri Nets, are used for modeling the system, resulting in system model M. During the modeling process, due to limitations in verification time and computer memory, abstraction techniques are necessary to simplify irrelevant or unimportant details to avoid state explosion.
- Specification: Prior to verification, the properties that the system must possess need to be described, usually expressed through temporal logic formulas, leading to property specifications φ, such as system safety and system liveness.
- Verification: A model-checking algorithm (tool) is developed that uses an exhaustive search of the state space for the formal verification of systems. Inputs for the algorithm consist of the model M of the system to be verified and the property specification φ to be checked. Upon the completion of verification, if no states are found that violate the property specification, this signifies that system model M complies with property specification φ. If system model M does not meet property specification φ, the model checking algorithm outputs a counterexample path demonstrating the system behavior that fails to meet the specification, thus clarifying why M fails to satisfy φ.
The model-checking algorithm primarily operates by traversing the state space to verify whether the property specifications are met within the system model. Given that autonomous ships are large-scale, real-time embedded systems with significant safety demands, they must uphold stringent safety features and precisely manage time constraints. This means preventing the system from acting when time constraints are not met and ensuring responses within specific time frames. Therefore, to better describe the time constraints of the system and to address the objective needs for system safety characteristics of autonomous ships, timed automata are introduced as the most widely used in real-time system model checking in this study.
Timed automata are denoted by a six-tuple , and the relevant parameters are as follows:
- is a finite set of locations.
- is the initial location.
- is a finite set of labels.
- is a finite set of clocks, with values being non-negative real numbers . For all clocks in , the rate of time passage is the same.
- is a mapping from locations to clock constraints, specifying a clock constraint from for each location in as the invariant of location , known as the location invariant. is a set of clock constraints defined on , with each clock constraint being constructed using the BNF syntax as , where means satisfying or , and denotes a non-negative real number.
- is a set of transitions, where the quintuple represents a transition from location to location labeled , which must satisfy the clock constraint ; represents the set of all clocks that are reset when the transition occurs, and .
Autonomous ships, being complex, large-scale, real-time embedded systems with high safety demands, must engage in real-time interactions with Shore Control Center (SCC) and other shore-based units, incorporating multiple subsystems that necessitate mutual communication and synchronized interwoven functioning. To realistically portray the behavior of autonomous ships, the addition of parallel combinations and constraints on single-timed automata is required [50]. This involves utilizing a network of timed automata to convert and delineate the exchange of information between multiple subsystems into interactions among the member automata.
Within timed automata, every timed automaton is considered a process. Communication among these processes is facilitated through channels or shared (global) variables. Synchronous communication is established via a handshake mechanism, and asynchronous communication is conducted using shared (global) variables. The formal definition of a timed automata network is as follows.
and are assumed to be two-timed automata with the disjoint clock sets and , denoted as . Consequently, the timed automata represent the parallel combination of and , i.e.,, where .
In the timed automata network, a location is a pair of positions where the elements of the pair correspond to the relevant quantities of the member automata. The location invariant is the conjunction of the location invariants of each member automata. Transitions of the same effect in each automata form a single transition in a parallel composition, where the source position of the transition is a combination of the transition source positions of the member automata. Similarly, the target position of the transition is also a combination of the transition target positions of the member automata.
3.3. The Proposed Method to Automatically Verify the Results of Hazard Analysis
Although the feasibility and effectiveness of STPA and its extended methods have been confirmed, the analysis process still heavily relies on the experience of the analysts, which can impact the completeness and objectivity of the hazard analysis results to some extent. Additionally, autonomous ships that are still under development and testing face substantial uncertainty in their system structures. The absence of adequate accident data and expert experience complicates the validation of their hazard analysis results.
To address the limitations mentioned, the lack of statistical data for establishing risk models in RBAT, and the questionable feasibility of applying classic risk assessment methods based on risk probability and consequence functions, the model checking from formal methods was introduced into the analytical process of the STPA extended method—STPA-SynSS, proposing a formal verification approach based on timed automata in risk-based assessment framework, as shown in Figure 2. Building upon the foundational hazard analysis conducted utilizing the STPA-SynSS framework, the method proposed herein establishes a network of timed automata models delineated with rigorous semantic precision. It employs model-checking tools alongside dynamically generated Backus–Naur Form (BNF) statements to facilitate the automatic verification of compliance with property specifications of the constructed system model, thereby enabling the formal verification of both the system’s modeling liveness and the correctness of the hazard analysis outcomes. Serving as a valuable addition to STPA and its extensions, model checking contributes to minimizing the subjective influences of human analysts during the hazard analysis process [51] and robustly confirms the critical role of safety constraints in hazard mitigation.
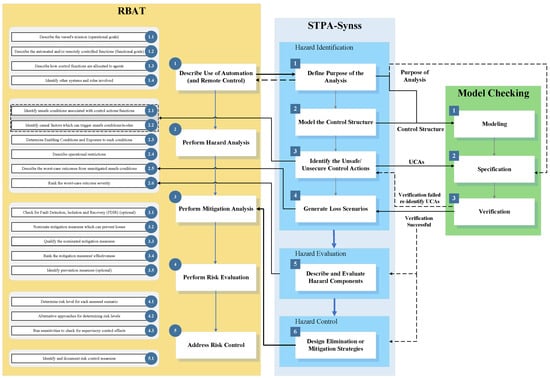
Figure 2.
The framework of the proposed method.
One key benefit of model checking is its fully automated verification process, which requires the use of corresponding model-checking tools for implementation. Appendix B presents an organized summary of the mainstream currently available model-checking tools. UPPAAL, a model-checking tool based on timed automata, utilizes a set of timed automata equipped with integer clock variables for modeling and verifying real-time systems. It conducts constraint-solving and functional testing by inputting models of timed automata and their to-be-verified properties, thereby facilitating the model checking of real-time systems. As an effective instrument for the verification of timed automata modeling, UPPAAL has achieved broad application across multiple domains, including modeling and verifying real-time systems, communication protocols, and controller networks [52,53,54]. In this study, UPPAAL is applied for the first time to the formal modeling and verification for autonomous ships to verify whether the system under examination meets the given property specifications, that is, to validate the set of properties along all reachable state paths.
UPPAAL utilizes a streamlined version of Timed Computation Tree Logic (TCTL) to characterize the properties of timed automata. In line with TCTL, its property query language comprises both path and state formulas, where the significance of logical connectives remains consistent. State formulas describe the various states of the model, while path formulas quantify the paths or trajectories of the model. Path formulas are divided into three categories: reachability, safety, and liveness. However, current research on the verification of real-time systems mainly concentrates on safety and liveness. The verification of system liveness involves assessing whether the system ultimately reaches a desired state using a cycle detection algorithm. This method, while consuming computational resources, provides a relatively simple verification approach. Conversely, safety verification checks whether the system attains any unsafe states during operation, achievable through a reachability analysis that involves traversing the state space of timed automata.
The verifier in UPPAAL employs a formal specification language based on the BNF syntax to delineate the properties awaiting verification with the following specific syntactic expressions:
Within this context, A and E serve as path quantifiers, with A representing ‘for all computation paths’, and E indicating ‘for some computation paths (indicating the existence of at least one path)’; [] and <> are utilized to denote states on quantified paths, with [] indicating that all states on the path fulfill the specified property p, and <> suggesting that at least one state on the path meets property p; p represents an expression for a specific property within the system (a logical expression awaiting verification); a denotes a variable, an integer variable expression, a time variable constraint, or a position within a timed automaton. Consequently, the explicit meanings are presented in Table 1, with the associated syntactic diagram displayed in Figure 3. Upon the completion of the construction of the timed automaton model for the system under verification, the to-be-verified properties can be inputted into the UPPAAL verifier using the BNF statements, thus automatically commencing the verification process.

Table 1.
Meaning of syntax in BNF and its equivalent properties.
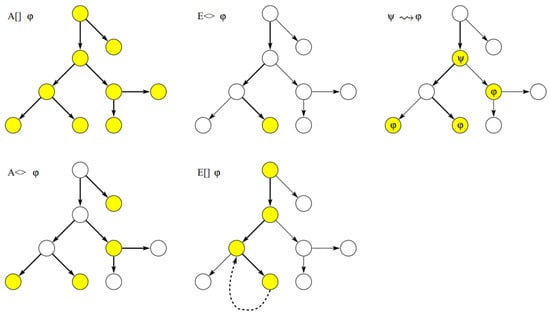
Figure 3.
Schematic diagram of BNF syntax.
As illustrated in Figure 2, model checking comprises three primary steps: modeling, specification, and verification. Functional requirements from step 1 of STPA-SynSS and control structures from step 2 of STPA-SynSS are utilized to build the network model of timed automata, representing system modeling. Upon confirming the responsibilities of model elements, the properties of the system must be clarified using UCAs identified in step 3 of STPA-SynSS, as well as information from step 1, such as system boundaries, objectives, unacceptable losses/accidents/events, system-level hazards, and safety constraints. These properties are articulated using the BNF statements, which then generate the property specifications of the system awaiting verification, termed specification. In the final stage, UPPAAL is employed to perform an exhaustive exploration of the system’s finite state space to assess the alignment between the system’s semantic model and its property specifications, thus ensuring the liveness of system modeling and the precision of the hazard analysis outcomes, referred to as verification.
It is crucial to highlight that the key to verifying the accuracy of hazard analysis results generated by STPA-SynSS lies in the verification of the identification result of UCAs. The accurate identification of UCAs within the system is essential for generating subsequent loss scenarios and developing effective hazard elimination or mitigation strategies. If the verification fails, a reiteration of UCA identification is required. Additionally, in constructing the UPPAAL model of timed automata, templates and channels correspond to model elements and control actions/feedback in the control structure. Simultaneously, the system’s guards, updates, clocks, and synchronization actions are incorporated into the simulation model.
4. Illustrative Case Study
In our previous study [44], a hazard analysis was conducted on the collision avoidance scenario for a remotely controlled ship (with seafarers onboard) using STPA-SynSS. We defined the purpose of the analysis, modeled the control structure, identified UCAs, and generated relevant loss scenarios. To demonstrate the continuity of our research, the application of the proposed method was executed on this same collision avoidance scenario as an illustrative case study, aiming to further validate the method’s applicability. Detailed results from the three phases are discussed in the following subsections.
4.1. Results from Phase 1 (Modeling)
In this case, the system boundary is defined as the safe navigation of a remotely controlled ship (with seafarers onboard) during the voyage, and the goal of the analysis is to support the introduction of autonomous ships while minimizing collision risk. In this step, six unacceptable losses and one unacceptable accident were defined.
In order to simplify the timed automata network model for remotely controlled ships (with seafarers onboard) and to emphasize the interactions between different timed automata, drawing on the functional requirements derived from step 1 of STPA-SynSS and the control structures developed in step 2 (as shown in Figure 4), the model elements were removed that have no practical impact on the collision avoidance scenario (considering only scenarios where both ownship and other ships are maneuverable), while simplifying and consolidating related control actions and feedback. Ultimately, a timed automata network model was established, known as , consisting of seven timed automata: SCC, Integrated Bridge System (IBS), Autonomous Navigation System (ANS), Autonomous Engine Monitoring and Control (AEMC) systems (including propulsion and steering systems, auxiliary engines, and other auxiliary machinery), manual control stations, communication devices (including AIS, GMDSS, VHF), and ship motion.
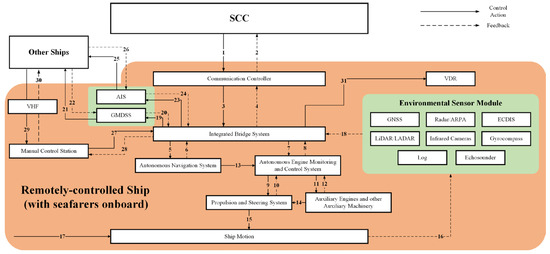
Figure 4.
The functional control structure for a remotely controlled ship (with seafarers onboard) [44].
In modeling remotely controlled ships with UPPAAL (version 4.1.25), model elements and control behaviors/feedback identified in STPA-SynSS step 2 need to be mapped into UPPAAL as templates and channels, as indicated in Table 2. The control structure is used to guide and track channel synchronization. Modeling is considered correct when the model encompasses all control actions/feedback, all states in the timed automata are accessible, timed automata synchronization is consistent, and there are no deadlocks in the model. The UPPAAL models for the SCC, IBS, ANS, and AEMC system, manual control stations, communication equipment, and ship motion timed automata are shown respectively in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, while the network of timed automata they compose is displayed in Figure 12.

Table 2.
Control actions/feedback based on functional control structure and corresponding UPPAAL channels.
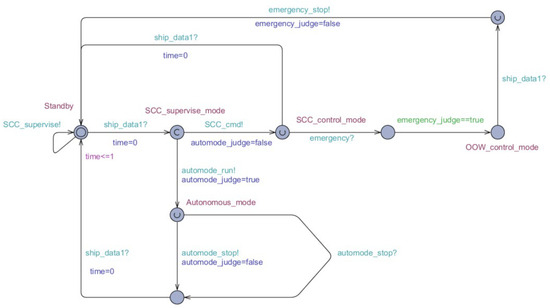
Figure 5.
UPPAAL model of timed automata of SCC.
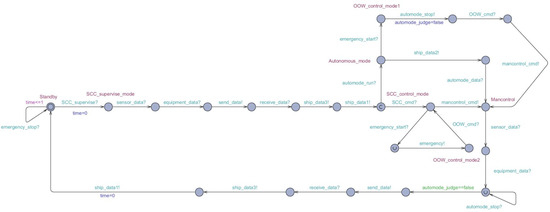
Figure 6.
UPPAAL model of timed automata of IBS.
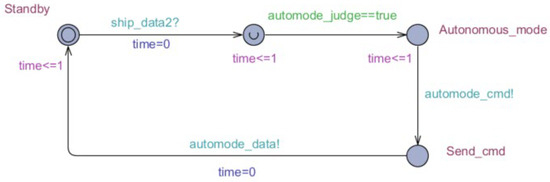
Figure 7.
UPPAAL model of timed automata of ANS.
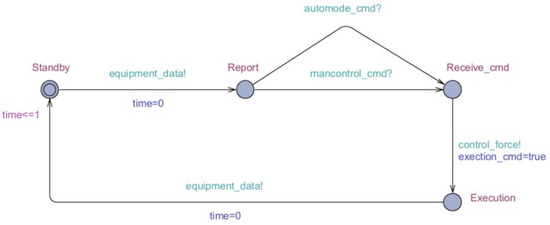
Figure 8.
UPPAAL model of timed automata of AEMC system.
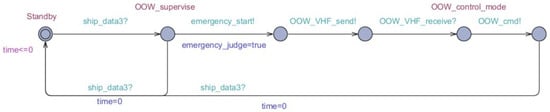
Figure 9.
UPPAAL model of timed automata of the manual control station.
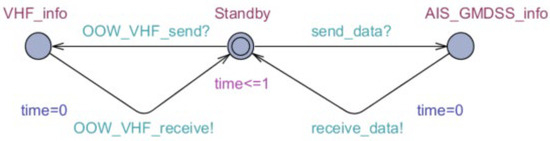
Figure 10.
UPPAAL model of timed automata of the communication device.
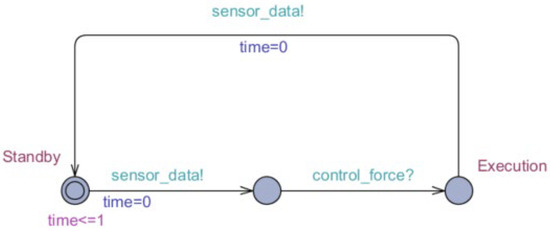
Figure 11.
UPPAAL model of timed automata of ship motion.
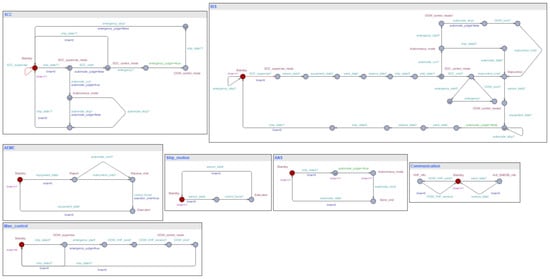
Figure 12.
UPPAAL model of timed automata network of the remotely-controlled ship.
4.2. Results from Phase 2 (Specification)
During the specification phase, it is necessary to rigorously describe the properties that the target system must satisfy using the BNF syntax. This serves as an input for the exhaustive search of the state space with the UPPAAL verifier in stage 3, thus fulfilling the verification of property specifications.
Formal verification primarily focuses on assessing the model’s liveness and safety, where liveness indicates that “good” events (actions) will eventually occur, denoting properties that are not constantly active but are ultimately present in the system. Meeting liveness criteria demonstrates the correctness and completeness of the system modeling and promotes or accomplishes the non-safety characteristics needed for system functionality, thus affecting the system’s reliability. The verification of liveness entails checking that all the model states are eventually reached or reachable and verifying the operational correctness of the system, as indicated by the BNF statements provided in Table 3.

Table 3.
BNF statements of system liveness.
Safety denotes that “bad” events (actions) are never supposed to happen, embodying traits that should be persistently upheld by the system. For remotely controlled ships in the collision avoidance scenario, verifying safety entails assessing whether the system could achieve an unsafe state, chiefly by exploring the state space of the timed automata network to conduct a reachability analysis of UCAs identified by STPA-SynSS. The BNF statement “E<>UCA” signifies “a path exists such that a UCA occurs in some state on that path.” Consequently, verifying this statement reflects whether UCAs that might cause hazardous states will occur, thus validating the safety of the system, i.e., if “E<>UCA” is true, then the UCA will occur, and if not, it will not.
In conducting a hazard analysis for the collision avoidance scenario with remotely controlled ships, the interaction between the IBS and AEMC systems served as an example, and seven UCAs were identified (as shown in Table 4). In this control loop, the IBS acted as the controller, and the AEMC system acted as the controlled entity, with control actions being course and speed control. The identified UCAs are mapped to the BNF statements, with the resulting property specifications displayed in Table 5.

Table 4.
UCAs of IBS as controller.

Table 5.
BNF statements of system safety.
4.3. Results from Phase 3 (Verification)
Once the construction of the timed automata network model for remotely controlled ships is finished, it can be simulated using the UPPAAL simulator. This simulation allows for observing state transitions during system operation, simulating interactions between timed automata, and checking for syntax errors in the model to ensure completeness and consistency. The initial simulation state is depicted in Figure 13. The UPPAAL simulator uses a message sequence chart (MSC) to present state transition diagrams for process transitions between timed automata in a temporally constrained sequence, showing active locations during these transitions.
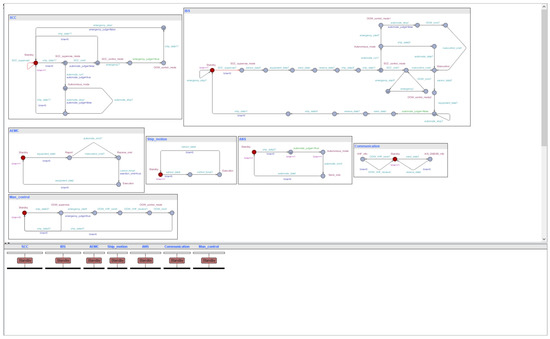
Figure 13.
The initial state of simulation for the UPPAAL model of the remotely-controlled ship.
Figure 14 shows the message sequence chart where the SCC monitors, controls, and maneuvers the ship. In this mode, the autonomous operation based on the ANS decisions is deactivated, and the OOW at the manual control station is only responsible for overseeing navigation. Whenever necessary or in emergencies, the OOW can assume control of the ship. The message sequence chart for normal conditions is depicted in Figure 14a, and the one for triggered emergency states is depicted in Figure 14b.
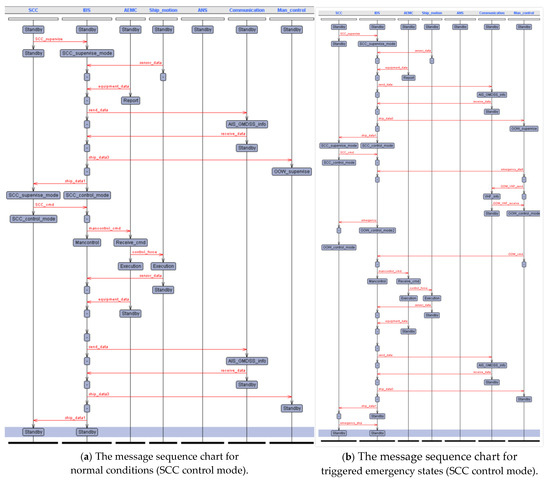
Figure 14.
Message sequence chart of SCC control mode.
Under the autonomous operation mode, remotely controlled ships continue to be supervised by SCC shore-based operators and the OOW. However, the IBS supplies the ANS with necessary data for route planning and collision avoidance, such as ship status and environmental sensor information. Commands from the ANS control the AEMC system to regulate the ship’s speed and course. The sequence chart for autonomous operation mode is displayed in Figure 15. Consistent with the SCC control mode, the OOW can assume control of the ship at any time in necessary or emergency situations. The message sequence chart for the normal state is shown in Figure 15a, and that for emergency conditions is shown in Figure 15b.
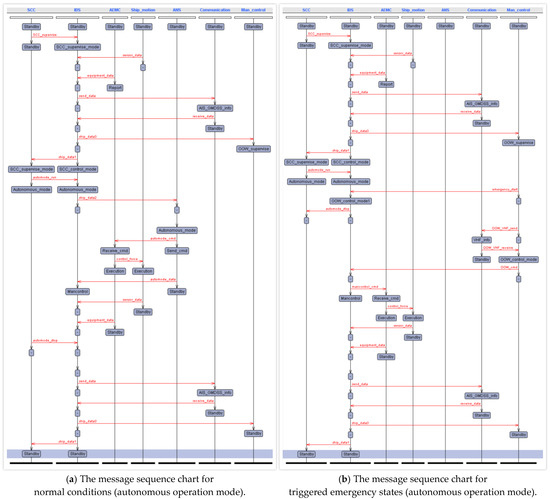
Figure 15.
Message sequence chart of autonomous operation mode.
Following the modeling, specification, and simulation of the target system, the UPPAAL verifier is used to perform an exhaustive search of the state space, thereby accomplishing the verification of the system’s liveness and safety. Results from the model simulation and system liveness verification reveal that all 10 property specifications listed in Table 3 were successfully verified (results displayed in Figure 16). This confirms that the system has no deadlocks and that all the subsystems or components function properly. Every system function is executed correctly, thus successfully verifying the accuracy of the control structure of remotely controlled ships (with seafarers onboard) developed using STPA-SynSS.

Figure 16.
Screenshot of UPPAAL verifier for system liveness.
On this basis, the crucial aspect of performing hazard analysis and producing outcomes with STPA-SynSS is identifying UCAs, as they are fundamental and central to the development of loss scenarios (STPA-SynSS step 4) and the formulation of hazard mitigation strategies (STPA-SynSS step 6). Hence, the correctness of identifying UCAs is especially critical. The verification result of system safety shows that all 11 property specifications listed in Table 5 passed the verification (as shown in Figure 17). This indicates the existence of at least one transition path that leads to the occurrence of UCA-1 to UCA-7, thereby affirming the presence of UCAs in the collision avoidance scenario of the remotely controlled ship (with seafarers onboard) and validating the accuracy of UCAs identification in this scenario.

Figure 17.
Screenshot of UPPAAL verifier for system safety.
5. Discussion
The continuous improvement in the safety level of autonomous ships is a common goal for all stakeholders in the maritime industry. A standardized hazard analysis process plays a crucial role in identifying, eliminating, and controlling potential hazards of autonomous ships. As the basis of hazard analysis, risks should be identified using suitable, recognized, and appropriate risk assessment techniques. To this end, RBAT was developed, as recommended in the draft MASS Code, to form a framework for a generic autonomous ship risk assessment tool in the absence of statistical data for establishing a risk model. The main impression is that RBAT can successfully identify and address key challenges associated with MASS, although it has been noted that refinements to the methodology are necessary to more precisely capture and distinguish between the varying risk levels across different scenarios.
To evaluate the risk by comprehensively considering the severity of the worst consequences of unexpected events and the effectiveness of mitigation actions to prevent losses in the absence of data support, STPA has emerged as an approach to improve the safety of modern complex systems in concert, which demonstrated the outstanding capability to identify and mitigate the unsafety/insecurity control actions that might lead to the losses of autonomous systems. However, the method of modeling and analysis through manual deduction remains controversial within the industry, particularly regarding the validity and authority of its results, as it is challenging to eliminate the human subjective influence during the process. Hence, the effort to introduce a certain level of formalization into STPA steps is well received.
5.1. Collaboration Between Model Checking and STPA
The workflow proposed in this study combines the model-checking approach with the STPA-SynSS process, and it leverages the output information from steps 1, 2, and 3 of STPA-SynSS to construct the timed automata network model, define its properties, and perform the automatic verification of hazard analysis results. This encompasses the modeling, specification, and verification stages in model checking, thereby ensuring the correctness of system modeling activities and hazard analysis results. The method aims to automatically verify the correctness of hazard analysis results while addressing the challenges of minimizing human influence in the analysis process.
To conclude the case study, we consider that the proposed method of combining STPA and model checking using UPPAAL has been successfully applied in autonomous ships. The process of aligning STPA with the UPPAAL model required considerable effort, but both approaches proved mutually beneficial [38]. The formalization of system behavior within an automata model raised several uncertainties that needed to be addressed in order to proceed with the proposed approach. As a result, the understanding of the system and potential hazardous scenarios was significantly enhanced. Conversely, the STPA identified UCA and loss scenarios that had not been considered during the initial system modeling.
5.2. Key Findings from the Case Study
The automated verification was achieved by modeling the timed automata network of the remotely controlled ship in UPPAAL. This work was possible because the requirements of automated verification were easily met by employing traversal strategies and algorithms over a finite state space, conducting an exhaustive explicit or implicit search of all reachable states and behaviors reflected in the given system or model in UPPAAL. Liveness, reachability, and safety properties are all employed for this verification.
The control structure is employed to guide and track the synchronization of channels. When the model incorporates all control behaviors and feedback, all states of the timed automata are accessible, synchronization within the automata is consistent, the model is free of deadlocks, and the correctness of the model can be confirmed. Simulation results and system activity verification in the case study demonstrate that the system is free of deadlocks, all subsystems and components operate correctly, and all system functions are executed as intended. This effectively verifies the correctness of the control structure for the remote-controlled ship (with seafarers onboard) modeled based on STPA-SynSS. Consequently, liveness verification holds a foundational position, as it indicates the correctness and integrity of the system modeling and can promote or complete the unsafe characteristics of the system function requirements, which determine the reliability of the system.
In the case study, a timed automata network model, which consists of seven timed automata, was established. This model, drawing on the functional requirements and control structures, simulated the dynamic behavior of the remotely controlled ship in the collision avoidance scenario. Reachability checks whether all model states are eventually reached or are reachable. The BNF statements for system safety and the verification results show that at least one transition path leads to the occurrence of all UCAs identified within the system, proving the existence of UCAs in the collision avoidance scenario of the remotely controlled ship (with seafarers onboard), thereby validating the correctness of the UCA identification for this scenario based on STPA-SynSS. The accuracy of the hazard analysis results is further effectively verified, and the closed loop of the hazard analysis of STPA is achieved. This case study shows that the formal method based on model checking can solve the verification difficulty of the hazard analysis results of autonomous ships through the liveness and reachability properties.
5.3. Potential for Industry Adoption
In conducting hazard analysis for the collision avoidance scenario with remotely controlled ships, seven UCAs were identified between the control loop of the IBS and AEMC systems. It is essential to model the hierarchical safety control structure based on the responsibilities and functional requirements of all model elements when constructing the control structure. From the perspective of system engineering, system safety is viewed as an emergence of the system and controlling this emergence is achieved by imposing constraints on the behavior of individual components and their interactions. From a high level of abstraction, STPA aims to model the system through its control structure as a set of feedback control loops. This method captures functional relationships and interactions while identifying unsafe control actions and their associated loss scenarios. As a result, without simulating the model based on system liveness, the integrity and consistency of the model cannot be ensured. In this case, the modeling process fails to support or achieve the non-safety-related functional requirements of the system, and the reliability of the system and the correctness of modeling results are uncertain. Consequently, all subsequent steps of the STPA methodology deviate from the intended objectives.
In the generated control loop between IBS and the AEMC system, as shown in Figure 18, if the UCAs are incorrectly identified, the designed targeted hazard mitigation measures fail to be effective. This could lead to the evolution of collision risks between encountering ships in a close-quarters situation and immediate danger, even resulting in a deviation from their OE. As a result, the likelihood of the ship collision accident occurrence would significantly increase. It is essential to verify the identified UCAs based on a general reachability analysis. If the identification results fail verification, it is necessary to return to step 3 to re-identify the UCAs, ensuring the correctness of generating loss scenarios and designing mitigation strategies.
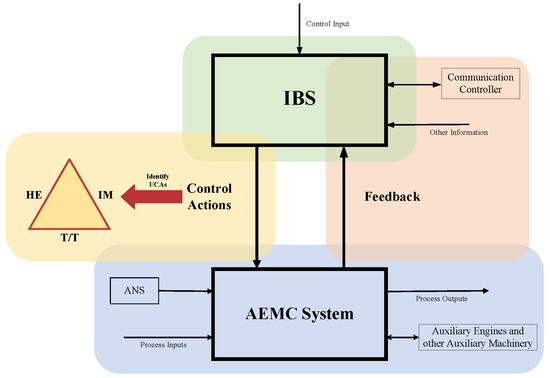
Figure 18.
Control loop of IBS and AEMC system.
After the iterative identification of UCAs and the verification of system activity, the targeted generation of hazard elimination or mitigation strategies is crucial for maritime practitioners, especially navigators. In the collision avoidance scenario for remotely-controlled ships, the consequences resulting from “course and speed control are not provided (UCA-1/2)” are more severe, drawing more attention from navigators. In this case study, the control loop is mapped to physical components, and specific causal factors are derived by refining safety and security constraints to facilitate the generation of loss scenarios and the decomposition/description of hazard ingredients. The hazard is an objective state that exists independent of human intention, and it can transition from a potential condition to an accident state when the elements within a hazard align in a specific combination. The existence of a hazard requires the presence of three hazard ingredients, including hazard element (HE), initiating mechanism (IM), and target and threat (T/T), as shown in the hazard triangle in Figure 18. To minimize the occurrence of ship collision accidents caused by “course and speed control are not provided” as much as possible, it is particularly crucial to design elimination/mitigation strategies that eliminate hazards, reduce the possibility of hazard transformation, and limit their consequences from the perspective of system safety and security-driven optimization.
The designed hazard elimination and mitigation measures are taken as input to implement the mitigation analysis in RBAT and identify mechanisms that can prevent unsafe conditions from escalating into accidents. Mitigation measures may involve the implementation of alternative control strategies aimed at re-entering the operational envelope, even if only in a degraded yet acceptable state, or transitioning the system into a fallback mode to maintain safety while efforts are made to restore nominal control. Fallback states represent predefined operational modes designed for situations in which continued operation within the nominal envelope is no longer feasible due to abnormal conditions. The transition into such states can be enabled through mitigation measures implemented by a single function or a combination of multiple functions. These same functions, or additional ones, may also facilitate the recovery of the system to a normal or degraded operational condition that ensures both safety and security. Thus, mitigation in this context entails the capacity to tolerate or recover from failures before they escalate into hazardous states, to regain control and restore the system to its intended operational domain, or to enter a stable fallback configuration that prevents further degradation and minimizes the risk of loss.
5.4. Limitations and Prospects
In comparison to classical STPA, STPA-SynSS can identify a greater number of UCAs and potential loss scenarios. This study focuses on the operational scenario of collision avoidance for a remotely controlled ship (with seafarers onboard). Two control loops with IBS and AEMC as control centers are constructed. The identified UCAs were mapped to the BNF statements; however, noteworthily, due to the limited number of inputted UCAs, no state space explosion occurred during the entire analysis process. The combinatorial explosion remains a major drawback of model-checkers since it requires exploring the entire state space when providing an optimal trace (in terms of length or duration of the sequences) [32]. With the deepening of future research, the analysis process of UCAs at the component level may promote state space explosion, but the solution to the state space explosion still needs further processing. Future extensions of our method could adopt a compositional modeling strategy, where complex systems are partitioned into smaller subsystems that are verified independently or hierarchically. Abstracting state variables and timing constraints where precision is not critical can help reduce state explosions without compromising safety guarantees.
It should be acknowledged that the current method, based on timed automata and UPPAAL, is limited to deterministic discrete-event systems. It does not accommodate probabilistic behavior or continuous dynamics often found in hybrid systems. Future extensions may consider integrating stochastic modeling tools or hybrid system verification frameworks to address these more complex behaviors in autonomous maritime systems.
Moreover, given the limited description of autonomous ships, the hierarchical control structure defined in this study represents only an illustrative case study. The draft MASS Code emphasizes the need to address the diversity in operational modes and scenarios for autonomous ships, reflecting their ability to adapt to varying modes of operation and environmental conditions. Since the future operational scenarios are not limited to collision avoidance scenarios, in future studies, it is suggested to generate exhaustive scenarios for different modes of operation and further demonstrate the capabilities of automated verification tools.
6. Conclusions
In this study, a formal verification method based on timed automata is utilized to verify the hazard analysis of autonomous ship navigation safety. This method is comprised of three steps and was applied to an autonomous ship. Compared with the more traditional approaches, the proposed method is more conducive to the integration of model checking into hazard analysis work. The formal verification method based on timed automata is demonstrated to be capable of overcoming the limitations associated with the accuracy and completeness of hazard analysis results derived from the traditional accident cause theory and manual deduction in the field of autonomous ships.
The method employs steps such as modeling, specification, and verification for model checking to automatically validate the control structure of the system that needs verification and the identified UCAs constructed by STPA-SynSS, thus assessing the correctness and completeness of the hazard analysis results. Using remotely controlled ships (with seafarers onboard) as a case study, a hazard analysis of the collision avoidance scenario is conducted, followed by the establishment of a timed automata network model for this scenario based on rigorous semantics. The model elements, control actions, and feedback identified by STPA-SynSS are mapped as templates and channels into UPPAAL to construct the corresponding timed automata, UPPAAL model. Finally, by utilizing the UPPAAL simulator and verifier to perform an automated exhaustive search of the system’s state space, the complete model is simulated, and the hazard analysis results are validated. The verification results indicate that the timed automata network model for remotely controlled ships, based on the control structure, is free of deadlocks and operates correctly. At least one transition path exists that leads to the occurrence of the UCAs identified by STPA-SynSS, thereby confirming the correctness of the STPA-SynSS hazard analysis results.
The results obtained with the proposed approach indicate that combining the two techniques improves the knowledge obtained about the system under design and the consistency of the design changes proposed to tackle the safety constraints identified in STPA. Moreover, the method proposed in this study emphasizes the significance of the collaborative work between safety and system engineering in the product development process. Future studies will focus on extending the applicability of this method to a broader range of autonomous systems while further refining the model to enhance both the efficiency and accuracy of the verification process. Particular emphasis will be placed on mitigating the risk of combinatorial explosion, a common challenge in the verification of large-scale models, by exploring advanced optimization techniques and scalable verification frameworks. This automated hazard verification method can serve as a reference for other intelligent systems with inherent potential hazards.
Author Contributions
Conceptualization, X.-Y.Z.; formal analysis, X.-Y.Z., X.Y., and W.Z.; funding acquisition, X.-Y.Z.; investigation, X.S., X.Y., and S.N.; methodology, X.-Y.Z.; resources, X.S. and S.N.; software, X.-Y.Z. and S.J.; validation, X.-Y.Z., Y.M., and W.Z.; visualization, S.J. and Y.M.; writing—original draft, X.-Y.Z. and S.J.; writing—review and editing, X.-Y.Z., S.J. and Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the National Key R&D Program of China (Grant No. 2023YFB4302300) and the National Natural Science Foundation of China (NSFC) (Grant No. 52301416, 52201408).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Xu Sun was employed by the company China Classification Society. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A

Table A1.
List 32 references in Figure 1.
Table A1.
List 32 references in Figure 1.
| No. | Year | Number of RIF | References |
|---|---|---|---|
| 1 | 2024 | 14 | Zhou, Y., Liu, Z., Wang, X., Xie, H., Tao, J., Wang, J. and Yang, Z. Human errors analysis for remotely controlled ships during collision avoidance. Front. Mar. Sci. 2024, 11, 1473367. |
| 2 | 2024 | 18 | Li, C., Zhao, J., Ding, G., Zhang, K., Li, W., Li, Y., Wang, Y. and Wen, J. The Study of Risk Assessment Method for Ship Berthing Based on the “Human-Ship-Environment” Synergy. J. Mar. Sci. Eng. 2024, 12(11), 2022. |
| 3 | 2024 | 18 | Zhang, W., Liu, Z. and Ma, X. Research on Navigation Risk Assessment of Unmanned Ship Under Complex Navigation Conditions. J. Mar. Sci. Eng. 2024, 12(11), 1947. |
| 4 | 2024 | 31 | Li, X. and Yuen, K.F. A human-centred review on maritime autonomous surfaces ships: impacts, responses, and future directions. Transport Rev. 2024, 44(4), 791-810. |
| 5 | 2024 | 53 | Zhang, W., Zhang, Y. and Zhang, C. Navigation risk assessment of intelligent ships based on DS-Fuzzy weighted distance Bayesian network. Ocean Eng. 2024, 313, 119452. |
| 6 | 2024 | 14 | Orzechowski, S.C., Verheyen, W. and Sys, C. A systematic literature review of factors influencing the regulation of autonomous inland shipping in Europe. Eur. Transport Res. Rev. 2024, 16(1), 54. |
| 7 | 2024 | 16 | Li, W., Chen, W., Guo, Y., Hu, S., Xi, Y. and Wu, J. Risk Performance Analysis on Navigation of MASS via a Hybrid Framework of STPA and HMM: Evidence from the Human–Machine Co-Driving Mode. J. Mar. Sci. Eng. 2024, 12(7), 1129. |
| 8 | 2024 | 35 | Li, P., Wang, Y. and Yang, Z. Risk assessment of maritime autonomous surface ships collisions using an FTA-FBN model. Ocean Eng. 2024, 309, 118444. |
| 9 | 2024 | 11 | Kim, J. A Fundamental Study of the Sustainable Key Competencies for Remote Operators of Maritime Autonomous Surface Ships. Sustainability-Basel 2024, 16(12), 4875. |
| 10 | 2024 | 15 | Fan, C., Montewka, J., Bolbot, V., Zhang, Y., Qiu, Y. and Hu, S. Towards an analysis framework for operational risk coupling mode: A case from MASS navigating in restricted waters. Reliab. Eng. Syst. Saf. 2024, 248, 110176. |
| 11 | 2024 | 35 | Shiokari, M., Itoh, H., Yuzui, T., Ishimura, E., Miyake, R., Kudo, J. and Kawashima, S. Structure model-based hazard identification method for autonomous ships. Reliab. Eng. Syst. Saf. 2024, 247, 110046. |
| 12 | 2024 | 9 | Sezer, S.I., Ahn, S.I., Akyuz, E., Kurt, R.E. and Gardoni, P. A hybrid human reliability analysis approach for a remotely-controlled maritime autonomous surface ship (MASS- degree 3) operation. Appl. Ocean Res. 2024, 147, 103966. |
| 13 | 2024 | 5 | Veitch, E., Alsos, O.A., Cheng, T., Senderud, K. and Utne, I.B. Human factor influences on supervisory control of remotely operated and autonomous vessels. Ocean Eng. 2024, 299, 117257. |
| 14 | 2024 | 17 | Luo, X., Ling, H., Xing, M. and Bai, X. A dynamic-static combination risk analysis framework for berthing/unberthing operations of maritime autonomous surface ships considering temporal correlation. Reliab. Eng. Syst. Saf. 2024, 245, 110015. |
| 15 | 2023 | 12 | Rødseth, Ø.J., Wennersberg, L.A.L. and Nordahl, H. Improving safety of interactions between conventional and autonomous ships. Ocean Eng. 2023, 284, 115206. |
| 16 | 2023 | 32 | Wan, C., Zhao, Y., Zhang, D. and Fan, L. A system dynamics-based approach for risk analysis of waterway transportation in a mixed traffic environment. Maritime Policy and Management 2024, 51(6), 1147-1169. |
| 17 | 2023 | 25 | Li, W., Chen, W., Hu, S., Xi, Y. and Guo, Y. Risk evolution model of marine traffic via STPA method and MC simulation: A case of MASS along coastal setting. Ocean Eng. 2023, 281, 114673. |
| 18 | 2023 | 4 | Zhang, W. and Zhang, Y. Navigation Risk Assessment of Autonomous Ships Based on Entropy–TOPSIS–Coupling Coordination Model. J. Mar. Sci. Eng. 2023, 11(2), 422. |
| 19 | 2023 | 6 | Park, C., Kontovas, C., Yang, Z. and Chang, C. A BN driven FMEA approach to assess maritime cybersecurity risks. Ocean Coast Manage 2023, 235, 106480. |
| 20 | 2023 | 4 | Zhang, W. and Zhang, Y. Research on coupling mechanism of intelligent ship navigation risk factors based on N-K model. J. Mar. Sci. Technol. 2023, 28(1), 195-207. |
| 21 | 2023 | 18 | Zhang, W. and Zhang, Y. Research on classification and navigational risk factors of intelligent ship. Brodogradnja 2023, 74(4), 105-128. |
| 22 | 2022 | 111 | Luo, X., He, H., Zhang, X., Ma, Y. and Bai, X. Failure Mode Analysis of Intelligent Ship Positioning System Considering Correlations Based on Fixed-Weight FMECA. Processes 2022, 10(12), 2677. |
| 23 | 2022 | 86 | Luo, J., Geng, X., Li, Y. and Yu, Q. Study on the Risk Model of the Intelligent Ship Navigation. Wireless Commun. Mobile Comput. 2022, 2022, 1-9. |
| 24 | 2021 | 23 | Guo, C., Haugen, S. and Utne, I.B. Risk assessment of collisions of an autonomous passenger ferry. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability 2023, 237(2), 425-435. |
| 25 | 2021 | 89 | Bolbot, V., Theotokatos, G., Wennersberg, L.A., Faivre, J., Vassalos, D., Boulougouris, E., Jan Rødseth, Ø., Andersen, P., Pauwelyn, A. and Van Coillie, A. A novel risk assessment process: Application to an autonomous inland waterways ship. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability 2023, 237(2), 436-458. |
| 26 | 2021 | 5 | Fan, C., Montewka, J. and Zhang, D. Towards a Framework of Operational-Risk Assessment for a Maritime Autonomous Surface Ship. Energies 2021, 14(13), 3879. |
| 27 | 2021 | 16 | Chang, C., Kontovas, C., Yu, Q. and Yang, Z. Risk assessment of the operations of maritime autonomous surface ships. Reliab. Eng. Syst. Saf. 2021, 207, 107324. |
| 28 | 2020 | 54 | Ramos, M.A., Thieme, C.A., Utne, I.B. and Mosleh, A. A generic approach to analysing failures in human – System interaction in autonomy. Saf. Sci. 2020, 129, 104808. |
| 29 | 2020 | 55 | Fan, C., Wróbel, K., Montewka, J., Gil, M., Wan, C. and Zhang, D. A framework to identify factors influencing navigational risk for Maritime Autonomous Surface Ships. Ocean Eng. 2020, 202, 107188. |
| 30 | 2019 | 50 | Zhang, X., Zhang, Q., Yang, J., Cong, Z., Luo, J. and Chen, H. Safety Risk Analysis of Unmanned Ships in Inland Rivers Based on a Fuzzy Bayesian Network. J. Adv. Transp. 2019, 2019, 1-15. |
| 31 | 2018 | 27 | Wróbel, K., Montewka, J. and Kujala, P. Towards the development of a system-theoretic model for safety assessment of autonomous merchant vessels. Reliab. Eng. Syst. Saf. 2018, 178, 209-224. |
| 32 | 2018 | 26 | Wróbel, K., Montewka, J. and Kujala, P. System-theoretic approach to safety of remotely-controlled merchant vessel. Ocean Eng. 2018, 152, 334-345. |
Appendix B

Table A2.
Comparison of model-checking tools.
Table A2.
Comparison of model-checking tools.
| Model-Checking Tools | Application Area | Modeling Language | Property Description Language | Counterexample Generation | GUI | Counterexample Visualization | Operating Platform | ||
|---|---|---|---|---|---|---|---|---|---|
| Conventional | Probabilistic | Real-Time | |||||||
| CADP | √ | √ | LOTOS FC2 FSP LNT | AFMC MCL XTL | Y | Y | Y | Mac OS Linux Solaris Windows | |
| DREAM | √ | C++ Timed Automata | Monitor Automata | Y | N | N | Windows Unix-related | ||
| LTSmin | √ | √ | Promela μCRL mCRL2 DVE Input Language | μ-Calculus LTL CTL* | Y | N | N | Mac OS X Linux Windows | |
| mCRL2 | √ | √ | mCRL2 | μ-Calculus | Y | Y | Y | Mac OS Linux Solaris Windows | |
| NuSMV | √ | SMV Input Language | CTL LTL PSL | Y | N | N | Mac OS X Linux Windows | ||
| MRMC | √ | √ | Plain MC | CSL CSRL PCTL PRCTL | N | N | N | Mac OS Linux Windows | |
| PAT | √ | √ | √ | CSP# Timed CSP Probabilistic CSP | LTL Assertion | Y | Y | Y | Windows OS with Mono Support |
| PRISM | √ | PEPA PRISM Language Plain MC | CSL PLTL PCTL | N | Y | N | Mac OS Linux Windows | ||
| SPIN | √ | Promela | LTL | Y | Y | Y | Windows Unix-related | ||
| TAPAs | √ | CCSP | CTL μ-Calculus | Y | Y | Y | Mac OS Windows Unix-related | ||
| UPPAAL | √ | Timed Automata C subset | TCTL subset | Y | Y | Y | Mac OS Linux Windows | ||
| TLA+ Model Checker | √ | TLA+ PlusCal | TLA | Y | Y | N | Mac OS Linux Windows | ||
References
- Charpentier, V.; Slamnik-Kriještorac, N.; Landi, G.; Caenepeel, M.; Vasseur, O.; Marquez-Barja, J.M. Paving the way towards safer and more efficient maritime industry with 5G and Beyond edge computing systems. Comput. Netw. 2024, 250, 110499. [Google Scholar] [CrossRef]
- Chua, C.; Li, X.; Tan, K.H.; Yuen, K.F. Building sustainable performance in the maritime industry via digital resources and innovation. Transp. Policy 2024, 149, 282–299. [Google Scholar] [CrossRef]
- Sun, M.; Tong, T.; Jiang, M.; Zhu, J.X. Innovation trends and evolutionary paths of green fuel technologies in maritime field: A global patent review. Int. J. Hydrogen Energy 2024, 71, 528–540. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, P.; Zhen, L. Green development of the maritime industry: Overview, perspectives, and future research opportunities. Transp. Res. Part E Logist. Transp. Rev. 2023, 179, 103322. [Google Scholar] [CrossRef]
- IMO. Development of a Goal-Based Instrument for Maritime Autonomous Ships (MASS); IMO: London, UK, 2024. [Google Scholar]
- Chaal, M.; Ren, X.; BahooToroody, A.; Basnet, S.; Bolbot, V.; Banda, O.A.V.; Gelder, P.V. Research on risk, safety, and reliability of autonomous ships: A bibliometric review. Saf. Sci. 2023, 167, 106256. [Google Scholar] [CrossRef]
- Liu, C.; Chu, X.; Wu, W.; Li, S.; He, Z.; Zheng, M.; Zhou, H.; Li, Z. Human–machine cooperation research for navigation of maritime autonomous surface ships: A review and consideration. Ocean Eng. 2022, 246, 110555. [Google Scholar] [CrossRef]
- Tao, J.; Liu, Z.; Wang, X.; Cao, Y.; Zhang, M.; Loughney, S.; Wang, J.; Yang, Z. Hazard identification and risk analysis of maritime autonomous surface ships: A systematic review and future directions. Ocean Eng. 2024, 307, 118174. [Google Scholar] [CrossRef]
- Lehmann, F.; Roop, P.S.; Ranjitkar, P. Extending Particle Hopping Models for road traffic with Timed Automata. Physical A 2020, 553, 124107. [Google Scholar] [CrossRef]
- Nazaruddin, Y.Y.; Tamba, T.A.; Pradityo, K.; Aristyo, B.; Widyotriatmo, A. Safety Verification of a Train Interlocking Timed Automaton Model. IFAC-Papersonline 2019, 52, 331–335. [Google Scholar] [CrossRef]
- EMSA. RBAT-Method Description; EMSA: Lisbon, Portugal, 2024. [Google Scholar]
- Yang, X.; Zhou, T.; Zhou, X.Y.; Zhang, W.J.; Mu, C.R.; Xu, S. A framework to identify failure scenarios in the control mode transition process for autonomous ships with dynamic autonomy. Ocean Coast Manag. 2024, 249, 107003. [Google Scholar] [CrossRef]
- Zhou, X.; Jin, S.; Ren, X.; Sun, X.; Meng, X.; Nie, S.; Zhang, W. A framework to assess the operational state of autonomous ships with multi-component degrading systems. Ocean Eng. 2025, 327, 121000. [Google Scholar] [CrossRef]
- Fan, C.; Wróbel, K.; Montewka, J.; Gil, M.; Wan, C.; Zhang, D. A framework to identify factors influencing navigational risk for Maritime Autonomous Surface Ships. Ocean Eng. 2020, 202, 107188. [Google Scholar] [CrossRef]
- Wróbel, K.; Montewka, J.; Kujala, P. System-theoretic approach to safety of remotely-controlled merchant vessel. Ocean Eng. 2018, 152, 334–345. [Google Scholar] [CrossRef]
- Wróbel, K.; Montewka, J.; Kujala, P. Towards the development of a system-theoretic model for safety assessment of autonomous merchant vessels. Reliab. Eng. Syst. Saf. 2018, 178, 209–224. [Google Scholar] [CrossRef]
- Ramos, M.A.; Utne, I.B.; Mosleh, A. On factors affecting autonomous ships operators performance in a Shore Control Center. In Proceedings of the 14th Probabilistic Safety Assessment and Management, Los Angeles, CA, USA, 16–21 September 2018; pp. 16–21. [Google Scholar]
- Zhang, X.; Zhang, Q.; Yang, J.; Cong, Z.; Luo, J.; Chen, H. Safety Risk Analysis of Unmanned Ships in Inland Rivers Based on a Fuzzy Bayesian Network. J. Adv. Transp. 2019, 2019, 4057195. [Google Scholar] [CrossRef]
- Chang, C.; Kontovas, C.; Yu, Q.; Yang, Z. Risk assessment of the operations of maritime autonomous surface ships. Reliab. Eng. Syst. Saf. 2021, 207, 107324. [Google Scholar] [CrossRef]
- Fan, C.; Bolbot, V.; Montewka, J.; Zhang, D. Advanced Bayesian study on inland navigational risk of remotely controlled autonomous ship. Accid. Anal. Prev. 2024, 203, 107619. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Wang, Y.; Yang, Z. Risk assessment of maritime autonomous surface ships collisions using an FTA-FBN model. Ocean Eng. 2024, 309, 118444. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y.; Qiao, W. Risk Scenario Evaluation for Intelligent Ships by Mapping Hierarchical Holographic Modeling into Risk Filtering, Ranking and Management. Sustainability 2022, 14, 2103. [Google Scholar] [CrossRef]
- Bolbot, V.; Theotokatos, G.; Wennersberg, L.A.; Faivre, J.; Vassalos, D.; Boulougouris, E.; Jan Rødseth, Ø.; Andersen, P.; Pauwelyn, A.; Van Coillie, A. A novel risk assessment process: Application to an autonomous inland waterways ship. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2023, 237, 436–458. [Google Scholar] [CrossRef]
- Wang, R.; Zheng, W.; Liang, C.; Tang, T. An integrated hazard identification method based on the hierarchical Colored Petri Net. Saf. Sci. 2016, 88, 166–179. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, J. Safety Analysis of Communication-Based Train Control System by STPA and Colored Petri Net. In Cyberspace Data and Intelligence, and Cyber-Living, Syndrome, and Health, International 2019 Cyberspace Congress, CyberDI and CyberLife, Beijing, China, December 16–18, 2019, Proceedings, Part I; Ning, H., Ed.; Springer: Singapore, 2019; pp. 433–449. [Google Scholar]
- Yan, F.; Ma, J.; Li, M.; Niu, R.; Tang, T. An Automated Accident Causal Scenario Identification Method for Fully Automatic Operation System Based on STPA. IEEE Access 2021, 9, 11051–11064. [Google Scholar] [CrossRef]
- Zhu, D.; Tan, H.; Yao, S. Petri Nets-based method to elicit component-interaction related safety requirements in safety-critical systems. Comput. Electr. Eng. 2018, 71, 162–172. [Google Scholar] [CrossRef]
- Valdez Banda, O.A.; Kannos, S.; Goerlandt, F.; van Gelder, P.H.A.J.; Bergström, M.; Kujala, P. A systemic hazard analysis and management process for the concept design phase of an autonomous vessel. Reliab. Eng. Syst. Saf. 2019, 191, 106584. [Google Scholar] [CrossRef]
- Hwang, T.; Youn, I. Development of a Graph-Based Collision Risk Situation Model for Validation of Autonomous Ships’ Collision Avoidance Systems. J. Mar. Sci. Eng. 2023, 11, 2037. [Google Scholar] [CrossRef]
- Fan, S.; Shi, K.; Weng, J.; Yang, Z. Letting losses be lessons: Human-machine cooperation in maritime transport. Reliab. Eng. Syst. Saf. 2025, 253, 110547. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Y. Navigation Risk Assessment of Autonomous Ships Based on Entropy–TOPSIS–Coupling Coordination Model. J. Mar. Sci. Eng. 2023, 11, 422. [Google Scholar] [CrossRef]
- Gouyon, D.; Pétin, J.; Cochard, T.; Devic, C. Architecture assessment for safety critical plant operation using reachability analysis of timed automata. Reliab. Eng. Syst. Saf. 2020, 199, 106923. [Google Scholar] [CrossRef]
- Johansen, T.; Blindheim, S.; Torben, T.R.; Utne, I.B.; Johansen, T.A.; Sørensen, A.J. Development and testing of a risk-based control system for autonomous ships. Reliab. Eng. Syst. Saf. 2023, 234, 109195. [Google Scholar] [CrossRef]
- Wang, H.; Zhong, D.; Zhao, T. Avionics system failure analysis and verification based on model checking. Eng. Fail. Anal. 2019, 105, 373–385. [Google Scholar] [CrossRef]
- Ma, Z.; Li, X.; Liu, Z.; Huang, R.; He, N. Model checking fuzzy computation tree logic of multi-agent systems based on fuzzy interpreted systems. Fuzzy Sets Syst. 2024, 485, 108966. [Google Scholar] [CrossRef]
- Alexiou, N.; Basagiannis, S.; Petridou, S. Formal security analysis of near field communication using model checking. Comput. Secur. 2016, 60, 1–14. [Google Scholar] [CrossRef]
- Bae, K.; Meseguer, J. Model checking linear temporal logic of rewriting formulas under localized fairness. Sci. Comput. Program. 2015, 99, 193–234. [Google Scholar] [CrossRef]
- Dakwat, A.L.; Villani, E. System safety assessment based on STPA and model checking. Saf. Sci. 2018, 109, 130–143. [Google Scholar] [CrossRef]
- Leveson, N. Engineering a Safer World: Systems Thinking Applied to Safety; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Leveson, N. A systems approach to risk management through leading safety indicators. Reliab. Eng. Syst. Saf. 2015, 136, 17–34. [Google Scholar] [CrossRef]
- Chaal, M.; Valdez Banda, O.A.; Glomsrud, J.A.; Basnet, S.; Hirdaris, S.; Kujala, P. A framework to model the STPA hierarchical control structure of an autonomous ship. Saf. Sci. 2020, 132, 104939. [Google Scholar] [CrossRef]
- Wróbel, K.; Gil, M.; Montewka, J. Towards a method evaluating control actions in stpa-based model of ship-ship collision avoidance process. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, OMAE 2018, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Zhou, X.; Liu, Z.; Wang, F.; Wu, Z.; Cui, R. Towards applicability evaluation of hazard analysis methods for autonomous ships. Ocean Eng. 2020, 214, 107773. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, Z.; Wang, F.; Wu, Z. A system-theoretic approach to safety and security co-analysis of autonomous ships. Ocean Eng. 2021, 222, 108569. [Google Scholar] [CrossRef]
- Cheng, T.; Utne, I.B.; Wu, B.; Wu, Q. A novel system-theoretic approach for human-system collaboration safety: Case studies on two degrees of autonomy for autonomous ships. Reliab. Eng. Syst. Saf. 2023, 237, 109388. [Google Scholar] [CrossRef]
- Fan, S.; Yang, Z. Safety and security co-analysis in transport systems: Current state and regulatory development. Transp. Res. Part A Policy Pract. 2022, 166, 369–388. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, D.; Han, B.; Wan, C. Risk and reliability analysis for maritime autonomous surface ship: A bibliometric review of literature from 2015 to 2022. Accid. Anal. Prev. 2023, 187, 107090. [Google Scholar] [CrossRef] [PubMed]
- Clarke, E.M.; Emerson, E.A. Design and synthesis of synchronization skeletons using branching time temporal logic. In Workshop on Logic of Programs; Kozen, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 52–71. [Google Scholar]
- Queille, J.P.; Sifakis, J. Specification and verification of concurrent systems in CESAR. In Proceedings of the 5th Colloquium on International Symposium on Programming; Dezani-Ciancaglini, M., Montanari, U., Eds.; Springer: Berlin/Heidelberg, Germany, 1982; pp. 337–351. [Google Scholar]
- Alur, R.; Dill, D.L. Automata-theoretic Verification of Real-Time Systems. In Formal Methods for Real-Time Computing; Heitmeyer, C., Mandrioli, D., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1996; pp. 55–82. [Google Scholar]
- Magureanu, G.; Gavrilescu, M.; Pescaru, D. Validation of static properties in unified modeling language models for cyber physical systems. J. Zhejiang Univ. Sci. C 2013, 14, 332–346. [Google Scholar] [CrossRef]
- Cha, S.; Son, H.; Yoo, J.; Jee, E.; Seong, P.H. Systematic evaluation of fault trees using real-time model checker UPPAAL. Reliab. Eng. Syst. Saf. 2003, 82, 11–20. [Google Scholar] [CrossRef]
- Vicenzutti, A.; Menis, R.; Sulligoi, G. All-Electric Ship-Integrated Power Systems: Dependable Design Based on Fault Tree Analysis and Dynamic Modeling. IEEE Trans. Transp. Electrif. 2019, 5, 812–827. [Google Scholar] [CrossRef]
- Vogel, T.; Carwehl, M.; Rodrigues, G.N.; Grunske, L. A property specification pattern catalog for real-time system verification with UPPAAL. Inf. Softw. Technol. 2023, 154, 107100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).