Faulted-Pole Discrimination in Shipboard DC Microgrids Using S-Transformation and Convolutional Neural Networks
Abstract
1. Introduction
2. Literature Review
2.1. AI Applications in DC-Grid Fault Protection
2.2. Pole Selection Research in DC Grids
3. S-Transformation and Convolutional Neural Networks
3.1. S-Transformation
3.1.1. Continuous S-Transformation
3.1.2. Discrete S-Transformation
3.2. Convolutional Neural Networks
3.2.1. Convolutional Layer
3.2.2. Pooling Layer
3.2.3. Fully Connected Layer
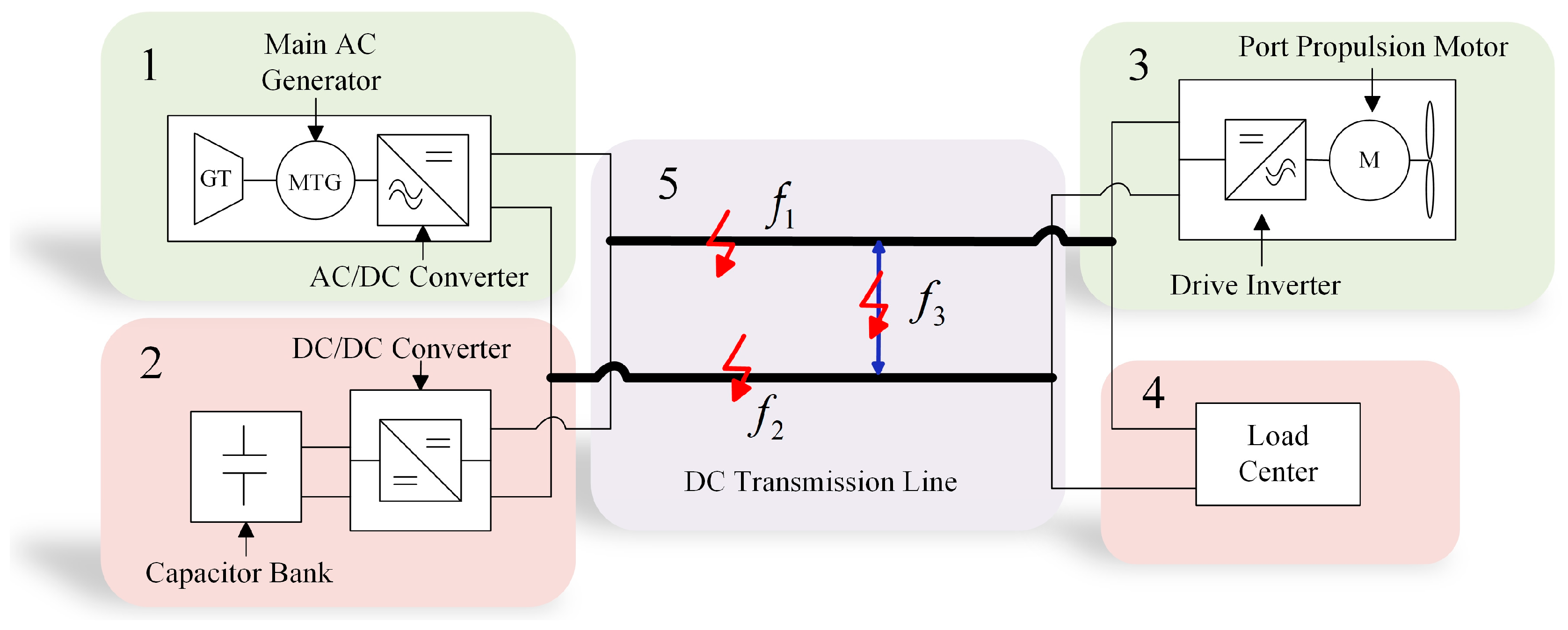
4. Modeling and Analysis
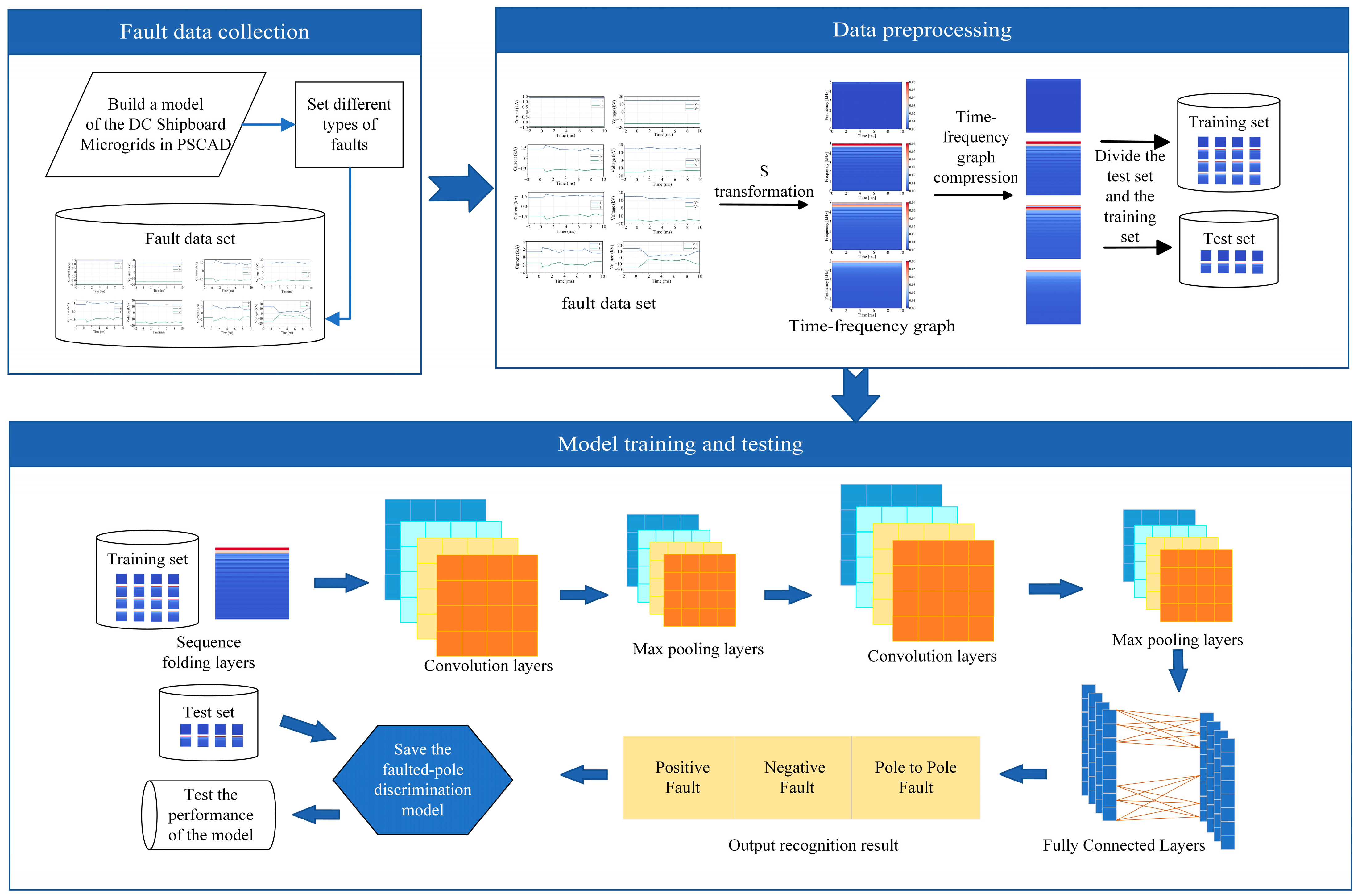
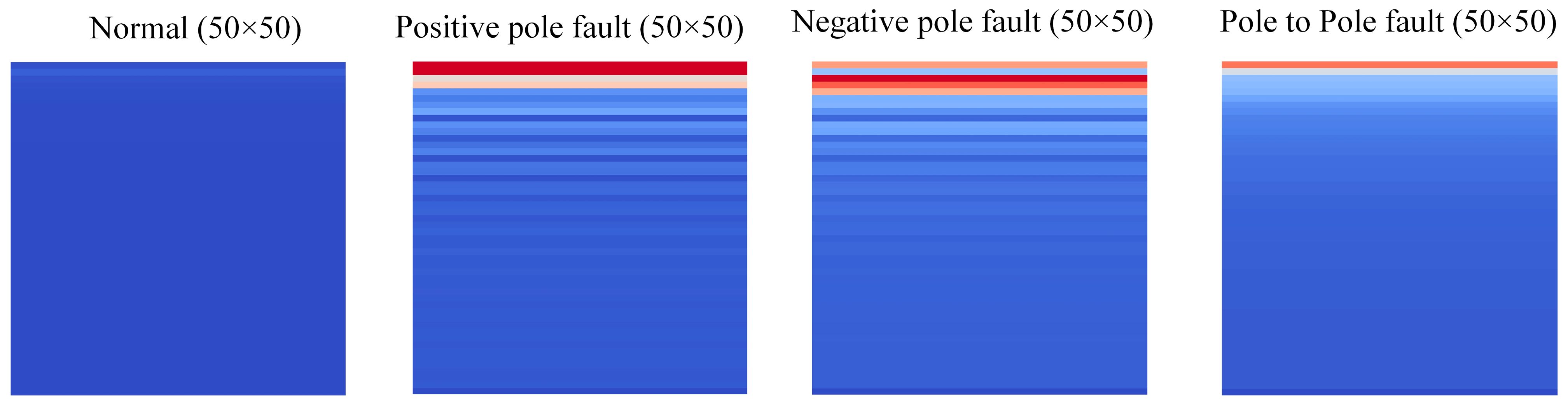
4.1. Data Preprocessing
4.2. Model Training and Testing
4.2.1. Forward Propagation
4.2.2. Loss Calculation
4.2.3. Backward Propagation
4.3. CNN Parameter Settings
4.3.1. Convolutional Layer and Pooling Layer
4.3.2. Learning Rate
4.3.3. Batch Size
5. Simulation and Verification
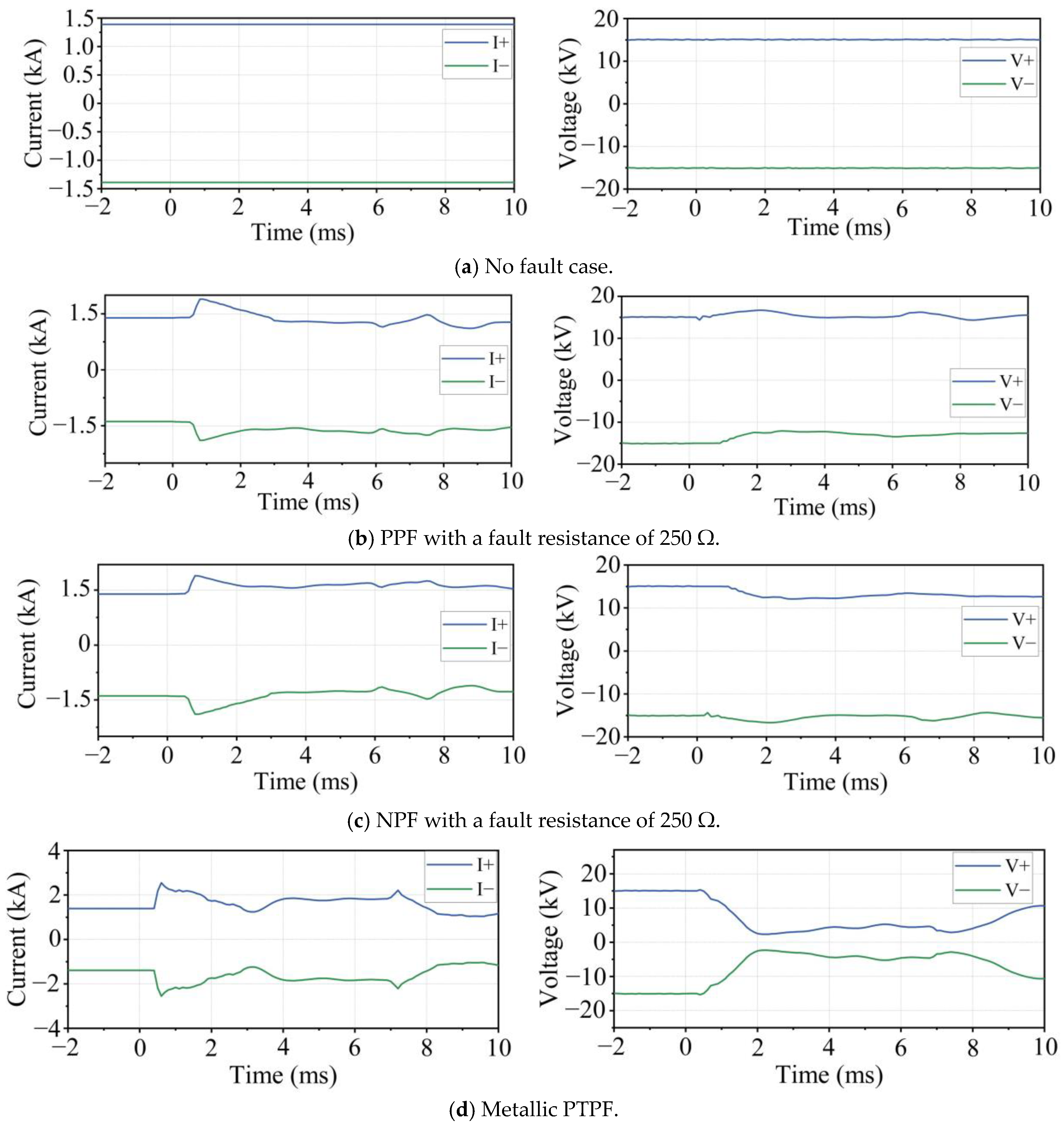
5.1. PPF, NPF, and PTPF
5.2. Sensitivity to Fault Distance
5.3. Sensitivity to Fault Resistance
5.4. Comparative Analysis with Existing Classification Models
- CNN combined with Support Vector Machine (CNN-SVM) [39];
- Wavelet Transform combined with CNN (WT-CNN) [40].
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, Y.; Jin, B.; Liu, Y.; Wei, X.; Wang, K.; Zhang, X. Modeling and Simulation of Medium Voltage DC Power System for All Electric Ships. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; IEEE: New York, NY, USA, 2024; pp. 1962–1965. [Google Scholar]
- Li, Z.; Chen, J.; Li, K.; Xu, Z.; Liu, Y.; Wang, M. Robust Model Predictive Control for Onboard Interleaved Multilevel Boost DC-DC Converter in DC Shipboard Microgrids. IEEE Trans. Transp. Electrif. 2025, 11, 8876–8888. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, J.; Guo, C.; Tan, Z.; Wang, Y.; Wei, N.; Song, Y. Fault Severity Classification Based Coordination Control Strategy of Fault Current Limiter and Modular Multilevel Converter for Adaptive Fault Current Limiting. J. Mod. Power Syst. Clean Energy 2025, 13, 1432–1443. [Google Scholar]
- Maydison, H.; Zhang, H.; Han, N.; Oh, D.; Jang, J. Optimized Diesel–Battery Hybrid Electric Propulsion System for Fast Patrol Boats with Global Warming Potential Reduction. J. Mar. Sci. Eng. 2025, 13, 1071. [Google Scholar] [CrossRef]
- Paipa-Sanabria, E.; González-Montoya, D.; Coronado-Hernández, J.R. Green Technologies for Environmental Air and Water Impact Reduction in Ships: A Systematic Literature Review. J. Mar. Sci. Eng. 2025, 13, 839. [Google Scholar] [CrossRef]
- Habyarimana, M.; Adebiyi, A.A. A Review of Artificial Intelligence Applications in Predicting Faults in Electrical Machines. Energies 2025, 18, 1616. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, C.; Hao, Z.; Monti, A.; Ponci, F. Data-driven Fault Detection and Isolation in DC Microgrids Without Prior Fault Data: A Transfer Learning Approach. Appl. Energy 2023, 336, 120708. [Google Scholar] [CrossRef]
- Yang, Y.; Tu, F.; Huang, S.; Tu, Y.; Liu, T. Research on CNN-LSTM DC Power System Fault Diagnosis and Differential Protection Strategy Based on Reinforcement Learning. Front. Energy Res. 2023, 11, 1258549. [Google Scholar] [CrossRef]
- Yousaf, M.Z.; Khalid, S.; Tahir, M.F.; Tzes, A.; Raza, A. A novel dc fault protection scheme based on intelligent network for meshed dc grids. Int. J. Electr. Power Energy Syst. 2023, 154, 109423. [Google Scholar] [CrossRef]
- Shanmugapriya, V.; Vidyasagar, S.; Raju, D.K. Post-fault voltage recovery and voltage instability assessment of DC microgrid with Deep Transfer-learning Convolution Neural Network. Electr. Power Syst. Res. 2025, 239, 111234. [Google Scholar] [CrossRef]
- Bayati, N.; Balouji, E.; Baghaee, H.R.; Hajizadeh, A.; Soltani, M.; Lin, Z.; Savaghebi, M. Locating high-impedance faults in DC microgrid clusters using support vector machines. Appl. Energy 2022, 308, 118338. [Google Scholar] [CrossRef]
- Liu, T.; Yan, J.; Liu, Y.; Chung, C.Y. Cascading Failure Screening Based on Gradient Boosting Decision Tree for HVDC Sending-End Systems with High Wind Power Penetration. IEEE Trans. Power Syst. 2025, 99, 1–13. [Google Scholar] [CrossRef]
- Salehimehr, S.; Miraftabzadeh, S.M.; Brenna, M. A novel machine learning-based approach for fault detection and location in low-voltage DC microgrids. Sustainability 2024, 16, 2821. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, J.; Li, Q.; Gao, X.; Yu, R.; Guo, J.; Yang, B. Long short-term memory network-based HVDC systems fault diagnosis under knowledge graph. Electronics 2023, 12, 2242. [Google Scholar] [CrossRef]
- Dash, P.K.; Pattnaik, S.R.; Prasad, E.N.; Bisoi, R. Detection and classification of DC and feeder faults in DC microgrid using new morphological operators with multi-class AdaBoost algorithm. Appl. Energy 2023, 340, 121013. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, L.; Yang, S.; Gao, Y. A series arc fault diagnosis method in DC distribution systems based on multiscale features and random forests. IEEE Sens. J. 2022, 23, 2605–2617. [Google Scholar] [CrossRef]
- Deb, A.; Jain, A.K. An effective data-driven machine learning hybrid approach for fault detection and classification in a standalone low-voltage DC microgrid. Electr. Eng. 2024, 106, 6199–6212. [Google Scholar] [CrossRef]
- Veerapandiyan, S.; Sugavanam, V. On-line fault identification, location, and seamless service restoration using transfer learning-based convolution neural network for low-voltage DC microgrid. Electr. Power Compon. Syst. 2023, 51, 785–808. [Google Scholar] [CrossRef]
- Li, J.; Song, G.; Yan, J.; Li, Y.; Xu, Z. Data-driven Fault Detection and Classification for MTDC Systems by Integrating HCTSA and Softmax Regression. IEEE Trans. Power Deliv. 2021, 37, 893–904. [Google Scholar] [CrossRef]
- Yang, Y.; Tai, N.; Fan, C.; Yang, L.; Chen, S. Resonance Frequency-based Protection Scheme for Ultra-High-Voltage Direct-Current Transmission Lines. IET Gener. Transm. Distrib. 2018, 12, 318–327. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Fu, Y. Fault-Line Selection and Fault-Type Recognition in DC Systems Based on Graph Theory. Prot. Control Mod. Power Syst. 2018, 3, 27. [Google Scholar] [CrossRef]
- Rahmani, R.; Sadeghi, S.H.H.; Askarian-Abyaneh, H.; Emadi, M.J. An entropy-based scheme for protection of DC microgrids. Electr. Power Syst. Res. 2024, 228, 110010. [Google Scholar] [CrossRef]
- Salehi, M.; Taher, S.A.; Sadeghkhani, I.; Shahidehpour, M. A poverty severity index-based protection strategy for ring-bus low-voltage DC microgrids. IEEE Trans. Smart Grid 2019, 10, 6860–6869. [Google Scholar] [CrossRef]
- Tiwari, R.S.; Sharma, J.P.; Gupta, O.H.; Ahmed Abdullah Sufyan, M. Extension of pole differential current based relaying for bipolar LCC HVDC lines. Sci. Rep. 2025, 15, 16142. [Google Scholar] [CrossRef]
- Shamsoddini, M.; Vahidi, B.; Razani, R.; Mohamed, Y.A.R.I. A novel protection scheme for low voltage DC microgrid using inductance estimation. Int. J. Electr. Power Energy Syst. 2020, 120, 105992. [Google Scholar] [CrossRef]
- Ma, J.; Xiao, Z.; Cheng, P. A pilot protection scheme for flexible HVDC transmission lines based on modulus power. Int. J. Electr. Power Energy Syst. 2022, 137, 107849. [Google Scholar] [CrossRef]
- Chu, X.; Lv, H. Coupling characteristic analysis and a fault pole detection scheme for single-circuit and double-circuit HVDC transmission lines. Electr. Power Syst. Res. 2020, 181, 106179. [Google Scholar] [CrossRef]
- An, N.; Shu, H.; Yang, B.; Cao, P.; Song, J.; Guo, Y. Voltage Correlation Based Single Pole-to-Ground Fault Detection of MMC-HVDC Transmission Line. IEEE Access 2020, 9, 118124–118133. [Google Scholar] [CrossRef]
- Qin, H.; Peng, F.; Pan, Z.; Zhong, Y.; Liu, T.; Cao, R. A Single-Ended Protection Scheme for Flexible HVDC Transmission Lines Based on the Fréchet Distance of the Rate of Change of Fault Voltage Traveling Waves. IEEE Access 2025, 13, 128716–128728. [Google Scholar] [CrossRef]
- Farshad, M. Detection and classification of internal faults in bipolar HVDC transmission lines based on K-means data description method. Int. J. Electr. Power Energy Syst. 2019, 104, 615–625. [Google Scholar] [CrossRef]
- Lazzari, R.; Piegari, L.; Grillo, S.; Carminati, M.; Ragaini, E.; Bossi, C.; Tironi, E. Selectivity and Security of DC Microgrid Under Line-to-Ground Fault. Electr. Power Syst. Res. 2018, 165, 238–249. [Google Scholar] [CrossRef]
- Datta, S.; Chattopadhyaya, A.; Chattopadhayay, S.; Das, A. S-transform based kurtosis analysis for detection of LG and LL faults in 14 Bus microgrid system. IETE J. Res. 2022, 68, 3766–3777. [Google Scholar] [CrossRef]
- Mishra, S.; Gupta, S.; Yadav, A.; Abdelaziz, A.Y. Traveling wave-based fault localization in FACTS-compensated transmission line via signal decomposition techniques. Energies 2023, 16, 1871. [Google Scholar] [CrossRef]
- Song, G.; Cheng, J.; Grattan, K.T.V. Recognition of microseismic and blasting signals in mines based on convolutional neural network and stockwell transform. IEEE Access 2020, 8, 45523–45530. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 53. [Google Scholar] [CrossRef] [PubMed]
- Bacevicius, M.; Paulauskaite-Taraseviciene, A. Machine learning algorithms for raw and unbalanced intrusion detection data in a multi-class classification problem. Appl. Sci. 2023, 13, 7328. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Wu, K. CNN-based Fault Phase Identification Method of Double Circuit Transmission Lines. Electr. Power Compon. Syst. 2020, 48, 833–843. [Google Scholar] [CrossRef]
- Lan, S.; Chen, M.J.; Chen, D.Y. A Novel HVDC Double-Terminal Non-Synchronous Fault Location Method Based on Convolutional Neural Network. IEEE Trans. Power Deliv. 2019, 34, 848–857. [Google Scholar] [CrossRef]
- Gnanamalar, A.J.; Bhavani, R.; Arulini, A.S.; Veerraju, M.S. CNN–SVM Based Fault Detection, Classification, and Location of Multi-Terminal VSC–HVDC System. J. Electr. Eng. Technol. 2023, 18, 3335–3347. [Google Scholar] [CrossRef]
- Paul, D.; Mohanty, S.K. Fault Classification in Transmission Lines Using Wavelet and CNN. In Proceedings of the 2019 IEEE 5th International Conference for Convergence in Technology (I2CT), Pune, India, 29–31 March 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]


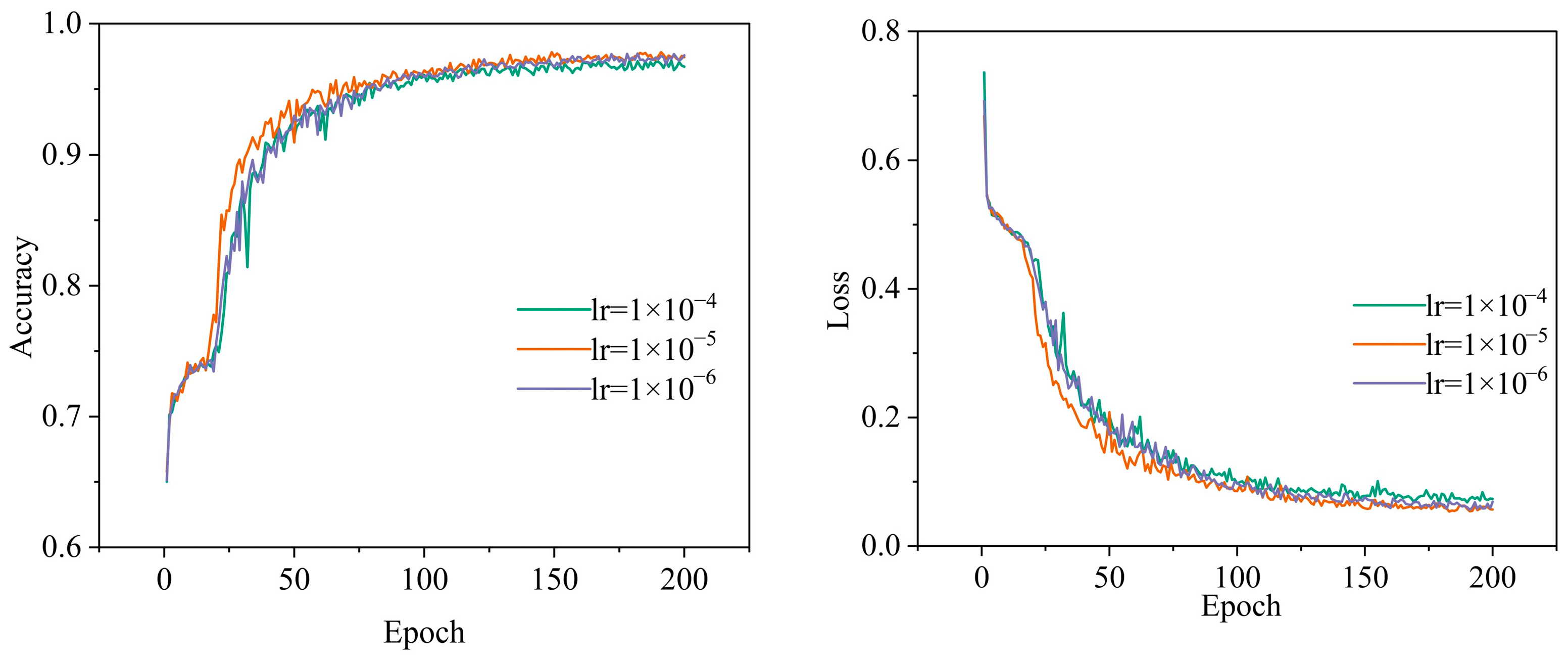
| Learning-Rate Lower Bound | Training Time/s | Accuracy |
|---|---|---|
| 0.0001 | 103.63 | 0.9821 |
| 0.00001 | 101.81 | 0.9898 |
| 0.000001 | 121.13 | 0.9868 |
| Batch Size | Training Time/s | Accuracy |
|---|---|---|
| 16 | 150.31 | 0.9793 |
| 32 | 103.12 | 0.9898 |
| 64 | 92.84 | 0.9821 |
| Item | Parameter |
|---|---|
| System version | Windows11 x64 |
| Processor model (CPU) | Intel(R) Core (TM) i5-12600F, Santa Clara, CA, USA |
| Processing speed | 3.7 GHz |
| Memory (RAM) | 16 GB |
| GPU | RTX3060 |
| Parameter | Possible Configuration |
|---|---|
| Types | PPF, NPF, PTPF |
| Ship-power load | 0, 5%, 10%, 15%, …, 100% |
| Fault distance | 0, 10%, 20%, 30%, …, 100% |
| Fault resistance (Ω) | 0, 5, 10, 20, 40, 50, 80, 100, 150, 200, 250, 300 |
| Fault Distance (%) | Fault Type | Discrimination Result | Fault Type | Discrimination Result | Fault Type | Discrimination Result |
|---|---|---|---|---|---|---|
| 0 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 5 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 10 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 20 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 40 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 60 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 90 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| 100 | PPF | PPF | NPF | NPF | PTPF | PTPF |
| Fault Resistance (Ω) | Fault Type | Discrimination Result | Fault Type | Discrimination Result |
|---|---|---|---|---|
| 0 | PPF | PPF | NPF | NPF |
| 10 | PPF | PPF | NPF | NPF |
| 50 | PPF | PPF | NPF | NPF |
| 100 | PPF | PPF | NPF | NPF |
| 150 | PPF | PPF | NPF | NPF |
| 200 | PPF | PPF | NPF | NPF |
| 250 | PPF | PPF | NPF | NPF |
| 300 | PPF | PPF | NPF | NPF |
| Algorithm | Classification Accuracy of Different Defect Types (%) | Total Accuracy (%) | Training Time/s | ||
|---|---|---|---|---|---|
| PPF | NPF | PTPF | |||
| CNN | 98.68 | 95.11 | 99.53 | 97.27 | 168.80 |
| CNN-SVM | 60.78 | 98.02 | 99.56 | 71.31 | 42.57 |
| WT-CNN | 93.53 | 99.12 | 100.00 | 96.43 | 190.47 |
| S-CNN | 98.40 | 99.55 | 100.00 | 98.98 | 103.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Wang, Z.; Gao, N.; Wang, K.; Jin, B.; Chen, H.; Li, B. Faulted-Pole Discrimination in Shipboard DC Microgrids Using S-Transformation and Convolutional Neural Networks. J. Mar. Sci. Eng. 2025, 13, 1510. https://doi.org/10.3390/jmse13081510
Yang Y, Wang Z, Gao N, Wang K, Jin B, Chen H, Li B. Faulted-Pole Discrimination in Shipboard DC Microgrids Using S-Transformation and Convolutional Neural Networks. Journal of Marine Science and Engineering. 2025; 13(8):1510. https://doi.org/10.3390/jmse13081510
Chicago/Turabian StyleYang, Yayu, Zhenxing Wang, Ning Gao, Kangan Wang, Binjie Jin, Hao Chen, and Bo Li. 2025. "Faulted-Pole Discrimination in Shipboard DC Microgrids Using S-Transformation and Convolutional Neural Networks" Journal of Marine Science and Engineering 13, no. 8: 1510. https://doi.org/10.3390/jmse13081510
APA StyleYang, Y., Wang, Z., Gao, N., Wang, K., Jin, B., Chen, H., & Li, B. (2025). Faulted-Pole Discrimination in Shipboard DC Microgrids Using S-Transformation and Convolutional Neural Networks. Journal of Marine Science and Engineering, 13(8), 1510. https://doi.org/10.3390/jmse13081510








