Navigating Coastal Vulnerability: Introducing the Coastal Fuzzy Vulnerability Index (CFVI)
Abstract
1. Introduction
2. Coastal Vulnerability Approaches
- (1)
- Coastal Vulnerability Index (CVI)
- (2)
- Physical Vulnerability Index (FVI)
- (3)
- Socioeconomic Vulnerability Index (SVI)
- (4)
- Environmental Vulnerability Index (EVI)
- (5)
- Integrated Coastal Vulnerability Index (ICVI)
- (6)
- Multi-hazard Vulnerability Index (MVI)
3. Coastal Vulnerability Indices Empirical Mathematics
- (1)
- The geometric mean implication is not correct because it is not the square root, but rather the square root of 6th order, as follows:
- (2)
- If the logarithm of both sides in Equation (2) are taken, then the nonlinearity relationship between CVI and each of the variable appears in the same form of nonlinearity equally, which may not correspond to physical effects in the natural coastal zones
- (3)
- Why is such an artificial nonlinearity integrated and what is the logical base or empirical basis of Equation (2) is not explained in open literature
- (4)
- Why are only the vulnerability classes 1, 2, 3, 4, and 5 are considered as inputs into Equations (1) and (2) and the variable available data values are not considered individually?
4. Coastal Vulnerability Indices Logical Structures
4.1. Bivalent Logic (BL)
- (1)
- All five classifications, “V. Low”, “Low”, “Moderate”, “High”, and “V. High”, have the same belonging values: 0 (false), implying no risk, or 1 (true), implying risk
- (2)
- All data values have an equal belonging degree in each classification group. Although there are wide data ranges, any value falling in this range is not different from the others, so their effects concern the vulnerability calculation. Once a class is considered risky, all the values in this class have the same effect without distinction among them. This point shows that in CVI calculation, the direct effect of each data value is not considered at all
- (3)
- There is an abrupt transition between neighboring classes, which is quite illogical, but can be considered as an assumption that does not match the real natural situation. There should be smooth transitions between classes, as will be explained in the next section
- (4)
- Each class is considered as mutually exclusive and without any overlapping, i.e., no relationship between the successive classes
- (5)
- In Table 1, four variables have increasing direction from right to left, but shoreline erosion and mean tide length have opposite increasing direction. Thus, it is not possible to compare them graphically, but the bivalent logical graphs, in Figure 1 are shown along the same direction and hence ready for comparison of variables without with the classification labels of “V. low”, “Low”, “Moderate”, “High”, and “V. high” labels that may be in reverse order with other four variables.
4.2. Fuzzy Logic (FL)
- (1)
- Each data set in five risk class is attached with a membership degree (MD) that includes all decimal numbers between 0 and 1. Thus, each data value has its contribution to the overall vulnerability calculation
- (2)
- The middle value of each data range is considered to have the highest MD value equal to 1, and the others include all decimal values between 0 and 1
- (3)
- Each data range is represented by triangular forms instead of rectangles, and the zero MDs on both sides interact with neighboring data range triangle peak values as having 0 MDs
- (4)
- Since at both ends of data ranges in each variable has > and < extreme signs, the end fuzzy sets are arranged as trapezium fuzzy sets
- (5)
- The whole procedure of fuzzy sets is referred to as the fuzzification of the data ranges, which helps to consider not a lump procedure but individual data assessment for each data range, as specified in Table 1.
- (1)
- In the BL approach, five crisp classes (1-“Very low”, 2-“Low”, 3-“Moderate”, 4-“High”, and 5-“Very high”) are represented in the form of FL sets as (see Figure 2)
- (2)
- Fuzzification of classes leads to two MDs for any variable numerical data value within each of the five classes
- (3)
- The decision regarding the choice between these two values depends on the researcher’s purpose. If the higher value is adopted, the ORing procedure (membership maximization, ) procedure of fuzzy inference is used. This means that the variable higher-class MD is adapted for CFVI calculation
- (4)
- In the case of adaptation of the decision of small MD selection, the ANDing connection (minimization of membership, ) of FL [22] is effective, which means that a smaller CFVI value than the previous step will be obtained
- (5)
- Considering the last two steps, the initial equation expressions can be written not in the form of arithmetic mean as in Equation (1), but in the form nonlinear logarithm as in Equation (2). If each of the variable MD is symbolized as , and six variable data values as a, b, c, d, e, and f, then the maximum CFVI, CFVIMax, and the minimum CFVImin can be expressed as follows:
- (1)
- Equation (4) does not have linearity like Equation (1); they are based on nonlinearity, because there are no specific mathematical formulations in FL procedures, but there are different MDs for each variable data values. Since nonlinearity is hidden in FL procedures [23], there is no need for Equation (4)’s artificial importation of nonlinearity as in Equation (2), explained in Section 2
- (2)
- If the same extreme values are applied to Equation (4) with extreme a, b, c, d, e, and f data value MDs, one can obtain the minimum and maximum CFVI values, and all other data sets in between will remain between these two values, as will be explained in the next section
- (3)
- In extreme cases, all the extremely high (low) data values for each variable in Table 1 will have MDs equal to 1; therefore, Equation (4) will have the arithmetic average forms as was in Equation (1), because equality of MDs to 1 will eliminate the nonlinearity structure of these equations, and the final equations in terms of extremely high and low data values will result in the form of Equation (2):
- (4)
- One can deduct from this result that Equation (2) is valid outside the high and low variable extremes, because there is no vulnerability classification for these ranges in Table 1.
5. Results
- (1)
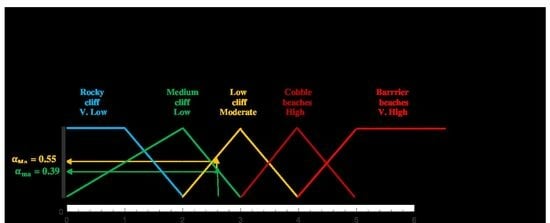
- Let provide a value on the horizontal axis in Figure 2a. It can be seen that = 0.55 and = 0.39
- (2)
- In Figure 2b, the input of the coastal slope as % on the horizontal axis gives the maximum and minimum MDs as = 0.39 and = 0.73, respectively
- (3)
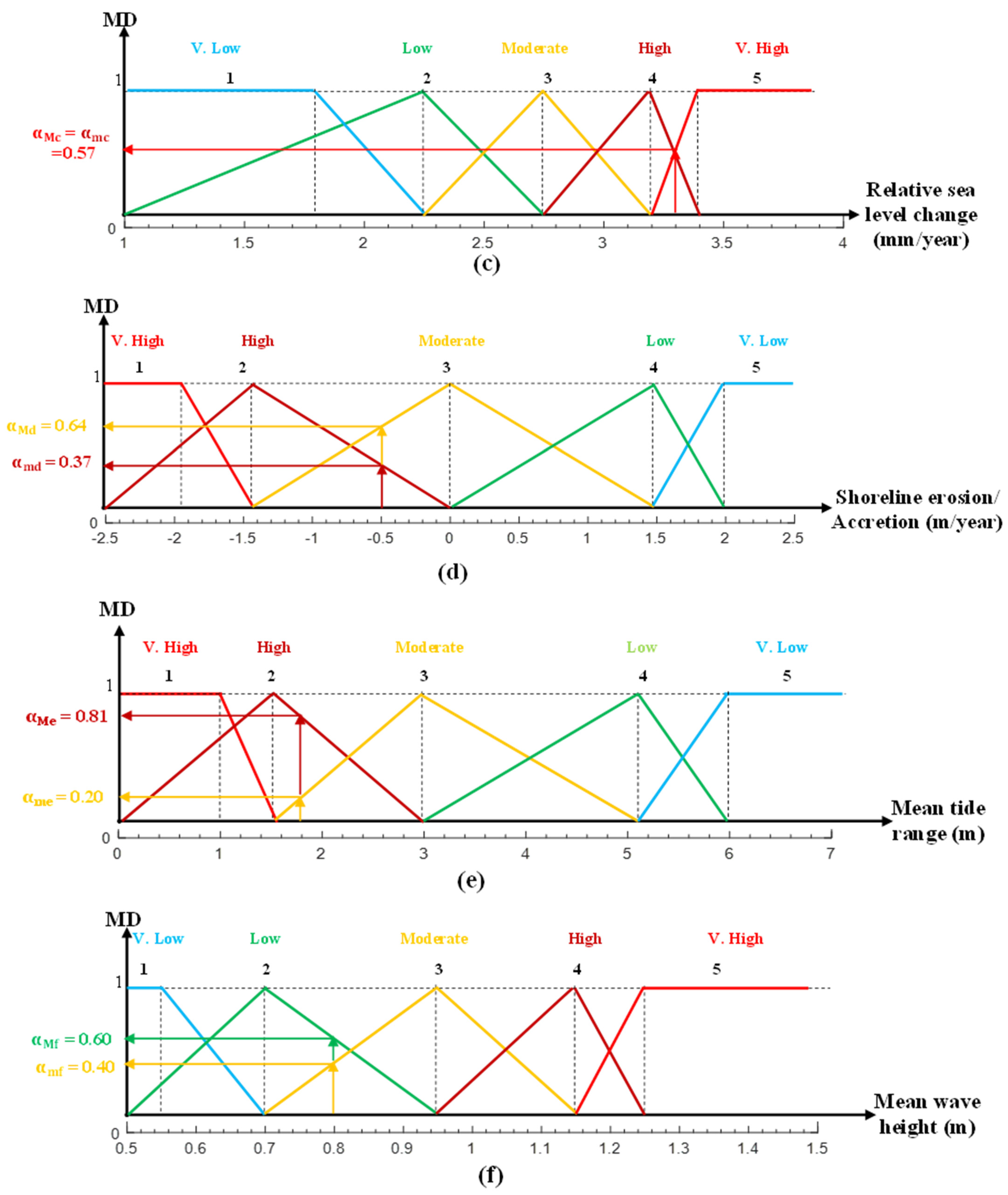
- In Figure 2c, the input value of 3.3 mm/year relative sea level gives = 0.57; thus, the MDs are equal
- (4)
- For the erosion rate d = −0.5, the MDs are shown in Figure 2d, and their values are = 0.64 and = 0.37, respectively
- (5)
- The mean tidal range is fitted as 1.8 m, which leads to the MD values in Figure 2e as = 0.81 and = 0.20
- (6)
- Finally, the MD in Figure 2e values 2f yield = 0.60 and = 0.40 for a 1.8 m mean wave height.
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pachauri, R.K.; Mayer, L. Intergovernmental Panel on Climate Change, IPCC Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC Summary for Policy Makers; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Pethick, J.S.; Crooks, S. Development of a coastal vulnerability index: A geomorphological perspective. Environ. Conserv. 2019, 27, 359–367. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Wong, P.P.; Burkett, V.R.; Codignotto, J.O.; Hay, J.E.; Ragoonaden, S.; Woodroffe, C.D. Coastal systems and low-lying areas. In Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 315–356. [Google Scholar]
- Simac, N.; Faivre, S. Overview of Coastal Vulnerability Indices with Reference to Physical Characteristics of the Croatian Coast of Istria. Hydrology 2023, 10, 14. [Google Scholar] [CrossRef]
- Kuleli, T.; Bayazit, S. An integrated approach to the spatial distribution of the coastal infrastructure vulnerability by using coastal vulnerability index and hot spot analysis: A case study of Kusadasi-Selcuk. Nat. Hazards 2024, 120, 14117–14151. [Google Scholar] [CrossRef]
- Pantusa, D.; D’Alessandro, F.; Frega, F.; Francone, A.; Tomasicchio, G.R. Improvement of a coastal vulnerability index and its application along the Calabria Coastline, Italy. Sci. Rep. 2022, 12, 21959. [Google Scholar] [CrossRef] [PubMed]
- Dal Cin, R.; Simeoni, U. Coastal zoning and vulnerability: Application to the Middle Adriatic (Italy). Coast. Zone 1989, 89, 98–110. [Google Scholar]
- Williams, A.T.; Davies, P.; Chrr, R.; Koh, A.; Bodéré, J.C.; Hallegouet, B. A checklist assessment of dune vulnerability and protection in Devon and Cornwall, UK. Coast. Zone 1993, 93, 3394–3408. [Google Scholar]
- Quelennec, R.E. The Corine ‘Coastal Erosion Project’: Identification of coastal erosion problems and data base on the littoral environment of eleven European countries. Coast. Zone 1989, 89, 4594–4601. [Google Scholar]
- Kantamaneni, K. Coastal infrastructure vulnerability: An integrated assessment model. Nat. Hazards 2014, 84, 139–154. [Google Scholar] [CrossRef]
- Alcántara-Carrió, J.; Echavarría, L.M.G.; Jaramillo-Vélez, A. Is the coastal vulnerability index a suitable index? Review and proposal of alternative indices for coastal vulnerability to sea level rise. Geo-Mar. Lett. 2024, 44, 8. [Google Scholar] [CrossRef]
- Theocharidis, C.; Doukanari, M.; Kalogirou, E.; Christofi, D.; Mettas, C.; Kontoes, C.; Hadjimitsis, D.; Argyriou, A.V.; Eliades, M. Coastal Vulnerability Index (CVI) Assessment: Evaluating Risks Associated with Human-Made Activities along the Limassol Coastline, Cyprus. Remote Sens. 2024, 16, 3688. [Google Scholar] [CrossRef]
- Köroğlu, A.; Ranasinghe, R.; Jimenez, J.; Dastgheib, A. Comparison of coastal vulnerability index applications for Barcelona. Ocean Coast. Manag. 2019, 178, 104799. [Google Scholar] [CrossRef]
- Oloyede, M.O.; Williams, A.B.; Ode, G.O.; Benson, N.U. Coastal Vulnerability Assessment: A Case Study of the Nigerian Coastline. Sustainability 2022, 14, 2097. [Google Scholar] [CrossRef]
- Mullick, R.A.; Tanim, A.H.; Islam, S.M.S. Coastal vulnerability analysis of Bangladesh coast using fuzzy logic based geospatial techniques. Ocean. Coast. Manag. 2019, 174, 154–169. [Google Scholar] [CrossRef]
- Tahri, M.; Maanan, M.; Bouksim, H.; Hakdaoui, M. Using Fuzzy Analytic Hierarchy Process multi-criteria and automatic computation to analyse coastal vulnerability. Prog. Phys. Geogr. 2017, 41, 268–285. [Google Scholar] [CrossRef]
- Hammar-Klose, E.S.; Thieler, E.R. Coastal Vulnerability to Sea-Level Rise: A preliminary Database for the US Atlantic, Pacific and Gulf of Mexico Coasts. US Geological Survey, Coastal and Marine Geology Program. 2001. Available online: https://pubs.usgs.gov/dds/dds68/htmldocs/project.htm (accessed on 30 March 2019).
- Hamid, A.I.A.; Din, A.H.M.; Yusof, N.; Abdullah, N.M.; Omari, A.H.; Khanan, M.F.A. Coastal Vulnerability Index Development: A review. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2019 6th International Conference on Geomatics and Geospatial Technology (GGT 2019), Kuala Lumpur, Malaysia, 1–3 October 2019; Volume XLII-4/W16. [Google Scholar]
- Zadeh, L.A. Fuzzy algorithms. Inf. Control 1968, 12, 94–102. [Google Scholar] [CrossRef]
- Zadeh, L.A. Towards a theory of fuzzy systems. In Aspects of Network and System Theory; Kalman, R.E., DeClaris, N., Eds.; World Scientific Publishing Co Pte Ltd.: Singapore, 1971. [Google Scholar]
- Ross, J.T. Fuzzy Logic with Engineering Applications; McGraw-Hill, Inc.: New York, NY, USA, 1995; p. 593. [Google Scholar]
- Şen, Z. Fuzzy Logic and Hydrological Modeling; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: Oxfordshire, UK, 2020; p. 340. [Google Scholar]
- Gornitz, V.; Daniels, R.C.; White, T.W.; Birdwell, K.R. The Development of a Coastal Risk Assessment Database: Vulnerability to Sea-Level Rise in the U.S. Southeasts (DE-AC05-84OR21400); US Government Report, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1993. [Google Scholar]
- Shaw, J.; Taylor, R.B.; Forbes, D.L.; Ruz, M.H.; Solomon, S. Sensitivity of the Coasts of Canada to Sea-Level Rise; Geological Survey of Canada: Ottawa, Canada, 1998; Volume 505, pp. 1–7. [Google Scholar]
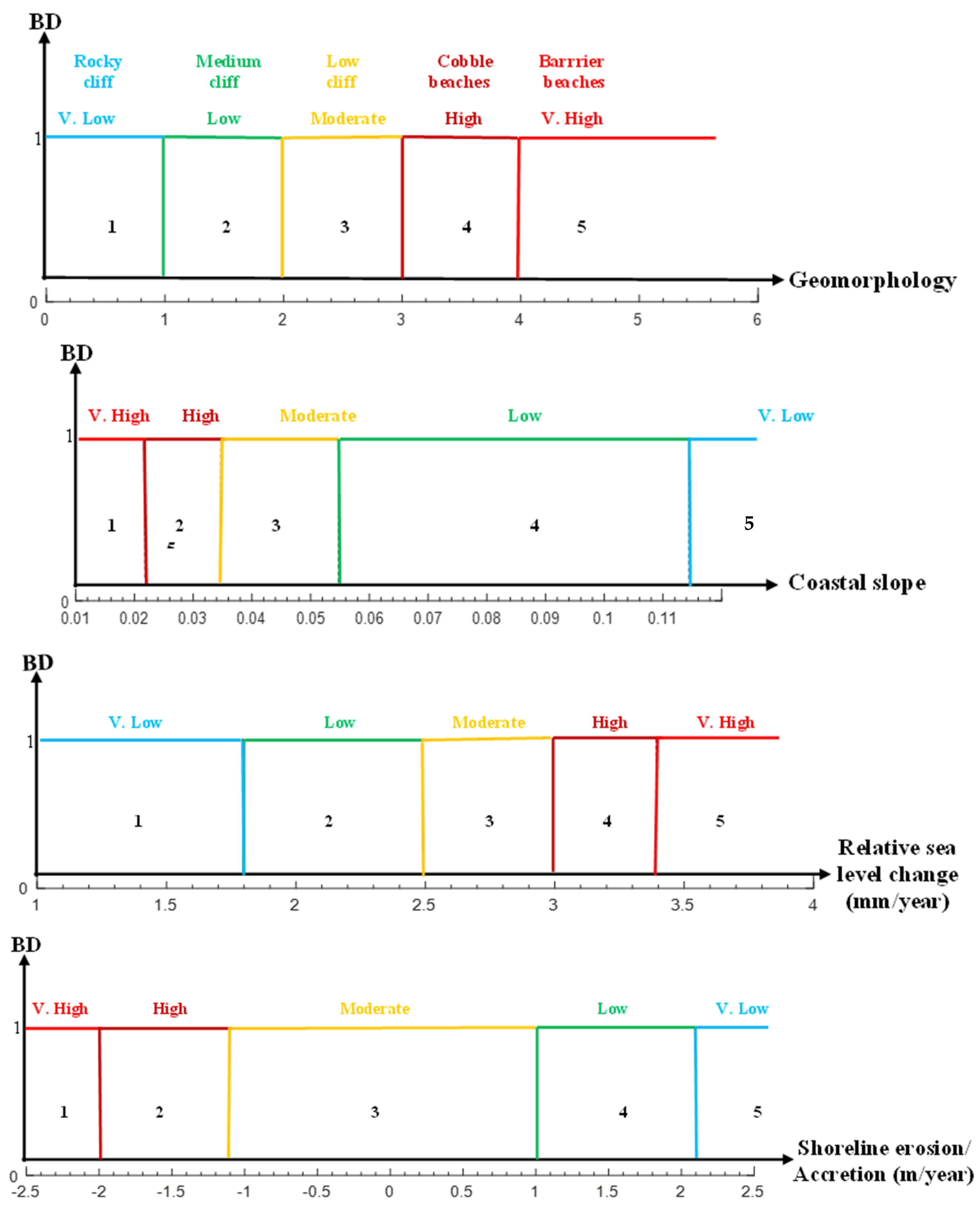
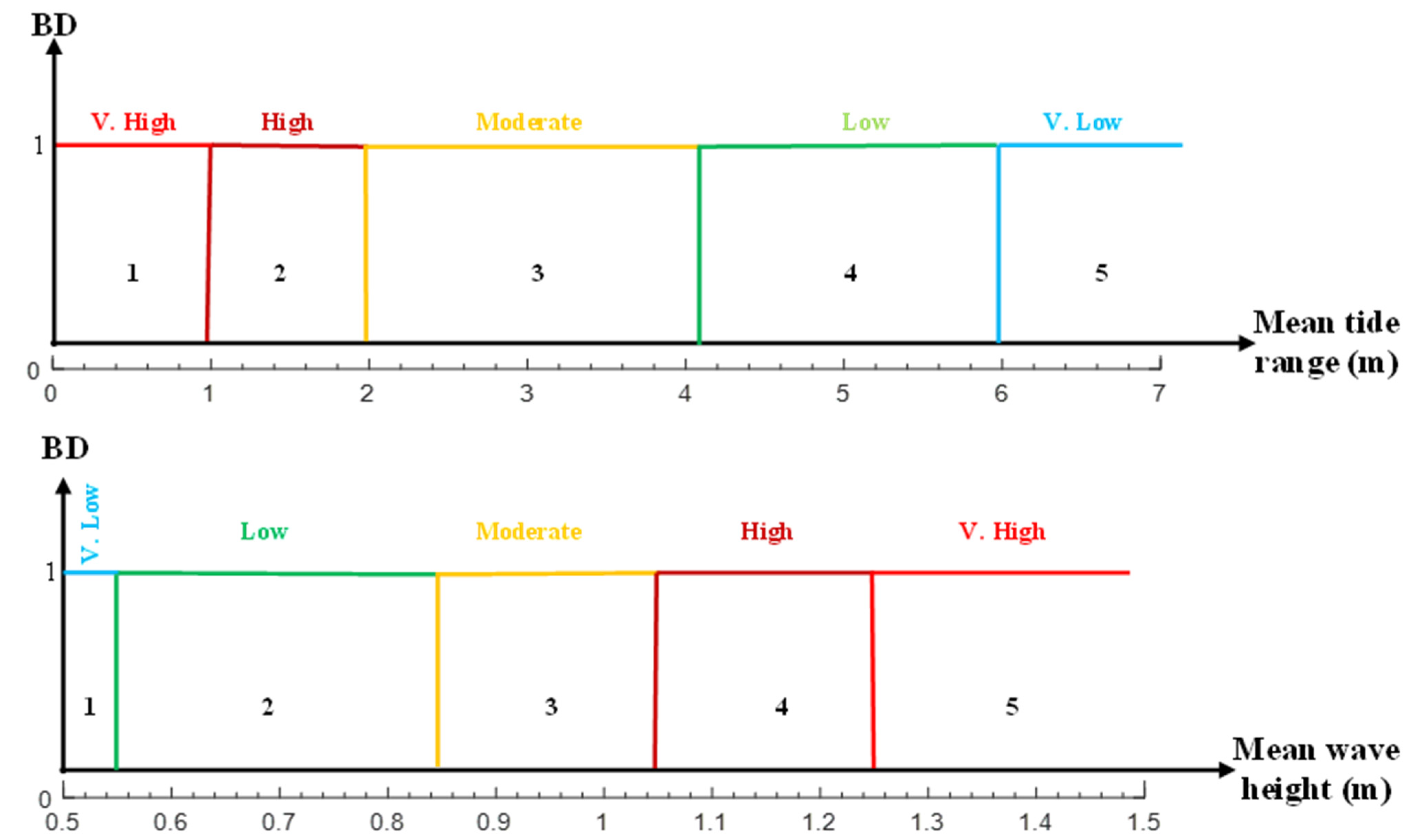
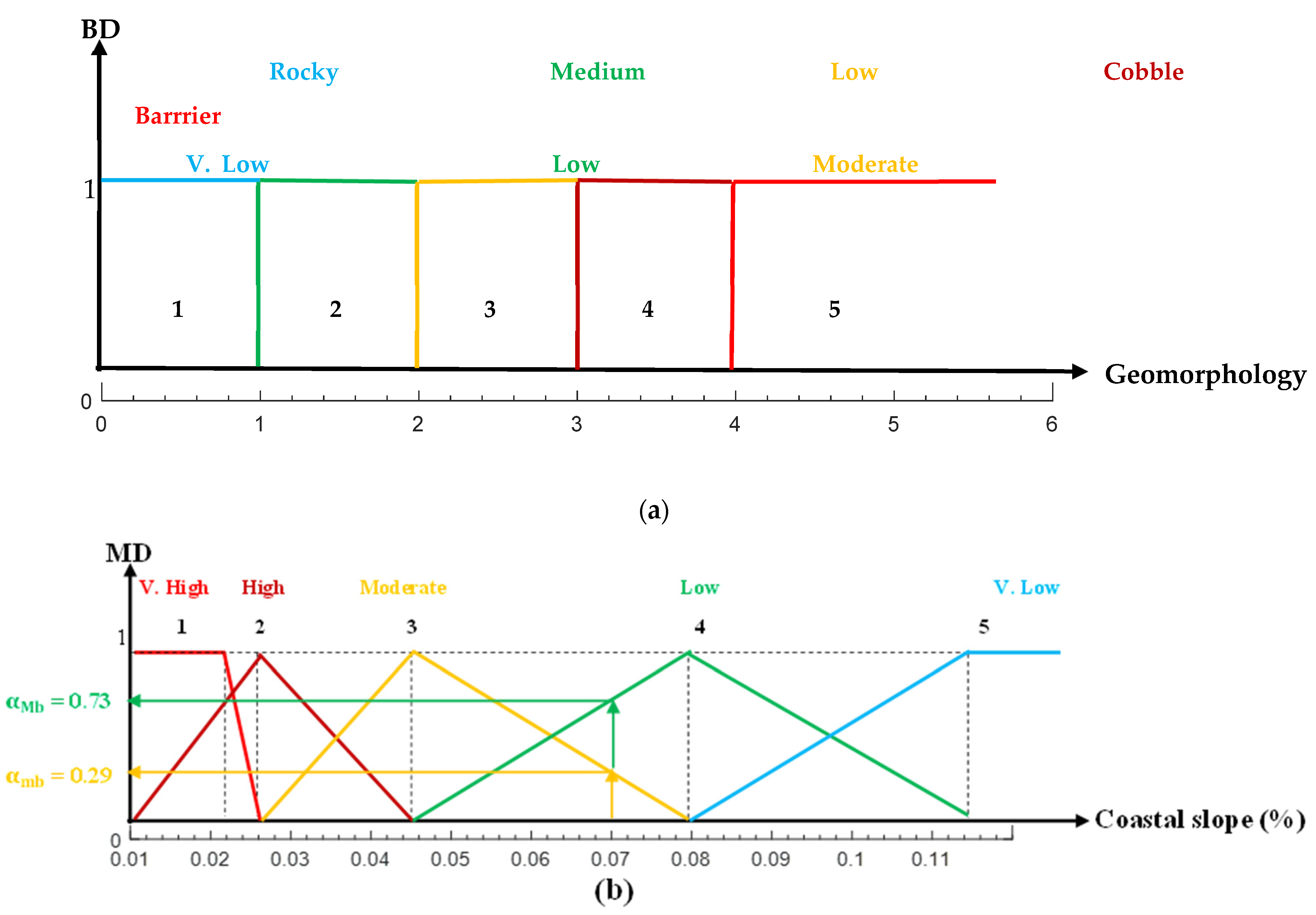
| Variables | Classifications | ||||
|---|---|---|---|---|---|
| “Very low” | “Low” | “Moderate” | “High” | “Very high” | |
| 1 | 2 | 3 | 4 | 5 | |
| Geomorphology | Rocky, cliffed coasts, Fjords, Fjards | Medium cliffs, Indented coasts | Low cliffs, Glacial drift, Alluvial plains | Cobble beaches, Estuary, Lagoon | Barrier and sand beaches, Salt marshes, Mud flats, Deltas, Mangrove, Coral reefs |
| Coastal slope (%) | >0.115 | 0.115–0.055 | 0.055–0.035 | 0.035–0.022 | <0.022 |
| Relative sea level Change (mm/year) | <1.8 | 1.8–2.5 | 2.5–3.0 | 3.0–3.4 | >3.4 |
| Shoreline erosion/ Accretion (m/year) | >2.0 Accretion | 1.0–2.0 | −1.0–+1.0 Stable | −1.0–−2.0 | <−2.0 Erosion |
| Mean tide range (m) | >6.0 | 4.0–6.0 | 2.0–4.0 | 1.0–2.0 | <1.0 |
| Mean wave height (m) | <0.55 | 0.55–0.85 | 0.85–1.05 | 1.05–1.25 | >1.25 |
| Variable Names | Vulnerability | Data Values | CFVI Calculations | |||
|---|---|---|---|---|---|---|
| Geomorphology | “Moderate” | 0.55 | 0.39 | 2.6 | 1.43 | 1.01 |
| Coastal slope | “Low | 0.73 | 0.29 | 0.1 | 0.05 | 0.02 |
| Relative sea level change (m/year) | “High” | 0.57 | 0.57 | 3.3 | 1.88 | 1.88 |
| Shoreline erosion | “Moderate” | 0.64 | 0.37 | −0.5 | −0.32 | −0.19 |
| Mean tide range (m) | “High” | 0.81 | 0.20 | 1.8 | 1.46 | 0.36 |
| Mean wave height (m) | “Low” | 0.60 | 0.40 | 0.8 | 0.48 | 0.32 |
| SUM | 3.90 | 2.22 | 4.98 | 3.41 | ||
| CFVImin = 1.28 | CFVIMax = 1.54 | |||||
| Variable Names | Vulnerability | Data Values | CFVI Calculations | |||
|---|---|---|---|---|---|---|
| Geomorphology | “High” | 0.69 | 0.32 | 4.30 | 2.97 | 1.38 |
| Coastal slope | “Moderate” | 0.56 | 0.42 | 0.04 | 0.02 | 0.01 |
| Relative sea level change (m/year) | “Moderate” | 0.57 | 0.55 | 2.50 | 1.43 | 1.38 |
| Shoreline erosion | “Low” | 0.99 | 0.01 | 1.50 | 1.49 | 0.02 |
| Mean tide range (m) | “Moderate” | 0.81 | 0.15 | 2.80 | 2.27 | 0.42 |
| Mean wave height (m) | “High” | 0.78 | 0.78 | 1.10 | 0.86 | 0.86 |
| SUM | 4.40 | 2.23 | 9.02 | 4.06 | ||
| CFVIMax = 2.05 | CFVImin = 1.82 | |||||
| Variable Names | Vulnerability | Maximum Data Values | Minimum Data Values | CFVI Calculations | |||
|---|---|---|---|---|---|---|---|
| Geomorphology | “Moderate” | 1.00 | 1.00 | 5.00 | 1.0 | 5.00 | 1.00 |
| Coastal slope | “Low | 1.00 | 1.00 | 0.12 | 0.1 | 0.12 | 0.12 |
| Relative sea level change (m/year) | “High” | 1.00 | 1.00 | 3.40 | 1.6 | 3.40 | 1.60 |
| Shoreline erosion | “Moderate” | 1.00 | 1.00 | 2.50 | −2.0 | 2.50 | −2.00 |
| Mean tide range (m) | “High” | 1.00 | 1.00 | 6.00 | 1.0 | 6.00 | 1.00 |
| Mean wave height (m) | “Low” | 1.00 | 1.00 | 1.25 | 0.6 | 1.25 | 0.55 |
| SUM | 6.00 | 6.00 | 18.27 | 2.27 | |||
| CFVIMax = 3.04 | CFVImin = 0.38 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şen, Z. Navigating Coastal Vulnerability: Introducing the Coastal Fuzzy Vulnerability Index (CFVI). J. Mar. Sci. Eng. 2025, 13, 978. https://doi.org/10.3390/jmse13050978
Şen Z. Navigating Coastal Vulnerability: Introducing the Coastal Fuzzy Vulnerability Index (CFVI). Journal of Marine Science and Engineering. 2025; 13(5):978. https://doi.org/10.3390/jmse13050978
Chicago/Turabian StyleŞen, Zekâi. 2025. "Navigating Coastal Vulnerability: Introducing the Coastal Fuzzy Vulnerability Index (CFVI)" Journal of Marine Science and Engineering 13, no. 5: 978. https://doi.org/10.3390/jmse13050978
APA StyleŞen, Z. (2025). Navigating Coastal Vulnerability: Introducing the Coastal Fuzzy Vulnerability Index (CFVI). Journal of Marine Science and Engineering, 13(5), 978. https://doi.org/10.3390/jmse13050978