Study on Suppression of Vortex-Induced Vibrations of a Rotating Cylinder with Dual Splitter Plates
Abstract
1. Introduction
2. Numerical Approach
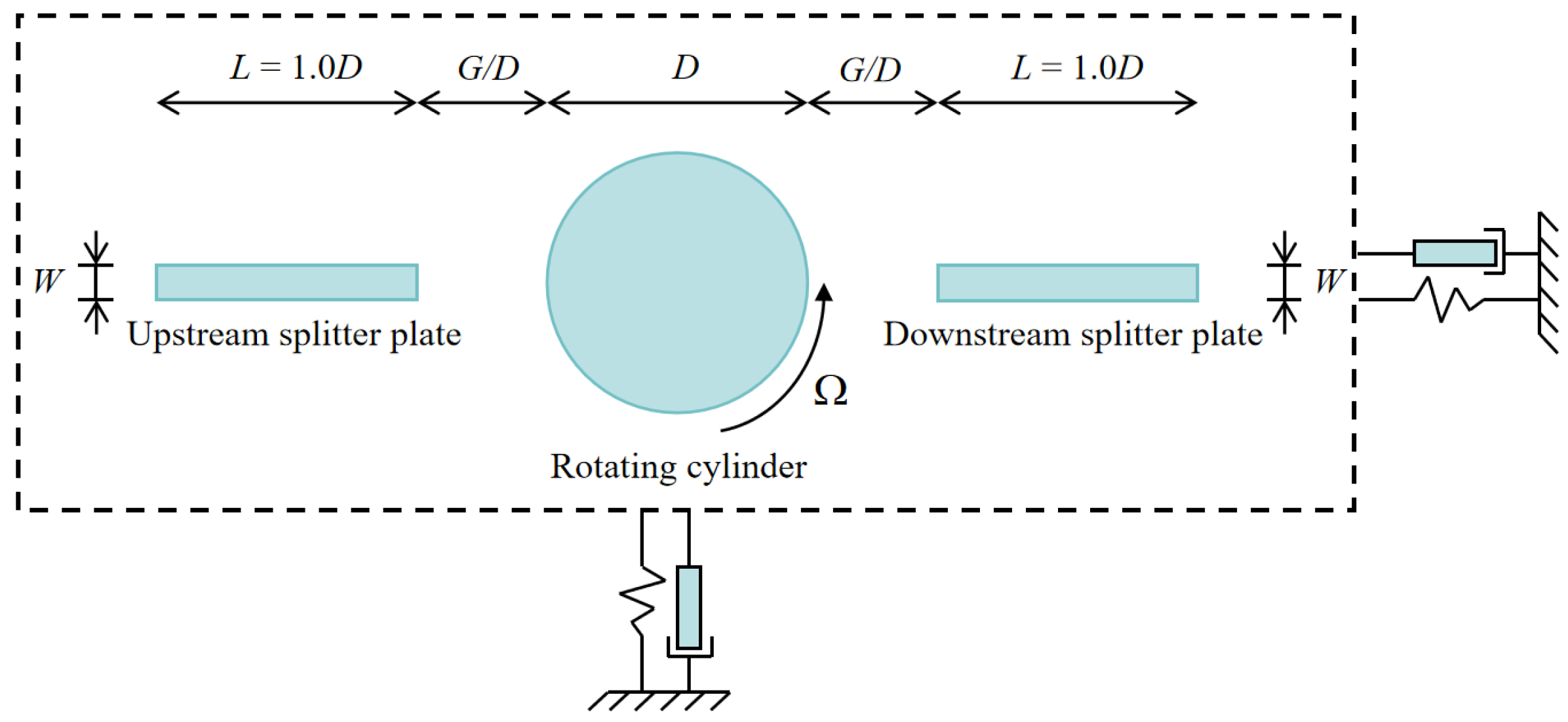
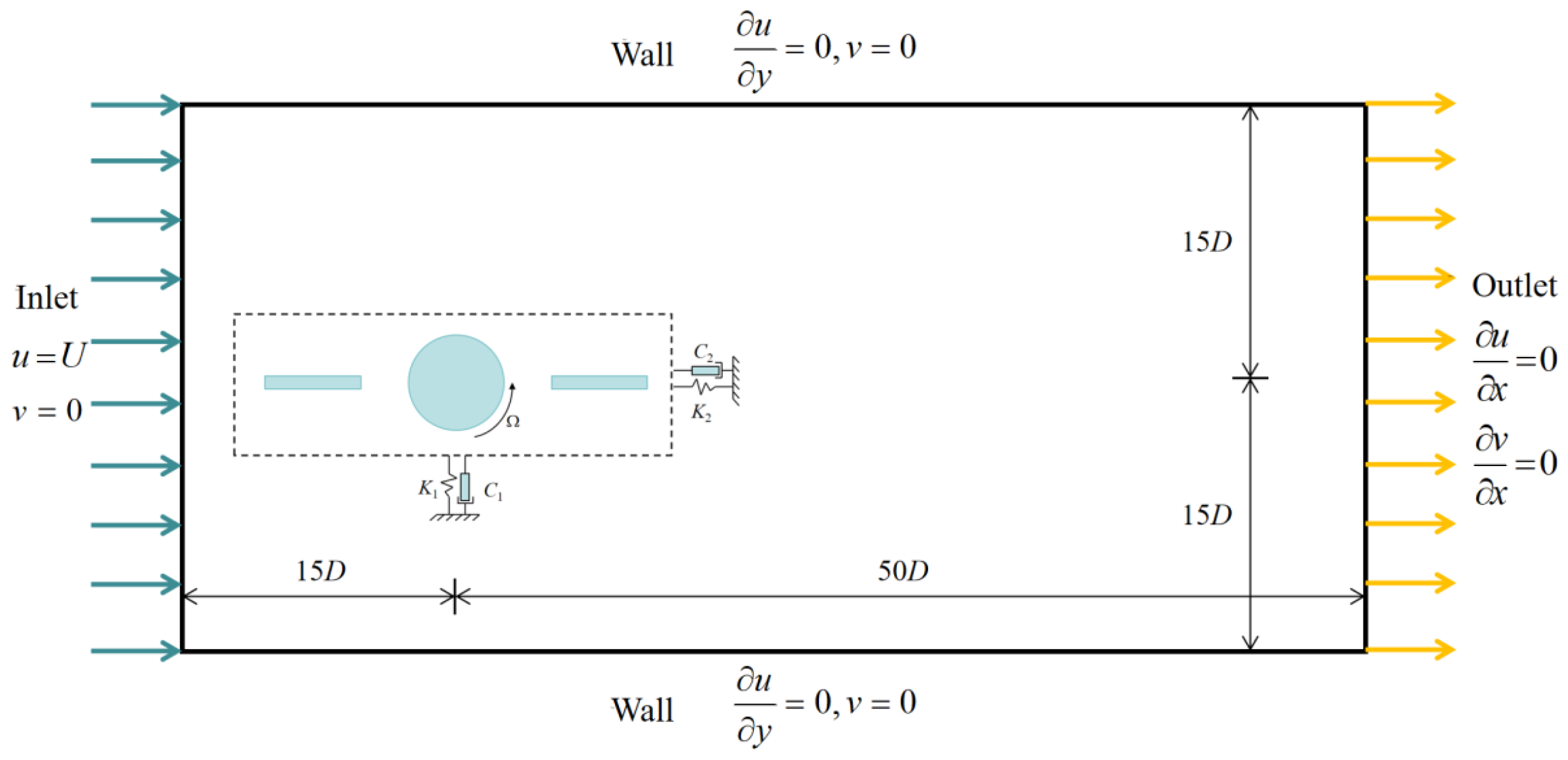
2.1. Problem Description and Computational Model
2.2. Governing Equations and Numerical Method
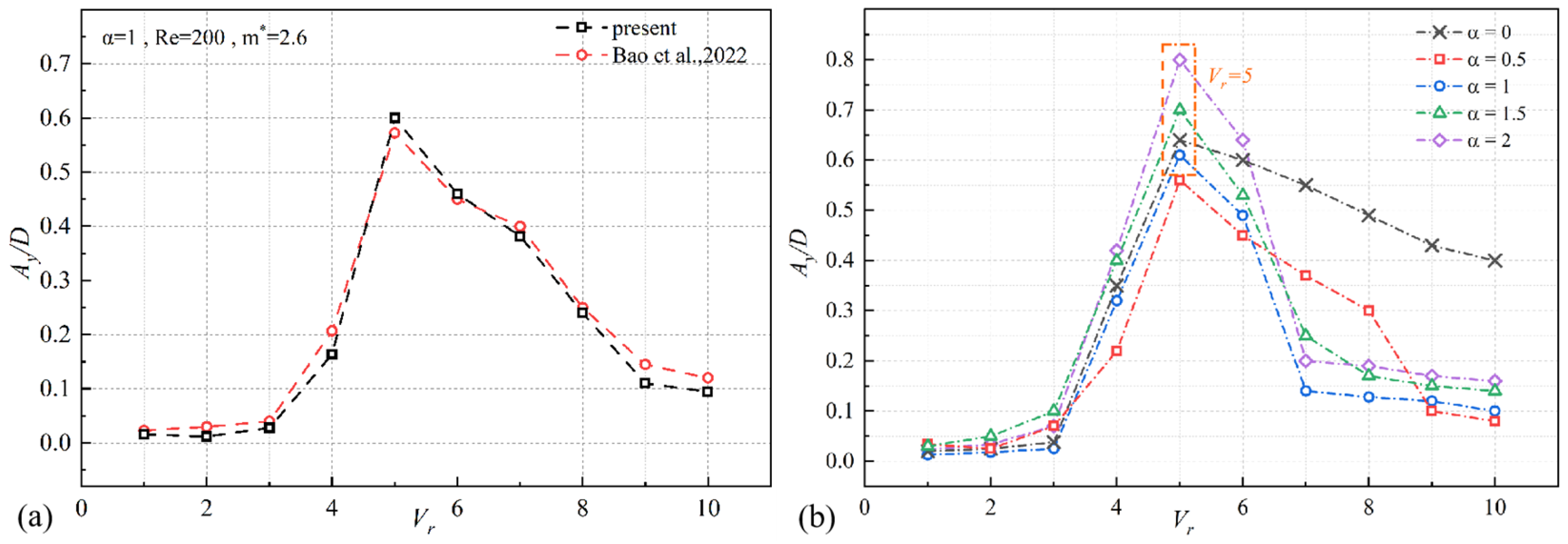
3. Mesh Dependency Study and Validation
4. Results and Discussion
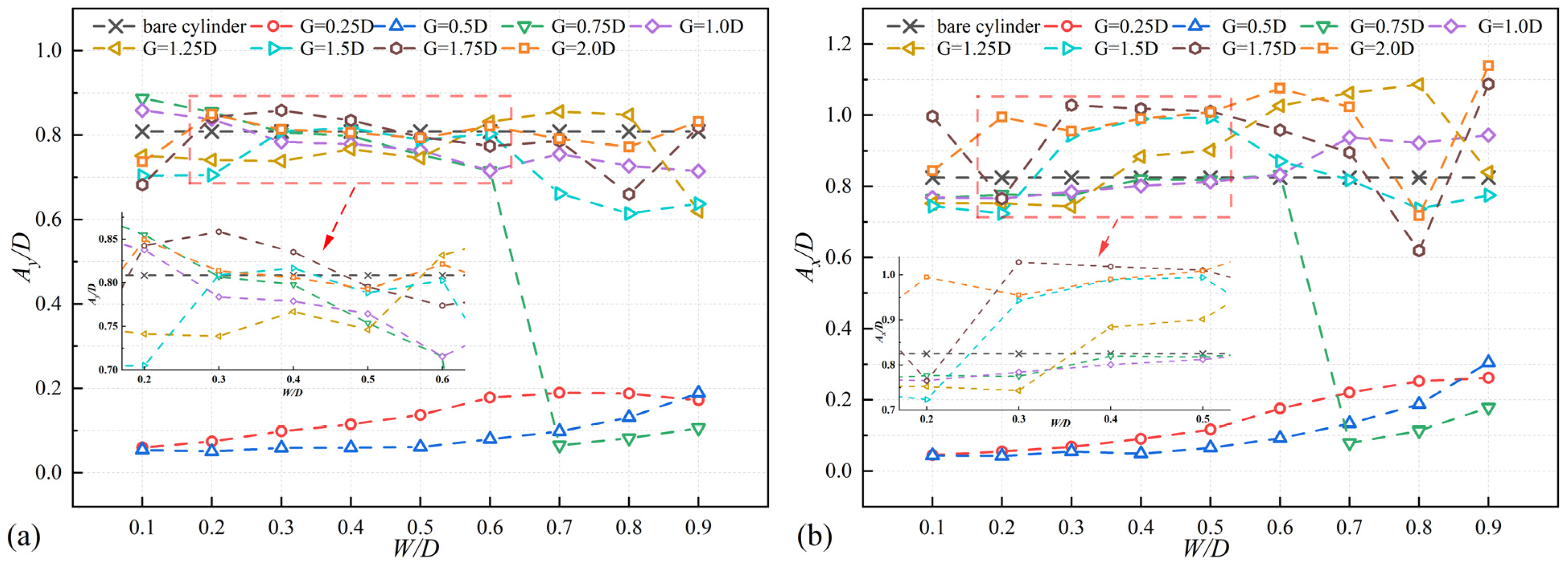
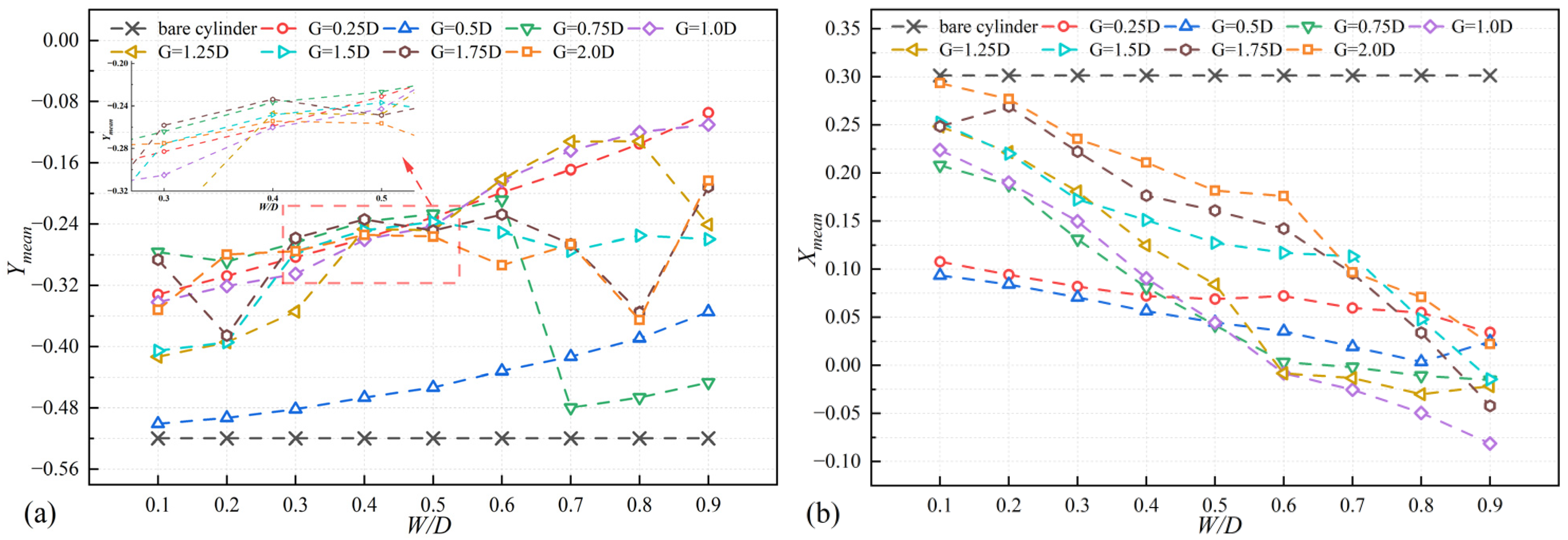
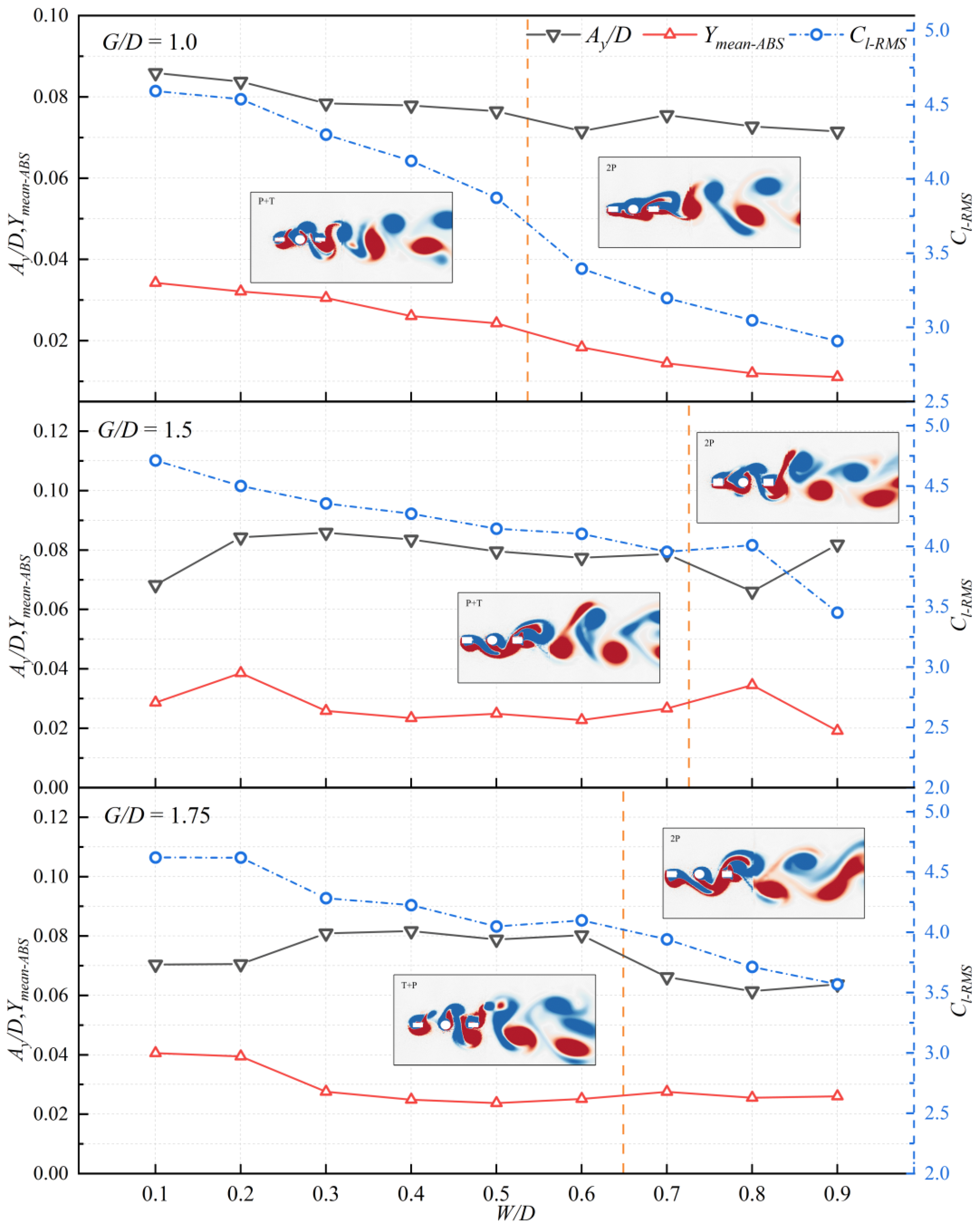
4.1. Response Amplitude
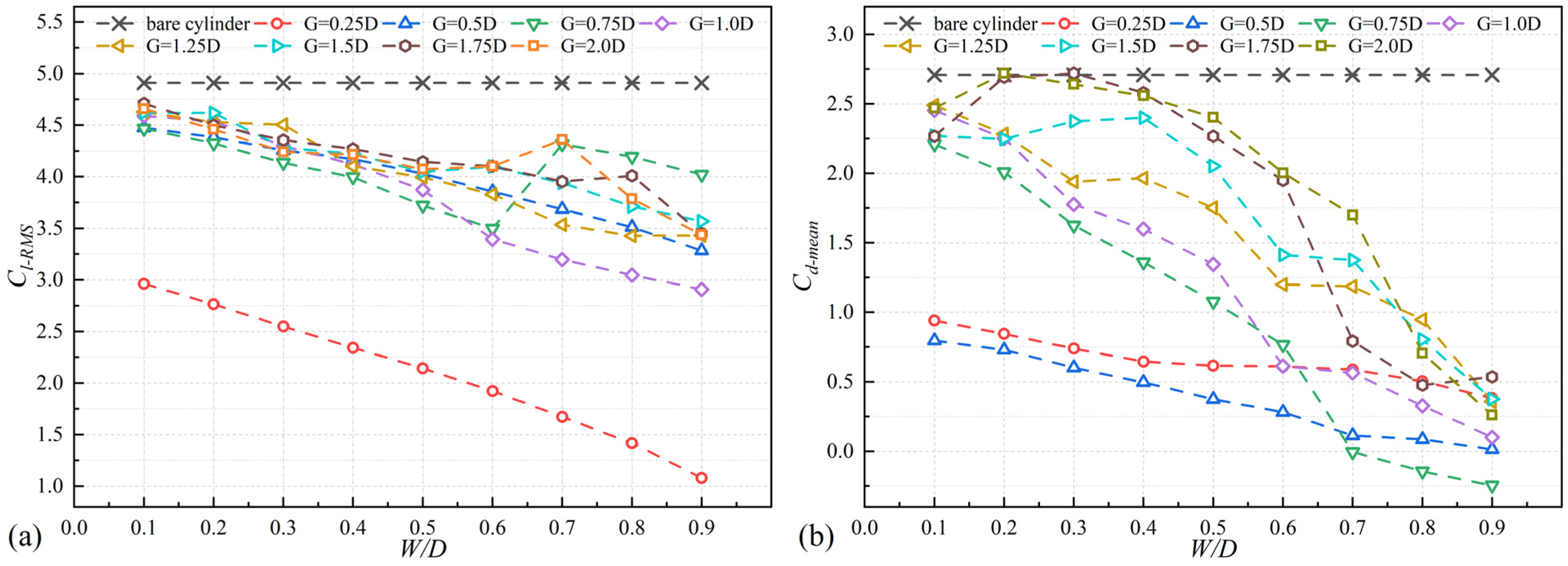
4.2. Hydrodynamics Coefficients
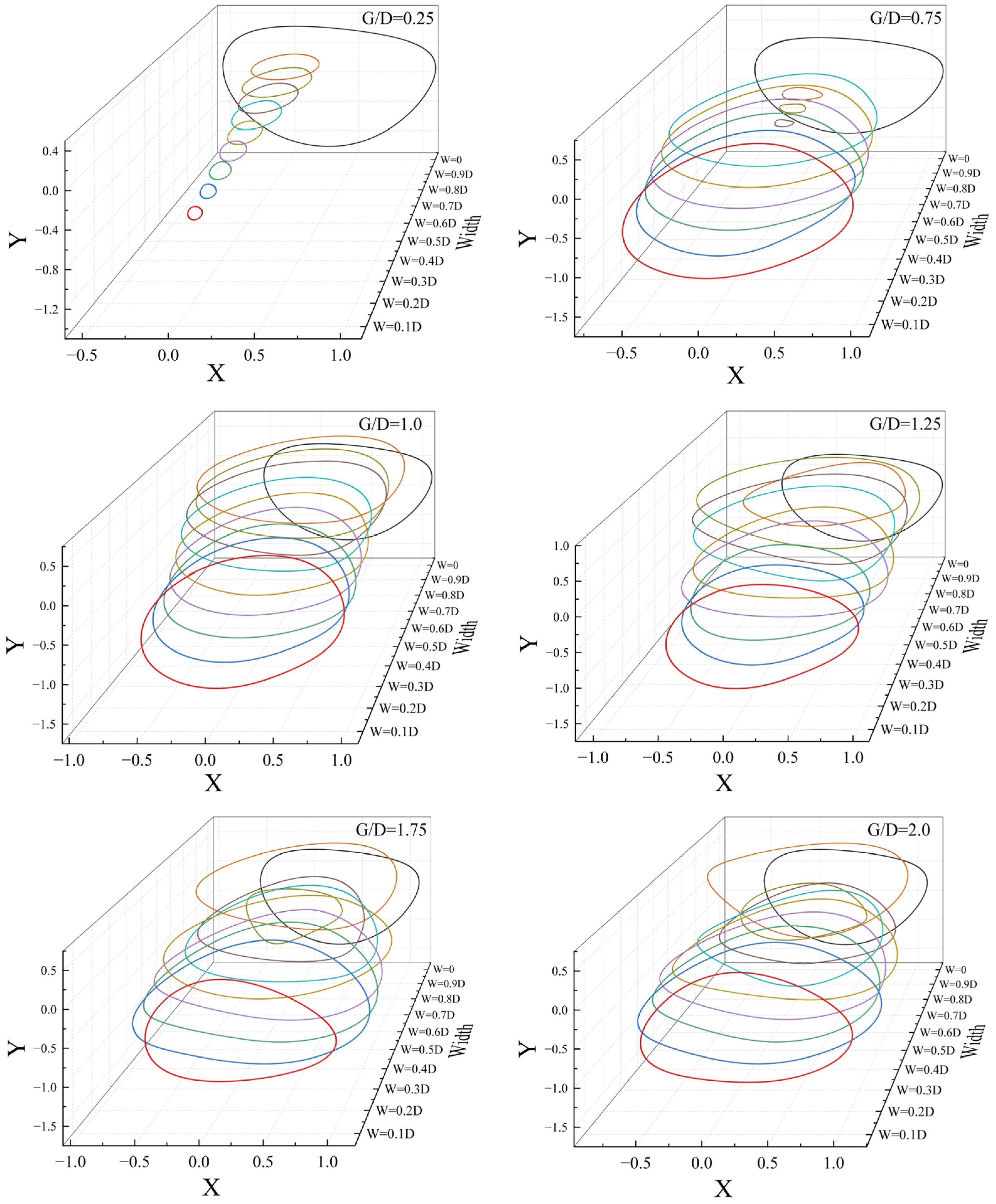
4.3. Cylindrical Vibration Trajectory
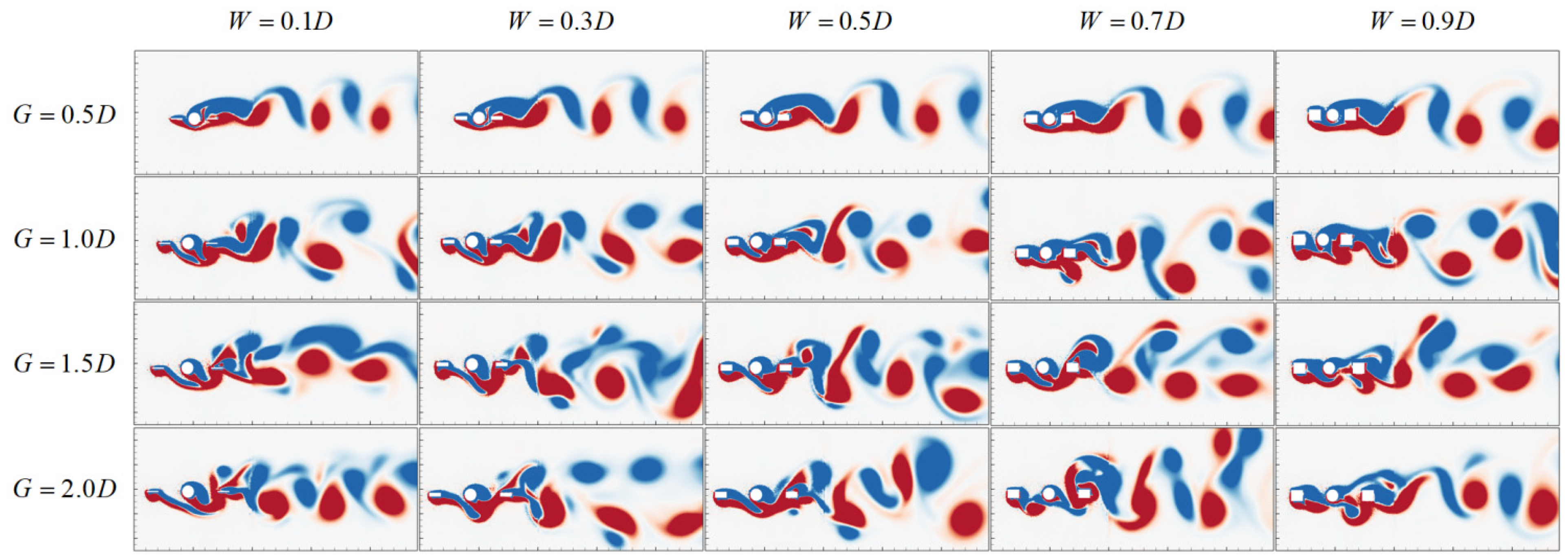
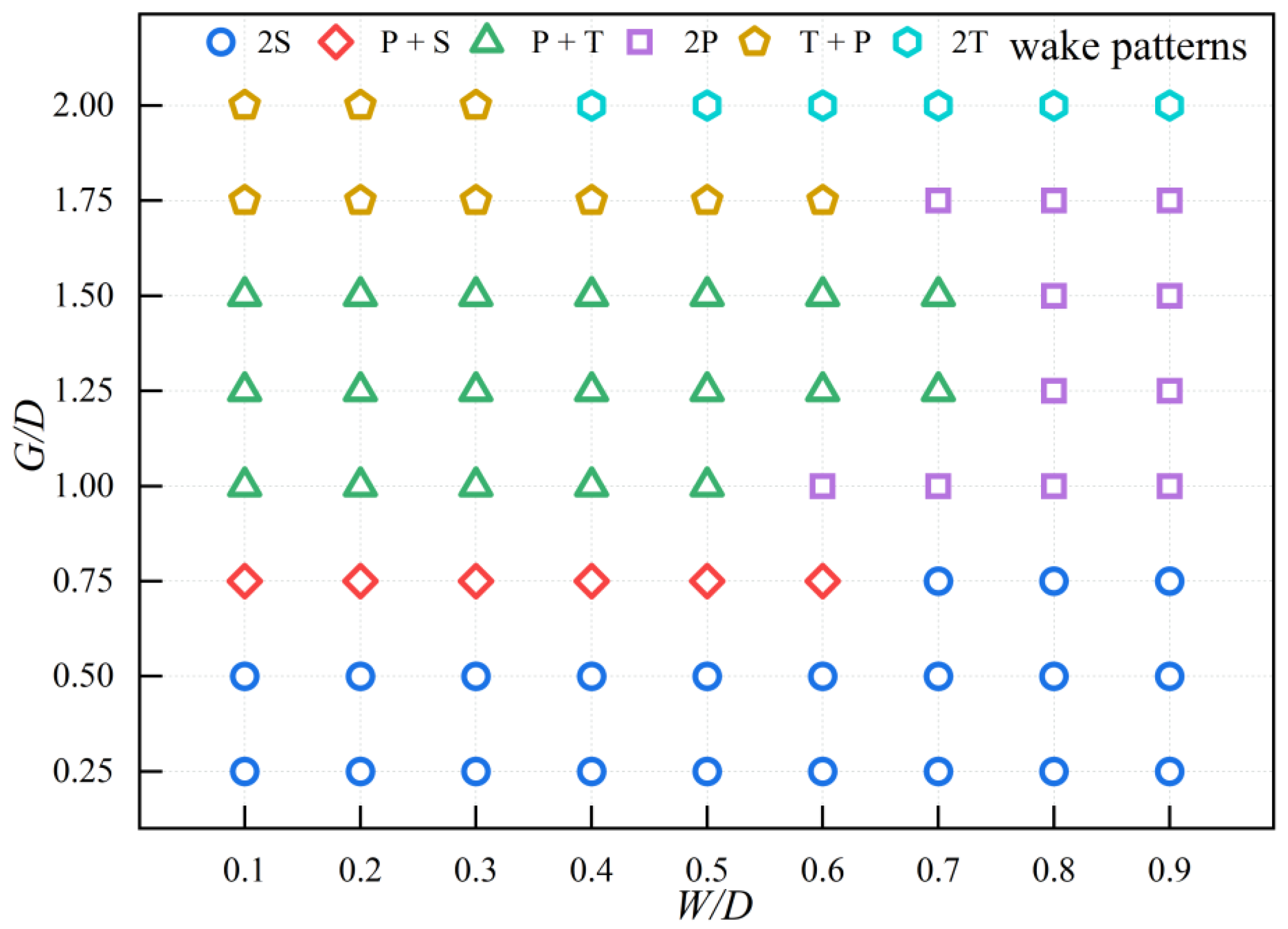
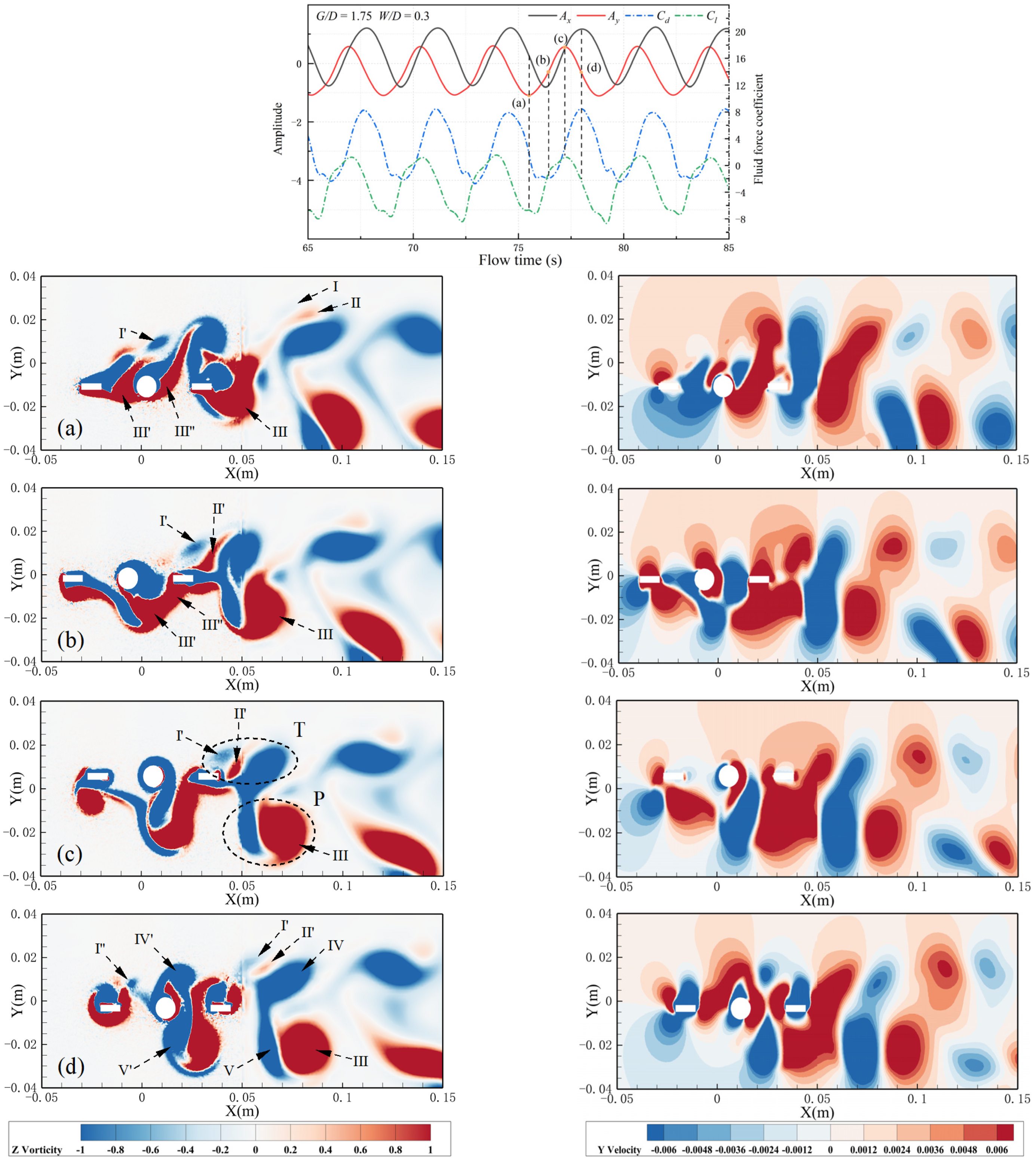
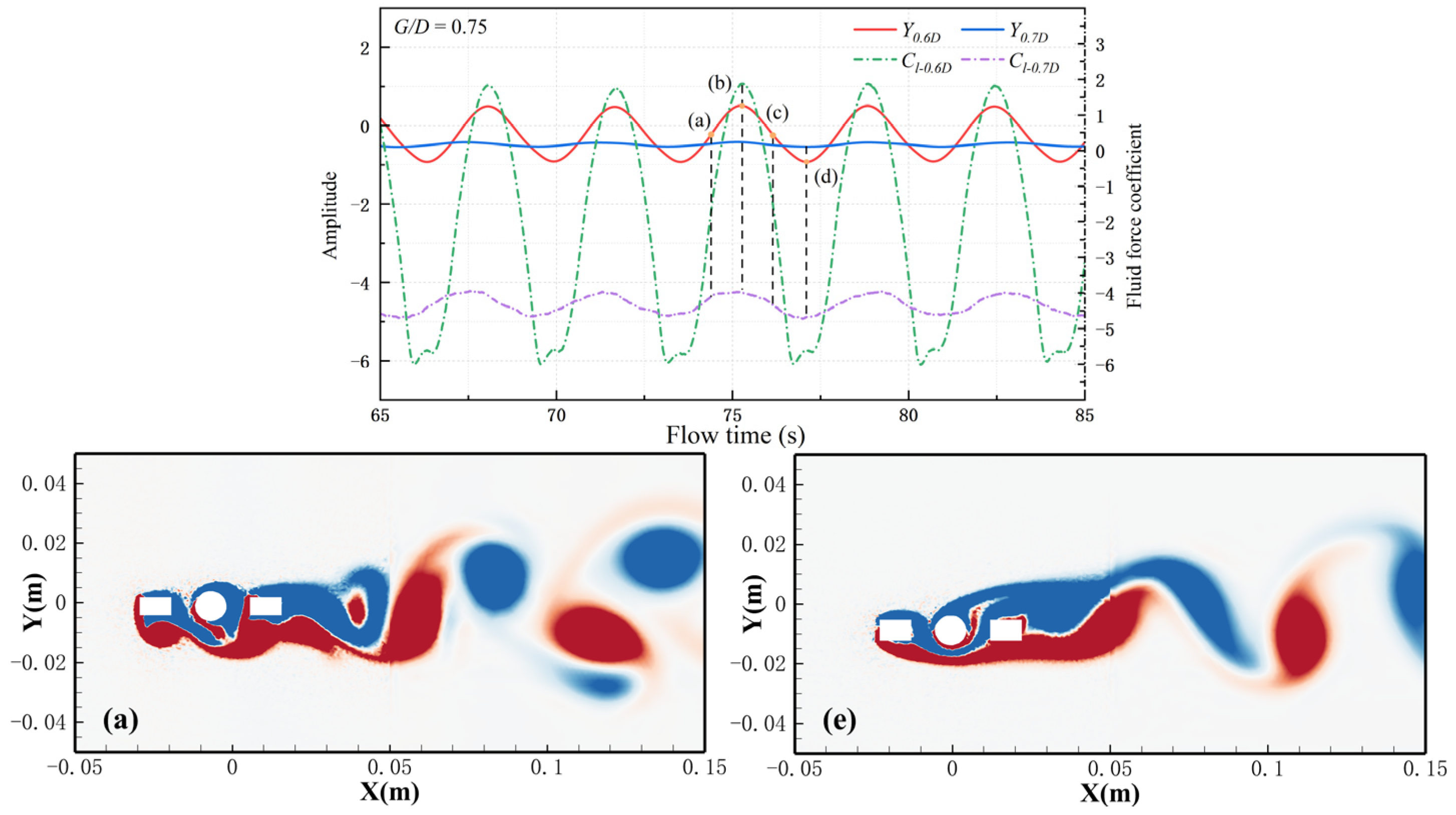
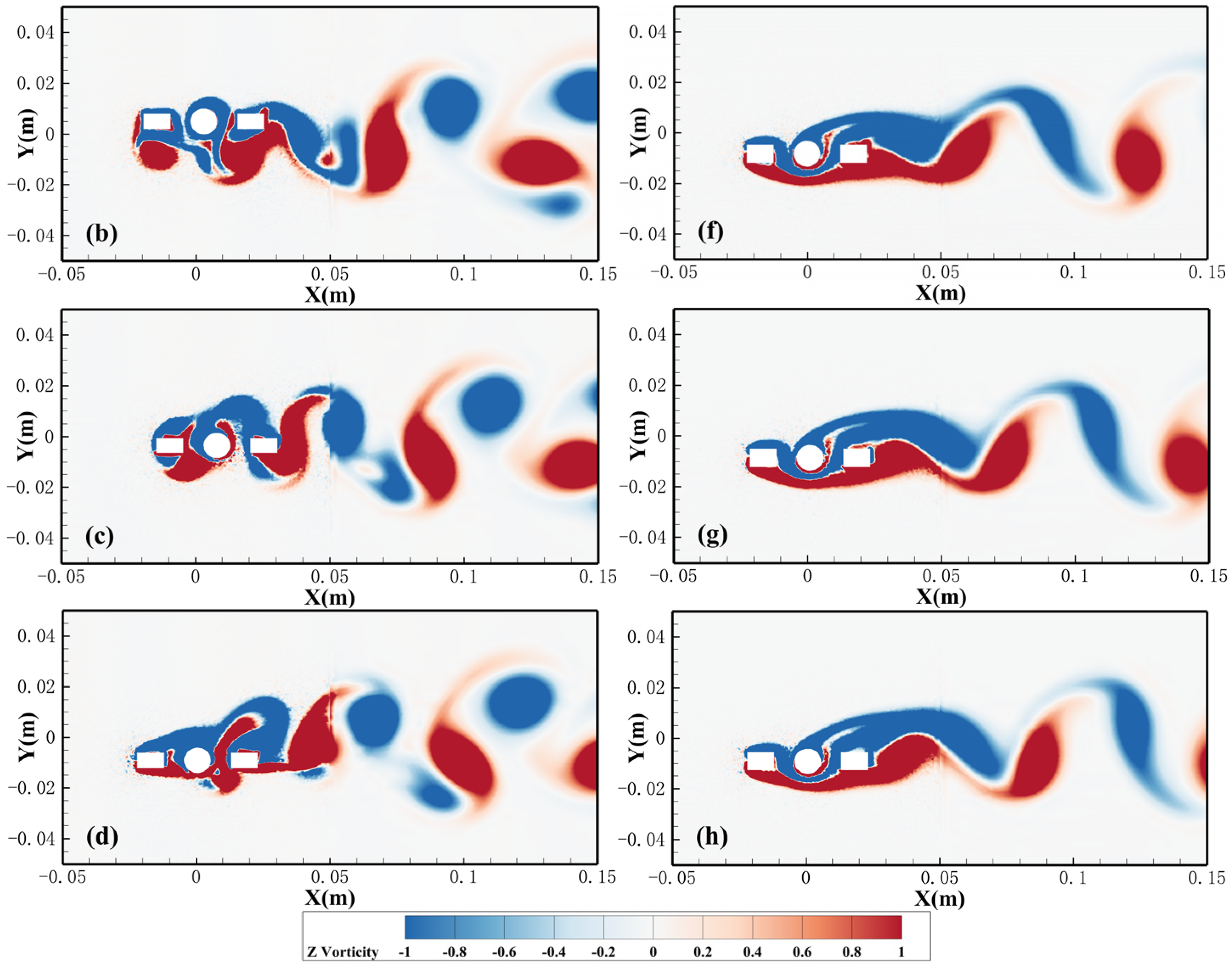
4.4. Wake Pattern
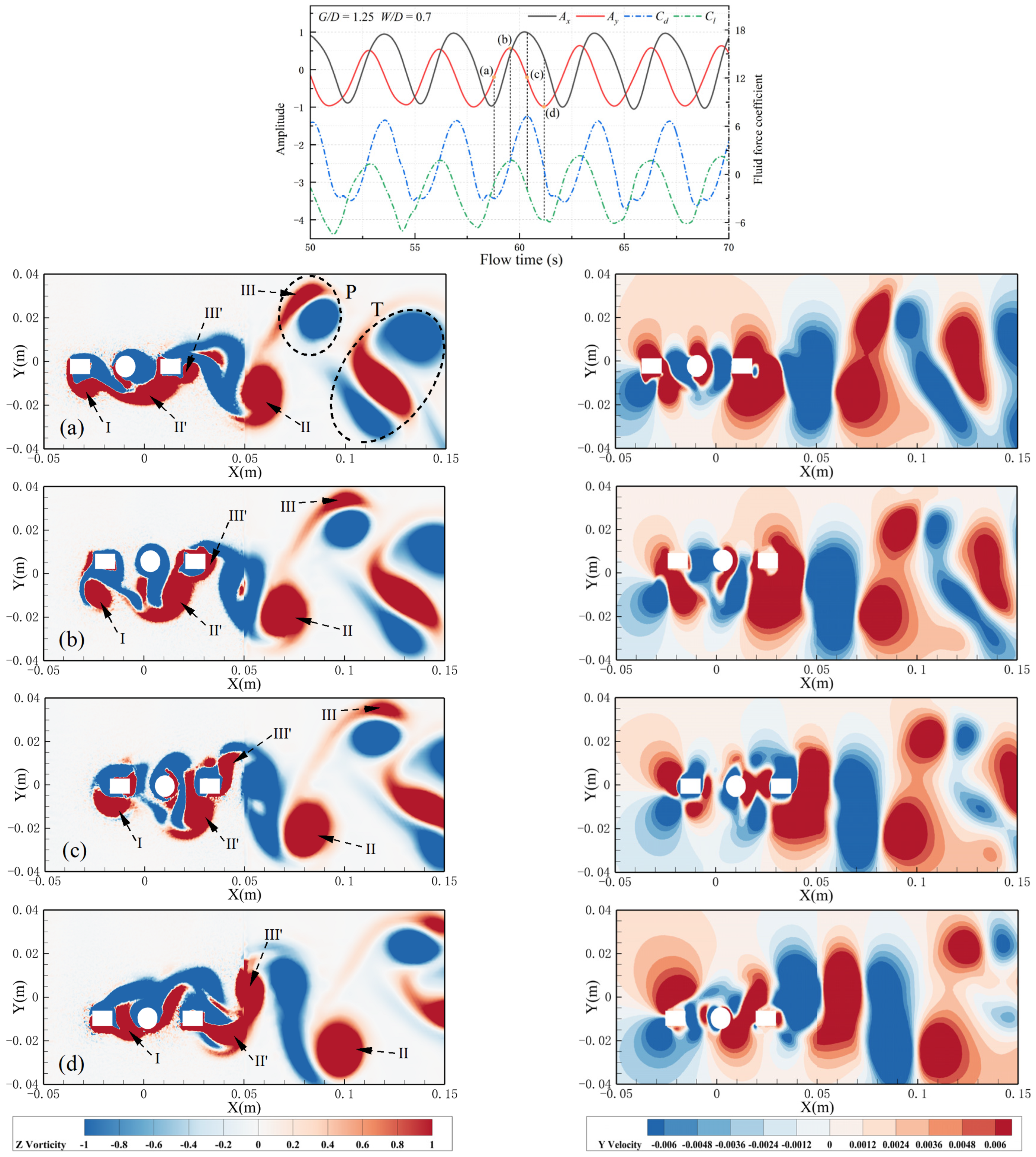
4.5. Vibration–Hydrodynamic–Wake Interactions
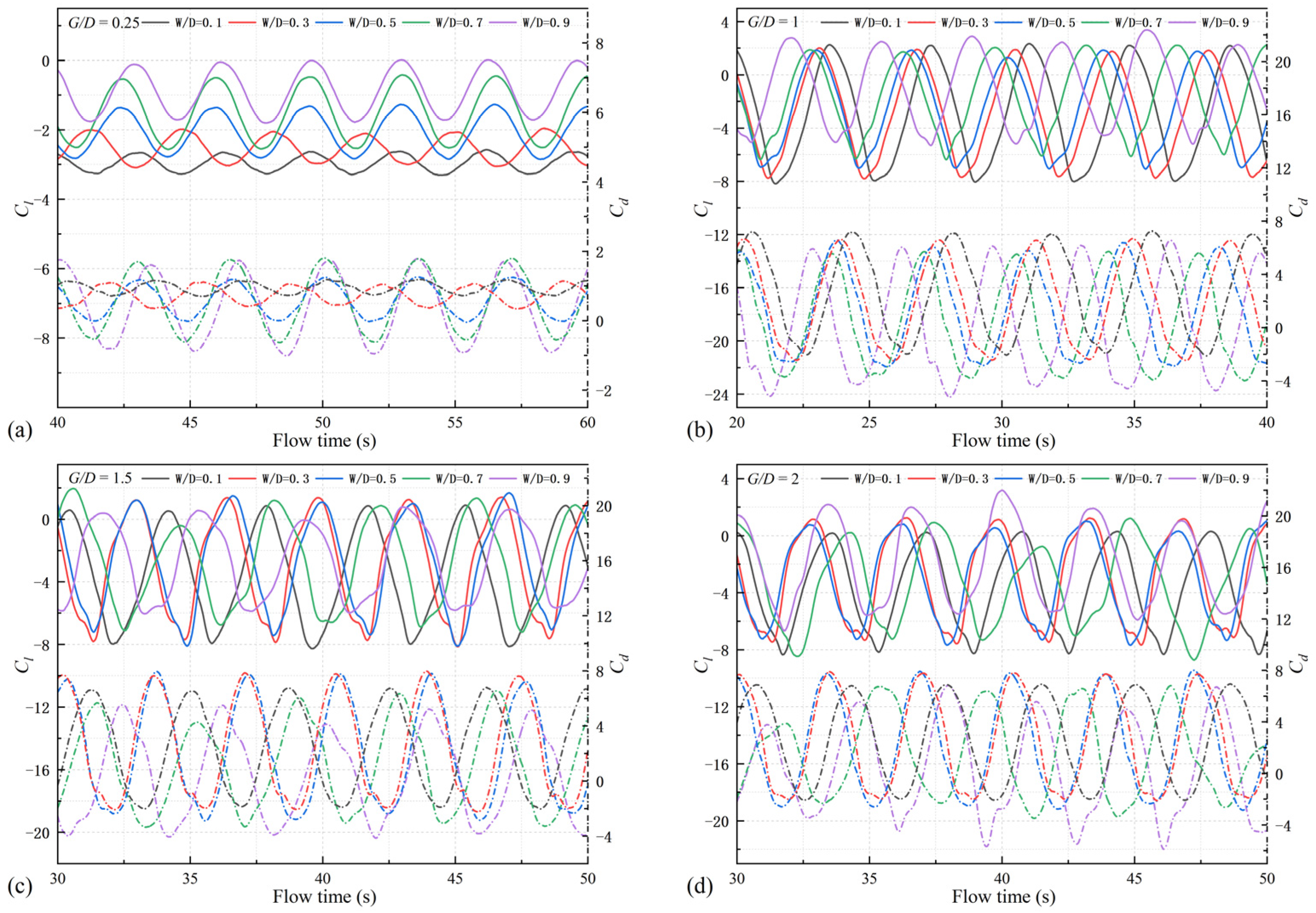
4.6. Lift and Drag Force Sensitivity
5. Conclusions
- (1)
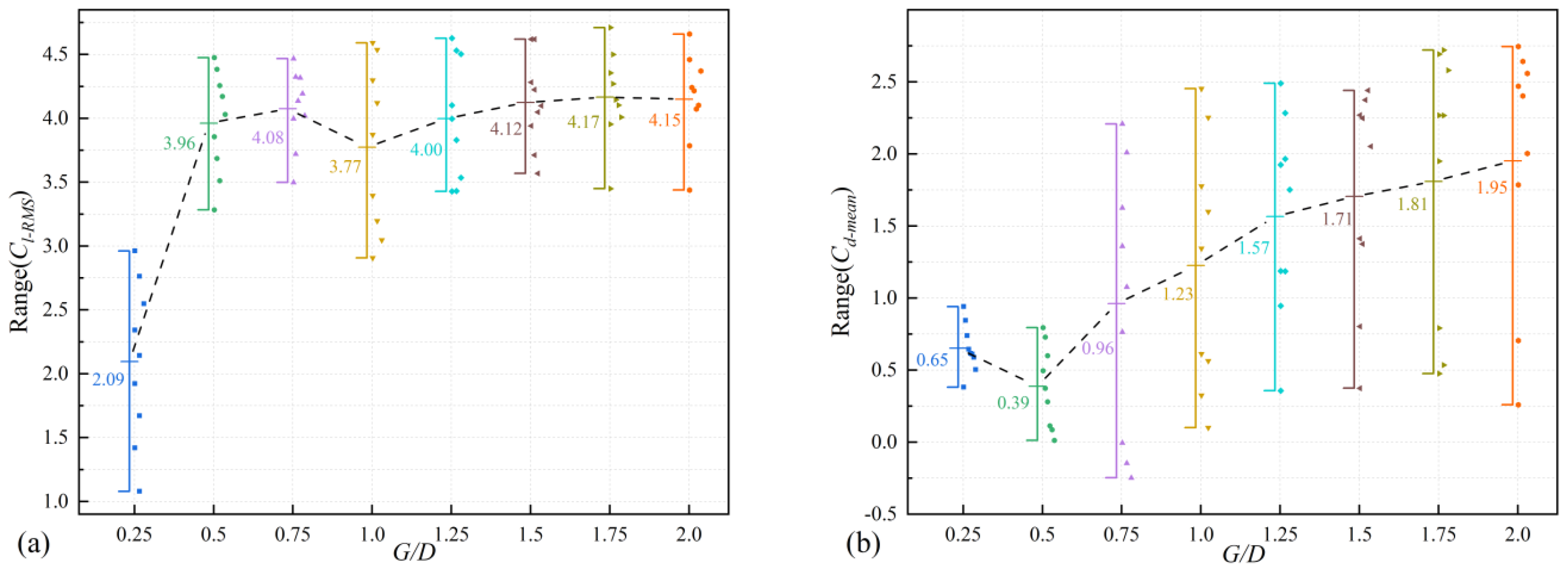
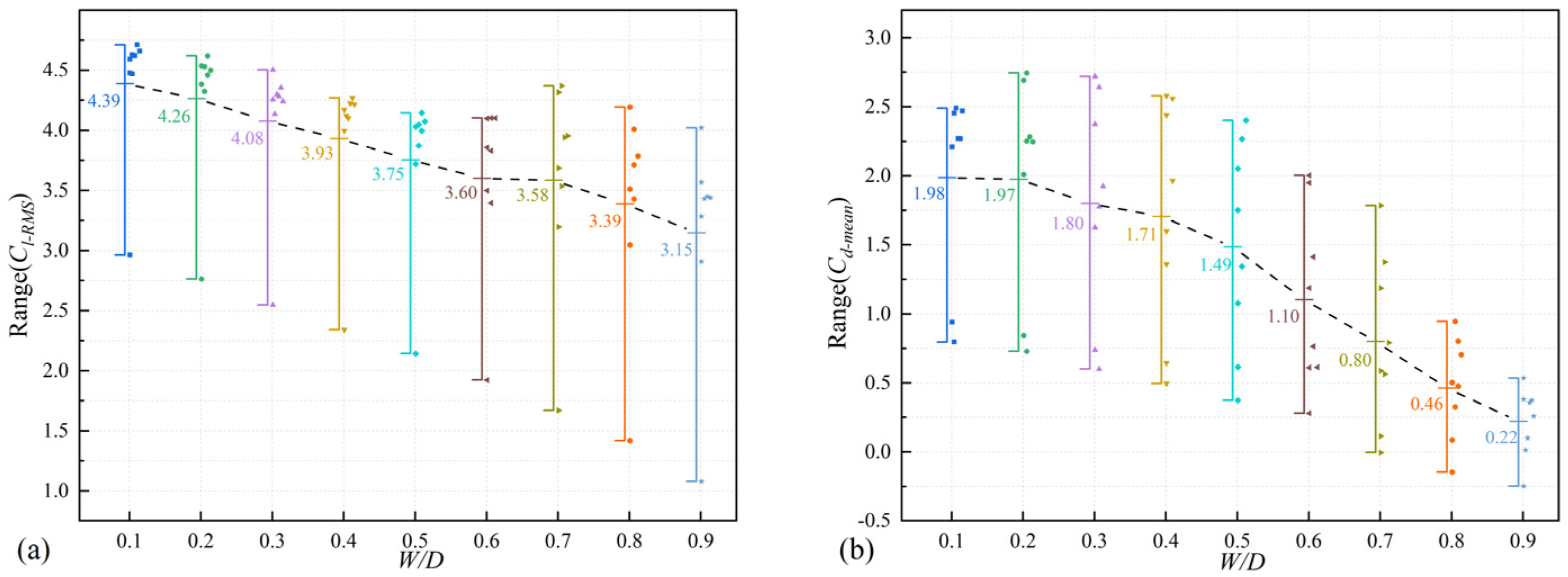
- There is a clear difference in amplitude and lift–drag curves between low gap distances and high gap distances. At low gap distances, the amplitude is low and increases with an increase in the width. In contrast, at high gap distances, the amplitude is high and less influenced by the width. At low gap distances (G/D = 0.25, 0.5), both cross-flow and in-line displacements change smoothly with minimal variation. For high gap distances (G/D > 0.5), selecting an appropriate width can achieve in-line mean displacement (Xmean) of 0. Both the mean drag coefficient (Cd-mean), and the root mean square of the lift coefficient (Cl-RMS) shows a decreasing trend as the width increases. The width has a significant suppression effect on Cd-mean and Cl-RMS.
- (2)
- Six different wake patterns are observed under different gap distances and widths. Changes in gap distance and width can lead to transformations in wake patterns. At gap distances of G/D = 0.25 and 0.5, the wake pattern remains a stable 2S pattern regardless of the width. For G/D = 0.75, when the width (W/D) reaches 0.7, the vortex shedding pattern transitions from the original P+S pattern to a 2S pattern. For G/D = 1.75, with an increase in the width, the vortex shedding pattern shifts from the original T+P pattern to a 2P pattern, and one negative vortice that detaches from the upstream splitter plate disappears. The number of shedding vortices increases, along with their merging and disappearance, combined with the interactions between vortice force fields, results in increasingly complex and unstable vortex shedding behaviors. The complex and unstable vortex behaviors can lead to uneven forces and amplify the vibration response of the cylinder, which compromises structure stability.
- (3)
- The sensitivity of lift and drag coefficients to variations in gap distance and width differs. For gap distances greater than 0.25, the lift coefficient is generally sensitive to changes in the width and the sensitivity of the drag coefficient to the width increases as the width increases. Conversely, the lift coefficient shows little sensitivity to changes in the gap distances and the sensitivity of the drag coefficient to the gap distance decreases as the width increases.
- (4)
- For the suppression of amplitudes, with low gap distances (G/D = 0.25, 0.5), the amplitude suppression is more effective at G/D = 0.5 compared to G/D = 0.25. Effective amplitude suppression can be achieved across all tested width (W/D = 0.1–0.9), with small width providing better suppression effects. When using high gap distances, for G/D = 0.75, effective suppression of both cross-flow and in-line amplitudes can be achieved with width from 0.7 to 0.9. At G/D values of 1.5, 1.75, and 2.0, there is a significant reduction in amplitude when W/D is set to 0.8. Specifically, at G/D = 1.25 and W/D = 0.9. In summary, it is advisable to use configurations where W/D ranges from 0.1 to 0.6 and G/D is 0.5, or where W/D ranges from 0.7 to 0.9 and G/D is 0.75. These setups offer comparable levels of amplitude suppression, achieving effective vibration suppression.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Re | Reynolds number |
| Gap distance | |
| Length of plate | |
| Width of plate | |
| Rotation rate | |
| Reduced velocity | |
| Mass ratio | |
| Lift coefficient | |
| Drag coefficient | |
| The root mean square of the lift coefficient | |
| Time-averaged drag coefficient | |
| Spring constant | |
| Damping coefficient | |
| Diameter of the cylinder | |
| Density of the fluid | |
| Damping ratio | |
| Strouhal number | |
| Uniform incoming fluid velocity | |
| Angular velocity | |
| v | Kinematic viscosity |
| Cross-flow amplitude | |
| In-line amplitude | |
| Cross-flow mean displacement | |
| In-line mean displacement | |
| Ymean-ABS | absolute value of cross-flow mean displacement |
| Xmean-ABS | absolute value of in-line mean displacement |
References
- Jeng, D.-S.; Zhang, H. An integrated three-dimensional model of wave-induced pore pressure and effective stresses in a porous seabed: II. Breaking waves. Ocean Eng. 2005, 32, 1950–1967. [Google Scholar] [CrossRef]
- Trim, A.D.; Braaten, H.; Lie, H.; Tognarelli, M.A. Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 2005, 21, 335–361. [Google Scholar] [CrossRef]
- Zhao, M. A review of recent studies on the control of vortex-induced vibration of circular cylinders. Ocean Eng. 2023, 285, 115389. [Google Scholar] [CrossRef]
- Wu, H.; Sun, D.P.; Lu, L.; Teng, B.; Tang, G.Q.; Song, J.N. Experimental investigation on the suppression of vortex-induced vibration of long flexible riser by multiple control rods. J. Fluids Struct. 2012, 30, 115–132. [Google Scholar] [CrossRef]
- Lu, L.; Liu, M.; Teng, B.; Cui, Z.; Tang, G.; Zhao, M.; Cheng, L. Numerical investigation of fluid flow past circular cylinder with multiple control rods at low Reynolds number. J. Fluids Struct. 2014, 48, 235–259. [Google Scholar] [CrossRef]
- Zhu, H.; Yao, J. Numerical evaluation of passive control of VIV by small control rods. Appl. Ocean Res. 2015, 51, 93–116. [Google Scholar] [CrossRef]
- Chen, W.; Bao, Y.; Chai, W.; Li, J.; Rheem, C.K.; Lin, Y.; Li, X. Investigation of the combined effect of control rods and forced rotation on a cylinder. Phys. Fluids 2023, 35, 103605. [Google Scholar] [CrossRef]
- Ishihara, T.; Li, T. Numerical study on suppression of vortex-induced vibration of circular cylinder by helical wires. J. Wind Eng. Ind. Aerodyn. 2020, 197, 104081. [Google Scholar] [CrossRef]
- Hao, Z.; Sun, C.; Lu, Y.; Bi, K.; Zhou, T. Suppression of vortex-induced vibration and phase-averaged analysis of the wake generated by a circular cylinder covered with helical grooves. Fluids 2022, 7, 194. [Google Scholar] [CrossRef]
- Xu, W.; Luan, Y.; Liu, L.; Wu, Y.X. Influences of the helical strake cross-section shape on vortex-induced vibrations suppression for a long flexible cylinder. China Ocean Eng. 2017, 31, 438–446. [Google Scholar] [CrossRef]
- Zhu, H.; Gao, Y.; Zhou, T. Flow-induced vibration of a locally rough cylinder with two symmetrical strips attached on its surface: Effect of the location and shape of strips. Appl. Ocean Res. 2018, 72, 122–140. [Google Scholar] [CrossRef]
- Chen, W.; Wang, S.; Shi, X.; Rheem, C.K.; Lin, Y.; Liu, E. Numerical simulation of surface roughness effects on the vortex-induced vibration of a circular cylinder at a subcritical Reynolds number. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100430. [Google Scholar] [CrossRef]
- Chen, W.; Du, A.; Lin, Y.; Shao, J.; Gu, J.; Gong, J.; Rheem, C.K.; Wen, B.; Li, X. Investigation of vortex-induced vibrations of rotating cylinders with different surface roughnesses. Phys. Fluids 2024, 36, 043614. [Google Scholar] [CrossRef]
- Sun, C.; Zhou, T.; An, H.; Zhu, H.; Cheng, L. On the study of vortex-induced vibration of circular cylinders covered with different roughness. Appl. Ocean Res. 2022, 124, 103215. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Fan, D.; Zheng, H.; Hu, Z. The roles of rigid splitter plates in flow-induced vibration of a circular cylinder. Phys. Fluids 2020, 34, 114114. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, W. Flow control and vibration response of a circular cylinder attached with a wavy plate. Ocean Eng. 2020, 212, 107537. [Google Scholar] [CrossRef]
- Zeng, L.; Zhao, F.; Wang, H.; Liu, Y.; Tang, H. Control of flow-induced vibration of a circular cylinder using a splitter plate. Phys. Fluids 2023, 35, 087104. [Google Scholar] [CrossRef]
- Zhu, H.; Li, G.; Wang, J. Flow-induced vibration of a circular cylinder with splitter plates placed upstream and downstream individually and simultaneously. Appl. Ocean Res. 2020, 97, 102084. [Google Scholar] [CrossRef]
- Sarpkaya, T. A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 2004, 19, 389–447. [Google Scholar] [CrossRef]
- Williamson, C.H.K.; Govardhan, R. Vortex-induced vibrations. Annu. Rev. Fluid Mech. 2004, 36, 413–455. [Google Scholar] [CrossRef]
- Guan, G.; He, K.; Wang, P.; Yang, Q. Study on the parameters of detached splitter plate for VIV suppression. Ocean Eng. 2022, 266, 113092. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, Q.; Tang, T.; Alam, M.M.; Zhou, T. Flow structures around a circular cylinder with bilateral splitter plates and their dynamic characteristics. Ocean Eng. 2023, 269, 113547. [Google Scholar] [CrossRef]
- Chen, J.; Wu, J. Control of flow-induced vibration of a circular cylinder with a porous splitter plate. Ocean Eng. 2023, 281, 114780. [Google Scholar] [CrossRef]
- Mittal, C.; Sharma, A. Flow-induced vibration of a flexible splitter-plate in the wake of a stationary cylinder. Phys. Fluids 2021, 33, 113607. [Google Scholar] [CrossRef]
- Cui, G.P.; Feng, L.H.; Hu, Y.W. Flow-induced vibration control of a circular cylinder by using flexible and rigid splitter plates. Ocean Eng. 2022, 249, 110939. [Google Scholar] [CrossRef]
- Liu, H.; Han, X.; Williams, J.J.R.; Xie, R.; Lin, P. 3D numerical study of splitter plate’s effect on a flexible cylinder VIV. Ocean Eng. 2023, 269, 113397. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; An, H.; Lu, L. Three-dimensional numerical simulation of vortex-induced vibration of an elastically mounted rigid circular cylinder in steady current. J. Fluids Struct. 2014, 50, 292–311. [Google Scholar] [CrossRef]
- Ogunremi, A.R.; Sumner, D. The effect of a splitter plate on the flow around a finite prism. J. Fluids Struct. 2015, 59, 1–21. [Google Scholar] [CrossRef]
- Liang, S.; Wang, J.; Xu, B.; Wu, W.; Lin, K. Vortex-induced vibration and structure instability for a circular cylinder with flexible splitter plates. J. Wind Eng. Ind. Aerodyn. 2018, 174, 200–209. [Google Scholar] [CrossRef]
- Bao, Y.; Zhang, X.; Lin, Y.; Shao, J.; Chen, W.; Rheem, C.K.; Li, X. Investigation of coupled response on cylindrical eccentricity induced vibration and flow induced vibration. Ocean Eng. 2024, 305, 117978. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Zhang, W.; Shao, J.Y.; Chen, W.; Rheem, C.K.; Tang, G.; Li, X. Numerical investigation of the flow-induced vibration of a rotation pipe with internal flow. Ocean Eng. 2024, 294, 116809. [Google Scholar] [CrossRef]
- Du, L.; Sun, X. Suppression of vortex-induced vibration using the rotary oscillation of a cylinder. Phys. Fluids 2015, 27, 023603. [Google Scholar] [CrossRef]
- Bourguet, R.; Lo Jacono, D. Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 2014, 740, 342–380. [Google Scholar] [CrossRef]
- Bao, Y.; Lin, Y.; Chen, W.; Rheem, C.K.; Li, X. Numerical investigation of wake and flow-induced vibrations of a rotating cylinder in flow. Ocean Eng. 2022, 262, 112207. [Google Scholar] [CrossRef]
- Du, A.; Chen, W.; Lin, Y.; Chi, Q.; Rheem, C.K.; Wen, B.; Liu, Z.; Li, X. Vortex-induced vibration of a rotating cylinder with dual splitter plates. Phys. Fluids 2024, 36, 083623. [Google Scholar] [CrossRef]
- Tang, T.; Zhu, H.; Chen, Q.; Zhang, J.; Gao, Y. Dynamic response of a circular cylinder in the presence of a detached splitter plate: On the gap distance sensitivity. J. Fluids Struct. 2023, 119, 103888. [Google Scholar] [CrossRef]
- Zou, Q.; Ding, L.; Wang, H.; Wang, J.; Zhang, L. Two-degree-of-freedom flow-induced vibration of a rotating circular cylinder. Ocean Eng. 2019, 191, 106505. [Google Scholar] [CrossRef]
- Wong, K.W.L.; Zhao, J.; Jacono, D.L.; Thompson, M.C.; Sheridan, J. Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 2017, 829, 486–511. [Google Scholar] [CrossRef]
- Serson, D.; Meneghini, J.R.; Carmo, B.S.; Volpe, E.V.; Gioria, R.S. Wake transition in the flow around a circular cylinder with a splitter plate. J. Fluid Mech. 2014, 755, 582–602. [Google Scholar] [CrossRef]
- Dehkordi, B.G.; Jafari, H.H. On the suppression of vortex shedding from circular cylinders using detached short splitter-plates. J. Fluids Eng. 2010, 132, 044501. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Gharib, N. Numerical investigations on the flow control over bumped surface circular cylinders. Ocean Eng. 2021, 240, 109943. [Google Scholar] [CrossRef]
- Canuto, D.; Taira, K. Two-dimensional compressible viscous flow around a circular cylinder. J. Fluid Mech. 2015, 785, 349–371. [Google Scholar] [CrossRef]
- Bourguet, R. Two-degree-of-freedom flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 2020, 897, A31. [Google Scholar] [CrossRef]
- Gu, J.; Fernandes, A.C.; Han, X.; Kuang, X.; Chen, W. Numerical investigation of Reynolds number effects on vortex-induced vibrations at low and moderate Re regimes. Ocean Eng. 2022, 245, 110535. [Google Scholar] [CrossRef]
- Brasa, M.; Chassaing, P.; Minh, H.H. Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 1986, 165, 79–130. [Google Scholar] [CrossRef]
- Bao, Y.; Zhou, D.; Tu, J.H. Flow interference between a stationary cylinder and an elastically mounted cylinder arranged in proximity. J. Fluids Struct. 2011, 27, 1425–1446. [Google Scholar] [CrossRef]
- Wu, J.; Shu, C.; Zhao, N. Numerical investigation of vortex-induced vibration of a circular cylinder with a hinged flat plate. Phys. Fluids 2014, 26, 063601. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L.; Lu, L. Vortex induced vibrations of a rotating circular cylinder at low Reynolds number. Phys. Fluids 2014, 26, 073602. [Google Scholar] [CrossRef]
- Li, R.; Gong, J.; Chen, W.; Li, J.; Chai, W.; Rheem, C.K.; Li, X. Numerical Investigation of Vortex-Induced Vibrations of a Rotating Cylinder near a Plane Wall. J. Mar. Sci. Eng. 2023, 11, 1202. [Google Scholar] [CrossRef]
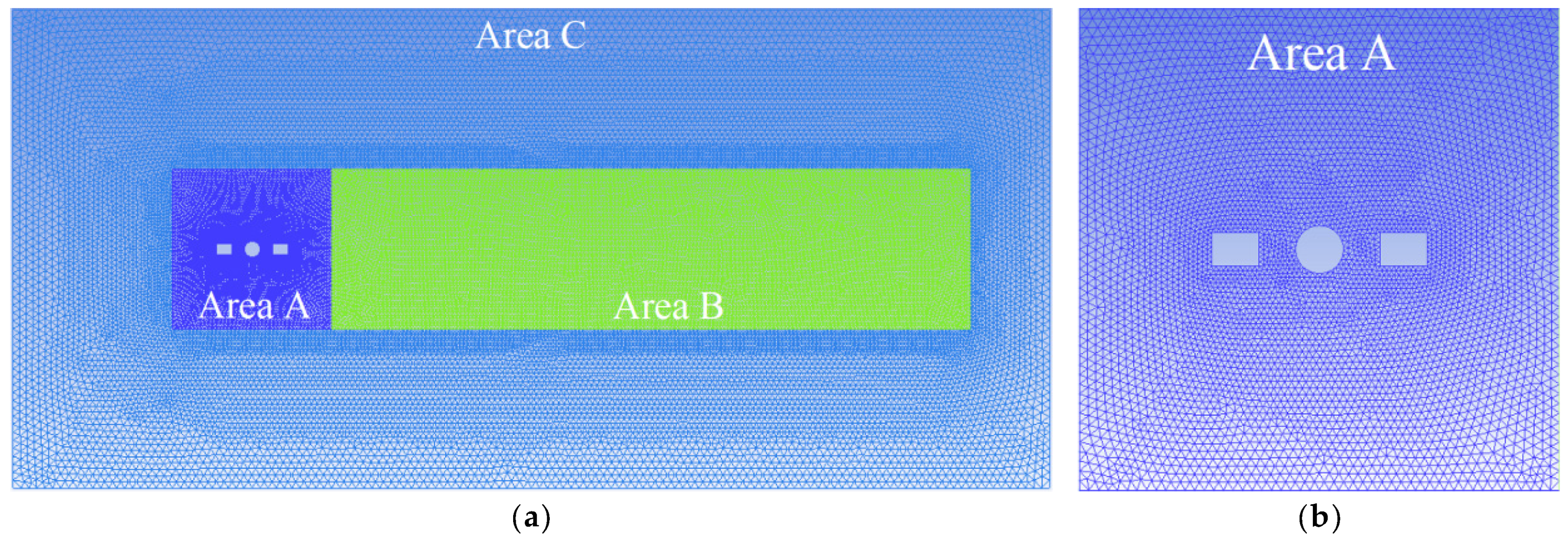

| Mesh | ||||
|---|---|---|---|---|
| (A) | (B) | (C) | ||
| SIZE I | 0.02–0.05 | 0.05–0.10 | 0.10–0.30 | |
| SIZE II | 0.04–0.08 | 0.08–0.16 | 0.16–0.40 | |
| SIZE III | 0.05–0.10 | 0.10–0.20 | 0.20–0.50 | |
| SIZE IV | 0.10–0.20 | 0.20–0.40 | 0.40–0.70 | |
| SIZE V | 0.20–0.30 | 0.30–0.50 | 0.50–0.80 |
| Case | Mesh | Elements | ||
|---|---|---|---|---|
| A1 | Size I | 1.33 | 0.19 | 389,775 |
| A2 | Size II | 1.34 | 0.19 | 148,085 |
| A3 | Size III | 1.36 | 0.19 | 96,423 |
| A4 | Size IV | 1.40 | 0.19 | 22,374 |
| A5 | Size V | 1.42 | 0.20 | 4743 |
| Braza et al. [45] | 1.38 | 0.20 | \ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Qi, Q.; Sun, Z.; Yang, Y.; Han, Y.; Chen, W.; Shao, J.; Wen, B.; Li, X. Study on Suppression of Vortex-Induced Vibrations of a Rotating Cylinder with Dual Splitter Plates. J. Mar. Sci. Eng. 2025, 13, 971. https://doi.org/10.3390/jmse13050971
Li J, Qi Q, Sun Z, Yang Y, Han Y, Chen W, Shao J, Wen B, Li X. Study on Suppression of Vortex-Induced Vibrations of a Rotating Cylinder with Dual Splitter Plates. Journal of Marine Science and Engineering. 2025; 13(5):971. https://doi.org/10.3390/jmse13050971
Chicago/Turabian StyleLi, Jiaqi, Qiongfang Qi, Zonghao Sun, Yongkang Yang, Yaowen Han, Wei Chen, Jiangyan Shao, Binrong Wen, and Xiaobin Li. 2025. "Study on Suppression of Vortex-Induced Vibrations of a Rotating Cylinder with Dual Splitter Plates" Journal of Marine Science and Engineering 13, no. 5: 971. https://doi.org/10.3390/jmse13050971
APA StyleLi, J., Qi, Q., Sun, Z., Yang, Y., Han, Y., Chen, W., Shao, J., Wen, B., & Li, X. (2025). Study on Suppression of Vortex-Induced Vibrations of a Rotating Cylinder with Dual Splitter Plates. Journal of Marine Science and Engineering, 13(5), 971. https://doi.org/10.3390/jmse13050971







