Elastic Wave Phase Inversion in the Local-Scale Frequency–Wavenumber Domain with Marine Towed Simultaneous Sources
Abstract
1. Introduction
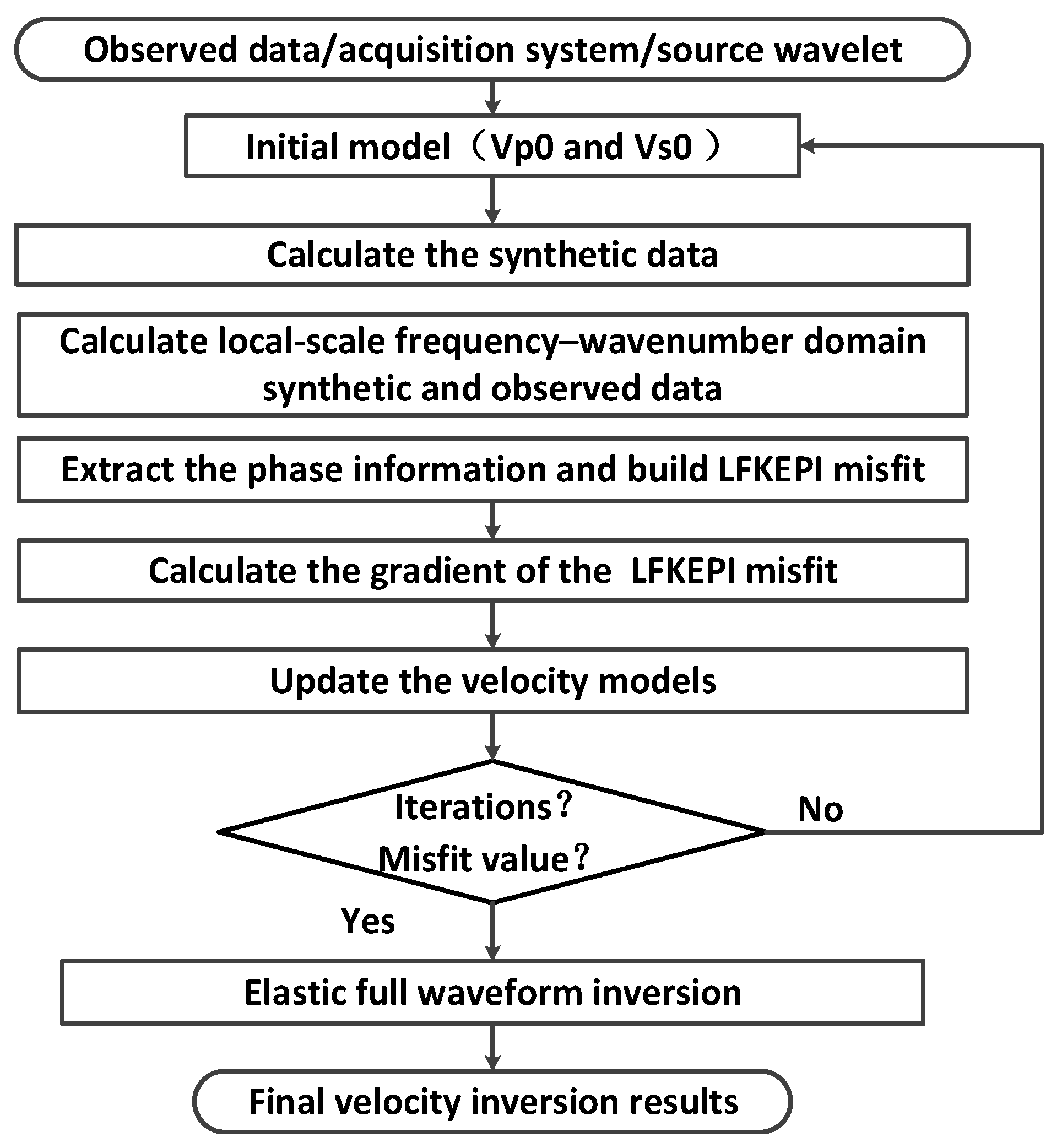
2. Methodology of Elastic Parameter Inversion
2.1. Review of Elastic Full Waveform Inversion
2.2. Elastic Wave Phase Inversion in the Frequency Domain
2.3. Elastic Wave Phase Inversion in the Local-Scale Frequency–Wavenumber Domain
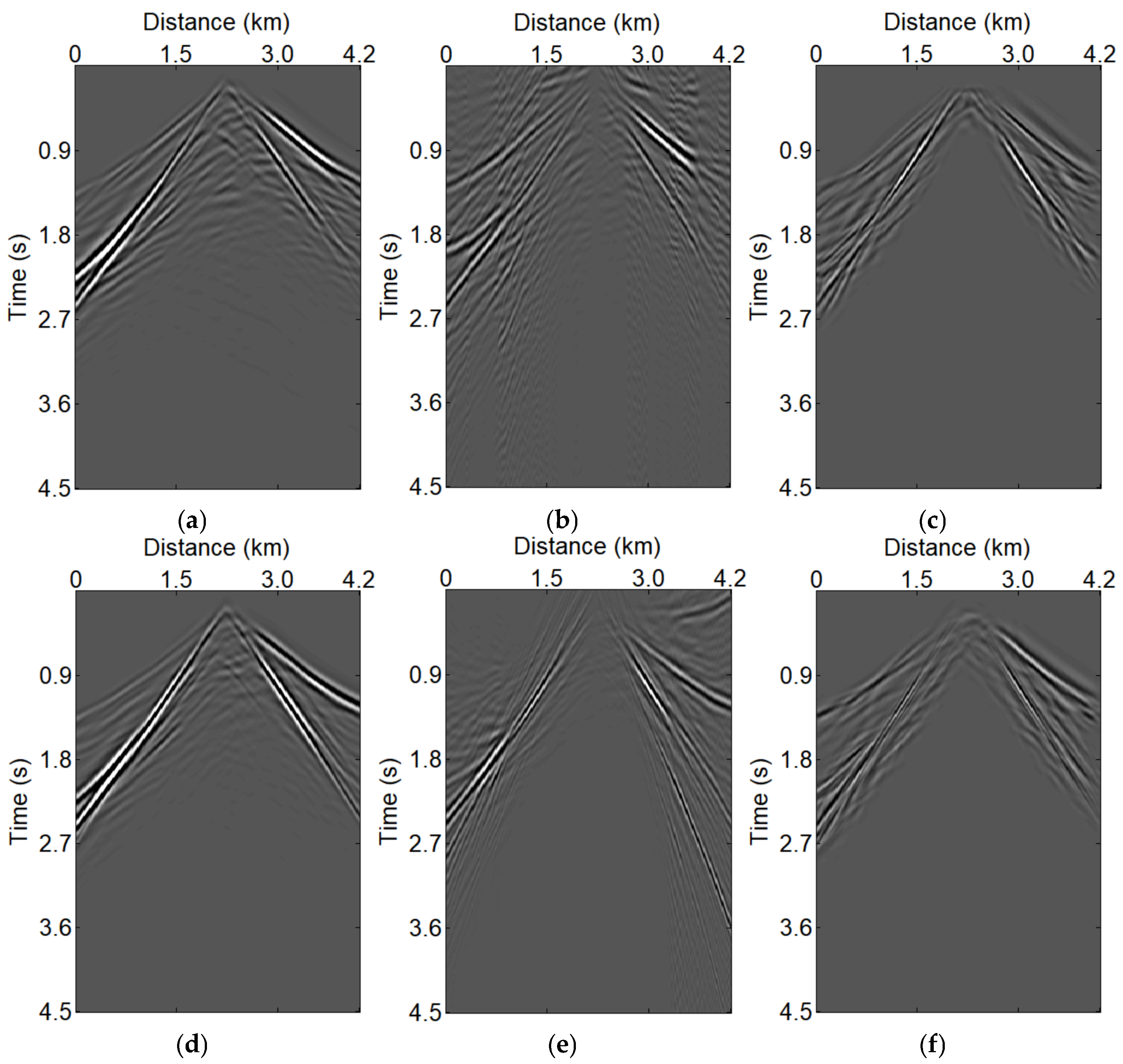
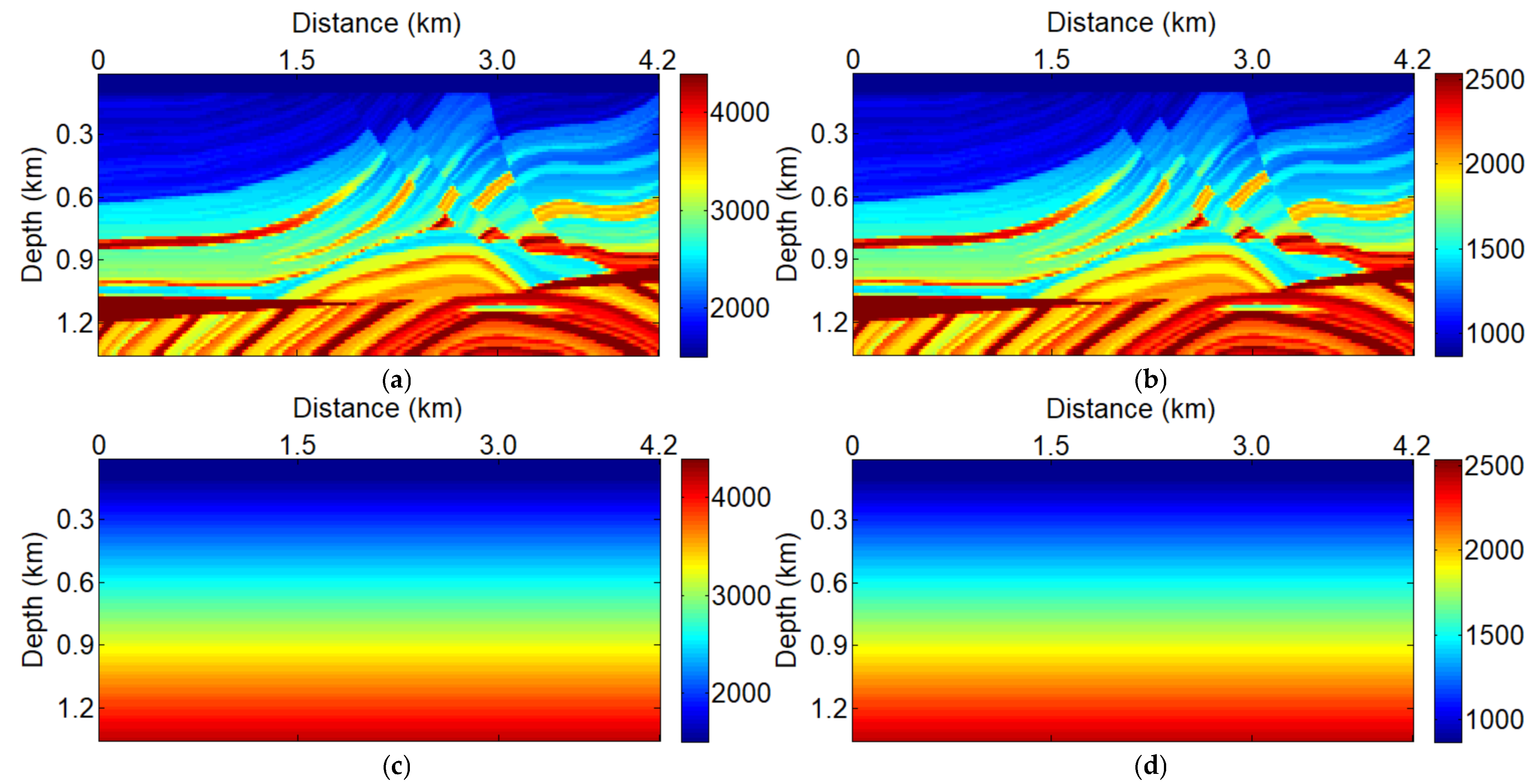
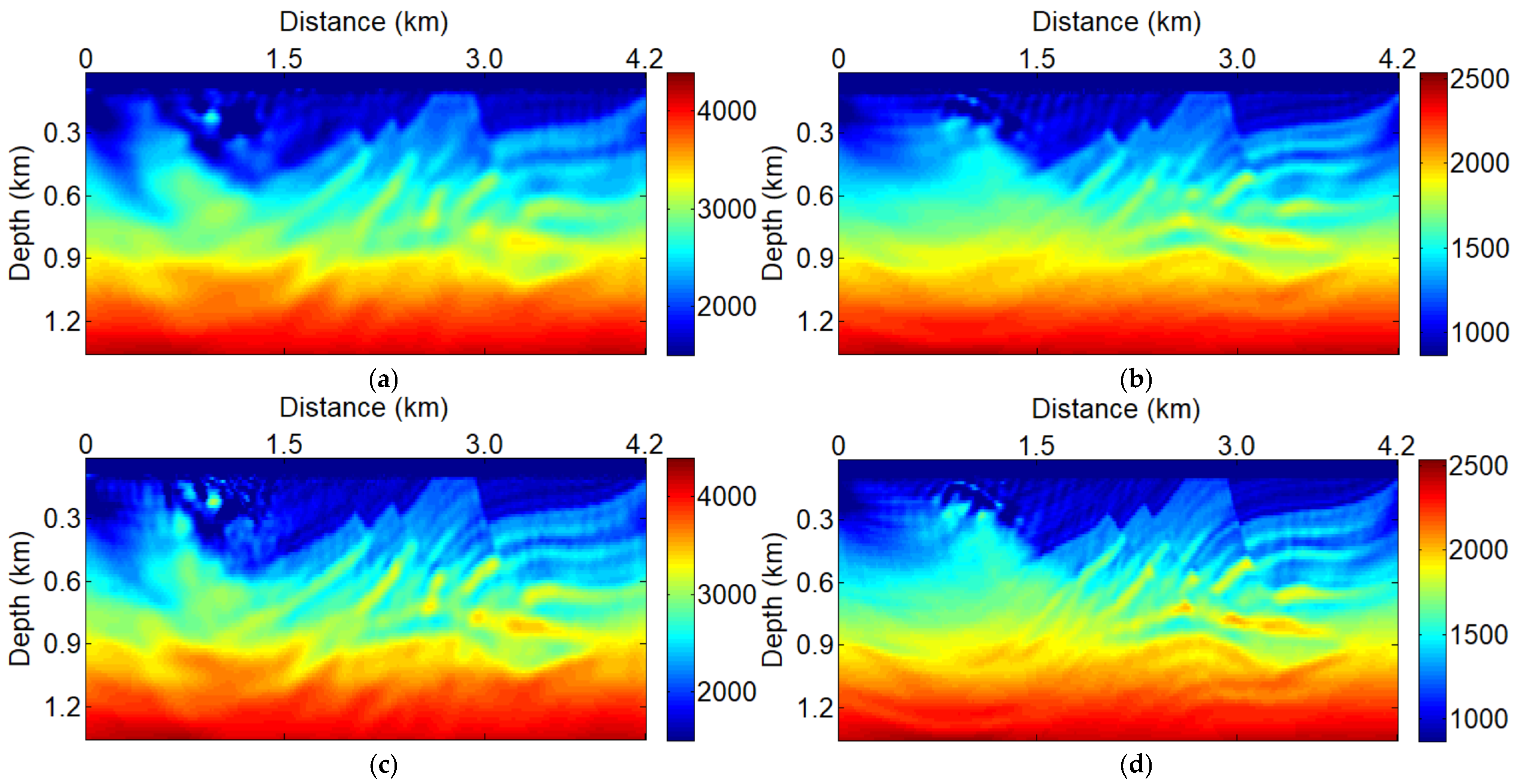
3. Numerical Testing
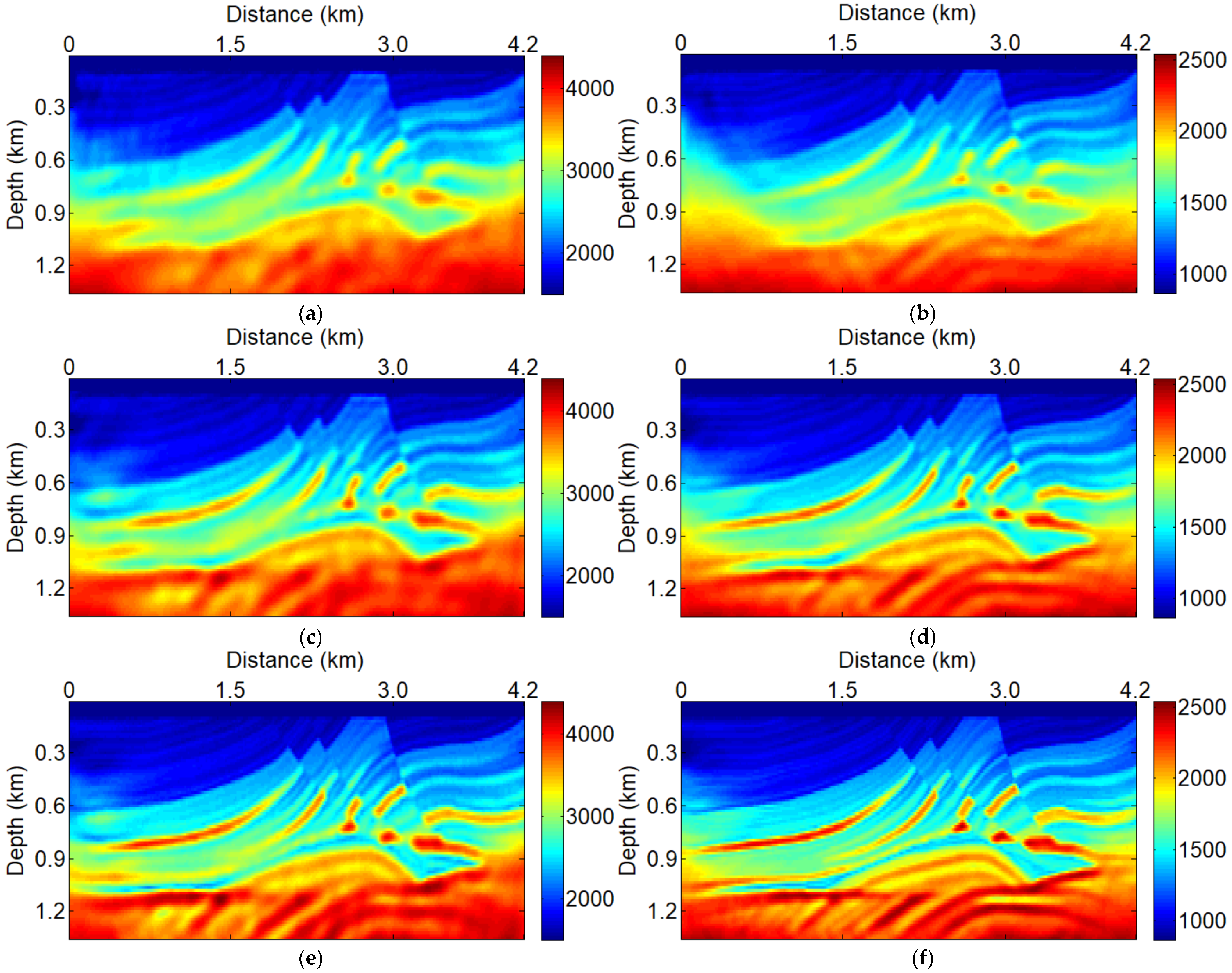
3.1. Land Seismic Acquisition System
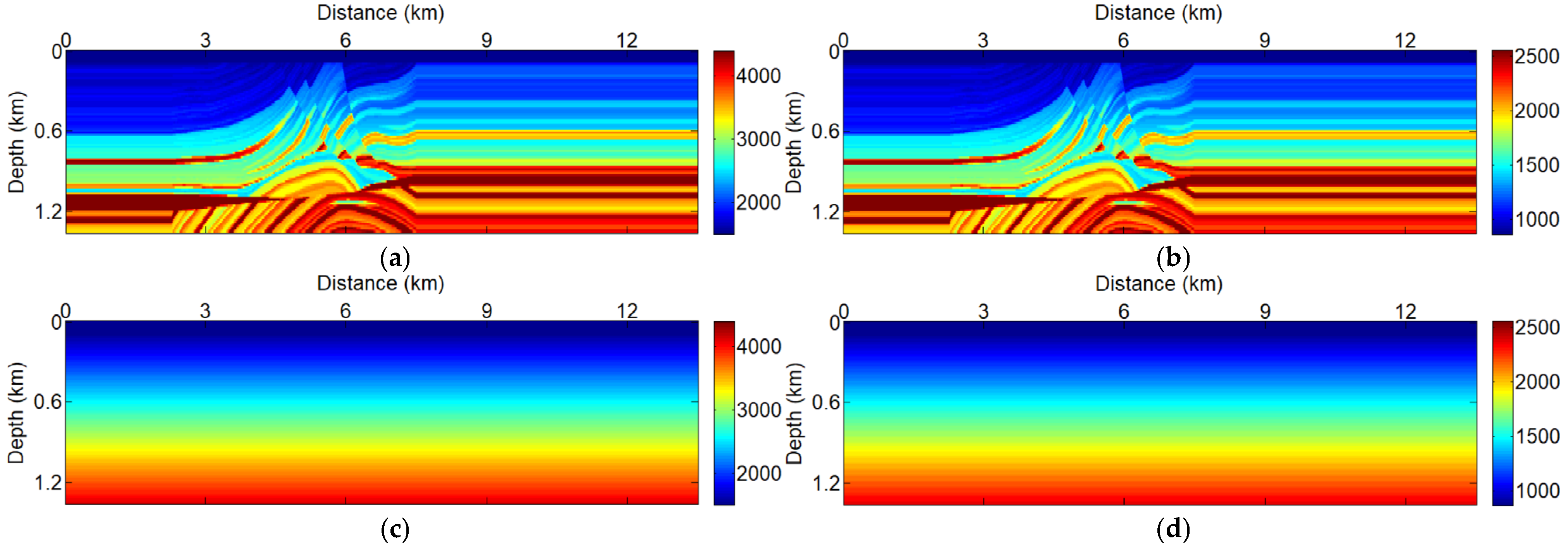
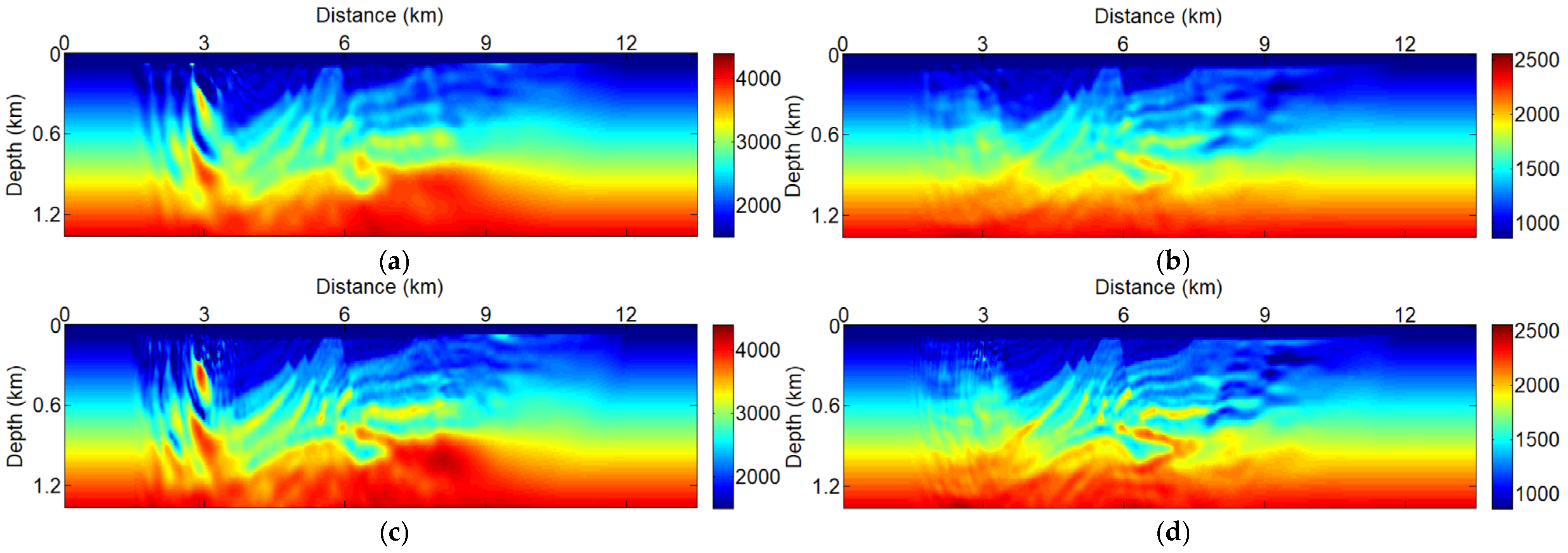
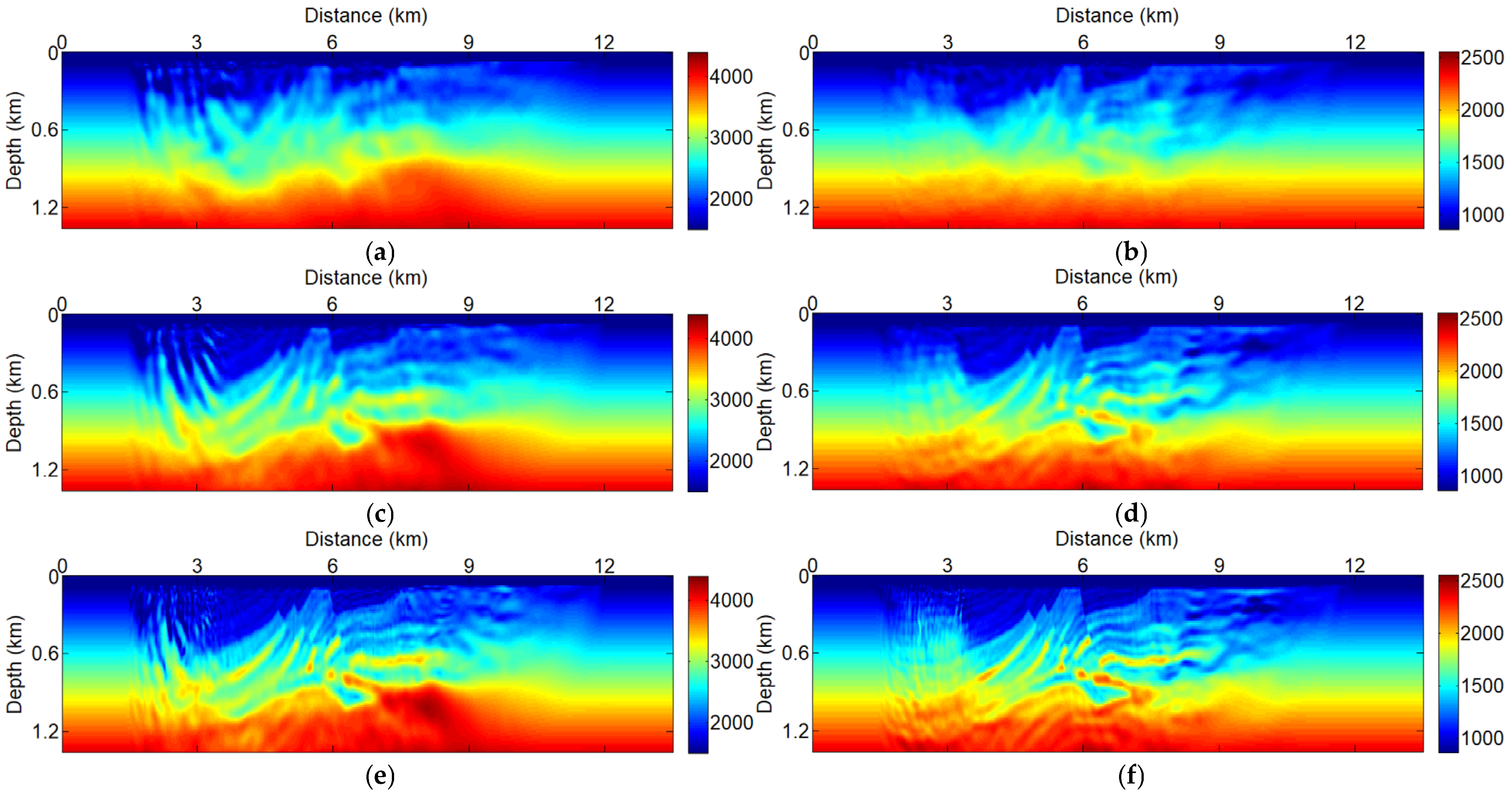
3.2. Marine Towed Seismic Acquisition Systems with Simultaneous Sources
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FWI | Full waveform inversion |
| EFWI | Elastic full waveform inversion |
| LFKEPI | Elastic Wave Phase Inversion in Local-scale Frequency–Wavenumber Domain |
| FEPI | Elastic Wave Phase Inversion in Frequency Domain |
References
- Lailly, P.; Bednar, J. The seismic inverse problem as a sequence of before stack migrations. In Conference on Inverse Scattering: Theory and Application; SIAM: Philadelphia, PA, USA, 1983; pp. 206–220. [Google Scholar]
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Tarantola, A. A strategy for nonlinear elastic inversion of seismic reflection data. Geophysics 1986, 51, 1893–1903. [Google Scholar] [CrossRef]
- Plessix, R.-E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophys. J. Int. 2006, 167, 495–503. [Google Scholar] [CrossRef]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Wu, R.-S.; Luo, J.; Wu, B. Seismic envelope inversion and modulation signal model. Geophysics 2014, 79, Wa13–Wa24. [Google Scholar] [CrossRef]
- Alkhalifah, T. Full-model wavenumber inversion: An emphasis on the appropriate wavenumber continuation. Geophysics 2016, 81, R89–R98. [Google Scholar] [CrossRef]
- Alkhalifah, T.; Choi, Y. From tomography to full-waveform inversion with a single objective function. Geophysics 2014, 79, R55–R61. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, Y. Crosshole seismic waveform tomography–I. Strategy for real data application. Geophys. J. Int. 2006, 166, 1224–1236. [Google Scholar] [CrossRef]
- Crase, E.; Wideman, C.; Noble, M.; Tarantola, A. Nonlinear elastic waveform inversion of land seismic reflection data. J. Geophys. Res. Solid Earth 1992, 97, 4685–4703. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Wan, X.; Sun, M.; Dong, L. Elastic multi-parameter full-waveform inversion for anisotropic media. Chin. J. Geophys. 2019, 62, 1809–1823. (In Chinese) [Google Scholar]
- Bunks, C.; Saleck, F.M.; Zaleski, S.; Chavent, G. Multiscale seismic waveform inversion. Geophysics 1995, 60, 1457–1473. [Google Scholar] [CrossRef]
- Pratt, R.G.; Shin, C.; Hicks, G.J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion. Geophys. J. Int. 1998, 133, 341–362. [Google Scholar] [CrossRef]
- Guo, X.B.; Liu, H.; Shi, Y. Time domain full waveform inversion based on frequency attenuation. Chin. J. Geophys. 2016, 59, 3777–3787. (In Chinese) [Google Scholar]
- Chen, S.C.; Chen, G.X. Time-damping full waveform inversion of multi-dominant-frequency wavefields. Chin. J. Geophys. 2017, 60, 3229–3237. (In Chinese) [Google Scholar] [CrossRef]
- Shin, C.; Ho Cha, Y. Waveform inversion in the Laplace-Fourier domain. Geophys. J. Int. 2009, 177, 1067–1079. [Google Scholar] [CrossRef]
- Kwon, J.; Jun, H.; Song, H.; Jang, U.G.; Shin, C. Waveform inversion in the shifted Laplace domain. Geophys. J. Int. 2017, 210, 340–353. [Google Scholar] [CrossRef]
- Ha, W.; Shin, C. Deconvolution-Based Objective Functions for Full Waveform Inversion in the Laplace Domain. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5904708. [Google Scholar] [CrossRef]
- Chi, B.X.; Dong, L.G.; Liu, Y.Z. Full waveform inversion method using envelope objective function without low frequency dataJ. J. Appl. Geophys. 2014, 109, 36–46. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, R.S.; Han, L. Seismic Envelope Inversion Based on Hybrid Scale Separation for Data with Strong Noises. Pure Appl. Geophys. 2019, 176, 165–188. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, R.S.; Han, L.G.; Zhang, P. Joint Multiscale Direct Envelope Inversion of Phase and Amplitude in the Time–Frequency Domain. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5108–5120. [Google Scholar] [CrossRef]
- Zhang, P.; Han, L.; Zhang, F.; Feng, Q.; Chen, X. Wavefield Decomposition-Based Direct Envelope Inversion and Structure-Guided Perturbation Decomposition for Salt Building. Minerals 2021, 11, 919. [Google Scholar] [CrossRef]
- Chen, G.; Yang, W.; Liu, Y.; Luo, J.; Jing, H. Envelope-Based Sparse-Constrained Deconvolution for Velocity Model Building. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4501413. [Google Scholar] [CrossRef]
- Wang, Y.; Chi, B.; Dong, L. Envelope normalized reflection waveform inversion. Geophys. Prospect. 2024, 73, 895–909. [Google Scholar] [CrossRef]
- Xiong, K.; Lumley, D.; Zhou, W. Improved seismic envelope full-waveform inversion. Geophysics 2023, 88, R421–R437. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, R.S.; Huang, X.; Long, Y.; Xu, Y.; Han, L.G. Phase-amplitude-based polarized direct envelope inversion in the time-frequency domain. Geophysics 2022, 87, R245–R260. [Google Scholar] [CrossRef]
- Sirgue, L.; Pratt, R.G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics 2004, 69, 231–248. [Google Scholar] [CrossRef]
- Luo, J.; Wu, R.-S.; Gao, F. Time-domain full waveform inversion using instantaneous phase information with damping. J. Geophys. Eng. 2018, 15, 1032. [Google Scholar] [CrossRef]
- Bednar, J.B.; Shin, C.; Pyun, S. Comparison of waveform inversion, part 2: Phase approach. Geophys. Prospect. 2007, 55, 465–475. [Google Scholar] [CrossRef]
- Sun, Y. Time-domain phase inversion. SEG Tech. Program Expand. Abstr. 1993, 12, 1396. [Google Scholar]
- Fu, L.; Guo, B.; Schuster, G.T. Multiscale phase inversion of seismic data. Geophysics 2017, 83, R159–R171. [Google Scholar] [CrossRef]
- Choi, Y. Time-domain pure-phase inversion of wavefield in exponential damping. J. Appl. Geophys. 2022, 204, 104734. [Google Scholar] [CrossRef]
- Fichtner, A.; Kennett, B.L.N.; Igel, H.; Bunge, H.-P. Theoretical background for continental-and global-scale full-waveform inversion in the time–frequency domain. Geophys. J. Int. 2008, 175, 665–685. [Google Scholar] [CrossRef]
- Hu, Y.; Han, L.; Wu, R.; Xu, Y. Multi-scale time-frequency domain full waveform inversion with a weighted local correlation-phase misfit function. J. Geophys. Eng. 2019, 16, 1017–1031. [Google Scholar] [CrossRef]
- Kang, P.; Hu, Y.; Liu, R.; Sun, C.; Zhao, Z.; Yuan, P.; Zhen, M.; Meng, Y.; Xu, Y. Local-scale frequency-wavenumber domain phase inversion. Prog. Geophys. 2025, 40, 155–165. [Google Scholar]
- Zhu, H.; Fomel, S. Building good starting models for full-waveform inversion using adaptive matching filtering misfit. Geophysics 2016, 81, U61–U72. [Google Scholar] [CrossRef]
- Warner, M.; Guasch, L. Adaptive waveform inversion. Theory J. Geophys. 2016, 81, R429–R445. [Google Scholar] [CrossRef]
- Hu, Y.; Han, L.; Zhang, P.; Ge, Q. Time-frequency domain multi-scale full waveform inversion based on adaptive non-stationary phase correction. Chin. J. Geophys. 2018, 61, 2969–2988. (In Chinese) [Google Scholar]
- Tao, L.; Gu, Z.; Ren, H. Improving the Seismic Impedance Inversion by Fully Convolutional Neural Network. J. Mar. Sci. Eng. 2025, 13, 262. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, L.-Y.; Li, Q.; Deng, W.; Han, L. Frequency-Wavenumber Domain Elastic Full Waveform Inversion with a Multistage Phase Correction. Remote Sens. 2022, 14, 5916. [Google Scholar] [CrossRef]




| EFWI | FEPI + EFWI | LFKEPI + EFWI | |
|---|---|---|---|
| Vp | 0.0168 | 0.024 | 0.0045 |
| Vs | 0.0188 | 0.0151 | 0.0048 |
| SS-EFWI | SS-FEPI + SS-EFWI | SS-LFKEPI + SS-EFWI | |
|---|---|---|---|
| Vp | 0.0191 | 0.0151 | 0.0143 |
| Vs | 0.0182 | 0.0179 | 0.0173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, S.; Hu, Y.; Huang, X.; Fang, J.; Jiang, Z. Elastic Wave Phase Inversion in the Local-Scale Frequency–Wavenumber Domain with Marine Towed Simultaneous Sources. J. Mar. Sci. Eng. 2025, 13, 964. https://doi.org/10.3390/jmse13050964
Qu S, Hu Y, Huang X, Fang J, Jiang Z. Elastic Wave Phase Inversion in the Local-Scale Frequency–Wavenumber Domain with Marine Towed Simultaneous Sources. Journal of Marine Science and Engineering. 2025; 13(5):964. https://doi.org/10.3390/jmse13050964
Chicago/Turabian StyleQu, Shaobo, Yong Hu, Xingguo Huang, Jingwei Fang, and Zhihai Jiang. 2025. "Elastic Wave Phase Inversion in the Local-Scale Frequency–Wavenumber Domain with Marine Towed Simultaneous Sources" Journal of Marine Science and Engineering 13, no. 5: 964. https://doi.org/10.3390/jmse13050964
APA StyleQu, S., Hu, Y., Huang, X., Fang, J., & Jiang, Z. (2025). Elastic Wave Phase Inversion in the Local-Scale Frequency–Wavenumber Domain with Marine Towed Simultaneous Sources. Journal of Marine Science and Engineering, 13(5), 964. https://doi.org/10.3390/jmse13050964






