Reservoir Characterization Based on Bayesian Amplitude Versus Offset Inversion of Marine Seismic Data
Abstract
1. Introduction
2. Novel Four-Term Reparameterization for the AVO Approximation
3. Bayesian AVO Inversion for Young’s Modulus and Poisson’s Ratio
| Algorithm 1. Process of IRLS method to solve Equation (17) | |
| 1: | Input data , . |
| 2: | Construct the operator, , . |
| 3: | Select , , and set maximum iteration number K and tolerance . |
| 4: | Initialize the solution, . |
| 5: | Calculate . |
| 6: | Solve the |
| 7: | If , output , else , |
| 8: | Repeat step 5–7, until the maximum iteration is reached . |
4. Results of Reservoir Characterization
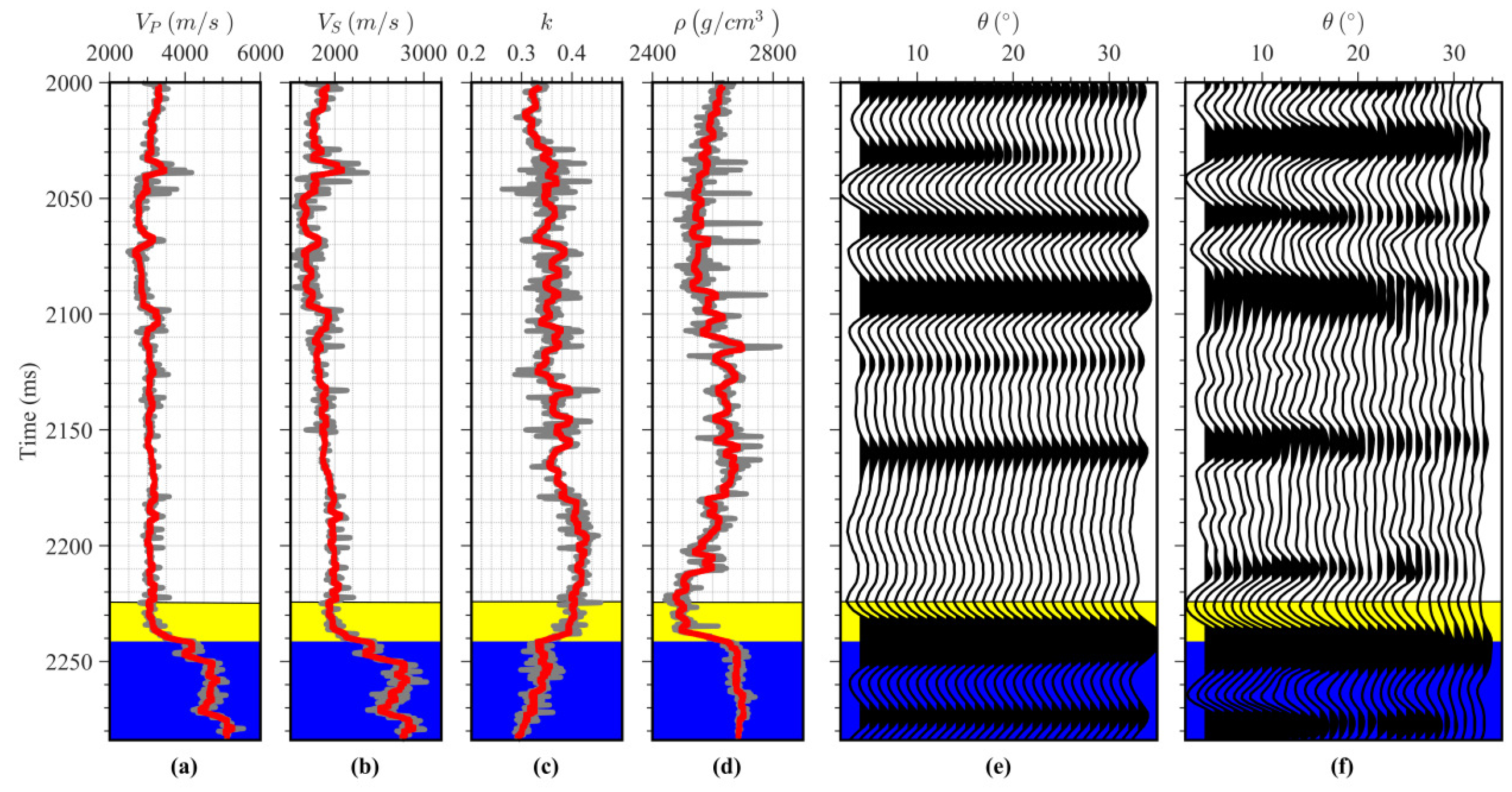
4.1. Two-Dimensional Real Data Example for Reservoir Characterization
4.2. Three-Dimensional Real Data Example for Reservoir Characterization

5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Young’s modulus | |
| Poisson’s ratio | |
| density | |
| incidence angle | |
| small perturbation | |
| ¯ | background value |
| the square of S-to-P-wave velocity ratio | |
| temporal samples | |
| numbers of incidence angles | |
| seismic angle gather vector | |
| kernel matrix | |
| model parameter vector | |
| noise vector | |
| variances of measured noise | |
| variances of model parameters | |
| data error matrix term | |
| Cauchy-sparse constraint term | |
| low-frequency model constraint term | |
| diagonal matrix | |
| Toeplitz matrix | |
| wavelet matrix | |
| coefficient-weighting matrix | |
| zero matrix | |
| identity matrix | |
| integral matrix |
Appendix A
Appendix A.1. Derivation of the Novel Four-Term Reparameterization for the AVO Approximation
Appendix A.2. Process of Bayesian AVO Inversion for Young’s Modulus and Poisson’s Ratio
References
- Zong, Z.; Yin, X. Direct inversion of Young’s and Poisson impedances for fluid discrimination. Geofluids 2016, 16, 1006–1016. [Google Scholar] [CrossRef]
- Singleton, S. Geophysical data processing, rock property inversion, and geomechanical model building in a Midland Basin development project, Midland/Ector Counties, Texas. Lead. Edge 2018, 37, 182–189. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, G. Amplitude variation with incident angle and azimuth inversion for Young’s impedance, Poisson’s ratio and fracture weaknesses in shale gas reservoirs. Geophys. Prospect. 2019, 67, 1898–1911. [Google Scholar] [CrossRef]
- Sayers, C.M.; Koesoemadinata, A.; Dasgupta, S.; Sudhakar, V.; Hearn, R. Predicting drilling performance in unconventional reservoirs using seismic inversion. In The SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2020; pp. 310–314. [Google Scholar]
- Avseth, P.; Mukerji, T.; Mavko, G. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Arévalo-López, H.S.; Dvorkin, J.P. Porosity, mineralogy, and pore fluid from simultaneous impedance inversion. Lead. Edge 2016, 35, 423–429. [Google Scholar] [CrossRef]
- Keynejad, S.; Sbar, M.L.; Johnson, R.A. Comparison of model-based generalized regression neural network and prestack inversion in predicting Poisson’s ratio in Heidrun Field, North Sea. Lead. Edge 2017, 36, 938–946. [Google Scholar] [CrossRef]
- Rickman, R.; Mullen, M.; Petre, J.; Grieser, W.; Kundert, D. A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett shale. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers (SPE): Denver, CO, USA, 2008. [Google Scholar]
- Guo, Z.; Li, X.; Liu, C.; Feng, X.; Shen, Y. A shale rock physics model for analysis of brittleness index, mineralogy and porosity in the Barnett shale. J. Geophys. Eng. 2013, 10, 25006. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Guo, S.; Xing, Z.; Liu, Z. The effect of shale properties on the anisotropic brittleness criterion index from laboratory study. J. Geophys. Eng. 2015, 12, 866–874. [Google Scholar] [CrossRef]
- Wu, H.; Dong, S.; Huang, Y.; Wang, H.; Chen, G. Brittleness index calculation and evaluation for CBM reservoirs based on AVO simultaneous inversion. J. Appl. Geophys. 2016, 134, 191–198. [Google Scholar] [CrossRef]
- Harris, N.B.; Miskimins, J.L.; Mnich, C.A. Mechanical anisotropy in the Woodford Shale, Permian Basin: Origin, magnitude, and scale. Lead. Edge 2011, 30, 284–291. [Google Scholar] [CrossRef]
- Sena, A.; Castillo, G.; Chesser, K.; Voisey, S.; Estrada, J.; Carcuz, J.; Carmona, E.; Hodgkins, P. Seismic reservoir characterization in resource shale plays: Stress analysis and sweet spot discrimination. Lead. Edge 2011, 30, 758–764. [Google Scholar] [CrossRef]
- Gray, D.; Anderson, P.; Logel, J.; Delbecq, F.; Schmidt, D.; Schmid, R. Estimation of stress and geomechanical properties using 3D seismic data. First Break 2012, 30, 59–68. [Google Scholar] [CrossRef]
- Sharma, R.K.; Chopra, S. Determination of lithology and brittleness of rocks with a new attribute. Lead. Edge 2015, 34, 554–564. [Google Scholar] [CrossRef]
- Sayers, C.; Lascano, M.; Gofer, E.; Den Boer, L.; Walz, M.; Hannan, A.; Dasgupta, S.; Goodway, W.; Perez, M.; Purdue, G. Geomechanical model for the Horn River formation based on seismic AVA inversion. In the SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Dallas, TX, USA, 2016. [Google Scholar]
- Pan, X.; Zhang, G.; Yin, X. Estimation of effective geostress parameters driven by anisotropic stress and rock physics models with orthorhombic symmetry. J. Geophys. Eng. 2017, 14, 1124–1137. [Google Scholar] [CrossRef]
- Zoeppritz, K. On reflection and propagation of seismic waves. Gottinger Nachrichten 1919, 1, 66–84. [Google Scholar]
- Wang, Y.H. Approximations to the Zoeppritz equations and their use in AVO analysis. Geophysics 1999, 64, 1920–1927. [Google Scholar] [CrossRef]
- Downton, J.E. Seismic Parameter Estimation from AVO Inversion. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Yin, X.Y.; Zhang, S.X. Bayesian inversion for effective pore-fluid bulk modulus based on fluid-matrix decoupled amplitude variation with offset approximation. Geophysics 2014, 79, R221–R232. [Google Scholar] [CrossRef]
- Dai, R.; Yin, C.; Peng, D. AVA inversion of pre-stack seismic data with cross-gradient constraints. J. Appl. Geophys. 2022, 199, 104594. [Google Scholar] [CrossRef]
- Fatti, J.L.; Smith, G.C.; Vail, P.J.; Strauss, P.J.; Levitt, P.R. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the geostack technique. Geophysics 1994, 59, 1137–1362. [Google Scholar] [CrossRef]
- Russell, B.H. Prestack seismic amplitude analysis: An integrated overview. Interpretation 2014, 2, C19–C36. [Google Scholar] [CrossRef]
- Debski, W.; Tarantola, A. Information on elastic parameters obtained from the amplitudes of reflected waves. Geophysics 1995, 60, 1426–1436. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, G. Model parameterization and PP-wave Amplitude Versus Angle and Azimuth (AVAZ) direct inversion for fracture quasi-weaknesses in weakly anisotropic elastic media. Surv. Geophys. 2018, 39, 937–964. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, G.; Yin, X. Elastic impedance variation with angle and azimuth inversion for brittleness and fracture parameters in anisotropic elastic media. Surv. Geophys. 2018, 39, 965–992. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, P.; Zhang, G.; Guo, Z.; Liu, J. Seismic characterization of fractured reservoirs with elastic impedance difference versus angle and azimuth: A low-frequency poroelasticity perspective. Geophysics 2021, 86, M123–M139. [Google Scholar] [CrossRef]
- Zong, Z.; Yin, X.; Wu, G. Elastic impedance parameterization and inversion with Young’s modulus and Poisson’s ratio. Geophysics 2013, 78, N35–N42. [Google Scholar] [CrossRef]
- Sharifi, J.; Hafezi Moghaddas, N.; Lashkaripour, G.R.; Javaherian, A.; Mirzakhanian, M. Application of extended elastic impedance in seismic geomechanics. Geophysics 2019, 84, R429–R446. [Google Scholar] [CrossRef]
- Zhou, L.; Li, J.; Chen, X.; Liu, X.; Chen, L. Prestack amplitude versus angle inversion for Young’s modulus and Poisson’s ratio based on the exact Zoeppritz equations. Geophys. Prospect. 2017, 65, 1462–1476. [Google Scholar] [CrossRef]
- Ma, Q.; Sun, Z. Direct inversion of Young’s modulus and Poisson’s ratio using exact Zoeppritz equations based on double constraints. J. Seism. Explor. 2019, 28, 175–204. [Google Scholar]
- Grana, D.; Russell, B.; Mukerji, T. Petrophysical inversion based on f-s-r amplitude-variation-with-offset linearization and canonical correlation analysis. Geophysics 2022, 87, M247–M258. [Google Scholar] [CrossRef]
- Li, P.; Grana, D.; Liu, M. Bayesian neural network and Bayesian physics-informed neural network via variational inference for seismic petrophysical inversion. Geophysics 2024, 89, M185–M196. [Google Scholar] [CrossRef]
- Grana, D.; Liu, M.; de Figueiredo, L. GeosPIn: A MATLAB library for geostatistical petrophysical inversion. Geophysics 2024, 89, F77–F88. [Google Scholar] [CrossRef]
- Liu, M.; Grana, D.; Mukerji, T. Geostatistical inversion for subsurface characterization using Stein variational gradient descent with autoencoder neural network: An application to geologic carbon sequestration. J. Geophys. Res. Solid Earth 2024, 129, e2024JB029073. [Google Scholar] [CrossRef]
- Grana, D.; de Figueiredo, L.; Paparozzi, E.; Ravasio, A. Hierarchical Bayesian AVO-facies inversion using I p and Vp/Vs parametrization. Geophysics 2025, 90, 1–53. [Google Scholar] [CrossRef]
- Mallick, S. AVO and elastic impedance. Lead. Edge 2001, 20, 1094–1104. [Google Scholar] [CrossRef]
- Smith, G.C.; Gidlow, P.M. Weighted stacking for rock property estimation and detection of gas. Geophys. Prospect. 1987, 35, 993–1014. [Google Scholar] [CrossRef]
- Aleardi, M.; Tognarelli, A. The limits of narrow and wide-angle AVA inversions for high Vp/Vs ratios: An application to elastic seabed characterization. J. Appl. Geophys. 2016, 131, 54–68. [Google Scholar] [CrossRef]
- Downton, J.E.; Roure, B. Interpreting azimuthal Fourier coefficients for anisotropic and fracture parameters. Interpretation 2015, 3, ST9–ST27. [Google Scholar] [CrossRef]
- Scales, J.A.; Tenorio, L. Prior information and uncertainty in inverse problems. Geophysics 2001, 66, 389–397. [Google Scholar] [CrossRef]
- Sacchi, M.D. Reweighting strategies in seismic deconvolution. Geophys. J. Int. 1997, 129, 651–656. [Google Scholar] [CrossRef]
- Alemie, W.; Sacchi, M.D. High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution. Geophysics 2011, 76, R43–R55. [Google Scholar] [CrossRef]
- Saneifar, M.; Aranibar, A.; Heidari, Z. Rock classification in the Haynesville Shale based on petrophysical and elastic properties estimated from well logs. Interpretation 2015, 3, A65–A75. [Google Scholar] [CrossRef]
- Russell, B.; Hampson, D.; Chun, J. Noise elimination and the Radon transform, Part 1. Lead. Edge 1990, 9, 18–23. [Google Scholar] [CrossRef]
- Contreras, A.; Torres-Verdín, C.; Fasnacht, T. Sensitivity analysis of data-related factors controlling AVA simultaneous inversion of partially stacked seismic amplitude data: Application to deepwater hydrocarbon reservoirs in the central Gulf of Mexico. Geophysics 2007, 72, C19–C29. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; W.H. Freeman and Company: New York City, NY, USA, 2002. [Google Scholar]
- Shuey, R.T. A simplification of the Zoeppritz equations. Geophysics 1985, 50, 609–614. [Google Scholar] [CrossRef]
- Gray, F.; Chen, T.; Goodway, W. Bridging the gap: Using AVO to detect changes in fundamental elastic constants. In 69th Annual International Meeting, SEG, Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 1999; pp. 852–855. [Google Scholar]
- Russell, B.H.; Gray, D.; Hampson, D.P. Linearized AVO and poroelasticity. Geophysics 2011, 76, C19–C29. [Google Scholar] [CrossRef]
- Lee, S.J.; Han, S.W.; Hyun, S.M.; Lee, H.J.; Kim, J.H.; Kim, Y.I. Measurement of Young’s modulus and Poisson’s ratio for thin Au films using a visual image tracing system. Curr. Appl. Phys. 2009, 9, S75–S78. [Google Scholar] [CrossRef]
- Udoh, P.J.; Nsien, E.F.; Abasiekwere, U.A. On the relationship between young’s modulus, shear modulus and Poisson’s ratio. World J. Appl. Sci. Technol. 2023, 15, 354–361. [Google Scholar] [CrossRef]
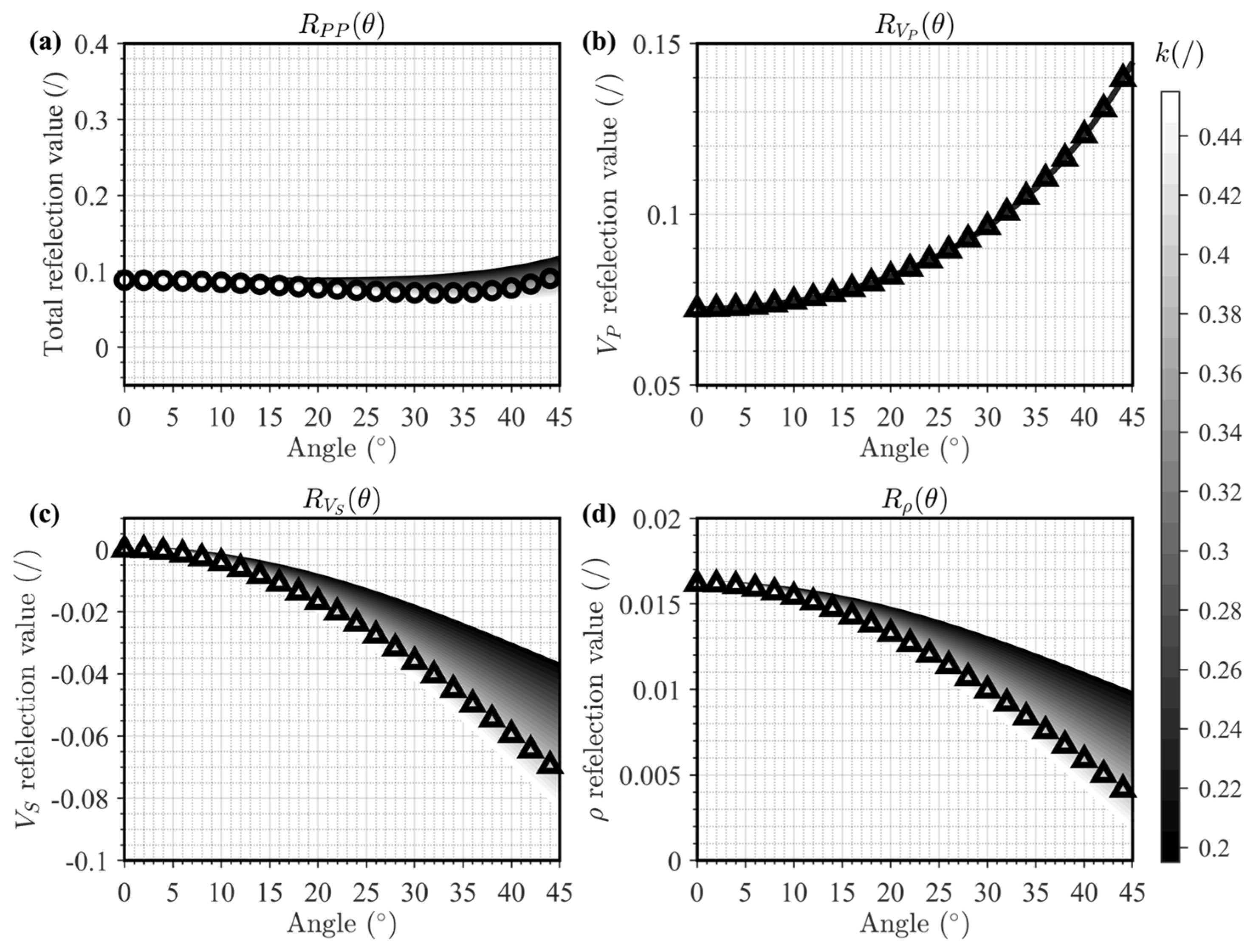
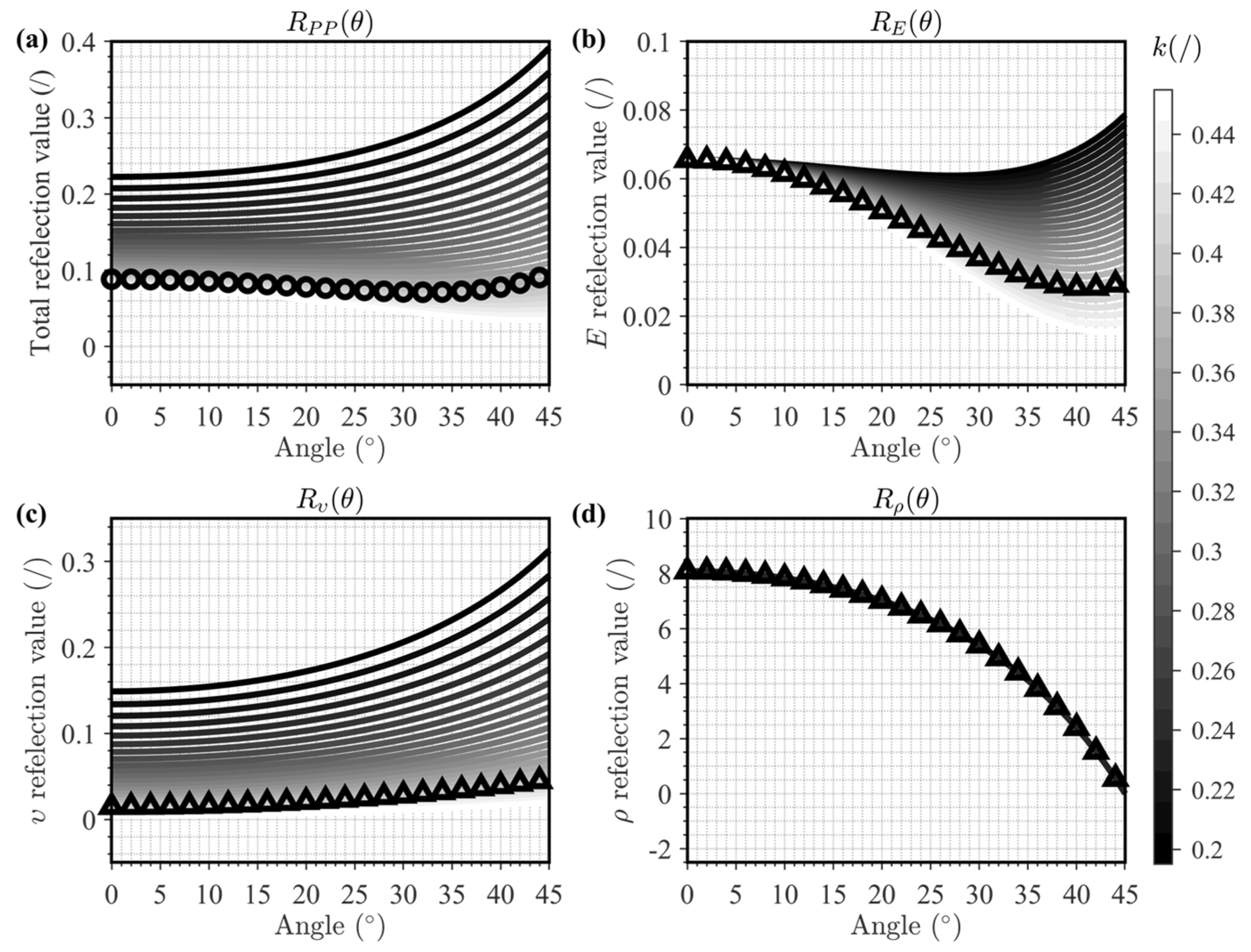
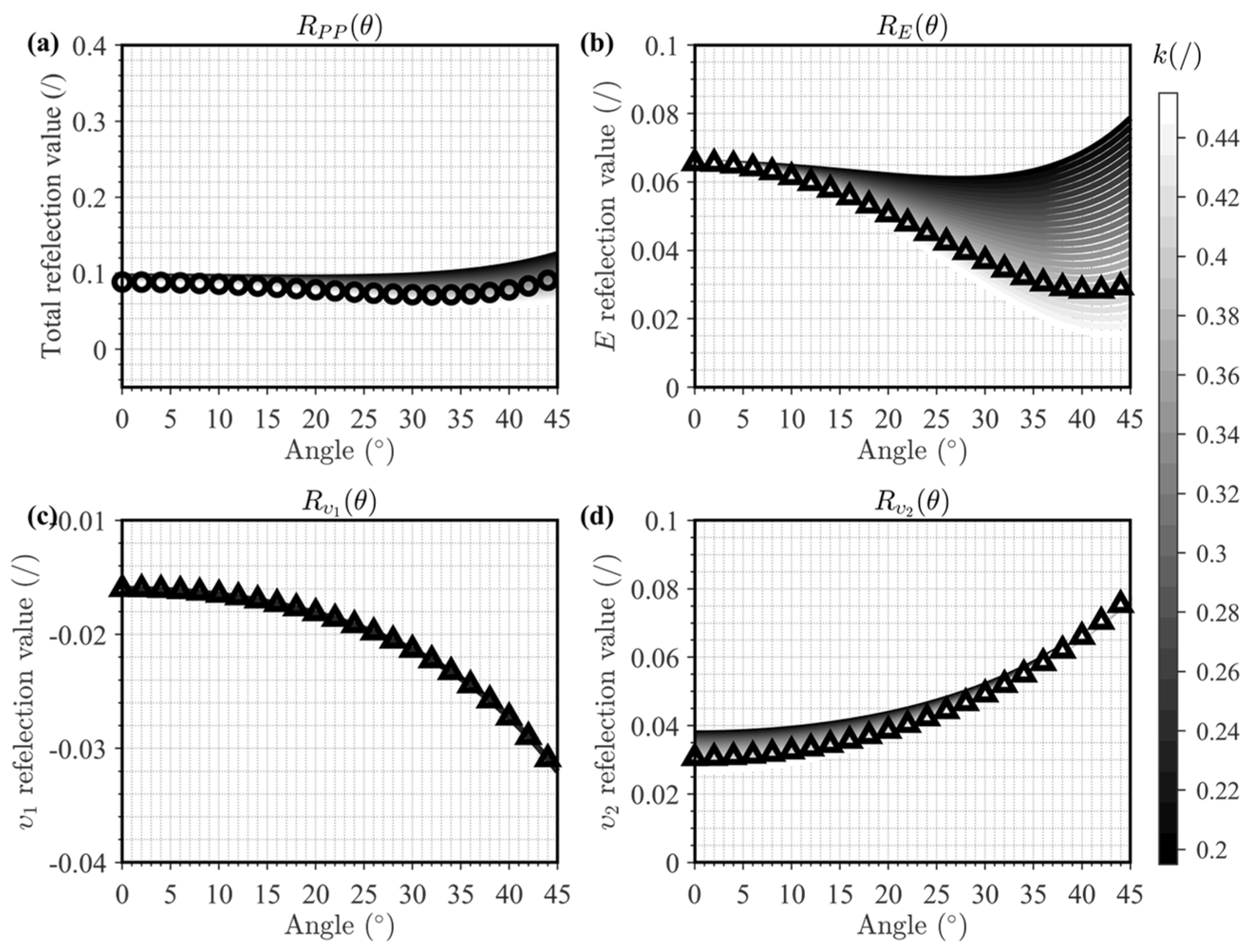
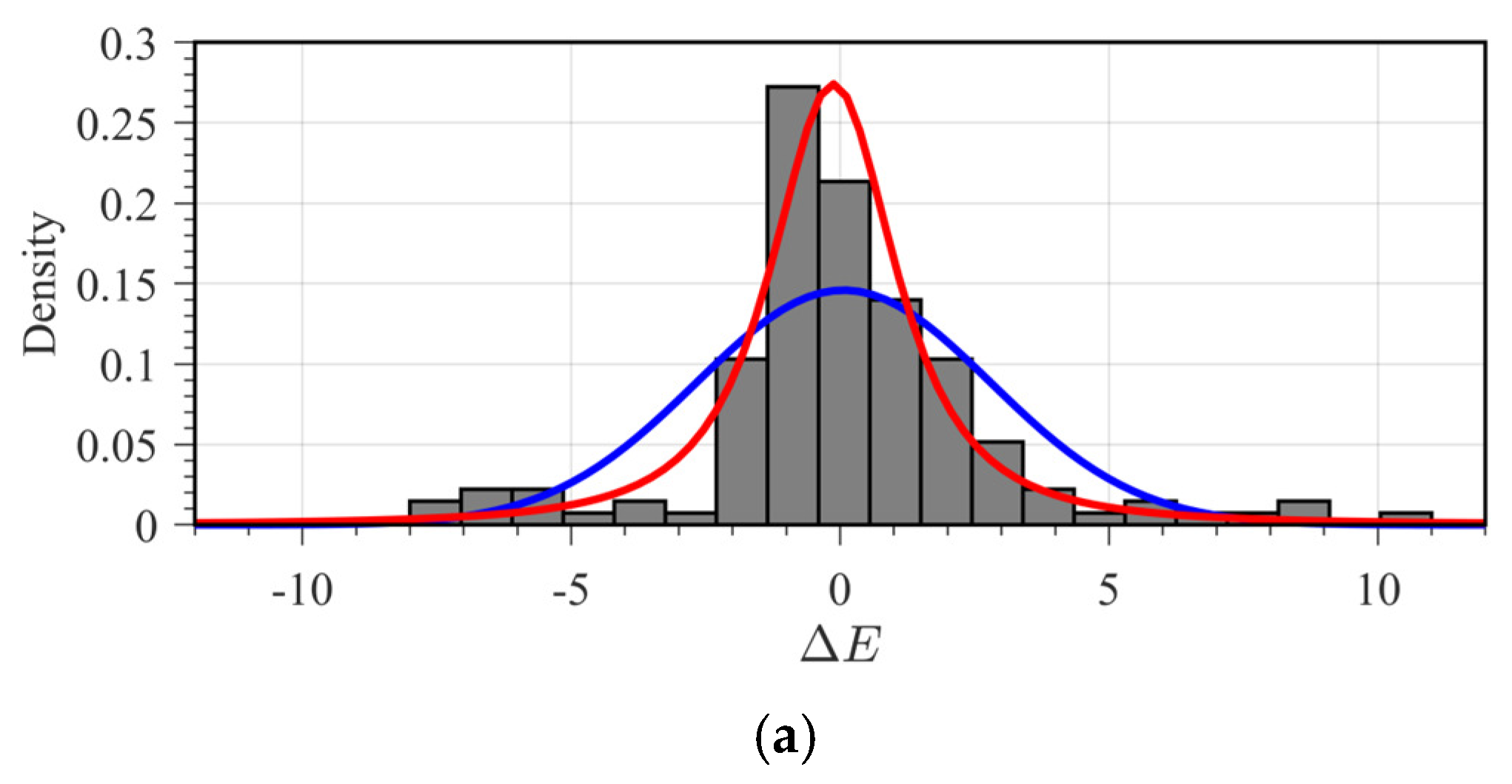
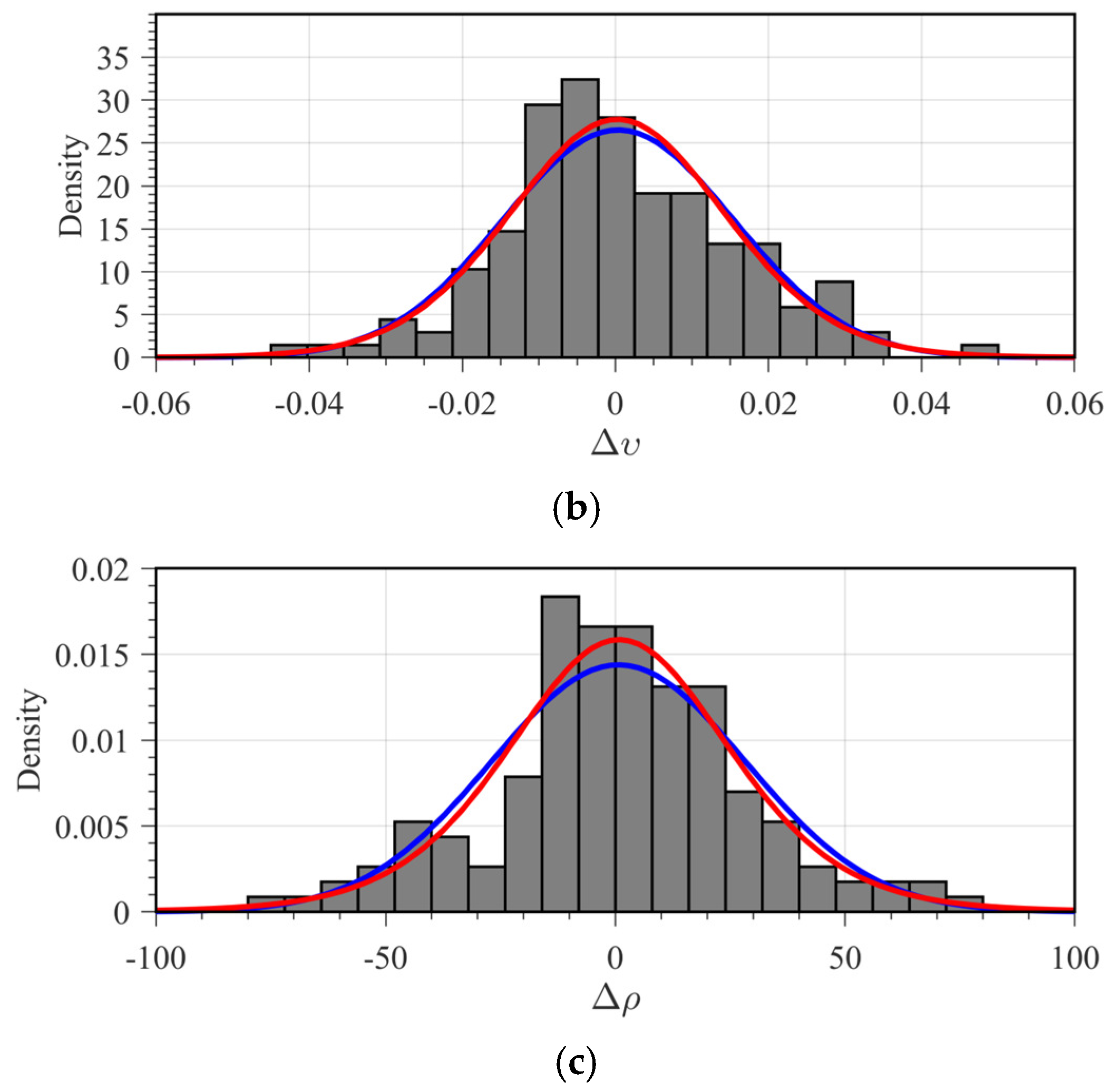
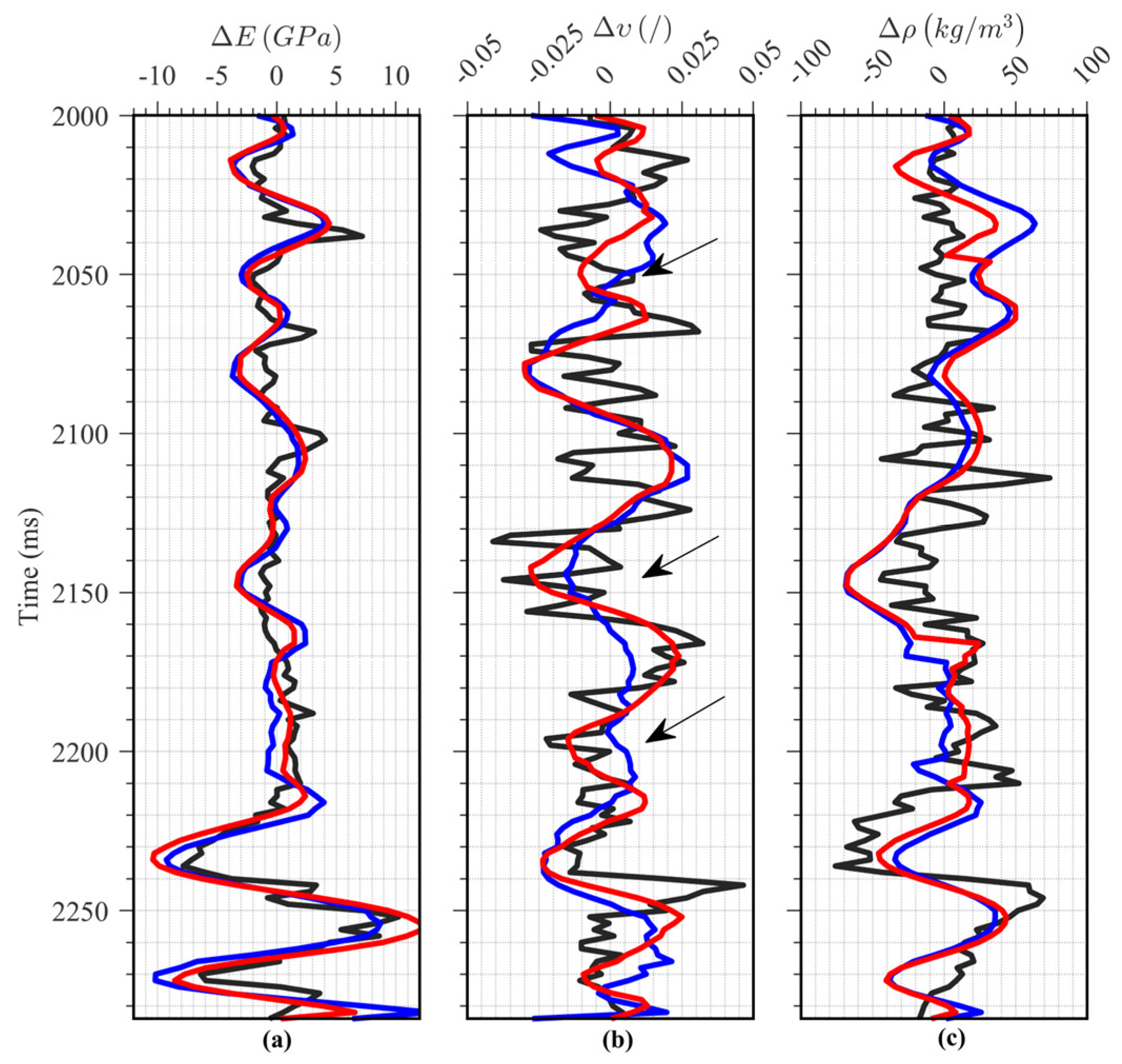

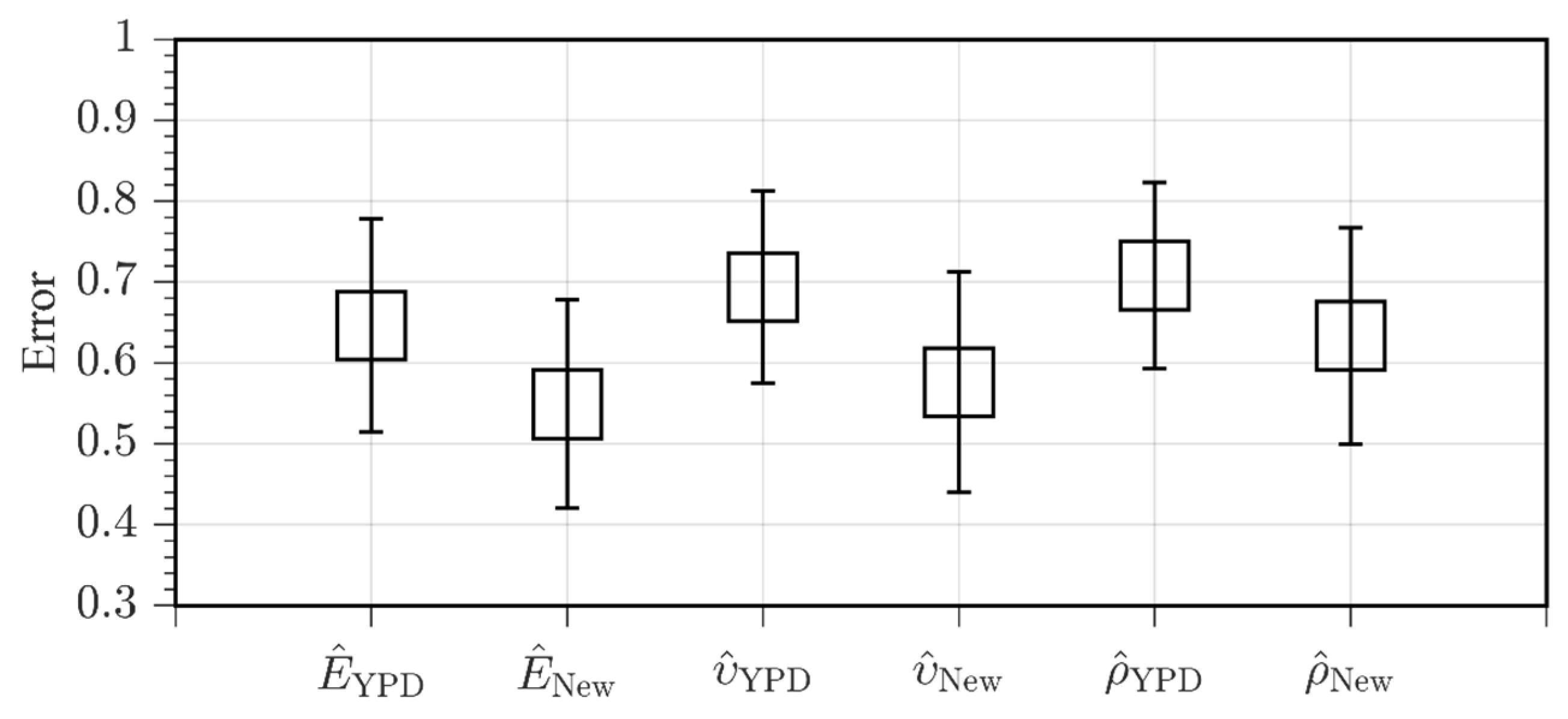

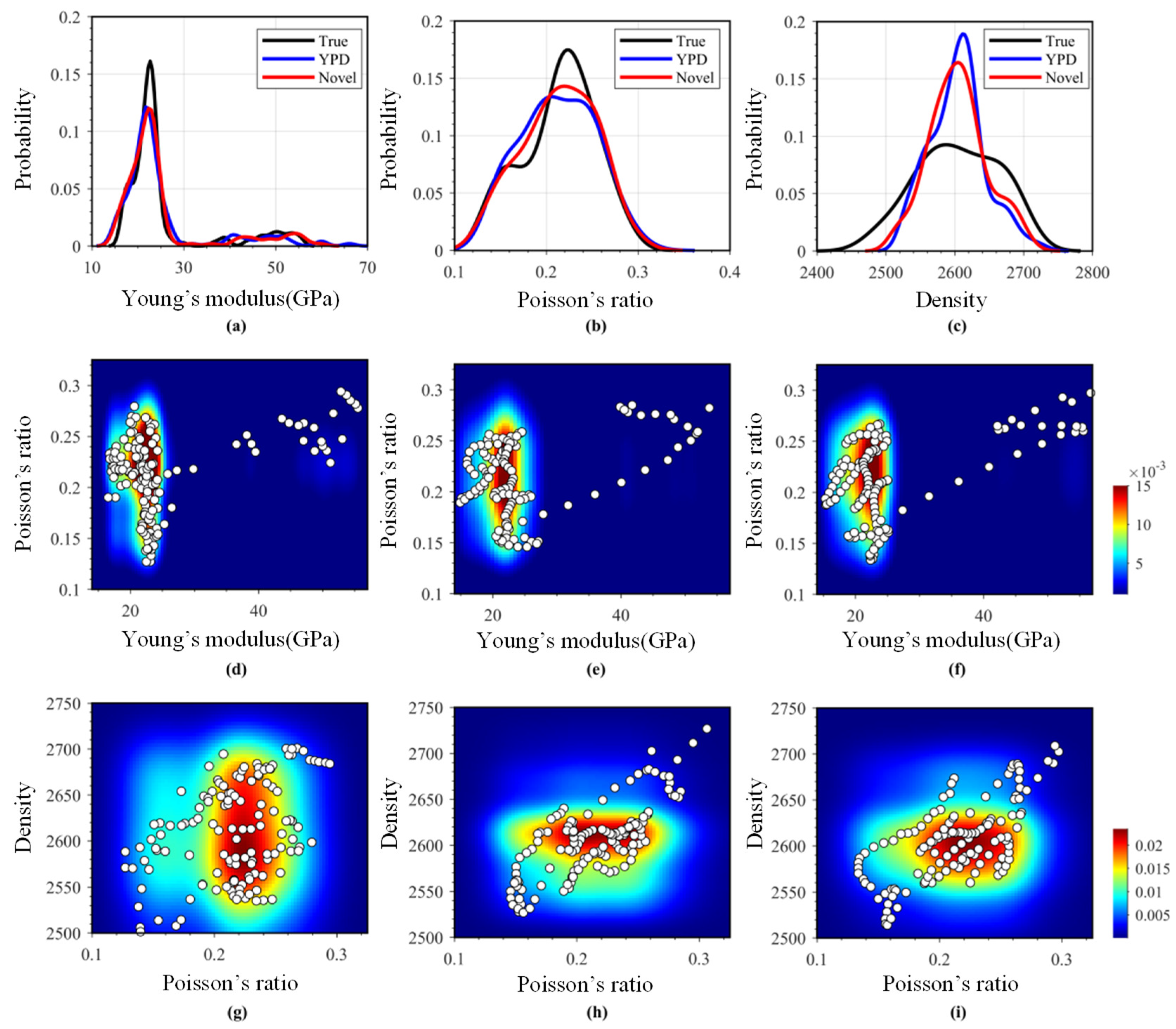

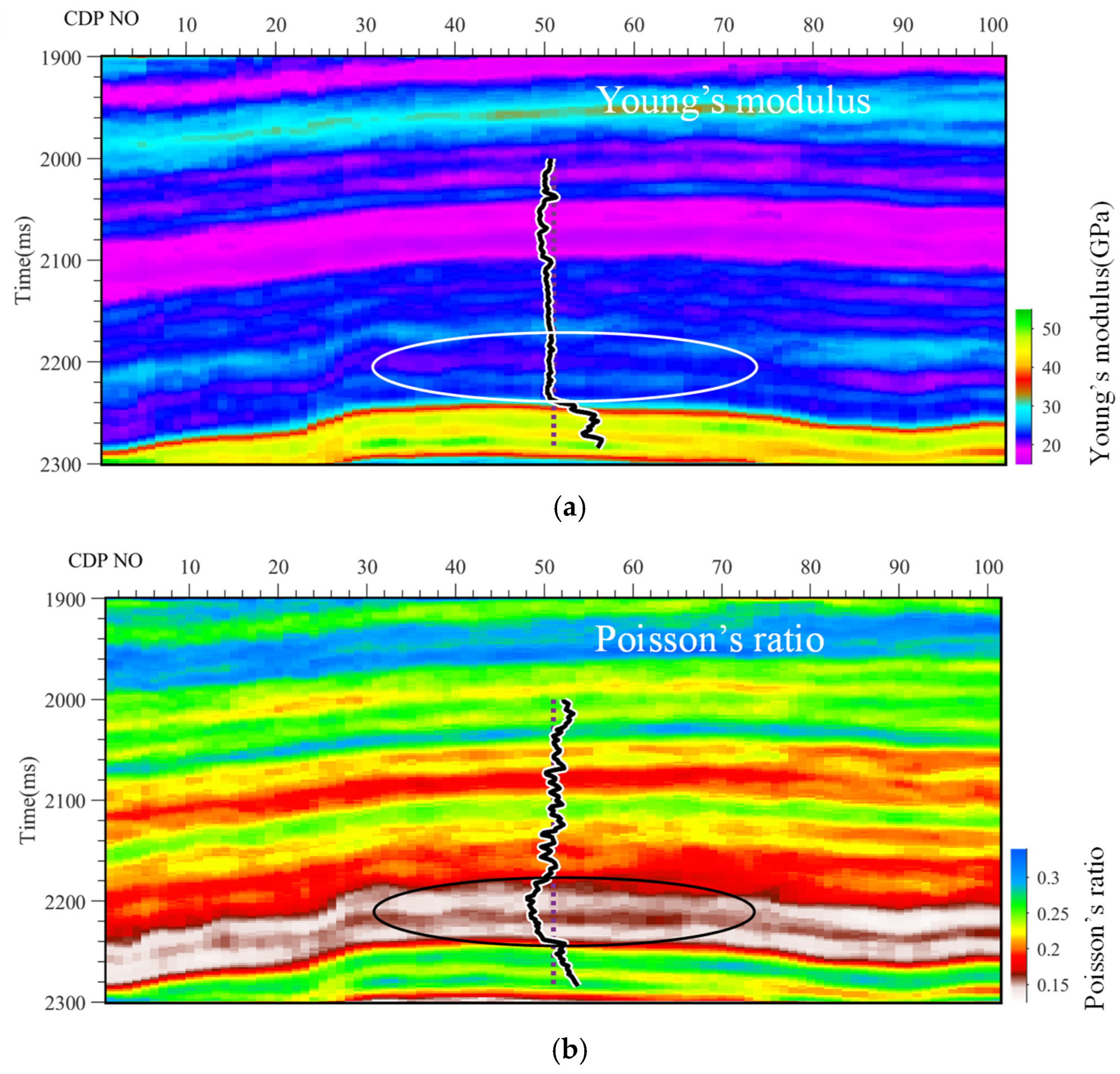
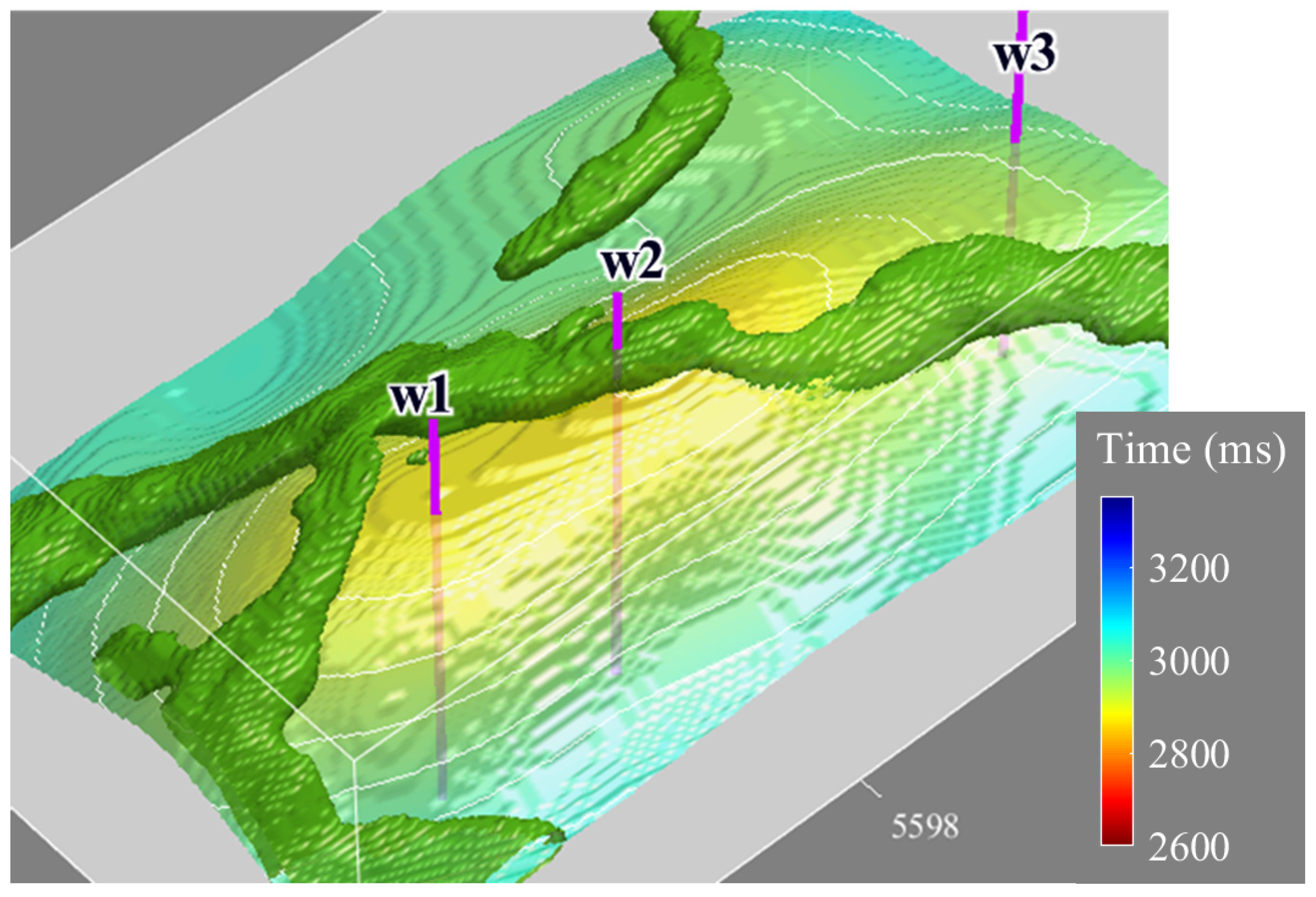
| Layer | VP (m/s) | VS (m/s) | ρ (g/cm3) | E (GPa) | (−) | (−) | (−) | (−) |
|---|---|---|---|---|---|---|---|---|
| 1 | 3106 | 1976 | 2494 | 22.59 | 0.16 | 0.84 | 1.47 | 0.41 |
| 2 | 3590 | 2170 | 2606 | 29.75 | 0.21 | 0.79 | 1.72 | 0.37 |
| RC (%) | 14.5 | 9.4 | 4.4 | 27.4 | 27.0 | 6.1 | 15.7 | 10.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Pan, X.; Sun, W.; Li, C.; Zheng, Y.; Zhao, X. Reservoir Characterization Based on Bayesian Amplitude Versus Offset Inversion of Marine Seismic Data. J. Mar. Sci. Eng. 2025, 13, 948. https://doi.org/10.3390/jmse13050948
Wang J, Pan X, Sun W, Li C, Zheng Y, Zhao X. Reservoir Characterization Based on Bayesian Amplitude Versus Offset Inversion of Marine Seismic Data. Journal of Marine Science and Engineering. 2025; 13(5):948. https://doi.org/10.3390/jmse13050948
Chicago/Turabian StyleWang, Jianhua, Xinpeng Pan, Wenbo Sun, Chao Li, Ying Zheng, and Xiaolong Zhao. 2025. "Reservoir Characterization Based on Bayesian Amplitude Versus Offset Inversion of Marine Seismic Data" Journal of Marine Science and Engineering 13, no. 5: 948. https://doi.org/10.3390/jmse13050948
APA StyleWang, J., Pan, X., Sun, W., Li, C., Zheng, Y., & Zhao, X. (2025). Reservoir Characterization Based on Bayesian Amplitude Versus Offset Inversion of Marine Seismic Data. Journal of Marine Science and Engineering, 13(5), 948. https://doi.org/10.3390/jmse13050948






