Marine Voyage Optimization and Weather Routing with Deep Reinforcement Learning
Abstract
1. Introduction
2. Literature Review
3. Theoretical Background
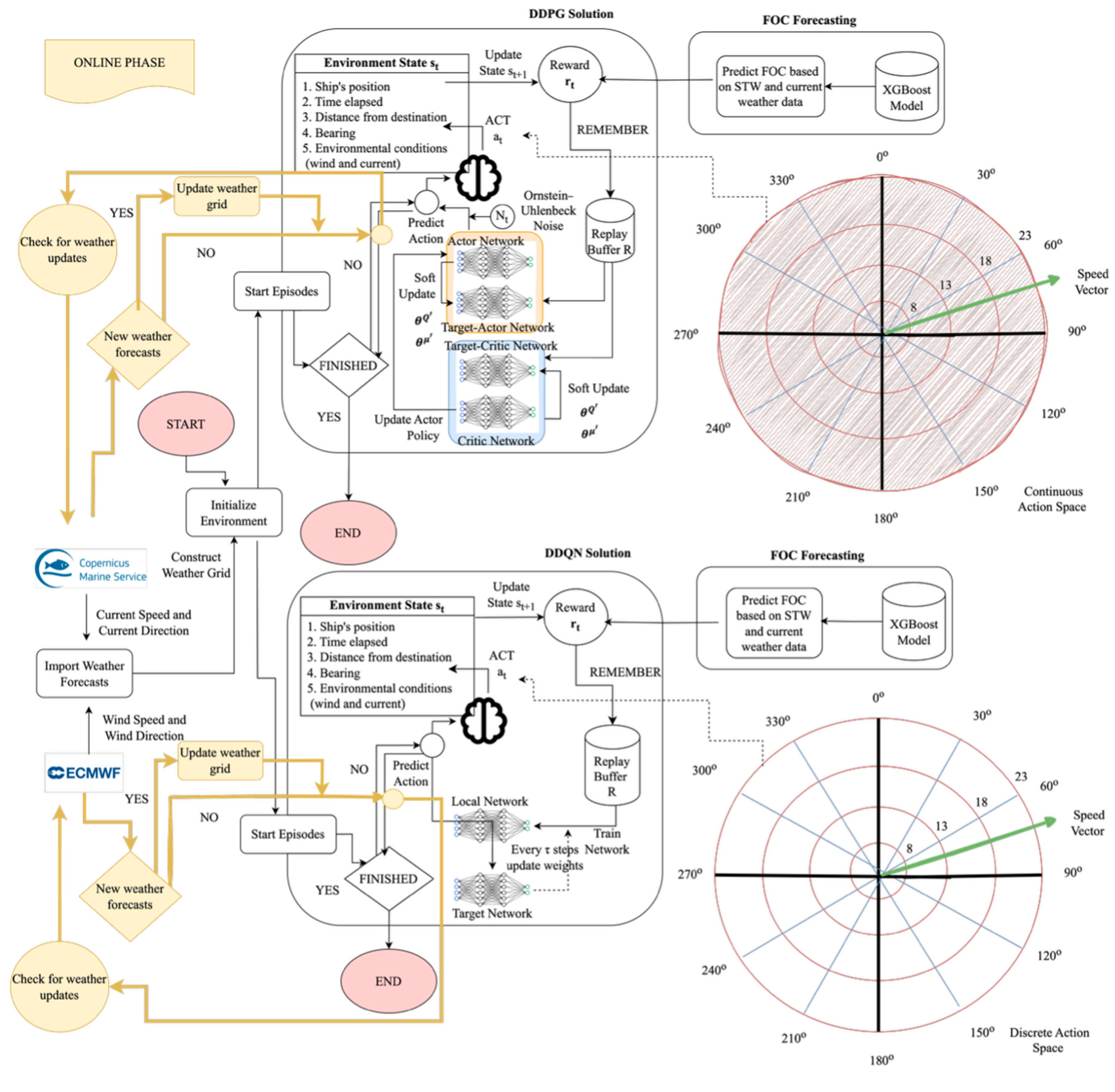
3.1. Double Deep Q-Network (DDQN)
| Algorithm 1: Double Deep Q-Learning |
| 1: Initialize replay buffer R with memory size N |
| 2: Initialize action-value function Q with random weights θ |
| 3: Initialize target action-value function with weights |
| 4: For episode = 1 to M do |
| 5: Initialize vessel’s starting state (position, course, speed, current and forecasted weather conditions) |
| 6: For timestep = 1 to T do |
| 7: With probability ε select a random action (STW and bearing) |
| 8: Otherwise select |
| 9: Execute action in the simulation environment, observe reward (based on fuel consumption, ETA deviation, constraint violations) and new state 10: Store transition in R 11: Sample random minibatch of transitions from R 12: Use the online network to select the action 13: Set 14: Perform a gradient descent step on with respect to the network parameters θ 15: Every C steps reset 16: End For 17: End For |
3.2. Deep Deterministic Policy Gradient (DDPG)
| Algorithm 2: Deep Deterministic Policy Gradient (DDPG) |
| 1: |
| 2: Initialize target networks: |
| 3: Initialize replay buffer R |
| 4: For episode = 1 to M do |
| 5: for action exploration (Ornstein–Uhlenbeck) 6: (vessel position, course, speed, current and forecasted weather conditions) |
| 7: For timestep = 1 to T do |
| 8: Select continuous action: (vector of vessel STW and bearing) |
| 9: Execute action in the environment and observe reward and observe new state |
| 10: in replay buffer R 11: from R 12: Compute target value: 13: Update critic by minimizing the loss 14: Update actor policy using the sampled policy gradient: 15: 16: Update the target networks with soft updates: 17: 18: End For 19: End For |
4. Methodology
4.1. Simulation Environment
- Geographical Position: The ship’s current coordinates (longitude and latitude).
- Elapsed Time: The time since the journey began, measured in seconds.
- Distance to Destination: The remaining distance to the target point.
- Environmental Conditions: Weather forecasts, including wind direction, wind speed, current direction, and current speed, interpolated based on the ship’s ETA.
- Discrete Action Space (DDQN): The agent selects a bearing in the range of [0°, 180°], with intervals of 10°, and STW values between 8 and 22 knots with unit intervals. Most commercial vessels, such as bulk carriers, container ships, and tankers, typically operate within this speed range under normal conditions to avoid excessive fuel consumption and mechanical stress. Smaller intervals (e.g., 5°) for bearings were found to increase the likelihood of suboptimal policies due to insufficient exploration and an excessive number of alternative routes.
- Continuous Action Space (DDPG): The agent can select any bearing in the range of [0°, 360°) and any STW in the range defined for the discrete action space.
4.2. Problem Formulation
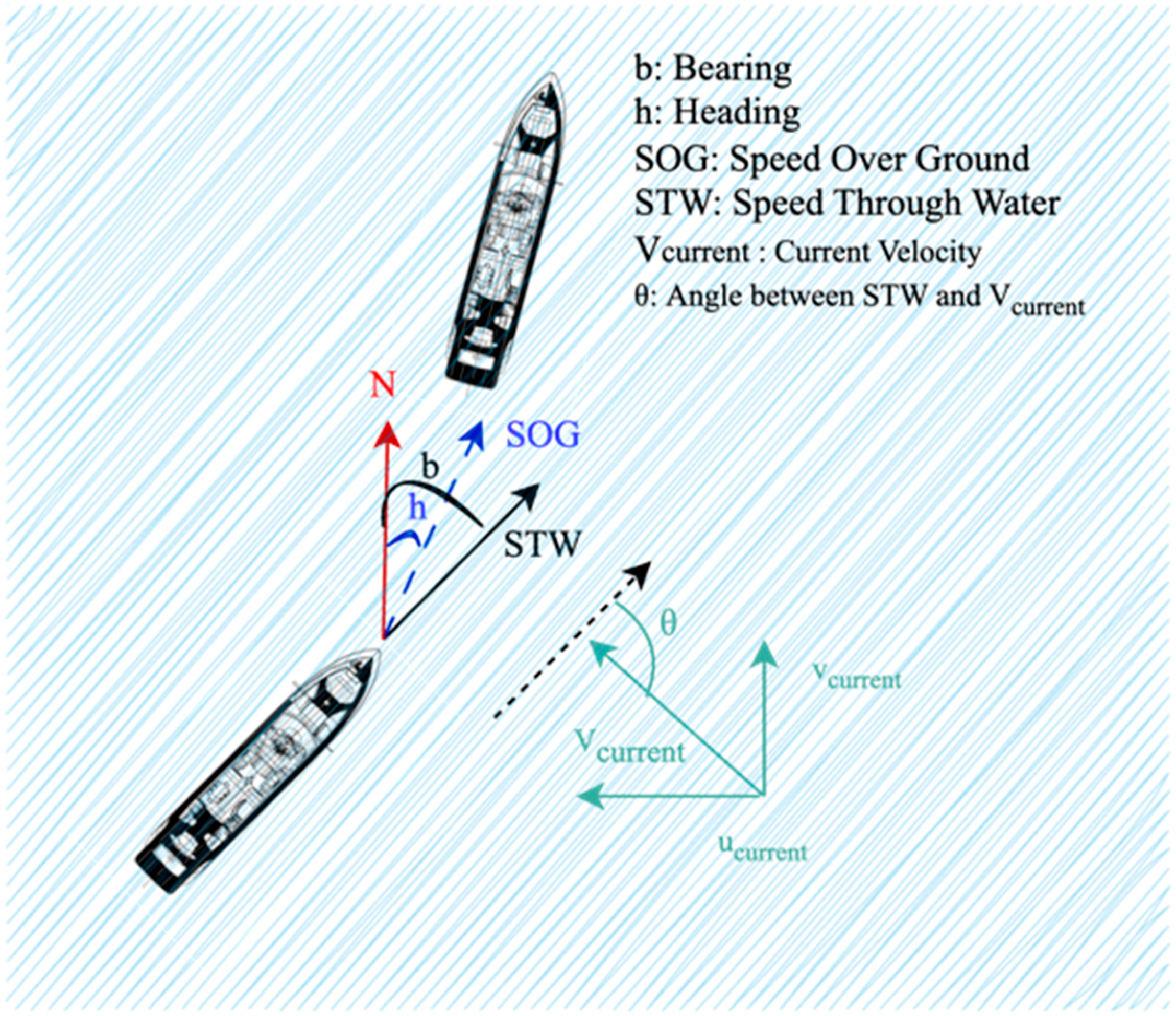
- is the Speed Through Water (knots);
- is the ocean current velocity (m/s);
- is the ship’s movement direction;
- is the current’s direction;
- is the angle between the ship’s speed and current direction (degrees);
- 0.037 is a unit conversion constant (m/s to nautical miles per minute).
- Dr: Reduction in the distance to destination. This encourages progress towards the destination by comparing the vessel’s current and previous Haversine distances to the target. This ensures timely feedback for every action taken.
- Pt: Penalty associated with travel time exceeding expected thresholds. It is applied when the vessel deviates from the ideal JIT arrival window.
- Ps: Speed penalty. This penalty ensures that the vessel operates at an optimal speed, minimizing fuel consumption while adhering to JIT constraints.
- PO: Obstacle penalty. This is a large penalty that is applied if the vessel crosses an obstacle.
- Weighting factors applied to each respective component.
- : Boolean variable that is true if the ship crosses an obstacle (e.g., land).
- : Final reward.
- Arrival reward.
- : Boolean variable that is true if the ship arrives within the JIT constraints.
- : Distance to destination.
- : Acceptable distance range for successful arrival.
- T: Maximum allowable steps per episode.
4.3. Phased Optimization Approach
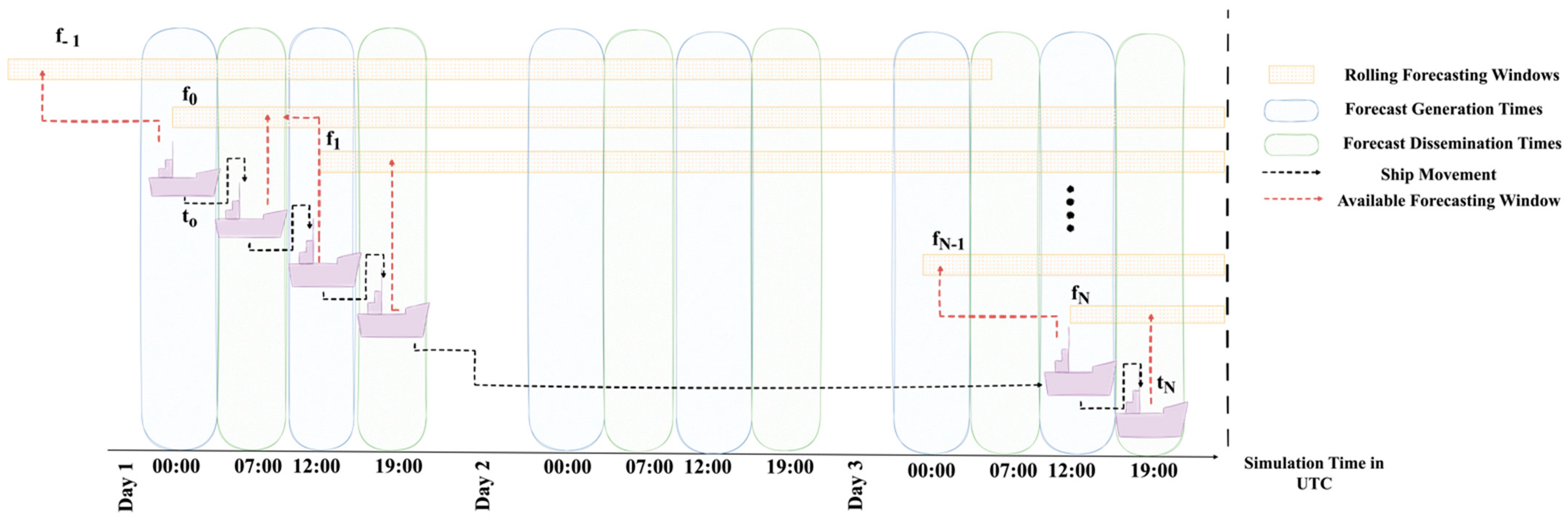
4.4. Weather Integration
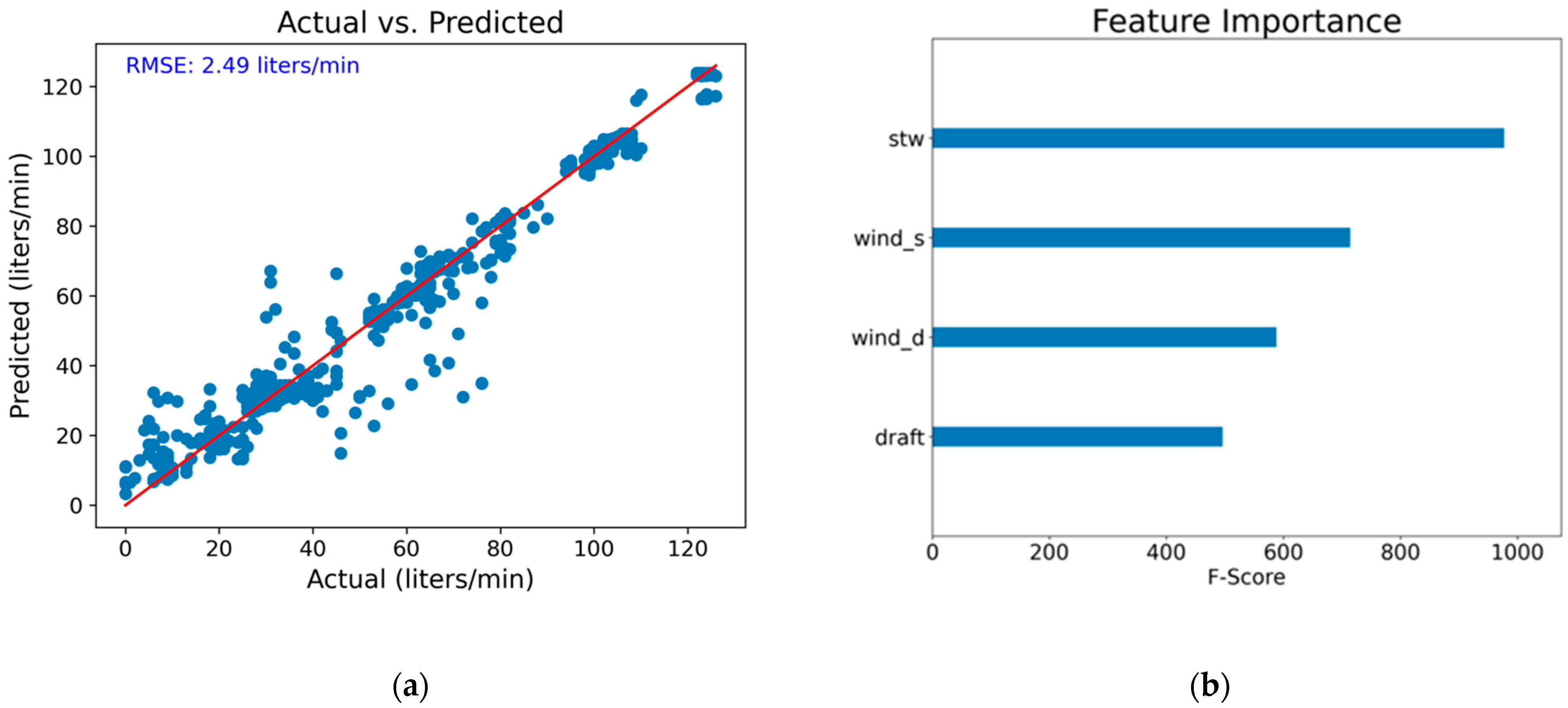
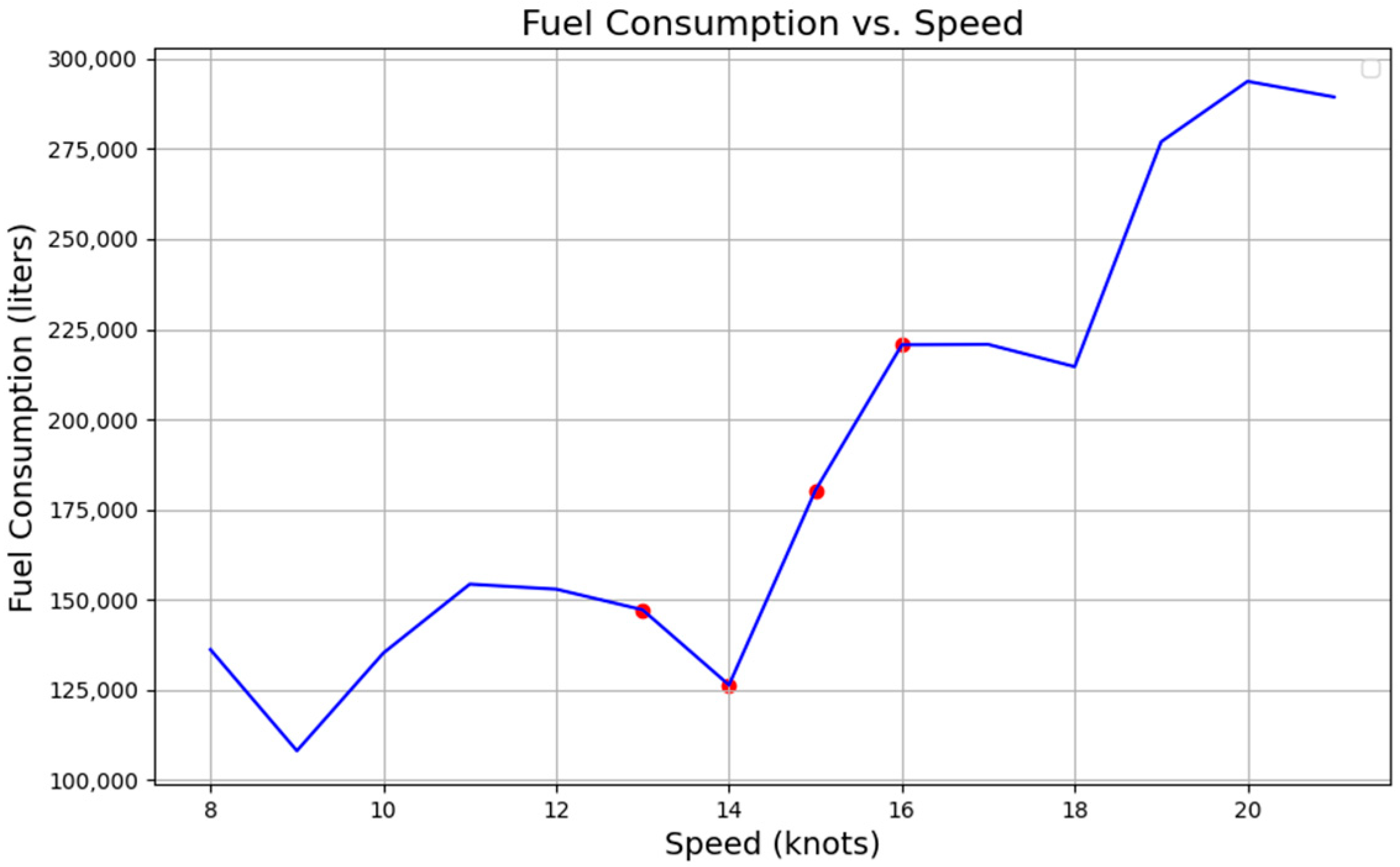
4.5. Fuel Oil Consumption (FOC) Modeling
4.6. Computational Setup
5. Results and Discussion
5.1. Results
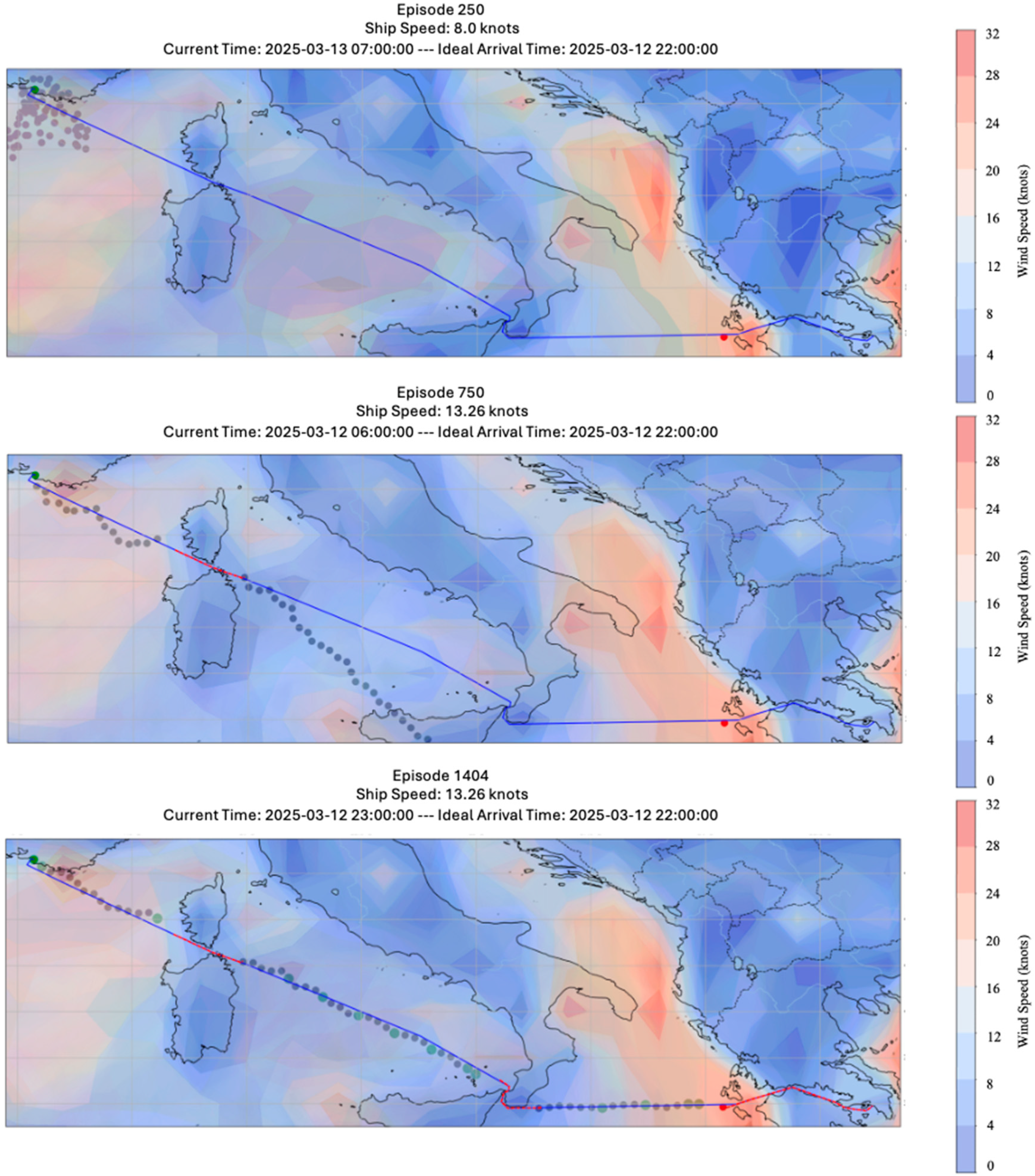
5.1.1. DDQN Results
5.1.2. DDPG Results
5.1.3. Adaptation to Real-Time Weather
5.1.4. Hyperparameter Tuning
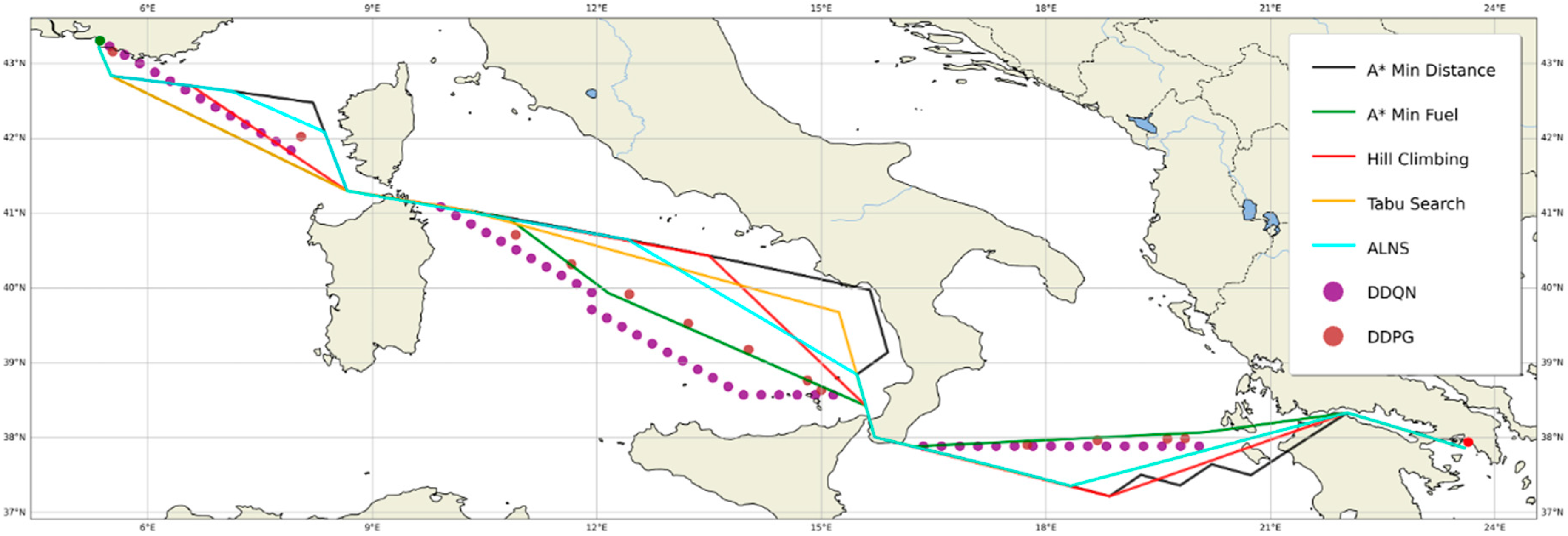
5.2. Benchmarking
5.2.1. Shortest Path Based on Maritime Graph
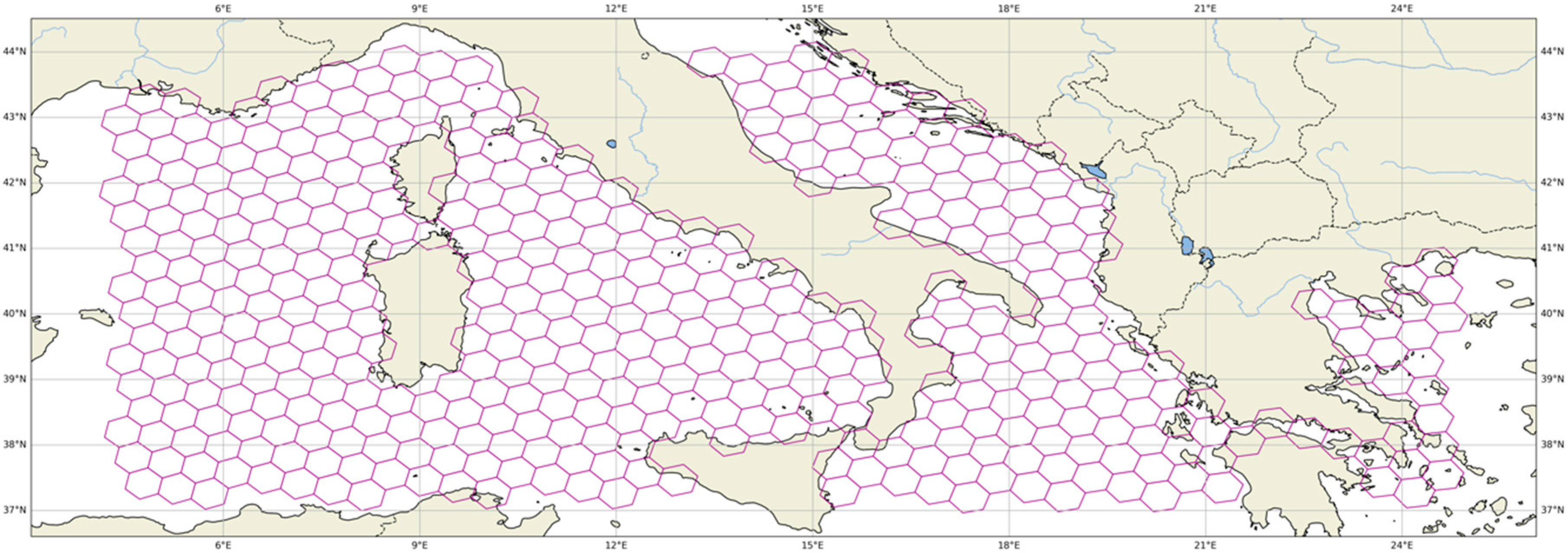
5.2.2. Grid-Based Benchmarks—The H3 Grid
- Uniform Connectivity: Each hexagon has six neighbors, ensuring consistent connectivity throughout the grid, which simplifies pathfinding and avoids the distortions caused by square grids.
- Isotropic Representation: Hexagons reduce directional bias, providing a more accurate representation of movement in all directions—a critical factor in maritime navigation.
- Multi-Resolution Analysis: H3 supports multiple resolution levels spanning from 1 m2 (level 15) up to 4 × 106 km2 (level 1), allowing the grid’s granularity to be tuned according to the problem’s complexity and computational limits.
5.2.3. A* Search
5.2.4. Hill Climbing
5.2.5. Tabu Search
5.2.6. Adaptive Large Neighborhood Search (ALNS)
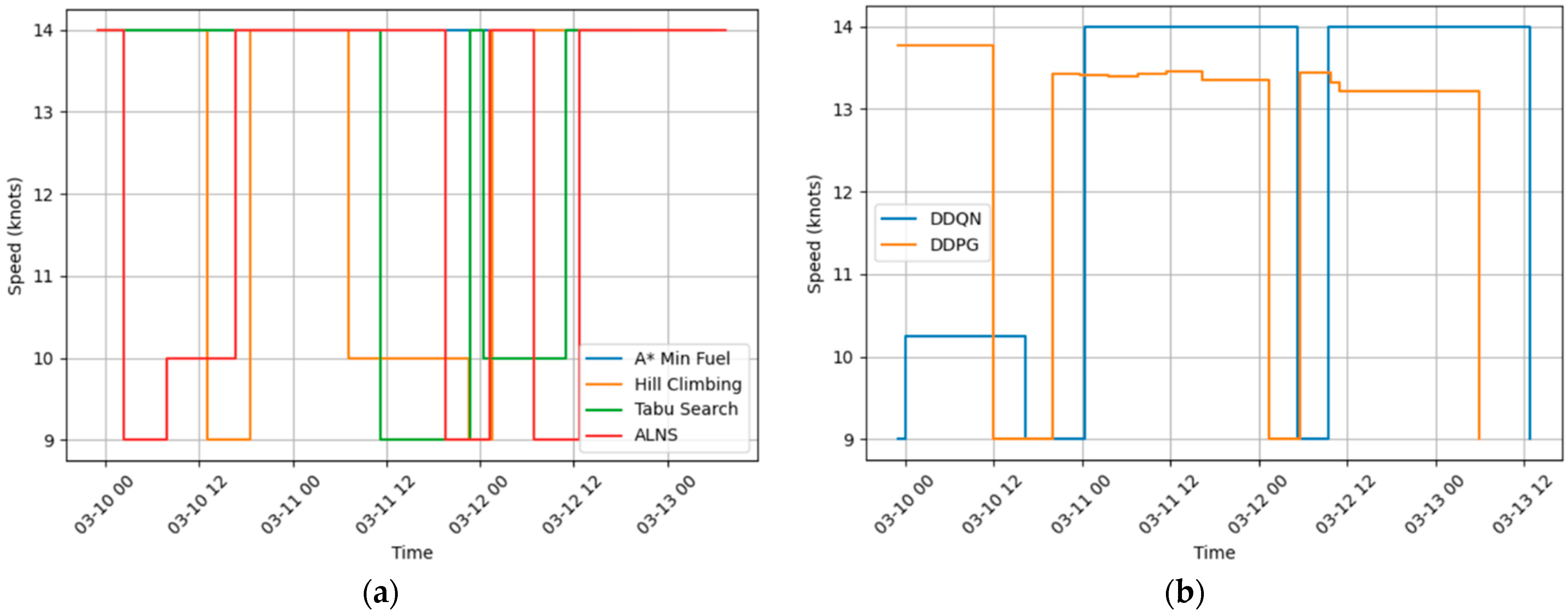
5.2.7. Algorithm Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RL | Reinforcement Learning |
| DRL | Deep Reinforcement Learning |
| DDQN | Double Deep Q Network |
| DPG | Deterministic Policy Gradient |
| DDPG | Deep Deterministic Policy Gradient |
| ML | Machine learning |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| GHG | Greenhouse gas |
| ETA | Estimated time of arrival |
| ALNS | Adaptive Large Neighborhood Search |
| DP | Dynamic Programming |
| STW | Speed Through Water |
| SOG | Speed Over Ground |
| JIT | Just-In-Time |
| FOC | Fuel Oil Consumption |
| CDS | Copernicus Data Store |
| UTC | Coordinated Universal Time |
| API | Application Programming Interface |
| LSTM | Long Short Term Memory |
| ReLU | Rectified Linear Unit |
Appendix A
| DDQN | DDPG | |
|---|---|---|
| General | ||
| Environment | An orthogonal environment of the latitude/longitude coordinates defined by the routing problem with geospatial information on sea and land locations and a grid with weather data availability | Same as DDQN |
| State | A combination the ship state and the weather conditions of the environment | Same as DDQN |
| Action | 19 angle values (every 10 degrees) × 15 speed values = 285 possible actions | Continuous angle values in the [0,360°) range and continuous speed values in the [8,22] range |
| Reward | A combination of distance, fuel consumption, and time of arrival (Equation (8)) | Same as DDQN |
| Network Architecture | ||
| Input | The input size depends on the side of the grid, which is dynamic and is generated to enclose the origin and destination points | Same as DDQN |
| Fully connected hidden layer | 2 hidden layers with 400 and 300 units, respectively. | Actor network: A total of 2 hidden layers with 400 and 300 units, respectively Critic network: A total of 2 state layers with 128 and 64 layers, respectively; 2 action layers with 128 and 64 layers, respectively; and 2 layers for their concatenation with 64 and 32 layers, respectively |
| Rectified Linear Units (ReLU) | Between all hidden layers | Between all hidden layers |
| Output of the network | Q-values for each possible action | Action network: A total of 2 Tanh layers to bound angle and speed Critic Network: Q-value without activation function |
| Optimization | Adam | Adam |
| Hyper-Parameters | ||
| Decay | ε-decay: 0.998 | Noise decay: 0.998 |
| Discount factor (γ) | 0.99 | 0.99 |
| Learning rate (α) | 0.0001 | 1 × 10−6 for the actor network and 5 × 10−7 for the critic network |
| Target network updates (τ) | 0.001 and updates every 5 steps | 0.005 and 2 updates per step |
| Experience replay memory | 4000 | 10,000 |
| Network update | Mini-batch sizes of 256 | Mini-batch sizes of 256 |
| Exploration policy | ε-greedy with the ε decreasing linearly from 1 to 0.05 | Temporally correlated noise (Ornstein–Uhlenbeck process) with θ = 0.2 and σ = 0.2 |
| Regularization | N/A | N/A |
| Number of episodes | 1500 episodes | 1500 episodes |
| DDQN (Pre-Training) | DDQN (Fine-Tuning) | DDPG (Pre-Training) | DDPG (Fine-Tuning) | |
|---|---|---|---|---|
| Learning rate (α) | 0.0001 | 8 × 10−5 (−20%) | N/A | N/A |
| Learning rate of actor network () | N/A | N/A | 1 × 10−6 | 5 × 10−7 (−50%) |
| Learning rate of critic network () | N/A | N/A | 5 × 10−7 | 2.5 × 10−7 (−50%) |
| Update every n steps (DDQN) and updates per step (DDPG) | 5 | 4 (−20%) | 2 | 3 (+50%) |
| Experience replay memory | 4000 | 1000 (−75%) | 10,000 | 2500 (−75%) |
| Initial ε (DDQN) and noise multiplier (DDPG) | 1.0 | 0.3 (−70%) | 1.0 | 0.3 (−70%) |
| Number of episodes | 1500 | 130 (−91%) | 1500 | 300 (−80%) |
References
- United Nations Conference on Trade and Development—UNCTAD, 2019. Review of Maritime Transport. UNCTAD/RMT/2019. United Nations Publication. Available online: http://unctad.org/en/PublicationsLibrary/rmt2019_en.pdf (accessed on 5 February 2025).
- Stopford, M. Maritime Economics 3e; Routledge: London, UK, 2008. [Google Scholar]
- IPCC. AR6 Synthesis Report. Climate Change 2023. Available online: https://www.ipcc.ch/report/ar6/syr/ (accessed on 20 May 2024).
- IPCC. Sixth Assessment Report. Working Group III: Mitigation of Climate Change. Available online: https://www.ipcc.ch/report/ar6/wg3/ (accessed on 20 May 2024).
- International Maritime Organization (IMO): MEPC.304(72), Initial IMO Strategy on Reduction of GHG Emissions from Ships; International Maritime Organization: London, UK, 2018.
- International Maritime Organization (IMO): MEPC.80/(WP.12), 2023 IMO Strategy on Reduction of GHG Emissions from Ships; International Maritime Organization: London, UK, 2023.
- European Commission. Reducing Emissions from the Shipping Sector. 2024. Available online: https://climate.ec.europa.eu/eu-action/transport/reducing-emissions-shipping-sector_en (accessed on 21 March 2025).
- OGCI & Concawe. Technological, Operational and Energy Pathways for Maritime Transport to Reduce Emissions Towards 2050 (Issue 6C). Oil and Gas Climate Initiative. 2023. Available online: https://www.ogci.com/wp-content/uploads/2023/05/OGCI_Concawe_Maritime_Decarbonisation_Final_Report_Issue_6C.pdf (accessed on 27 April 2025).
- Bullock, S.; Mason, J.; Broderick, J.; Larkin, A. Shipping and the Paris climate agreement: A focus on committed emissions. BMC Energy 2020, 2, 5. [Google Scholar] [CrossRef]
- Bouman, E.A.; Lindstad, E.; Rialland, A.I.; Strømman, A.H. State-of-the-art technologies, measures, and potential for reducing GHG emissions from shipping—A review. Transp. Res. Part D Transp. Environ. 2017, 52, 408–421. [Google Scholar] [CrossRef]
- Zis, T.P.; Psaraftis, H.N.; Ding, L. Ship weather routing: A taxonomy and survey. Ocean. Eng. 2020, 213, 107697. [Google Scholar] [CrossRef]
- International Maritime Organization. Just in Time Arrival Guide. 2021. Available online: https://greenvoyage2050.imo.org/wp-content/uploads/2021/01/GIA-just-in-time-hires.pdf (accessed on 27 April 2025).
- Sun, Y.; Fang, M.; Su, Y. AGV Path Planning based on Improved Dijkstra Algorithm. J. Phys. Conf. Series 2021, 1746, 012052. [Google Scholar] [CrossRef]
- Mannarini, G.; Salinas, M.L.; Carelli, L.; Petacco, N.; Orović, J. VISIR-2: Ship weather routing in Python. Geosci. Model Dev. 2024, 17, 4355–4382. [Google Scholar] [CrossRef]
- Sen, D.; Padhy, C. An Approach for Development of a Ship Routing Algorithm for Application in the North Indian Ocean Region. Appl. Ocean. Res. 2015, 50, 173–191. [Google Scholar] [CrossRef]
- Gao, F.; Zhou, H.; Yang, Z. Global path planning for surface unmanned ships based on improved A∗ algorithm. Appl. Res. Comput. 2020, 37. [Google Scholar]
- Kaklis, D.; Kontopoulos, I.; Varlamis, I.; Emiris, I.Z.; Varelas, T. Trajectory mining and routing: A cross-sectoral approach. J. Mar. Sci. Eng. 2024, 12, 157. [Google Scholar] [CrossRef]
- Xiang, J.; Wang, H.; Ouyang, Z.; Yi, H. Research on local path planning algorithm of unmanned boat based on improved Bidirectional RRT. Shipbuild. China 2020, 61, 157–166. [Google Scholar]
- James, R. Application of Wave Forecast to Marine Navigation; US Navy Hydrographic Office: Washington, DC, USA, 1957. [Google Scholar]
- Tao, W.; Yan, S.; Pan, F.; Li, G. AUV path planning based on improved genetic algorithm. In Proceedings of the 2020 5th International Conference on Automation, Control and Robotics Engineering (CACRE), Dalian, China, 19–20 September 2020; pp. 195–199. [Google Scholar]
- Vettor, R.; Guedes Soares, C. Multi-objective route optimization for onboard decision support system. In Information, Communication and Environment: Marine Navigation and Safety of Sea Transportation; Weintrit, A., Neumann, T., Eds.; CRC Press: Leiden, The Netherlands, 2015; pp. 99–106. [Google Scholar]
- Ding, F.; Zhang, Z.; Fu, M.; Wang, Y.; Wang, C. Energy-efficient path planning and control approach of USV based on particle swarm optimization. In Proceedings of the Conference on OCEANS MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; pp. 1–6. [Google Scholar]
- Lazarowska, A. Ship’s trajectory planning for collision avoidance at sea based on ant colony optimisation. J. Navig. 2015, 68, 291–307. [Google Scholar] [CrossRef]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean. Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- Pallotta, G.; Vespe, M.; Bryan, K. Vessel pattern knowledge discovery from ais data: A framework for anomaly detection and route prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef]
- Yoo, B.; Kim, J. Path optimization for marine vehicles in ocean currents using reinforcement learning. J. Mar. Sci. Technol. 2016, 21, 334–343. [Google Scholar] [CrossRef]
- Chen, C.X.Q.; Chen, F.M.; Zeng, X.J.; Wang, J. A knowledge-free path planning approach for smart ships based on reinforcement learning. Ocean Eng. 2019, 189, 106299. [Google Scholar] [CrossRef]
- Moradi, M.H.; Brutsche, M.; Wenig, M.; Wagner, U.; Koch, T. Marine route optimization using reinforcement learning approach to reduce fuel consumption and consequently minimize CO2 emissions. Ocean Eng. 2021, 259, 111882. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Hou, P.; Jiang, L. Using deep reinforcement learning for Autonomous Vessel Path Planning in Offshore Wind Farms. In Proceedings of the 2024 International Conference on Industrial Automation and Robotics, Singapore, 18–20 October 2024; pp. 1–7. [Google Scholar]
- Wu, Y.; Wang, T.; Liu, S. A Review of Path Planning Methods for Marine Autonomous Surface Vehicles. J. Mar. Sci. Eng. 2024, 12, 833. [Google Scholar] [CrossRef]
- Shen, Y.; Liao, Z.; Chen, D. Differential Evolution Deep Reinforcement Learning Algorithm for Dynamic Multiship Collision Avoidance with COLREGs Compliance. J. Mar. Sci. Eng. 2025, 13, 596. [Google Scholar] [CrossRef]
- You, Y.; Chen, K.; Guo, X.; Zhou, H.; Luo, G.; Wu, R. Dynamic Path Planning Algorithm for Unmanned Ship Based on Deep Reinforcement Learning. In Bio-Inspired Computing: Theories and Applications: 16th International Conference, BIC-TA 2021, Taiyuan, China, December 17–19, 2021, Revised Selected Papers, Part II; Springer: Singapore, 2021; pp. 373–384. [Google Scholar]
- Guo, S.; Zhang, X.; Zheng, Y.; Du, Y. An autonomous path planning model for unmanned ships based on deep reinforcement learning. Sensors 2020, 20, 426. [Google Scholar] [CrossRef]
- Zhang, R.; Qin, X.; Pan, M.; Li, S.; Shen, H. Adaptive Temporal Reinforcement Learning for Mapping Complex Maritime Environmental State Spaces in Autonomous Ship Navigation. J. Mar. Sci. Eng. 2025, 13, 514. [Google Scholar] [CrossRef]
- Xu, H.; Wang, N.; Zhao, H.; Zheng, Z. Deep reinforcement learning-based path planning of underactuated surface vessels. Cyber-Phys. Syst. 2019, 5, 1–17. [Google Scholar] [CrossRef]
- Gong, H.; Wang, P.; Ni, C.; Cheng, N. Efficient path planning for mobile robot based on deep deterministic policy gradient. Sensors 2022, 22, 3579. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, X.; Cao, Z.; Wang, S.; Liang, J.; Zhang, F.; Tang, J. An optimized path planning method for coastal ships based on improved DDPG and DP. J. Adv. Transp. 2021, 1, 7765130. [Google Scholar] [CrossRef]
- Walther, L.; Rizvanolli, A.; Wendebourg, M.; Jahn, C. Modeling and optimization algorithms in ship weather routing. Int. J. e-Navig. Marit. Econ. 2016, 4, 31–45. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, L. A Three-Dimensional Dijkstra’s algorithm for multi-objective ship voyage optimization. Ocean Eng. 2019, 186, 106131. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. Proc. AAAI Conf. Artif. Intell. 2016, 30, 2094–2100. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar]
- E.U. Copernicus Marine Service Information (CMEMS). Global Ocean Physics Analysis and Forecast. Available online: https://data.marine.copernicus.eu/product/GLOBAL_ANALYSISFORECAST_PHY_001_024/description (accessed on 10 March 2025).
- Yu, H.; Fang, Z.; Fu, X.; Liu, J.; Chen, J. Literature review on emission control-based ship voyage optimization. Transp. Res. Part D Transp. Environ. 2021, 93, 102768. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Y.; Li, X.; Schönborn, A.; Sun, Z. Data fusion and machine learning for ship fuel efficiency modeling: Part III—Sensor data and meteorological data. Commun. Transp. Res. 2022, 2, 100072. [Google Scholar] [CrossRef]
- Fan, A.; Yang, J.; Yang, L.; Wu, D.; Vladimir, N. A review of ship fuel consumption models. Ocean Eng. 2022, 264, 112405. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, L. Benchmark study of five optimization algorithms for weather routing. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, New York, NY, USA, 25–30 June 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017; Volume 57748, p. V07BT06A023. [Google Scholar]
- de la Jara, J.J.; Preciosoc, D.; Bud, L.; Redondo-Nebleb, M.V.; Milsond, R.; Ballester-Ripollc, R.; Gómez-Ullatec, D. WeatherRouting Bench 1.0: Towards Comparative Research in Weather Routing. 2025; submitted. [Google Scholar]
- Davis, S.C.; Boundy, R.G. Transportation Energy Data Book: Edition 40; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2022. [Google Scholar]
- Uber Technologies, Inc. H3—Hexagonal Hierarchical Geospatial Indexing System. Software; Uber Technologies, Inc.: San Francisco, CA, USA, 2018. [Google Scholar]
- Open-Meteo. Model Updates and Data Availability. 2025. Available online: https://open-meteo.com/en/docs/model-updates (accessed on 26 April 2025).
- Zavvos, E.; Zavitsas, K.; Latinopoulos, C.; Leemen, V.; Halatsis, A. Digital Twins for Synchronized Port-Centric Optimization Enabling Shipping Emissions Reduction. In State-of-the-Art Digital Twin Applications for Shipping Sector Decarbonization; Karakostas, B., Katsoulakos, T., Eds.; IGI Global: Hershey, PA, USA, 2024; pp. 137–160. [Google Scholar]
- International Maritime Organization (IMO). Navtex Manual, 2023 ed.; International Maritime Organization: London, UK, 2023. [Google Scholar]

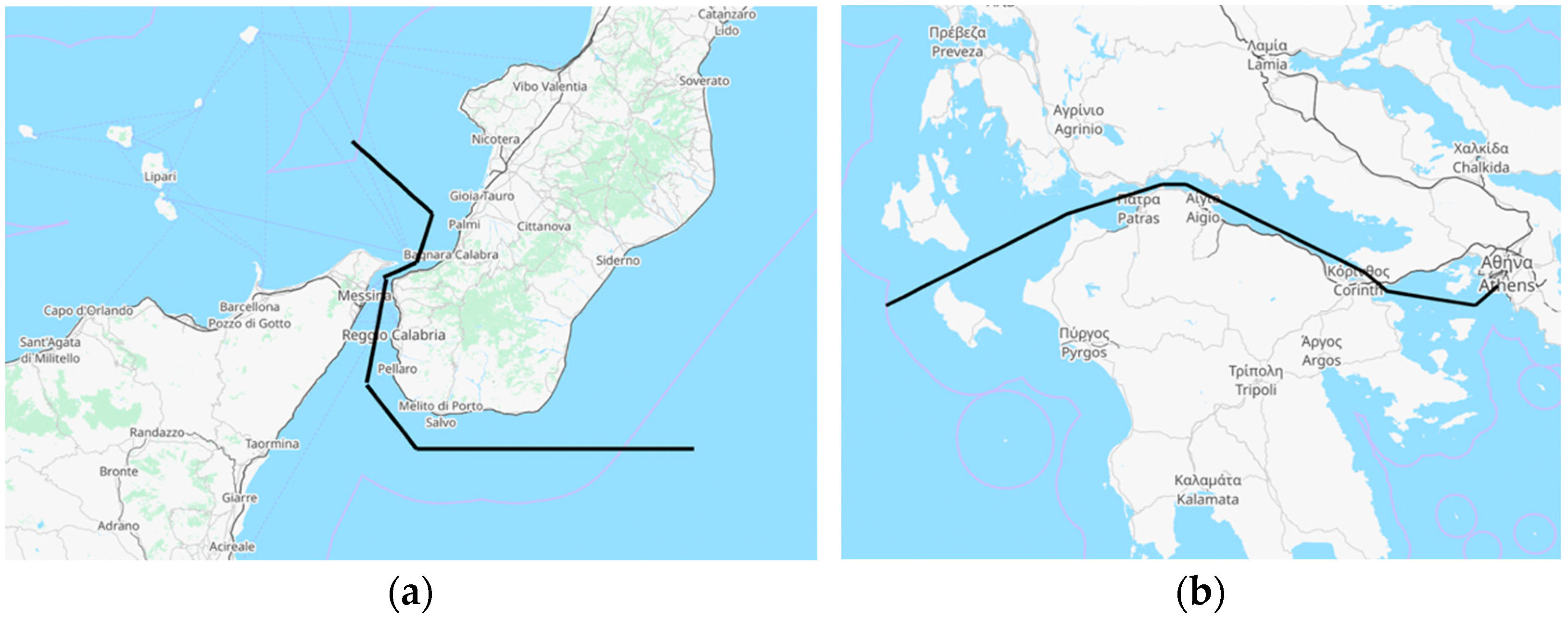

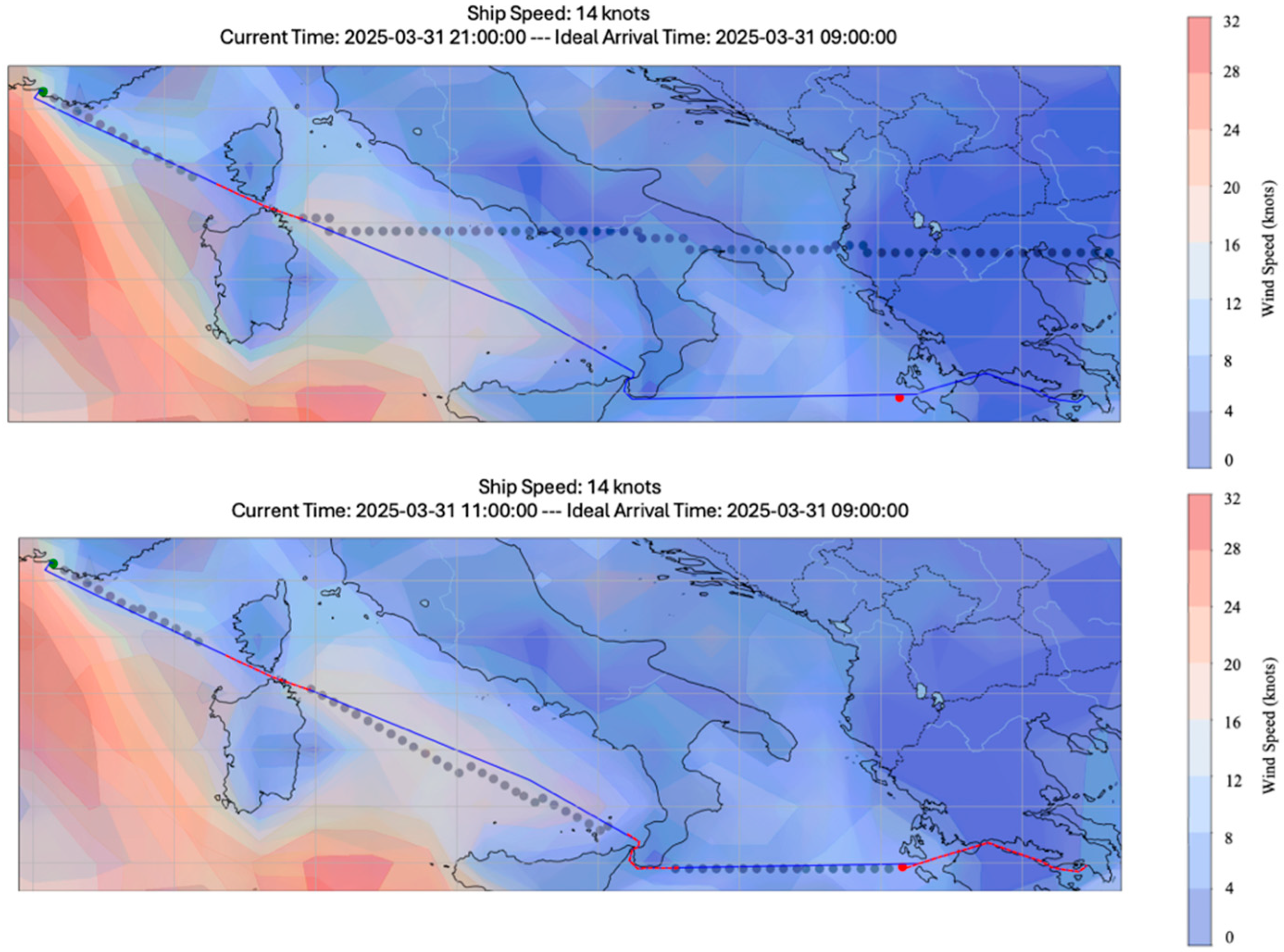
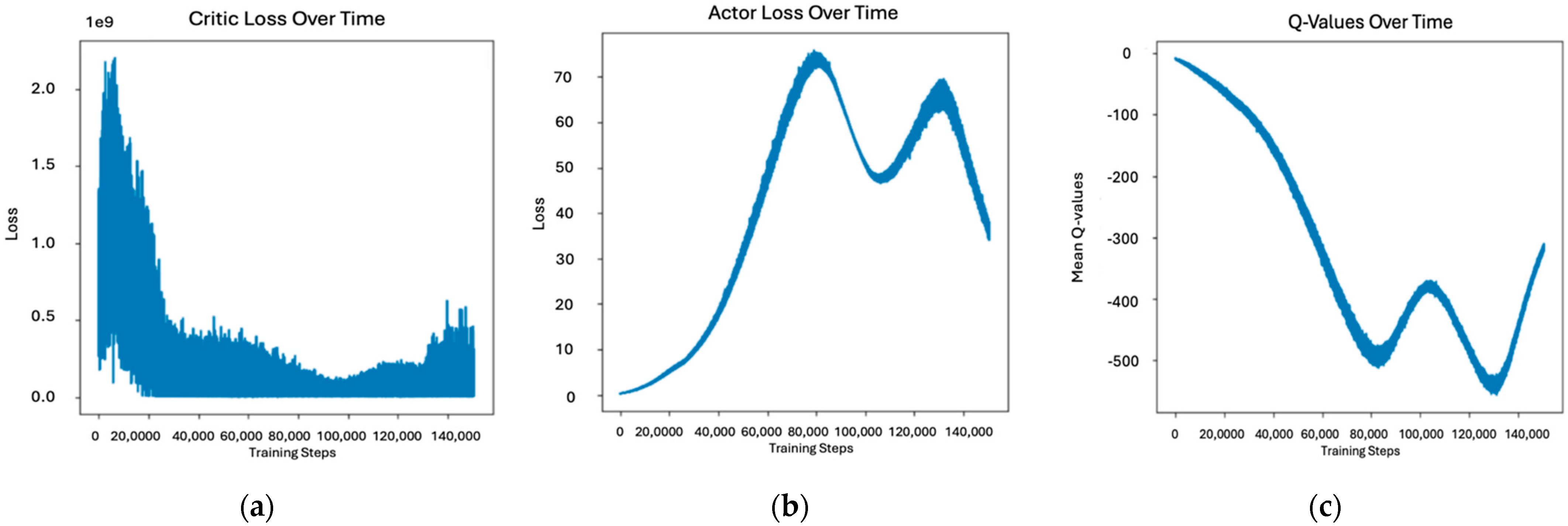

| Category | Model | Key Characteristics | Year |
|---|---|---|---|
| Classical Pathfinding Algorithms | Dijkstra [13,14,15] | Guarantees shortest path; computationally intensive; discrete | [2021, 2024, 2015] |
| A* Search [16,17] | Faster than Dijkstra; heuristic guidance; risk of local optima | [2020, 2024] | |
| Rapidly Exploring Random Tree (RTT) [18] | High-dimensional space exploration; discrete | 2020 | |
| Metaheuristics and Mathematical Optimization | Isochrone Method [19] | Time-based segments; multiple feasible paths | 1957 |
| Genetic Algorithms [20,21] | Flexible objective functions; evolutionary search | [2020, 2015] | |
| Particle Swarm Optimization [22] | Swarm-based optimization; iterative improvement | 2018 | |
| Ant Colony Optimization [23] | Probabilistic; path refinement via pheromone trails | 2015 | |
| Dynamic Programming [24] | Subproblem solving; high computational cost | 2018 | |
| 3D Graph Search [39] | Time as third dimension; dynamic environment | 2019 | |
| Machine Learning and Reinforcement Learning Models | Q-learning [27] | Self-learning; discrete state–action mapping | 2019 |
| Deep RL (DQN, DDPG, PPO) [28,29,30,33,35,37] | Model-free learning; real-time adaptation | [2021, 2024, 2024, 2020, 2019, 2021] | |
| Hybrid DRL [31,32] | Combines DRL with other optimization methods | [2025, 2021] | |
| DRL with LSTM [34,36] | Combines DRL with other neural network approaches | [2025, 2022] |
| DDQN (Offline Policy) | DDQN (Online Policy) | DDPG (Offline Policy) | DDPG (Online Policy) | |
|---|---|---|---|---|
| Fuel Consumption Reduction (%) | 6.6 | 8.3 | 10.7 | 11.9 |
| Method | Computation Time (s) | Fuel Consumption (Liters) | Average Speed (Knots) | Voyage Time (Hours) | Memory Usage | Adaptability to Weather | Applicability to Digital Twins |
|---|---|---|---|---|---|---|---|
| Graph-based Shortest Path (baseline) | 3.2 s | 126,382 | 14 * | 71.0 | Low | Low | Low |
| Distance-based A* Search | 15.6 | 137,553 (+8.8%) | 14 * | 78.2 | High | Low | Moderate |
| Fuel-based A* Search | 462 | 122,903 (−2.8%) | 14 * | 69.1 | High | Low | Moderate |
| Hill Climbing | 143 | 119,130 (−5.7%) | 11.62 | 79.9 | Low | Low | Low |
| Tabu Search | 150 | 108,946(−13.8%) | 13.58 | 77.4 | Moderate | Moderate | Moderate |
| ALNS | 128 | 114,178 (−9.7%) | 12.67 | 80.9 | Moderate | High | High |
| DDQN | 11,040 (920 for online) | 115,346 (−8.7%) | 12.30 | 85.8 ** | Very High | Very High | Very High |
| DDPG | 11,700 (1854 for online) | 110,409 (−12.6%) | 12.56 | 78.9 | Very High | Very High | Very High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latinopoulos, C.; Zavvos, E.; Kaklis, D.; Leemen, V.; Halatsis, A. Marine Voyage Optimization and Weather Routing with Deep Reinforcement Learning. J. Mar. Sci. Eng. 2025, 13, 902. https://doi.org/10.3390/jmse13050902
Latinopoulos C, Zavvos E, Kaklis D, Leemen V, Halatsis A. Marine Voyage Optimization and Weather Routing with Deep Reinforcement Learning. Journal of Marine Science and Engineering. 2025; 13(5):902. https://doi.org/10.3390/jmse13050902
Chicago/Turabian StyleLatinopoulos, Charilaos, Efstathios Zavvos, Dimitrios Kaklis, Veerle Leemen, and Aristides Halatsis. 2025. "Marine Voyage Optimization and Weather Routing with Deep Reinforcement Learning" Journal of Marine Science and Engineering 13, no. 5: 902. https://doi.org/10.3390/jmse13050902
APA StyleLatinopoulos, C., Zavvos, E., Kaklis, D., Leemen, V., & Halatsis, A. (2025). Marine Voyage Optimization and Weather Routing with Deep Reinforcement Learning. Journal of Marine Science and Engineering, 13(5), 902. https://doi.org/10.3390/jmse13050902









