1. Introduction
In the field of control systems for complex dynamic systems, especially ship-related control, the design of controllers is a critical research area. The control direction [
1,
2], which is a key factor, significantly affects the performance and stability of these systems. During the past twenty years, the control dilemma of continuous nonlinear systems accompanied by unknown control directions has captured the fascination of a great number of scholars. At present, the Nussbaum gain adaptive control approach [
3,
4] has become the principal research orientation where abundant research outcomes and remarkable breakthroughs have been attained. In 1983, Nussbaum [
5] initially put forward the Nussbaum gain theory. By way of a straightforward first-order system, it was demonstrated that this theory is capable of resolving the control issues of systems with indeterminate high-frequency control coefficients.
Concerning the problem of a solitary unknown control direction, extensive research on Nussbaum gain control has been conducted. For example, in 1998, Ye [
6] contrived a controller for a lower triangular system through the integration of backstepping design and the Nussbaum technique. In 2003, Shuzhi Sam [
7] carried out an investigation into adaptive control in the context of deficient prior knowledge regarding virtual control coefficients. In 2006, Zhou [
8] devised a backstepping Nussbaum gain controller for systems having unknown high-frequency gain matrix signs. Nevertheless, during the simulation process, only the circumstance of unknown signs was taken into consideration, while overlooking the situation of high-frequency sign fluctuations. In 2009, Bechlioulis [
9] introduced a robust adaptive control algorithm for a class of uncertain nonlinear perturbed systems that possess virtual control gain functions with unknown signs. In 2012, Jin [
10] indicated that when the control direction is unknown, the solution method founded on the Nussbaum function proposed by Nussbaum is of pivotal importance in this domain and still stands as the key means of addressing the problem of unknown control directions up until now. In 2024, Liu [
11] introduced a novel Nussbaum function design. This design was intended to tackle the coupling cancellation problem of traditional Nussbaum functions in multiple unknown control directions stochastic systems. The stability of the system was safeguarded through Lyapunov analysis. To relieve the computational strain, an innovative combination of a static composite event triggering mechanism (incorporating tracking error and control signal triggering conditions) and intermittent feedback was proposed, and a dynamic composite triggering mechanism was further developed for optimization. This overall plan substantially decreases the frequency of control updates while guaranteeing the boundedness of tracking errors.
Nevertheless, the traditional Nussbaum gain method has its flaws. The traditional approach has to factor in the scenario where the Nussbaum gain converges towards both positive and negative infinity. This makes it rather inconvenient for the proof of system stability. Hence, this paper endeavors to develop a new variety of Nussbaum function, which simplifies the process of proving the stability of a control system.
Reference [
12] probed into the correlation between the Mittag-Leffler function and the Nussbaum-type function. The research manifested that under certain particular conditions, the Mittag-Leffler function can be transformed into a Nussbaum-type function. This reference not only unveiled the characteristics of the Nussbaum-type function but also put forward numerous new types of Nussbaum-type functions.
For ship control systems, the ship course–keeping control system is a complex nonlinear system. It is influenced by multiple factors, including unknown control direction coefficients, uncertain parameters, and external disturbances. Traditional control methods often face challenges in achieving satisfactory control performance in such complex scenarios. Some early control strategies, although effective to a certain extent, failed to fully account for the complexity introduced by unknown control directions. For instance, they might have simplified the system model by assuming known control directions, which is far from the real-world situation where control directions can change due to various factors like ship specific dynamics or virtual control coefficients caused by the backstepping design method.
References [
13,
14] pointed out that since a sailboat is a time-varying system with strong disturbances and model uncertainties, the traditional PID controller does not perform well. The sailboat motion control methods based on fuzzy and neural networks in References [
13,
14] do not consider the dynamic model of the sailboat, so there are certain limitations in the analysis of system stability. Saoud et al. [
15] took the three-degrees-of-freedom sailboat model [
16] as the research object, ignored the yaw influence caused by the roll during the motion process of the sailboat, and designed a course controller by using the backstepping method and the switching function, achieving the course-keeping control of the sailboat. Xiao Lin et al. [
17] designed a ship motion course controller for a four-degrees-of-freedom sailboat mathematical model without external environmental disturbances by using the backstepping method. Based on Reference [
17], Wille et al. [
18] considered the influence of external disturbances and designed a course-keeping controller by using state feedback linearization. The mathematical models of ships studied by Saoud et al. [
15,
16] and Wille et al. [
18] are completely known, and the control directions in the controller design are also known, which has a certain gap from the actual engineering situation. In practical engineering, there are situations where the models of unmanned ships are uncertain and the control directions are unknown.
Shen [
19] pointed out that due to the fact that unmanned sailboats will encounter numerous unknown navigation hazards during sailing, along with marine interferences such as wind, waves, and currents in the external environment, and taking into account the strong uncertainties of the sailboat model as well as the delay characteristics of the steering gear, etc., all these factors can lead to the problem of the uncertainty of the control direction, or the occurrence of the problem of unknown indirect virtual control coefficients. Du [
20], aiming at the difficulty of the unknown control direction existing in the nonlinear control system of ship motion with parameter uncertainties, combined the backstepping algorithm with the Nussbaum gain method and proposed a new adaptive nonlinear control strategy, thus realizing the course-tracking control of ship motion.
Tian [
21], in order to improve the problem of the course-keeping control of ships with unknown control directions in the model and being disturbed by the external environment, introduced the Nussbaum gain technology into the backstepping method. The proposed algorithm is capable of solving the problem of the specified steady state performance control under the condition of the unknown control direction in the course-keeping control of ships. Du [
22] pointed out that if the influence of the steering gear and parameter uncertainties are considered in the design of the ship course controller, then the ship course control will turn into a nonmatching uncertain nonlinear control problem, especially the problem that the sign of its virtual control coefficient is unknown. By combining the Nussbaum function with the backstepping technology, he designed a course-tracking controller for ship motion and successfully solved the problem of the unknown sign of its virtual control coefficient.
In this paper, a special Nussbaum-type function, which is called the “unilateral Nussbaum function,” is defined. It is used to design an adaptive controller for a nonlinear system, which can simplify the design and proof of the adaptive Nussbaum gain method. It is necessary to analyze the situation that the Nussbaum gain converge to both and when the traditional Nussbaum gain method is used. But only the consideration of situation is necessary if the unilateral Nussbaum gain method is adopted. Therefore, it has better quality than the traditional Nussbaum function.
When the backstepping design method is applied to high-order systems, it is prone to the overparameterization problem, which makes the design extremely complicated. Due to its excellent robustness and order reduction characteristics, sliding mode control [
23,
24] has been widely used in many engineering systems.
In this paper, an adaptive sliding mode control is also adopted to reduce the complexity of the controller design for high-order systems. Meanwhile, a method that combines sliding mode control with the Nussbaum gain is introduced to address the problem of unknown control direction. The overparametric problem was considered in [
25], but the unknown control direction problem is neglected. Therefore, in this paper, the unilateral Nussbaum gain method is proposed and used in the ship course–keeping system with uncertainties and an unknown control direction. Meanwhile, aiming at the special nonlinear problems of ship systems, a class of dedicated RBF neural networks [
26,
27] was designed. Sliding mode control was used to reduce the order of the system, and it was combined with the Nussbaum method to simplify the design and analysis process of the traditional Nussbaum gain control. In this paper, we aim to address the research gaps in the existing method.
We apply this new method to the ship course–keeping control system. Through theoretical analysis and simulations, we verify the effectiveness of the proposed method, offering a novel solution for ship control systems with an unknown control direction in practical engineering applications. The innovative points of this article are as follows:
1. Innovation point regarding neural network: Considering the special nonlinear and uncertain characteristics of the ship, a dedicated RBF nonlinear neural network has been designed. Its basis functions are a combination of linear and cubic terms, which can rapidly compensate the uncertainties of the system.
2. Innovation point regarding the unknown control direction: The large system with the problem of an unknown control direction is decomposed into a two-dimensional situation. One dimension forms a new dynamic system with the sliding mode surface, while the other dimension is reserved for the stability analysis of the Nussbaum gain. The design for the problem of the unknown control direction is divided into two steps, systematically constructing an analytical method for this type of problem, especially simplifying the proof.
2. Methodology
2.1. Unilateral Nussbaum Gain Control of a Nonlinear System
To make the following introduction of a new Nussbaum gain method simple, we propose the definition of unilateral Nussbaum gain at first.
Definition 1. A function is called a “unilateral Nussbaum-type function” if it satisfies
Considering the traditional Nussbaum function, it is obvious that does not belong to a unilateral-type Nussbaum function, and belongs to the unilateral-type Nussbaum function.
The following lower triangular nonlinear system is used to illustrate the unilateral Nussbaum gain control method:
Considering the following N-order SISO system
where
is the unknown control direction,
, and define a new input variable as
, and design a sliding mode surface as
Therefore, the system can be rewritten as
Then, the unknown control direction does not exist in the system equation.
Assumption 1. There exists a control and a Lyapunov function such that the above system satisfies and the system is stable.
Lemma 1. For the abovementioned system, if we design and
where
is a unilateral Nussbaum gain function, then the above system is stable under the condition of unknown control direction.
The proof is as follows:
According to Assumption 1, there exists a Lyapunov function
Solving the derivative of the Lyapunov function, we obtain
Considering the control law, it is easy to obtain
Design the adaptive regulation law as
And using Proof by Contradiction, we assume
is unbounded, such as
, then we have
Then a contradiction appears and the above assumption does not satisfy and is bounded. It is easy to prove that all signals of the close system are bounded. With the help of Baralat lemma, we can prove that the system is stable.
2.2. Model of Ship Course–Keeping Control System with an Unknown Control Direction
The mathematical model of the ship course–keeping control system is as follows:
where
is an unknown control direction coefficient;
and
are unknown coefficients;
,
,
and
are known coefficients of system;
is the unknown disturbance, which is bounded and
,
is the bounded function and it is known;
is the yaw speed; and
is the heading angle. The control objective is to design rudder angle
, such that to make the system stable and make the heading angle trace the desired value.
First, we design a new control variable as
, then the above model can be rewritten as
where
,
. At this point, there is no problem of unknown control direction in the system since
is completely known, and the uncertainties of the model mainly focus on
and
. Next, the adaptive sliding mode control method is adopted to design
to make the above system stable.
2.3. Neural RBF Network and Sliding Mode Control for Ship Course–Keeping Control System Without Unknown Control Direction
Firstly, the ship course angle command is set as
, and the course angle error variable is defined as
A proportional–integral–derivative (PID)-type sliding mode surface is selected as
The derivative of the sliding mode surface is obtained as
Since the structure of the part is known, but only its parameters are uncertain, a special RBF neural network with a combination of cubic and linear terms is designed according to the characteristics of the abovementioned model to approximate the uncertain part of the system. And the robust adaptive control will be used to deal with .
The designed dual-input RBF single-output neural network is as follows:
where
and
are the weights of the neural network,
is the output of the neural network, and the basis functions of the neural network are defined as
The role of the basis functions is mainly to automatically adjust the influence of the weights according to the values of the sliding mode surface and the error, so as to achieve the approximation of the uncertain part. , , , and are parameters of the RBF network.
According to the result of the derivative of the sliding mode surface, the control law is designed in a backstepping manner as follows:
where
, in which
is an odd integer and
is a softening coefficient. It is not difficult to prove that
where
,
and
are constant control parameters.
After further arrangement, we obtain
Substituting Formula (22) into the derivative formula of the sliding mode surface, we obtain
Due to the approximation characteristics of the neural network, and because the structure of the neural network in this paper is consistent with the structure of the uncertain part of the system, there obviously exist optimal neural network weights
and
such that
where
is an arbitrarily small positive number. In fact, when the following equations are satisfied
It can be obtained that the optimal neural network weights
and
will ensure that
According to Formulas (25)–(27), we have
The weight error of the neural network is defined as follows:
According to Formulas (29) and (30), we have
First, considering the constant value characteristics of the optimal neural network weights
and
, we can solve the derivative of the weight error of the neural network as
In order to use the neural network to eliminate the uncertainty
, the weight adaptation law of the special RBF neural network with a combination of cubic and linear terms is designed as follows:
According to Formulas (32) and (33), if the Lyapunov function related to the neural network weights is selected as
The derivative of it is obtained as
After further arrangement, we obtain
The above design mainly uses the neural network to eliminate the uncertain part . Next, a robust adaptive control is designed to deal with .
2.4. Robust Control for Uncertainties of Ship Course–Keeping Control System with Unknown Control Direction
Considering the uncertainties of the ship course–keeping control system that
, we have
After further arrangement, we obtain
And defining
, according to Formulas (38) and (39), its derivative is obtained as
Therefore, the adaptive parameter adjustment law can be designed as
The estimation error of the unknown parameter is defined as
The Lyapunov function related to the parameter is selected as
The derivative of it is obtained as
According to Formulas (41)–(45), and considering that the sign change only brings a momentary disturbance to the system, we have
The Lyapunov function related to the sliding mode surface is selected as
The derivative of the Lyapunov function is obtained as
So far, the total Lyapunov function of the system is selected as
Using the control law designed as shown in the formula
, its derivative is obtained as
According to the Lyapunov stability theory, it is not difficult to prove that the system is stable, all signals are bounded, and thus the sliding mode surface variable converges to 0. Since the coefficients , and are positive and Hurwitz, and the sliding mode surface variable is selected as , it is not difficult to further prove that the error is stable; that is, approaches 0, so as to achieve the control goal of tracking the heading angle.
According to the above lemma 1, we can directly design and , at this time, in Assumption 1 is set as . Then, based on the above lemma, it is not difficult to prove that the above design can ensure the stability of our ship course–keeping system and the tracking of the heading angle.
After establishing the theoretical framework, the following section presents an example and simulation to verify the effectiveness of the proposed method.
3. Results and Discussion
In the context of maritime scenarios, considering the impacts of ocean waves, ocean currents, and sensor noise, ship models exhibit significant uncertainties. Mathematically, these uncertainties can be equivalently described as uncertainties in and the unknown values and sign changes of . Under the theoretical assumptions of an unknown control direction, sign changes, and complete reversals, the control difficulty of the abovementioned models is greater than the challenges posed by the impacts of ocean waves, ocean currents, and sensor noise.
3.1. Example
Using the abovementioned model, the parameter is selected as follows to do the simulation:
,
,
,
; The ship course angle command is selected as
, and design
And choose the unilateral Nussbaum gain function as
And choose simulation parameters as , , , , , , .
3.2. Simulation Results and Discussion
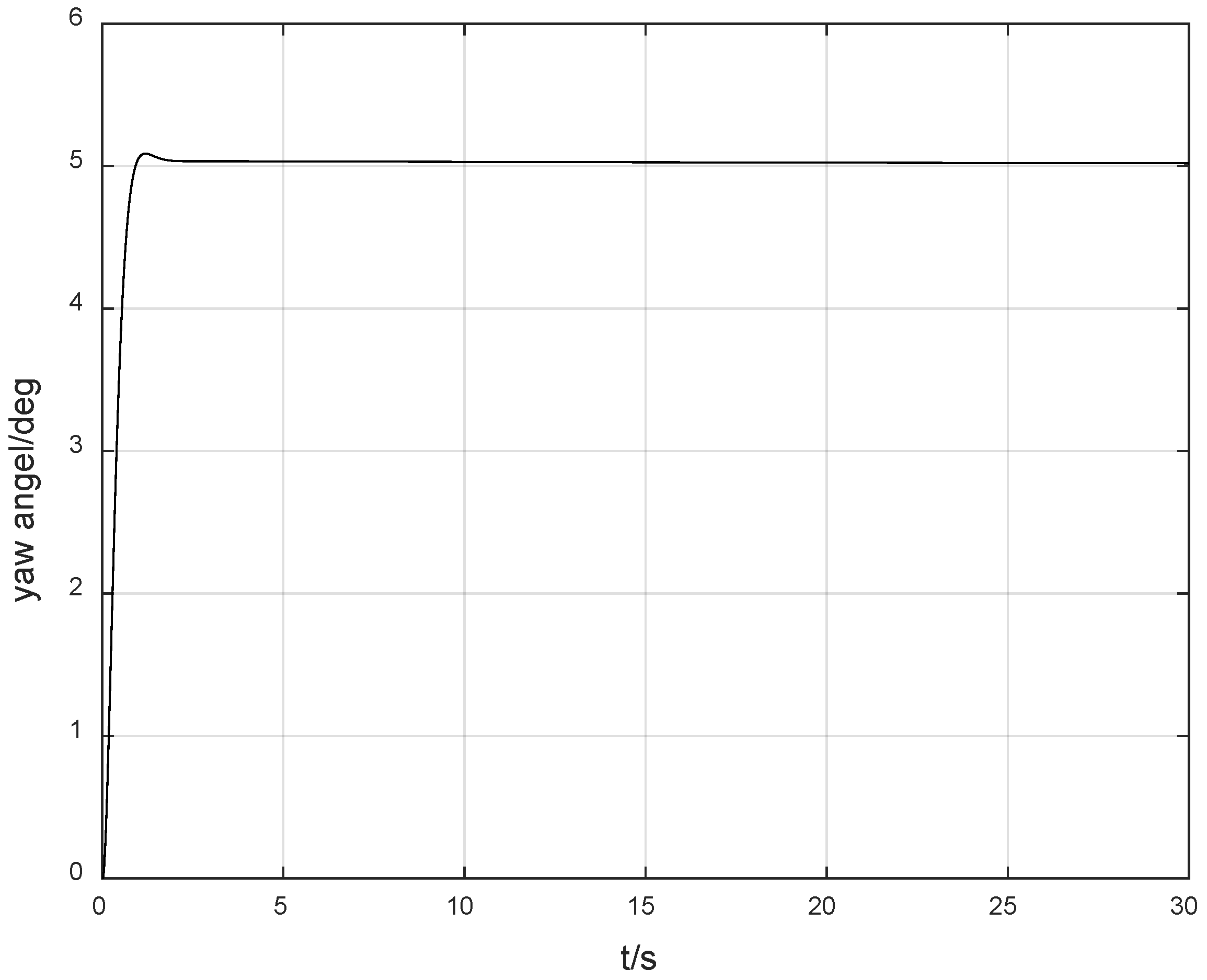
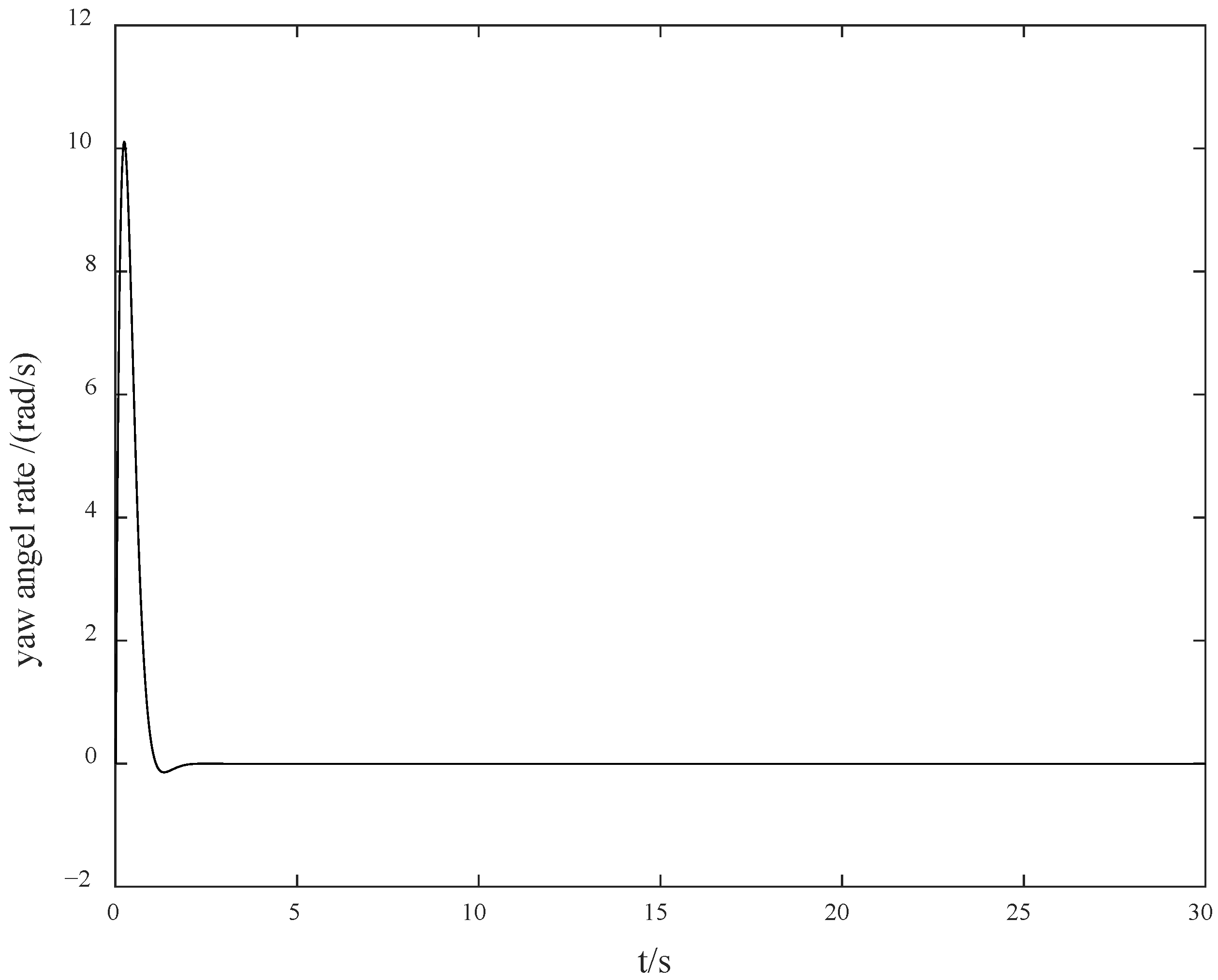
When the unknown control direction is not taken into account, we set
. At this time, the control effects are shown in
Figure 1 and
Figure 2.
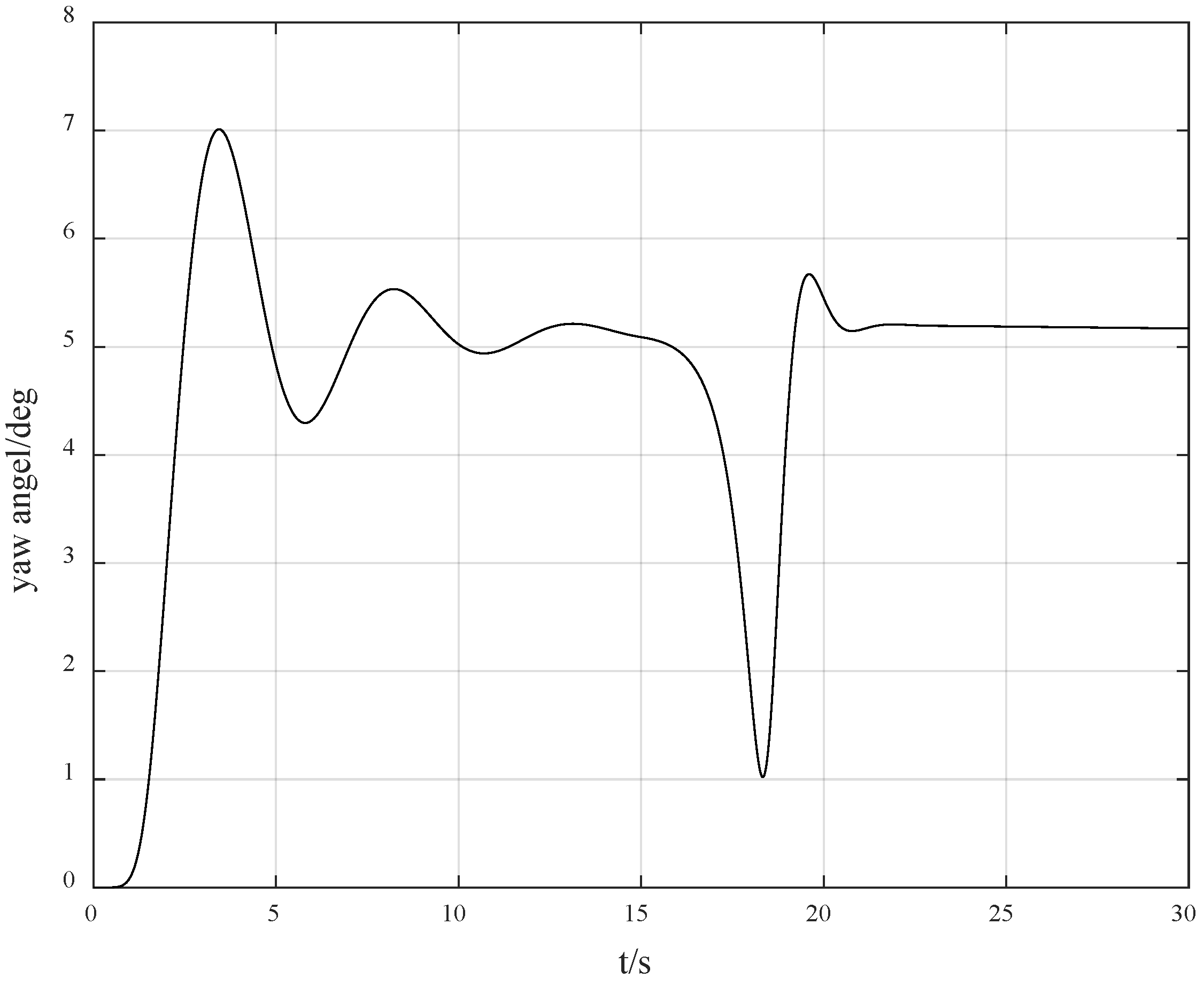
Figure 1 presents the yaw angle response curve of the ship, and
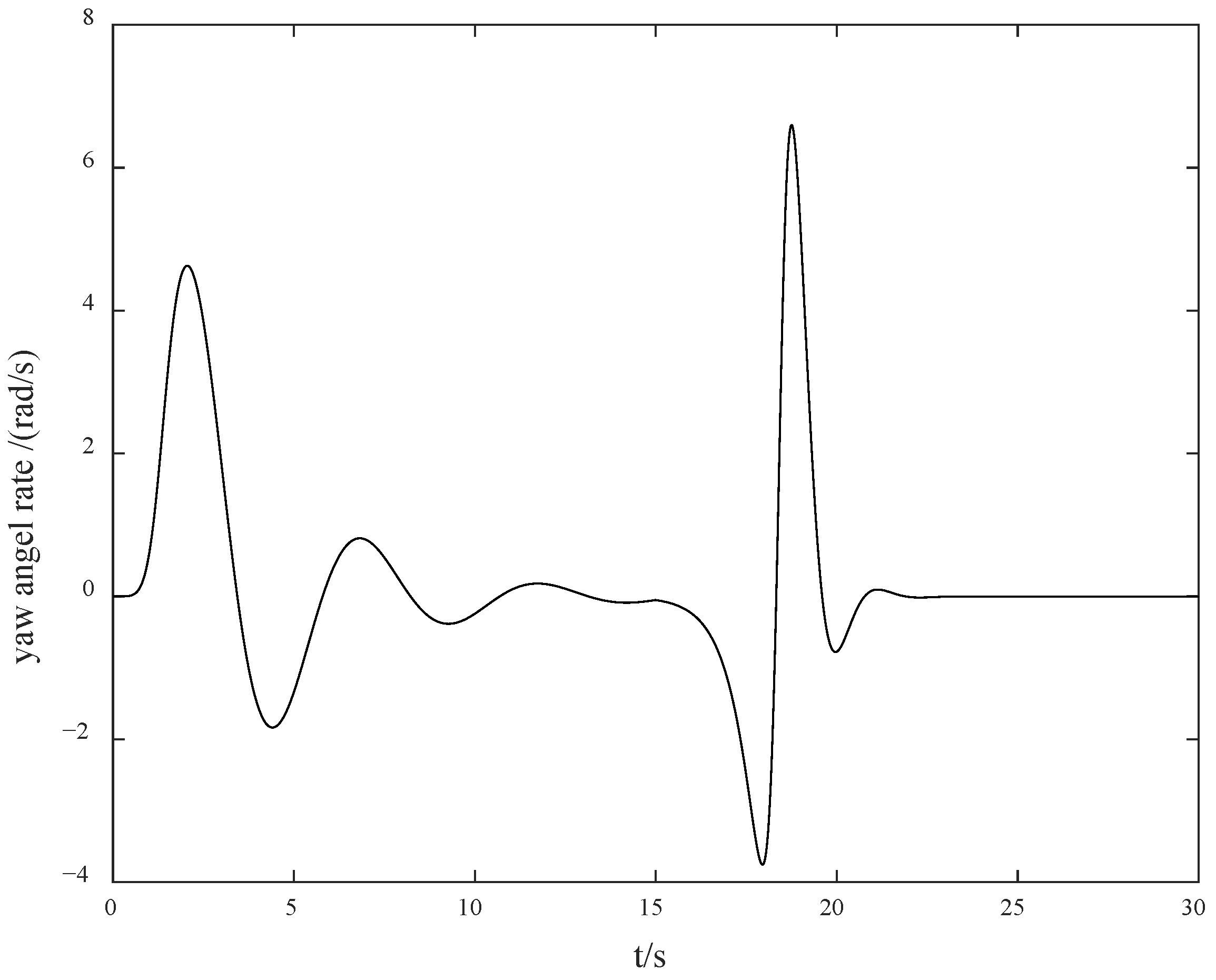
Figure 2 presents the yaw angle rate response curve. As shown in
Figure 1 and
Figure 2, the system response is relatively smooth, and the overshoot is small. Since the unknown control direction is not considered, the magnitude of the control gain can be reasonably selected, enabling the response curve of the entire system to have excellent dynamic performance. However, when the control direction is unknown, especially when a jump occurs, the difficulty of control will increase sharply. In particular, due to the unknown jump of the control direction, which is an unmeasurable and unpredictable jump, the system is likely to switch from negative feedback to positive feedback, resulting in a transient divergence phenomenon, thereby increasing the difficulty of control.
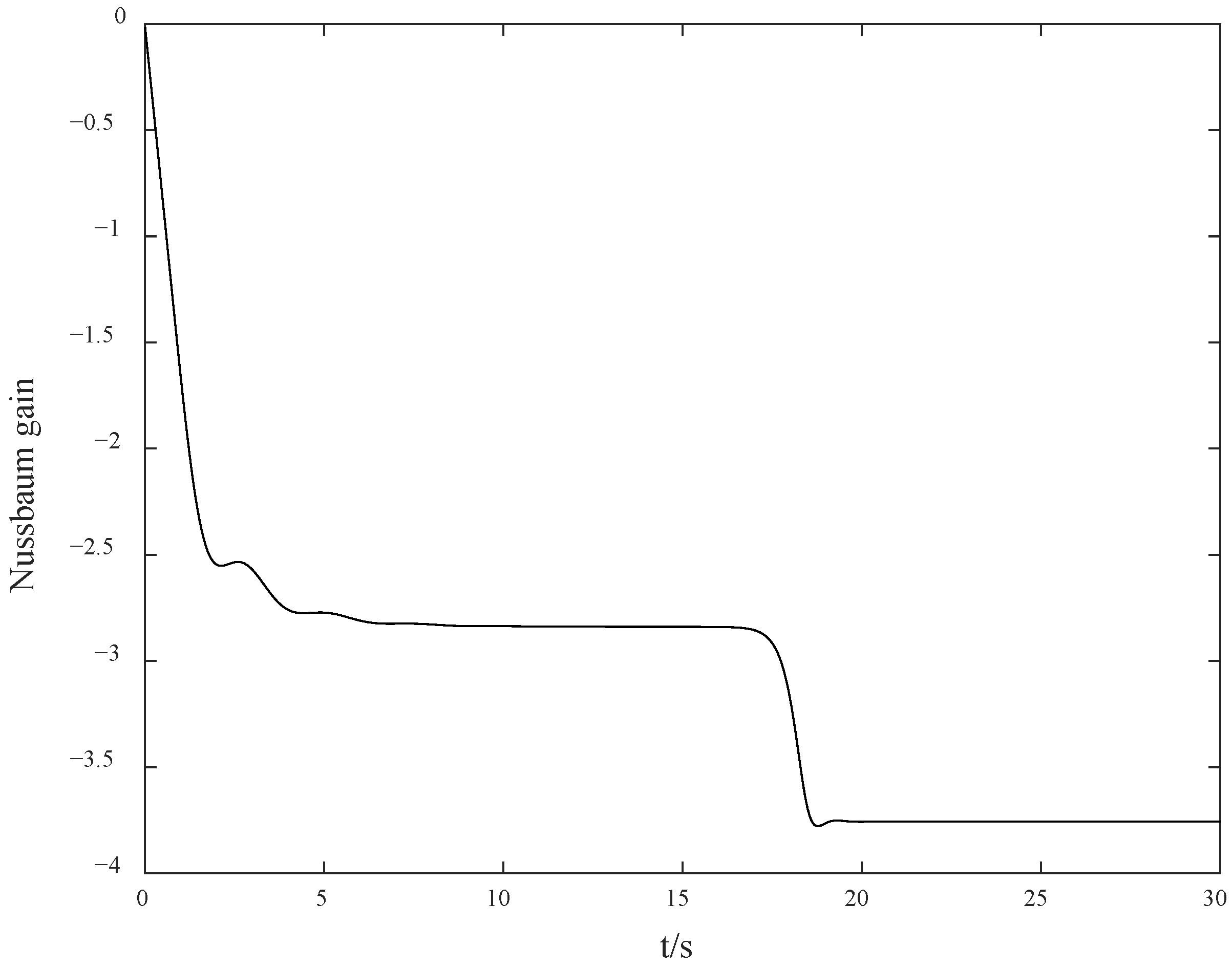
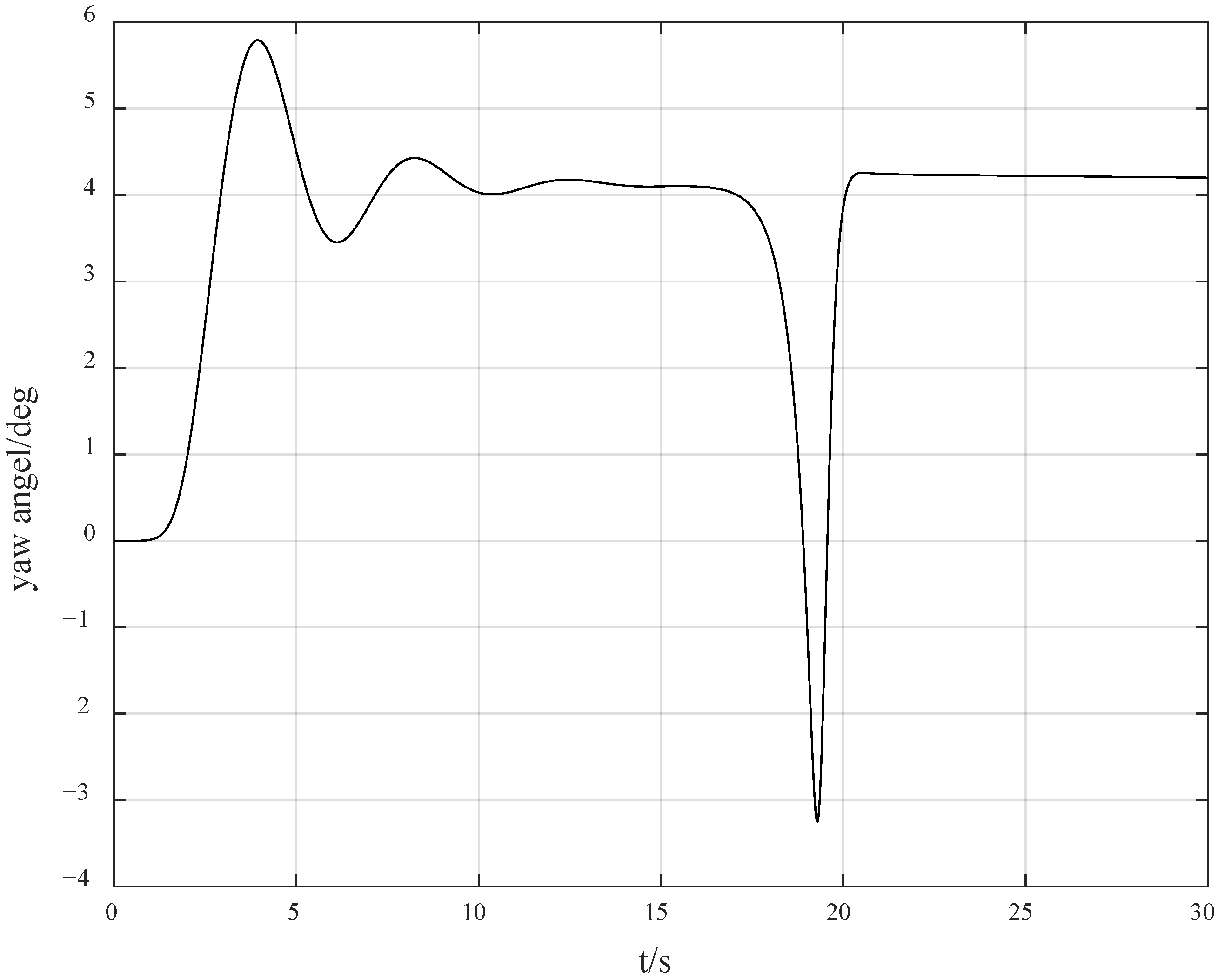
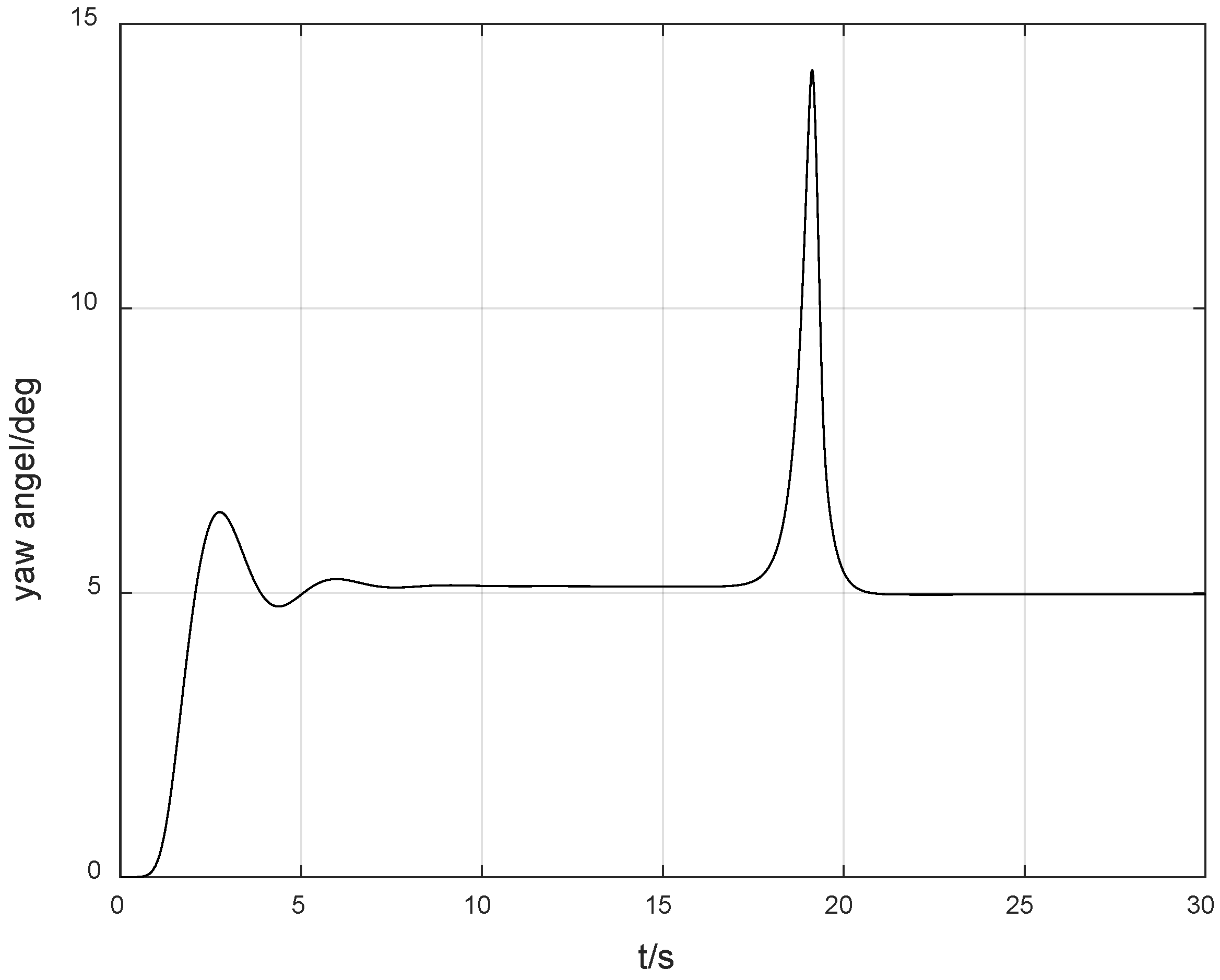
However, considering the possible problem of an unknown control direction in practical situations, we set
. As shown in
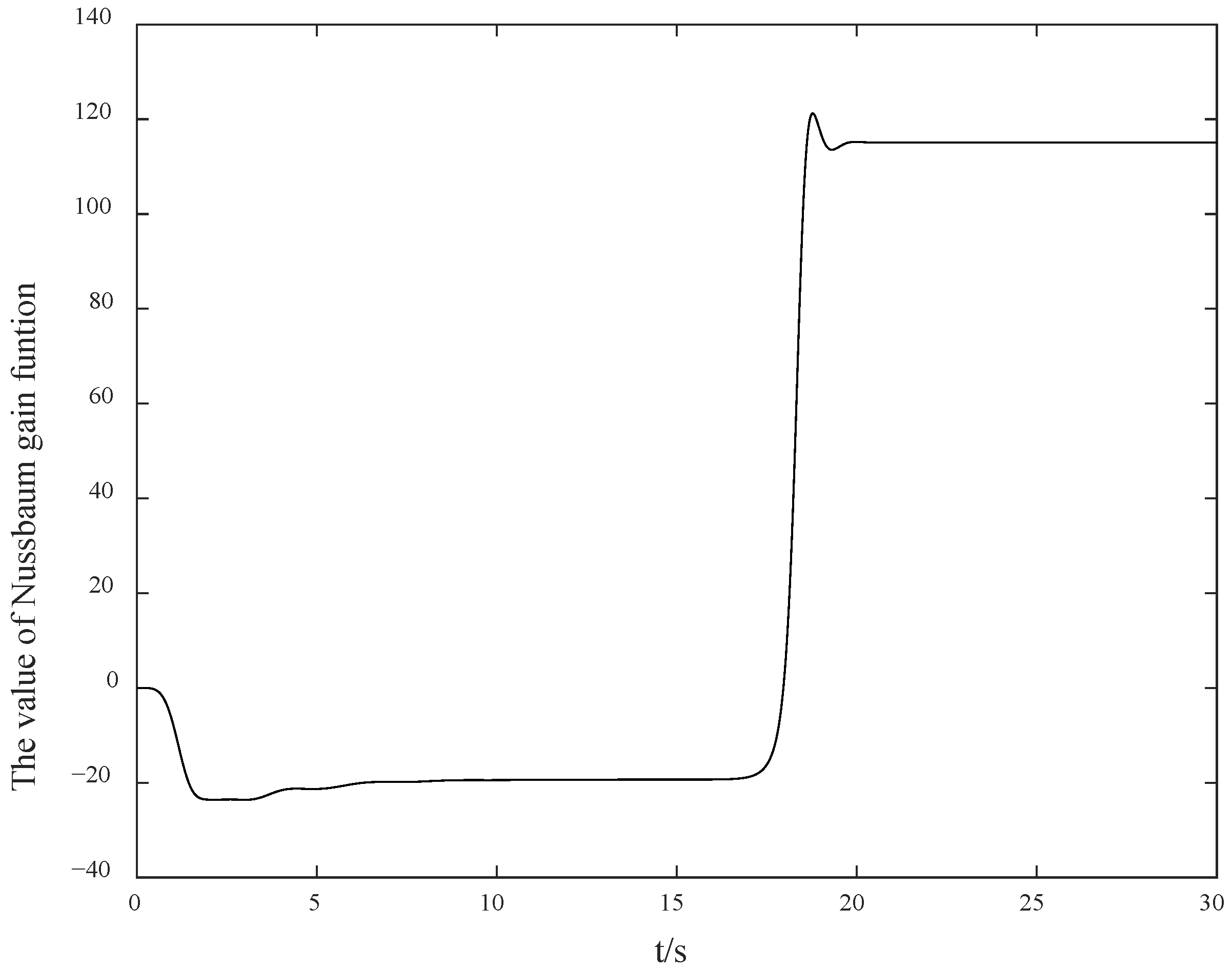
Figure 3, the search jump situation of the Nussbaum gain at this time is shown in
Figure 4. The yaw angle rate response curve under the condition of control direction jump is shown in
Figure 5, and the yaw angle response curve is shown in
Figure 6. It can be seen from
Figure 7 that the value of the Nussbaum gain function can quickly search following the jump of the control direction. From
Figure 5 and
Figure 6, it can be observed that due to the drastic challenges brought to the system by the jump of the control direction, the control method proposed in this paper can automatically adjust and find the appropriate control gain direction for compensation again, so that the overall gain direction of the system remains unchanged, thus keeping the system stable.
And if we choose a proper simulation parameters as
,
,
,
,
,
,
. The simulation results are shown in the following
Figure 6, and the overshoot can be reduced to 40%.
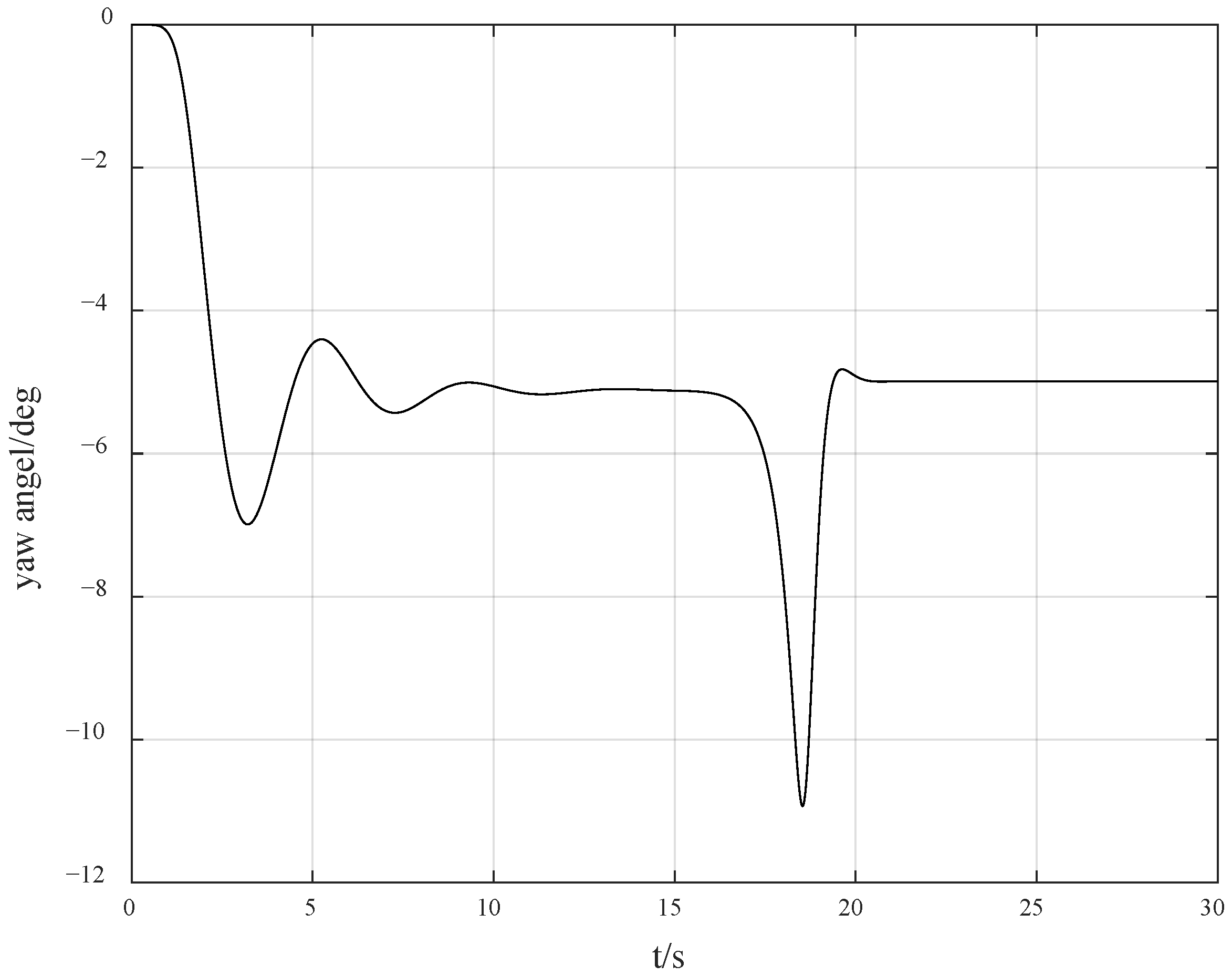
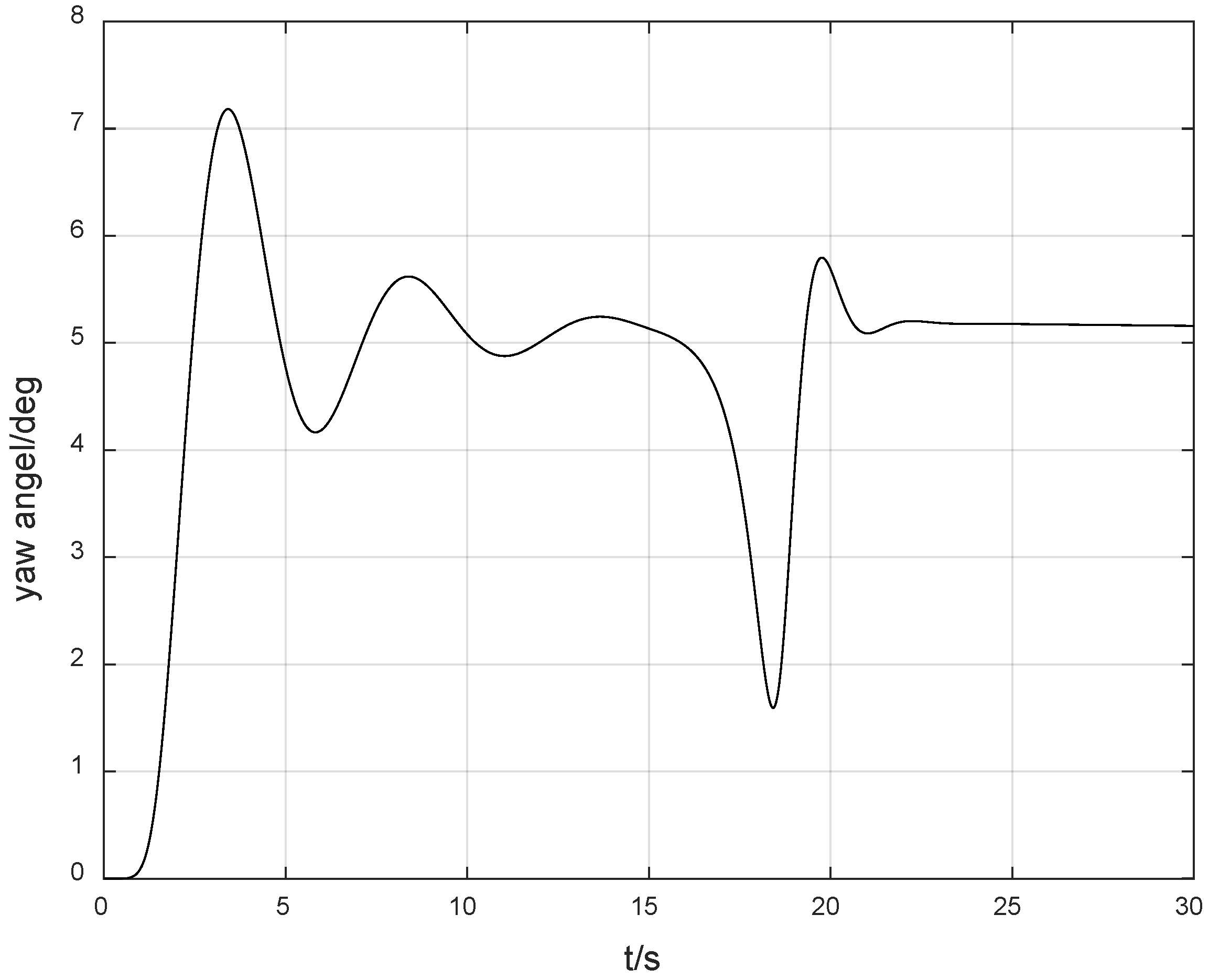
Furthermore, in order to verify the robustness of the method provided in this paper, we also perturbed the known parameters of the model, increasing them by 30%, respectively. Meanwhile, the desired yaw angle was set to −5 degrees, and the simulation results are as shown in
Figure 8.
And we test the situation that the desired yaw angle is changed to 4 degrees and the parameters are overall perturbed downward by 30%, then the simulation results are shown in
Figure 9.
As can be seen from
Figure 8 and
Figure 9, although the perturbation of known model parameters was not considered in the theoretical design, the controller can still maintain stability in the case of parameter perturbations. The abovementioned simulation results show that the method provided in this paper has excellent robustness. The main reason is that the control difficulty caused by the perturbation due to unknown direction is much greater than the harm to stability caused by the perturbation of the model.
From the simulation results of the three scenarios, namely known control direction, unknown control direction but known model parameters, and unknown control direction with model parameter perturbations, it can be seen that when the control direction is known, the overshoot of the output response is very small, and the control difficulty is relatively low. In the second scenario, where the control direction is unknown without considering model parameter perturbations, the control difficulty increases significantly. This is mainly manifested in the jump of the control direction to the opposite direction, which turns the system from negative feedback into something similar to positive feedback, causing the system to diverge in a short time and resulting in a large overshoot in the output. However, the unilateral Nussbaum gain control method proposed in this paper can identify the control direction in a short time and effectively compensate for it, thus ensuring the stability of the system. The simulation results of the third scenario further demonstrate the correctness and effectiveness of the method proposed in this paper. In particular, it shows that the greatest difficulty and challenge in control come from the unknown control direction rather than the uncertainty of model parameters.
In order to further illustrate the superiority of the method proposed in this paper, we employed the ordinary adaptive method to address the problem of control direction switching and carried out a comparative analysis. The simulation results are shown in
Figure 10 and
Figure 11.
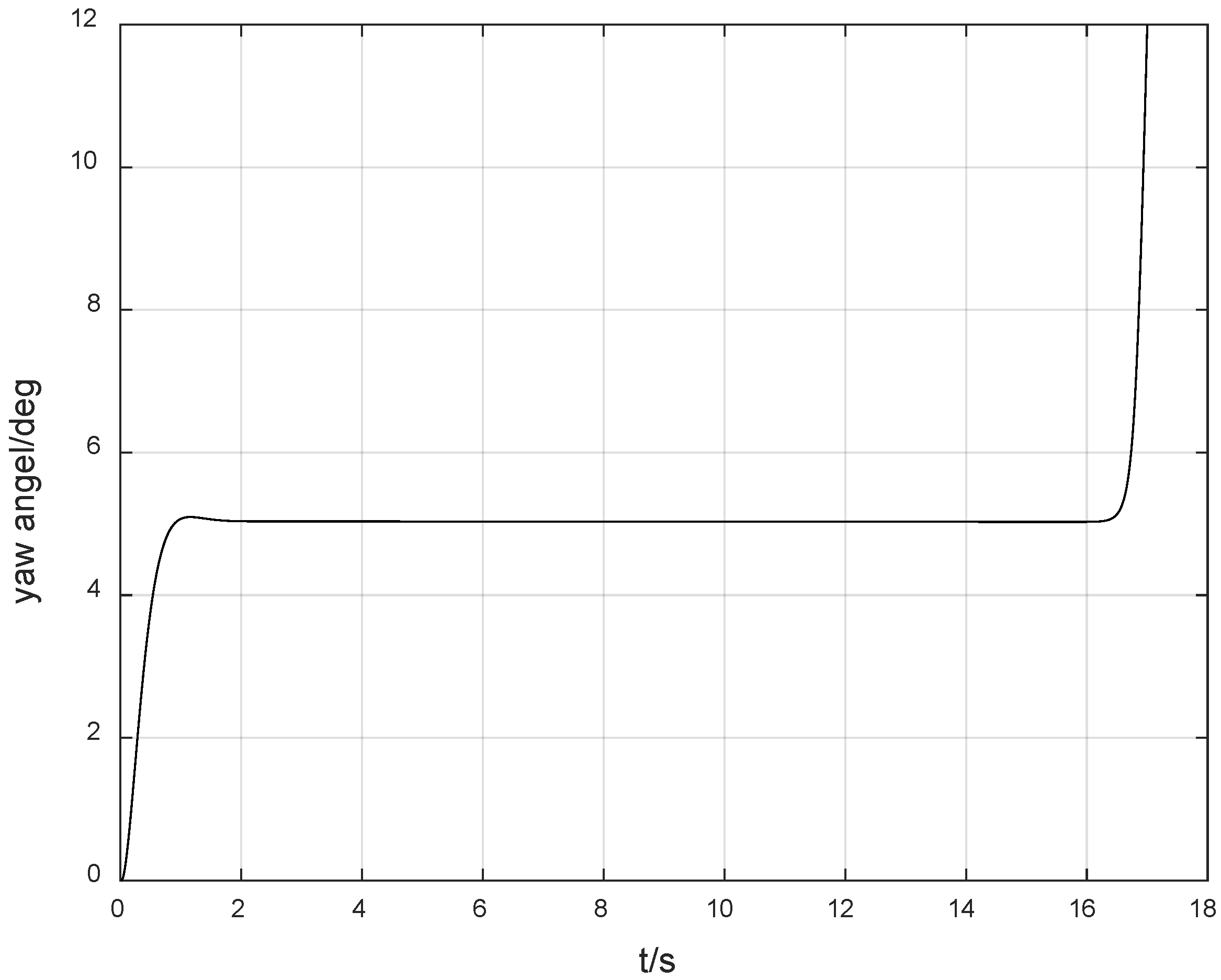
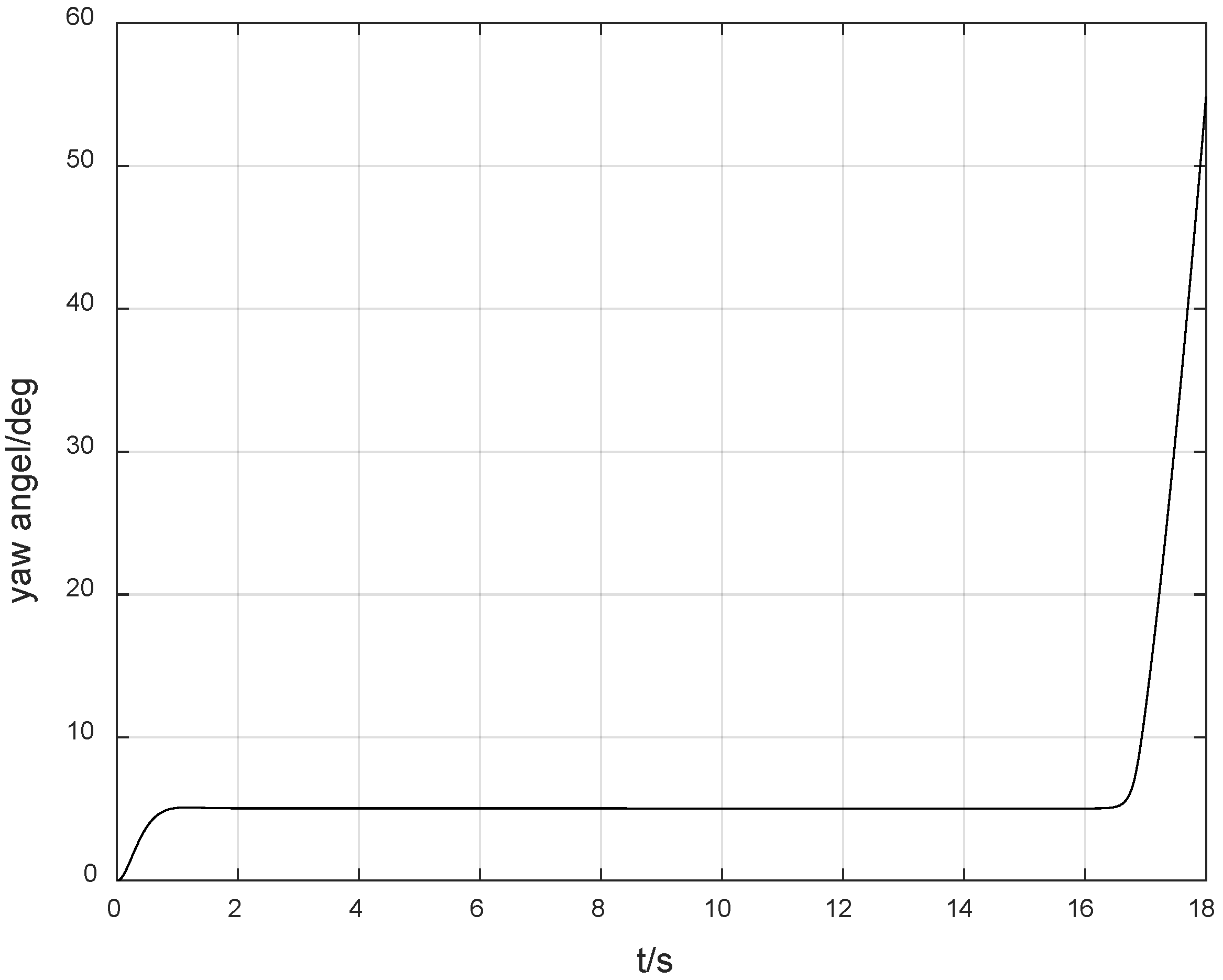
Figure 10 shows the experimental results of tracking the desired angle of 5 degrees using the ordinary adaptive method. It indicates that when the control direction is not switched, the system is stable. However, after the control direction is switched, the system diverges rapidly within 2 s. At the 18th second, that is, 3 s after the control direction is switched, the system response is as shown in
Figure 11. It can be seen that the system diverges very rapidly, and neither the conventional adaptive method nor the PID control method can deal with the instability problem caused by the unknown switching of the control direction. It can be seen that although the Nussbaum gain method results in an overshoot of 40%, it is still a good choice for the system controller design.
Furthermore, we increased the parameter perturbations to plus or minus 70%, and set the parameters of
and
to be 2 times and 20 times of
, respectively. The final simulation results are shown in
Figure 12. As can be seen from the simulation results, under significant parameter perturbations and with full consideration of uncertainties, the method proposed in this paper still exhibits excellent robustness.
In order to conduct a quantitative evaluation of the neural network’s performance in handling uncertainties, we have supplemented the results obtained without using the neural network. The results are shown in
Figure 13. It can clearly be seen that the overshoot is even larger, exceeding 120%. This indicates that the incorporation of the neural network can effectively handle and compensate for the impacts brought about by uncertainties, thus improving the performance of the system.
From the above simulation results, the rationality and effectiveness of the method proposed in this paper are verified. It can solve the huge challenges to the system stability caused by the sharp gain jumps in practical engineering, which endows the method proposed in this paper with high theoretical value and practical engineering value.
4. Conclusions
For the complex nonlinear dynamic model of the ship maneuvering system, a course angle tracking controller that combines neural networks, robust adaptive control, and sliding mode control has been designed. Moreover, the problem of unknown control direction has been taken into account, and a unilateral Nussbaum gain control function has been introduced to address it. The final simulation also demonstrates the effectiveness of the method proposed in this paper.
The main innovations and contributions of this paper are as follows. First, the large system with the problem of unknown control direction is decomposed into a two-dimensional situation. One dimension forms a new dynamic system with the sliding mode surface, while the other dimension is reserved for the stability analysis of the Nussbaum gain. Therefore, the design for the problem of unknown control direction is divided into two steps, systematically constructing an analytical method for this type of problem, especially simplifying the proof. Second, the unilateral Nussbaum gain method is combined with the sliding mode control method and applied to the control of the ship system. As a result, both the problem of unknown direction and the overparameterization problem in the backstepping design are solved. Third, considering the special nonlinear and uncertain characteristics of the ship, a dedicated RBF nonlinear neural network has been designed. Its basis functions are a combination of linear and cubic terms, enabling rapid compensation for the uncertainties of the system.
In the entire design of this paper, sliding mode control mainly ensures the stability of the system under other model uncertainties when there is no uncertainty in the control direction; that is, it guarantees the stability and robustness of the system under . On the other hand, Nussbaum gain control, based on sliding mode control, ensures the stability of the system in the presence of and the jump of its sign. Therefore, the entire design is closely linked, carefully crafted, and logically rigorous.
The research in this paper does not consider the dynamic characteristics of the actuators. If the second-order dynamic characteristics of the actuators are taken into account, the order of the entire system will increase, and the system design and stability analysis will become more complex. At the same time, the direct problem of the unknown control direction will transform into the problem of the unknown indirect control coefficients, and the entire design will be different. Moreover, this paper does not directly model the influences of ocean waves, ocean currents, and sensor noise. Instead, it merely describes the amplitude of the uncertainties mathematically. Therefore, it lacks sufficient physical persuasiveness. In our future research plan, more realistic marine scenarios will be incorporated, taking into account environmental disturbance factors such as wind, waves, ocean currents, and sensor noise. The main method is to model wind, waves, ocean currents, and sensor noise one by one at first, and then simplify the models. These models will be organized into common uncertainties that match theoretical analysis, and then theoretical design and experimental result analysis will be carried out. Finally, regarding the assumptions about uncertainties, for input uncertainties, it is necessary to assume that the bounding function is known. Therefore, in our future research, we will further relax the restrictions on uncertainties and conduct in-depth research on the abovementioned issues.