Fatigue Life Prediction of Submarine Pipelines with Varying Span Length and Position
Abstract
1. Introduction
2. Numerical Model
3. Numerical Results
3.1. Fatigue Life Analysis of the Pipeline Under Varying Span Length Due to Local Scour
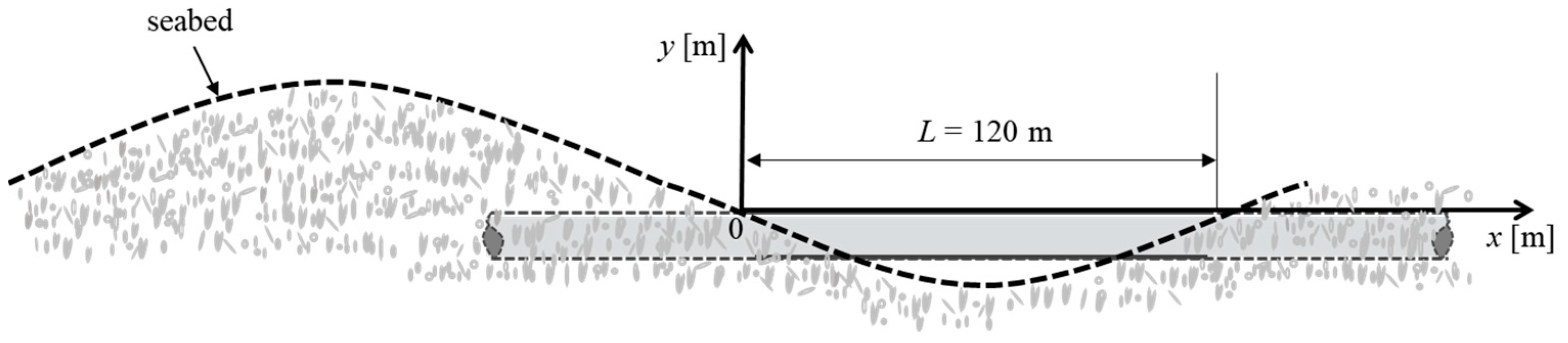
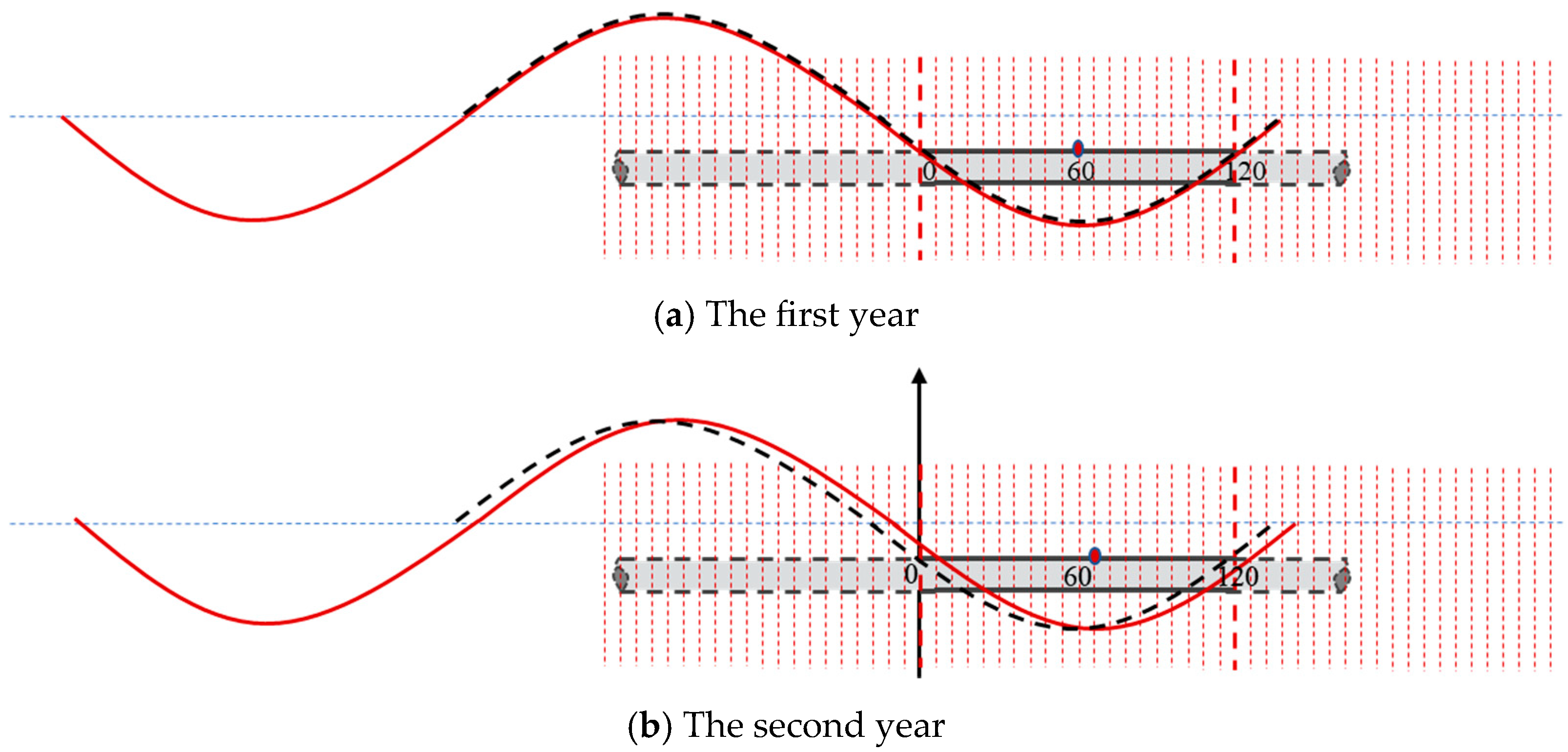
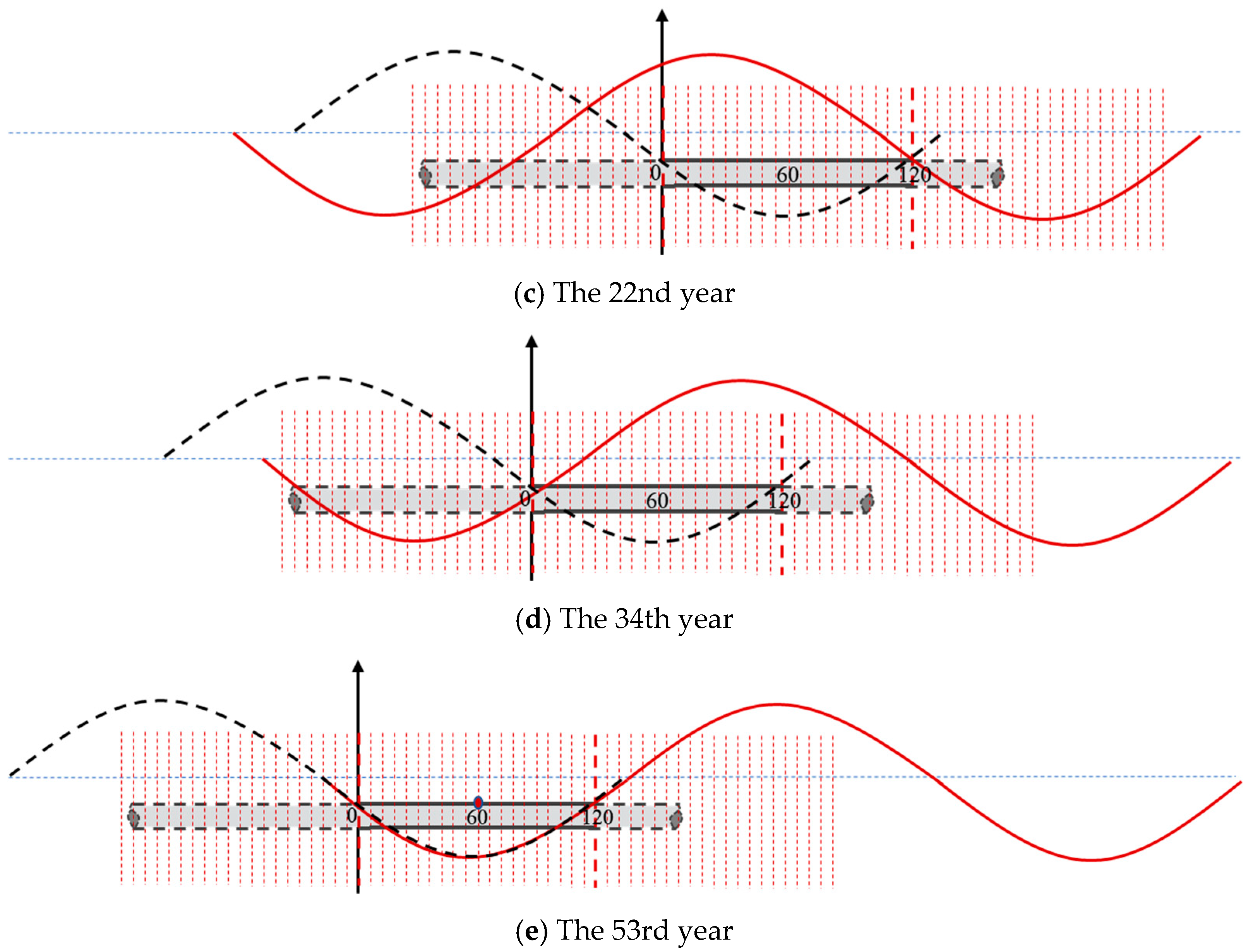
3.2. Fatigue Life Analysis of the Pipeline Under Changing Suspension Position Due to Sand Wave Migration
4. Conclusions and Recommendations for Further Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| VIV | vortex-induced vibration |
| POF | Probability of Failure |
| Probability density function | |
| COV | Coefficient of Variation |
References
- Kapuria, S.; Salpekar, V.Y.; Sengupta, S. Fatigue due to vortex-induced crossflow oscillations in free spanning pipelines supported on elastic soil bed. In Proceedings of the 9th International Offshore and Polar Engineering Conference, Brest, France, 30 May–4 June 1999. [Google Scholar]
- Fyrileiv, O.; Mørk, K. Structural response of pipeline free spans based on beam theory. In Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering, Oslo, Norway, 23–28 June 2002. [Google Scholar]
- Gamino, M. FSI Methodology for Analyzing VIV on Subsea Pipeline Free Spans with Practical Boundary Conditions. Ph.D. Thesis, Department of Mechanical Engineering Technology, University of Houston, Houston, TX, USA, 2013. [Google Scholar]
- Ulveseter, J.V.; Sævik, S.; Larsen, C.M. Vortex induced vibrations of pipelines with non-linear seabed contact properties. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2016-54424), Busan, South Korea, 19–24 June 2016. [Google Scholar]
- Yttervik, R.; Larsen, C.M.; Furnes, G.K. Fatigue from vortex-induced vibrations of free span pipelines using statistics of current speed and direction. In Proceedings of the ASME 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, 8–13 June 2003. [Google Scholar]
- Esplin, G.D.; Stappenbelt, B. Reducing conservatism in free spanning pipeline vortex-induced vibration fatigue analysis. Aust. J. Mech. Eng. 2011, 8, 11–20. [Google Scholar] [CrossRef]
- Gazis, N. A probabilistic approach for reliability assessment and fatigue analysis of subsea free spanning pipelines. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Dong, J.; Chen, X.D.; Wang, B.; Guan, W.X.; Yang, T.X.; Fan, Z.C. The effect of soil on the structural response and fatigue life of free span for submarine pipeline. In Proceedings of the ASME Pressure Vessels and Piping Conference, Boston, MA, USA, 19–23 July 2015. [Google Scholar]
- Palmer, A. 10−6 and all that: What do failure probabilities mean? J. Pipeline Eng. 2013, 2, 109–111. [Google Scholar]
- Shabani, M.M.; Taheri, A.; Daghigh, M. Reliability assessment of free spanning subsea pipeline. Thin-Walled Struct. 2017, 120, 116–123. [Google Scholar] [CrossRef]
- Shabani, M.M.; Shabani, H.; Goudarzi, N.; Taravati, R. Probabilistic modelling of free spanning pipelines considering multiple failure modes. Eng. Fail. Anal. 2019, 106, 104169. [Google Scholar] [CrossRef]
- Li, X.H.; Zhang, Y.; Abbassi, R.; Khan, F.; Chen, G.M. Probabilistic fatigue failure assessment of free spanning subsea pipeline using dynamic Bayesian network. Ocean. Eng. 2021, 234, 109323. [Google Scholar] [CrossRef]
- Pinna, R.; Weatherald, A.; Grulich, J.; Ronalds, B.F. Field observations and modelling of the self-burial of a North West Shelf pipeline. In Proceedings of the 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, 8–13 June 2003. [Google Scholar]
- Pu, J.J.; Xu, J.S.; Li, G.X. Self-burial and potential hazards of a submarine pipeline in the sand wave area in the South China Sea. J. Pipeline Syst. Eng. Pract. 2013, 4, 124–130. [Google Scholar] [CrossRef]
- Worden, K.; Farrar, C.R.; Manson, G.; Park, G. The fundamental axioms of structural health monitoring. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1639–1664. [Google Scholar] [CrossRef]
- West, B.M.; Locke, W.R.; Andrews, T.C.; Scheinker, A.; Farrar, C.R. Applying Concepts of Complexity to Structural Health Monitoring. In Structural Health Monitoring, Photogrammetry & DIC; Springer: Cham, Switzerland, 2019; Volume 6, pp. 205–215. [Google Scholar]
- Ceravolo, R.; Civera, M.; Lenticchia, E.; Miraglia, G.; Surace, C. Detection and localization of multiple damages through entropy in information theory. Appl. Sci. 2021, 11, 5773. [Google Scholar] [CrossRef]
- Thorsen, M.J.; Sævik, S.; Larsen, C.M. Fatigue damage from time domain simulation of combined in-line and cross-flow vortex-induced vibrations. Mar. Struct. 2015, 41, 200–222. [Google Scholar] [CrossRef]
- Passano, E.; Larsen, C.M.; Lie, H.; Wu, J. VIVANA Theory Manual. User Manual; Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Sumer, B.M. Hydrodynamics Around Cylindrical Structures; World Scientific: Singapore, 2006. [Google Scholar]
- Dowling, N.E.; Calhoun, C.A.; Arcari, A. Mean stress effects in stress-life fatigue and the Walker equation. Fatigue. Fract. Eng. M. 2009, 32, 163–179. [Google Scholar] [CrossRef]
- Palmgren, A. Die lebensdauer von Kugellagern. Verfahrenstechnik Berl. 1924, 68, 339–341. [Google Scholar]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. Sep. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Leckie, S.H.F.; Draper, S.; White, D.J.; Cheng, L.; Fogliani, A. Lifelong embedment and spanning of a pipeline on a mobile seabed. Coast. Eng. 2015, 95, 130–146. [Google Scholar] [CrossRef]
- Lin, Y.K.M. Probabilistic Theory of Structural Dynamics; McGraw-Hill: New York, NY, USA, 1967. [Google Scholar]
- Cao, Q.Y.; Hu, S.L.J.; Li, H.J. Global maximum response of linear systems with uncertain damping to irregular excitation. J. Eng. Mech. 2020, 146, 04020043. [Google Scholar] [CrossRef]
- Det Norske Veritas. Recommended Practice DNV-RP-F105: Free Spanning Pipelines; DNV: Oslo, Norway, 2006. [Google Scholar]
- He, Z.F.; Wei, Y.; Liu, S.L. Analysis of safe span length and fatigue life of submarine pipelines. COE 2020, 34, 119–130. [Google Scholar] [CrossRef]
- Knaapen, M.A.F. Sandwave migration predictor based on shape information. J. Geophys. Res. Earth Surf. 2005, 110, 3. [Google Scholar] [CrossRef]
- Hulscher, S.J.M.H.; van den Brink, G.M. Comparison between predicted and observed sand waves and sand banks in the North Sea. J. Geophys. Res. Ocean. 2001, 106, 9327–9338. [Google Scholar] [CrossRef]
- Bijker, R.; Wilkens, J.; Hulscher, S. Sandwaves: Where and why. In Proceedings of the Eighth International Offshore and Polar Engineering Conference, Montreal, QC, Canada, 24 May 1998. [Google Scholar]




| Parameter | Symbol | Value |
|---|---|---|
| Outside diameter/(m) | D | 0.55 |
| Wall thickness/(m) | d | 0.02 |
| Pipeline mass for unit length/(kg/m) | mp | 315 |
| Young’s modulus/(Pa) | E | 2.08 × 1011 |
| Bending stiffness of pipeline/(N/m) | EI | 2.9 × 108 |
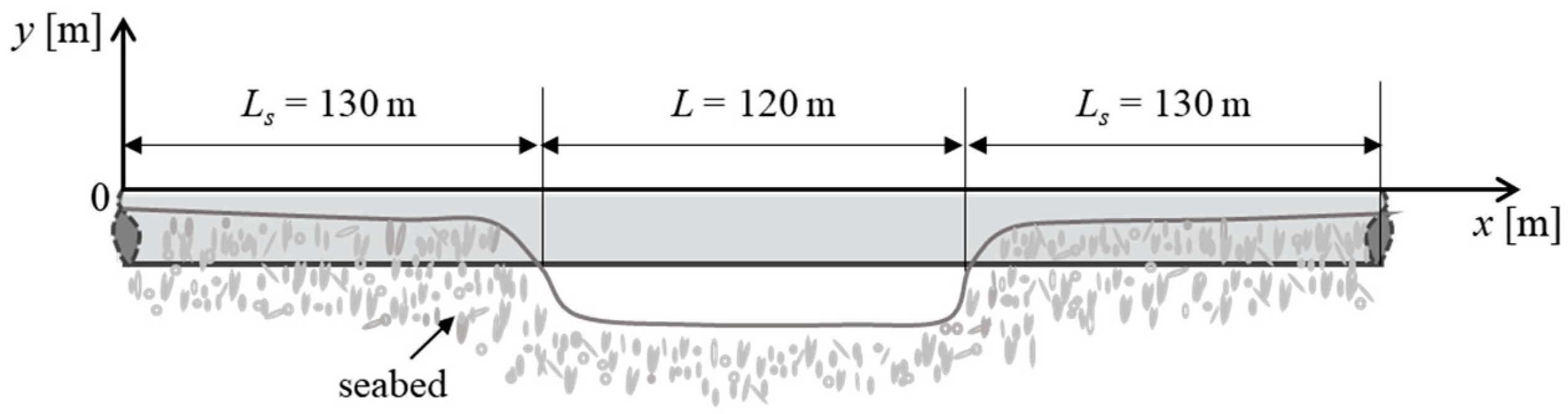
| Span length/(m) | L | 120 |
| Shoulder length/(m) | LS | 130 |
| Current velocity/(m/s) | U | 0.7 |
| Water density/(kg/m3) | ρ | 1025 |
| Vertical soil stiffness/(N/m) | kb | 40,000 |
| Span length (m) | 120 | 117 | …… | 63 | 60 | …… | 15 | 12 | …… | 0 |
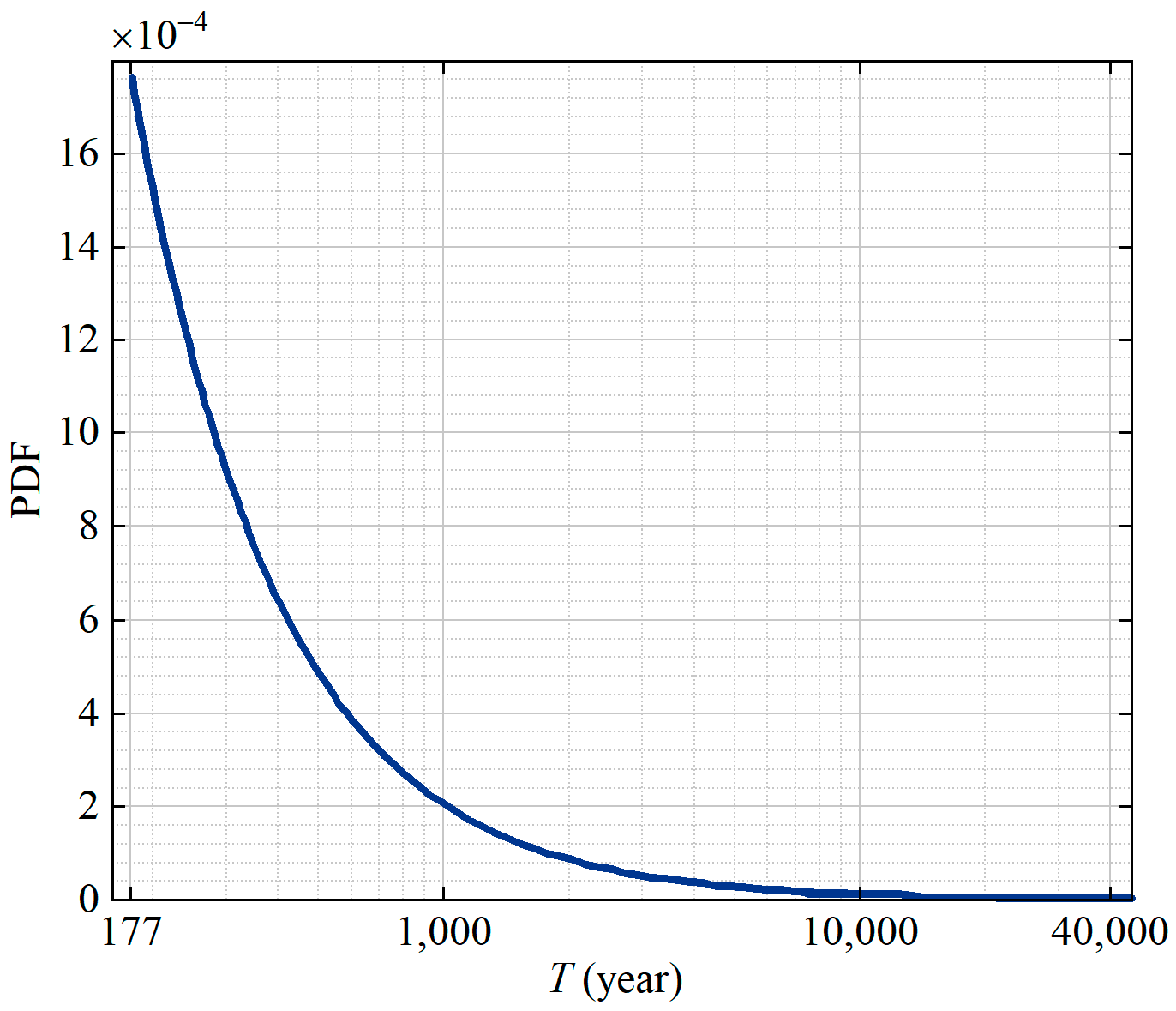
| Fatigue life (year) | 177 | 315 | …… | 1893 | 2494 | …… | ∞ | ∞ | …… | ∞ |
| Probability Density Curve | Truncated Gaussian | Rayleigh | Uniform |
|---|---|---|---|
| E(T)/(year) | 1837 | 1766 | 1876 |
| COV | COVL | COVT | |
|---|---|---|---|
| Probability Density Curve | |||
| Truncated Gaussian distribution | 0.4723 | 2.9459 | |
| Rayleigh distribution | 0.4649 | 2.7337 | |
| Uniform distribution | 0.5774 | 2.8033 | |
| Position (m) | ||||||
|---|---|---|---|---|---|---|
| In Year | 0 | 24 | 48 | 72 | 96 | 120 |
| 1 | 1.24 × 10−10 | 1.58 × 10−5 | 3.70 × 10−3 | 4.13 × 10−3 | 3.20 × 10−5 | 7.28 × 10−11 |
| 2 | 1.33 × 10−7 | 2.14 × 10−3 | 5.29 × 10−3 | 3.10 × 10−4 | 6.81 × 10−11 | |
| 3 | 1.13 × 10−10 | 8.95 × 10−4 | 5.63 × 10−3 | 1.13 × 10−3 | 1.33 × 10−10 | |
| 4 | 6.57 × 10−11 | 2.20 × 10−4 | 5.16 × 10−3 | 2.58 × 10−3 | 1.33 × 10−7 | |
| 5 | 1.24 × 10−10 | 1.58 × 10−5 | 3.70 × 10−3 | 4.13 × 10−3 | 3.20 × 10−5 | |
| 6 | 1.33 × 10−7 | 2.14 × 10−3 | 5.29 × 10−3 | 3.10 × 10−4 | ||
| 7 | 1.13 × 10−10 | 8.95 × 10−4 | 5.63 × 10−3 | 1.13 × 10−3 | ||
| 8 | 6.57 × 10−11 | 2.20 × 10−4 | 5.16 × 10−3 | 2.58 × 10−3 | ||
| 9 | 1.24 × 10−10 | 1.58 × 10−5 | 3.70 × 10−3 | 4.13 × 10−3 | ||
| 10 | 1.33 × 10−7 | 2.14 × 10−3 | 5.29 × 10−3 | |||
| 11 | 1.13 × 10−10 | 8.95 × 10−4 | 5.63 × 10−3 | |||
| 12 | 6.57 × 10−11 | 2.20 × 10−4 | 5.16 × 10−3 | |||
| 13 | 1.24 × 10−10 | 1.58 × 10−5 | 3.70 × 10−3 | |||
| 14 | 1.33 × 10−7 | 2.14 × 10−3 | ||||
| 15 | 1.13 × 10−10 | 8.95 × 10−4 | ||||
| 16 | 6.57 × 10−11 | 2.20 × 10−4 | ||||
| 17 | 1.24 × 10−10 | 1.58 × 10−5 | ||||
| 18 | 1.33 × 10−7 | |||||
| 19 | 1.13 × 10−10 | |||||
| 20 | 6.57 × 10−11 | |||||
| 21 | 1.24 × 10−10 | |||||
| …… | ||||||
| 33 | 7.28 × 10−11 | |||||
| 34 | 6.81 × 10−11 | |||||
| 35 | 1.33 × 10−10 | |||||
| 36 | 1.33 × 10−7 | |||||
| 37 | 3.20 × 10−5 | 7.28 × 10−11 | ||||
| 38 | 3.10 × 10−4 | 6.81 × 10−11 | ||||
| 39 | 1.13 × 10−3 | 1.33 × 10−10 | ||||
| 40 | 2.58 × 10−3 | 1.33 × 10−7 | ||||
| 41 | 4.13 × 10−3 | 3.20 × 10−5 | 7.28 × 10−11 | |||
| 42 | 5.29 × 10−3 | 3.10 × 10−4 | 6.81 × 10−11 | |||
| 43 | 5.63 × 10−3 | 1.13 × 10−3 | 1.33 × 10−10 | |||
| 44 | 5.16 × 10−3 | 2.58 × 10−3 | 1.33 × 10−7 | |||
| 45 | 3.70 × 10−3 | 4.13 × 10−3 | 3.20 × 10−5 | 7.28 × 10−11 | ||
| 46 | 2.14 × 10−3 | 5.29 × 10−3 | 3.10 × 10−4 | 6.81 × 10−11 | ||
| 47 | 8.95 × 10−4 | 5.63 × 10−3 | 1.13 × 10−3 | 1.33 × 10−10 | ||
| 48 | 2.20 × 10−4 | 5.16 × 10−3 | 2.58 × 10−3 | 1.33 × 10−7 | ||
| 49 | 1.58 × 10−5 | 3.70 × 10−3 | 4.13 × 10−3 | 3.20 × 10−5 | 7.28 × 10−11 | |
| 50 | 1.33 × 10−7 | 2.14 × 10−3 | 5.29 × 10−3 | 3.10 × 10−4 | 6.81 × 10−11 | |
| 51 | 1.13 × 10−10 | 8.95 × 10−4 | 5.63 × 10−3 | 1.13 × 10−3 | 1.33 × 10−10 | |
| 52 | 6.57 × 10−11 | 2.20 × 10−4 | 5.16 × 10−3 | 2.58 × 10−3 | 1.33 × 10−7 | |
| 53 | 1.24 × 10−10 | 1.58 × 10−5 | 3.70 × 10−3 | 4.13 × 10−3 | 3.20 × 10−5 | 7.28 × 10−11 |
| Sum in 53 years | 3.12 × 10−2 | 3.12 × 10−2 | 3.49 × 10−2 | 3.54 × 10−2 | 3.13 × 10−2 | 3.12 × 10−2 |
| Fatingue life (year) | 1697 | 1696 | 1518 | 1499 | 1696 | 1697 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, D.; Huang, X.; Zhao, D.; Yang, H.; Tang, G. Fatigue Life Prediction of Submarine Pipelines with Varying Span Length and Position. J. Mar. Sci. Eng. 2025, 13, 763. https://doi.org/10.3390/jmse13040763
Jiang D, Huang X, Zhao D, Yang H, Tang G. Fatigue Life Prediction of Submarine Pipelines with Varying Span Length and Position. Journal of Marine Science and Engineering. 2025; 13(4):763. https://doi.org/10.3390/jmse13040763
Chicago/Turabian StyleJiang, Daoyu, Xiaowei Huang, Deping Zhao, Haijing Yang, and Guoqiang Tang. 2025. "Fatigue Life Prediction of Submarine Pipelines with Varying Span Length and Position" Journal of Marine Science and Engineering 13, no. 4: 763. https://doi.org/10.3390/jmse13040763
APA StyleJiang, D., Huang, X., Zhao, D., Yang, H., & Tang, G. (2025). Fatigue Life Prediction of Submarine Pipelines with Varying Span Length and Position. Journal of Marine Science and Engineering, 13(4), 763. https://doi.org/10.3390/jmse13040763







