Abstract
Flexible pipes can be subjected to extreme bending load during installation and in situ operations, as well as high pressure from oil and gas field production fluids. Although field experience shows that the unlocking of the pressure armour layer is a rare failure mode, its consequences are potentially catastrophic. To investigate the unlocking mechanism of the pressure armour layer, a 3D nonlinear finite element model is developed, which contains three layers: a pressure armour layer with a “Zeta” shape cross-section, a polymer layer, and an analytical cylindrical surface representing the radial support from the carcass. The analysis is carried out with the ABAQUS Dynamic Explicit solver using a semi-automatic mass scaling factor. The study focuses on the possibility of pressure armour unlocking due to bending load, where the effects of geometric features of the pressure armour layer and internal pressure value on unlocking are investigated by varying corresponding parameters. The influence of these variables are discussed at the end. Ultimately, in conjunction with the numerical analysis results, critical reflections on the shortcomings of the model and suggestions for improvement are presented based on the numerical analysis results.
1. Introduction
With its superior mechanical properties and design flexibility, unbonded flexible risers have become pivotal O&G transportation equipment for deep-water field exploitation. Figure 1 presents a comprehensive internal architecture view of these risers. Unbonded flexible risers comprise metallic and polymeric layers. The metallic layers include carcass, pressure armour and tensile armour layers, while the polymetric components are comprised of inner and outer sheaths and anti-wear and high-strength anti-birdcage tapes. The pressure armour layer is manufactured by applying the Zeta-section steel wire winding and placement technique around the outer surface of the inner sheath. It conventionally consists of one continuous wire with a laying angle close to 90 degrees with regards to the generatrix. The fundamental duty of the pressure armour layer is to provide resistance against internal pressure. Furthermore, it also endures external loads such as crushing due to pipe handling, installation, or accidents. As with the interlocked carcass, its shape does not make the pipe watertight, still permitting fluid mobility between layers.
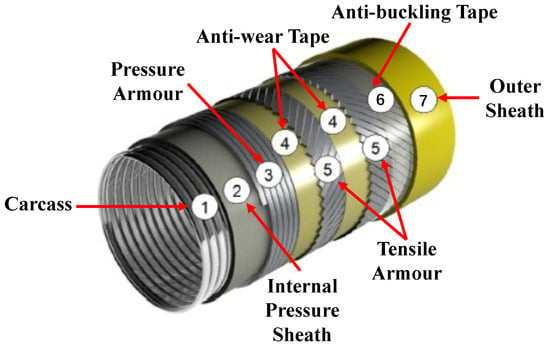
Figure 1.
Typical unbonded flexible riser cross-section.
As main international O&G operators turn their attention to deeper marine areas, the harsh operating environment poses even greater challenges for complex offshore production structures with movable components. Special working conditions demand flexible risers endure integrity under high temperature (HT), high pressure (HP), and extreme and alternating dynamic loads. The foregoing statements require that flexible riser manufacturers be more rigorous in the design and verification of products to avoid irreparable damage, as some failure modes, which are considered to have a low probability of occurrence in shallow or deep water, may feasibly be activated in the arduous environment of ultradeep waters.
In 1999, a pressure armour layer unlocking incident that occurred in an eight-inch flexible riser, which transported water, on the Norwegian continental shelf has been officially recorded by the CODAM database [1,2]. Further detail illustrates that the pressure armour was unlocked due to cracks caused by overbending [3]; the riser was then repaired with an entire restoration of the unlocking riser section. The failure mitigation method indicates the severity of the unlocking failure. The creeping and perforation of the inner sheath may occur if the riser is subjected to internal pressure due to the expansive void between the pressure armour wires [4]. One can infer that the inner sheath at the pressure armour wire unlocking location may experience continuous and progressive creep extrusion and perforation under the internal pressure of continuous production conditions. The outcome can be anticipated with the absence of radial restraint of the pressure armour layer, and ultimate failure may manifest, such as burst and leakage. Combining statistical data and relevant reports, the pressure armour layer unlocking can be recognized as a rare but disastrous failure mode, and it is unacceptable because of its threat to riser integrity, expense in terms of a remedy, and environmental contamination risk.
Thereafter, the unlocking failure has been investigated to some extent by the industry sector [4,5]. The possible unlocking initiators are summarized as follows: excessive axial tension, overbending, excessive torsion (at installation), polymer material creeping [6], failure of tensile or backup pressure armour wires, and external impact. It is possible to deduce that unlocking is achievable due to excessive axial tension and overbending. In addition, the loss of support from the neighbouring layers or other forms of pressure armour layer deterioration can facilitate the unlocking.
The present work focuses on the pressure armour layer unlocking caused by overbending, which a flexible riser section can experience after the birdcage incident. The birdcage phenomenon is a unique failure mode for tensile armour layers. Due to the hydrostatic end-cap effect, tensile armour layers can encounter considerable longitudinal compressive load during installation, well shutdown, etc. Flexible pipes are radially dilated as a result of such axial compressive loads. A radial failure mechanism with a substantial localized radial dislocation, namely a birdcage failure, will develop if such radial expansion is not effectively controlled [7]. Based on the preceding discussion, the inference regarding the pressure armour layer unlocking due to overbending is as follows: the tensile armour layer is separated from other inner layers in sections confronted with birdcage failure. Meanwhile, the riser’s resistance to bending loads is reduced. Consequently, the excessive bending that takes place in this segmentation will be transmitted to the inner layers. Concisely, the unlocking may become a secondary effect after the “birdcage”. It is important to evaluate if the pipe can still maintain its internal fluid tightness after the unlocking. It is deemed valuable to develop a methodology for the risk assessment of pressure armour unlocking after the flexible riser “birdcage” incident.
To date, limited studies are directly related to pressure armour layer unlocking. To simulate the contact behaviour between pressure armour wires, Lu et al. [8] developed a 3D FE model to simulate the loss of interlock of the pressure armour layer. By imposing a pre-calculated displacement on the inner sheath nodes, the bending behaviour is produced in the model. The pressure armour layer acts per the interlayer contact interaction to produce a uniform bending effect. The results showed that the finite element model (FEM) can be used to calculate the Damage Bending Radius (DBR) of the pressure armour layer with a measured cross-section profile. Lu et al. [9] proceeded by introducing the ingression of polymer material and thermo-plasticity into the previous research. Scenarios for the creeping of polymers into the pressure armour wires’ gap with different temperatures and different gap size distributions are devised and the resulting reduction in riser flexibility is investigated. The developed FEM is sufficient to simulate the bending of the pressure armour layer with polymer material ingression and gives reasonable stress analysis results according to different pressure armour wire spacing conditions.
Considering the practical function of pressure armour in supporting the inner sheath and protecting the pipe from external pressure or crushing, the mainstream research interest related to the pressure armour layer has been divided into the following two areas: burst and collapse analysis of the flexible riser. For burst analysis, Neto et al. [10,11] proposed three numerical models, including a 2D simplified equivalent ring model, a 3D ring approximation model for helically rolled pressure armour layer, and a full 3D model of the actual spiral structure. The conclusion shows that up to yielding, a 3D FE model is necessary for analysing the stress concentration. Increasing the strain hardening of the pressure armour gives a more significant difference between 2D and 3D models. Subsequently, Cuamatzi-Melendez et al. [12] presented a burst analysis analytically and numerically. The morphology modelling of the pressure armour layer and the polymer layer is of high significance for the unlocking simulation involving the internal pressure effect. The importance of using a 3D model to determine the real stress level in the pressure armour is claimed again, and as compared to a 2D FEM and analytical model, considering the winding pitch and actual profiles, the 3D model produces increased stress results. Liu et al. [13] investigated the internal pressure capacity and burst failure characteristics of an unbonded flexible riser, emphasizing the pressure armour layer. Detailed geometric properties and material elastoplastic behaviour of the pressure armour layer is incorporated into the FEM. In addition to burst, dry and wet annulus collapse failures are becoming more prominent with the increase in deployment depth [14]. Both the pressure armour layer and carcass are involved in the study because they are the key elements that give resistance to external pressure. Firstly, Paumier and Mesnage [15] reported ultradeepwater flexible riser qualification progress with field cases. A local residual stress assessment FEM and an in-house prediction tool of the PSI dynamic wire, namely the pressure armour wire, have been developed per corresponding standards [5,16]. In 2012, Neto et al. [17] developed a four-layer numerical model that considers the actual rolled shape of carcass and pressure armour with a few assumptions. This four-layer complete model was used as a benchmark to validate other simplified models developed by Neto et al. [18,19]. This series of studies is launched to clarify the mechanical behaviour of the pressure armour layer in the wet and dry collapse of straight and curved flexible pipes. Pilot nodes and clamping coupling conditions are used for curvature imposition on the overall flexible riser. For carcass collapse failure, a simplified or equivalent pressure armour layer does not cast significant influence. The text provides a detailed description of the material model section for flexible riser components and contact settings. Meanwhile, in 2017, Cuamatzi-Melendez et al. [20] worked on the FEM and theoretical analysis of two bisymmetric collapses. A helical pressure armour layer with a “Zeta” cross-section was used in an FEM. Simulation results finally proved the lateral resistance and restriction of the pressure armour layer for the carcass ovality before and after the eight-type carcass collapse. Recently, Zhu and Lei [21] analysed how the yield strength of the carcass and pressure armour layer affects flexible pipe collapse failure. Multi-Point Constraint (MPC) and similar finite element modelling methods are used in their study. Progress in simulation algorithms has led to sophisticated numerical models for unbonded flexible risers, capturing intricate geometric details and complex load interactions [22,23,24]. Structures from flexible risers that were once difficult to simulate, such as the pressure armour layer, can be alleviated to a certain extent. Liu et al. [25,26,27] explored flexible risers with non-uniform geometries under diverse loads, using explicit algorithms to ensure convergence despite complex contact and geometric profiles. Their work underscores the significant coupling effects of different load types on riser performance.
This study aims to investigate the unlocking mechanism of the pressure armour layer under uniform curvature and internal pressure, leading to unlocking failure. This failure mode is suspected to occur at the Touch Down Zone (TDZ), where elastoplastic deformation causes a loss of interlock between adjacent pressure armour wires, potentially resulting in outer layer failure, such as a birdcage failure of the tensile armour layer. Key factors influencing this process include material properties, structural geometry, and loading conditions. A 3D nonlinear asymmetric finite element model (FEM) is developed, incorporating the pressure armour layer, polymer inner sheath, and a cylindrical surface representing the carcass radial support. The FEM framework is presented in detail, covering the geometric configuration, material properties, meshing strategy, and boundary conditions. A comprehensive sensitivity analysis is performed, examining the effects of critical geometric parameters—such as pitch number, pitch distance, and internal diameter—along with variations in internal pressure. The results are discussed, focusing on the unlocking process, stress distribution, and the influence of various parameters on the unlocking curvature. Key observations and correlations are highlighted. Finally, the key findings are summarized, and future research directions are proposed, including experimental validation and potential improvements for practical design considerations.
2. Finite Element Modelling
This section presents the pressure armour layer unlocking features and FE modelling approach using ABAQUS 2021 software. The FE models are composed of three layers: a rigid surface, inner sheath, and pressure armour layer. Shell and solid elements are used both to ensure the FE simulation can reflect the practical engineering conditions and to reduce computation consumption. Taking into account the contribution of each layer and the extrapolation of the unlocking mentioned in the previous section, several hypotheses are established in advance.
- The structure is assumed to be stress-free in the initial state, and any prestress introduced by fabrication is ignored.
- Geometrical imperfections are not considered. It is assumed that the pressure armour is laid in a perfect helical configuration.
- The inner sheath is modelled as a tubular shell with uniform thickness and its extrusion into the gaps of pressure armour is not considered in the initial unloaded condition.
- It is assumed that the carcass will not be self-contacted and maintain its integrity during the whole simulation. For the sake of simplification, the radial support from the carcass layer is replicated by a frictionless rigid tubular surface.
- Considering that pressure armour layer unlocking may be a secondary effect of a birdcage failure, outer layers are removed to reproduce the birdcage failure and diminish the radially outward displacement constraint these outer layers place on the pressure armour layer.
2.1. Geometry and Material
2.1.1. Pressure Armour Layer
The work by Cuamatzi-Melendez et al. [12] provides the basic geometry and material information for the pressure armour wire and inner sheath. The pressure armour wire profile is claimed to be derived from API RP 17B [16] and matches the dimensions of a two-inch flexible riser. Basic dimensioning parameters and important stress–strain points are displayed in Table 1 and Figure 2, among which stands for internal diameter and , , , , , and are, respectively, Young’s modulus, Poisson’s ratio, yield stress, ultimate tensile stress, and ultimate tensile strain and density. Conclusions drawn from studies of burst failures indicate that a reproduction close to the practical three-dimensional helical structure of the pressure armour layer is important and accurate for stress analysis [12]. Thus, two asymmetry features, armour wire with a true Zeta cross-sectional shape and helical structure, are restored in the modelling. The profile revolved 90 degrees around the rotation axis with a 6.5 mm pitch distance, which equates to the 88.4 degrees helix angle of the pressure armour layer. Multiple discrete quarter armour wire turns are merged head to tail into a pressure armour layer instance with spiral conformation.

Table 1.
Geometry and material properties [12].
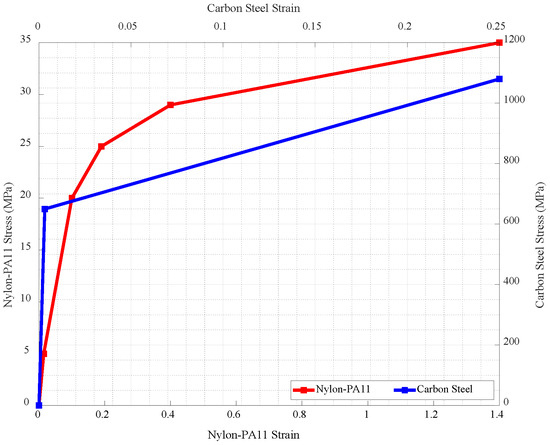
Figure 2.
Stress–strain curve of nylon PA11 and carbon steel material.
2.1.2. Inner Sheath
By incorporating the work from Cuamatzi-Melendez et al. [12] and Merino et al. [28], Polymer PA11 is used as the inner sheath material. The inner sheath is not regarded as the primary resisting layer due to its lower stiffness compared to other metallic layers. Nonetheless, transferring the internal pressure of the delivered fluid to the inner surface of the pressure armour layer is its primary function. Since the unlocking failure analysis only includes the external loading implementation until unlocking occurs, and excludes the unloading process, the stress–strain curve is shown in Figure 2 as a linear-hardening form. In FE models, the inner sheath presents a wall with equal thickness and a cylindrical shape generated by revolution with an inner surface distance from the central axis equal to the polymer layer’s inner radius.
2.1.3. Carcass
Essentially, the carcass layer is made of a thin steel strip that is spiralled into an S shape. The purpose of the unlocking investigation does not cover modelling complex carcass structures, which is a difficult task for both modelling and computation. During the overbending simulation, it is anticipated that the carcass layer will help maintain the global curvature’s regularity. Comparatively to a cylindrical thin-walled shell that does not take thickness into account, the carcass layer using a real cross-section necessitates more complicated operations to maintain the consistency of the overall model’s curvature. Additionally, a real cross-sectioned carcass’s complex contact behaviour would demand huge processing power during bending. Therefore, the simplification of the carcass as a thin-walled deformable cylinder surface, whose radius is equal to the inner diameter of the polymer layer, serves the goals of lowering computation costs and facilitating simple control of global curvature. (Note: in the following section, “carcass” will be replaced with “simplified surface” textually.)
2.2. Overbending Model
A simplified surface is generated along the positive X axis as the carcass layer. The inner sheath and pressure armour layer are spliced by the quarter inner sheath and pressure armour wire turns using the linear and radial pattern and joint head to tail into a whole. The centre of the left cross-section of the simplified surface coincides with the origin of the global coordinate system, and the longitudinal centres of all three layers are aligned in the middle.
Figure 3a shows the three-layer structure of the FE model. One feature of the pressure armour layer is its non-integer pitch number. The pitch number is always an integer plus half of one coil pressure armour wire. Figure 3b depicts the entire assembly of a 14.5-pitch model as well as the unbent and bent shapes of the pressure armour layer to aid in comprehension. It can be observed that half of one coil pressure armour wire at the bending extrados contributes to the bending balance and uniformity, which is important for the overbending-induced unlocking simulation.
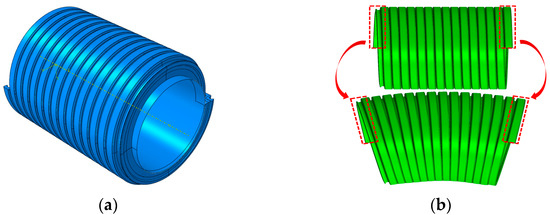
Figure 3.
FEM conformation: (a) the FEM’s three-layer structure; (b) unbent and bent shapes of the pressure armour layer.
The validity and processability of the simulation results primarily depend on the bending uniformity. The two extremity half coils, which are indicated by the red dashed square at the bending extrados side, where the structure is stretched, ensure the balance of displacement and rotational loading during the bending process.
2.2.1. Contact
The self-contact pairs of the pressure armour layer, interlayer contact pairs, and corresponding contact properties are specified as general contacts. The defined contact pairs’ domain and properties are shown in Table 2, and appropriate surface smoothing methods are assigned to eliminate the unwanted disturbance generated by coarse contact surfaces in the numerical solution. According to the works of Halloran et al. [29] and Dong et al. [30], the value of the friction coefficient for three contact pairs is provided. The friction between the simplified shell and polymer layer is ignored given that the former is merely designed to provide internal support and uniformly transfer the bending curvature to other external layers. The sectional drawing with magnified contact pair details is shown in Figure 4 and Figure 5. Within the figures, different contact domains are highlighted by annotation, and for the I-C contact pair, red and yellow lines are used to indicate master and slave surfaces. To prevent penetrations, “hard” contact is employed, which also brings the model closer to actual working conditions. The “Penalty” technique is used to improve convergence efficiency and reduce computation. Specially, the polymer layer is portioned into inner and outer parts for the meshes with different densities. The inner and outer polymer layers (see Figure 6) are unified as a consolidatory polymer layer with TIE constraints, which binds two meshes of different densities jointly and allows the inner and outer polymer layers to behave consistently to imitate a continuous undivided entity.

Table 2.
Defined contact pairs and contact properties.
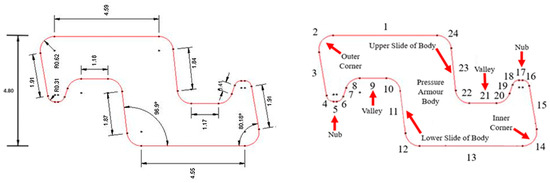
Figure 4.
Pressure armour profile and defined surfaces for contact pair definition (dimension in mm).
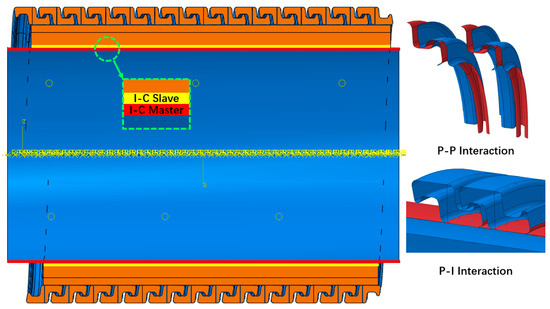
Figure 5.
Interaction settings and contact pairs.
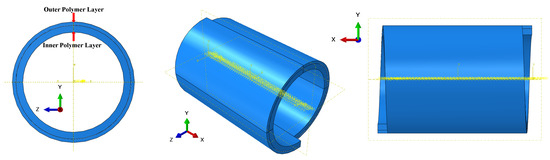
Figure 6.
Configuration of the inner sheath of the overbending model.
2.2.2. Mesh Topology
The challenge in meshing is to distinguish clearly between the mesh density of the master and slave surfaces while avoiding an excessive number of FE model elements. To provide a more thorough explanation of the meshing strategy, the description is divided into three points that correspond to the three layers.
- Simplified surface: For the sake of cross-section properties, the mesh of the simplified shell is generated by SFM3D4R element type, which is a 3D linear four-node quadrilateral surface element with reduced integration. The global seed size is fixed at 2 mm while the total length of the simplified shell in a 14.5-pitch model equals 104 mm. The linear eight-node hexahedral brick element with enhanced hourglass and distortion control is selected for both the polymer layer of the structured mesh and the pressure armour layer of the swept mesh.
- Inner sheath: The polymer layer is split into two sub-layers to reduce the element count, as shown in Figure 6. The specific reasons are as follows: (1) the primary function of the polymer layer is to transmit the internal pressure effect to the pressure armour layer, and a mesh density difference along the wall thickness direction does not affect the transfer of pressure loads; (2) the impacts of polymer deformation and ingression under internal pressure should be considered during simulation. The inner coarse mesh transfers the internal pressure primarily, while the outer polymer layer with a finer mesh can better represent the polymer’s deformation and ingression effect on the pressure armour layer. This strategy of different mesh densities between two sub-layers of inner sheath (see Figure 7) enables the model to be functional and reduces the element. The inner layer possesses a 4 mm thickness and is assigned a 1 mm mesh size, and the outer layer is 2 mm thick with a 0.5 mm mesh size. The number of elements in the inner and outer layers is 71,448 and 312,200.
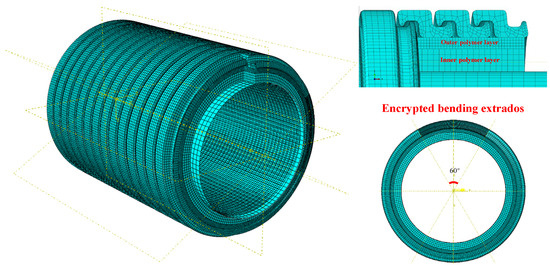 Figure 7. Global view of FEM meshing with local detail.
Figure 7. Global view of FEM meshing with local detail. - Pressure armour layer: Under the premise of maintaining the global mesh size at 1 mm, the pressure armour layer is encrypted emphatically at the nub region and the bending extrados region, where the unlocking is expected to happen. The bending extrados side of the pressure armour layer is segmented along the ring direction by radians (see the low right corner of Figure 7). The mesh sizes of the master and slave self-contact surfaces of the pressure armour layer are 0.1 mm to 0.2 mm, respectively. For a 14.5-pitch model, the problem size is determined to contain 982,580 elements with 4,369,692 DOFs.
Both the inner sheath and pressure armour wire are meshed with C3D8R elements with distortion and enhanced hourglass control. Structured mesh is used in the inner sheath. The schematic diagram of the mesh settings, the details of the bending extrados mesh partition, and the different mesh sizes of the inner and outer polymer layers are all shown in Figure 6 and Figure 7.
2.2.3. Boundary and Loading Conditions
The overbending model that includes internal pressure has two simulation steps, while the model without internal pressure just has one step. For comprehension, the overbending model with internal pressure is described as follows:
- First step—pressurization: The first step focuses on applying internal pressure. The pressurization step allows the inner sheath to expand radially, transferring the pressure load to the pressure armour layer, which is essential for the replication of realistic interlayer interactions during riser production. A coupling constraint is applied at two extremities to limit pressure armour layer displacement during pressurization. Internal pressure is imposed on the internal surface of the sheath layer and increased linearly until the target value mimics the gradual pressurization in real-world scenarios.
- Second step—bending: This step replicates the overbending conditions that a flexible riser may experience during installation or after a birdcage failure. By applying a uniform curvature, the model captures the stress and deformation patterns in the pressure armour layer, which are critical for unlocking analysis. Within this step, a global uniform curvature is applied while maintaining a constant internal pressure. Predetermined displacements and rotations, which are calculated based on distances between specific reference points and the model’s midpoint, are imposed at specified reference points to ensure bending uniformity. The curvature is applied incrementally until the unlocking condition is achieved, as determined by the loss of interlock between adjacent armour wires.
By implementing predetermined displacements and rotations at specified reference points, uniform curvature is guaranteed during the simulation of unlocking failures due to excessive bending. The information about coupling and boundary condition settings is presented sequentially in the following two subsections. The first subsection fully describes the coupling and boundary conditions setting, and the second subsection introduces the calculation procedure for the pre-defined displacements and rotations on the reference points for the uniform bending application.
2.2.4. Coupling and Boundary Condition Settings
The specifics of coupling and boundary condition settings consider the simulation steps and structural features of different components. A 14.5-pitch overbending model with internal pressure is taken as an example.
- Simplified surface: Figure 8 depicts the schematic of the coupling constraint on the simplified surface. Two cross-sectional centres at the left and right ends of the simplified surface serve as the first and last reference points controlling the simplified surface. The remaining reference points are spaced out evenly at 2 mm intervals along the central longitudinal axis, matching the simplified surface mesh density. “Kinematic” coupling is adopted to constrain translational and rotational DOFs of the coupled nodes in the Cartesian coordinate system. Therefore, the simplified surface transforms into a deformation-controllable instance to achieve a uniformly bent configuration and transmit the curvature to other outer layers.
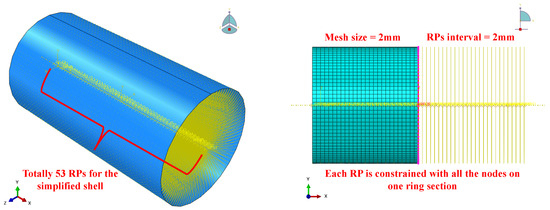
Figure 8.
Schematic of the coupling constraint on the simplified surface.
- Inner sheath: Figure 9 depicts the schematic of the coupling constraint on the inner sheath. Except for radial displacement U1, which permits the boundary of the inner sheath layer to radially expand under internal pressure, other DOFs are constrained with the reference points located at two extremities of the polymer layer.
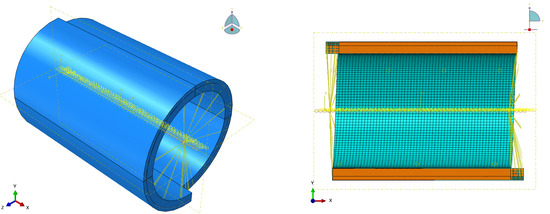
Figure 9.
Schematic of the coupling constraint on the inner sheath.
- Pressure armour layer: Figure 10 depicts the coupling constraint on the pressure armour wire. Pressure armour wire is coupled with two reference points at ends of the pressure armour layer. The half sectional coupling and purpose of the partition are shown in Figure 10. The cross-sectional profile is divided into two sections, as indicated by the yellow dot line. Throughout the entire simulation, the “coupled” portion in the armour wire will not contact the neighbouring armour wire and generate deformation. During the bending process, there will be significant contact and distortion effects in the “uncoupled” portion. Therefore, this method of splitting the profile into “coupled” and “uncoupled” sections will reduce the unexpected boundary effects brought on by the coupling constraints.
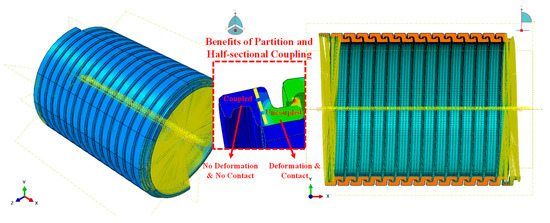
Figure 10.
Schematic of the coupling constraint on the pressure armour layer.
Uniform Bending Displacement Rotation Calculation Method
The global rotation angle is linearly loaded with a target minimum curvature radius of 0.1 m. The reference points’ displacement and rotation amplitudes over time are obtained based on distances between their location and the model’s midpoint. The midpoint of all the reference points for the simplified surface has been marked as in Figure 11.
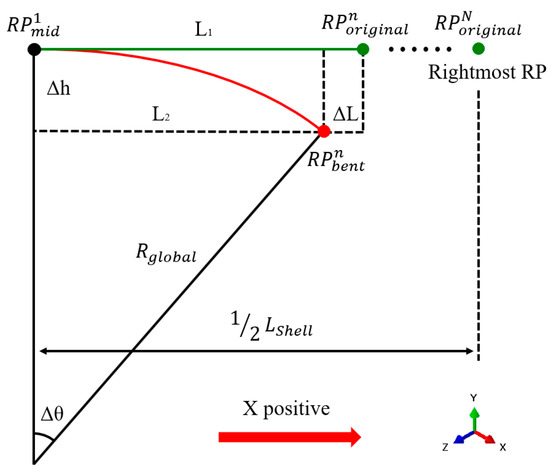

Figure 11.
Schematic of the translational and rotational displacement of the reference points during bending.
Only the right half of the model is depicted in Figure 11 to demonstrate the pre-defined displacement and rotation angle calculation process. The undeformed and deformed neutral axes, where all RPs are located, are represented by the green and red curves, respectively. There are a total of reference points, numbered from to , with standing for the th reference point. The distance between and on the undeformed neutral axis is , where is the overall length of the simplified surface. Assuming that the neutral axis is neither pulled nor compressed during the overbending process, the translational displacement of any along the X and Z axes, and the rotation around the Y axis, can be written as Equations (1)–(3).
In the above equations, is the current simulation time, stands for the duration of the overbending analysis step, is the target minimum curvature radius, and is the distance between and .
2.2.5. Unlocking Judgement Methodology
Bending moment and curvature (or curvature radius) are important characterization indicators for determining and studying the overbending-induced pressure armour layer unlocking failure. The bending moment characterizes the magnitude of the flexural load to which the riser section is subjected, while the curvature straightforwardly characterizes the riser’s bending degree geometrically. The determination and results with both indicators are introduced later, and the method for determining when the unlocking occurs is described in Figure 12. As an illustration, consider one nub pair at the bending extrados. The difference in distances between the apexes of the nubs and the centre of the bending circle is calculated according to Equation (4). The distance difference would be negative before the loss of interlock. As the bending proceeds, the apexes of nub1 and nub2 overlap, and the distance difference will equal 0, which can be viewed as the unlocking occurrence with a nub-ride-nub configuration. Following the apexes’ separation, the distance would turn negative. To sum up, the judgement method can be expressed as Equation (5), where the conversion of the positive and negative signs of the distance difference value allows for the detection of the unlocking.
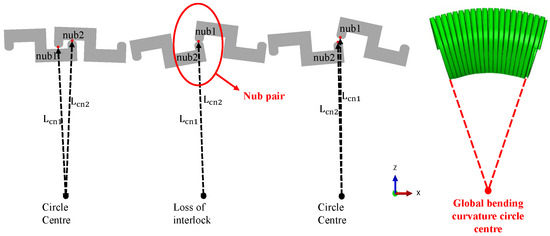
Figure 12.
Unlocking moment judgement diagram.
3. Pitch Number Sensitivity
The purpose of conducting a study on the number of pitches is to define an overbending FEM with a predetermined length that can yield results for a convergent unlocking radius or allowable error in comparison to the astringent value while using minimal computational resources. Therefore, this analysis can serve as the basis for the later investigation of other parameters. Figure 13 displays the relationship between the number of pitches and the unlocking curvature radius.
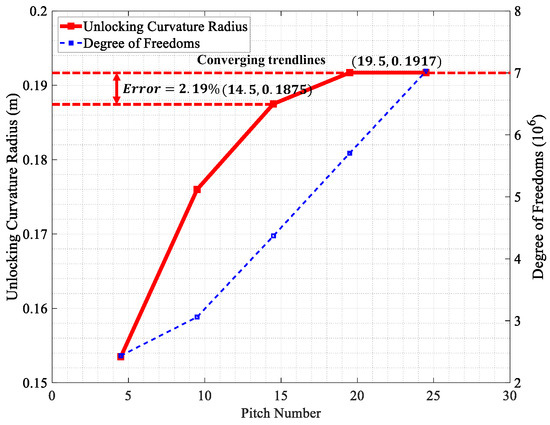
Figure 13.
Number of pitches vs. the unlocking curvature radius.
In this figure, 19.5-pitch and 24.5-pitch models produce the same unlocking curvature radius, and the converging value of the unlocking radius is 0.1917 m. Both earlier models, however, are limited by computational resources and are deemed uneconomical when compared with the 14.5-pitch model, which has a tolerable 2.19% error. The unlocking configurations for models of different lengths are shown in Figure 14. The red-dotted circle indicates specific unlocking nub pairs.
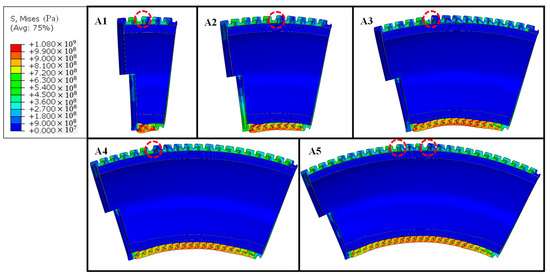
Figure 14.
Unlocking configurations for all cases in the pitch number study.
4. Results and Discussion
Parameter studies are performed by varying the model length and internal pressure. Associated unlocking processes and manifestations are described. According to the cross-section profile and parameters used in the FEM, the results are discussed and evaluated.
Four simulation groups are paralleled to study the unlocking process caused by overbending. The examined arguments include the number of pitches (model length), pitch distance, the internal diameter of the pressure armour layer, and the internal pressure. The case study for the number of pitches starts with a model length of 4.5 pitches and gradually increases to a model with a length of 24.5 pitches, with a common difference of 5 pitches. The pitch distance group includes three FEMs with pitch distances equal to 6, 6.5, and 7 mm, respectively. The case study for the pressure armour layer internal diameter includes three FEMs with internal diameters equal to 57.1, 69.8, and 82.5 mm. The inner surface of the flexible riser is applied with a uniform hydrostatic pressure of 0, 5, 10, and 15 MPa to study the influence of internal pressure. The general idea of overbending-induced unlocking is shown in Figure 15, before the presentation of the results and discussion.
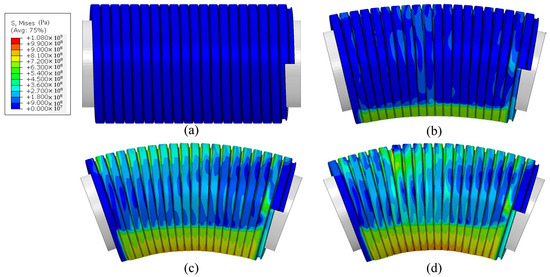
Figure 15.
Schematic diagram of the overbending-induced unlocking process.
Figure 15a demonstrates a 19.5-pitch model’s unbent conformation at the beginning of the simulation; Figure 15b depicts the pressure armour layer’s intrados as the first area to start becoming compressed; and Figure 15c depicts the extrados as the next area to reach the tensioned state. The order in which the intrados and extrados enter stressed conditions is unfixed and depends largely on the pitch distance. Stress develops as soon as contact is established and locking starts. With a greater pitch distance, the extrados can make contact first and transition into the tensioned state earlier. Eventually, the extrados region armour wire unlocks, as shown in Figure 15d. There is a transient nub-nub sliding effect immediately before the unlocking. Figure 16 illustrates the location where the sliding begins to occur. Profiles ① and ② are pulled out in opposite directions. Profile ①’s right nub twists due to elastoplastic deformation. After dividing the force produced by Profiles ① and ② on the middle contact pair into parallel and perpendicular component directions, it is found that both profiles present a clockwise rotating trend, which facilitates unlocking.
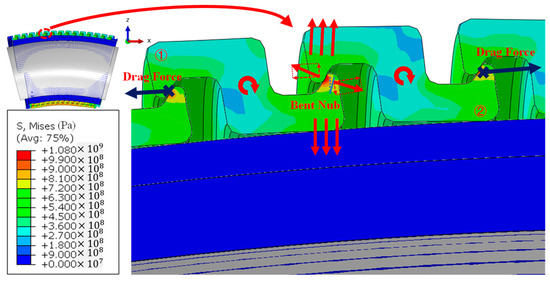
Figure 16.
Nub-nub sliding effect before overbending-induced unlocking.
As shown in Figure 17, an indication of the rotating trend is the angle formed between the inner surface of the pressure armour layer and the outer surface of the polymer layer. The rotating trend facilitates unlocking because two of the nubs in the middle nub pair move in opposite directions, apart from one another. As the curvature is further applied, static friction will eventually lose its ability to prevent the nub pair from separating and unlocking. Figure 17 represents the local stress distribution on the armour wire cross-section at the extrados. The stress contour demonstrates that most of the cross-section is still in an elastic state. Only a small portion of the nub region is susceptible to plastic deformation. The intrados of the pressure armour layer will be compacted while the extrados is tensioned during the bending. Despite the tremendous compressive force, it is unlikely that compression induces the unlocking. It is anticipated that the tensioned extrados will unlock.
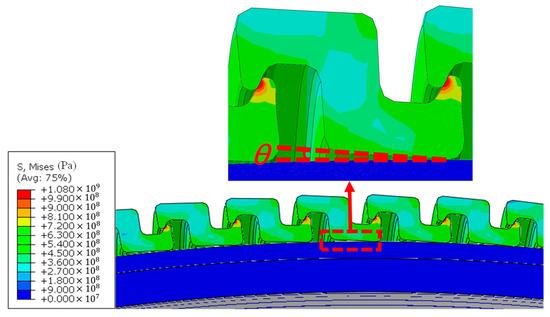
Figure 17.
Stress contour on the cross-section of the overbending model without internal pressure (Curvature radius = 0.2 m).
4.1. Influence of Pitch Distance
For the perfect flexible riser, the pressure armour wire should be distributed evenly. However, under external load, the pressure armour layer in a tube section where a birdcage failure has occurred may be stretched or contracted, causing the wire pitch of the failed section to differ from that of the adjacent section. It is noteworthy how this uneven distribution of wire pitch affects unlocking failure. Figure 18 shows the results of the study on pitch distance. The unlocking radius rises significantly with the pitch distance being elongated. It implies that an armour layer with a long pitch distance can make the unlocking failure easier. The pitch distance effect is schematically illustrated in Figure 19. From the view of deformation, overbending-induced unlocking can be separated into two phases: (1) armour wire is circumferentially tensioned due to internal pressure, and the two nubs move toward one another until they make contact; (2) two nubs undergo elastoplastic deformation until unlocking. Thus, the unlocking process can be expressed as Equation (6). represents the traction displacement required for the extrados unlocking. The traction displacement consists of two components: the relative distance between two nubs at the initial state, which will be eliminated by the sliding of two nubs, as shown on the right side of Figure 19; and , which is the elastoplastic deformation contributed by each nub pair after being stretched and making contact for the unlocking. It is assumed that there are nub pairs at the bending extrados side and the contribution of each nub pair is constant. It can be inferred from Equation (6) that the larger the pitch distance, the smaller sliding space between a nub pair, and then the less extrados stretching displacement that will be required for unlocking.
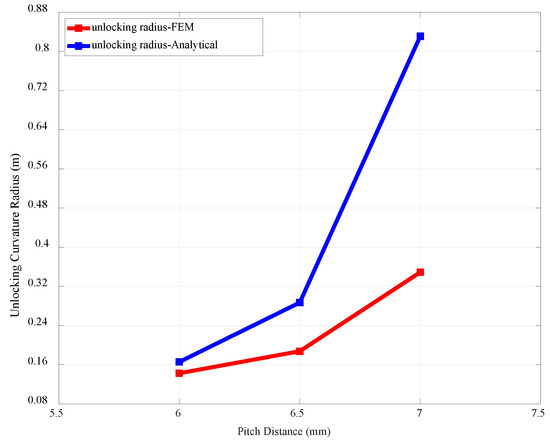
Figure 18.
Pitch distance versus unlocking radius.
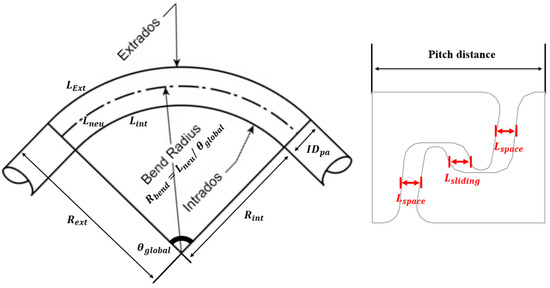
Figure 19.
Schematic of the pitch distance effect.
From the view of bending moment and curvature imposition, the relationship between extrados curvature radius and extrados stretch due to bending can be expressed as Equations (7) and (8). Since pressure armour layer internal diameter and pressure armour layer thickness are constants, extrados stretching and global bending radians are linearly related. Combining Equations (6)–(8) furnishes Equation (9). It implies that the model will have a smaller global curvature radius as decreases. Consequently, less bending load is required for unlocking if the riser section possesses a longer pitch distance.
Theoretically, elastoplastic deformation generated by the nub pairs is relatively small when compared with sliding distance , and computationally hard to calculate. Therefore, the elastoplastic deformation term is omitted for simplification. An approximate analytical solution for the bending curvature radius that triggers the unlocking failure can be written as Equation (10):
The theoretical solution for the bending curvature radius is presented with the FEM result in Figure 18. The results show that both the analytical and numerical solutions increase as the pitch distance increases, suggesting that a large pitch distance can facilitate the unlocking of the riser at low curvature. The analytical solution is larger than the theoretical solution because the elastoplastic deformation of nub pair after making contact is neglected. The error becomes progressively larger as the pitch distance increases, indicating that the elastoplastic deformation of nub pair cannot be omitted for large pitch distance cases. As the pitch distance increases, the influence of elastoplastic deformation on the unlocking becomes even more significant. This is consistent with the FE simulation results, as the nub pair needs to undergo significant elastoplastic deformation before unlocking as decreases.
Figure 20 depicts the stress contour for models with different pitch distances. For small pitch distance and normal pitch distance models, the intrados have already undergone continuous compression and severe deformation before the extrados engage contact. For the large pitch distance model, one nub pair at the extrados has unlocked, but the intrados region still has not been fully compacted. Moreover, in comparison to the first two models, the large pitch distance model generally presents a lower stress level and a less curved conformation, which suggests that a large pitch distance is a significant unlocking facilitation factor.
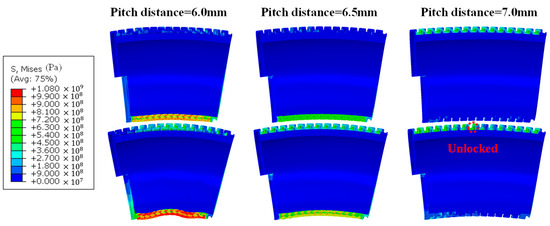
Figure 20.
Stress contour of different pitch distance models when the extrados or intrados engage fully in contact.
4.2. Influence of Pressure Armour Layer Internal Diameter
The internal diameter of the riser is a geometrically crucial parameter for its bending performance. Therefore, models with original thickness, pitch distance, no internal pressure, and different internal diameters are used to study its influence. Figure 21 demonstrates the unlocking curvature radius and , which is defined in Equation (11) as the bending degree of the riser at the unlocking moment.
where is the ratio of unlocking curvature diameter to pressure armour layer internal diameter . According to the trend in unlocking curvature radius, a model with a higher has a greater unlocking curvature radius, making the unlocking easier. This tendency is proven and supported by Equation (9). and are constant values in terms of the FEM studying the pitch distance effect, where drops as increases. Moreover, the model length is constant, and the unlocking curvature radius increases as decreases. Nevertheless, the curve in Figure 21 indicates that the model with the original demands greater curvature to unlock. There are two possible explanations: although it contradicts the previous inference, it may naturally exist in a non-monotonic relationship between and the unlocking curvature radius; (2) since is a crucial parameter, length sensitivity studies must be performed for cases with various to pinpoint the precise minimum pitch number for numerical simulation.
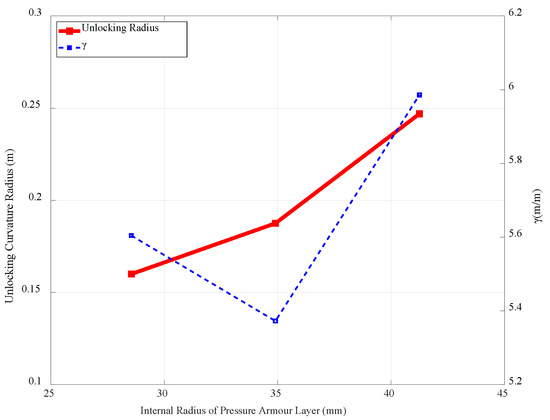
Figure 21.
Pressure armour layer internal radius versus unlocking radius.
Figure 22 shows the stress contour for the case study of . The bending curvature presents a significant decreasing tendency with the increase in . Additionally, as increases, the stress caused by intrados compression decreases as rises. However, the study only offers a cursory analysis of the impact of . Further investigation is required, along with a more precise and thorough explanation, to perform multiple case studies using FEMs.
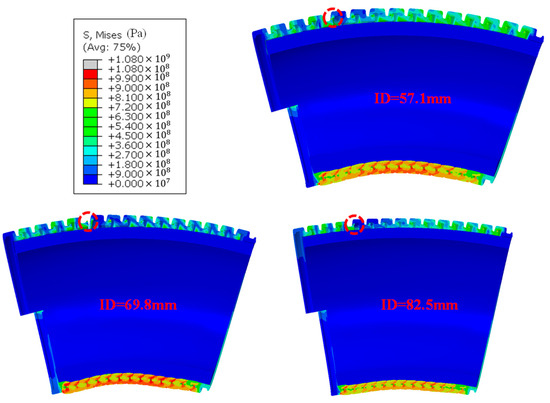
Figure 22.
Schematic of the unlocking configuration for models with different IDpa.
4.3. Influence of Internal Pressure
The flexible riser is subjected to internal pressure from the transported fluid during operation. If the axial load is not considered, namely the plane stress assumption, internal pressure can increase the circumferential stress level of the pressure armour wire, which is intuitively thought to be a favourable condition for unlocking. Consequently, simulation is conducted using models with a range of internal pressure values. Internal pressure loads of 5 MPa, 10 MPa, and 15 MPa are implemented in FEMs separately. The numerical results show that internal pressure increases the stress level of the armour wire section. The stress maxima are usually found in the inner corner region, as defined in Figure 4. Figure 23 depicts the stress contour within the armour wire section subjected to various internal pressures. The maximum von Mises stress levels in the wire are approximately 99.8 MPa, 200.9 MPa, and 300.2 MPa as the internal pressure rises from 5 MPa to 15 MPa.
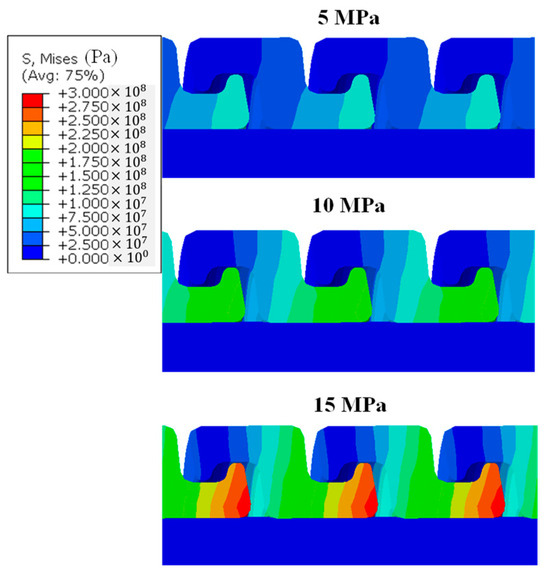
Figure 23.
Stress levels within the armour wire cross-section under different internal pressures.
The local stress contour of the model’s armour wire cross-section with 10 MPa internal pressure is shown in Figure 24. Three important phenomena can be observed: (1) the inner sheath is pressurized and pushed away from the simplified surface (carcass); (2) the inner sheath has been extruded into the gap between two adjacent armour wires. The pressurized extrusion effect is not pronounced because the polymer material is assumed without initial creeping ingression; (3) the inner sheath, which is radially outward expanded by internal pressure, inhibits the armour wire rotation effect illustrated in Figure 16 and Figure 17.
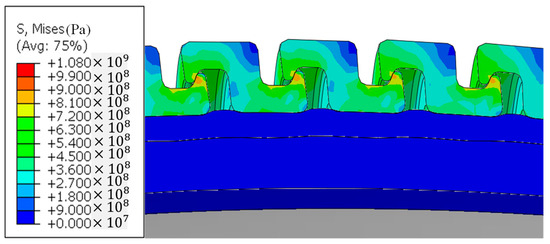
Figure 24.
Local cross-section stress contour of the overbending model with internal pressure (10 MPa, curvature radius = 0.2 m).
Figure 25 shows that as the internal pressure rises, the unlocking curvature radius grows. This can be explained by the push-out effect cast by the internal pressure as well as the elevated stress level in the armour wire caused by pressurization, which facilitates easier deformation once the nub pair makes contact. But as the internal pressure increases from 0 to 5 MPa, the riser shows a decrease in unlocking curvature radius. An explanation for this is that the pressure armour layer exhibits a loose spiral conformation in the absence of internal pressure. Therefore, being slightly internally pressurized may stabilize the loose spiral armour wire structure and reduce the unlocking risk to some extent. A mild internal pressure can transform the armour wire into a circumferentially tensioned state, which inhibits the rotation effect demonstrated in Figure 16 and Figure 17.
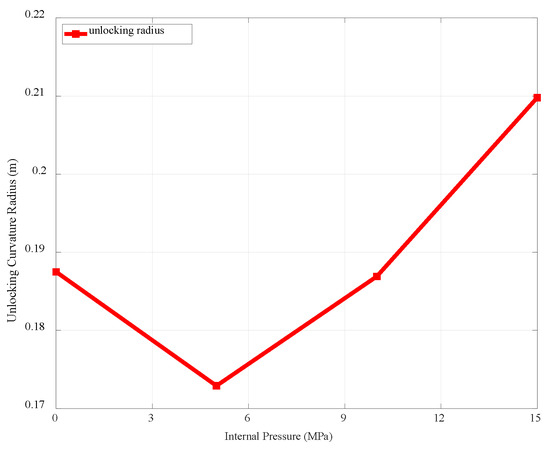
Figure 25.
Internal pressure versus the unlocking radius.
5. Conclusions and Perspective
To investigate the overbending-induced unlocking of the pressure armour layer, this paper presents a three-layer finite element model implemented with uniform bending by pre-defined displacement and rotation loads and boundary constraints. Nevertheless, it remains of interest and to be confirmed whether the numerical overbending simulation is compatible with the uniform bending conformation of a true 3D helical pressure armour layer structure and whether the boundary effects of the asymmetric FEM can be further attenuated when internal pressure and other external loads are applied. A number of pitch-sensitivity assessments are necessary because such assessments not only ensure the accuracy of subsequent numerical simulations but also computational efficiency. A three-layer, 14.5-pitch pressure armour layer FEM is confirmed after balancing computation time and relative error. Firstly, the unlocking curvature radius tends to increase as the internal diameter of the riser expands. A pressure armour layer with a larger internal diameter would produce larger displacements in both the extrados and intrados regions compared to models with a small internal diameter. The principle is analogous to the idea that long pitch distance facilitates unlocking. This leads to the conclusion that the armour wire profile thickness and internal diameter may be crucial variables for the analytical model of unlocking curvature radius. To determine the representativeness of the FEM, more case studies are required. Internal pressurization reduces the difficulty of unlocking to a limited extent. The unlocking curvature radius of the 15 MPa model is approximately 0.04 m greater than the unlocking curvature of the 5 MPa model. If extremely high internal pressure is applied, there is a chance that a pronounced result with a steep lift of the unlocking radius will be produced. However, there is a risk that extremely high internal pressure can cast significant boundary effects on the FEM, necessitating advanced measures to counteract them.
It is suggested that future work include laboratory experiments simulating overbending-induced pressure armour unlocking. A comparison of numerical accuracy could be established based on the experimental results and the FEM methodology could be revisited and calibrated. Both the effect of fabrication-induced prestress in pressure armour wire and the effect of polymeric layer extrusion into armour wire gaps also merit further investigation.
Author Contributions
R.W.: conceptualization, methodology, software, investigation, formal analysis, and writing—original draft; X.L.: conceptualization, investigation, formal analysis, and review; M.A.V.: conceptualization, formal analysis, writing—review and editing, and supervision; A.B.C.: conceptualization, formal analysis, and review. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors acknowledge the support for the support from PETROBRAS, Coordination for the Improvement of Higher Education Personnel (CAPES), CNPq (National Council of Scientific and Technological Development), National Science Foundation of China (No. 52201348), and Guangdong Basic and Applied Basic Research Foundation, China (No. 2024A1515011027).
Conflicts of Interest
Anderson Barata Custódio was employed by Petrobras. The remaining authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Nomenclature
| Young’s modulus | |
| internal diameter | |
| pressure armour layer internal diameter | |
| unlocking curvature diameter | |
| distance between nub1 and the bending curvature centre | |
| distance between nub2 and the bending curvature centre | |
| hoop length of the FEM along the neutral axis | |
| overall length of the simplified surface | |
| sliding distance between two adjacent nubs at the initial unbent state | |
| as the total number of reference points on one side of the FEM | |
| critical bending curvature that will trigger the unlocking | |
| extrados curvature radius | |
| minimum curvature radius applied in the FEM | |
| standing for the reference point at the model extremities | |
| real simulation time | |
| pressure armour layer thickness | |
| total simulation time of the overbending analysis step | |
| Poisson ratio | |
| yielding stress | |
| ultimate tensile strength | |
| ultimate tensile strain | |
| material density | |
| elastoplastic deformation contributed by each nub pair after being stretched and making contact for the unlocking | |
| global bending radians | |
| difference between distances of the two adjacent nubs to be unlocked with the bending curvature centre | |
| traction displacement required for the extrados unlocking | |
References
- Stigerørskader-Skader Og Hendelser Fra Petroleumstilsynets CODAM Database. Available online: https://www.havtil.no/contentassets/a13ec8ed3fc94e3a97b76aebb01bf6e3/stigeroersskader-2021-okt.pdf (accessed on 28 July 2021).
- Muren, J. PSA-NORWAY Flexible Pipes Failure Modes, Inspection, Testing and Monitoring. 2007. Available online: https://www.ptil.no/contentassets/a4c8365164094826a24499ef9f22742b/p5996rpt01rev02cseaflex_janmuren.pdf (accessed on 1 December 2007).
- Simonsen, A. Inspection and Monitoring Techniques for Un-Bonded Flexible Risers and Pipelines. Master’s Thesis, University of Stavanger, Stavanger, Norway, 2014. [Google Scholar]
- Fergestad, D.; Løtveit, S.A. Handbook on Design and Operation of Flexible Pipes; SINTEF Ocean: Trondheim, Norway, 2014; Volume 1, ISBN 9788271742652. [Google Scholar]
- API. 17J Specification for Unbonded Flexible Pipe; American Petroleum Institute: Washington, DC, USA, 2002. [Google Scholar]
- Ted Miller, FPSO Past Issues and Typical Claims 2012. Available online: https://slideplayer.com/slide/1567408/ (accessed on 28 July 2021).
- Li, X.; Vaz, M.A.; Custódio, A.B. Analytical Study of a Repair Methodology for Flexible Pipes Anti-Birdcage Tapes. Mar. Struct. 2019, 63, 289–303. [Google Scholar] [CrossRef]
- Lu, J.; Tan, Z.; Ma, F.; Sheldrake, T. Simulating Contact Behavior Between the Flexlok Wires. In International ANSYS Conference; Wellstream International Limited: Newcastle upon Tyne, UK, 2008. [Google Scholar]
- Lu, J.; Ma, F.; Tan, Z.; Sheldrake, T. The Impact of Flexbarrier Ingress on Flexlok Stress. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; Volume 3, pp. 533–538. [Google Scholar]
- Neto, A.G.; Martins, C.D.A.; Pesce, C.P.; Meirelles, C.O.C.; Malta, E.R.; Neto, T.F.B.; Godinho, C.A.F. Prediction of Burst in Flexible Pipes. J. Offshore Mech. Arct. Eng. 2013, 135, 011401. [Google Scholar] [CrossRef]
- Neto, A.G.; Martins, C.D.A.; Pesce, C.P.; Meirelles, C.O.C.; Malta, E.R.; Barbosa Neto, T.F.; Godinho, C.A.F. Burst Prediction of Flexible Pipes. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 5, pp. 511–520. [Google Scholar]
- Cuamatzi-Melendez, R.; Castillo-Hernández, O.; Vázquez-Hernández, A.O.; Albiter, A.; Vaz, M. Finite Element Modeling of Burst Failure in Unbonded Flexible Risers. Eng. Struct. 2015, 87, 58–69. [Google Scholar] [CrossRef]
- Liu, X.; Qu, Z.; Liu, Y.; He, J.; Si, G.; Wang, S.; Liu, Q. Numerical Simulation of Burst Failure in 2.5-Inch Unbonded Flexible Riser Pressure Armor Layers. Metals 2024, 14, 762. [Google Scholar] [CrossRef]
- Paumier, L.; Averbuch, D.; Felix-Henry, A. Flexible Pipe Curved Collapse Resistance Calculation. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; Volume 3, pp. 55–61. [Google Scholar]
- Paumier, L.; Mesnage, O. PSI Armour Wire for High Collapse Performance of Flexible Pipe. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; Volume 4, pp. 239–246. [Google Scholar]
- API. 17B Recommended Practice for Flexible Pipe; American Petroleum Institute: Washington, DC, USA, 2008. [Google Scholar]
- Neto, A.G.; de Arruda Martins, C.; Malta, E.R.; Godinho, C.A.; Neto, T.F.; de Lima, E.A. Wet and Dry Collapse of Straight and Curved Flexible Pipes: A 3D FEM Modeling. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Neto, A.G.; Martins, C.D.A.; Malta, E.R.; Tanaka, R.L.; Godinho, C.A.F. Simplified Finite Element Models to Study the Dry Collapse of Straight and Curved Flexible Pipes. J. Offshore Mech. Arct. Eng. 2016, 138, 021701. [Google Scholar] [CrossRef]
- Neto, A.G.; Martins, C.D.A.; Malta, E.R.; Tanaka, R.L.; Godinho, C.A.F. Simplified Finite Element Models to Study the Wet Collapse of Straight and Curved Flexible Pipes. J. Offshore Mech. Arct. Eng. 2017, 139, 061701. [Google Scholar] [CrossRef]
- Cuamatzi-Melendez, R.; Castillo-Hernández, O.; Vázquez-Hernández, A.O.; Vaz, M.A. Finite Element and Theoretical Analyses of Bisymmetric Collapses in Flexible Risers for Deepwaters Developments. Ocean. Eng. 2017, 140, 195–208. [Google Scholar] [CrossRef]
- Zhu, X.; Lei, Q. Collapse Characteristics of Flexible Pipes under External Pressure. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 312. [Google Scholar] [CrossRef]
- Yun, R.-H.; Jang, B.-S.; Kim, J. Du Improvement of the Bending Behavior of a Flexible Riser: Part I—Nonlinear Bending Behavior Considering the Shear Deformation of Polymer Layers. Appl. Ocean Res. 2020, 101, 102204. [Google Scholar] [CrossRef]
- Ruan, W.; Chen, M.; Nie, Q.; Xu, P.; Li, J.; Wang, X. Dynamic Response of Steel Lazy Wave Riser Considering the Excitation of Internal Solitary Wave and Ocean Currents. Ocean Eng. 2024, 294, 116708. [Google Scholar] [CrossRef]
- Ruan, W.; Nie, Q.; Han, X.; Li, J.; Bai, Y.; Fu, X. Accurate Modeling and Safety Evaluation of Dented Pipeline with Internal Pressure Based on Reverse Modeling Technique. Ships Offshore Struct. 2024, 1–11. [Google Scholar] [CrossRef]
- Liu, Q.; Xue, H.; Tang, W. Behavior of Unbonded Flexible Riser with Composite Armor Layers under Coupling Loads. Ocean Eng. 2021, 239, 109907. [Google Scholar] [CrossRef]
- Liu, Q.; Xue, H.; Tang, W.; Yuan, Y. Theoretical and Numerical Methods to Predict the Behaviour of Unbonded Flexible Riser with Composite Armour Layers Subjected to Axial Tension. Ocean Eng. 2020, 199, 107038. [Google Scholar] [CrossRef]
- Liu, Q.-S.; Qu, Z.-Y.; Wang, G.; He, J.-W.; Ni, J.-F. Advanced Analysis of Cross-Sectional Properties in Unbonded Flexible Risers with Composite Layers. Ships Offshore Struct. 2025, 1–14. [Google Scholar] [CrossRef]
- Merino, H.E.M.; de Sousa, J.R.M.; Magluta, C.; Roitman, N. Numerical and Experimental Study of a Flexible Pipe Under Torsion. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 5, pp. 911–922. [Google Scholar]
- O’Halloran, S.M.; Connaire, A.D.; Harte, A.M.; Leen, S.B. Modelling of Fretting in the Pressure Armour Layer of Flexible Marine Risers. Tribol. Int 2016, 100, 306–316. [Google Scholar] [CrossRef]
- Dong, L.; Huang, Y.; Zhang, Q.; Liu, G. An Analytical Model to Predict the Bending Behavior of Unbonded Flexible Pipes. J. Ship Res. 2013, 57, 171–177. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).