Research on LSTM-PPO Obstacle Avoidance Algorithm and Training Environment for Unmanned Surface Vehicles

Abstract

The current unmanned surface vehicle (USV) intelligent obstacle avoidance algorithm based on deep reinforcement learning usually adopts the mass point model to train in an ideal environment. However, in actual navigation, due to the influence of the ship model and the water surface environment, the training set is triggered. The reward function does not match the actual situation, resulting in a poor obstacle avoidance effect. In response to the above problems, this paper proposes a long and short memory network-proximal strategy optimization (LSTM-PPO) intelligent obstacle avoidance algorithm for non-particle models in non-ideal environments, and designs a corresponding deep reinforcement learning training environment. We integrate the motion characteristics of the unmanned boat and the influencing factors of the surface environment, based on the curiosity-driven set reward function, to improve its autonomous obstacle avoidance ability, combined with the LSTM network to identify and save obstacle information to improve the adaptability to the unknown environment; virtual simulation is performed in Unity. The engine builds a USV physical model and a refined water deep reinforcement learning training environment including a variety of obstacle models. The experimental results demonstrate that the LSTM-PPO algorithm exhibits an effective and rational obstacle avoidance effect, with a success rate of 86.7%, an average path length of 198.52 m, and a convergence time of 1.5 h. A comparison with the performance of three other deep reinforcement learning algorithms reveals that the LSTM-PPO algorithm exhibits a 21.5% reduction in average convergence time, an 18.5% reduction in average path length, and an approximately 20% enhancement in the success rate of obstacle avoidance in complex environments. These results indicate that the LSTM-PPO algorithm can effectively enhance the search efficiency and optimize the path planning in obstacle avoidance for unmanned boats, rendering it more rational.

1. Introduction

In autonomous navigation and obstacle avoidance tasks, unmanned surface vehicles (USVs) rely on sensors to perceive the environment and make decisions based on the data to navigate and avoid obstacles. Traditional rule-based methods, such as the artificial potential field and dynamic window approaches, often lack flexibility in complex environments and struggle with adapting to unknown obstacles and hydrodynamic changes. Recently, Reinforcement Learning (RL), a data-driven optimization technique, has gained popularity in intelligent decision making due to its ability to learn optimal strategies through interaction with the environment. Among RL methods, Deep Reinforcement Learning (DRL) combines deep learning’s capability to process high-dimensional data with RL’s decision-making optimization, offering an effective solution for adaptive and intelligent obstacle avoidance in USVs.

The unmanned boat is programmed to perform a series of tasks, including the collection of environmental data through the use of sensors. These data are then used to construct a model, which is subsequently integrated into the decision-making layer. This enables the boat to plan and execute autonomous obstacle avoidance maneuvers [1]. The field of unmanned boat navigation encompasses two principal categories of algorithms: global path planning and local path planning. Global path planning methods are designed to generate obstacle avoidance paths based on global map information, whereas local path planning methods are intended to generate local obstacle avoidance paths based on real-time sensor information [2].

The field of local path planning has a long history of research, with numerous algorithms having been proposed over the years. These include the artificial potential field method [3], the dynamic window method [4], the velocity barrier method [5,6], and many others. The advent of artificial intelligence has seen the advent of deep reinforcement learning methods [7,8,9], which combine deep learning and reinforcement learning, in the field of intelligent decision making. These methods have been applied with a view to enhancing the intelligence and environmental adaptability of local path planning. Deep reinforcement learning can be classified into two principal categories: value-based and policy-based algorithms. The value-based algorithms include, for example, the Deep Q Network [8] (DQN), Competitive Architecture-based DQN [10] (Dueling DQN), and so forth. Policy-based algorithms, on the other hand, encompass the Policy Gradient Algorithm [11] and the Trust Region Algorithm [12] (Trust Region). Barto et al. [13] introduced the Actor-Critic (AC) approach, which combines the advantages of both value-based and policy-based algorithms. This approach is the most commonly considered algorithmic framework for solving real-world problems due to its combination of the two aforementioned algorithms. Subsequently, the aforementioned framework was utilized to inform the development of additional algorithms, including the Deep Deterministic Policy Gradient (DDPG) algorithm [14], the Asynchronous Advantage Actor-Critic (A3C) algorithm [15], the Proximal Policy Optimization algorithm [16], and others.

The advancement of deep reinforcement learning has facilitated the successful implementation of this technology in the domain of unmanned platform control. In their study, Duguleana and Mogan [17] employed a combination of Q-learning and a neural network planner to develop collision-free trajectories for mobile robots. Fathinezhad et al. [18] put forth a methodology for electronic hockey robot collision avoidance that integrates supervised and reinforcement learning. In their study, Tai et al. [19] trained the Turtlebot robot using the DQN algorithm in deep reinforcement learning. This enabled the robot to navigate and avoid obstacles when facing unknown environments. Wang Ke et al. [20] proposed a selective training method based on minimum depth information to obtain the robot’s action decision result after inputting the depth information obtained from the sensors into the architecture. This method not only improves the training speed but also enhances the navigation ability. In a study conducted by Zhang et al. [21], a robot was programmed to complete a series of tasks, including navigation and manipulation, using a guided policy search with internal storage. Xu Guoyan et al. [22] put forth a method for avoiding obstacles in unmanned vehicles based on an enhanced DDPG deep reinforcement learning algorithm. This method is capable of continuously outputting the steering wheel angle and acceleration of an unmanned vehicle. In their study, Li et al. [23] employed multi-task learning and reinforcement learning techniques to achieve lateral decision control of vehicles in the VTORCS (Visual TORCS) environment. Huang, Zhiqing et al. [24] constructed a decision-making control model based on the deep reinforcement learning algorithm DDPG to achieve end-to-end autonomous decision making. Xu et al. [25] put forth an intelligent collision avoidance algorithm based on deep reinforcement learning, constrained by the International Regulations for Preventing Collisions at Sea (COLREGs). This algorithm employs deep neural networks to automatically extract state features, design a reward function, and track the current network weights to update the target network weights, thereby enhancing the algorithm’s stability and ability to learn optimal strategies. In their study, Joohyun and Nakwan [26] employed a deep reinforcement learning approach to address the collision avoidance challenge of an unmanned boat. They utilized the extracted deep reinforcement learning network parameters to compute the action value function for each behavioral candidate in real time. The coupling of various perturbation factors in the marine environment necessitates the real-time and robust functioning of obstacle avoidance algorithms for unmanned boats [27].

The selection and configuration of a suitable simulation training environment represents a significant challenge for researchers engaged in the development of deep reinforcement learning obstacle avoidance algorithms. These algorithms require a substantial amount of data collected from the environment to facilitate effective training, underscoring the importance of an appropriate training environment. In order to facilitate rapid interaction and ensure the stability of data collection, researchers typically select an optimal setting for training and validating obstacle avoidance algorithms. Notable examples include the straightforward Python-based GridWorld environment, which can be constructed independently through the use of standard libraries such as Pyglet, and which is limited to discrete action spaces; the intricate GridWorld environment proposed by Jun Wang et al. [28], which is employed to investigate competition and collaboration issues in the context of a large number of intelligences; and Open AI’s [29] proposed Particle environment, which enables the specification of the number of intelligences and the selection of tasks, and which is applicable to both discrete and continuous action spaces. In the context of training obstacle avoidance algorithms within the aforementioned simulation environment, intelligent bodies, such as unmanned boats, are typically idealized as prime models, with the water environment assumed to be an ideal one. This ideal environment setting model is markedly dissimilar from actual scenarios. Consequently, when confronted with diverse types of obstacles, the unmanned boat cannot implement targeted obstacle avoidance strategies.

Despite the notable accomplishments of reinforcement learning algorithms such as PPO, SAC, and A2C in addressing localized obstacle avoidance tasks for unmanned boats, their adaptive capacity in complex environments remains a significant area of concern. For instance, SAC exhibits constrained adaptability to environmental perturbations, despite its stability. PPO may lack the stability required to update its strategy during training due to its fixed-step optimization, and A2C employs a synchronous updating strategy that may not be sufficient to swiftly adapt to environmental changes in complex environments. Consequently, a reinforcement learning method that can leverage historical information is imperative for enhancing the adaptability and decision-making capabilities of intelligences in complex environments.

LSTM (Long Short-Term Memory) is a specific type of Recurrent Neural Network (RNN) that has the capacity to process time-series data effectively and make adaptive adjustments by leveraging historical information. In comparison to the PPO algorithm alone, the PPO combined with LSTM (LSTM-PPO) exhibits the capability to more accurately capture the historical state information of the unmanned boat and circumvent the constraints imposed by short-term observation. Consequently, this enhances the system’s obstacle avoidance proficiency and environmental adaptability.

This study proposes an LSTM-PPO deep reinforcement learning unmanned boat obstacle avoidance algorithm based on a reinforcement learning framework. The proposed algorithm combines a long short-term memory network (LSTM) and a proximal policy optimization (PPO) algorithm with the aim of improving the obstacle avoidance ability and safety of unmanned boats in complex environments. The main research objectives are as follows:

1.

The obstacle avoidance strategy of the unmanned boat is optimized. This can be accomplished by autonomously training the unmanned boat through reinforcement learning so that it can efficiently avoid obstacles in non-ideal complex environments and navigate to the target point. This will avoid the problem of strategy failure that may be caused by the training of traditional plasmonic models.

2.

Virtual LIDAR-based environment sensing is introduced. The local water environment information can be sensed by virtual LIDAR, so that the unmanned boat can accurately recognize obstacles and make reasonable obstacle avoidance decisions.

3.

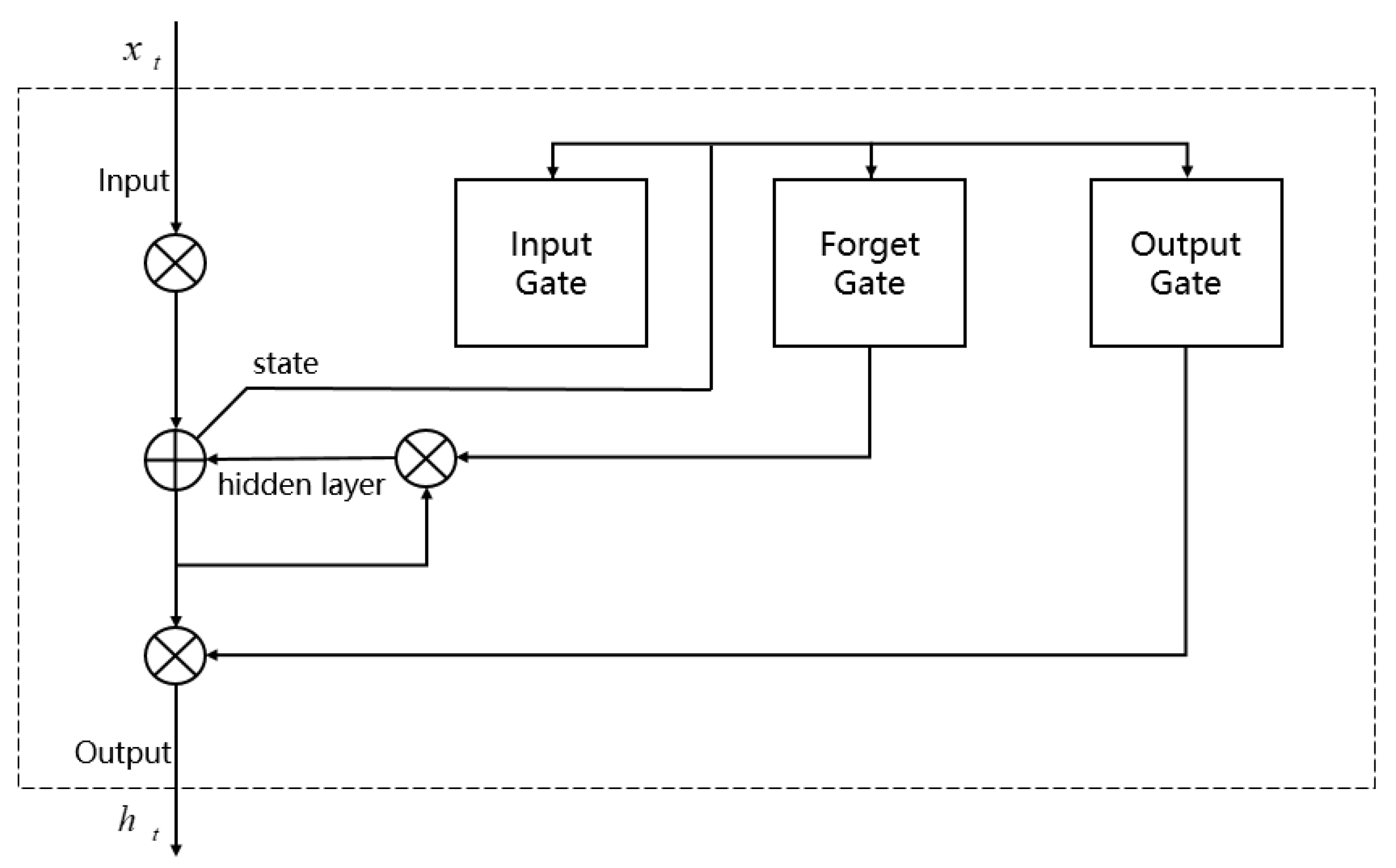
Using LSTM to process historical information, avoiding the limitations brought by single-step observation and enabling the unmanned boat to memorize the historical state and improve the coherence of obstacle avoidance decision.

4.

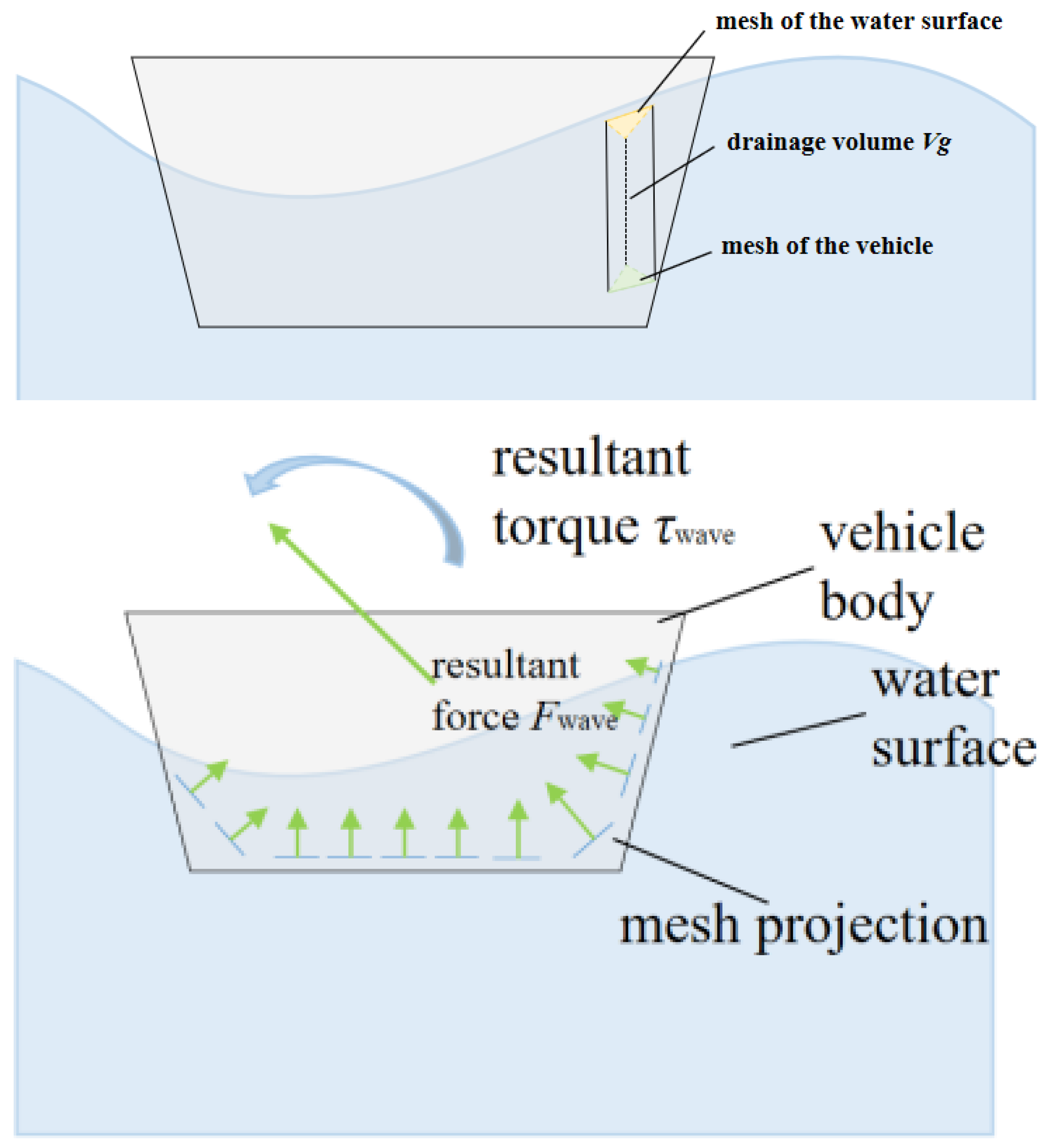
Considering the influence of hydrodynamic forces and dynamics by introducing water surface resistance and drift penalties in the training process to enhance the adaptability of the algorithm to the actual marine environment.

5.

Optimizing the design of reward function, considering the risk level of different obstacles in the design process and using the curiosity-driven mechanism to optimize the reward function to make it more reasonable and scientific.

6.

Verifying the performance of the algorithm, where a comparison with the algorithms A2C, SAC, and PPO is necessary to evaluate the advantages of LSTM-PPO in terms of training efficiency, obstacle avoidance path optimization, and success rate of obstacle avoidance.

In addressing these challenges, this paper presents an LSTM-PPO deep reinforcement learning unmanned boat intelligent obstacle avoidance algorithm for non-prime models in non-ideal environments, integrating long- and short-memory networks on the foundation of traditional proximal policy optimization decisions. LSTM-PPO has been shown to outperform PPO, SAC, and A2C in terms of long-term dependent modeling, leading to more stable decision making in complex environments. In contrast to PPO, which can result in local optima due to its fixed-step optimization strategy, and SAC, which exhibits degraded performance in high-noise environments, LSTM-PPO’s time-series modeling capability enables more effective adaptation to environmental changes and enhances the stability of obstacle avoidance.

Furthermore, the long-term memory mechanism of LSTM enables the unmanned boat to retain historical information when encountering complex obstacle layouts. This allows the boat to refer to the previous state when making decisions, thereby improving the rationality of path planning. This feature makes LSTM-PPO more advantageous than traditional PPO and SAC in complex marine environments, especially in obstacle avoidance path optimization and training stability.

This paper presents the findings of experiments conducted to verify the convergence of an algorithm in an obstacle avoidance training experiment. The experiment was conducted in a constructed refined water environment using a real USV physical model. The training environment of this study is a single-boat autonomous obstacle avoidance task, and the main objective is to optimize the local obstacle avoidance strategy of the unmanned boat. The reward function design does not directly consider the coordinated multi-boat avoidance rule in COLREGs. However, the obstacle avoidance strategies learned by the proposed LSTM-PPO algorithm can serve as a foundation for future research. These strategies can be combined with the COLREGs rule constraints when further extended to multi-boat environments, thereby enhancing the adaptability and safety of unmanned boats in complex maritime traffic environments. The performance enhancement of LSTM within the reinforcement learning framework is analyzed through comparative experiments with A2C, SAC, and PPO algorithms. These experiments compare the algorithm training time consumption, obstacle avoidance path length, obstacle avoidance success rate, and other indicators. The experimental results demonstrate that LSTM-PPO can improve the decision-making ability of USVs in complex environments, guarantee the reliability of obstacle avoidance of USVs, and lay the foundation for obstacle avoidance experiments in real-water environments.

The primary contributions of this study are enumerated below.

1.

The development of an unmanned boat obstacle avoidance algorithm based on LSTM-PPO, which integrates the LSTM memory capability to enhance the adaptability of PPO in non-ideal complex environments.

2.

The construction of a refined water simulation environment, training based on the physical model of the unmanned boat, and the introduction of hydrodynamic effects. Dynamic influence to train the unmanned boat in a way closer to the actual environment.

3.

Adopting the perception model based on virtual LiDAR to optimize the local environment cognition ability of the unmanned boat, so as to make its obstacle avoidance strategy more stable and reliable.

4.

Designing a multi-level reward mechanism to balance the factors of target point navigation, obstacle avoidance, sailing direction optimization, and hydrodynamic influence, so as to improve the rationality of obstacle avoidance decision making.

5.

Verifying the effectiveness of the algorithm through comparative experiments, and conducting experimental comparisons with A2C, SAC, and PPO to quantify the performance improvement of LSTM in reinforcement learning.

The results of this study provide an efficient reinforcement learning solution for intelligent obstacle avoidance of unmanned boats and lay a theoretical foundation for future application in real waters.

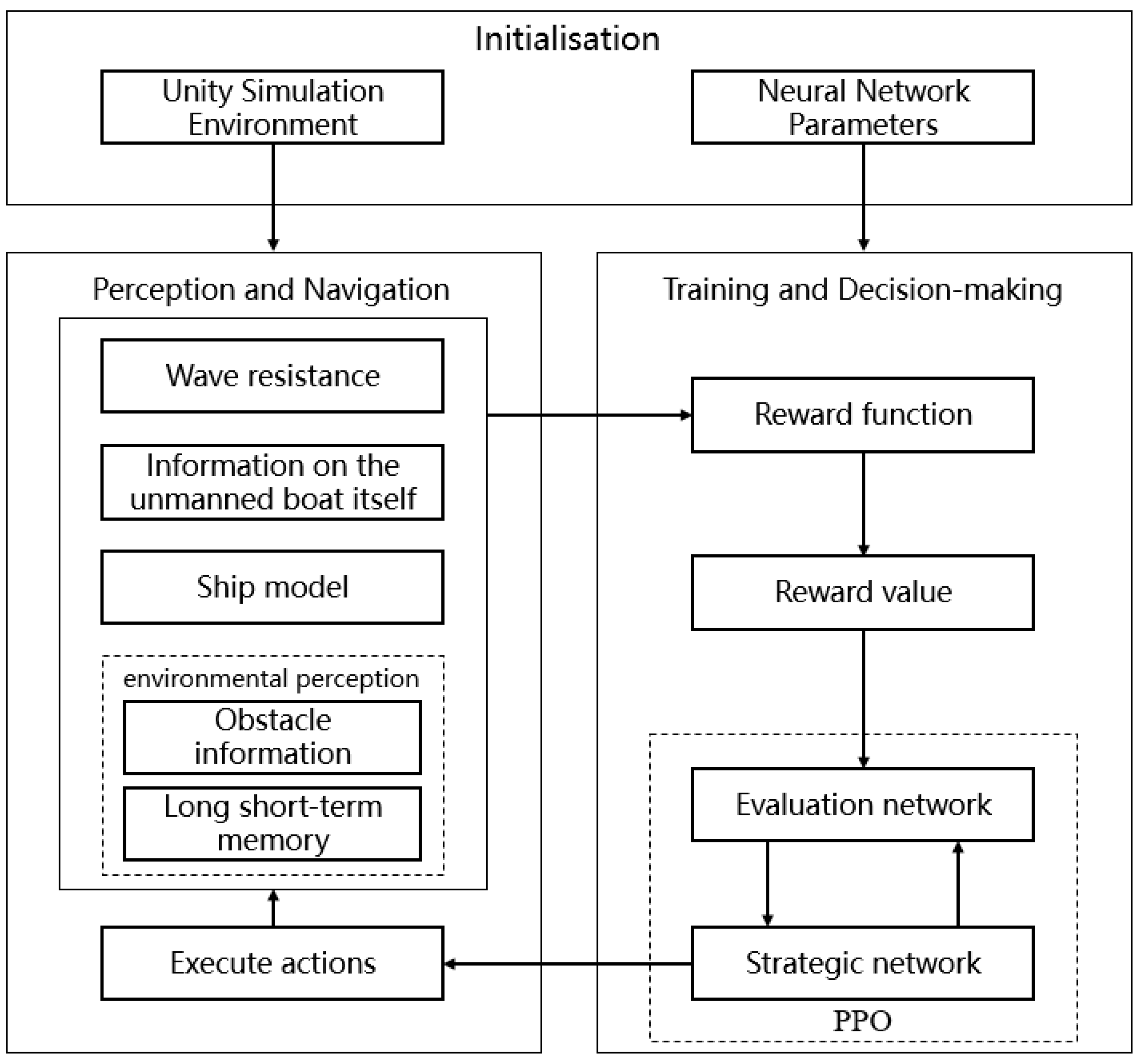
2. Methodology

The framework of the LSTM-PPO obstacle avoidance algorithm for unmanned boats is illustrated in Figure 1. The overall framework is divided into three modules: initialization, perception and navigation, and training and decision making. Initialization and setup of the state space for local obstacle avoidance in unmanned boats is the first step. This consists of environment information and parameters for a deep reinforcement learning neural network. The environment information is provided by the constructed Unity simulation environment, including the position and speed of local obstacles, the position and speed of unmanned boats, and the position of target points, among other data. The simulation environment utilizes this information in the perception and navigation module of the USV, whereas the neural network parameters, including the learning rate, maximum steps, sample training size, and so forth, are employed in the training and decision-making module. The aforementioned neural network parameters, which include the learning rate, maximum steps, and batch size, are utilized in the training and decision-making modules. In the sensing and navigation module, a long short-term memory (LSTM) network is introduced for environment sensing. Its memory is utilized to recognize and save obstacle information, thereby enhancing the adaptability of the unmanned boat to the unknown environment. In the training and decision-making module, the wave resistance, the unmanned boat’s own information, and the ship model provided by the refined simulation platform are introduced as influencing factors of the reward function, thereby enhancing the realism and reliability of the simulation platform. The appropriate reward function is established and provided to the neural network for training purposes. The PPO algorithm is employed to identify the optimal action as the subsequent motion decision for the unmanned boat, thereby enabling autonomous obstacle avoidance.

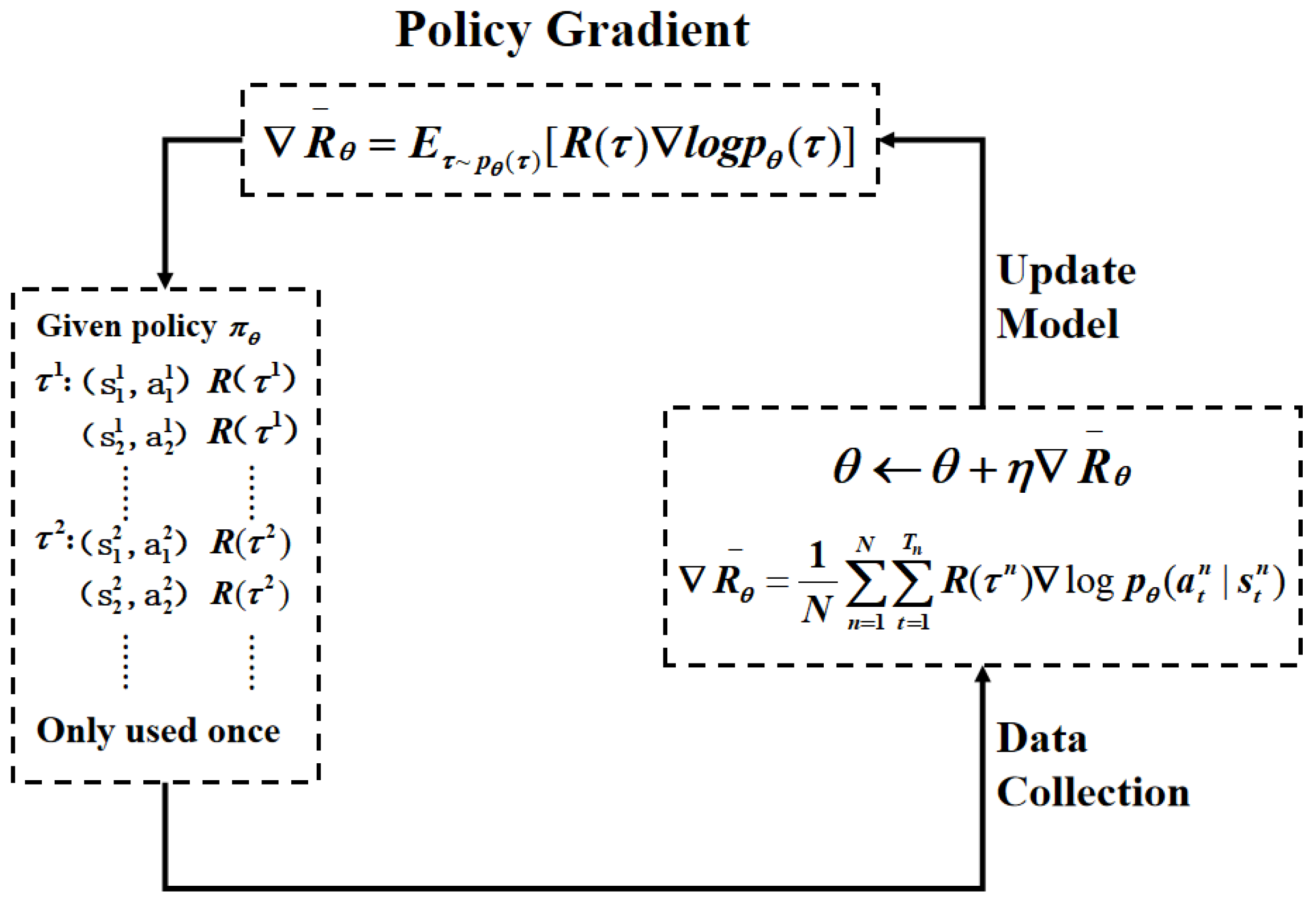
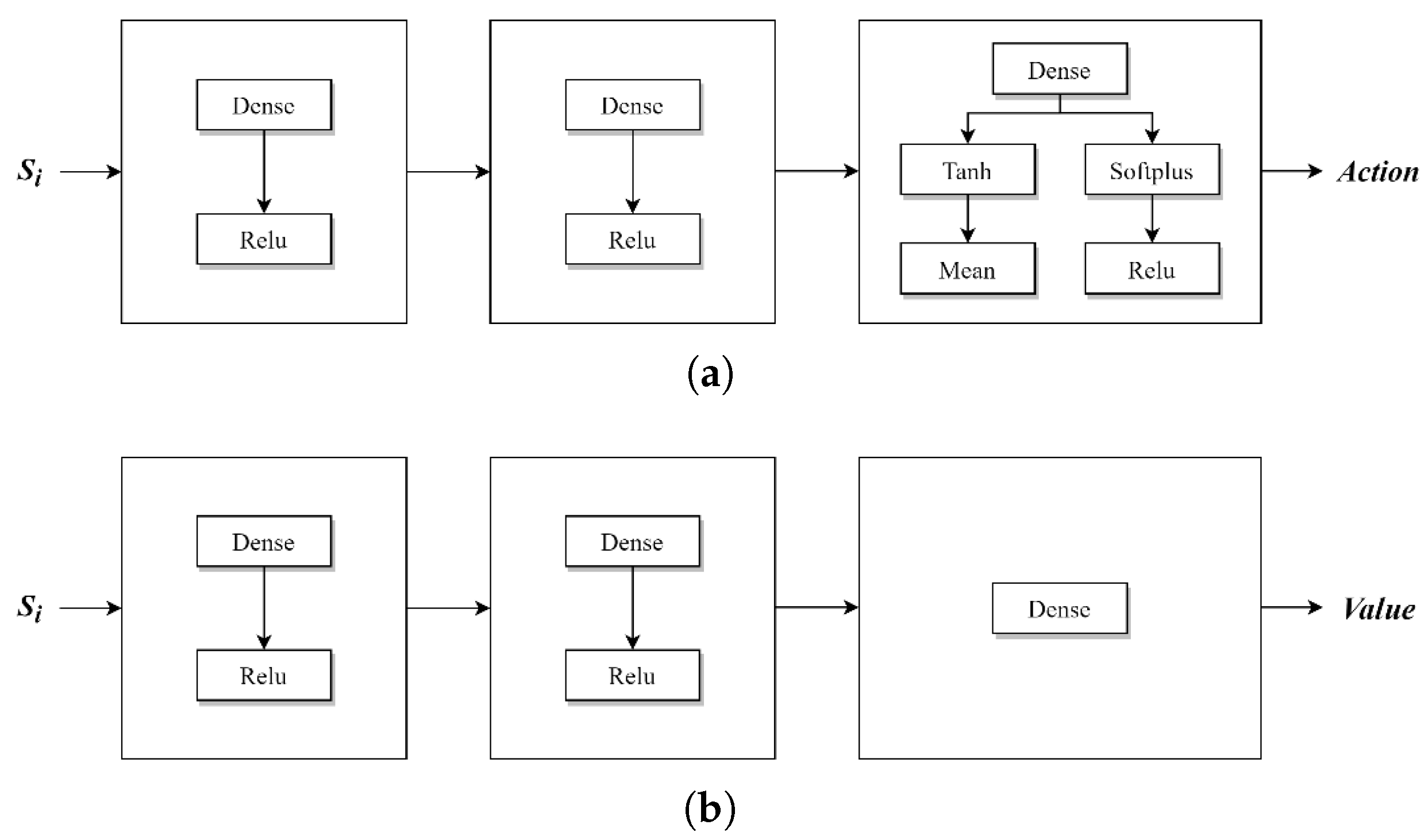
2.1. Obstacle Avoidance Strategy

Reinforcement learning algorithms can be classified into two main categories: value-based and policy-based methods. Value-based reinforcement learning methods, however, present significant challenges when applied to the task of unmanned boat obstacle avoidance. For instance, there is a dearth of capacity to manage continuous actions. The unmanned boat deploys a force with a specific value and direction to make decisions regarding obstacle avoidance. Consequently, this phenomenon necessitates the utilization of policy-based reinforcement learning methods for its modeling. Furthermore, value-based reinforcement learning methods lack the capacity to address the issue of constrained states. In the actual obstacle avoidance environment of the USV, two distinct states may exhibit identical characteristics after modeling, rendering the optimal solution inaccessible through value-based methods. Additionally, the optimal strategy for USV obstacle avoidance is often a random strategy, which value-based reinforcement learning methods are unable to resolve. In light of the aforementioned considerations, this paper employs the policy-based reinforcement learning method to identify the optimal policy through the use of a continuous function optimization approach. One of the most frequently utilized algorithms is the Policy Gradient (PG) algorithm [24]. The primary objective of the PG algorithm is to update the policy using the gradient ascent method in order to maximize the expected reward. The objective function for updating the network parameters is presented below:

$${\nabla }_{\theta }J\left({\pi }_{\theta }\right)={\mathbb{E}}_{\tau \sim {\pi }_{\theta }}\left[\sum _{t=0}^T{\nabla }_{\theta }{\log }_{{\pi }_{\theta }}(a_t\mid s_t)R\left(\tau \right)\right]$$

(1)

As illustrated in Figure 2, the data acquisition is initially conducted, the parameters are then updated in accordance with the obtained gradient ascent formula, and subsequently, the data are acquired with the updated parameters based on the updated strategy. This process is then repeated, and the cycle continues. It should be noted that following the updating of the parameters, the policy has been modified. Consequently, the preceding data are contingent upon the policy that was obtained prior to the aforementioned update. Therefore, it can only be utilized on a single occasion. In this manner, the PG algorithm can enhance the likelihood of an action with a high reward value occurring and simultaneously diminish the probability of a strategy with a low reward value occurring.

Nevertheless, experimental studies have demonstrated that the utilization of harvested expectations for the computation of state values results in a heightened degree of variability in behavioral patterns. This, in turn, gives rise to parameter updates that are likely to be suboptimal for the policy gradient. Accordingly, this paper employs the Actor-Critic approach, a policy gradient method that integrates the policy-based and value-based techniques.

The Actor-Critic algorithm framework is a widely utilized approach in the domain of real-world unmanned surface vehicle (USV) obstacle avoidance algorithms. It integrates two key algorithms: the value function estimation algorithm and the policy search algorithm. This integration enables the avoidance of policy degradation, a phenomenon that can arise due to errors in the value function estimation. Furthermore, this framework facilitates the effective resolution of USV obstacle avoidance problems, including those encountered in unmanned boat operations. At present, the majority of mainstream deep reinforcement learning algorithms, including A3C, PPO, and other algorithms, are based on this framework. Among the algorithms proposed, the PPO algorithm, developed by OpenAI in 2017 [23], represents a novel strategy gradient algorithm. While the strategy gradient algorithm is effective in practical problems with a certain degree of difficulty, it is highly sensitive to the number of iteration steps. As a result, it is challenging to select an appropriate step size, and it exhibits suboptimal data efficiency and robustness. To address this shortcoming, the PPO algorithm selects a new objective function for realizing small batch updates in multiple training steps. This addresses the problem of determining the step size in the policy gradient algorithm, which is difficult to determine. In this paper, we utilize the primary form of the PPO algorithm, designated as PPO-Clip, and introduce a novel ratio for elucidating the distinctions between the preceding and current strategies. This ratio is defined as follows:

$$r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}}$$

(2)

Let $r_t\left(\theta \right)$ represent the behavioral probability ratio. When a is greater than 1, it indicates that the probability of taking an action under the current strategy is greater than the probability of taking an action under the previous strategy. The objective function is currently designed as follows:

$$L\left(\theta \right)=E_t\left[{\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}}{A}_t\right]=E_t\left[r_t\left(\theta \right)A_t\right]$$

(3)

Next, in order to prevent significant discrepancies in policy updates during parameter updating, the Clip function is introduced. This entails the utilization of a truncation method to restrict the ratio of action probabilities to the interval [$1-\epsilon$, $1+\epsilon$] (where $\epsilon$ is the truncation constant), with the aim of enhancing the stability of the trained intelligences’ behavior. Accordingly, the objective function of PPO can be optimized as illustrated below:

$$L^{CLIP}=E_t\left[\min \left(r_t\left(\theta \right)A_t,clip\left(r_t\left(\theta \right),1-\epsilon ,1+\epsilon \right)A_t\right)\right]$$

(4)

When the value of Advantage Function $A_t$ (Advantage Function A) is greater than 0, it indicates that the current strategy action is beneficial to the optimization objective. In such cases, the probability of its occurrence should be increased, while ensuring that the range of strategy updating remains below $1+\epsilon$. Similarly, it can be demonstrated that when the value of $A_t$ is less than 0, the current strategy action is negative, and the probability of its occurrence should be reduced. Furthermore, the range of strategy updating should be lowered to $1-\epsilon$.

In order to ensure the safe navigation of unmanned boats, it is essential that they are able to acquire local environmental information. This enables them to avoid potential obstacles. This paper introduces the addition of reef-simulating static obstacles and a moving floating block simulating dynamic obstacles to the virtual simulation environment. Furthermore, the obstacle information detected by the virtual LiDAR is discretized into a finite number of states, and the resulting state space is formulated in a reasonable manner. The unmanned boat is equipped with a virtual LIDAR system that emits 180 rays for obstacle detection within a 180-degree radius in front of the vessel. The range of the emitted rays is 50 m. The environmental information that must be observed during the training process includes the location of the target point ($x_{goal}$, $y_{goal}$), the location of the obstacles ($x_{obstacle}$, $y_{obstacle}$), and the movement speed ($v_{obstacle-x}$, $v_{obstacle-y}$). Additionally, the location of the unmanned boat itself ($x_{USV}$, $y_{USV}$) and the movement speed ($v_{USV-x}$, $v_{USV-y}$) must be considered. The final environmental state is, thus, defined as follows:

$$\begin{array}{c}{s}_i=\{x_{goal},y_{goal},x_{USV},y_{USV},v_{USV-x},\hfill \\ v_{USV-y},x_{obstacle},y_{obstacle},v_{obstacle-x},v_{obstacle-y}\}\hfill \end{array}$$

(5)

In light of the uncertainty surrounding the number and location of obstacles in the surface environment, this paper proposes the integration of a long- and short-term memory network into the environment sensing module, based on the PPO-Clip algorithm. A long short-term memory (LSTM) is a recurrent neural network that is capable of processing continuous data information. In comparison to the utilization of the PPO algorithm exclusively, the integration of the LSTM network enhances the unmanned surface vehicle (USV) capacity for obstacle avoidance and its adaptability to unanticipated environmental conditions. The LSTM network architecture utilized in this research is illustrated in Figure 3. The state vector of the unmanned boat is input to the LSTM network in sequence. The number of preceding messages to be retained is determined by a forgetting gate, while the input gate stores the valid portion of the current message. Subsequently, the valid information is conveyed through the output gate and stored in the hidden state. The environment state is transformed into fixed-size vectors through the hidden state, and these vectors, which contain the environment state information, will be utilized as inputs to the PPO network for the localized obstacle avoidance decision of the unmanned boat.

The network structure of the PPO algorithm utilized in this paper is illustrated in Figure 4 below. It employs a strategy network structure devised to encompass three hidden layers (hidden layer), each comprising 128 neurons. The input to the network is the state $s_i$, and the output is the action selected according to the distribution, that is, the action undertaken by the unmanned boat in the subsequent step. The evaluation network design structure also comprises three hidden layers, each comprising 128 neurons. The input to the network is the state $s_i$, while the output is the state value function (state value function), that is, the expected value of the cumulative rewards at state $s_i$. This value is employed for the assessment of the quality of the state.

In the context of reinforcement learning tasks, the policy-gradient-based approach, known as PPO, has demonstrated efficacy in addressing challenges posed by continuous action spaces, characterized by its stable update mechanism. However, in complex environments, PPO is susceptible to the short-sightedness problem, as it relies exclusively on the current state for decision-making processes. To address this limitation, this paper proposes a novel approach that integrates the long short-term memory (LSTM) network with PPO. The LSTM network’s capacity to process time-series data is leveraged to enhance the adaptability of an unmanned boat in complex environments. The following section will provide a detailed comparison of LSTM-PPO with SAC and traditional PPO, highlighting its respective strengths and weaknesses.

LSTM-PPO has been demonstrated to exhibit enhanced stability in comparison with SAC (Soft Actor-Critic), a reinforcement learning method grounded in maximum entropy. SAC demonstrates a notable strength in its exploratory capacity; however, the incorporation of entropy terms during training can potentially induce instability, particularly in complex continuous control tasks, where the policy update volatility is substantial.

The PPO model incorporates a truncated policy update mechanism, a strategy that has been demonstrated to effectively curtail excessive policy alterations. In addition, the LSTM component serves to further refine the policy update process by storing and recalling the preceding state information. This collaborative approach enables the intelligent entity to exhibit enhanced adaptability to environmental fluctuations. The overarching objective function of the PPO model, subsequent to its integration with the LSTM component, is delineated as follows:

$$J\left(\theta \right)=\mathbb{E}\left[\min \left({\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t,h_t)}{{\pi }_{{\theta }_{\mathrm{old}}}\left(a_t\right|s_t,h_t)}}{A}_t,\mathrm{clip}\left({\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t,h_t)}{{\pi }_{{\theta }_{\mathrm{old}}}\left(a_t\right|s_t,h_t)}},1-\epsilon ,1+\epsilon \right)A_t\right)\right]$$

(6)

In this paradigm, the symbol ${\pi }_{\theta }$ represents the prevailing policy, while $h_t$ signifies a hidden state that is managed by the LSTM to store historical data, thereby ensuring more stable policy updates. The strategy loss function can be delineated as follows:

$$L^{CLIP}\left(\theta \right)=-\mathrm{E}\left[\min (r_t\left(\theta \right)A_t,\mathrm{clip}(r_t\left(\theta \right),1-\epsilon ,1+\epsilon )A_t)\right]$$

(7)

Among them, the formula $r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t,h_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t,h_t)}}$ is the probability sampling ratio (IMSR), which is used to measure the change between the old and new strategies. $A_t$ is the dominance function, which is used to evaluate how good the current action is compared to the average strategy. The CLIP operation limits the magnitude of the strategy change, preventing the strategy from being updated too much and ensuring the stability of the training.

The employment of a hidden state $h_t$ by LSTM facilitates the incorporation of historical information into the decision-making process, thereby mitigating short-term fluctuations and enhancing the strategy gradient’s smoothness. In environments characterized by complexity, SACs may become over-explored, a phenomenon that LSTM-PPO, operating in conjunction with the long-term memory function of LSTM, seeks to counteract by reducing strategy volatility and enhancing training stability.

LSTM-PPO has been demonstrated to exhibit greater adaptability to complex environments in comparison with PPO. PPO makes decisions based solely on the current state, whereas LSTM has the capacity to accumulate historical information by maintaining a hidden state, $h_t$. This capacity enables USVs to take into consideration longer-term environmental trends. The core computational process of LSTM is as follows.

The forget gate determines whether to discard past cell state information:

$$f_t=\sigma (W_f[h_{t-1},x_t]+b_f)$$

(8)

The function of the input gate is to determine the manner in which new information from the current time step is added to the cell state:

$$i_t=\sigma (W_i[h_{t-1},x_t]+b_i)$$

(9)

New information candidate value calculation:

$$\underset{t}{\overset{\sim }{C}}=\tanh (W_C[h_{t-1},x_t]+b_C)$$

(10)

Update cell state $C_t$:

$$C_t=f_t\ast C_{t-1}+i_t\ast \underset{t}{\overset{\sim }{C}}$$

(11)

Output gate calculates the hidden state:

$$o_t=\sigma (W_o[h_{t-1},x_t]+b_o)$$

(12)

Compute the hidden state $h_t$:

$$h_t=o_t\ast \tanh \left(C_t\right)$$

(13)

where $f_t$ is the oblivion gate, $i_t$ is the input gate, $C_t$ is the cell state, $o_t$ is the output gate, and $h_t$ is the hidden state.

The following advantages are yielded by the combination of LSTM and PPO through the above LSTM computation: improvement of time information utilization and enabling the intelligent body to adapt to the long-term changes of the environment rather than relying only on the current state by maintaining the historical observation information. Furthermore, LSTM-PPO enhances the continuity of decision making, a crucial aspect of unmanned craft navigation in complex environments, by mitigating the effects of excessive strategy changes in standard PPO, thereby ensuring smoother trajectory updates through the time-dependent mechanism. Finally, LSTM-PPO adapts to partially observable environments, a critical capability for unmanned craft navigation, by leveraging the time-dependent mechanism to improve stability and navigate complex scenarios with greater precision. In the context of the Partially Observable Markov Decision Process (POMDP), LSTM’s capacity to accumulate historical state information facilitates the formulation of more optimal strategies, even in the presence of missing information. Conversely, PPO has the capability to integrate past observation data into the decision-making process, thereby enhancing the strategy’s resilience in dynamic environments, particularly in scenarios where the unmanned vessel must repeatedly adjust its heading to evade obstacles. The incorporation of past observations into the decision-making process by PPO enhances the strategy’s resilience in dynamic environments, particularly in scenarios where the USV must continuously adjust its heading to evade obstacles.

The following evaluation metrics are employed in this paper to further validate the effectiveness of LSTM-PPO:

• Convergence speed: Statistics on the reward convergence of LSTM-PPO, PPO, and SAC during the training process are used to verify the data utilization efficiency of the LSTM structure in complex environments.
• Obstacle avoidance success rate: The obstacle avoidance success rate of the three algorithms under different environment settings (e.g., obstacle density, etc.) is compared.
• Trajectory smoothness is analyzed by examining the motion trajectories of USVs under different algorithms. This analysis verifies whether LSTM-PPO reduces unnecessary trajectory oscillations and improves navigation smoothness.

2.2. Reward and Penalty Functions

This paper considers the multi-faceted factors involved in the design of reward and punishment functions for unmanned boats performing obstacle avoidance. These factors include navigation towards the target point, obstacle avoidance, and arrival at the target point with minimal time and path cost. In the reward function for obstacle avoidance, different penalties are set according to the risk level of the obstacle, which serves to enhance the success rate of obstacle avoidance of the unmanned boat. Furthermore, this paper integrates the unmanned boat characteristics into the reward and punishment function, thereby facilitating the adjustment of the unmanned boat’s bow direction to enhance the vessel’s efficiency in reaching the designated destination. Concurrently, this approach mitigates the risk of the unmanned boat becoming adrift, thus enhancing the algorithm’s applicability to unmanned boat obstacle avoidance scenarios.

In the reward and punishment function equations, the variables $x_{USV}$ and $y_{USV}$ represent the horizontal and vertical coordinate positions of the unmanned boat USV, respectively, while $x_{goal}$ and $y_{goal}$ represent the horizontal and vertical coordinate positions of the target point, respectively. The variables $x_{obstacle}$ and $y_{obstacle}$ represent the horizontal and vertical coordinate positions of the obstacles detected by the virtual LIDAR, respectively.

As the distance between the unmanned surface vehicle (USV) and the target point decreases, it can be inferred that the USV is approaching the target point. In order to facilitate the navigation of the unmanned boat towards the destination point, it is necessary to define a reward function, designated as $R_{distance}$, which is received when the unmanned boat is in motion towards the target point. It is further required that the reward received is proportional to the distance between the unmanned boat and the target point. The formula for calculating $R_{distance}$ is provided below for reference:

$$R_{distance}={\displaystyle \frac{1}{\sqrt{{\left(x_{USV}-x_{goal}\right)}^2+{\left(y_{USV}-y_{goal}\right)}^2}}}$$

(14)

Once the distance between the unmanned boat and the target point reaches 8 m, the boat will cease movement and decelerate due to the resistance of the water surface. It will then proceed to reach the destination point. When the unmanned boat successfully arrives, the unmanned boat will receive a reward $R_{end}$.

The unmanned boat employs LIDAR sensors to detect localized obstacles, subsequently initiating obstacle avoidance maneuvers upon acquiring pertinent information regarding these obstacles. In this paper, a penalty is imposed on the unmanned boat through $R_{collision}$ when the virtual LiDAR detects that the distance between the unmanned boat and the obstacle is less than or equal to 35 m. This penalty is implemented to train the unmanned boat to complete the obstacle avoidance process. In this paper, the design of $R_{collision}$ considers the fact that obstacles at different distances present varying levels of risk. When the distance between the unmanned boat and the obstacle is closer, the larger the penalty the unmanned boat receives, which encourages the unmanned boat to avoid localized obstacles as soon as possible and enhances safety. The formula for $R_{collision}$ is as follows:

$$R_{collision}=-{\displaystyle \frac{1}{\sqrt{{\left(x_{USV}-x_{goal}\right)}^2+{\left(y_{USV}-y_{goal}\right)}^2}}}$$

(15)

It is imperative that, during the navigation of the unmanned boat, the direction of the bow remains in close proximity to the target point. The angle between the direction of the bow and the line connecting the center of gravity of the unmanned craft to the target point is designated as ${\theta }_{distance}$. A low value of this angle indicates that the bow direction is in close proximity to the target point. In this paper, rewards are provided in the form of $R_{direction}$, with the magnitude of the reward increasing in proportion to the degree of alignment between the bow direction and the target point. Consequently, the bow of the unmanned boat is oriented in the direction of the target point to the greatest extent possible, thereby facilitating more efficient navigation to the target point. The formula for $R_{direction}$ is as follows:

$$R_{direction}=\cos {\theta }_{direction}$$

(16)

Unmanned surface vehicles (USVs) are subject to water surface drag during navigation. When the transverse speed of the USV exceeds the longitudinal speed, the USV may drift in a manner that is dangerous to the vehicle and those in the vicinity. In the event of unmanned boat drift to avoid a penalty, a penalty $R_{drift}$ is applied. The formula for $R_{drift}$ is as follows:

$$R_{drift}=\left\{\begin{array}{c}-1,\left|\mu \right|<\left|vs.\right|\hfill \\ 0,else\hfill \end{array}\right.$$

(17)

In order to reduce the time required for the unmanned boat to reach the designated point, a penalty is applied following each action taken by the unmanned boat. This results in a reduction in the overall sailing time.

It is imperative to note that several of the aforementioned rewards possess varying degrees of influence in the obstacle avoidance process of the unmanned boat. Consequently, these rewards must be augmented with commensurate weights prior to their amalgamation into a definitive reward function. The multiple weights are then calibrated to an optimal magnitude within the algorithm, thereby ensuring an enhanced obstacle avoidance effect. Specifically, the weights function to incentivize the USV to approach the target point for the purpose of avoiding collisions with obstacles, while also encouraging reasonable heading adjustments to reduce trajectory offsets. In the actual experiment, the weights are adjusted via the following methodologies.

1.

Staged adjustment: At varying stages of training, the weights undergo staged adjustments. Initially, the weight assigned to obstacle avoidance is augmented to ensure that the unmanned boat can prioritize obstacle avoidance; as the training progresses, the weight allocated to path optimization is incrementally increased to facilitate more efficient navigation by the unmanned boat.

2.

Heuristic adjustment: according to the actual difficulties encountered by the USV during training (e.g., frequent collisions or large path deviation), we adjust the corresponding weights in real time. When encountering more collisions, we enhance the obstacle avoidance reward; if the trajectory deviates too far from the target, we increase the weight of path optimization.

3.

Cross-validation method: In different experimental setups, we utilize cross-validation to ascertain the optimal combination of weights, and gradually adjust the weights through multiple experiments, and finally select the weight setting that can balance obstacle avoidance and path optimization in most cases. Through these adjustments, the reward function is able to balance the effects of obstacle avoidance and path optimization in different training phases and different experimental conditions, thus improving the overall navigation performance of the unmanned boat.

The overall structure of the reward function is as follows:

$$R={\lambda }^{T}R={\left[\begin{array}{c}{\lambda }_{end}\hfill \\ {\lambda }_{distance}\hfill \\ {\lambda }_{collision}\hfill \\ {\lambda }_{direction}\hfill \\ {\lambda }_{drift}\hfill \\ {\lambda }_{time}\hfill \end{array}\right]}^T\left[\begin{array}{c}{R}_{end}\hfill \\ R_{distance}\hfill \\ R_{collision}\hfill \\ R_{direction}\hfill \\ R_{drift}\hfill \\ R_{time}\hfill \end{array}\right]$$

(18)

In this study, our reward function implicitly considers ocean dynamics factors, such as hydrodynamic drag and wave interference, and guides the unmanned boat to learn a stable navigation strategy through reasonable incentive and penalty mechanisms. However, we recognize that there is still room for optimizing the existing reward design in more complex marine environments, such as those with dynamic obstacles and complex current fields. Subsequent research endeavors will center on broadening the training environment by incorporating dynamic obstacles. This will enable the USV to not only evade static obstacles but also optimize its navigation strategy in a high-speed moving target environment, thereby accounting for the relative speed of obstacles, the maneuvering ability of the USV (e.g., optimal steering radius), and the reasonableness of the obstacle-avoidance path planning, etc., so as to enhance the algorithm’s adaptability and robustness in more complex environments.

In order to achieve the integration of the deep reinforcement learning algorithm and the virtual training ground as outlined in this paper, a three-module design has been developed: the Learning Environment, the Python API (version 2020.3.10), and the External Communicator. The Learning Environment comprises the physical model of the drone boat and the virtualized scene of the real map. The Python API, on the other hand, contains the deep reinforcement learning algorithms employed for training purposes, including the LSTM-PPO algorithm utilized in this paper. It should be noted that, in contrast to the Learning Environment, the Python API is not integrated into Unity. Instead, it is situated externally and communicates with Unity through the External Communicator.

As shown in Figure 5 below, the aforementioned modules were utilized as a foundation for the development of supplementary components, which were integrated into the learning environment with the objective of facilitating the organization of the virtual training ground. The Agent, Brain, and Academy modules were developed to facilitate the creation of a comprehensive learning environment. The Agent can be attached to the physical model of the drone boat in the Unity scene. It is responsible for generating the observation results, executing the received actions, and assigning rewards (positive or negative) at the appropriate time. Each Agent is associated with only one Brain. The Brain encapsulates the Agent’s decision-making logic and decides the actions that should be taken by the Agent under the corresponding circumstances by storing each Agent’s strategy. The Academy is used to direct the observation and decision-making process of the Agent. It allows the specification of several environment parameters, such as the rendering quality. The Brain encapsulates the decision-making logic of the Agent. It does so by saving the strategy of each Agent, which allows it to decide the action to be taken by the Agent in the corresponding situation. In other words, the Brain realizes the function of receiving the observation results and rewards from the Agent and returning the action. The Academy is used to direct the observation and decision-making process of the Agent. It allows the specification of a number of environment parameters, such as the rendering quality and the environment running speed parameters. The External Communicator is placed in the Academy.

In accordance with the aforementioned methodology for the design of modules and add-ons, the global Academy was established within the learning environment. Furthermore, all potential observation variables and action spaces of the unmanned boat within the virtual environment were defined in the Brain, with the objective of associating them with the Agent component. This constituted the final step in the preparation for the implementation of the LSTM-PPO algorithm in the virtual training ground.

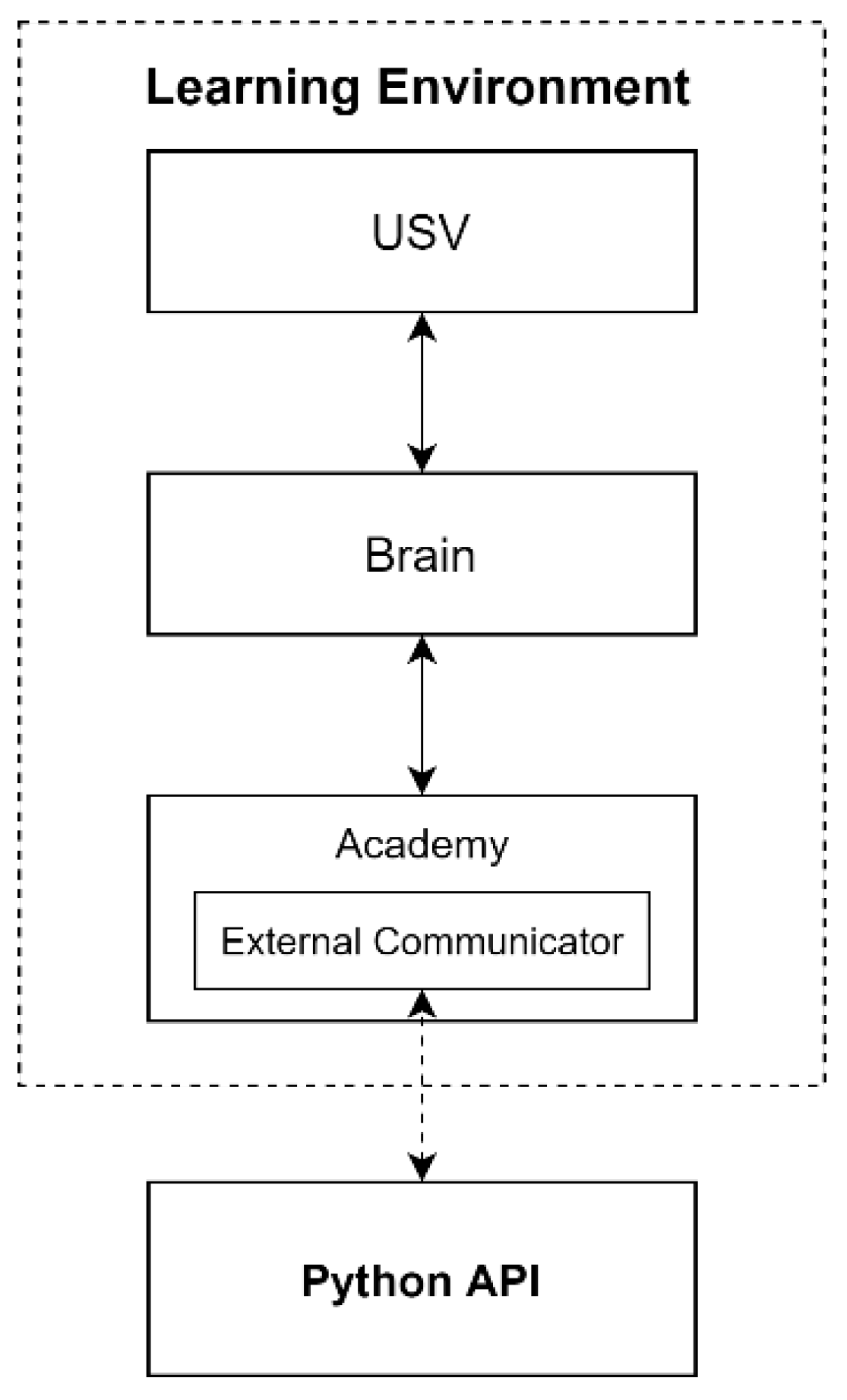
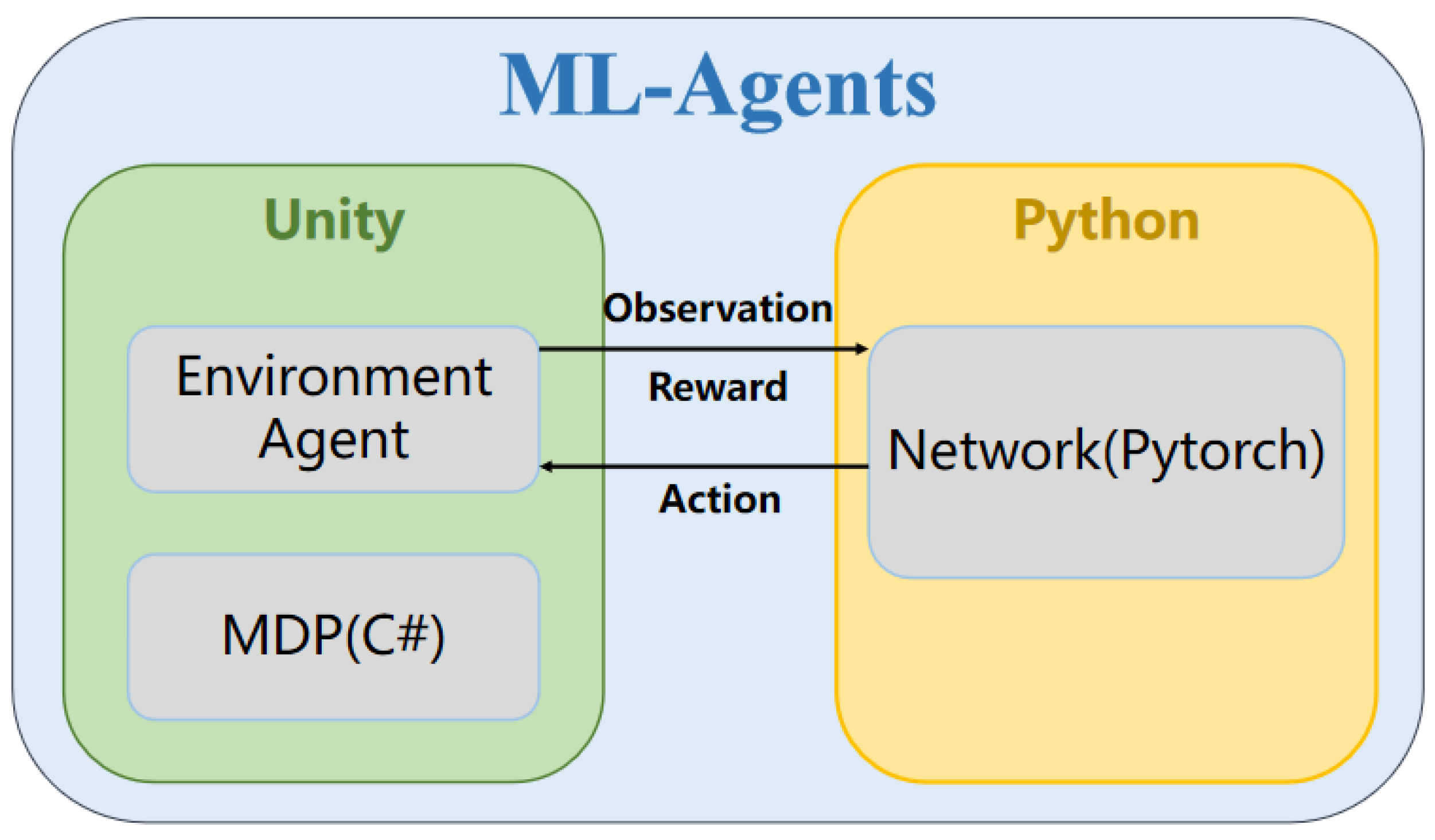
3. Training Environment

Unmanned boats must be capable of navigating complex and changing water environments, such as waves, to successfully complete their missions. Consequently, the construction of a high-fidelity 3D model and navigation environment for unmanned boats is imperative to ensure the reliability of the obstacle avoidance algorithm and the training environment. In this paper, we propose a physical model based on an actual unmanned boat in the Unity3D simulation engine, integrating it with a real water scene to create an unmanned boat navigation environment for training and simulation testing.

Unity’s ML-Agents toolkit is a specialized framework designed for reinforcement learning training, offering a comprehensive environment for developing customized Unity scenarios as Markov decision processes. Utilizing the Gym Wrapper feature, these scenarios can be seamlessly transformed into training environments for reinforcement learning. The integration of Python facilitates the training and optimization of neural networks, enhancing the overall capabilities of the system. The training environment employed in this study is predicated on the ML-Agents framework, wherein a Unity waterscape scene is constructed, a Markov decision process is delineated, and the scene is enveloped within a Gym-style training environment. The engineering framework is shown in Figure 6 below.

3.1. Navigation Water Construction

In order to achieve a high degree of similarity between the simulation training results and the real ship experimental effect, a sea island scene test site was used as a prototype to build a three-dimensional virtual training environment. The Ocean component is employed to construct the water environment, and the sea surface rendered by the Ocean component exhibits a strong sense of realism. This component can simulate the effects of water surface light reflection, reflection, etc., and the range and amplitude of its waves can be customized to control, so as to achieve a more realistic water surface effect. Furthermore, to enhance the simulation’s precision, the water surface is utilized not only for visual rendering but also in conjunction with the Dynamic Water Physics Toolkit to facilitate grid-based hydrodynamics calculations. This enables the USV to be influenced by the actual ocean environment forces. The floating blocks introduced in subsequent training environments function as non-autonomous moving obstacles in regions impacted by hydrodynamics.

In the context of the simulation environment, a multi-faceted approach is employed to enhance the realism of the simulation of the effect of the ocean environment on the USV. This approach involves the consideration of the buoyancy effect (as depicted in Equation (19)) by the USV model, in conjunction with the integration of the hydrodynamic effect, encompassing waves, currents, and other dynamical factors. This multi-faceted approach serves to augment the realism of the simulation environment. The calculation of these forces is predicated on the ocean hydrodynamics model and is facilitated by the Dynamic Water Physics Toolkit of Unity3D [30].

The calculation of buoyancy is based on a meshing method, in which the buoyancy of each triangular mesh is determined by the volume of water discharged from the submerged portion. The following equation illustrates this calculation:

$$F_{\mathrm{buoyancy}}=\sum _{i=0}^n{\{}_{0,\hspace{1em}\mathrm{others}}^{-{\rho }_{\mathrm{fluid}}g·V_g^i,\hspace{1em}\mathrm{if}\mathrm{mesh}\mathrm{is}\mathrm{underwater}}$$

(19)

where ${\rho }_{\mathrm{fluid}}$ denotes the water density, g signifies the gravitational acceleration, n represents the total number of triangular grids in the hull, and $V_g^i$ is the drainage volume of the ith grid.

In order to simulate a realistic marine environment, the dynamic effects of waves and currents are incorporated into the simulation. These forces are calculated based on a hydrodynamic model, as demonstrated in the following equations:

$$F_{wave}=\sum _{i=0}^n{\{}_{0,\hspace{1em}\mathrm{others}}^{C_w{k}_{\mathrm{dot}}^i·n_{\mathrm{boat}}^i\left|\right|v_{\mathrm{wave}}^i|{|}^2{S}_{\mathrm{area}}^i,\hspace{1em}\mathrm{if}\mathrm{the}\mathrm{mesh}\mathrm{is}\mathrm{underwater}}$$

(20)

where $C_w$ is the force coefficient, $n_{\mathrm{boat}}^i$ is the normal vector of the ith grid, $n_{\mathrm{ocean}}$ is the normal vector of the water surface grid, Equation $k_{\mathrm{dot}}^i=n_{\mathrm{boat}}^i·n_{\mathrm{ocean}}$ is the dot product of the two normal vectors, $v_{\mathrm{wave}}^i$ is the velocity of the water flow on the ith grid, and $S_{\mathrm{area}}^i$ is the area of the ith grid.

As shown in Figure 7, This model can be used not only to calculate the wave forces on USVs, but also to further extrapolate the moments generated by waves on USVs, thus improving maneuverability studies.

Conventional water environments are characterized by the presence of obstacles such as reefs, shores, and trees, in addition to water surfaces. Therefore, it is necessary to construct obstacles in virtual environments. In the Unity3D platform, objects are modeled with different levels of fineness. When the camera is positioned at a greater distance from the object in the platform, the coarse model is rendered to minimize the computer’s performance consumption. Conversely, when the camera is positioned closer to the object, the fine model is rendered to ensure the demonstration of more details regarding the terrain, water surface, obstacles, and other elements. This approach ensures the performance of the platform while simulating the real scene with greater fidelity.

Despite the incorporation of hydrodynamic effects within the simulation environment, residual discrepancies persist. The interaction between waves and USV is of particular interest in the context of oceanic simulations, where waves in the actual ocean exhibit more complex non-linear characteristics, such as surges and short-period waves. These characteristics are primarily modeled by gridded hydrodynamic methods in the simulation. In the future, the incorporation of wave models based on Fourier series holds potential in enhancing the realism of wave characteristics. The impact of ocean currents on the simulation is another crucial factor to consider. Presently, the simulation employs a uniform flow field to emulate ocean currents; however, the actual ocean currents possess varying levels of velocity gradients, which may influence the attitude control of the USV. To enhance the precision of the ocean current simulation, a more sophisticated hydrodynamic calculation method (e.g., CFD model) can be implemented.

The presence of floating objects in the actual ocean environment has the potential to impact the stability of USV navigation. The current simulation does not incorporate the dynamics of floating objects, which can be addressed by integrating rigid body dynamics components (e.g., Unity3D Buoyancy Effector).

The aforementioned methods have been demonstrated to effectively bridge the gap between the simulation environment and the real world, thereby enhancing the applicability and reliability of the simulation environment.

3.2. USV Physical Model

In this study, the USV120 USV is utilized as a prototype in a laboratory setting. Its 3D model is designed using SolidWorks software (version 2020), converted into an .FBX file in 3D Max software (version 2020), and imported into the Assets of Unity3D project. This process yields a physical model of the USV that closely resembles the USV120 USV in terms of its appearance and retains the physical characteristics of the unmanned boat. This model is presented in Figure 8.

In order to align the motion process of the virtual unmanned boat with that of the actual unmanned boat, the motion characteristics of the unmanned boat are simulated using the MMG separated ship motion model.

Two right-handed coordinate systems are employed to describe the motion of the unmanned boat, as illustrated in Figure 8. The OXYZ coordinate system is a right-handed system fixed to the Earth’s surface. The XY plane is in the static horizontal plane, and the z-axis is vertically downward and positive. The OXYZ coordinate system is a right-handed system moving with the boat. The origin is at the center of gravity of the unmanned boat. The x-axis points to the bow of the boat, the y-axis points to the starboard side, and the z-axis points to the keel. The longitudinal velocity of the unmanned boat is designated as u, the transverse velocity is represented by v, and the angular velocity of the turning bow is denoted as r.

The mathematical equations that define the motion of a ship according to the MMG model are as follows:

$$\left\{\begin{array}{c}\left(m+m_x\right)\dot{u}-\left(m+m_y\right)vr=X_H+X_P+X_R\\ \left(m+m_y\right)\dot{v}s.+\left(m+m_x\right)ur=Y_H+Y_R\\ \left(I_{zz}+J_{zz}\right)\dot{r}=N_H+N_R\end{array}\right.$$

(21)

In the context of this study, the variables m, $m_z$, and $m_x$ are defined as the mass of the unmanned boat, the longitudinal additional mass of the unmanned boat, and the transverse additional mass of the unmanned boat, respectively. Variables $\dot{u}$ and $\dot{v}$ represent the longitudinal and transverse velocities, respectively. Variables $I_{zz}$ and $J_{zz}$ correspond to the rotational moment of inertia of the hull around the z-axis and the additional rotational moment of inertia. The capitalized letters X and Y represent the components of the force acting on the unmanned surface vehicle (USV) along the x and y axes. The letter N represents the rotational moment of the external force on the USV around the y axis. The subscripts H, P, and R represent the forces on the USV from water, the propeller, and the rudder, respectively.

For the purposes of facilitating calculation, Equation (21) is converted to a form analogous to Equation (22).

$$\left\{\begin{array}{c}\dot{u}={\displaystyle \frac{X_H+X_P+X_R+\left(m+m_y\right)vr}{m+m_x}}\\ \dot{v}s.={\displaystyle \frac{Y_H+Y_R-\left(m+m_x\right)ur}{m+m_y}}\\ \dot{r}={\displaystyle \frac{N_H+N_R}{I_{zz}+J_{zz}}}\end{array}\right.$$

(22)

The objective is to calculate the individual forces and moments acting on the unmanned boat using Unity3D and C scripting. In order to add force, the member function AddRelativeForce is called; similarly, the function AddRelativeTorque is called to add torque. The values situated to the right of the initial and second equations in the aforementioned equation are conveyed to the AddRelativeForce function, while the values situated to the right of the first and second equations are conveyed to the AddRelativeTorque function.

3.3. Obstacle Sensing

Unmanned boats navigating in the surface environment may encounter a variety of obstacles, including islands, floating debris, and other moving vessels. The assurance of secure, obstacle-free navigation is contingent upon the efficacy of collision avoidance strategies in the presence of both static and dynamic obstacles. In the context of actual boat navigation, radar sensors are typically employed to identify potential obstacles. The resulting detection data are then integrated into the unmanned boat’s decision-making system as local environmental information, enabling the autonomous vessel to navigate around these obstacles. The most common radar detection and collision avoidance sensors include ultrasonic radar, millimeter wave radar, marine radar, and LIDAR, among others. Among these, LIDAR is most commonly employed for the purposes of detection and ranging when unmanned boats are sailing. This is due to the fact that it offers a wide detection range, high accuracy in distance and speed detection, and high stability. The ranging sensor utilized in the laboratory is the LIDAR sensor, which is carried on the actual unmanned boat. The virtual LIDAR sensor has also been constructed in the Unity3D simulation platform. This is used to simulate the process of detecting and ranging the local environment and obstacles when the unmanned boat is sailing on the surface of the water. The fluctuations in altitude when sailing an unmanned boat have a negligible impact on the outcome of path planning. Consequently, this paper considers path planning for an unmanned boat as path planning in a two-dimensional plane. In the simulation platform, a virtual 2D LiDAR sensor is constructed on the unmanned boat model. When the unmanned boat navigates in the surface environment, the virtual 2D LiDAR sensor acquires obstacle information and environmental information of the non-navigable area.

C scripts are written in Unity3D to simulate the laser emission and other functions of LIDAR, including obstacle detection, using the Physics.Raycast method. The Physics.Raycast method can be employed to emit a ray of a specified length. If the ray collides with an obstacle within the specified range, it is indicative of the detection of an obstacle within that range. By employing the Physics.Raycast method to generate a multitude of rays from the front of the unmanned boat, which converge to form a plane at a specific elevation, it is feasible to scan and detect obstacles across a range of planes. Figure 9 illustrates the scanning state of the LIDAR on the unmanned boat. The angular range of LIDAR detection is set to 180° in front of the unmanned boat, with a ray emitted every 1°. The distance range of detection, or the length of the ray, is set to 50 m. The LIDAR system generates a series of arrays that store the detection results of each ray. Each array contains a set of numerical data, including the distance to an obstacle, the bearing of the obstacle, and the obstacle’s movement speed. In the absence of an obstacle within the detection range, the values represented in this detection array are all set to the negative integer −1. The local environment and obstacle information stored in the array will be utilized as inputs for the unmanned boat’s obstacle avoidance decision-making process, thereby enabling the unmanned boat to avoid unknown local obstacles.

The accuracy of virtual LIDAR is susceptible to perturbations caused by wave reflections in a surface environment. Furthermore, LIDAR’s capacity to detect underwater obstacles is limited, and its ability to discern low reflectivity or transparent targets is constrained. Additionally, the sensor’s field of view is confined to 180° in the frontal direction, impeding comprehensive environmental perception and potentially leading to the failure to detect obstacles in a timely manner, whether they are situated laterally or posteriorly.

In light of the limitations of virtual LIDAR, the prospect of integrating additional sensors into unmanned vessels in the future is a viable proposition. Such integration would serve to enhance the environmental awareness of the vessel. For instance, the implementation of sonar would facilitate the detection of underwater obstacles, while AIS could be employed to ascertain the position of surrounding vessels. Additionally, the integration of millimeter-wave radar would ensure the capability for all-weather obstacle detection. The incorporation of camera and computer vision capabilities would facilitate the identification of significant targets, such as sea beacons and docks. The integration of these disparate sensors promises to provide a more comprehensive environmental picture and enhance the reliability of obstacle avoidance decisions.

In the future, improvements in this field could include the implementation of multi-sensor fusion algorithms, which would integrate data from different sensors to create a more accurate environment perception model. Concurrently, the incorporation of deep learning technology would optimize target detection capability, thereby improving the decision-making accuracy in complex environments. Through these optimization means, the intelligent body could better adapt to the real marine environment and improve the reliability of the obstacle avoidance system.

4. Simulation Verification

In this paper, a challenging route is selected within the aforementioned constructed refined water environment, as illustrated in Figure 10. The yellow circle represents the initial point of departure for the USV, while the red circle denotes the final destination. Firstly, experiments are conducted to verify convergence with varying numbers of training iterations along the route. Secondly, experiments are carried out to compare the proposed algorithm with the more commonly used A2C, SAC, and PPO algorithms. Finally, experiments are conducted to verify the algorithm’s adaptability to unknown environments by setting up multiple floats and floats as shown in Figure 11.

The placement of these obstacles was guided by the following criteria:

• Variety of obstacle distribution: The algorithm was tested for its ability to adapt to complex distributions of static obstacles, with fixed obstacles (i.e., floats) and randomly generated obstacles (i.e., floats) utilized for this purpose.
• Path complexity control: The density and distribution of obstacles were adapted in different experimental environments to ensure that there was a progressive increase in difficulty from simple environments (no obstacles) to complex environments (high density of obstacles). This was performed to test the algorithm’s ability to generalize across different environments.
• Path feasibility: The feasibility of the path was evaluated to ensure that after obstacles were placed, a reasonable and feasible path still existed, allowing the USV to arrive at the target point through reasonable decision making without falling into an unsolvable state.

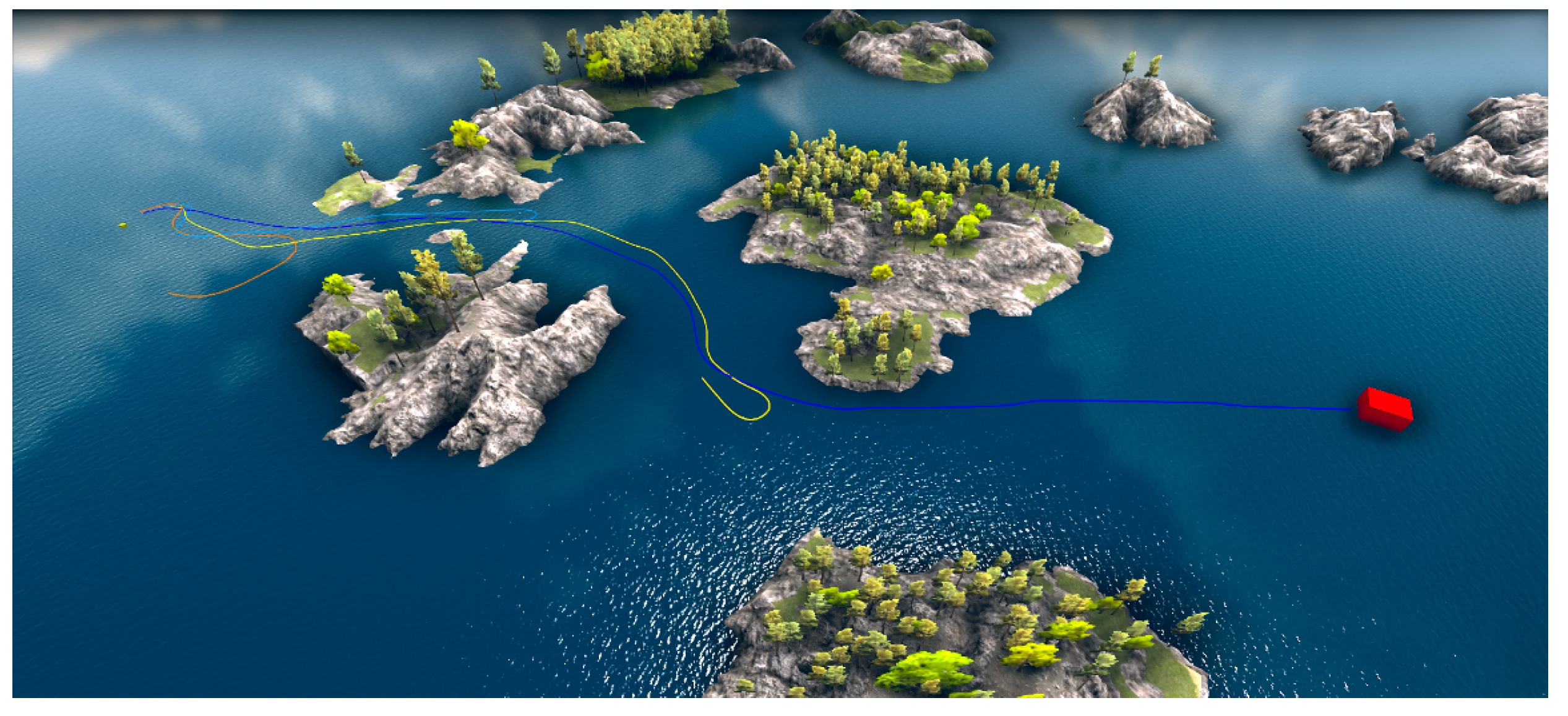
4.1. Comparison of LSTM-PPO, PPO, SAC, and A2C Algorithm Sailing Experiments

The LSTM-PPO algorithm is evaluated in comparison with the PPO, SAC, and A2C algorithms in a navigational water scenario. This scenario encompasses both a simple water environment, as illustrated in Figure 10, and a complex environment with obstacles, such as buoys, as shown in Figure 11.

In order to comprehensively evaluate the performance of the LSTM-PPO algorithm, the following error metrics are utilized in this paper:

-

Obstacle avoidance success rate: the proportion of unmanned boats that successfully avoid all the obstacles and reaches the target point in multiple experiments.

-

Path length: reflects the path planning efficiency of the unmanned boats in the obstacle avoidance process.

-

Convergence time: refers to the time required for the algorithm to reach stable performance during training.

The algorithms are assessed in terms of their convergence time and path length in Figure 10 and their obstacle avoidance success rate in Figure 11. The evaluation is conducted with the same starting point and target location for all algorithms. The results are presented in

Table 1. Comparison of experimental results of algorithms. * Number represents the algorithm used in this study.

Algorithm	Convergence Time/h	Path Length/m	Avoidance Success Rate
A2C	2.5	256.34	53.8%
PPO	1.9	224.72	67.4%
SAC	1.8	210.37	63.8%
LSTM-PPO *	1.5	198.52	86.7%

.

The results demonstrate that the LSTM-PPO algorithm, as proposed in this paper, reduces the average convergence time by 21.5% in comparison to the other three deep reinforcement learning algorithms. Furthermore, the average path length is reduced by 18.5%, and the success rate of obstacle avoidance is enhanced by approximately 20% in the constructed fine-grained and complex environment. Accordingly, the algorithm presented in this paper is designed to enhance the search efficiency and rationality of the unmanned boat’s path planning when navigating around obstacles.

The reward value alterations throughout the training process of each algorithm are illustrated in Figure 12. The horizontal axis in the figure represents the number of training rounds, and the vertical axis represents the normalized result of the training reward value. It can be observed that the LSTM-PPO algorithm exhibits the most rapid convergence speed and the least degree of fluctuation after reaching convergence, in comparison to the other three deep reinforcement learning algorithms. This indicates that this algorithm demonstrates an effective obstacle avoidance effect and high stability.

The results of the experiments, which demonstrate the path planning and obstacle avoidance trajectories of the four algorithms, are presented in Figure 13. Figure 13 illustrates the trajectories of the PPO and SAC algorithms, represented by light blue and yellow, respectively. It can be observed that the unmanned boat employs a strategy of deviating from obstacles to avoid them, which may result in reduced efficiency. The dark blue trajectory represents the A2C algorithm, and it can be seen that the unmanned boat navigates between obstacles, which may increase the risk of collision. It can be seen that all three are not applicable to the obstacle avoidance and path planning of the actual unmanned boat. The trajectory obtained by the unmanned boat when using the LSTM-PPO algorithm is represented by the red line segment in Figure 13. It can be concluded that reasonable obstacle avoidance results can be achieved.

In order to ascertain the experimental nature of the algorithm in an unknown environment, obstacles such as floats and pontoons are incorporated into the refined simulation environment. The successful and unsuccessful trajectories in the obstacle avoidance process are then intercepted, as illustrated in Figure 14. When the unmanned boat encounters obstacles, it is deemed to have failed in its obstacle avoidance attempt. As evidenced by the data in Table 1, the LSTM-PPO algorithm exhibits the highest success rate in obstacle avoidance within the refined simulation environment, demonstrating notable adaptability.

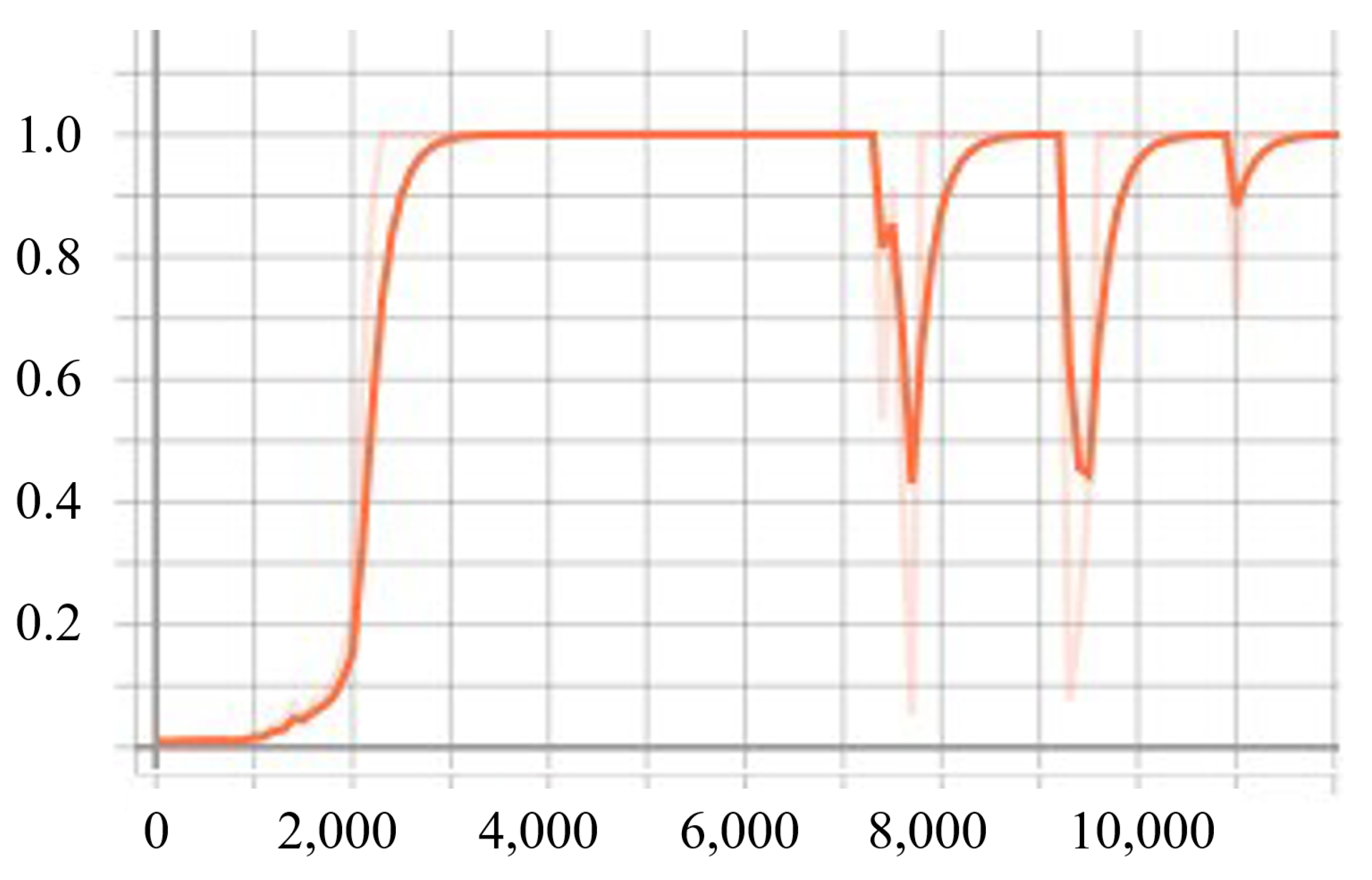
4.2. Algorithm Convergence Verification

In order to ascertain the convergence of the algorithm, Figure 15 illustrates the simulation results for training times of 50, 100, 1000, and 4000 (corresponding to the curves depicted in orange, yellow, cyan, and blue, respectively, in the figure). It is evident that the unmanned boat is unable to reach the intended destination effectively at the outset of the training period, primarily due to the lack of sufficient learning. With the progression of training, the unmanned boat demonstrates an emerging capacity for obstacle avoidance, although its path planning abilities remain relatively limited. Following 4000 iterations of the training process, the unmanned boat demonstrates a markedly enhanced capacity for path planning and obstacle avoidance. It is now able to navigate safely around obstacles and reach its destination via the optimal route.

Figure 16 illustrates the alteration in reward value throughout the training process of the LSTM-PPO algorithm. The horizontal axis in the figure represents the number of training rounds, and the vertical axis represents the normalized result of the training reward value. As the number of training instances increases, the reward value obtained by the unmanned boat gradually approaches the maximum value, exhibiting a certain degree of fluctuation within a defined range. Once the reward value has reached convergence, it can be concluded that the unmanned boat has demonstrated effective local path planning capabilities and has successfully navigated through a variety of environmental obstacles to reach the designated target point.

5. Results and Discussion

5.1. Analysis of the Failure Reasons of SAC, PPO, and A2C Algorithms

A rigorous examination of the outcomes will be undertaken to elucidate the underlying causes of the failure of each algorithm.

Excessive exploration, resulting in bypass, has been identified as contributing to the failure of SAC. The data analysis is presented below.

The convergence time was found to be 1.8 h, which is 20% slower than that of the LSTM-PPO. This suggests that the training efficiency is lower. The path length was determined to be 210.37 m, which is 6.0% longer than that of the LSTM-PPO. This indicates that the path planned by SAC has a detour problem. The success rate of obstacle avoidance was found to be 63.8%, which is 22.9% lower than that of LSTM-PPO, indicating that SAC is unable to avoid obstacles stably.

The failure of the strategy can be attributed to several factors. Primarily, the entropy regulation mechanism of SAC leads to an over-exploratory strategy that hinders the ability to converge rapidly. Additionally, the training process exhibits significant fluctuations, as illustrated in Figure 10, reward curve. In the process of obstacle avoidance, the over-exploratory behavior of SAC results in unnecessary detours by the unmanned boat during navigation, thereby increasing the navigation distance (the path is 6.0% longer than that of the LSTM-PPO). The instability in the decision-making process of SAC contributes to an obstacle avoidance success rate of only 63.8%, which is significantly lower than the 86.7% success rate achieved by the LSTM-PPO.

Conservative decision making and redundant obstacle avoidance paths have been identified as contributing to the failure of PPO. The data analysis is presented below.

The convergence time was found to be 1.9 h, which is 26.7% longer than that of LSTM-PPO. This result indicates that PPO requires a more extended training period. The path length was determined to be 224.72 m, which is 13.2% longer than that of LSTM-PPO. This suggests that the path planned by PPO is more cautious and differs from the optimal route. The success rate of obstacle avoidance was found to be 67.4%, which is 19.3% lower than that of LSTM-PPO, indicating that PPO is less adaptive in the obstacle avoidance task.

The failure can be attributed to several factors. Primarily, the policy update limitation of PPO results in the USV’s conservative decision making, leading to over-avoidance during obstacle avoidance. This, in turn, results in an additional 13.2% growth in the path. While PPO converges faster than SAC, it is still 26.7% slower than LSTM-PPO, primarily due to the limitation of the step size of its policy optimization, which leads to low learning efficiency. The success rate of obstacle avoidance is 67.4%, which is 19.3% lower than that of LSTM-PPO, indicating that PPO is unable to make the best decision in complex environments.

Simple decision making and ease of selection of dangerous paths have been identified as contributing to the failure of A2C. The data analysis is shown below.

The convergence time was found to be 2.5 h, which is 66.7% longer than that of the LSTM-PPO algorithm, which is the slowest among all algorithms. The path length was determined to be 256.34 m, which is 29.1% longer than that of the LSTM-PPO algorithm. This finding indicates that the path planned by A2C is extremely inefficient. The success rate of obstacle avoidance was 53.8%, which is 29.1% lower than that of the LSTM-PPO algorithm. This finding suggests that A2C is more prone to collisions and exhibits the poorest obstacle avoidance ability.

The failure can be attributed to the synchronization update mechanism of A2C employing a simplified decision-making approach, prompting the USV to select the shortest but high-risk path in complex environments. This ultimately increases the probability of collision (obstacle avoidance success rate of only 53.8%). The reward value of A2C fluctuates significantly during the training process, and it exhibits the slowest convergence speed (2.5 h), which is 66.7% slower than the LSTM-PPO, indicating that it possesses a very low learning efficiency. Due to the inadequate strategy updating method of A2C, it is unable to fully learn a reasonable obstacle avoidance strategy during the training process, and the final path is the worst.

5.2. Analysis of LSTM-PPO Success Reasons

The high success rate of LSTM-PPO can be attributed to the LSTM structure’s capacity to store historical information and memorize the environmental distribution of obstacles. This enables the USV to make a timelier decision regarding obstacle avoidance. The LSTM’s long-term memory capability facilitates USVs’ ability to maintain stable decision making in complex environments, thereby avoiding the frequent path adjustments that are characteristic of SAC, PPO, and A2C. The high success rate of LSTM-PPO can be attributed to the following factors.

The objective is to enhance the convergence speed and reduce the training time. The convergence time of LSTM-PPO is 1.5 h, which is 16.7% faster than SAC, 26.7% faster than PPO, and 66.7% faster than A2C. LSTM can utilize historical data more efficiently, which contributes to a more stable training process and faster convergence speed.

Regarding the optimization of routes and the minimization of sailing time, the mean path length of LSTM-PPO is 198.52 m, which is 6.0% shorter than SAC, 13.2% shorter than PPO, and 29.1% shorter than A2C. LSTM optimizes the planning of routes through the utilization of long-term memory, thereby reducing unnecessary detours and enhancing sailing efficiency.

The success rate of obstacle avoidance is highest for LSTM-PPO, which achieves 86.7% success, significantly surpassing the rates of A2C (53.8%), SAC (63.8%), and PPO (67.4%). This outcome demonstrates that LSTM enhances the stability of obstacle avoidance decisions by leveraging long-term memory, thereby empowering the USV to formulate optimal path planning in complex environments.

5.3. Convergence Speed and Stability Analysis

Convergence speed comparison: the LSTM-PPO converges within 1.5 h, which is 16.7%, 26.7%, and 66.7% faster than SAC, PPO, and A2C, respectively. SAC and A2C converge slower due to the unstable way of policy updating and the large fluctuation of the reward value during the training process (see Figure 10 for the reward curve).

Fluctuations in the reward value have been demonstrated to have a significant impact on stability. The LSTM-PPO has been shown to exhibit the least fluctuation in reward value during training, leading to the most stable decision making after convergence. In contrast, SAC and A2C have been observed to demonstrate substantial fluctuations in the reward value after training. This suggests that their strategies are unstable, resulting in a suboptimal obstacle avoidance ability.

5.4. Research Limitations

A review of existing research highlights several limitations of LSTM-PPO that must be considered for its practical application. Although the model shows superior obstacle avoidance in simulation, there are still key challenges to address when deploying it in real-world environments.

This study examines the computational complexity and real-time performance of the LSTM structure, which increases computational overhead and may hinder real-time decision making on embedded devices with limited computing power. Additionally, the study does not incorporate COLREG rules, the international collision avoidance regulations at sea, which may lead to decisions that deviate from established navigation norms in multi-boat scenarios. The study also highlights limitations in applicability and scalability. The experiments focus solely on single-boat obstacle avoidance, and the adaptability of LSTM-PPO in multi-task (e.g., cruising, target tracking) and multi-boat collaborative environments remains unaddressed. Furthermore, the simplified simulation environment excludes real-world marine factors like wind, waves, and currents, and its simplified dynamics may impact practical applications.

5.5. Directions for Future Improvement

To ensure the suitability of LSTM-PPO for real-time USV obstacle avoidance, its computational efficiency must be optimized in several areas. The complexity of the LSTM model can be reduced through techniques such as Knowledge Distillation and Pruning, ensuring its compatibility with low-power embedded devices like the NVIDIA Jetson Nano. Additionally, real-time performance can be enhanced by incorporating multi-threaded computation or TensorRT acceleration, which would speed up obstacle avoidance decision making. Furthermore, testing on different embedded platforms, such as the NVIDIA Jetson AGX Xavier and ARM processors, is necessary to evaluate the model’s applicability across various hardware. Based on these tests, the model structure can be further optimized to improve performance on specific platforms.

Integration of COLREG Rules: Future work will focus on enhancing the practical applicability of LSTM-PPO by integrating COLREG rules into its obstacle avoidance decision-making process. The proposed framework will incorporate COLREG rules into the training, including constraints like starboard avoidance and overtaking prevention, to be embedded in the reward function. This integration is expected to improve the USV’s adherence to navigational norms, ensuring safe and efficient operation in complex maritime environments. The combination of reinforcement learning and COLREG rules will play a key role in developing obstacle avoidance strategies that comply with international maritime regulations. Additionally, future research will involve the creation of multi-vessel scenarios, such as rendezvous, pursuit, and overrun situations, in simulations to assess LSTM-PPO’s decision-making capabilities under these rule constraints, further improving its real-world applicability.

Extension of LSTM-PPO to Multi-Task USV Applications: The extension of LSTM-PPO to multi-task USV applications involves expanding the current single-obstacle avoidance task to include additional tasks, enhancing the algorithm’s generalizability. Multi-task learning will train LSTM-PPO to handle tasks such as cruising, target tracking, and obstacle avoidance, enabling adaptation to a wider range of aquatic scenarios. With an adaptive reinforcement learning approach, the USV will dynamically adjust its strategy based on task requirements, improving overall flexibility. Furthermore, future testing will incorporate more complex tasks, such as underwater target search and environmental monitoring, to assess the multi-task adaptability of LSTM-PPO.

Research on Multi-Vessel Collaboration Strategies for Enhanced Group Obstacle Avoidance: As future USVs are required to operate in multi-vessel collaborative environments, optimizing LSTM-PPO for multi-agent scenarios is crucial. Adopting a Multi-Agent Reinforcement Learning (MARL) framework will enable multiple USVs to share information, coordinate obstacle avoidance, and improve flotilla collaboration efficiency. A distributed decision-making system will explore how decentralized learning can enhance coordination among USVs, making the system suitable for unmanned ship formation tasks. Additionally, multi-vessel simulation experiments will be conducted to assess the obstacle avoidance and path optimization capabilities of LSTM-PPO in such environments, further enhancing its practical applicability.

Real-Water Testing and Environment Adaptation Optimization: In order to ensure the applicability of LSTM-PPO in real-water environments, the following can be carried out in the future:

• Real-Water Testing: Test LSTM-PPO in different waters (lakes, offshore, etc.) and analyze the obstacle avoidance effect under the interference of wind, waves, and water currents.
• Optimization of dynamic model: The incorporation of wind, wave, and current modeling within the simulation environment is recommended. This will enable LSTM-PPO to adapt to diverse marine environments and enhance its practical application capabilities.

The integration of multi-sensor data, encompassing LiDAR, radar, and vision sensor data, is a critical component in enhancing the environmental perception capabilities of LSTM-PPO. This integration facilitates the augmentation of LSTM-PPO’s adaptability to complex environments, thereby ensuring its effective functioning in dynamic and varied contexts.

6. Conclusions

In this study, an autonomous obstacle avoidance algorithm based on LSTM-PPO is proposed for an unmanned craft, which addresses the problems of unstable and insufficient adaptability of traditional SAC and PPO in complex environments, stores historical obstacle distribution information through LSTM structure to improve the unmanned craft’s understanding of the environment and the coherence of the obstacle avoidance decision, and combines with the optimized reward function to improve the training efficiency. Comparison experiments are conducted in the constructed refined water environment, and the results show that LSTM-PPO can complete the autonomous obstacle avoidance task more efficiently and stably, compared with A2C, SAC and PPO, and shows significant advantages in convergence speed, path optimization, and success rate of obstacle avoidance.

While the present study demonstrates the effectiveness of the algorithm in a simulated environment, certain limitations remain. The experimental setup mainly involves static obstacles and non-autonomous dynamic obstacles, and its validity in real-world water bodies has yet to be verified. Future work should assess its performance under various environmental conditions, such as wind, waves, and current interference, while optimizing the dynamics modeling to improve the algorithm’s robustness. Additionally, the scope of the present study is limited to single-boat obstacle avoidance, but future extensions could include multi-boat interaction scenarios using Multi-Agent Reinforcement Learning (MARL), enabling collaborative obstacle avoidance and enhancing group operations of unmanned boats. Furthermore, the current training data are primarily from simulations, but incorporating real-world data in future studies will improve the model’s ability to navigate complex environments. Integrating the COLREG rules into the reward function will further ensure the safety and usability of unmanned boats in real-world applications.