Abstract
The hydrodynamic coefficients of underwater robots can be used to evaluate their maneuverability and motion stability and to design motion controllers, thereby reducing experimental time and costs. In this paper, an Autonomous Underwater Vehicle (AUV) with a negative-lift profile is designed. The spatially constrained motion method, combined with neural networks, is utilized to identify all the hydrodynamic coefficients in the standard hydrodynamic equations of the AUV. Subsequently, based on the goodness-of-fit, the significance of the hydrodynamic coefficients is evaluated to yield a simplified hydrodynamic equation. Given the cost constraints, it was not feasible to obtain precise experimental data on hydrodynamic coefficients to validate the accuracy of the CFD calculation method. Therefore, the hydrodynamic coefficients were used to construct a dynamic model for the AUV, and an MPC controller was designed based on this model. Finally, simulations and pool tests were conducted on the AUV, and a comparative analysis of the simulation results with the pool test results revealed that although there were certain errors in the calculation of the hydrodynamic coefficients, the controller constructed within this margin of error was still capable of effectively controlling the AUV. This fully demonstrates the feasibility and applicability of using CFD methods to calculate hydrodynamic coefficients and establishing model predictive control methods based on these coefficients in practical applications.
1. Introduction
Optimizing and accurately identifying the hydrodynamic coefficients of AUVs are the foundation for the subsequent design and analysis of motion control [1]. Precise and simplified hydrodynamic equations can help researchers understand the hydrodynamic performance of the underwater vehicle, and further research based on this understanding can better identify potential issues. Additionally, evaluating the stability and maneuverability of underwater vehicles requires the use of hydrodynamic coefficients, and analyzing and improving these coefficients can enhance the stability and robustness of underwater robots.
Among the methods for identifying hydrodynamic coefficients of underwater robots, commonly used ones include model testing, semi-theoretical and semi-empirical methods, as well as computational fluid dynamics (CFD) numerical simulation methods [2], and the recently emerging deep learning-based methods [3]. Model testing is currently the most accurate research method for identifying hydrodynamic coefficients, but it requires a long test period and high cost, making it difficult to apply efficiently in the early design stages of AUVs [4,5,6,7]. The semi-theoretical and semi-empirical estimation method possesses strong economic efficiency and practicality, but its applicability and accuracy are difficult to guarantee. For underwater vehicles with complex shapes and numerous appendages, the calculation errors tend to be larger [8]
With the rapid development of the computer industry, computing power has now met the demands of most CFD models for hydrodynamic coefficient identification. Therefore, the use of CFD numerical simulation methods for identifying hydrodynamic coefficients has gained widespread application. Towing tank numerical simulation is a commonly used method in CFD simulation technology for studying underwater vehicles [9]. Although traditional towing tank numerical simulation can accurately solve relevant hydrodynamic coefficients, such methods require multiple modeling and solving processes to obtain several hydrodynamic coefficients, which increases the computational cycle and the cost of vehicle design. However, the spatial captive model method can calculate all the hydrodynamic coefficients in the standard equation through a single modeling process [10]. After solving all the hydrodynamic coefficients, the standard equation can be simplified through important analysis, which addresses the difficulty of simplifying complex-shaped vehicles. Compared to traditional methods that involve multiple modeling and combinations of different techniques, the spatial captive model method offers superior overall stability, as it requires only one modeling process.
The determination of AUVs’ hydrodynamic coefficients, whether through experiments or CFD, inherently involves a certain degree of uncertainty. During mission execution, AUVs are further subjected to complex, variable, and unpredictable ocean current disturbances. Additionally, the inherent strong nonlinearity and high coupling characteristics of their dynamic models make the control task particularly challenging. Model Predictive Control (MPC), as an advanced control strategy, effectively constrains the inputs and states of AUVs within physical or safety limits, ensuring that the system state remains within the designated constraints while enhancing the efficiency and effectiveness of control inputs through the solution of optimization problems.
To address the uncertainties in external environmental disturbances, one can design a disturbance observer [11] or utilize a Kalman filter-integrated navigation and guidance algorithm [12] to estimate the disturbance caused by uncertain water flow disturbances. These estimates are then integrated into a nonlinear MPC controller, effectively compensating for the disturbances. As for the imprecisions in parameter estimation, an adaptive control method can be adopted to enhance the nonlinear MPC, ensuring the asymptotic convergence of the control system even in the presence of uncertainties [13]. Wu et al. proposed a data-driven tracking control method via a fuzzy state observer for AUVs under uncertain disturbances and time delays, showcasing the effectiveness of adaptive control strategies in handling environmental uncertainties [14]. The application of MPC in AUVs primarily focuses on the following areas: AUV motion control. Nonlinear MPC (NMPC) in AUVs achieves higher model accuracy at the cost of reduced computational efficiency, and the high computational requirements often limit its direct application in real-time control systems. A strategy to improve computational efficiency is to simplify the complexity of the MPC model. Linearized MPC [15] or decoupling and reduced-order methods applied to AUV models [16] significantly enhance computational efficiency by reducing the computational burden and have achieved certain successes in practical applications. However, for highly nonlinear and strongly coupled systems like AUVs, these two methods may fail to accurately capture their internal dynamic characteristics, potentially even introducing significant deviations, resulting in unsatisfactory control performance. NMPC is employed to handle nonlinear dynamics and achieve high-precision tracking. Robust MPC (RMPC) or Stochastic MPC (SMPC) are introduced to address environmental uncertainties [17,18]. AUVs need to plan paths and avoid obstacles in complex environments. By incorporating obstacle constraints into the MPC optimization problem, MPC can be combined with graph search algorithms or potential field methods to enable obstacle avoidance and global path planning [19,20]. For multiple AUVs working together to complete tasks, a Distributed MPC (DMPC) framework is designed, where each AUV independently optimizes and shares information, enabling multi-AUV formation control [21] or collaborative detection [22]. Most importantly, MPC is a model-based optimal control algorithm. By including an energy consumption term in the objective function, MPC allows AUVs can optimize energy usage to extend mission duration [23,24]. Some scholars have pointed out that research on MPC for vector-propelled AUVs remains insufficient [25]. Sriharsha Bhat [26] noted in their research that their team was the first to achieve real-time MPC control for an agile underactuated AUV. Compared to multi-thruster AUVs, vector-propelled AUVs exhibit higher energy efficiency, but their flexibility and agility are relatively lower, and the control difficulty is greater. Additionally, the hydrodynamic characteristics of underactuated AUVs with unconventional shapes are more complex, and their motion states exhibit strong coupling, which further increases the control difficulty. MPC excels in solving Multi-Input Multi-Output (MIMO) problems and can account for state constraints and physical input constraints of the AUV system, making it highly suitable for controlling such complex AUV systems.
The contributions of this paper are as follows: (1) We designed and developed a negative-lift-shaped AUV capable of rapid diving, which utilizes a single vector thruster for motion control. To the best of our knowledge, there is currently no such AUV with a special shape and vector propulsion capability. (2) To address the challenges of complex hydrodynamic characteristics and the difficulty in obtaining hydrodynamic models for underactuated AUVs with unconventional shapes, this paper proposes a method that combines a spatially constrained motion model with a neural network-based approach to identify all hydrodynamic coefficients in the standard hydrodynamic equations of the AUV. The identified hydrodynamic coefficients can be directly applied to MPC, reducing the workload of hydrodynamic identification through experiments and improving the efficiency of control algorithm design. (3) To achieve automatic control, theoretical modeling of the full AUV’s states is conducted by considering the physical constraints of vector thrusters, and an NMPC is established for real-time prediction and optimization. (4) This paper conducts numerical studies and experiments on the position and attitude responses of the AUV during motion to ensure that the proposed NMPC method can achieve real-time control of the AUV and to validate the performance of the AUV prototype. The findings provide a reference for the design of controllers for future AUVs with special shapes and input constraints.
Section 2 introduces the 3D models of two types of vehicles, the presentation of the standard equations of hydrodynamics, and the CFD numerical simulation model. STAR-CCM+ Marine trial (a trial version) is the CFD software used in this study. Section 3 first elaborates on the modeling method for spatially constrained motion and then explains how neural networks are utilized to identify hydrodynamic coefficients. It further compares the identification results from neural networks with CFD calculations, assessing the accuracy of identification using goodness-of-fit metrics. Lastly, it outlines the process of reducing 88 hydrodynamic coefficient terms for the AUV to 20 key terms. Section 4 focuses on the modeling strategy for MPC: To minimize error introduction, the core of the MPC model employs precise nonlinear six-degree-of-freedom dynamic equations. Additionally, it discusses the practical application effectiveness of MPC. To enhance computational efficiency and performance in real-world applications, this section designs multiple optimized objective cost functions and varying-length prediction horizons, determining the optimal control strategy through simulation analysis. Furthermore, to mitigate the adverse effects of external environmental disturbances on MPC control accuracy, the AUV control tests are specifically conducted in a still-water pool environment.
2. Model Introduction
In this paper, CFD software is used to establish the hydrodynamic model of underwater vehicles and to calculate towing-tank numerical simulations. The modeling process primarily includes the 3D models of two types of vehicles, the presentation of the standard hydrodynamic equations, and the development of the CFD numerical simulation model.
2.1. AUV Model
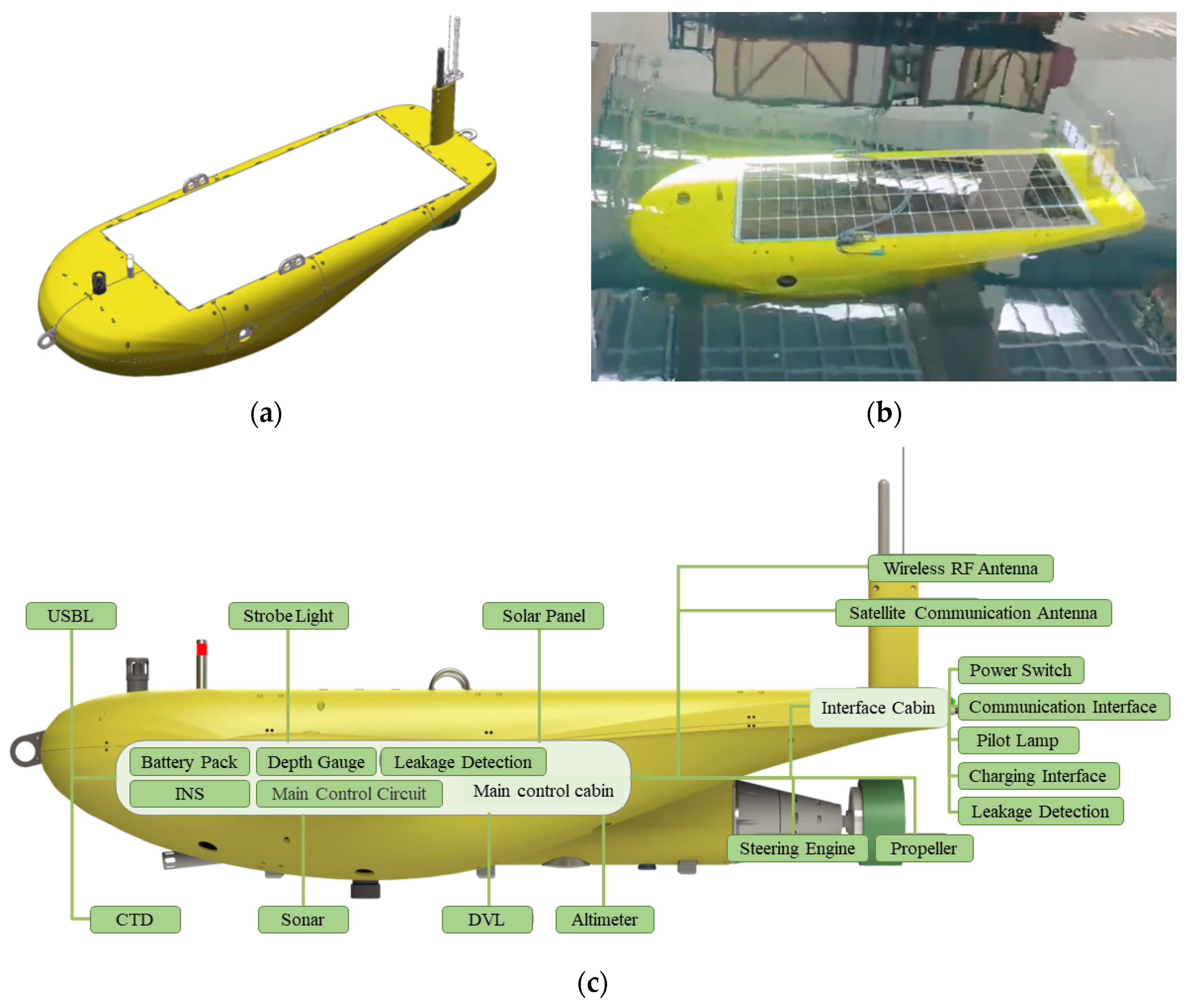
The Institute of Deep-Sea Science and Engineering (IDSSE) has independently developed a complex-profile AUV, as shown in Figure 1. The outer shell of the AUV is made of fiberglass, while the main control cabin and structural frame are constructed from aluminum alloy and incorporate an appropriate amount of buoyancy materials. Compared to the currently mainstream revolving-hull underwater vehicles, this underwater vehicle has an irregular shape, featuring a complex streamlined exterior and a gliding-wing design. This unique design endows the AUV with exceptional hydrodynamic performance, thereby placing more stringent demands on the precision and flexibility of its control system.
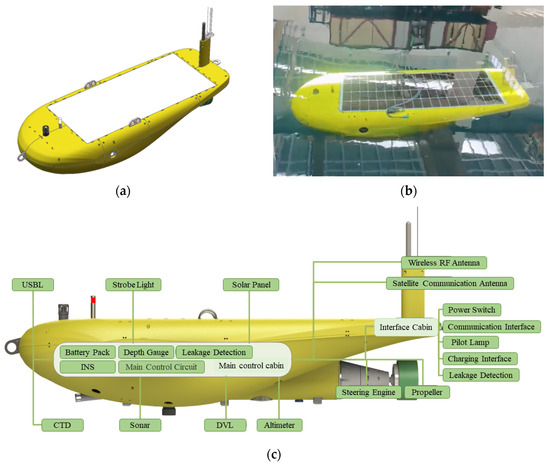
Figure 1.
3D model and actual entity of the AUV: (a) 3D model; (b) actual entity; (c) sensor layout.
The design of this underwater vehicle, which has an irregular shape, is primarily driven by its specific mission requirements. The vehicle is designed to install a horizontal solar panel on its upper surface to enhance endurance, which prevents it from being designed in a conventional torpedo or flat shape. This complex profile AUV can achieve positive buoyancy and negative lift based on its geometric characteristics and physical properties. Specifically, when the vehicle is stationary, it floats on the water surface due to positive buoyancy. However, when the vehicle is cruising at a certain speed, it submerges due to the influence of negative lift. This design allows the vehicle to descend to the desired depth during normal cruising, while in emergencies, it can simply stop moving and float to the surface solely through the action of positive buoyancy. Unlike the approach in this paper, which utilizes negative lift to overcome positive buoyancy, some related studies have explored optimal motion control for AUVs with positive buoyancy [27]. The AUV has a total length of 2.39 m, a beam of 0.83 m, a depth of 0.52 m, a design weight of 210 kg, and a designed positive buoyancy of 1 kg.
2.2. Hydrodynamic Coefficient Motion Equation
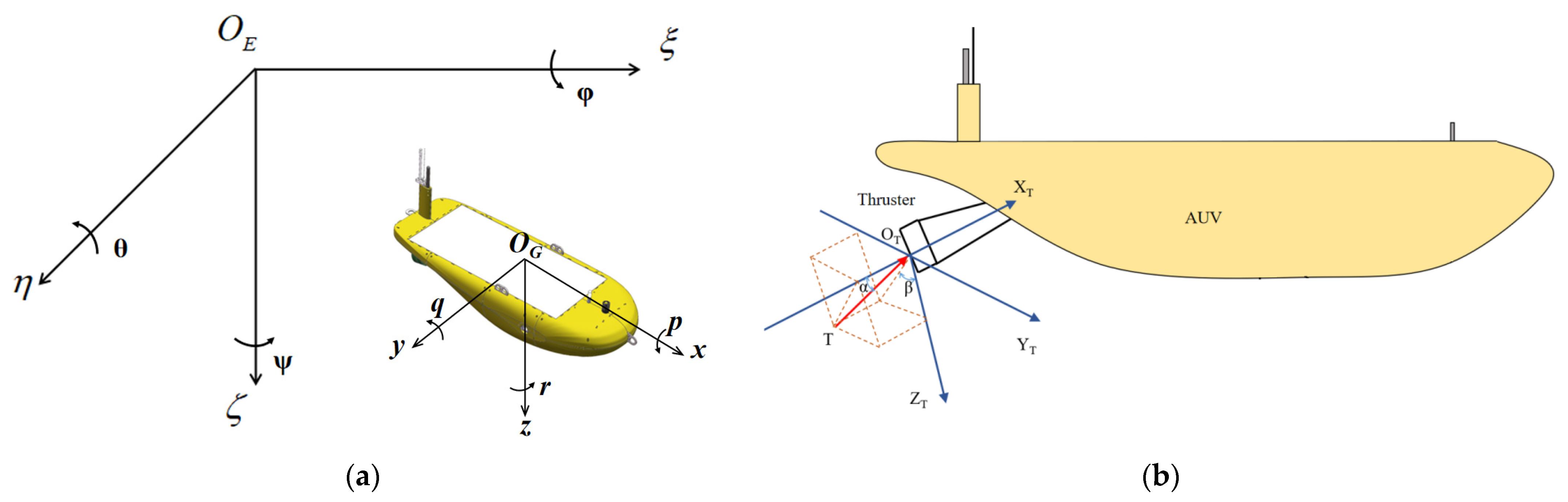
Before delving into the kinematic and dynamic analysis of underwater vehicles, it is imperative to establish an appropriate coordinate system. This paper adopts the coordinate system and notation recommended by the International Towing Tank Conference (ITTC). The following introduction takes the AUV model as an example. As depicted in Figure 2, the study of underwater vehicles typically involves defining two coordinate systems: an inertial coordinate system () and a body-fixed coordinate system ().
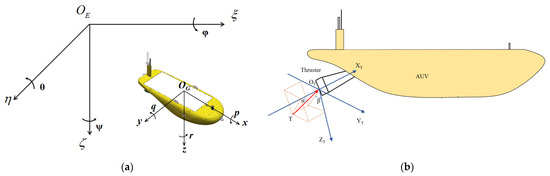
Figure 2.
Description of the coordinate systems: (a) Inertial coordinate system and a body-fixed coordinate system; (b) Thruster coordinate system.
The inertial coordinate system can be selected arbitrarily. Generally, points to the north, points to the east, and points to the center of the earth along the direction of gravity. The origin of the body coordinate system is taken from the center of gravity or geometric center of the underwater vehicle. is parallel to the central axis of the vehicle, pointing forward as positive; is parallel to the geometric datum plane of the vehicle, pointing to the right side of the vehicle; is perpendicular to the plane of and points to the bottom of the vehicle.
The third reference frame is the thruster frame, which defines the thrust force and the relative tilt angles of the thruster and SAUV [T, , ]. The red arrow indicates the thrust T provided by the vectored thruster. The thrust T can be rotated by adjusting α and β. Where , , denotes the distance from the center of gravity of SAUV to the center of the thrust-vectoring mechanism.
The one-dimensional vector F consists of the hydrodynamic force and hydrodynamic torque experienced by the AUV while submerged underwater:
In the formula, represents the projection component of the resultant force on the body-fixed coordinate system , and is the projection component of the resultant torque on the body-fixed coordinate system .
Without considering the influence of factors such as propellers, rudders, gravity, and buoyancy and only focusing on the effect of water on the underwater robot during its movement, the hydrodynamic force and torque of the AUV are functions of velocity , acceleration , angular velocity , and angular acceleration .
In the formula, and are the velocity components and angular velocity components of the AUV’s combined velocity under the body coordinate system axes, respectively. Currently, the most widely used and authoritative hydrodynamic coefficient motion equation for underwater vehicles is , which was published by the Taylor Naval Ship Research and Development Center. The standard equation for hydrodynamic coefficients is established as:
The standard equation for hydrodynamic coefficients is complex, with numerous coupling terms. To obtain all the hydrodynamic coefficients in the above equation, numerous tests would be required, and some hydrodynamic coefficients are difficult to measure using conventional testing equipment. However, the CFD method can yield reliable results without building a physical model of the underwater vehicle, offering the advantage of reducing time and financial costs. Therefore, most researchers consider CFD simulation to be an effective means of optimizing algorithms.
2.3. CFD Model
2.3.1. Governing Equation
The Navier–Stokes equations in CFD encompass three fundamental governing equations: the continuity equation, the momentum equation, and the energy equation. Assuming the fluid is incompressible and adheres to the conservation of mass, the continuity equation is represented as:
Regarding the fluid motion around an underwater vehicle, when it is considered to be viscous flow, the rate of change of momentum in any infinitesimal control volume of the fluid is equal to the algebraic sum of all forces acting on it. The momentum equation is expressed as:
By solving these equations, the behavior of the fluid surrounding the underwater vehicle can be accurately characterized.
2.3.2. Turbulence Model
In turbulence numerical simulation techniques, there are several main methods: Direct Numerical Simulation (DNS), Reynolds-Averaged Navier–Stokes Simulation (RANS), and Large Eddy Simulation (LES). While DNS can theoretically produce the most accurate results, it is not suitable for practical engineering projects due to the excessively large computational resources required. Large Eddy Simulation also demands fine grid division and significant computational resources. Considering computational efficiency and cost, this paper adopts the RANS equations as the fundamental governing equations. However, when solving RANS equations, the number of unknowns in the equations exceeds the number of equations, leading to an unclosed equation set that is unsolvable. Therefore, turbulence models can be added to close the system of equations and enable its solution. In this study, the standard k-ε model is chosen, which has high computational efficiency and good stability, thus being widely used in this field. The model can be described by the following two equations:
where
In the above equation: represents the eddy viscosity; denotes the turbulent kinetic energy; signifies the energy dissipation rate; U is the fluid velocity; and stands for the Hamiltonian operator. The values of other constants are shown in Table 1 below.

Table 1.
Constant values in the k-ε turbulence model.
2.3.3. Calculation Domain
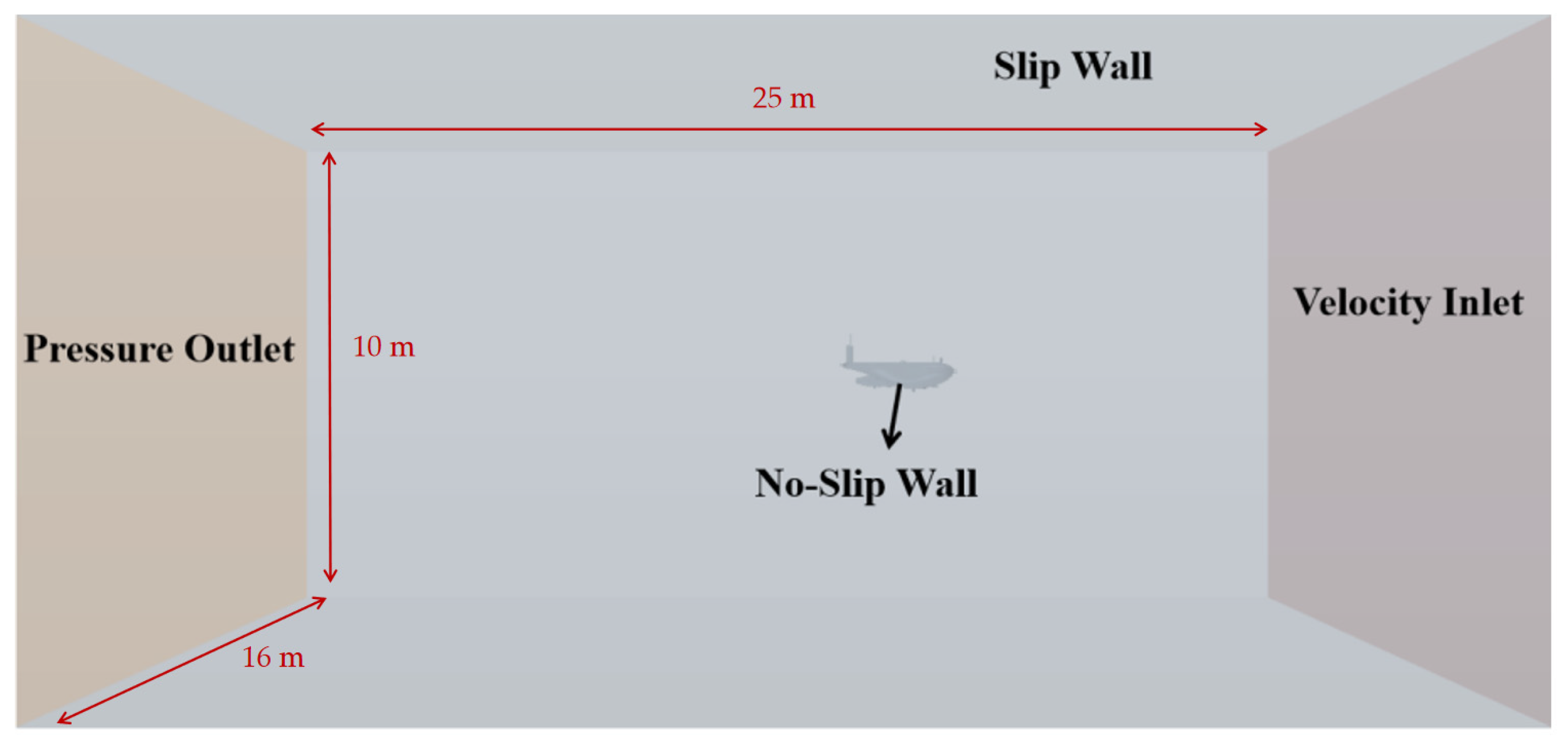
For the calculation of hydrodynamic forces on underwater vehicles, it is first necessary to determine a virtual computational boundary within the computational domain defined by the virtual boundary. Using the concept of relative motion, the movement of the underwater vehicle is transformed into a static state of the vehicle while the surrounding environmental flow field is in motion. This approach simplifies the calculations and saves computational resources. The computational domain for the AUV is a cuboid with dimensions of 25 m in length, 16 m in width, and 10 m in height. The inlet is set as a velocity inlet; the outlet is set as a pressure outlet with a relative pressure of zero; the four perimeter boundaries are set as slip walls; and the vehicle surface is set as a no-slip wall, as shown in Figure 3.
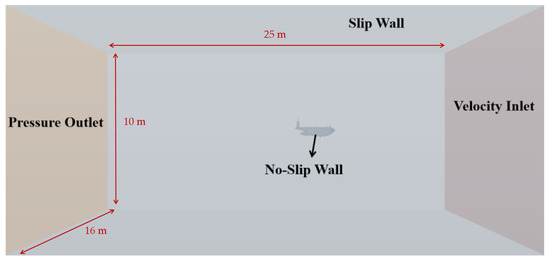
Figure 3.
Schematic diagram of calculation domain.
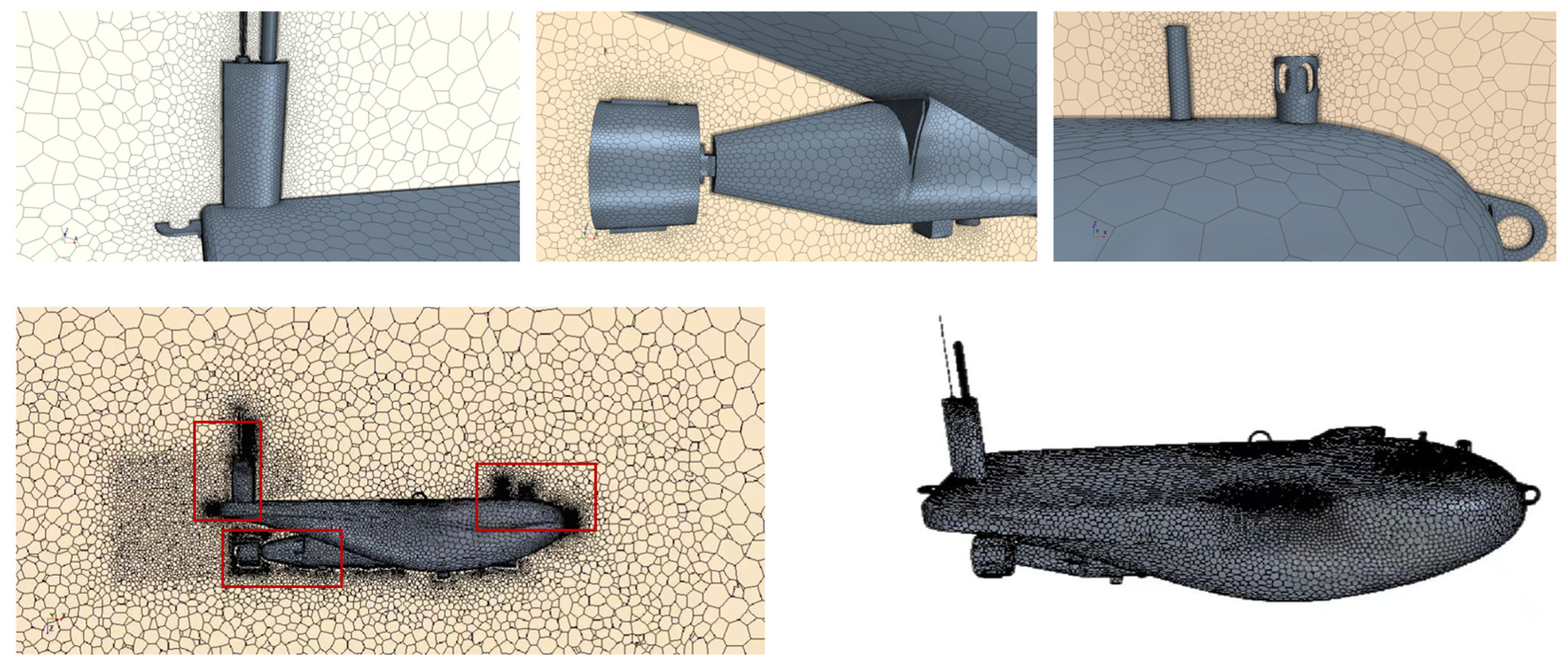
2.3.4. Mesh Generation
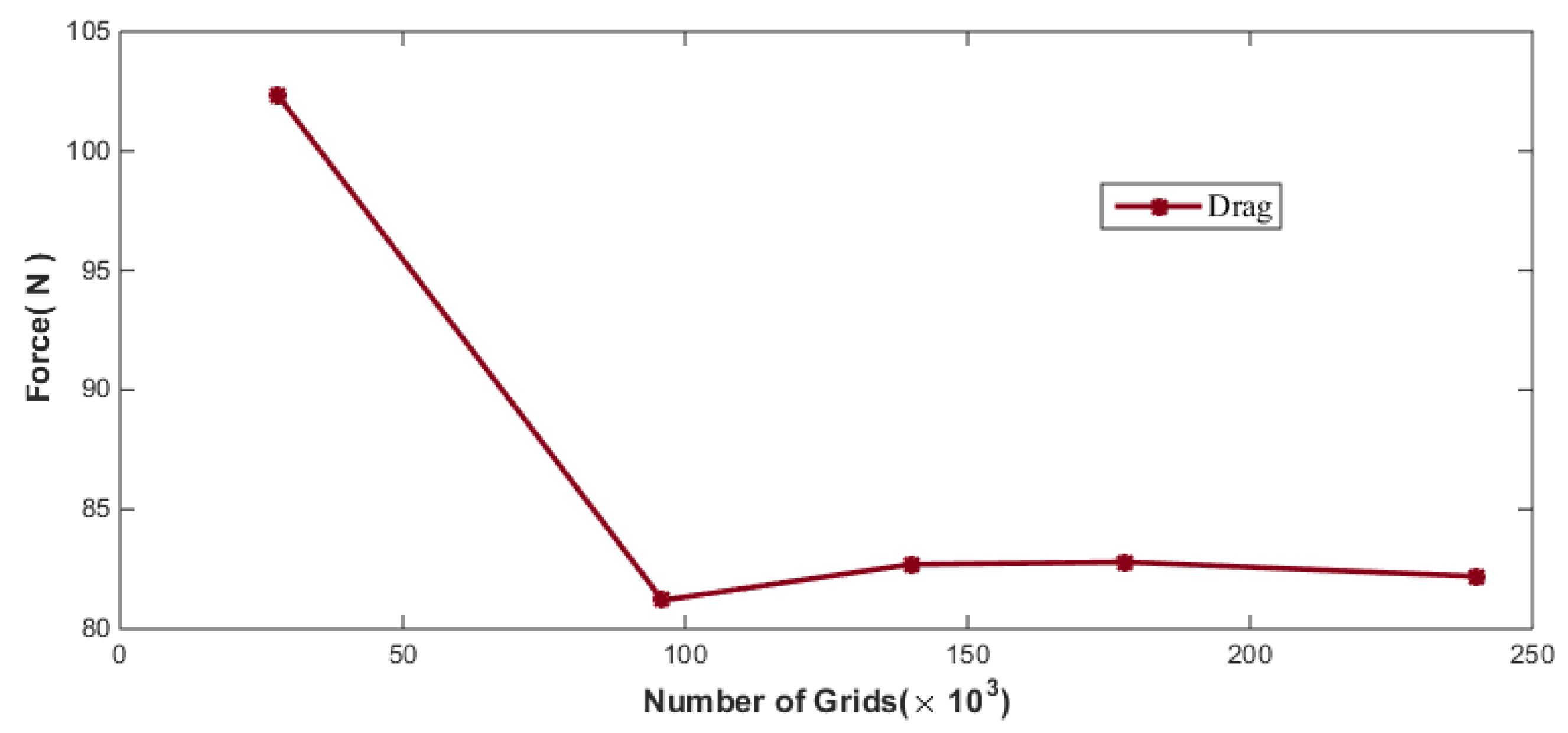
The SAUV has a more intricate shape and possesses a greater number of appendages. By replacing the cut-cell grids in the grid generator with polyhedral grids, the generated grids are better suited to the complex shape of the vehicle. Meanwhile, appropriate grid refinement is required at the appendages and regions with significant shape changes of the vehicle, ensuring a smooth transition in grid density between the refined areas and other regions to enhance computational stability and convergence. If the grid size is too large, the calculations will not be accurate. As the grid is refined, the calculations will approach the true values more closely, but after a certain point, further grid refinement will not significantly improve the results and instead will unnecessarily increase the computational burden on the computer. Therefore, to balance accuracy and computational efficiency, a grid independence test is necessary before conducting CFD simulations. The resistance encountered by the SAUV at a speed of 2.5 kn for different grid configurations was tested, and the calculation results are shown in Figure 4 below.
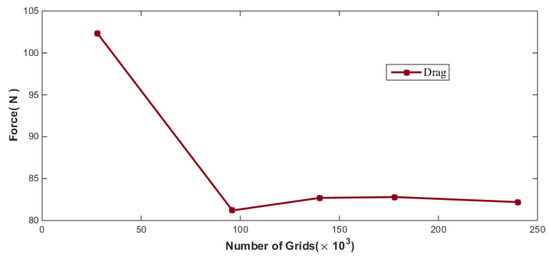
Figure 4.
The variation in SAUV calculation results with the corresponding number of grids.
A grid independence validation was conducted on the SAUV, resulting in a total grid count of 1.4 million for straight-line course numerical simulations. A grid size of 5 cm was set within a spatial range of 2 m around the AUV. As the SAUV has numerous appendages, different grid sizes were assigned based on the geometric dimensions of the appendages, with the smallest grid size being 0.16 cm. In the computational domain farther away from the AUV, a grid size of 80 cm was set. The final grid distribution of the SAUV itself and its surrounding fluid domain is shown in Figure 5 below. Figure 5 shows the overall mesh division of the AUV and the enlarged views of different parts, including the AUV tail antenna, the AUV tail vector thruster, and the AUV head components. The enlarged views of the near-wall mesh discretization highlight the mesh resolution around the key components of the AUV for enhanced clarity.
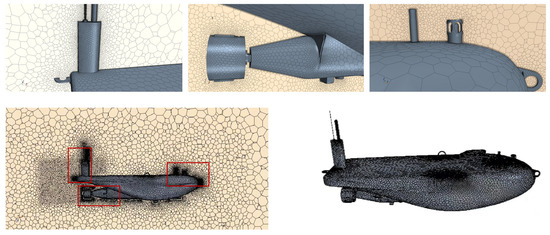
Figure 5.
AUV Grid Diagram.
In the setup of boundary conditions, as the surface of the underwater vehicle is defined as a no-slip wall, the near-wall region exhibits significant gradients in flow properties, where viscous effects dominate. To quantify the flow characteristics in this region, the wall function method is employed to establish the relationship between shear stress and velocity distribution. Specifically, by assuming that the near-wall fluid velocity follows a logarithmic law with respect to the wall-normal distance, the wall shear stress can be derived from this velocity profile. This approach essentially correlates the shear stress with velocities at different wall-normal positions through wall functions. In CFD simulations, the dimensionless parameter is commonly used to characterize the normalized distance from the first grid layer to the wall. Its approximate expression is:
is dimensionless wall distance, is the height of the first grid layer, and is the characteristic length of the vehicle. , the Reynolds number, based on the AUV’s characteristic length and flow velocity, is . Using this formula, the required can be inversely calculated to achieve the target . This guides the refinement of near-wall grids to ensure the validity of the wall function method.
3. Hydrodynamic Coefficient Calculation Based on CFD
3.1. Modeling for Spatial Captive Motion
Planar-constrained motion [10] refers to confining a vehicle to perform irregular motion within a plane in order to calculate the relevant hydrodynamic coefficients within that plane. These constraints restrict the degrees of freedom of the body motion, allowing for the isolation and precise calculation of individual hydrodynamic coefficients. Specifically, the body was constrained to move in a single degree of freedom (e.g., surge, sway, heave, roll, pitch, or yaw) at a time, while the other degrees of freedom were fixed. This approach ensures that the hydrodynamic forces and moments are directly associated with the specific motion under investigation, thereby reducing coupling effects and the accuracy of the coefficient determination.
The spatially constrained motion approach was employed to determine the hydrodynamic coefficients in this study. This method involves restricting the motion of the body to a single DOF at a time while keeping all other DOFs fixed. By isolating each motion, the hydrodynamic forces and moments associated with that specific motion can be accurately quantified, thereby enabling the calculation of the corresponding hydrodynamic coefficients. To simulate the irregular motion of the vehicle, motion equations for each degree of freedom of the AUV are defined in the motion module of the CFD software as follows:
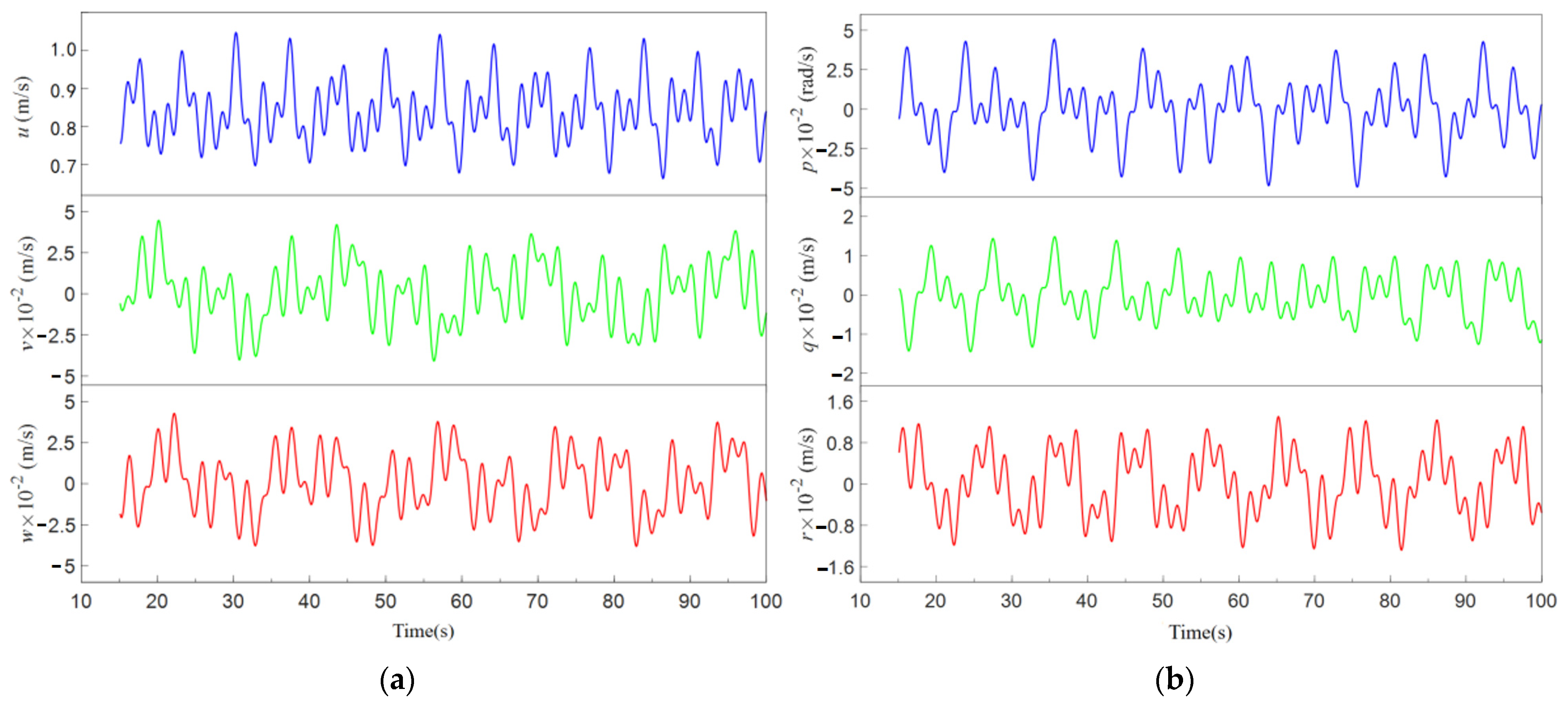
In this equation, represents the motion state variables of the vehicle, including the velocity components and angular velocity components , with being the initial reference value. The sum of the three sine functions can simulate the irregular random perturbations in six directions that are superimposed on the vehicle’s motion based on the cruise speed. By reasonably setting the amplitude and frequency of the sine waves, the motion acceleration and range of the vehicle’s irregular perturbations can be made to match actual motion conditions.
By incorporating the motion state variables of the AUV defined in Figure 6 into the CFD software, the vehicle is set to move according to the given states. A 110 s unsteady calculation is performed on the model, with a time step of 0.1 s, to calculate the changes in hydrodynamic forces and moments over time. This constitutes the modeling and calculation method for spatial captive motion.
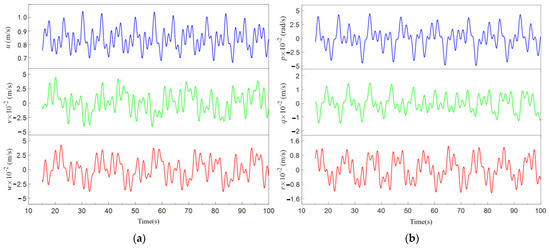
Figure 6.
Variation of velocity and angular velocity components in the body-fixed coordinate: (a) Velocity; (b) Angular velocity.
3.2. Identification of Hydrodynamic Coefficients
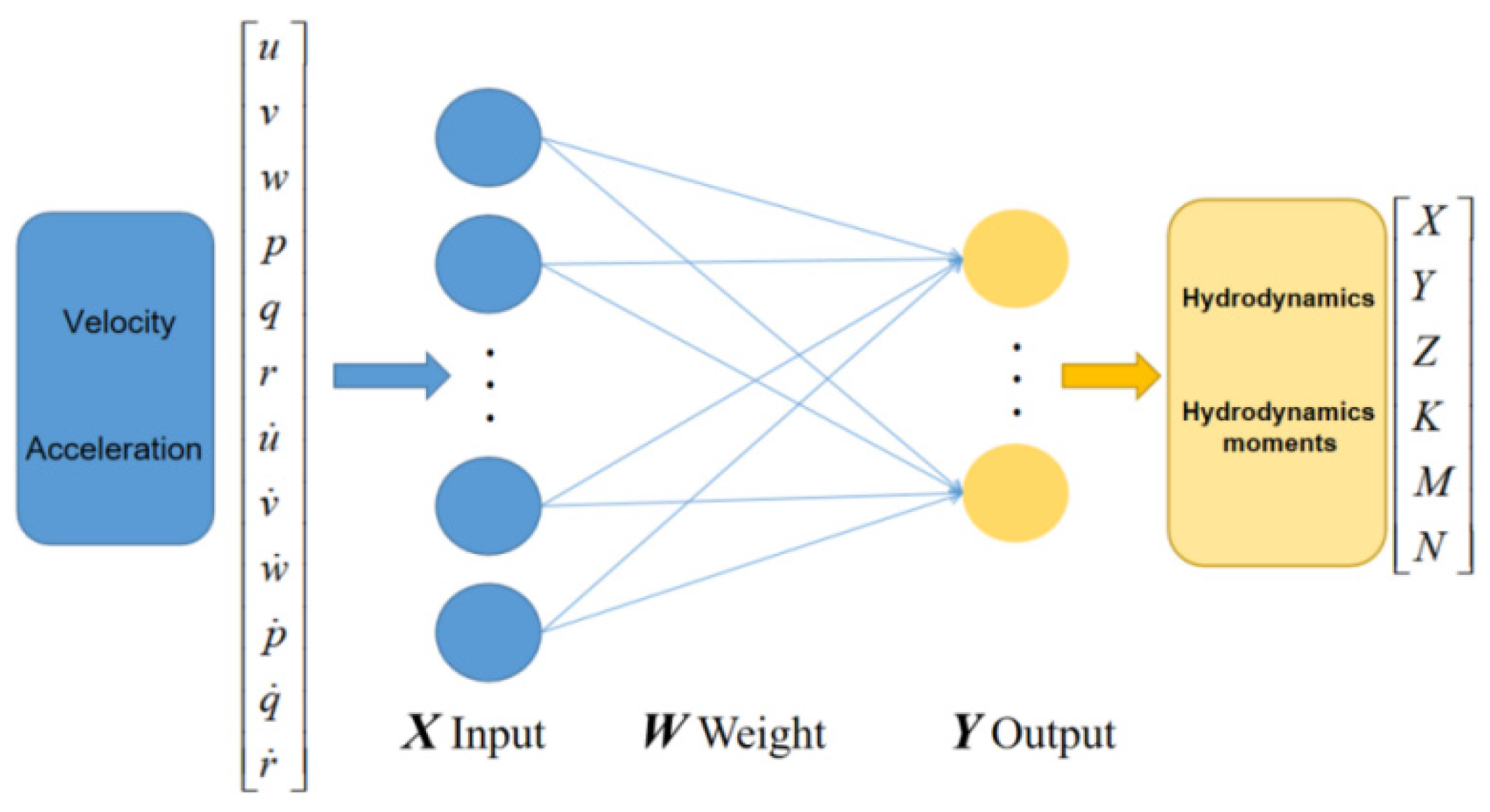
For the hydrodynamic equation , multiple sets of independent variables and dependent variables can be obtained through a single calculation using the spatial captive motion model. The functional relationship between the independent and dependent variables is denoted as f, and the expansion of function f is given by Equations (4)–(9). The various hydrodynamic coefficients in function f are the unknown parameters to be determined. A neural network can be trained to fit these unknown hydrodynamic coefficients, and the weight coefficients of the neural network correspond to the hydrodynamic coefficients that need to be fitted. The neural network computational method is efficient, and the model construction is simple. Furthermore, by using neural networks to process data, a black-box model can be established, bypassing the need to solve hydrodynamic coefficients directly and obtaining the relationship between motion states and force conditions. This approach can reduce the errors caused by ignoring higher-order terms in the hydrodynamic standard equations derived from Taylor expansions. The application of neural network methods to calculate hydrodynamic prediction models provides a new research direction for dynamic modeling. The basic structure of a neural network is shown in Figure 7 below.
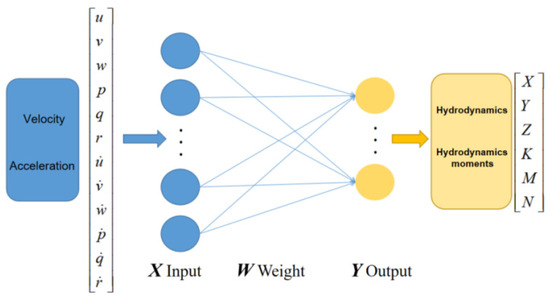
Figure 7.
The basic structure of a neural network.
The motion equations of AUV typically contain nonlinear and coupled terms, which are often related to velocity, acceleration, and other state variables. For such complex nonlinear systems, directly using a simple shallow neural network may indeed struggle to fully capture their dynamic characteristics.
In this subsection, CFD simulation results are utilized to fit the hydrodynamic coefficients. Under specific conditions (such as when velocity is known), the relationship between the hydrodynamic coefficients and certain input parameters (possibly velocity, angle, etc.) is approximately linear within the current simulation range. Therefore, it is feasible to use the least squares method or a shallow neural network to fit these coefficients.
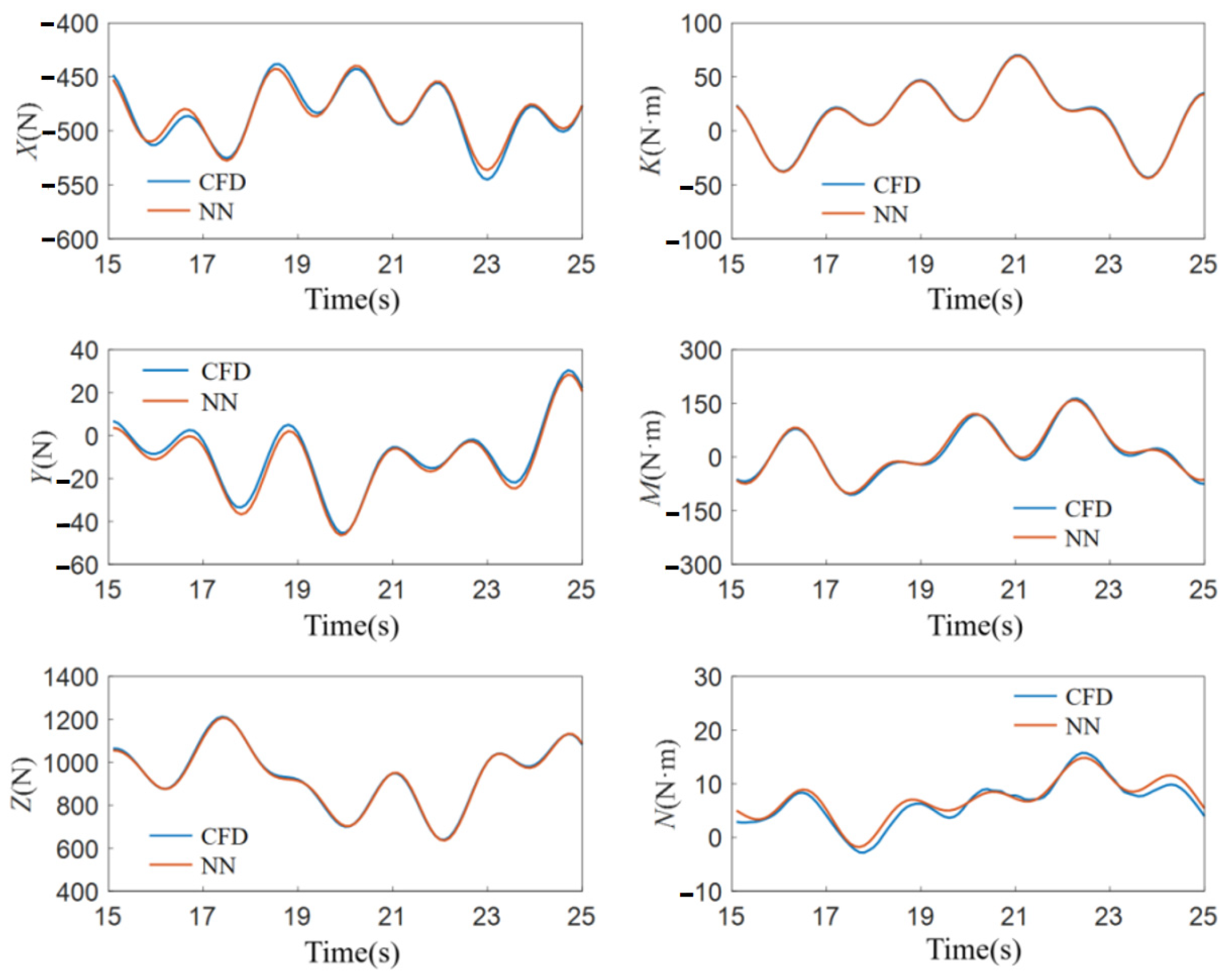
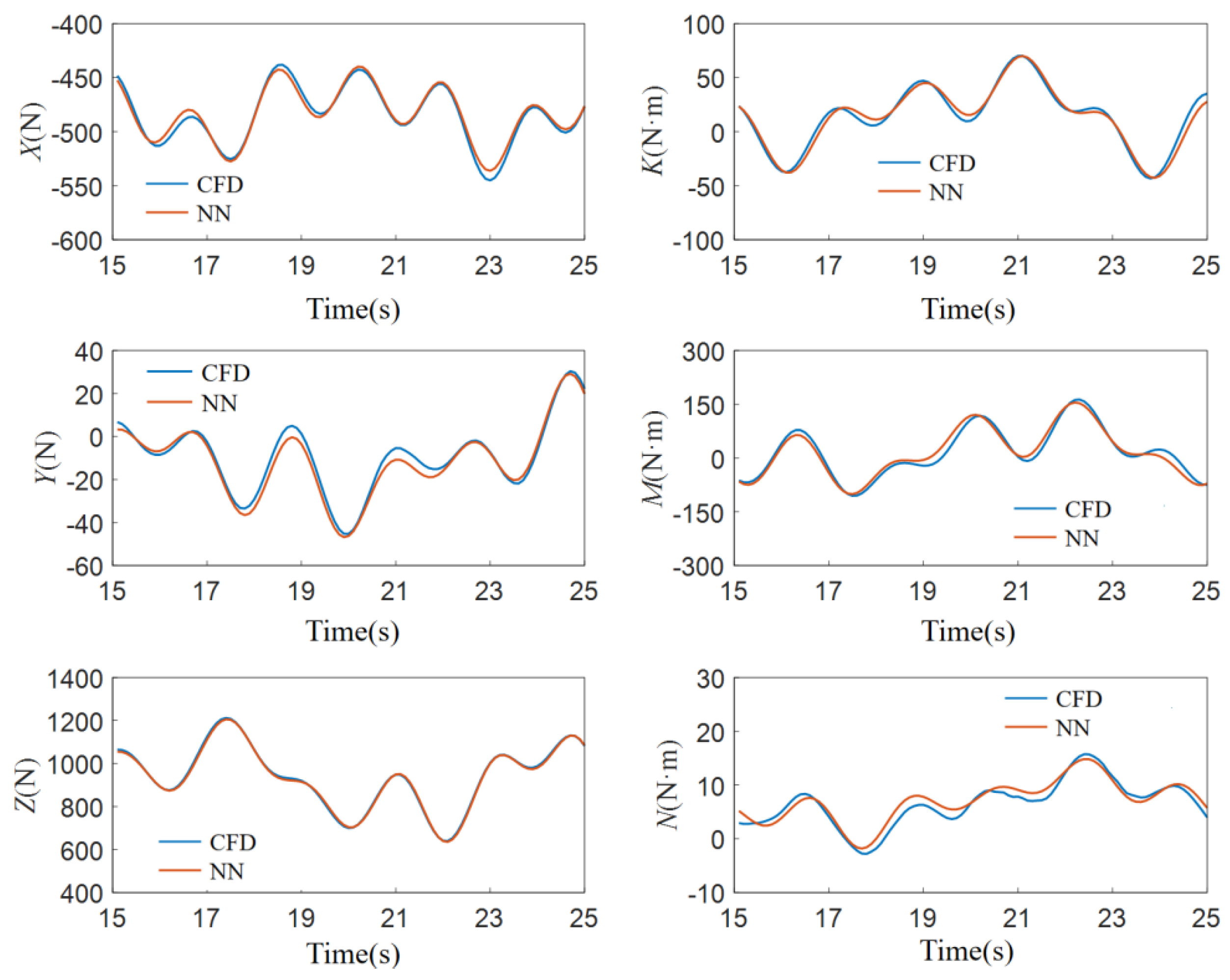
The CFD numerical simulation generated data spanning 110 s, with each time-step corresponding to a data group that includes the motion state, hydrodynamics, and torque. The CFD simulation was set with a time step of 0.1 s, resulting in a total of 1100 data groups. Excluding the first 150 unstable data groups within the first 15 s, there are 950 remaining data groups available for neural network training and testing. The 100 data groups from 15.1 s to 25 s are used as the test set, while the 850 data groups from 25.1 s to 110 s are used as the neural network’s training set. The test set is input into the neural network for testing. The blue lines in Figure 8 represent the output results of the neural network, while the red lines represent the CFD calculation results based on the spatial constraint motion model.
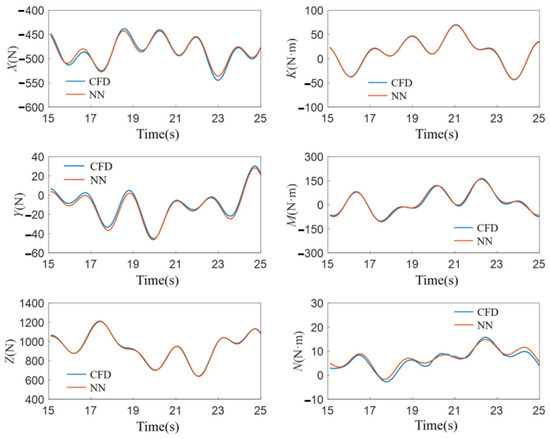
Figure 8.
Comparison of Calculation Results for AUV.
In this paper, the coefficient of determination, a statistical measure of goodness-of-fit, , is introduced as an indicator of the accuracy of the neural network model’s fitting. The closer the value of is to 1, the better the neural network model fits the observed values. Conversely, the closer the value of is to 0, the worse the neural network model fits the observed values. The goodness-of-fit and error analyses are performed on the data from the test set between 15.1 s and 25 s. The goodness-of-fit and the absolute values of the maximum errors for each of the six force components of the AUV are shown in Table 2.

Table 2.
Maximum Absolute Errors and Hydrodynamic Coefficients for AUV.
Based on the results of the hydrodynamic coefficient fitting for the AUV, the following analysis and conclusions can be drawn: the results of the spatial captive motion combined with neural networks for both the AUV model largely overlap with the CFD simulation results. As can be seen from Table 2, the goodness-of-fit for both models is mostly greater than 0.95. For the AUV, the maximum hydrodynamic error occurs on the X-component curve, which does not exceed 10 . The maximum error in the hydrodynamic torque occurs on the M-component curve, which does not exceed 15 .
3.3. Selection of Key Hydrodynamic Coefficients
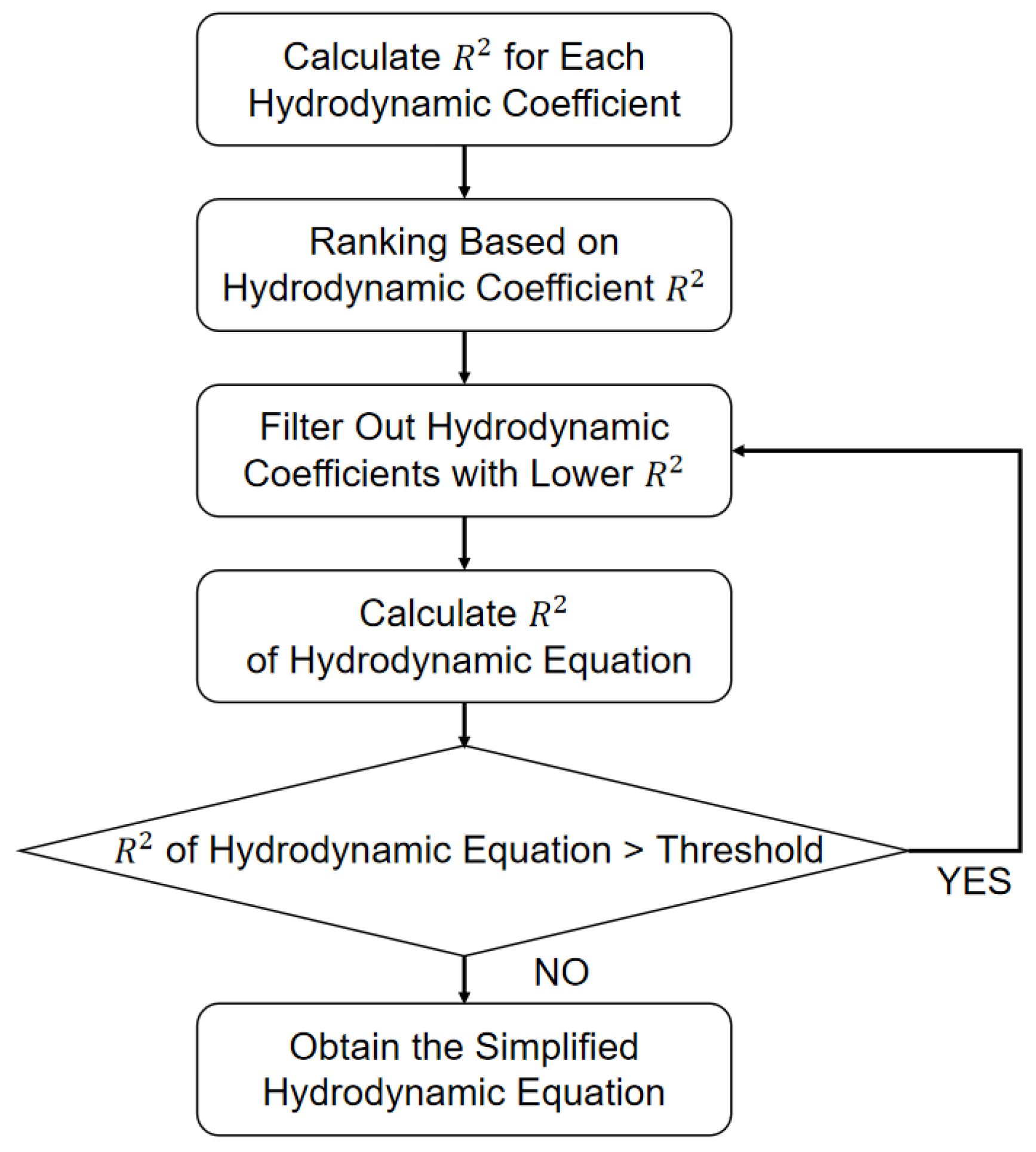
The importance of each hydrodynamic coefficient in the equations varies. Therefore, it is necessary to screen the hydrodynamic coefficients while ensuring the accuracy of the model, eliminating those that are less important and have unstable calculations. Eliminating an unimportant hydrodynamic coefficient in this equation is also based on the goodness-of-fit . Based on the data in Table 2, the initial threshold for the goodness-of-fit can be set at 0.95 or 0.90. The flowchart for simplifying the equations is shown in Figure 9 below.
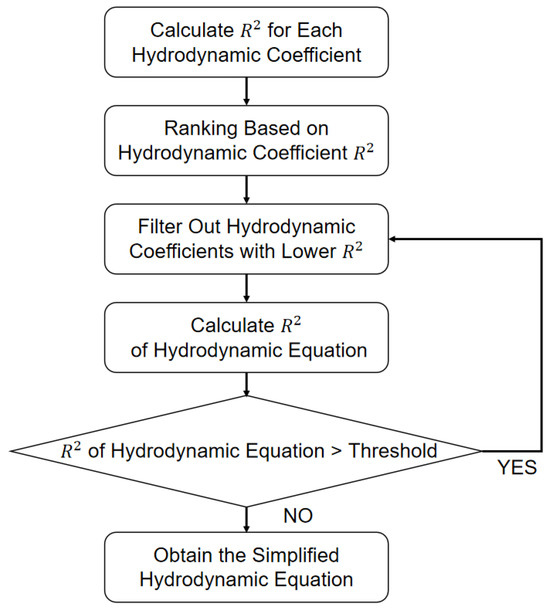
Figure 9.
Simplified flowchart of hydrodynamic equation.
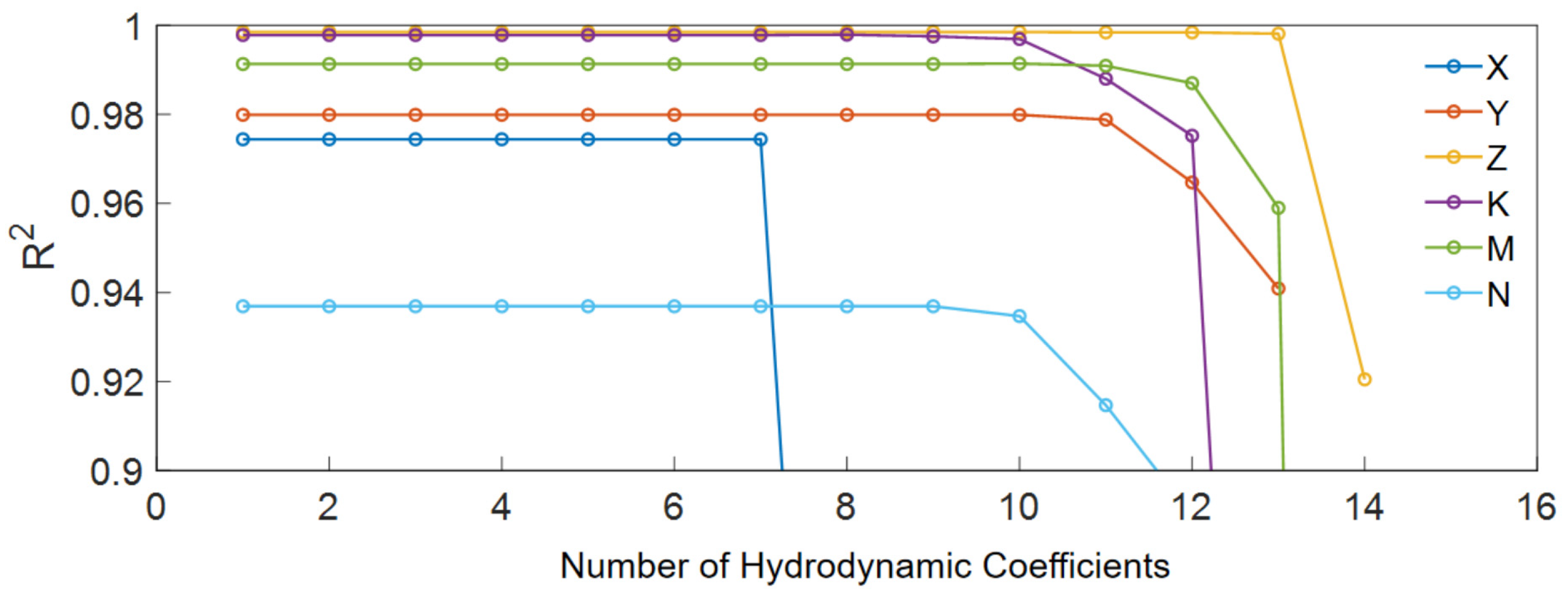
Figure 10 depicts the change in the goodness-of-fit of the AUV as the number of simplified terms varies. As the importance of the eliminated hydrodynamic coefficients increases and a certain term is reached, the goodness-of-fit experiences a significant drop. Further elimination of hydrodynamic coefficients will result in the goodness-of-fit falling below the threshold of 0.95.
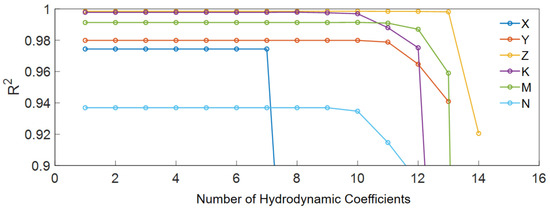
Figure 10.
The goodness-of-fit of AUV varies with the number of simplified terms.
Through the screening of hydrodynamic coefficients, the simplified hydrodynamic equations for the AUV are:
Figure 11 compares the calculation results of the simplified hydrodynamic coefficient models for the AUV with the CFD calculation results before simplification. Table 3 presents the goodness-of-fit and error between the calculation results of the simplified hydrodynamic coefficient models for the AUV and the CFD calculation results before simplification, respectively. For the AUV model, there is currently no comprehensive experimental data on hydrodynamic coefficients to serve as a basis for the accuracy of the spatially constrained motion method. By using the spatial captive motion model combined with neural networks, all the hydrodynamic coefficients of the AUV can be identified.
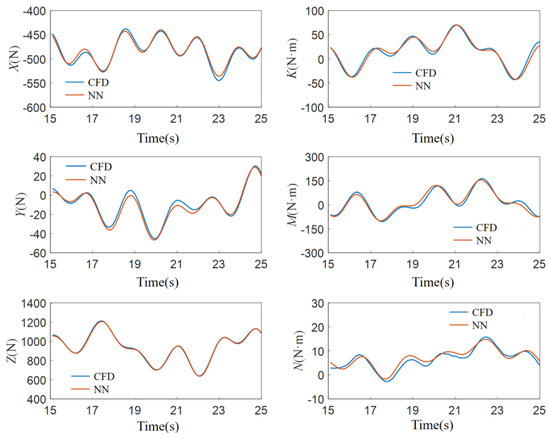
Figure 11.
Comparison of simplified hydrodynamic models for AUV.

Table 3.
Maximum Absolute Errors and Hydrodynamic Coefficients for AUV after screening.
Table 4 shows the key hydrodynamic coefficients of the AUV after screening.

Table 4.
Shows the key hydrodynamic coefficients of the AUV after screening.
By incorporating the hydrodynamic coefficients in Table 4 into the simplified hydrodynamic Equations (16)–(21) of the AUV, one can predict the hydrodynamic force and moment experienced by the AUV under a specific motion state.
4. Motion Control of AUV Based on MPC
The preceding article calculated the hydrodynamic characteristics of the AUV by applying the spatially constrained motion method. However, for the fully appended model of the AUV, due to cost constraints, there is a lack of comprehensive and precise experimental data on hydrodynamic coefficients to directly validate the accuracy of this calculation method. To address this deficiency, this section proposes utilizing a kinematic and dynamic model based on the existing hydrodynamic coefficients of the AUV, first conducting open-loop control simulations and experiments to preliminarily assess the response characteristics of the AUV. Subsequently, when the MPC method is introduced for closed-loop control simulation and experimentation of AUVs, insufficient accuracy in the hydrodynamic coefficients adopted by the model will directly impact the effective implementation of the MPC control strategy, potentially leading to the unsuccessful application of the MPC method or failure to achieve the desired control effects. If the control accuracy falls within an acceptable range, it indicates that the preceding hydrodynamic calculations possess a certain degree of accuracy.
4.1. Open-Loop Control Simulation and Experimentation for AUV
The dynamic model of the AUV is based on the six-degree-of-freedom spatial motion equations and has undergone a simplification process for the hydrodynamic coefficients, resulting in the simplified equations presented below:
The kinematic relationships of the AUV are as follows:
When conducting an open-loop simulation, the dynamic state of the system is denoted as , the kinematic state is denoted as , and the system input is denoted as . When different values of are applied, different kinematic states are obtained. The schematic diagram of the open-loop control is shown in the following Figure 12 below.
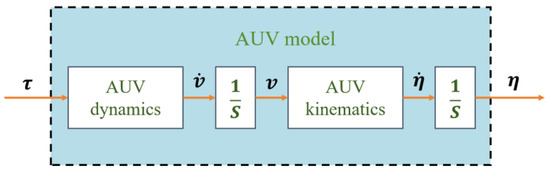
Figure 12.
The schematic diagram of open-loop control simulation for AUV.
The AUV studied employs a vector thruster as its propulsion unit. The thrust magnitude T of this thruster is adjustable within the range of [0, 112N], while the angles used to adjust the thrust direction encompass two dimensions: ranging from [−20°, 20°] and ranging from [−90°, 90°]. and control the AUV’s motion in the vertical and horizontal planes, respectively. For a more detailed explanation of these parameters, please refer to reference [28].
During simulation analysis, the thrust magnitude T is directly used as an input parameter for the simulation model. However, in actual experimental procedures, due to the difficulty in accurately measuring the true thrust magnitude of the thruster directly, the power of the thruster is chosen as the control input parameter. Furthermore, open-water tests on the vector thruster have been conducted in reference [28], establishing a corresponding relationship between power and thrust in still-water conditions, which provides an important basis for the control strategy during experiments. The AUV is an underactuated system capable of controlling state variables such as velocity , yaw angle , and pitch angle . Both the water tank testing environment and the simulation and experimentation results are illustrated in Figure 13 and Figure 14 below.

Figure 13.
AUV in the water tank.
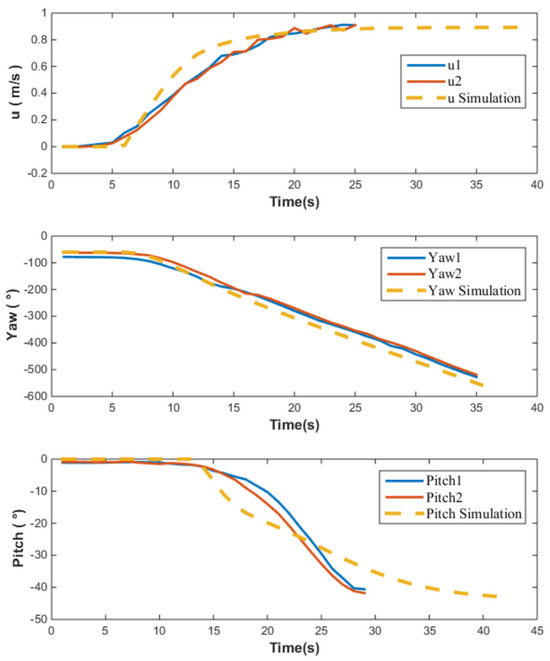
Figure 14.
Open-loop simulation and test results of AUV.
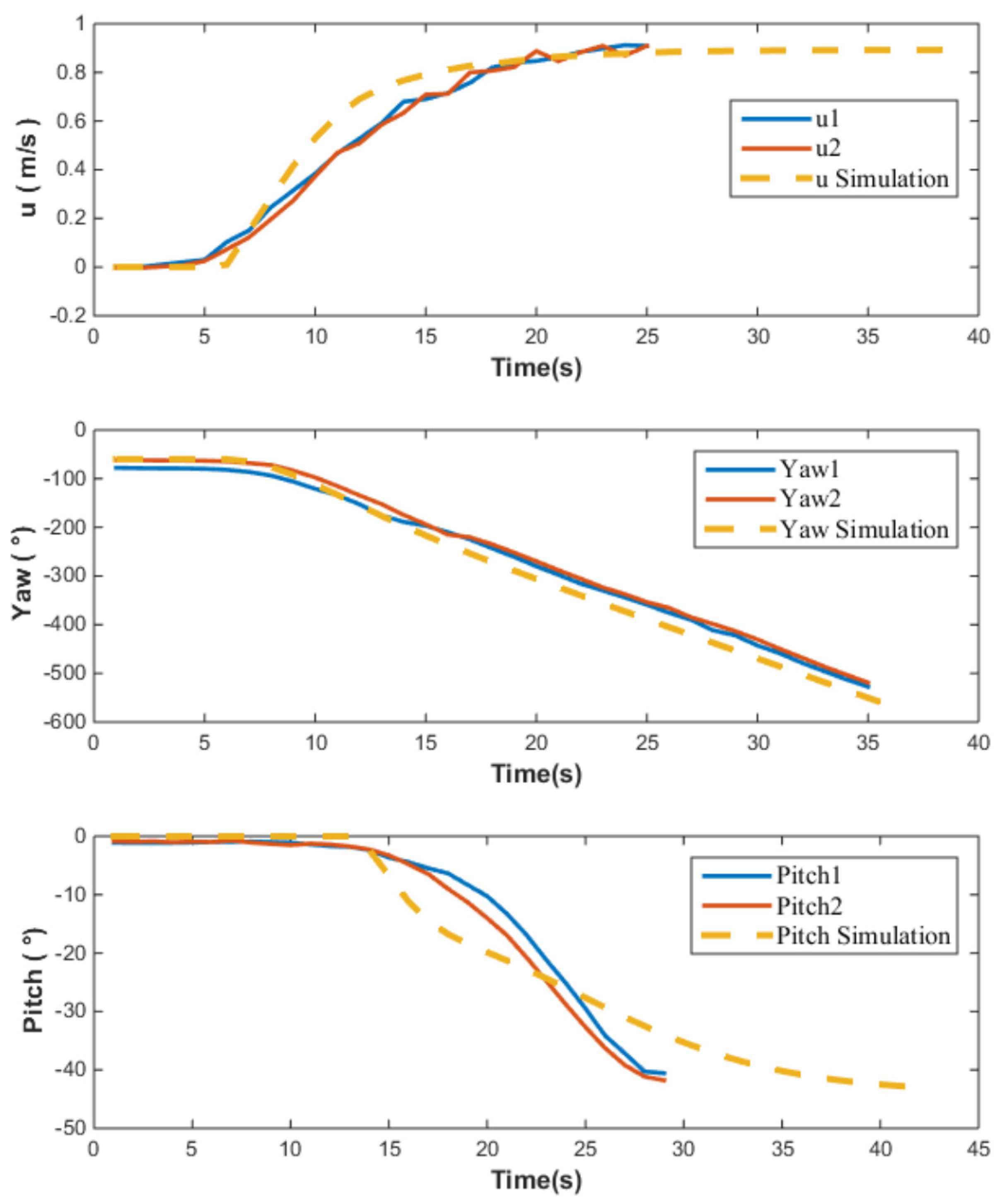
When the system input is , the changes in velocity u during two separate trials and simulations are presented. The maximum velocity achieved by the AUV is 0.9 m/s; however, the simulated acceleration exceeds that observed in both experimental trials. This indicates the presence of certain errors in the hydrodynamic coefficients .
When the system input is , the changes in the heading (yaw angle) during two separate trials and simulations are presented. The results from the experiments and simulations are relatively close, which suggests that the relevant hydrodynamic coefficients possess a certain degree of accuracy.
When the system input is , the variations in the pitch angle during two separate trials and simulations are shown. There is a significant error between the experimental and simulation results. The AUV has a negative-lift shape, which exhibits poor structural symmetry. Compared to the calculation of other hydrodynamic coefficients, the calculation error for the hydrodynamic coefficients related to pitch motion is larger.
In summary, by comparing the results of the open-loop control experiments with simulations, the accuracy of hydrodynamic coefficients can be approximately estimated. The consistency between the AUV simulation results and the open-loop control experiments in some data validates that the hydrodynamic coefficients calculated earlier possess certain referential values. However, for those hydrodynamic coefficients with larger errors, it is imperative to explore and consider other effective error compensation methods when designing the closed-loop controller to ensure the precision and stability of the system control.
4.2. MPC Simulation and Experimentation for AUV
In order to reduce the errors introduced by model linearization and decoupling, the MPC controller designed in this section is constructed directly based on the nonlinear six-degree-of-freedom dynamic Equations (22)–(27). The system state of the AUV is denoted as , and the system input is . From the above equation, the general expression of the AUV can be derived as:
Generally, MPC is used for trajectory tracking control of AUVs. In this paper, to verify the accuracy of the hydrodynamic coefficients, the validation of the AUV is conducted in an undisturbed indoor pool. Due to the limited test site, the speed control, depth control, and yaw control of the AUV are verified in the pool. Based on the above equation, the MPC formula for AUV motion control can be established as follows:
In the above equation, represents the cost function. And denotes the error state cost, which can be adjusted according to the state variables that need to be controlled. is the terminal cost function. Typically, for an underactuated AUV performing simultaneous speed control, depth control, and yaw control, the error state cost at this time is:
For the practical application of the algorithm, there may be a situation where the computing power of the MCU is insufficient, requiring the simplification of the error state cost to improve computational efficiency. In this case, when only depth control and heading control are performed, the error state cost is as follows:
For depth control of an underactuated AUV, it is common to first control the pitch angle and then indirectly control the depth. In this scenario, the error state cost is:
where , , , and are the target speed, target depth, and target yaw, respectively. , , and are the predicted speed, predicted depth, and predicted yaw of the AUV under the predicted input . is the speed error, is the depth error, is the yaw error. represents the control error. is the weight coefficient for the velocity control performance index, is the weight coefficient for the pitch angle control, is the weight coefficient for the heading angle control, is the weight coefficient for the depth control, and is the weight coefficient for the control input.
To derive the terminal cost function, the system model needs to be linearized, resulting in an approximate linearized model as follows:
where , . Solve the Riccati equation to obtain .
Determine the local linear stabilizing feedback gain for the system.
Given , , solve the Riccati equation to obtain .
Obtain the terminal cost function.
where , is a K function, which is defined as follows:
The K function, denoted as : ( is defined as a positive real number), is a continuous and strictly increasing function, with the property that .
where , the defined minimum value is denoted as , and the corresponding optimal input sequence is denoted as .
The optimal state prediction trajectory corresponding to u* is denoted as:
When the system transitions to the next state, , there is a control law that governs this transition.
satisfies the following conditions:
where
At this time, the performance index corresponding to the control rate (or control law) satisfies:
Therefore, it can be obtained as follows:
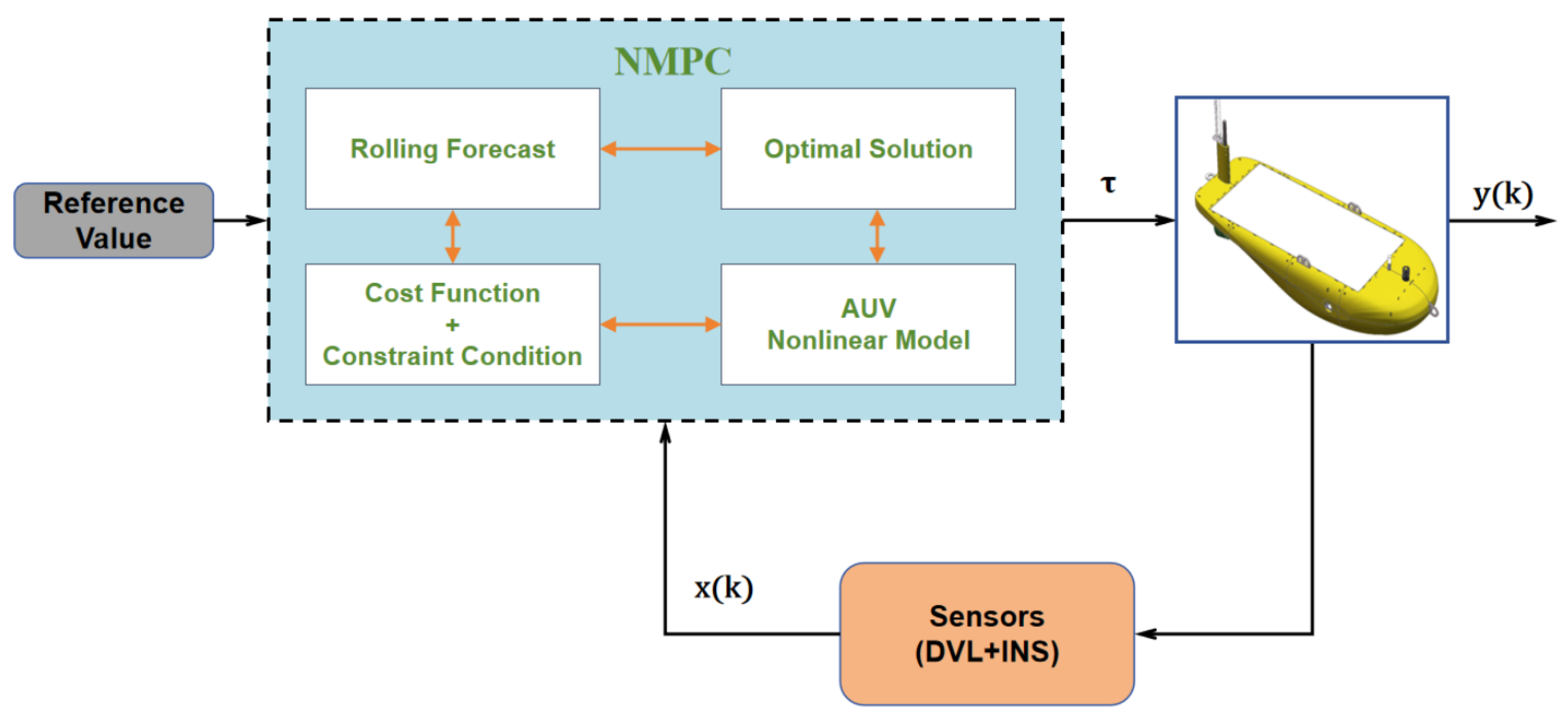
Let be a Lyapunov function. When the rolling horizon control law is , the system is stable. The main principle of MPC is illustrated in Figure 15 below:
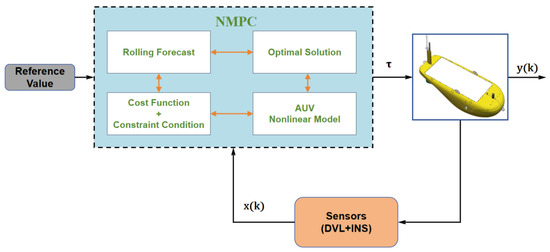
Figure 15.
The schematic diagram of the MPC controller for AUV.
Since the MCU used by the AUV is a Raspberry Pi 4B, which has limited computing power, it is necessary to pre-determine some suitable test parameters through simulation before conducting actual tests. Additionally, other test parameters need to be determined based on the physical constraints of the AUV, such as the angle adjustment speed of the vector thrusters, sampling frequency, and execution frequency.
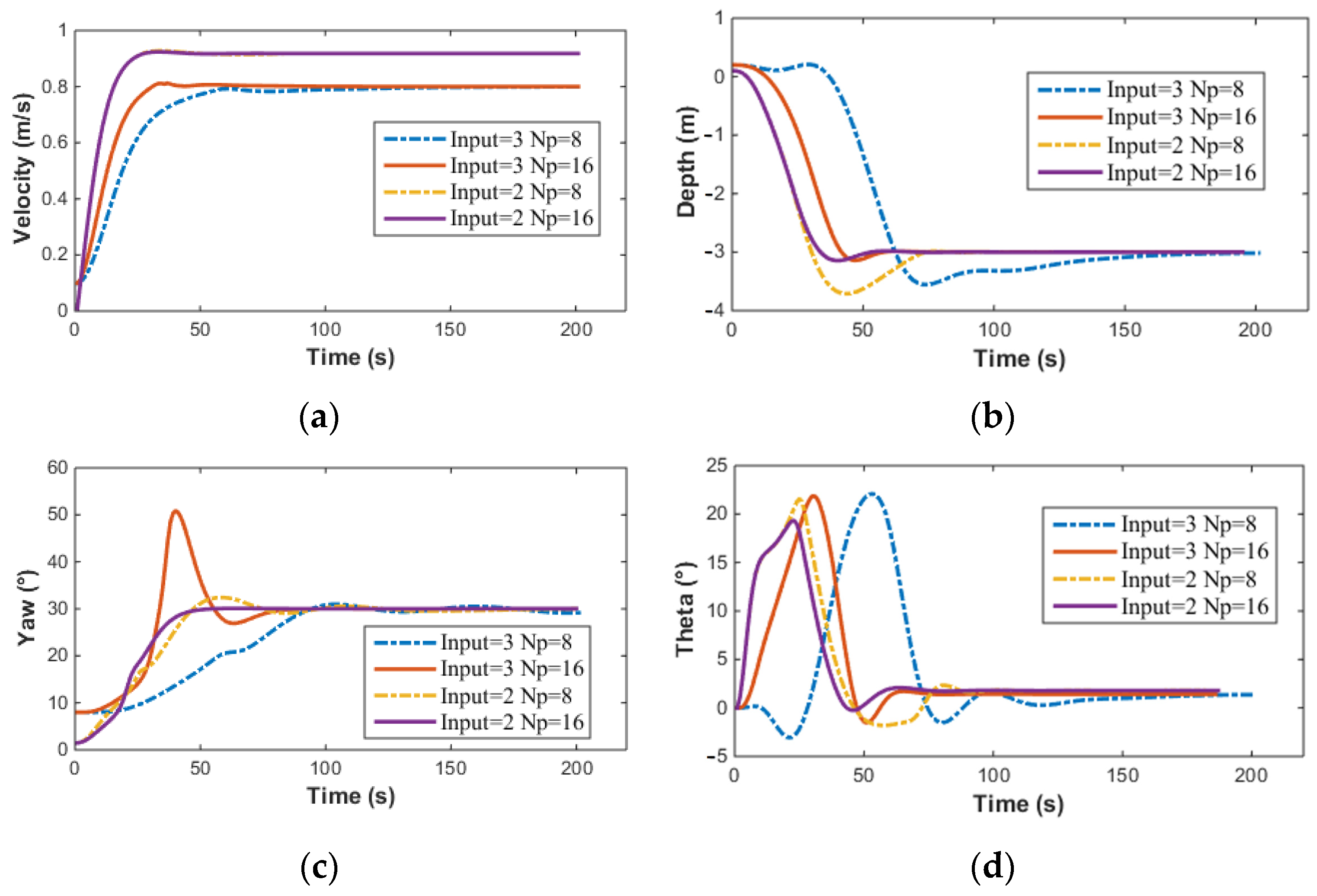
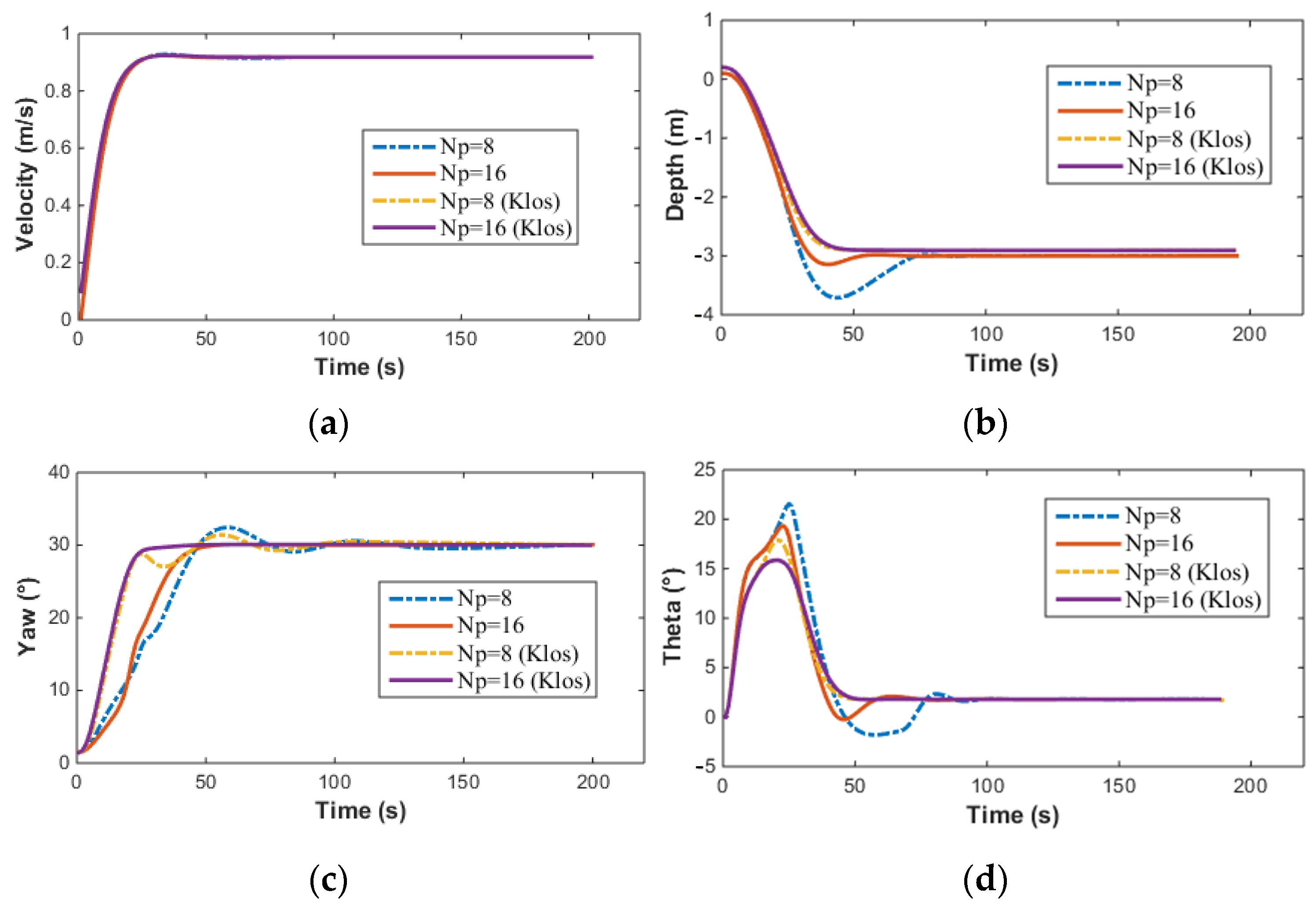
When the underactuated AUV performs simultaneous speed control, depth control, and yaw control, the error state cost is denoted as , with weight coefficients , , , , and U = 1 m/s, , m, . The prediction horizon is set to 8 and 16, respectively, for these simulations. When the underactuated AUV performs only depth control and yaw control, the error state cost is calculated with the same weight coefficients , , , and m, . The prediction horizon is also set to 8 and 16 for these simulations. The simulation results are presented in Figure 16 and Figure 17.
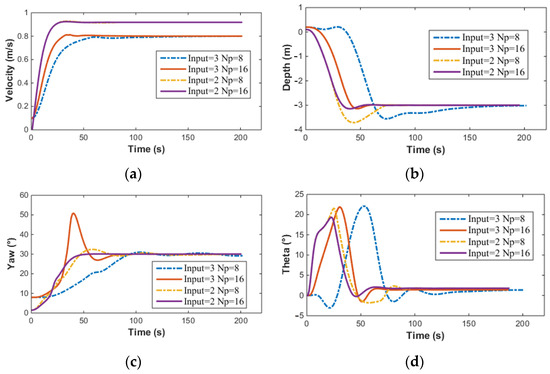
Figure 16.
MPC simulation results of AUV: (a) Velocity; (b) Depth; (c) Yaw; (d) Theta.
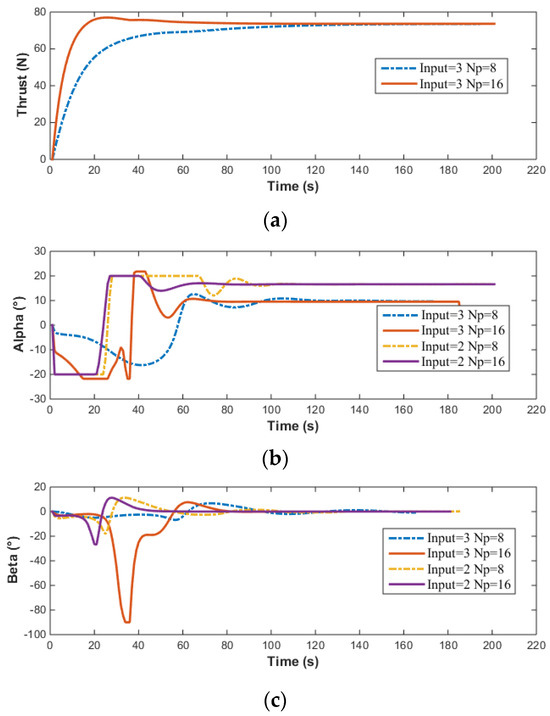
Figure 17.
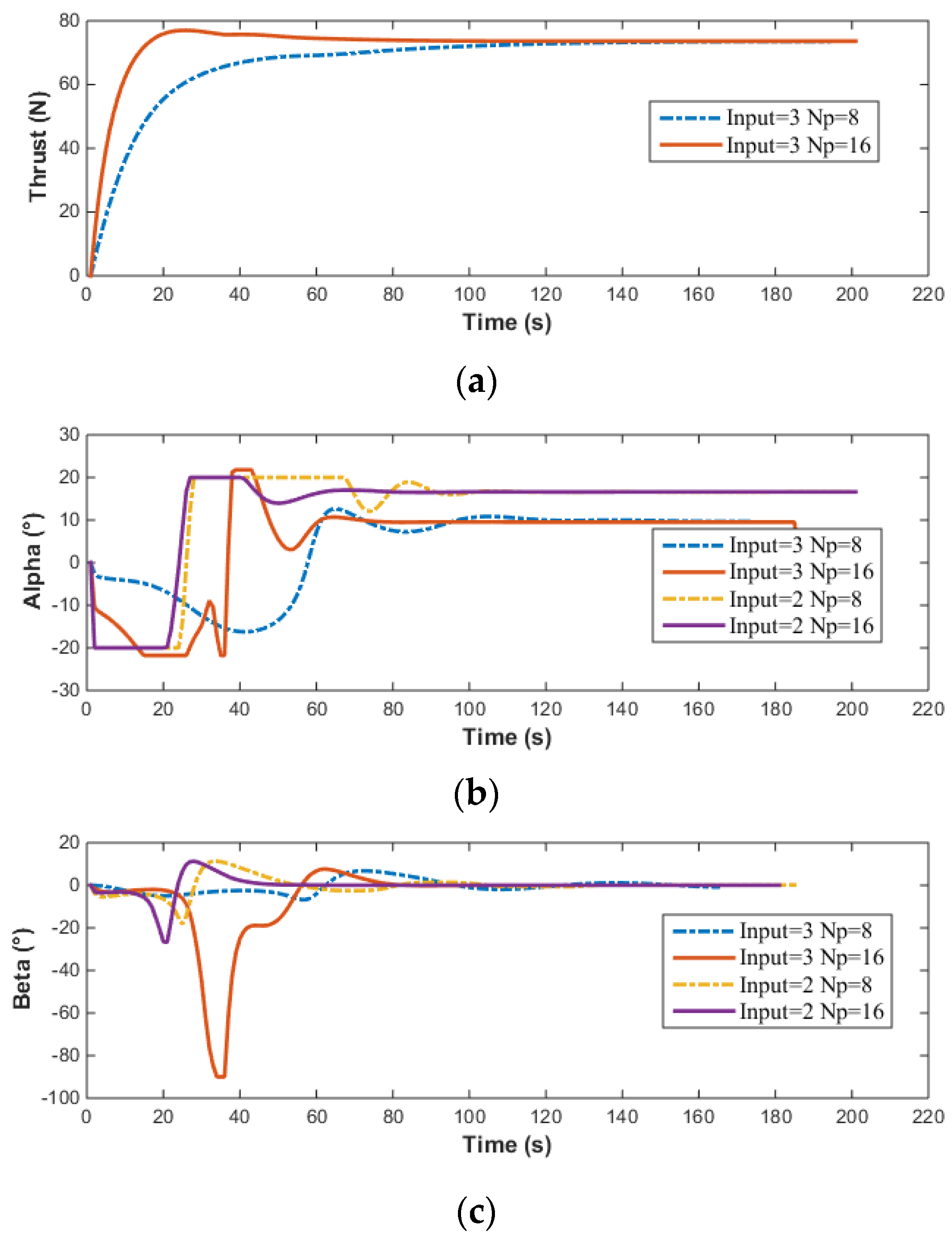
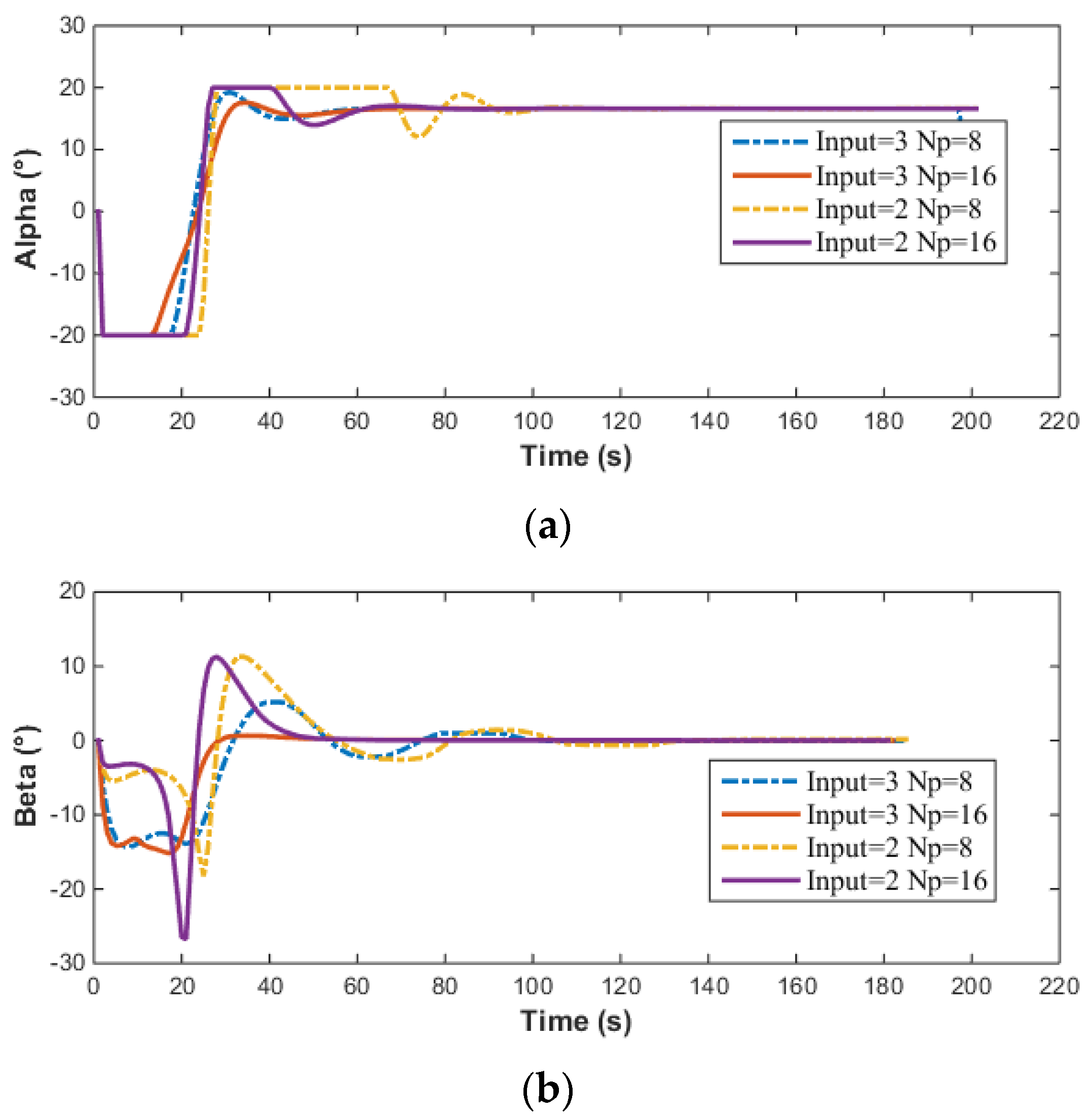
Input of vector thruster in MPC simulation of AUV: (a) Thrust; (b) Alpha; (c) Beta.
At this point, the input to the vector thruster is:
The above simulation results compare the effects of the prediction horizon and the number of control inputs on the simulation results. The smaller the prediction horizon, the lower the required computing power. A shorter prediction horizon requires less computational power. However, the control precision when is significantly higher than when . As the prediction horizon increases, the overshoot decreases, the adjustment time shortens, and the control precision improves. Additionally, it can be observed that the control input becomes smoother as the prediction horizon increases.
From Figure 17, it can also be noted that when no velocity control is applied to the AUV, the velocity converges to . However, when velocity control is implemented, the AUV converges to the target velocity . It is evident from the graphs that under the same prediction horizon , implementing velocity control does not change the control precision of the heading angle, the pitch angle, or the depth, but their adjustment times increase significantly. Furthermore, the time taken by the MPC solver also increases when velocity control is applied. The corresponding computation times for the three cost functions mentioned are presented in Table 5 below.

Table 5.
Calculate time cost.
After considering both computational power and control precision, the prediction horizon is determined to be 16, and no velocity control is applied. It is also important to note that the depth control of underactuated AUVs is typically not achieved by directly controlling the depth but rather indirectly through the control of the pitch angle. When employing the Line-Of-Sight (LOS) method, the target pitch angle is given by:
In the above equation, represents the look-ahead distance, which is typically determined based on the motion characteristics of the AUV. In this paper, for the experiments and simulations, the target depth is set to . Moreover, due to the AUV’s negative-lift shape, its motion in the vertical plane is inherently unstable, and the control input from the vector thruster is limited. In practical control, it is necessary to constrain the pitch angle variation range of the AUV. By setting and substituting it into the equation above, we can calculate the maximum range of pitch angle variation for the AUV during its descent from the water surface to the target depth as:
During the simulation, the error state cost function is set to with a weight coefficient , , , and the parameters m, are defined. The prediction horizon is set to both 8 and 16, and the simulation results are compared against those obtained with an error state cost function. The results are presented in Figure 18 and Figure 19 as shown.
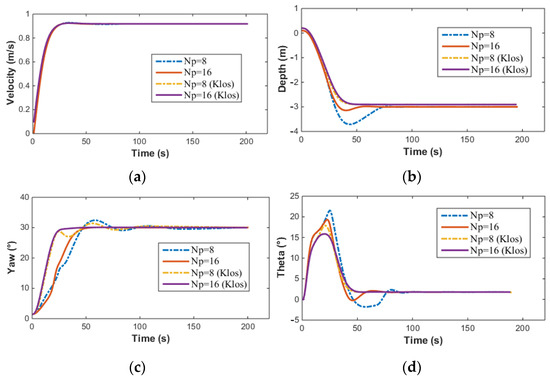
Figure 18.
MPC simulation results of AUV: (a) Velocity; (b) Depth; (c) Yaw; (d) Theta.
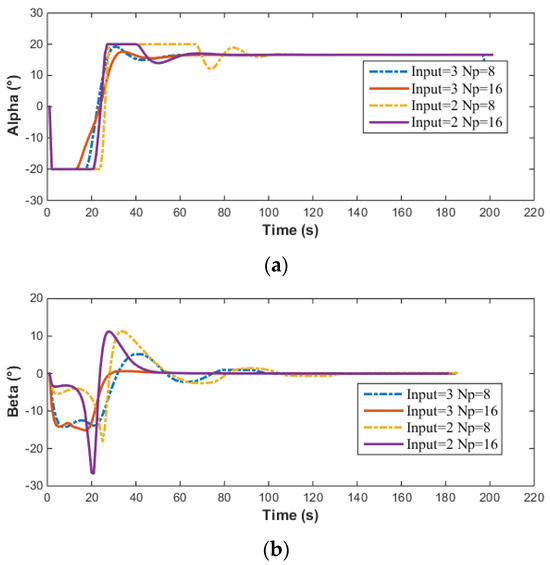
Figure 19.
Input of vector thruster in MPC simulation of AUV: (a) Alpha; (b) Beta.
At this point, the input to the vector thruster is:
In Figure 18, and represents the results of depth control based on the LOS method. Since no velocity control is implemented, the velocity response curves for both methods are identical. For depth control, due to the limitation on the pitch angle, when using the LOS method, the maximum pitch angle of the AUV is , and there is no overshoot in the depth control. The simulation results demonstrate that the LOS-based depth control method achieves better performance. The object of this study is the AUV with vector propulsion. According to Equation (1), the control inputs , , and of the AUV are mutually coupled. When controlling three variables simultaneously (speed, heading, depth), the NMPC controller must resolve coupled dynamics and trade-offs between conflicting objectives (e.g., AUV uses a vector thruster, and speed adjustment will inevitably disrupt depth stability). This higher-dimensional optimization problem introduces stronger nonlinear interactions, making convergence more sensitive to the prediction horizon (Np). In contrast, the two-input case (fixed speed) simplifies the problem by decoupling speed dynamics, thereby reducing computational complexity and improving solution consistency. Multi-variable NMPC with a long horizon is more sensitive to the initial guess of the optimization. As shown in Figure 19, in the case of three-input, a suboptimal initial guess leads to a longer convergence time and may cause the solution to diverge, whereas the two-input scenario benefits from simpler dynamics and more stable convergence.
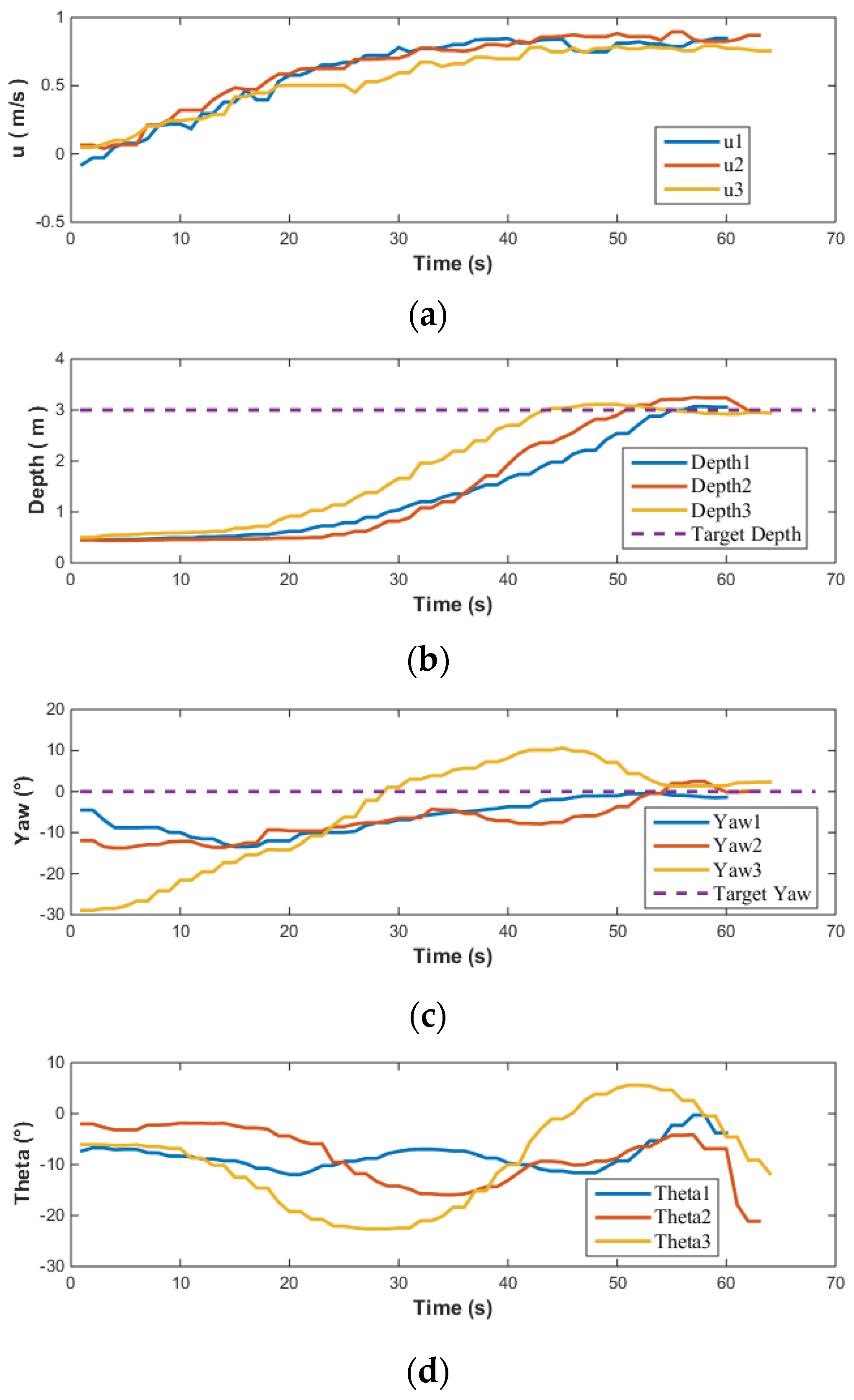
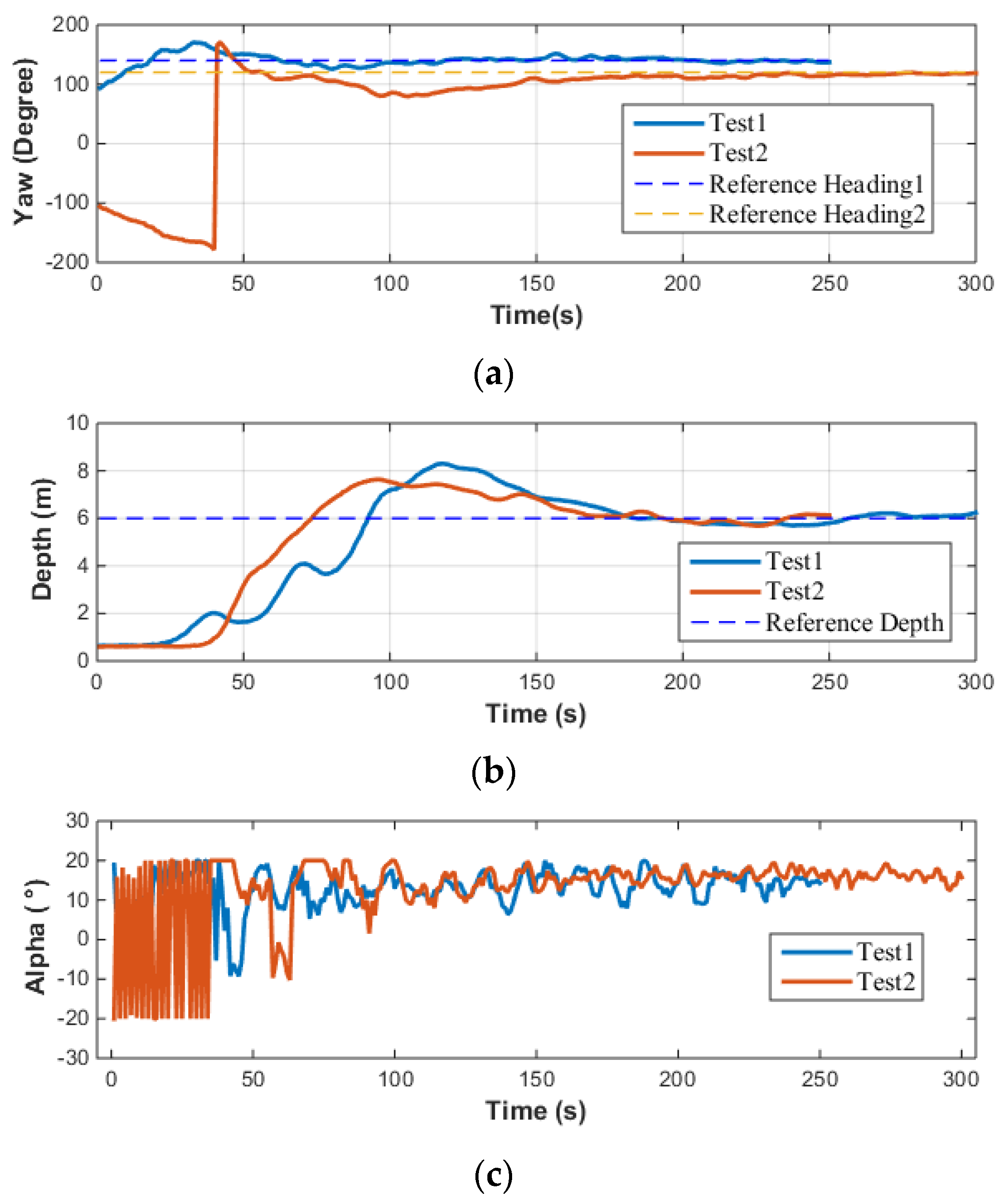
Through simulation analysis, the MPC utilizing the LOS method was identified as the control scheme for the AUV. As disturbances were not considered in the simulation, to validate the effectiveness of the MPC control scheme under conditions free from external interferences and ensure consistency between the simulation and actual test environment, tests were conducted in a still water tank environment without any disturbance. The objective of the tests was to indirectly judge whether the accuracy of the AUV’s hydrodynamic coefficient calculations met the actual engineering application requirements by evaluating its control precision. The following Figure 20 demonstrates the consistency between the control parameters used in the LOS-based depth control method for the AUV and those set during simulation, showcasing the results obtained from multiple tests conducted in the water tank environment.
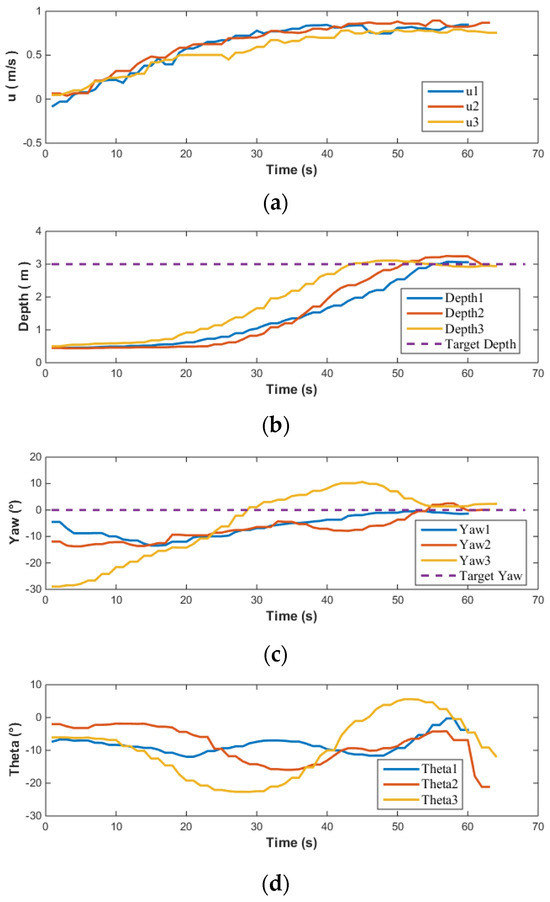
Figure 20.
Water tank test results of AUV based on MPC: (a) Velocity(u); (b) Depth; (c) Yaw; (d) Theta.
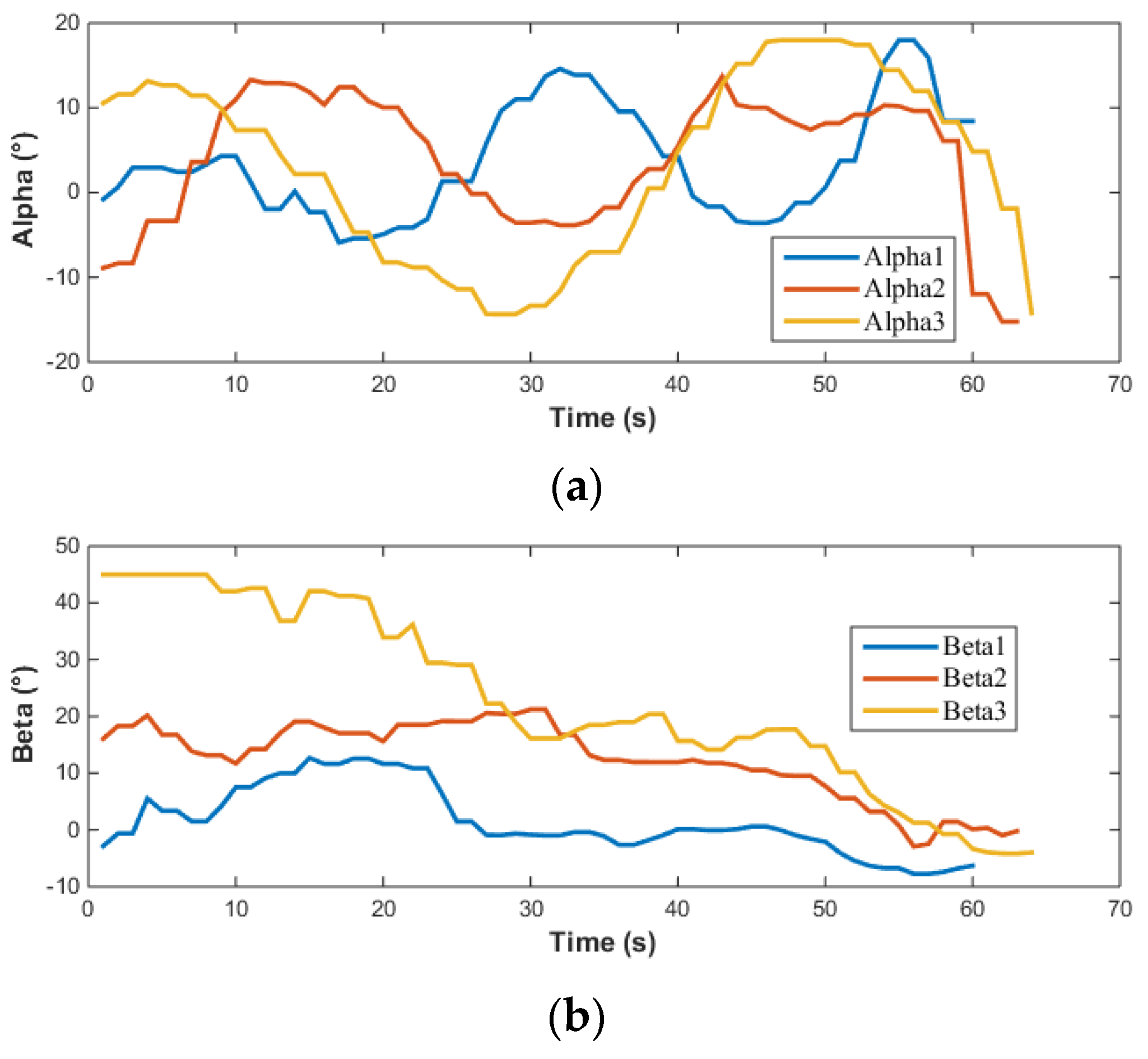
It can be observed from Figure 20 that while the speed of the AUV was not specifically controlled, the three test results exhibited good repeatability. In terms of depth control, the AUV showed minimal overshoot, and the depth in all three tests converged to the target depth. For heading angle control, given that the pool is oriented north-south, when the AUV moves linearly in this direction, its natural heading angle is 0°. Consequently, when setting up the heading control experiment, the target heading angle is set to 0°, and the heading control capability is evaluated by assigning various initial heading angles to the AUV. The experimental results indicated that even with varying initial heading angles, the AUV’s heading angle control maintained high precision, successfully adjusting and maintaining the heading angle near 0°. The largest difference between simulation and testing lies in the control of the pitch angle. Overall, the pitch angle varies within a limited range of approximately . The sources of error here are similar to those in open-loop testing. In practical engineering applications of AUVs, where accurate hydrodynamic coefficients may not be readily available, it is necessary to consider the impact of errors and design MPC controllers with higher robustness. Furthermore, the actual input to the AUV’s vector thruster is illustrated in Figure 21 below.
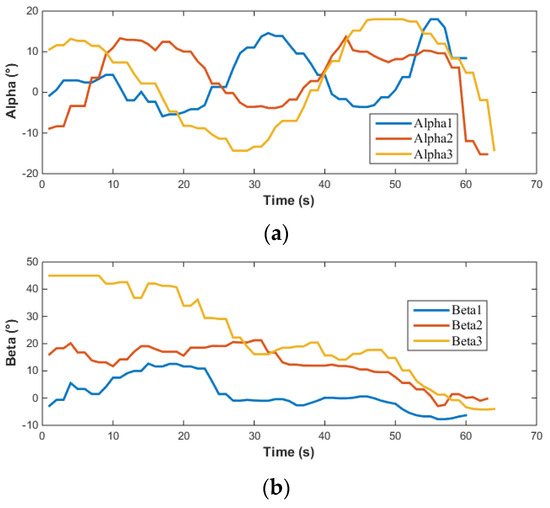
Figure 21.
Input of vector thruster for AUV in water tank experiments: (a) Alpha; (b) Beta.
Figure 22 shows that the actuator of the vector thruster undergoes a relatively slow change process, which satisfies the physical constraints of the vector thruster.
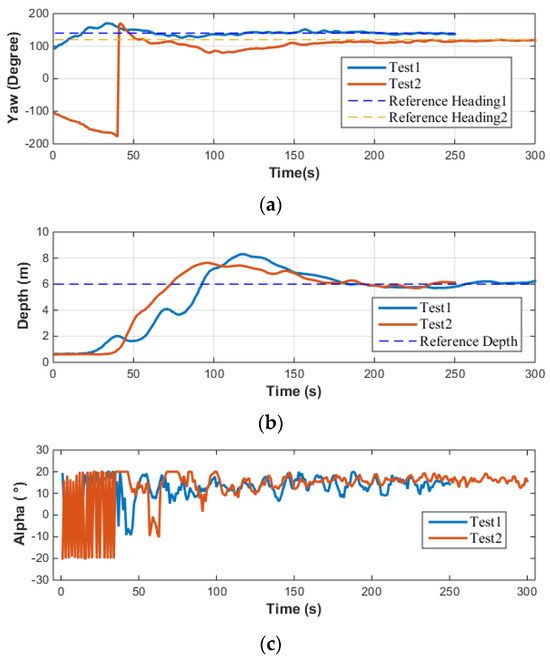
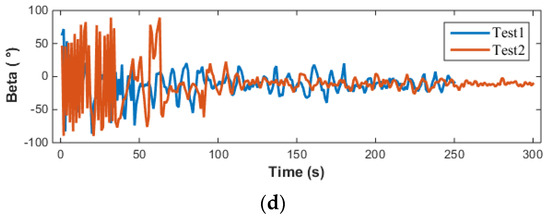
Figure 22.
Offshore test results of AUV based on PID control: (a) Yaw; (b) Depth; (c) Alpha; (d) Beta.
Prior to conducting MPC control tests, extensive open-loop tests in the pool and model-free PID control tests offshore were performed on this AUV. Figure 22 describes the design approach and relevant test results of a PID controller designed specifically for the AUV’s vector thruster. Comparing the control effects of MPC and PID, PID control is prone to overshooting, while MPC exhibits no overshooting phenomenon. When contrasting the vector thruster outputs, and (i.e., the inputs to the AUV), obtained through MPC and PID, respectively, it becomes evident that when a PID-based control strategy is adopted, the AUV’s motion control system, inherently a complex multi-input multi-output system, experiences significant coupling effects among its various thrust inputs. This coupling results in more drastic variations in the vector thruster outputs ( and ) after decoupling via PID control, thereby increasing the actuator’s operating frequency and ultimately leading to a substantial increase in control energy consumption. More crucially, the current control system fails to adequately consider the physical performance constraints of the vector thruster, such as output frequency limitations, which prevent the actual output values from matching the high-frequency outputs decoupled by PID control. This causes control delays and may even lead to degraded control performance or complete loss of control. Additionally, during actual offshore testing, the vector thruster’s frequent high-frequency outputs exacerbate the risk of mechanical failures or actuator damage, further complicating maintenance efforts. In contrast, the vector thruster outputs obtained through MPC exhibit smoother variations, effectively eliminating the drawbacks associated with PID control.
5. Conclusions
By establishing the spatial captive motion numerical simulation models for the AUV, a large number of vehicle motion states and corresponding hydrodynamic forces were obtained through CFD calculations using these models. These data serve as training data for the single-layer neural network to identify hydrodynamic coefficients, thus enabling the identification of all hydrodynamic coefficients in the standard hydrodynamic equations.
By evaluating the impact of individual hydrodynamic coefficient terms on the model’s goodness-of-fit, the importance of each coefficient is ranked. Subsequently, the hydrodynamic coefficients are screened and simplified while maintaining the accuracy of the model. The standard hydrodynamic equations before simplification contained 88 hydrodynamic coefficients. After simplification, the hydrodynamic equations for the AUV are reduced to 20 coefficients.
The hydrodynamic coefficients obtained through CFD calculations were used to construct the dynamic model of the AUV. Subsequently, the NMPC controller designed using this model was validated theoretically through motion simulations. Following the simulations, water tank tests were conducted, and the experimental results demonstrated that the NMPC controller, constructed with CFD-derived hydrodynamic coefficients, could efficiently control the AUV in practical applications. This series of achievements fully proves the feasibility and applicability of using CFD-calculated hydrodynamic coefficients to establish NMPC methods in real-world scenarios.
Author Contributions
H.Z. designed the mechanical structure of the AUV. L.L. drafted the manuscript and reviewed it critically. C.Y. provided the software implementation strategy for the AUV. Y.C. agreed to be accountable for all aspects of the work, ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. H.X. completed the design and optimization of the AUV. Y.X. completed the experiments mentioned in the manuscript. G.Z. provided the hardware implementation strategy for the AUV. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by the Hainan Provincial Joint Project of Sanya Yazhou Bay Science and Technology City, Grant No: 2021CXLH0003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hou, S.; Zhang, Z.; Lian, H.; Xing, X.; Gong, H.; Xu, X. Hull Shape Optimization of Small Underwater Vehicle Based on Kriging-Based Response Surface Method and Multi-Objective Optimization Algorithm. Brodogradnja 2022, 73, 111–134. [Google Scholar] [CrossRef]
- Mansoorzadeh, S.; Javanmard, E. An Investigation of Free Surface Effects on Drag and Lift Coefficients of an Autonomous Underwater Vehicle (AUV) Using Computational and Experimental Fluid Dynamics Methods. J. Fluids Struct. 2014, 51, 161–171. [Google Scholar] [CrossRef]
- Wang, D.; Wan, J.; Shen, Y.; Qin, P.; He, B. Hyperparameter Optimization for the LSTM Method of AUV Model Identification Based on Q-Learning. J. Mar. Sci. Eng. 2022, 10, 1002. [Google Scholar] [CrossRef]
- Xu, F.; Zou, Z.J.; Yin, J.C.; Cao, J. Identification Modeling of Underwater Vehicles’ Nonlinear Dynamics Based on Support Vector Machines. Ocean Eng. 2013, 67, 68–76. [Google Scholar] [CrossRef]
- Javanmard, E.; Mansoorzadeh, S. A new CFD method for determination of translational added mass coefficients of an underwater vehicle. Ocean Eng. 2020, 215, 107857. [Google Scholar] [CrossRef]
- La Gala, F.; Dubbioso, G.; Ortolani, F.; Sellini, M. Preliminary Evaluation of Control and Manoeuvring Qualities for the AUTODROP-UUV Vehicle. IFAC Proc. Vol. 2012, 45, 132–137. [Google Scholar] [CrossRef]
- Avila, J.P.J.; Adamowski, J.C. Experimental Evaluation of the Hydrodynamic Coefficients of a ROV through Morison’s Equation. Ocean Eng. 2011, 38, 2162–2170. [Google Scholar] [CrossRef]
- Algarín, R.; Bula, A. Numerical Computation of the Hydrodynamic Coefficients on Planing Hulls in the Six Degrees of Freedom. Ocean Eng. 2021, 241, 110021. [Google Scholar] [CrossRef]
- Javanmard, E.; Mansoorzadeh, S. A Computational Fluid Dynamics Investigation on the Drag Coefficient Measurement of an AUV in a Towing Tank. J. Appl. Fluid Mech. 2019, 12, 947–959. [Google Scholar] [CrossRef]
- Gao, T.; Wang, Y.; Pang, Y.; Chen, Q.; Tang, Y. A Time-Efficient CFD Approach for Hydrodynamic Coefficient Determination and Model Simplification of Submarine. Ocean Eng. 2018, 154, 16–26. [Google Scholar] [CrossRef]
- Zhang, G.; Yan, W.; Gao, J.; Liu, C. High-Gain Observer-Based Model Predictive Control for Cross Tracking of Underactuated Autonomous Underwater Vehicles. In Proceedings of the 2016 IEEE International Conference on Underwater System Technology: Theory and Applications (USYS), Penang, Malaysia, 13–14 December 2016; pp. 115–120. [Google Scholar]
- Fan, S.; Li, B.; Xu, W.; Xu, Y. Impact of Current Disturbances on AUV Docking: Model-Based Motion Prediction and Countering Approaches. IEEE J. Ocean. Eng. 2017, 43, 888–904. [Google Scholar] [CrossRef]
- Gao, J.; Liu, C.; Proctor, A. Nonlinear Model Predictive Dynamic Positioning Control of an Underwater Vehicle with an Onboard USBL System. J. Mar. Sci. Technol. 2016, 21, 57–69. [Google Scholar] [CrossRef]
- Wu, C.; Dai, Y.; Shan, L.; Zhu, Z. Date-Driven Tracking Control via Fuzzy-State Observer for AUV under Uncertain Disturbance and Time-Delay. J. Mar. Sci. Eng. 2023, 11, 207. [Google Scholar] [CrossRef]
- Jagtap, P.; Raut, P.; Kumar, P.; Gupta, A.; Singh, N.; Kazi, F. Control of Autonomous Underwater Vehicle Using Reduced Order Model Predictive Control in Three Dimensional Space. IFAC-Pap. 2016, 49, 772–777. [Google Scholar] [CrossRef]
- Chen, Y.; Bian, Y. Tube-Based Event-Triggered Path Tracking for AUV against Disturbances and Parametric Uncertainties. Electronics 2023, 12, 4248. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Karras, G.C.; Marantos, P.; Kyriakopoulos, K.J. A Robust Predictive Control Approach for Underwater Robotic Vehicles. IEEE Trans. Control Syst. Technol. 2019, 28, 2352–2363. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y. Distributed Implementation of Nonlinear Model Predictive Control for AUV Trajectory Tracking. Automatica 2020, 115, 108863. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Nikou, A.; Dimarogonas, D.V. Robust Trajectory Tracking Control for Underactuated Autonomous Underwater Vehicles in Uncertain Environments. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1288–1301. [Google Scholar] [CrossRef]
- Li, X.; Yu, S.; Gao, X.; Yan, Y.; Zhao, Y. Path Planning and Obstacle Avoidance Control of UUV Based on an Enhanced A* Algorithm and MPC in Dynamic Environment. Ocean Eng. 2024, 302, 117584. [Google Scholar] [CrossRef]
- Xu, B.; Wang, Z.; Li, W.; Yu, Q. Distributed Robust Model Predictive Control-Based Formation-Containment Tracking Control for Autonomous Underwater Vehicles. Ocean Eng. 2023, 283, 115210. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Zhang, H. Distributed Dynamic Predictive Control for Multi-AUV Target Searching and Hunting in Unknown Environments. Machines 2022, 10, 366. [Google Scholar] [CrossRef]
- Yang, N.; Chang, D.; Johnson-Roberson, M.; Sun, J. Robust Energy-Optimal Path Following Control for Autonomous Underwater Vehicles in Ocean Currents. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 5119–5124. [Google Scholar]
- Yang, N.; Chang, D.; Johnson-Roberson, M.; Sun, J. Energy-Optimal Control for Autonomous Underwater Vehicles Using Economic Model Predictive Control. IEEE Trans. Control Syst. Technol. 2022, 30, 2377–2390. [Google Scholar] [CrossRef]
- Bhat, S.; Panteli, C.; Stenius, I.; Dimarogonas, D.V. Nonlinear Model Predictive Control for Hydrobatics: Experiments with an Underactuated AUV. J. Field Robot. 2023, 40, 1840–1859. [Google Scholar] [CrossRef]
- Gao, T.; Luo, Y.; Lv, C.; Luo, W.; Fu, X.; Zhao, N.; Luo, X.; Shen, Y. Model Predictive Control for an Autonomous Underwater Robot with Fully Vectored Propulsion. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 10482–10488. [Google Scholar]
- Wang, Z.; Wei, Z.; Yu, C.; Cao, J.; Yao, B.; Lian, L. Dynamic Modeling and Optimal Control of a Positive Buoyancy Diving Autonomous Vehicle. Brodogradnja 2023, 74, 19–40. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, L.; Yu, C.; Chen, Y.; Xiong, H.; Xing, Y.; Zheng, G. The Design and Application of a Vectored Thruster for a Negative Lift-Shaped AUV. Actuators 2024, 13, 228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).