Robust Relative Space Motion Control of Underwater Vehicles Using Time Delay Estimation
Abstract
1. Introduction
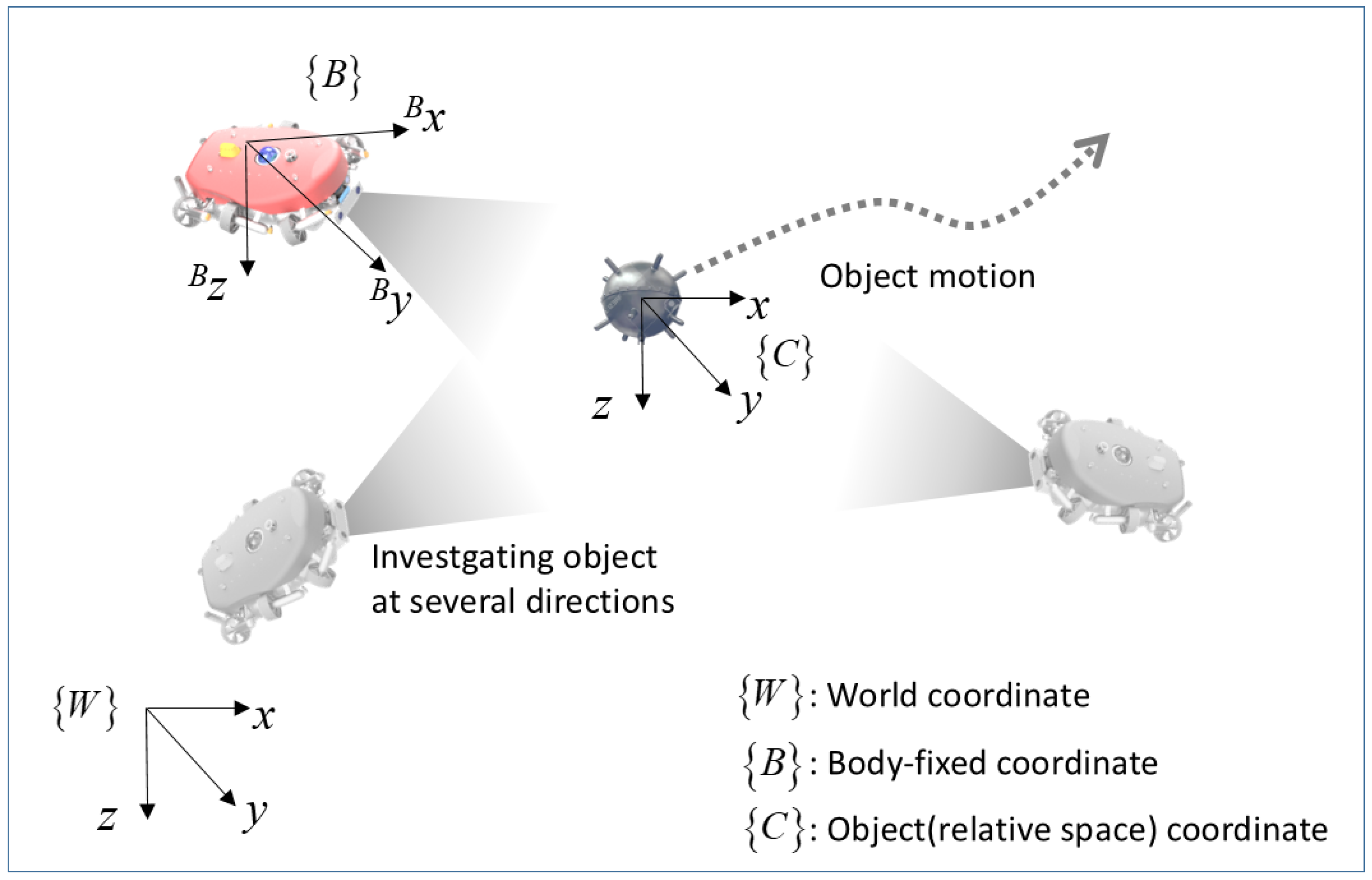
2. Dynamics of Underwater Vehicles in the Relative Space
3. Robust Control for Tracking Trajectories in Relative Space
3.1. Design of Robust Relative Motion Controller
3.2. Stability Anlaysis
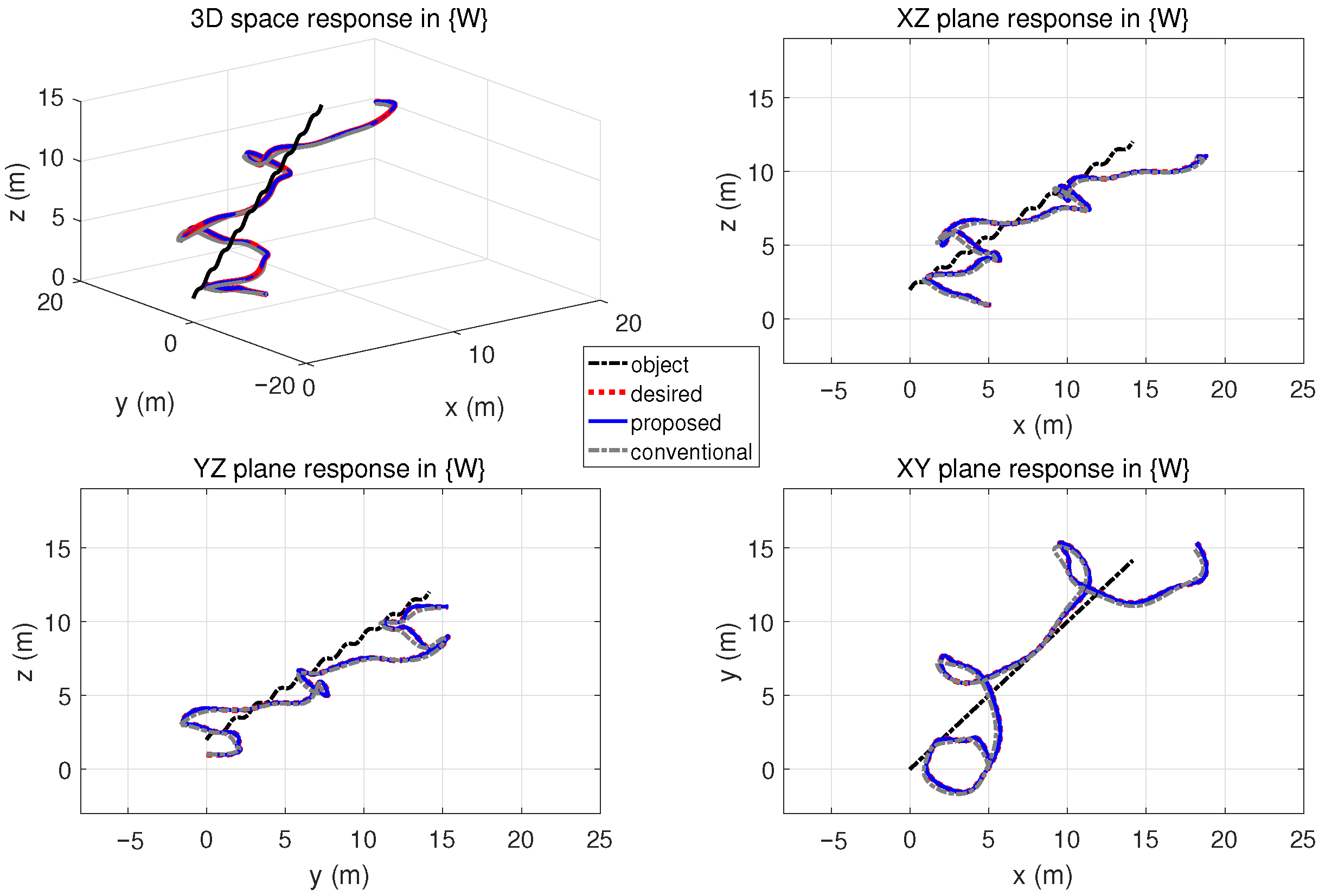
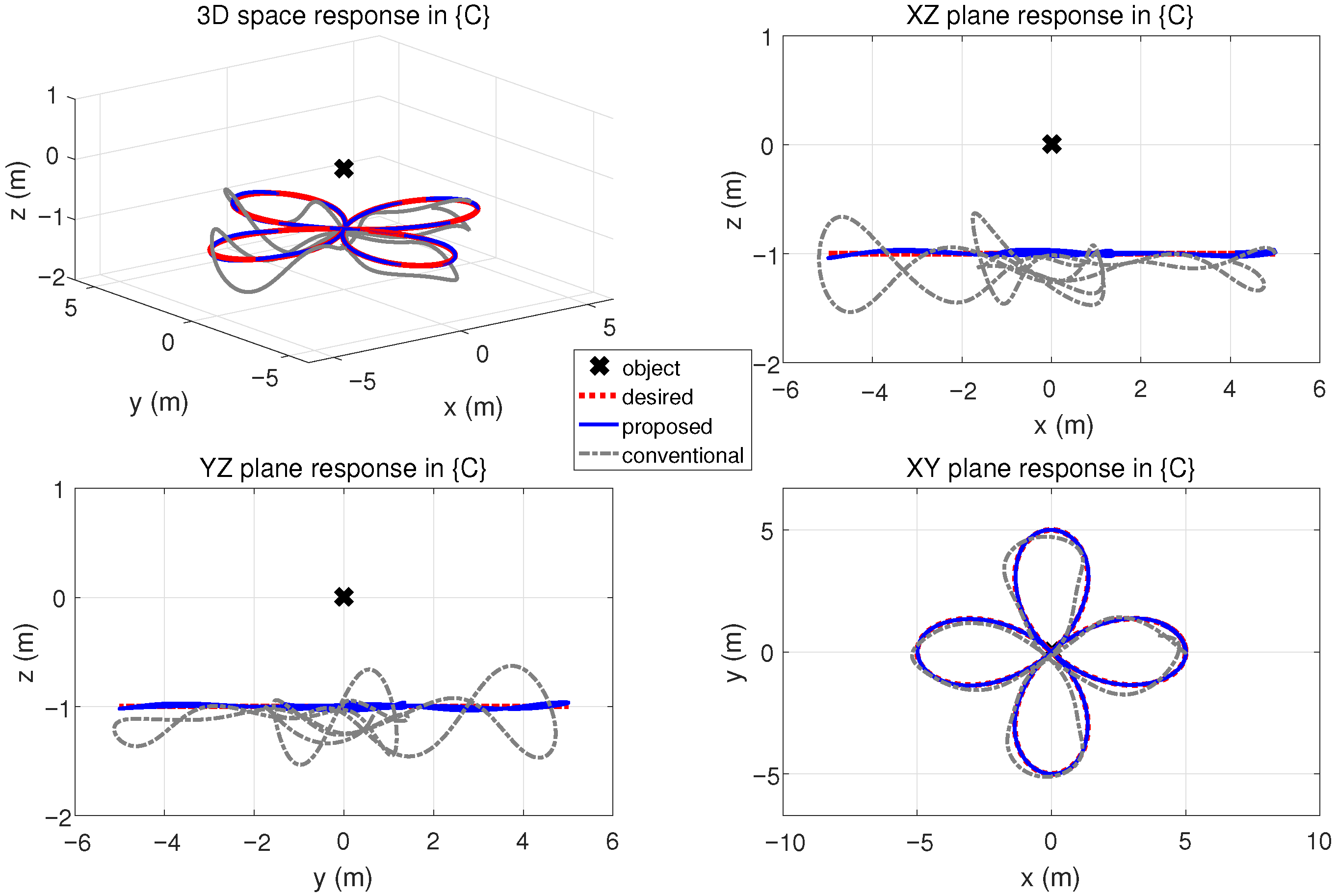
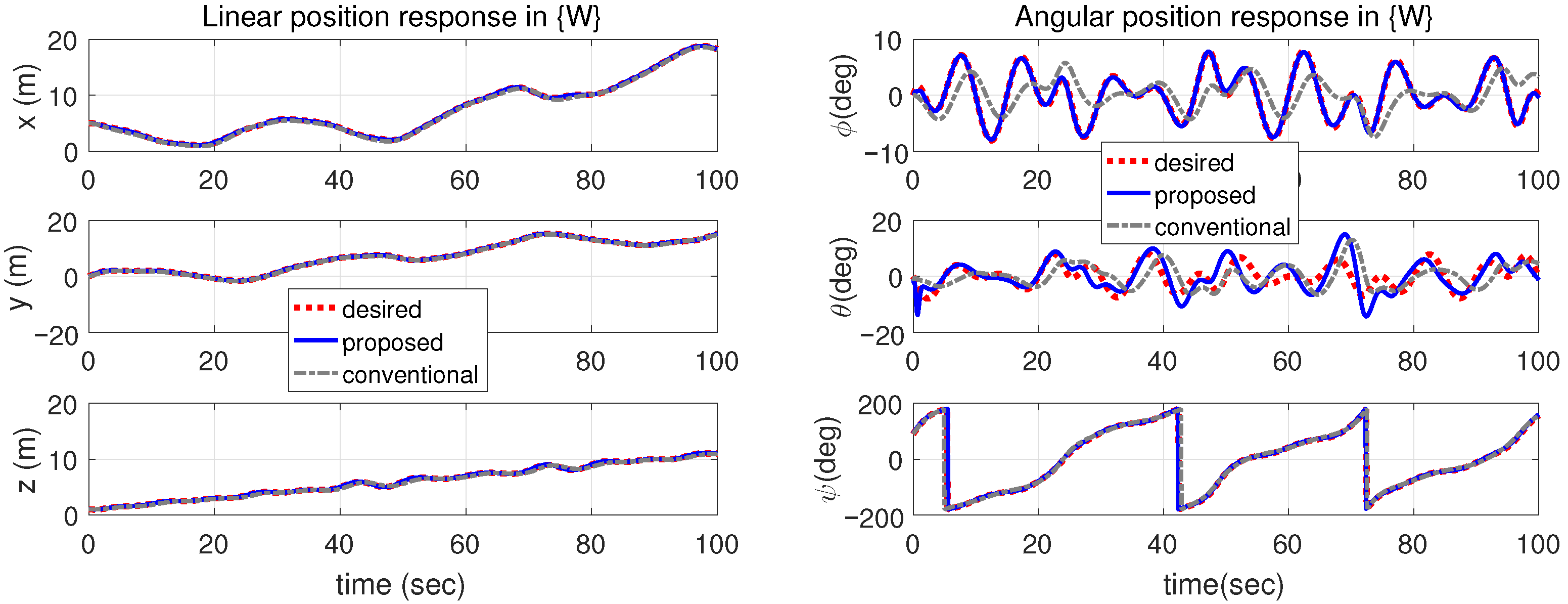
4. Simulation
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| World coordinate frame | |
| Body-fixed coordinate frame of the vehicle | |
| Object (relative) coordinate frame | |
| Rotation matrix from frame to | |
| Linear velocity of expressed in | |
| Angular velocity of expressed in | |
| Inertia matrix of the underwater vehicle | |
| Coriolis and centripetal matrix | |
| Hydrodynamic damping matrix | |
| Restoring forces and moments (gravity and buoyancy) | |
| Control input vector in frame | |
| Environmental disturbance vector | |
| Linear and angular velocity vector in | |
| Linear and angular velocity vector expressed in | |
| Adjoint transformation (Jacobian) from to | |
| Additional velocity term due to motion of (Equation (5)) | |
| Position of origin w.r.t. | |
| Linear and angular velocities of w.r.t. | |
| Augmented nonlinear term (Equation (3)) | |
| Nonlinear term transformed into (Equation (12)) | |
| Estimated nonlinear term via TDE | |
| L | Sampling interval (time delay) |
| Desired input in relative frame | |
| Proportional / derivative gain matrices | |
| Position / velocity error in | |
| Rotational error vector (Equation (28)) | |
| Time-delay estimation (TDE) error | |
| Forcing functions in TDE error dynamics | |
| Identity matrix | |
| Transpose of • |
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| TDC | Time Delay Control |
| TDE | Time Delay Estimation |
| BIBO | Bounded Input Bounded Output |
Appendix A. Proof of Lemma 1
Appendix B. Proof of (11)
Appendix C. Proof of Lemma 2
Appendix D. Proof of Theorem 1
References
- Kartal, S.K.; Cantekin, R.F. Autonomous underwater pipe damage detection positioning and pipe line tracking experiment with unmanned underwater vehicle. J. Mar. Sci. Eng. 2024, 12, 2002. [Google Scholar] [CrossRef]
- Kang, H.; Cho, G.R.; Jin, H.; Kim, M.G.; Li, J.H.; Jin, S.; Lee, J.; Min, J. Robot-Based Diver Safety Support Scenario and Concept Design for NADIA. J. Ocean Eng. Technol. 2025, 39, 235–247. [Google Scholar] [CrossRef]
- Cho, G.R.; Kang, H.; Kim, M.G.; Park, S.; Jin, H.; Jin, S. Operational Space Fomulation of Time Delay Control for Underwater Vehicles and its Extension to Diver Guidance. In Proceedings of the 2025 IEEE Underwater Technology (UT), Taipei, Taiwan, 2–5 March 2025; pp. 1–8. [Google Scholar]
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Yan, T.; Xu, Z.; Yang, S.X.; Gadsden, S.A. Formation control of multiple autonomous underwater vehicles: A review. Intell. Robot. 2023, 3, 1–22. [Google Scholar] [CrossRef]
- Zheng, R.; Song, T.; Sun, Q.; Guo, J. Review on underwater docking technology of AUV. Chin. J. Ship Res. 2018, 13, 43–49. [Google Scholar]
- Sun, Y.; Ran, X.; Cao, J.; Li, Y. Deep submergence rescue vehicle docking based on parameter adaptive control with acoustic and visual guidance. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420919955. [Google Scholar] [CrossRef]
- Li, D.-j.; Chen, Y.-h.; Shi, J.-g.; Yang, C.-j. Autonomous underwater vehicle docking system for cabled ocean observatory network. Ocean Eng. 2015, 109, 127–134. [Google Scholar] [CrossRef]
- Somerton, D.A.; Williams, K.; Campbell, M.D. Quantifying the behavior of fish in response to a moving camera vehicle by using benthic stereo cameras and target tracking. Fish. Bull. 2017, 115, 343–354. [Google Scholar] [CrossRef]
- Neettiyath, U.; Thondiyath, A. Dynamic formations of autonomous underwater vehicles using state estimation. In Proceedings of the Conference on Advances In Robotics, Pune, India, 4–6 July 2013; pp. 1–6. [Google Scholar]
- Zheng, L.; Ma, Y.; Yu, H.; Tang, Y. Multicooperation of Turtle-inspired amphibious spherical robots. Sci. Rep. 2025, 15, 2932. [Google Scholar] [CrossRef]
- Furukawa, T.; Matsuda, T. A Positioning Method Based on Path Control of Multiple Autonomous Underwater Vehicles. In Proceedings of the OCEANS 2024-Singapore, Singapore, 15–18 April 2024; pp. 1–5. [Google Scholar]
- García-Valdovinos, L.G.; Salgado-Jiménez, T.; Bandala-Sánchez, M.; Nava-Balanzar, L.; Hernández-Alvarado, R.; Cruz-Ledesma, J.A. Modelling, design and robust control of a remotely operated underwater vehicle. Int. J. Adv. Robot. Syst. 2014, 11, 1. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Karras, G.C.; Marantos, P.; Kyriakopoulos, K.J. A robust predictive control approach for underwater robotic vehicles. IEEE Trans. Control Syst. Technol. 2019, 28, 2352–2363. [Google Scholar] [CrossRef]
- Heshmati-Alamdari, S.; Nikou, A.; Dimarogonas, D.V. Robust trajectory tracking control for underactuated autonomous underwater vehicles in uncertain environments. IEEE Trans. Autom. Sci. Eng. 2020, 18, 1288–1301. [Google Scholar] [CrossRef]
- Kumar, R.P.; Dasgupta, A.; Kumar, C. Robust trajectory control of underwater vehicles using time delay control law. Ocean Eng. 2007, 34, 842–849. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, C.; Sen, D.; Dasgupta, A. Discrete time-delay control of an autonomous underwater vehicle: Theory and experimental results. Ocean Eng. 2009, 36, 74–81. [Google Scholar] [CrossRef]
- Kim, J.; Joe, H.; Yu, S.c.; Lee, J.S.; Kim, M. Time-delay controller design for position control of autonomous underwater vehicle under disturbances. IEEE Trans. Ind. Electron. 2016, 63, 1052–1061. [Google Scholar] [CrossRef]
- Li, J.; Zhu, G.; Lu, J.; Chen, C. FTILOS-based self-triggered adaptive neural path following control for 4DOF underactuated unmanned surface vehicles. Ocean Eng. 2024, 295, 116947. [Google Scholar] [CrossRef]
- Zhu, G.; Li, J.; Ma, Y.; Hu, S. FT-ILOS-based adaptive fuzzy path following of USVs under input saturation via parallel-self-triggered approach. IEEE J. Ocean. Eng. 2025, 50, 2744–2755. [Google Scholar] [CrossRef]
- Liu, J.; Yu, F.; He, B.; Soares, C.G. A review of underwater docking and charging technology for autonomous vehicles. Ocean Eng. 2024, 297, 117154. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Shen, Y.; Dai, N.; He, B. Multi-AUV cooperative control and autonomous obstacle avoidance study. Ocean Eng. 2024, 304, 117634. [Google Scholar] [CrossRef]
- Ni, T.; Sima, C.; Zhang, W.; Wang, J.; Guo, J.; Zhang, L. Vision-based underwater docking guidance and positioning: Enhancing detection with YOLO-D. J. Mar. Sci. Eng. 2025, 13, 102. [Google Scholar] [CrossRef]
- Chen, B.; Hu, J.; Ghosh, B.K. Finite-time coordination controls for multiple autonomous underwater vehicle systems. Eng. Rep. 2024, 6, e12804. [Google Scholar] [CrossRef]
- Youcef-Toumi, K.; Ito, O. A time delay controller for systems with unknown dynamics. J. Dyn. Syst. Meas. Control 1990, 112, 133–142. [Google Scholar] [CrossRef]
- Hsia, T.; Gao, L. Robot manipulator control using decentralized linear time-invariant time-delayed joint controllers. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 2070–2075. [Google Scholar]
- Cho, G.R.; Chang, P.H.; Park, S.H.; Jin, M. Robust tracking under nonlinear friction using time-delay control with internal model. IEEE Trans. Control Syst. Technol. 2009, 17, 1406–1414. [Google Scholar]
- Cho, G.R.; Li, J.H.; Park, D.; Jung, J.H. Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation. Ocean Eng. 2020, 201, 107131. [Google Scholar] [CrossRef]
- Cho, G.R.; Kang, H.; Kim, M.G.; Lee, M.J.; Li, J.H.; Kim, H.; Lee, H.; Lee, G. An Experimental Study on Trajectory Tracking Control of Torpedo-like AUVs Using Coupled Error Dynamics. J. Mar. Sci. Eng. 2023, 11, 1334. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Zhang, G.; Xing, Y.; Zhang, W.; Li, J. Prescribed Performance Control for USV-UAV via a Robust Bounded Compensating Technique. IEEE Trans. Control Netw. Syst. 2025, 12, 2289–2299. [Google Scholar] [CrossRef]
- Marani, G.; Yuh, J. Introduction to Autonomous Manipulation. Case Study with an Underwater Robot, SAUVIM; Springer: Berlin/Heidelberg, Germany, 2014; Volume 102. [Google Scholar]
- Lee, T. Exponential stability of an attitude tracking control system on SO(3) for large-angle rotational maneuvers. Syst. Control Lett. 2012, 61, 231–237. [Google Scholar] [CrossRef]
- Jung, S.; Hsia, T.C.; Bonitz, R.G. Force tracking impedance control of robot manipulators under unknown environment. IEEE Trans. Control Syst. Technol. 2004, 12, 474–483. [Google Scholar] [CrossRef]
- Hsia, T. Simple robust schemes for cartesian space control of robot manipulators. Int. J. Robot. Autom. 1994, 9, 167–174. [Google Scholar]
- Jin, M.; Lee, J.; Chang, P.H.; Choi, C. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control. IEEE Trans. Ind. Electron. 2009, 56, 3593–3601. [Google Scholar]
- Jung, J.; Chang, P.; Stefanov, D. Discretisation method and stability criteria for non-linear systems under discrete-time time delay control. IET Control Theory Appl. 2011, 5, 1264–1276. [Google Scholar] [CrossRef]
- Wu, C.J. 6-Dof Modelling and Control of a Remotely Operated Vehicle. Ph.D. Thesis, College of Science and Engineering, Flinders University, Adelaide, Australia, 2018. [Google Scholar]
- Zhang, G.; Sun, Z.; Li, J.; Huang, J.; Qiu, B. Iterative learning control for path-following of ASV with the ice floes auto-select avoidance mechanism. IEEE Trans. Intell. Transp. Syst. 2025, 26, 13927–13938. [Google Scholar] [CrossRef]


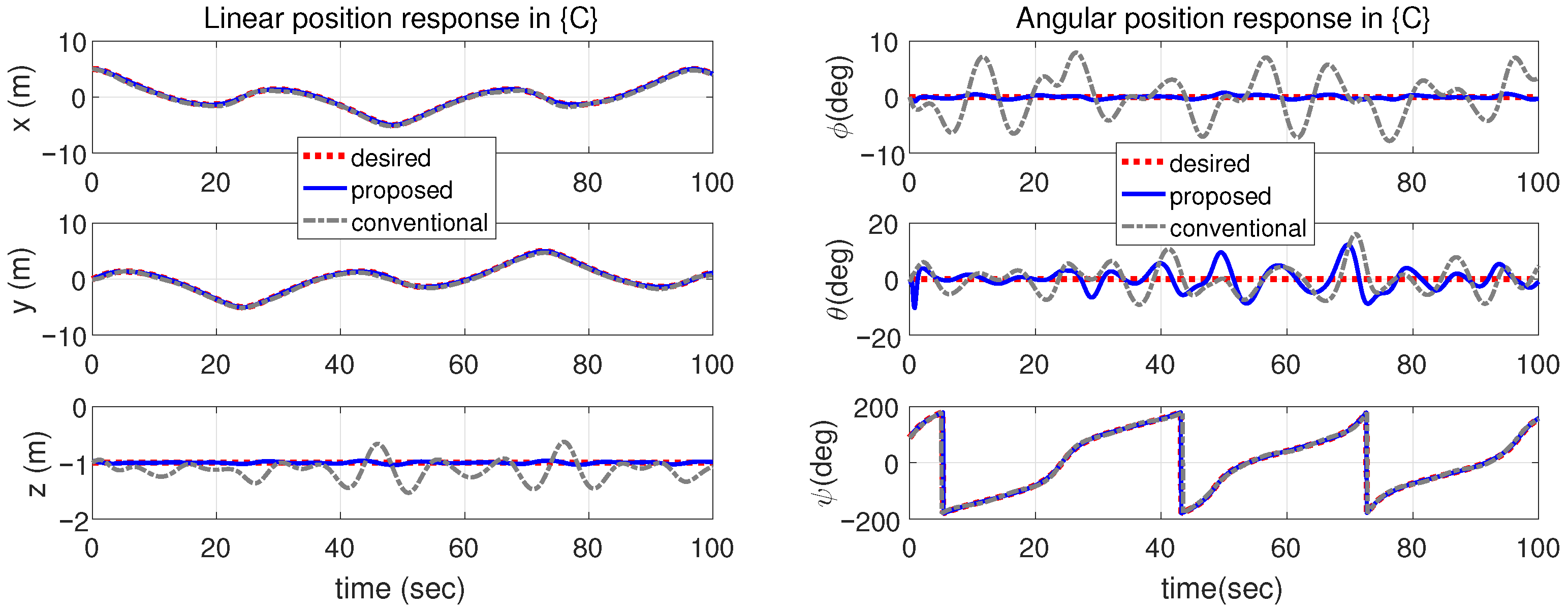

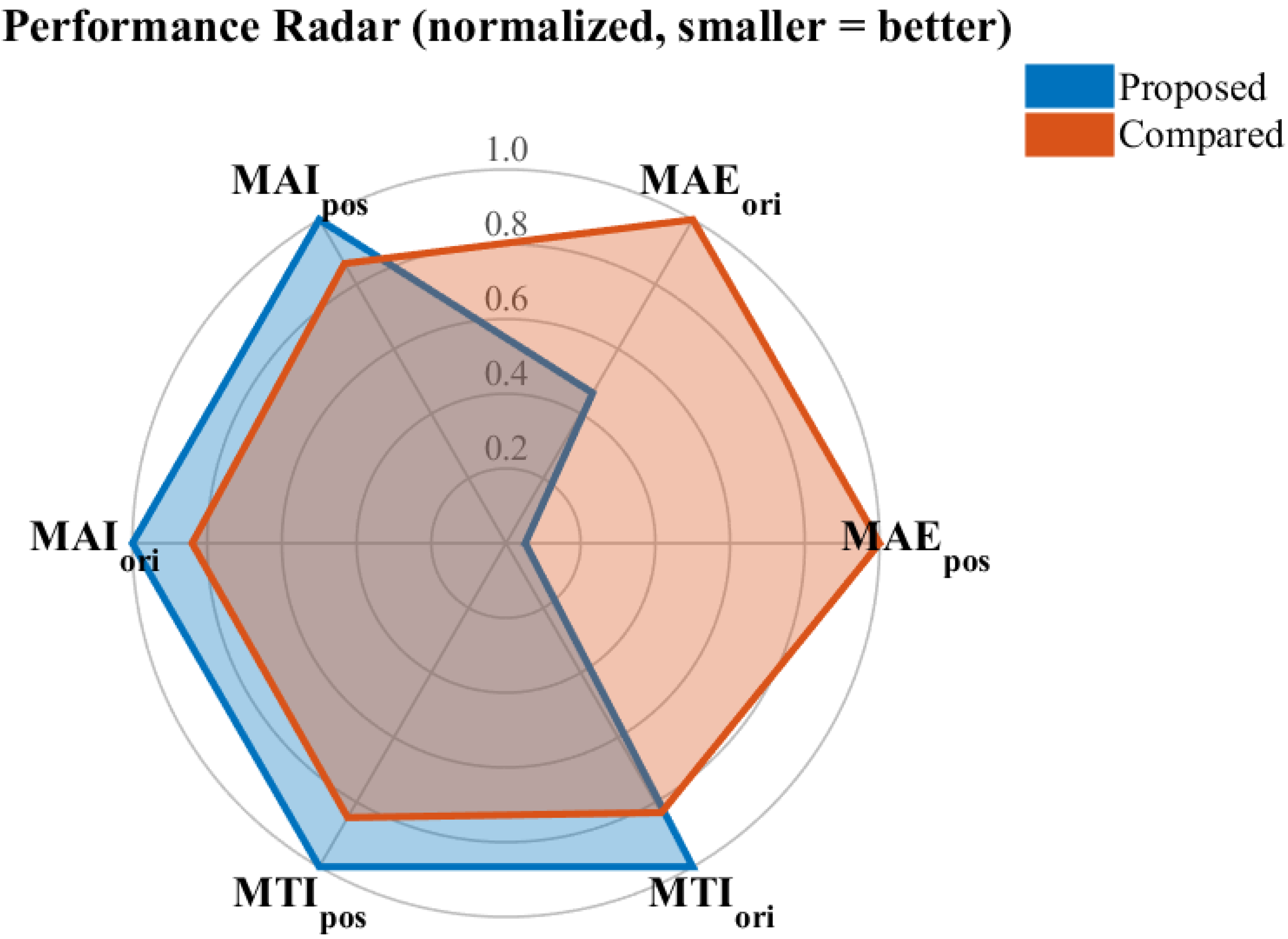
| Controller | x | y | z | Roll | Pitch | Yaw |
|---|---|---|---|---|---|---|
| ① Proposed (mm, deg) | 10.9 | 13.6 | 16.0 | 0.286 | 3.873 | 0.709 |
| ② Compared (mm, deg) | 219.3 | 220.4 | 220.0 | 3.898 | 4.911 | 3.729 |
| ①/② × 100(%) | 4.97 | 6.17 | 7.27 | 7.33 | 78.85 | 19.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, G.R.; Kang, H.; Kim, M.-G.; Park, S.; Bae, C.; Jin, H.-S.; Jin, S.; Li, J.-H. Robust Relative Space Motion Control of Underwater Vehicles Using Time Delay Estimation. J. Mar. Sci. Eng. 2025, 13, 2214. https://doi.org/10.3390/jmse13112214
Cho GR, Kang H, Kim M-G, Park S, Bae C, Jin H-S, Jin S, Li J-H. Robust Relative Space Motion Control of Underwater Vehicles Using Time Delay Estimation. Journal of Marine Science and Engineering. 2025; 13(11):2214. https://doi.org/10.3390/jmse13112214
Chicago/Turabian StyleCho, Gun Rae, Hyungjoo Kang, Min-Gyu Kim, Sungho Park, Chulhee Bae, Han-Sol Jin, Seongho Jin, and Ji-Hong Li. 2025. "Robust Relative Space Motion Control of Underwater Vehicles Using Time Delay Estimation" Journal of Marine Science and Engineering 13, no. 11: 2214. https://doi.org/10.3390/jmse13112214
APA StyleCho, G. R., Kang, H., Kim, M.-G., Park, S., Bae, C., Jin, H.-S., Jin, S., & Li, J.-H. (2025). Robust Relative Space Motion Control of Underwater Vehicles Using Time Delay Estimation. Journal of Marine Science and Engineering, 13(11), 2214. https://doi.org/10.3390/jmse13112214








