Evaluation of Different AI-Based Wave Phase-Resolved Prediction Methods
Abstract
1. Introduction
2. Data and Error Evaluation Methods
2.1. Data Sources
2.2. Error Evaluation Methods
3. Method and Theory
3.1. Physical Basis of Phase-Resolved Wave Intelligent Prediction
3.2. Overview of Phase-Resolved Wave Intelligent Prediction Model
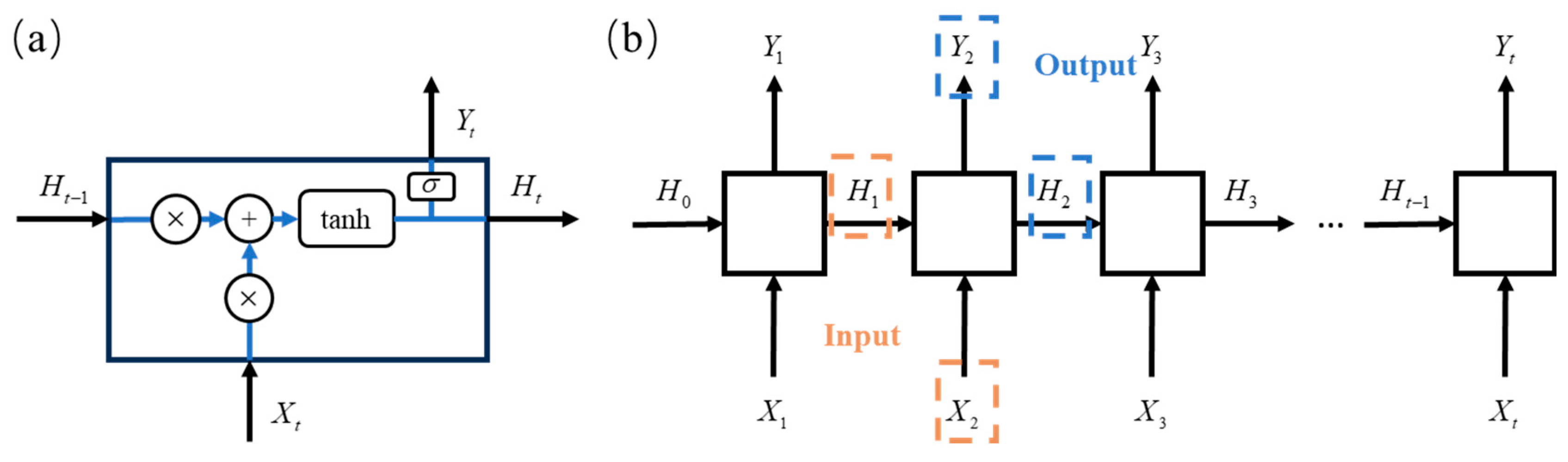
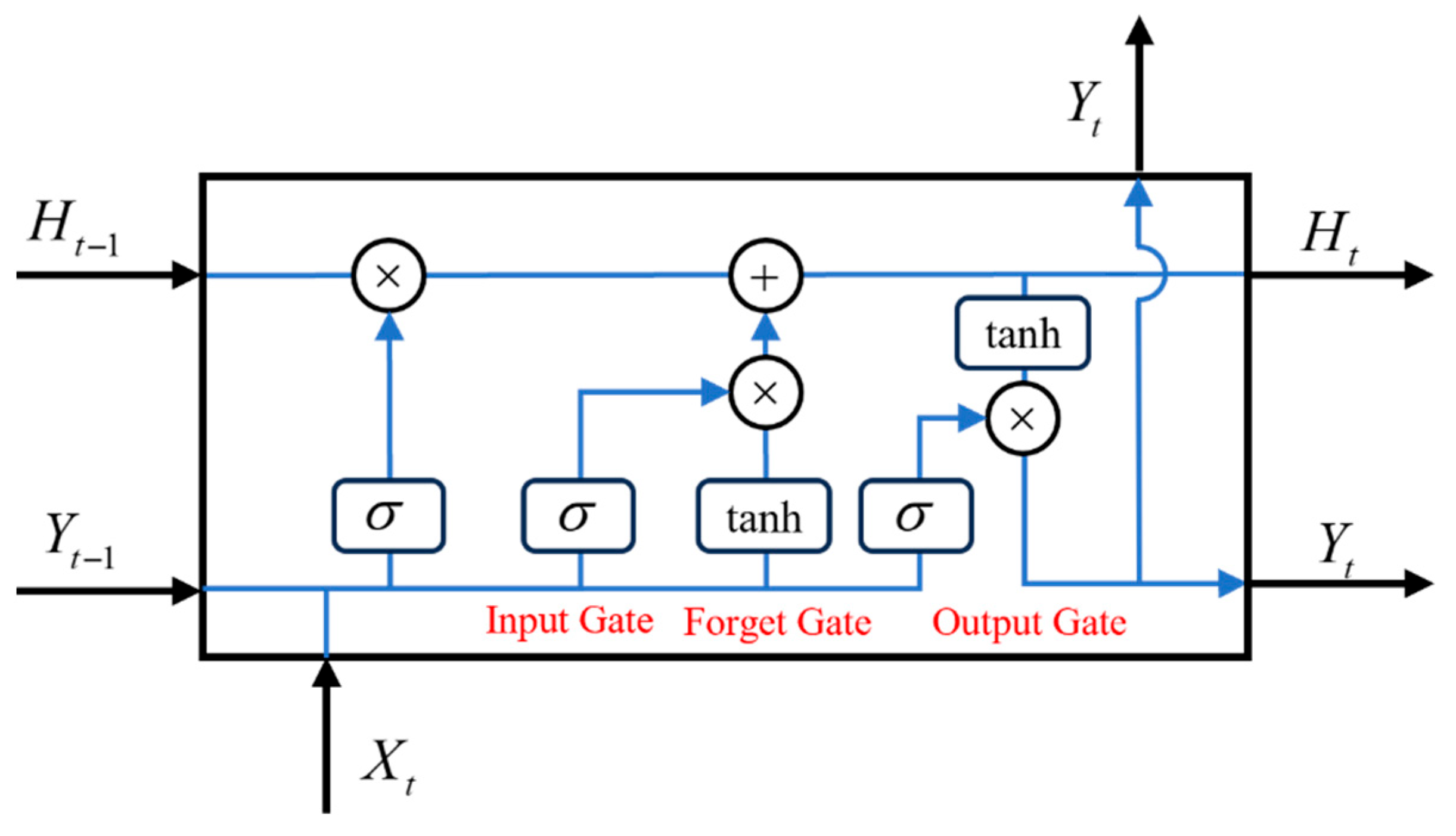
3.2.1. Recurrent Neural Network for Wave Prediction (RNN-WP)
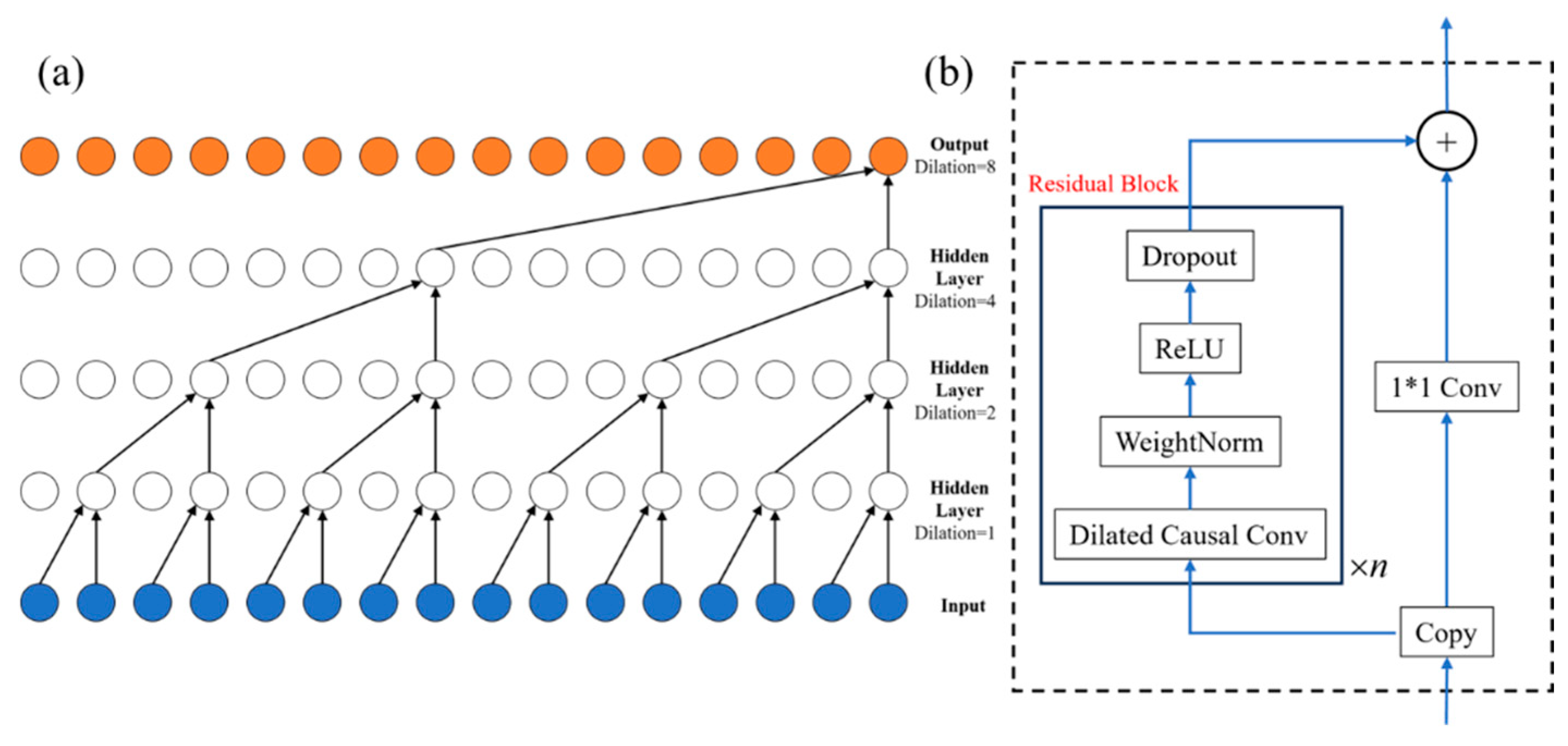
3.2.2. Temporal Convolutional Network for Wave Prediction (TCN-WP)
4. Results and Analysis
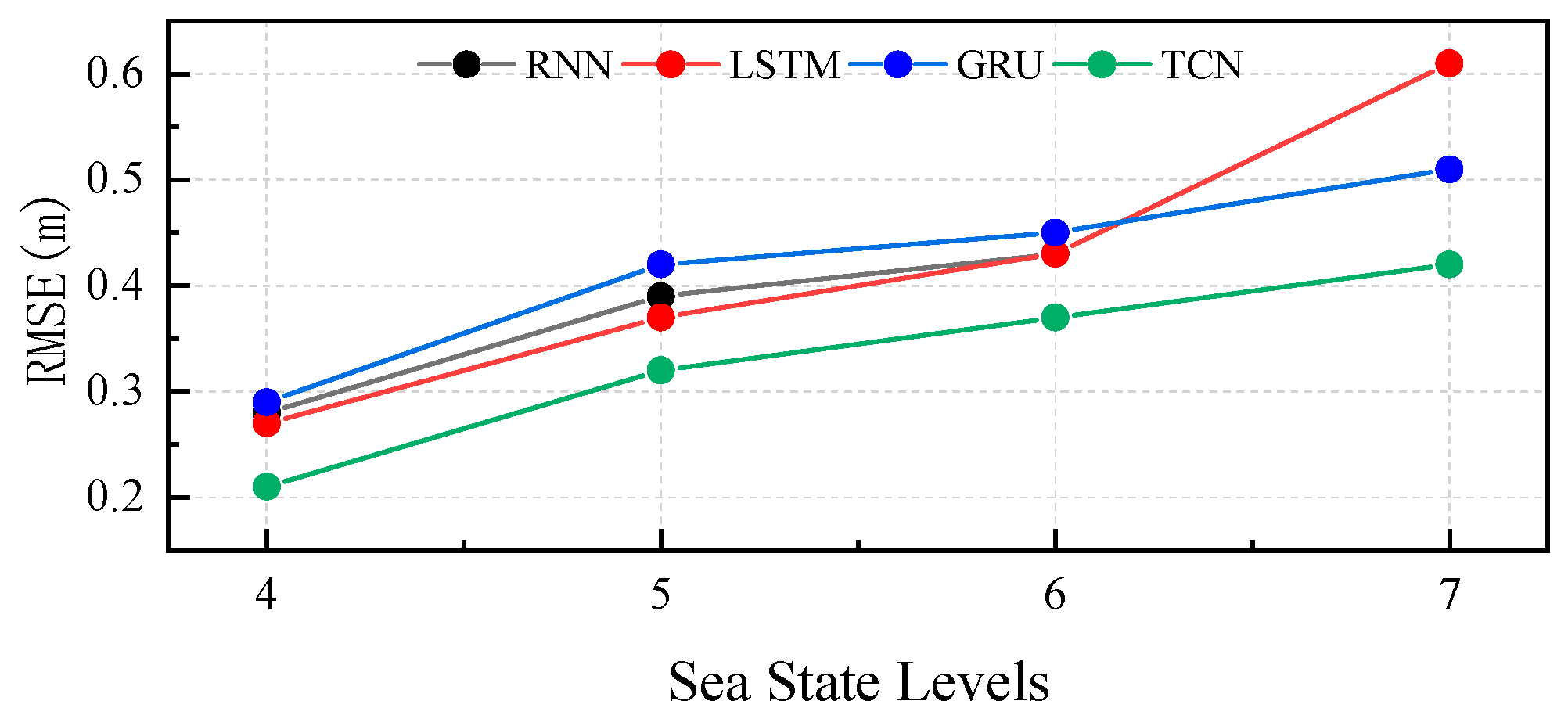
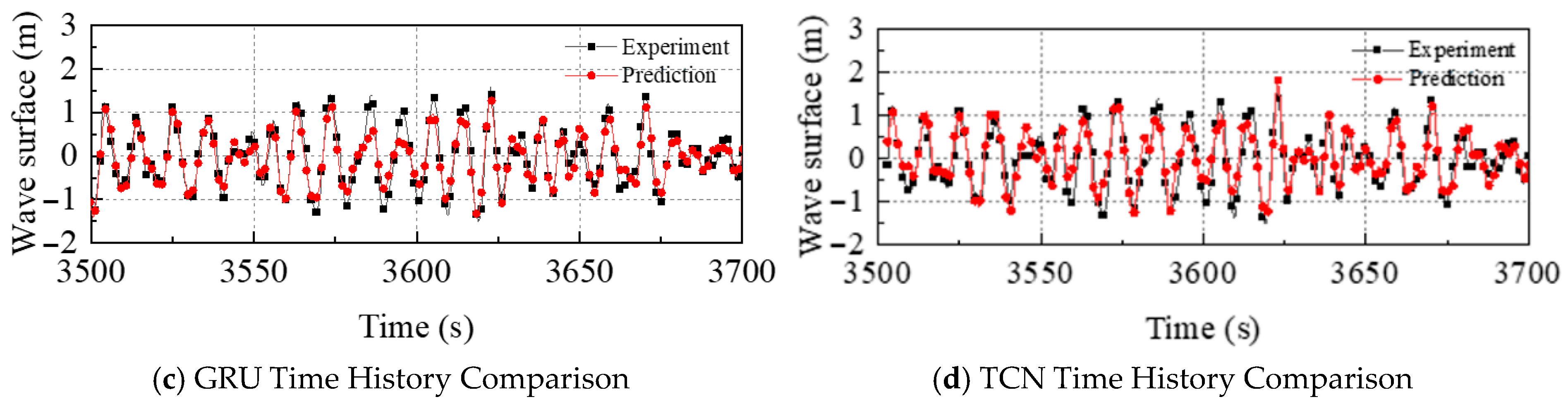
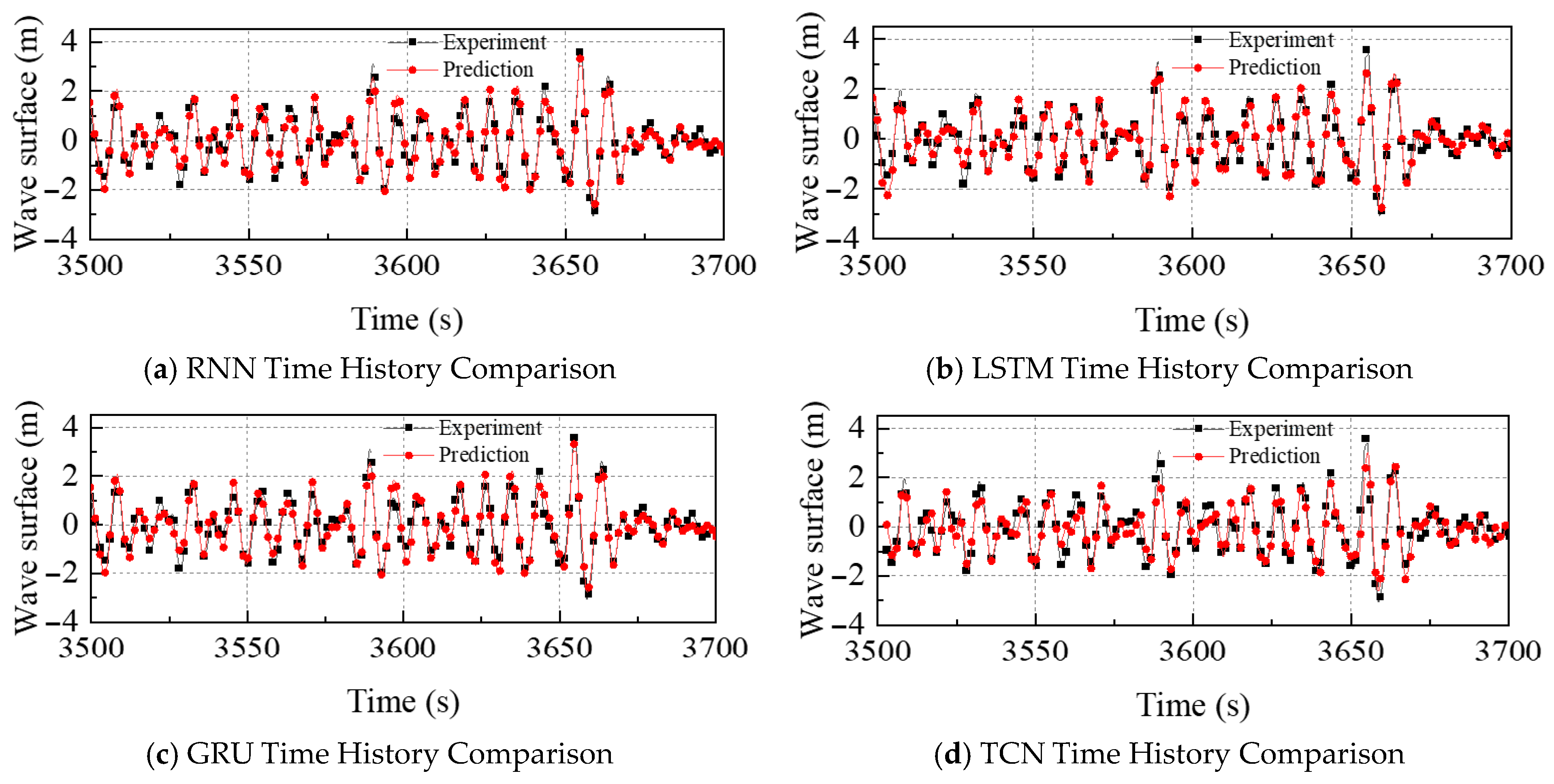
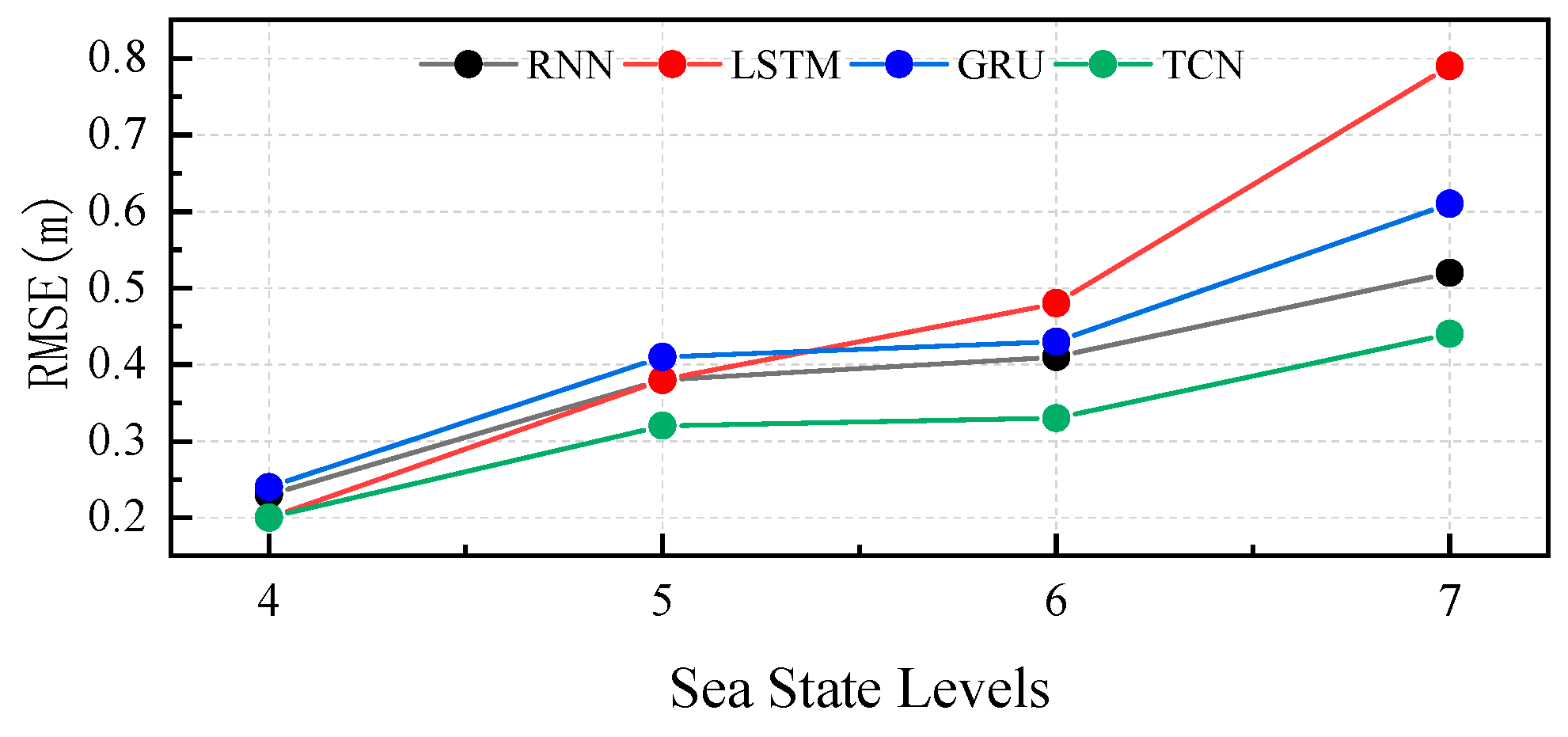
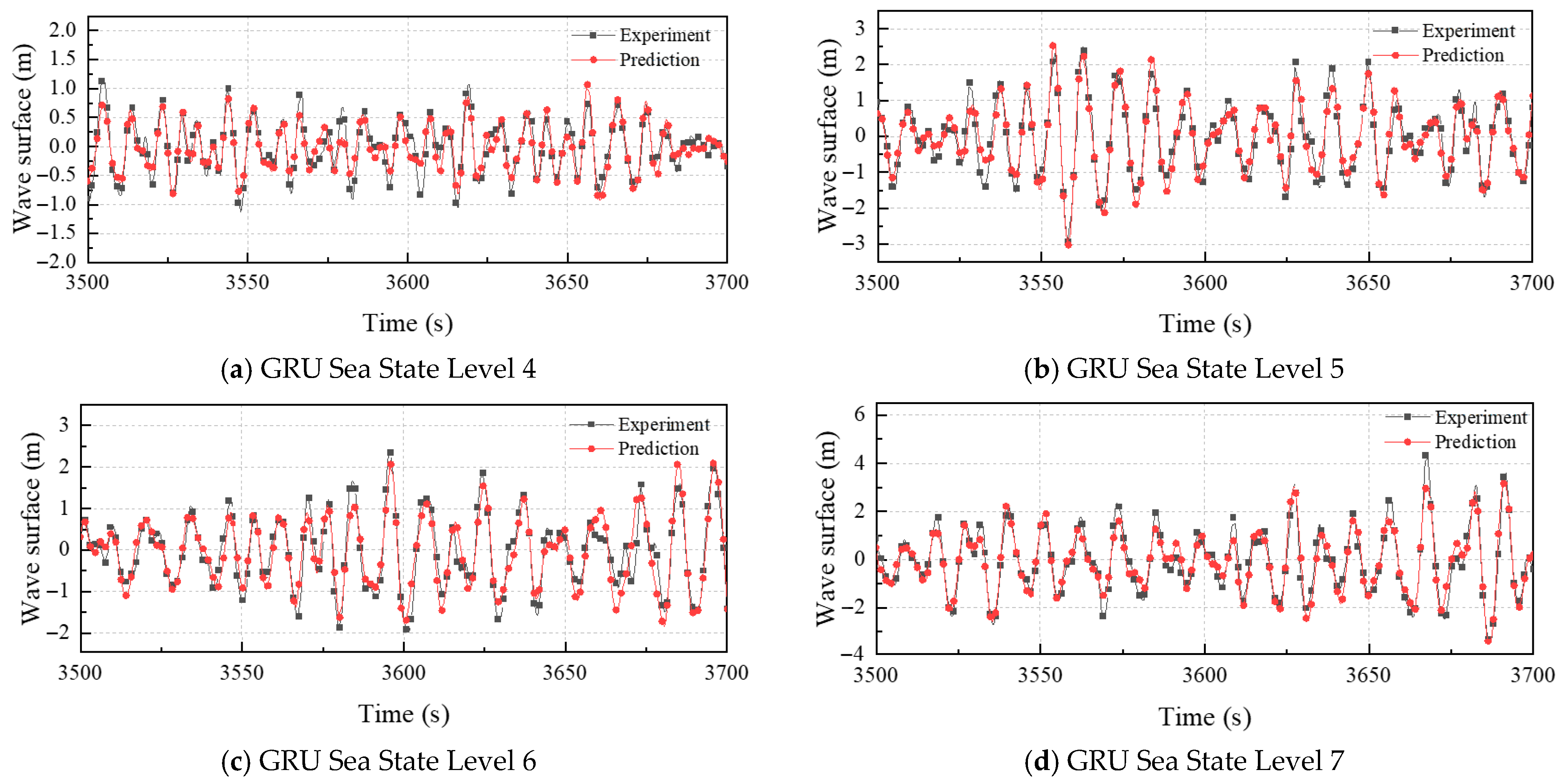
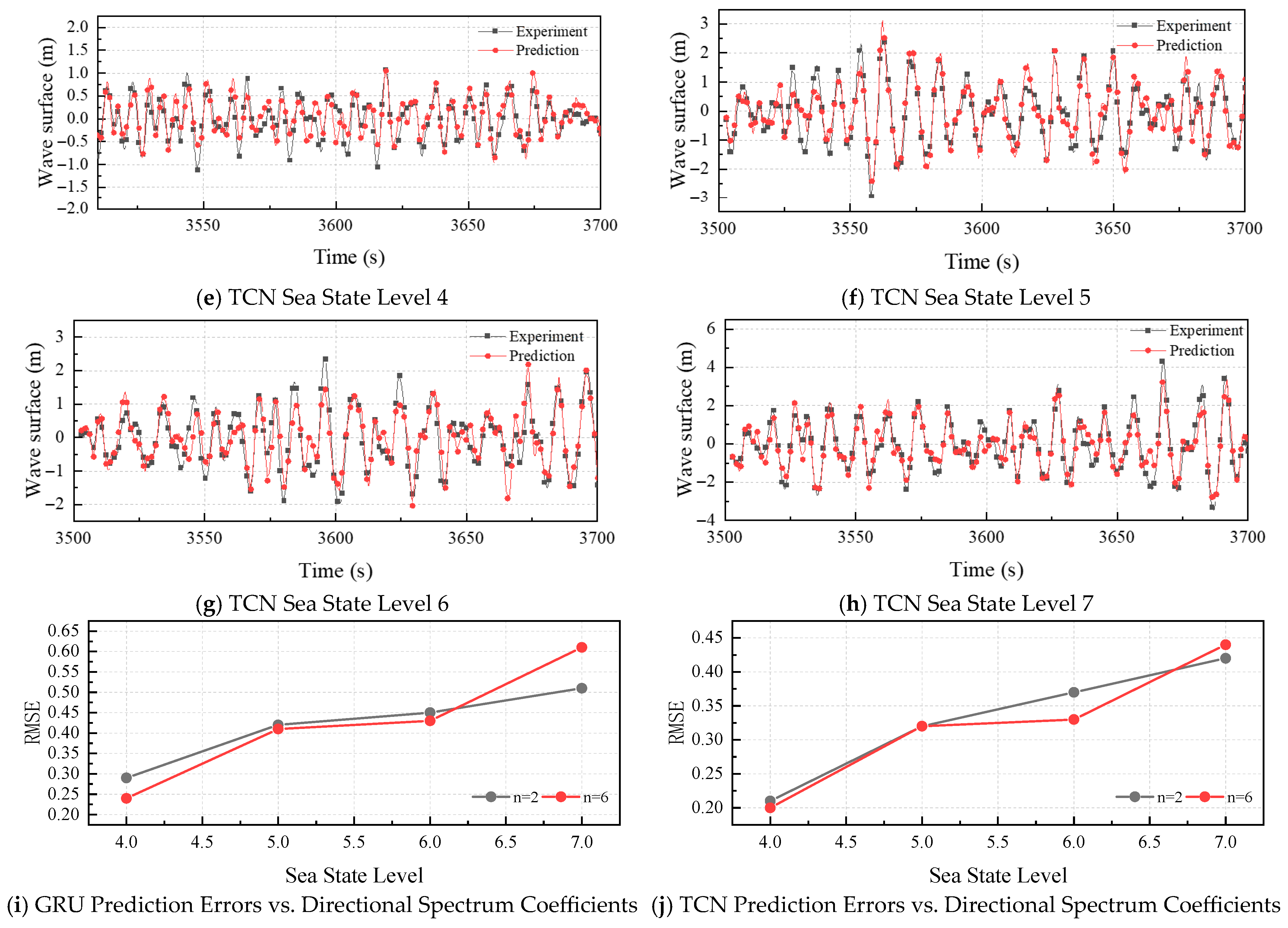
4.1. Influence of Sea State
4.2. Influence of Directional Spectrum
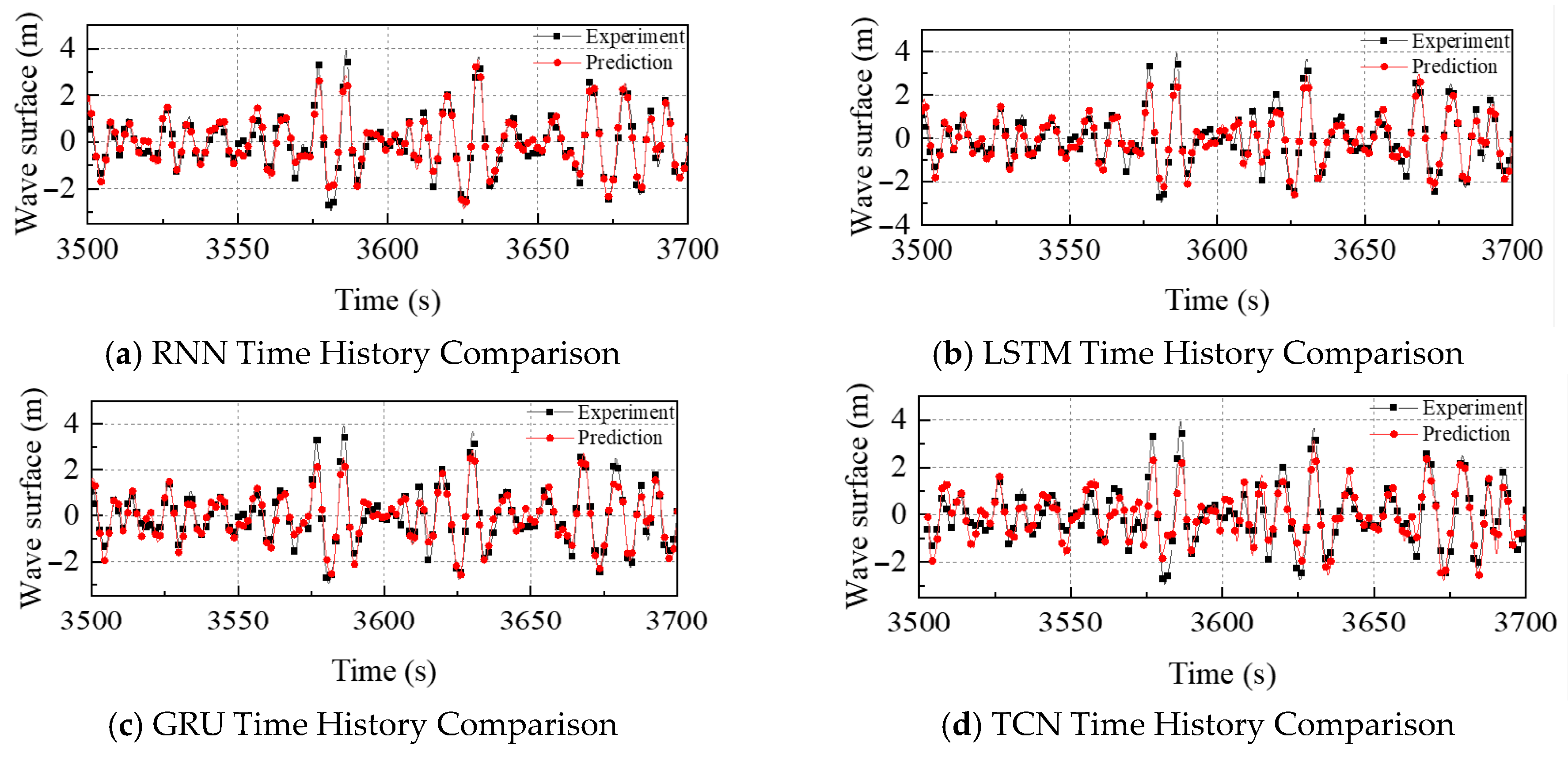
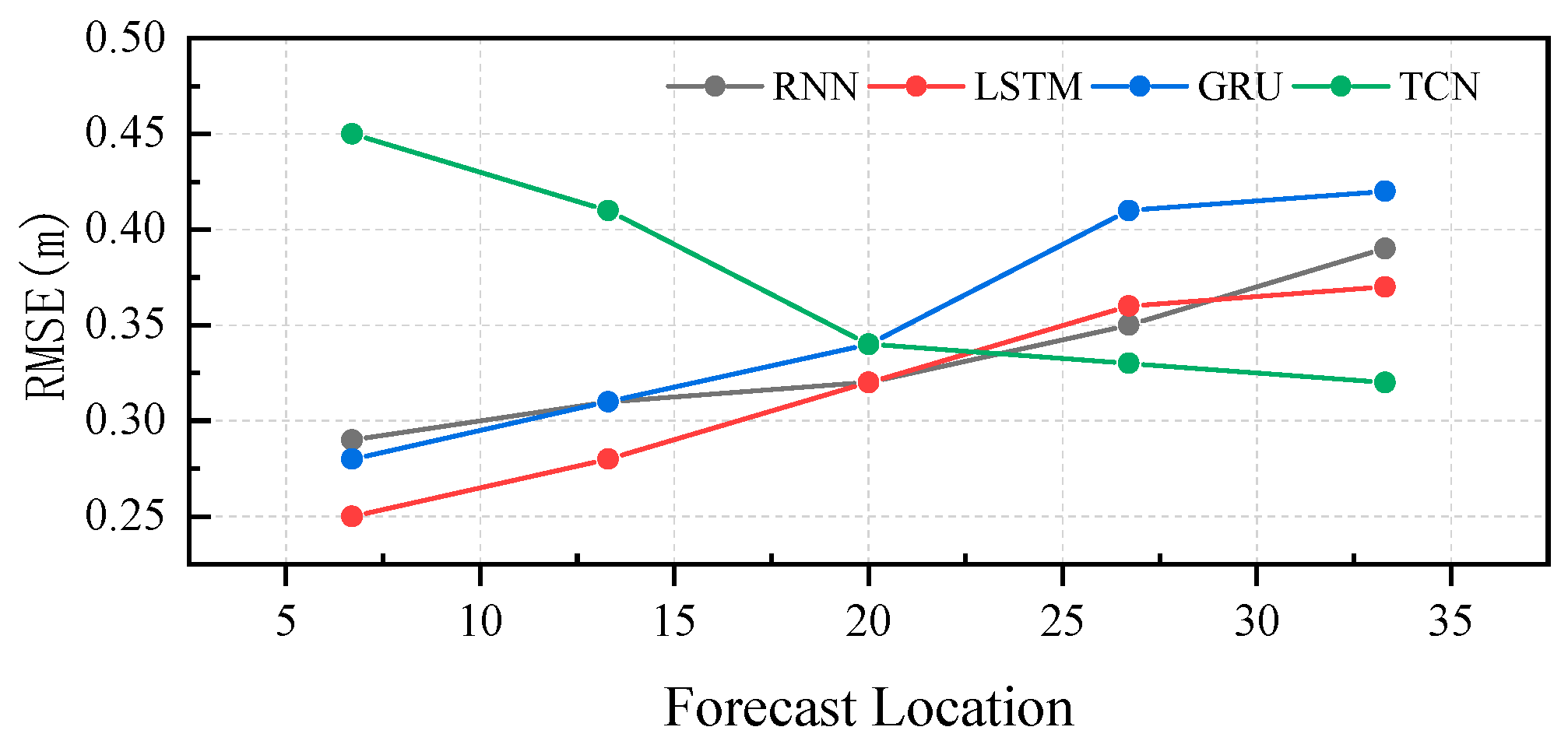
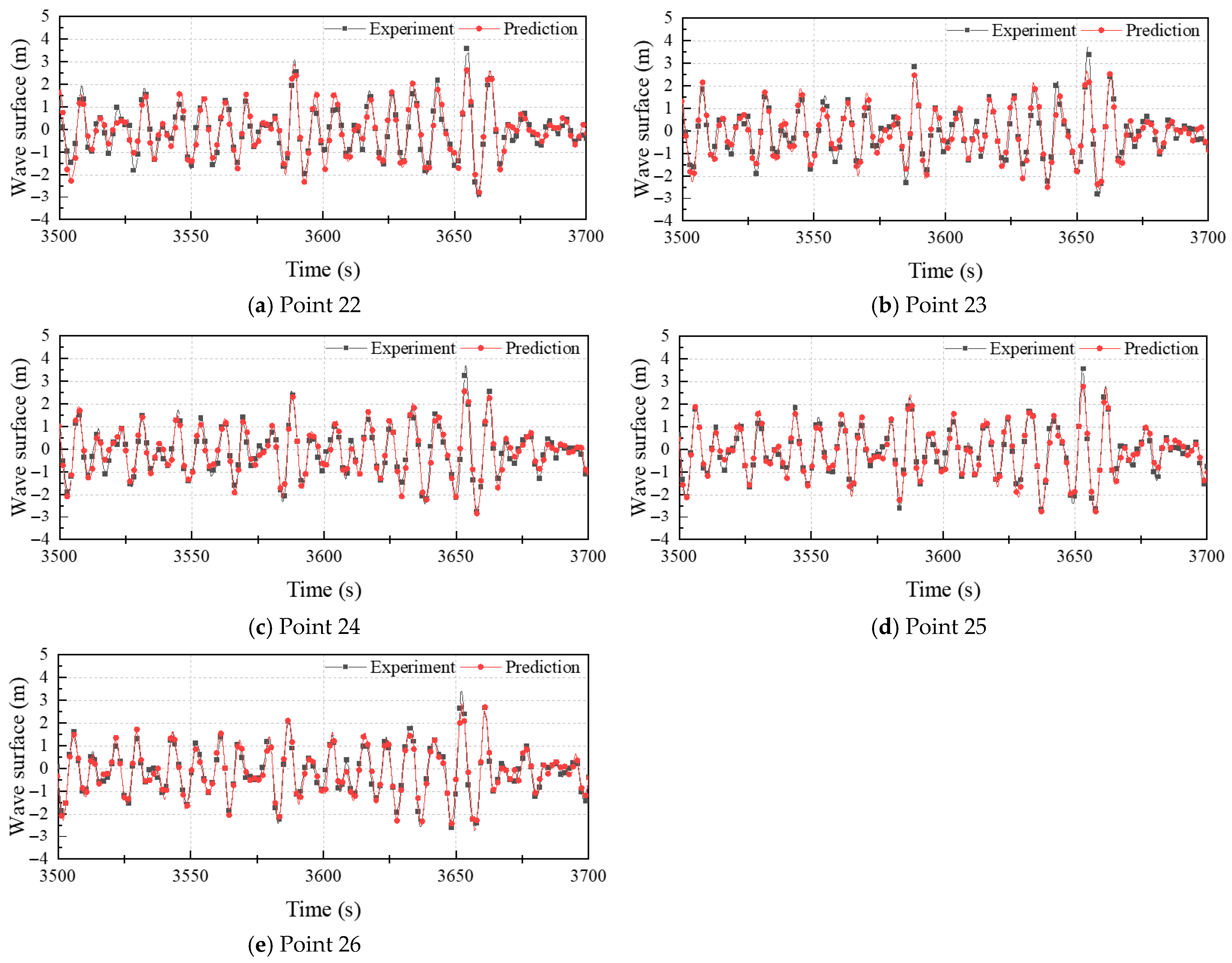
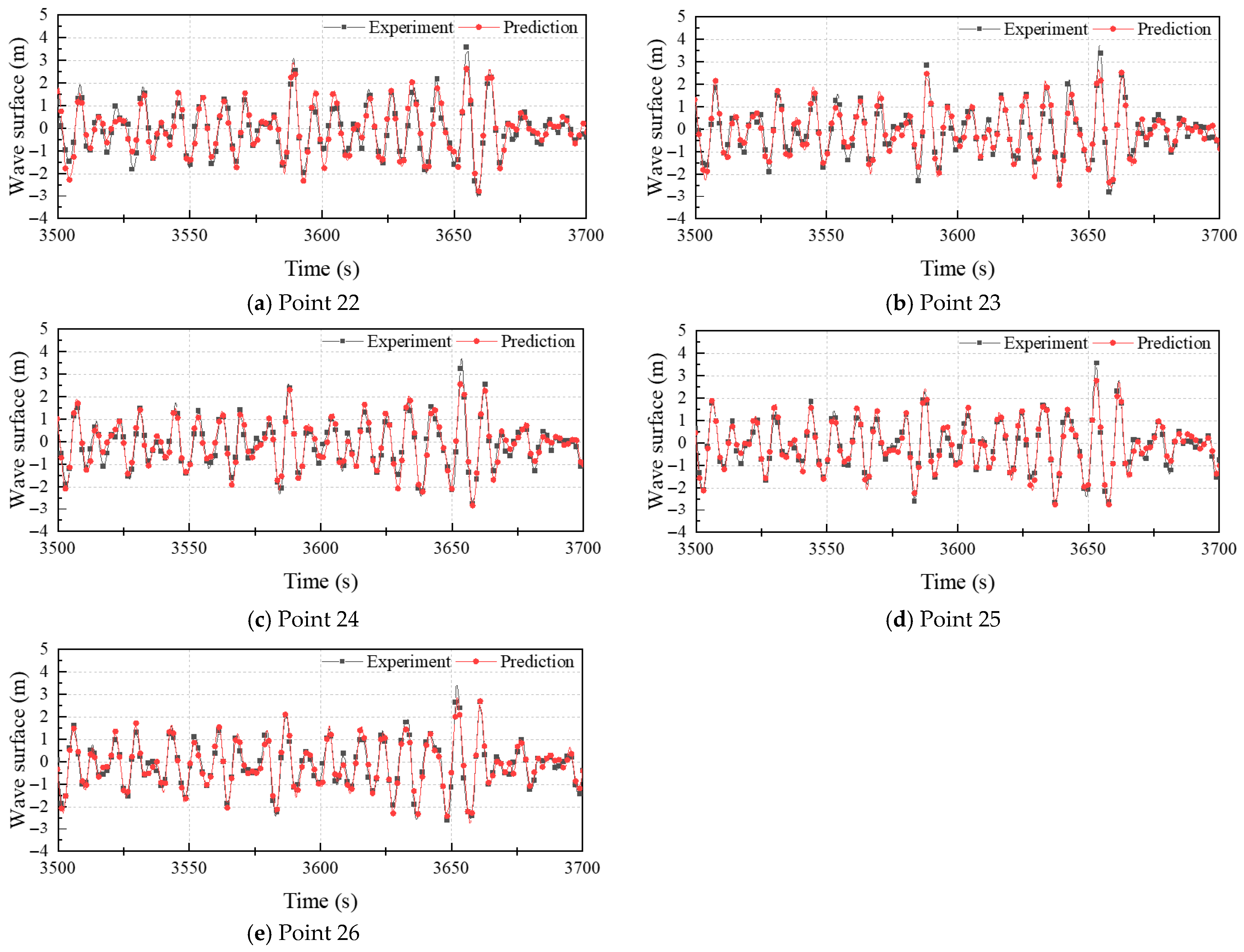
4.3. Influence of Prediction Distance
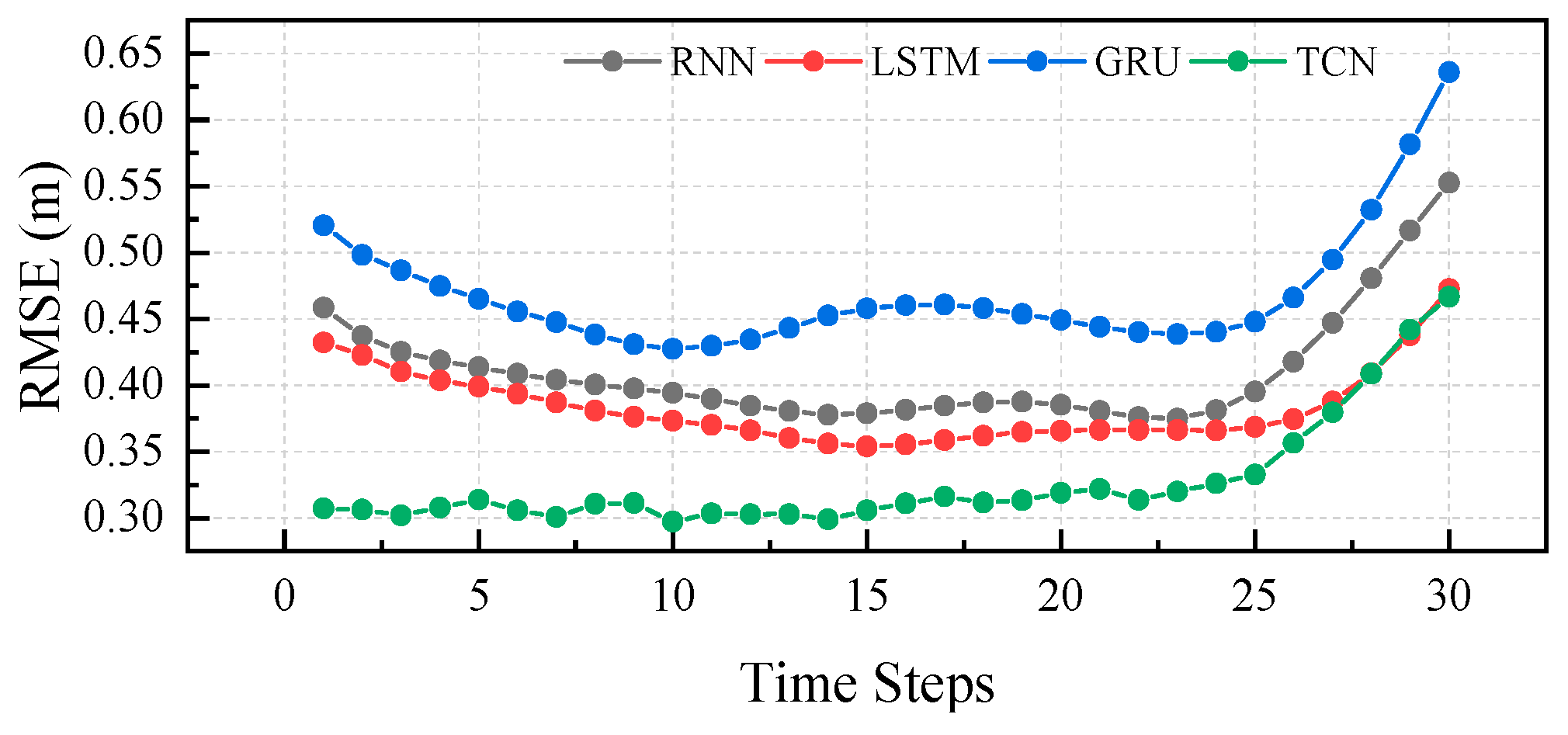
4.4. Influence of Prediction Lead Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kourafalou, V.; De Mey, P.; Staneva, J.; Ayoub, N.; Barth, A.; Chao, Y.; Cirano, M.; Fiechter, J.; Herzfeld, M.; Kurapov, A.; et al. Coastal Ocean Forecasting: Science foundation and user benefits. J. Oper. Oceanogr. 2015, 8 (Supp. 1), s147–s167. [Google Scholar] [CrossRef]
- Makris, C.; Papadimitriou, A.; Baltikas, V.; Spiliopoulos, G.; Kontos, Y.; Metallinos, A.; Androulidakis, Y.; Chondros, M.; Klonaris, G.; Malliouri, D.; et al. Validation and Application of the Accu-Waves Operational Platform for Wave Forecasts at Ports. J. Mar. Sci. Eng. 2024, 12, 220. [Google Scholar] [CrossRef]
- Ravdas, M.; Zacharioudaki, A.; Korres, G. Implementation and validation of a new operational wave forecasting system of the Mediterranean Monitoring and Forecasting Centre in the framework of the Copernicus Marine Environment Monitoring Service. Nat. Hazards Earth Syst. Sci. 2018, 18, 2675–2695. [Google Scholar] [CrossRef]
- Kerczek, C.V.; Davis, S.H. Linear stability theory of oscillatory Stokes layers. J. Fluid Mech. 1974, 62, 753–773. [Google Scholar] [CrossRef]
- Dalzell, J.F. A note on finite depth second-order wave–wave interactions. Appl. Ocean Res. 1999, 21, 105–111. [Google Scholar] [CrossRef]
- Wang, G.; Pan, Y. Data Assimilation for Phase-Resolved Ocean Wave Forecast. In Proceedings of the ASME 2020 39th International Conference on Ocean, Offshore and Arctic Engineering, Virtual Online, 3–7 August 2020; ASME: New York, NY, USA, 2020; Volume 6B, p. V06BT06A071. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, X. Deterministic reconstruction and prediction model of multi-level nonlinear wave fields. In Proceedings of the 16th National Conference on Hydrodynamics & 32nd National Symposium on Hydrodynamics, Wuxi, China, 30 October 2021; Volume II, pp. 831–841. (In Chinese). [Google Scholar]
- Mohapatra, S.C.; Amouzadrad, P.; Bispo, I.B.S.; Guedes Soares, C. Hydrodynamic response to current and wind on a large floating interconnected structure. J. Mar. Sci. Eng. 2025, 13, 63. [Google Scholar] [CrossRef]
- Schäffer, H.A.; Madsen, P.A.; Deigaard, R. A Boussinesq model for waves breaking in shallow water. Coast. Eng. 1993, 20, 185–202. [Google Scholar] [CrossRef]
- Zhao, B. Numerical Simulation Methods for Three-Dimensional Nonlinear Water Waves Based on G-N Theory. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2010. (In Chinese). [Google Scholar]
- Stuhlmeier, R.; Stiassnie, M. Deterministic wave forecasting with the Zakharov equation. J. Fluid Mech. 2021, 913, A50. [Google Scholar] [CrossRef]
- Lange, H. On Dysthe’s nonlinear Schrödinger equation for deep water waves. Transp. Theory Stat. Phys. 2000, 29, 509–524. [Google Scholar] [CrossRef]
- Aziz, T.M. Statistics of nonlinear wave crests and groups. Ocean Eng. 2006, 33, 1589–1622. [Google Scholar] [CrossRef]
- Tsai, P.-H.; Fischer, P.; Iliescu, T. A time-relaxation reduced order model for the turbulent channel flow. J. Comput. Phys. 2025, 521 Pt 1, 113563. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, H.; Zhao, X.; Ding, J.; Xu, D. Multiple-input operator network prediction method for nonlinear wave energy converter. Ocean Eng. 2025, 317, 120106. [Google Scholar] [CrossRef]
- Quang, T.L.; Dao, M.; Lu, X. Prediction of near-field uni-directional and multi-directional random waves from far-field measurements with artificial neural networks. Ocean Eng. 2023, 278, 114307. [Google Scholar] [CrossRef]
- Ma, X.; Duan, W.; Huang, L.; Qin, Y.; Yin, H. Phase-resolved wave prediction for short crest wave fields using deep learning. Ocean Eng. 2022, 262, 112170. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Jin, S.; Greaves, D. Phase-resolved real-time ocean wave prediction with quantified uncertainty based on variational Bayesian machine learning. Appl. Energy 2022, 324, 119711. [Google Scholar] [CrossRef]
- Wedler, M.; Stender, M.; Klein, M.; Hoffmann, N. Machine learning simulation of one-dimensional deterministic water wave propagation. Ocean Eng. 2023, 284, 115222. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, D.; Zou, L.; Wang, A. Freak wave prediction based on LSTM neural networks. J. Huazhong Univ. Sci. Tech. 2020, 48, 47–51. (In Chinese) [Google Scholar]
- Kim, Y.; Ha, Y.; Choi, J. Preliminary study on wave height prediction with convolutional neural network. In Proceedings of the Thirty-first (2021) International Ocean and Polar Engineering Conference, Corfu, Greece, 20–25 June 2021; International Society of Offshore and Polar Engineers: Reston, VA, USA, 2021; p. I–21–3133. [Google Scholar]
- Yu, S. Ocean Wave Simulation and Prediction. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2018. [Google Scholar]
- Duan, W.; Ma, X.; Huang, L.; Liu, Y.; Duan, S. Phase-resolved wave prediction model for long-crest waves based on machine learning. Computer. Methods Appl. Mech. Eng. 2020, 372, 113350. [Google Scholar] [CrossRef]
- Law, Y.Z.; Santo, H.; Lim, K.Y.; Chan, E.S. Deterministic wave prediction for unidirectional sea-states in real-time using artificial neural network. Ocean Eng. 2020, 195, 106722. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Dong, Q.; Chen, G.; Li, X. Phase-resolved wave prediction with linear wave theory and physics-informed neural networks. Appl. Energy 2024, 355, 121602. [Google Scholar] [CrossRef]
- Ehlers, S.; Klein, M.; Heinlein, A.; Wedler, M.; Desmars, N.; Hoffmann, N.; Stender, M. Machine learning for phase-resolved reconstruction of nonlinear ocean wave surface elevations from sparse remote sensing data. Ocean Eng. 2023, 288, 116059. [Google Scholar] [CrossRef]
- Agyekum, E.B.; PraveenKumar, S.; Eliseev, A.; Velkin, V.I. Design and construction of a novel simple and low-cost test bench point-absorber wave energy converter emulator system. Inventions 2021, 6, 20. [Google Scholar] [CrossRef]
- WMO. WMO Sea-Ice Nomenclature; WMO-No. 558; World Meteorological Organization: Geneva, Switzerland, 2018; ISBN 978-92-63-10558-5. [Google Scholar]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures, Chinese ed.; Yang, J.; Xiao, L.; Ge, C., Translators; Shanghai Jiao Tong University Press: Shanghai, China, 2008; ISBN 978-7-313-03029-9. [Google Scholar]
- Belmont, M.R.; Horwood, J.M.K.; Thurley, R.W.F.; Baker, J. Filters for linear sea-wave prediction. Ocean Eng. 2006, 33, 2332–2351. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Sepp Hochreiter, Jürgen Schmidhuber; Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [CrossRef]
- Chung, J.; Gülçehre, Ç.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]





| Reference | Model Architecture | Experimental Conditions | Prediction Task | Key Contribution |
|---|---|---|---|---|
| [21] | LSTM | Island-reef physical model, JONSWAP spectrum, uni-directional waves. | Single- and multi-step freak-wave prediction. | Demonstrated LSTM capability for short-term extreme-wave forecasting. |
| [22] | CNN | Wave basin: long-crested & short-crested seas, 3-D spectrum. | 0–3 s wave-height regression. | Real-time mapping of spatial wave features by convolutional kernels. |
| [23] | Elman RNN | Numerical flume, finite depth, uni-directional waves. | Nonlinear phase-resolved forecast. | Introduced recurrent feedback to capture nonlinear phase evolution. |
| [25] | ANN | Towing-tank long-crested waves, sea states 3–4. | 0–4 s deterministic surface-elevation time series. | Hybridized linear dispersion with ANN error correction. |
| [26] | LWT-PINN | Wave-tank irregular long-crested waves, steepness 0.0174–0.0349, finite water depth. | Deterministic time-history forecast of downstream surface elevation for the next 15 s. | First PINN to predict real waves; 13.7 s high-fidelity horizon with 0.13 s compute, 2.5× longer than classical linear predictor. |
| [27] | U-Net + Fourier Neural Operator | Synthetic 1-D radar-snapshot data, multiple historic time slices. | Phase-resolved reconstruction from sparse radar snapshots. | Replaced heavy optimization with NN mapping; FNO learns global wave-physics relationship in Fourier space, yielding real-time capable and sea-state-robust reconstruction. |
| Sea State Level | Significant Wave Height (m) | Spectral Peak Frequency (s) |
|---|---|---|
| 4 | 2/2.1 | 9.5 |
| 5 | 3.5/3.7 | 10 |
| 6 | 5/5.34 | 11 |
| 7 | 6/6.34 | 12 |
| Model Names | RNN | LSTM | GRU | TCN | |
|---|---|---|---|---|---|
| Sea State Levels | |||||
| 4 | 0.28 | 0.27 | 0.29 | 0.21 | |
| 5 | 0.39 | 0.37 | 0.42 | 0.32 | |
| 6 | 0.43 | 0.43 | 0.45 | 0.37 | |
| 7 | 0.61 | 0.61 | 0.51 | 0.42 | |
| Model Names | RNN | LSTM | GRU | TCN | |
|---|---|---|---|---|---|
| Sea State Levels | |||||
| 4 | 0.23 | 0.20 | 0.24 | 0.20 | |
| 5 | 0.38 | 0.38 | 0.41 | 0.32 | |
| 6 | 0.41 | 0.48 | 0.43 | 0.33 | |
| 7 | 0.52 | 0.79 | 0.61 | 0.44 | |
| Model Names | RNN | LSTM | GRU | TCN | |
|---|---|---|---|---|---|
| Prediction Location | |||||
| 22 | 0.39 | 0.37 | 0.42 | 0.32 | |
| 23 | 0.35 | 0.36 | 0.41 | 0.33 | |
| 24 | 0.32 | 0.32 | 0.34 | 0.34 | |
| 25 | 0.31 | 0.28 | 0.31 | 0.41 | |
| 26 | 0.29 | 0.25 | 0.28 | 0.45 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, S.; Yang, D.; Chen, H.; Ma, X.; Li, M. Evaluation of Different AI-Based Wave Phase-Resolved Prediction Methods. J. Mar. Sci. Eng. 2025, 13, 2196. https://doi.org/10.3390/jmse13112196
Cao S, Yang D, Chen H, Ma X, Li M. Evaluation of Different AI-Based Wave Phase-Resolved Prediction Methods. Journal of Marine Science and Engineering. 2025; 13(11):2196. https://doi.org/10.3390/jmse13112196
Chicago/Turabian StyleCao, Shunli, Dezheng Yang, Hangyu Chen, Xuewen Ma, and Mao Li. 2025. "Evaluation of Different AI-Based Wave Phase-Resolved Prediction Methods" Journal of Marine Science and Engineering 13, no. 11: 2196. https://doi.org/10.3390/jmse13112196
APA StyleCao, S., Yang, D., Chen, H., Ma, X., & Li, M. (2025). Evaluation of Different AI-Based Wave Phase-Resolved Prediction Methods. Journal of Marine Science and Engineering, 13(11), 2196. https://doi.org/10.3390/jmse13112196




