An IPSO-RC-Based Study on Dynamic Coordination Excitation and Optimal Capacity Allocation for Marine Hybrid Energy Systems
Abstract
1. Introduction
2. Literature Review
2.1. Optimization Method for the Capacity Configuration of Energy-Storage Systems
2.2. Energy Management Strategy for Fuel Cell Ships
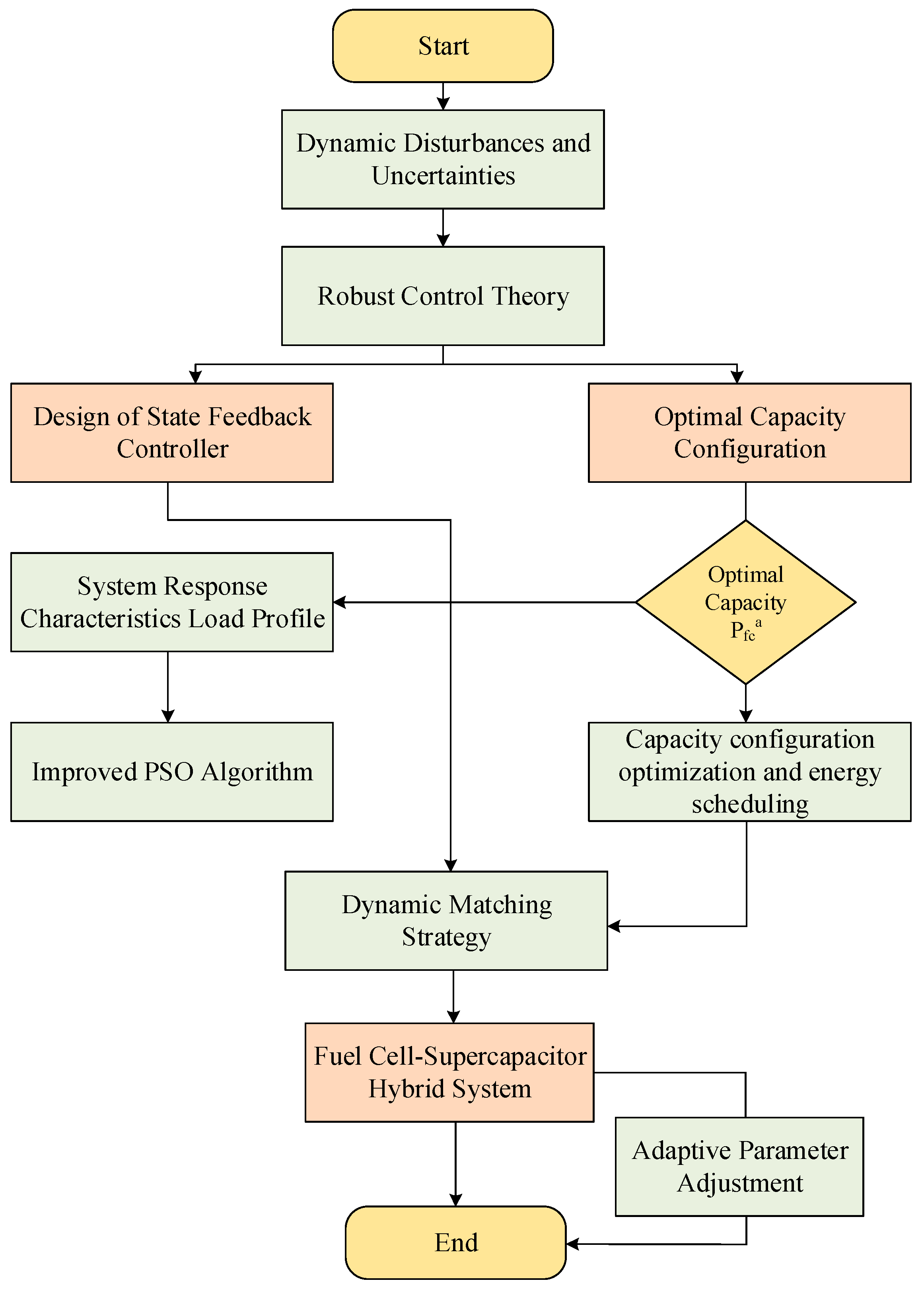
3. Modeling of Ship Hybrid Energy Systems Based on Robust Control
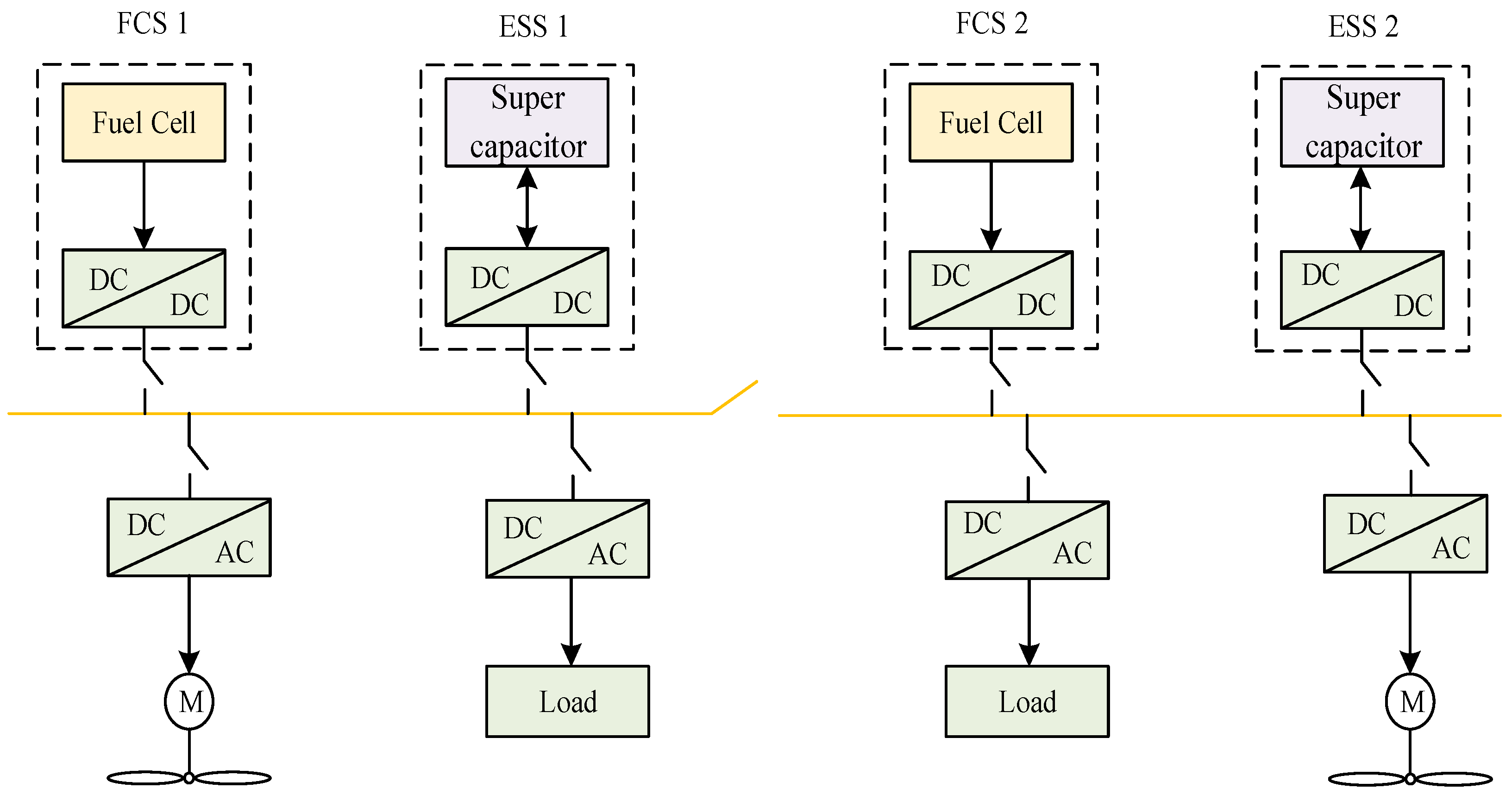
3.1. Ship Power System
3.2. System State Feedback Controller Based on Robust Control Theory
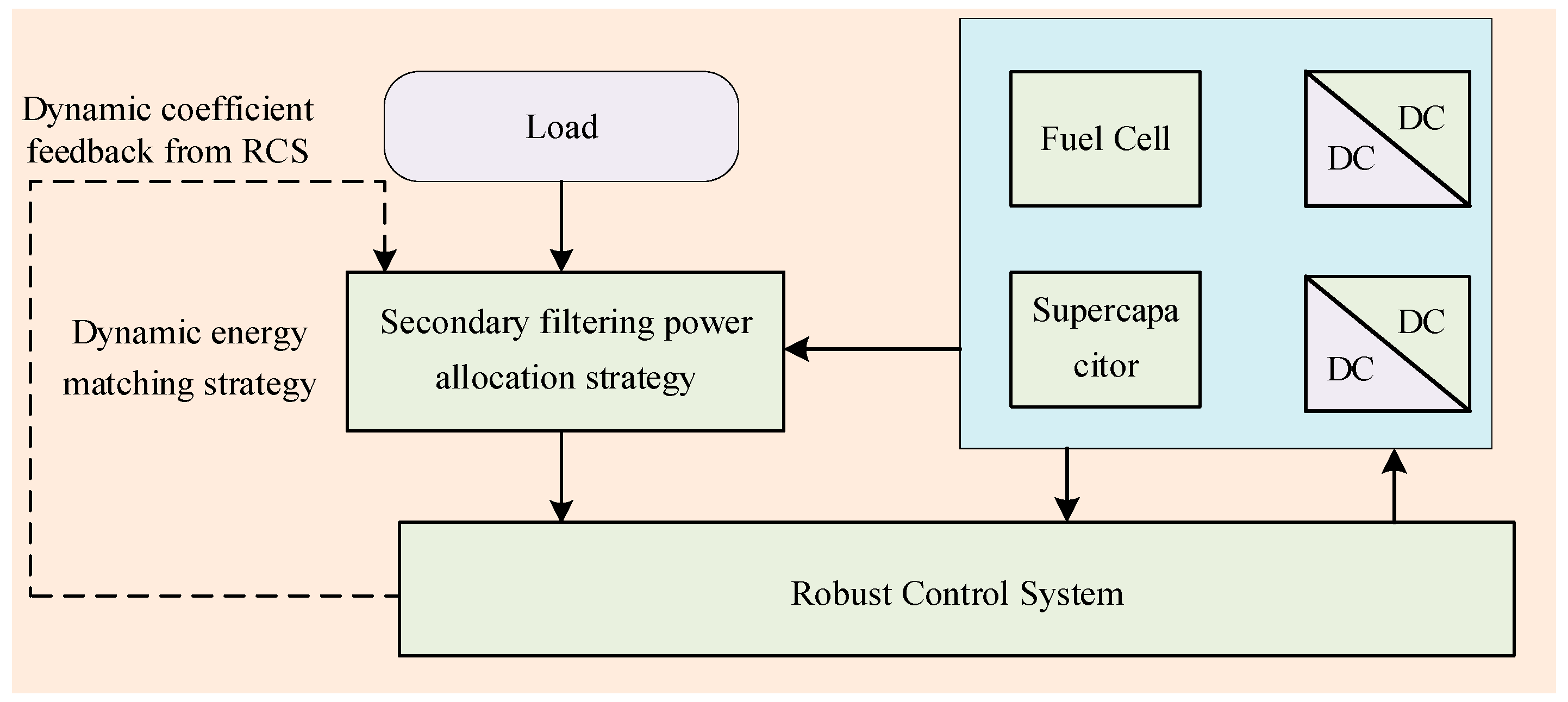
4. Cooperative Method for Capacity Configuration and Operational Strategy of Marine Hybrid Energy Systems
4.1. Optimization of Energy Storage Capacity Allocation Based on PSO
4.2. Design and Optimization of Dynamic Energy Matching Strategies
4.3. Adaptive Adjustment and Optimization of State Feedback Controller Parameters
5. Modeling and Analysis
5.1. Experimental Design and Test Environment
5.2. Verification of a Marine Hybrid System Based on Robust Control
5.2.1. Comparative Analysis of Capacity Configuration Optimization Experiment Results
5.2.2. Comparative Analysis of System Security and Stability Test Results
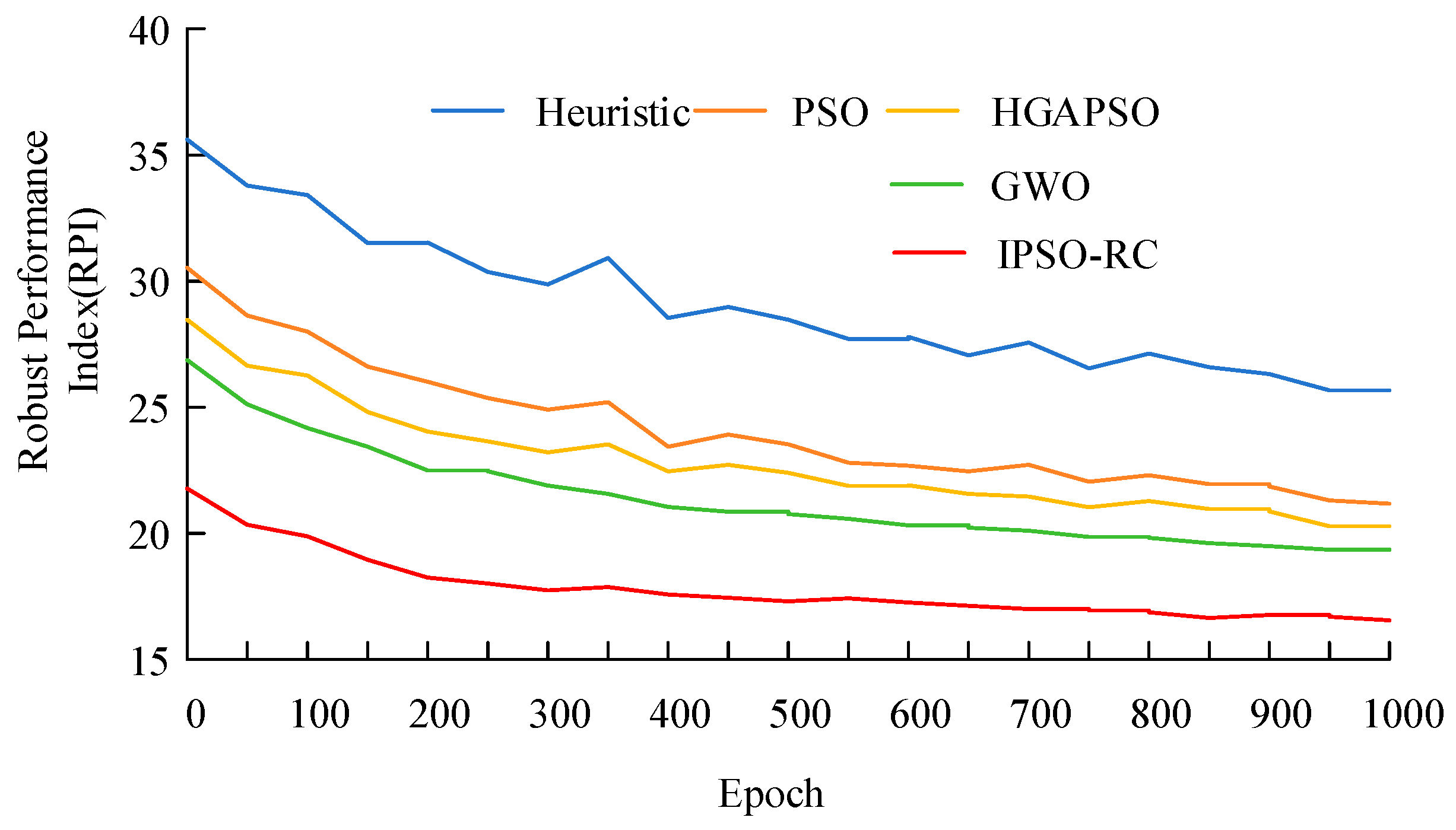
5.2.3. Verification and Evaluation of System Robustness
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Lu, B.; Li, R.; Li, Y. Research progress on multi-clean energy hybrid system and the key technologies of ships. Ship Sci. Technol. 2020, 17, 6–11. [Google Scholar]
- Aly, M.; Ahmed, E.; Rezk, H. Marine Predators Algorithm Optimized Reduced Sensor Fuzzy-Logic Based Maximum Power Point Tracking of Fuel Cell-Battery Standalone Applications. IEEE Access 2021, 9, 27987–28000. [Google Scholar] [CrossRef]
- Hou, L.; Zai, X.; Meng, Y.; Liang, S.; Cao, Y. Influence of Rhamnolipids Biosurfactant on the Anodic Electrochemical Performance in Marine Sediment Microbial Fuel Cell and the Acceleration Degradation of Crude Petroleum. J. Ocean. Univ. China 2025, 24, 139–146. [Google Scholar] [CrossRef]
- Serbin, S.; Washchilenko, N.; Cherednichenko, O. Application analysis of a hybrid solid oxide fuel cell-gas turbine system for marine power plants. Ships Offshore Struct. 2021, 1, 866–876. [Google Scholar] [CrossRef]
- Fang, S.; Chen, D.; Fan, X. Novel intelligent adaptive sliding mode control for marine fuel cell system via hybrid algorithm. Energy AI 2025, 19, 100464. [Google Scholar] [CrossRef]
- He, R.; Zhu, C.; Feng, W. Distributed Multi-Train Robust Predictive Control with a Target Switching Mechanism. J. Transp. Syst. Eng. Inf. Technol. 2025, 1, 1–20. [Google Scholar]
- Milićević, S.; Blagojević, I.; Milojević, S.; Bukvić, M.; Stojanović, B. Numerical Analysis of Optimal Hybridization in Parallel Hybrid Electric Powertrains for Tracked Vehicles. Energies 2024, 17, 3531. [Google Scholar] [CrossRef]
- Chen, L.; Guan, W.; Zhao, Y. Review and Prospect of Standard Research for Hydrogen Fuel Cell Powered Ships. Transm. Energy Conserv. Environ. Prot. 2023, 4, 1–6. [Google Scholar]
- Accetta, A.; Pucci, M. Energy Management System in DC Micro-Grids of Smart Ships: Main Gen-Set Fuel Consumption Minimization and Fault Compensation. IEEE Trans. Ind. App. 2019, 55, 3097–3113. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Yuan, J.; Chen, Y. Optimized configuration of hydrogen fuel cells and energy storage batteries for cruise ships. J. Power Source 2021, 3, 330–334. [Google Scholar]
- Pang, S.; Yang, C.; Liu, R. Multi-objective optimization method of energy storage system capacity allocation for marine microgrid lithium battery. Ship Res. 2020, 15, 22–28. [Google Scholar]
- Pan, Z.; Shang, L.; Gao, G.; Hu, H. Optimization of composite energy storage system and energy management strategy for fuel cell hybrid ships. J. Dalian Marit. Univ. 2021, 3, 78–85. [Google Scholar]
- Haseltalab, A.; Sapra, H. Component sizing and energy management for SOFC-based ship power systems. Energy Convers. Manag. 2021, 245, 114625. [Google Scholar] [CrossRef]
- Letafat, A.; Rafiei, M.; Sheikh, M. Simultaneous energy management and optimal components sizing of a zero-emission ferry boat. J. Energy Storage 2020, 28, 101215. [Google Scholar] [CrossRef]
- Bao, X.; Xu, X.; Zhang, Y. Optimal Sizing of Battery Energy Storage System in a Shipboard Power System with considering Energy Management Optimization. Discrete Dyn. Nat. Soc. 2021, 2021, 9032206. [Google Scholar] [CrossRef]
- Kistner, L.; Bensman, A. Optimal design of power gradient limited solid oxide fuel cell systems with hybrid storage support for ship applications. Energy Convers. Manage. 2021, 243, 114396. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Zhang, J. An adaptive multi-objective joint optimization framework for marine hybrid energy storge system design considering energy management strategy. J. Energy Storage 2023, 68, 107689. [Google Scholar] [CrossRef]
- Valer-Garcia, J.; Atutxa-Lekue, I. On the optimal design of hybrid-electric power systems for offshore vessels. IEEE Trans. Transport. Electrif. 2019, 5, 324–334. [Google Scholar] [CrossRef]
- Du, Z.; Chen, Q.; Guan, C.; Chen, H. Improvement and Optimization Configuration of Inland Ship Power and Propulsion System. J. Mar. Sci. Eng. 2023, 11, 135. [Google Scholar] [CrossRef]
- Sheng, C.; Fu, J.; Li, D. Energy management strategy based on healthy state for a PEMFC/Lithium-ion batteries hybrid power system. Energy Convers. Manage. 2022, 271, 116330. [Google Scholar] [CrossRef]
- Fan, A.; Li, Y.; Liu, H. Development trend and hotspot analysis of ship energy management. J. Clean. Prod. 2023, 389, 135899. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Guan, C. Optimization of sizing and frequency control in battery/supercapacitor hybrid energy storage system for fuel cell ship. Energy 2020, 197, 72–85. [Google Scholar] [CrossRef]
- Faddel, S.; Saad, A.; Hariri, M. Coordination of hybrid energy storage for ship power systems with pulsed loads. IEEE Trans. Ind. Appl. 2020, 56, 1136–1145. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, H.; Han, J. Optimal SOC control and rule-based energy management strategy for fuel-cell-based hybrid vessel including batteries and supercapacitors. J. Mar. Sci. Eng. 2023, 11, 398. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.; Li, Q. Research on energy management strategy for a hybrid power system of ship’s aluminum-air battery and lithium-ion battery. Energy Storage Syst. Eng. 2023, 12, 2871–2880. [Google Scholar]
- Fam, M.; Tay, Z.; Konovessis, D. An artificial neural network for fuel efficiency analysis for cargo vessel operation. Ocean Eng. 2022, 264, 112437. [Google Scholar] [CrossRef]
- Gao, F.; Qiang, Y.; Gao, Z. Energy management strategy for fuel cell trams combining online and offline control. J. Jilin Univ. 2024, 10, 3064–3076. [Google Scholar]
- Yuan, Y.; Chen, M.; Wang, J. A novel hybrid energy management strategy of a diesel-electric hybrid ship based on dynamic programing and model predictive control. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 644–657. [Google Scholar] [CrossRef]
- Rafiei, M.; Boudjadar, J.; Khooban, M. Energy management of a zero-emission ferry boat with a fuel-cell-based hybrid energy system: Feasibility assessment. IEEE Trans. Ind. Electron 2021, 68, 1739–1748. [Google Scholar] [CrossRef]
- Hong, J.; Ma, S.; Liang, F.; Yang, J.; Zhang, H. System integration and intelligent management of hydrogen fuel cells based on digital twin technology. Chin. J. Eng. 2025, 1, 2095–9389. [Google Scholar]
- Chiachío, M.; Megía, M.; Chiachío, J.; Fernandez, J.; Jalón, M. Structural digital twin framework: Formulation and technology integration. Autom. Constr. 2022, 140, 104333. [Google Scholar] [CrossRef]
- IEEE 1709-2010; IEEE Recommended Practice for 1kV to 35kV Medium-Voltage DC Power Systems on Ships. IEEE: New York, NY, USA, 2010.
- Xu, L.; Guerrero, J.; Lashab, A. A review of DC shipboard microgrids-part I: Power architectures, energy storge, and power converters. IEEE Trans. Power Electron. 2022, 37, 5155–5172. [Google Scholar] [CrossRef]
- Li, H.; Sun, C.; Li, J.; Mei, J.; Jiang, J.; Fan, F.; Yang, W.; Zhuo, R.; Song, K. Self-Tuning Oxygen Excess Ratio Control for Proton Exchange Membrane Fuel Cells Under Dynamic Conditions. Processes 2024, 12, 2807. [Google Scholar] [CrossRef]
- Mei, J.; Meng, X.; Tang, X.; Li, H.; Hasanien, H.; Alharbi, M.; Dong, Z.; Shen, J.; Sun, C.; Fan, F.; et al. An Accurate Parameter Estimation Method of the Voltage Model for Proton Exchange Membrane Fuel Cells. Energies 2024, 17, 2917. [Google Scholar] [CrossRef]
- Meng, X.; Liu, M.; Mei, J.; Li, X.; Grigoriev, S.; Hasanien, H.; Tang, X.; Li, R.; Sun, C. Polarization loss decomposition-based online health state estimation for proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2025, 157, 150162. [Google Scholar] [CrossRef]
- Bassam, A.; Phillips, A.; Turnock, S. Development of a multi-scheme energy management strategy for a hybrid fuel cell driven passenger ship. Int. J. Hydrog. Energy 2017, 42, 623–635. [Google Scholar] [CrossRef]
- Lu, S.; Yin, Z.; Liao, S. An asymmetric encoder-decoder model for zn-ion battery lifetime prediction. Energy Rep. 2022, 8, 33–50. [Google Scholar] [CrossRef]
- Yang, P.; Yu, L.; Wang, X. Multi-objective planning and optimization of microgrid lithium iron phosphate battery energy storage system consider power supply status and CCER transactions. Int. J. Hydrog. Energy 2022, 47, 29925–29944. [Google Scholar] [CrossRef]
- Li, S.; He, H.; Su, C. Data driven battery modeling and management method with again phenomenon considered. Appl. Energy 2020, 275, 115340. [Google Scholar] [CrossRef]
- Lu, X.; Wang, H. Optimal sizing and energy management for cost-effective PEV hybrid energy storage systems. IEEE Trans. Ind. Inform. 2020, 16, 3407–3416. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Soleymani, M.; Macias, A. Online power and efficiency estimation of a fuel cell system for adaptive energy management design. Energy Convers. Manag. 2020, 16, 3407–3416. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, G.; Li, Y. An adaptive Kalman filter with inaccurate noise covariances in the presence of outliers. IEEE Trans. Autom. Control 2022, 67, 374–381. [Google Scholar] [CrossRef]
- Sun, F.; Liu, Y.; Gan, H. Multi-Objective Optimization of Energy Storage Configuration and Dispatch in Diesel-Electric Propulsion Ships. J. Mar. Sci. Eng. 2025, 9, 1808. [Google Scholar] [CrossRef]
- Zhao, Y.; Wen, S.; Zhao, Q. Deep Reinforcement Learning-Based Energy Management Strategy for Green Ships Considering Photovoltaic Uncertainty. J. Mar. Sci. Eng. 2025, 13, 565. [Google Scholar] [CrossRef]
- Nivolianiti, E.; Karnavas, Y.L.; Charpentier, J.-F. Fuzzy Logic-Based Energy Management Strategy for Hybrid Fuel Cell Electric Ship Power and Propulsion System. J. Mar. Sci. Eng. 2024, 12, 1813. [Google Scholar] [CrossRef]
- Zheng, H.; Ye, J.; Luo, F. Two-stage stochastic robust optimization for capacity allocation and operation of integrated energy systems. Electr. Power Syst. Res. 2025, 239, 111253. [Google Scholar] [CrossRef]
- Sadeq, A. Energy Storage Systems: A Comprehensive Guide, 1st ed.; Aristo Academy: Hyogo, Japan, 2023. [Google Scholar]
- Ge, Y.; Zhang, J.; Zhou, K.; Zhu, J.; Wang, Y. Research on Energy Management for Ship Hybrid Power System Based on Adaptive Equivalent Consumption Minimization Strategy. J. Mar. Sci. Eng. 2023, 11, 1271. [Google Scholar] [CrossRef]
| Research Objective/Method Summary | Control Type | Optimization Included | Validation Method | Reported Efficiency/Advantages | Limitations Compared with IPSO-RC |
|---|---|---|---|---|---|
| DC microgrid EMS for intelligent ships: aims to minimize fuel consumption and compensate for faults | Rule-/droop- based + optimization scheduling | Yes (convex/ numerical optimization) | Simulation | Reduced fuel consumption and fluctuation suppression | Focuses on fuel economy and fault compensation; lacks handling of strong nonlinearity, time-varying uncertainty, and coordinated capacity design |
| Cruise ship: capacity configuration of fuel cell and battery | Rule-/static strategy | Yes (capacity optimization) | Voyage simulation | Ensures power supply over full voyage | Mostly offline capacity optimization; lacks robustness to dynamic disturbances |
| Marine microgrid battery capacity multi-objective optimization | Rule-based | Yes (multi- objective evolutionary algorithm) | Simulation | Balances cost and lifetime | Not deeply coupled with online energy allocation or robust control |
| SOFC ship: integrated capacity sizing and EMS optimization | Optimization-oriented | Yes (coupled optimization) | Simulation | Improved fuel-cell efficiency | Targets steady-state efficiency; lacks adaptive and filtering mechanisms for harsh sea conditions |
| Zero-emission ferry: joint optimization of energy management and sizing | Optimization/scheduling | Yes (multi-objective) | Feasibility analysis + simulation | Balances OPEX and CAPEX | Limited adaptive learning and robustness; lacks compensation for parameter drift |
| Offshore ship hybrid system optimal design | Planning/multi-objective | Yes (NSGA-II) | Simulation | Balanced design trade-offs | Focuses on offline design; lacks online adaptation and time-varying filtering |
| Fuel cell ship: battery/supercapacitor hybrid with frequency-based load division | Rule-based (fixed or semi-variable filtering) | Partly (capacity/parameter) | Simulation | Effectively suppresses high-frequency load | Filtering parameters fixed or semi-fixed; poor adaptability to strong nonlinearity or time-varying operation |
| Fuel cell + battery + supercapacitor: SOC optimization and rule-based EMS | Rule + optimization | Yes (SOC-based objectives) | Simulation | Balances response and lifetime | Still rule-driven; lacks robust control and online identification coupling |
| Diesel–electric hybrid: combined DP and MPC EMS | MPC/optimization | Yes (offline DP + online MPC) | Simulation + noise analysis | High economy; considers noise | Based on predictive model; lacks online capacity coordination and adjustable robust feedback gain K |
| Modern zero-emission ship: stochastic MPC-based EMS | MPC (with degradation constraints) | Yes (stochastic optimization) | Simulation | Balances cost and battery degradation | Relies on accurate modeling and probabilistic assumptions; lacks online self-learning of matching coefficients |
| Parameter Name | Data Type | Unit | Min Value | Max Value | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Fuel Cell Voltage | Continuous | V | 700 | 1000 | 850 | 50 |
| Fuel Cell Current | Continuous | A | 0.5 | 95 | 45 | 15 |
| Supercapacitor Voltage | Continuous | V | 400 | 460 | 430 | 10 |
| Supercapacitor SOC | Percentage | % | 20 | 98 | 60 | 15 |
| Load Power | Continuous | W | 1000 | 5000 | 3000 | 1500 |
| DC Bus Voltage | Continuous | V | 690 | 1100 | 900 | 100 |
| Controller Output Gain | Control Value | - | 0 | 1 | 0.55 | 0.2 |
| System Temperature | Continuous | °C | 25 | 60 | 40 | 7 |
| Component | Parameter | Symbol | Value/ Range | Unit | Data Source |
|---|---|---|---|---|---|
| Fuel Cell Stack (PEMFC) | Rated Power | P_FC | 5 kW | W | Manufacturer spec (Ballard Nexa) |
| Nominal Voltage | V_FC | 850 | V | Experimental measurement | |
| Max Current | I_FC, max | 90 | A | Experimental | |
| Efficiency (rated) | _FC | 52–58% | - | Manufacturer | |
| Stack Temp Range | T_FC | 25–60 | °C | Sensor record | |
| Supercapacitor Bank | Equivalent Capacitance | C_SC | 450 F | F | Maxwell data sheet |
| Rated Voltage | V_SC | 450 | V | Experimental | |
| ESR | R_SC | 25 m | Data sheet | ||
| Bidirectional DC/DC Converter | Switching Frequency | f_sw | 10 | kHz | Controller spec |
| Efficiency | _conv | 0.96 | - | Bench measurement | |
| Load Model | Dynamic Load Range | P_L | 1–5 | kW | Simulated propulsion curve |
| Frequency Component | f_L | 0.1 | Hz | Derived from sea-state data | |
| Controller | Sampling Frequency | f_s | 100–200 | Hz | Design value |
| Communication Delay | _com | 10–20 | ms | Bench measurement |
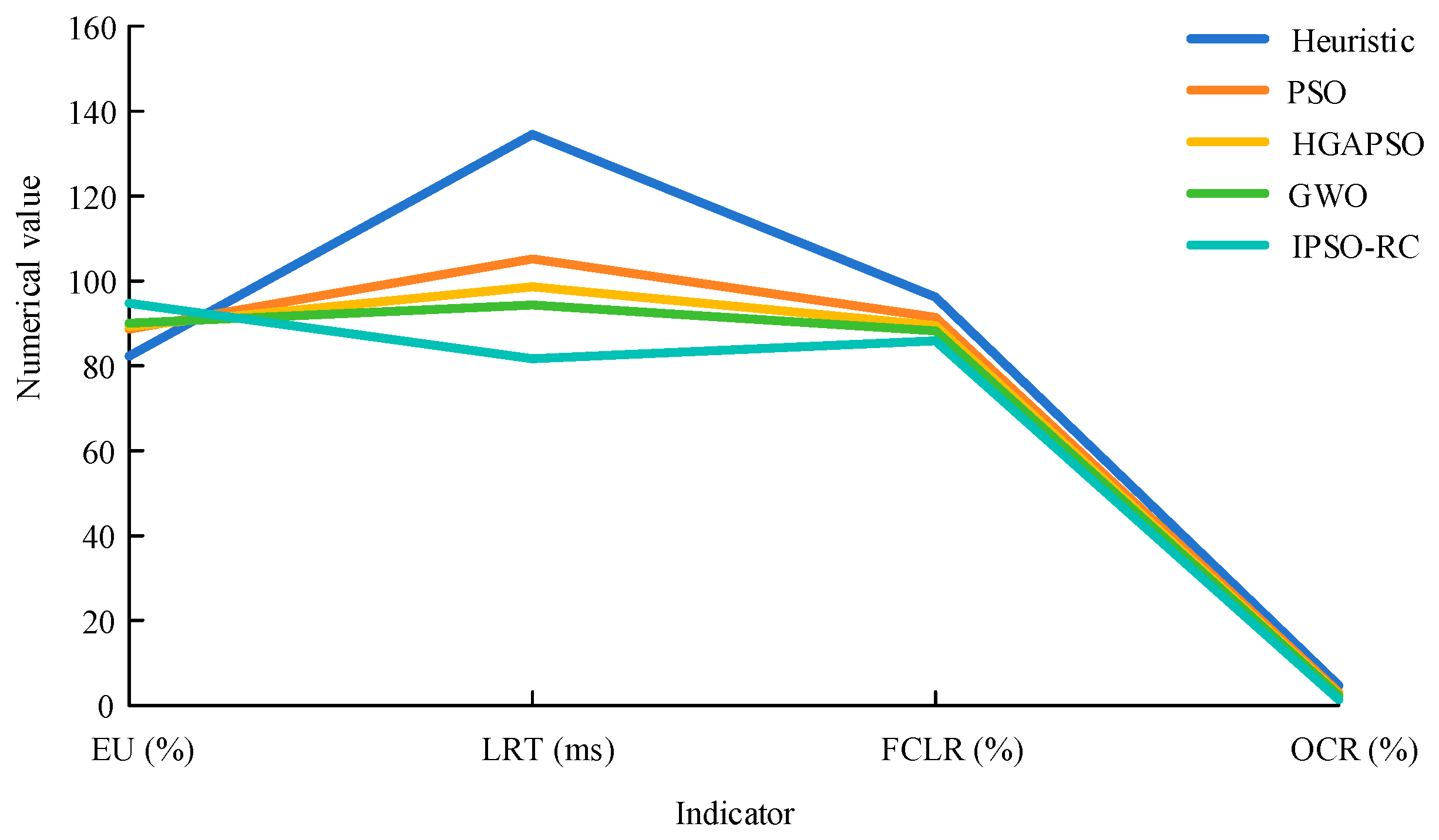
| Algorithm | EU (%) | LRT (ms) | FCLR (%) | OCR (%) |
|---|---|---|---|---|
| Heuristic | 82.31 | 134.5 | 96.2 | 4.7 |
| PSO | 88.67 | 105.2 | 91.4 | 3.1 |
| HGAPSO | 89.23 | 98.6 | 89.5 | 2.6 |
| GWO | 90.01 | 94.3 | 88.2 | 2.3 |
| IPSO-RC | 94.75 | 81.7 | 85.9 | 1.4 |
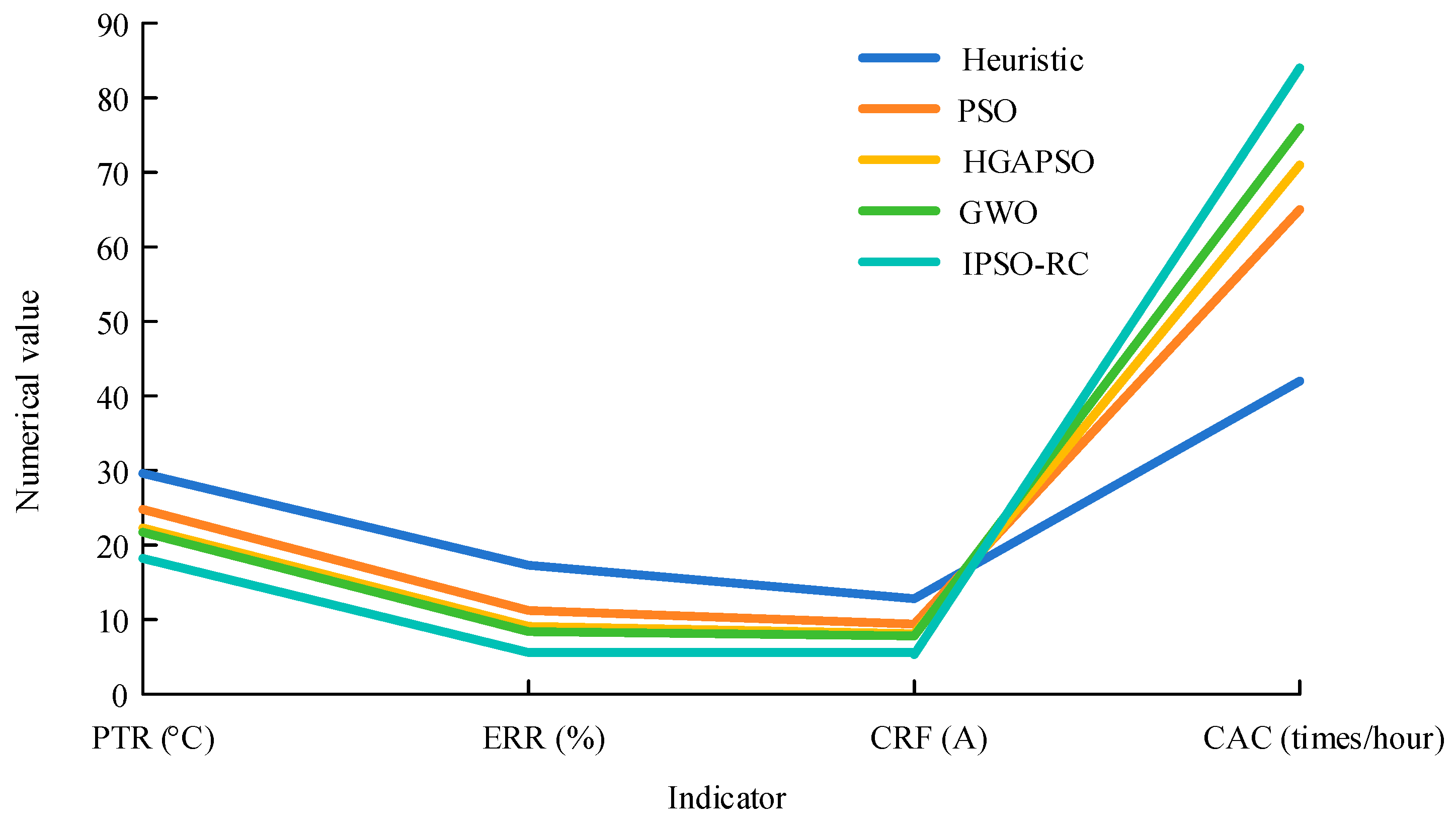
| Algorithm | PTR (°C) | ERR (%) | CRF (A) | CAC (Times/Hour) |
|---|---|---|---|---|
| Heuristic | 29.6 | 17.3 | 12.8 | 42 |
| PSO | 24.8 | 11.2 | 9.4 | 65 |
| HGAPSO | 22.3 | 9.1 | 8.1 | 71 |
| GWO | 21.7 | 8.4 | 7.8 | 76 |
| IPSO-RC | 18.2 | 5.6 | 5.3 | 84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Guo, Y.; Yang, Y.; Han, B. An IPSO-RC-Based Study on Dynamic Coordination Excitation and Optimal Capacity Allocation for Marine Hybrid Energy Systems. J. Mar. Sci. Eng. 2025, 13, 2197. https://doi.org/10.3390/jmse13112197
Liu H, Guo Y, Yang Y, Han B. An IPSO-RC-Based Study on Dynamic Coordination Excitation and Optimal Capacity Allocation for Marine Hybrid Energy Systems. Journal of Marine Science and Engineering. 2025; 13(11):2197. https://doi.org/10.3390/jmse13112197
Chicago/Turabian StyleLiu, Huanbo, Yi Guo, Yayu Yang, and Bing Han. 2025. "An IPSO-RC-Based Study on Dynamic Coordination Excitation and Optimal Capacity Allocation for Marine Hybrid Energy Systems" Journal of Marine Science and Engineering 13, no. 11: 2197. https://doi.org/10.3390/jmse13112197
APA StyleLiu, H., Guo, Y., Yang, Y., & Han, B. (2025). An IPSO-RC-Based Study on Dynamic Coordination Excitation and Optimal Capacity Allocation for Marine Hybrid Energy Systems. Journal of Marine Science and Engineering, 13(11), 2197. https://doi.org/10.3390/jmse13112197






