Study on Cyclic Tensile Shakedown Behaviour of Flexible Risers Considering Winding Process
Abstract
1. Introduction
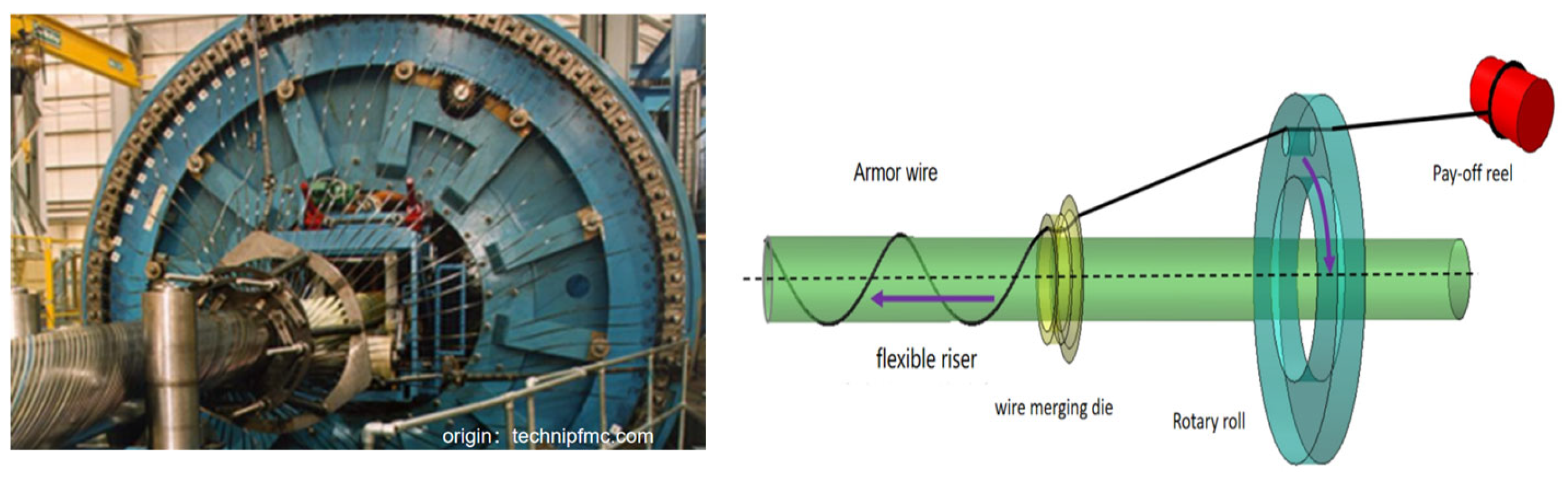
2. Simulation Model of the Winding Process of Tensile Armour Layers
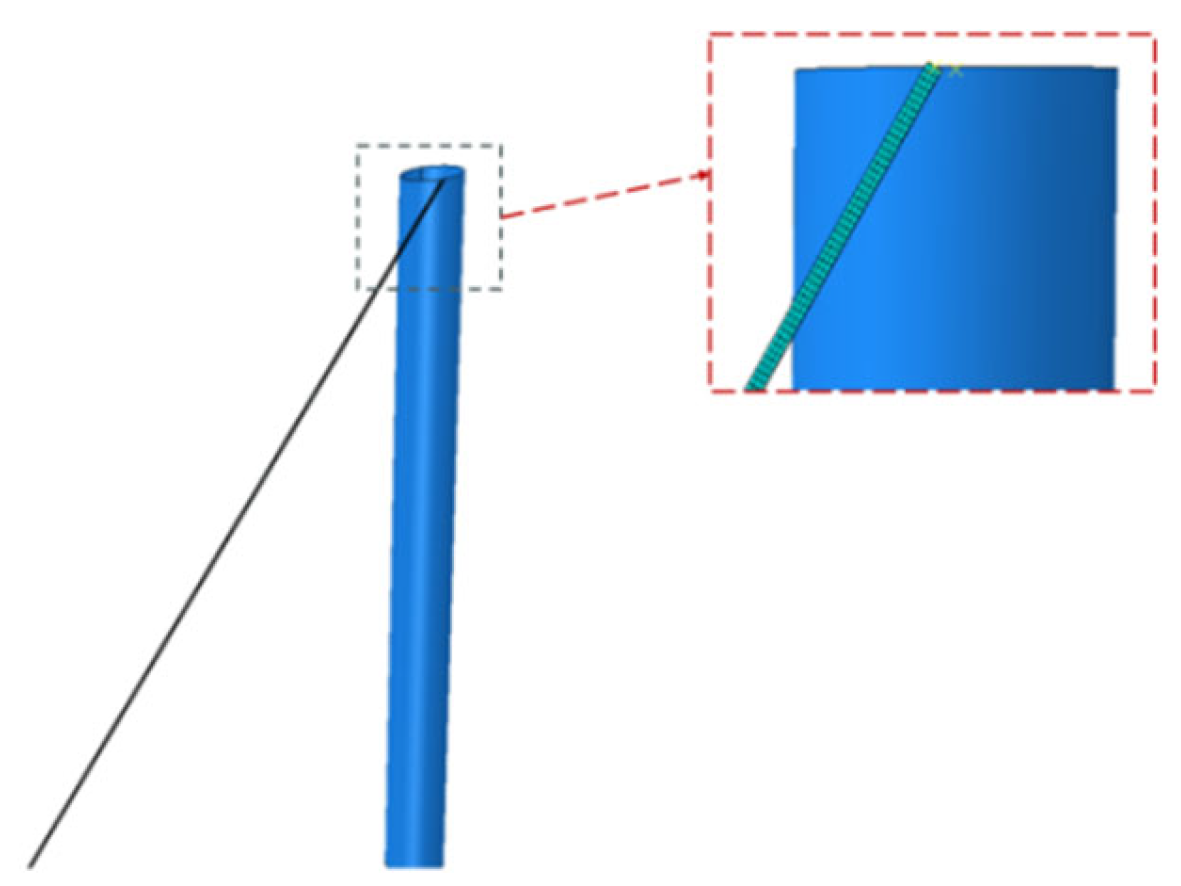
2.1. Establishment of the Numerical Model for the Winding Process of Armour Wires
2.2. Analysis of Residual Stress in Steel Wire Cross-Section After Winding
3. Tensile Loading–Unloading Model of Armour Wires with Processing-Induced Residual Stress
3.1. Model Establishment
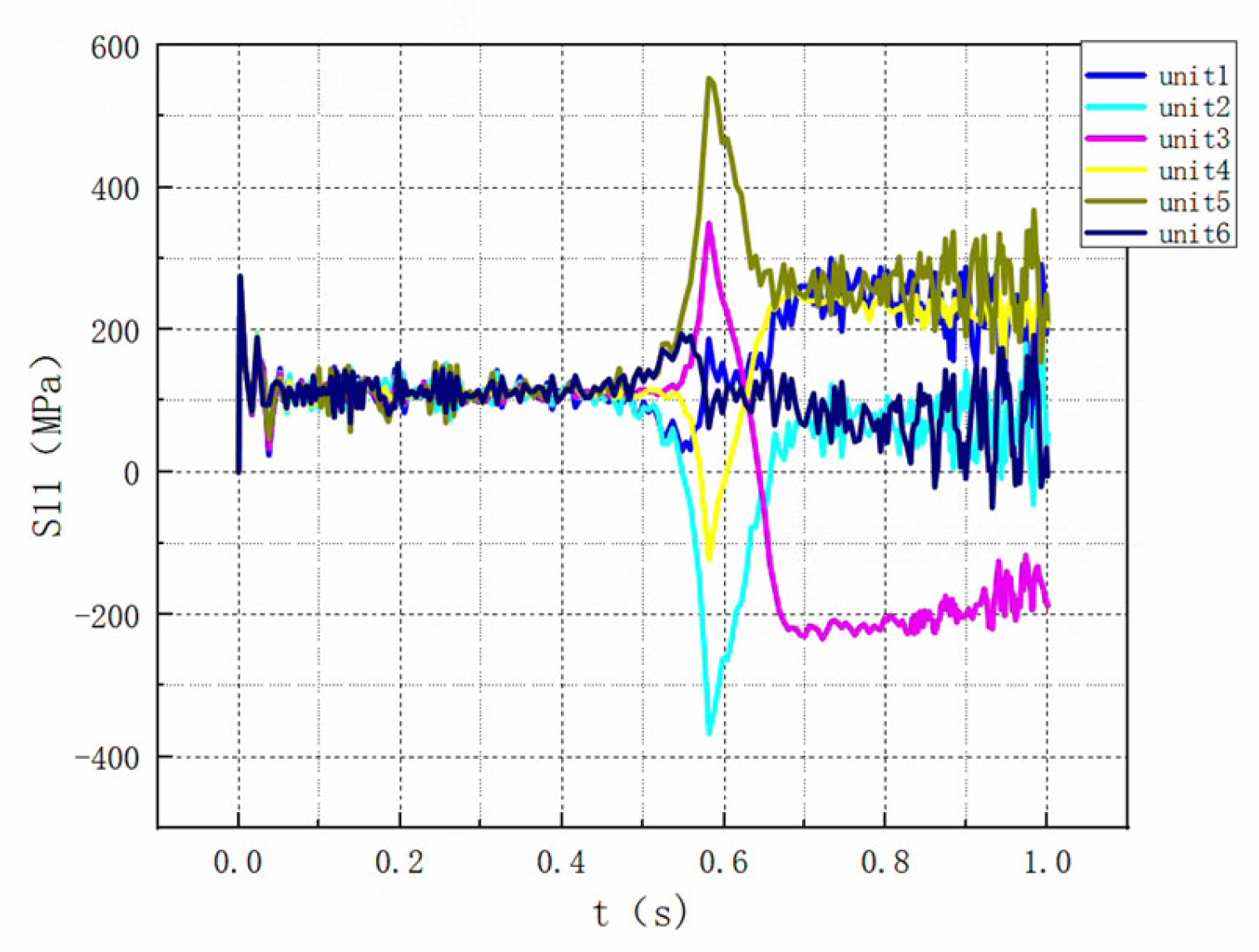
3.2. Discussion on the Residual Stress Distribution in Steel Wire Cross-Section After Loading and Unloading
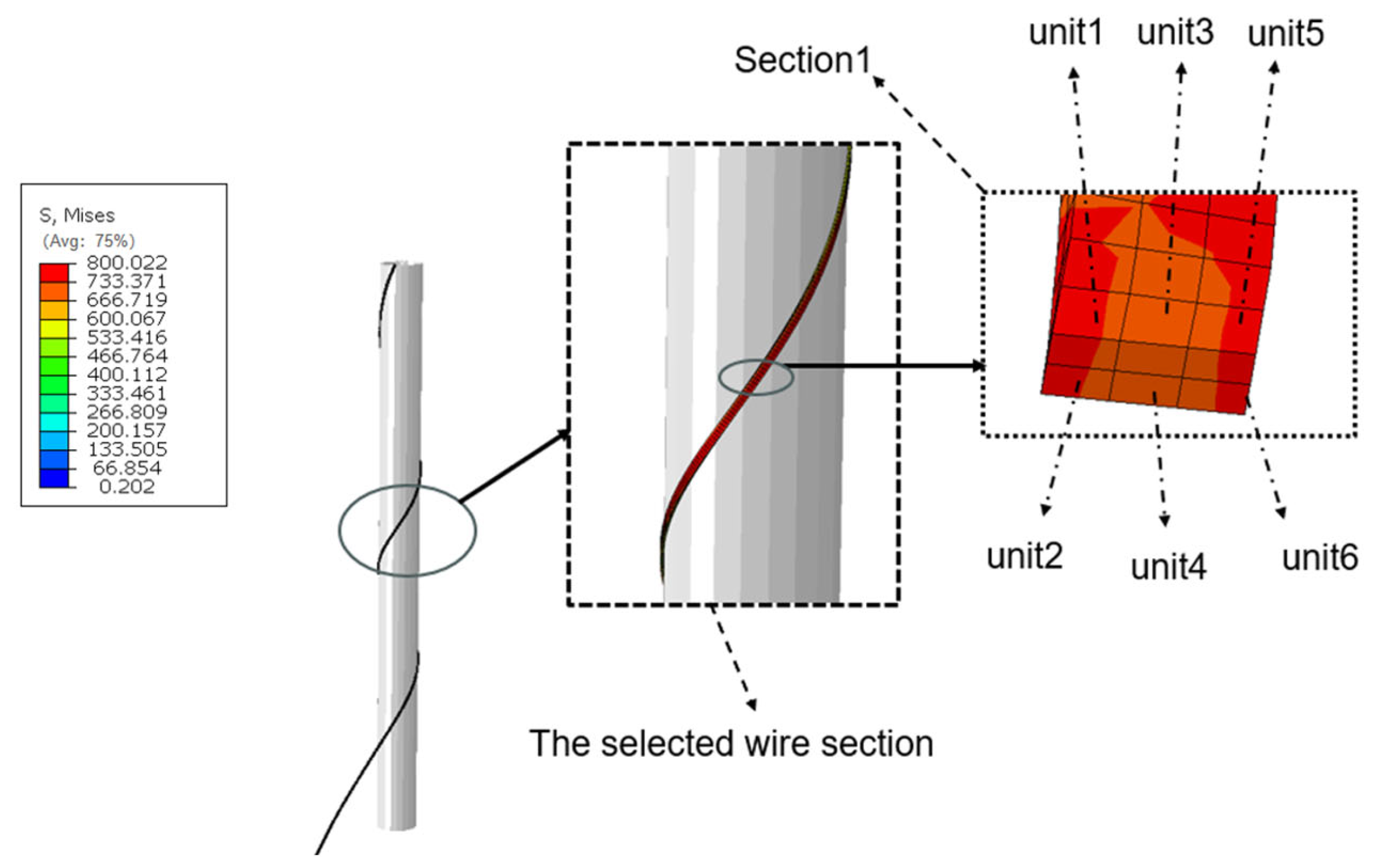
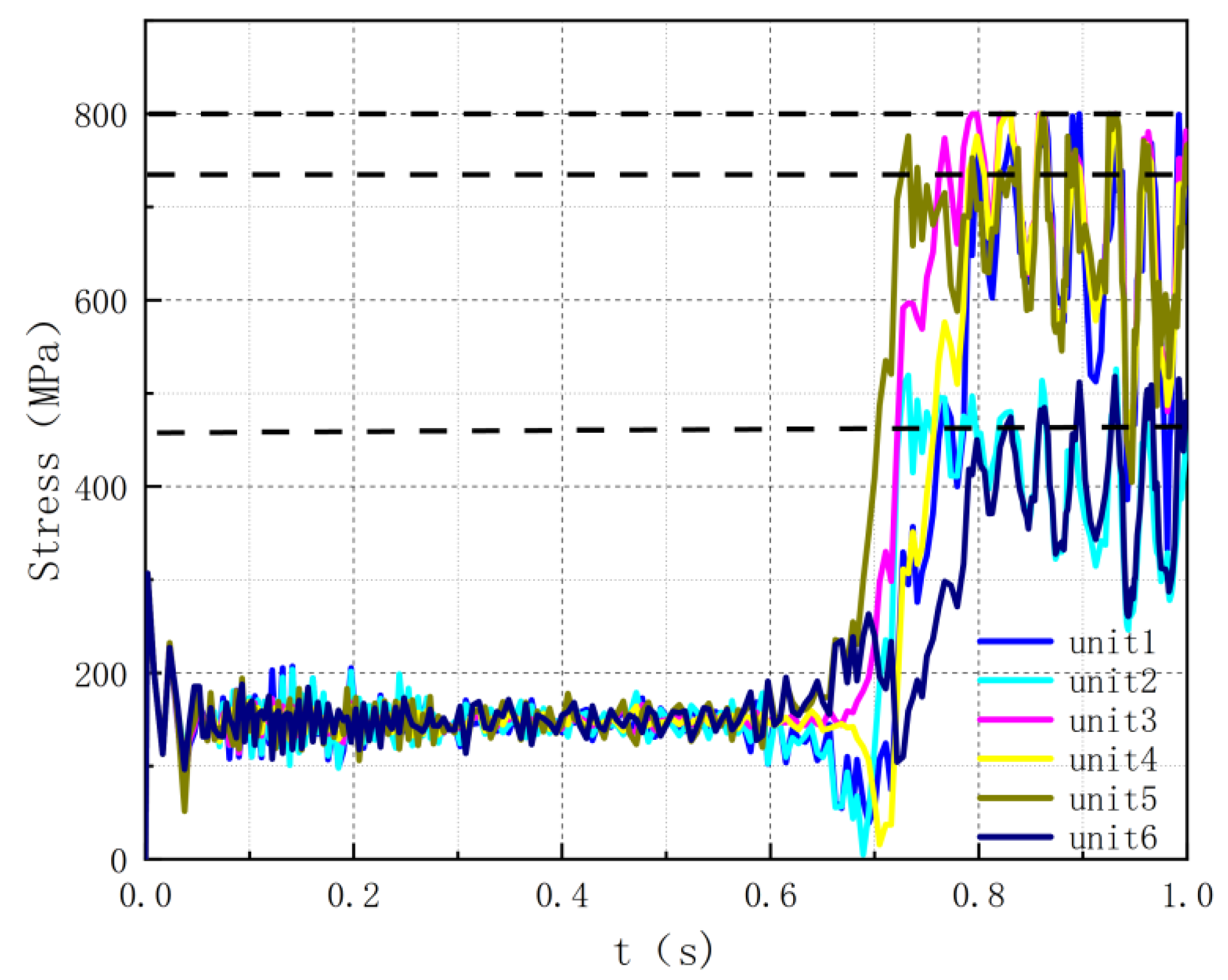
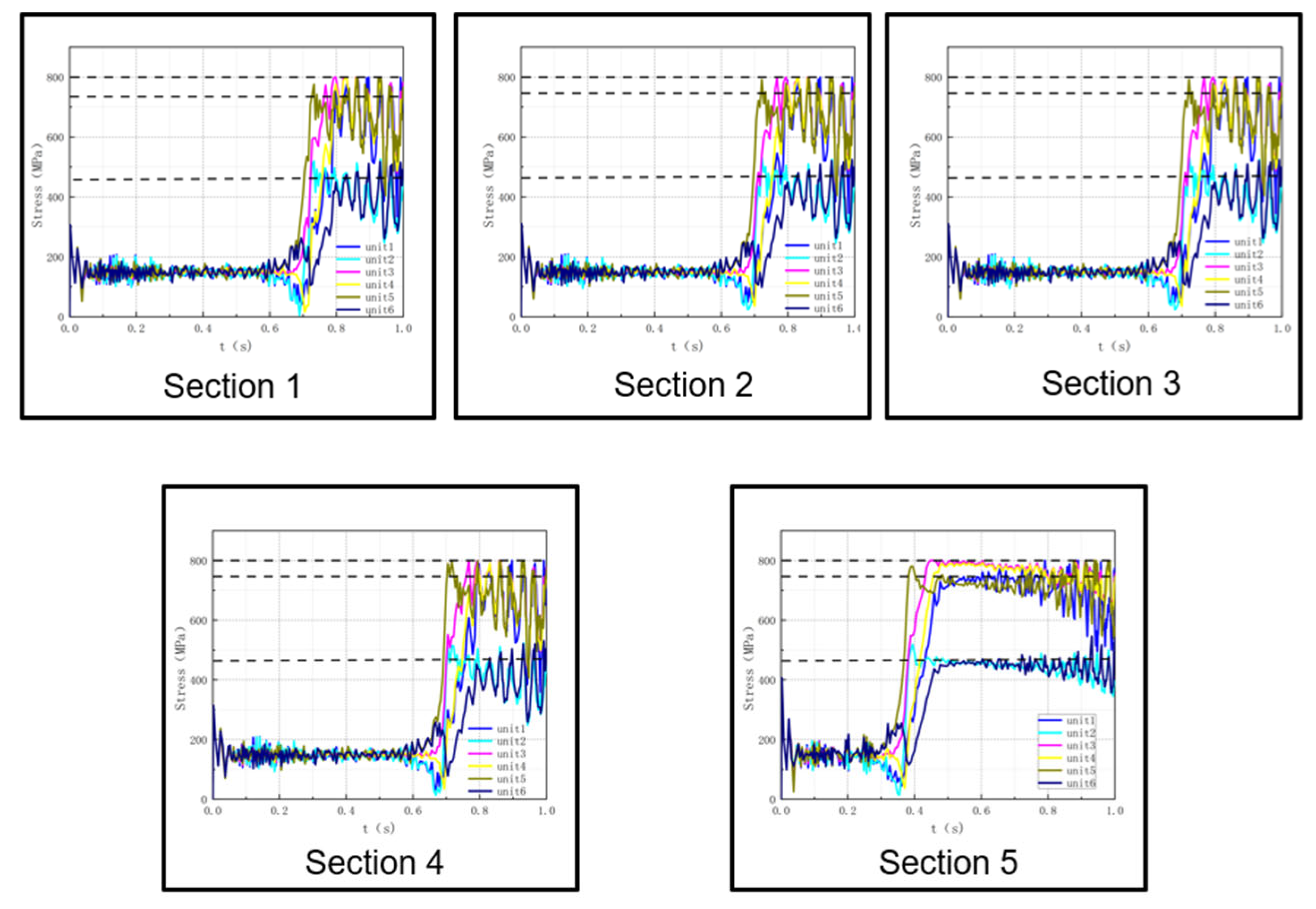
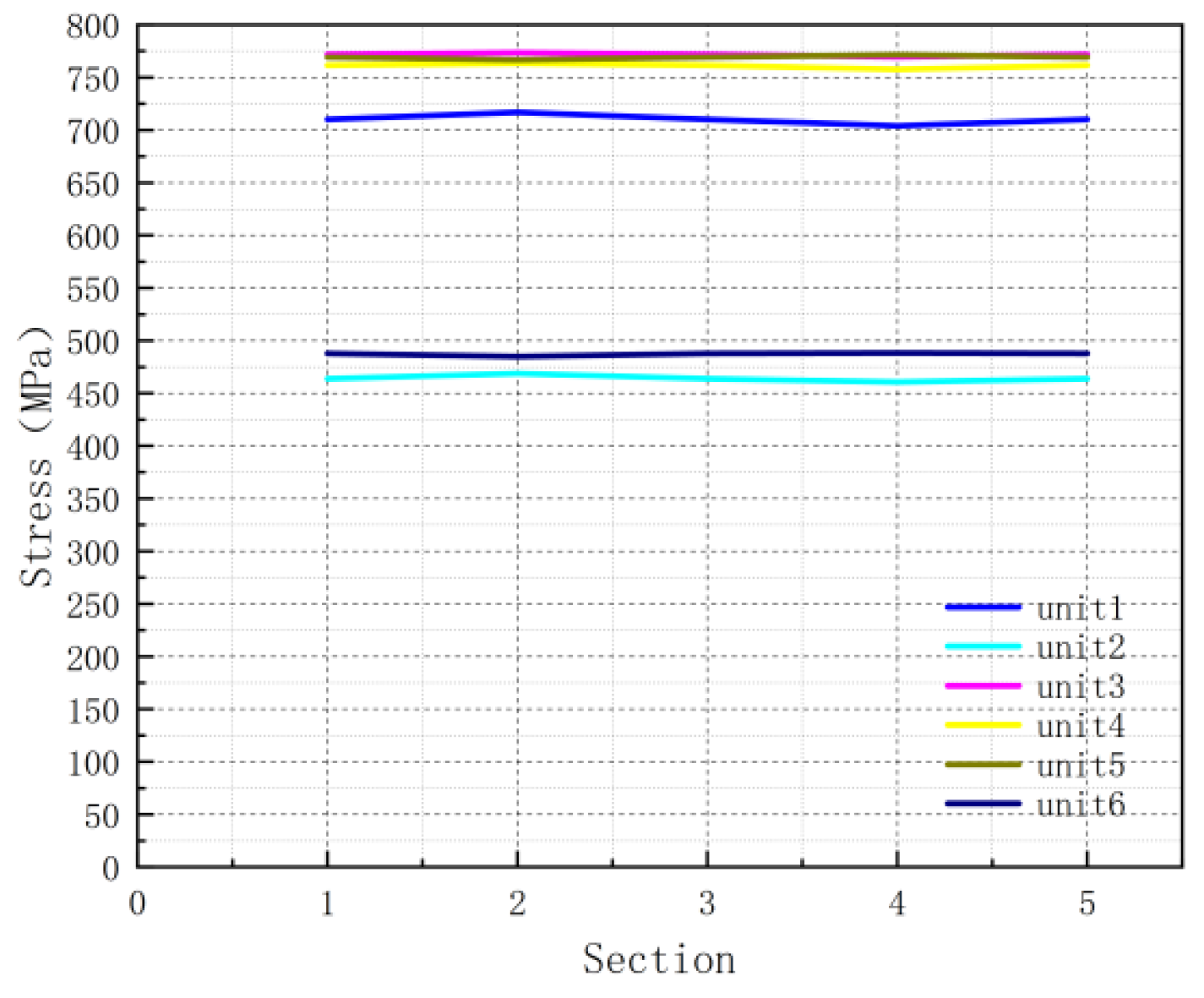
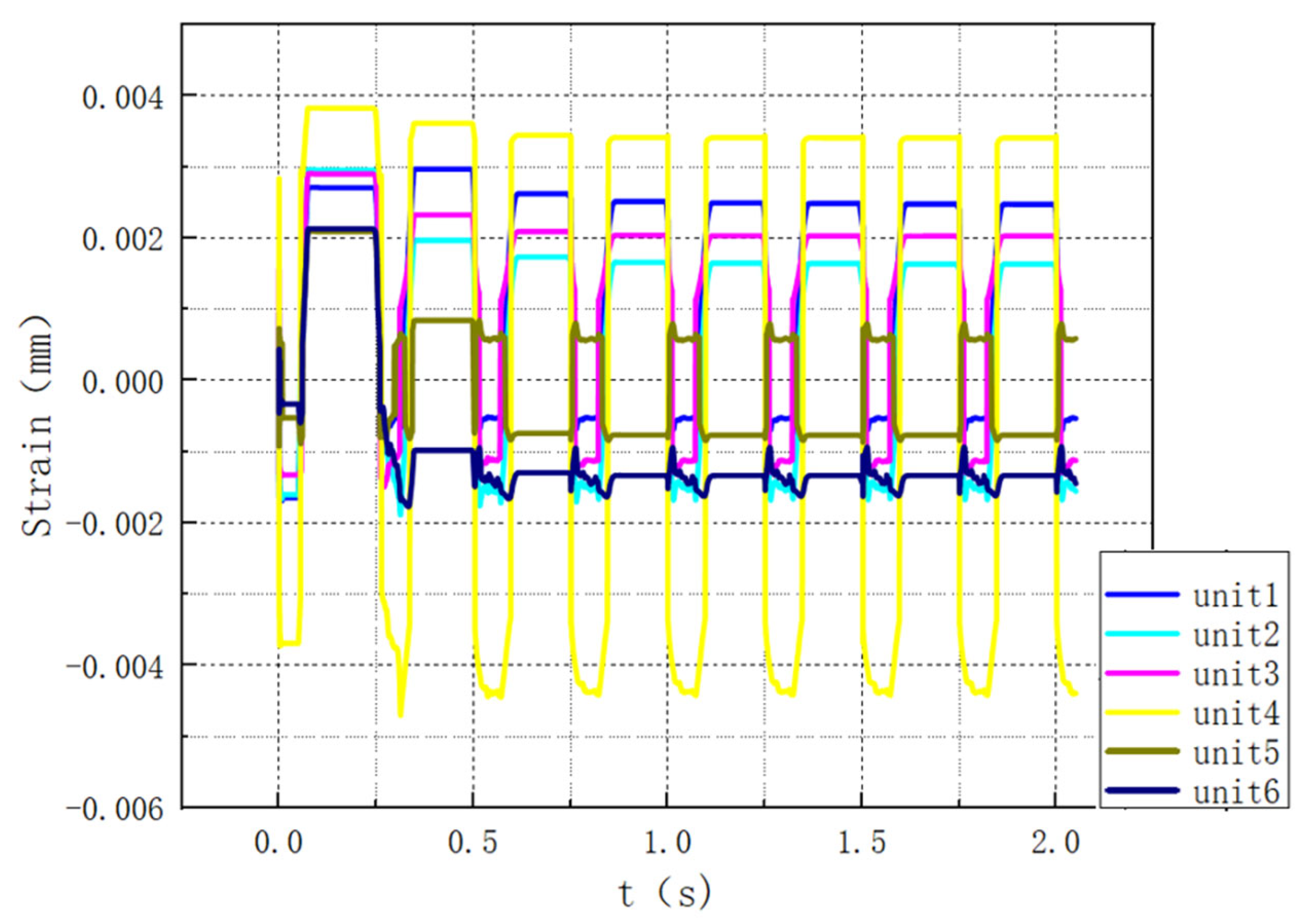
4. Study on Cyclic Tension Shakedown Behaviour
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Knapp, R. Nonlinear analysis of a helically armoured cable with nonuniform mechanical properties in tension and torsion. In Proceedings of the Ocean 75 Conference, San Diego, CA, USA, 22–25 September 1975; IEEE: New York, NY, USA, 1975; pp. 155–164. [Google Scholar]
- Knapp, R.H. Derivation of a new stiffness matrix for helically armoured cables considering tension and torsion. Int. J. Numer. Methods Eng. 1979, 14, 515–529. [Google Scholar] [CrossRef]
- Knapp, R.H. Torque and stress balanced design of helically armoured cables. J. Eng. Ind. 1981, 103, 61–66. [Google Scholar] [CrossRef]
- Lanteigne, J. Theoretical estimation of the response of helically armoured cables to tension, torsion, and bending. J. Appl. Mech. 1985, 52, 423–432. [Google Scholar] [CrossRef]
- LeClair, R.A.; Costello, G.A. Axial, bending and torsional loading of a strand with friction. J. Offshore Mech. Arct. Eng. 1988, 110, 38–42. [Google Scholar] [CrossRef]
- Jolicoeur, C.; Cardou, A. A numerical comparison of current mathematical models of twisted wire cables under axisymmetric loads. J. Energy Resour. Technol. 1991, 113, 241–249. [Google Scholar] [CrossRef]
- Witz, J.A.; Tan, Z. On the axial-torsional structural behaviour of flexible pipes, umbilicals and marine cables. Mar. Struct. 1992, 5, 205–227. [Google Scholar] [CrossRef]
- Custódio, A.; Vaz, M. A nonlinear formulation for the axisymmetric response of umbilical cables and flexible pipes. Appl. Ocean. Res. 2002, 24, 21–29. [Google Scholar] [CrossRef]
- Ramos, R., Jr.; Pesce, C.P. A consistent analytical model to predict the structural behavior of flexible risers subjected to combined loads. J. Offshore Mech. Arct. Eng. 2004, 126, 141–146. [Google Scholar] [CrossRef]
- Yue, Q.; Lu, Q.; Yan, J.; Zheng, J.; Palmer, A. Tension behavior prediction of flexible pipelines in shallow water. Ocean. Eng. 2013, 58, 201–207. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, H.; Chen, Y.; Guan, Y.; Wang, Y.; Dai, L. Modeling of multi-strand wire ropes subjected to axial tension and torsion loads. Int. J. Solids Struct. 2015, 58, 233–246. [Google Scholar] [CrossRef]
- Foti, F.; di Roseto, A.D.L. Analytical and finite element modelling of the elastic–plastic behaviour of metallic strands under axial–torsional loads. Int. J. Mech. Sci. 2016, 115, 202–214. [Google Scholar] [CrossRef]
- Blkich, H. Über die Bemessung statisch unbestimmter Stahlwerke unter Berücksichtigung des elastischplastischen Berhaltens des Baustoffes. Bauingenieur 1932, 13, 261–267. [Google Scholar]
- Melan, E. Theorie Statisch Unbestimmter Systeme aus Ideal-Plastischem Baustoff; Hölder-Pichler-Tempsky in Komm: Prambachkirchen, Austria, 1936. [Google Scholar]
- Melan, E. Zur plastizität des räumlichen kontinuums. Ing.-Arch. 1938, 9, 116–126. [Google Scholar] [CrossRef]
- Koiter, W.T. A new general theorem on shakedown of elastic-plastic structures. Proc. Koninkl. Ned. Akad. Wet. B 1956, 59, 24–34. [Google Scholar]
- Ponter, A.R.S.; Karadeniz, S. An extended shakedown theory for structures that suffer cyclic thermal loading, Part 1: Theory. J. Appl. Mech. 1985, 52, 877–882. [Google Scholar] [CrossRef]
- Polizzotto, C. On the conditions to prevent plastic shakedown of structures: Part I—Theory. J. Appl. Mech. 1993, 60, 15–19. [Google Scholar] [CrossRef]
- Prager, W. A new method of analyzing stresses and strains in work-hardening plastic solids. J. Appl. Mech. 1956, 23, 493–496. [Google Scholar] [CrossRef]
- Besseling, J.F. A theory of elastic, plastic, and creep deformations of an initially isotropic material showing anisotropic strain-hardening, creep recovery, and secondary creep. J. Appl. Mech. 1958, 25, 529–536. [Google Scholar] [CrossRef]
- Armstrong, P.J.; Frederick, C.O. A Mathematical Representation of the Multiaxial Bauschinger Effect; Nuclear Laboratories: Berkeley, CA, USA, 1966; Volume 731. [Google Scholar]
- Chaboche, J.L. Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Han, K.; Chen, Z.-F.; Wang, W.; Shi, L.; Lu, K.-Q. A short review of ratcheting effect in pressurized piping. Int. J. Press. Vessel. Pip. 2023, 205, 105009. [Google Scholar] [CrossRef]
- Fernando, U.S.; Davidson, M.; Simpson, C.; Pirling, T.; Yan, K.; Callaghan, M.D.; Roy, M.; Francis, J.A.; Withers, P.J. Measurement of residual stress shakedown in pressure/tensile armour wires of flexible pipes by neutron diffraction. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Sævik, S.; Gray, L.; Phan, A. A method for calculating residual and transverse stress effects in flexible pipe pressure spirals. In Proceedings of the 20th International Conference on Offshore Mechanics and Arctic Engineering (OMAE 2001 CD), Rio de Janeiro, Brazil, 3–8 June 2001; pp. 3–8. [Google Scholar]
- Fernando, U.S.; Tan, Z.; Sheldrake, T.; Clements, R. The stress analysis and residual stress evaluation of pressure armour layers in flexible pipes using 3D finite element models. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004; Volume 37459, pp. 57–65. [Google Scholar]
- Tang, M.; Yan, J.; Chen, J.; Yang, Z.; Yue, Q. Residual Stress Evaluation and Buckling Analysis of Carcass Layers in Flexible Pipes Using 3D Finite Element Model. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015. [Google Scholar]
- Lu, Q.; Wu, S.; Wang, D.; Yang, Z.; Yin, Y.; Hu, H.; Yan, J.; Yue, Q. Study on mechanical behavior of tensile armour wires of marine flexible pipes and cables during winding process. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Glasgow, UK, 9–14 June 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 58806. [Google Scholar]
- Pan, Y.; Zheng, L.; Yang, S.; Wang, Y. A review of fatigue analysis of marine flexible risers. Geoenergy Sci. Eng. 2024, 246, 213555. [Google Scholar] [CrossRef]
- Bao, R.; Liu, J.; Xiao, Z. Stress and failure analysis of composite flexible riser subjected to torsion and thermomechanical loading. In Proceedings of the International Ocean and Polar Engineering Conference, Rhodes, Greece, 16–21 June 2024; ISOPE: Mountain View, CA, USA, 2024. [Google Scholar]




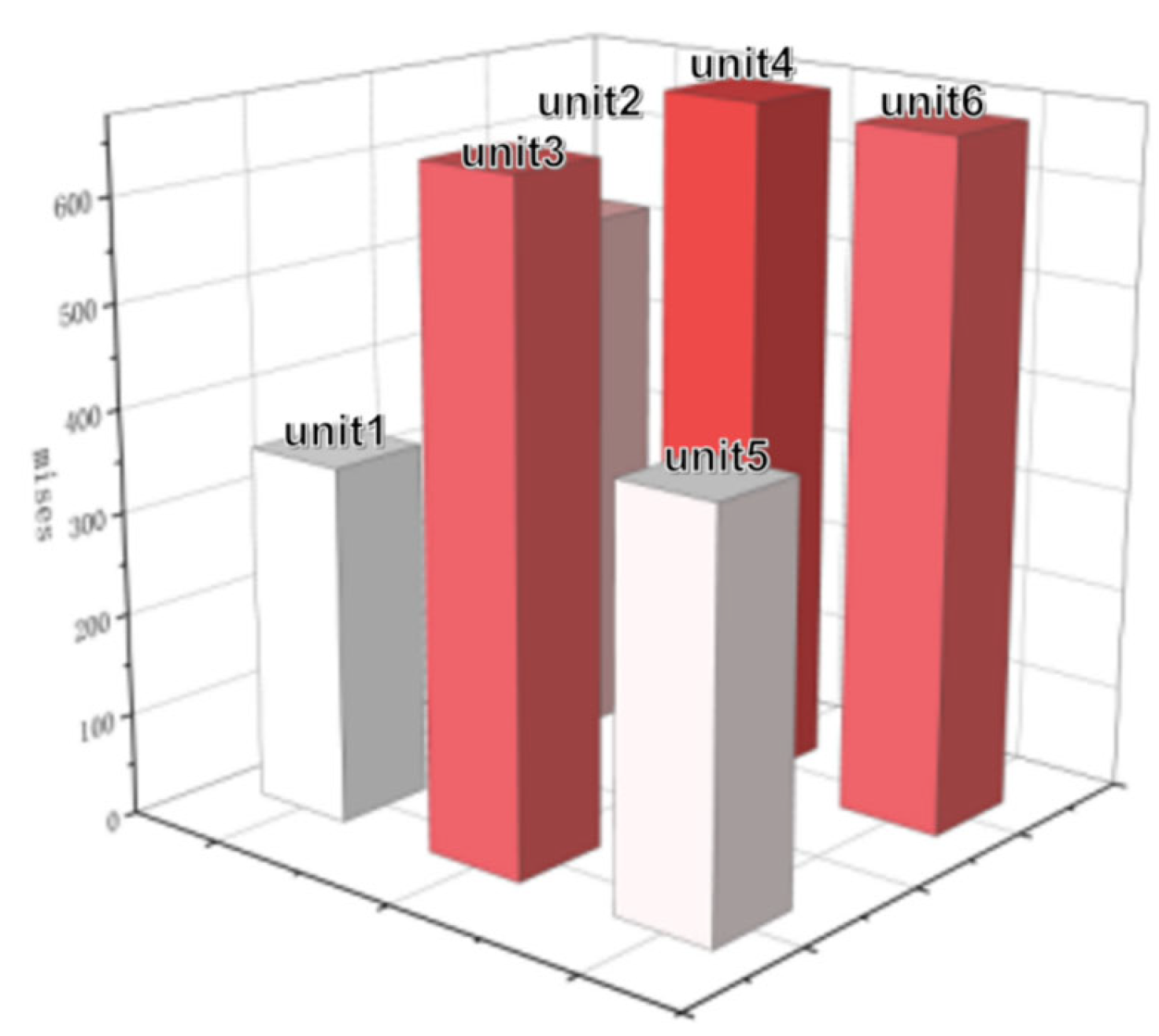
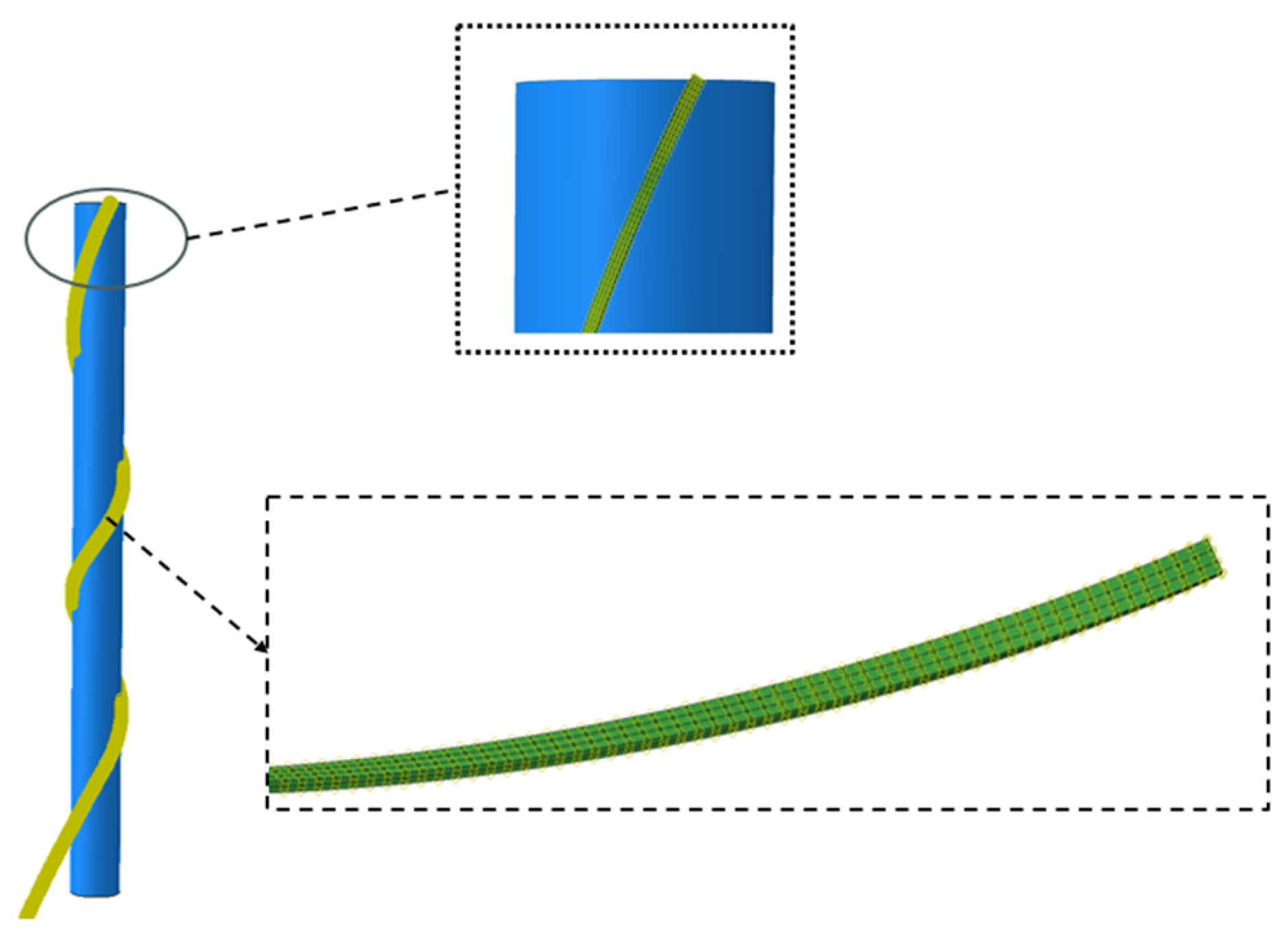




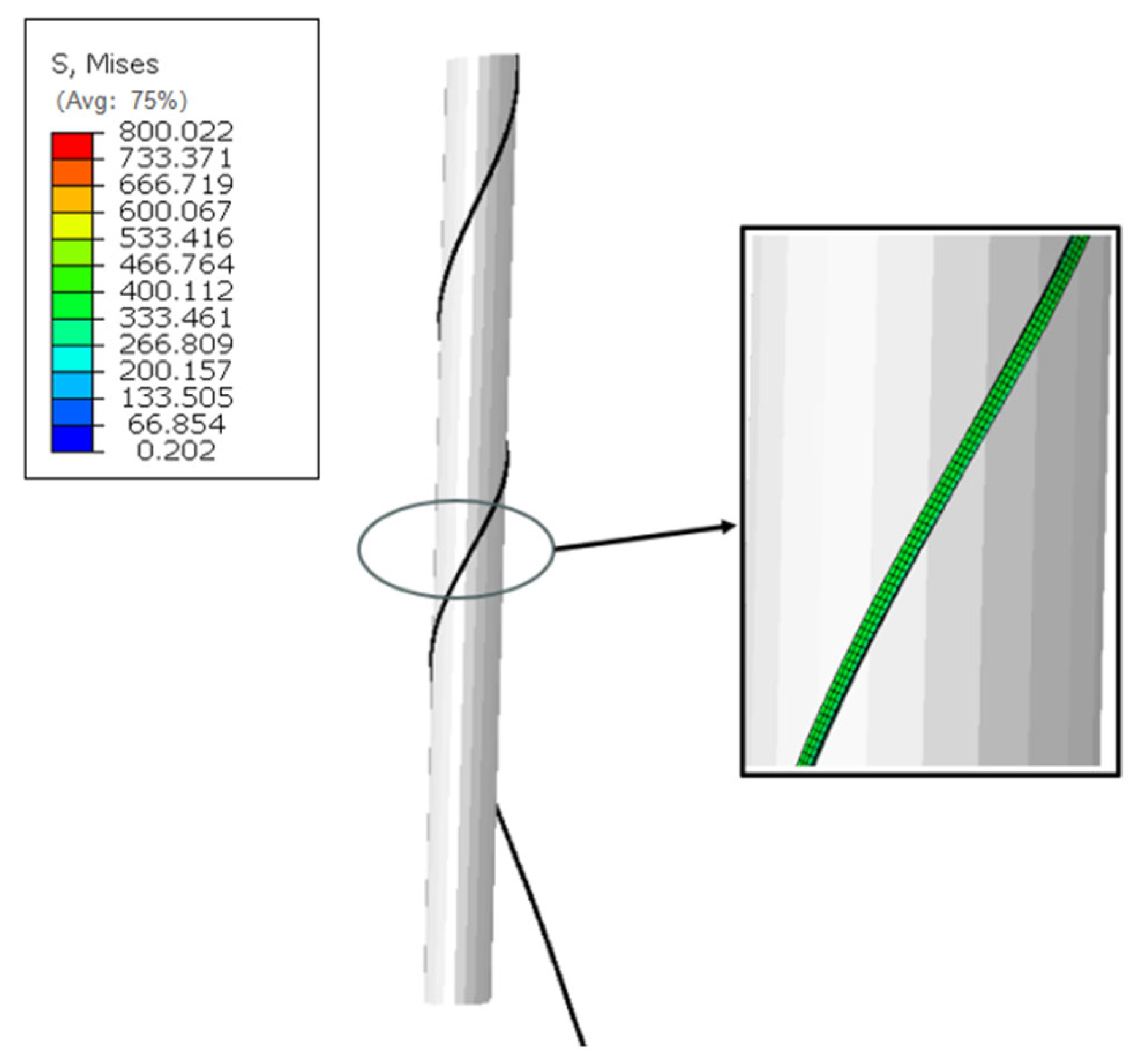

| Width | Thickness | Winding Radius | Winding Angle | Elastic Modulus | Yield Strength | Wire Merging Die Radius |
|---|---|---|---|---|---|---|
| 12 mm | 4 mm | 127 mm | 30° | 2 × 105 MPa | 800 Mpa | 132 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Liu, J.; Shang, E.; Yue, X.; Shen, Z. Study on Cyclic Tensile Shakedown Behaviour of Flexible Risers Considering Winding Process. J. Mar. Sci. Eng. 2025, 13, 2186. https://doi.org/10.3390/jmse13112186
Wu S, Liu J, Shang E, Yue X, Shen Z. Study on Cyclic Tensile Shakedown Behaviour of Flexible Risers Considering Winding Process. Journal of Marine Science and Engineering. 2025; 13(11):2186. https://doi.org/10.3390/jmse13112186
Chicago/Turabian StyleWu, Shanghua, Junyu Liu, Ersu Shang, Xiufeng Yue, and Zhuoyuan Shen. 2025. "Study on Cyclic Tensile Shakedown Behaviour of Flexible Risers Considering Winding Process" Journal of Marine Science and Engineering 13, no. 11: 2186. https://doi.org/10.3390/jmse13112186
APA StyleWu, S., Liu, J., Shang, E., Yue, X., & Shen, Z. (2025). Study on Cyclic Tensile Shakedown Behaviour of Flexible Risers Considering Winding Process. Journal of Marine Science and Engineering, 13(11), 2186. https://doi.org/10.3390/jmse13112186






