Simulation Application of Computational Fluid Dynamics for the Variable Structure Underwater Vehicle
Abstract
1. Introduction
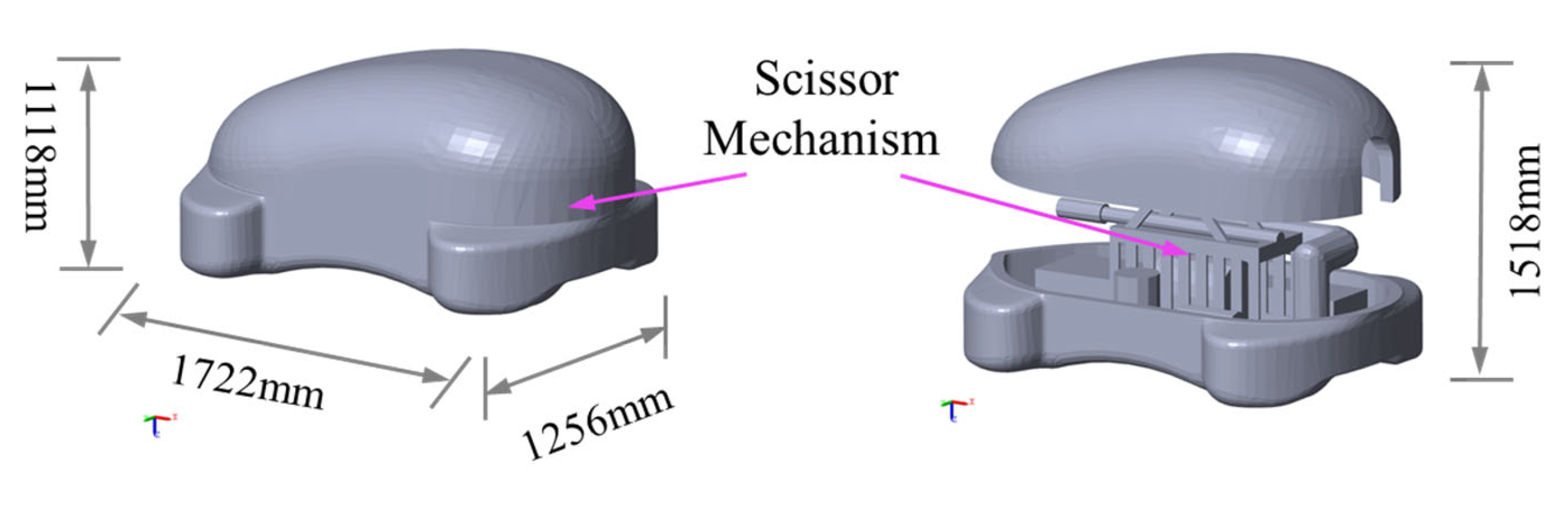
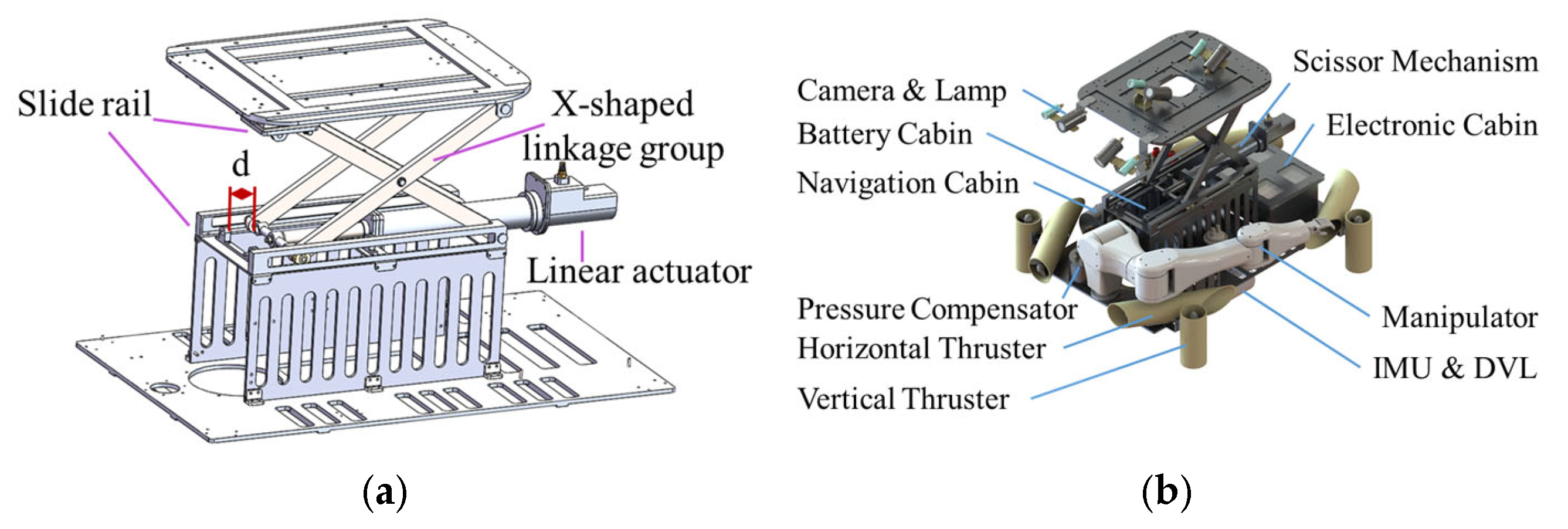
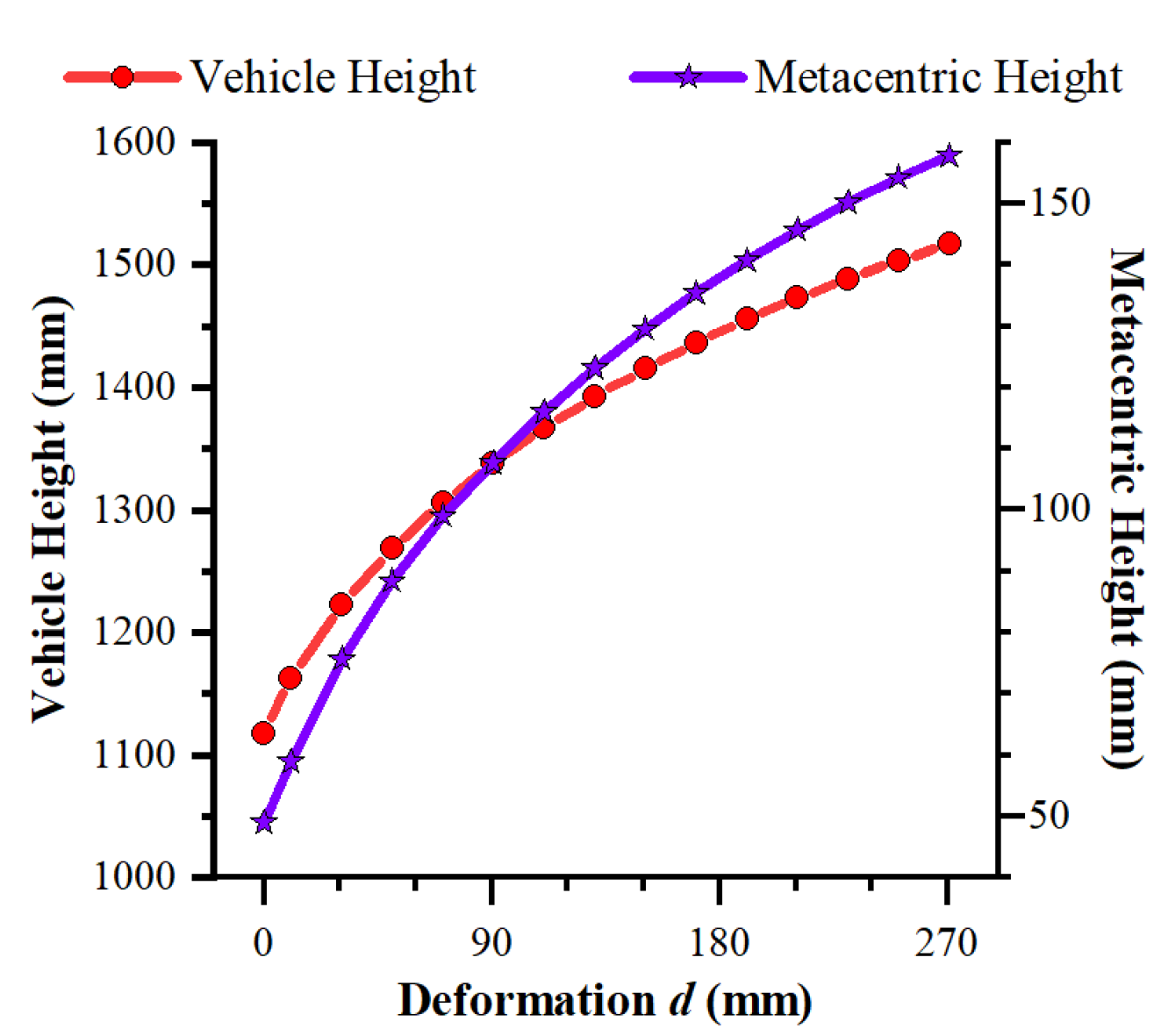
2. Underwater Vehicle Mechanism
3. CFD Simulation Strategy
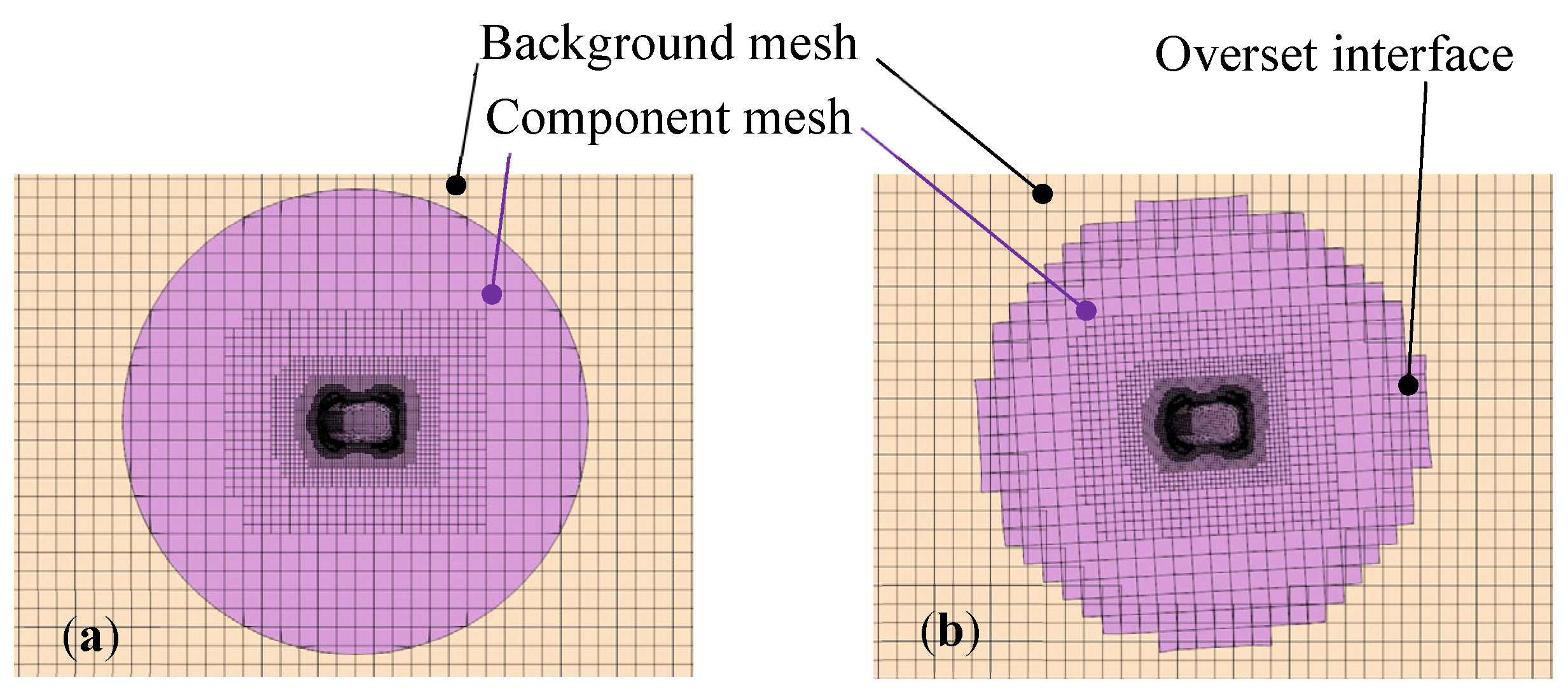
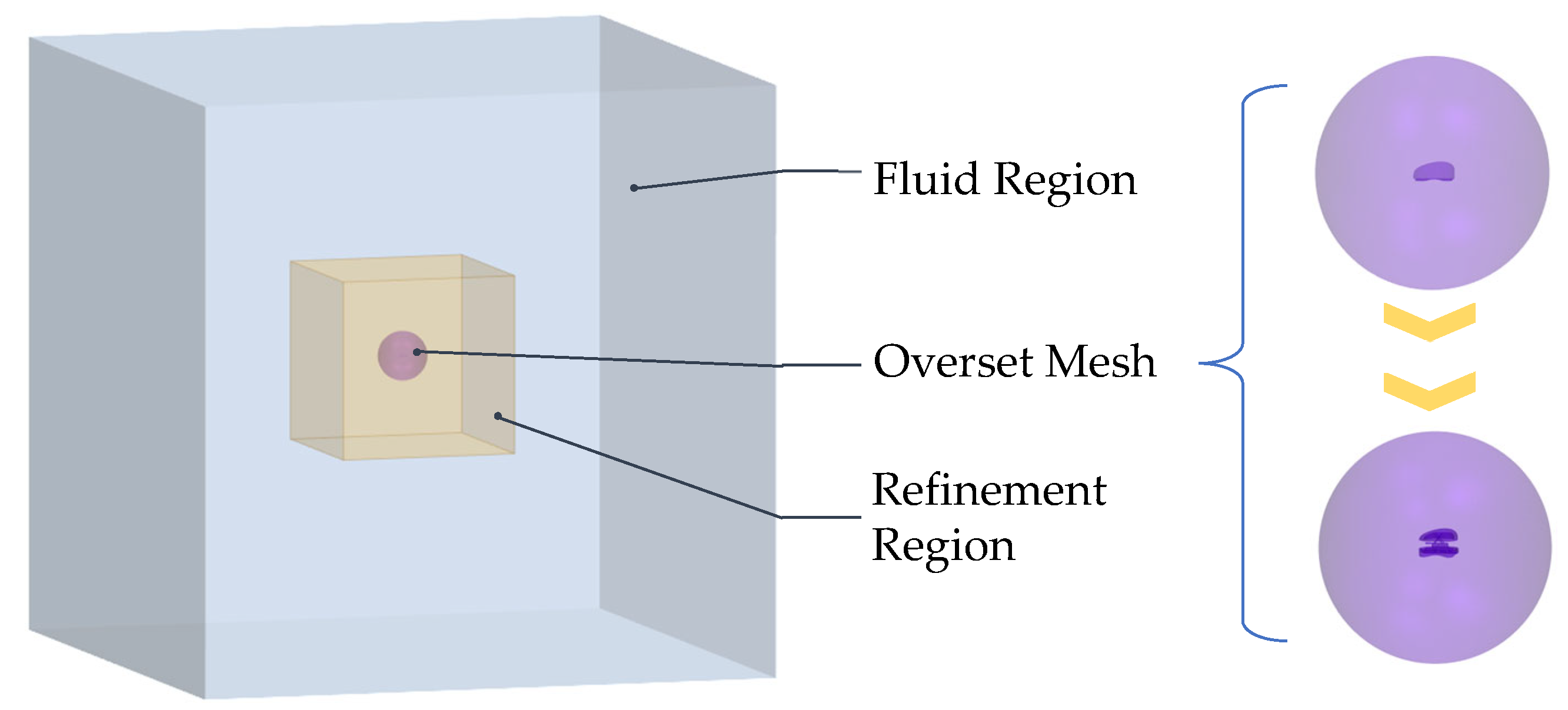
3.1. Parallel Meshing
3.2. Boundary Layer Configuration
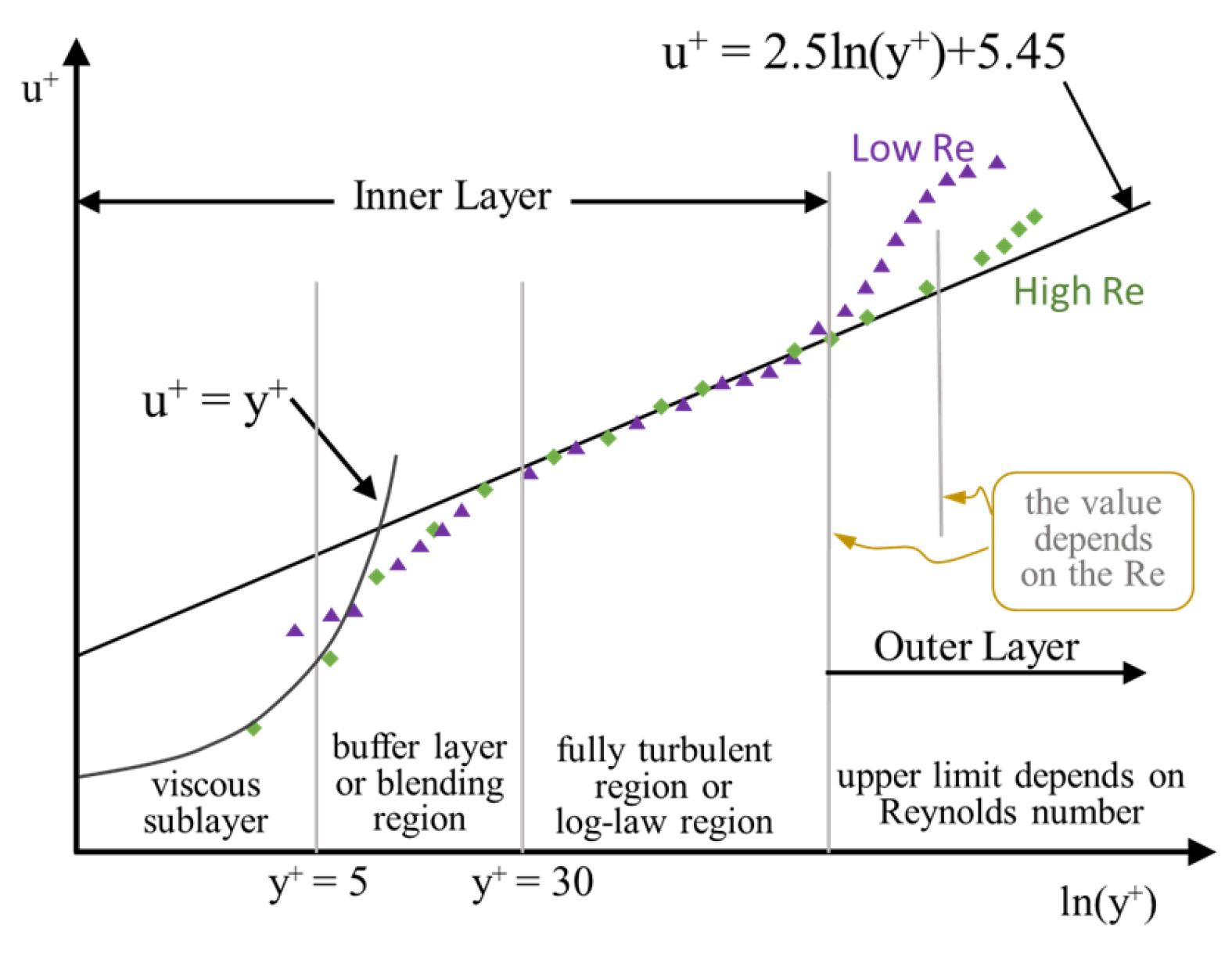
3.3. Turbulence Model
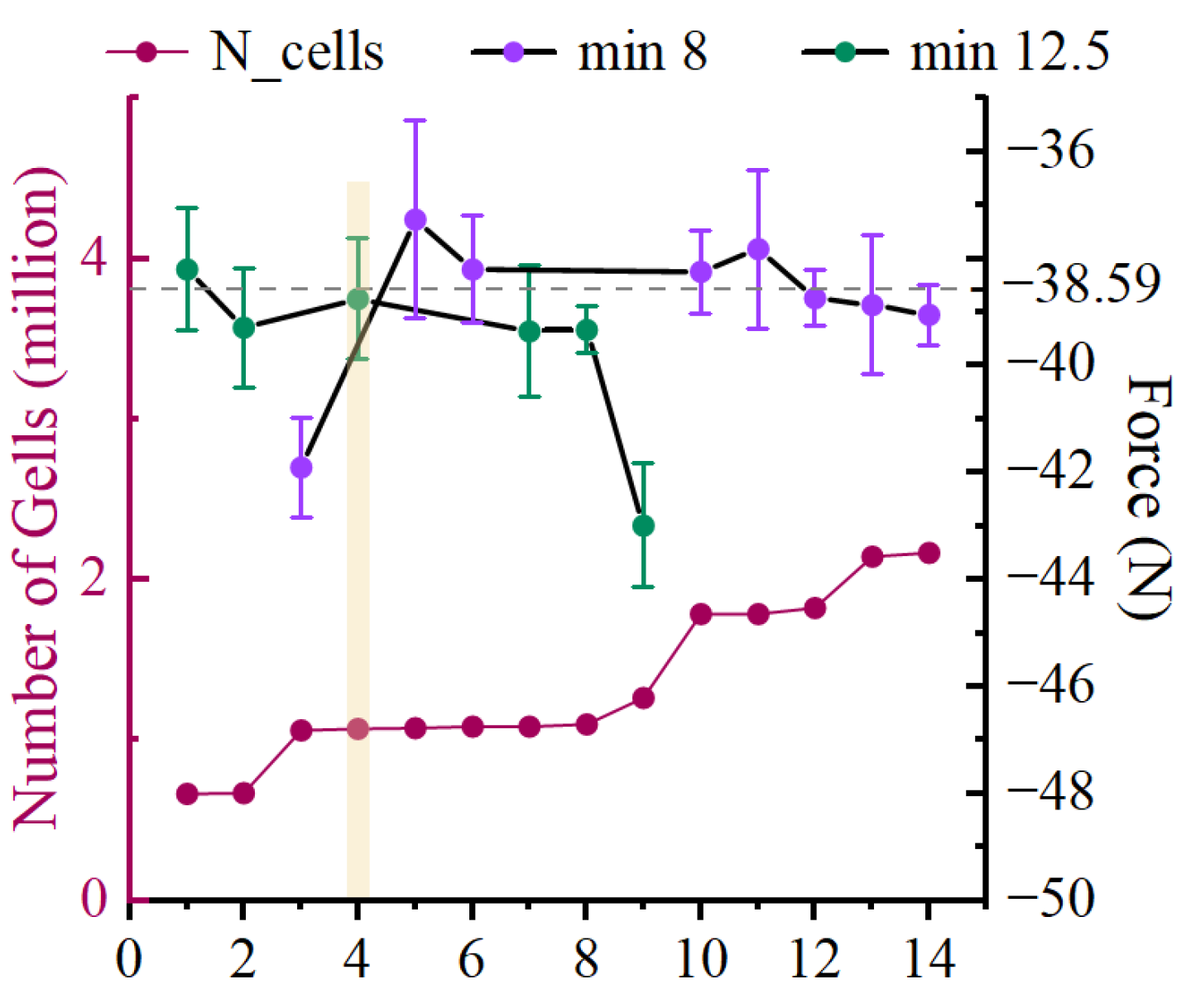
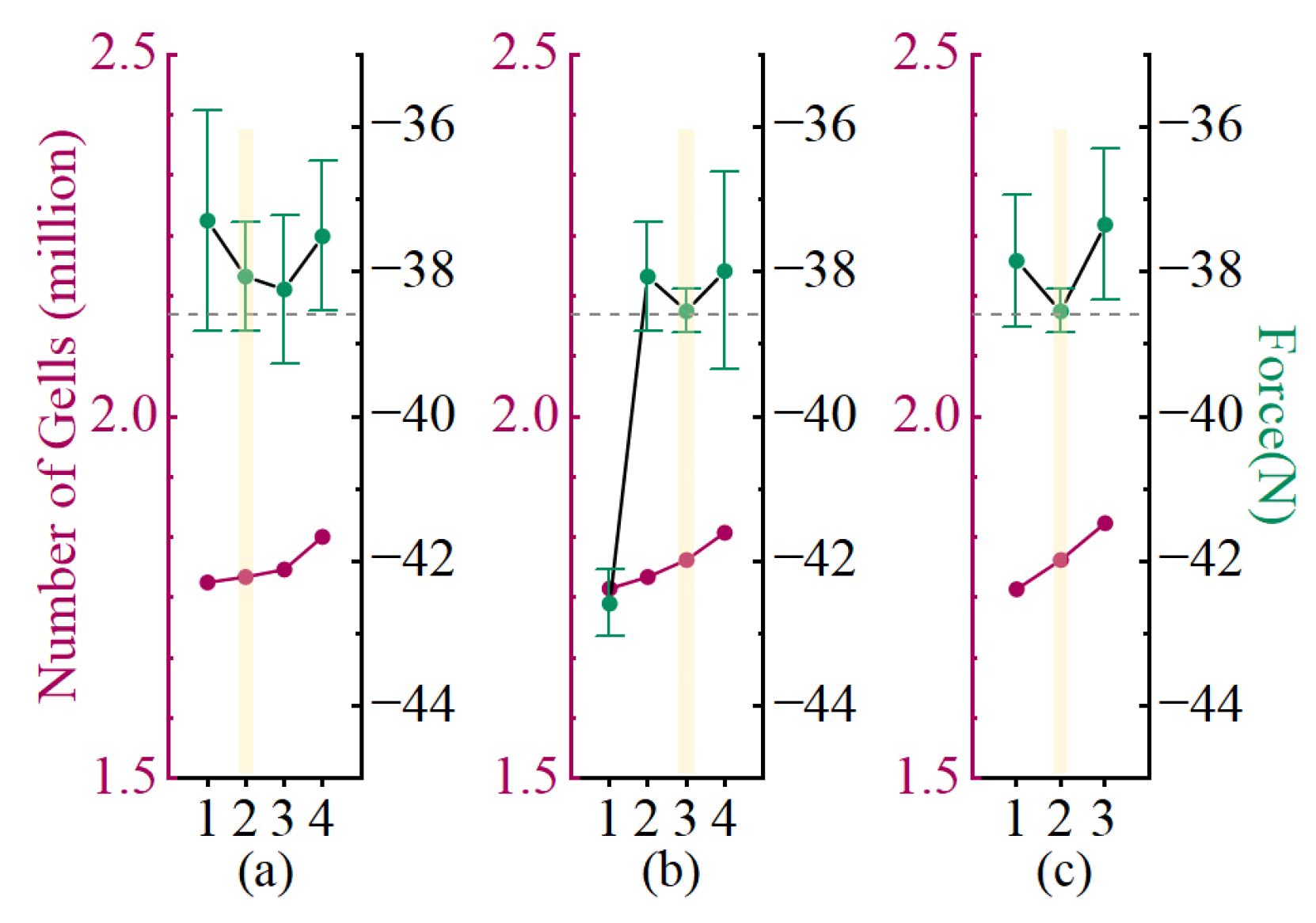
3.4. Grid Independence Verification
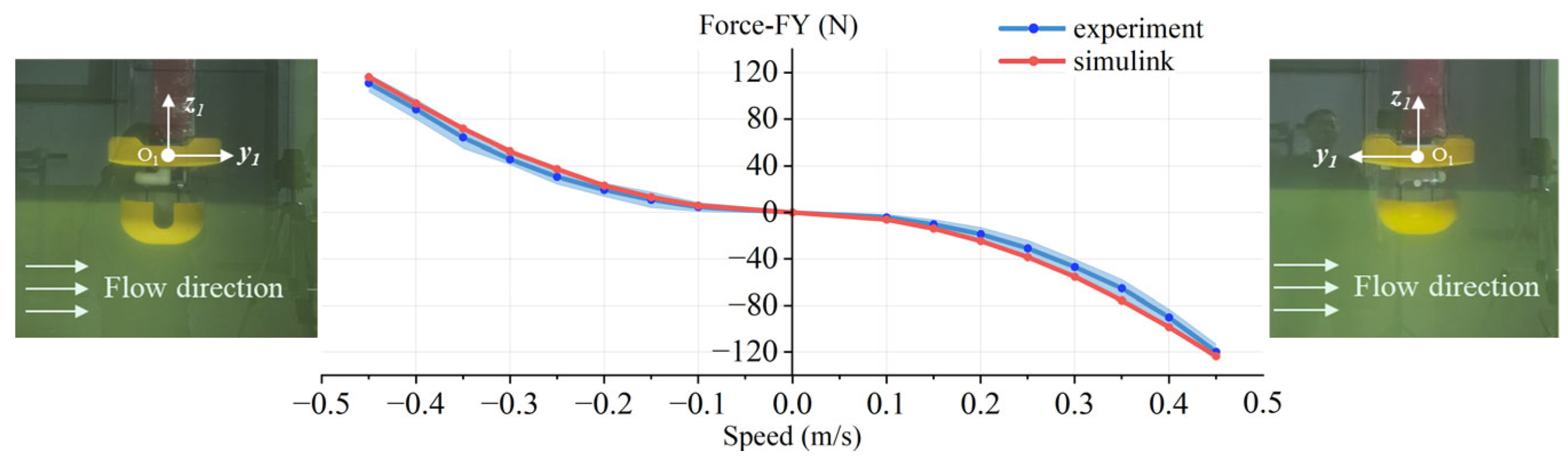
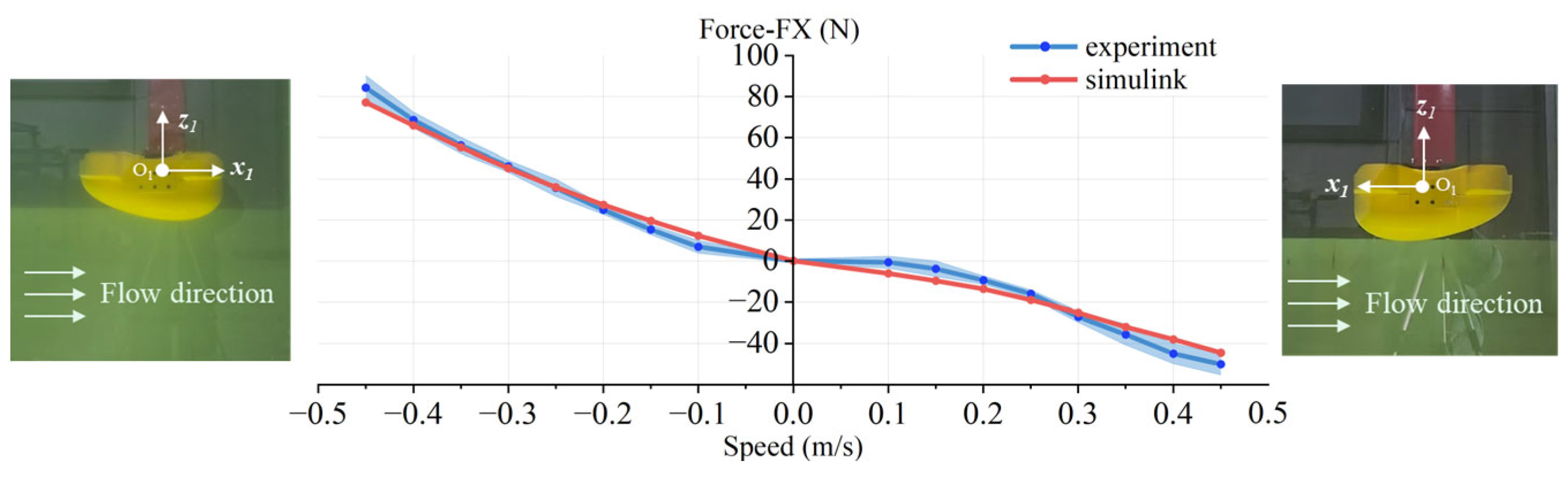
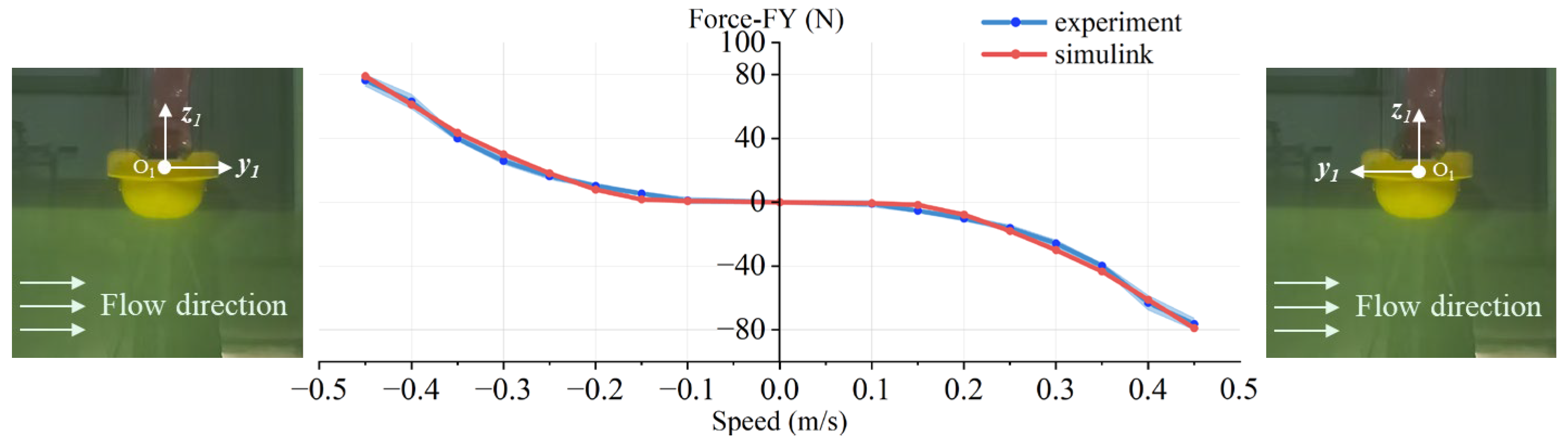
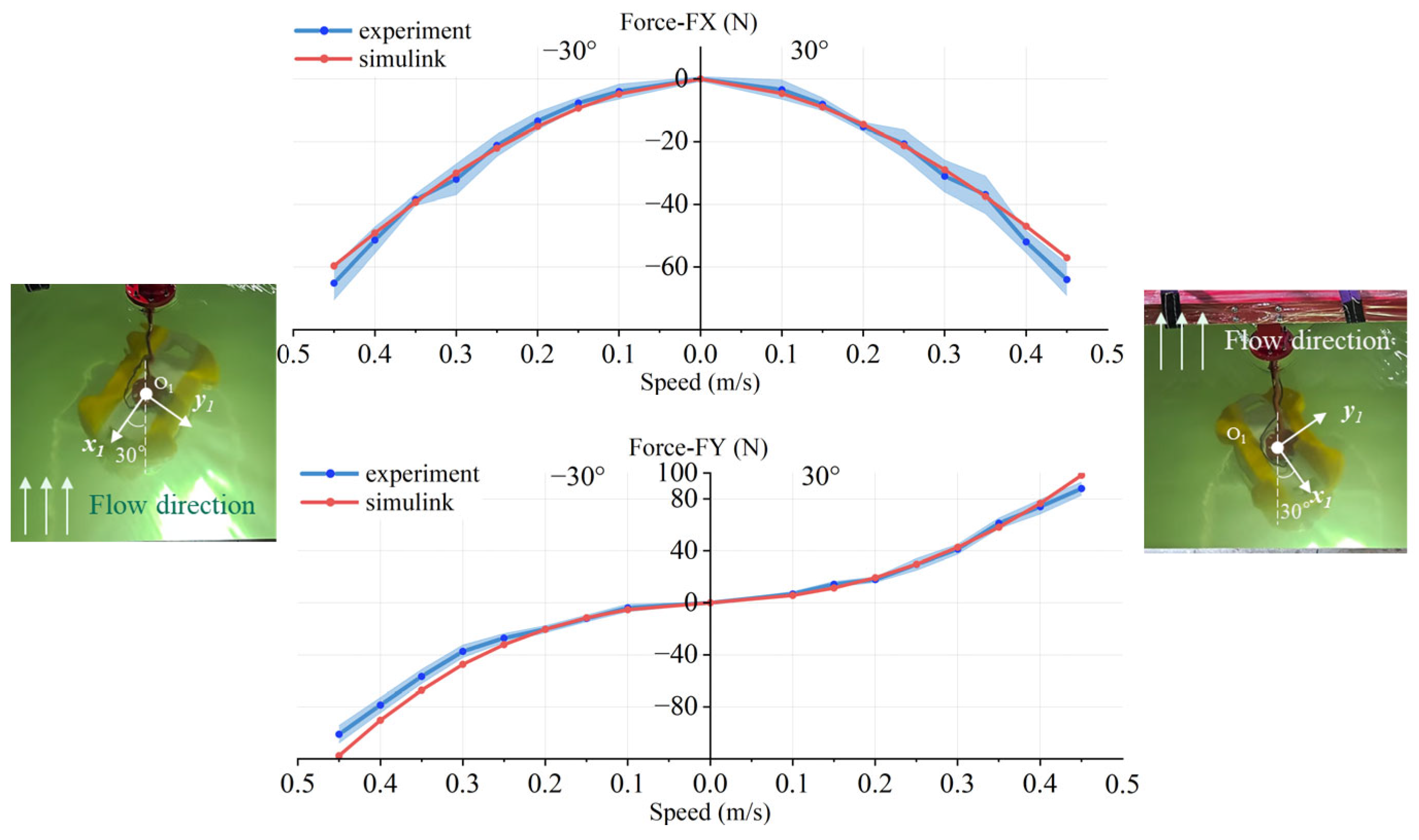
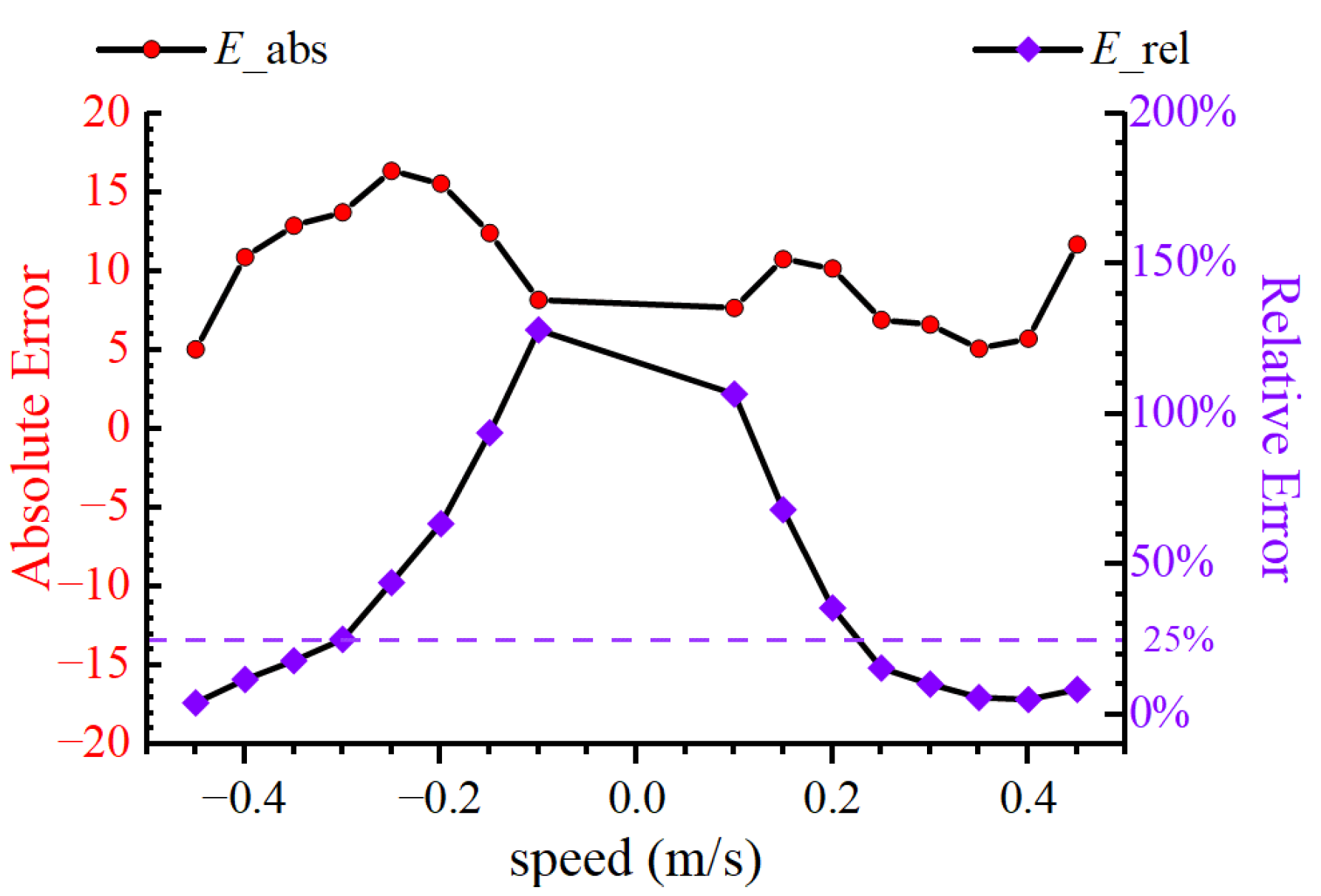
4. Comparison Between Simulation and Experiment
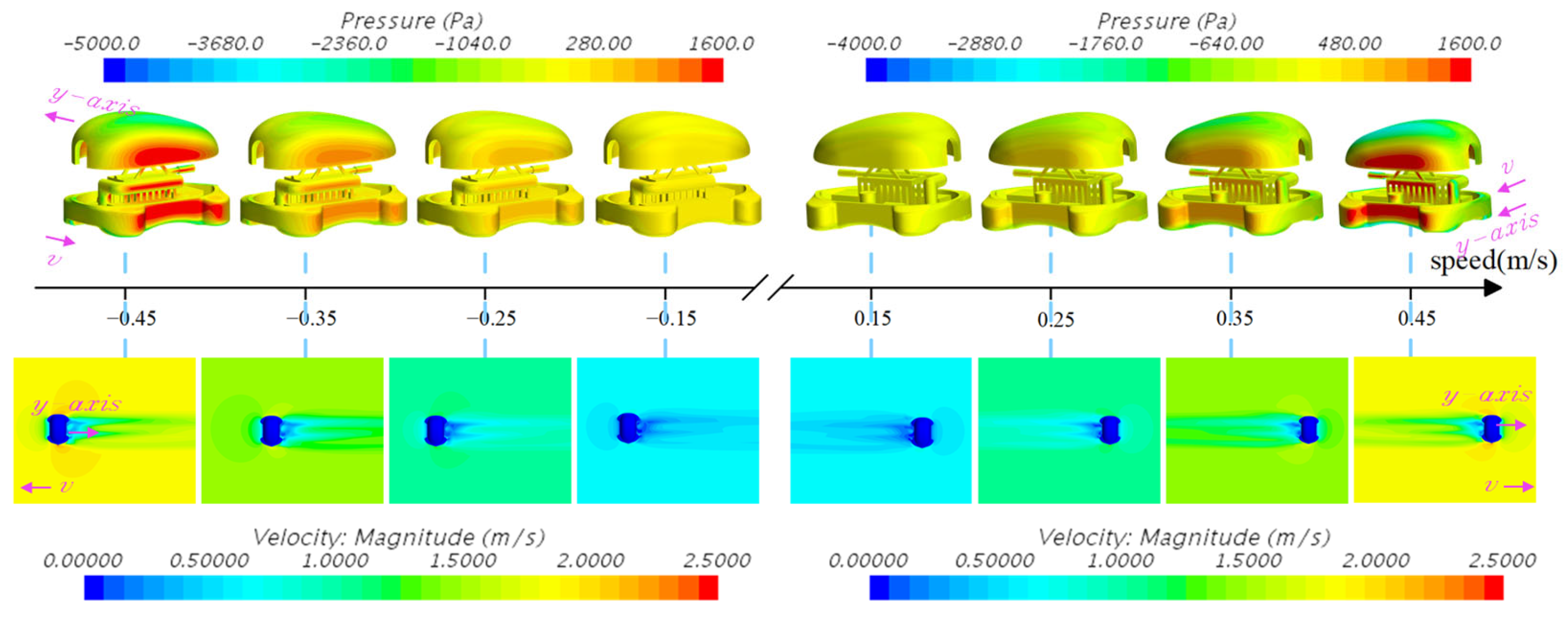
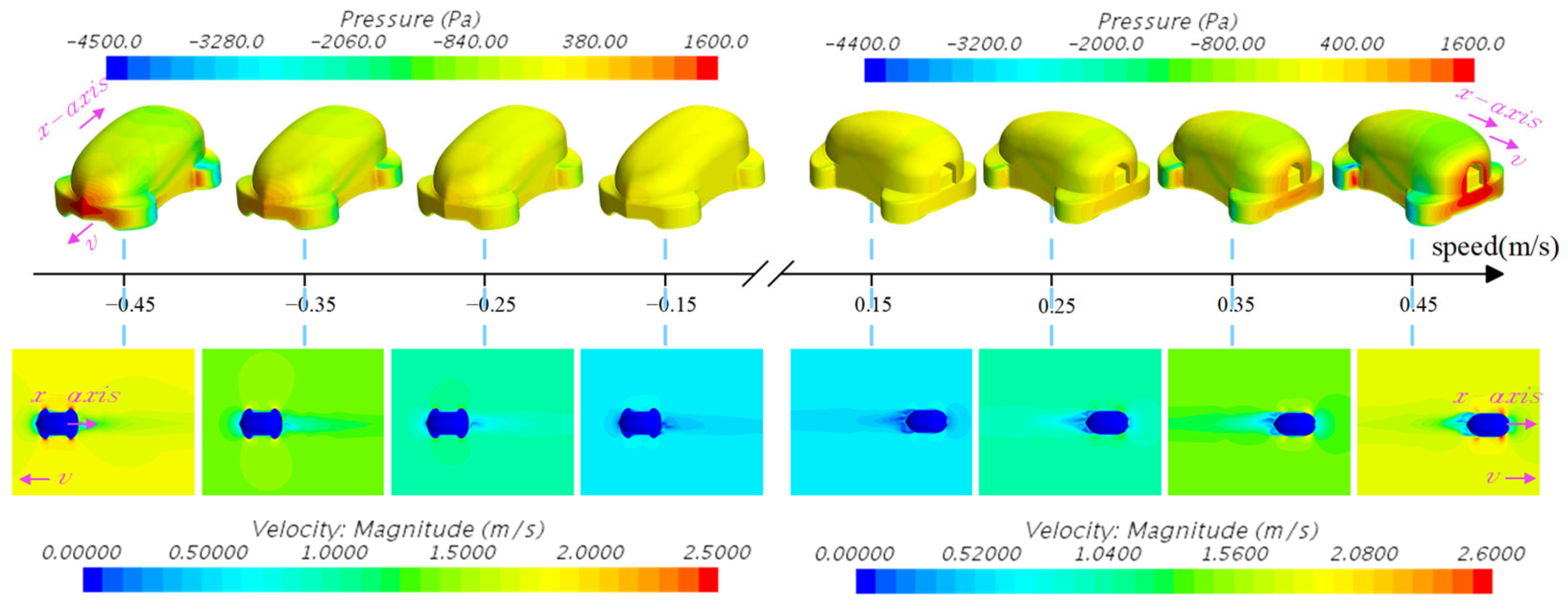
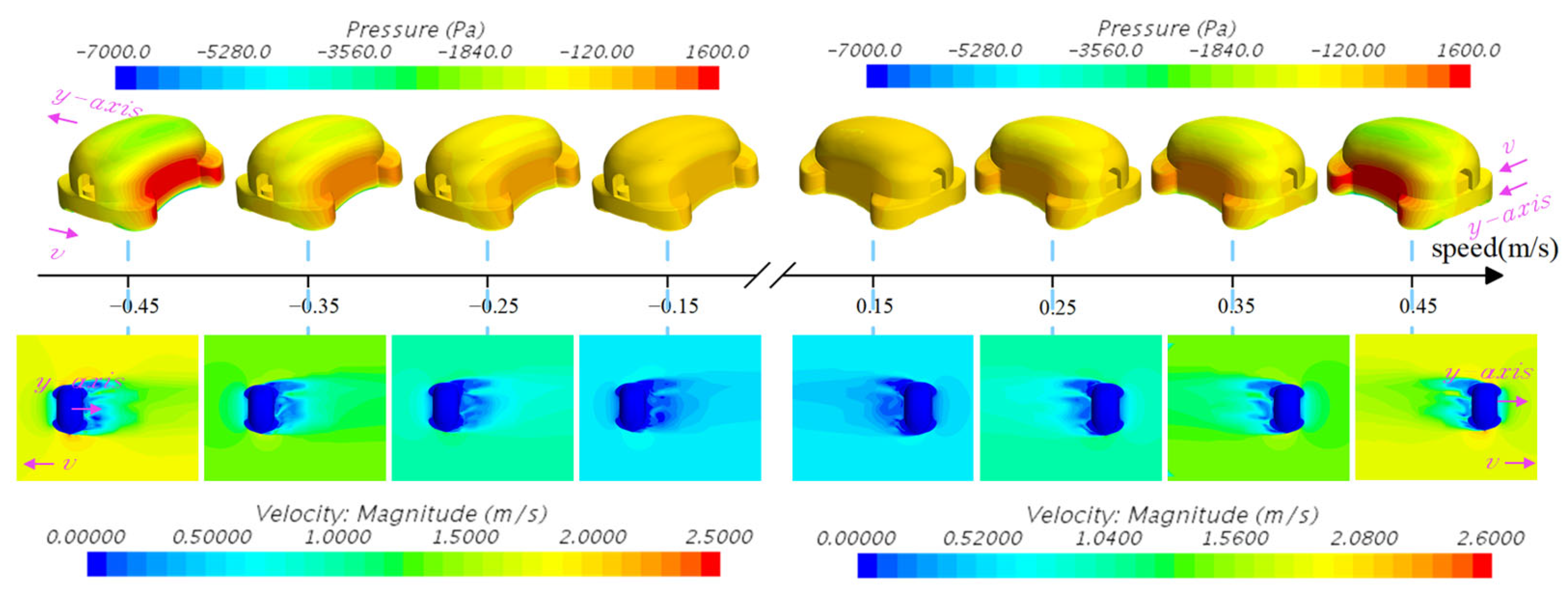
4.1. Simulation Results
4.2. Experimental Validation in the Circulating Water Channel
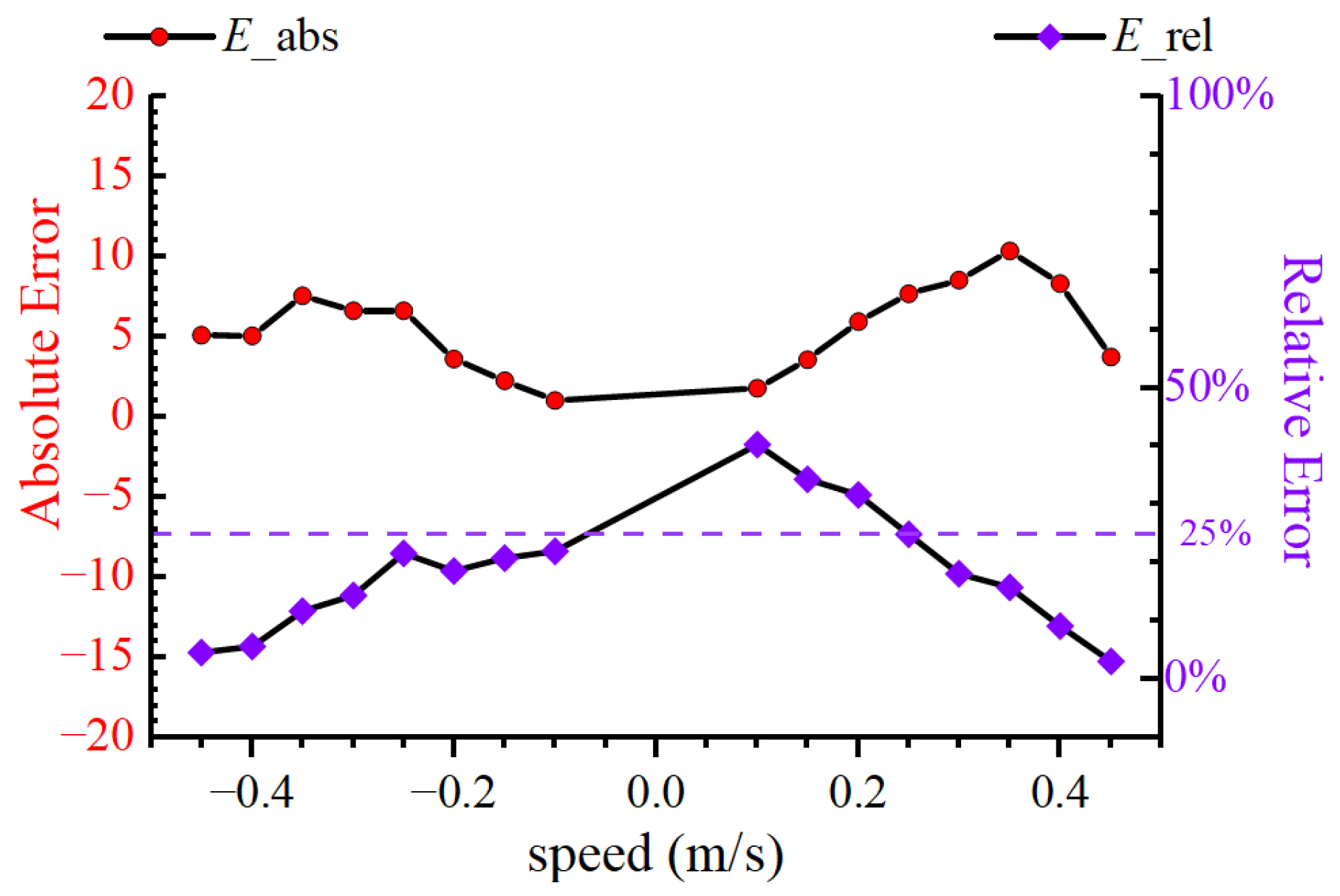
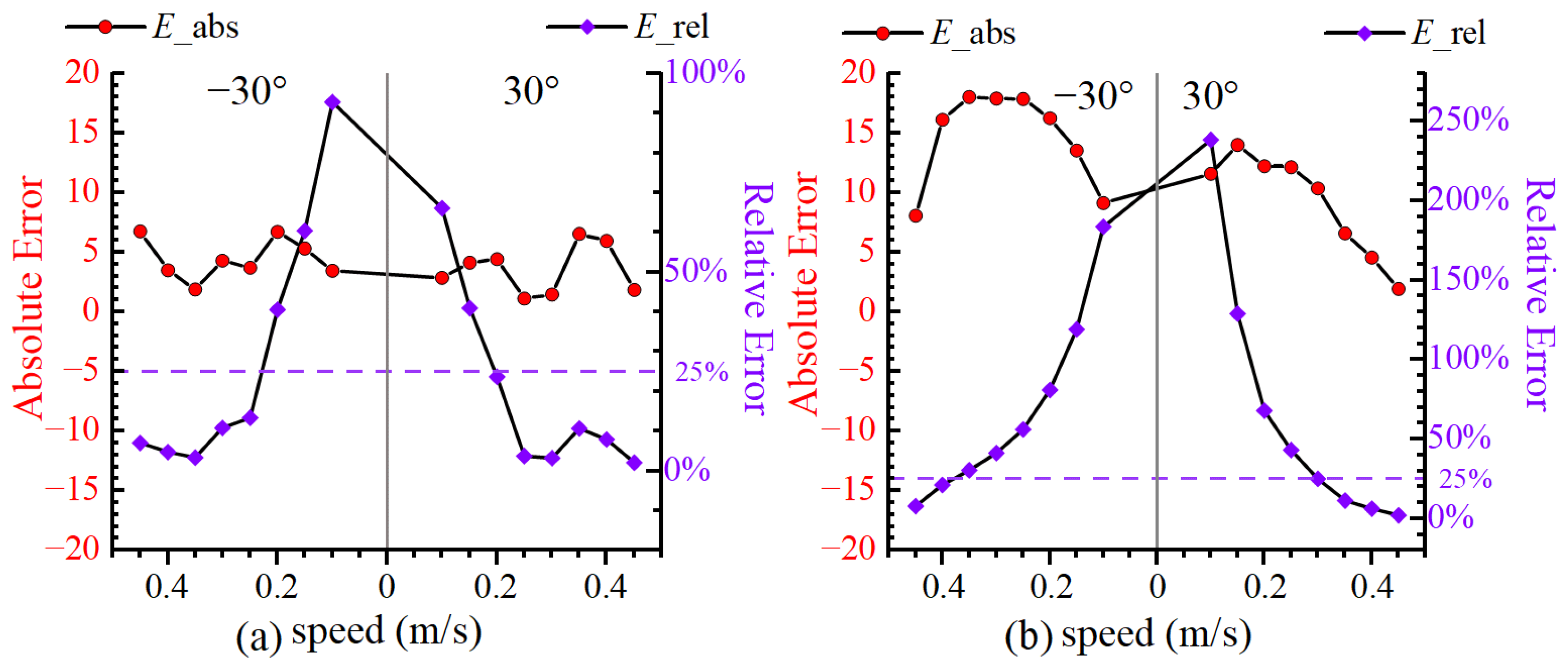
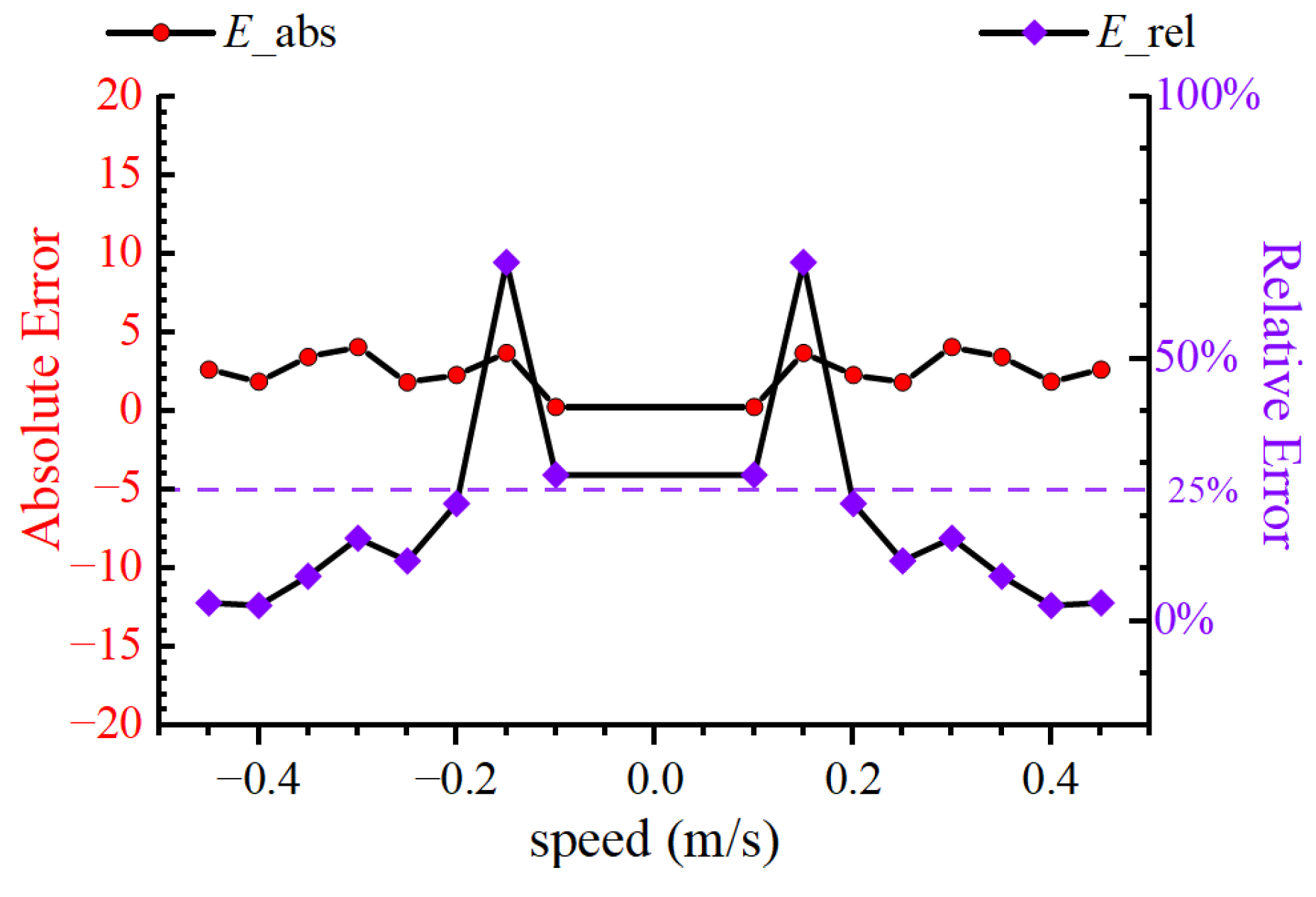
4.3. Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| No. | y+ | Boundary Layer | Minimum Surface Size (mm) | Number of Cells | Force (N) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer Number | First Cell Height (mm) | Growth Rate | Total | Background Mesh | Component Mesh | Mean | SD | |||
| 1 | 30 | 5 | 2.71 | 1.59 | min 12.5 | 0.66757 | 0.5139 | 0.15367 | −38.2 | 1.14 |
| 2 | 20 | 5 | 2.71 | 1.59 | min 12.5 | 0.67267 | 0.519 | 0.15367 | −39.29 | 1.11 |
| 3 | 60 | 5 | 5.42 | 1.22 | min 8 | 1.06527 | 0.9116 | 0.15367 | −41.9 | 0.93 |
| 4 | 60 | 15 | 5.42 | 1 | min 12.5 | 1.07307 | 0.9194 | 0.15367 | −38.75 | 1.13 |
| 5 | 30 | 5 | 2.71 | 1.59 | min 8 | 1.07807 | 0.9244 | 0.15367 | −37.27 | 1.84 |
| 6 | 20 | 5 | 1.81 | 1.82 | min 8 | 1.08567 | 0.932 | 0.15367 | −38.2 | 1.01 |
| 7 | 30 | 15 | 2.7 | 1.01 | min 12.5 | 1.08747 | 0.9338 | 0.15367 | −39.36 | 1.23 |
| 8 | 20 | 15 | 1.81 | 1.06 | min 12.5 | 1.09867 | 0.945 | 0.15367 | −39.33 | 0.43 |
| 9 | 30 | 20 | 2.71 | 1 | min 12.5 | 1.26567 | 1.112 | 0.15367 | −42.98 | 1.17 |
| 10 | 60 | 15 | 5.42 | 1 | min 8 | 1.78837 | 1.6347 | 0.15367 | −38.25 | 0.77 |
| 11 | 30 | 15 | 2.7 | 1.01 | min 8 | 1.78867 | 1.635 | 0.15367 | −37.82 | 1.48 |
| 12 | 20 | 15 | 1.81 | 1.06 | min 8 | 1.82657 | 1.6729 | 0.15367 | −38.74 | 0.52 |
| 13 | 30 | 20 | 2.71 | 1 | min 8 | 2.14567 | 1.992 | 0.15367 | −38.86 | 1.31 |
| 14 | 20 | 20 | 1.81 | 1.02 | min 8 | 2.16897 | 2.0153 | 0.15367 | −39.05 | 0.56 |
Appendix A.2
| (a) Grid Independence Verification of Refinement Mesh | ||||||||
|---|---|---|---|---|---|---|---|---|
| No. | Overset Mesh. Region (∮(m)) | Refinement Region (m) | Flow Domain (m) | Mesh Number (million) | Force(N) | |||
| Total | Background Mesh | Component Mesh | Mean | SD | ||||
| 1 | 4 | 8 | 40 | 1.7708 | 1.6347 | 0.1361 | −37.3 | 1.53 |
| 2 | 4 | 10 | 40 | 1.77891 | 1.6347 | 0.14421 | −38.06 | 0.75 |
| 3 | 4 | 12 | 40 | 1.78837 | 1.6347 | 0.15367 | −38.25 | 1.03 |
| 4 | 4 | 16 | 40 | 1.83424 | 1.6347 | 0.19954 | −37.51 | 1.04 |
| (b) Grid Independence Verification of Component Mesh | ||||||||
| No. | Overset Mesh. Region (∮(m)) | Refinement Region (m) | Flow Domain (m) | Mesh Number (million) | Force(N) | |||
| Total | Background Mesh | Component Mesh | Mean | SD | ||||
| 1 | 3 | 10 | 40 | 1.76211 | 1.6179 | 0.14421 | −42.58 | 0.46 |
| 2 | 4 | 10 | 40 | 1.77891 | 1.6347 | 0.14421 | −38.065 | 0.808 |
| 3 | 7 | 10 | 40 | 1.80171 | 1.6575 | 0.14421 | −38.55 | 0.3 |
| 4 | 10 | 10 | 40 | 1.83932 | 1.6445 | 0.19482 | −37.99 | 1.36 |
| (c) Grid Independence Verification of Background Mesh | ||||||||
| No. | Overset Mesh. Region (∮(m)) | Refinement Region (m) | Flow Domain (m) | Mesh Number (million) | Force(N) | |||
| Total | Background Mesh | Component Mesh | Mean | SD | ||||
| 1 | 7 | 10 | 35 | 1.76189 | 1.6575 | 0.10439 | −37.85 | 0.915 |
| 2 | 7 | 10 | 40 | 1.80171 | 1.6575 | 0.14421 | −38.55 | 0.3 |
| 3 | 7 | 10 | 45 | 1.85232 | 1.6575 | 0.19482 | −37.35 | 1.05 |
References
- Keymasi-Khalaji, A.; Haghjoo, M. Passivity-based stabilizing controller for an underwater robot. Ocean Eng. 2024, 302, 117656. [Google Scholar] [CrossRef]
- Rath, B.N.; Subudhi, B. A robust model predictive path following controller for an Autonomous Underwater Vehicle. Ocean Eng. 2022, 244, 110265. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Tseng, S.-H.; Chen, Y.-H. The experimental study on maneuvering derivatives of a submerged body SUBOFF by implementing the Planar Motion Mechanism tests. Ocean Eng. 2018, 170, 120–135. [Google Scholar] [CrossRef]
- De Moraes, C.C.; Faltinsen, O.M.; Esperança, P.T.T.; Sphaier, S.H.; Lugni, C. Free-surface interaction of a fully appendaged AUV: An experimental study using the Planar Motion Mechanism method for calculating hydrodynamic coefficients. Ocean Eng. 2025, 324, 120670. [Google Scholar] [CrossRef]
- Guo, R.; Zan, Y.; Luo, X.; Ma, X.; Xu, T.; Han, D.; Li, D.; Bai, X. Evaluation of hydrodynamic coefficients and sensitivity analysis of a work-class remotely operated vehicle using planar motion mechanism tests. Ocean Eng. 2024, 312, 119037. [Google Scholar] [CrossRef]
- Joonyoung, K.; Kihun, K.; Choi, H.S.; Woojae, S.; Kyu-Yeul, L. Estimation of hydrodynamic coefficients for an AUV using nonlinear observers. IEEE J. Ocean. Eng. 2002, 27, 830–840. [Google Scholar] [CrossRef]
- De Barros, E.A.; Pascoal, A.; de Sa, E. AUV dynamics: Modelling and parameter estimation using analytical, semi-empirical, and CFD methods. IFAC Proc. Vol. 2004, 37, 369–376. [Google Scholar] [CrossRef]
- Fang, M.-C.; Wang, S.-M.; Mu-Chen, W.; Lin, Y.-H. Applying the self-tuning fuzzy control with the image detection technique on the obstacle-avoidance for autonomous underwater vehicles. Ocean Eng. 2015, 93, 11–24. [Google Scholar] [CrossRef]
- Liu, J.; Yu, F.; He, B.; Yan, T. Hydrodynamic numerical simulation and prediction of bionic fish based on computational fluid dynamics and multilayer perceptron. Eng. Appl. Comput. Fluid Mech. 2022, 16, 858–878. [Google Scholar] [CrossRef]
- Li, Z.; Tao, J.; Sun, H.; Luo, Y.; Ding, L.; Deng, Z. Hydrodynamic calculation and analysis of a complex-shaped underwater robot based on computational fluid dynamics and prototype test. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Mishra, V.; Vengadesan, S.; Bhattacharya, S. Translational Added Mass of Axisymmetric Underwater Vehicles with Forward Speed Using Computational Fluid Dynamics. J. Ship Res. 2011, 55, 185–195. [Google Scholar] [CrossRef]
- Javanmard, E.; Mansoorzadeh, S.; Mehr, J.A. A new CFD method for determination of translational added mass coefficients of an underwater vehicle. Ocean Eng. 2020, 215, 107857. [Google Scholar] [CrossRef]
- Shad, A.; Mansoorzadeh, S. Calculation of Linear Damping Coefficients by Numerical Simulation of Steady State Experiments. J. Appl. Fluid Mech. 2016, 9, 653–660. [Google Scholar] [CrossRef]
- Le, T.-L.; Hong, D.-T. Computational Fluid Dynamics Study of the Hydrodynamic Characteristics of a Torpedo-Shaped Underwater Glider. Fluids 2021, 6, 252. [Google Scholar] [CrossRef]
- Guo, R.; Zan, Y.; Han, D.; Li, Z.; Huang, F.; Sun, Y.; Sun, N. Flow memory effect on viscous hydrodynamic loads of a remotely operated vehicle undergoing drift motions. Appl. Ocean Res. 2025, 155, 104461. [Google Scholar] [CrossRef]
- Ardeshiri, S.; Hossein Mousavizadegan, S. An efficient method to calculate the maneuvering coefficient of underwater vehicles. Ocean Eng. 2022, 266, 113168. [Google Scholar] [CrossRef]
- Tariq, M.A.; Mahmood, Z.M.; Qureshi, M.A.; Khan, N.; Javaid, M.J.; Hussain, B. CFD-based study of appendages design for dynamic stability of underwater vehicle. J. Mar. Sci. Technol. 2025, 30, 658–676. [Google Scholar] [CrossRef]
- Kang, S.; Yu, J.; Zhang, J.; Hu, F.; Jin, Q. Research on accurate modeling of hydrodynamic interaction forces on AUVs operating in tandem. Ocean Eng. 2022, 251, 111125. [Google Scholar] [CrossRef]
- Li, X.; Zhang, D.; Zhao, M.; Wang, X.; Shen, Y. Hydrodynamic Analysis and Drag-Reduction Design of an Unmanned Underwater Vehicle Based on Computational Fluid Dynamics. J. Mar. Sci. Eng. 2024, 12, 1388. [Google Scholar] [CrossRef]
- Zhou, H.; Wei, Z.; Hu, W. Hydrodynamic performance and maneuverability design for a compound eVTOL configuration based unmanned aerial underwater vehicle. Ocean Eng. 2025, 319, 120210. [Google Scholar] [CrossRef]
- Xu, S.; Wu, J.; Lv, H.; Ma, C.; Yang, X.; Wang, H.; Dou, Y. Numerical simulation and hydrodynamics analysis of a tethered underwater robot with control equipment. J. Mar. Sci. Technol. 2022, 27, 368–382. [Google Scholar] [CrossRef]
- Li, X.; Zhao, M.; Zhao, F.; Yuan, Q.; Ge, T. Study on hydrodynamic performance of Heavier-than-water AUV with overlapping grid method. Ocean Syst. Eng. 2014, 4, 1–19. [Google Scholar] [CrossRef]
- Tian, Q.; Li, S.; Yang, L.; Shao, S.; Zhang, B.; Gao, Y.; Shuai, M. Robots in Torch Relay at the Beijing 2022 Olympic and Paralympic Winter Games. Robot 2022, 44, 513–521. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, Q.; Lu, Y.; Li, S.; Li, Z.; Zhang, Q.; Liu, X. The New Robots for Underwater Torch Relay at the Beijing 2022 Winter Olympic Games. Robot 2022, 44, 538–545. [Google Scholar] [CrossRef]
- ITTC. Uncertainty Analysis in CFD: Verification and Validation—Methodology and Procedures. In ITTC—Quality Manual, Procedure 7.5-03-01-01, Rev. 01; ITTC: Zürich, Switzerland, 2002. [Google Scholar]
- Chandar, D.; Boppana, B.; Kumar, V. A Comparative Study of Different Overset Grid Solvers Between OpenFOAM, StarCCM+ and Ansys-Fluent. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Wu, J.; Xu, S.; Liao, H.; Ma, C.; Yang, X.; Wang, H.; Zhang, T.; Han, X. Maneuverability and Hydrodynamics of a Tethered Underwater Robot Based on Mixing Grid Technique. J. Mar. Sci. Eng. 2021, 9, 561. [Google Scholar] [CrossRef]
- Wikipedia. Geometric Series. Wikimedia Foundation, Inc., San Francisco, CA, USA. 2021. Available online: https://en.wikipedia.org/wiki/Geometric_series (accessed on 18 October 2025).
- Klein, R.I. Star formation with 3-D adaptive mesh refinement: The collapse and fragmentation of molecular clouds. J. Comput. Appl. Math. 1999, 109, 123–152. [Google Scholar] [CrossRef]
- Almohammadi, K.M.; Ingham, D.B.; Ma, L.; Pourkashan, M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine. Energy 2013, 58, 483–493. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, D.; Zhang, Q.; Tian, Q.; Wang, Y.; Wang, X. Simulation Application of Computational Fluid Dynamics for the Variable Structure Underwater Vehicle. J. Mar. Sci. Eng. 2025, 13, 2175. https://doi.org/10.3390/jmse13112175
Liu X, Li D, Zhang Q, Tian Q, Wang Y, Wang X. Simulation Application of Computational Fluid Dynamics for the Variable Structure Underwater Vehicle. Journal of Marine Science and Engineering. 2025; 13(11):2175. https://doi.org/10.3390/jmse13112175
Chicago/Turabian StyleLiu, Xiaomeng, Dehao Li, Qifeng Zhang, Qiyan Tian, Yiqun Wang, and Xiaohui Wang. 2025. "Simulation Application of Computational Fluid Dynamics for the Variable Structure Underwater Vehicle" Journal of Marine Science and Engineering 13, no. 11: 2175. https://doi.org/10.3390/jmse13112175
APA StyleLiu, X., Li, D., Zhang, Q., Tian, Q., Wang, Y., & Wang, X. (2025). Simulation Application of Computational Fluid Dynamics for the Variable Structure Underwater Vehicle. Journal of Marine Science and Engineering, 13(11), 2175. https://doi.org/10.3390/jmse13112175







