Energy-Efficient Scheduling for Distributed Hybrid Flowshop of Offshore Wind Blade Manufacturing Considering Limited Buffers
Abstract
1. Introduction
- This paper extends the DHFSP problem by establishing a multi-objective mixed-integer linear programming (MILP) model that simultaneously considers the strong coupling constraints of SDST and LB.
- A hybrid optimization algorithm combining evolutionary algorithm and reinforcement learning is proposed. It utilizes the dynamic decision-making capability of DDQN to overcome the drawbacks of MOEAs and adaptively selects five knowledge-driven search operators.
- Two critical path-based energy-saving strategies are introduced; they reduce the machine’s idle time through right-shift and speed-scaling mechanisms, thereby cutting down the total energy consumption.
2. Materials and Methods
2.1. Problem Description
- If job j has already been processed at stage s − 1 and a machine m at stage s is free and prepared, job j is assigned to machine m and begins processing at stage s.
- If job j has already been processed at stage s − 1 and no machine at stage s is free and prepared, but there are spaces in the buffer between stages s − 1 and s, then job j is allocated to the buffer in stage s − 1 and waits for one free and prepared machine m at stage s.
- If job j has already been processed at stage s − 1, no machine at stage s is free and prepared, and there is no space in the buffer between stages s − 1 and s, then job j is blocked at the processing machine at stage s − 1 until one space becomes available in the buffer.
- If job j is in situation 3 and the buffer is full, but a machine m at stage s becomes free and prepared, then job j is assigned to machine m and begins processing at stage s.
- All jobs are available at time zero, and there is no precedence constraint for the jobs in any factory.
- Machine breakdowns, order insertions, and other dynamic disturbances are not taken into consideration.
- Job transportation times and machine speed changeover times are ignored.
- Processing energy consumption is positively correlated with speed level; the higher the speed, the shorter the processing time.
- Only processing and idle energy consumptions are considered; machine start/stop, setup, and jobs transport energy consumptions are ignored.
- When a job is blocked on a machine, the machine incurs idle energy consumption.
- Once a machine starts processing a job, interruption is not allowed.
- After a job has been assigned to one factory and machine, it cannot be transferred.
- Each job cannot be processed on more than one machine simultaneously, and each machine can process at most one job at a time.
2.2. MILP Model
3. Methodology
3.1. Framework of DDQN-MOCE
3.2. Encoding and Decoding
3.3. Global Searching
3.4. Energy-Efficient Strategy
- EM1: Identify Pc and Oc, collect all Of, calculate the maximum allowable delay time for Of, and delay the start processing time of Of as late as possible without increasing cmax.
- EM2: Identify Pc and Oc, collect all Of, obtain all available speed options lower than the current speed of the machine processing Of, and select the slowest available speed for the machine without increasing cmax.
| Algorithm 1: Energy-Efficient Strategy EM1 |
| Input: current solution Sol decoded schedule schedule makespan cmax Output: updated solution Solnew 1: Pc ← IdentifyCriticalPath(schedule, cmax) // Identify the critical path 2: Oc ← [operations in Pc] // Collect all critical operations from the critical path 3: Of ← [operations in schedule but not in Oc] // Collect all non-critical operations 4: Sort Of by finish time in descending order 5: for each operation o in Of do 6: tstart ← o.Start 7: tfinish ← o.Finish 8: tproc ← tfinish − tstart 9: delaymax ← tproc 10: tnew_start ← tstart + delaymax 11: tnew_finish ← tnew_start + tproc 12: if tnew_finish ≤ cmax then 13: o.Start ← tnew_start 14: o.Finish ← tnew_finish 15: end if 16: end for 17: return Solnew |
| Algorithm 2: Energy-Efficient Strategy EM2 |
| Input: current solution Sol decoded schedule schedule makespan cmax set of available speed levels V Output: updated solution Solnew 1: Pc ← IdentifyCriticalPath(schedule, cmax) // Identify the critical path 2: Oc ← [operations in Pc] // Collect all critical operations from the critical path 3: Of ← [operations in schedule but not in Oc] // Collect all non-critical operations 4: for each operation o in Of do 5: j ← o.Job 6: s ← o.Stage 7: vcurrent ← Sol.speed_selection[j][s] 8: Vslower ← {v ∈ V | v < vcurrent} 9: if Vslower ≠ ∅ then 10: vnew ← max(Vslower) 11: tproc_new ← GetProcessingTime(o.Factory, o.Stage, o.Machine, j, vnew) // Calculate new processing time 12: if o.Start + tproc_new ≤ cmax then 13: Sol.speed_selection[j][s] ← vnew // Update speed in the solution 14: end if 15: end if 16: end for 17: return Solnew |
3.5. Local-Search Operators
- LS1: Randomly choose a job sequence and two positions within it. Swap the corresponding jobs to obtain a new processing order.
- LS2: Randomly choose a machine. Exclude its current speed and then randomly assign one of the remaining available speed levels.
- LS3: Randomly choose a factory. Exclude its current factory and then randomly assign one of the remaining eligible factories.
- ES1: Execute EM1 to delay all Ofa as late as possible.
- ES2: Execute EM2 to set the slowest feasible speed for all Ofs.
3.6. DDQN-Based Local Search
- State space: The state space is composed of three dimensions, namely job sequence, factory assignment, and machine selection. For the job sequence dimension, the JS vector is normalized and mapped into the range [0, 1]. For the factory assignment dimension, the FS vector is transformed into a one-hot encoding. For the machine selection dimension, the SS matrix is first flattened by reshaping it into a one-dimensional vector row-wise and then globally normalized.
- Action space: The discrete action space is defined as action ∈ {0, 1, 2, 3, 4}, corresponding to preset heuristic operators LS1–ES2. An ε-greedy policy is adopted. If the random number is below ε, an operator is chosen at random. Otherwise, the state vector is tensorized and forwarded to the evaluation network, and the operator yielding the maximum Q-value is selected.
- Reward function: To reconcile the dual objectives of minimizing cmax and tec, a hierarchical reward function with embedded priorities is devised. When both cmax and tec are improved, the reward is 20; when only cmax is improved, the reward is 15; when only tec is improved, the reward is 10; and when neither is improved, the reward is 0.
- Network training: When the number of stored samples is sufficient, the neural network begins training. For every NU step of training, the parameters θ1 of the evaluation network QE are fully aligned with the parameters θ2 of the target network QT. Subsequently, bs experience samples are randomly sampled from the replay pool, from which the state St, action At, reward Rt, and next state St+1 are extracted. QE predicts the Q-value of St based on the Q-value of the current state–action pair and all Q-values of St+1, thereby selecting action At+1. On the other hand, QE calculates the Q-value corresponding to At+1 and updates the Q-value. Finally, based on the learning rate α, the parameters of QE are updated using the Adam optimizer.
| Algorithm 3: Training process of D2QN |
| Input: QE(θ1): evaluated Q-network with parameters θ1 QT(θ2): target Q-network with parameters θ2 E: replay buffer (deque) batch_size: number of samples per batch (bs) learning_rate: optimizer learning rate (α) discount_factor: reward discount γ update_target_every: steps interval to update target network (NU) current_step: total training step counter Epoch: number of optimizations passes Output: Updated QE(θ1) and QT(θ2) 1: if len(E) < bs then 2: return // not enough samples to train 3: if current_step mod NU == 0 then 4: θ2 ← θ1 // update target network 5: for epoch in range (Epoch) do 6: T ← random sample of size bs from E 7: Extract (St, At, Rt, St+1) from T // all values are tensors 8: q_eval ← QE(St)[At] // gather Q-value of selected action 9: q_next_eval ← QE(St+1) // all Q-values for next state from QE 10: At+1 ← argmax(q_next_eval) // select best next action 11: q_next_target ← QT(St+1)[At+1] // get target Q-value from QT 12: q_target ← Rt + γ * q_next_target // compute target Q-value 13: L ← MSE(q_eval, q_target) // mean squared error loss 14: Adam (QE(θ1), α, L). // Update QE(θ1) using Adam optimizer with loss L and learning rate α |
4. Results and Discussion
4.1. Instances and Metrics
4.2. Parameter Settings
4.3. Effectiveness of the Algorithm Components
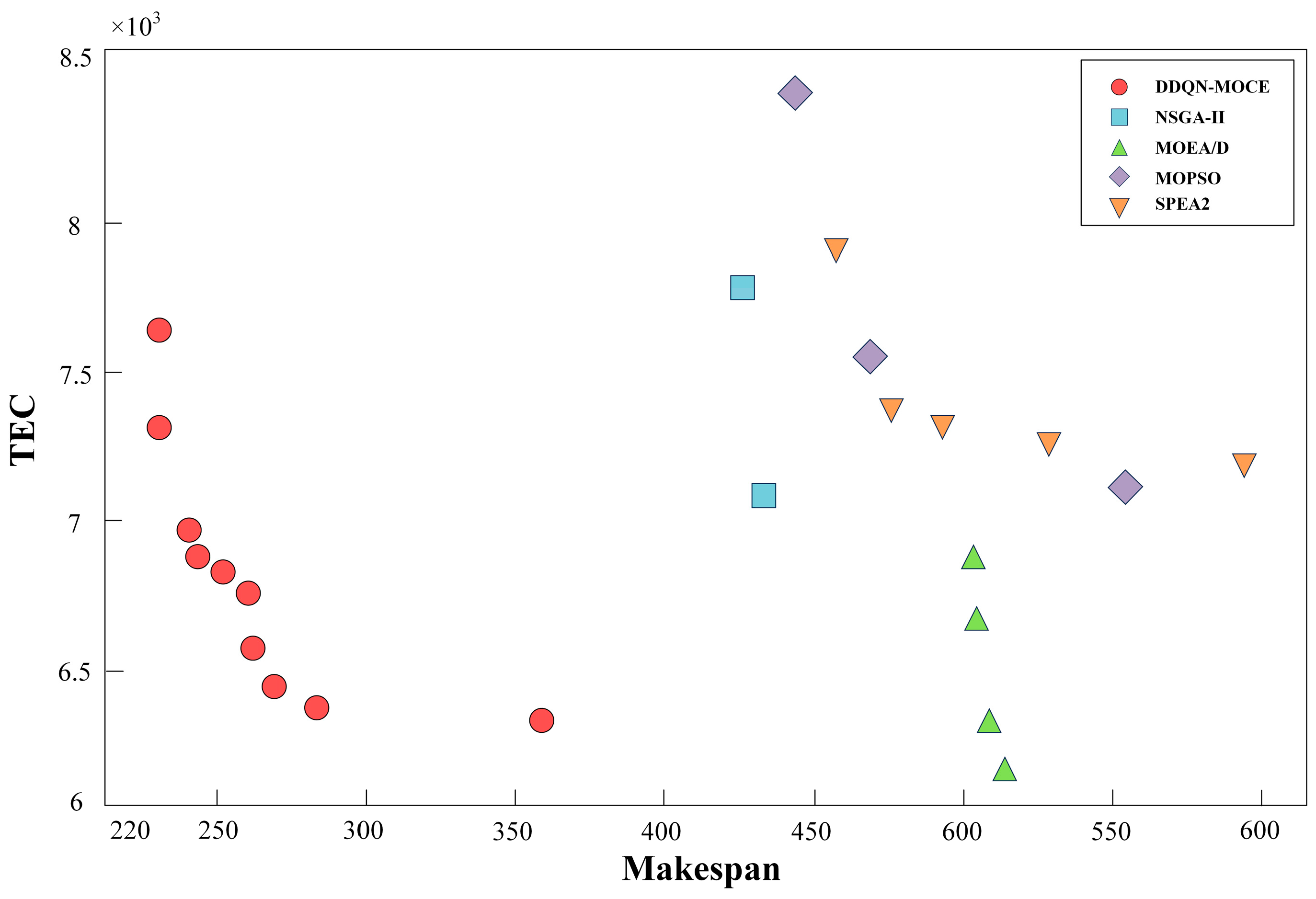
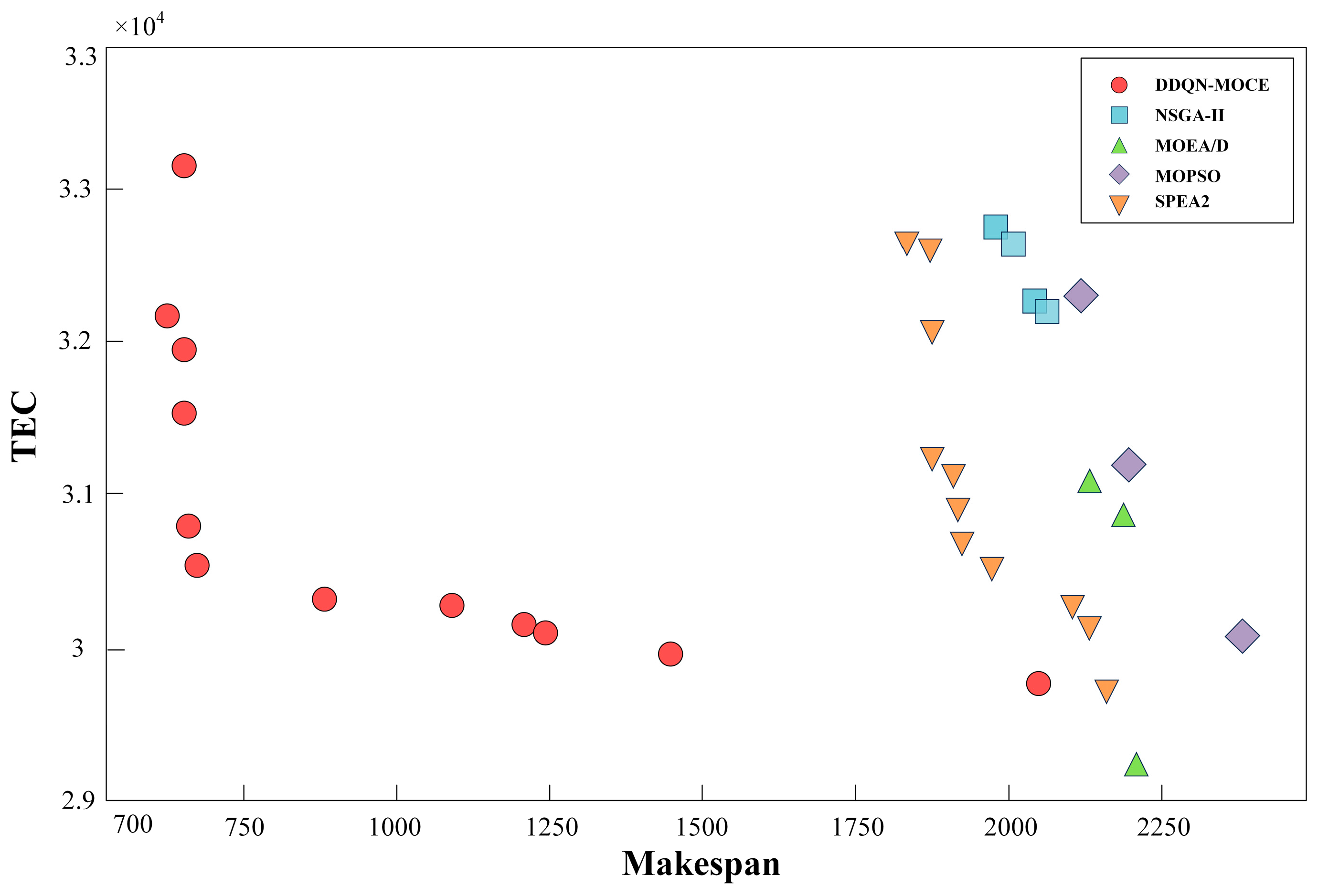
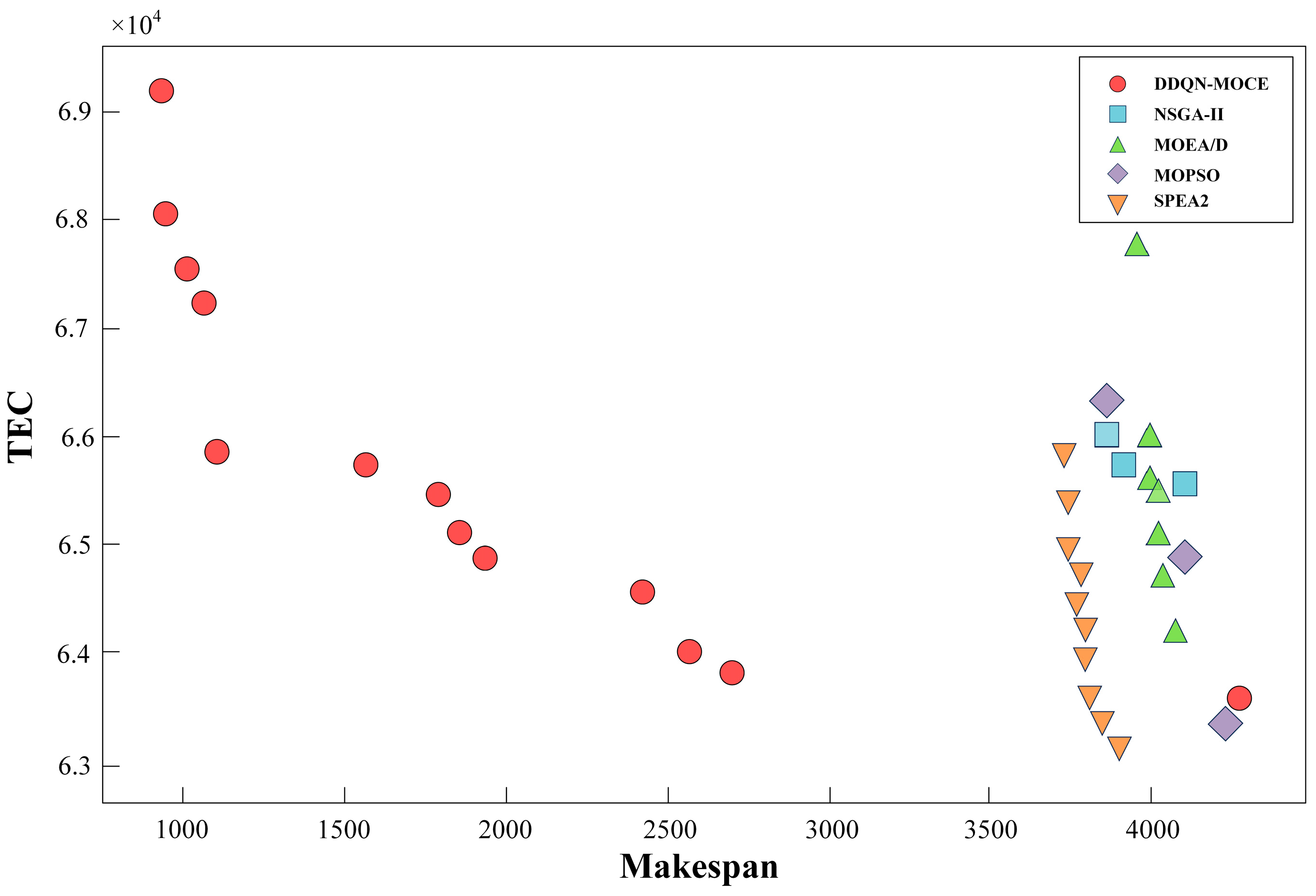
4.4. Comparisons to Other Algorithms
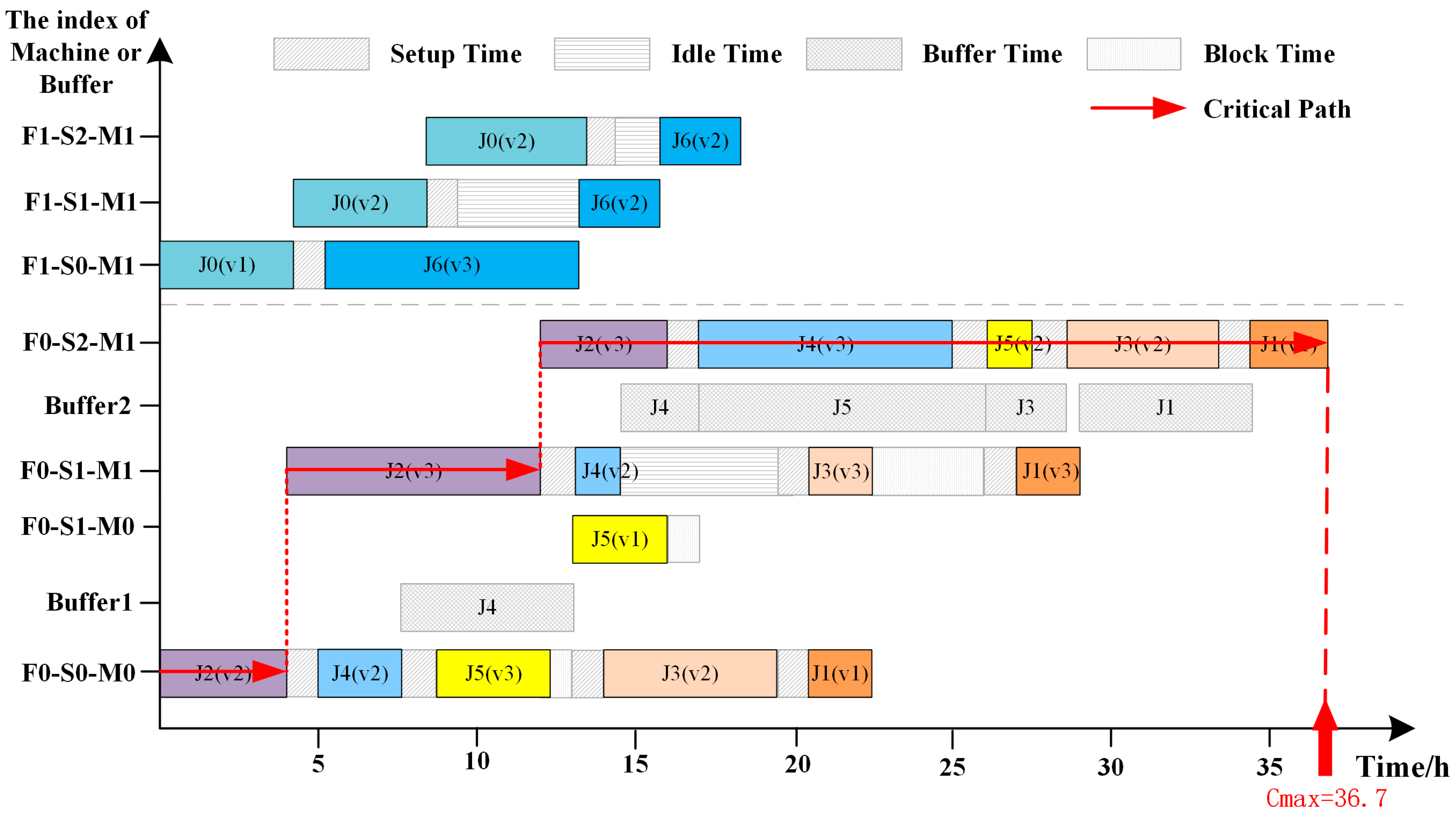
4.5. Comparisons on a Real-World Case
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, X.; Wang, X.; Xu, W.; Yuan, L.; Xiong, C.; Chen, J. Offshore Wind Power: Progress of the Edge Tool, Which Can Promote Sustainable Energy Development. Sustainability 2024, 16, 7810. [Google Scholar] [CrossRef]
- Kim, A.; Kim, H.; Choe, C.; Lim, H. Feasibility of offshore wind turbines for linkage with onshore green hydrogen demands: A comparative economic analysis. Energy Convers. Manag. 2023, 277, 116662. [Google Scholar] [CrossRef]
- Yang, J.; Chang, Y.; Zhang, L.; Hao, Y.; Yan, Q.; Wang, C. The life-cycle energy and environmental emissions of a typical offshore wind farm in China. J. Clean. Prod. 2018, 180, 316–324. [Google Scholar] [CrossRef]
- Farina, A.; Anctil, A. Material consumption and environmental impact of wind turbines in the USA and globally. Resour. Conserv. Recycl. 2022, 176, 105938. [Google Scholar] [CrossRef]
- Neufeld, J.S.; Schulz, S.; Buscher, U. A systematic review of multi-objective hybrid flow shop scheduling. Eur. J. Oper. Res. 2023, 309, 1–23. [Google Scholar] [CrossRef]
- Levine, A.; Cook, J. Transportation of Large Wind Components: A Permitting and Regulatory Review; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2016. [Google Scholar] [CrossRef]
- Shao, W.; Shao, Z.; Pi, D. Multi-local search-based general variable neighborhood search for distributed flow shop scheduling in heterogeneous multi-factories. Appl. Soft Comput. 2022, 125, 109138. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X. A knowledge-driven constructive heuristic algorithm for the distributed assembly blocking flow shop scheduling problem. Expert Syst. Appl. 2022, 202, 117269. [Google Scholar] [CrossRef]
- Niu, W.; Li, J.-q.; Jin, H.; Qi, R.; Sang, H.-y. Bi-objective optimization using an improved NSGA-II for energy-efficient scheduling of a distributed assembly blocking flowshop. Eng. Optim. 2022, 55, 719–740. [Google Scholar] [CrossRef]
- Shi, H.; Si, H.; Qin, J. Energy-Efficient Scheduling for Resilient Container-Supply Hybrid Flow Shops Under Transportation Constraints and Stochastic Arrivals. J. Mar. Sci. Eng. 2025, 13, 1153. [Google Scholar] [CrossRef]
- Li, J.; Lin, P.; Wu, X.; Song, D.; Yang, B.; Zhou, L. Scheduling optimization of ship plane block flow line considering dual resource constraints. Sci. Rep. 2024, 14, 30765. [Google Scholar] [CrossRef]
- Zhong, Z.; Guo, Y.; Zhang, J.; Yang, S. Energy-aware Integrated Scheduling for Container Terminals with Conflict-free AGVs. J. Syst. Sci. Syst. Eng. 2023, 32, 413–443. [Google Scholar] [CrossRef]
- Njiri, J.G.; Söffker, D. State-of-the-art in wind turbine control: Trends and challenges. Renew. Sustain. Energy Rev. 2016, 60, 377–393. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Ma, Z. A Hybrid Local Search Algorithm for the Sequence Dependent Setup Times Flowshop Scheduling Problem with Makespan Criterion. Sustainability 2017, 9, 2318. [Google Scholar] [CrossRef]
- Clarke, J.; McIlhagger, A.; Archer, E.; Dooher, T.; Flanagan, T.; Schubel, P. A Feature-Based Cost Estimation Model for Wind Turbine Blade Spar Caps. Appl. Syst. Innov. 2020, 3, 17. [Google Scholar] [CrossRef]
- Yaurima, V.; Burtseva, L.; Tchernykh, A. Hybrid flowshop with unrelated machines, sequence-dependent setup time, availability constraints and limited buffers. Comput. Ind. Eng. 2009, 56, 1452–1463. [Google Scholar] [CrossRef]
- Hakimzadeh Abyaneh, S.; Zandieh, M. Bi-objective hybrid flow shop scheduling with sequence-dependent setup times and limited buffers. Int. J. Adv. Manuf. Technol. 2011, 58, 309–325. [Google Scholar] [CrossRef]
- Han, Y.; Li, J.; Sang, H.; Liu, Y.; Gao, K.; Pan, Q. Discrete evolutionary multi-objective optimization for energy-efficient blocking flow shop scheduling with setup time. Appl. Soft Comput. 2020, 93, 106343. [Google Scholar] [CrossRef]
- Zhao, F.; Xu, Z.; Bao, H.; Xu, T.; Zhu, N.; Jonrinaldi. A cooperative whale optimization algorithm for energy-efficient scheduling of the distributed blocking flow-shop with sequence-dependent setup time. Comput. Ind. Eng. 2023, 178, 109082. [Google Scholar] [CrossRef]
- Zhao, F.; Di, S.; Wang, L. A Hyperheuristic With Q-Learning for the Multiobjective Energy-Efficient Distributed Blocking Flow Shop Scheduling Problem. IEEE Trans. Cybern. 2023, 53, 3337–3350. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Zhang, Y.; Tian, H.; He, L. A cooperative adaptive genetic algorithm for reentrant hybrid flow shop scheduling with sequence-dependent setup time and limited buffers. Complex Intell. Syst. 2023, 10, 781–809. [Google Scholar] [CrossRef]
- Luo, Y.; Liang, X.; Zhang, Y.; Tang, K.; Li, W. Energy-Aware Integrated Scheduling for Quay Crane and IGV in Automated Container Terminal. J. Mar. Sci. Eng. 2024, 12, 376. [Google Scholar] [CrossRef]
- Müller, A.; Grumbach, F.; Kattenstroth, F. Reinforcement Learning for Two-Stage Permutation Flow Shop Scheduling—A Real-World Application in Household Appliance Production. IEEE Access 2024, 12, 11388–11399. [Google Scholar] [CrossRef]
- Wang, Y.-J.; Wang, G.-G.; Tian, F.-M.; Gong, D.-W.; Pedrycz, W. Solving energy-efficient fuzzy hybrid flow-shop scheduling problem at a variable machine speed using an extended NSGA-II. Eng. Appl. Artif. Intell. 2023, 121, 105977. [Google Scholar] [CrossRef]
- Schulz, S.; Neufeld, J.S.; Buscher, U. A multi-objective iterated local search algorithm for comprehensive energy-aware hybrid flow shop scheduling. J. Clean. Prod. 2019, 224, 421–434. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Jiang, E.; Wang, L.; Wang, J. Decomposition-based multi-objective optimization for energy-aware distributed hybrid flow shop scheduling with multiprocessor tasks. Tsinghua Sci. Technol. 2021, 26, 646–663. [Google Scholar] [CrossRef]
- Zhang, W.; Xiao, G.; Gen, M.; Geng, H.; Wang, X.; Deng, M.; Zhang, G. Enhancing multi-objective evolutionary algorithms with machine learning for scheduling problems: Recent advances and survey. Front. Ind. Eng. 2024, 2, 1337174. [Google Scholar] [CrossRef]
- Geng, K.; Liu, L.; Wu, S. A reinforcement learning based memetic algorithm for energy-efficient distributed two-stage flexible job shop scheduling problem. Sci. Rep. 2024, 14, 30816. [Google Scholar] [CrossRef]
- Shi, J.; Liu, W.; Yang, J. An Enhanced Multi-Objective Evolutionary Algorithm with Reinforcement Learning for Energy-Efficient Scheduling in the Flexible Job Shop. Processes 2024, 12, 1976. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI conference on artificial intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar] [CrossRef]
- Han, B.-A.; Yang, J.-J. Research on adaptive job shop scheduling problems based on dueling double DQN. IEEE Access 2020, 8, 186474–186495. [Google Scholar] [CrossRef]
- Zhang, Z.-Q.; Qian, B.; Hu, R.; Yang, J.-B. Q-learning-based hyper-heuristic evolutionary algorithm for the distributed assembly blocking flowshop scheduling problem. Appl. Soft Comput. 2023, 146, 110695. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Wang, K.; Wang, L.; Liu, J.; Wang, J.; Wang, X.V. Reinforcement learning for distributed hybrid flowshop scheduling problem with variable task splitting towards mass personalized manufacturing. J. Manuf. Syst. 2024, 76, 188–206. [Google Scholar] [CrossRef]
- Deng, L.; Di, Y.; Wang, L. A Reinforcement-Learning-Based 3-D Estimation of Distribution Algorithm for Fuzzy Distributed Hybrid Flow-Shop Scheduling Considering On-Time-Delivery. IEEE Trans. Cybern. 2024, 54, 1024–1036. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.; Wang, L.; Lu, C.; Pan, Z.; Zhuang, X. Double DQN-Based Coevolution for Green Distributed Heterogeneous Hybrid Flowshop Scheduling With Multiple Priorities of Jobs. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6550–6562. [Google Scholar] [CrossRef]
- Yang, Z.; Bi, L.; Jiao, X. Combining Reinforcement Learning Algorithms with Graph Neural Networks to Solve Dynamic Job Shop Scheduling Problems. Processes 2023, 11, 1571. [Google Scholar] [CrossRef]
- Zhao, F.; Yin, F.; Wang, L.; Yu, Y. A Co-Evolution Algorithm With Dueling Reinforcement Learning Mechanism for the Energy-Aware Distributed Heterogeneous Flexible Flow-Shop Scheduling Problem. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 1794–1809. [Google Scholar] [CrossRef]
- Cao, S.; Li, R.; Gong, W.; Lu, C. Inverse model and adaptive neighborhood search based cooperative optimizer for energy-efficient distributed flexible job shop scheduling. Swarm Evol. Comput. 2023, 83, 101419. [Google Scholar] [CrossRef]
- Wang, G.; Li, X.; Gao, L.; Li, P. Energy-efficient distributed heterogeneous welding flow shop scheduling problem using a modified MOEA/D. Swarm Evol. Comput. 2021, 62, 100858. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, X.; Zhang, R. An Enhanced MOPSO Algorithm for Energy-Efficient Single-Machine Production Scheduling. Sustainability 2019, 11, 5381. [Google Scholar] [CrossRef]
- He, F.; Shen, K.; Guan, L.; Jiang, M. Research on Energy-Saving Scheduling of a Forging Stock Charging Furnace Based on an Improved SPEA2 Algorithm. Sustainability 2017, 9, 2154. [Google Scholar] [CrossRef]



| Study | Marine Domain | Problem | SDST | Buffer | Objective (s) | Algorithm | Dynamic Operator Selection |
|---|---|---|---|---|---|---|---|
| Our study | √ (Offshore wind blade manufacturing) | DHFSP | √ | √ (Limited) | Makespan, Tec | EA + DDQN | √ |
| Shi et al. [10] | √ (Container production) | HFSP | × | √ (Only one and infinite) | Makespan, Tec | MGCOA + Q-Learning | √ |
| Li et al. [11] | √ (Ship plane) | Blocking FSP | × | √ (Limited) | Makespan | GWO + NEH | × |
| Zhong et al. [12] | √ (Container logistics) | Joint scheduling of AGVs and YCs | × | √ (Limited) | Tec | A bi-level GA | × |
| Yaurima et al. [16] | × (Television) | HFSP | √ | √ (Limited) | Makespan | GA | × |
| Hakimzadeh et al. [17] | × (PCB assembly) | HFSP | √ | √ (Limited) | Makespan, Tardiness | NSGA-II/SPGA-II | × |
| Han et al. [18] | × (Theoretical workshop scheduling) | Blocking FSP | √ | × | Makespan, Tec | Self-adaptive discrete MOEA | × |
| Zhao et al. [19] | × (Theoretical workshop scheduling) | Blocking DFSP | √ | × | Makespan, Tec, Tardiness | Cooperative Whale Optimization Algorithm | × |
| Zhao, Di, and Wang [20] | × (Theoretical workshop scheduling) | Blocking DFSP | × | × | Tec, Tardiness | Hyperheuristic with Q-Learning | √ |
| Zheng et al. [21] | × (Theoretical workshop scheduling) | Reentrant HFSP | √ | √ | Total weighted completion time | GA+ACS+Modified Greedy Heuristic | × |
| Müller et al. [23] | × (Household appliance production) | Two-stage permutation FSP | √ | √ (Limited) | Idle times, setup efforts | PPO | √ |
| Zhang et al. [33] | × (Theoretical workshop scheduling) | Assembly blocking DFSP | × | × | Makespan | Hyper-Heuristic EA+Q-Learning | √ |
| Chen et al. [34] | × (Mass personalized manufacturing, | Variable Task Splitting DHFSP | × | × | Makespan, Tec | MOEA/D + Q-Learning | √ |
| Deng et al. [35] | × (Mass-customization) | Fuzzy DHFSP | √ | × | Makespan, Tec | 3D-EDA + Q-Learning | √ |
| Li et al. [36] | × (Large engineering equipment) | Heterogeneous DHFSP | × | × | Total weighted Tardiness, Tec | EA + DDQN | √ |
| Yang et al. [37] | × (Smart Factory) | Dynamic JSP | × | × | The earlier and later completion time | GNN + DDQN | √ |
| Notations | Descriptions |
|---|---|
| J | Job set, indexed by j, j ∈ J = {0, …, n − 1} |
| F | Factory set, indexed by f |
| S | Stage set, indexed by s |
| Mfs | The set of machines at stage s of factory f, indexed by i, i ∈ Mfsc = {0, …, mfs} |
| L | Speed set, indexed by v, v ∈ L = {1, 2, 3}, corresponding to high-speed, medium-speed, and low-speed |
| pijsfv | The processing time of job j on machine i at stage s of factory f under speed v |
| pijj′sf | The setup time of job j to job j′ on machine i at stage s of factory f |
| τifv | The energy consumption per unit time (kW) on machine i of factory f under speed v |
| φifv | The idle energy consumption per unit time (kW) on machine i of factory f under speed v |
| vl | Speed factor of speed level l |
| bsf | The buffer capacity at stage s of factory f |
| M | A positive number that is large enough |
| cmax | Maximum completion time (makespan) |
| tec | The total energy consumption |
| yjf | Decision variable, if job j is allocated in factory f, yjf = 1; otherwise, yjf = 0 |
| xijsfv | Decision variable, if job j is processed on machine i at stage s of factory f under speed v, xijsfv = 1; otherwise, xijsfv = 0 |
| zijj′sf | Decision variable, if job j′ is the successor of job on machine i at stage s of factory f, zijj′sf = 1; otherwise, zijj′sf = 0 |
| wjsf | Decision variable, if job j occupies the buffer at stage s of factory f, wjsf = 1; otherwise, wjsf = 1 |
| sijsf | Continuous variable, starting time of job j on machine i at stage s of factory |
| cijsf | Continuous variable, completion time of job j on machine i at stage s of factory |
| Problem Scale | D1 | D2 | DDQN-MOCE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HV | Spacing | GD | HV | Spacing | GD | HV | Spacing | GD | |
| 3-2-20 | 0.8654 | 0.0714 | 0.1677 | 0.9019 | 0.0598 | 0.1437 | 1.0261 * | 0.0507 | 0.0603 |
| 3-5-20 | 0.6565 | 0.0606 | 0.3352 | 0.7134 | 0.0899 | 0.3200 | 0.9072 | 0.0297 | 0.1368 |
| 3-8-20 | 0.7477 | 0.0607 | 0.2743 | 0.7823 | 0.0555 | 0.2639 | 0.9630 | 0.0592 | 0.1028 |
| 4-2-20 | 0.7987 | 0.0517 | 0.2105 | 0.8438 | 0.0553 | 0.1994 | 0.8379 | 0.0432 | 0.1261 |
| 4-5-20 | 0.8095 | 0.0966 | 0.2694 | 0.8573 | 0.0670 | 0.229 | 1.0238 | 0.0447 | 0.0925 |
| 4-8-20 | 0.5782 | 0.0627 | 0.4098 | 0.6523 | 0.0647 | 0.3768 | 0.9243 | 0.0319 | 0.1342 |
| 5-2-20 | 0.7868 | 0.0804 | 0.2804 | 0.8435 | 0.0821 | 0.2305 | 0.8928 | 0.0619 | 0.1302 |
| 5-5-20 | 0.7545 | 0.075 | 0.3261 | 0.8024 | 0.0574 | 0.2787 | 0.9238 | 0.0339 | 0.1605 |
| 5-8-20 | 0.6837 | 0.073 | 0.2981 | 0.7120 | 0.0708 | 0.2712 | 0.8794 | 0.0674 | 0.1106 |
| 3-2-50 | 0.7308 | 0.0735 | 0.2143 | 0.7938 | 0.0806 | 0.1775 | 0.9355 | 0.0707 | 0.0881 |
| 3-5-50 | 0.8130 | 0.0604 | 0.2091 | 0.8552 | 0.0765 | 0.1898 | 0.9339 | 0.0515 | 0.1033 |
| 3-8-50 | 0.5971 | 0.0711 | 0.3377 | 0.6471 | 0.0625 | 0.3008 | 0.9222 | 0.0451 | 0.1453 |
| 4-2-50 | 0.7444 | 0.0468 | 0.2342 | 0.8388 | 0.0621 | 0.1852 | 0.8035 | 0.0340 | 0.1410 |
| 4-5-50 | 0.6755 | 0.0754 | 0.3118 | 0.706 | 0.0702 | 0.298 | 0.8553 | 0.0621 | 0.1191 |
| 4-8-50 | 0.7402 | 0.0642 | 0.2291 | 0.792 | 0.0528 | 0.1963 | 0.9061 | 0.0574 | 0.0827 |
| 5-2-50 | 0.6237 | 0.0621 | 0.2754 | 0.7229 | 0.0703 | 0.1642 | 0.7662 | 0.0384 | 0.1398 |
| 5-5-50 | 0.5641 | 0.0468 | 0.3611 | 0.6883 | 0.0518 | 0.2667 | 0.8057 | 0.0265 | 0.1387 |
| 5-8-50 | 0.6243 | 0.0526 | 0.2999 | 0.7104 | 0.0677 | 0.2487 | 0.8347 | 0.0363 | 0.0947 |
| 3-2-100 | 0.7956 | 0.0512 | 0.2246 | 0.8707 | 0.0868 | 0.1658 | 1.0079 | 0.0591 | 0.0885 |
| 3-5-100 | 0.4721 | 0.0584 | 0.4226 | 0.6921 | 0.031 | 0.215 | 0.7828 | 0.0440 | 0.1505 |
| 3-8-100 | 0.7753 | 0.0296 | 0.2064 | 0.8151 | 0.0349 | 0.1848 | 0.9802 | 0.0378 | 0.0835 |
| 4-2-100 | 0.7869 | 0.0556 | 0.2372 | 0.8766 | 0.0547 | 0.1544 | 0.9106 | 0.0652 | 0.1356 |
| 4-5-100 | 0.7944 | 0.0695 | 0.2028 | 0.8948 | 0.0401 | 0.1352 | 0.9388 | 0.0490 | 0.0997 |
| 4-8-100 | 0.458 | 0.0458 | 0.3434 | 0.6002 | 0.0340 | 0.1681 | 0.6673 | 0.0176 | 0.1314 |
| 5-2-100 | 0.7686 | 0.0596 | 0.1865 | 0.8443 | 0.0548 | 0.1354 | 0.9220 | 0.0586 | 0.0867 |
| 5-5-100 | 0.5252 | 0.0417 | 0.5013 | 0.767 | 0.0409 | 0.3121 | 0.7196 | 0.0399 | 0.2825 |
| 5-8-100 | 0.7419 | 0.0457 | 0.2632 | 0.8679 | 0.0461 | 0.1711 | 0.9866 | 0.0516 | 0.0986 |
| 3-2-200 | 0.6307 | 0.052 | 0.3675 | 0.8156 | 0.0646 | 0.1978 | 0.8842 | 0.0686 | 0.1406 |
| 3-5-200 | 0.6494 | 0.0271 | 0.2172 | 0.7614 | 0.0264 | 0.1728 | 0.9285 | 0.0377 | 0.0646 |
| 3-8-200 | 0.5227 | 0.0529 | 0.3597 | 0.7294 | 0.0698 | 0.1983 | 0.7395 | 0.0588 | 0.1419 |
| 4-2-200 | 0.4253 | 0.0515 | 0.4872 | 0.6195 | 0.0500 | 0.1944 | 0.8108 | 0.0441 | 0.1347 |
| 4-5-200 | 0.4035 | 0.0416 | 0.571 | 0.6264 | 0.0365 | 0.2819 | 0.7476 | 0.0228 | 0.2512 |
| 4-8-200 | 0.6418 | 0.0277 | 0.2914 | 0.8268 | 0.0309 | 0.1885 | 0.9603 | 0.0365 | 0.0781 |
| 5-2-200 | 0.657 | 0.0637 | 0.2925 | 0.7572 | 0.0589 | 0.2133 | 0.7509 | 0.0444 | 0.2310 |
| 5-5-200 | 0.6101 | 0.0627 | 0.3198 | 0.7727 | 0.0586 | 0.1428 | 0.8557 | 0.0677 | 0.1458 |
| 5-8-200 | 0.2978 | 0.0406 | 0.5810 | 0.5328 | 0.0362 | 0.3373 | 0.6959 | 0.0304 | 0.1999 |
| Problem Scale | DDQN-MOCE vs. D1 | DDQN-MOCE vs. D2 | D1 vs. D2 | |||
|---|---|---|---|---|---|---|
| C(DDQN-MOCE, D1) | C(D1, DDQN-MOCE) | C(DDQN-MOCE, D2) | C(D2, DDQN-MOCE) | C(D1, D2) | C(D2, D1) | |
| 3-2-20 | 0.9190 * | 0.0150 | 0.8843 | 0.0506 | 0.2542 | 0.5711 |
| 3-5-20 | 0.7971 | 0.0125 | 0.7496 | 0.0100 | 0.3020 | 0.5825 |
| 3-8-20 | 0.7453 | 0.0171 | 0.7631 | 0.01 | 0.2722 | 0.4859 |
| 4-2-20 | 0.6492 | 0.1125 | 0.504 | 0.1319 | 0.3492 | 0.5411 |
| 4-5-20 | 0.8921 | 0.0100 | 0.8807 | 0.01 | 0.2214 | 0.5982 |
| 4-8-20 | 0.9301 | 0 | 0.8656 | 0 | 0.2670 | 0.5896 |
| 5-2-20 | 0.7062 | 0.0614 | 0.6648 | 0.0855 | 0.2393 | 0.5643 |
| 5-5-20 | 0.762 | 0.0083 | 0.7386 | 0.0225 | 0.3015 | 0.5432 |
| 5-8-20 | 0.7393 | 0.005 | 0.7694 | 0.0050 | 0.3120 | 0.6115 |
| 3-2-50 | 0.8949 | 0.0328 | 0.8665 | 0.0405 | 0.2065 | 0.6764 |
| 3-5-50 | 0.7316 | 0.0401 | 0.7120 | 0.1404 | 0.3075 | 0.5778 |
| 3-8-50 | 0.8294 | 0.0155 | 0.6965 | 0.0127 | 0.2724 | 0.6567 |
| 4-2-50 | 0.4654 | 0.0556 | 0.4612 | 0.1306 | 0.1776 | 0.6863 |
| 4-5-50 | 0.6182 | 0.0351 | 0.6735 | 0.0536 | 0.3046 | 0.5196 |
| 4-8-50 | 0.7957 | 0.0369 | 0.7405 | 0.0542 | 0.2710 | 0.5985 |
| 5-2-50 | 0.647 | 0 | 0.4565 | 0.1146 | 0.1405 | 0.7785 |
| 5-5-50 | 0.7791 | 0 | 0.6855 | 0.0125 | 0.1701 | 0.7332 |
| 5-8-50 | 0.776 | 0.0394 | 0.7449 | 0.0610 | 0.1944 | 0.7225 |
| 3-2-100 | 0.8647 | 0.0354 | 0.7498 | 0.1170 | 0.1766 | 0.7108 |
| 3-5-100 | 0.7036 | 0.053 | 0.4325 | 0.0967 | 0.0167 | 0.8703 |
| 3-8-100 | 0.9547 | 0.0167 | 0.9168 | 0.0301 | 0.2504 | 0.6254 |
| 4-2-100 | 0.7946 | 0.1143 | 0.5523 | 0.2960 | 0.1637 | 0.7684 |
| 4-5-100 | 0.8151 | 0.0985 | 0.6421 | 0.2099 | 0.1161 | 0.8272 |
| 4-8-100 | 0.3717 | 0.0167 | 0.1035 | 0.0250 | 0.0507 | 0.8935 |
| 5-2-100 | 0.7896 | 0.1137 | 0.6198 | 0.2693 | 0.1534 | 0.7164 |
| 5-5-100 | 0.6918 | 0.0196 | 0.3874 | 0.1871 | 0.0183 | 0.8841 |
| 5-8-100 | 0.9679 | 0.0211 | 0.818 | 0.1091 | 0.0495 | 0.8823 |
| 3-2-200 | 0.894 | 0.0251 | 0.6784 | 0.2359 | 0.0493 | 0.889 |
| 3-5-200 | 0.9798 | 0.0020 | 0.9605 | 0.0249 | 0.1959 | 0.7300 |
| 3-8-200 | 0.6907 | 0.0012 | 0.4663 | 0.1435 | 0.0367 | 0.8832 |
| 4-2-200 | 0.7145 | 0.0394 | 0.164 | 0.6361 | 0.0163 | 0.9142 |
| 4-5-200 | 0.4587 | 0.0250 | 0.2247 | 0.2833 | 0.0368 | 0.8821 |
| 4-8-200 | 0.9781 | 0.0065 | 0.8672 | 0.0907 | 0.0918 | 0.8404 |
| 5-2-200 | 0.6637 | 0.1639 | 0.3531 | 0.4403 | 0.1514 | 0.7339 |
| 5-5-200 | 0.6065 | 0.1052 | 0.2975 | 0.4207 | 0.0881 | 0.8479 |
| 5-8-200 | 0.5275 | 0 | 0.1169 | 0.325 | 0 | 0.9292 |
| Variants | HV | Spacing | GD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | p-Value | Rank | p-Value | Rank | p-Value | ||||
| D1 | 3.00 | 64.89 | 8.12 × 10−15 | 2.31 | 10.06 | 6.55 × 10−3 | 3.00 | 68.22 | 1.53 × 10−15 |
| D2 | 1.89 | 2.11 | 1.94 | ||||||
| DDQN-MOCE | 1.11 | 1.58 | 1.06 | ||||||
| Problem Scale | DDQN-MOCE | NSGA-II | MOEA/D | MOPSO | SPEA2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 3-2-20 | 1.0677 * | 0.0610 | 0.2339 | 0.0306 | 0.5702 | 0.1658 | 0.2016 | 0.0195 | 0.3696 | 0.1336 |
| 3-5-20 | 1.0333 | 0.0785 | 0.2466− | 0.0310 | 0.4344− | 0.0854 | 0.2556− | 0.0229 | 0.4055− | 0.1090 |
| 3-8-20 | 1.0369 | 0.0721 | 0.4569− | 0.0513 | 0.5755− | 0.1278 | 0.4010− | 0.0372 | 0.5757− | 0.1175 |
| 4-2-20 | 1.0096 | 0.0791 | 0.365− | 0.0551 | 0.5644− | 0.1534 | 0.2892− | 0.0315 | 0.4025− | 0.0994 |
| 4-5-20 | 0.9807 | 0.0765 | 0.3639− | 0.0548 | 0.5033− | 0.0963 | 0.4427− | 0.0369 | 0.5166− | 0.0812 |
| 4-8-20 | 0.9569 | 0.0723 | 0.4560− | 0.0570 | 0.5314− | 0.1222 | 0.4573− | 0.0378 | 0.6158− | 0.1179 |
| 5-2-20 | 0.9369 | 0.1001 | 0.5679− | 0.0731 | 0.7036− | 0.1359 | 0.4877− | 0.0488 | 0.6364− | 0.1526 |
| 5-5-20 | 0.9385 | 0.0655 | 0.4055− | 0.0615 | 0.5635− | 0.1445 | 0.3693− | 0.0360 | 0.5518− | 0.1480 |
| 5-8-20 | 0.8455 | 0.1193 | 0.4605− | 0.0885 | 0.5581− | 0.1183 | 0.5071− | 0.0578 | 0.5966− | 0.0977 |
| 3-2-50 | 0.9162 | 0.0547 | 0.3771− | 0.0365 | 0.4610− | 0.0569 | 0.5459− | 0.0290 | 0.6008− | 0.0384 |
| 3-5-50 | 0.8638 | 0.0687 | 0.2106− | 0.0265 | 0.2871− | 0.0573 | 0.2504− | 0.0247 | 0.2956− | 0.0775 |
| 3-8-50 | 1.0165 | 0.0758 | 0.1878− | 0.0346 | 0.2472− | 0.0539 | 0.2517− | 0.0297 | 0.3039− | 0.0543 |
| 4-2-50 | 0.9356 | 0.0871 | 0.1358− | 0.0147 | 0.2763− | 0.0764 | 0.1197− | 0.0079 | 0.2016− | 0.0596 |
| 4-5-50 | 0.9284 | 0.0863 | 0.2086− | 0.0376 | 0.2766− | 0.0647 | 0.2285− | 0.0241 | 0.3108− | 0.0527 |
| 4-8-50 | 0.9988 | 0.0722 | 0.2374− | 0.0306 | 0.2648− | 0.0735 | 0.2592− | 0.0163 | 0.3119− | 0.0422 |
| 5-2-50 | 1.0291 | 0.0806 | 0.1415− | 0.0212 | 0.2691− | 0.0653 | 0.1473− | 0.0151 | 0.2119− | 0.0844 |
| 5-5-50 | 1.0463 | 0.0688 | 0.1672− | 0.0162 | 0.2394− | 0.0535 | 0.1751− | 0.0151 | 0.2498− | 0.0590 |
| 5-8-50 | 0.9028 | 0.0530 | 0.373− | 0.0430 | 0.6562− | 0.1816 | 0.3412− | 0.0314 | 0.5505− | 0.1341 |
| 3-2-100 | 0.7965 | 0.0536 | 0.2008− | 0.0305 | 0.2497− | 0.0449 | 0.2889− | 0.0201 | 0.3358− | 0.0529 |
| 3-5-100 | 1.0676 | 0.0819 | 0.1587− | 0.0124 | 0.2045− | 0.0339 | 0.1682− | 0.0130 | 0.1943− | 0.0348 |
| 3-8-100 | 0.9066 | 0.0228 | 0.2305− | 0.0070 | 0.2410− | 0.0237 | 0.2400− | 0.0135 | 0.2674− | 0.0120 |
| 4-2-100 | 0.9499 | 0.0616 | 0.2358− | 0.0252 | 0.3246− | 0.0633 | 0.2307− | 0.0136 | 0.3206− | 0.0498 |
| 4-5-100 | 0.8442 | 0.0609 | 0.1901− | 0.0234 | 0.2204− | 0.0284 | 0.1857− | 0.0180 | 0.2474− | 0.0358 |
| 4-8-100 | 0.9703 | 0.1403 | 0.0709− | 0.0085 | 0.1054− | 0.0287 | 0.0770− | 0.0050 | 0.1065− | 0.0184 |
| 5-2-100 | 0.8745 | 0.0455 | 0.3043− | 0.0251 | 0.3257− | 0.0397 | 0.4155− | 0.0229 | 0.4186− | 0.0254 |
| 5-5-100 | 0.9904 | 0.0869 | 0.1141− | 0.0162 | 0.1689− | 0.0328 | 0.1236− | 0.0104 | 0.1775− | 0.0353 |
| 5-8-100 | 0.8401 | 0.0351 | 0.2012− | 0.0321 | 0.2127− | 0.0161 | 0.2145− | 0.0155 | 0.2577− | 0.0238 |
| 3-2-200 | 0.8716 | 0.0386 | 0.1818− | 0.0185 | 0.2396− | 0.0433 | 0.1967− | 0.0123 | 0.2418− | 0.0350 |
| 3-5-200 | 0.9019 | 0.0220 | 0.2227− | 0.0152 | 0.2271− | 0.0261 | 0.2327− | 0.0098 | 0.2490− | 0.0250 |
| 3-8-200 | 1.0519 | 0.0728 | 0.1102− | 0.0180 | 0.1701− | 0.0256 | 0.1182− | 0.0151 | 0.1469− | 0.0221 |
| 4-2-200 | 0.9274 | 0.0987 | 0.1216− | 0.0098 | 0.2091− | 0.0474 | 0.1353− | 0.0094 | 0.1744− | 0.0461 |
| 4-5-200 | 1.0067 | 0.0967 | 0.1075− | 0.0129 | 0.1295− | 0.0222 | 0.1244− | 0.0088 | 0.1510− | 0.0237 |
| 4-8-200 | 0.8410 | 0.0244 | 0.1861− | 0.0086 | 0.2032− | 0.0267 | 0.2016− | 0.0068 | 0.2116− | 0.0211 |
| 5-2-200 | 0.8350 | 0.0914 | 0.1938− | 0.0324 | 0.2583− | 0.0469 | 0.3284− | 0.0261 | 0.3431− | 0.0313 |
| 5-5-200 | 1.1051 | 0.0196 | 0.1350− | 0.0078 | 0.1750− | 0.0187 | 0.1499− | 0.0117 | 0.1966− | 0.0095 |
| 5-8-200 | 1.0542 | 0.4001 | 0.0575− | 0.0138 | 0.1017− | 0.0367 | 0.0622− | 0.0147 | 0.1046− | 0.0416 |
| Problem Scale | DDQN−MOCE | NSGA−II | MOEA/D | MOPSO | SPEA2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 3-2-20 | 0.0283 | 0.0185 | 0.0126≈ * | 0.0155 | 0.0158≈ | 0.0235 | 0.0426− | 0.0219 | 0.0146≈ | 0.0144 |
| 3-5-20 | 0.0284 | 0.0206 | 0.0213≈ | 0.0244 | 0.0100+ | 0.0143 | 0.0288≈ | 0.0246 | 0.0280≈ | 0.0129 |
| 3-8-20 | 0.0532 | 0.0410 | 0.0136+ | 0.0199 | 0.0268+ | 0.0320 | 0.0444≈ | 0.0368 | 0.0432≈ | 0.0303 |
| 4-2-20 | 0.0253 | 0.0274 | 0.0056+ | 0.0094 | 0.0151≈ | 0.0170 | 0.0638− | 0.0559 | 0.0282≈ | 0.0318 |
| 4-5-20 | 0.0502 | 0.0429 | 0.0419≈ | 0.0451 | 0.0344≈ | 0.0352 | 0.0430≈ | 0.0336 | 0.0411≈ | 0.0340 |
| 4-8-20 | 0.0646 | 0.0398 | 0.0222+ | 0.0217 | 0.0370+ | 0.0285 | 0.0820− | 0.0662 | 0.0410+ | 0.0260 |
| 5-2-20 | 0.0337 | 0.0395 | 0.0123+ | 0.0196 | 0.0223+ | 0.0392 | 0.0554− | 0.0496 | 0.0325≈ | 0.0476 |
| 5-5-20 | 0.0426 | 0.0234 | 0.0253+ | 0.0361 | 0.0214+ | 0.0279 | 0.0626− | 0.0402 | 0.0491≈ | 0.0373 |
| 5-8-20 | 0.0488 | 0.0413 | 0.0474≈ | 0.0387 | 0.0250+ | 0.0354 | 0.0549≈ | 0.0436 | 0.0486≈ | 0.0358 |
| 3-2-50 | 0.0400 | 0.0361 | 0.0358≈ | 0.0254 | 0.0264≈ | 0.0366 | 0.0682− | 0.0607 | 0.0529≈ | 0.0324 |
| 3-5-50 | 0.0364 | 0.0320 | 0.0350≈ | 0.0353 | 0.0343≈ | 0.0384 | 0.0517− | 0.0385 | 0.0322≈ | 0.0206 |
| 3-8-50 | 0.0460 | 0.0257 | 0.0470≈ | 0.0589 | 0.0330≈ | 0.0360 | 0.0478≈ | 0.0363 | 0.0550≈ | 0.0333 |
| 4-2-50 | 0.0054 | 0.0018 | 0.0014≈ | 0.0046 | 0.0015≈ | 0.0065 | 0.0224− | 0.0167 | 0.0046≈ | 0.0100 |
| 4-5-50 | 0.0462 | 0.0316 | 0.0459≈ | 0.0446 | 0.0321≈ | 0.0346 | 0.0550≈ | 0.0549 | 0.046≈ | 0.0294 |
| 4-8-50 | 0.0653 | 0.0392 | 0.0372+ | 0.0350 | 0.0317+ | 0.0359 | 0.0834− | 0.0669 | 0.0371+ | 0.0282 |
| 5-2-50 | 0.0272 | 0.0304 | 0.0127≈ | 0.0261 | 0.0141≈ | 0.0280 | 0.0382≈ | 0.0292 | 0.0268≈ | 0.0320 |
| 5-5-50 | 0.0224 | 0.0244 | 0.0276≈ | 0.0233 | 0.0304≈ | 0.0218 | 0.0412− | 0.0365 | 0.0320≈ | 0.0229 |
| 5-8-50 | 0.0718 | 0.0424 | 0.0199+ | 0.0213 | 0.0362+ | 0.0287 | 0.0627≈ | 0.0607 | 0.0290+ | 0.0193 |
| 3-2-100 | 0.0457 | 0.0388 | 0.0460≈ | 0.0354 | 0.0282+ | 0.0366 | 0.0644− | 0.0281 | 0.0439≈ | 0.0193 |
| 3-5-100 | 0.0315 | 0.0255 | 0.0163≈ | 0.0168 | 0.0316≈ | 0.0359 | 0.0540− | 0.0446 | 0.0296≈ | 0.0259 |
| 3-8-100 | 0.0512 | 0.0141 | 0.0151+ | 0.0016 | 0.0250+ | 0.0116 | 0.0338+ | 0.0173 | 0.0287+ | 0.0072 |
| 4-2-100 | 0.0392 | 0.0323 | 0.0068+ | 0.0144 | 0.0293≈ | 0.0265 | 0.0708− | 0.0380 | 0.0183+ | 0.0234 |
| 4-5-100 | 0.0438 | 0.0362 | 0.0326≈ | 0.0341 | 0.026+ | 0.0316 | 0.0690− | 0.0424 | 0.0471≈ | 0.0375 |
| 4-8-100 | 0.0167 | 0.0182 | 0.0233≈ | 0.0194 | 0.0210≈ | 0.0183 | 0.0360− | 0.0118 | 0.0153≈ | 0.0069 |
| 5-2-100 | 0.0365 | 0.0361 | 0.0456≈ | 0.0314 | 0.0345≈ | 0.0320 | 0.0599− | 0.0520 | 0.0350≈ | 0.0210 |
| 5-5-100 | 0.0540 | 0.0404 | 0.0168+ | 0.0185 | 0.0213+ | 0.0170 | 0.0478≈ | 0.0258 | 0.0328 | 0.0245 |
| 5-8-100 | 0.0631 | 0.0155 | 0.0248+ | 0.0184 | 0.0335+ | 0.0187 | 0.0688≈ | 0.0247 | 0.0418+ | 0.0229 |
| 3-2-200 | 0.0399 | 0.0215 | 0.0336≈ | 0.0320 | 0.0206≈ | 0.0249 | 0.0580− | 0.0376 | 0.0231≈ | 0.0158 |
| 3-5-200 | 0.0389 | 0.0225 | 0.0181+ | 0.0172 | 0.0188+ | 0.0217 | 0.0280≈ | 0.0160 | 0.0239≈ | 0.0196 |
| 3-8-200 | 0.0541 | 0.0297 | 0.0302+ | 0.0246 | 0.0380≈ | 0.0237 | 0.0602≈ | 0.0343 | 0.0413≈ | 0.0243 |
| 4-2-200 | 0.0412 | 0.0344 | 0.0253+ | 0.0282 | 0.0223+ | 0.0273 | 0.0721− | 0.0466 | 0.0168+ | 0.0230 |
| 4-5-200 | 0.0237 | 0.0242 | 0.0246≈ | 0.0201 | 0.0201≈ | 0.0284 | 0.0630− | 0.0577 | 0.0369≈ | 0.0276 |
| 4-8-200 | 0.0362 | 0.0190 | 0.0125+ | 0.0112 | 0.0240≈ | 0.0175 | 0.0308≈ | 0.0326 | 0.0191+ | 0.0087 |
| 5-2-200 | 0.0646 | 0.0446 | 0.0427+ | 0.0587 | 0.0246+ | 0.0358 | 0.0960− | 0.0756 | 0.0486+ | 0.0319 |
| 5-5-200 | 0.0580 | 0.0335 | 0.0441≈ | 0.0198 | 0.0446≈ | 0.0299 | 0.1342− | 0.0389 | 0.0563≈ | 0.0387 |
| 5-8-200 | 0.0188 | 0.0233 | 0.0208≈ | 0.0229 | 0.0176≈ | 0.0083 | 0.0294≈ | 0.0294 | 0.0300≈ | 0.0132 |
| Problem Scale | DDQN-MOCE | NSGA-II | MOEA/D | MOPSO | SPEA2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| 3-2-20 | 0.0573 * | 0.0288 | 0.7482 | 0.0325 | 0.3454 | 0.1432 | 0.8237 | 0.0453 | 0.5562 | 0.1498 |
| 3-5-20 | 0.0910 | 0.0402 | 0.7239 | 0.0492 | 0.5247 | 0.0800 | 0.8019 | 0.0452 | 0.5915 | 0.0968 |
| 3-8-20 | 0.0731 | 0.0304 | 0.4332 | 0.0457 | 0.4211 | 0.1193 | 0.6246 | 0.0493 | 0.4620 | 0.0943 |
| 4-2-20 | 0.0676 | 0.0319 | 0.5155 | 0.0666 | 0.3782 | 0.1300 | 0.7215 | 0.0571 | 0.5492 | 0.1030 |
| 4-5-20 | 0.0979 | 0.0445 | 0.5433 | 0.0724 | 0.4595 | 0.0993 | 0.5637 | 0.0476 | 0.4890 | 0.0687 |
| 4-8-20 | 0.1097 | 0.0611 | 0.4900 | 0.0679 | 0.4958 | 0.1318 | 0.6068 | 0.0574 | 0.4522 | 0.1029 |
| 5-2-20 | 0.1097 | 0.0549 | 0.2623 | 0.0579 | 0.2167 | 0.1092 | 0.4538 | 0.0665 | 0.2741 | 0.1059 |
| 5-5-20 | 0.1019 | 0.0408 | 0.4410 | 0.0619 | 0.0214 | 0.0279 | 0.5100 | 0.0345 | 0.3732 | 0.1137 |
| 5-8-20 | 0.1206 | 0.0515 | 0.3999 | 0.0570 | 0.2877 | 0.0958 | 0.3705 | 0.0486 | 0.3148 | 0.0552 |
| 3-2-50 | 0.0974 | 0.0369 | 0.4613 | 0.0440 | 0.3304 | 0.0787 | 0.2865 | 0.0315 | 0.2533 | 0.0286 |
| 3-5-50 | 0.1308 | 0.0517 | 0.5399 | 0.0768 | 0.3279 | 0.0791 | 0.4580 | 0.0674 | 0.3807 | 0.0944 |
| 3-8-50 | 0.0706 | 0.0337 | 0.7698 | 0.0413 | 0.7617 | 0.0460 | 0.7761 | 0.0354 | 0.7370 | 0.0385 |
| 4-2-50 | 0.0865 | 0.0471 | 0.8253 | 0.0307 | 0.6324 | 0.0976 | 0.9262 | 0.0269 | 0.7396 | 0.0941 |
| 4-5-50 | 0.1710 | 0.0652 | 0.8308 | 0.0420 | 0.7461 | 0.0900 | 0.8435 | 0.0400 | 0.7495 | 0.0518 |
| 4-8-50 | 0.0684 | 0.0214 | 0.6664 | 0.0366 | 0.5982 | 0.0996 | 0.6556 | 0.0244 | 0.5737 | 0.0506 |
| 5-2-50 | 0.1045 | 0.0486 | 0.9357 | 0.0354 | 0.7688 | 0.0818 | 0.9965 | 0.0379 | 0.8594 | 0.1118 |
| 5-5-50 | 0.0738 | 0.0350 | 0.8958 | 0.0332 | 0.8043 | 0.0751 | 0.9394 | 0.0336 | 0.8086 | 0.0661 |
| 5-8-50 | 0.1042 | 0.0306 | 0.4460 | 0.0407 | 0.1856 | 0.0885 | 0.4688 | 0.0326 | 0.2870 | 0.0917 |
| 3-2-100 | 0.1147 | 0.0381 | 0.5419 | 0.0708 | 0.3892 | 0.0727 | 0.3935 | 0.0422 | 0.3305 | 0.0743 |
| 3-5-100 | 0.0872 | 0.0464 | 0.9068 | 0.0275 | 0.8636 | 0.0413 | 0.9522 | 0.0250 | 0.8905 | 0.0405 |
| 3-8-100 | 0.0477 | 0.0091 | 0.2147 | 0.0259 | 0.0929 | 0.0308 | 0.1805 | 0.0223 | 0.1248 | 0.0499 |
| 4-2-100 | 0.0828 | 0.0358 | 0.3546 | 0.0634 | 0.2275 | 0.0699 | 0.3434 | 0.0432 | 0.1765 | 0.0492 |
| 4-5-100 | 0.1274 | 0.0404 | 0.4311 | 0.0636 | 0.2554 | 0.1014 | 0.3957 | 0.0401 | 0.2349 | 0.0814 |
| 4-8-100 | 0.1441 | 0.1000 | 1.1610 | 0.0242 | 1.1698 | 0.0151 | 1.0774 | 0.0610 | 1.0891 | 0.0423 |
| 5-2-100 | 0.1043 | 0.0242 | 0.3176 | 0.0463 | 0.2717 | 0.0556 | 0.2138 | 0.0448 | 0.1801 | 0.0388 |
| 5-5-100 | 0.1331 | 0.0691 | 0.9802 | 0.0340 | 0.9127 | 0.0476 | 1.0129 | 0.0264 | 0.9125 | 0.0477 |
| 5-8-100 | 0.0647 | 0.0199 | 0.2679 | 0.0825 | 0.1362 | 0.0336 | 0.2455 | 0.0639 | 0.1784 | 0.0317 |
| 3-2-200 | 0.0851 | 0.0292 | 0.3507 | 0.0562 | 0.1913 | 0.0799 | 0.2961 | 0.0395 | 0.2046 | 0.0644 |
| 3-5-200 | 0.0596 | 0.0133 | 0.1852 | 0.0327 | 0.1236 | 0.0396 | 0.1445 | 0.0217 | 0.1035 | 0.0298 |
| 3-8-200 | 0.0561 | 0.0258 | 0.8426 | 0.1236 | 0.7164 | 0.2439 | 0.8373 | 0.1670 | 0.6577 | 0.2110 |
| 4-2-200 | 0.1452 | 0.0642 | 0.9511 | 0.0200 | 0.9731 | 0.0173 | 0.9731 | 0.0173 | 0.8880 | 0.0491 |
| 4-5-200 | 0.1210 | 0.0575 | 1.0327 | 0.0286 | 0.9835 | 0.0390 | 1.0274 | 0.0210 | 0.9761 | 0.0419 |
| 4-8-200 | 0.0745 | 0.0170 | 0.1716 | 0.0406 | 0.0850 | 0.0388 | 0.1371 | 0.0210 | 0.0849 | 0.0332 |
| 5-2-200 | 0.2494 | 0.0976 | 0.6416 | 0.0967 | 0.4730 | 0.1141 | 0.4608 | 0.0558 | 0.4375 | 0.0775 |
| 5-5-200 | 0.0510 | 0.0266 | 0.7880 | 0.1288 | 0.7267 | 0.1370 | 0.7777 | 0.1568 | 0.6780 | 0.2039 |
| 5-8-200 | 0.0127 | 0.0381 | 1.1701 | 0.0677 | 1.0534 | 0.0978 | 1.1887 | 0.0779 | 1.0779 | 0.1117 |
| Problem Scale | DDQN-MOCE vs. NSGA-II | DDQN-MOCE vs. MOEA/D | DDQN-MOCE vs. MOPSO | DDQN-MOCE vs. SPEA2 | ||||
|---|---|---|---|---|---|---|---|---|
| A | A′ | B | B′ | C | C′ | D | D′ | |
| 3-2-20 | 1 * | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3-5-20 | 1 | 0 | 0.9300 | 0 | 1 | 0 | 0.9857 | 0 |
| 3-8-20 | 1 | 0 | 0.9333 | 0.0063 | 1 | 0 | 0.9583 | 0 |
| 4-2-20 | 1 | 0 | 0.9833 | 0 | 1 | 0 | 1 | 0 |
| 4-5-20 | 1 | 0 | 0.9625 | 0 | 1 | 0 | 0.9833 | 0 |
| 4-8-20 | 1 | 0 | 0.7392 | 0.01 | 0.9500 | 0 | 0.7296 | 0.0183 |
| 5-2-20 | 0.95 | 0.0083 | 0.7786 | 0.0424 | 1 | 0 | 0.7500 | 0.0563 |
| 5-5-20 | 1 | 0 | 0.7300 | 0 | 1 | 0 | 0.8959 | 0 |
| 5-8-20 | 0.9292 | 0.0167 | 0.5975 | 0.0133 | 0.8083 | 0 | 0.7761 | 0.0260 |
| 3-2-50 | 1 | 0 | 0.8333 | 0 | 0.6167 | 0.0353 | 0.6359 | 0.0324 |
| 3-5-50 | 1 | 0 | 0.7508 | 0 | 0.9333 | 0 | 0.8758 | 0 |
| 3-8-50 | 1 | 0 | 1 | 0 | 1 | 0 | 0.9917 | 0 |
| 4-2-50 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 4-5-50 | 1 | 0 | 0.95 | 0 | 1 | 0 | 0.9644 | 0 |
| 4-8-50 | 1 | 0 | 0.95 | 0 | 0.9333 | 0 | 0.8973 | 0 |
| 5-2-50 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5-5-50 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5-8-50 | 1 | 0 | 0.3831 | 0.1375 | 1 | 0 | 0.6619 | 0 |
| 3-2-100 | 1 | 0 | 0.8708 | 0 | 0.8250 | 0.0100 | 0.7315 | 0.0100 |
| 3-5-100 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3-8-100 | 0.9000 | 0 | 0.2467 | 0 | 0.7333 | 0 | 0.7633 | 0 |
| 4-2-100 | 0.9875 | 0 | 0.6833 | 0.0115 | 0.9000 | 0.0076 | 0.4938 | 0.016 |
| 4-5-100 | 0.9833 | 0 | 0.7042 | 0.0201 | 0.8667 | 0 | 0.6791 | 0.011 |
| 4-8-100 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5-2-100 | 1 | 0 | 1 | 0 | 0.6833 | 0 | 0.7240 | 0.0045 |
| 5-5-100 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5-8-100 | 0.7850 | 0 | 0.4883 | 0.005 | 0.5045 | 0.0113 | 0.5293 | 0.0125 |
| 3-2-200 | 1 | 0 | 0.7167 | 0 | 0.8833 | 0 | 0.7028 | 0 |
| 3-5-200 | 0.9750 | 0 | 0.7958 | 0.0035 | 0.6667 | 0.0063 | 0.5256 | 0.0158 |
| 3-8-200 | 1 | 0 | 0.9107 | 0 | 1 | 0 | 0.9702 | 0 |
| 4-2-200 | 1 | 0 | 1 | 0 | 1 | 0 | 0.9417 | 0 |
| 4-5-200 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 4-8-200 | 0.9000 | 0.0016 | 0.5221 | 0.0091 | 0.6750 | 0.0076 | 0.5275 | 0.0112 |
| 5-2-200 | 1 | 0 | 0.9625 | 0 | 0.9333 | 0 | 0.9599 | 0 |
| 5-5-200 | 0.8750 | 0 | 0.8047 | 0 | 0.8750 | 0 | 0.8179 | 0 |
| 5-8-200 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Algorithm | HV | Spacing | GD | Solution Count |
|---|---|---|---|---|
| DDQN-MOCE | 0.9140 * | 0.0469 | 0.1044 | 10 |
| NSGA-II | 0.4143 | 0.0010 | 0.4426 | 2 |
| MOEA/D | 0.4389 | 0.0080 | 0.3042 | 4 |
| MOPSO | 0.3398 | 0.0313 | 0.5334 | 3 |
| SPEA2 | 0.3382 | 0.0580 | 0.5389 | 5 |
| Algorithm | HV | Spacing | GD | Solution Count |
|---|---|---|---|---|
| DDQN-MOCE | 0.9778 * | 0.1447 | 0.1046 | 12 |
| NSGA-II | 0.1981 | 0.0026 | 0.7145 | 4 |
| MOEA/D | 0.2848 | 0.1494 | 0.5684 | 3 |
| MOPSO | 0.2474 | 0.0102 | 0.6577 | 3 |
| SPEA2 | 0.3995 | 0.0322 | 0.5325 | 11 |
| Algorithm | HV | Spacing | GD | Solution Count |
|---|---|---|---|---|
| DDQN-MOCE | 0.9044 * | 0.1151 | 0.0494 | 13 |
| NSGA-II | 0.1509 | 0.0185 | 0.3821 | 3 |
| MOEA/D | 0.1680 | 0.0963 | 0.3523 | 7 |
| MOPSO | 0.1951 | 0.0315 | 0.2528 | 3 |
| SPEA2 | 0.2873 | 0.0216 | 0.2045 | 10 |
| Algorithms | HV | Spacing | GD | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | p-Value | Rank | p-Value | Rank | p-Value | ||||
| DDQN-MOCE | 1.00 | 124.42 | 6.07 × 10−26 | 3.69 | 88.89 | 2.27 × 10−18 | 1.03 | 111.51 | 3.46 × 10−23 |
| NSGA-II | 4.75 | 1.92 | 4.33 | ||||||
| MOEA/D | 2.86 | 1.81 | 2.65 | ||||||
| MOPSO | 4.06 | 4.75 | 4.35 | ||||||
| SPEA2 | 2.33 | 2.83 | 2.64 | ||||||
| Metric | Algorithm | Mean | Std | Best | Worst |
|---|---|---|---|---|---|
| HV | DDQN-MOCE | 0.7622 * | 0.0337 | 0.8427 | 0.7083 |
| NSGA-II | 0.3111 | 0.0299 | 0.3577 | 0.227 | |
| MOEA/D | 0.3247 | 0.0787 | 0.4789 | 0.2027 | |
| MOPSO | 0.3252 | 0.0263 | 0.3796 | 0.2842 | |
| SPEA2 | 0.4013 | 0.0745 | 0.5276 | 0.2627 | |
| Spacing | DDQN-MOCE | 0.0597 | 0.046 | 0.0161 | 0.1691 |
| NSGA-II | 0.0224 | 0.0276 | 0 | 0.1176 | |
| MOEA/D | 0.0367 | 0.0332 | 0 | 0.1154 | |
| MOPSO | 0.0329 | 0.0231 | 0.0016 | 0.0915 | |
| SPEA2 | 0.0337 | 0.0197 | 0.0014 | 0.0737 | |
| GD | DDQN-MOCE | 0.0851 | 0.0339 | 0.0179 | 0.1423 |
| NSGA-II | 0.2572 | 0.0613 | 0.1196 | 0.404 | |
| MOEA/D | 0.1772 | 0.084 | 0.0153 | 0.3861 | |
| MOPSO | 0.2594 | 0.0436 | 0.1779 | 0.3394 | |
| SPEA2 | 0.1674 | 0.0633 | 0.0529 | 0.3165 | |
| Time (seconds) | DDQN-MOCE | 500.91 | 53.34 | 380.54 | 633.27 |
| NSGA-II | 2441.01 | 174.24 | 2076.11 | 2558.04 | |
| MOEA/D | 882.96 | 62.00 | 756.09 | 927.11 | |
| MOPSO | 636.36 | 39.80 | 542.45 | 662.86 | |
| SPEA2 | 305.66 | 22.20 | 261.38 | 341.79 |
| C-metric | DDQN-MOCE | NSGA-II | MOEA/D | MOPSO | SPEA2 |
|---|---|---|---|---|---|
| DDQN-MOCE | - | 1 * | 0.5 | 1 | 1 |
| NSGA-II | 0 | - | 0 | 0.6667 | 0 |
| MOEA/D | 0 | 0 | - | 1 | 0.75 |
| MOPSO | 0 | 0 | 1 | - | 0.75 |
| SPEA2 | 0 | 0 | 0 | 0 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, Q.; Duan, J.; Qin, J.; Zhou, Y. Energy-Efficient Scheduling for Distributed Hybrid Flowshop of Offshore Wind Blade Manufacturing Considering Limited Buffers. J. Mar. Sci. Eng. 2025, 13, 2176. https://doi.org/10.3390/jmse13112176
Zhang Q, Zhang Q, Duan J, Qin J, Zhou Y. Energy-Efficient Scheduling for Distributed Hybrid Flowshop of Offshore Wind Blade Manufacturing Considering Limited Buffers. Journal of Marine Science and Engineering. 2025; 13(11):2176. https://doi.org/10.3390/jmse13112176
Chicago/Turabian StyleZhang, Qinglei, Qianyuan Zhang, Jianguo Duan, Jiyun Qin, and Ying Zhou. 2025. "Energy-Efficient Scheduling for Distributed Hybrid Flowshop of Offshore Wind Blade Manufacturing Considering Limited Buffers" Journal of Marine Science and Engineering 13, no. 11: 2176. https://doi.org/10.3390/jmse13112176
APA StyleZhang, Q., Zhang, Q., Duan, J., Qin, J., & Zhou, Y. (2025). Energy-Efficient Scheduling for Distributed Hybrid Flowshop of Offshore Wind Blade Manufacturing Considering Limited Buffers. Journal of Marine Science and Engineering, 13(11), 2176. https://doi.org/10.3390/jmse13112176





