Performance Improvement of a Multiple Linear Regression-Based Storm Surge Height Prediction Model Using Data Resampling Techniques
Abstract
1. Introduction
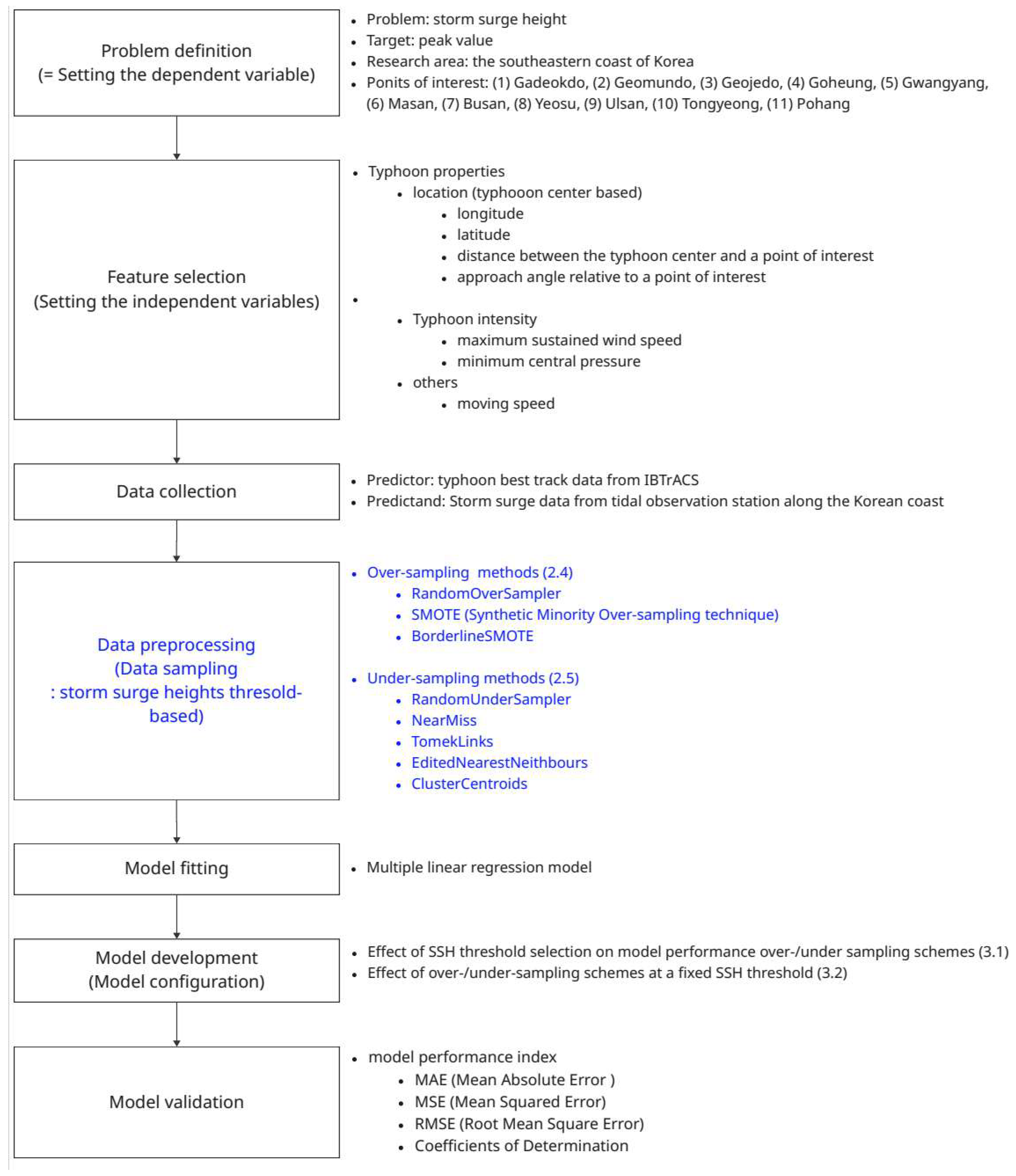
2. Data and Methodology
2.1. Research Area
2.2. Data
2.2.1. Predictors
2.2.2. Predictand
2.3. Multiple Linear Regression Technique
2.4. Data Sampling Technique—Over-Sampling
2.5. Data Sampling Technique—Under-Sampling
2.6. Objective Functions
3. Results
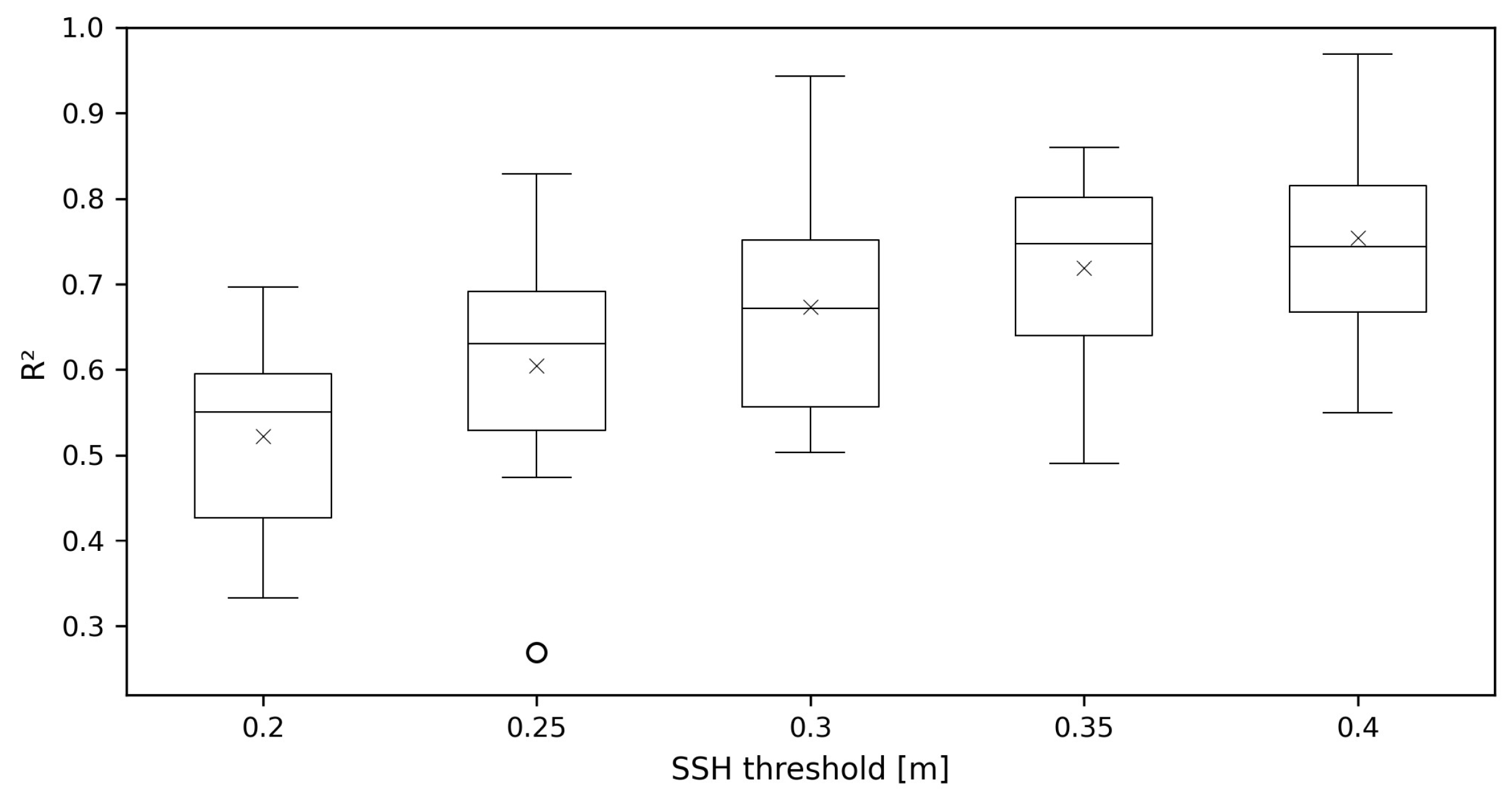
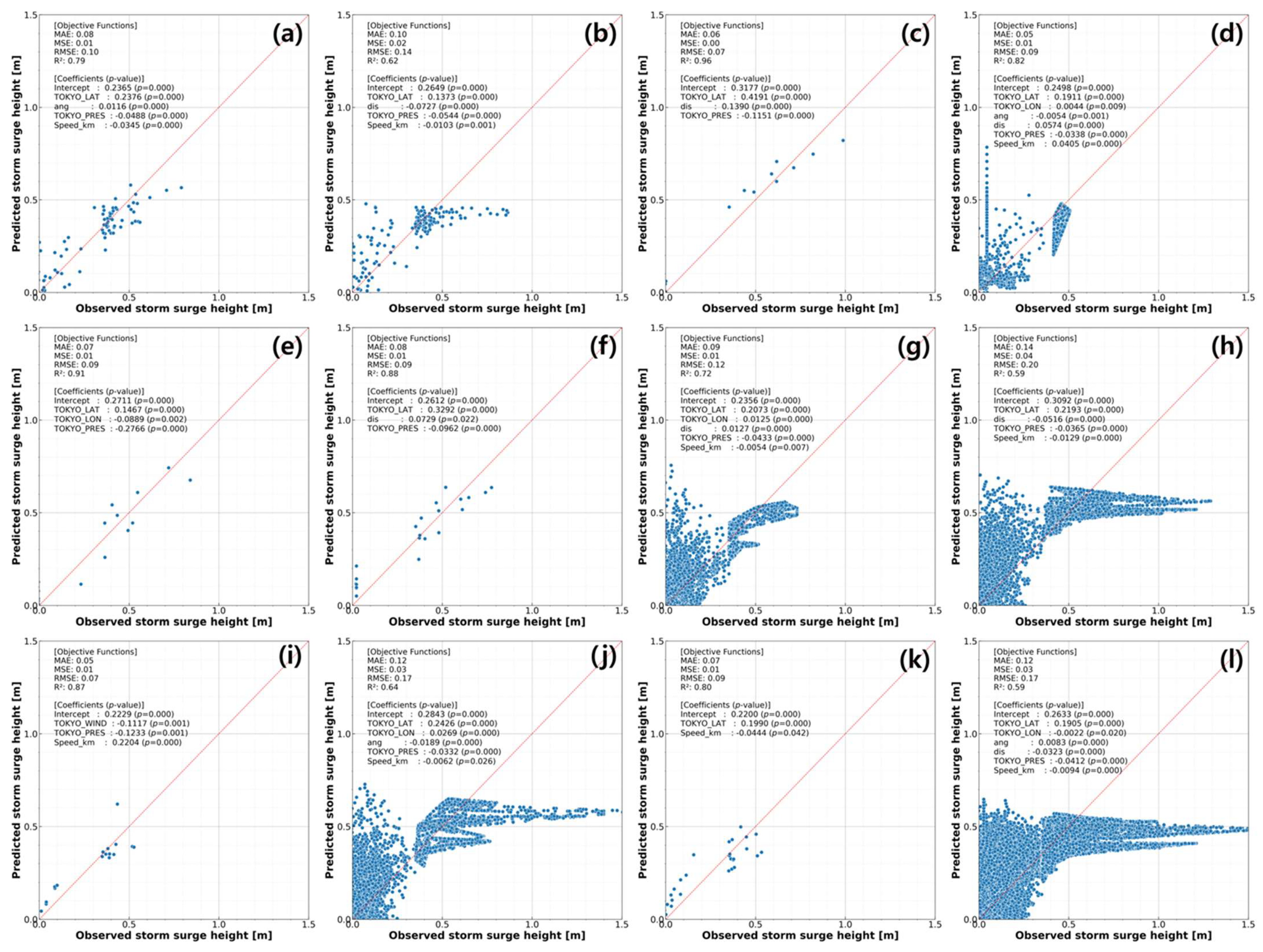
3.1. Effect of SSH Threshold Selection on Model Performance Under Over- and Under-Sampling Schemes
3.2. Effects of Over-/Under-Sampling Schemes at a Fixed SSH Threshold
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Border | Borderline SMOTE; |
| Centroids | Cluster Centroids; |
| ENN | Edited Nearest Neighbours; |
| GTSR | Global Tide and Surge Reanalysis; |
| IBTrACS | International Best Track Archive for Climate Stewardship; |
| MAE | Mean Absolute Error; |
| MLR | Multiple Linear Regression; |
| MSE | Mean Squared Error; |
| NCEI | National Centers for Environmental Information; |
| NOAA | National Oceanic and Atmospheric Administration; |
| R2 | Coefficient of Determination; |
| RMSE | Root Mean Square Error; |
| ROS | Random Over Sampler; |
| RSMC | Regional Specialized Meteorological Centre; |
| RUS | Random Under Sampler; |
| SMOTE | Synthetic Minority Over-Sampling Technique; |
| SSH | Storm Surge Height; |
| TCWC | Tropical Cyclone Warning Center; |
| Tomek | Tomek Links. |
Appendix A
| No. | Typhoon Name | Pmin | Umax | Typhoon Lifetime | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | IRVING | 958 | 75 | 1979 | 8 | 7 | ~ | 1979 | 8 | 20 |
| 2 | JUDY | 980 | 50 | 1979 | 8 | 15 | ~ | 1979 | 8 | 27 |
| 3 | KEN | 991 | 43 | 1979 | 8 | 30 | ~ | 1979 | 9 | 10 |
| 4 | IDA | 996 | NaN | 1980 | 7 | 5 | ~ | 1980 | 7 | 15 |
| 5 | NORRIS | 1002 | NaN | 1980 | 8 | 23 | ~ | 1980 | 8 | 31 |
| 6 | ORCHID | 967 | 70 | 1980 | 9 | 1 | ~ | 1980 | 9 | 16 |
| 7 | IKE | 1006 | NaN | 1981 | 6 | 7 | ~ | 1981 | 6 | 17 |
| 8 | JUNE | 990 | 45 | 1981 | 6 | 15 | ~ | 1981 | 6 | 26 |
| 9 | OGDEN | 983 | NaN | 1981 | 7 | 26 | ~ | 1981 | 8 | 1 |
| 10 | AGNES | 970 | 55 | 1981 | 8 | 25 | ~ | 1981 | 9 | 6 |
| 11 | CLARA | 1004 | NaN | 1981 | 9 | 13 | ~ | 1981 | 10 | 2 |
| 12 | CECIL | 975 | 55 | 1982 | 8 | 1 | ~ | 1982 | 8 | 19 |
| 13 | ELLIS | 955 | 70 | 1982 | 8 | 17 | ~ | 1982 | 9 | 4 |
| 14 | FORREST | 968 | 70 | 1983 | 9 | 16 | ~ | 1983 | 9 | 30 |
| 15 | ALEX | 1004 | NaN | 1984 | 6 | 28 | ~ | 1984 | 7 | 6 |
| 16 | HOLLY | 965 | 70 | 1984 | 8 | 12 | ~ | 1984 | 8 | 23 |
| 17 | GERALD | 1002 | NaN | 1984 | 8 | 14 | ~ | 1984 | 8 | 24 |
| 18 | JUNE | 1002 | NaN | 1984 | 8 | 25 | ~ | 1984 | 9 | 3 |
| 19 | HAL | 996 | NaN | 1985 | 6 | 11 | ~ | 1985 | 6 | 28 |
| 20 | JEFF | 992 | 45 | 1985 | 7 | 18 | ~ | 1985 | 8 | 3 |
| 21 | KIT | 970 | 70 | 1985 | 7 | 30 | ~ | 1985 | 8 | 17 |
| 22 | LEE | 980 | 60 | 1985 | 8 | 8 | ~ | 1985 | 8 | 16 |
| 23 | ODESSA | 985 | 55 | 1985 | 8 | 19 | ~ | 1985 | 9 | 2 |
| 24 | PAT | 965 | 70 | 1985 | 8 | 24 | ~ | 1985 | 9 | 2 |
| 25 | BRENDAN | 980 | 70 | 1985 | 9 | 25 | ~ | 1985 | 10 | 8 |
| 26 | NANCY | 994 | 45 | 1986 | 6 | 18 | ~ | 1986 | 6 | 27 |
| 27 | VERA | 960 | 70 | 1986 | 8 | 13 | ~ | 1986 | 9 | 2 |
| 28 | ABBY | 996 | NaN | 1986 | 9 | 9 | ~ | 1986 | 9 | 24 |
| 29 | THELMA | 960 | 78 | 1987 | 7 | 6 | ~ | 1987 | 7 | 18 |
| 30 | ALEX | 994 | NaN | 1987 | 7 | 21 | ~ | 1987 | 8 | 2 |
| 31 | DINAH | 940 | 85 | 1987 | 8 | 19 | ~ | 1987 | 9 | 3 |
| 32 | ELLIS | 990 | 40 | 1989 | 6 | 18 | ~ | 1989 | 6 | 25 |
| 33 | JUDY | 970 | 65 | 1989 | 7 | 20 | ~ | 1989 | 7 | 29 |
| 34 | VERA | 1002 | NaN | 1989 | 9 | 11 | ~ | 1989 | 9 | 19 |
| 35 | OFELIA | 996 | NaN | 1990 | 6 | 15 | ~ | 1990 | 6 | 26 |
| 36 | ROBYN | 992 | 40 | 1990 | 6 | 29 | ~ | 1990 | 7 | 14 |
| 37 | ABE | 996 | NaN | 1990 | 8 | 22 | ~ | 1990 | 9 | 3 |
| 38 | CAITLIN | 945 | 80 | 1991 | 7 | 18 | ~ | 1991 | 7 | 30 |
| 39 | GLADYS | 975 | 50 | 1991 | 8 | 13 | ~ | 1991 | 8 | 24 |
| 40 | UNNAMED | 994 | 35 | 1991 | 8 | 21 | ~ | 1991 | 8 | 31 |
| 41 | KINNA | 965 | 70 | 1991 | 9 | 8 | ~ | 1991 | 9 | 16 |
| 42 | MIREILLE | 935 | 95 | 1991 | 9 | 13 | ~ | 1991 | 10 | 1 |
| 43 | JANIS | 965 | 70 | 1992 | 7 | 30 | ~ | 1992 | 8 | 13 |
| 44 | IRVING | 994 | 40 | 1992 | 7 | 30 | ~ | 1992 | 8 | 5 |
| 45 | KENT | 980 | 50 | 1992 | 8 | 3 | ~ | 1992 | 8 | 20 |
| 46 | POLLY | 1000 | NaN | 1992 | 8 | 23 | ~ | 1992 | 9 | 4 |
| 47 | TED | 992 | 45 | 1992 | 9 | 14 | ~ | 1992 | 9 | 27 |
| 48 | OFELIA | 990 | 40 | 1993 | 7 | 24 | ~ | 1993 | 7 | 29 |
| 49 | PERCY | 980 | 55 | 1993 | 7 | 25 | ~ | 1993 | 8 | 1 |
| 50 | ROBYN | 945 | 85 | 1993 | 7 | 30 | ~ | 1993 | 8 | 14 |
| 51 | YANCY | 955 | 75 | 1993 | 8 | 27 | ~ | 1993 | 9 | 7 |
| 52 | RUSS | 1004 | NaN | 1994 | 6 | 2 | ~ | 1994 | 6 | 12 |
| 53 | WALT | 992 | 40 | 1994 | 7 | 11 | ~ | 1994 | 7 | 28 |
| 54 | BRENDAN | 992 | 45 | 1994 | 7 | 25 | ~ | 1994 | 8 | 3 |
| 55 | DOUG | 985 | 48 | 1994 | 7 | 30 | ~ | 1994 | 8 | 13 |
| 56 | ELLIE | 970 | 65 | 1994 | 8 | 3 | ~ | 1994 | 8 | 19 |
| 57 | FRED | 1004 | NaN | 1994 | 8 | 12 | ~ | 1994 | 8 | 26 |
| 58 | SETH | 975 | 55 | 1994 | 9 | 30 | ~ | 1994 | 10 | 16 |
| 59 | FAYE | 950 | 75 | 1995 | 7 | 12 | ~ | 1995 | 7 | 25 |
| 60 | JANIS | 990 | NaN | 1995 | 8 | 17 | ~ | 1995 | 8 | 30 |
| 61 | RYAN | 985 | 60 | 1995 | 9 | 14 | ~ | 1995 | 9 | 25 |
| 62 | EVE | 980 | 60 | 1996 | 7 | 10 | ~ | 1996 | 7 | 27 |
| 63 | KIRK | 960 | 75 | 1996 | 7 | 28 | ~ | 1996 | 8 | 18 |
| 64 | PETER | 975 | 60 | 1997 | 6 | 15 | ~ | 1997 | 7 | 4 |
| 65 | TINA | 975 | 60 | 1997 | 7 | 21 | ~ | 1997 | 8 | 10 |
| 66 | OLIWA | 970 | 65 | 1997 | 8 | 28 | ~ | 1997 | 9 | 19 |
| 67 | YANNI | 975 | 55 | 1998 | 9 | 24 | ~ | 1998 | 10 | 2 |
| 68 | NEIL | 980 | 50 | 1999 | 7 | 22 | ~ | 1999 | 7 | 28 |
| 69 | OLGA | 975 | 60 | 1999 | 7 | 26 | ~ | 1999 | 8 | 5 |
| 70 | PAUL | 992 | 35 | 1999 | 7 | 31 | ~ | 1999 | 8 | 9 |
| 71 | RACHEL | 1000 | NaN | 1999 | 8 | 5 | ~ | 1999 | 8 | 11 |
| 72 | SAM | 1004 | NaN | 1999 | 8 | 17 | ~ | 1999 | 8 | 27 |
| 73 | WENDY | 1006 | NaN | 1999 | 8 | 29 | ~ | 1999 | 9 | 7 |
| 74 | ZIA | 990 | 40 | 1999 | 9 | 11 | ~ | 1999 | 9 | 17 |
| 75 | ANN | 994 | 38 | 1999 | 9 | 14 | ~ | 1999 | 9 | 20 |
| 76 | BART | 940 | 85 | 1999 | 9 | 17 | ~ | 1999 | 9 | 29 |
| 77 | DAN | 1012 | NaN | 1999 | 10 | 1 | ~ | 1999 | 10 | 12 |
| 78 | KAI-TAK | 994 | 35 | 2000 | 7 | 2 | ~ | 2000 | 7 | 12 |
| 79 | BOLAVEN | 985 | 40 | 2000 | 7 | 19 | ~ | 2000 | 8 | 2 |
| 80 | BILIS | 1001 | NaN | 2000 | 8 | 17 | ~ | 2000 | 8 | 27 |
| 81 | PRAPIROON | 965 | 70 | 2000 | 8 | 24 | ~ | 2000 | 9 | 4 |
| 82 | SAOMAI | 970 | 60 | 2000 | 8 | 31 | ~ | 2000 | 9 | 19 |
| 83 | XANGSANE | 1003 | NaN | 2000 | 10 | 24 | ~ | 2000 | 11 | 2 |
| 84 | CHEBI | 1000 | NaN | 2001 | 6 | 19 | ~ | 2001 | 6 | 25 |
| 85 | RAMMASUN | 965 | 65 | 2002 | 6 | 26 | ~ | 2002 | 7 | 7 |
| 86 | NAKRI | 996 | NaN | 2002 | 7 | 7 | ~ | 2002 | 7 | 13 |
| 87 | FENGSHEN | 980 | 50 | 2002 | 7 | 13 | ~ | 2002 | 7 | 28 |
| 88 | RUSA | 960 | 70 | 2002 | 8 | 22 | ~ | 2002 | 9 | 3 |
| 89 | KUJIRA | 1000 | NaN | 2003 | 4 | 8 | ~ | 2003 | 4 | 25 |
| 90 | SOUDELOR | 975 | 60 | 2003 | 6 | 7 | ~ | 2003 | 6 | 24 |
| 91 | MAEMI | 935 | 90 | 2003 | 9 | 4 | ~ | 2003 | 9 | 16 |
| 92 | MINDULLE | 984 | 45 | 2004 | 6 | 21 | ~ | 2004 | 7 | 5 |
| 93 | NAMTHEUN | 996 | 40 | 2004 | 7 | 24 | ~ | 2004 | 8 | 3 |
| 94 | MEGI | 970 | 65 | 2004 | 8 | 13 | ~ | 2004 | 8 | 22 |
| 95 | CHABA | 955 | 80 | 2004 | 8 | 17 | ~ | 2004 | 9 | 5 |
| 96 | SONGDA | 945 | 75 | 2004 | 8 | 26 | ~ | 2004 | 9 | 10 |
| 97 | MEARI | 975 | 60 | 2004 | 9 | 18 | ~ | 2004 | 10 | 2 |
| 98 | MATSA | 998 | NaN | 2005 | 7 | 29 | ~ | 2005 | 8 | 9 |
| 99 | NABI | 955 | 75 | 2005 | 8 | 28 | ~ | 2005 | 9 | 9 |
| 100 | KHANUN | 1000 | NaN | 2005 | 9 | 5 | ~ | 2005 | 9 | 13 |
| 101 | CHANCHU | 996 | NaN | 2006 | 5 | 7 | ~ | 2006 | 5 | 19 |
| 102 | EWINIAR | 975 | 60 | 2006 | 6 | 29 | ~ | 2006 | 7 | 12 |
| 103 | WUKONG | 980 | 45 | 2006 | 8 | 12 | ~ | 2006 | 8 | 21 |
| 104 | SHANSHAN | 950 | 80 | 2006 | 9 | 9 | ~ | 2006 | 9 | 19 |
| 105 | MAN-YI | 955 | 70 | 2007 | 7 | 6 | ~ | 2007 | 7 | 23 |
| 106 | USAGI | 960 | 80 | 2007 | 7 | 27 | ~ | 2007 | 8 | 4 |
| 107 | PABUK | 995 | NaN | 2007 | 8 | 4 | ~ | 2007 | 8 | 15 |
| 108 | NARI | 960 | 75 | 2007 | 9 | 11 | ~ | 2007 | 9 | 18 |
| 109 | WIPHA | 1005 | NaN | 2007 | 9 | 14 | ~ | 2007 | 9 | 20 |
| 110 | KROSA | 1010 | NaN | 2007 | 10 | 1 | ~ | 2007 | 10 | 14 |
| 111 | KALMAEGI | 994 | NaN | 2008 | 7 | 11 | ~ | 2008 | 7 | 24 |
| 112 | LINFA | 998 | NaN | 2009 | 6 | 13 | ~ | 2009 | 6 | 30 |
| 113 | MORAKOT | 998 | NaN | 2009 | 8 | 2 | ~ | 2009 | 8 | 13 |
| 114 | DIANMU | 985 | 50 | 2010 | 8 | 6 | ~ | 2010 | 8 | 13 |
| 115 | KOMPASU | 970 | 70 | 2010 | 8 | 27 | ~ | 2010 | 9 | 6 |
| 116 | MALOU | 992 | 50 | 2010 | 8 | 31 | ~ | 2010 | 9 | 10 |
| 117 | MERANTI | 1003 | NaN | 2010 | 9 | 6 | ~ | 2010 | 9 | 14 |
| 118 | MEARI | 980 | 55 | 2011 | 6 | 20 | ~ | 2011 | 6 | 27 |
| 119 | MUIFA | 973 | 63 | 2011 | 7 | 26 | ~ | 2011 | 8 | 15 |
| 120 | KULAP | 1012 | NaN | 2011 | 9 | 5 | ~ | 2011 | 9 | 11 |
| 121 | KHANUN | 991 | 43 | 2012 | 7 | 13 | ~ | 2012 | 7 | 20 |
| 122 | DAMREY | 965 | 70 | 2012 | 7 | 27 | ~ | 2012 | 8 | 4 |
| 123 | TEMBIN | 980 | 55 | 2012 | 8 | 17 | ~ | 2012 | 9 | 1 |
| 124 | BOLAVEN | 960 | 65 | 2012 | 8 | 18 | ~ | 2012 | 9 | 1 |
| 125 | SANBA | 940 | 85 | 2012 | 9 | 10 | ~ | 2012 | 9 | 18 |
| 126 | LEEPI | 1002 | NaN | 2013 | 6 | 16 | ~ | 2013 | 6 | 23 |
| 127 | DANAS | 965 | 65 | 2013 | 10 | 1 | ~ | 2013 | 10 | 9 |
| 128 | NEOGURI | 975 | 50 | 2014 | 7 | 2 | ~ | 2014 | 7 | 13 |
| 129 | MATMO | 994 | NaN | 2014 | 7 | 16 | ~ | 2014 | 7 | 26 |
| 130 | NAKRI | 980 | 50 | 2014 | 7 | 27 | ~ | 2014 | 8 | 4 |
| 131 | FUNG-WONG | 998 | 35 | 2014 | 9 | 17 | ~ | 2014 | 9 | 25 |
| 132 | VONGFONG | 975 | 60 | 2014 | 10 | 1 | ~ | 2014 | 10 | 16 |
| 133 | CHAN-HOM | 973 | 58 | 2015 | 6 | 29 | ~ | 2015 | 7 | 13 |
| 134 | HALOLA | 994 | 45 | 2015 | 7 | 6 | ~ | 2015 | 7 | 26 |
| 135 | SOUDELOR | 998 | 35 | 2015 | 7 | 29 | ~ | 2015 | 8 | 12 |
| 136 | GONI | 945 | 85 | 2015 | 8 | 13 | ~ | 2015 | 8 | 30 |
| 137 | NAMTHEUN | 994 | 45 | 2016 | 8 | 30 | ~ | 2016 | 9 | 5 |
| 138 | MERANTI | 1004 | NaN | 2016 | 9 | 8 | ~ | 2016 | 9 | 17 |
| 139 | CHABA | 965 | 70 | 2016 | 9 | 24 | ~ | 2016 | 10 | 7 |
| 140 | NANMADOL | 985 | 55 | 2017 | 7 | 1 | ~ | 2017 | 7 | 8 |
| 141 | PRAPIROON | 965 | 60 | 2018 | 6 | 27 | ~ | 2018 | 7 | 5 |
| 142 | JONGDARI | 992 | 45 | 2018 | 7 | 23 | ~ | 2018 | 8 | 4 |
| 143 | LEEPI | 998 | 40 | 2018 | 8 | 10 | ~ | 2018 | 8 | 15 |
| 144 | SOULIK | 963 | 73 | 2018 | 8 | 15 | ~ | 2018 | 8 | 30 |
| 145 | KONG-REY | 975 | 65 | 2018 | 9 | 27 | ~ | 2018 | 10 | 7 |
| 146 | DANAS | 985 | 43 | 2019 | 7 | 14 | ~ | 2019 | 7 | 23 |
| 147 | FRANCISCO | 975 | 65 | 2019 | 8 | 1 | ~ | 2019 | 8 | 11 |
| 148 | LINGLING | 963 | 73 | 2019 | 8 | 30 | ~ | 2019 | 9 | 12 |
| 149 | TAPAH | 975 | 60 | 2019 | 9 | 17 | ~ | 2019 | 9 | 23 |
| 150 | MITAG | 988 | 50 | 2019 | 9 | 24 | ~ | 2019 | 10 | 5 |
| 151 | HAGUPIT | 996 | NaN | 2020 | 7 | 30 | ~ | 2020 | 8 | 12 |
| 152 | JANGMI | 996 | 40 | 2020 | 8 | 6 | ~ | 2020 | 8 | 14 |
| 153 | BAVI | 950 | 85 | 2020 | 8 | 20 | ~ | 2020 | 8 | 29 |
| 154 | MAYSAK | 950 | 80 | 2020 | 8 | 26 | ~ | 2020 | 9 | 7 |
| 155 | HAISHEN | 945 | 85 | 2020 | 8 | 30 | ~ | 2020 | 9 | 10 |
References
- Muis, S.; Verlaan, M.; Winsemius, H.C.; Aerts, J.C.; Ward, P.J. A global reanalysis of storm surges and extreme sea levels. Nat. Commun. 2016, 7, 11969. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 1–2391. [Google Scholar]
- Papadopoulos, N.; Gikas, V. Combined Coastal Sea Level Estimation Considering Astronomical Tide and Storm Surge Effects: Model Development and Its Application in Thermaikos Gulf, Greece. J. Mar. Sci. Eng. 2023, 11, 2033. [Google Scholar] [CrossRef]
- Antunes, C.; Lemos, G. A probabilistic approach to combine sea level rise, tide and storm surge into representative return periods of extreme total water levels: Application to the Portuguese coastal areas. Estuar. Coast. Shelf Sci. 2025, 313, 109060. [Google Scholar] [CrossRef]
- Palmer, K.; Watson, C.S.; Power, H.E.; Hunter, J.R. Quantifying the Mean Sea Level, Tide, and Surge Contributions to Changing Coastal High Water Levels. J. Geophys. Res. Ocean. 2024, 129, e2023JC020737. [Google Scholar] [CrossRef]
- Goring, D.G.; Stephens, S.A.; Bell, R.G.; Pearson, C.P. Estimation of Extreme Sea Levels in a Tide-Dominated Environment Using Short Data Records. J. Waterw. Port Coast. Ocean. Eng. 2011, 137, 150–159. [Google Scholar] [CrossRef]
- Yang, J.-A.; Kim, S.; Mori, N.; Mase, H. Bias correction of simulated storm surge height considering coastline complexity. Hydrol. Res. Lett. 2017, 11, 121–127. [Google Scholar] [CrossRef]
- Yang, J.-A.; Kim, S.; Mori, N.; Mase, H. Assessment of long-term impact of storm surges around the Korean Peninsula based on a large ensemble of climate projections. Coast. Eng. 2018, 142, 1–8. [Google Scholar] [CrossRef]
- Yang, J.-A.; Kim, S.; Son, S.; Mori, N.; Mase, H. Correction to: Assessment of uncertainties in projecting future changes to extreme storm surge height depending on future SST and greenhouse gas concentration scenarios. Clim. Chang. 2020, 162, 443–444. [Google Scholar] [CrossRef]
- Kim, H.-S.; Lee, S.-W. Storm Surge Caused by the Typhoon “Maemi” in Kwangyang Bay in 2003. J. Korea. Soc. Ocean 2004, 9, 119–129. [Google Scholar]
- National Disaster Information Center. Typhoon Maemi’s Damage. Available online: https://web.archive.org/web/20150924093447/http://www.safekorea.go.kr/dmtd/contents/room/ldstr/DmgReco.jsp?q_menuid=&q_largClmy=3 (accessed on 17 September 2025).
- Seo, S.N.; Kim, S.I. Storm Surges in West Coast of Korea by Typhoon Bolaven (1215). J. Korean Soc. Coast. Ocean Eng. 2014, 26, 41–48. [Google Scholar] [CrossRef]
- Munhwa Broadcasting Corporation. Available online: https://imnews.imbc.com/replay/2016/nw1500/article/4133688_30224.html#:~:text=%EB%8B%AB%EA%B8%B0 (accessed on 17 September 2025). (In Korean).
- Yonhap News Agency. Available online: https://science.ytn.co.kr/program/view.php?mcd=0082&key=2020090711443611297#:~:text=%EB%B9%84%EA%B3%B5%EC%8B%9D%20%EA%B8%B0%EB%A1%9D%EC%9D%B4%EC%A7%80%EB%A7%8C%2C%20%EC%A0%9C%EC%A3%BC%20%EC%82%B0%EA%B0%84%EC%97%90%20%ED%95%98%EB%A3%A8,1%2C000mm%EC%9D%98%20%ED%8F%AD%EC%9A%B0%EA%B0%80%20%EC%B2%98%EC%9D%8C%20%EA%B4%80%EC%B8%A1%EB%90%90%EC%8A%B5%EB%8B%88%EB%8B%A4 (accessed on 17 September 2025). (In Korean).
- National Fire Agency. Available online: https://www.nfa.go.kr/nfa/news/disasterNews/;jsessionid=nCcZd2oihNduR2POx2RrAiWG.nfa12?boardId=bbs_0000000000001896&mode=view&cntId=161424 (accessed on 17 September 2025).
- Tadesse, M.; Wahl, T.; Cid, A. Data-Driven Modeling of Global Storm Surges. Front. Mar. Sci. 2020, 7, 260. [Google Scholar] [CrossRef]
- Tian, Q.; Luo, W.; Tian, Y.; Gao, H.; Guo, L.; Jiang, Y. Prediction of storm surge in the Pearl River Estuary based on data-driven model. Front. Mar. Sci. 2024, 11, 1390364. [Google Scholar] [CrossRef]
- Ayyad, M.; Hajj, M.R.; Marsooli, R. Machine learning-based assessment of storm surge in the New York metropolitan area. Sci. Rep. 2022, 12, 19215. [Google Scholar] [CrossRef] [PubMed]
- Sadler, J.M.; Goodall, J.L.; Morsy, M.M.; Spencer, K. Modeling urban coastal flood severity from crowd-sourced flood reports using Poisson regression and Random Forest. J. Hydrol. 2018, 559, 43–55. [Google Scholar] [CrossRef]
- Sun, K.; Pan, J. Model of Storm Surge Maximum Water Level Increase in a Coastal Area Using Ensemble Machine Learning and Explicable Algorithm. Earth Space Sci. 2023, 10, e2023EA003243. [Google Scholar] [CrossRef]
- Yang, J.-A.; Lee, Y. Development of a Storm Surge Prediction Model Using Typhoon Characteristics and Multiple Linear Regression. J. Mar. Sci. Eng. 2025, 13, 1655. [Google Scholar] [CrossRef]
- Metters, D. (Ed.) Machine Learning to Forecast Storm Surge. Forum of Operational Oceanography, Melbourne. Available online: https://www.researchgate.net/publication/336779021_Machine_learning_to_forecast_storm_surge (accessed on 12 October 2019).
- Lee, Y.; Jung, C.; Kim, S. Spatial distribution of soil moisture estimates using a multiple linear regression model and Korean geostationary satellite (COMS) data. Agric. Water Manag. 2019, 213, 580–593. [Google Scholar] [CrossRef]
- Korea Hydrographic and Oceanographic Agency. Available online: https://www.khoa.go.kr (accessed on 25 July 2025).
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T-TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]
- Jensen, C.; Mahavadi, T.; Schade, N.H.; Hache, I.; Kruschke, T. Negative Storm Surges in the Elbe Estuary-Large-Scale Meteorological Conditions and Future Climate Change. Atmosphere 2022, 13, 1634. [Google Scholar] [CrossRef]
- Dinápoli, M.G.; Simionato, C.G.; Alonso, G.; Bodnariuk, N.; Saurral, R. Negative storm surges in the Río de la Plata Estuary: Mechanisms, variability, trends and linkage with the Continental Shelf dynamics. Estuar. Coast. Shelf Sci. 2024, 305, 108844. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J. Applied Linear Statistical Models, 5th ed.; McGraw-Hill: Irwin, ID, USA; New York, NY, USA, 2004. [Google Scholar]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Tras. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Sets; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Batista, G.E.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.-Y.; Mao, B.-H. (Eds.) Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- LemaÃŽtre, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A python toolbox to tackle the curse of imbalanced datasets in machine learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Mani, I.; Zhang, I. (Eds.) kNN approach to unbalanced data distributions: A case study involving information extraction. In Proceedings of the Workshop on Learning from Imbalanced Datasets; ICML: Washington, UT, USA, 2003. [Google Scholar]
- Tomek, I. Two modifications of CNN. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 769–772. [Google Scholar]
- Wilson, D.L. Asymptotic properties of nearest neighbor rules using edited data. IEEE Trans. Syst. Man Cybern. 1972, SMC-2, 408–421. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large rwer basin with point and nonpoint sources 1. J. Am. Water Resour. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
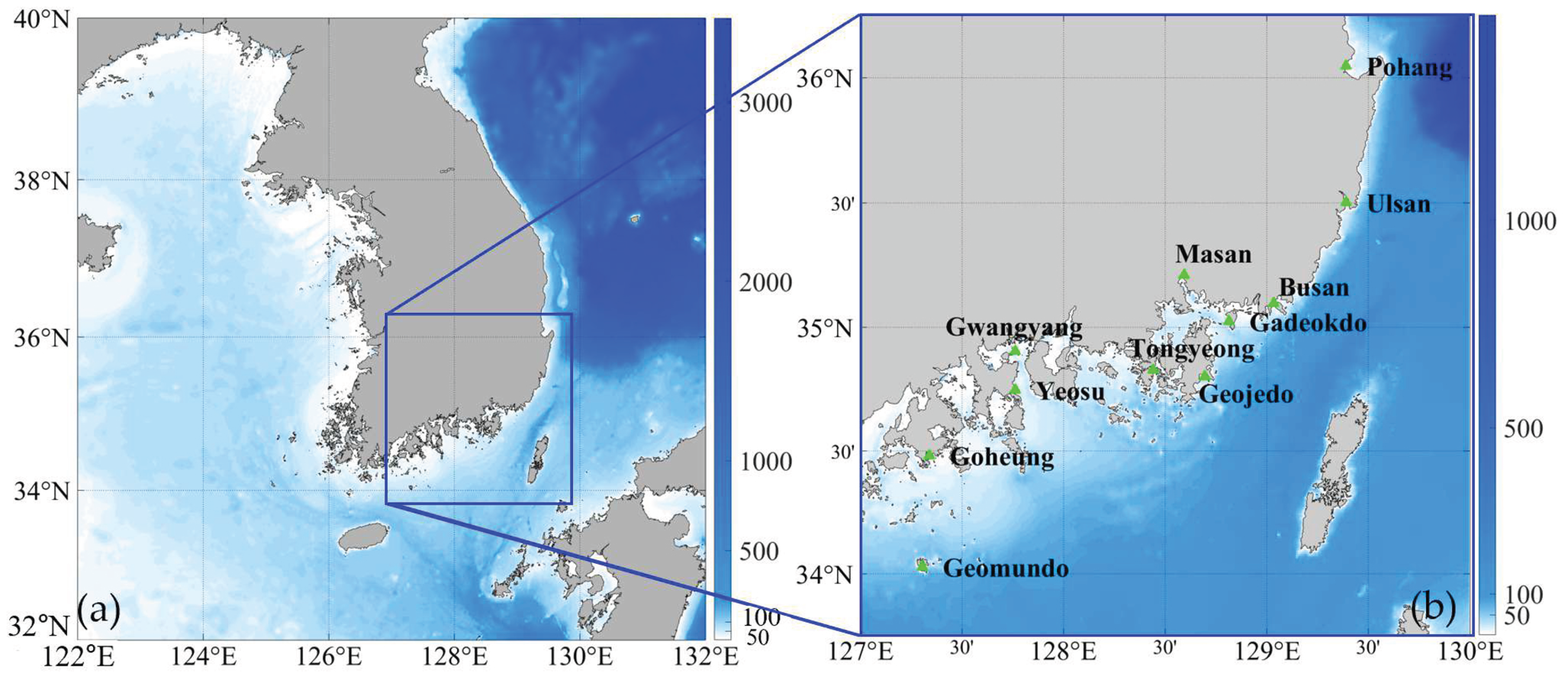



| Point Name | Longitude [°] | Latitude [°] |
|---|---|---|
| Geomundo | 127.308889 | 34.02833 |
| Goheung | 127.342778 | 34.48111 |
| Yeosu | 129.387222 | 35.50194 |
| Gwangyang | 127.754722 | 34.90361 |
| Tongyeong | 128.434722 | 34.82778 |
| Masan | 128.588889 | 35.21 |
| Geojedo | 128.699167 | 34.80139 |
| Gadeokdo | 128.810833 | 35.02417 |
| Busan | 129.035278 | 35.09639 |
| Ulsan | 127.765833 | 34.74722 |
| Pohang | 129.383889 | 36.04722 |
| Station | Storm Surge Height Threshold [m] | ||||
|---|---|---|---|---|---|
| 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | |
| Geomundo | 0.3927 | 0.4741 | 0.5526 | 0.6246 | 0.6164 |
| Goheung | 0.5559 | 0.6464 | 0.9435 | 0.6556 | 0.9687 |
| Yeosu | 0.392 | 0.5164 | 0.561 | 0.4905 | 0.5494 |
| Gwangyang | 0.6442 | 0.8293 | 0.699 | 0.8083 | 0.7436 |
| Tongyeong | 0.4603 | 0.5424 | 0.5036 | 0.5985 | 0.6365 |
| Masan | 0.333 | 0.2695 | 0.8562 | 0.8597 | 0.8457 |
| Geojedo | 0.6967 | 0.7585 | 0.5712 | 0.7775 | 0.698 |
| Gadeokdo | 0.5502 | 0.5987 | 0.6716 | 0.7942 | 0.7854 |
| Busan | 0.5295 | 0.6307 | 0.713 | 0.6901 | 0.7799 |
| Ulsan | 0.6343 | 0.6693 | 0.5489 | 0.8593 | 0.7388 |
| Pohang | 0.5512 | 0.7137 | 0.7904 | 0.7469 | 0.9318 |
| Total | 0.4355 | 0.4965 | 0.5708 | 0.5808 | 0.6255 |
| Station | Sampling Techniques (Over Sampling Technique–Under Sampling Technique) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ROS–Centroids | ROS–ENN | ROS–NearMiss | ROS–RUS | ROS–Tomek | Border–ENN | Border–RUS | SMOTE–ENN | SMOTE–RUS | |
| Geomundo | 0.5368 | 0.5956 | 0.2718 | 0.6246 | 0.5847 | 0.6202 | 0.5960 | 0.6078 | 0.5960 |
| Goheung | 0.6641 | 0.7692 | 0.4306 | 0.6556 | 0.7667 | 0.8235 | 0.6552 | 0.7892 | 0.6552 |
| Yeosu | 0.4611 | 0.5595 | 0.2125 | 0.4905 | 0.5489 | 0.5849 | 0.4977 | 0.5908 | 0.4977 |
| Gwangyang | 0.8960 | 0.8226 | 0.9059 | 0.8083 | 0.8199 | 0.8400 | 0.7360 | 0.8357 | 0.7360 |
| Tongyeong | 0.5234 | 0.5979 | 0.1649 | 0.5985 | 0.5879 | 0.6404 | 0.5813 | 0.6413 | 0.5813 |
| Masan | 0.6329 | 0.7817 | 0.4353 | 0.8597 | 0.7724 | 0.8217 | 0.8770 | 0.8027 | 0.8770 |
| Geojedo | 0.9599 | 0.8196 | 0.9510 | 0.7775 | 0.8167 | 0.8387 | 0.6082 | 0.8350 | 0.6082 |
| Gadeokdo | 0.6276 | 0.7076 | 0.2998 | 0.7942 | 0.6978 | 0.7388 | 0.7860 | 0.7188 | 0.7860 |
| Busan | 0.6513 | 0.6983 | 0.3990 | 0.6901 | 0.6910 | 0.7210 | 0.6974 | 0.7161 | 0.6974 |
| Ulsan | 0.8712 | 0.6288 | 0.3518 | 0.8593 | 0.6283 | 0.6647 | 0.8266 | 0.6571 | 0.8266 |
| Pohang | 0.7984 | 0.7534 | 0.3224 | 0.7469 | 0.7510 | 0.7790 | 0.7509 | 0.7801 | 0.7509 |
| Total | 0.4894 | 0.5614 | 0.0802 | 0.5808 | 0.5534 | 0.5691 | 0.5681 | 0.5870 | 0.5681 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.-A.; Lee, Y. Performance Improvement of a Multiple Linear Regression-Based Storm Surge Height Prediction Model Using Data Resampling Techniques. J. Mar. Sci. Eng. 2025, 13, 2173. https://doi.org/10.3390/jmse13112173
Yang J-A, Lee Y. Performance Improvement of a Multiple Linear Regression-Based Storm Surge Height Prediction Model Using Data Resampling Techniques. Journal of Marine Science and Engineering. 2025; 13(11):2173. https://doi.org/10.3390/jmse13112173
Chicago/Turabian StyleYang, Jung-A, and Yonggwan Lee. 2025. "Performance Improvement of a Multiple Linear Regression-Based Storm Surge Height Prediction Model Using Data Resampling Techniques" Journal of Marine Science and Engineering 13, no. 11: 2173. https://doi.org/10.3390/jmse13112173
APA StyleYang, J.-A., & Lee, Y. (2025). Performance Improvement of a Multiple Linear Regression-Based Storm Surge Height Prediction Model Using Data Resampling Techniques. Journal of Marine Science and Engineering, 13(11), 2173. https://doi.org/10.3390/jmse13112173







