Experimental Investigation of a Novel Single-Shank Drag Anchor Design

Abstract

Drag embedment anchor (DEA) constitutes a compelling anchoring solution for an array of floating structures, attributable to its exceptional efficiency in holding capacity and the comparatively modest expenditures incurred in manufacturing and installation. The holding capacity of DEAs is, to a large extent, dictated by the penetration depth achieved during installation. In hard soils, such as dense sand and stiff clay, the penetration depth of DEAs is often limited due to the large soil resistance acting on the shank structure, which in turn limits its holding capacity. In this paper, a novel anchor design with a single flat shank is proposed, which can greatly reduce the soil resistance on the shank during installation, in the hope of improving the penetration depth and consequently the holding capacity of DEAs. To verify this design assumption, a comprehensive suite of large deformation numerical simulations is carried out in both clayey and sandy soils. In addition, a series of physical model tests are performed in uniform sand. The results from both the numerical simulations and the model tests confirm the superior penetrability and holding capacity of the proposed single-shank anchor design.

1. Introduction

Exploitation of marine resources and development of offshore renewables have significantly prompted the deployment of a range of floating structures, such as floating mobile offshore drilling units (MODUs), Floating Production Storage and Offloading Systems (FPSOs), and floating offshore wind turbines (FWTs) [1,2]. A mooring system, which consists of mooring lines and anchors, is a critical component for the station keeping of floating structures against a variety of environmental loads. Drag embedment anchor (DEA) is widely utilized in catenary mooring systems and distinguishes itself from other anchor types with advantages in high holding capacity efficiency, low fabrication cost, and relatively cheap installations [3,4]. For this reason, drag anchors are widely used for securing floating offshore structures.

However, the application of DEAs in hard soils such as dense sand and stiff clay is limited due to its shallow ultimate embedment depth (UED) induced by the difficulty in penetration. During installation, the drag anchor is firstly lowered from the installation vessel to the seabed, where the penetration angle (θ, as illustrated in Figure 1) is relatively large. Through the horizontal movement of the anchor chain, which is towed by an anchor-handling vessel (AHV) or through the cross-tensioning of two counteracting anchors, the drag anchor gradually penetrates the seabed. The increase in embedment depth is usually accompanied by changes in the anchor’s posture. Figure 1 illustrates the typical penetration trajectory of a drag anchor, where the anchor is shown to gradually rotate anticlockwise as it gains penetration.

Limit equilibrium studies by Neubecker and Randolph [5,6] have shown that the forces acting on the drag anchor during installation consist of the fluke force F_f, the shank force F_s, the chain tension T_a, the anchor self-weight W_a, and the force behind the fluke F_fb, as illustrated in Figure 2. It has been found in both numerical and experimental studies that the increase in soil strength increases the resistance acting on the shank (i.e., F_s), which accelerates the rotation of the DEA (i.e., θ decreases faster) during the dragging process, leading to a smaller ultimate embedment depth and consequently reduced ultimate holding capacity [7,8,9,10].

Based on this knowledge, a novel single-shank drag anchor design is proposed, which is illustrated in Figure 3c. Compared with conventional double-shank drag anchor designs, such as the Vryhof MK6 anchor [11] illustrated in Figure 3a, the two inclined shanks connected by several bracing plates are replaced with a single flat shank. The assumption is that by reducing the soil resistance acting on the shank structure, the rotation of the anchor can be slowed down in hard soils, thereby increasing the penetrability and ultimately the holding capacity.

The purpose of the current study is to explore the soundness of the above assumption. Firstly, a series of large-deformation finite element (LDFE) numerical simulations were carried out using the Coupled Eulerian–Lagrangian (CEL) method. Comparative installation simulations for three anchor designs, including the conventional double-shank anchor (DSA), the single-shank anchor (SSA), and the double-shank anchor with no bracing (DSANB, Figure 3b), were carried out in a range of clayey and sandy soils. To confirm the numerical observations, a series of carefully designed model tests exploring the same group of anchor designs were subsequently conducted in uniform sand. This paper reports the results of the numerical simulations and the physical model tests, which all confirm the above assumptions.

2. Methodology

The methodologies adopted in the current study are elaborated on in this section, including the numerical modeling method and parameter settings of the large-deformation finite element model and the set-up of the physical model experiments.

2.1. Coupled Eulerian–Lagrangian Method

A numerical analysis model was established in general finite element software Abaqus 2017 [12]. The conventional Lagrangian finite element method can only handle small deformations due to the non-convergence induced by element distortion. To solve this problem, the Coupled Eulerian–Lagrangian (CEL) method was developed and has become a powerful tool in analyzing large-deformation problems [13,14,15]. The CEL method has been utilized in a variety of geotechnical engineering applications, such as the excavation of deep soft rock tunnels [16], spudcan installation [17,18], ship anchor dragging [19], cone penetration tests, submarine pipeline buckling, and free-fall penetrometer tests [20]. Its efficiency and accuracy in simulating practical engineering problems have already been extensively demonstrated. For this reason, the CEL method was applied in the current study to simulate the installation process of drag embedment anchors (DEAs). The DEAs and anchor chains are defined as Lagrangian bodies, while the soil domain is defined as a Eulerian body. In this way, the physical boundaries and motions of DEAs and chain units can be precisely tracked as Lagrangian bodies, and the soil can flow ‘freely’ in a preconfigured Eulerian mesh, preventing the problem of element distortion.

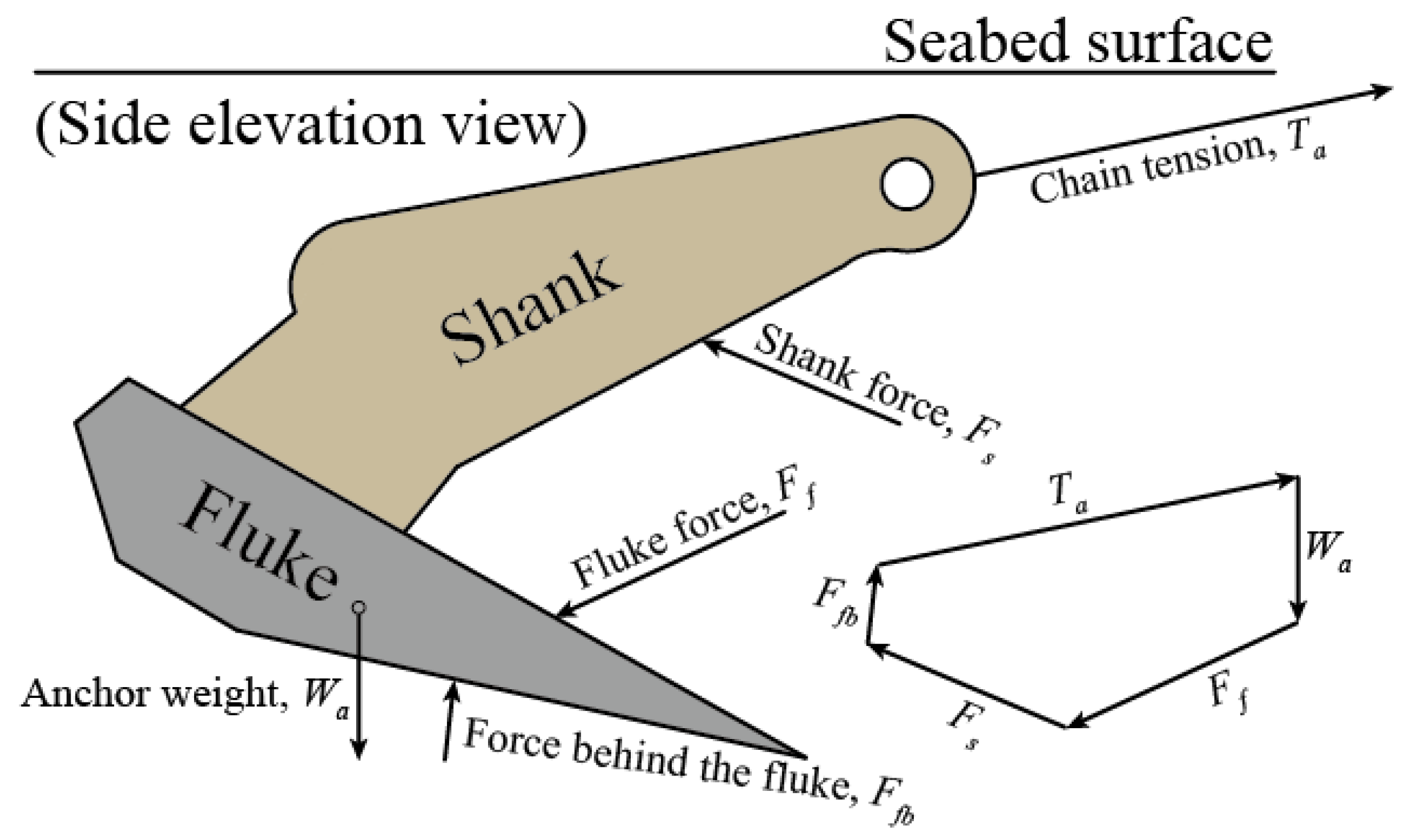
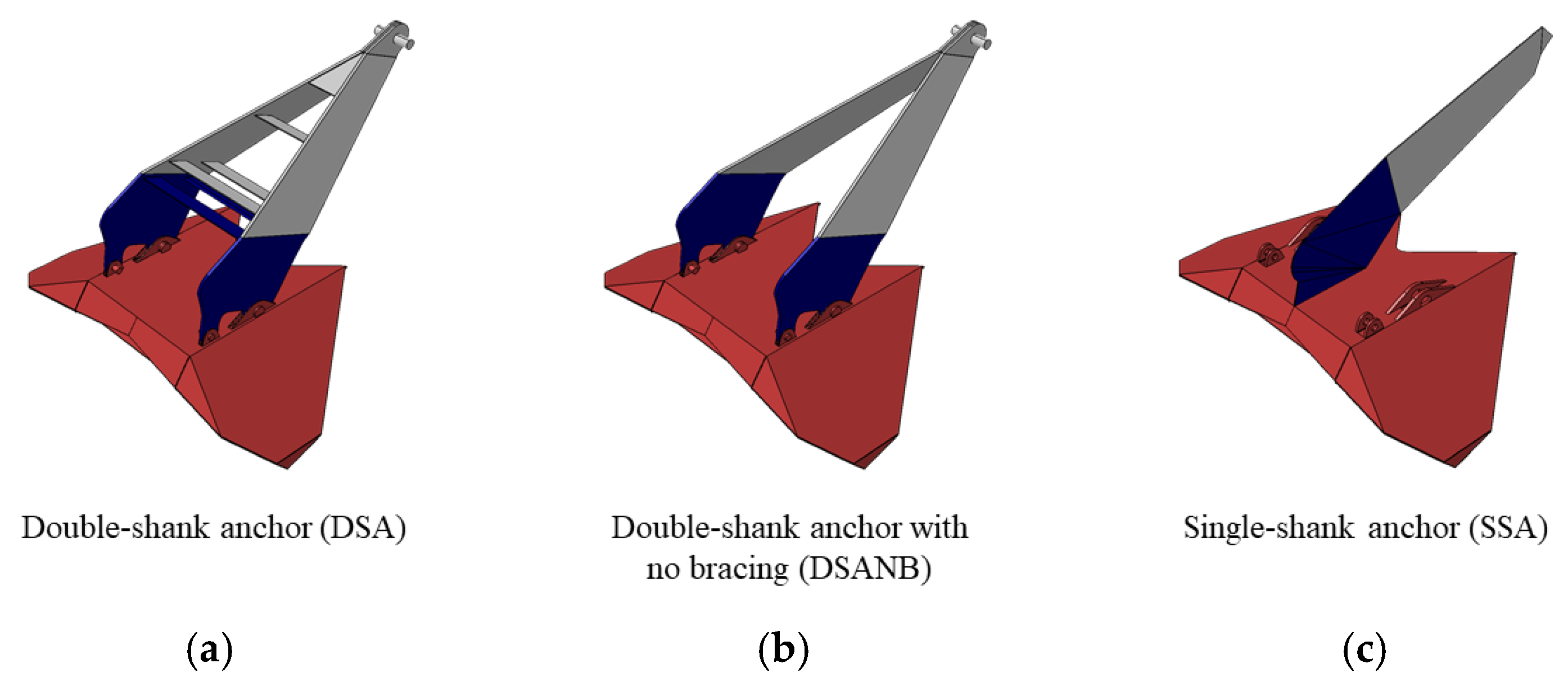
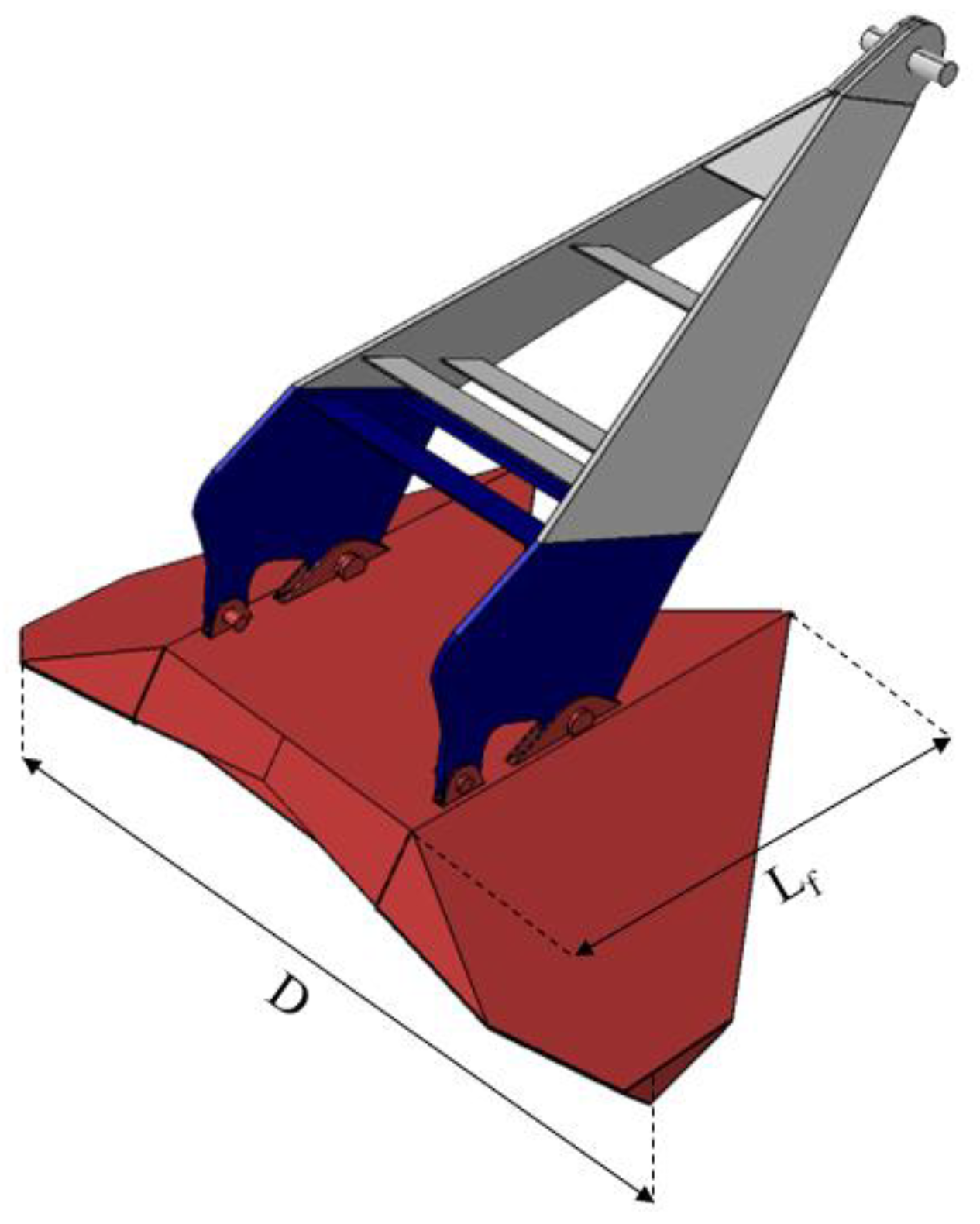
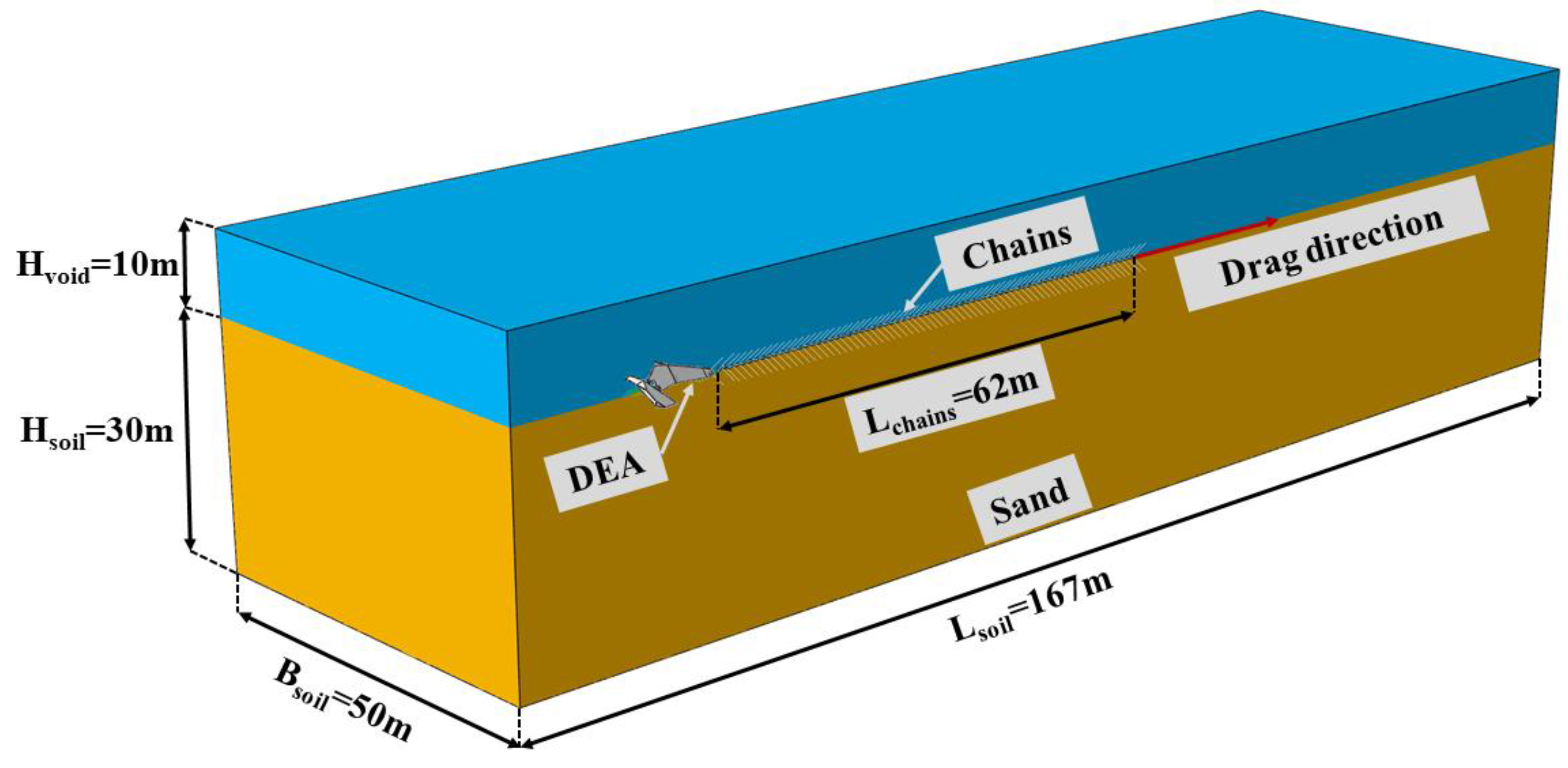
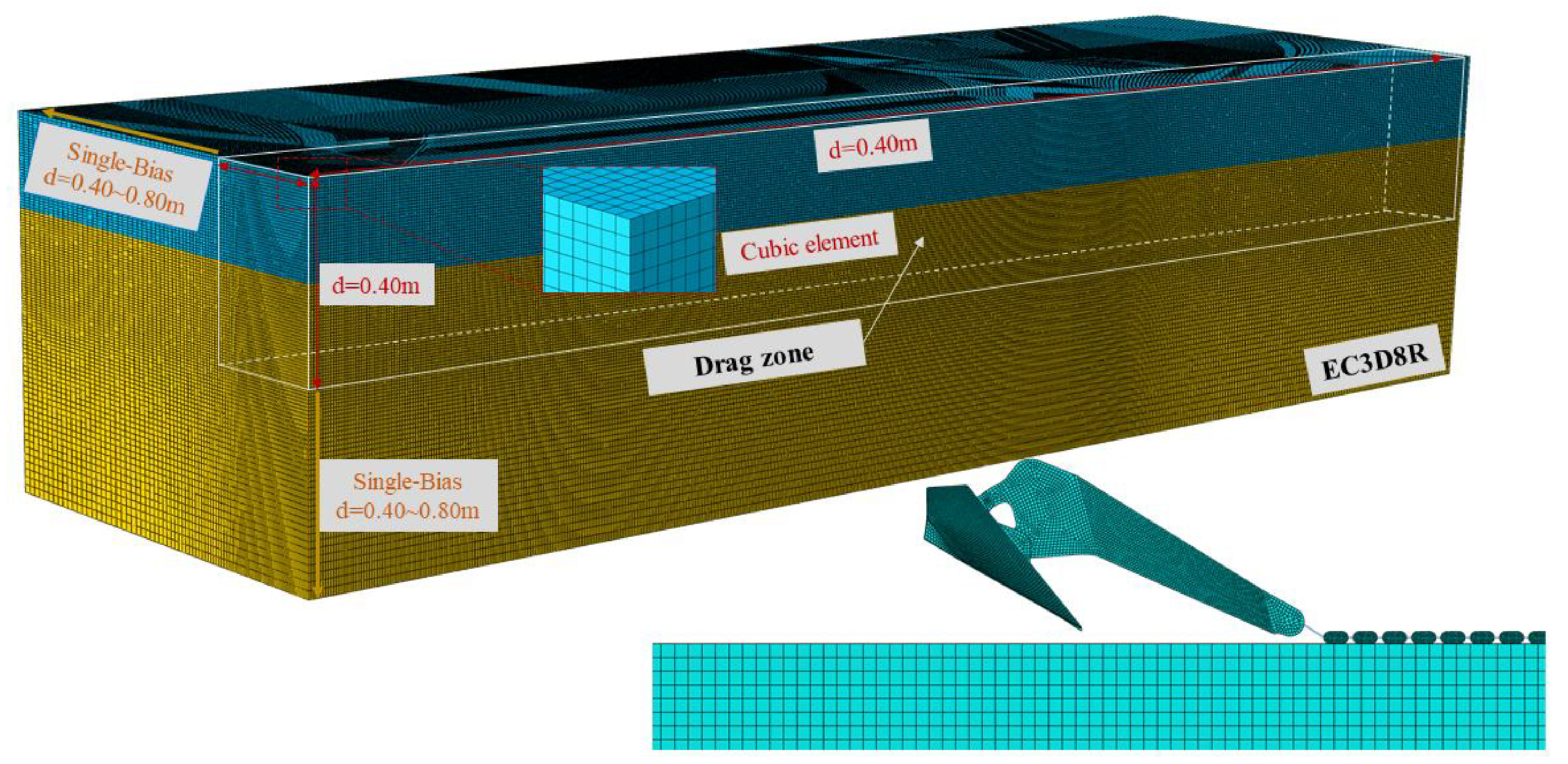
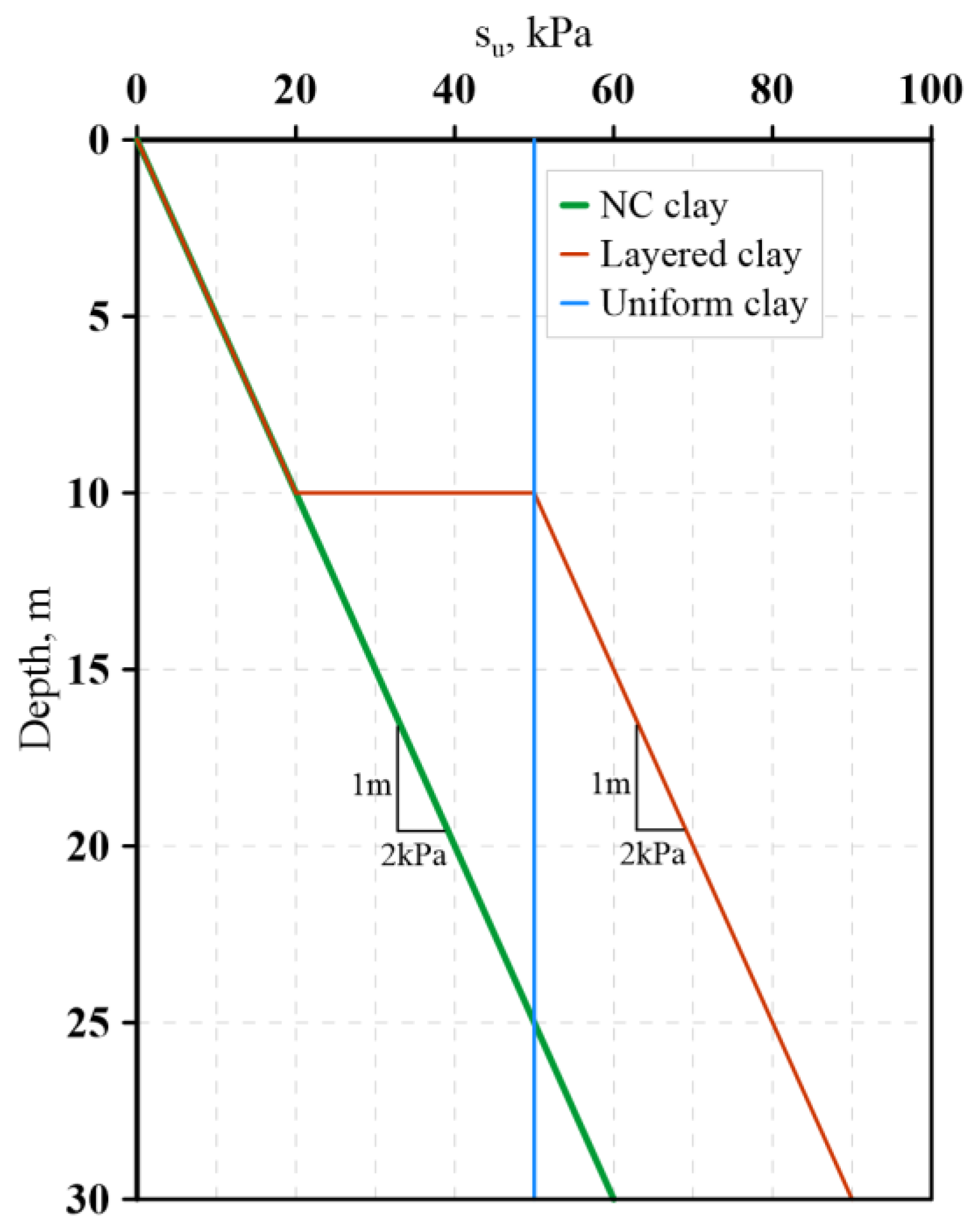
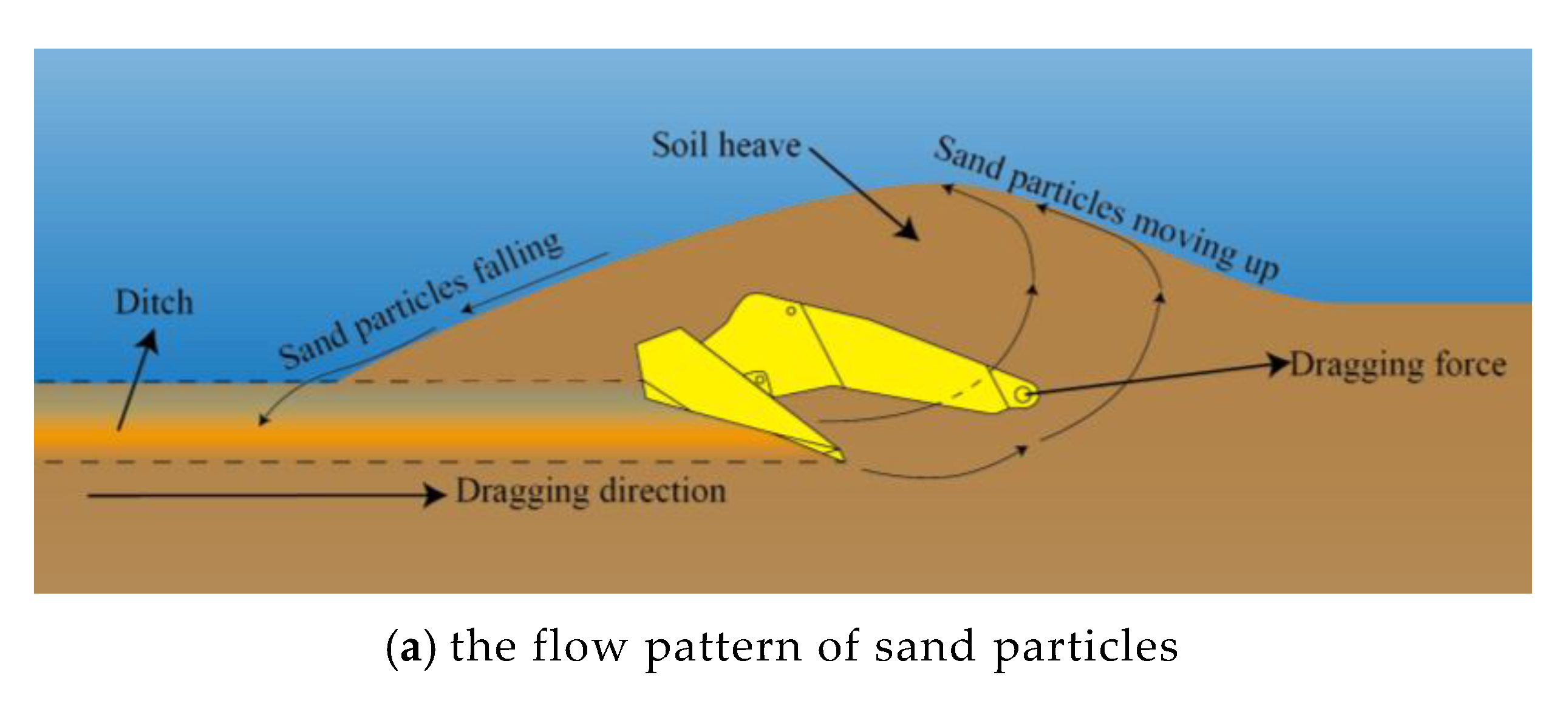
2.2. Simulation of the Drag Anchor and the Seabed Soil

Figure 3 illustrates the three anchor designs examined in CEL simulations: the double-shank anchor (DSA), the double-shank anchor with no bracing (DSANB), and the currently proposed single-shank anchor (SSA). The shape and dimensions of the DSA are based on a Vryhof Stevpris MK6 anchor [11] with a dry weight of 50 tonnes. The fluke length (L_f) is 6.42 m and the fluke width (D) is 10.11 m, as shown in Figure 4. The DSANB has the same dimensions as the DSA but with all the braces between the inclined shanks removed. Similarly, The SSA is obtained by replacing the inclined shanks of DSA with a flat plate shank on the symmetric plane.

In order to minimize the effects of mass properties among the three anchor designs, as illustrated in Figure 3, different material densities were calculated and assigned to different parts of the anchor (as indicated by the color shading in Figure 3), aiming to keep the mass centroid of the anchors at the same position. Although small mass differences (about 10%) still exist among the three anchors, they are expected to only have minimal influence on the overall performance of DEAs, according to O’Neill [7].

The ultimate embedment depth and holding capacity of drag anchors are strongly influenced by the fluke–shank angle, θ_fs (i.e., the angle between the fluke and shank, as illustrated in Figure 5). Three fluke–shank angles are commonly used in practice for various soil conditions:

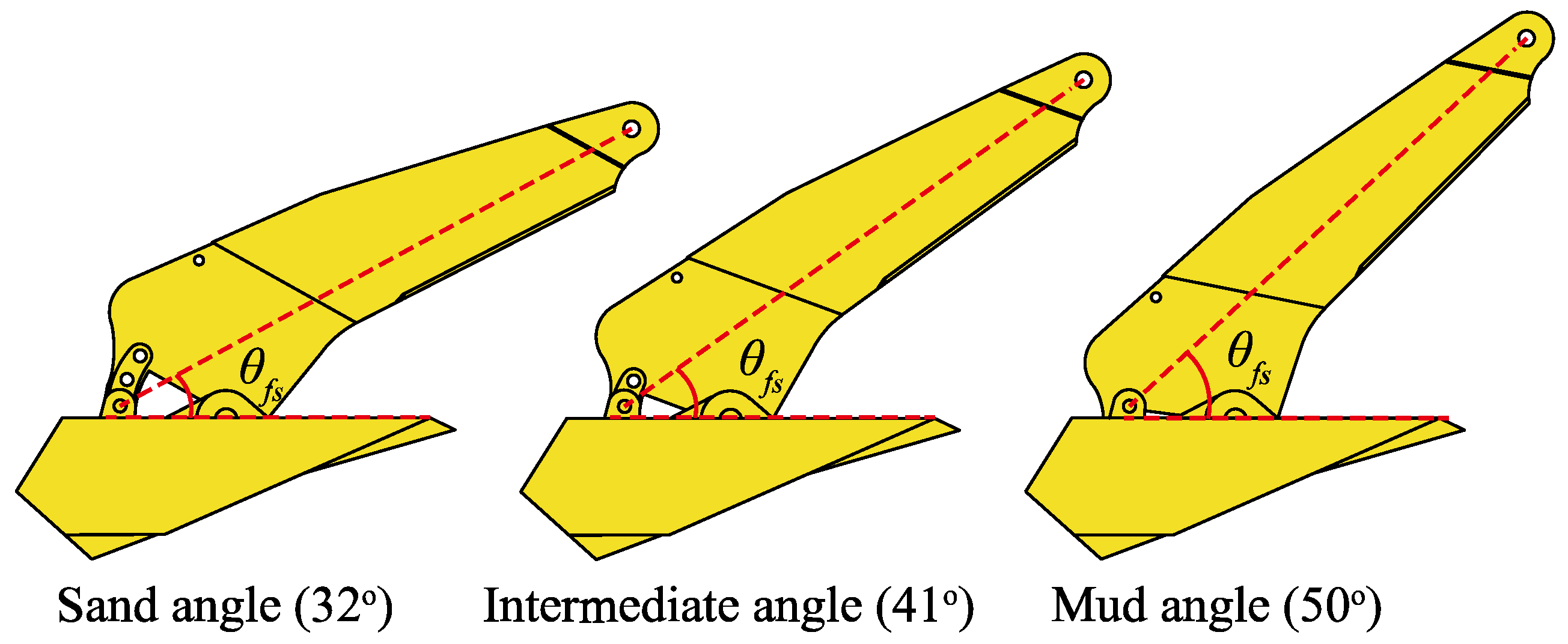
• θ_fs = 32°: in sand and medium to hard clays;
• θ_fs = 41°: in layered or complex soil conditions;
• θ_fs = 50°: in soft clay.

In the current numerical simulations, two fluke–shank angles were considered, the mud angle (θ_fs = 50°) in clayey seabed and the sand angle (θ_fs = 32°) in sandy seabed.

Figure 6 illustrates the overall set-up of CEL models, which include the soil domain, the drag anchor, and the chains. The dimensions of the Eulerian domain were 167 m, 50 m, and 40 m, respectively, for the length, width, and depth, which were found to be large enough to avoid the boundary effects according to a parametric sensitivity analysis [21]. The upper 10 m of the Eulerian domain was void with no material assignment, while the remaining part of the Eulerian domain was filled with soil at the beginning of the simulation. In order to reduce computational time, only half of the problem was modeled, taking advantage of the symmetry of this process.

The Eulerian domain was discretized with EC3D8R elements, and the anchor and chains were meshed with C3D8R elements. Figure 7 illustrates the mesh of the Eulerian domain. The mesh size (d) of the cubic soil elements in the Eulerian domain in the vicinity of the anchors’ trajectory (marked as the drag zone in Figure 7) was set to 0.4 m so that the movement of the soil was accurately captured. For numerical efficiency, the mesh was singe-biased away from the drag zone, which means that the mesh becomes progressively coarser in directions away from the drag zone. The size of the element increases from 0.4 m at the boundary of the drag zone to 0.8 m at the boundaries of the Eulerian domain. Parametric sensitivity analyses indicate that the currently adopted mesh was optimized in terms of numerical efficiency and accuracy [21].

In order to fully explore the performance of the currently proposed single-shank design, installation analyses were performed in both clayey and sandy seabed. The clayey soils were modeled using the elastic-perfect plastic Tresca model, which is described with a submerged unit weight (γ′), an undrained shear strength (s_u), Young’s modulus (E), and Poisson’s ratio (µ). In the simulations reported in this study, E = 200 s_u and µ = 0.49 were adopted. Three different undrained shear strength profiles were considered: a normally consolidated (NC) clay with s_u linearly increasing with depth, a layered profile with normally consolidated clay in the upper 10 m underlain with over-consolidated clay, and a uniform (over-consolidated) clay with a constant s_u with depth. The three clay profiles are illustrated in Figure 8. The effective unit weight γ′ was taken to be 6.5 kN/m³ for the normally consolidated clay, 8 kN/m³ for the uniform (over-consolidated) clay, and 9.8 kN/m³ for the lower layer of the layered profile.

The variation in s_u and E with depth was achieved using a predefined field in Abaqus. In this case, a temperature field was defined, whose value was set equal to the soil depth. In the Abaqus material property definition, the undrained shear strength and Young’s modulus are defined to vary with the field variable. Note that in the simulations of the NC and the layered profiles, a s_u of 0.1 kPa was assigned to the mudline in order to avoid numerical instabilities.

Sandy soil was modeled using the Mohr–Coulomb model, which is described with the submerged unit weight (γ′), internal friction angle (φ), cohesion (c), Young’s modulus (E), and Poisson’s ratio (µ). In this study, a sand profile with φ = 30° was considered, while γ′ = 9.8 kN/m³, c = 1 kPa, E = 12 MPa, and μ = 0.3 were adopted.

In summary, five sets of comparative analyses were performed, and each set included three CEL simulations corresponding to three anchor geometries (Figure 3). Set 1 corresponds to a normally consolidated clay (NC clay) profile; Set 2 corresponds to a layered clay profile; Set 3 corresponds to a uniform (over-consolidated) clay profile; and Set 4 corresponds to a homogeneous sand profile with φ = 30°.

It typically took about 48 to 96 h for a single simulation with parallel computing using 64 cores (2.3 GHz) and 224 GB RAM, depending on the type and strength of the soil. Simulations in sand required more time than those in clay, and simulations in hard soil consumed more time than in soft soil.

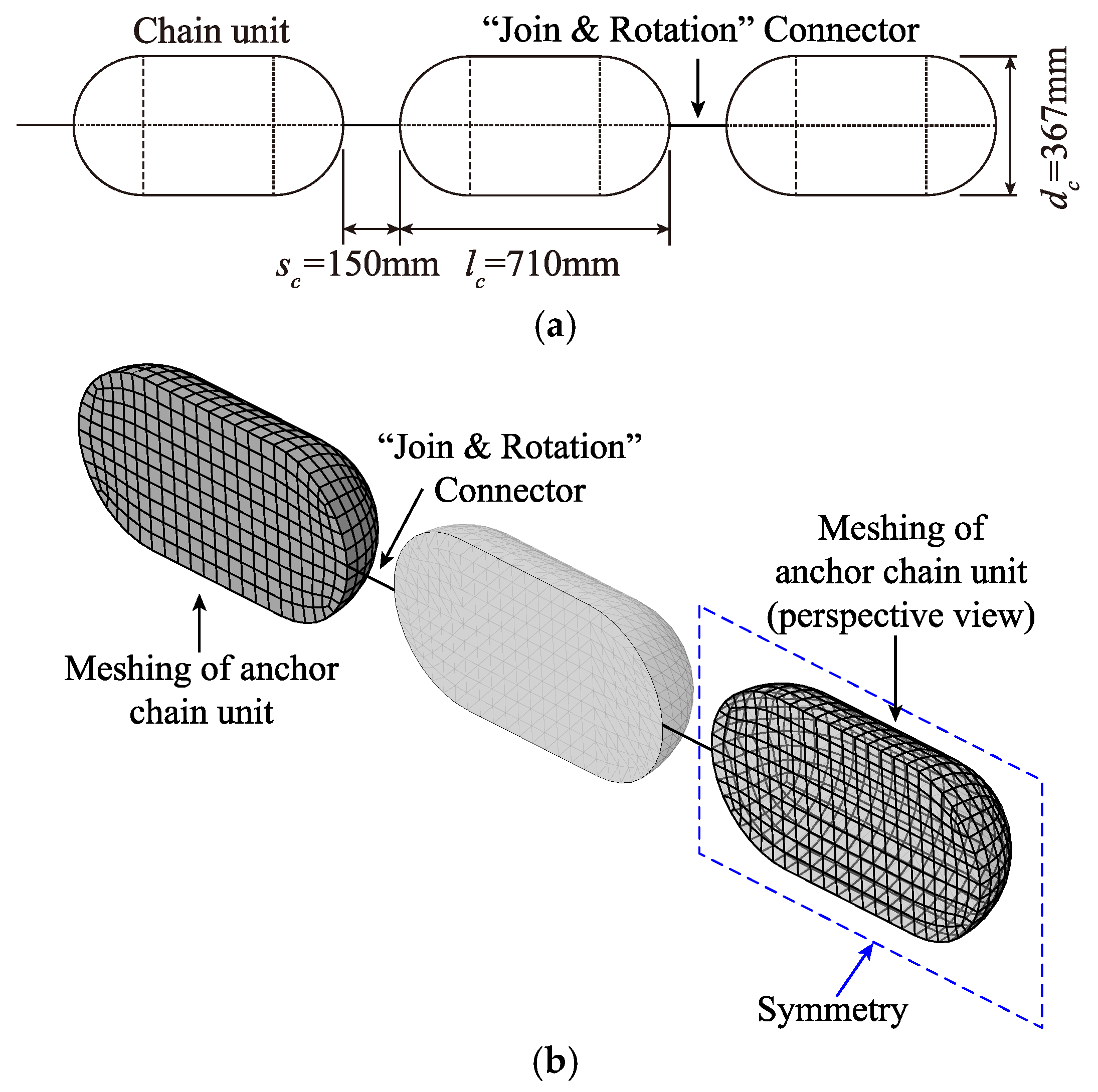
2.3. Simulation of the Chain

In order to accurately simulate the entire installation process of DEAs in the seabed, the chains were simulated, and their interaction with soils was taken into consideration. Based on the method proposed in [21], which is an improvement of the method proposed in [9,22] the R3S142 studless mooring chain unit was simplified into a series of evenly spaced round-ended cylinders joined using “Join + Rotation” connectors in Abaqus/Explicit (Figure 9). The dimensions of the simplified anchor chain unit are presented in Figure 9a. In this study, 70 anchor chain units were simulated with a total length of 60 m. Based on weight equivalency, the submerged unit weight of the chains’ material was set to 37.66 kN/m³.

2.4. Analysis Steps and Boundary Conditions

There are in total three analysis steps involved in each simulation, and the details are described below:

(1)

The “geostatic” step. The purpose of this step is to generate the initial stress field within the soil domain.

(2)

The “initialization” step. Gravity is activated on the anchor and the chains in this step, and the anchor achieves a small initial penetration due to its weight.

(3)

The “drag” step. A horizontal pulling velocity is applied to the last chain unit, and the anchor penetrates the seabed under the pulling motion.

The boundary conditions and interactions among the DEA, the chain units, and the soil in the CEL model are detailed below:

• For the Eulerian domain, side boundaries (including the bottom of the soil) are prescribed with a zero-velocity boundary condition normal to the surfaces.
• A Eulerian outflow boundary with a “no reflection” option is applied on the side boundaries of the Eulerian domain (except the bottom of the soil). This is essential for modeling infinite domains.
• The vertical symmetry plane of the model is assigned a symmetry boundary condition.
• A constant drag velocity is prescribed at the reference point (RP) of the last chain unit, which aims to simulate the dragging of the anchor-holding vehicle in practical engineering.
• The contact between the DEA and the soil, and the chain units and the soil, is defined using “general contact”. The tangential behavior follows the Coulomb friction law, with a friction coefficient of 0.5. The normal behavior is defined as “hard contact, allow separation after contact”.

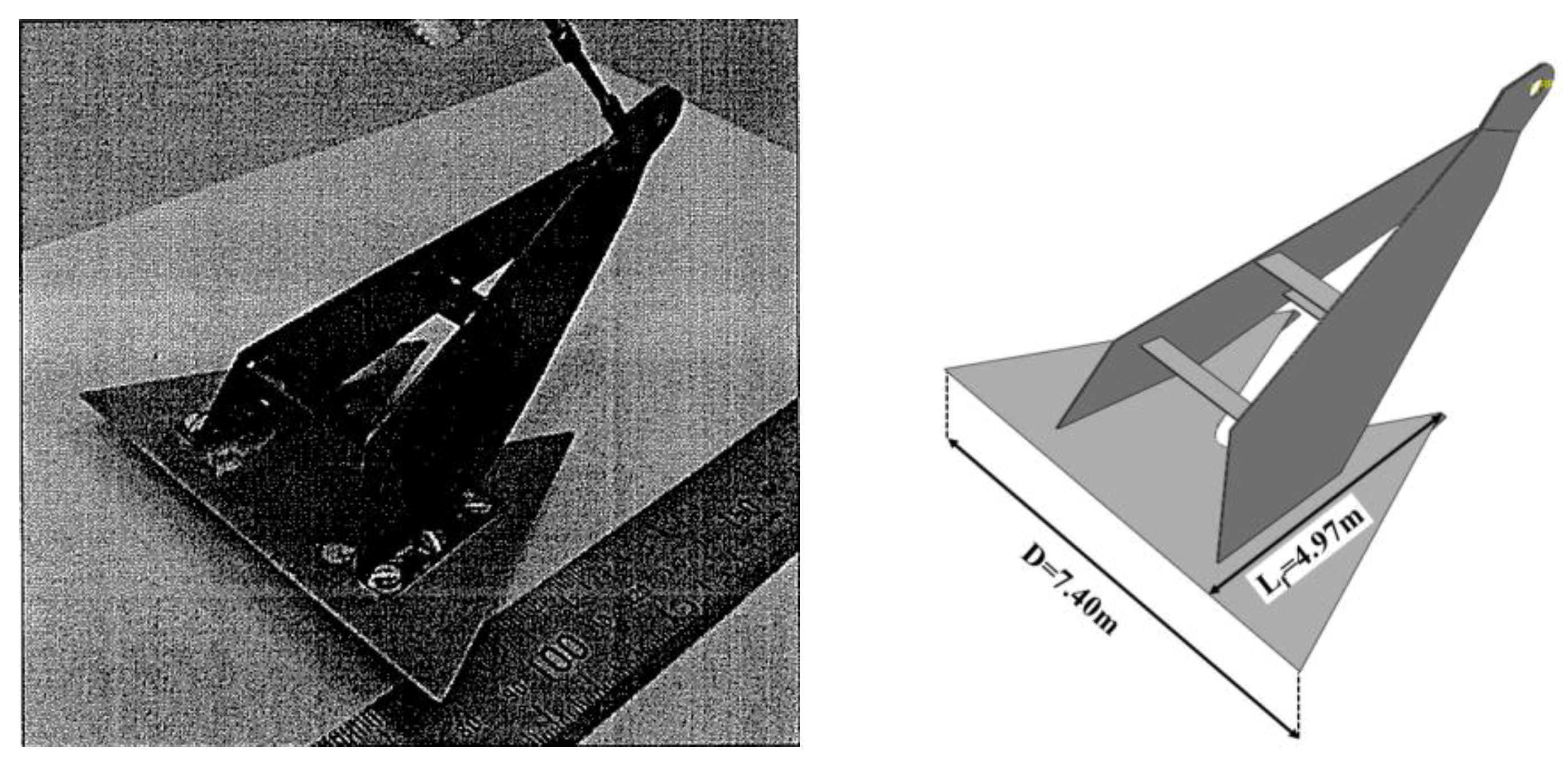
2.5. Verification of the CEL Method Against Centrifuge Test

A series of centrifuge tests were conducted at UWA and reported in [7]. The centrifuge tests covered a range of soils, including kaolin clay, silica sand, and calcareous sand, which provide a suitable benchmark for the current study. To validate the numerical model, a centrifuge test carried out in calcareous sand was backanalyzed using the proposed CEL method. A 1:80 model of a 32t Vryhof Stevpris anchor with a fluke–shank angle θ_fs of 32° was adopted in the centrifuge test (Figure 10), and the numerical model was developed with the prototype geometry of the centrifuge test, as illustrated in Figure 10. In the centrifuge test, the DEA was firstly placed at one end of the test pit with an initial pre-embedment and a penetration angle (θ) of 38°, as illustrated in Figure 11a. The test was performed by applying a dragging motion to the anchor. The calcareous sand used in the centrifuge tests was modeled using the Mohr–Coulomb model. A friction angle of 42.7° and a submerged unit weight of 8.33 kN/m³ were selected according to [7], and Young’s modulus (E = 12 MPa) and Poisson’s ratio (μ = 0.3) were empirically determined. A velocity boundary condition (v_c = 0.2 m/s) was applied at the end of the chains, pulling the anchor into the soil. Figure 11b illustrates the conditions around the anchor with a drag distance of 20 m.

Figure 12 compares the results of the centrifuge test and CEL simulation. Anchor efficiency was calculated as η_a = T_a/W_a, where T_a represents the dragging force at the padeye, and W_a stands for the weight of the anchor. The horizontal padeye drag length x_a and embedment depths of padeye (d_a) and fluke tip (d_t) are normalized by the fluke length L_f. The results reveal overall good agreement between the centrifuge test and the CEL simulation, which verifies the reliability of the CEL method.

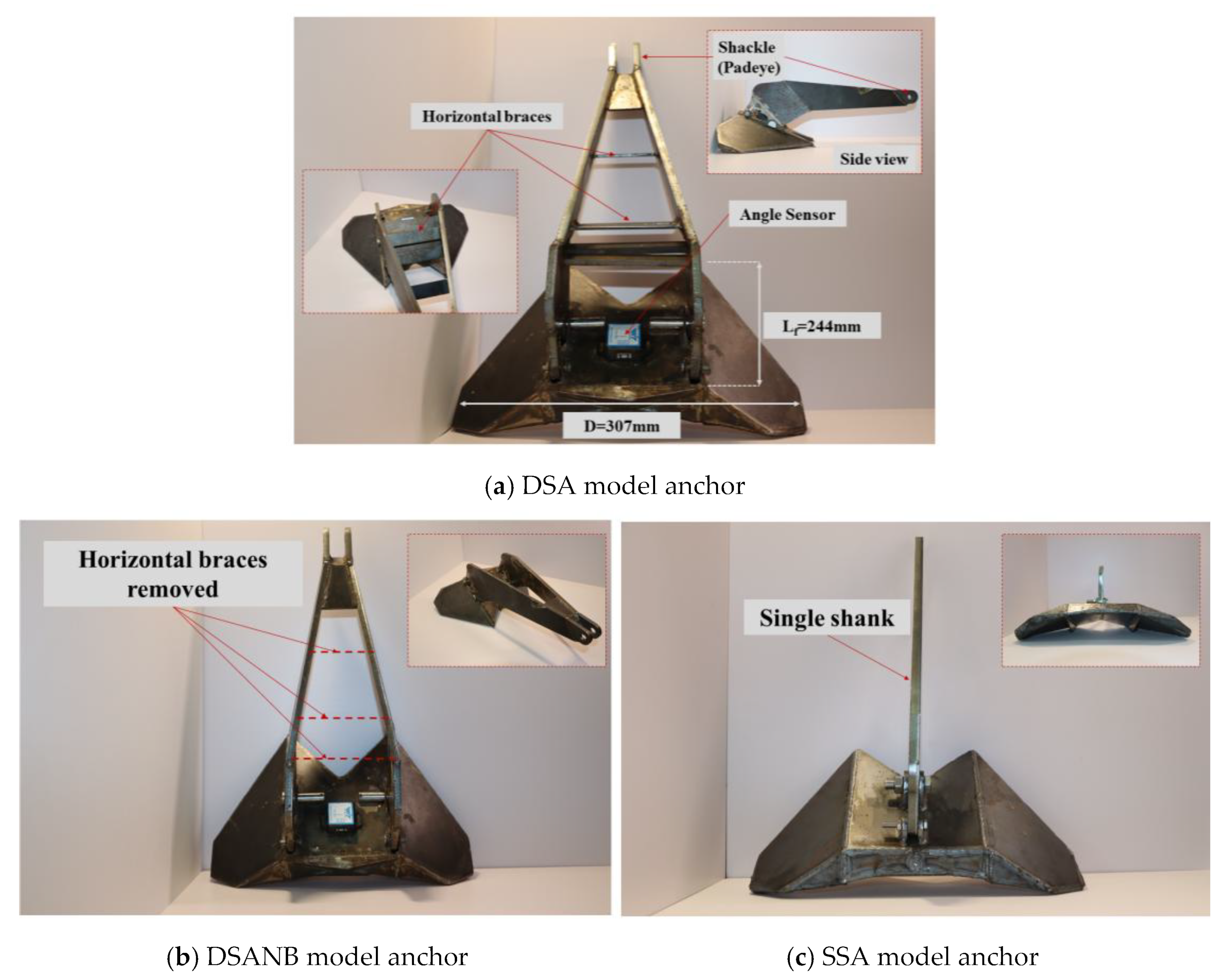
2.6. Set-Up of Model Tests in Sand

In order to confirm the observations seen in the numerical simulations, a series of three scaled physical model tests were conducted at Southeast University. The physical model tests examined the same three anchor designs investigated in the numerical simulations. The double-shank anchor (DSA) model (shown in Figure 13a) was scaled from a 25-tonne Vryhof Stevpris MK6 anchor with a scaling factor of 30. The fluke length (L_f) was 244 mm, and the fluke width (D) was 307 mm. The double-shank anchor with no bracing (DSANB, Figure 13b) and single-shank anchor (SSA, Figure 13c) share the same fluke as the DSA model. The mass of the model anchor was 6.55 kg, 6.03 kg, and 5.74 kg for the DSA, DSANB, and SSA, respectively. This is heavier than what should be scaled from a 25-tonne prototype with a scaling factor of N³ and N = 30, which gives about 1 kg. This mismatch is mainly due to fabrication constraints. However, in the context of drag embedment anchors (DEAs) used in marine engineering, the mass of the anchor exerts minimal influence on its dynamic response during the drag installation process. This is primarily because the anchor’s trajectory, embedment depth, and ultimate holding capacity are dominated by soil resistance forces—driven by factors such as the undrained shear strength of the seabed soil, fluke–shank angle, and anchor line geometry—rather than the anchor’s inertial weight. For instance, comparative analyses of lightweight (e.g., acrylic) versus heavier (e.g., steel) anchor models show only slight initial differences in line tension and penetration, which quickly converge to equilibrium behavior governed by soil interaction, with the anchor’s unit weight being comparable to or overshadowed by the surrounding soil [23].

As for the chain, considering an R3S studless chain with a diameter of 142 mm in the prototype results in a chain with a diameter of 4.7 mm at model scale. For the model tests, a studless chain with a 6 mm diameter was selected, which is available off the shelf.

The set-up for the model tests is illustrated in Figure 14. The dimensions of the testing pit were 3660 mm for length, 3660 mm for width, and 600 mm for height. In total, three drag channels were planned in one soil sample, and the distribution is shown in Figure 14b. At the start of each test, the model anchor was placed on the surface of the sand sample near one end of the testing pit, 500 mm away from the end boundary. Anchor chains were linked to the shackle (padeye) of the model anchor and run horizontally on the sand surface along the dragging direction. A winch was located 8 m from the end of the testing pit and positioned in such a way that a purely horizontal pulling action was applied to the chain. A load cell (with a capacity of 10 kN and a resolution of 0.1 kN) was connected between the end of the chains and the steel wire of the winch. The drag force measured with the load cell was recorded using a data logger and a computer. An angle sensor (Figure 13) was installed at the center of the fluke for DSA and DSANB tests to monitor the change in the fluke angle during the penetration process. However, the angle sensor was not used in the SSA test as the space was occupied by the single-shank connection to the fluke. A relatively low dragging velocity of 1.68 m/min, which is the lowest achievable velocity by the winch, was adopted in the experiments, resulting in an essentially quasi-static installation process. Note that no attempt was made to match what should be scaled from the actual dragging velocity in the field or from the numerical simulations. This is because as long as the dragging velocity is slow enough to ensure a quasistatic dragging process, it does not influence the test results.

The sand used in the model tests was sampled and tested in the laboratory, with its physical parameters summarized in

Table 1. Physical and mechanical parameters of testing sand.

d10 mm	d50 mm	Dry Density γd, (g·cm−3)	Water Content w, %	Relative Density Dr, %	Internal Friction Angle φ, °
0.13	0.30	1.473	0.93	33	35.85

. The sand was almost dry with an internal friction angle of 35.85 degrees measured with triaxial compression tests. In general, φ tends to decrease slightly as stress increases, due to factors like reduced dilatancy, changes in particle interlocking, and stress-path dependencies in granular assemblies. In the current study, the internal friction angle was measured at the prototype-scale stress level and may be smaller than that at the model scale. To be specific, triaxial tests of this kind of sand cannot be carried out at the model-scale stress level due to sample preparation problems, and the prototype internal friction angle is used here for reference. The testing bed was prepared via stratified tamping. The testing bed was prepared layer by layer for a total of four layers, and each layer had a target height of 15 cm. According to the target relative density (33%) and target height of each layer, the mass of sand for each layer was calculated. After evenly placing the correct amount of sand in the testing pit, a hand-held tamping machine was used to temp the sand to the target height. The surface of the sand was then roughened with a rake and another sand layer was prepared above it until the whole testing bed was prepared. The surface of the finished testing bed was smoothed carefully with a wood stick before anchor testing.

It should be noted that for the model tests, the stress level was low compared to that of the prototype, which is known to be important particularly for model tests in sand. In this study, the intention was not to directly associate the numerical analyses performed at the prototype scale with the 1 g experiments. Rather, the numerical simulations and physical model testing were adopted as two independent approaches, which have their respective strengths and limitations, for the verification of the novel anchor concept proposed in this study.

3. Results and Discussions

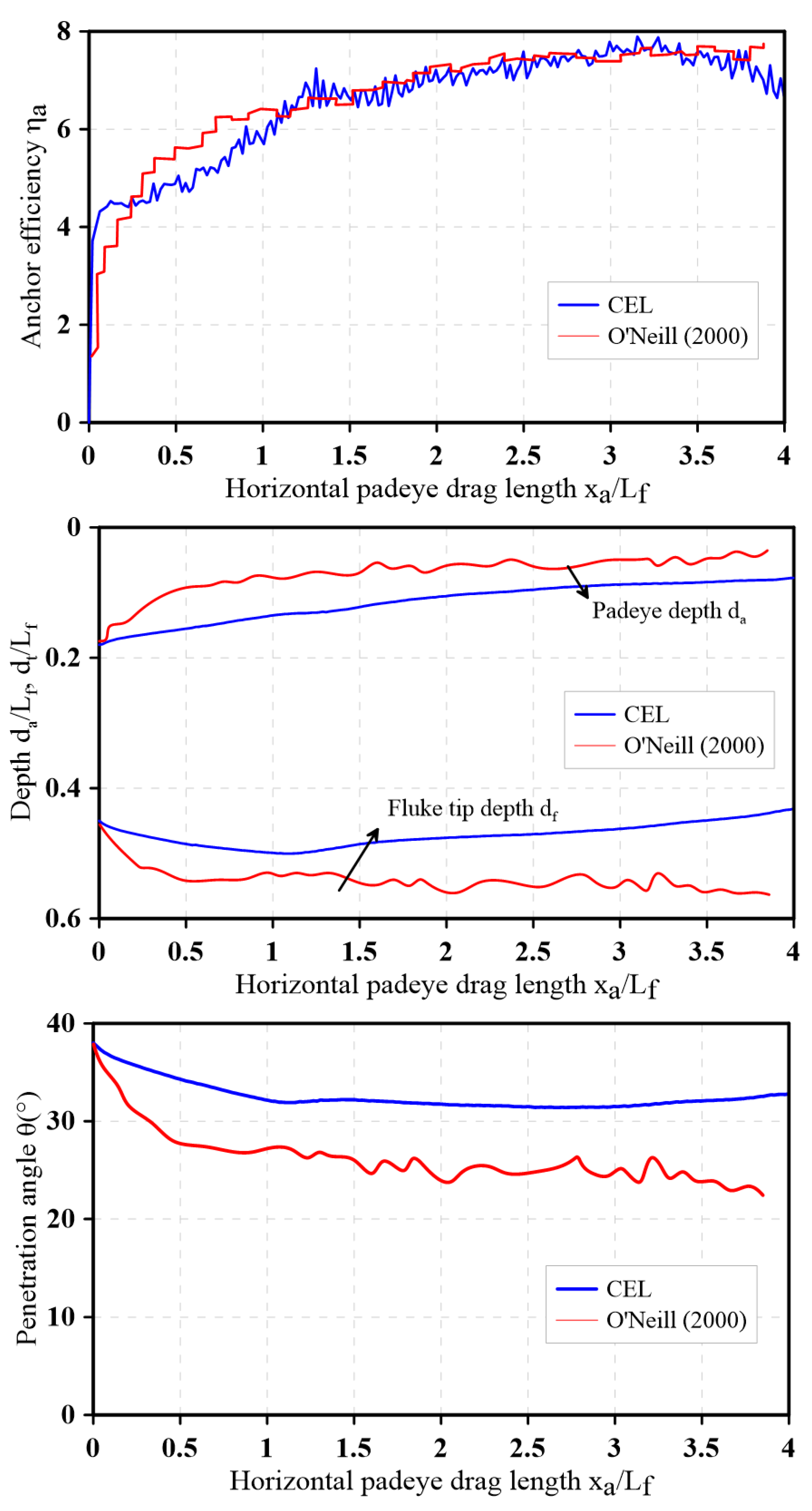
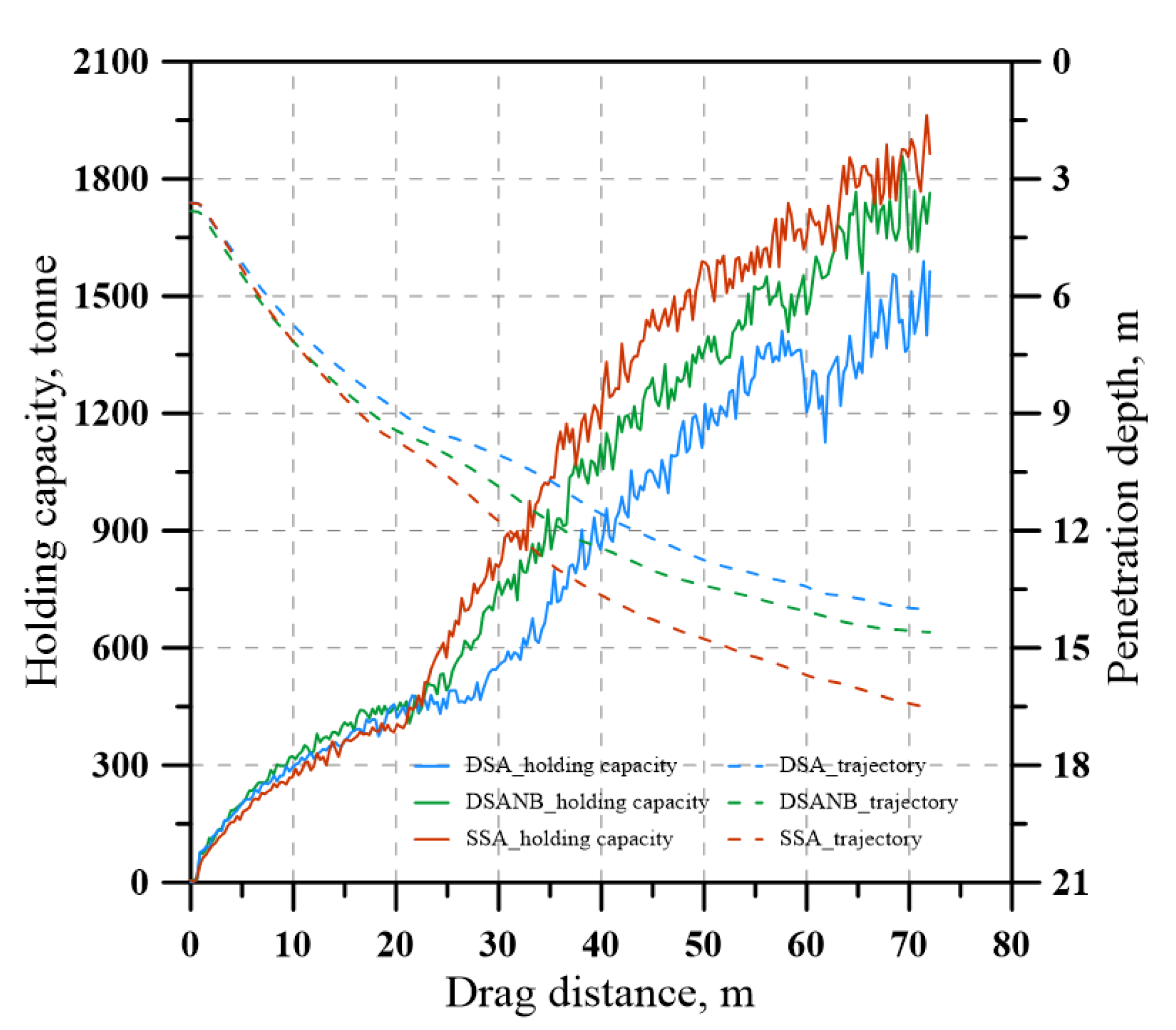
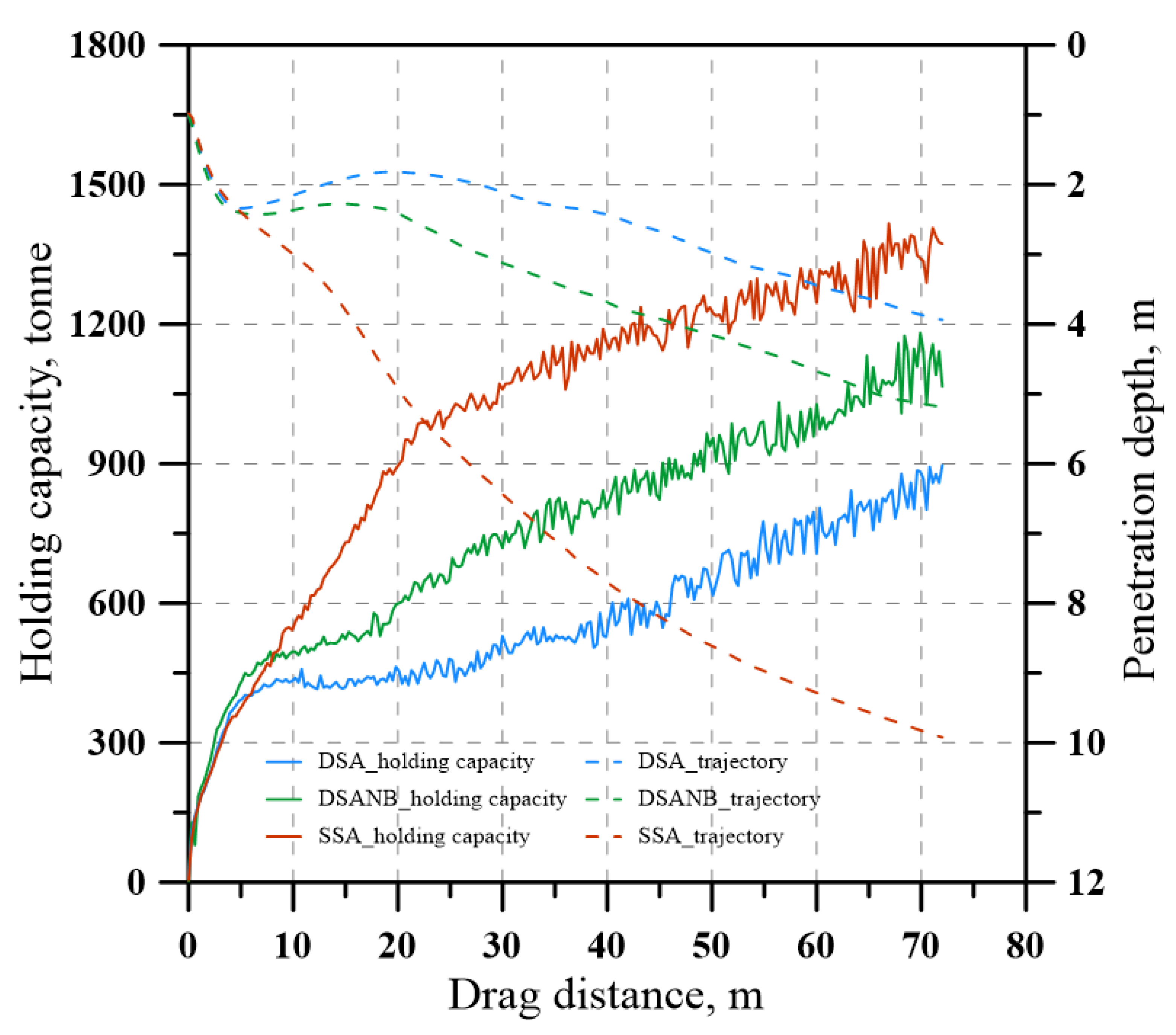
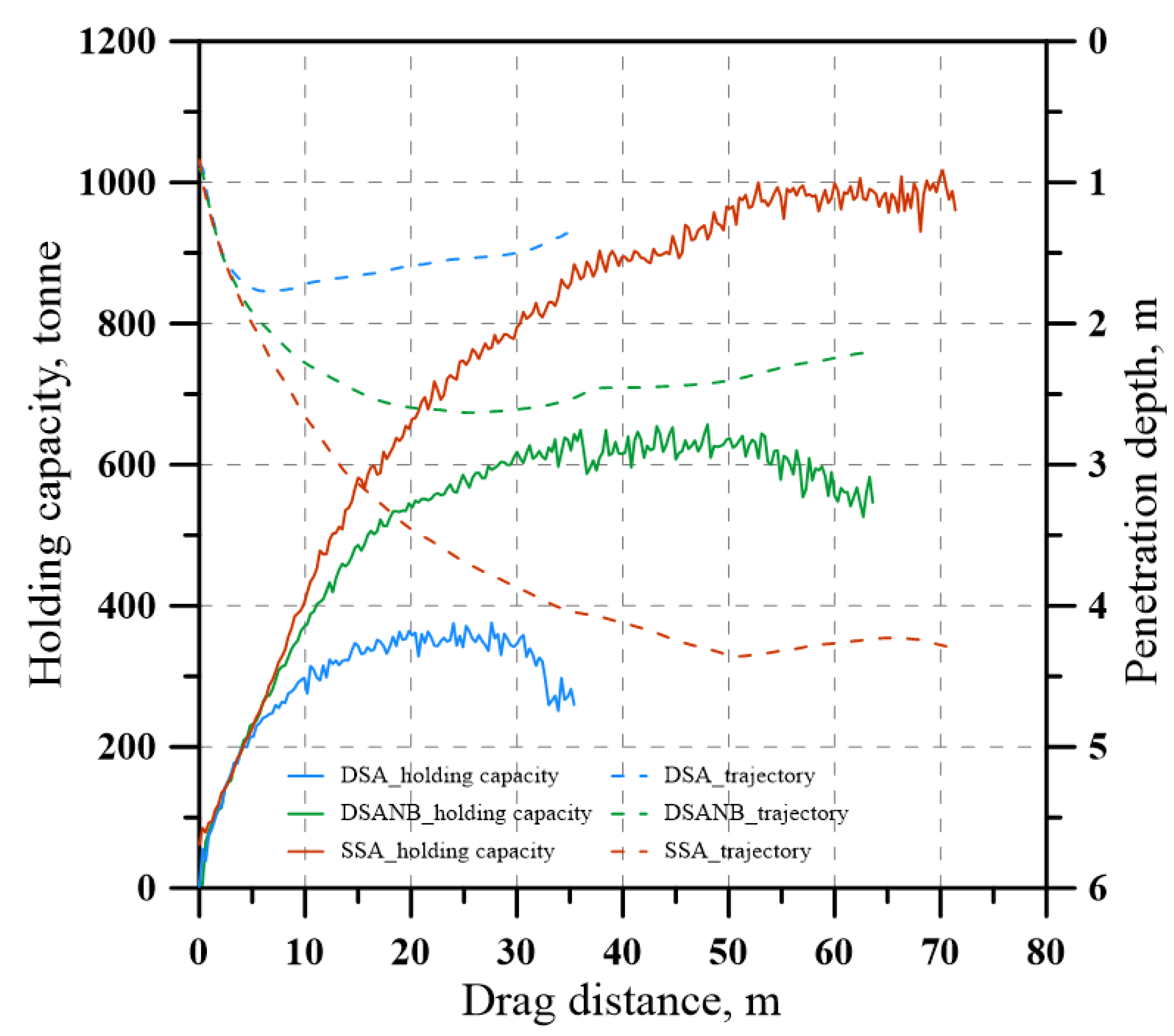
3.1. Results of Numerical Studies

Figure 15 presents the numerical simulation results of the three anchors in normally consolidated clay, which has a s_u profile linearly increasing with depth (as shown in Figure 8). At the beginning of the dragging process, an initial penetration depth (approximately 0.50 m) is reached due to the anchors’ self-weight. During the dragging process, it can be seen that the trajectory curves of anchors (penetration depth against drag distance) almost overlap each other for the first few meters of dragging, and the same is true for the holding capacity. However, as the drag distance increases, the differences in penetration performance and holding capacity among the three anchors gradually grow. The currently proposed single-shank anchor (SSA) has the largest penetration depth and holding capacity, while the double-shank anchor (DSA) has the lowest penetration depth and holding capacity. The removal of the horizontal braces of DSA brings its response closer to that of the SSA. At a drag distance of 70 m, the largest difference in embedment depth between the three anchors is about 2.0 m, and the holding capacity of SSA is 11% higher than that of the DSA. It is evident that, in normally consolidated clay, none of the anchor configurations attains its ultimate holding capacity within a drag distance of approximately 10 times the fluke length. Extrapolating from the observed trends, this disparity in capacity development is projected to widen with prolonged dragging, thereby underscoring the superior performance of the DSANB and SSA designs.

Figure 16 presents the results in a layered soil profile, which consists of normally consolidated clay underlain with over-consolidated clay. It shows that the holding capacity and penetration trajectories of the three anchors are basically identical during the initial installation phase (for a drag distance less than around 20 m). However, as the SSA starts entering the second clay layer at a drag distance of 21.9 m, the response of the single-shank anchor starts diverging from that of the other two anchors. When the drag distance reaches 25 m, the fluke tips of the DSA and DSANB also start entering the underlying strong layer, which is signified by the upward turning of the resistance versus drag distance curve. At a drag distance around 55 m, the DSA reaches its ultimate embedment depth, and the holding capacity plateaus, while the SSA and the DSANB achieve further embedment with a drag distance beyond 55 m. At a 55 m drag distance, the three drag anchors show significant differences in penetration depth and holding capacity. The embedment depth and holding capacity of the SSA are 20.4% and 25.8% higher than those of the DSA, respectively. It is evident that the SSA demonstrates superior penetrability in shallow soft clay, attaining the layer boundary ahead of both the DSANB and DSA configurations. This penetrability advantage is even more pronounced in stiffer clays, wherein the SSA sustains the highest holding capacity across the full duration of the dragging process.

Figure 17 presents the results of the numerical simulations in uniform (over-consolidated) clay with a constant undrained shear strength (s_u) with depth. Different from the other two clay profiles, the seabed has high undrained shear strength right from the mudline. Once the drag distance reaches 5 m, at which point the shank starts to come into contact with the seabed, the responses of the three anchors start to diverge. As shown in Figure 17, the double-shank anchors (with or without horizontal braces) plow through the soil for drag distance between 5 and 20 m without gaining penetration depth. Thereafter, the DSA only achieves an additional penetration of 2.1 m with an additional 52 m of drag distance. The DSANB shows better penetrability and gains an additional 2.8 m of penetration for the same additional drag distance. The SSA penetrates continuously and achieves a tip penetration of 9.9 m at 72 m drag distance, which is about 2.5 times that of the DSA. The holding capacity of the SSA shows a 54% enhancement compared to the DSA for the same drag distance. As evident from the trajectory curves in Figure 17, immediately upon shank penetration into the soil, the DSA and DSANB configurations initiate uplift and partial extraction (drag distance < 20 m), whereas the SSA persists in embedding, albeit at a diminished velocity. This divergent kinematic response precipitates the pronounced escalation in holding capacity for the SSA across the 5–20 m drag interval. At 20 m, the SSA attains a holding capacity that is 2.3 times that of the DSA, underscoring its suitability for applications in stiff soils subject to constrained drag distances.

Figure 18 presents the results of the numerical simulations in the homogenous sand layer with φ = 30°. As illustrated, the DSA penetrates continuously and achieves the largest tip penetration of 1.7 m at a 6 m drag distance. With further dragging, the DSA starts to rotate, and the depth of the tip point decreases, while the depth of the fluke tail increases. The DSA only achieves an ultimate holding capacity of 325 tonnes at a 18 m drag distance. It should be noted that the DSA is not fully embedded in the seabed soil until the abort of the calculation. On the other hand, the SSA achieves a tip penetration of 4.4 m at a 50 m drag distance, which is about 2.6 times that of the DSA, and the ultimate holding capacity of the SSA is about 2.9 times that of the DSA. By removing the braces of the DSA, the penetrability and holding capacity is greatly improved, although still considerably lower than the SSA. Drag embedment anchors are typically not applied in sandy soils owing to their limited penetration depths and propensity for unstable responses, such as anchor rolling. Design guidelines [3] mandate pretensioning to at least 100% of the anticipated design capacity during installation for permanent moorings, thereby safeguarding operational integrity but substantially increasing the installation expenses. Nonetheless, as illustrated in Figure 18, the SSA exhibits a markedly superior holding performance relative to the DSA in sandy profiles—surpassing the advantages observed in clayey soils—thereby rendering it viable for practical engineering implementations.

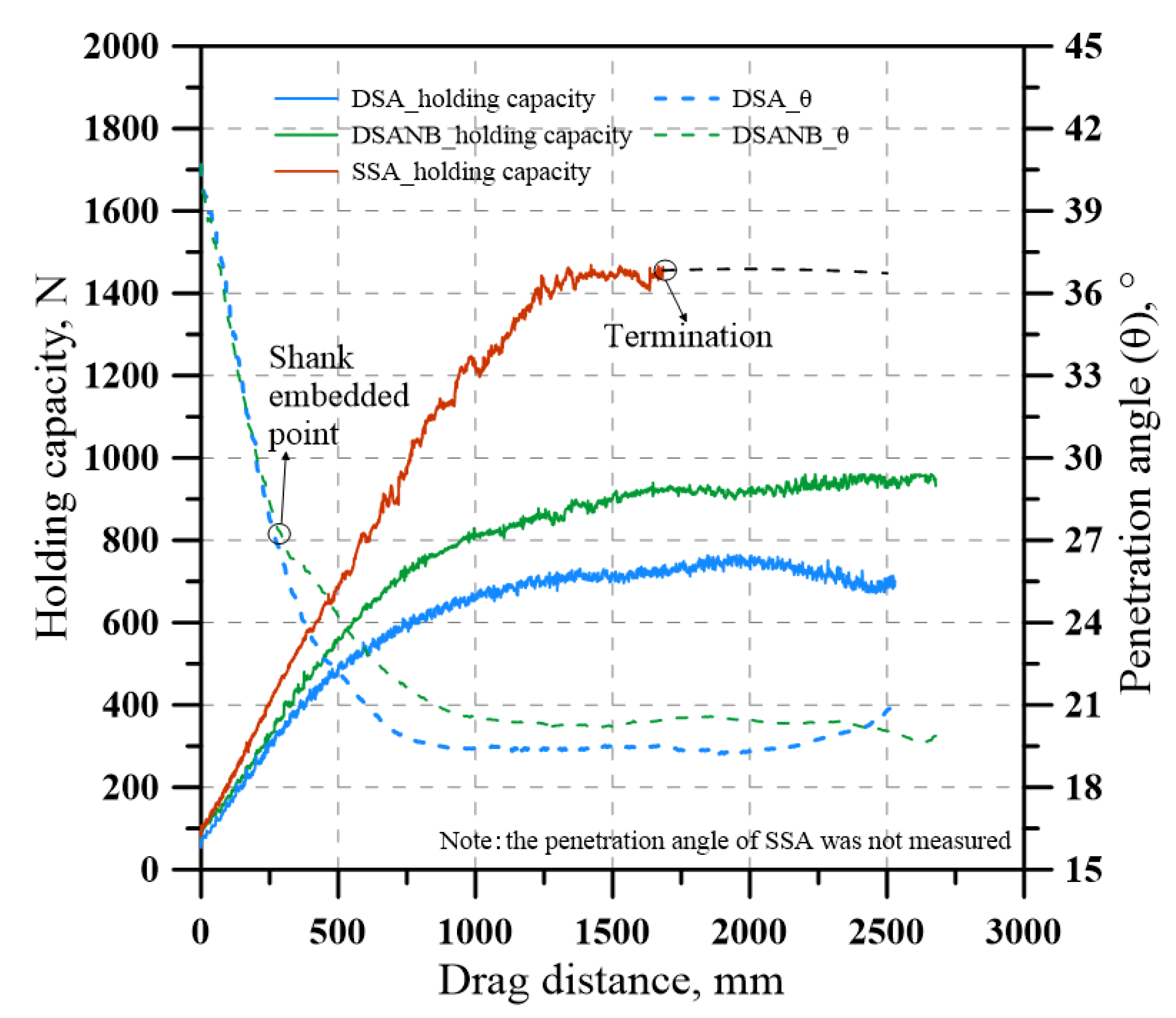
3.2. Results of the Physical Model Tests

Figure 19a illustrates the flow pattern of sand particles during the dragging process of the DEAs. After the anchor is embedded into the soil, a soil heave with a typical “horseshoe” shape forms above the anchor, as shown in Figure 19b. As the dragging process continues, sand particles on the soil heave fall down into the ditch behind the anchor. At the same time, the sand particles “plowed” by the fluke move upwards, becoming a part of the soil heave. The balance of the sand particle movements during the dragging process makes the shape and size of the soil heave remain relatively unchanged, which is also observed in the numerical simulations.

For the case of the DSA, when the sand particles are forced to move upwards due to the plowing motion of the anchor, some of the particles flow around the shank structure, while other sand particles are forced to pass through the narrow space between the braces. This creates considerable frictional and end resistances, and a soil plug is eventually formed, as illustrated in Figure 19c. A plugged shank structure drastically increases the soil resistance acting on the shank, prompting quick rotation of the anchor and eventually preventing the anchor from further penetration. In contrast, for the double-shank anchor without braces and the single-shank anchor, the soil plug is not observed. Considering the difference in stress level between the model tests and prototype tests, it should be noted that the reduced dilatancy of sand under a high stress level may prevent or delay the soil plug from forming, and further investigation is needed to confirm this assumption.

The results of the three model tests are presented in Figure 20. An initial holding capacity, approximately 100 N, was observed at the beginning of the tests due to an initial embedment depth caused by the self-weight penetration of the anchors. The load–displacement curves obtained from the physical model tests basically resembles those obtained from CEL simulations. The highest holding capacity was obtained with the single-shank anchor, which is 93.3% higher than the double-shank anchor. In removing the braces of the double shank anchors, its holding capacity is increased by 30.6%. Examination of the penetration angle measured with the angle senor in the DSA and DSANB tests reveals that once the shank is embedded in the soil, the penetration behaviors of the two anchors start to diverge and so does the holding capacity. The penetration angle plays a dominant role in the penetrability of drag anchors. A comparison of the penetration angles for the DSANB and DSA configurations indicates that the omission of horizontal braces optimizes overall penetrability, marked by consistently larger penetration angles across the entire dragging trajectory. An analogous improvement is inferred for the SSA, which simplifies the double-shank assembly into a single flat shank, notwithstanding the absence of direct penetration angle measurements. It should be noted that the SSA dragging test was prematurely terminated prior to attaining the predetermined drag distance. This interruption occurred as the anchor penetrated deeper into the soil, resulting in a progressively increasing out-of-plane roll angle that precipitated a loss of penetrability—a phenomenon commonly observed in practical engineering applications [24]. This event manifested as an abrupt inflection in the SSA holding capacity curve, beyond which no further increment in capacity was evident, prompting the cessation of the test.

4. Conclusions

In this study, the efficiency of a proposed single-shank anchor (SSA) design was examined through comprehensive large-deformation finite element simulations using the Coupled Eulerian–Lagrangian method in both clayey and sandy soil profiles. Small-scale physical model tests in sandy soil are also carried out to further verify the penetration and holding performance of the SSA. A numerical analysis model was established in general finite element Abaqus [21] and verified with a centrifuge test benchmark conducted at the University of Western Australia [7], with a less than ten percent holding capacity prediction error. Both the numerical and physical experimental results confirm the design assumption that by reducing the soil resistance acting on the shank, the penetrability of the anchor can be greatly improved. The largest effect is seen in hard materials, such as stiff clay and sand, where the holding capacity can be more than doubled by adopting the proposed single-shank design.

Despite the advantages of the SSA design, it should, however, be recognized that the study presented herein has only dealt with the geotechnical aspect of the drag anchor design, assuming the anchors have rigid bodies. The structural design of a single-shank anchor design is anticipated to be demanding, especially at the connection between the shank and the fluke, which holds a substantial bending moment.