Reliability and Risk Assessment of Hydrogen-Powered Marine Propulsion Systems Based on the Integrated FAHP-FMECA Framework
Abstract
1. Introduction
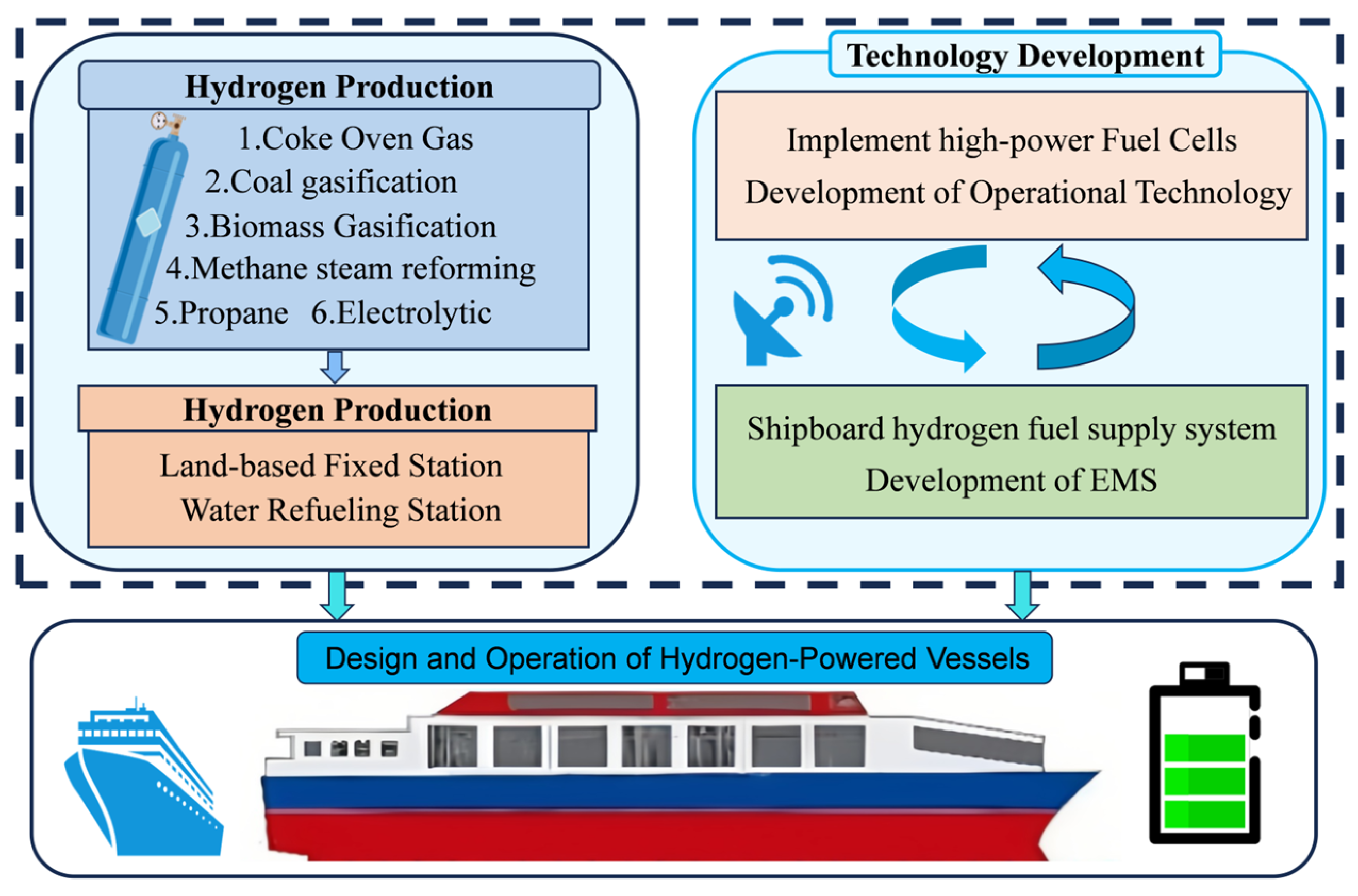
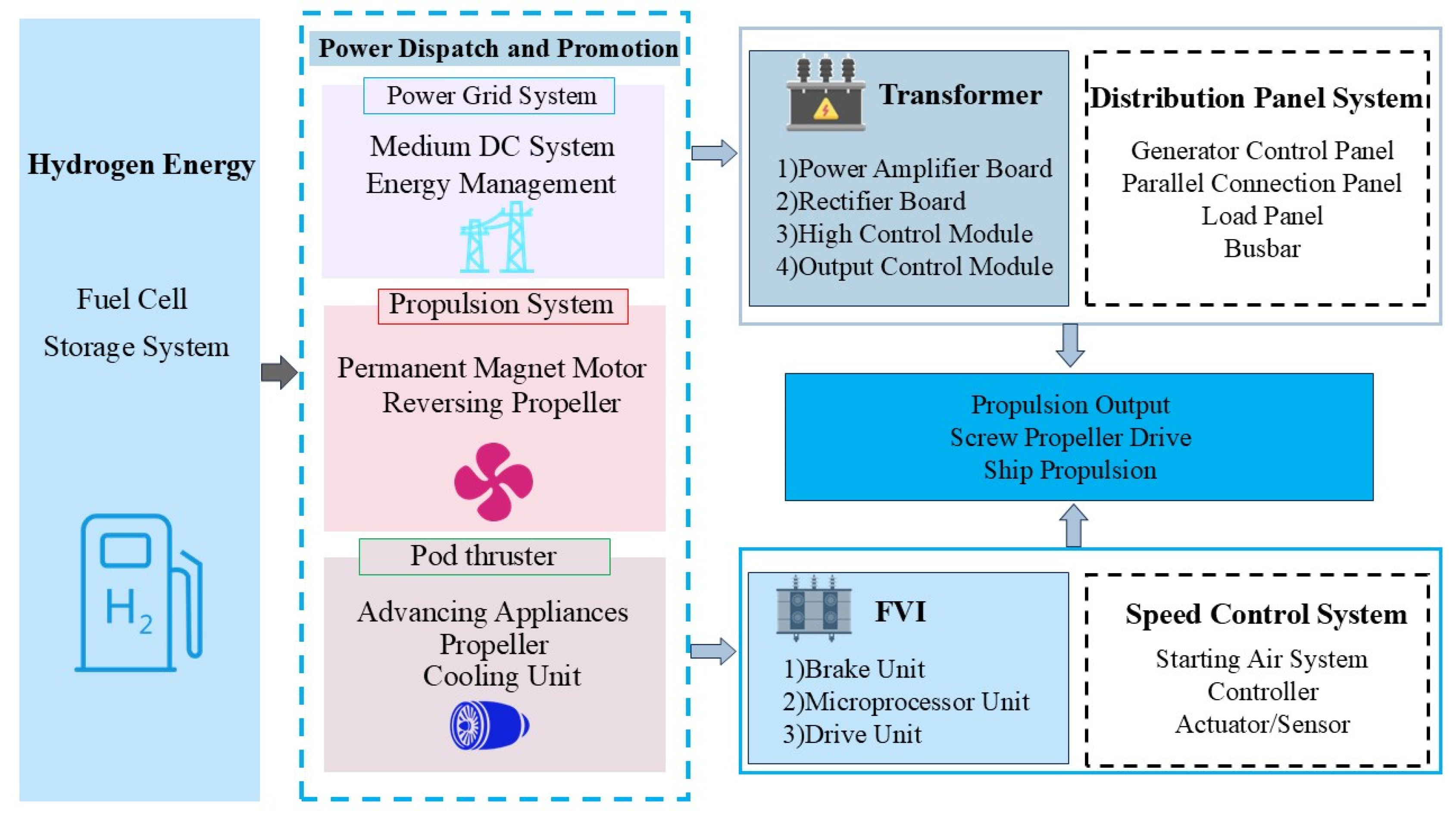
2. Hydrogen Energy Ship Propulsion System
2.1. Composition and Functions of the Hydrogen Energy Power System
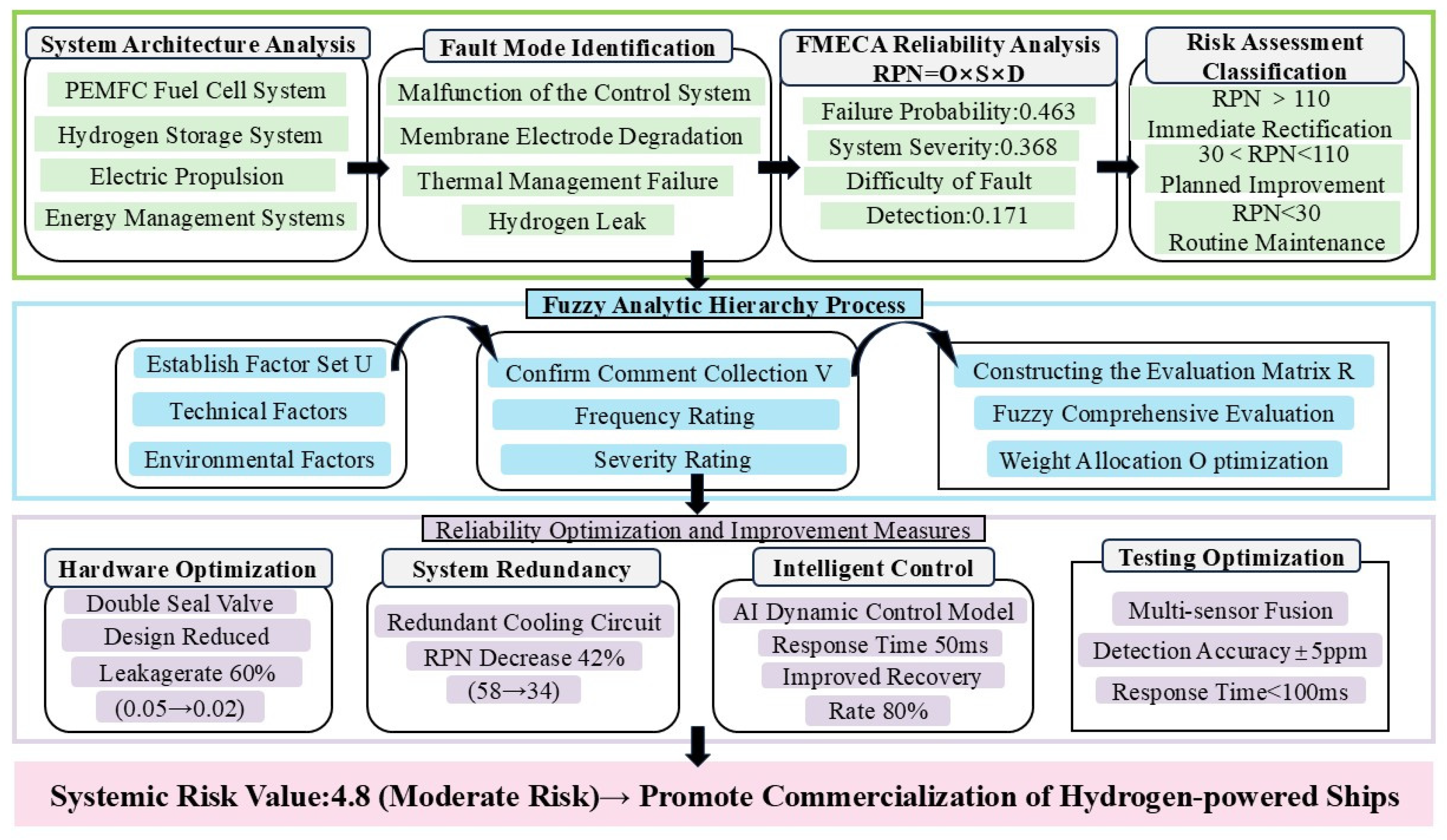
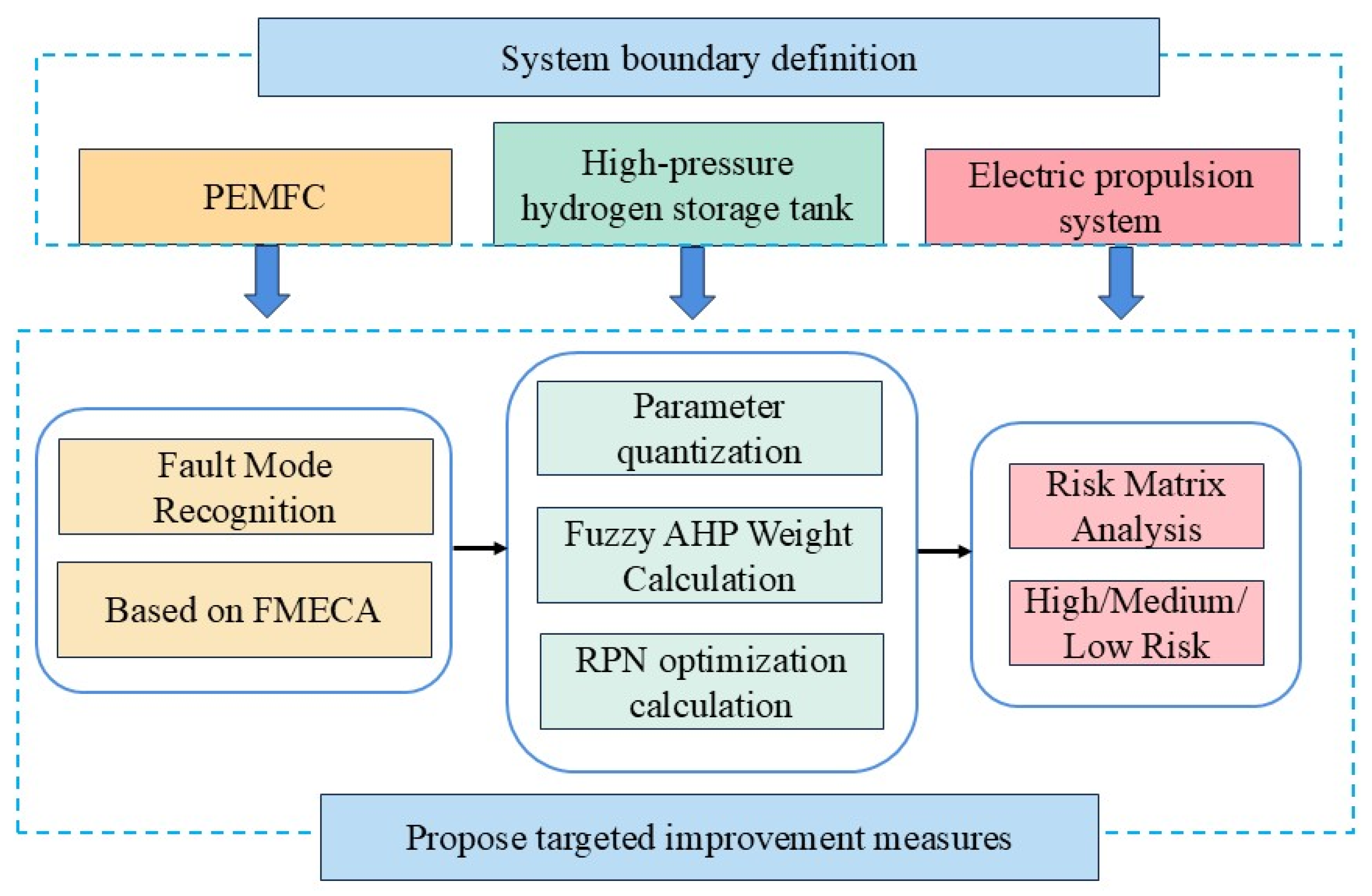
2.2. Fault Analysis and Risk Assessment of Hydrogen Energy Systems: From Boundary Definition to Pattern Recognition
3. Reliability Analysis of Fuel Cell Hybrid Marine Propulsion System
3.1. Fundamental Reliability Theory and Fuzzy Comprehensive Evaluation Method
3.1.1. Fundamentals of Reliability
3.1.2. Analytic Hierarchy Process
3.1.3. Fuzzy Comprehensive Evaluation
- (1)
- Single-factor evaluation
- (2)
- Construction of the comprehensive evaluation matrix
- (3)
- Determination of fuzzy sets for factor weights
- (4)
- Determination of the Comprehensive Evaluation Model
- (5)
- Comprehensive Evaluation
3.2. Determination of Evaluation Parameters
3.3. Fuzzy Evaluation Framework Construction
3.3.1. Evaluation Factor Set (U) Construction
- (1)
- Hydrogen-powered System Factor Set (U1):
- (2)
- Hydrogen fuel generator system factor set (U2):
3.3.2. Evaluation Comments Collection (V) Confirmed
3.3.3. Construction of Fuzzy Evaluation Matrix (R)
3.3.4. Determination of the Weights of Various Factors
3.4. Risk Priority Number Calculation
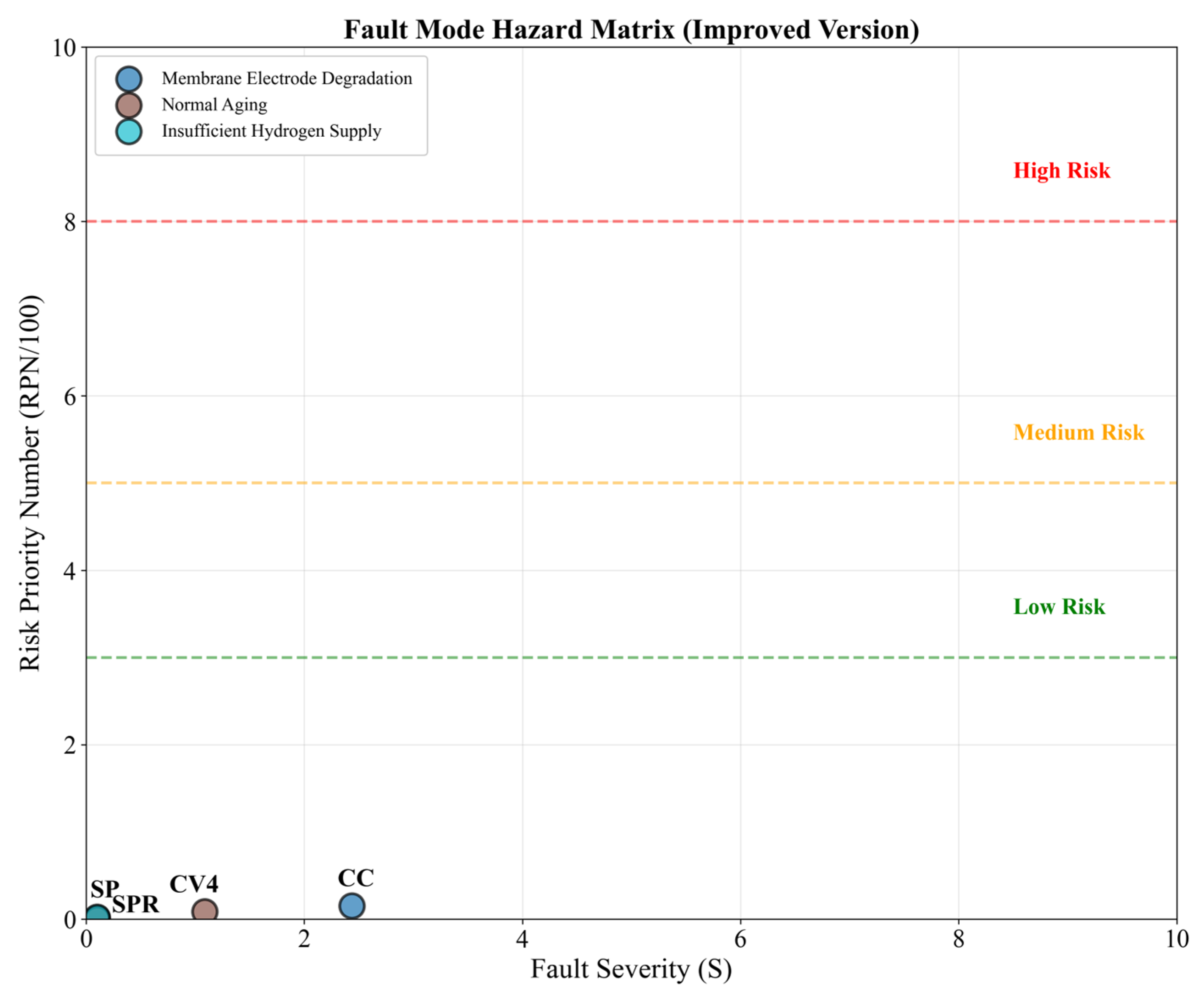
3.5. Hazard and Hazard Matrix Analysis
4. Reliability Analysis Results of Hydrogen-Powered Ship Propulsion Systems
4.1. Fuzzy Evaluation Results of Hydrogen Power System
4.1.1. Fuzzy Evaluation
4.1.2. Fuzzy Comprehensive Evaluation
4.1.3. Evaluation Results
4.2. Hydrogen Fuel Generator System
4.2.1. Primary Fuzzy Evaluation
4.2.2. Secondary Fuzzy Comprehensive Evaluation
4.2.3. Clarification of Evaluation Results
5. Discussion
5.1. Core Analysis of Research Findings and Engineering Implications
5.2. Comparison with Previous Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Liao, P.; Long, F.; Han, F.; Ji, Y. Maritime electrification pathways for sustainable shipping: Technological advances, environmental drivers, challenges, and prospects. eTransportation 2025, 26, 100462. [Google Scholar] [CrossRef]
- Alsunousi, M.; Kayabasi, E. The role of hydrogen in synthetic fuel production strategies. Int. J. Hydrogen Energy 2024, 54, 1169–1178. [Google Scholar] [CrossRef]
- Cao, M.; Wang, Z.; Tang, H.; Li, S.; Han, F.; Ji, Y. Electric-Thermal-Gas Synergistic Dynamics in PEMFC-LIB Hybrid Systems for Hydrogen Ships: A Multi-Scale Evaluation Framework. eTransportation 2025, 25, 100430. [Google Scholar] [CrossRef]
- El-Adawy, M.; Nemitallah, M.A.; Abdelhafez, A. Towards sustainable hydrogen and ammonia internal combustion engines: Challenges and opportunities. Fuel 2024, 364, 131090. [Google Scholar] [CrossRef]
- El-Adawy, M.; Dalha, I.B.; Ismael, M.A.; Al-Absi, Z.A.; Nemitallah, M.A. Review of Sustainable Hydrogen Energy Processes: Production, Storage, Transportation, and Color-Coded Classifica tions. Energy Fuels 2024, 38, 22686–22718. [Google Scholar] [CrossRef]
- Locke, K. The urgency of hydrogen: Environmental issues and the need for change. Future Sustain. 2024, 2, 46–58. [Google Scholar] [CrossRef]
- Shahid, M.Z.; Farooqi, A.S.; Fajri, K.; El-Adawy, M.; Hamdy, M.; Farooqi, A.S.; Abdelaziz, O.Y.; Hossain, M.M.; Nemitallah, M.A. Clean hydrogen production via sorption enhanced water gas shift reaction: A comprehensive review. Int. J. Hydrogen Energy 2025, 100, 1483–1512. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R.; Dutta, S. Review and outlook of hydrogen production through catalytic processes. Energy Fuels 2024, 38, 2601–2629. [Google Scholar] [CrossRef]
- Wang, Z.; Liao, P.; Liu, S.; Ji, Y.; Han, F. Scenario-based energy management optimization of hydrogen-electric-thermal systems in sustainable shipping. Int. J. Hydrogen Energy 2025, 99, 566–578. [Google Scholar] [CrossRef]
- Daya, A.A.; Lazakis, I. Systems reliability and data driven analysis for marine machinery maintenance planning and decision making. Machines 2024, 12, 294. [Google Scholar] [CrossRef]
- Wang, Z.; Liao, P.; Long, F.; Wang, Z.; Han, F. Coordinated optimization of multi-energy systems in sustainable ships: Synergizing power-to-gas, carbon capture, hydrogen blending, and carbon trading mechanisms. Int. J. Hydrogen Energy 2025, 165, 150755. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, X.; Ma, Y.; Liao, P.; Ji, Y.; Han, F. Advanced energy management and optimal scheduling for integrated offshore gas-hydrogen-electricity-heat systems. Energy 2025, 319, 135091. [Google Scholar] [CrossRef]
- Durukan, O.; Akyuz, E.; Destanoğlu, O.; Arslanoğlu, Y.; Sezer, S.I. Quantitive HAZOP and DS evidence theory-fault tree analysis approach to predict fire and explosion risk in inert gas system on-board tanker ship. Ocean. Eng. 2024, 308, 118274. [Google Scholar] [CrossRef]
- Yigin, B.; Celik, M. A prescriptive model for failure analysis in ship machinery monitoring using Generative Adversarial Networks. J. Mar. Sci. Eng. 2024, 12, 493. [Google Scholar] [CrossRef]
- Xiong, Z.; Yuan, Y.; Tong, L.; Li, X.; Shen, B. Dynamic performance analysis of proton exchange membrane fuel cell in marine applications. Energy 2024, 310, 133218. [Google Scholar] [CrossRef]
- Inal, O.B.; Zincir, B.; Dere, C.; Charpentier, J.-F. Hydrogen Fuel Cell as an Electric Generator: A Case Study for a General Cargo Ship. J. Mar. Sci. Eng. 2024, 12, 432. [Google Scholar] [CrossRef]
- Di Bernardo, R.; Di Cecca, B.; Coppola, T.; Spazzafumo, G.; Speranza, D. Preliminary design of a 75 m Mega Yacht with diesel-Electric hybrid propulsion powered with hydrogen FCs. Int. J. Hydrogen Energy 2025, 137, 917–924. [Google Scholar] [CrossRef]
- Zou, L.; Li, B.; Han, B.; Liu, Y.; Wang, X.; Bi, M.; Shu, C.M. Release of high-pressure hydrogen from type III tank in a fire scenario:Analysis and prediction of jet flame length and thermal response characteristics. Fuel 2024, 372, 132153. [Google Scholar] [CrossRef]
- Sazelee, N.; Ismail, M. Recent advances in catalyst enhanced LiAlH4 for solidstate hydrogen storage:a review. Int. J. Hydrogen Energy 2021, 46, 9123–9141. [Google Scholar] [CrossRef]
- Huo, Y.Z. Hydrogen Energy Commercial Vehicle Boom: Automotive-Grade Methanol Reforming Hydrogen Production Power System Technology. Commer. Veh. 2022, 6, 80–82. [Google Scholar]
- Yu, G.Y. A Study on the Energy Management Strategy of Shipboard Hybrid Power Systems Based on MATLAB/Simulink. Intern. Combust. Engine Accessories 2021, 20, 21–22. [Google Scholar]
- Cheng, P.; Pan, T.; Li, R.; Liang, N. Research on optimal matching of renewable energy power generation system and ship power system. IET Renew. Power Gener. 2022, 16, 1649–1660. [Google Scholar] [CrossRef]
- Dong, Y.; Han, Z.; Li, C.; Ma, S.; Ma, Z. Research on the optimal planning method of hydrogen-storage units in wind–hydrogen energy system considering hydrogen energy source. Energy Rep. 2023, 9, 1258–1264. [Google Scholar] [CrossRef]
- Karatuğ, Ç.; Tadros, M.; Ventura, M.; Soares, C.G. Strategy for ship energy efficiency based on optimization model and data-driven approach. Ocean. Eng. 2023, 279, 114397. [Google Scholar] [CrossRef]
- Park, I.-C.; Seo, B.-C.; Lee, S.-H.; Park, J.-H.; Seo, H.-S. A study on slamming impact load characteristics of energy storage system case for ships. J. Mar. Sci. Eng. 2022, 11, 44. [Google Scholar] [CrossRef]
- Jina, C.; Hayeon, K.; Ron, L.; Elangovan, D.; John, V. Fuzzy Analytical Hierarchy Process-based Risk Priority Number Approach in Failure Modes and Effects Analysis for Magnetic Resonance Imaging-guided High-dose-rate Brachytherapy for Gynecologic Cancer. Adv. Radiat. Oncol. 2025, 10, 101731. [Google Scholar]
- Rabie, K.; Khaled, L.; Laid, G. A Multi-criteria Weighted Risk Priority Number Model for Evaluating Failure Modes and Effects: A Case Study. J. Fail. Anal. Prev. 2025, 25, 895–905. [Google Scholar] [CrossRef]
- Wang, G.; Ding, S.; Yang, X.; Huang, S.; Zhou, G.; Liu, L.; Li, H.; Jia, L.; Diao, W.; Sun, Y.; et al. Risk assessment and quality management in AIO based on CT-linac for nasopharyngeal carcinoma: An improved FMEA and FTA approach. Med. Phys. 2025, 52, 2425–2437. [Google Scholar] [CrossRef]
- Feng, L.; Laibin, Z.; Shaohua, D.; Lushuai, X.; Hang, Z.; Lin, C. Risk Assessment of Bolt-Gasket-flange Connection (BGFC) Failures at Hydrogen Transfer Stations Based on Improved FMEA. Int. J. Hydrogen Energy 2024, 50, 700–716. [Google Scholar]
- Cao, M.; Wang, L.W.; Chen, B. A Review of the Assessment of the Technical Condition of Marine Power Systems. Ship Electr. Eng. Technol. 2022, 42, 34–36. [Google Scholar]
- Zheng, N.; Ding, X.; Zhou, Y.; Zhang, H.; Duan, L.; Zhang, M. Dynamic modeling and response characteristics of a solar-driven polygeneration system coupled with hydrogen and thermal energy storage. Energy Convers. Manag. 2023, 293, 117496. [Google Scholar] [CrossRef]
- Luo, X.; He, H.; Zhang, X.; Ma, Y.; Bai, X. Failure mode analysis of intelligent ship positioning system considering correlations based on fixed-Weight FMECA. Processes 2022, 10, 2677. [Google Scholar] [CrossRef]
- Wang, Z.; Tang, H.; Wu, Z.; Ji, Y.; Han, F. Evaluating fuel cell power systems for coastal and inland waterway vessels: Technical and economic perspectives. Energy Convers. Manag. 2025, 323, 119200. [Google Scholar] [CrossRef]
- Tang, H.; Wang, Z.; Li, J.; Li, S.; Ji, Y.; Han, F. Cross-scale modeling and 6E analysis of a cold storage Rankine-Carnot battery and PEMFC coupled system for liquid hydrogen maritime transportation. Energy 2025, 319, 134987. [Google Scholar] [CrossRef]
- Joibary, S.M.M.; Rahgoshay, S.; Rahimi-Esbo, M.; Firouzjaee, K.D. Numerical investigation of the influence of different cooling flow channels on the thermal and water saturation distribution in a real dimensional polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2023, 48, 2762–2787. [Google Scholar] [CrossRef]
- Pal, A.; Gupta, M.; Chauhan, S.S.; Pippal, S.K.; Sinha, A.; Kumar, S. Fuel Cell Vehicles: Technology, Challenges & Future Prospects. In Proceedings of the 2025 International Conference on Cognitive Computing in Engineering, Communications, Sciences and Biomedical Health Informatics (IC3ECSBHI), Greater Noida, India, 16–18 January 2025; IEEE: New York, NY, USA, 2025; pp. 420–425. [Google Scholar]
- Sebastian, S.; Wijewardane, S.; Srinivasan, S. Recent advances in hydrogen production, storage, and fuel cell Technologies with an emphasis on inventions, innovations, and commercialization. Sol. Compass 2023, 8, 100065. [Google Scholar] [CrossRef]
- Balestra, L.; Yang, R.C.; Schjølberg, I.; Utne, I.B. Towards safety barrier analysis of hydrogen powered maritime vessels, ocean engineering. In Proceedings of the ASME 2021 40th International Conference on Ocean, Offshore and Arctic Engineering, Virtual, 21–30 June 2021. [Google Scholar]
- Pei, Z.; Kang, Y.; Long, F. Research and development of inland green and smart ship technologies in China. Appl. Sci. 2024, 14, 2316. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, X.; Cui, D.; Yang, M.; Cheng, M.; Ji, Y. Research Progress of Fuel Cell Technology in Marine Applications: A Review. J. Mar. Sci. Eng. 2025, 13, 721. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Orfanoudakis, G.I.; Katsigiannis, Y.A.; Karapidakis, E.S. Hydrogen production from wave power farms to refuel hydrogen-powered ships in the mediterranean sea. Hydrogen 2024, 5, 494–518. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, B.; Zhu, J.; Yao, C. A Hybrid System Approach to Energy Optimization in Gas–Electric Hybrid Powertrains. Sustainability 2025, 17, 8160. [Google Scholar] [CrossRef]
- Ceylan, B.O. Marine diesel engine turbocharger fouling phenomenon risk assessment application by using fuzzy FMEA method. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2024, 238, 514–530. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Tian, J.; Li, J.; Xiong, Z.; Liu, C.; Zhao, W.; Cui, J. Risk Analysis of Offshore Test Process for Ultra High Temperature and High Pressure Wellhead Equipment System Based on FMECA. Curr. Sci. 2025, 5, 1604–1617. [Google Scholar] [CrossRef]
- Chang, K.-H.; Lai, H.-H.; Huang, B.-J. Combining the Fuzzy Analytic Hierarchy Process Method with the Weighted Aggregated Sum Product Assessment Method to Address Internet Platform Selection Problems in an Environment with Incomplete Information. Appl. Sci. 2024, 14, 4390. [Google Scholar] [CrossRef]


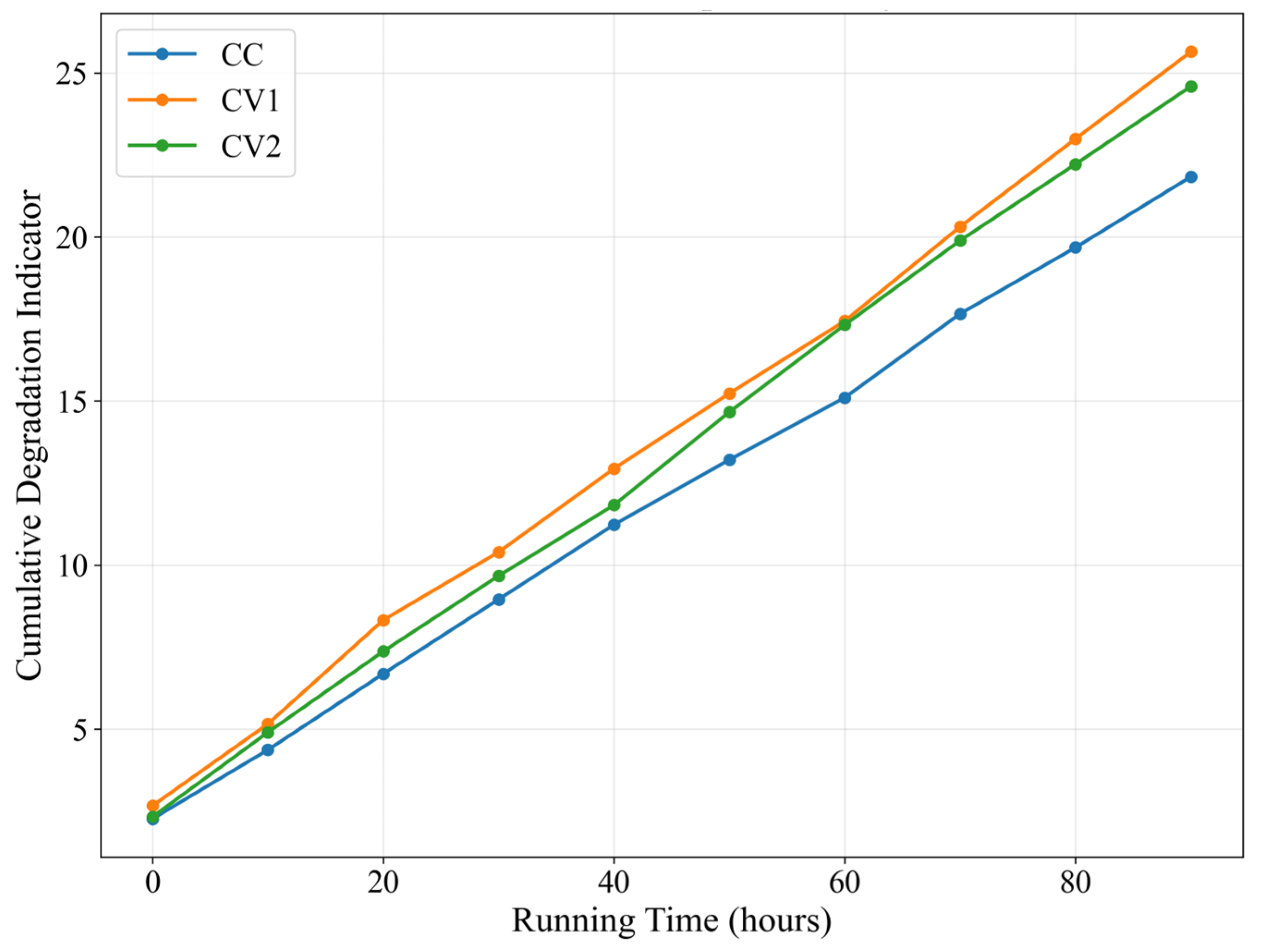
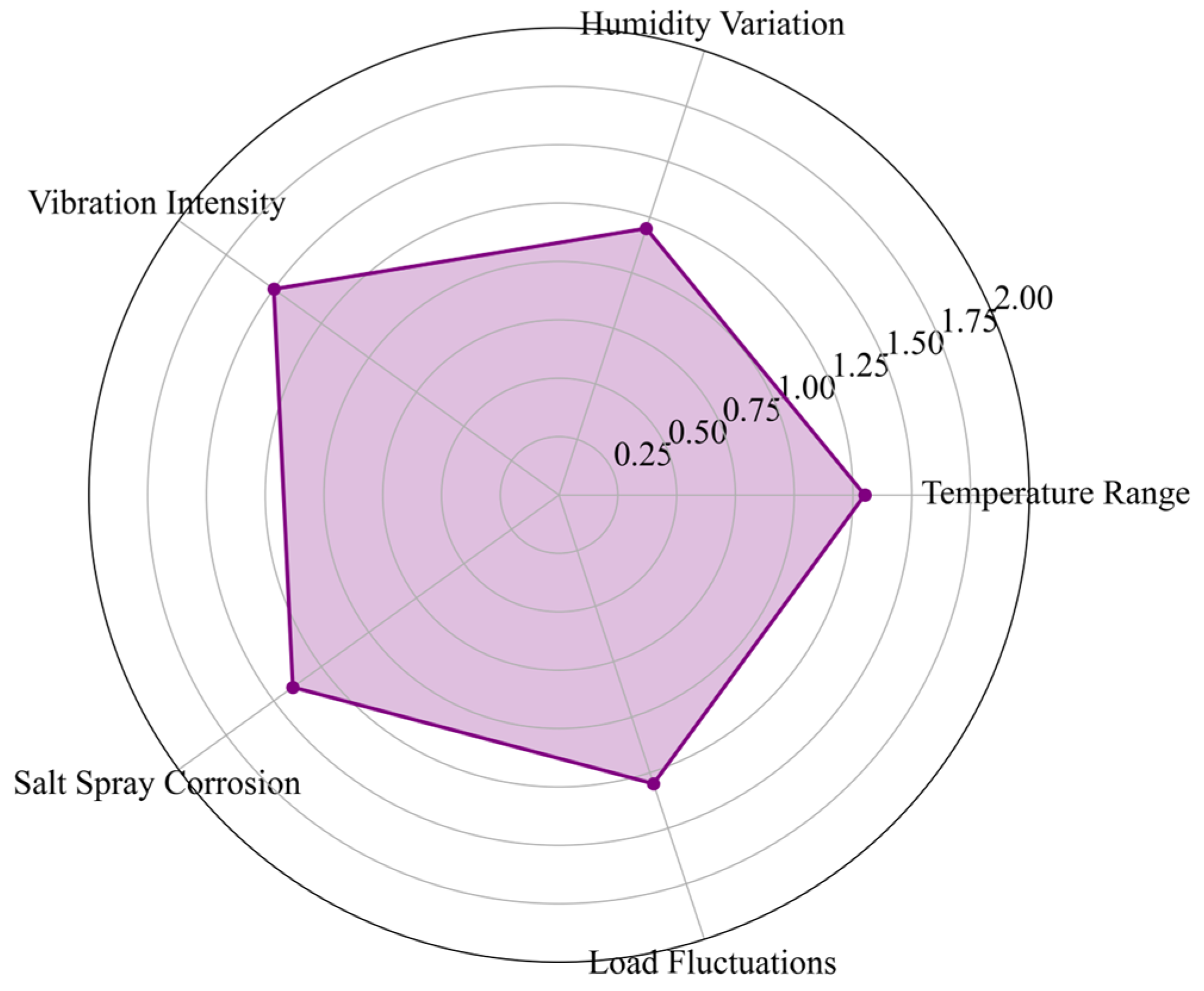
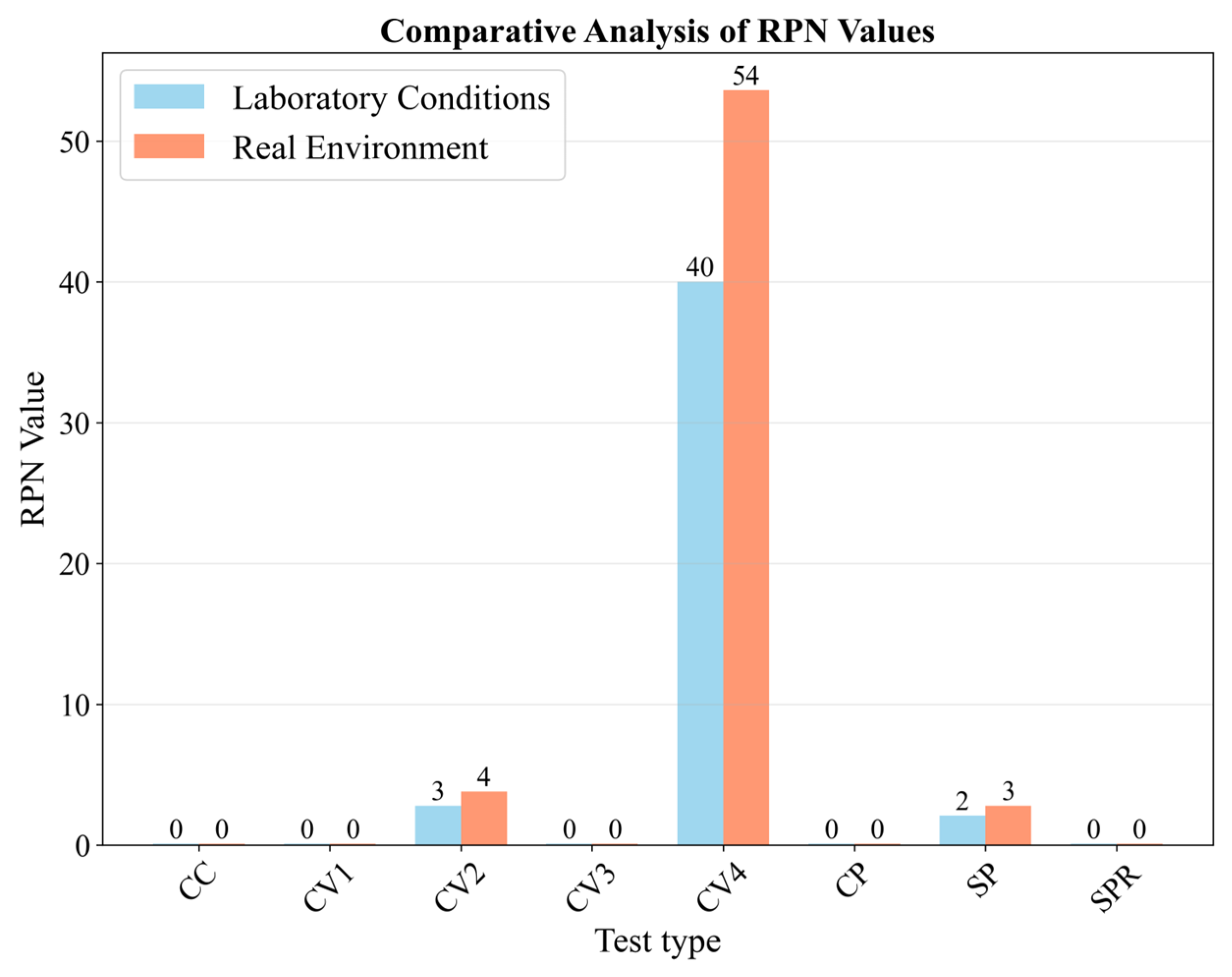
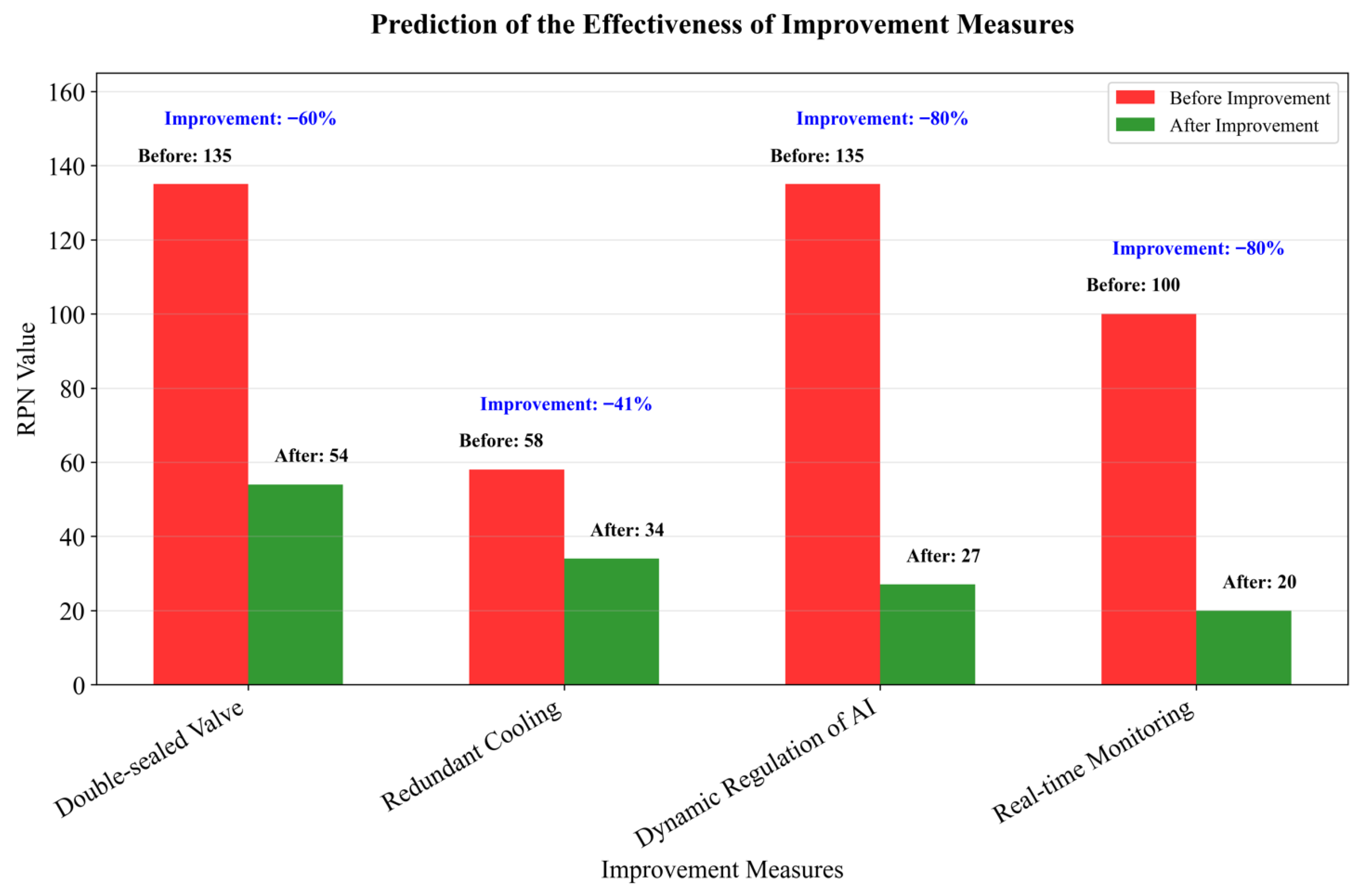
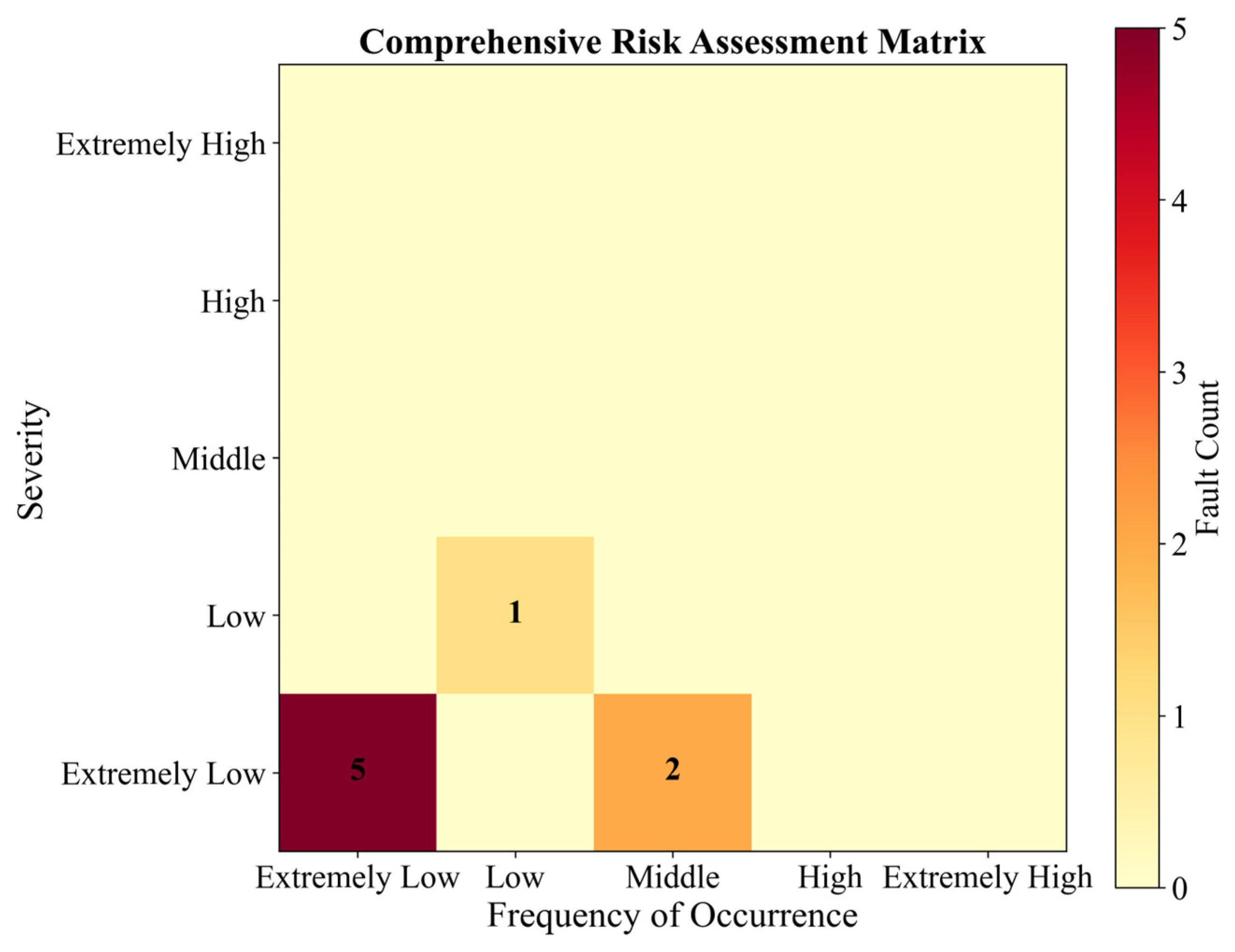
| Fault Categories | Severity Level | Detection Methods |
|---|---|---|
| Hydrogen Leakage | Level I (Catastrophic) | Multipoint sensors combined with thermal imaging |
| Membrane Electrode Degradation | Level II (Severe) | Impedance spectroscopy paired with polarization curve analysis |
| Cooling System Failure | Level III (Moderate) | Temperature and flow monitoring |
| Control System Abnormality | Level III (Moderate) | Self-diagnosis integrated with redundant verification |
| Hydrogen Storage System Issues | Level II (Severe) | Pressure, Temperature, and Strain Monitoring |
| Power System Failure | Level III (Moderate) | Real-Time Monitoring of Electrical Parameters |
| Level | Failure Mode Occurrence Probability | Reference Probability Value | |
|---|---|---|---|
| 1 | Extremely rare occurrence | The probability of failure is extremely low | 1/500,000 |
| 2 | Rare occurrence | The probability of failure is relatively low | 1/18,000 |
| 3 | 1/4500 | ||
| 4 | Occasional occurrence | The probability of failure is moderate | 1/1000 |
| 5 | 1/400 | ||
| 6 | 1/80 | ||
| 7 | Sometimes occurrence | The probability of failure is high | 1/40 |
| 8 | 1/20 | ||
| 9 | Frequent occurrence | The probability of failure is extremely high | 1/8 |
| 10 | 1/2 | ||
| Level | Severity of Failure Modes | |
|---|---|---|
| 1 | Almost no impact | Faults that do not affect the system’s performance and remain unnoticed by users |
| 2 | Slight impact | Faults that have a slight impact on the system’s functionality may be detected by users and lead to minor complaints |
| 3 | ||
| 4 | Moderate | Faults that cause a degradation in system performance will make users feel discomfort and dissatisfaction |
| 5 | ||
| 6 | ||
| 7 | Severe | Major faults that interrupt operation or cause failures in comfort-providing subsystems may result in significant user dissatisfaction; however, such faults do not lead to safety consequences nor do they violate governmental regulations |
| 8 | ||
| 9 | Catastrophic | Fatal faults that result in loss of life or property damage, or faults that fail to comply with governmental regulations |
| Level | Fault Mode Detection Difficulty | |
|---|---|---|
| 1 | Direct discovery | Potential faults that are very easy to detect |
| 2 | ||
| 3 | Routine examination | Potential faults that the testing procedure has a high probability of detecting |
| 4 | ||
| 5 | Certain degree of difficulty | Potential faults that the testing procedure may detect |
| 6 | ||
| 7 | Additional testing | Potential faults that the testing procedure is unlikely to detect |
| 8 | ||
| 9 | Nearly undetectable | Potential faults that the testing procedure cannot detect |
| Criteria for Judgment | Definition |
|---|---|
| 1 | For , and are of equal importance |
| 3 | For , is slightly more important than |
| 5 | For , is noticeably more important than |
| 7 | For , is strongly more important than |
| 9 | For , is extremely more important than |
| 2, 4, 6, 8 | The level of importance lies between the two adjacent judgment scales mentioned above |
| Frequency of Occurrence | Severity Detection | Difficulty | Priority | |
|---|---|---|---|---|
| Frequency of Occurrence | - | 1 | 3 | 0.463 |
| Severity Detection | 1 | - | 2 | 0.368 |
| Difficulty | 1/3 | 1/2 | - | 0.170 |
| IR = Inconsistency ratio = 0.018 | ||||
| Comparison Dimension | WRI | RPN |
|---|---|---|
| Weight allocation | Based on FAHP and expert experience, considering the characteristics of hydrogen-powered ships, the weights are uneven. | Default weights are equal, without considering the system’s specifics. |
| Data Processing | 0–1 standardization to eliminate the problem of uneven intervals between ordinal scales, making the data continuous and comparable. | 1–10 ordinal scale, intervals have no physical meaning, data are discrete |
| Coupling Adapter | Quantifiable comprehensive risk of multi-field coupled failures, adapted to the characteristics of hydrogen-powered systems | Unable to reflect the interdependence of parameters, only suitable for simple systems |
| Practical verification | Consistent with actual ship failure data and laboratory test results, the risk ranking is accurate. | Prone to ‘domination by extreme values,’ leading to distorted risk ranking |
| System Module | Failure Modes | Failure Frequency | Severity | Detection Difficulty | RPN Value | Risk Level | Improvement Suggestions |
|---|---|---|---|---|---|---|---|
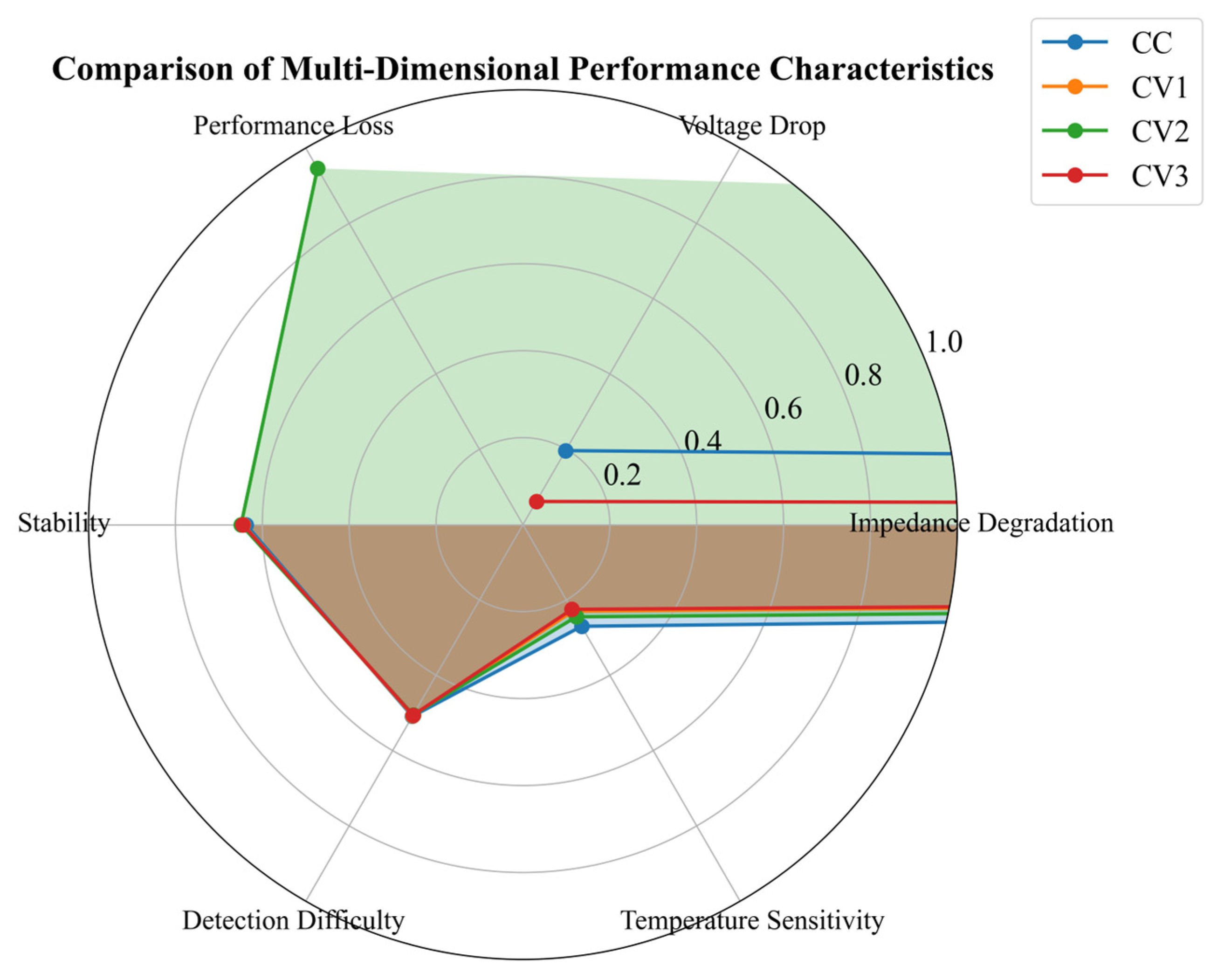
| PEMFC Sytem—CC | Membrane Electrode Degradation | 0.123 | 0.244 | 0.509 | 15.3 | Low Risk | Regularly replace the membrane electrodes and optimize the catalyst layer |
| PEMFC Sytem—CV2 | Insufficient Oxygen Supply | 0.600 | 0.010 | 0.405 | 2.4 | Low Risk | Enhance oxygen flow monitoring and optimize the gas supply pipeline |
| PEMFC Sytem—CV4 | Normal Aging | 0.254 | 0.109 | 0.309 | 8.6 | Low Risk | Establish a preventive maintenance plan |
| PEMFC Sytem—SP | Normal aging | 0.411 | 0.010 | 0.306 | 1.3 | Low Risk | Routine maintenance is sufficient |
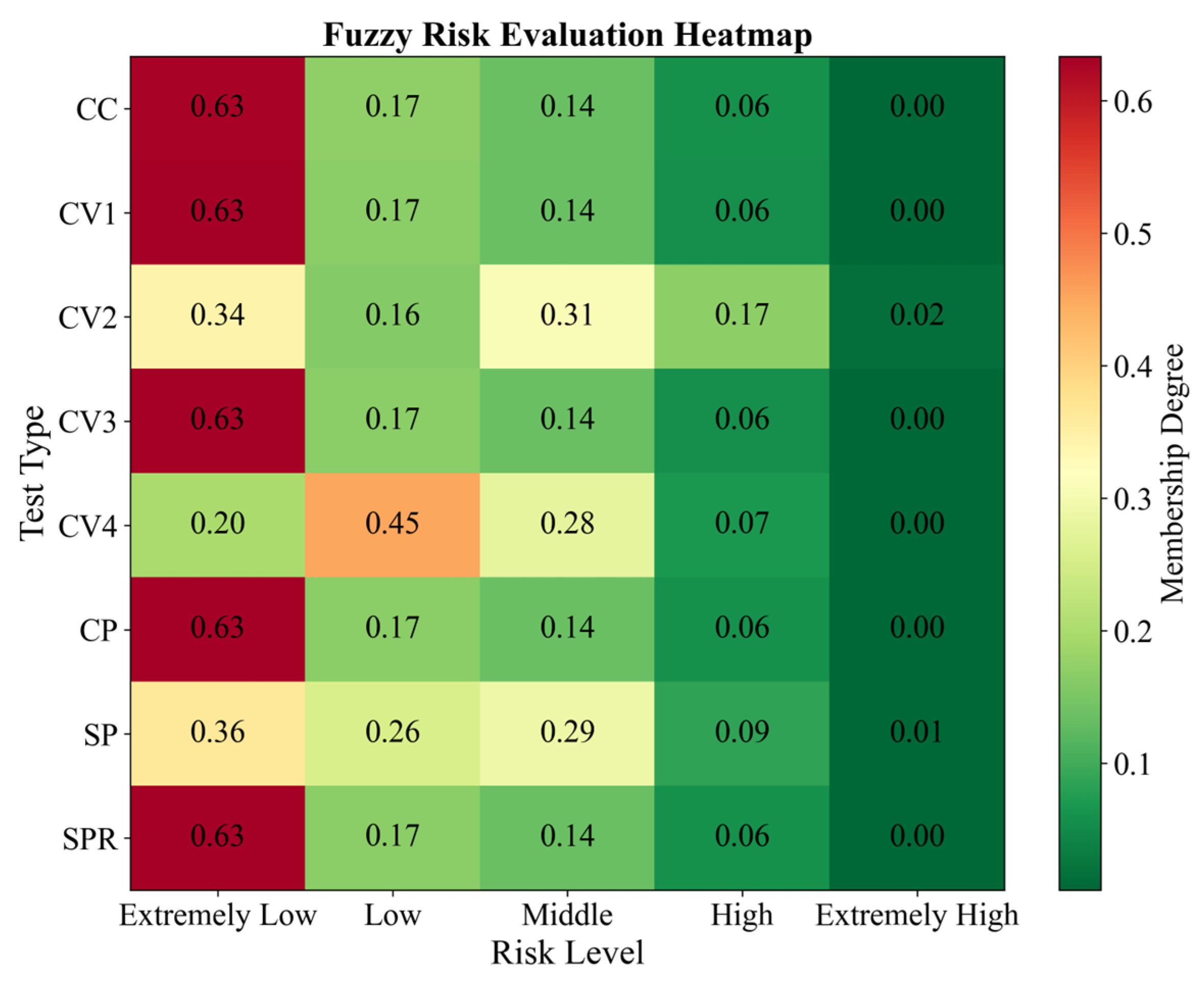
| Test Type | Risk Level | Risk Index | Highest Membership | Degree Weight Type | Comprehensive Evaluation |
|---|---|---|---|---|---|
| CC | Low | 2 | 0.371 | Standard | The system operates stably, and the membrane electrodes require periodic inspection |
| CV1 | Extremely low | 1 | 0.682 | Standard | The system exhibits excellent performance |
| CV2 | Extremely low | 1 | 0.395 | Adjustment | Attention should be given to the stability of the hydrogen supply |
| CV3 | Extremely low | 1 | 0.682 | Standard | The system exhibits excellent performance |
| CV4 | Low | 2 | 0.439 | Standard | The system operates normally |
| CP | Extremely low | 1 | 0.681 | Standard | The system exhibits excellent performance |
| SP | Extremely low | 1 | 0.410 | Standard | The system operates stably |
| SPR | Extremely low | 1 | 0.682 | Standard | The system exhibits excellent performance |
| Environmental Factors | Correction Factor | Weight | Weighted Contribution |
|---|---|---|---|
| Temperature Range | 1.3 | 0.25 | 0.325 |
| Humidity Variation | 1.2 | 0.20 | 0.240 |
| Vibration Intensity | 1.5 | 0.25 | 0.375 |
| Salt Spray | 1.4 | 0.20 | 0.280 |
| Corrosion Load Fluctuation | 1.3 | 0.10 | 0.130 |
| Correction Factor | 1.35 | ||
| Comparison Dimension | This Study | Past Research | Differences and Advantages |
|---|---|---|---|
| Research System Boundaries | Hydrogen storage-PEMFC-Propulsion motor-Full energy management chain | Single subsystem | Identify the cascade failure chain: Hydrogen supply deficiency→PEMFC voltage fluctuation→Inverter overload |
| Risk Assessment Method | FAHP weight + marine environmental correction | Traditional FMECA (without environmental correction) | Resolving weight ambiguity issues |
| Output of Improvement Measures | Quantify the effect | Qualitative recommendations | Provide actionable metrics for project implementation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Han, F.; Li, H.; Zhou, J.; Wang, Z. Reliability and Risk Assessment of Hydrogen-Powered Marine Propulsion Systems Based on the Integrated FAHP-FMECA Framework. J. Mar. Sci. Eng. 2025, 13, 2115. https://doi.org/10.3390/jmse13112115
Wang M, Han F, Li H, Zhou J, Wang Z. Reliability and Risk Assessment of Hydrogen-Powered Marine Propulsion Systems Based on the Integrated FAHP-FMECA Framework. Journal of Marine Science and Engineering. 2025; 13(11):2115. https://doi.org/10.3390/jmse13112115
Chicago/Turabian StyleWang, Meng, Fenghui Han, Huairui Li, Jingkai Zhou, and Zhe Wang. 2025. "Reliability and Risk Assessment of Hydrogen-Powered Marine Propulsion Systems Based on the Integrated FAHP-FMECA Framework" Journal of Marine Science and Engineering 13, no. 11: 2115. https://doi.org/10.3390/jmse13112115
APA StyleWang, M., Han, F., Li, H., Zhou, J., & Wang, Z. (2025). Reliability and Risk Assessment of Hydrogen-Powered Marine Propulsion Systems Based on the Integrated FAHP-FMECA Framework. Journal of Marine Science and Engineering, 13(11), 2115. https://doi.org/10.3390/jmse13112115






