Abstract
The capacity estimation of lithium-ion batteries, serving as an auxiliary power source in fuel cell vessels, is crucial for ensuring system stability and enhancing operational efficiency. Accurate capacity estimation technology not only helps extend battery lifespan but also enhances the energy management and scheduling capabilities of the entire vessel. To address the challenge of accurately estimating lithium-ion battery capacity under complex operating conditions, this study extracts universal health factors from battery data under varied charging and discharging scenarios and combines these with a deep learning model to enhance prediction accuracy. First, battery data from three complex conditions are analyzed, extracting partial charge and discharge data. The distance correlation coefficient calculates the correlation between each factor and the capacity sequence, informing the priority of universal health factors. A TCN-BiGRU model is then developed, with hyperparameters determined by the Kepler optimization algorithm (KOA). Cells from a battery pack under consistent conditions are used for training, while other cells in the same pack serve as the test set. Evaluation metrics include mean absolute error (MAE) and root-mean-square error (RMSE). The testing shows that the MAE and RMSE for full-life capacity estimation remain around 1%, with most cells achieving values under 1%. The results indicate that the proposed method effectively aids in accurate capacity estimation for individual cells in complex operating environments.
1. Introduction
Maritime transportation is undergoing a profound transformation driven by global imperatives toward carbon neutrality and sustainable development [,]. Among the emerging technologies, fuel cell hybrid power systems—particularly those integrating proton exchange membrane fuel cells (PEMFCs) and lithium-ion batteries—have emerged as pivotal solutions for decarbonizing maritime operations. These systems offer dual advantages of high energy conversion efficiency and near-zero emissions, as highlighted in studies on fuel cell technologies for sustainable ship power [,]. PEMFCs demonstrate superior environmental performance compared to hydrogen-fueled internal combustion engines, with negligible CO2 and particulate emissions [], while hybrid configurations combining PEMFCs and lithium-ion batteries optimize the energy flow under fluctuating loads [,]. As emphasized in comprehensive reviews of PEMFC hybrid systems [], the lithium-ion battery subsystem serves as a critical energy buffer, addressing peak power demands and stabilizing the grid during transient operations. However, the accurate capacity estimation of these batteries remains a critical bottleneck for ensuring reliable energy management in fuel cell ships, where complex maritime environments—including variable sea states, temperature gradients, and intermittent fuel cell output—exacerbate degradation uncertainties []. Unlike land-based energy systems, maritime applications impose unique challenges on battery management, including (1) dynamic load fluctuations, as propulsion demands in ships vary significantly with sea states, ship speed, and auxiliary equipment usage, leading to frequent charging/discharging cycles that accelerate battery degradation [,]; (2) harsh environmental conditions as salt fog, humidity, and temperature gradients in marine environments exacerbate electrochemical side reactions (e.g., SEI film growth), complicating capacity estimation [,]; (3) safety-critical requirements, since a reliable capacity estimation is essential for avoiding navigational failures caused by unexpected battery depletion, particularly in remote maritime operations [].
Lithium-ion batteries in fuel cell ships serve as critical auxiliary power sources, supporting peak power demands and enhancing system stability under fluctuating loads. However, their performance degradation over time—manifested through capacity loss and increased internal resistance—poses challenges for long-term reliability, energy management, and navigation safety [,]. An accurate and timely capacity estimation is essential not only for extending battery lifespan but also for optimizing energy scheduling and preventing unexpected system failures. This task is particularly challenging due to the complex, non-linear aging processes influenced by temperature, charge/discharge cycles, and load conditions [,], which collectively lead to irreversible capacity fade and power loss.
Traditional capacity estimation methods, such as electrochemical models, rely on physical and chemical principles but are often limited by complex parameterization and sensitivity to environmental conditions, which makes them difficult to be generalized across different battery chemistries and operating scenarios [,]. To address these limitations, data-driven methods—leveraging machine learning and deep learning techniques—have emerged as promising alternatives. These approaches extract degradation patterns from historical data, offering improved adaptability and prediction accuracy without extensive domain-specific knowledge [,]. Methods such as convolutional neural networks (CNNs), recurrent neural networks (RNNs), long short-term memory (LSTM), and hybrid models combining machine learning with physical insights have demonstrated significant potential in estimating battery capacity under diverse conditions [].
Data-driven approaches have emerged as promising alternatives, but their application in maritime contexts is hindered by two key limitations. First, the multi-scale nature of battery signals—encompassing high-frequency noise from power electronics and low-frequency degradation trends—requires robust feature separation techniques. As noted in reviews of maritime battery health modeling [], most deep learning models directly process raw voltage/current data, overlooking the hierarchical structure of capacity dynamics. Second, the complex coupling between operational parameters (e.g., temperature, depth of discharge) and battery aging [,] demands architectures capable of capturing multivariate dependencies. Studies on hybrid energy storage sizing [] emphasize that a suboptimal capacity estimation can lead to premature battery failure or inefficient energy allocation, underscoring the need for adaptive, physics-informed deep learning frameworks.
Recent advancements in hybrid modeling approaches integrate physics-informed data features with machine learning algorithms to enhance prediction robustness and interpretability []. For example, attention mechanisms and ensemble learning methods have been applied to capture nonlinear degradation patterns across varying conditions [,], while optimization techniques like particle swarm optimization (PSO) and genetic algorithms (GA) automate hyperparameter selection to improve model performance [,,]. Despite these progressions, challenges remain in achieving high accuracy under complex and fluctuating operational environments, such as in electric vehicles and ships with highly variable discharging cycles []. These methods share two critical limitations for fuel cell ships: (1) dependence on specific working conditions because most models are trained on land-based datasets (e.g., EV driving cycles), neglecting marine-specific load profiles; (2) lack of universal feature extraction, since existing studies rely on condition-specific health factors whereas fuel cell ships require robust features extractable from partial charge/discharge data.
This paper addresses these challenges by proposing a method that mines universal health factors applicable to most complex working conditions and integrates them with a TCN-BiGRU deep learning model. Specifically, partial charging/discharging data under different conditions are analyzed to identify universal health factors using the distance correlation coefficient (DCC), which prioritizes factors based on their correlation with capacity data. A TCN-BiGRU model is then developed, where the temporal convolutional network (TCN) extracts features from input health factors, and the bidirectional gated recurrent unit (BiGRU) performs capacity regression. Key model parameters are optimized using the Kepler optimization algorithm (KOA). Unlike prior work on battery health estimation in maritime systems [,], which primarily focuses on state of health (SOH)/remaining useful life (RUL) prediction, this study targets real-time capacity estimation—a critical parameter for fuel cell ship energy scheduling. By combining universal feature extraction with adaptive deep learning, our framework bridges the gap between laboratory-scale models and practical marine applications, offering a scalable solution for battery packs in hybrid power systems.
The remaining sections are structured as follows: Section 2 provides an overview of the battery degradation dataset used for model training and testing, details the process of extracting generic health factors, and the related theories, and outlines the overall pipeline of the estimation method; Section 3 exhibits the estimation results and errors of the proposed method; Section 4 discusses the results; and finally, Section 5 concludes the article.
2. Battery Experiment Data and the KOA-TCN-BiGRU Model
2.1. MIT Battery Dataset
The Massachusetts Institute of Technology (MIT) conducted a systematic cycling test on 45 LFP/C batteries of the model A123 APR18650M1A, with the test ambient temperature maintained at a constant 30 °C [], in order to study the aging and performance changes of the batteries under standard operating conditions. During the experimental process, the discharge conditions of all batteries were kept the same, and all of them were discharged to 2 V using 4 C constant current, with C/20 as the cut-off current to ensure the comparability of the experiments. The charging process, on the other hand, adopted a staged constant current (CC) and constant voltage (CV) strategy, which specifically included multiple charging stages with a short rest time in between, to simulate the charging behavior in real use. In order to deeply analyze the influence of charging strategies on battery performance, two batteries with highly similar charging strategies (numbered M1 and M2) were selected as representative samples for a subsequent detailed study, and their test parameters and related experimental results are summarized in Table 1 and Figure 1.

Table 1.
Cycling test conditions for M1 and M2.
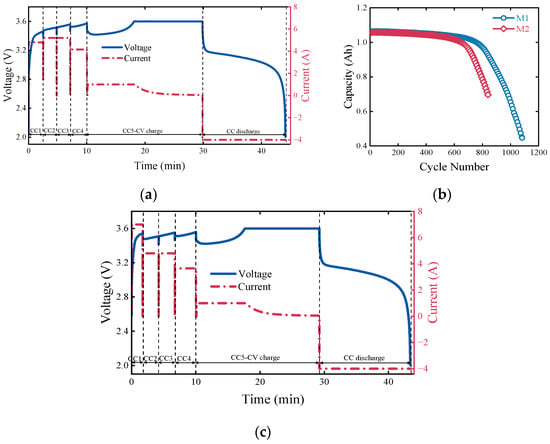
Figure 1.
(a,c) Complete charge/discharge curves for batteries M1 and M2; (b) capacity decay curves for M1 and M2.
2.2. Oxford Dataset
The dataset provided by Oxford contains a complete record of the ageing process of eight Kokam lithium-ion batteries with a rated capacity of 740 mAh []. The experiment was conducted at a constant ambient temperature of 40 °C, and the batteries were subjected to 2 C constant current charge/discharge cycles based on ARTEMIS urban driving conditions to simulate the battery workload in a real urban traffic environment. In order to monitor the changes in battery performance, after every 100 simulated cycles, the researchers conducted a 1 C constant-current charge/discharge characterization test on the batteries to assess their capacity changes. It is worth noting that the discharge process cut-off for the simulated condition cycle was ~3.6 V, while the discharge cut-off voltage in the characterization test was lower, at ~2.7 V, to obtain more comprehensive performance data. The relevant test conditions are detailed in Table 2. Figure 2a demonstrates the capacity decay curves of the eight batteries during the aging process, while Figure 2b,c present the changes of voltage and current during charging and discharging, respectively, which provide an important data base for subsequent modelling and capacity estimation.

Table 2.
Cycle test conditions for Cells 1–8.
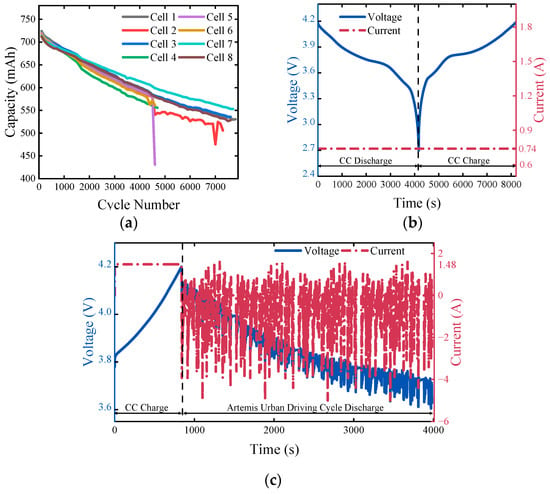
Figure 2.
(a) Capacity decay curve of Cells 1–8; (b) voltage and current variation curves under characteristic test conditions; (c) variation curves of voltage and current under simulated working conditions.
It is worth noting that cells 1 and 8 showed faster decay rates, likely due to manufacturing tolerances or subtle differences in thermal management during testing. This variability underscores the importance of individual cell modeling, as addressed by our approach using intra-pack training/testing splits. In addition, the decay curve followed a roughly linear trend after an initial stabilization phase, aligning with electrochemical impedance growth and SEI film thickening mechanisms. The inflection point at ~4000 cycles for Cell 5 suggests accelerated aging due to repeated deep discharges in the ARTEMIS urban cycle, validating the sensitivity of capacity fade to duty cycle severity. At 40 °C, the higher ambient temperature accelerated the capacity decay compared to the values in the MIT dataset (30 °C, Figure 1b), consistent with Arrhenius kinetics, where a 10 °C increase elevated the degradation rates by 20–30% []. This highlights the necessity of thermal normalization in cross-condition capacity estimation, a challenge addressed by our universal health factor framework.
2.3. Battery Aging Experiment Under Simulated Ship Sailing Conditions
The purpose of this experiment was to evaluate the cycling performance and capacity degradation characteristics of a LiFePO4/C (LFP/C) cylindrical power battery under typical sailing conditions []. The NEWARE CTE-4008D-5V30A battery tester was chosen for the experimental setup, which has a high accuracy measurement capability of 0.05% FS and is operated by a central control computer and an upper computer. The structure of the experimental system is shown in Figure 3a. During the test, the battery was connected to the tester through the fixture and the data transmission line, the specific battery test conditions were set in the host computer to carry out cyclic aging experiments for the battery under a variety of conditions, and the data of the battery’s charging and discharging currents, voltages, and capacities were captured by the tester and then saved in the upper computer during the experiments. The middle computer acted as a communication hub connecting the host computer and the tester to realize the bidirectional transmission of commands and data. The test objects were two OXUN brand IFR26650 cylindrical lithium iron phosphate batteries, numbered C1 and C2, whose basic parameters are shown in Table 3, the working conditions simulated in the experiment were derived from the actual sailing data of the all-electric passenger ship “Jun Lv Hao” on 2 July 2023, and the original data were derived from the operation records of the battery cluster of the ship. The original data are shown in Figure 3b, and the real picture of the ship is exhibited in Figure 4. In the experimental design, in order to let the tested single cell discharge according to the real output current trajectory and at the same time to ensure experimental safety, the real output current was reduced by a certain proportion in the following way: firstly, the sampling time of the original working condition was shortened from 5 s to 1 s in order to save the experimental time and make the current more dynamic at the same time; secondly, the ampere–time integration method was used to calculate the discharge capacity under the real working condition after the discharge time was shortened; subsequently, the result obtained by dividing the discharge capacity value by 80% of the rated capacity of the battery under test was taken as the reduction ratio of the real output current; and finally, the output current under the real working condition after the discharge time was shortened was reduced according to this ratio to obtain the final simulated discharging condition. This method can make the trajectory of the reduced output current the same as the trajectory of the original condition, so as to simulate the sailing condition of the ship. The experimental cycle consisted of the following steps: charging at a constant current of 2 C to a voltage of 3.65 V and then charging at a constant voltage (CV) until the current dropped to 0.2 C, followed by a 5 min standstill; after that, executing a simulated operating condition discharge, which would consume 80% of the capacity of the battery under test; and then, executing another 4 C constant-current, high-speed discharge (with a cutoff voltage of 2 V) before stopping for 5 min again to complete the full cycle. The test was stopped when the battery capacity fell below 80% of the rated capacity []. The entire experiment was carried out at about 10–15 °C. The decay trend of the battery capacity is shown in Figure 3c, while the voltage and current change curves during charging and discharging are shown in Figure 3d. The complete test conditions and set parameters of this experiment are detailed in Table 4.
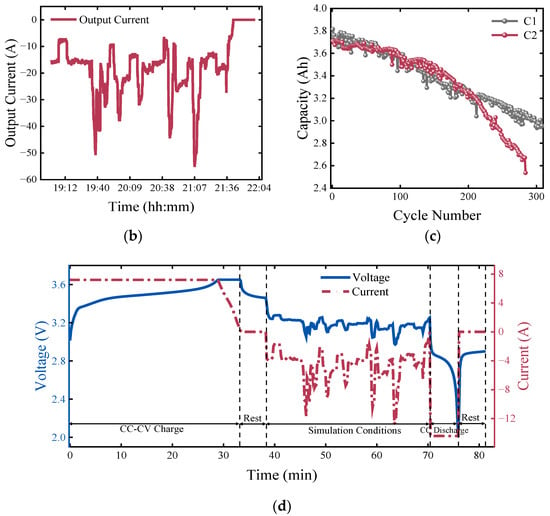
Figure 3.
(a) Battery testing system; (b) the current output under sailing conditions aboard the “Jun Lv Hao” passenger ship; (c) capacity decline curves for C1 and C2; (d) voltage and current change curves during cyclic testing.

Table 3.
Parameters of the IFR26650 LFP/C cylindrical power cell.

Figure 4.
Image of the “Jun Lv Hao” passenger ship.

Table 4.
Cycle test conditions for C1 and C2.
2.4. Data Analysis
This section aims to systematically analyze the experimental data of different types of lithium-ion batteries, focusing on the extraction of representative and universal health factors from the voltage and current curves under a variety of charging and discharging conditions, to provide a factor basis for whole-life capacity estimation. In practice, batteries are usually not fully discharged to their lowest cut-off voltage during use, but retain a certain amount of charge, and the common lower limit of discharge is about 30% SOC. Accordingly, the characteristic voltages of different types of batteries are defined; so, for NCM/C batteries, 30% SOC roughly corresponds to an open-circuit voltage (OCV) of 3.6 V, while the OCV of LFP/C batteries at the same SOC level is 3 V. Therefore, to ensure the practical significance and wide applicability of the analysis, the charging data of the batteries in the study interval from 30% SOC to 98% SOC were selected. In this range, the OCV of NCM/C batteries is from 3.6 V to 4 V, and that of LFP/C batteries is from 3 V to 3.6 V. This range can effectively reflect the performance evolution of batteries during aging in real scenarios.
2.4.1. Method of Extracting Universal Health Factors During the Charging Phase
The most common charging protocol is constant-current and constant-voltage charging, and as long as there is a constant-current stage, the incremental capacity (IC) curve can be extracted from it []. Incremental capacity analysis (ICA) for constant-current conditions is very helpful in capturing the health factor of a battery. This section takes Cell1, M1 and C1 as examples to describe the process of extracting universal health factors based on some constant-current charging data. First, the voltage curves and IC curves of the three cells in the constant-current charging stage for some SOC intervals under full life were plotted, as shown in Figure 5a–f. The SOH value can well characterize the available capacity of a battery. As the SOH value decreased under different cycles, the life of the battery was also constantly decaying. Along the direction of the black dashed arrow, the darker the color of the curve in the graph, the worse the SOH, and the less the capacity available for the current cycle.
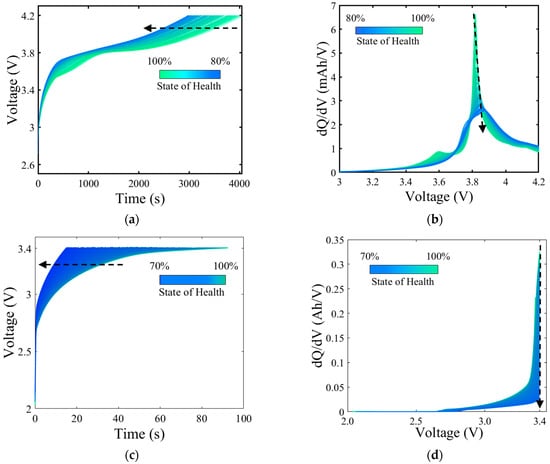
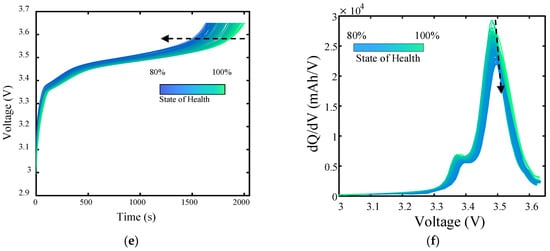
Figure 5.
Voltage curves and IC curves of partial constant-current charging stages. (a,b) Cell 1; (c,d) M1; (e,f) C1.
In the analysis of the charging data of the M1 battery, it was found that its fast charging process consisted of several constant-current charging stages with different multiplicities. In order to assess the feasibility of extracting the health factor in the constant-current stage, a section of the small-multiplier constant-current charging interval (shown in Figure 5c) located between 30 and 98% SOC was selected for the study as the target for factor extraction. As the number of cycles increased, the charging time required for this constant-current interval gradually shortened, which intuitively reflected the decreasing trend of the battery capacity. In order to further reveal this change, the study introduced the incremental capacity (IC) curve, which is the derivative of the charging capacity with respect to the terminal voltage. The IC curve can be used to describe the rate of change in capacity corresponding to the change in unit voltage of a battery during constant-current charging and can sensitively reflect the change in the electrochemical reaction of the battery material during aging, which is an effective tool to characterize the state of health of a battery. Under constant-current conditions, the IC value at different times of each cycle can be easily calculated by Equation (1):
Then, the IC curve cluster was plotted with the IC value as the ordinate and the voltage as the abscissa, and a Gaussian filter was used to smooth it []. Taking M1 with a complex charging condition as an example, although the selected constant-current charging condition was less than 2 min, the incremental capacity analysis of this stage could still be performed. Often at the beginning of charging, the voltage will have a short and rapid rise and then enter the stage of slow rise, that is, the voltage platform stage []. This stage is the main stage of battery capacity increase, causing the IC curve to change and peak. However, due to the reaction between the electrode material and the electrolyte during the charging and discharging process, lithium ions are consumed, and the electrolyte interface film is thickened, causing the peak of the IC curve to decrease as the battery capacity decays. This also directly leads to a gradual decrease in the area surrounded by the IC curve. In addition, in Figure 5b,f, the peak of the IC curve gradually shifts to the right, that is, as the battery capacity decays, the peak gradually appears in the later stage of the voltage platform. This is because the activity of lithium ions decreases, affecting the ion ability to correctly embed and de-embed, which also directly leads to the corresponding voltage point when the peak appears to gradually increase as the battery capacity decays. In summary, for the constant-current charging stage, the universal health factors that could be extracted were the charging time of the fixed SOC segment (HF1), the peak value of the IC curve (HF2), the voltage point corresponding to the peak of the IC curve (HF3), and the area surrounded by the IC curve (HF4).
Taking Cell1, M1 and C1 as examples, the universal health factors during the charging stage are shown in Figure 6. HF1, HF2 and HF4 of the three cells are plotted in Figure 6a–c respectively, and HF3 of Cell1 and C1 is plotted separately in Figure 6d.
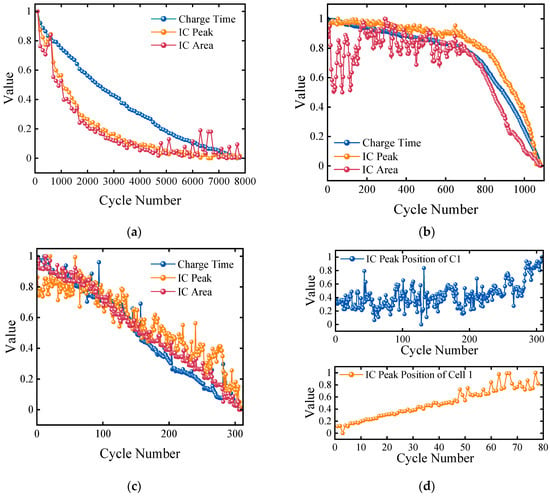
Figure 6.
Schematic diagram of universal health factors during the charging phase. (a) Cell 1; (b) M1; (c) C1; (d) the voltage point corresponding to the peak value of Cell 1 and C1.
It is worth noting that not all batteries allow for the full extraction of these four factors. For example, for batteries like M1 with complex charging conditions and a very short constant-current charging segment, the peak points of the IC curves of many cycles do not appear; so, the factor of the voltage point corresponding to the peak cannot be extracted. In practice, the four universal health factors should be selected in combination with the actual working conditions. In addition, in order to avoid the influence of training data of different magnitudes on the model, all universal health factors were standardized using range normalization according to Equation (2) before training the model.
2.4.2. Extraction of Universal Health Factors During the Dynamic Discharging Phase
Under complex discharge conditions, the traditional differential capacity analysis (ICA) method based on constant-current discharge is no longer applicable, and common health factors, such as discharge time, lack consistency and generality under different discharge conditions. Therefore, there is an urgent need to explore common health indicators that can be stably extracted under non-constant-current, real-world operating conditions. C1 was taken as a research object to analyze its performance under complex simulated discharge conditions. The battery was discharged from 98% SOC, and as the number of cycles increased, it was observed that the voltage curve at the end of the discharge gradually sank, showing a gradually deepening color (shown in Figure 7a). This change indicates that the voltage drop rate of the battery kept accelerating under the same discharge starting state. Further analysis revealed that there was an obvious negative correlation between the voltage drop rate and the battery lifetime: as the lifetime declined, the voltage drop per unit time increased. This phenomenon provided a basis for extracting the universal health factor, denoted as HF5, which is highly correlated with the battery health state in complex discharge scenarios. The voltage across the battery after each cycle of discharge was recorded, as shown in Figure 7b.
Figure 7.
(a) Voltage curve cluster of full-life simulation working conditions; (b) universal health factors under dynamic discharge conditions.
2.4.3. Correlation Analysis
The DCC was introduced to overcome the limitations of the Pearson correlation coefficient, which measures only linear associations and fails to effectively capture nonlinear dependencies [,]. It was employed to measure the correlation between the health factors and the capacity, with the capacity series denoted as:
Denote the sequence of health factors for each cell as:
where n represents the number of universal health factors, and m denotes the cycle life for each cell.
The distance correlation coefficients were calculated for each health factor sequence in relation to the capacity sequences using the following formula:
where and represent the standard deviation of the distance for the capacity and the health factors, respectively.
The universal health factors extracted are directly linked to critical electrochemical processes in lithium-ion batteries. The charging time (HF1) reflects the declining lithium-ion diffusion efficiency in electrodes, which is accelerated by SEI film thickening and active material loss during aging []. The IC peak (HF2) and IC area (HF4) are sensitive to the redox reaction kinetics at the electrode–electrolyte interface. A declining peak indicates reduced lithium-ion availability due to electrode particle cracking or electrolyte consumption []. The IC peak position (HF3) shifts to higher voltages with aging, signaling increased charge transfer resistance from SEI film growth []. The terminal voltage after simulation (HF5) under dynamic discharge correlates with the battery’s internal resistance, which rises due to lithium plating and electrode degradation under non-constant-current loads [].
Table 5 lists the distance correlation coefficients between the factors of the batteries in each training set and their capacity decay sequences. Since the voltage data after each simulated condition were not recorded in the data file of Cell1, HF5 was not extracted. In addition, since the discharge condition of M1 was a constant-current condition, and each cycle was discharged at a constant current to the lower cut-off voltage, HF5 could not be extracted. It is not difficult to find from the table that the features extracted from the short-time constant-current charging stage showed a high correlation with the capacity; only HF3 of C1 had a low correlation, which may be related to external factors such as experimental equipment and data recording. Furthermore, the dynamic load-induced capacity fluctuations exhibited nonlinear correlations with HF5, which the DCC could identify more effectively. During the subsequent model testing, the batteries’ input factors in the test set were not evaluated for their correlation with the capacity, as the capacity sequences of these batteries are unknown in practical applications.

Table 5.
Results of the correlation analysis between each health factor and the capacity.
2.5. The KOA-TCN-BiGRU Method
2.5.1. KOA
The Kepler optimization algorithm (KOA) is an intelligent optimization algorithm inspired by Kepler’s laws of planetary motion, the core idea of which is to find the global optimal solution by simulating a planet’s orbit around the Sun []. In this algorithm, each individual in the search space is analogous to a ‘planet’, and the optimal solution is regarded as the “sun”. The position and motion state of an individual are dynamically updated with iterations, thus allowing for gradually approaching the global optimal solution. The optimization process of KOA consists of the following three key steps []:
- Step 1: Initialization
Denote the population size as N and the solution space dimension as d. The initial position of the i th planet in the j th dimension is randomly generated by []:
Additionally, the orbital eccentricity of each planet is similarly initialized with a random number []:
The orbital period is randomly generated based on a normal distribution []:
- Step 2: Defining the Gravitational Force
The gravitational relationship between the planets and the Sun is defined, and the magnitude of the attraction is calculated based on the differences in their positional distance and fitness (i.e., mass) [], defined as:
where is a small constant preventing division by zero; ; and are the normalized masses of and , respectively; is the gravitational constant decaying with iteration; and is the normalized Euclidean distance. The formulas for , , and are as follows []:
- Step 3: Calculating an Object’s Velocity and Updating Objects’ Positions
The KOA includes two types of updates, “far planets” and “near planets”, based on the relative distance of the planets from the Sun, to enhance exploration and utilization, respectively []. When a planet moves away from the Sun, its new position is calculated by the following formula []:
As the planet approaches the Sun, its new position is obtained using the elliptical orbit deformation formula []:
For any planet, the new position is retained if it is better than the old position, otherwise the old position continues to be retained []:
2.5.2. TCN
The temporal convolutional network (TCN) is intended to extract key features without relying on prior capacity information, thereby providing a foundation for accurate capacity estimation in real-world scenarios. At the same time, the short-term, medium-term and long-term “capacity evolution patterns” are mined by using convolution kernels of different scales.
The TCN [] is a convolution-based deep learning architecture tailored for sequence modeling tasks. Compared to the traditional recurrent neural networks (RNNs), the TCN offers improved parallelism, flexible receptive field control, and stable gradient propagation, which makes it highly suitable for long-term dependency modeling with time series data such as those related to battery health evolution.
A TCN block typically integrates three core components:
(1) Causal convolution: To preserve the temporal order and avoid future data leakage, causal convolution ensures that the prediction at time t is only influenced by inputs from time t and earlier. The prediction probability is formulated as []:
(2) Dilated convolution: To capture long-range dependencies without increasing the network depth significantly, dilated convolutions introduce a dilation factor d, allowing the receptive field to grow exponentially with the number of layers. The output of a dilated convolution is given by []:
where is the kernel size, is the dilation rate, and is the filter weight at position .
(3) Residual connections: To mitigate gradient vanishing and enhance convergence, residual connections are used. The residual output is computed as []:
where is the input, is the output of convolution operations, and is an activation function.
Through the combination of causal, dilated convolutions and residual learning, the TCN effectively models complex temporal features and maintains stable training even in deep architectures. This makes it particularly suitable for capturing nonlinear and multi-scale degradation patterns in lithium-ion battery capacity sequences.
The overall structure of the TCN comprises dilated convolution and residual connection modules, as illustrated in Figure 8. The ReLU (rectified linear unit) activation function is applied within the residual modules to introduce non-linearity, which is critical for capturing the complex, non-linear degradation patterns in battery capacity trajectories. The “ReLU” addresses the vanishing gradient problem common in deep networks, enabling the model to learn hierarchical features effectively. Specifically, in each residual block, the ReLU is used after the dilated convolution layers to enhance the model’s ability to distinguish subtle changes in health factors, such as the voltage plateau shifts and IC curve variations shown in Figure 5. This design choice aligns with previous studies [,], which demonstrated that the ReLU improves convergence speed and feature representation in time series modeling tasks, particularly for capturing the non-linear relationship between battery aging mechanisms and capacity fade. “Conv” refers to the convolution kernel sliding over the input data to extract local patterns. To enhance the model’s ability to capture historical dependencies and improve its overall performance, the residual connection module is commonly incorporated, consisting of several essential components. Firstly, one-dimensional dilated causal convolution enlarges the receptive field without increasing the computational complexity, effectively captures long-term dependencies, and prevents future information leakage through its causal design. Secondly, weight normalization standardizes the parameter distribution and improves the training stability, while a dropout layer mitigates the risk of overfitting by randomly deactivating certain neurons. Finally, a 1 × 1 convolution layer adjusts the input and output channel dimensions to maintain consistency within the residual connection.
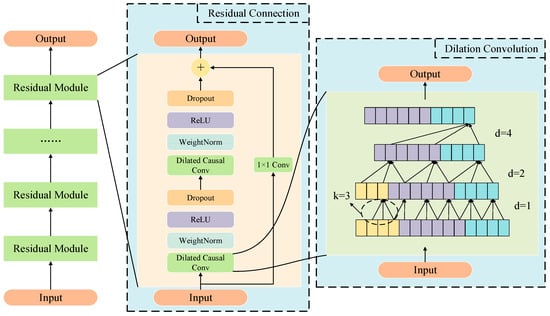
Figure 8.
TCN structure diagram.
2.5.3. BiGRU
The bidirectional gated recurrent unit (BiGRU) is widely used in time series prediction and other fields and involves running two standard GRU networks simultaneously in forward and reverse directions to achieve the comprehensive modeling of information before and after the current moment in the sequence, which enhances the ability of capturing the context. The overall structure of the GRU is depicted in Figure 9. The overall structure of the TCN combined with the BiGRU is shown in Figure 10.
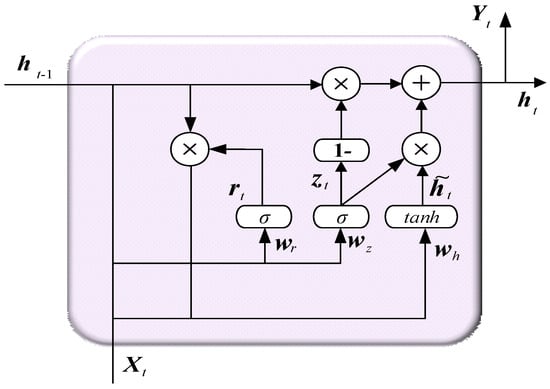
Figure 9.
GRU structure diagram.
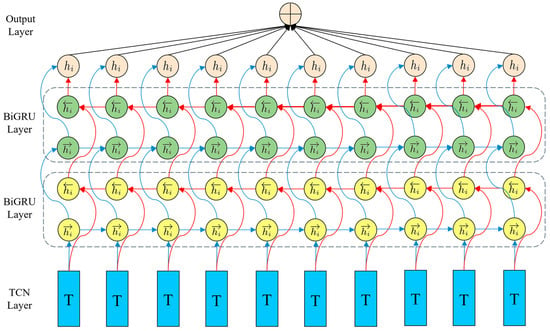
Figure 10.
TCN-BiGRU structure diagram.
The BiGRU is an enhanced recurrent neural network architecture that integrates the outputs of two independent GRU layers processing sequences in forward and backward directions, enabling bidirectional temporal dependency modeling. Its core mechanism comprises update and reset gates: the update gate determines the retention ratio of historical information through a sigmoid function, while the reset gate governs the degree of hidden state forgetting. The forward GRU layer processes input sequences chronologically, whereas the backward GRU layer operates inversely. The final hidden states from both directions are fused through fully connected layers. This bidirectional information flow empowers the model to capture long-range dependencies while effectively mitigating gradient vanishing issues. Compared with the conventional unidirectional GRU, the BiGRU demonstrates superior contextual modeling capability and parameter efficiency through its dual-directional feature integration. The formulas for the update gate , reset gate , candidate hidden states and hidden states are as follows []:
The current capacity of a cell is not only directly affected by the current working conditions, but also closely related to its historical state changes and future trends. Therefore, when building an estimation model, the correlation between the before and the after states in the time series must be fully considered to improve the accuracy and robustness of the estimation. To achieve this goal, this paper introduces a bidirectional gated recurrent unit (BiGRU) structure in model training. The BiGRU effectively enhanced the model’s ability to understand global time series features by modeling the time series in both directions simultaneously—i.e., processing historical information in the forward direction and capturing future trends in the reverse direction. In this structure, the hidden layer output at each moment is not only determined by the current input and the forward hidden state of the previous moment but also fuses the output of the reverse hidden layer, thus realizing a richer expression of information. This two-way fusion mechanism enables the model to capture the dynamic change characteristics of the battery capacity evolution problem in a more comprehensive way when dealing with it, providing strong support for accurate modeling []. In the BiGRU, its hidden layer output is determined by the current input , the output of the previous moment and the output of the inverse hidden layer combined as follows []:
2.5.4. Estimation Process
In real scenarios, several cells of the same type are often connected in series and parallel to form battery packs, battery groups, and battery clusters. Therefore, three sets of training sets and test sets were set. For Cells 1–8, the eight cells were in the same working condition; so, Cell 1 was used as the training set, and Cells 2–8 were used as the test set. Similarly, among M1, M2, C1 and C2, M1 and C1 were used as training sets, and another cell under the same working condition was used as the test set. This section takes the test process of Cells 2–8 as an example to describe the model construction, training and testing process in detail. The overall framework of the proposed method is drawn in Figure 11.
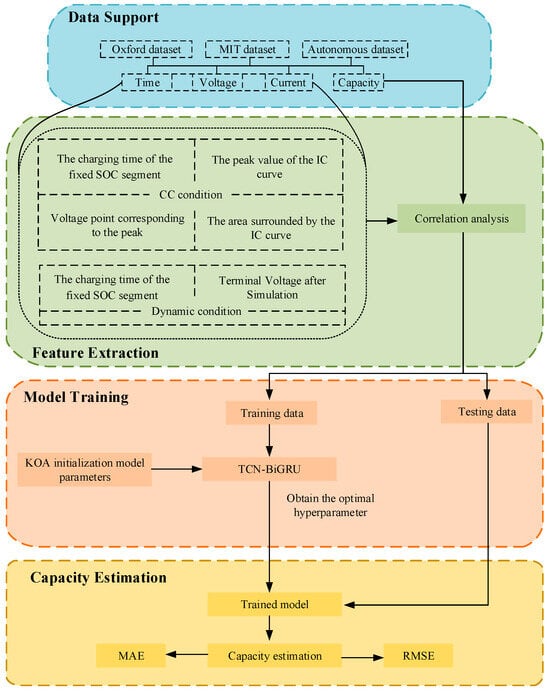
Figure 11.
Framework of the proposed capacity estimation method.
The proposed deep learning model was implemented in MATLAB R2023a using the “layerGraph()” and “addLayers()” functions. The model was designed for a multi-input single-output prediction task, where multiple health-related variables are used to predict the current capacity of lithium-ion battery cells under complex working conditions. The dataset used for training comprised several universal health indicators and their corresponding capacity labels. After preprocessing and normalization using the “mapminmax()” function, the input features of each cell were structured as sequences of size 4 × 78 (4 health factors over 78 characteristic test times), while the output was the corresponding capacity sequence of size 1 × 78. All data were reshaped into cell array format to suit a sequence-based model input. The model architecture integrates a TCN and a BiGRU. The network was constructed in a modular fashion with the following components:
- (1)
- Input layer: the sequenceInputLayer(f) function is used, where = 4;
- (2)
- TCN module: two causal convolution blocks with dilation factors = 1, 2; each block includes a “convolution1dLayer”, a “layerNormalizationLayer”, a “dropoutLayer” and residual connections via an “additionLayer”; number of filters: 64; kernel size: 5; dropout rate: 0.005;
- (3)
- BiGRU module: two GRU layers of size 35—one for the forward sequence, one for the backward sequence (via “FlipLayer”); the outputs were concatenated with the “concatenationLayer”;
- (4)
- Output layer: a fully connected layer followed by the “regressionLayer”.
The initial (unoptimized) model is trained using the trainNetwork() function. The training settings are as follows: optimizer, adam; maximum epochs, 100; initial learning rate, 0.01; gradient threshold, 1; number of neurons in the GRU layer, 35; L2 regularization, 0.0001; and training environment, CPU. These settings ensures convergence while preventing overfitting on relatively small sample sequences.
In order to improve the performance of the battery capacity estimation model, the KOA is used to automatically tune the key hyperparameters. These hyperparameters to be optimized included the number of neurons in the GRU layer, the L2 regularization coefficient, and the initial learning rate, all three of which had an important impact on the convergence speed and prediction accuracy of the model. In the optimization process, the KOA updates the individuals in the search space by simulating the motion patterns of the planets around the Sun and measures the prediction accuracy of the model on the validation set using the mean absolute percentage error (MAPE) as the objective function:
where is the length of the sequence, and and represent the true and the predicted values, respectively. Initially, the initial value of the objective function (i.e., the optimal solution) is set to infinity. The iteration continues until the parameter that minimizes the MAPE value is found, provided that the objective function value continues to improve upon the previously recorded optimum after each iteration.
Once trained, the model was used to predict the capacity of the test set using the “predict()” function, taking the Cells 2–8’s factor data as input, and provided the capacity as output. The predicted outputs were then denormalized with the “mapminmax(‘reverse’, …)” function.
2.6. Uncertainty Analysis
The reliability of capacity estimation is inherently linked to the precision of the experimental devices and the stability of the operational conditions. This section systematically evaluates potential uncertainty sources in the experimental setup and their impacts on the reported results.
The NEWARE CTE-4008D-5V30A battery tester used in this study has a nominal measurement accuracy of 0.05% full scale (FS) for voltage and current []. However, cumulative errors may arise from the following elements:
- (1)
- Voltage/current sampling resolution: limited by the analog-to-digital converter (ADC) precision, small-amplitude signals (e.g., low-current charging phases) may introduce quantization errors, potentially distorting the incremental capacity (IC) curves and derived health factors (HF1–HF4).
- (2)
- Thermal drift in sensors: ambient temperature control during the experiments was maintained at 30 ± 1 °C for the MIT datasets and at 10–15 °C for the “Jun Lv Hao” simulation [,]; fluctuations beyond this range could alter battery impedance and capacity, leading to inconsistent health factor extraction.
- (3)
- Contact resistance in test fixtures: intermittent electrical connections during long-term cycling tests may cause abrupt voltage drops, misattributed as capacity degradation in the model.
3. Results
3.1. Evaluation Criteria
The overall trend of the estimation error was captured by two assessment metrics: the MAE and the RMSE. The calculation was as follows:
3.2. Estimated Results and Errors for Each Cell Capacity
The capacity estimation results of each cell in the test set and the error results with the true value are plotted in Figure 12. Figure 12a–l,p show the estimation results and errors of Cells 2–8; Figure 12n,q report the estimation results and errors of M2, respectively; Figure 12q,r display the estimation results and errors of C2, respectively. The MAE and RMSE values of the predicted capacity sequence and the true capacity sequence are shown in Figure 13 and Figure 14 in the form of bar charts and pie charts, respectively.
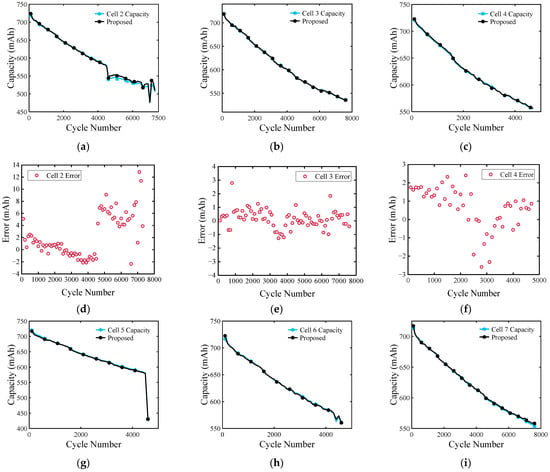
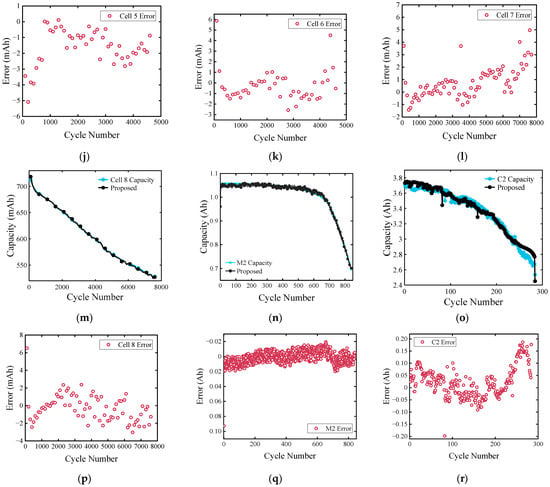
Figure 12.
Full-life capacity estimation results and errors. (a–m,p) Cells 2–8; (n,q) M2; (o,r) C2.
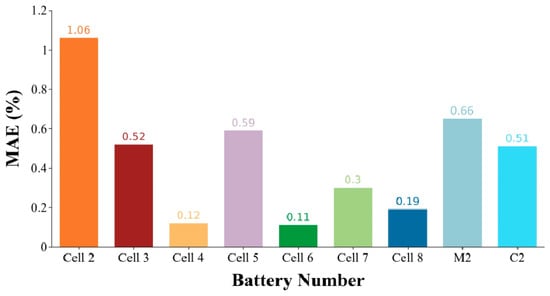
Figure 13.
MAE calculation results for each cell.
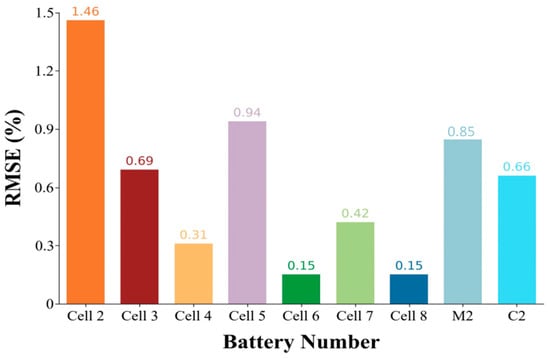
Figure 14.
RMSE calculation results for each cell.
4. Discussion
Judging from the estimation results, the proposed method can achieve good results for the full-life capacity estimation of single cells in a battery pack working under the same working conditions.
For Cells 2–8, the capacity decay trajectory of each cell can be well grasped. The fluctuations at the end of the life of Cell2 and Cell5 can also be well captured. At the end of the life of Cell 2, the maximum capacity prediction error was only 14 mAh; for Cell 5, the maximum capacity prediction error was only 5 mAh, which could well capture the sudden change of capacity. For the other cells in the same group, Figure 13 and Figure 14 clearly show that the overall prediction error indicators MAE and RMSE of the full-life capacity decay curve were kept below 1%. This shows the prediction performance of the developed model. For Cell 2–8 under Oxford dataset conditions (40 °C, Figure 2), the MAE of 0.52–1.06% highlights the model’s robustness at elevated temperatures. In contrast, M2’s higher early-life error (1.20% MAE) correlated with thermal drift in its multi-stage charging protocol, where rapid current changes induced localized heating (Figure 1c). This underscores the importance of integrating real-time temperature feedback into deep learning frameworks for maritime applications.
For M2, due to the complex charging conditions, the correlation between the universal characteristic factors that could be extracted and the capacity sequence was not high, which directly affected the estimation ability of the model. Therefore, in the early stage of life, the estimation error of the developed model was slightly larger, but near the end of life, the error gradually decreased to 6 mAh, and the MAE and RMSE values were also stable, under 1%.
For C2, HF5 could provide information that was strongly correlated with capacity attenuation, which is of great help for capacity estimation under complex working conditions. Although the error tended to increase in the later period, the MAE and RMSE values were both below 1% overall.
A comparison with some of the latest available methods on a common tested battery dataset was performed as fairly as possible, the evaluation metrics used for the comparison were set as mean absolute error (MAE) and root-mean-square error (RMSE), and the results of the comparison are recorded in Table 6.

Table 6.
The comparation of the proposed method with other published methods.
The CNN-CBAM-LSTM model [], presented the lowest error values on multiple cells with the Oxford dataset but used data from two cells (Cell 1 and Cell 8) to train the model; IWOA-VFOS-ELM [] used Cell 1 and Cell 2 to train the model, and Cell 3, Cell 6, Cell 7 and Cell 8 for testing. For battery M2 under dynamic operating conditions, only the PINN model [] had a slightly higher estimation accuracy than the proposed method, but its computational complexity may hinder its real-time implementation on onboard embedded systems. It can be seen that the proposed method was able to maintain the best estimation accuracy most of the time with the least amount of training data, which can indicate the superior performance of the proposed method.
The observed estimation errors (MAE/RMSE < 1%) reflect not only the model’s performance but also the cumulative impact of experimental uncertainties. For example, the slightly higher errors in M2’s early-life estimation (Figure 12n) may have stemmed from ADC resolution limitations during its multi-stage charging protocol, which amplified the noise in HF1–HF4 extraction. Similarly, the late-life error increase for C2 (Figure 12r) could be linked to thermal drift in the NEWARE tester’s current sensor, which introduced spurious fluctuations in HF5 during high-power discharge cycles. These findings underscore the importance of integrating real-time sensor diagnostics into future iterations of the model to further improve its robustness.
5. Conclusions
This paper focused on the capacity estimation of lithium battery systems for fuel cell vessels. In order to cope with the challenge of capacity estimation under dynamic working conditions, the use of universal health factors combined with a deep learning model is proposed, and the following conclusions were drawn.
The correlation between a characteristic factor and the capacity sequence greatly affects the prediction performance of the model. According to previous studies, the health factors extracted from the complete charge and discharge data are often more correlated with the capacity sequence. When the battery is fully charged and discharged, the extracted factors can better characterize the battery capacity decay. However, in real scenarios, features can only be extracted from part of the charge and discharge data, and in order to cope with variable working conditions, extracting highly correlated and universal health factors provides great help for capacity estimation. In addition, the TCN was introduced to further extract features from the input health factors instead of performing a manual screening, because in real scenarios, the input factors can only be selected based on prior knowledge of the characteristic factor priority, and the health factors cannot be correlated with the capacity sequence of the tested battery cell. The introduction of the intelligent optimization algorithm KOA to determine the key parameters avoids manual parameter adjustment. From the results, the TCN-BiGRU model performs well and can be used for the capacity estimation of single cells working under complex working conditions in real scenarios.
While this study provides a robust framework for capacity estimation under complex marine conditions, several avenues for future research warrant exploration to further enhance the model’s applicability and scalability:
(1) Scalability to large-scale battery packs: The current model was validated on single cells within a battery pack, but extending it to multi-string battery systems (e.g., series–parallel configurations in fuel cell ships) requires addressing inter-cell variability and thermal runaway risks. For large-format pouch cells or batteries with >10 Ah capacity, the thermal and ionic transport dynamics may differ, requiring adjusted feature extraction or additional physics-based corrections.
(2) Exploration of advanced battery chemistries: The study focused on LFP/C batteries, but emerging technologies like solid-state lithium metal batteries or lithium–sulfur batteries demand adapted health factor extraction strategies.
(3) Long-term performance under dynamic environmental conditions: The current experiments were limited to controlled temperatures (25–40 °C), but the maritime environments often involve wide temperature gradients (e.g., from −10 °C in cold regions to 60 °C in engine rooms). Future work will focus on developing thermal-aware hybrid models that couple electrochemical thermal models (e.g., Newman’s porous electrode theory []) with TCN-BiGRU, enabling real-time capacity estimation under extreme marine temperatures, and validating across ice-class vessel scenarios (−10 °C to 60 °C).
Author Contributions
Conceptualization and methodology, J.T.; software, Q.S.; validation, Y.L., Y.C. and Q.S.; formal analysis and investigation, J.T.; resources, X.Y.; data curation, J.T.; writing—original draft preparation, J.T. and T.T.; writing—review and editing, X.Y.; visualization and supervision, L.L. and X.Z.; project administration and funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (Grant No: 2023YFB4301704) and the China National Key Laboratory of Electromagnetic Energy Technology Open Fund (Grant No: 61422172220403).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| PEMFCs | Proton-exchange membrane fuel cells |
| SEI | Solid–electrolyte interphase |
| CNN | Convolutional neural network |
| RNN | Recurrent neural network |
| LSTM | Long short-term memory |
| TCN | Temporal convolutional network |
| BiGRU | Bidirectional gated recurrent unit |
| KOA | Kepler optimization algorithm |
| DCC | Distance correlation coefficient |
| C(k) | Capacity for the kth cycle |
| DCC of the capacity series to the i th factor | |
| Predicted probability | |
| Convolutional output | |
| True value of capacity | |
| MIT | Massachusetts Institute of Technology |
| SOH | State of health |
| RUL | Remaining useful life |
| SOC | State of charge |
| CC | Constant current |
| CV | Constant voltage |
| ICA | Incremental capacity analysis |
| HF | Health factor |
| MAE | Mean absolute error |
| RMSE | Root-mean-square error |
| MAPE | Mean absolute percentage error |
| Value of the kth cycle of the ith factor | |
| Gravitation between planets and the Sun | |
| Network output of dilation convolution | |
| Output of the residual connection | |
| Predicted capacity value |
References
- Wang, Z.; Li, M.; Zhao, F.; Ji, Y.; Han, F. Status and Prospects in Technical Standards of Hydrogen-Powered Ships for Advancing Maritime Zero-Carbon Transformation. Int. J. Hydrogen Energy 2024, 62, 925–946. [Google Scholar] [CrossRef]
- Li, X.; Ju, L.; Geng, G.; Jiang, Q. Data-Driven State-of-Health Estimation for Lithium-Ion Battery Based on Aging Features. Energy 2023, 274, 127378. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, B.; Wang, Y.; Li, M.; Liu, H.; Han, F. Analysis and Evaluation of Fuel Cell Technologies for Sustainable Ship Power: Energy Efficiency and Environmental Impact. Energy Convers. Manag. X 2024, 21, 100482. [Google Scholar] [CrossRef]
- Gürbüz, H.; Akçay, H.; Demirtürk, S.; Topalcı, Ü. Techno-Enviro-Economic Comparison Analysis of a PEMFC and a Hydrogen-Fueled SI Engine. Appl. Therm. Eng. 2024, 243, 122528. [Google Scholar] [CrossRef]
- Lü, X.; Qu, Y.; Wang, Y.; Qin, C.; Liu, G. A Comprehensive Review on Hybrid Power System for PEMFC-HEV: Issues and Strategies. Energy Convers. Manag. 2018, 171, 1273–1291. [Google Scholar] [CrossRef]
- Lu, J.; Abed, A.M.; Nag, K.; Fayed, M.; Deifalla, A.; Al-Zahrani, A.; Ghamry, N.A.; Galal, A.M. Optimization of a Near-Zero-Emission Energy System for the Production of Desalinated Water and Cooling Using Waste Energy of Fuel Cells. Chemosphere 2023, 336, 139035. [Google Scholar] [CrossRef]
- Vanem, E.; Salucci, C.B.; Bakdi, A.; Alnes, Ø.Å.S. Data-Driven State of Health Modelling—A Review of State of the Art and Reflections on Applications for Maritime Battery Systems. J. Energy Storage 2021, 43, 103158. [Google Scholar] [CrossRef]
- Naseri, F.; Barbu, C.; Sarikurt, T. Optimal Sizing of Hybrid High-Energy/High-Power Battery Energy Storage Systems to Improve Battery Cycle Life and Charging Power in Electric Vehicle Applications. J. Energy Storage 2022, 55, 105768. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.; Yao, L.; Zheng, J.; Fang, Z.; Shen, Y. A Comprehensive Review of the Lithium-Ion Battery State of Health Prognosis Methods Combining Aging Mechanism Analysis. J. Energy Storage 2023, 65, 107347. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A Review of the State of Health for Lithium-Ion Batteries: Research Status and Suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
- Ju, L.; Li, X.; Geng, G.; Jiang, Q. Degradation Diagnosis of Lithium-Ion Batteries Considering Internal Gas Evolution. J. Energy Storage 2023, 71, 108084. [Google Scholar] [CrossRef]
- Ju, L.; Long, P.; Geng, G.; Jiang, Q. Open Circuit Voltage—State of Charge Curve Calibration by Redefining Max–Min Bounds for Lithium-Ion Batteries. J. Energy Storage 2024, 79, 110224. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A Novel Gaussian Process Regression Model for State-of-Health Estimation of Lithium-Ion Battery Using Charging Curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Gu, X.; See, K.W.; Li, P.; Shan, K.; Wang, Y.; Zhao, L.; Lim, K.C.; Zhang, N. A Novel State-of-Health Estimation for the Lithium-Ion Battery Using a Convolutional Neural Network and Transformer Model. Energy 2023, 262, 125501. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Health Indicator and Gaussian Process Regression Model. IEEE Access 2019, 7, 39474–39484. [Google Scholar] [CrossRef]
- Sun, J.; Kainz, J. State of Health Estimation for Lithium-Ion Batteries Based on Current Interrupt Method and Genetic Algorithm Optimized Back Propagation Neural Network. J. Power Sources 2024, 591, 233842. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Li, P.; Lin, X.; Bian, X. Data-Driven Battery State of Health Estimation Based on Random Partial Charging Data. IEEE Trans. Power Electron. 2022, 37, 5021–5031. [Google Scholar] [CrossRef]
- Chen, L.; Bao, X.; Lopes, A.M.; Xu, C.; Wu, X.; Kong, H.; Ge, S.; Huang, J. State of Health Estimation of Lithium-Ion Batteries Based on Equivalent Circuit Model and Data-Driven Method. J. Energy Storage 2023, 73, 109195. [Google Scholar] [CrossRef]
- Liu, F.; Liu, X.; Su, W.; Lin, H.; Chen, H.; He, M. An Online State of Health Estimation Method Based on Battery Management System Monitoring Data. Int. J. Energy Res. 2020, 44, 6338–6349. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Z.; Liu, P.; Zhao, Y.; Cui, D.; Wang, Z. Data-Driven Battery State-of-Health Estimation and Prediction Using IC Based Features and Coupled Model. J. Energy Storage 2023, 72, 108413. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic Health Condition for Lithium Battery Using the Partial Incremental Capacity and Gaussian Process Regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-Health Estimation for Li-Ion Batteries by Combing the Incremental Capacity Analysis Method with Grey Relational Analysis. J. Power Sources 2019, 410–411, 106–114. [Google Scholar] [CrossRef]
- Chang, C.; Wang, Q.; Jiang, J.; Wu, T. Lithium-Ion Battery State of Health Estimation Using the Incremental Capacity and Wavelet Neural Networks with Genetic Algorithm. J. Energy Storage 2021, 38, 102570. [Google Scholar] [CrossRef]
- Tang, T.; Yang, X.; Li, M.; Li, X.; Huang, H.; Guan, C.; Huang, J.; Wang, Y.; Zhou, C. Deep Learning Model-Based Real-Time State-of-Health Estimation of Lithium-Ion Batteries under Dynamic Operating Conditions. Energy 2025, 317, 134697. [Google Scholar] [CrossRef]
- Attia, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.-H.; Chen, M.H.; Cheong, B.; Perkins, N.; Yang, Z.; et al. Closed-Loop Optimization of Fast-Charging Protocols for Batteries with Machine Learning. Nature 2020, 578, 397–402. [Google Scholar] [CrossRef]
- Xu, H.; Wu, L.; Xiong, S.; Li, W.; Garg, A.; Gao, L. An Improved CNN-LSTM Model-Based State-of-Health Estimation Approach for Lithium-Ion Batteries. Energy 2023, 276, 127585. [Google Scholar] [CrossRef]
- He, J.; Bian, X.; Liu, L.; Wei, Z.; Yan, F. Comparative Study of Curve Determination Methods for Incremental Capacity Analysis and State of Health Estimation of Lithium-Ion Battery. J. Energy Storage 2020, 29, 101400. [Google Scholar] [CrossRef]
- Goh, H.H.; Lan, Z.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C. Estimation of the State of Health (SOH) of Batteries Using Discrete Curvature Feature Extraction. J. Energy Storage 2022, 50, 104646. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, Y.; Wang, C.; Tian, J.; Chen, X.; Li, H.; Zhang, Q. A Data-Driven Method for Extracting Aging Features to Accurately Predict the Battery Health. Energy Storage Mater. 2023, 57, 460–470. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Azeem, S.A.A.; Jameel, M.; Abouhawwash, M. Kepler Optimization Algorithm: A New Metaheuristic Algorithm Inspired by Kepler’s Laws of Planetary Motion. Knowl.-Based Syst. 2023, 268, 110454. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Mao, R.; Li, L.; Hua, W.; Zhang, J. Remaining Useful Life Prediction for Lithium-Ion Batteries with a Hybrid Model Based on TCN-GRU-DNN and Dual Attention Mechanism. IEEE Trans. Transp. Electrif. 2023, 9, 4726–4740. [Google Scholar] [CrossRef]
- Zhou, G.; Guo, Z.; Sun, S.; Jin, Q. A CNN-BiGRU-AM Neural Network for AI Applications in Shale Oil Production Prediction. Appl. Energy 2023, 344, 121249. [Google Scholar] [CrossRef]
- Tang, A.; Jiang, Y.; Yu, Q.; Zhang, Z. A Hybrid Neural Network Model with Attention Mechanism for State of Health Estimation of Lithium-Ion Batteries. J. Energy Storage 2023, 68, 107734. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, H.; Zhang, Y.; Shen, S.; Shen, J.; Liu, Y. State of Health Estimation for Lithium-Ion Batteries Based on Temperature Prediction and Gated Recurrent Unit Neural Network. J. Power Sources 2022, 521, 230892. [Google Scholar] [CrossRef]
- Duan, W.; Song, S.; Xiao, F.; Chen, Y.; Peng, S.; Song, C. Battery SOH Estimation and RUL Prediction Framework Based on Variable Forgetting Factor Online Sequential Extreme Learning Machine and Particle Filter. J. Energy Storage 2023, 65, 107322. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Garg, A.; Gao, L. Enhancing Real-Time Degradation Prediction of Lithium-Ion Battery: A Digital Twin Framework with CNN-LSTM-Attention Model. Energy 2024, 286, 129681. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Y.; Zhao, Z.; Xia, H.; Chen, Z.; Zhang, Y. Automatic Feature Extraction-Enabled Lithium-Ion Battery Capacity Estimation Using Random Fragmented Charging Data. IEEE Trans. Transp. Electrif. 2024, 10, 8845–8856. [Google Scholar] [CrossRef]
- Tao, T.; Ji, C.; Dai, J.; Rao, J.; Wang, J.; Sun, W.; Romagnoli, J. Data-Based Health Indicator Extraction for Battery SOH Estimation via Deep Learning. J. Energy Storage 2024, 78, 109982. [Google Scholar] [CrossRef]
- Hu, X.; Che, Y.; Lin, X.; Onori, S. Battery Health Prediction Using Fusion-Based Feature Selection and Machine Learning. IEEE Trans. Transp. Electrif. 2021, 7, 382–398. [Google Scholar] [CrossRef]
- Che, Y.; Deng, Z.; Lin, X.; Hu, L.; Hu, X. Predictive Battery Health Management with Transfer Learning and Online Model Correction. IEEE Trans. Veh. Technol. 2021, 70, 1269–1277. [Google Scholar] [CrossRef]
- Wang, F.; Zhai, Z.; Zhao, Z.; Di, Y.; Chen, X. Physics-Informed Neural Network for Lithium-Ion Battery Degradation Stable Modeling and Prognosis. Nat. Commun. 2024, 15, 4332. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-Driven Capacity Estimation of Commercial Lithium-Ion Batteries from Voltage Relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).