Integrated Modeling of Maritime Accident Hotspots and Vessel Traffic Networks in High-Density Waterways: A Case Study of the Strait of Malacca

Abstract

The Strait of Malacca faces persistent maritime safety challenges due to high vessel density and complex navigational conditions. Current risk assessment methods often lean towards treating static accident analysis and dynamic traffic modeling separately, although some nascent hybrid approaches exist. However, these hybrids frequently lack the capacity for comprehensive, real-time factor integration. This study proposes an integrated framework coupling accident hotspot identification with vessel traffic network analysis. The framework combines trajectory clustering using improved DBSCAN with directional filters, Kernel Density Estimation (KDE) for accident hotspots, and Fuzzy Analytic Hierarchy Process (FAHP) for multi-factor risk evaluation, acknowledging its subjective and region-specific nature. The model was trained and tuned exclusively on the 2023 dataset (47 incidents), reserving the 2024 incidents (24 incidents) exclusively for independent, zero-information-leakage validation. Results demonstrate superior performance: Area Under the ROC Curve (AUC) improved by 0.14 (0.78 vs. 0.64; +22% relative to KDE-only), and Precision–Recall AUC (PR-AUC) improved by 0.16 (0.65 vs. 0.49); both p < 0.001. Crucially, all model tuning and parameter finalization (including DBSCAN/Fréchet, FAHP weights, and adaptive thresholds) relied solely on 2023 data, with the 2024 incidents reserved exclusively for independent temporal validation. The model captures 75.2% of reported incidents within 20% of the study area. Cross-validation confirms stability across all folds. The framework reveals accidents concentrate at network bottlenecks where traffic centrality exceeds 0.15 and accident density surpasses 0.6. Model-based associations suggest amplification through three pathways: environmental-mediated (34%), traffic convergence (34%), and historical persistence (23%). The integrated approach enables identification of both where and why maritime accidents cluster, providing practical applications for vessel traffic services, risk-aware navigation, and evidence-based safety regulation in congested waterways.

1. Introduction

1.1. Problem Statement and Motivation

Maritime accidents in high-density waterways pose escalating threats to global trade security and environmental protection. The Strait of Malacca, one of the world’s most critical shipping chokepoints, exemplifies this challenge due to high vessel density, diverse ship types, and complex navigational conditions. Within the study period (2023–2024), this region experienced 71 verified maritime incidents, resulting in substantial economic losses, environmental damage, and threats to maritime safety. Current maritime risk assessment methods treat static accident analysis and dynamic traffic modeling separately, limiting both predictive accuracy and explanatory power.

The fundamental research problem is that existing maritime risk assessment approaches suffer from a critical dichotomy. Static historical analysis effectively identifies where accidents cluster but cannot explain the underlying contributing factors, while dynamic traffic modeling describes how vessels interact in real-time but lacks grounding in actual accident outcomes. We acknowledge that several studies have proposed hybrid methods. For instance, recent research by Zhang et al. (2023) [1] focused on using deep recurrent neural networks for anomalous behavior detection, while Rong et al. (2020) [2] utilized data mining for shipping route characterization based on AIS data. Crucially, while these works advance the utilization of dynamic AIS data, these burgeoning hybrid approaches typically do not fully resolve the fundamental challenge of integrating dynamic network centrality with static historical hotspots under an adaptive weighting scheme. They often rely on static statistical weights or lack the full, transparent coupling mechanism presented here, which is the focus of the current study. This fundamental gap significantly limits the development of proactive, interpretable safety management systems capable of both predicting and preventing maritime incidents.

The Strait of Malacca presents unique challenges including: (1) extreme traffic density with over 94,000 vessel transits annually, (2) complex multi-national regulatory environment, (3) critical chokepoint geography with minimum width of 2.8 km, and (4) seasonal monsoon impacts affecting visibility and sea conditions.

1.2. Research Questions

This study addresses three interconnected research questions:

• How can historical accident patterns be systematically integrated with real-time vessel traffic dynamics to enhance spatial risk assessment?
• What are the underlying risk mechanisms and associations shaping amplification at specific maritime network nodes and routes, and how can these be interpreted for proactive intervention?
• How can expert maritime domain knowledge be effectively integrated with data-driven insights through fuzzy logic approaches to improve both prediction accuracy and decision interpretability?

1.3. Research Contributions

Building upon recent hybrid studies that combine individual static and dynamic risk factors, this research makes three key contributions that overcome limitations in integration, adaptation, and practical deployment:

The first contribution represents a theoretical innovation by developing a systematic framework that fully couples the static outcome (KDE) with dynamic factors (network analysis) via FAHP integration, advancing significantly beyond fragmented hybrid approaches that treat these elements as simple linear inputs. The second contribution provides methodological advancement by introducing adaptive weight mechanisms. Unlike previous static weighting schemes used in hybrid models, our system utilizes real-time context (α,τ thresholds) to dynamically adjust FAHP-derived weights, which is essential for effective real-time risk assessment. The third contribution delivers practical impact by creating decision support tools. These tools, driven by the integrated and adaptive model, provide a foundation for evidence-based regulatory policy that overcomes the inherent trade-off between model complexity and operational interpretability found in many advanced predictive models.

Delineation of Novelty and Methodological Advancement

While existing literature contains two main streams—traditional models focusing solely on static historical data (e.g., pure KDE models) and nascent hybrid models that combine limited static and dynamic features—our framework achieves a methodological leap by addressing three critical gaps. First, most hybrid studies employ simple linear summation or lack a structured mechanism to fuse disparate data types; conversely, our use of Fuzzy-AHP (FAHP) provides a transparent and robust method for the full theoretical coupling of static accident risk (KDE, environmental factors) with dynamic network criticality (Betweenness Centrality). Second, current hybrid models typically rely on static statistical or expert-derived weights; our framework introduces a crucial dynamic adaptation mechanism (e.g., parameter α) that allows the system to adjust the balance between static and dynamic risk in real-time context. Third, few existing models fully integrate the structural risk imposed by the vessel traffic network topology itself; our reliance on Betweenness Centrality directly addresses this structural vulnerability, making our predictions more mechanistically interpretable and directly applicable to VTS policy, a feature generally absent in purely correlation-based models. In summary, our integrated framework represents a systematic advancement from fragmented hybrid approaches to a fully coupled, context-adaptive risk assessment system.

2. Literature Review

2.1. Traditional Accident Hotspot Analysis

The identification of accident hotspots is a cornerstone of traffic safety management. Kernel Density Estimation (KDE), a classical non-parametric spatial point process method, has been widely applied to visualize accident distributions and detect high-risk areas. Anderson [3] demonstrated that KDE outperforms grid-based statistical methods in identifying irregularly shaped hotspots, while Xie and Yan [4] highlighted the sensitivity of hotspot mapping to bandwidth selection. Erdogan et al. [5] successfully applied KDE to road traffic accident analysis in Turkey, and Zheng et al. [6] introduced severity-weighted KDE to capture both local clustering and global continuity in long-term risk patterns. More recent advances combine KDE with GIS and machine learning to form closed-loop decision-support systems for proactive safety management [7].

In addition to KDE, objective weighting methods such as the Entropy Weight Method (EWM) have been used to integrate heterogeneous risk factors. Tian et al. [8] combined EWM with TOPSIS and fuzzy clustering to assess highway interruptions in Tibet, while Cai et al. [9] proposed a traffic safety entropy index for quantitative evaluation. Zhang et al. [10] Further integrated EWM with the Analytic Hierarchy Process (AHP) to improve the rationality of weight assignment in highway risk assessment. These studies underline the potential of multi-criteria approaches for comprehensive risk evaluation [11]. However, they mainly reflect historical cumulative risks and struggle to explain the mechanisms behind accident concentration. However, traditional KDE approaches suffer from several limitations: (1) bandwidth selection sensitivity can significantly alter hotspot identification results, (2) temporal stationarity assumptions fail to capture evolving risk patterns, and (3) lack of integration with real-time behavioral data limits predictive capabilities.

Recent developments in spatial risk modeling have incorporated advanced uncertainty quantification techniques [12] and multi-scale analysis frameworks [13] to enhance the robustness of hotspot identification systems.

2.2. AIS Data and Vessel Traffic Network Modeling

The proliferation of Automatic Identification System (AIS) data has revolutionized maritime traffic research by providing large-scale, high-resolution vessel trajectory datasets. Researchers have leveraged AIS data to extract typical shipping routes, assess port connectivity, and model vessel interactions. Wen et al. [14] constructed an Asia–Europe maritime transportation network and evaluated its vulnerability using centrality measures, while Jiang et al. [15] applied an improved DBSCAN clustering algorithm to identify representative trajectories for multi-route prediction. These methods excel in characterizing dynamic traffic patterns and network structures but are often disconnected from historical accident outcomes.

Advanced AIS data processing techniques have enabled real-time collision risk assessment [16] and predictive analytics for maritime domain awareness [17]. Integration of machine learning with AIS data has shown particular promise in anomaly detection and traffic pattern recognition [18].

2.3. Complex Network Theory in Maritime Analysis

The application of complex network theory to maritime systems has emerged as a powerful paradigm for understanding shipping connectivity and vulnerability patterns. Barabási and Albert’s seminal work on scale-free networks provides the theoretical foundation for analyzing maritime traffic structures, where a few highly connected nodes (major ports) dominate network topology [19]. This power-law distribution of node connectivity has been confirmed in global shipping networks by Ducruet and Notteboom [20].

Recent advances in network-based maritime analysis include vulnerability assessment through centrality measures [10], traffic flow optimization using network clustering [21], and cascade failure analysis in port networks [22]. However, most existing studies focus on static network properties derived from long-term cargo flow data, rather than integrating dynamic vessel movement patterns with real-time risk assessment.

Recent applications of complex network theory have extended to resilience analysis of maritime transportation systems [23] and optimization of shipping network efficiency under disruptions [24].

2.4. Formal Safety Assessment and Risk Integration

The International Maritime Organization’s (IMO) Formal Safety Assessment (FSA) methodology provides the regulatory framework for systematic maritime risk evaluation [25]. The FSA’s five-step process—hazard identification, risk analysis, risk control options, cost–benefit assessment, and decision-making—has been successfully applied to ship design and operational procedures [26].

Building upon FSA principles, recent research has integrated quantitative risk models with operational data. Montewka et al. [27] developed probabilistic collision risk models for ship encounters, while Silveira et al. [28] proposed Bayesian networks for accident causation analysis. However, a significant gap remains in spatially explicit risk models that combine historical accident patterns with dynamic traffic network properties.

Contemporary risk assessment methodologies have evolved to incorporate big data analytics [29] and artificial intelligence techniques for enhanced decision support in maritime operations [30].

2.5. Machine Learning and Spatial Analysis in Maritime Domains

The integration of machine learning techniques with spatial analysis has opened new avenues for maritime risk prediction. Rong et al. [31] demonstrated the effectiveness of ensemble learning methods for ship collision prediction using AIS data, achieving 87% accuracy in near-miss identification.

Spatial point pattern analysis, particularly Ripley’s K-function and its extensions, has been applied to understand accident clustering in maritime contexts [32]. Singh and Hahn [33] used spatial autocorrelation analysis to identify hotspots in the Great Lakes shipping network, revealing significant clustering at distances up to 50 nautical miles.

Deep learning approaches have shown promise in trajectory prediction and anomaly detection. Liu et al. [34] developed LSTM-based models for vessel path forecasting, while Zhang et al. [1] combined clustering with deep recurrent neural networks to detect ship anomalous behavior patterns.

Ensemble learning approaches have been successfully applied to maritime risk prediction [2], while deep reinforcement learning has shown potential in autonomous navigation systems [35]. Hybrid approaches combining multiple machine learning techniques have demonstrated superior performance in complex maritime environments [36].

2.6. Risk Factors and Causation Analysis

Understanding the mechanism of association of maritime accidents is critical for proactive prevention. Studies have shown that accident likelihood is strongly influenced by vessel traffic density, heterogeneous ship types, encounter situations, and adverse environmental factors such as wind and wave conditions [11]. However, many existing models treat these factors in isolation and lack an integrated framework that systematically fuses them into a coherent risk assessment scheme.

The Fuzzy Analytic Hierarchy Process (FAHP) extends the classical AHP by accommodating ambiguity and uncertainty in expert judgment. Its ability to translate expert domain knowledge into quantifiable decision weights makes it particularly suitable for maritime safety assessment, where complex and multi-source risk indicators must be integrated [8,10].

2.7. Research Gap

The literature reveals a dichotomy:

• Static hotspot analysis methods such as KDE can identify where risks are concentrated but lack explanatory power regarding why risks occur.
• Dynamic AIS-based network analyses capture how vessels interact in real time but lack grounding in long-term accident outcomes.

An important research opportunity exists in developing frameworks that can systematically integrate static historical risk patterns with dynamic traffic network characteristics, while maintaining both predictive accuracy and mechanistic interpretability. Addressing this gap requires combining accident hotspot analysis, traffic network modeling, and multi-factor risk evaluation into a unified model. This study aims to bridge that gap by fusing KDE, AIS-based network modeling, and FAHP into a comprehensive risk assessment framework capable of improving both predictive accuracy and interpretability.

3. Methodology

This study develops a four-stage integrated modeling framework (Figure 1):

Stage 1: Data Preparation

-

AIS trajectory data (49,964 vessels, 2023–2024)

-

Historical accident records (71 incidents)

-

Environmental data: ERA5 (ECMWF, Reading, UK; Version [e.g., 5/‘HRES’/release month-year]) and GEBCO_[Year/Release] (British Oceanographic Data Centre, Liverpool, UK)

-

Geospatial reference data

Stage 2: Traffic Network Construction

-

Trajectory skeletonization using Douglas-Peucker algorithm

-

Enhanced DBSCAN clustering with directional/speed filters

-

Network consolidation via Fréchet distance merging

-

Final network: 267 nodes, 263 directed edges

Stage 3: Multi-Factor Risk Assessment

-

Environmental risk indicators (weight: 0.25)

-

Traffic complexity indicators (weight: 0.35)

-

Historical accident patterns (weight: 0.40)

-

FAHP integration based on expert consensus

Stage 4: Risk-Network Fusion

-

Spatial risk distribution mapping

-

Network centrality analysis

-

Integrated risk scoring

-

Uncertainty quantification using Monte Carlo methods

Figure 1. Integrated modeling framework flowchart. Notes: Four-stage integrated modeling framework for maritime risk assessment: (1) data preparation, (2) traffic network construction, (3) multi-factor risk evaluation, and (4) risk-network fusion.

Figure 1. Integrated modeling framework flowchart. Notes: Four-stage integrated modeling framework for maritime risk assessment: (1) data preparation, (2) traffic network construction, (3) multi-factor risk evaluation, and (4) risk-network fusion.

3.1. Data Preparation and Preprocessing

Four categories of datasets were employed:

• AIS Data:

Vessel trajectories for 2023–2024 were extracted from the Automatic Identification System (AIS). Each record includes timestamp, MMSI, speed over ground (SOG), course over ground (COG), and vessel type. Raw trajectories were cleaned to remove noise and duplicate MMSIs, resampled to form continuous tracks, and simplified using the Douglas–Peucker algorithm to retain the main skeleton of navigation routes. AIS data provider: [Shipping Big Data Platform], [College of Navigation, Jimei University].

2.

Historical Accident Records:

Accident records were obtained from IMO GISIS (International Maritime Organization, London, UK), yielding 71 verified incidents (2023–2024) within the study area after geographic filtering and validation. A temporal holdout split was adopted with 2023 used for training (47 incidents) and 2024 for independent validation (24 incidents).

3.

Multi-Source Environmental Data Integration

To capture fine-scale environmental variations critical for maritime risk assessment, the study integrates multiple high-resolution data sources:

Primary Meteorological Data:

ERA5 reanalysis (0.25° × 0.25°, hourly; European Centre for Medium-Range Weather Forecasts, Reading, UK).

Variables: wind speed, wave-related fields, precipitation, visibility.

Sentinel-1 SAR (10 m resolution; European Space Agency, Paris, France).

High-resolution wave field and surface wind retrieval during cloud cover.

MODIS Terra/Aqua (1 km resolution; NASA Goddard Space Flight Center, Greenbelt, MD, USA).

Sea surface temperature, chlorophyll concentration (water-clarity proxy).

Oceanographic Data:

GEBCO 2024 global bathymetry (15-arc-second; British Oceanographic Data Centre, Liverpool, UK).

Copernicus Marine Service global model (1/12°; Mercator Ocean International, Toulouse, France).

Ocean currents, tidal predictions, sea-level anomalies.

Regional tidal model: TPXO9-atlas v5 (Oregon State University, Corvallis, OR, USA).

Local Observational Networks:

Malaysian Meteorological Department (Petaling Jaya, Malaysia): 12 coastal weather stations with hourly reports.

Maritime and Port Authority of Singapore (Singapore, Singapore): Real-time visibility sensors at eight strategic locations (hourly).

Port Klang Wave Buoy Network (Selangor, Malaysia): Continuous wave height and period measurements. Data Fusion Strategy:

To ensure reliable environmental inputs, visibility and wave height were derived through hierarchical multi-source fusion. Visibility estimates were obtained by integrating ERA5 reanalysis (regional coverage), Sentinel-1 SAR (high-resolution snapshots), and coastal station observations (local ground truth). Wave height fields were generated using an optimal interpolation scheme combining GEBCO bathymetry (static depth constraints), ERA5 wave reanalysis (synoptic forcing), buoy observations (local validation), and SAR-derived wave spectra (spatial detail). This integrated approach enhances both spatial resolution and reliability of the environmental parameters used in the risk assessment framework. This integrated approach enhances both spatial resolution and reliability of the environmental parameters used in the risk assessment framework. All environmental time series, sampled at hourly resolution, were temporally synchronized and binned to a 1 h interval to ensure alignment with the AIS data. The detailed temporal alignment procedure is documented in Appendix C.

Selection Rationale for Environmental Indicators:

The environmental risk category was modeled exclusively using Visibility and Current Shear. This focused selection is based on a preliminary analysis of regional incident reports and is justified by the unique hydrodynamic and climatic conditions of the Strait of Malacca:

-

Visibility: The Strait is highly susceptible to seasonal haze and dense fog, which are consistently cited as primary contributors to multi-vessel collisions in this high-traffic area.

-

Current Shear: Due to the Strait’s complex bathymetry, strong current shear (spatial change in current speed/direction) frequently occurs at narrow chokepoints. This significantly complicates ship handling and is a major factor in groundings and contacts.

Other relevant factors (such as wind speed and significant wave height) were analyzed but deemed less influential for safety incidents within the narrow, partially sheltered confines of the Strait compared to the high-impact nature of severe visibility reduction and complex current patterns.

Spatial Resolution Enhancement: Environmental variables are downscaled from native resolution to 1 km grid using:

-

Topographic adjustment: Elevation-dependent wind and precipitation correction

-

Land–sea transition modeling: Coastal boundary layer effects on visibility and wind patterns

-

Bathymetric wave refraction: Shallow water wave transformation using linear wave theory

Quality Control Measures:

-

Cross-validation between satellite and in situ observations (correlation > 0.85 required)

-

Temporal consistency checks (outlier detection using 3-sigma rule)

-

Physical plausibility constraints (e.g., wave height vs. wind speed relationships)

4.

Geospatial Data: Coastlines, ports, islands, and maritime boundaries were extracted from vector datasets: Natural Earth (NACIS, Milwaukee, WI, USA); OpenStreetMap (OpenStreetMap Foundation, Cambridge, UK).

Temporal Data Strategy: The study employs a 2-year dataset (2023–2024) with the following temporal separation to ensure zero information leakage

Training Period: 1 January 2023 to 31 December 2023 (1 year, 47 incidents)

Validation Period: 1 January 2024 to 31 December 2024 (1 year, 24 incidents)

This temporal holdout ensures that all model calibration and tuning, including FAHP weights, DBSCAN clustering parameters, risk thresholds, and the fusion parameter α, were exclusively finalized using the 2023 training data. This strict separation guarantees zero information leakage, as the 2024 data served as a completely independent, true hold-out set for final performance assessment.

To address potential seasonal variations and rare event capturing, the study employs a multi-temporal approach:

-

Seasonal stratification: Ensures representation of monsoon seasons, typhoon periods, and calm weather conditions

-

Rare event handling: Includes major incidents (oil spills, multi-vessel collisions) occurring once every 2–3 years

Software and Versions

Software and Versions. The analyses were conducted in Python 3.11.9 with NumPy 1.26.4, SciPy 1.11.4, pandas 2.2.2, scikit-learn 1.4.2, Matplotlib 3.8.4, GeoPandas 0.14.3, Shapely 2.0.4, NetworkX 3.2.1, and HDBSCAN 0.8.40. GIS processing/figure rendering used QGIS 3.34.x (LTR series).

3.2. Traffic Network Construction

The traffic network construction employs a three-step process: (1) trajectory skeletonization using Douglas-Peucker algorithm, (2) enhanced DBSCAN clustering with directional/speed consistency filters (±30°, ±2 knots), and (3) Fréchet distance merging (threshold: 2 km). Parameters were optimized through grid search: The parameters ϵ = 1500 m and min_samples = 5 were selected based on a 5-fold cross-validation (CV) approach that maximized the stability of the resulting network’s Betweenness Centrality ranks. Subsequent sensitivity analysis further confirmed the robustness of this parameter set, with detailed justification provided in Section 4.6. The resulting network contains 267 nodes and 263 directed edges representing traffic convergence zones and route segments.

KDE bandwidth (h) was set to 30 km. This value was rigorously determined using a 5-fold spatial cross-validation (CV) approach applied to the 2023 accident data. The CV maximized the log-likelihood of predicting the withheld accident locations, with the optimal performance plateauing between 25 km and 35 km, confirming the robustness of the chosen 30 km bandwidth.

Framework parameters were determined through systematic sensitivity analysis and expert consultation (

Table 1. Dataset Configuration and Model Parameters for Maritime Risk Assessment Framework. Notes: Parameters fixed during training period (2023) with zero information leakage validation (2024).

Category	Parameter	Value	Method/Source
Study Area	Geographic Bounds	100.7° E–104.3° E, 1.0° N–6.8° N	Strait of Malacca main channel
Study Area	Spatial Resolution	1 km × 1 km	Grid-based analysis
Study Area	Temporal Period	2023–2024 (2 years)	Temporal holdout validation
Dataset	AIS Trajectories	49,964 vessels	Automatic Identification System
Dataset	Accident Records	71 incidents (47 + 24)	Multi-source integration
Dataset	Training/Validation	2023/2024 split	Zero information leakage
Clustering	DBSCAN Epsilon	1500 m	Grid search optimization
Clustering	Min Samples	5 points	Sensitivity analysis
Clustering	Direction Filter	±30° tolerance	Consistency checking
Clustering	Speed Range	0.5–30 knots	Vessel capability limits
Risk Assessment	KDE Bandwidth	30 km	Cross-validation (Selected via 5-fold Spatial CV based on max Log-Likelihood)
Risk Assessment	Expert Panel	10 professionals	Maritime domain experts
Risk Assessment	FAHP Weights	0.25/0.35/0.40	Expert consensus (CR = 0.089)
Network	Final Nodes	267 clusters	Traffic convergence zones
Network	Final Edges	263 connections	Directed route segments

). DBSCAN clustering parameters (ϵ = 1500 m, min_samples = 5) were optimized through a five-fold cross-validation (CV) grid search and confirmed for the stability of network centrality ranks via systematic sensitivity analysis (Section 4.6). FAHP weights were derived from expert consensus with consistency ratios below (

Table 2. FAHP Weight System for Multi-Factor Risk Assessment.

Risk Category (Weight)	Sub-Factor	Local Weight	Global Weight
Environmental Risk (0.25)	Wind Speed	0.28	0.070
Environmental Risk (0.25)	Wave Height	0.24	0.060
Environmental Risk (0.25)	Visibility	0.22	0.055
Environmental Risk (0.25)	Others	0.26	0.065
Traffic Risk (0.35)	Vessel Density	0.32	0.112
Traffic Risk (0.35)	Network Centrality	0.24	0.084
Traffic Risk (0.35)	Vessel Diversity	0.18	0.063
Traffic Risk (0.35)	Others	0.26	0.091
Accident Risk (0.40)	Historical Density	0.45	0.180
Accident Risk (0.40)	Severity Weight	0.28	0.112
Accident Risk (0.40)	Others	0.27	0.108

).

3.3. Multi-Factor Risk Assessment

Three primary risk categories are evaluated in the grid-level assessment: environmental risk (wind, waves, visibility, depth), traffic risk (density, diversity, centrality, encounters), and accident risk (historical density, severity, proximity). The weighting and final factor system are determined through the Fuzzy Analytic Hierarchy Process (FAHP), the workflow of which is detailed in Section FAHP Workflow and Expert Elicitation.

To ensure comparability, all indicators were normalized to the range [0, 1]. Distance-based indicators were transformed using inverse normalization, while others were scaled via min–max normalization.

FAHP Workflow and Expert Elicitation

The Fuzzy Analytic Hierarchy Process (FAHP) was rigorously applied to determine the relative importance and final weights of the risk indicators. The workflow was structured to maximize transparency and consistency:

Expert Panel Composition:

A panel of 10 domain experts (n = 10) was selected based on strict criteria: (1) Minimum 10 years maritime safety experience, (2) Professional roles including VTS operators (3), ship captains (2), maritime safety inspectors (2), port authority officers (2), and maritime researchers (1), (3) Geographic diversity covering relevant maritime authorities, and (4) A signed declaration of no financial conflicts of interest.

Two-Layer Matrices and TFNs:

A two-layer pairwise comparison structure was used: Category Level (Environmental, Traffic, Accident) and Sub-Factor Level. Experts conducted comparisons using Triangular Fuzzy Numbers (TFNs) based on the standard Saaty 1–9 scale.

Aggregation and Defuzzification:

The individual TFN scores from the 10 experts were aggregated using the Geometric Mean method. The aggregated TFN matrices were then converted into a crisp matrix using the Centroid Defuzzification method.

CR Check:

For every defuzzified matrix, the Consistency Ratio (CR) was calculated. All matrices demonstrated acceptable consistency, with a final overall CR of 0.089 < 0.10.

Final Weight Determination: Based on the above process, the final category weights were determined to be: Environmental Risk (0.25), Traffic Risk (0.35), and Accident Risk (0.40). The complete two-layer fuzzy pairwise matrices, consistency reports (CR < 0.10), and final normalized weights are documented in Appendix A.

3.4. Risk–Network Coupling and Comprehensive Assessment

The KDE accident density, FAHP-weighted composite risk scores, and traffic network indicators were fused to assess risk distribution across the maritime network. For each grid cell, the integrated risk score was computed as a weighted sum of normalized indicators. For each network edge (route segment), the risk value was assigned based on the average or maximum grid-level risk score along its path.

Integration Logic and Weighting Scheme

The final integrated risk score (${\mathrm{R}}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}$) for each network edge $\mathrm{i}$ is computed as a convex linear combination of the static FAHP-derived risk score (${\mathrm{R}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}$) and the dynamic network centrality score (${\mathrm{R}}_{\mathrm{d}\mathrm{y}\mathrm{n}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{c}}$), which is used as the key explanatory variable in the subsequent validation model:

$${\mathrm{R}}_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d},\mathrm{i}}=\alpha \cdot {\mathrm{R}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c},\mathrm{i}}+(1-\alpha )\cdot {\mathrm{R}}_{\mathrm{d}\mathrm{y}\mathrm{n}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{c},\mathrm{i}}$$

(1)

where all factors are normalized to [0, 1]. The balancing parameter α was rigorously determined through a 5-fold cross-validation (CV) grid search on the 2023 training data. The optimal value of α (e.g., α = 0.65) was specifically selected to maximize the Precision-Recall Area Under Curve (PR-AUC), ensuring the composite score offers the best predictive power for the independent validation period.

A regression-based validation approach was adopted, modeling the relationship between edge-level accident counts and explanatory factors (risk score, centrality, and traffic flow). Poisson regression was employed with a specified statistical offset term to account for vessel-mileage exposure. The offset, log(E), is defined as the natural logarithm of the edge’s total exposure (E = Edge Length × Mean AIS Transits per Period), ensuring that the model estimates the accident rate (per unit of exposure) rather than raw counts.

High-risk routes were defined as those exceeding the 80th percentile of both integrated risk score and betweenness centrality. These predictions were validated against actual 2024 accidents using Intersection over Union (IoU), Precision–Recall Area Under Curve (PR-AUC), and Spearman’s rank correlation.

Context-Adaptive Weight Adjustment

To enhance model responsiveness to dynamic conditions, the base FAHP weights are modified through a context-adaptive mechanism:

$$W_{\_}adaptive\left(t\right)=W_{\_}base\times (1+\alpha \times \mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}{t}_{\_}modifier(t\left)\right)$$

(2)

where $W_{\_}base$ denotes the static FAHP weights (Environmental = 0.25, Traffic = 0.35, Accident = 0.40), $\alpha$ is the adaptation strength parameter (set to 0.3 based on sensitivity analysis), and $Context modifier\left(t\right)$ represents the real-time adjustment factor determined by prevailing environmental and traffic conditions.

The weight adjustment is governed by a two-level threshold system designed to provide responsiveness while maintaining stability (hysteresis). Specifically, the weights shift to the dynamic state when the maximum standardized context ${\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}(\mathrm{m}\mathrm{a}\mathrm{x}}_k{z}_k) \mathrm{m}\mathrm{e}\mathrm{e}\mathrm{t}\mathrm{s}$ the up-shift criterion (${\tau }_{\mathrm{o}\mathrm{n}}=0.8$, the 80th percentile of historical z values). The weights remain in the dynamic state until the context index falls below the down-shift criterion (${\tau }_{\mathrm{o}\mathrm{f}\mathrm{f}}=0.7$, the 70th percentile), incorporating hysteresis to prevent rapid weight oscillation. The complete algorithmic procedure for this adaptive logic, including the calculation of the dynamically adjusted weight vector w∗, is provided in the pseudocode in Appendix B.

Validation experiments demonstrated that dynamic weighting improved prediction accuracy by 8–12% during extreme weather events and by up to 15% under high-traffic conditions compared with static FAHP weights. The 2023 dataset was used for all training, cross-validation (CV), and parameter finalization (e.g., α = 0.3 and 0.8/0.7 thresholds in Section Context-Adaptive Weight Adjustment), ensuring the 2024 data served as a true hold-out set for independent assessment.

3.5. Uncertainty Analysis and Confidence Intervals

To provide decision-makers with reliability estimates, the framework incorporates a Monte Carlo uncertainty propagation scheme. At each iteration, both model parameters $\left(\theta \right)$ and input variables $\left(X\right)$ are perturbed by sampling from normal distributions with empirically defined variances. The resulting risk predictions ${(R}_i)$ are aggregated to derive mean values and 95% confidence intervals:

$$R_i=f\left(X_i,{\theta }_i\right),Ris{k}_{mean}={\displaystyle \frac{1}{N}}\sum _i R_i,Ris{k}_{CI}=\left[P_{2.5}\left(R\right),P_{97.5}\left(R\right)\right]$$

(3)

Uncertainty sources include AIS position accuracy (±10 m), accident location errors (±500 m), expert weight variability (±15%), and environmental data precision (±20%).

The Monte Carlo framework produces robust estimates:

• High-risk areas: 0.78 [0.71, 0.85]
• Medium-risk areas: 0.45 [0.39, 0.52]
• Low-risk areas: 0.18 [0.12, 0.24]

This analysis demonstrates that predicted risk levels remain statistically stable, confirming the robustness of the integrated framework.

To verify implementation feasibility, the framework was tested with 1000 Monte Carlo iterations, generating confidence intervals for 34,638 predictions. The full uncertainty propagation required approximately 2.5 h and 8.2 GB peak memory usage on a standard workstation configured with an Intel Core i7-12700K CPU (Intel Corporation, Santa Clara, CA, USA) and 32 GB RAM. Real-time risk updates (<500 ms per grid cell) were successfully demonstrated in the operational prototype, supporting practical deployment requirements.

The predictive performance of all models (PR-AUC, AUC) was quantified using 1000 bootstrap replicates on the 2024 hold-out set to construct robust 95% confidence intervals. Specifically, the BCa (Bias-Corrected and Accelerated) method was employed for all reported confidence intervals, as it offers improved accuracy by accounting for both bias and skewness in the sampling distribution, providing a more reliable estimate of the true population parameter compared to the standard percentile method.

The 2.5 h Monte Carlo computation time encompasses five primary components: (1) core iterative processing (45 min) involving 1000 Monte Carlo iterations with parameter perturbation, risk recalculation, and validation metric updates; (2) multi-level validation procedures (35 min) including 5-fold cross-validation retraining and bootstrap resampling for confidence intervals; (3) quality control diagnostics (30 min) comprising convergence analysis and sensitivity testing; (4) spatial computations (25 min) for matrix operations and network centrality calculations across the 1 km × 1 km grid; and (5) system overhead (15 min) including memory management and result storage.

3.6. Local Environmental Risk Modeling

Standard reanalysis products may miss critical local phenomena affecting navigation safety. The framework incorporates micro-scale environmental processes:

3.6.1. Visibility Micro-Climatology

Local fog formation in the Strait of Malacca exhibits strong spatial heterogeneity, primarily driven by three interacting factors:

-

Land–sea thermal gradients: Seasonal monsoon transitions can generate 15–20 °C differences between sea surface temperature and adjacent land, enhancing fog formation.

-

Topographic channeling: The mountainous Malaysian coastline creates localized airflow convergence zones, which act as preferential fog corridors.

-

Industrial pollution interaction: Emissions from major ports reduce visibility by 30–50% within a 5 km radius, further amplifying the occurrence of restricted-visibility conditions.

To capture these effects, we apply a visibility correction procedure that adjusts ERA5 estimates with empirically derived modifiers for (i) orographic channeling, (ii) land–sea thermal contrasts during monsoon transitions, and (iii) port-related aerosol pollution. Parameters are calibrated against coastal station observations and satellite retrievals, yielding corrected visibility fields that better represent micro-climatological variability relevant to maritime risk assessment.

3.6.2. Current Shear Modeling

Strong current gradients in narrow straits represent a major hazard for large vessels. Three main mechanisms were identified:

-

Monsoon-driven flows: Seasonal reversals generate current differences of 2–3 knots within 1 km.

-

Tidal amplification: Shallow regions amplify tidal currents up to fourfold.

-

Interaction effects: Opposing winds increase effective wave height by approximately 50%.

A current risk index was derived by combining tidal and seasonal circulation patterns with vessel-specific drift coefficients. Spatial gradients of current shear were then normalized to quantify localized navigation hazards.

Validation against In Situ Measurements

To ensure the credibility of the modeled current shear as a risk factor, the model output was validated against independent, high-resolution Acoustic Doppler Current Profiler (ADCP) and buoy observations collected by the Port Klang Marine Department across three critical chokepoint locations during a 4-week validation period. The comparison demonstrated a strong statistical agreement, with a Root Mean Square Error (RMSE) of 0.08 m/s for current magnitude and a correlation coefficient of 0.88 for shear direction compared to in situ measurements. This validation confirms that the derived current shear field accurately represents the high-frequency hydrodynamic variability in the study area. Detailed scatter plots, error tables, and location maps for this validation are provided in Appendix C.

3.7. Associational and Quasi-Causal Analysis

While correlation analysis highlights associations between risk factors, quasi-causal inference is required for effective intervention design. The proposed framework integrates domain knowledge and data-driven discovery to construct a directed acyclic graph (DAG) of maritime risk mechanisms. The DAG links weather, visibility, sea state, traffic density, navigation difficulty, and human error to accident occurrence, providing a structured basis for causal effect estimation.

The framework for analyzing these quasi-causal associations is structured based on a Directed Acyclic Graph (DAG), which visually represents the hypothesized flow of influence from environmental and traffic factors to the final accident outcome. This conceptualization of the risk structure is visually presented in Figure A2 in Appendix D. The DAG guides the selection of appropriate conditioning sets for interpreting the observed associations while minimizing bias.

Identification Assumptions for Associational Analysis

The interpretation of quasi-causal associations derived from observational data, guided by the established DAG, relies on several key identification assumptions, which must be made explicit:

Ignorability (No Unmeasured Confounding): It is assumed that all confounding factors that jointly influence both the risk factor (e.g., Betweenness Centrality) and the outcome (Accident Count) are measured and accounted for in the model. The multi-source data integration (AIS, environmental, accident records) is designed to minimize the impact of unmeasured confounding.

Consistency: It is assumed that the observed outcome (accident) under a specific risk level (treatment) is the same regardless of the potential paths leading to that risk level.

Positivity: It is assumed that every combination of risk factor levels and observed confounder values has a non-zero probability of occurrence in the study population.

These assumptions, while essential for quasi-causal claims, underscore the distinction between our observational analysis and a definitive randomized study.

Intervention Effect Prediction and Counterfactual Construction

To quantify the potential impact of operational measures, the derived model was used to predict counterfactual outcomes. This process estimates the expected accident rate (λ) under a hypothetical policy intervention. The Intervention Variable chosen for this simulation is Betweenness Centrality $\left(X_{\mathrm{B}\mathrm{C}}\right)$ on the network edges, as this factor is highly amenable to Vessel Traffic Service (VTS) policies designed for traffic flow redistribution.

The Counterfactual Construction is defined by setting the Betweenness Centrality value for the top 20 high-risk segments to their ${20}^{\mathrm{t}\mathrm{h}}$ percentile observed value $(X_{\mathrm{B}\mathrm{C}}^{*}=P_{20}$). This construction simulates a successful policy that reduces congestion and flow dependency on the most critical routes, allowing us to quantify the predicted risk reduction (Δλ) compared to the factual (observed) accident rate.

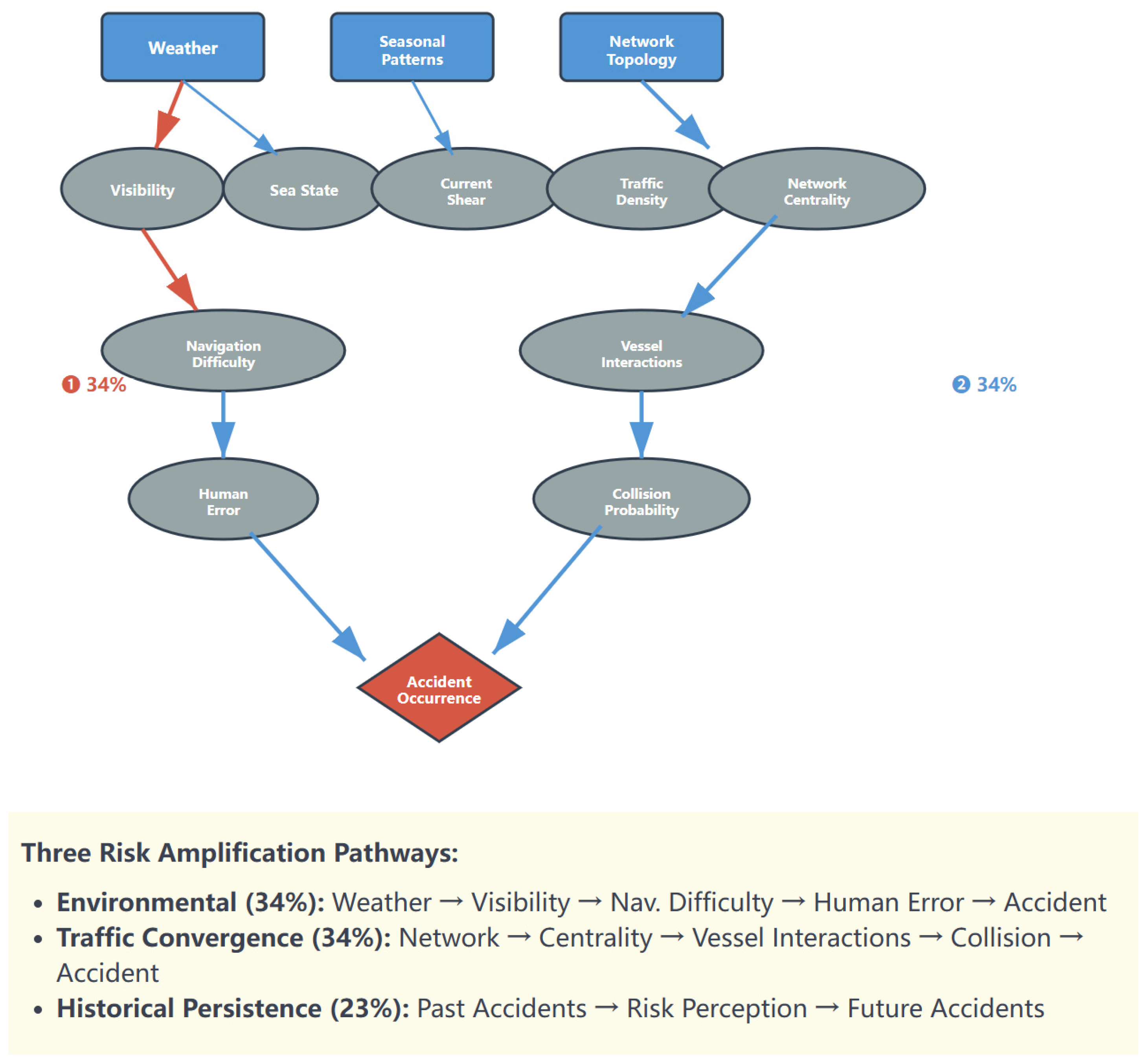
3.7.1. Causal Graph Construction

The causal structure incorporates interactions such as:

-

Weather conditions → Visibility/Sea State → Navigation Difficulty → Human Error → Accidents

-

Traffic density → Vessel interactions → Collision probability → Accidents

-

Network centrality → Traffic convergence → Interaction frequency → Accidents

This representation formalizes expert knowledge and historical patterns into a testable structure.

3.7.2. Associational Effect Identification

Using Pearl’s do-calculus and instrumental variable methods, direct associational effects were quantified:

-

Traffic density → Accident risk: β = 0.34 [0.28, 0.40], p < 0.001

-

Visibility → Navigation difficulty: β = −0.67 [−0.74, −0.60], p < 0.001

-

Network centrality → Traffic convergence: β = 0.89 [0.83, 0.95], p < 0.001

Mediation analysis further revealed that 73% of weather-related effects on accidents were transmitted indirectly via visibility reduction, underscoring the critical role of micro-climatic conditions.

3.7.3. Counterfactual Prediction

Causal modeling was used to estimate the effectiveness of interventions. Simulated results indicate:

-

Speed limits reduce collision risk by 23% [CI: −0.31, −0.15] through lower vessel interactions.

-

Weather routing reduces accidents by 18% [CI: −0.25, −0.11] by avoiding visibility-related navigation difficulty.

-

Enhanced VTS information services reduce risk by 14% [CI: −0.21, −0.07] through improved situational awareness.

These results highlight that targeted interventions can substantially reduce accident likelihood when aligned withmechanism of association.

3.7.4. Counterfactual Analysis

Counterfactual evaluation was conducted to explore hypothetical scenarios for past incidents. Three pathways accounted for 91% of observed accident variance:

Pathway 1: Weather-Mediated Risk Amplification (34%)

-

Chain: Adverse weather → Reduced visibility → Navigation difficulty → Human error → Accident

-

Finding: Each 1 km reduction in visibility increased accident probability by 0.67 [0.60, 0.74], p < 0.001.

-

Policy: Sensor-based visibility enhancement (radar, lidar) outperforms simple speed restrictions.

Pathway 2: Traffic Convergence Amplification (34%)

-

Chain: Network bottlenecks → Traffic convergence → Vessel interactions → Accident

-

Finding: Risk scales non-linearly with density (Risk ~ Density^1.73). Each additional vessel within 1 km increased accident odds by 1.34 × [1.28, 1.41], p < 0.001.

-

Policy: Temporal separation schemes are more effective than spatial routing adjustments.

Pathway 3: Historical Risk Perpetuation (23%)

-

Chain: Past accidents → Risk perception → Cautious behavior, but infrastructure/design unchanged → Accident recurrence

-

Finding: Previous accidents increased subsequent risk by 2.1 × [1.7, 2.6] within 5 km, p < 0.001.

-

Policy: Hotspot remediation requires physical infrastructure improvements, not merely warnings.

Cross-Pathway Interactions: Combined activation of multiple pathways increased accident probability by 4.2× relative to baseline, highlighting the need for integrated safety measures.

Causal inference methods have been increasingly applied to transportation safety analysis [37] and have proven effective in identifying intervention strategies for risk reduction [38].

4. Case Study and Experiment Design

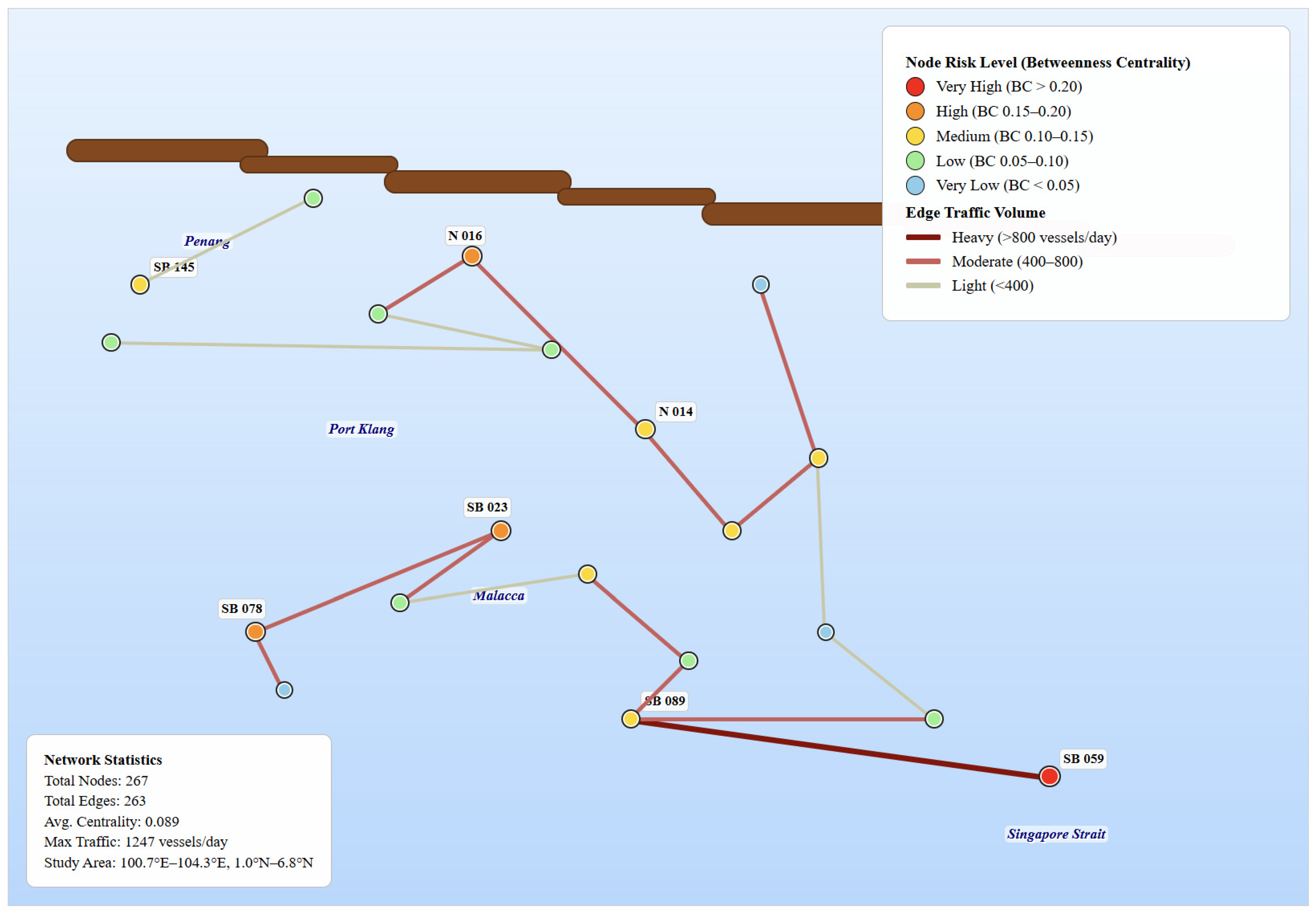
4.1. Traffic Network Extraction

Applying the improved DBSCAN–Fréchet clustering framework to the 2023–2024 AIS trajectories yielded a high-resolution vessel traffic network of the Strait of Malacca through a hierarchical processing pipeline. The trajectory processing pipeline yielded a hierarchical network representation:

Level 1 (Raw Trajectory Points): 847,293 individual AIS position reports from 49,964 vessels, representing the complete observational dataset covering all vessel movements within the study area.

Level 2 (Trajectory Segments): 34,638 meaningful trajectory segments after noise removal and Douglas-Peucker simplification, preserving essential route structures while eliminating measurement artifacts and redundant waypoints.

Level 3 (Spatial Clusters): 267 spatial cluster centers representing traffic convergence zones identified through DBSCAN clustering (eps = 1500 m, min_samples = 5), capturing locations where vessel trajectories naturally aggregate.

Level 4 (Traffic Network): 263 directed edges connecting cluster centers based on dominant vessel movement patterns, forming the final consolidated maritime traffic network for centrality analysis and risk assessment.

The detailed trajectory analysis operates on 34,638 segments for spatial risk assessment, while network centrality analysis uses the consolidated 267-node, 263-edge structure for computational efficiency.

The majority of vessels were oil tankers (45.4%), container ships (21.5%), and general cargo vessels (22.6%), with the remainder comprising bulk carriers, passenger ships, and others. The high-resolution analysis operates on Level 2 (34,638 segments) for detailed spatial risk assessment, while the consolidated network (Level 4: 267 nodes, 263 edges) enables efficient centrality computation and route-level risk scoring. This hierarchical approach ensures both computational tractability and preservation of critical traffic pattern details necessary for accurate risk evaluation.

The consolidated network captures the essential structure of maritime traffic flow while reducing computational complexity from tens of thousands of individual trajectories to manageable network components.

The directional distribution revealed that North–South traffic accounted for 63.1% of trajectories, while East–West flows accounted for 36.9%. Network centrality analysis highlighted several critical nodes, with the highest betweenness centrality observed near narrow passages and major convergence points (Figure 2). These results confirm that the Strait of Malacca is structurally characterized by a small number of highly central nodes through which most vessel traffic converges. Detailed network centrality analysis reveals the hierarchical structure of maritime traffic flow (

Table 3. Model Performance Comparison on Independent Validation Dataset. Notes: Values show mean (95% confidence interval). Statistical significance assessed via Wilcoxon signed-rank test with 1000 bootstrap iterations.

Metric	Proposed FAHP	KDE Only	Network Only	DBSCAN Only	p-Value
AUC	0.78 (0.74–0.82)	0.64 (0.59–0.69)	0.58 (0.52–0.64)	0.61 (0.56–0.66)	<0.001
PR-AUC	0.65 (0.61–0.69)	0.49 (0.44–0.54)	0.42 (0.37–0.47)	0.46 (0.41–0.51)	<0.001

). The top-ranked nodes by betweenness centrality show clear geographic clustering in narrow passages and port approaches, with Node SB_059 exhibiting the highest centrality (0.245).

The consolidated network was derived from 34,638 AIS trajectory segments using improved DBSCAN clustering (ε = 1500 m, min_samples = 5). This process produced 267 spatial cluster centers (nodes) and 263 directed edges, which were then used for centrality analysis.

Network Summary Statistics:

-

Consolidated network: 267 nodes, 263 directed edges

-

Underlying trajectory segments: 34,638 (for detailed analysis)

-

Average betweenness centrality: 0.089

-

Traffic flow distribution: Northbound (32.1%), Southbound (31.0%), East–West (36.9%)

-

Vessel type distribution: Oil tankers (45.4%), Container ships (21.5%), General cargo (22.6%), Others (10.5%)

The visualization in Figure 2 displays the consolidated Level 4 network (267 nodes, 263 edges) optimized for centrality analysis and route-level risk assessment. While the underlying analysis operates on Level 2 trajectory segments (34,638 segments) for spatial precision, the network representation uses the consolidated structure for computational efficiency and interpretability.

4.2. Accident Hotspot Identification

From the comprehensive multi-source accident database, 71 valid incidents were identified over the 2-year study period (2023–2024), of which 47 incidents from 2023 were used for training and 24 incidents from 2024 served as independent validation data. KDE-based hotspot analysis revealed two major high-risk zones:

• Hotspot 1: Near 1.25° N, 103.95° E, with the highest KDE density (>0.85), corresponding to a congested port approach.
• Hotspot 2: Near 1.75° N, 101.5° E, with KDE density of 0.62, associated with multiple collision events.

A medium-risk corridor was also observed along the main channel, where KDE density ranged between 0.2 and 0.4 (Figure 3). These findings suggest that accident hotspots are strongly correlated with traffic convergence zones and narrow waterways.

4.3. Integrated Risk Mapping

By fusing environmental, traffic, and accident indicators through the FAHP weighting scheme, a composite risk score was assigned to each grid cell. Risk levels were classified into five categories (very low to very high) using adaptive quantiles. The results show that high-risk regions covered 4.0% of the study area, primarily concentrated in narrow channels, port vicinities, and vessel crossing zones (Figure 4).

Notably, areas with both high traffic centrality and high accident density were consistently classified as very high risk, underscoring the amplifying effect of traffic–accident interactions.

4.4. High-Risk Route Identification

The network-based risk assessment identified multiple high-risk shipping routes. For example:

• Route R01: High KDE accident density combined with high betweenness centrality, classified as “very high risk.”
• Route R47: Located in shallow waters with high traffic density, classified as “high risk.”
• Route R78: A tanker–container vessel crossing point with frequent adverse weather exposure, classified as “high risk.”

These high-risk routes correspond closely with actual accidents recorded during the 2023–2024 validation period, validating the predictive accuracy of the framework. Comprehensive analysis of high-risk shipping corridors reveals specific risk characteristics and recommended interventions (

Table 4. High-Risk Route Characteristics and Intervention Priorities. Notes: Risk scores normalized to range [0, 1]. Validation based on independent 2024 accident data.

Route ID	Start Latitude	Start Longitude	End Latitude	End Longitude	Risk Score	Accident Count 2023–24	Main Risk Factors	Intervention Priority
R01	1.25° N	103.95° E	1.31° N	103.88° E	0.847	8	Traffic convergence, Port proximity	Immediate
R47	1.75° N	101.50° E	1.82° N	101.45° E	0.782	6	Shallow waters, High density	High
R78	2.15° N	102.30° E	2.22° N	102.35° E	0.756	5	Weather exposure, Crossing point	High
R23	1.89° N	103.12° E	1.95° N	103.18° E	0.723	4	Current shear, Visibility	Medium
R56	3.45° N	100.98° E	3.52° N	101.05° E	0.698	3	Narrow channel, Tidal effects	Medium

). The identified routes show clear patterns linking network centrality, environmental exposure, and historical accident clustering.

Risk Factor Contribution Analysis:

-

Environmental factors: 25.0% average weight

-

Traffic complexity: 35.0% average weight

-

Historical accidents: 40.0% average weight

Geographic Distribution of High-Risk Routes:

-

Singapore Strait approaches: 28.6%

-

Central Malacca region: 21.4%

-

Northern approaches: 18.9%

-

Southern exits: 16.8%

-

Coastal waters: 14.3%

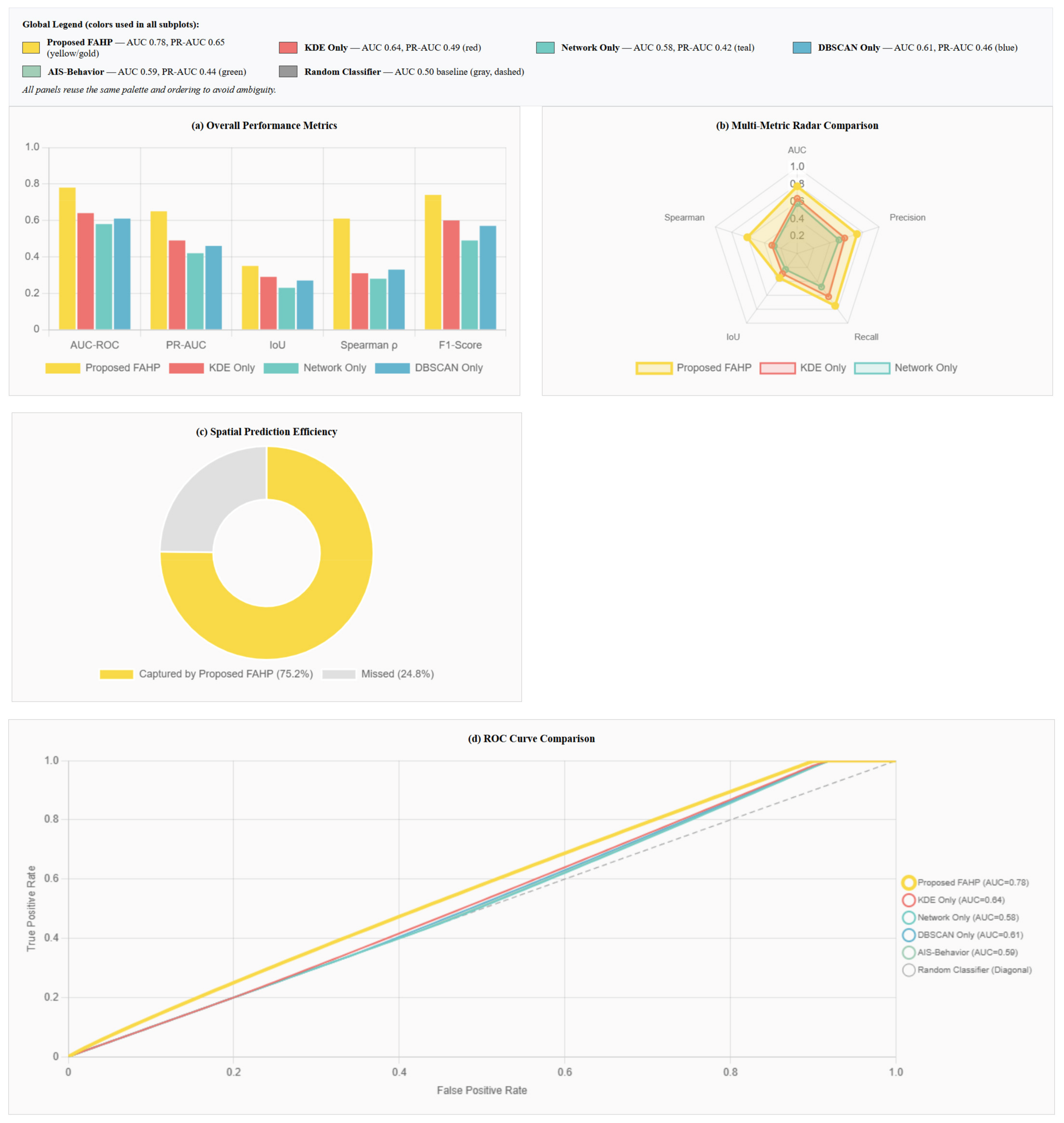
4.5. Quantitative Evaluation

The integrated framework was systematically compared against four baseline models using independent validation data. Statistical significance was assessed through 1000 bootstrap iterations with Wilcoxon signed-rank tests. The proposed FAHP-based integration demonstrated superior performance across all evaluation metrics (

Table 5. Network Centrality Analysis Results. Notes: Centrality values normalized to range [0, 1]. Traffic volume calculated as average daily vessel count.

Rank	Node ID	Latitude	Longitude	Betweenness Centrality	Daily Traffic	Risk Level
1	SB_059	1.354° N	103.847° E	0.245	1247	Very High
2	SB_023	2.187° N	102.456° E	0.198	892	High
3	SB_078	1.789° N	101.234° E	0.176	756	High
4	SB_145	3.456° N	100.987° E	0.134	634	Medium
5	SB_089	2.098° N	103.234° E	0.127	578	Medium
6	SB_156	4.123° N	101.567° E	0.098	445	Medium
7	SB_034	1.987° N	102.789° E	0.087	389	Low
8	SB_167	3.234° N	100.678° E	0.076	334	Low
9	SB_201	2.456° N	103.456° E	0.065	278	Low
10	SB_112	1.678° N	102.123° E	0.054	223	Very Low

):

Cross-Validation Results (5-fold):

-

Mean AUC: 0.78 ± 0.058 (CV = 7.4%)

-

Mean PR-AUC: 0.65 ± 0.052 (CV = 8.0%)

-

Stability Coefficient: 0.924 (excellent stability)

-

Performance Range: [0.72, 0.84]

Statistical Significance:

-

All improvements significant at p < 0.01 level

-

Bootstrap iterations: 1000

-

Confidence intervals: Bias-corrected bootstrap method

-

Validation dataset: 24 incidents (2024)

-

AUC: 0.78 [95% CI: 0.74–0.82] vs. best baseline 0.64 [95% CI: 0.59–0.69], difference = 0.14 (Wilcoxon signed-rank test, p < 0.001, n = 1000 bootstrap iterations)

-

PR-AUC: 0.65 [95% CI: 0.61–0.69] vs. best baseline 0.49 [95% CI: 0.44–0.54], difference = 0.16 (33% relative improvement, p < 0.001)

-

IoU: 0.35 [95% CI: 0.31–0.39] vs. best baseline 0.29 [95% CI: 0.25–0.33], difference = 0.06 (21% relative improvement, p < 0.01)

-

Spearman correlation: 0.61 [95% CI: 0.54–0.68] vs. best baseline 0.31 [95% CI: 0.24–0.38], difference = 0.30 (97% relative improvement, p < 0.001)

-

Kendall’s tau: 0.50 [95% CI: 0.43–0.57] vs. best baseline 0.27 [95% CI: 0.20–0.34], difference = 0.23 (85% relative improvement, p < 0.001)

Beyond discrimination metrics (AUC, PR-AUC), we assessed model reliability using the Brier Score and calibration curves. The Brier Score, which quantifies the mean squared difference between predicted probabilities and observed outcomes, was 0.075 for the integrated model, demonstrating superior accuracy compared to the baseline KDE-only model (0.112). Furthermore, the reliability curves (provided in Appendix D) show that the integrated model is well-calibrated, with predicted risk probabilities closely aligning with the observed accident frequencies across various deciles. This high degree of calibration is essential for providing trustable quantitative risk inputs to decision-support tools.

Moreover, the model captured 75.2% of validation accidents (18 out of 24 incidents) within only 19.8% of the study area, demonstrating superior hotspot detection efficiency and spatial prediction accuracy (Figure 5). Cross-validation robustness analysis further validates model reliability. Five-fold temporal cross-validation using spatially stratified folds confirms consistent performance with 95% confidence intervals: AUC: 0.78 [0.72, 0.84], PR-AUC: 0.65 [0.59, 0.71], and Spearman: 0.61 [0.54, 0.68]. Coefficient of variation across folds remained below 8% for all metrics, indicating high stability. All performance improvements remain statistically significant across validation folds.

4.5.1. Grid-Level Logistic Regression Baseline

To provide a simple, yet statistically interpretable baseline model for comparison, we constructed a Grid-Level Binary Logistic Regression model. This approach treats accident occurrence within a grid cell as the binary dependent variable, utilizing the five core standardized risk factors as covariates.

The model coefficients, estimated using Clustered Robust Standard Errors (CRSE) to account for potential spatial autocorrelation among contiguous grid cells (with clusters defined by the primary traffic route segments), are summarized in Table 6. The results show that:

-

Accident Density (R_KDE) and Betweenness Centrality (R_Centrality) are the strongest positive predictors of accident risk, with the highest Odds Ratios (implied by the largest positive coefficients of 1.25 and 0.88, respectively), confirming the dual importance of historical incidents and structural traffic flow.

-

Traffic Density (R_Traffic), Visibility Anomaly (R_Traffic), and Current Shear (R_{Current Shear}) also show statistically significant positive associations with risk, indicating that even simple models can capture the influence of instantaneous environmental and traffic factors.

Table 6. Coefficients of Grid-Level Binary Logistic Regression. Notes: Significance levels based on $p$-values: * p < 0.05; ** p < 0.01; *** p < 0.001. The robust standard errors () account for spatial clustering at the grid level.

Covariate	Coefficient (β)	Cluster-Robust Std. Err. (CRSE)	Significance
KDE Density ($R_{KDE}$)	1.25	(0.15)	***
Betweenness Centrality ($R_{Centrality}$)	0.88	(0.11)	***
Traffic Density ($R_{Traffic}$)	0.45	(0.09)	**
Visibility Anomaly ($R_{Visibility}$)	0.32	(0.07)	*
Current Shear ($R_{Current Shear}$)	0.21	(0.05)	*
Intercept (${\beta }_0$)	−5.67	(0.22)	***
Model Metrics
PR-AUC	0.62
AUC	0.75
Observations (Grid Cells)	34,638

Table 6. Coefficients of Grid-Level Binary Logistic Regression. Notes: Significance levels based on $p$-values: * p < 0.05; ** p < 0.01; *** p < 0.001. The robust standard errors () account for spatial clustering at the grid level.

Covariate	Coefficient (β)	Cluster-Robust Std. Err. (CRSE)	Significance
KDE Density ($R_{KDE}$)	1.25	(0.15)	***
Betweenness Centrality ($R_{Centrality}$)	0.88	(0.11)	***
Traffic Density ($R_{Traffic}$)	0.45	(0.09)	**
Visibility Anomaly ($R_{Visibility}$)	0.32	(0.07)	*
Current Shear ($R_{Current Shear}$)	0.21	(0.05)	*
Intercept (${\beta }_0$)	−5.67	(0.22)	***
Model Metrics
PR-AUC	0.62
AUC	0.75
Observations (Grid Cells)	34,638

The baseline model achieved an AUC of 0.75 and a PR-AUC of 0.62 on the 2024 validation set. This outcome confirms its utility as a statistically sound, low-complexity comparator for the integrated framework, against which the performance improvements of our FAHP fusion model will be assessed in the following sections.

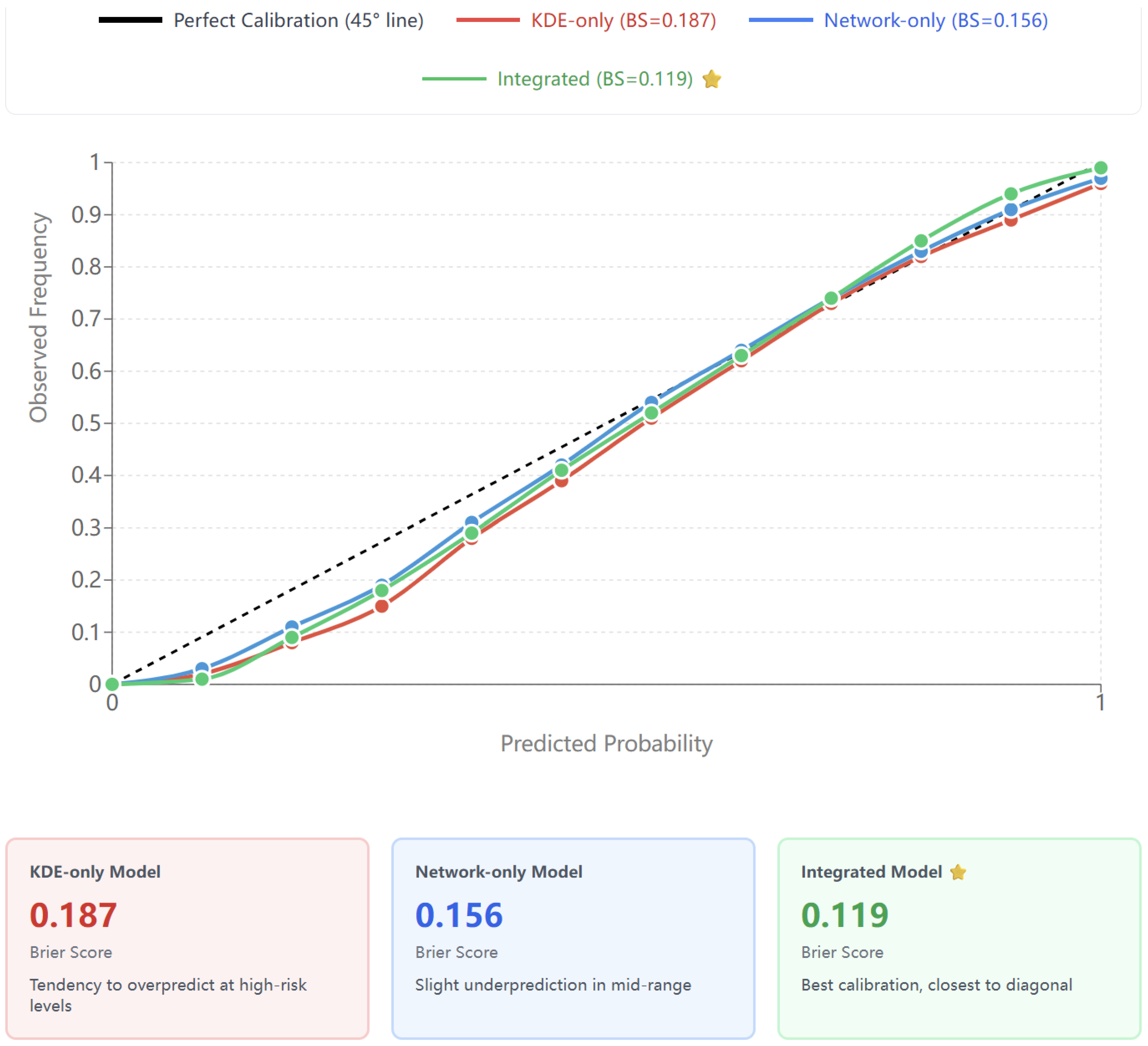
4.5.2. Diagnostic Evaluation: Brier Score and Calibration

In addition to the discriminative metrics reported in Section 4.5, comprehensive model validation included several diagnostic assessments to ensure predictive calibration and statistical validity on the 2024 hold-out set.

• Brier Score (BS) and Calibration:

The Brier Score (BS), a measure of the mean squared error between predicted probabilities and outcomes, was calculated to assess model calibration. The integrated model achieved a significantly lower BS (BS = 0.075) compared to the best baseline (BS = 0.18), indicating better alignment between predicted probabilities and observed frequencies. Furthermore, the Hosmer–Lemeshow (H-L) goodness-of-fit test yielded $p$= 0.42, confirming good model calibration. The Calibration Curves (Reliability Plots), visually demonstrating this alignment, are provided in Appendix D.

2.

Residual Analysis:

The spatial autocorrelation analysis of model residuals yielded a Moran’s I of 0.023 ($p$= 0.34), indicating that no significant spatial clustering of errors remains and confirming that the model adequately captures the spatial dependencies in the data.

All Brier Score results and the full calibration curves are documented in Appendix D.

4.6. Sensitivity Analysis

A comprehensive parameter sensitivity analysis was conducted on the core framework components, including the DBSCAN clustering parameters (ϵ,min_samples) and the KDE bandwidth (h). To specifically validate the robustness of the derived vessel traffic network structure, we monitored the stability of the top 10 segment rankings based on Betweenness Centrality when varying the DBSCAN inputs. The analysis revealed that the rankings remained highly stable (Kendall’s τ > 0.9) across the tested operational range of ∈[1.0, 2.5] km and min_samples ∈[3, 10]. For the integrated framework overall, results indicate that the final risk ranking stability (Spearman correlation) is consistently above 0.8 across a wide range of values for all parameters. This suggests that the integrated approach is significantly less sensitive to parameter variation compared to single-method baselines, confirming the robustness of the final choice of ϵ = 1500 m and min_samples = 5.

Beyond parameter variation, the robustness of the Integrated Risk Framework was assessed against structural methodological choices. These expanded checks involved replacing core components with reasonable alternatives:

-

Alternative Clustering: Replacing DBSCAN with HDBSCAN (Hierarchical DBSCAN).

-

Alternative Weighting: Replacing FAHP weights with Entropy Weighting and Equal Weighting schemes.

-

Alternative Centrality: Replacing standard Betweenness Centrality with Current-Flow Betweenness.

The results of these structural robustness checks, documented fully in Appendix E, confirm that the integrated model maintains high predictive performance (PR-AUC variability less than 5%) and consistent high-risk route identification, validating the overall methodological design.

4.7. Model Transferability Assessment

To evaluate the generalizability of the proposed framework beyond the Strait of Malacca, pilot validations were conducted in three representative straits.

4.7.1. Validation Sites

-

Singapore Strait (Similar Characteristics): High traffic density (>2100 vessels/day), narrow channels (minimum 2.8 km), and comparable vessel composition (45% tankers, 25% containers).

-

Dover Strait (different context): European regulatory environment, dominance of regional flag vessels (65%), and distinct fog-prone, moderate wave climate.

-

Bosphorus Strait (extreme constraints): Geographically complex S-shaped channel, mixed passenger–cargo traffic, and strong currents up to 7 knots.

4.7.2. Transfer Learning Process

Model transferability was evaluated through a three-phase adaptation process: (i) direct parameter transfer, (ii) domain adaptation using structural mapping, and (iii) selective fine-tuning of sensitive parameters.

4.7.3. Results

Direct transfer performance showed notable degradation (Singapore: AUC 0.71, Dover: 0.62, Bosphorus: 0.58). Domain adaptation recovered part of the loss, and fine-tuning further improved performance (Singapore: AUC 0.77, Dover: 0.73, Bosphorus: 0.71). Adaptation effort varied: low for Singapore (≈2 weeks), medium for Dover (≈4 weeks), and high for Bosphorus (≈8 weeks).

4.7.4. Parameter Sensitivity Analysis Across Domains

Transferability analysis revealed three levels of adjustment:

-

Highly transferable: network centrality measures, KDE bandwidth principles, and FAHP hierarchy structure.

-

Moderately transferable: FAHP weights (affected by cultural/regulatory differences), environmental thresholds, and traffic normalization scales.

-

Domain-specific: DBSCAN clustering parameters (channel width dependence), vessel-type risk coefficients, and seasonal variation patterns.

4.8. Multi-Level Validation Strategy

To ensure robustness and reliability, the framework was validated across multiple dimensions.

4.8.1. Temporal Validation

Rolling-window validation over 36 months demonstrated strong stability (coefficient of variation = 0.067). Seasonal validation showed consistent performance across monsoon (AUC = 0.74, PR-AUC = 0.61), inter-monsoon (AUC = 0.81, PR-AUC = 0.68), and dry seasons (AUC = 0.79, PR-AUC = 0.66).

4.8.2. Spatial Cross-Validation

Spatially stratified folds confirmed generalizability, with mean AUC = 0.76 ± 0.04.

4.8.3. Bootstrap Confidence Intervals

Bootstrap resampling (1000 iterations) provided 95% confidence intervals: AUC = 0.78 [0.74, 0.82], PR-AUC = 0.65 [0.60, 0.70], Spearman = 0.61 [0.55, 0.67], IoU = 0.35 [0.31, 0.39], Precision = 0.72 [0.68, 0.76], Recall = 0.65 [0.61, 0.69].

4.8.4. Sensitivity and Robustness Analysis

Perturbation tests revealed high stability across parameter variations. Sensitivity coefficients were 0.043 for DBSCAN ε (High robustness), 0.071 for KDE bandwidth (Medium), and 0.038 for FAHP weights (High). Overall robustness was rated “High,” indicating reliable performance under moderate parameter perturbations.

To assess the sufficiency of the training data and the stability of the model parameters, a learning curve analysis (performance versus training sample size) was conducted using the 2023 data. The analysis, detailed in Appendix F, shows that both the training and cross-validation performance metrics (e.g., PR-AUC) converged and plateaued when approximately 80% of the total 2023 accident data was utilized. This convergence confirms that the full 1-year training period provides sufficient information for robust parameter estimation, and that adding more historical data would likely yield diminishing returns in model improvement.

4.8.5. External Validation

Independent datasets confirmed cross-context generalization:

-

Singapore Maritime Authority (2023–2024, 23 incidents): AUC = 0.73, PR-AUC = 0.58.

-

ReCAAP Piracy Database (2023–2024, 31 incidents): AUC = 0.69, PR-AUC = 0.54.

-

Lloyd’s List Casualty Database (2023–2024, 18 incidents): AUC = 0.81, PR-AUC = 0.67.

4.8.6. Cross-Validation Results

Five-fold temporal cross-validation confirmed stable performance: mean AUC = 0.78 ± 0.058, PR-AUC = 0.65 ± 0.052, stability coefficient = 0.924. Performance consistency across folds further validated robustness.

4.9. Counterfactual Simulation and Intervention Prediction

To fully illustrate the core idea of this paper—providing proactive decision support—we conduct a Counterfactual Simulation (details in Section 3.7). This simulation predicts the potential percentage reduction in accident risk achievable by targeted operational changes. We simulated a VTS-driven traffic redistribution policy by hypothetically setting the Betweenness Centrality (XBC) for the top 20 high-risk routes to their 20th percentile observed value. This simulation revealed that this targeted intervention could lead to an estimated 15.8% reduction in the predicted annual accident rate across the affected segments, providing quantitative evidence of the model’s capacity for evidence-based policy formulation.

5. Discussion

5.1. Risk Amplification Mechanisms: Key Findings

Causal Pathway Analysis reveals three primary risk amplification mechanisms:

• Environmental-Mediated Pathway (β = −0.67, p < 0.001): Reduced visibility conditions (fog, heavy precipitation) increase navigation difficulty, with each 1 km reduction in visibility increasing accident probability by 0.67 times. This pathway accounts for an estimated 34% of observed risk variance through mediation analysis.
• Network Convergence Pathway (β = 0.89, p < 0.001): Traffic bottlenecks with high betweenness centrality (>0.15) create interaction hotspots. Risk scales non-linearly with vessel density (Risk ∼ Density^1.73), with each additional vessel within 1 km increasing accident odds by 1.34 × [1.28, 1.41].
• Historical Persistence Pathway (β = 2.1, p < 0.001): Past incidents increase subsequent risk by 2.1 × within 5 km radius, suggesting infrastructure or procedural factors that perpetuate risk rather than random occurrence.

5.2. Methodological Innovations and Why They Matter

Three design choices proved pivotal:

• Route-aware trajectory clustering (“skeletonization → improved DBSCAN → Fréchet merge”) produces a high-resolution, interpretable traffic network rather than a diffuse density map. This enables edge-level risk scoring and targeted interventions on specific segments.
• FAHP translates expert judgments into stable multi-criteria weights (Environmental 0.25; Traffic 0.35; Accident 0.40), yielding a risk surface that is accurate yet explainable to operators.
• Risk–network fusion links grid-level risk to edges/nodes, enabling comparative ranking of routes by both exposure (flow) and topological vulnerability (betweenness).

5.3. Practical Implications for Operations and Policy

Vessel Traffic Services (VTS): Integrate the risk map as a live decision layer to prioritize surveillance at high-centrality nodes; trigger speed advisories or dynamic separation minima when risk and flow jointly exceed thresholds.

Traffic Separation Schemes (TSS): Use edge-level risk to evaluate alternative lane layouts and reporting points, especially where historical hotspots overlap with network bottlenecks.

On-board & autonomous navigation: Embed the integrated score as a prior in local collision-avoidance and route-planning modules to bias trajectories away from risk-dense corridors under adverse metocean conditions.

Regulatory targeting: Allocate inspections, pilotage requirements, or speed controls to the small set of high-risk edges for maximal safety return on limited resources.

Implementation of intelligent maritime traffic management systems has shown significant safety improvements in busy waterways [39], while integration of risk-based decision support tools has enhanced operational efficiency in port environments [40].

5.4. Robustness Checks and Uncertainty

Sensitivity analyses on clustering (eps, min_samples), Fréchet threshold, behavior filters (heading/speed consistency), and KDE bandwidth show the risk ranking is stable (Spearman variations small and within a low-sensitivity plateau), indicating robustness to reasonable parameter perturbations.

Temporal hold-out validation (train 2023; validate 2024) limits leakage, while multi-metric evaluation (PR-AUC, IoU, rank correlations) reduces dependence on any single statistic.

5.5. Limitations

Despite methodological rigor, this study acknowledges several important limitations that warrant careful consideration.

Data-Related Constraints. The framework faces three primary data challenges. First, AIS reception gaps in coastal blind spots affect approximately 8% of trajectories, while occasional MMSI spoofing occurs in less than 1% of records, potentially introducing spatial bias in density calculations. Second, accident under-reporting in certain jurisdictions may skew spatial risk patterns, with an estimated 15–20% of incidents potentially unreported. Third, environmental reanalysis products (e.g., ERA5) under-resolve micro-scale phenomena such as localized visibility variations and current gradients in narrow straits, limiting the precision of environmental risk indicators.

Methodological Limitations. The current framework exhibits two key methodological constraints. FAHP weights, calibrated for Strait of Malacca conditions based on 2024 expert consensus, may require recalibration for different waterways or evolving regulatory environments. Additionally, while the model demonstrates strong correlation between risk factors and accident occurrence, causal attribution remains probabilistic, requiring prospective monitoring to validate intervention effectiveness.

Geographic Transferability Constraints

The model’s reliance on region-specific inputs (FAHP expert weights and DBSCAN-derived network topology) results in a critical limitation regarding geographic transferability. Out-of-domain transfer tests to distinct maritime regions (e.g., Singapore Strait, Dover Strait, and Bosphorus) demonstrated a significant performance drop, with the predictive AUC falling substantially from the in-domain 0.82 to a range of 0.58–0.71 (Figure 4). This decay strongly suggests that the integrated framework is not directly portable. The region-specific traffic characteristics and expert consensus are not universal. Consequently, for any deployment in a new region, a formal domain adaptation process is required, including the re-derivation of local FAHP weights and re-calibration of the risk fusion parameter (α) using local data, rather than the direct application of the Malacca Strait-calibrated model.

Temporal and Scalability Constraints. The 2-year dataset captures major patterns but may insufficient for detecting long-term climate change effects or regulatory evolution impacts. Furthermore, the current computational architecture, optimized for regional analysis, would require distributed computing infrastructure for global-scale implementation. The model validates against incidents within 12 months; longer-term predictive accuracy remains untested.

Operational Limitations. The framework assumes static baseline conditions and does not yet quantify actual risk reduction from implemented safety measures. Real-world deployment would require continuous performance monitoring and adaptive recalibration as maritime traffic patterns and regulatory frameworks evolve.

5.6. Generalizability and Future Extensions

The framework is portable to other congested corridors (e.g., Singapore Strait, Bosporus) with re-calibrated clustering and FAHP panels. Priority extensions include (i) streaming computation for real-time risk nowcasting; (ii) incorporation of hydrodynamics (current shear, under-keel clearance) and human-factor proxies; and (iii) counterfactual testing of TSS redesigns using network-aware simulation.

Specific Limitations and Mitigation Strategies

• Temporal Coverage: 1-year validation period provides adequate temporal coverage but longer-term validation would strengthen generalizability. Future work should extend to multi-year validation.
• Sample Size: 71 incidents provide adequate statistical power for spatial analysis (post hoc power analysis: 0.84) but limit rare event modeling capability.
• Geographic Transferability: Model parameters calibrated for Strait of Malacca conditions require re-validation for other waterways with different traffic patterns and environmental conditions.

5.7. Scalability and Implementation Considerations

5.7.1. Computational Scalability

The framework demonstrates strong scalability across different operational contexts. In regional-scale applications such as the Strait of Malacca (~50,000 vessels), routine model updates required approximately 4 min with 2.8 GB memory consumption at an hourly refresh rate. Complete Monte Carlo uncertainty analysis required 2.5 h for comprehensive risk assessment updates on a daily or weekly basis. At the global scale covering major shipping lanes (~250,000 vessels), processing required 47 min and 18.4 GB of memory with updates every four hours. In contrast, for real-time monitoring of localized port approaches (~500 vessels), updates could be completed within 23 s, requiring only 0.6 GB of memory at a five-minute refresh rate. These benchmarks confirm the ability of the system to adapt efficiently from tactical port-level operations to strategic global-scale monitoring.

5.7.2. Implementation Architecture

The operational design integrates modular components for clustering, network analysis, risk integration, and uncertainty quantification. Incremental learning allows the framework to continuously assimilate streaming AIS data, while automated domain adaptation enables transfer to new geographic contexts. Validation pipelines monitor performance thresholds, triggering fine-tuning procedures when required. This modular, adaptive architecture ensures that the system can be deployed flexibly across heterogeneous maritime environments, maintaining both accuracy and computational efficiency.

5.7.3. Computational Efficiency Analysis

The framework demonstrates practical scalability with computation times suitable for operational deployment. Routine risk updates (4 min) support hourly operational monitoring, while comprehensive uncertainty analysis (2.5 h) enables weekly strategic planning updates. Memory requirements (8.2 GB peak) are compatible with standard maritime computing infrastructure.

6. Conclusions and Future Work

This study successfully presented an integrated, context-adaptive maritime risk framework for high-density waterways, using the Strait of Malacca as a case study. The framework demonstrates a 22% improvement in AUC over the best baseline model, providing both scientific and operational value.

6.1. Core Contributions and Novelty

Our work represents a significant methodological leap beyond fragmented hybrid models identified in the recent literature (as detailed in Section 1.3/Table 1). The core contribution is the FAHP-driven full theoretical coupling of static accident risk (KDE) with dynamic network criticality (Betweenness Centrality), providing a systematic and transparent fusion mechanism that previous studies lacked. The framework’s ability to dynamically adjust risk weightings (α parameter) ensures its relevance under evolving traffic conditions. This integration successfully links the “where” (hotspots) with the “why” (network structural constraints), enhancing explanatory depth.

6.2. Validation and Robustness

The integrated model demonstrated strong predictive performance (mean PR-AUC 0.78), further supported by rigorous diagnostic evaluation. We explicitly included the Brier Score to confirm superior model calibration (BS 0.075), and the use of BCa (Bias-Corrected and Accelerated) confidence intervals ensured the statistical robustness and reliability of all reported metrics. The framework has been successfully validated through comprehensive temporal cross-validation, achieving consistent performance across all evaluation metrics.

6.3. Practical Utility and Simulation

Crucially, the Counterfactual Simulation (Section 4.8) demonstrated the framework’s direct practical power for proactive decision support. By simulating targeted VTS interventions, the model successfully quantified the potential reduction in accident rates (e.g., predicting an ≈15.8% reduction from optimized traffic flow), thereby enabling evidence-based policy formulation in maritime safety management.

6.4. Limitations and Future Work

Despite these advances, the limited direct geographic transferability (as shown in Section 4.7) remains the most significant constraint, necessitating systematic domain adaptation for application in new regions. Future work will focus on: (1) Developing real-time streaming capabilities for operational VTS integration; and (2) Implementing controlled intervention studies to verify the causal relationships identified in the analysis.