Mesoscale Linear Elastic Modeling and Homogenization of Marine Energy Composites
Abstract
1. Introduction
2. Materials and Imaging
2.1. Manufacturing
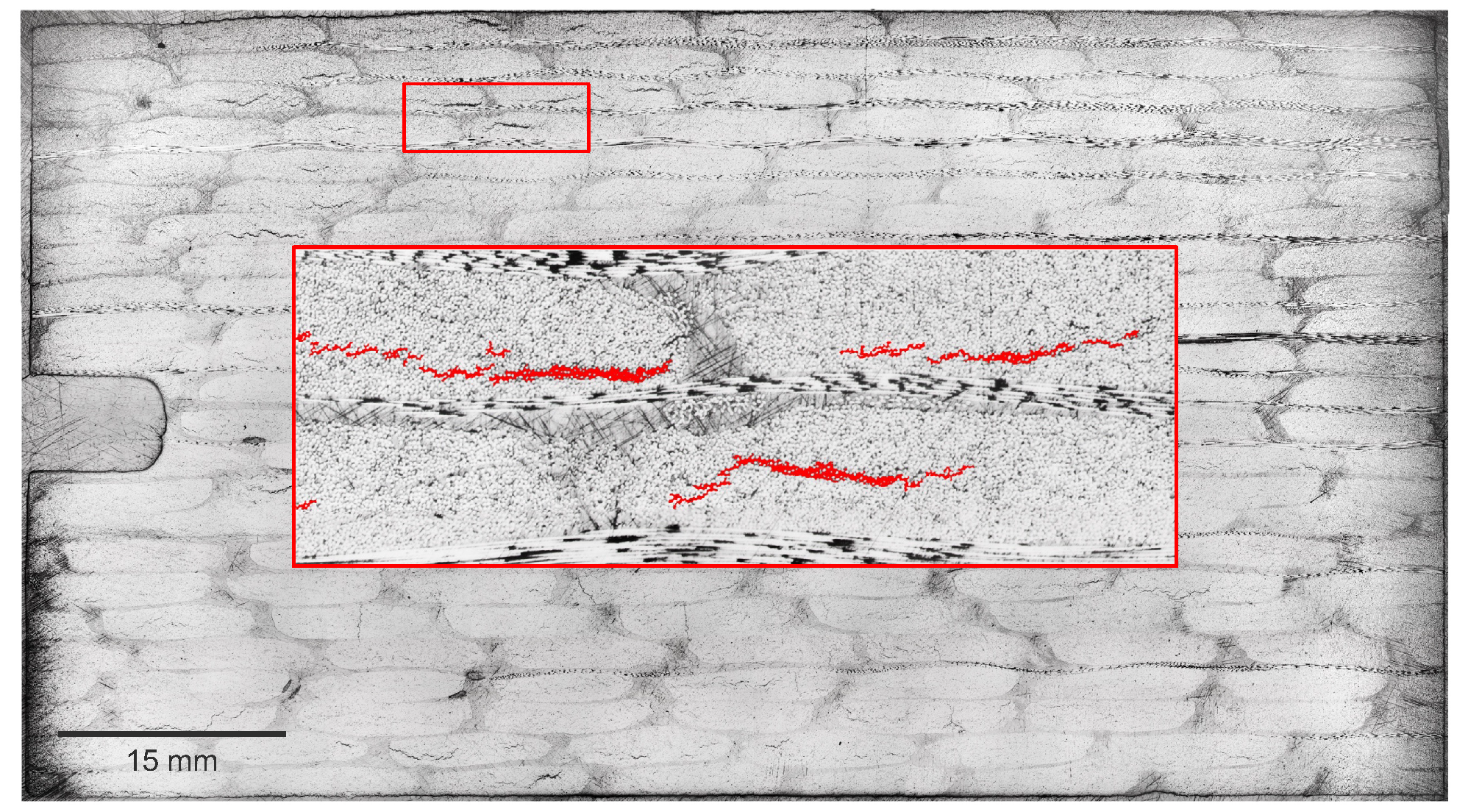
2.2. Image Acquisition and Segmentation
3. Methods
3.1. Idealized Mesoscale Modeling Approach
| Variable | Unit | Nominal | Lower | Upper | Reference |
|---|---|---|---|---|---|
| Warp tow width | cm | 0.35 | 0.30 | 0.40 | XCT |
| Warp tow height | cm | 0.06 | 0.05 | 0.07 | XCT |
| Weft tow width | cm | 0.35 | 0.30 | 0.40 | XCT |
| Weft tow height | cm | 0.012 | 0.01 | 0.02 | XCT |
| Warp tow gap | cm | 0.03 | 0.0 | 0.04 | XCT |
| Weft tow gap | cm | 0.30 | 0.0 | 0.80 | XCT |
| Tow fiber volume fraction | – | 0.575 | 0.55 | 0.70 | Exp., XCT |
| Matrix diffusivity | mm2/s | 8.5 × 10−7 | 7.0 × 10−7 | 9.65 × 10−7 | Exp., [42] |
| Matrix modulus | GPa | 2.50 | 2.10 | 3.60 | Exp., [43] |
| Matrix Poisson’s ratio | – | 0.347 | 0.30 | 0.45 | Exp., [43] |
| Matrix exp. coef. | – | 0.30 | 0.1761 | 0.33 | Exp., [44] |
| Fiber modulus | GPa | 73.0 | 65.0 | 85.0 | [45,46] |
| Fiber Poisson’s ratio | – | 0.22 | 0.10 | 0.30 | [45,46] |
3.2. Image-Based Mesoscale Modeling Approach
4. Results and Discussion
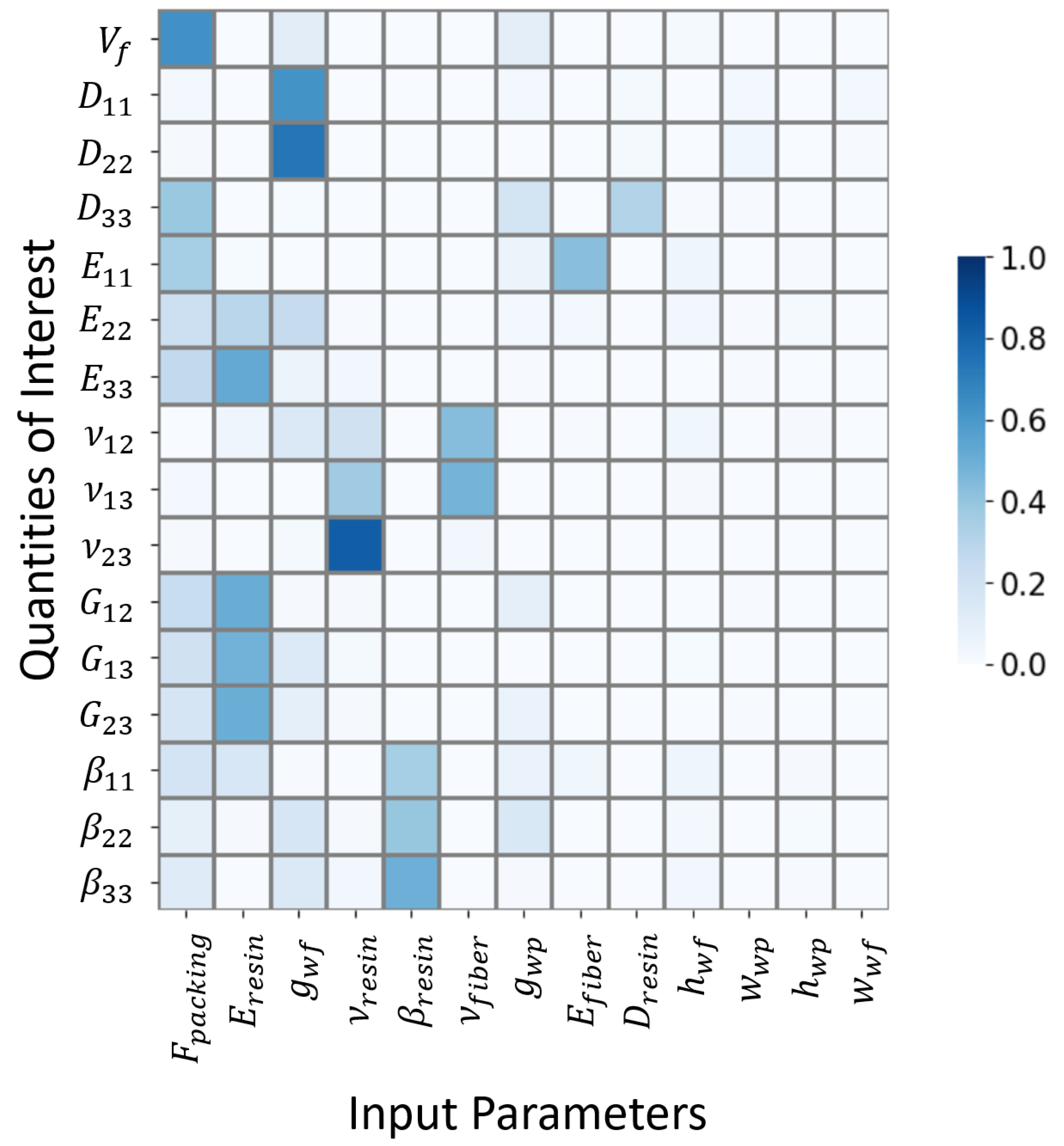
4.1. Idealized Model Results and Sensitivity Analysis
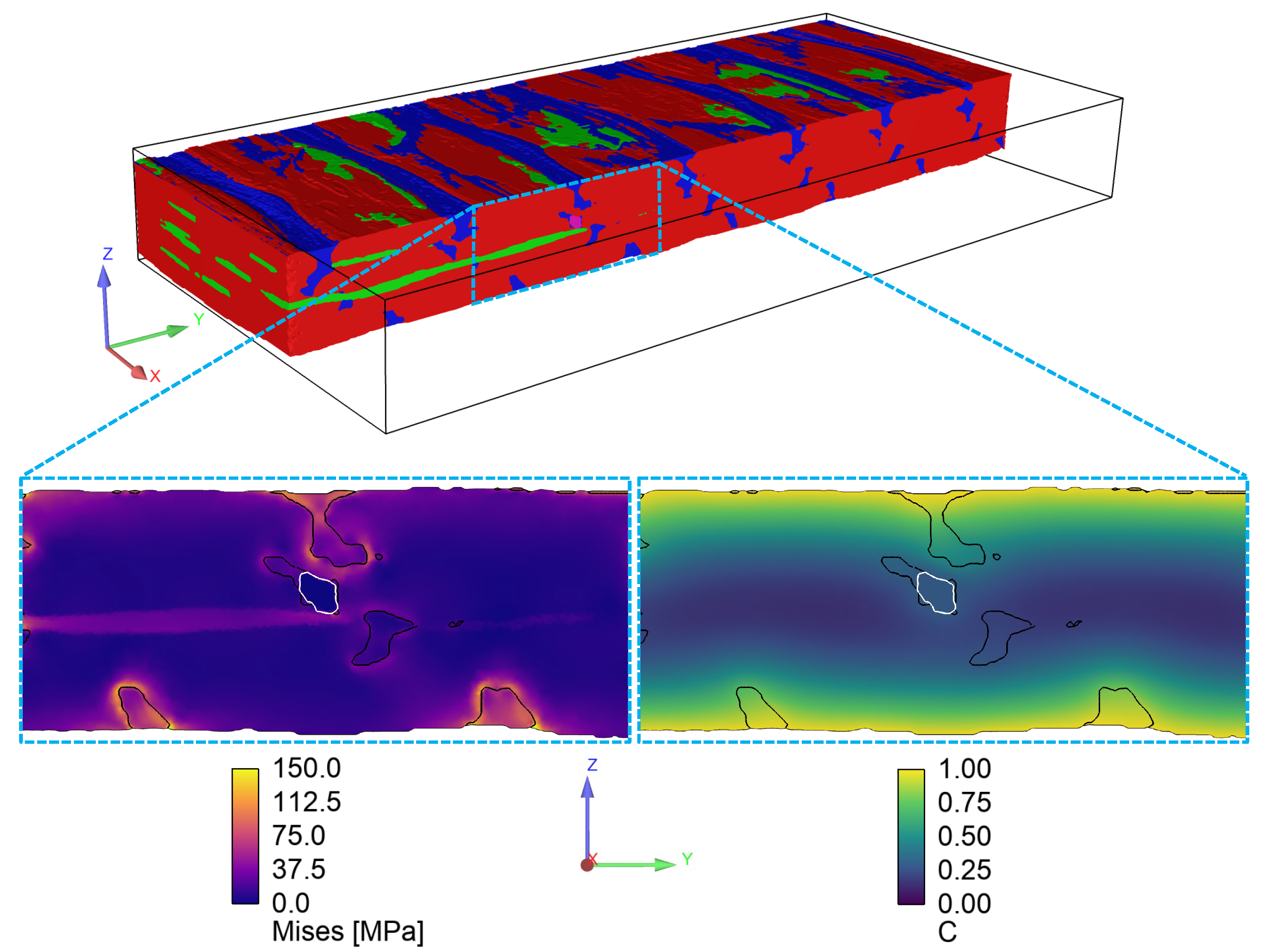
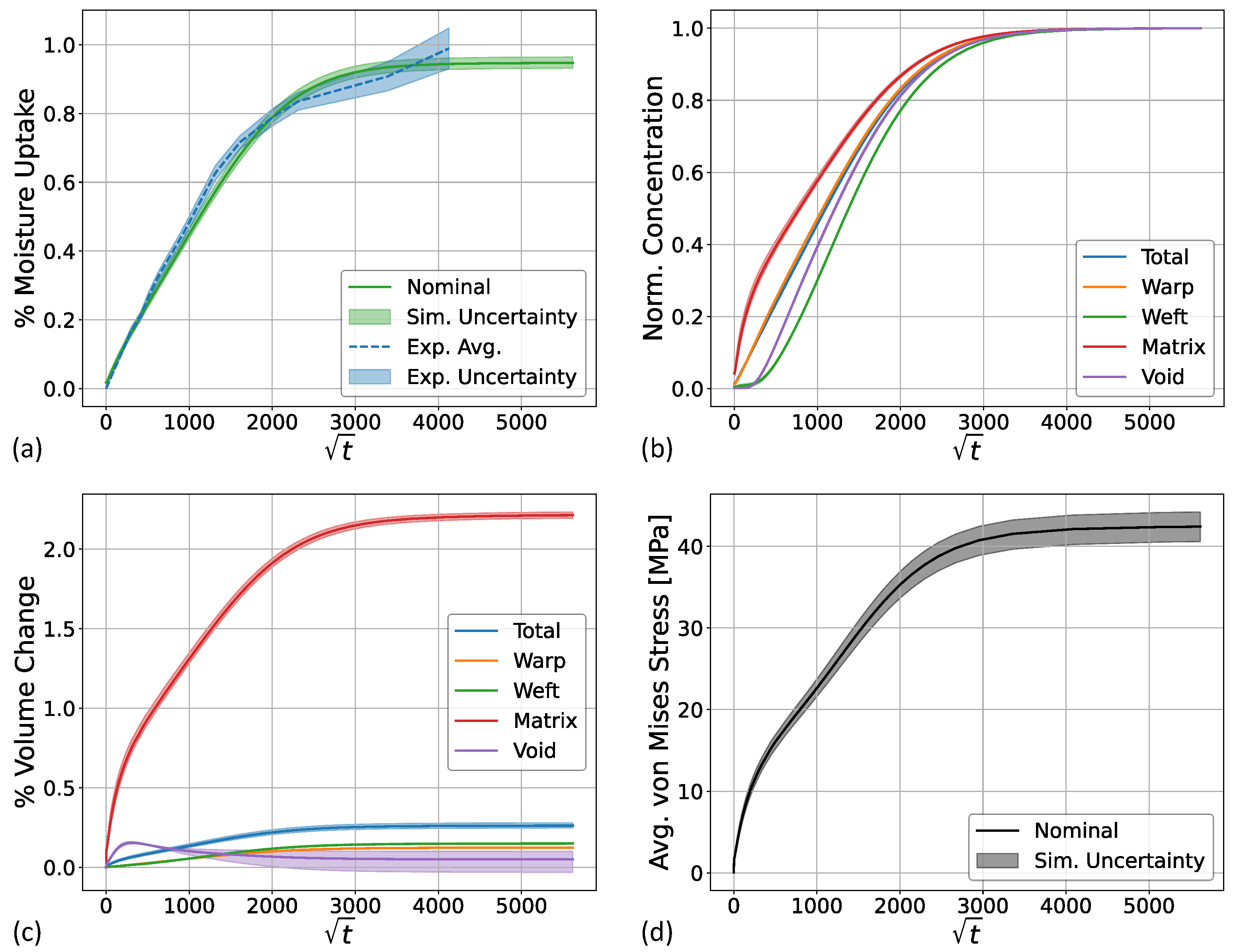
4.2. Image-Based Modeling Results
5. Conclusions
- The idealized geometry constructed in this work can easily be generated, which enables many hundreds of simulations to be executed and used to perform a parametric sensitivity analysis on model input parameters.
- Based on the distribution of experimental data of effective properties, it was shown that the predicted values for moduli, Poisson’s ratios, and diffusion coefficients agreed well when utilizing the idealized geometry. Predicted hygroscopic swelling coefficients, however, exhibited greater disagreement. This disagreement likely stems from moisture absorption-induced damage, where cracks were observed after full saturation. Accounting for these damage features is the subject of future efforts.
- Construction of the image-based geometry by leveraging deep learning based image segmentation is robust at identifying the key features of interest. Predicted moisture uptake from the image-based geometry showed good agreement with experimental data, but slightly under-predicted moisture uptake at early times.
- Image segmentation uncertainty was explored by probing the 5- and 95-percentile probability map segmentation of the resin. Increased resin volume fraction generated from the 5th-percentile showed improved results compared to the nominal case. Moisture uptake, however, was still under-predicted at early times. One area of future improvement identified stems from acquiring additional X-ray CT images with enhanced resolution and contrast to validate the image segmentation accuracy. These results demonstrate the need for high-quality image data when performing image-based simulations.
- Image-based simulation results further highlighted regions of stress concentration on fiber/resin interfaces as expected, which also correlated well with regions of high resin concentration. These results stem from the high hygroscopic swelling of the resin relative to the tows. These results ultimately inform areas/regions where failure is likely to initiate.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, E.; Gunawan, B.; Nicholas, J.; Ingraham, M.; Hernandez-Sanchez, B.A. A multicontinuum-theory-based approach to the analysis of fiber-reinforced polymer composites with degraded stiffness and strength properties due to moisture absorption. J. Mar. Sci. Eng. 2023, 11, 421. [Google Scholar] [CrossRef]
- Rubino, F.; Nisticò, A.; Tucci, F.; Carlone, P. Marine application of fiber reinforced composites: A review. J. Mar. Sci. Eng. 2020, 8, 26. [Google Scholar] [CrossRef]
- Chen, N.Z.; Sun, H.H.; Soares, C.G. Reliability analysis of a ship hull in composite material. Compos. Struct. 2003, 62, 59–66. [Google Scholar] [CrossRef]
- Guo, K.; Deng, Y.; Ren, Y.; Jiang, H. Multi-scale moisture diffusion modeling and analysis of carbon/Kevlar-fiber hybrid composite laminates under the hygrothermal aging environment. Polym. Degrad. Stab. 2024, 229, 110952. [Google Scholar] [CrossRef]
- Ursache, Ş.; Cerbu, C.; Hadăr, A. Characteristics of Carbon and Kevlar Fibres, Their Composites and Structural Applications in Civil Engineering—A Review. Polymers 2023, 16, 127. [Google Scholar] [CrossRef]
- Shubha, M.; Parimala, H.; Vijayan, K. Moisture uptake by Keviar fibres. J. Mater. Sci. Lett. 1993, 12, 60–62. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Yu, T.; Li, Q.; Li, Z. Anisotropic behaviors of moisture absorption and hygroscopic swelling of unidirectional flax fiber reinforced composites. Compos. Struct. 2022, 297, 115941. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Prediction of orthotropic hygroscopic swelling of fiber-reinforced composites from isotropic swelling of matrix polymer. J. Compos. Sci. 2019, 3, 10. [Google Scholar] [CrossRef]
- Arun, K.; Basavarajappa, S.; Sherigara, B. Damage characterisation of glass/textile fabric polymer hybrid composites in sea water environment. Mater. Des. 2010, 31, 930–939. [Google Scholar] [CrossRef]
- Wu, L.; Murphy, K.; Karbhari, V.M.; Zhang, J.S. Short-term effects of sea water on E-glass/vinylester composites. J. Appl. Polym. Sci. 2002, 84, 2760–2767. [Google Scholar] [CrossRef]
- Verdant Power. 2025. Available online: https://verdantpower.com/ (accessed on 26 September 2025).
- ORPC. 2025. Available online: https://orpc.co/ (accessed on 26 September 2025).
- Raye, R.; Nichols, C.; Bharath, A.; Candon, C.; Baca, E. Data Acquisition and Control for Marine Energy Devices: Cost Considerations; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024.
- Ulvgård, L.; Kamf, T.; Risberg, A.; Leijon, M. Portable data acquisition system for offshore applications. IEEE J. Ocean. Eng. 2018, 44, 719–727. [Google Scholar] [CrossRef]
- Hayman, B.; Wedel-Heinen, J.; Brøndsted, P. Materials challenges in present and future wind energy. Mrs Bull. 2008, 33, 343–353. [Google Scholar] [CrossRef]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Collins, L.N.; Roberts, S.A. Mesoscale simulation of woven composite design decisions. arXiv 2021, arXiv:2104.13554. [Google Scholar] [CrossRef]
- Foster, C.W.; Collins, L.N.; Panerai, F.; Roberts, S.A. Assessing Parameterized Geometric Models of Woven Composites using Image-Based Simulations. arXiv 2023, arXiv:2302.09480. [Google Scholar] [CrossRef]
- Trembacki, B.L.; Mistry, A.N.; Noble, D.R.; Ferraro, M.E.; Mukherjee, P.P.; Roberts, S.A. Mesoscale analysis of conductive binder domain morphology in lithium-ion battery electrodes. J. Electrochem. Soc. 2018, 165, E725–E736. [Google Scholar] [CrossRef]
- Sinchuk, Y.; Pannier, Y.; Gueguen, M.; Tandiang, D.; Gigliotti, M. Computed-tomography based modeling and simulation of moisture diffusion and induced swelling in textile composite materials. Int. J. Solids Struct. 2018, 154, 88–96. [Google Scholar] [CrossRef]
- Vanaerschot, A.; Panerai, F.; Cassell, A.; Lomov, S.V.; Vandepitte, D.; Mansour, N.N. Stochastic characterisation methodology for 3-D textiles based on micro-tomography. Compos. Struct. 2017, 173, 44–52. [Google Scholar] [CrossRef]
- ASTM D3039/D3039M-08; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D3518/D3518M-18; Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM-D5229; Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- Zhang, G.; Allaire, D.; Cagan, J. Taking the guess work out of the initial guess: A solution interval method for least-squares parameter estimation in nonlinear models. J. Comput. Inf. Sci. Eng. 2021, 21, 021011. [Google Scholar] [CrossRef]
- Mourad, A.H.I.; Abdel-Magid, B.M.; El-Maaddawy, T.; Grami, M.E. Effect of seawater and warm environment on glass/epoxy and glass/polyurethane composites. Appl. Compos. Mater. 2010, 17, 557–573. [Google Scholar] [CrossRef]
- Miller, D.; Mandell, J.; Samborsky, D.; Hernandez-Sanchez, B.; Griffith, D.T. Performance of composite materials subjected to salt water environments. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012; p. 1575. [Google Scholar]
- Hexion. EPIKOTE™ Resin MGS™ RIMR 135 and EPIKURE™ Curing Agent MGS™ RIMH 134–RIMH 137. 2006. Available online: https://www.metyx.com/wp-content/uploads/PDF_Files/Hexion/TDS/TDS%20RIMH%20137.pdf (accessed on 26 September 2025).
- Comet. Dragonfly. 2023. Available online: https://dragonfly.comet.tech/ (accessed on 26 September 2025).
- Novikov, A.A.; Major, D.; Wimmer, M.; Lenis, D.; Bühler, K. Deep sequential segmentation of organs in volumetric medical scans. IEEE Trans. Med. Imaging 2018, 38, 1207–1215. [Google Scholar] [CrossRef]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar] [CrossRef]
- Krygier, M.C.; LaBonte, T.; Martinez, C.; Norris, C.; Sharma, K.; Collins, L.N.; Mukherjee, P.P.; Roberts, S.A. Quantifying the unknown impact of segmentation uncertainty on image-based simulations. Nat. Commun. 2021, 12, 5414. [Google Scholar] [CrossRef]
- Noble, D.R.; Newren, E.P.; Lechman, J.B. A conformal decomposition finite element method for modeling stationary fluid interface problems. Int. J. Numer. Methods Fluids 2010, 63, 725–742. [Google Scholar] [CrossRef]
- Roberts, S.A.; Mendoza, H.; Brunini, V.E.; Noble, D.R. A verified conformal decomposition finite element method for implicit, many-material geometries. J. Comput. Phys. 2018, 375, 352–367. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified composite micromechanics equations for hygral, thermal and mechanical properties. In Proceedings of the Annual Conference of the Society of the Plastics Industry (SPI) Reinforced Plastics/Composites Institute, Houston, TX, USA, 7–11 February 1983. number NASA-TM-83320. [Google Scholar]
- Yu, W. Multiscale Structural Mechanics: Top-Down Modelling of Composites Using the Structural Genome; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- SIERRA Thermal/Fluid Development Team. SIERRA Multimechanics Module: Aria User Manual, Version 5.10; Technical Report SAND2022-12436; Sandia National Laboratories: Albuquerque, NM, USA, 2022. [CrossRef]
- Adams, B.M.; Bohnhoff, W.J.; Dalbey, K.R.; Ebeida, M.S.; Eddy, J.P.; Eldred, M.S.; Hooper, R.W.; Hough, P.D.; Hu, K.T.; Jakeman, J.D.; et al. DAKOTA, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis (V.6.16 User’s Manual); Sandia National Laboratories: Albuquerque, NM, USA, 2021. [CrossRef]
- Winokur, J. Empirical Sensitivity Analysis for Scalar and Field Quantities; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2020.
- Li, C.; Mahadevan, S. An efficient modularized sample-based method to estimate the first-order Sobol’ index. Reliab. Eng. Syst. Saf. 2016, 153, 110–121. [Google Scholar] [CrossRef]
- TORE. TUHH Open Research. 2024. Available online: https://tore.tuhh.de/ (accessed on 7 April 2025).
- University, M.S. 3D Static Elastic and Strength Properties of a Glass/Epoxy Unidirectional Laminate. 2024. Available online: https://www.montana.edu/composites/documents/3D%20Static%20Property%20Report-2.pdf (accessed on 7 April 2025).
- Teverovsky, A. Environmentally Induced Swelling and Shrinkage of Molding Compounds in PEMs; NASA/GSFC: Greenbelt, MD, USA, 2002.
- MatWeb. MatWeb Material Property Data. 2024. Available online: https://www.matweb.com (accessed on 7 April 2025).
- Ruggiero, A.; Merola, M.; Carlone, P.; Archodoulaki, V.M. Tribo-mechanical characterization of reinforced epoxy resin under dry and lubricated contact conditions. Compos. Part Eng. 2015, 79, 595–603. [Google Scholar] [CrossRef]
- van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; the scikit-image contributors. Scikit-image: Image processing in Python. PeerJ. 2014, 2, e453. [Google Scholar] [CrossRef] [PubMed]
- Wong, E.; Koh, S.; Lee, K.; Rajoo, R. Advanced moisture diffusion modeling and characterisation for electronic packaging. In Proceedings of the 52nd Electronic Components and Technology Conference 2002, San Diego, CA, USA, 28–31 May 2002; (Cat. No. 02CH37345). IEEE: New York, NY, USA, 2002; pp. 1297–1303. [Google Scholar]
- Cao, B.; Wang, J.; Tang, S.; Zhang, Z.; Li, Y. Experimental and numerical study on moisture diffusion behavior of 3D woven composite. Compos. Part Appl. Sci. Manuf. 2024, 185, 108280. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Neumann, S.; Marom, G. Prediction of moisture diffusion parameters in composite materials under stress. J. Compos. Mater. 1987, 21, 68–80. [Google Scholar] [CrossRef]
- Miller, D.A.; Samborsky, D.D.; Stoffels, M.T.; Voth, M.M.; Nunemaker, J.D.; Newhouse, K.J.; Hernandez-Sanchez, B.A. Summary of Marine and Hydrokinetic (MHK) Composites Testing at Montana State University; Technical, Report; Sandia National Laboratories: Albuquerque, NM, USA; Montana State University: Bozeman, MT, USA, 2020. [CrossRef]
- Gibson, R.F. Principles of Composite Material Mechanics; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Kappenthuler, S.; Seeger, S. Assessing the long-term potential of fiber reinforced polymer composites for sustainable marine construction. J. Ocean. Eng. Mar. Energy 2021, 7, 129–144. [Google Scholar] [CrossRef]
- Li, B.; Baxevanakis, K.P.; Silberschmidt, V.V. Water Diffusion in Additively Manufactured Polymers: Effect of Voids. J. Compos. Sci. 2024, 8, 319. [Google Scholar] [CrossRef]
- Wang, M. Multiscale water diffusivity prediction of plain woven composites considering void defects. Sci. Eng. Compos. Mater. 2024, 31, 20220236. [Google Scholar] [CrossRef]

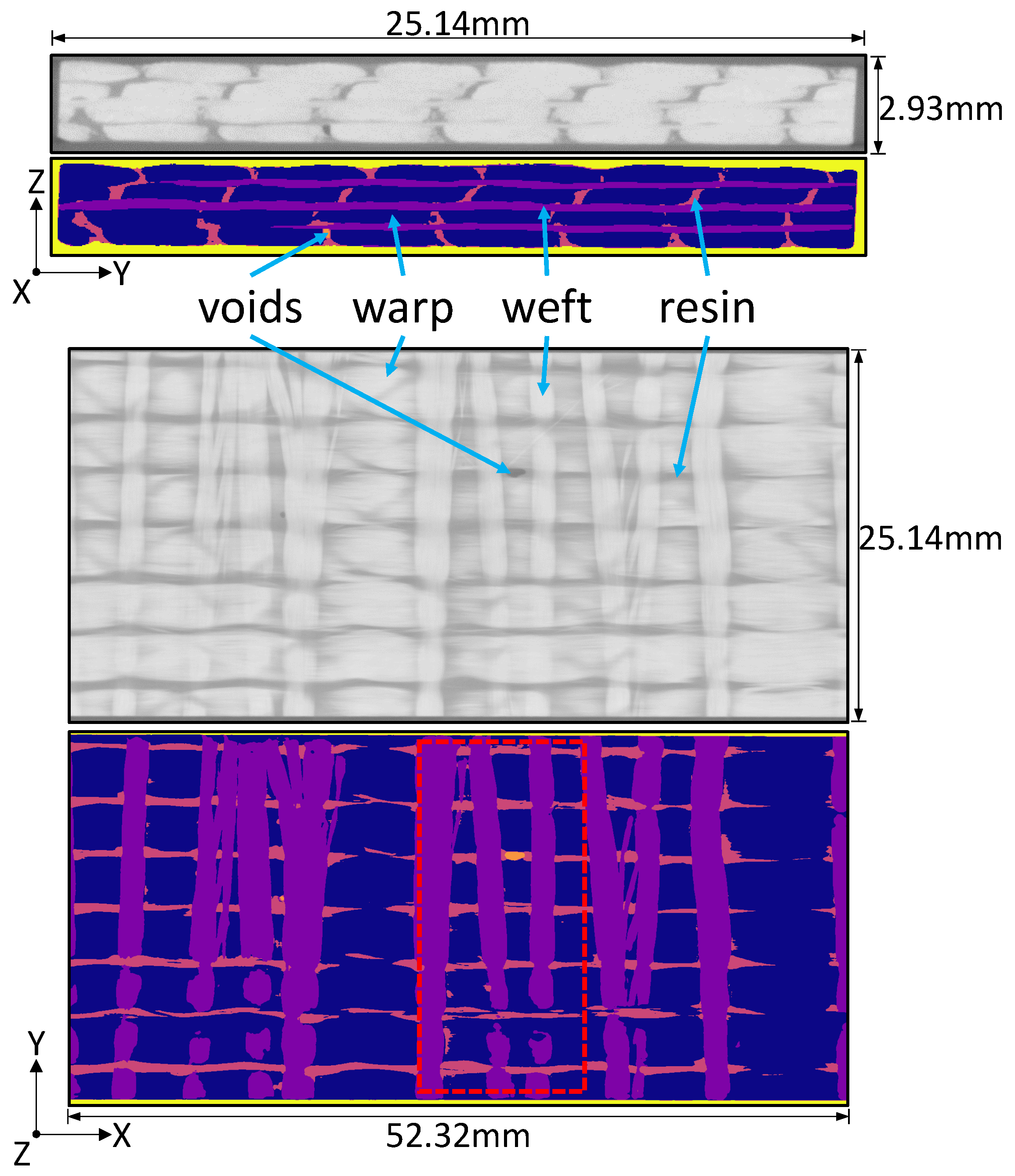
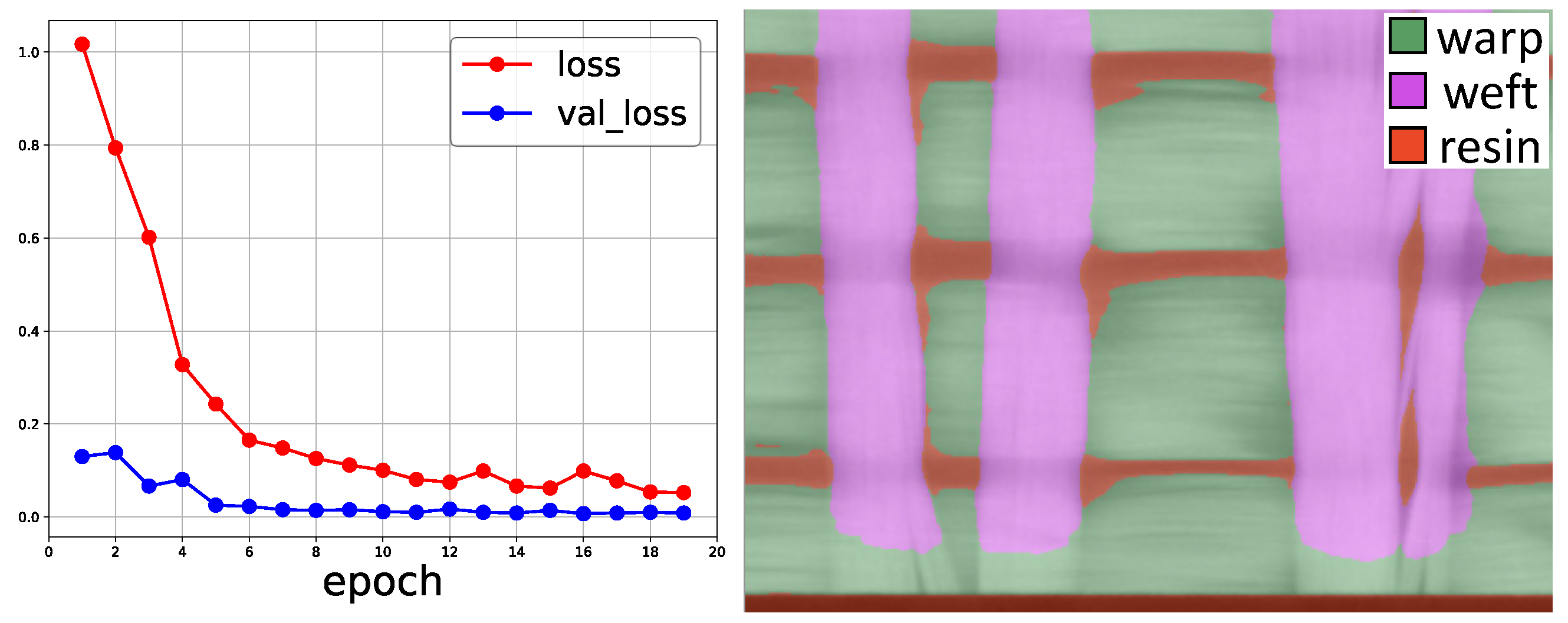
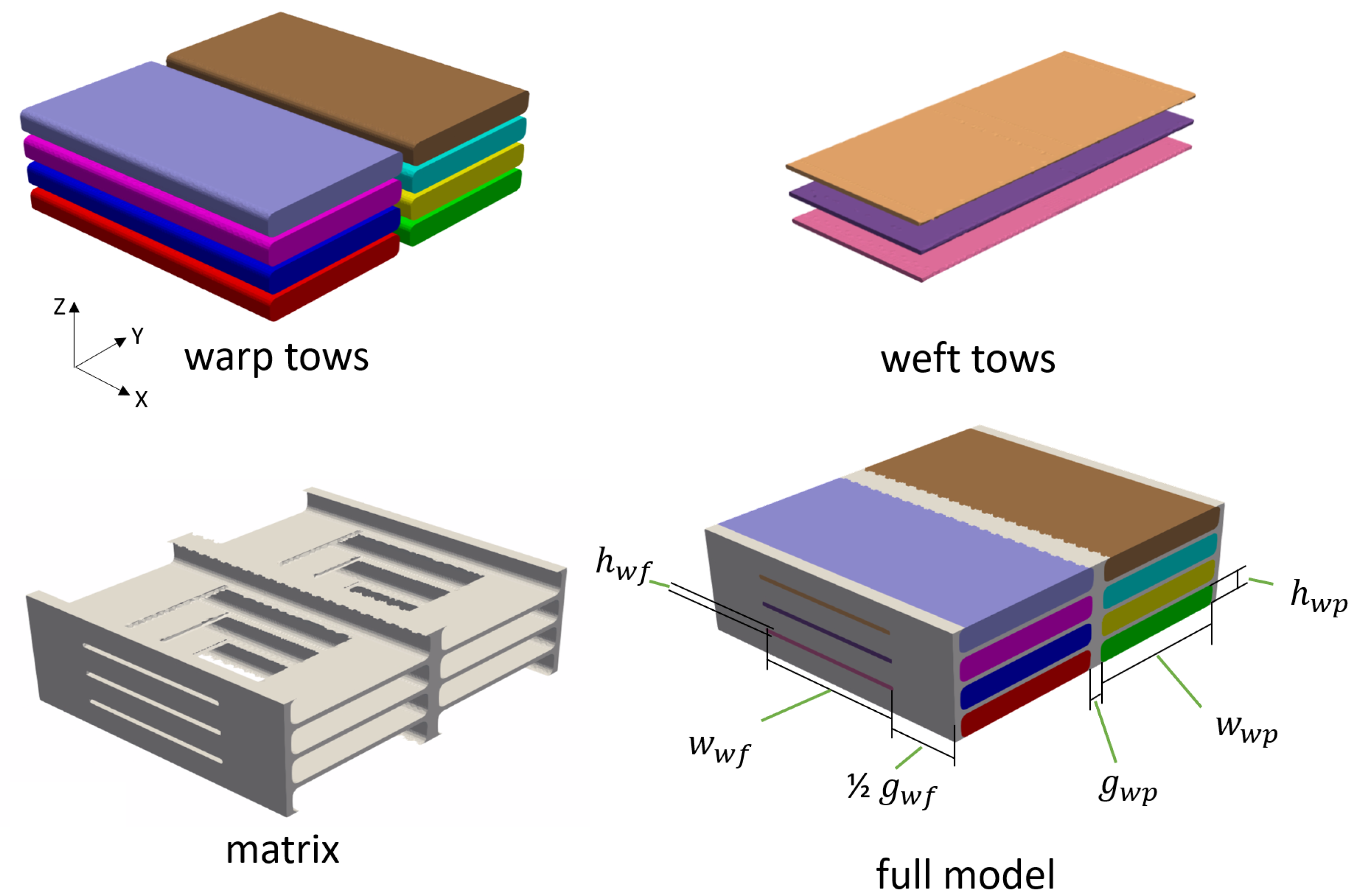


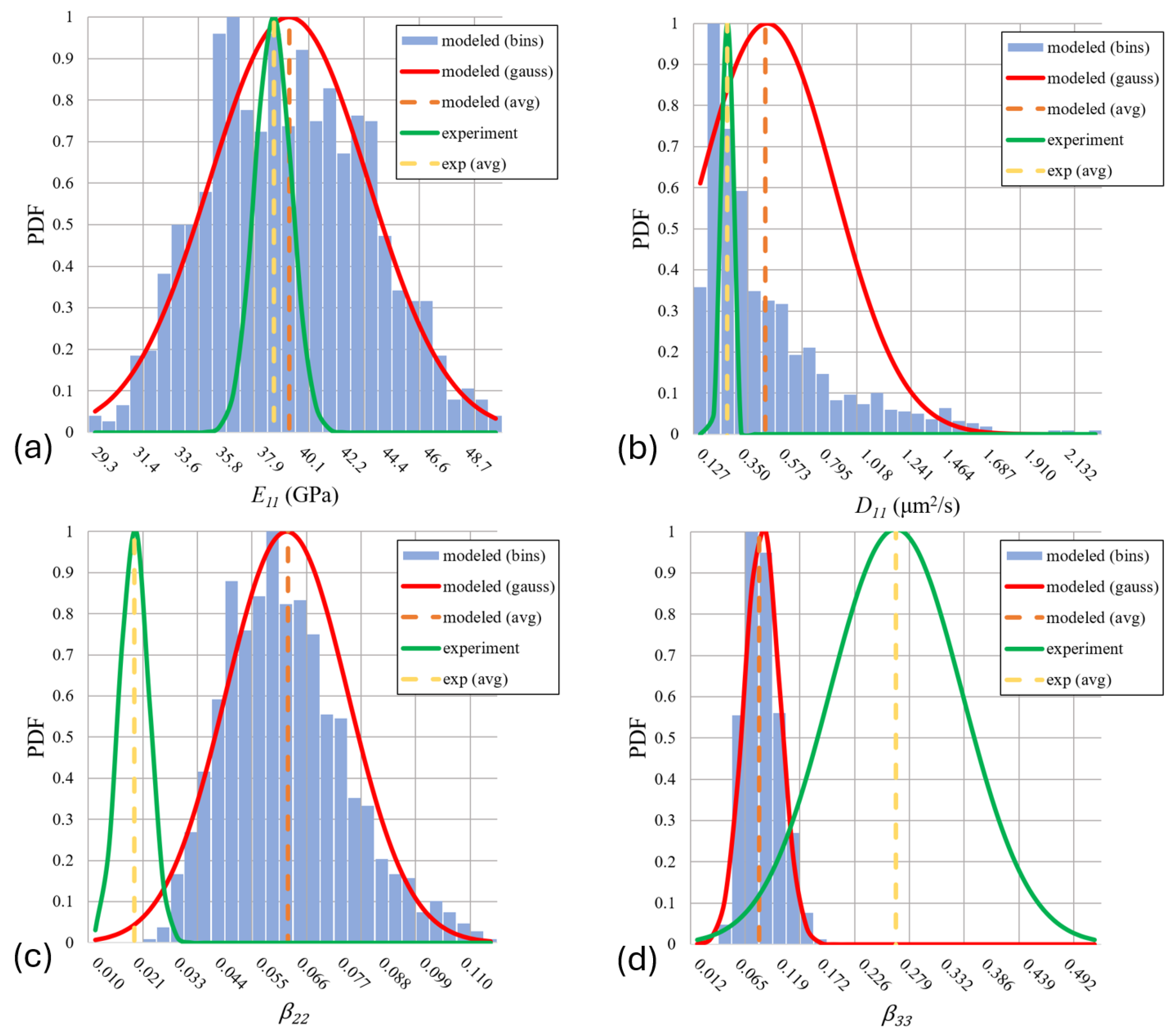
| Composite Property | Unit | Min. | Max. | Avg. | Std. Dev. | # Samples |
|---|---|---|---|---|---|---|
| Young’s modulus | GPa | 36.50 | 39.65 | 38.56 | 1.00 | 11 |
| Young’s modulus | GPa | 12.99 | 15.08 | 14.15 | 0.60 | 11 |
| Shear modulus G | GPa | 4.04 | 4.48 | 4.36 | 0.16 | 5 |
| Poisson’s ratio | — | 0.23 | 0.31 | 0.28 | 0.04 | 4 |
| Swelling coefficient | — | 0.016 | 0.027 | 0.021 | 0.004 | 8 |
| Swelling coefficient | — | 0.17 | 0.36 | 0.27 | 0.086 | 4 |
| Diffusion coefficient D a | mm2/s | 2.39 × 10−7 | 2.68 × 10−7 | 2.51 × 10−7 | 0.13 × 10−7 | 4 |
| Diffusion coefficient D b | mm2/s | 2.45 × 10−7 | 2.75 × 10−7 | 2.59 × 10−7 | 0.13 × 10−7 | 4 |
| Resin Property | Unit | Min. | Max. | Avg. | Std. Dev. | # Samples |
| Young’s modulus E | GPa | 2.41 | 2.88 | 2.53 | 0.16 | 10 |
| Poisson’s ratio | — | 0.36 | 0.40 | 0.38 | 0.03 | 2 |
| Diffusion coefficient D a | mm2/s | 7.49 × 10−7 | 9.58 × 10−7 | 8.41 × 10−7 | 0.70 × 10−7 | 9 |
| Diffusion coefficient D b | mm2/s | 8.01 × 10−7 | 9.62 × 10−7 | 8.58 × 10−7 | 0.53 × 10−7 | 9 |
| Density | g/cm3 | 1.13 | 1.14 | 1.15 | 0.004 | 9 |
| Maximum Moisture uptake | % | 3.22 | 3.28 | 3.25 | 0.02 | 9 |
| Property | Analytical Formula |
|---|---|
| Axial diffusivity | |
| Transverse diffusivity | |
| Longitudinal modulus | |
| Transverse modulus | |
| Shear modulus | |
| Shear modulus | |
| Poisson’s ratio | |
| Poisson’s ratio | |
| Longitudinal exp. coef. | |
| Transverse exp. coef. |
| QOI | Unit | Model Avg. | Model Std. Dev. | Exp. Avg. | Exp. Std. Dev. |
|---|---|---|---|---|---|
| Volume fraction | – | 0.545 | 0.0447 | 0.513 | 0.018 |
| Longitudinal diffusivity | mm2/s | 4.92 × 10−7 | 3.68 × 10−7 | 2.55 × 10−7 | 1.07 × 10−8 |
| Transverse diffusivity | mm2/s | 2.78 × 10−7 | 1.84 × 10−7 | – | – |
| Out of plane diffusivity | mm2/s | 2.14 × 10−7 | 3.44 × 10−8 | – | – |
| Longitudinal modulus | GPa | 39.4 | 4.14 | 38.56 | 0.954 |
| Transverse modulus | GPa | 13.4 | 2.33 | 14.15 | 0.573 |
| Out of plane modulus | GPa | 10.6 | 1.85 | – | – |
| Poisson’s ratio | – | 0.216 | 0.0370 | 0.275 | 0.032 |
| Poisson’s ratio | – | 0.304 | 0.0424 | – | – |
| Poisson’s ratio | – | 0.363 | 0.0501 | – | – |
| Shear modulus | GPa | 3.65 | 0.676 | 4.36 | 0.163 |
| Shear modulus | GPa | 3.53 | 0.664 | – | – |
| Shear modulus | GPa | 3.33 | 0.625 | – | – |
| Longitudinal exp. coef. | – | 0.0111 | 0.00313 | – | – |
| Transverse exp. coef. | – | 0.0624 | 0.0166 | 0.021 | 0.004 |
| Out of plane exp. coef. | – | 0.0961 | 0.0228 | 0.270 | 0.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Creveling, P.J.; Anderson, E.M.; Blank, O.; Miller, D.; Hernandez-Sanchez, B.A. Mesoscale Linear Elastic Modeling and Homogenization of Marine Energy Composites. J. Mar. Sci. Eng. 2025, 13, 2043. https://doi.org/10.3390/jmse13112043
Creveling PJ, Anderson EM, Blank O, Miller D, Hernandez-Sanchez BA. Mesoscale Linear Elastic Modeling and Homogenization of Marine Energy Composites. Journal of Marine Science and Engineering. 2025; 13(11):2043. https://doi.org/10.3390/jmse13112043
Chicago/Turabian StyleCreveling, Peter J., Evan M. Anderson, Olivia Blank, David Miller, and Bernadette A. Hernandez-Sanchez. 2025. "Mesoscale Linear Elastic Modeling and Homogenization of Marine Energy Composites" Journal of Marine Science and Engineering 13, no. 11: 2043. https://doi.org/10.3390/jmse13112043
APA StyleCreveling, P. J., Anderson, E. M., Blank, O., Miller, D., & Hernandez-Sanchez, B. A. (2025). Mesoscale Linear Elastic Modeling and Homogenization of Marine Energy Composites. Journal of Marine Science and Engineering, 13(11), 2043. https://doi.org/10.3390/jmse13112043






