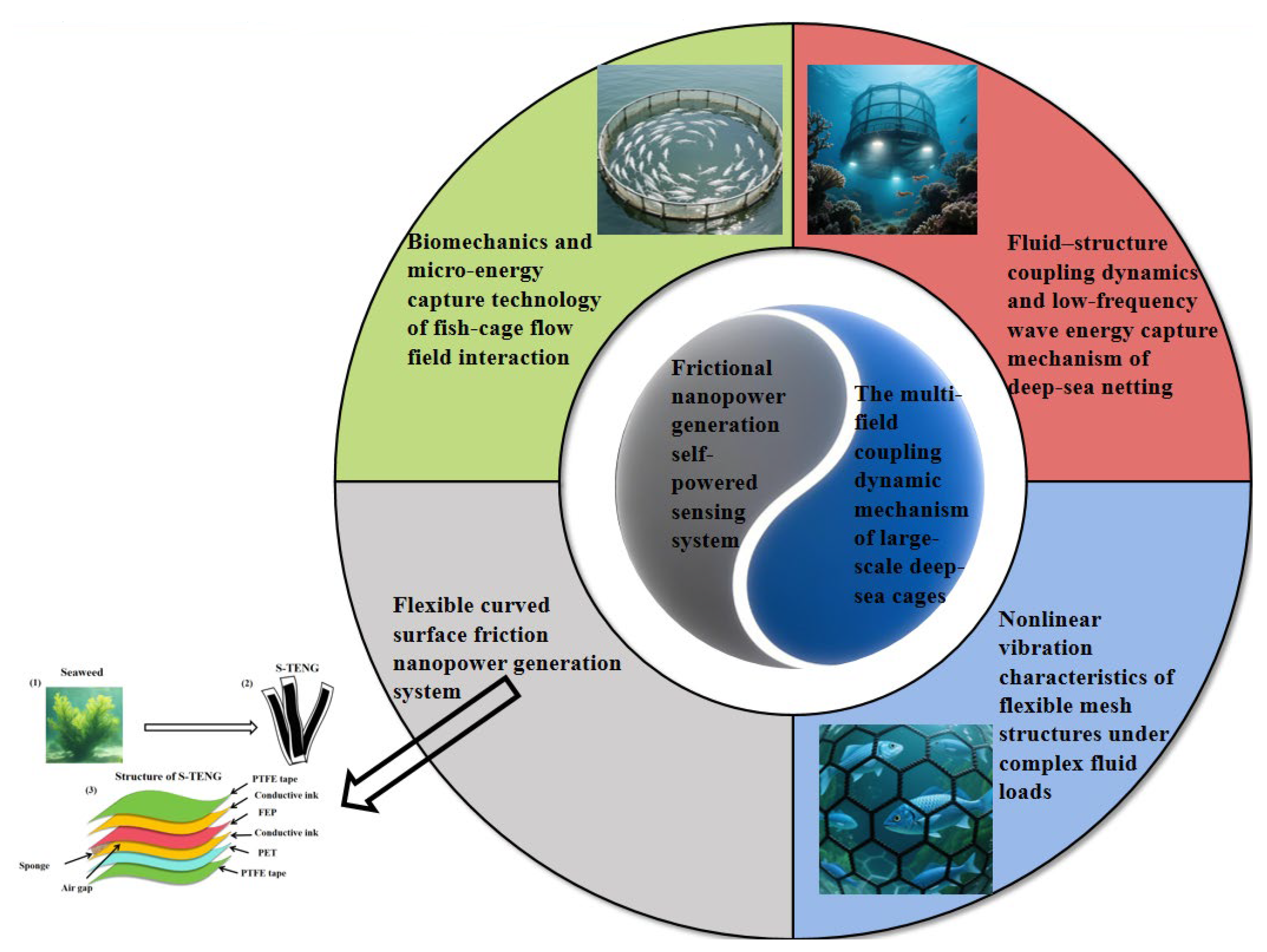
From Multi-Field Coupling Behaviors to Self-Powered Monitoring: Triboelectric Nanogenerator Arrays for Deep-Sea Large-Scale Cages
Abstract
1. Introduction
2. Flow–Solid Coupling Dynamics of Deep-Sea Cage Nets and Low-Frequency Wave Energy Capture Mechanism
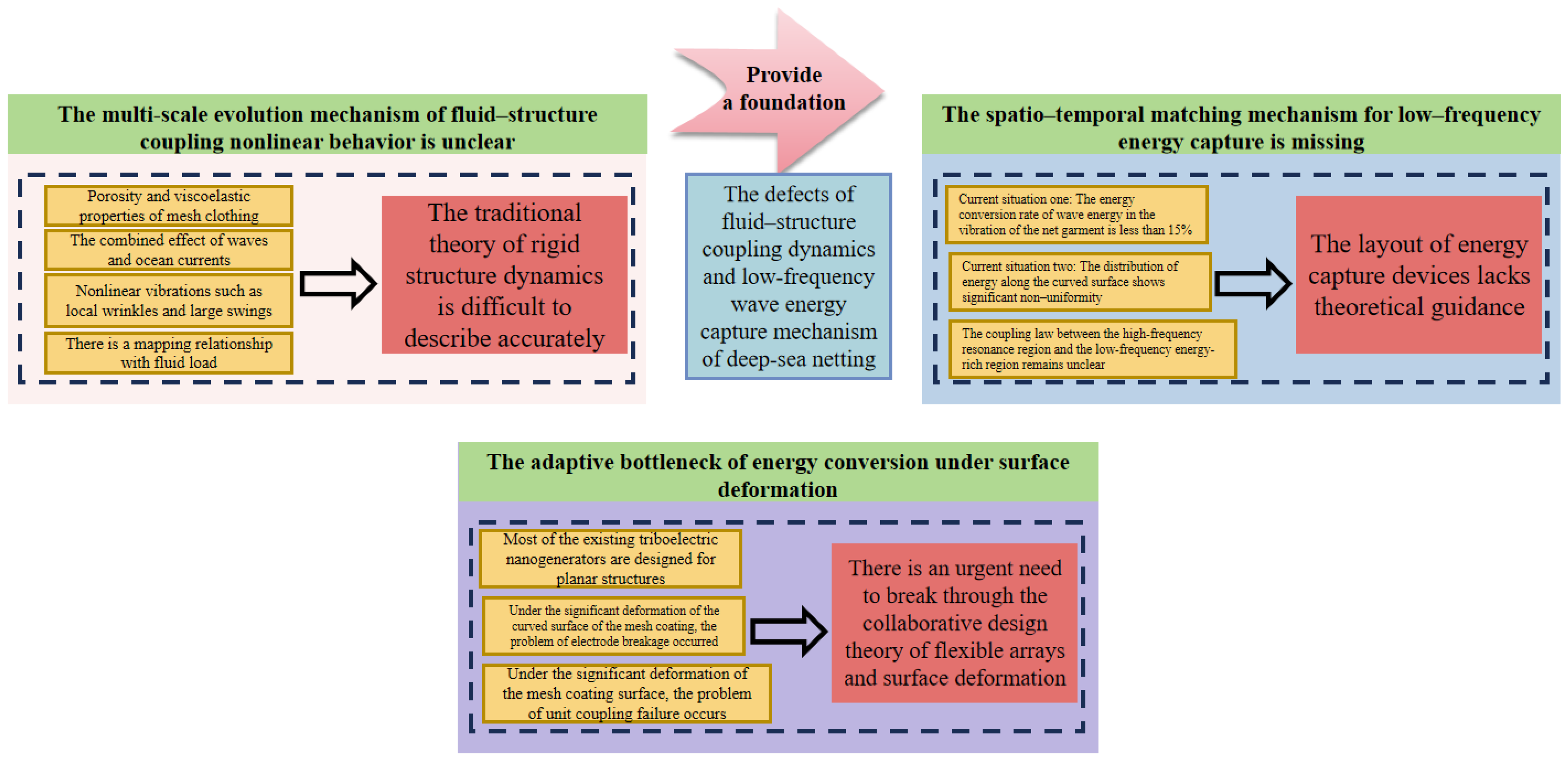
- The multi-scale evolution mechanism of fluid–structure coupling nonlinear behavior is unclear: the nonlinear vibrations such as local wrinkles and large swings caused by the porosity and viscoelastic properties of the mesh fabric under the combined action of waves and ocean currents are significantly affected by the scale effect in terms of the mapping relationship between the amplitude, frequency, and fluid load. The traditional rigid structure dynamics theory is difficult to accurately describe the coupling process of “fluid-induced deformation and load redistribution” of flexible mesh fabrics.
- The spatio-temporal matching mechanism for low-frequency energy capture is missing: the energy conversion rate of wave energy in the vibration of the mesh jacket is less than 15%, and the distribution of energy along the curved surface shows significant non-uniformity. The coupling effect law between the high-frequency resonance region (such as the edge of the mesh jacket) and the low-frequency energy-rich region (such as the center of the mesh jacket) is not yet clear, resulting in a lack of theoretical guidance for the layout of the energy capture device.
- The adaptive bottleneck of energy conversion under surface deformation: the existing triboelectric nanogenerators are mostly designed for planar structures. Under the significant deformation of the mesh coating surface, problems such as electrode fracture and unit coupling failure are prone to occur. Moreover, the seawater corrosion resistance life of the TENG materials is mostly between 6 and 12 months. There is an urgent need to break through the collaborative design theory of flexible arrays and surface deformation.
2.1. Nonlinear Vibration Characteristics of Net Flexible Structures Under Complex Fluid Loads
2.1.1. Construction of Multi-Factor Fluid–Structure Coupling Dynamics Model
- A dynamic porosity model with spatial heterogeneity was constructed using the Brinkman–Darcy equation:
- 2.
- Introduce the fractional-order Burgers viscoelastic constitutive model, describe the frequency-dependent characteristics of the material through Caputo fractional-order derivatives, and construct a nonlinear constitutive equation considering the historical effects of strain:
- 3.
- Develop a fluid–structure coupling solver based on the immersion boundary method to achieve a precise solution of the bidirectional coupling of flow field and structure under large deformation conditions.
2.1.2. Research on Nonlinear Vibration Evolution Mechanism in Complex Flow Fields
- 1.
- Multimodal coupling vibration characteristics: Analyze the nonlinear phenomena such as parametric resonance and internal resonance of the mesh structure under the coupling action of regular waves, irregular waves, and shear flow;
- 2.
- Instability critical criterion: A periodic disturbance stability analysis framework is established through Floquet theory to determine the critical conditions for the transformation of the structure from steady-state vibration to chaotic motion under different flow velocity ratios. The vibration system of the net garment under the combined action of waves and the current is regarded as a system of periodic linear differential equations, and its dynamic equation can be expressed as follows:
- 3.
- Local fold evolution law: Based on the curvature mode decomposition method, the central difference method is used to calculate the curvature modes of each measurement point of the net garment:
2.1.3. Intelligent Mapping Model of Vibration Response and Load Characteristics
- The random forest algorithm is adopted to rank the importance of features, and a vibration amplitude prediction model based on XGBoost is constructed to achieve the prediction of the probability distribution of response extremum. The vibration response of the net garment under the combined action of waves and the current shows significant nonlinearity (such as local wrinkles and large swings), and there is a complex coupling relationship between its vibration amplitude and fluid load as well as structural parameters. XGBoost is based on the iterative optimization logic of gradient boosting trees (GBDT). By constructing regression trees one by one to minimize prediction errors, it can efficiently fit the nonlinear mapping relationship between multiple factors and vibration amplitudes. Compared with traditional linear models that cannot capture nonlinear features such as a “sudden increase in flow velocity causing sudden changes in vibration amplitude”, XGBoost uses a “residual compensation” mechanism. Each new tree corrects the prediction error of the previous model in each round, and the final integrated strong learner can accurately depict the dynamic evolution law of the net garment vibration.
- Develop a convolutional long short-term memory network, integrate flow field time series data with structural response signals, and establish an end-to-end vibration state prediction framework.
2.2. Spatiotemporal Distribution Characteristics of Wave-Induced Net Motion Energy
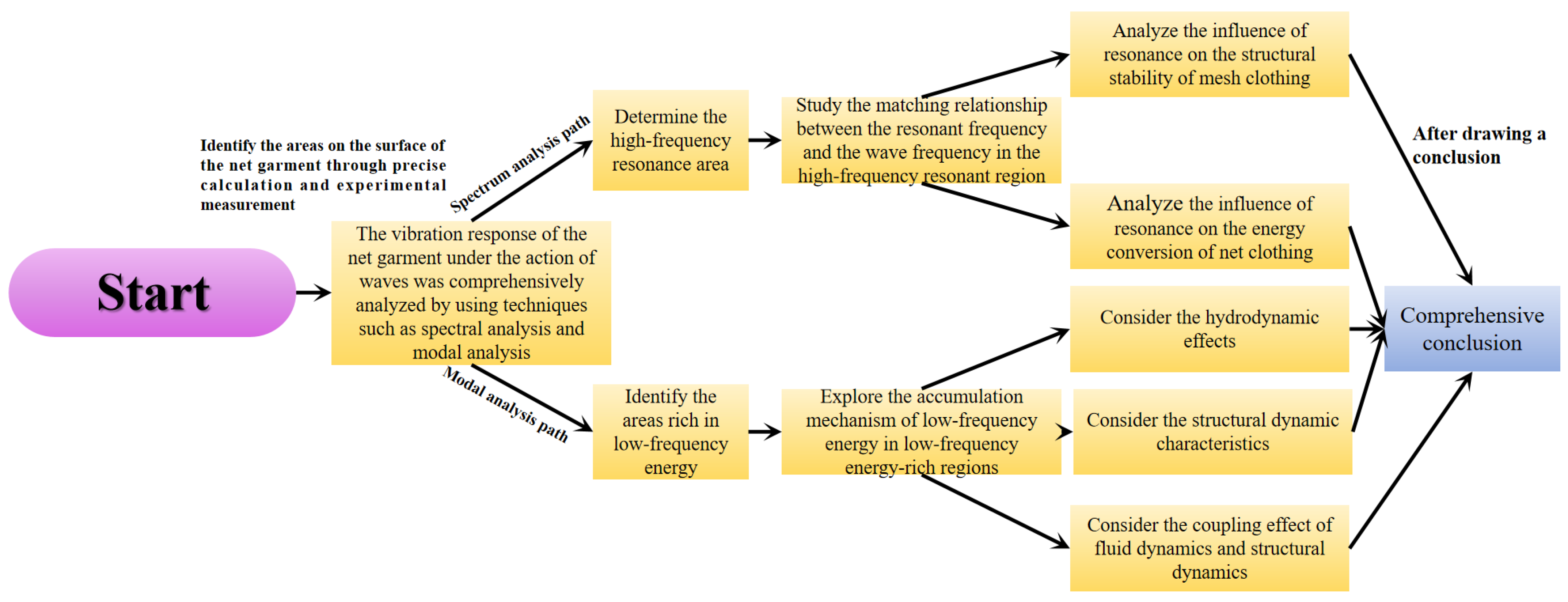
2.2.1. Quantitative Model of Multimodal Energy Conversion Efficiency
2.2.2. Analysis of Topological Characteristics of Energy Spatio-Temporal Distribution
2.2.3. The Correlation Mechanism Between Resonance Modes and Energy Accumulation
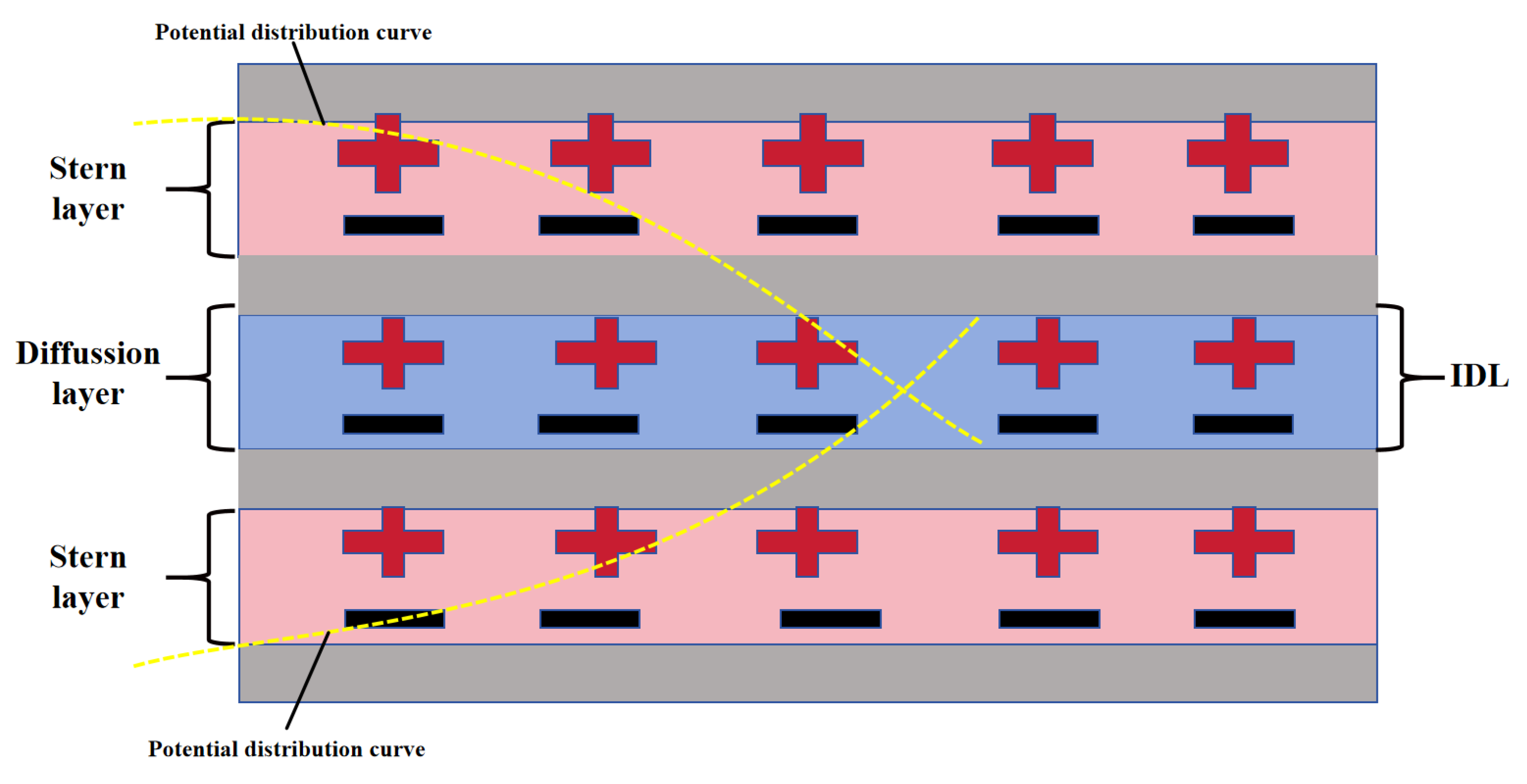
2.3. Design of Curved Surface-Adaptive TENG Arrays
2.4. Quantitative Analysis of Power Demand for Core Equipment in Deep-Sea Aquaculture Systems
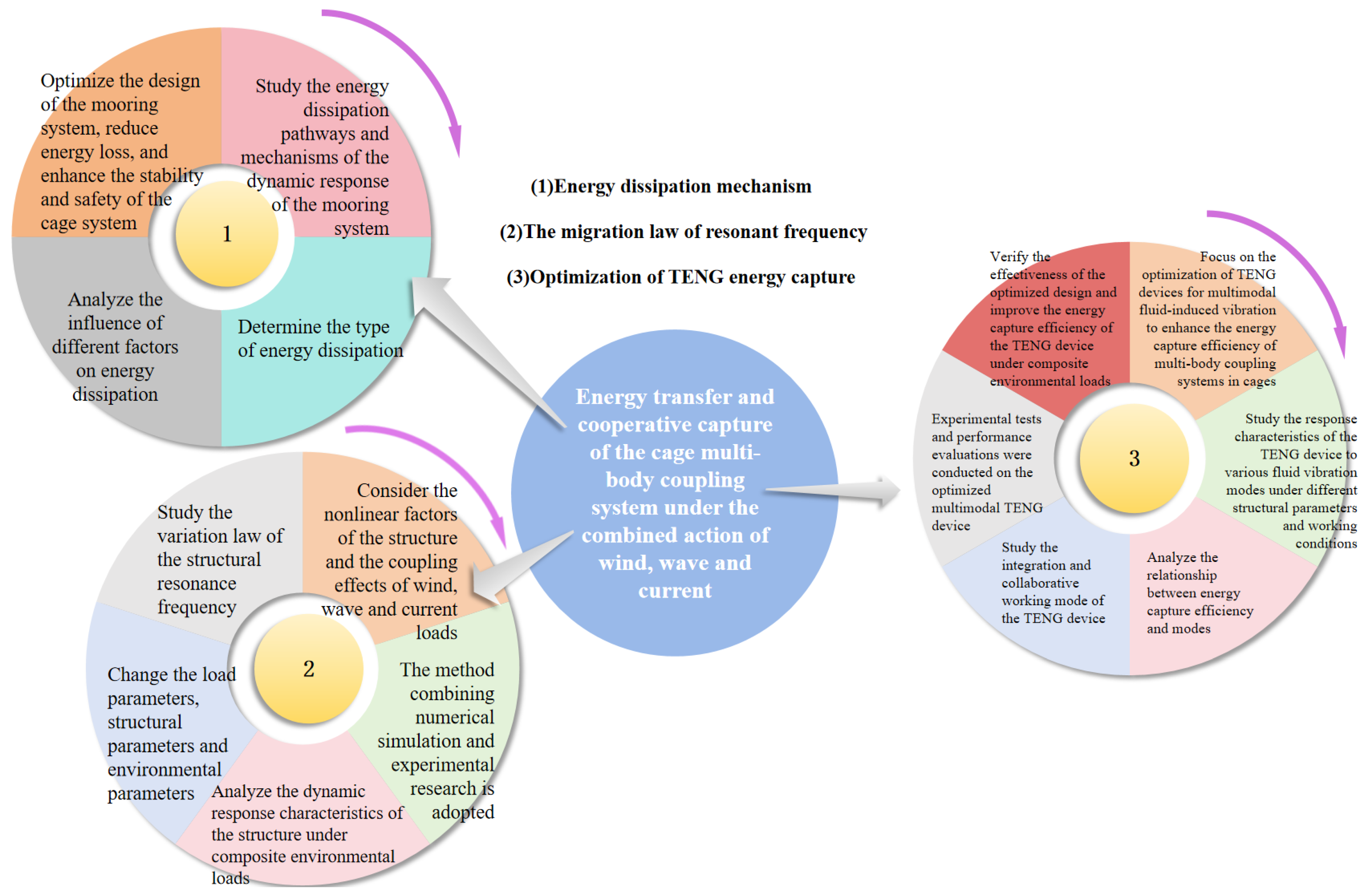
3. Energy Transfer and Cooperative Capture of Multi-Body Coupling Cage Systems Under Combined Wind–Wave–Current Actions
3.1. Energy Dissipation Mechanism of Dynamic Response of Multi-Degrees-of-Freedom Mooring Systems
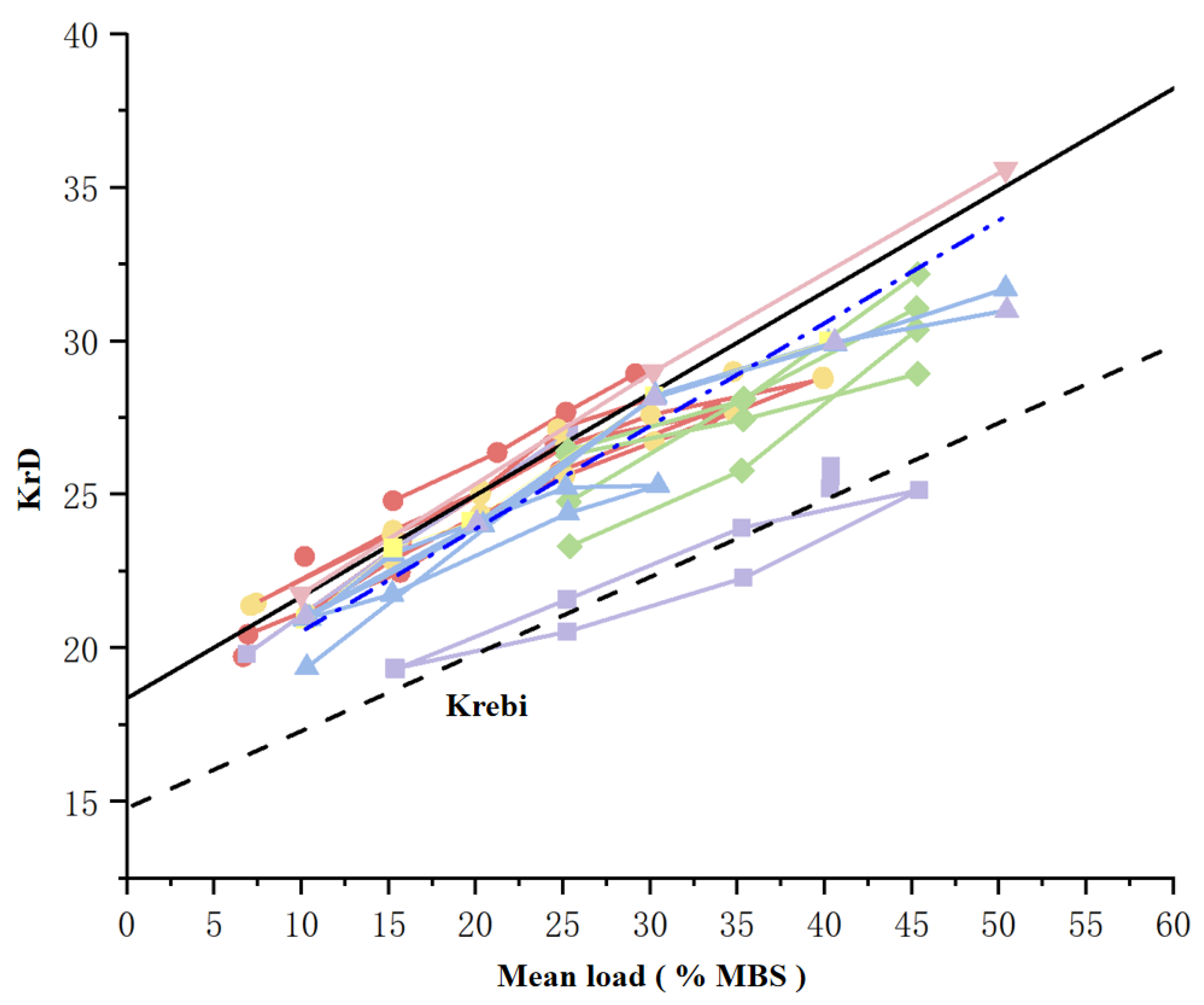
3.1.1. Internal Friction Dissipation of the Mooring Line Material
- Through three-parameter fitting, they wrote the elongation L(t) on each creep (or recovery) platform as follows:
- 2.
- In L(t), they use
- 3.
- Then, the linearized quasi-stiffness is regarded as the secant stiffness between the last consecutive period (duration ) endpoints. The load is normalized through the rope MBS to obtain the dimensionless quasi-static stiffness KrS.
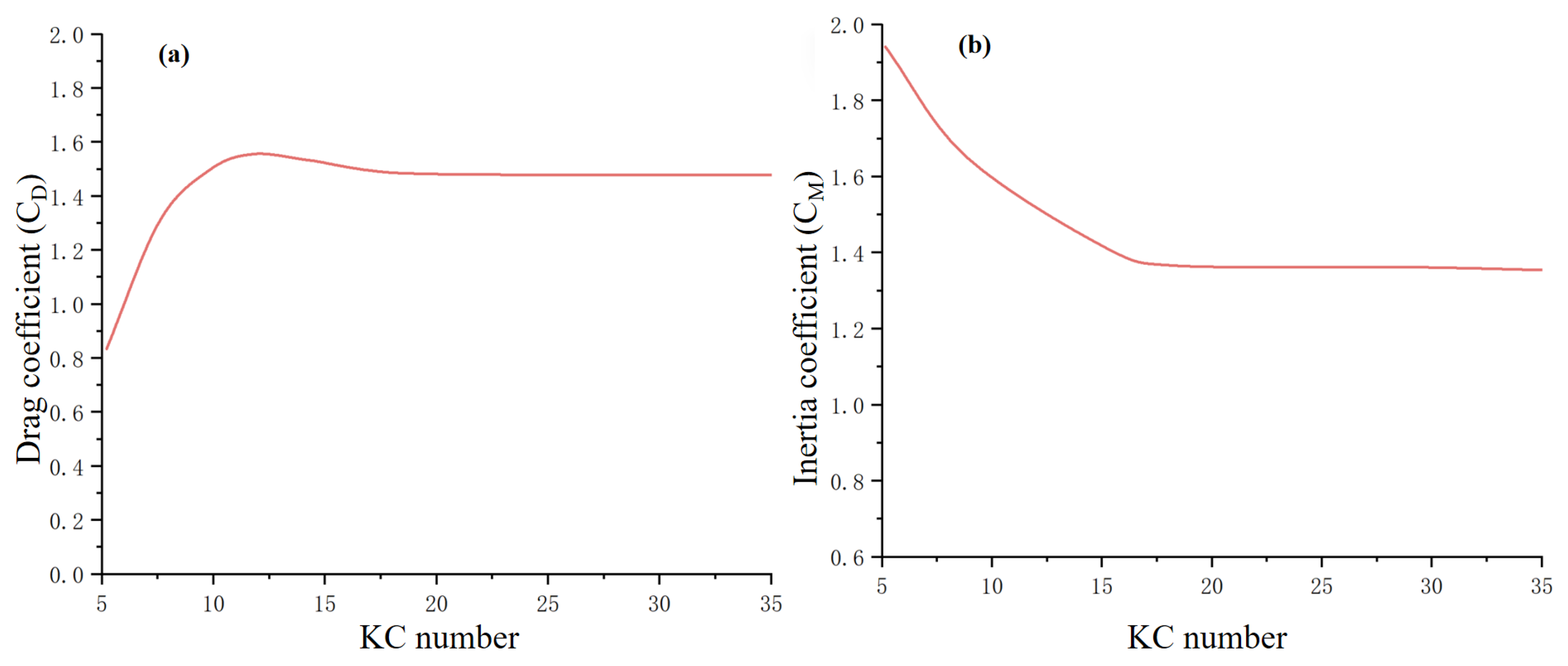
3.1.2. Viscous Frictional Dissipation of Seawater
3.2. Migration Law of Structural Resonance Frequency Under Composite Environmental Loads
3.2.1. The Influence of Load Parameters on Resonant Frequency
3.2.2. The Regulatory Role of Structural Parameters
3.2.3. Coupling Effects of Nonlinear Factors
3.3. Optimization of TENG Devices for Multi-Modal Fluid-Induced Vibration
4. Biomechanics of Interactions Between Fish Schools and Cage Flow Fields and Micro-Energy Harvesting Technology
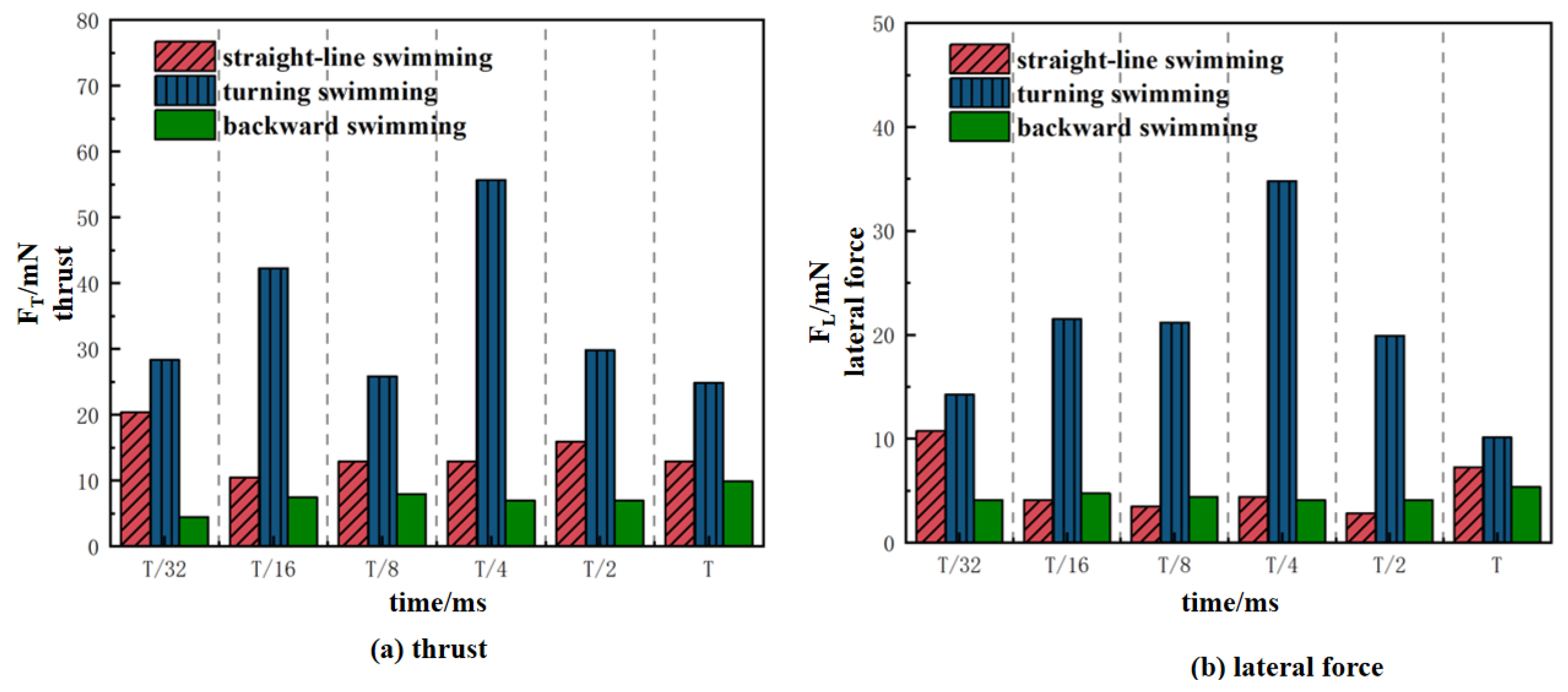
4.1. Characteristics of the Vortex Energy Field Induced by Fish Tail Swing Motion
4.1.1. Experimental Study on the Characteristics of Vortex Energy Fields
- The reference basis for the core measurement technology of the experimental platform:
- 2.
- Comparison indicators for performance verification of the experimental platform:
4.1.2. Numerical Simulation of Vortex Energy Field Characteristics
- 1.
- The revelation of the vortex energy evolution mechanism by two-dimensional unsteady models:
- 2.
- Analysis of the vortex energy development law under the dynamic mesh RANS method:
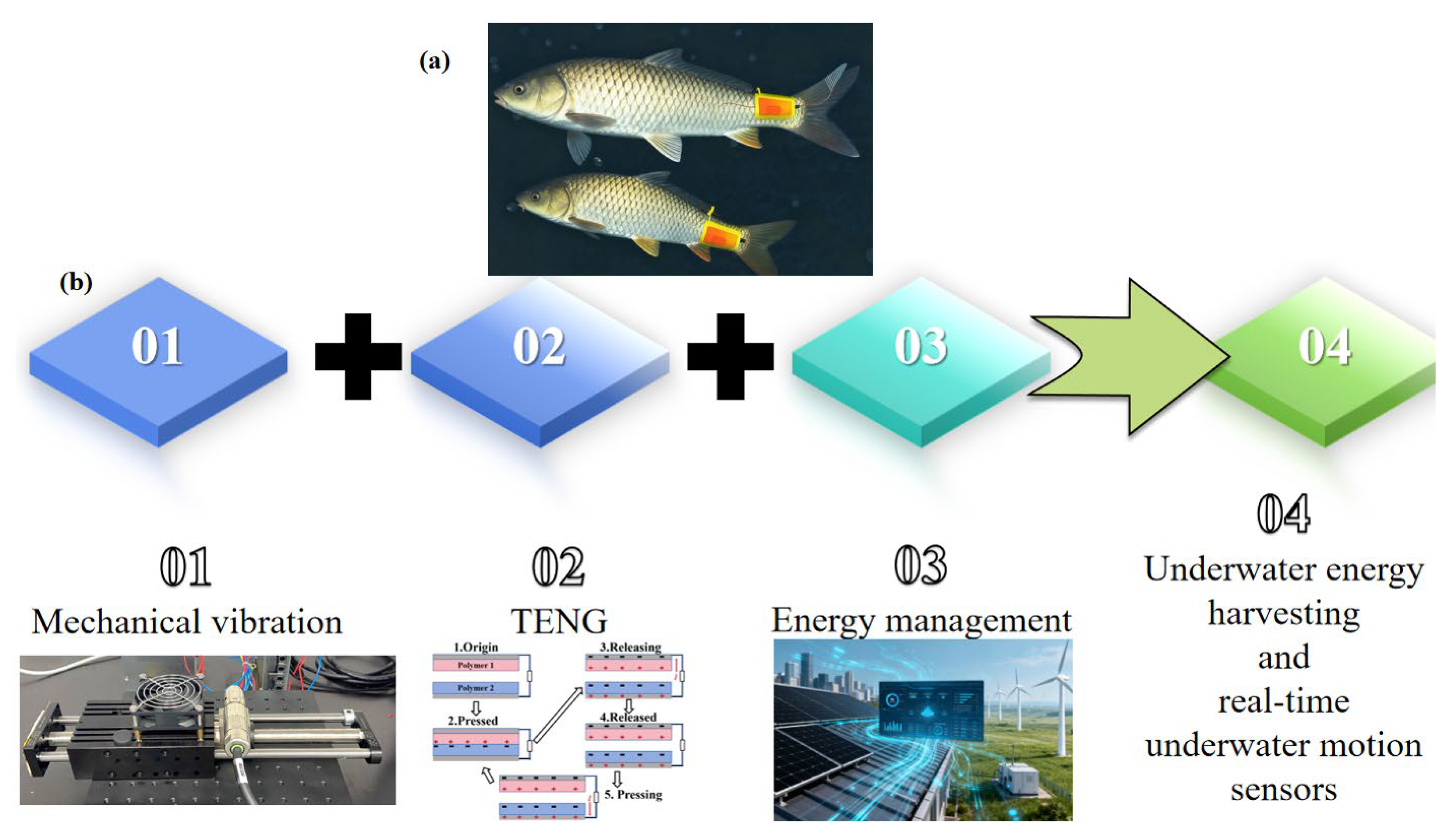
4.2. Self-Driving Principle of Bionic Flexible TENG Sensors
4.3. Multi-Physical Field Coupling Micro-Energy Management System
- 1.
- CFD model establishment:
- 2.
- DEM model establishment:
- 3.
- Coupling of CFD and DEM models:
- 4.
- Model verification:
- 5.
- Case study:
4.3.1. CFD Model
4.3.2. DEM Model
4.3.3. Coupling of CFD and DEM Models
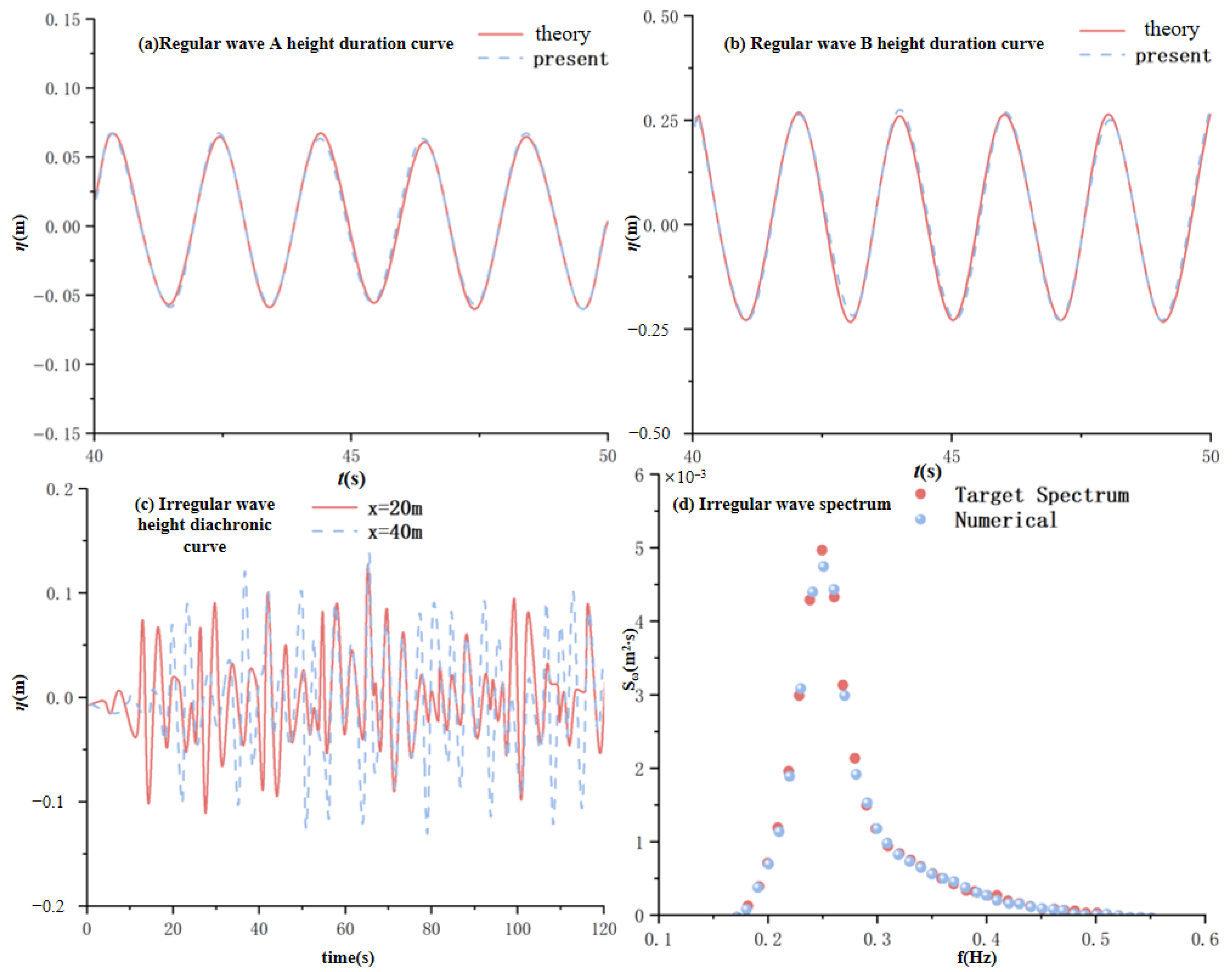
4.4. Model Verification and Convergence Analysis
4.4.1. Grid Sensitivity Analysis
4.4.2. Verification of Convergence of Time Steps
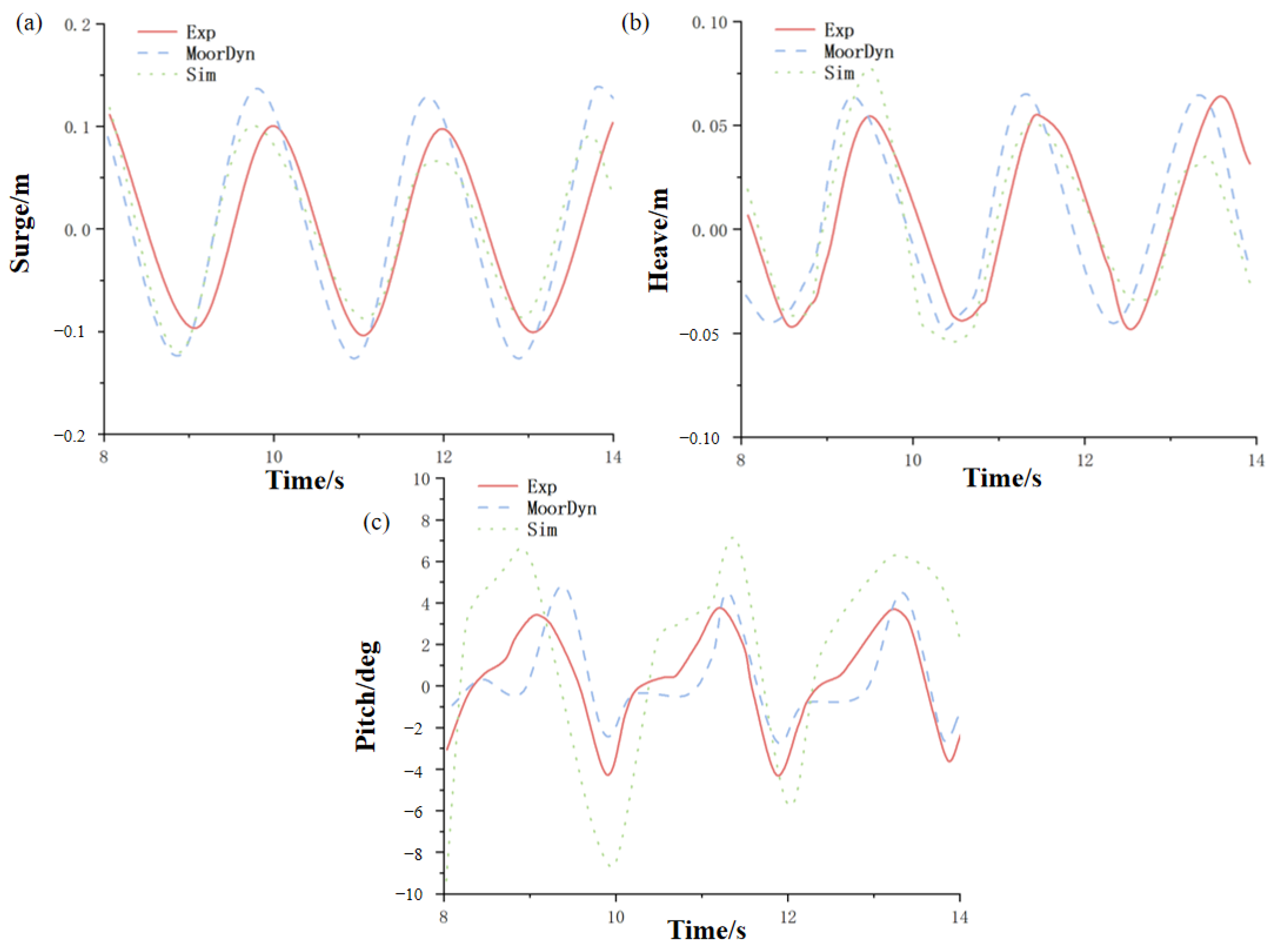
4.4.3. Verification by Comparison with Experimental Data
5. Conclusions
5.1. Limitations
5.1.1. Limitations in Multi-Field Coupling Dynamic Mechanism Research
5.1.2. Deficiencies in Self-Powered Sensing System Development
5.1.3. Gaps in Fish–Cage Flow Field Interactions and Micro-Energy Capture
5.2. Prospects
5.2.1. Optimization of Multi-Field Coupling Dynamic Model
5.2.2. Upgrade of Self-Powered Sensing System
5.2.3. Deepening of Fish–Cage Flow Field Interaction and Micro-Energy Capture Research
5.2.4. Broader Application Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, G.; Ni, X.; Mo, J. Research status and development trend of profound Marine aquaculture equipment technology. J. Dalian Ocean. Univ. 2018, 33, 123–129. (In Chinese) [Google Scholar] [CrossRef]
- Chen, Y.; Fang, R.; Qiao, J. China’s Marine aquaculture development research. J. Agric. Econ. 2012, 72–77+112. (In Chinese) [Google Scholar] [CrossRef]
- Zhu, Y.; Ju, X.; Chen, Y. Current Situation, Problems and Countermeasures of Deep-sea Cage Aquaculture in China. China Fish. Econ. 2017, 35, 72–78. (In Chinese) [Google Scholar]
- Hou, H.; Ju, X.; Chen, Y. The development trends of Deep-sea cage aquaculture abroad and its implications for China. World Agric. 2017, 162–166. (In Chinese) [Google Scholar] [CrossRef]
- Song, R.; Zhou, M.; Li, Y.; Zhang, H.; Lin, Z. Research Progress on Key Technologies of Deep-sea Cage Aquaculture Equipment. Mech. Eng. 2015, 134–138. (In Chinese) [Google Scholar]
- Hou, Y.; Li, Y.; Li, G.; Tong, X.; Wang, Y. Oil-spill detection sensor using ultraviolet-induced fluorescence for routine surveillance in coastal environments. Appl. Phys. B 2022, 128, 41. [Google Scholar] [CrossRef]
- Gonzaga, B.A.; Alves, D.L.; Albuquerque, M.D.G.; Espinoza, J.M.D.A.; Almeida, L.P.; Weschenfelder, J. Development of a Low-cost Ultrasonic Sensor for Groundwater Monitoring in Coastal Environments: Validation using Field and Laboratory Observations. J. Coast. Res. 2020, 95 (Suppl. 1), 1001–1005. [Google Scholar] [CrossRef]
- Xie, Y. Based on the Internet of Things of Marine Water Quality Wise Observation Solution Research. Master’s Thesis, Shanghai Ocean University, Shanghai, China, 2020. (In Chinese). [Google Scholar]
- Diaz, K.; Teh, Y. Design and Power Management of a Secured Wireless Sensor System for Salton Sea Environmental Monitoring. Electronics 2020, 9, 544. [Google Scholar] [CrossRef]
- Zhang, Y. Review on the Development of Marine Environment Monitoring Equipment Technology. Digit. Ocean. Underw. Attack Def. 2018, 1, 7–14. (In Chinese) [Google Scholar]
- Rodrigues, C.; Nunes, D.; Clemente, D.; Mathias, N.; Correia, J.M.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Pereira, A.; Ventura, J. Emerging triboelectric nanogenerators for ocean wave energy harvesting: State of the art and future perspectives. Energy Environ. Sci. 2020, 13, 2657–2683. [Google Scholar] [CrossRef]
- Liu, L.; Hu, T.; Zhao, X.; Lee, C. Recent progress in blue energy harvesting based on triboelectric nanogenerators. Nanoenergy Adv. 2024, 4, 156–173. [Google Scholar] [CrossRef]
- Jiang, Y.; Liang, X.; Jiang, T.; Wang, Z.L. Advances in triboelectric nanogenerators for blue energy harvesting and marine environmental monitoring. Engineering 2024, 33, 204–224. [Google Scholar] [CrossRef]
- Isabel, G.; Rodrigues, C.; Ventura, J. Sea state adaptation enhances power output of triboelectric nanogenerators for tailored ocean wave energy harvesting. Adv. Energy Mater. 2024, 14, 2302627. [Google Scholar]
- Li, X.; Xu, L.; Wang, Z.L. Networking strategies of triboelectric nanogenerators for harvesting ocean blue energy. Nanoenergy Adv. 2024, 4, 70–96. [Google Scholar] [CrossRef]
- Tan, D.; Chi, S.; Ou, X.; Zhou, J.; Wang, K. Some Advances in nonlinear frictional nanopower generation Energy capture technology. Acta Mech. Sin. 2024, 56, 2495–2510. (In Chinese) [Google Scholar]
- Gao, J.; Zhao, B.; Yang, C.; Rui, H.Y.; Gang, X.H. Development Trends and Prospects of Offshore Energy Storage Technology. Adv. New Renew. Energy 2020, 8. (In Chinese) [Google Scholar]
- Wang, Y. Research on Friction Nano-Electromagnetic Composite Flow Energy Capture and Energy Supply for Observation Nodes. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2023. (In Chinese). [Google Scholar]
- Dong, J. Research on Self-Powering Technology of Marine Buoys Based on Stackable Triboelectric Nanogenerators. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2021. (In Chinese). [Google Scholar]
- Lin, Z.W. Triboelectric nanogenerators as new energy technology for self-powered systems and as active mechanical and chemical sensors. ACS Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef]
- Li, P.; Tian, Y.; Qin, H.; Wei, B.; Deng, Z. Analysis of Flow Field Characteristics and Deformation of Nylon Mesh Based on Fluid-Structure Coupling. China Offshore Platf. 2023, 38, 48–56. (In Chinese) [Google Scholar]
- Ma, J. Energy Transfer Analysis of Multi-Body Systems. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2008. (In Chinese). [Google Scholar]
- Zhang, C. Fish Flow Field Interference Mechanism Research. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2022. (In Chinese). [Google Scholar]
- Lin, X. Research on the Hydrodynamic Mechanism of Fish and Bird Migration. Ph.D. Thesis, Nanchang Hangkong University, Nanchang, China, 2017. (In Chinese). [Google Scholar]
- Tang, M. Flow Wave Net Structure Hydrodynamic Characteristics Research. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2020. (In Chinese). [Google Scholar]
- Zhang, K.; Liu, B.; Chen, H.; Chen, J.; Yao, H.D. Solving fluid-structure interaction of flexible net structures in current and waves based on a coupled truss–porous medium model. Ocean. Eng. 2025, 329, 121115. [Google Scholar] [CrossRef]
- Schäfer, F.; Kniesburges, S.; Uffinger, T.; Becker, S.; Grabinger, J.; Link, G.; Kaltenbacher, M. Numerical simulation of fluid-structure-and fluid-structure-acoustic interaction based on a partitioned coupling scheme. In High Performance Computing in Science and Engineering, Garching/Munich 2007: Transactions of the Third Joint HLRB and KONWIHR Status and Result Workshop, Leibniz Supercomputing Centre, Garching/Munich, Germany 3–4 December 2007; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wang, M.; Li, G.; Xia, C.; Jing, X.; Wang, R.; Liu, Q.; Cai, X. Facile preparation of cyclodextrin polymer materials with rigid spherical structure and flexible network for sorption of organic contaminants in water. Chem. Eng. J. 2021, 411, 128489. [Google Scholar] [CrossRef]
- Rosén, T.; Mittal, N.; Roth, S.V.; Zhang, P.; Lundell, F.; Söderberg, L.D. Flow fields control nanostructural organization in semiflexible networks. Soft Matter 2020, 16, 5439–5449. [Google Scholar] [CrossRef]
- Hu, Z. Numerical Simulation Research on the Structural Safety of Net Jackets in Large Deep-Sea and Far-Sea Cages. Ph.D. Thesis, Shandong University, Jinan, China, 2024. (In Chinese). [Google Scholar]
- Hu, B.; Yang, X. Current Situation and Development Trend of Deep-sea Aquaculture Cages at Home and Abroad. Silicon Val. 2008, 28–29. (In Chinese) [Google Scholar]
- Pan, Y.; Zhang, J.; Li, L.; Liu, C.; Sun, Z.; Hong, J. Numerical simulation of hydrodynamic characteristics of ultra-large diameter aquaculture cages under waves action. Ocean. Eng. 2025, 338, 121981. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Jiang, H. Wave energy converter with floating-point absorber and catenary mooring: Dynamic coupling analysis. Front. Mar. Sci. 2024, 11, 1338330. [Google Scholar] [CrossRef]
- Ma, Y.; Si, K.; Xie, Y.; Liang, Z.; Wu, J.; Zhang, D.; Zhang, Y.; Cai, R. Global Marine Ranching Research: Progress and Trends through Bibliometric Analysis. Eng. Solut. Mech. Mar. Struct. Infrastruct. 2024, 1, 1–23. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, B.; Zhang, Y.; Zhu, K.; Yan, J. Study on Dynamic Characteristics and Fracture Failure of Rigid Truss Trawl System During Towing Process. J. Mar. Sci. Eng. 2025, 13, 586. [Google Scholar] [CrossRef]
- Gui, F.; Zhu, H.; Feng, D. Research Progress on Hydrodynamic Characteristics of Marine Aquaculture Netting. Fish. Mod. 2019, 46, 9–14. (In Chinese) [Google Scholar]
- Li, N.; Li, X.; Shi, W.; Liu, C. Numerical Simulation of Hydrodynamic Characteristics of Planar Mesh under Wave-Current Action. J. Shanghai Ocean. Univ. 2024, 33, 509–520. (In Chinese) [Google Scholar]
- Wu, H.; Liu, Q.; Fan, W. Research on Hydrodynamic Loads of Cage Nets and Net Jackets in Aquaculture. Mod. Fish. 2023, 50, 43–51. (In Chinese) [Google Scholar]
- Zhang, Y.M.; Bi, C.W.; Feng, L.; Huang, L.Y. Hydrodynamic response analysis of the aquaculture net under the combined action of irregular waves and currents. Ships Offshore Struct. 2024, 1–17. [Google Scholar] [CrossRef]
- Ling, A.; Liang, Y.; Zhao, D.; Fan, Z.; Zhao, Y. Marine aquaculture hydrodynamic characteristics is reviewed. The flexible net structure. Fish. Sci. Prog. 2024, 45, 223–236. (In Chinese) [Google Scholar] [CrossRef]
- He, W.; Liu, W.; Fu, S.; Wu, H.; Shan, C.; Wang, Z.; Xi, Y.; Wang, X.; Guo, H.; Liu, H.; et al. Ultrahigh Performance Triboelectric Nanogenerator Enabled by Charge Transmission in Interfacial Lubrication and Potential Decentralization Design. Research 2022, 2022, 9812865. [Google Scholar] [CrossRef]
- Zhang, C.; He, L.; Zhou, L.; Yang, O.; Yuan, W.; Wei, X.; Liu, Y.; Lu, L.; Wang, J.; Wang, Z.L. Active resonance triboelectric nanogenerator for harvesting omnidirectional water-wave energy. Joule 2021, 5, 1613–1623. [Google Scholar] [CrossRef]
- Li, X.; Zhang, D.; Zhang, D.; Li, Z.; Wu, H.; Zhou, Y.; Wang, B.; Guo, H.; Peng, Y. Solid-liquid triboelectric nanogenerator based on vortex-induced resonance. Nanomaterials 2023, 13, 1036. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, L.; Wang, T.; Jiang, Y.; Tian, Y.; Jin, T.; Yue, T.; Lee, C. Self-sustainable flow-velocity detection via electromagnetic/triboelectric hybrid generator aiming at IoT-based environment monitoring. Nano Energy 2021, 90, 106501. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Ma, T.; Kong, Y.; Gao, S.; Han, Q. Symmetrical Triboelectric In Situ Self-Powered Sensing and Fault Diagnosis for Double-Row Tapered Roller Bearings in Wind Turbines: An Integrated and Real-Time Approach. Adv. Sci. 2025, 12, 2500981. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Wu, J.; Zhang, K.; Lu, J.; Li, J.; Hazarika, D.; Jin, H.; Luo, J. An instantaneous self-powered wireless sensing system based on a triboelectric nanogenerator and the human body. Nanoscale 2024, 16, 19355–19363. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Yan, J.; Wang, X.; Pang, H.; Sun, C.; Sun, Y.; Wang, L.; Zhang, D. Research on the Performance of a Liquid–Solid Triboelectric Nanogenerator Prototype Based on Multiphase Liquid. Micromachines 2025, 16, 78. [Google Scholar] [CrossRef]
- Yang, K.F.; Xie, Y.; Si, K.; Yang, K.Q.; Zeng, S.; Zhang, D. Research Progress on Friction Nanogenerator Technology for Wave Energy Harvesting. Eng. Solut. Mech. Mar. Struct. Infrastruct. 2024. [Google Scholar] [CrossRef]
- Yan, J.; Sheng, Y.; Zhang, D.; Tang, Z. Research Progress in Fluid Energy Collection Based on Friction Nanogenerators. Micromachines 2023, 15, 40. [Google Scholar] [CrossRef]
- Chen, P.; Zhu, X.; Tian, G.; Feng, X. Recent advances of TENGs for marine applications: Opportunities and challenges coexist. Nano Energy 2025, 142, 111212. [Google Scholar] [CrossRef]
- Li, M.; Jin, S.; Meng, A.; Song, J.; Xu, Z.; Chen, Y.; Zeng, Y. A performance study on the drum-type energy harvesting device based on triboelectric nanogenerator. J. Electrost. 2025, 135, 104066. [Google Scholar] [CrossRef]
- Ji, C. Research on Flexible Acoustic Sensor Based on PDMS-AgNWs. Ph.D. Thesis, Taiyuan University of Technology, Taiyuan, China, 2019. (In Chinese). [Google Scholar]
- Deng, X.; Li, D.; Yang, J.; Wang, J. Research on Friction and Wear Properties of High-Performance High-Temperature Resistant Polymer Composites. Bull. Polym. Sci. 2008, 41–46. (In Chinese) [Google Scholar]
- Chen, X.; Chen, J.; Huang, L.; Nie, S.; Xu, W.; Yin, Y.; Zhang, S.; Pei, F.; Yu, K.; Su, W.; et al. Highly conductive omnidirectionally stretchable 2D transparent copper mesh electrodes and applications in optoelectronic devices. Adv. Mater. Technol. 2023, 8, 2201406. [Google Scholar] [CrossRef]
- Sun, P.; Wang, L.; Wang, L. Deepwater semi-submersible platform anchoring auxiliary power positioning system power consumption research. Ocean. Eng. 2010, 28, 24–30. (In Chinese) [Google Scholar] [CrossRef]
- Wen, X.; Gjerde, A.; Ong, M.C. Numerical investigation of pre-tension effects in mooring systems on global responses of gravity-type fish farms. Ocean. Eng. 2025, 337, 121832. [Google Scholar] [CrossRef]
- Wang, B.; Wang, H.; Liu, Z.; Cao, Z.; Yang, D.; Wang, F. Research Progress on Structural Design and Performance Analysis of Mooring System for Aquaculture Cages. J. Shanghai Ocean. Univ. 2025, 34, 176–187. (In Chinese) [Google Scholar]
- Liu, F.; Jiang, Z.; Cheng, T.; Xu, Y.; Zhu, H.; Wang, G.; Sun, G.; Zhang, Y. Study on the Dynamic Response of Mooring System of Multiple Fish Cages under the Combined Effects of Waves and Currents. J. Mar. Sci. Eng. 2024, 12, 1648. [Google Scholar] [CrossRef]
- Wang, H.; Gu, S.; Ma, G.; Huang, W.; Sun, Y.; Du, Z. Dynamic performance analysis of grid mooring system for gravity cages. Ships Offshore Struct. 2025, 20, 1143–1160. [Google Scholar] [CrossRef]
- Abdellah Mohammed, Y.; Sadek, M.G.; Alharthi, H.; Abdel-Jaber, G.T.; Backar, A.H. Characteristic properties of date-palm fibre/sheep wool reinforced polyester composites. J. Bioresour. Bioprod. 2023, 8, 430–443. [Google Scholar] [CrossRef]
- Michel, F.; Davies, P. Characterization of polyester mooring lines. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; Volume 48180. [Google Scholar]
- Liu, X.; Li, Z.; Zhu, D.; Gong, Q. Dynamic viscoelastic properties of polyethylene terephthalate. Plastics 2024, 53, 137–142. (In Chinese) [Google Scholar]
- da Silva, L.S.; Cazzolato, B.S.; Sergiienko, N.Y.; Ding, B.; Morishita, H.M.; Pesce, C.P. Statistical linearization of the Morison’s equation applied to wave energy converters. J. Ocean. Eng. Mar. Energy 2020, 6, 157–169. [Google Scholar] [CrossRef]
- Beji, S. Formulation of wave and current forces acting on a body and resistance of ships. Ocean. Eng. 2020, 218, 108121. [Google Scholar] [CrossRef]
- Liu, G.; Wang, Q.; Tian, X.; Xie, Y. The ocean structure small scale research and progress on hydrodynamic coefficients of pile. Chin. J. Ocean. Univ. (Nat. Sci. Ed.) 2020, 50, 136–144. (In Chinese) [Google Scholar] [CrossRef]
- Wang, F.; Zhang, J.; Zhu, Y.; Geng, Z.; Wang, F. Research and Progress on Hydrodynamics of Boat-type Aquaculture cages. Ships 2025, 36, 27. (In Chinese) [Google Scholar]
- Wang, G.; Tao, L.; Rong, B.; Rui, X. Research Progress of Dynamic Simulation Methods for Multi-field Coupled Systems. Adv. Mech. 2023, 53, 468–495. (In Chinese) [Google Scholar]
- Lin, M.; Wu, Q.; Tian, H.; Huang, L.; Huang, G.; Liu, B.; Wang, X.; Wang, G. Tension of mooring ropes and safety of jacket Foundation structure in the integrated system of offshore wind turbines and aquaculture cages. Acta Fish. Sin. 2024, 48, 107–119. (In Chinese) [Google Scholar]
- Kuan, J.; Čanić, S.; Muha, B. Fluid-poroviscoelastic structure interaction problem with nonlinear geometric coupling. J. Math. Pures Appl. 2024, 188, 345–445. [Google Scholar] [CrossRef]
- Bungartz, H.J.; Lindner, F.; Mehl, M.; Uekermann, B. A plug-and-play coupling approach for parallel multi-field simulations. Comput. Mech. 2015, 55, 1119–1129. [Google Scholar] [CrossRef]
- Gong, S.; Gao, J.; Yan, M.; Song, Z.; Shi, H. Effects of floater motion on wave loads during steady-state gap resonance occurring between two non-identical boxes. Ocean. Eng. 2025, 323, 120649. [Google Scholar] [CrossRef]
- Zeng, X.; Shi, W.; Feng, X.; Shao, Y.; Li, X. Investigation of higher-harmonic wave loads and low-frequency resonance response of floating offshore wind turbine under extreme wave groups. Mar. Struct. 2023, 89, 103401. [Google Scholar] [CrossRef]
- Ling, H.; Yang, P.; Zhang, Z.; Wang, Z. Complex wave loads and hydroelastic responses of a very large tourism floating platform ‘Ocean Diamond’. Ocean. Eng. 2022, 265, 112608. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, D.; He, H.; Yang, F.; Li, W.; Chen, Y. Dynamic Response and Fatigue Analysis of a New Marine Gravitational Energy Storage System Under Wave Loads. J. Mar. Sci. Eng. 2024, 12, 2196. [Google Scholar] [CrossRef]
- Fan, Y.; Zhao, Z.; Yu, J.; Wu, L. Net hydrodynamic load impact factor analysis. Mar. Eng. 2025, 47, 1–6+77. (In Chinese) [Google Scholar] [CrossRef]
- Mi, S.; Wang, M.; Avital, E.J.; Williams, J.J.; Chatjigeorgiou, I.K. An implicit Eulerian–Lagrangian model for flow-net interaction using immersed boundary method in OpenFOAM. Ocean. Eng. 2022, 264, 112843. [Google Scholar] [CrossRef]
- Cao, H.; Wan, D. Research on the Development and Application of Numerical Wave Water Pool Based on OpenFOAM. In Strive to Be Strong and Realize the Dream of the Maritime Frontier—Proceedings of the 8th Plenary Session of the Ship Mechanics Academic Committee of the China Shipbuilding Society; State Key Laboratory of Marine Engineering, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University: Shanghai, China, 2014; pp. 319–332. (In Chinese) [Google Scholar]
- Chen, C.; Wang, W.; Zheng, J.; Zheng, Y.; Shi, X.; Liu, C. Water flow under the action of the flat metal net water resistance characteristic numerical simulation. J. Dalian Ocean. Univ. 2017, 32, 363–368. (In Chinese) [Google Scholar] [CrossRef]
- Huang, X.; Guo, G.; Tao, Q.; Hu, Y. Numerical Simulation of Deformation Characteristics under Force of HDPE Circular Gravity Cage. South. Fish. Sci. 2013, 9, 126–131. (In Chinese) [Google Scholar]
- Chen, Y.; Pang, G.; Huang, X.; Li, G.; Yuan, T.; Hu, Y.; Tao, Q. The influence of net coating on the structural response of self-elevating truss cages. South. Fish. Sci. 2024, 20, 43–53. (In Chinese) [Google Scholar]
- Scherz, L.; Kriegesmann, B.; Pedersen, C.B. A condition number-based numerical stabilization method for geometrically nonlinear topology optimization. Int. J. Numer. Methods Eng. 2024, 125, e7574. [Google Scholar] [CrossRef]
- Ceglie, M.; Violano, G.; Afferrante, L.; Menga, N. Hysteresis in Approach-Retraction Frictional Contacts with Geometric and Material Nonlinearity. Mater. Sci. Forum 2025, 1151, 109–115. [Google Scholar] [CrossRef]
- Dai, H. Research on Fluid-Structure Coupled Nonlinear Vibration Mechanism and Its Driving Utilization. In Abstracts of the 19th National Conference on Nonlinear Vibration and the 16th National Conference on Nonlinear Dynamics and Motion Stability; Department of Engineering Mechanics, School of Aeronautics and Astronautics, Huazhong University of Science and Technology: Wuhan, China, 2023; Volume 4, (In Chinese). [Google Scholar] [CrossRef]
- Pan, Y. Research on Ocean Energy Harvesting and Sensing Technology Based on Nanopower Generation. Master’s Thesis, Beijing University of Technology, Beijing, China, 2024. (In Chinese). [Google Scholar]
- Liang, N.; Miao, C.; Cui, H.; Wang, J.; Yang, X. Simulation Study on Coupling System of Raft Wave Energy Conversion and Triboelectric Nanogenerator Energy Output. Adv. New Renew. Energy 2022, 10, 265–270. (In Chinese) [Google Scholar] [CrossRef]
- Pan, C.Y.; Dai, Z.H.; Ma, H.X.; Zheng, J.R.; Leng, J.; Xie, C.; Yuan, Y.P.; Yang, W.C.; Yaliun, Y.X.; Song, X.M.; et al. Self-powered and speed-adjustable sensor for abyssal ocean current measurements based on triboelectric nanogenerators. Nat. Commun. 2024, 15, 6133. (In Chinese) [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhang, J.; Liu, Y.; Sun, K.; Zhang, C.; Wu, W.; Teng, F. Numerical assessment of the environmental impacts of deep sea cage culture in the Yellow Sea, China. Sci. Total Environ. 2020, 706, 135752. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Hao, Y.; Yang, J.; Su, W.; Zhang, H.; Wang, J.; Wang, Z.; Li, X. Recent advances in triboelectric nanogenerators for marine exploitation. Adv. Energy Mater. 2023, 13, 2300387. [Google Scholar] [CrossRef]
- Yu, J.; Guo, Y.; Yang, L. Solid-liquid Triboelectric Nanogenerator. J. Mech. Eng. 2021, 57, 160–181. (In Chinese) [Google Scholar]
- Zhu, H.; Liang, J.; Wang, S.; Huang, J.; Chen, Z. A multimodal PDMS triboelectric nanogenerator sensor based on anodised aluminium oxide template preparation for object recognition. J. Mater. Chem. A 2023, 11, 24158–24168. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Li, X.; Xu, C.; Halim, J.; Cao, S.; Rosen, J.; Strömme, M. A mechanically robust spiral fiber with ionic–electronic coupling for multimodal energy harvesting. Mater. Horiz. 2024, 11, 3643–3650. [Google Scholar] [CrossRef]
- Jin, S.Y. Based on Drum TENG Device of Energy Collection and Vibration Testing Research. Master’s Thesis, Hangzhou University of Electronic Science and Technology, Hangzhou, China, 2024. (In Chinese). [Google Scholar]
- Yang, H. Structural Design and Performance Research of a Triboelectric Nanogenerator for Water Wave Energy Harvesting. Master’s Thesis, Zhejiang Normal University, Jinhua, China, 2024. (In Chinese). [Google Scholar]
- Park, S.G.; Zhou, J.; Dong, S.; Li, Q.; Yoshida, T.; Kitazawa, D. Characteristics of the flow field inside and around a square fish cage considering the circular swimming pattern of a farmed fish school: Laboratory experiments and field observations. Ocean. Eng. 2022, 261, 112097. [Google Scholar] [CrossRef]
- Gansel, L.C.; Rackebrandt, S.; Oppedal, F.; McClimans, T.A. Flow fields inside stocked fish cages and the near environment. J. Offshore Mech. Arct. Eng. 2014, 136, 031201. [Google Scholar] [CrossRef]
- Dong, S.; Park, S.G.; Zhou, J.; Li, Q.; Yoshida, T.; Kitazawa, D. Flow Field Inside and Around a Square Fish Cage Considering Fish School Swimming Pattern. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Virtual, 21–30 June 2021; Volume 85154. [Google Scholar]
- Tang, M.F.; Xu, T.J.; Dong, G.H.; Zhao, Y.P.; Guo, W.J. Numerical simulation of the effects of fish behavior on flow dynamics around net cage. Appl. Ocean. Res. 2017, 64, 258–280. [Google Scholar] [CrossRef]
- Borazjani, I.; Mohsen, D. The fish tail motion forms an attached leading edge vortex. Proc. R. Soc. B Biol. Sci. 2013, 280, 20122071. [Google Scholar] [CrossRef]
- Guo, C.; Liang, Z.; Han, Y.; Kui, Y.; Xu, P.; Sun, L. Experimental Study on Linear Accelerated Swimming of Zebrafish. Acta Mech. Sin. 2022, 54, 2446–2459. (In Chinese) [Google Scholar]
- Yang, G.; Hu, X.; Zhang, B.; Long, Z.; Zhang, Y.; Shi, X. Analysis of Dynamic Characteristics of Free-Swimming Grass Carp Based on Particle Image Velocimetry (PIV). J. Dalian Ocean. Univ. 2021, 4, 833–841. (In Chinese) [Google Scholar] [CrossRef]
- Hu, W. Numerical and analytical study on a tail-flaping model for fish fast C-start. Acta Mech. Sin. 2004, 20, 16–23. (In Chinese) [Google Scholar] [PubMed]
- Su, B.; Zhai, S.; Bai, Y.; Zhang, J. Analysis of hydrodynamic and vortex Structure Characteristics of Tail Fin Swing Propulsion. J. Ship Mech. 2024, 28, 220–228. (In Chinese) [Google Scholar]
- Cui, Z.; Jiang, H.; He, J.; Tong, Z. Research Progress and Key Technology Analysis of Swimming Mechanism of BCF bionic fish. J. Mech. Eng. 2015, 51, 177–184. (In Chinese) [Google Scholar] [CrossRef]
- Tong, B. The Propulsion Mechanism of Fish ‘Wavy Swimming’. Mech. Chin. Pract. 2000, 22. (In Chinese) [Google Scholar]
- Chu, W.; Yuan, Q.; Kong, X.; Zhang, Z.; Li, H.; Qian, W. Analysis of Tail fin Propulsion Mechanism and Influencing Parameters of Swimming Ability of Fish. J. Shanghai Ocean. Univ. 2022, 31, 1224–1234. (In Chinese) [Google Scholar]
- Sun, W.; Liu, S.; Wu, G.; Zhou, Y.; Ren, X. Research Progress on the Swimming mechanism of fish. J. Dalian Ocean. Univ. 2024, 39, 698–707. (In Chinese) [Google Scholar]
- Xu, P.; Liu, J.; Liu, X.; Wang, X.; Zheng, j.; Wang, S.; Chen, T.; Wang, H.; Wang, C.; Fu, X.; et al. A bio-inspired and self-powered triboelectric tactile sensor for underwater vehicle perception. Npj Flex. Electron. 2022, 6, 25. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, C.; Zhong, L.W. The sealed bionic fishtail-structured TENG based on anticorrosive paint for ocean sensor systems. Nano Energy 2023, 108, 108210. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Wang, C. Application Progress of Flexible Wearable Sensing Technology in Smart Fishery. Trans. Chin. Soc. Agric. Eng. 2023, 39, 1–13. (In Chinese) [Google Scholar]
- Zhang, B.; Hu, X.; Yang, G.; Long, Z.; Huang, H.; Shi, X. Study on the Dynamics of Juvenile Grass Carp Cruising Based on Pressure Field. J. Hydroelectr. Power 2021, 40, 79–88. (In Chinese) [Google Scholar]
- Clukey, E.C.; Silva, A.J. Permeability of deep-sea clays: Northwestern Atlantic. Mar. Georesources Geotechnol. 1982, 5, 1–26. [Google Scholar] [CrossRef]
- Du, J.; Hu, L.; Sun, J.; Song, Q.; Chen, M.; Xiao, J. Tribo-corrosion Performance of 7075-T6 Al-alloy in 3.5%NaCl Solution. J. Chin. Soc. Corros. Prot. 2025, 45, 803–811. [Google Scholar] [CrossRef]
- Chen, Z.; Mei, Y.; Liu, S.; Li, H.; Liu, L.; Lei, X.; Zhou, Y.; Gao, X. Electronic Packaging reliability: Past, Present and future. J. Mech. Eng. 2021, 57, 248–268. (In Chinese) [Google Scholar]
- Sun, Y.; Zheng, Y.; Wang, R.; Lei, T.; Liu, J.; Fan, J.; Shou, W.; Liu, Y. 3D micro-nanostructure based waterproof triboelectric nanogenerator as an outdoor adventure power source. Nano Energy 2022, 100, 107506. [Google Scholar] [CrossRef]

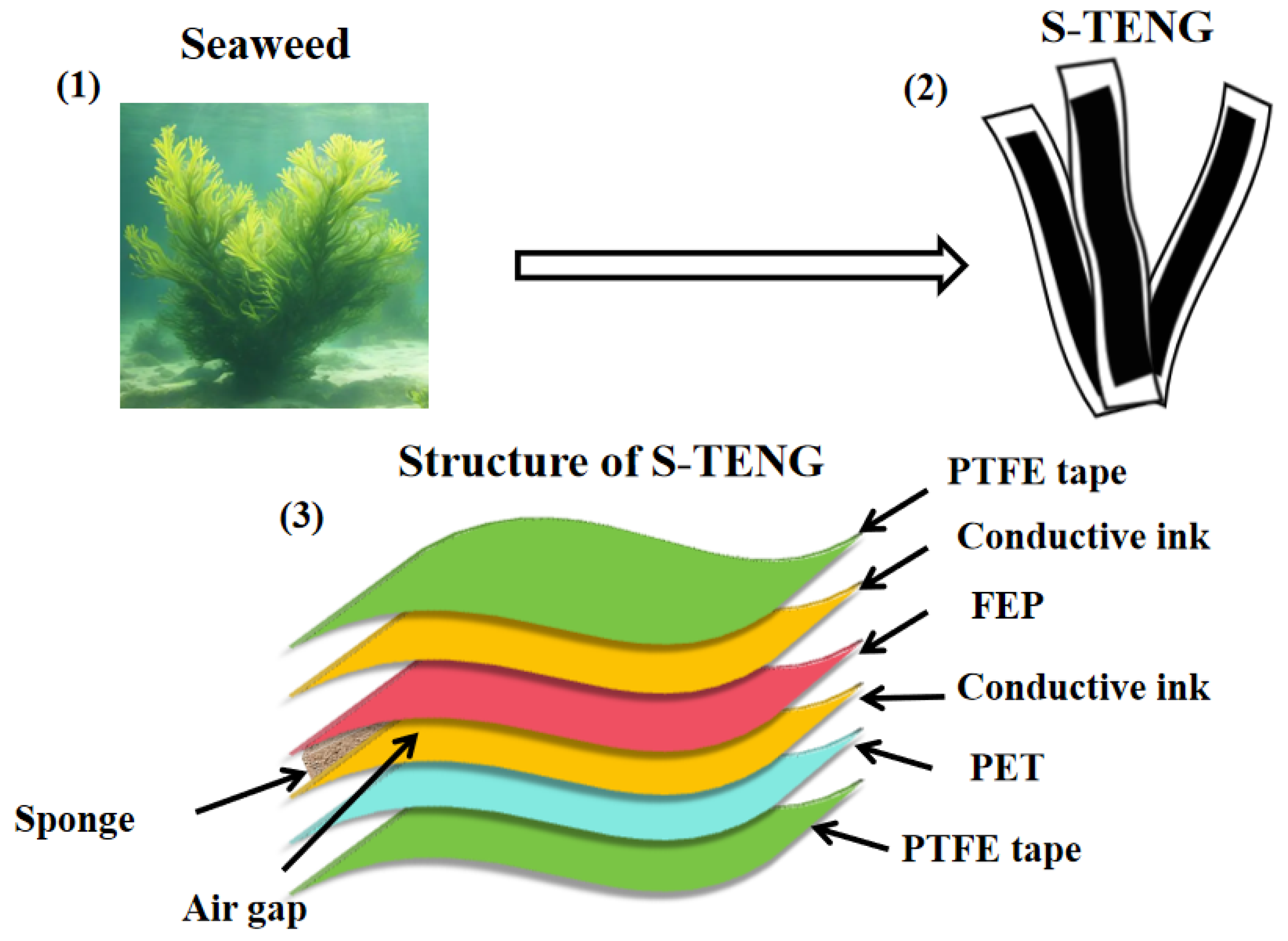
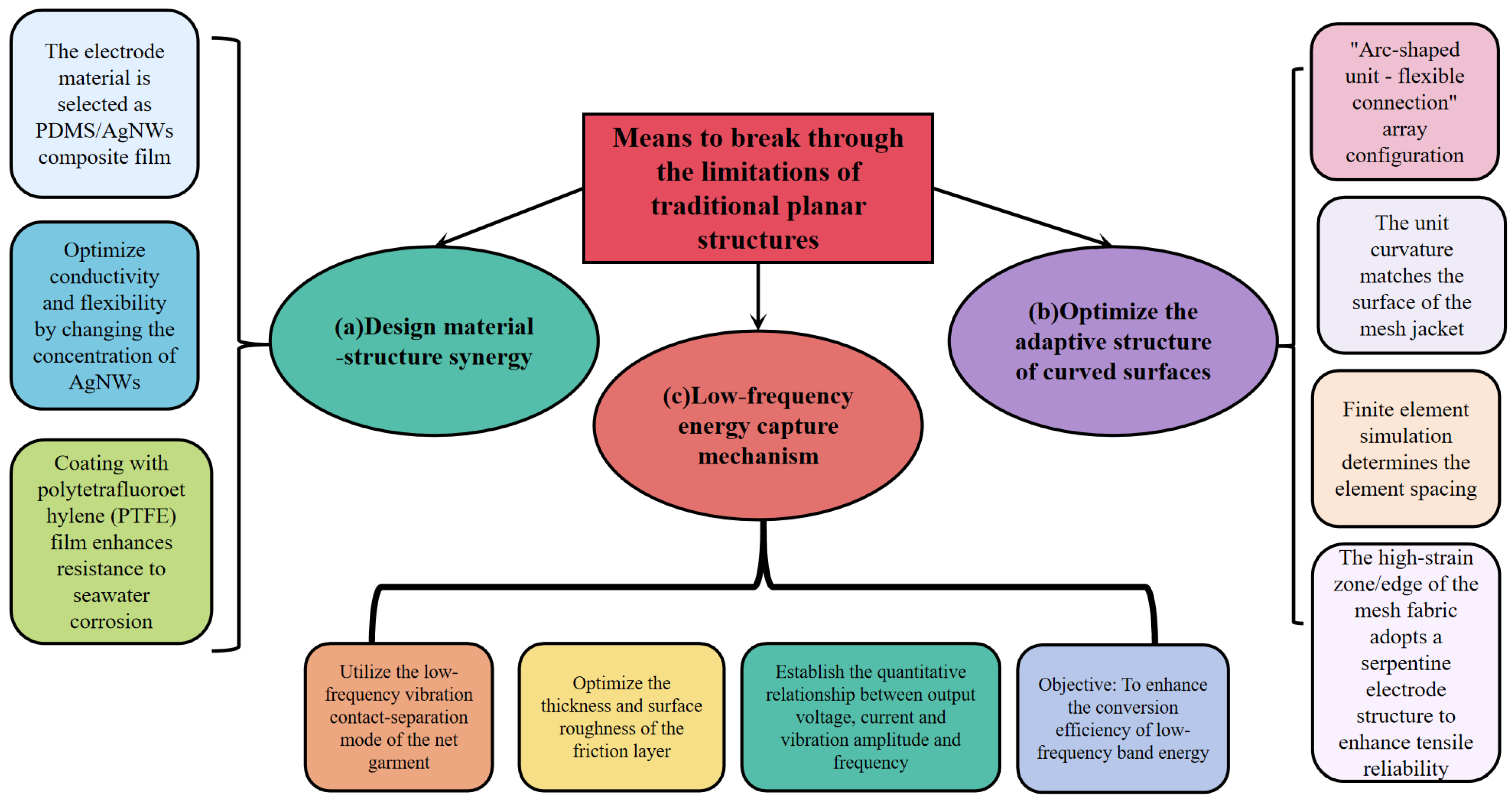
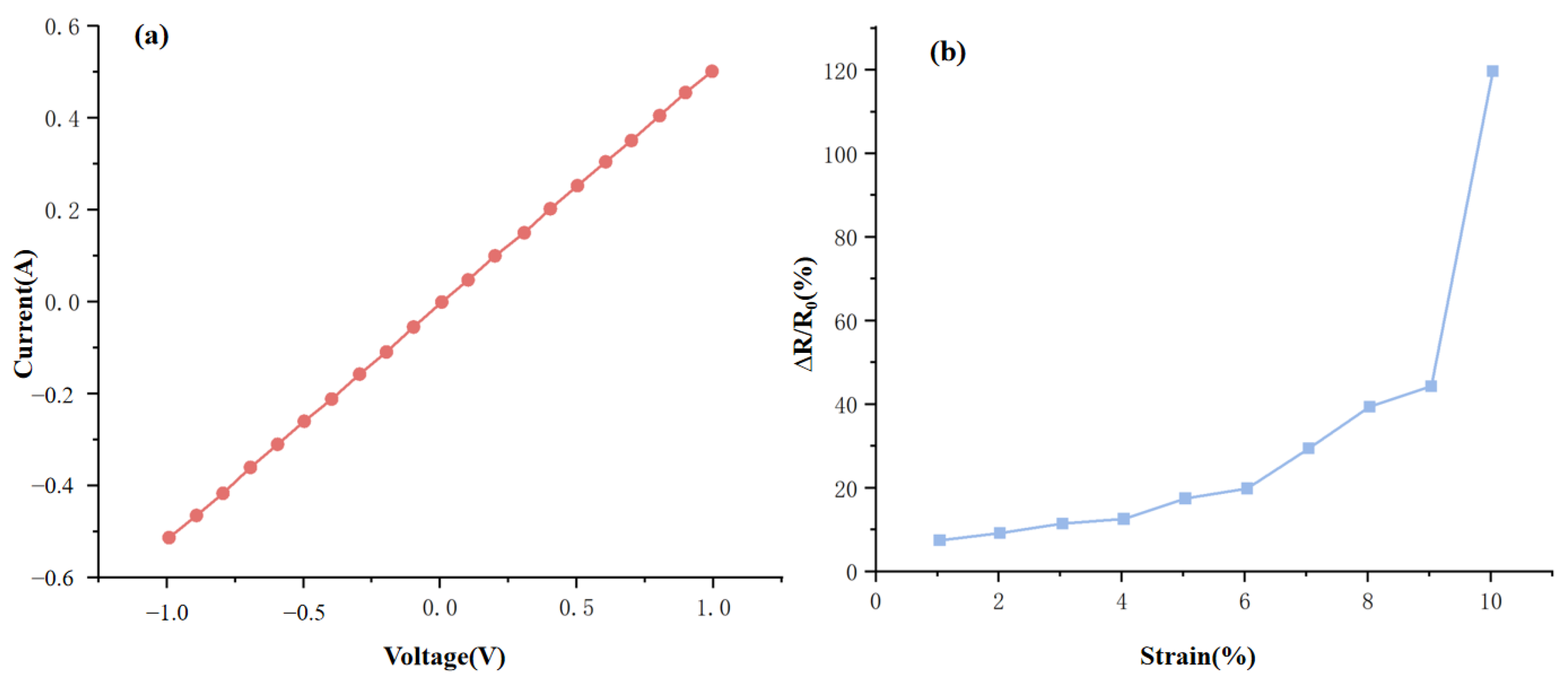
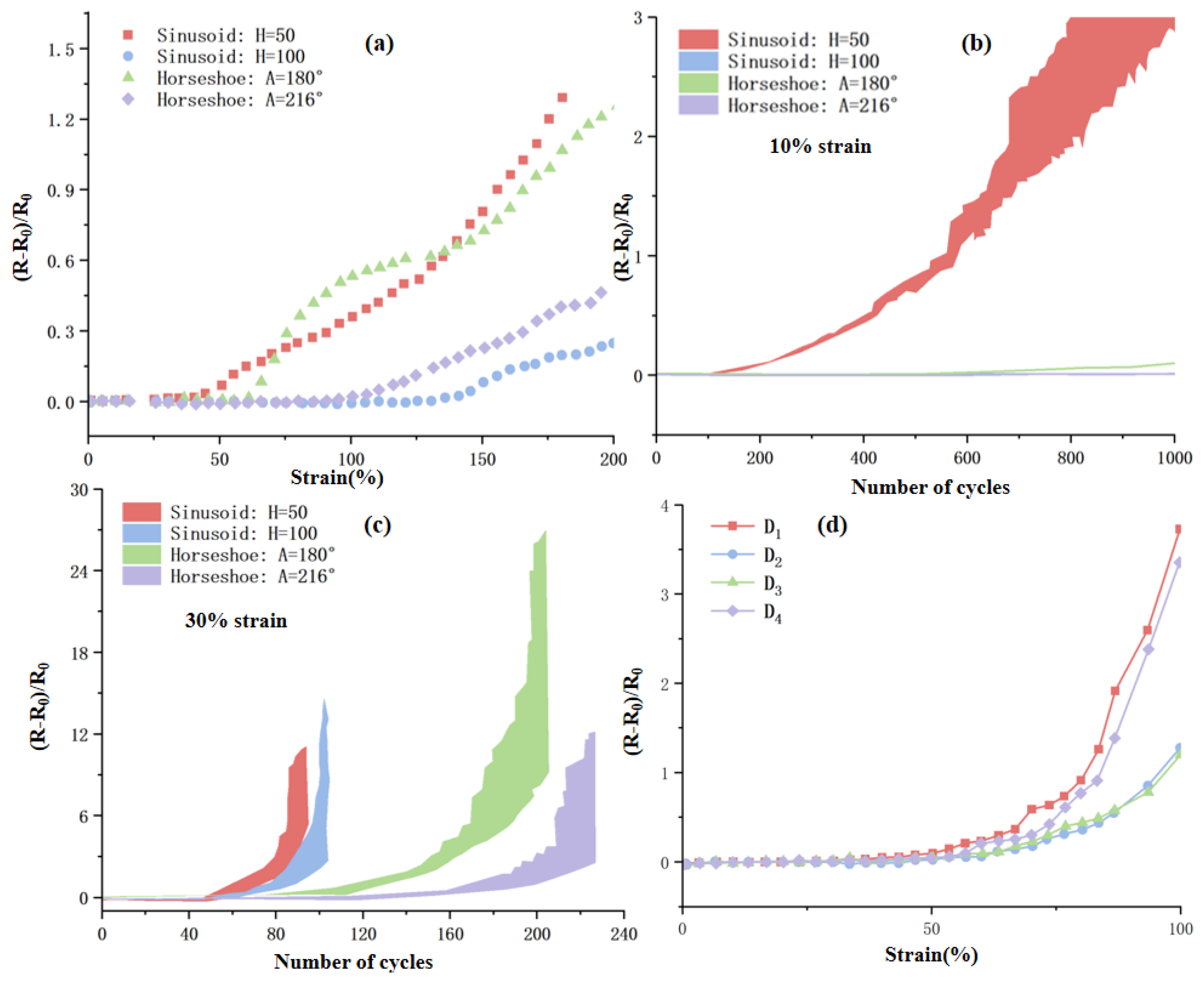


| Modulus Value 0 | Status | Vibration Amplitude |
|---|---|---|
| All | The net garment is in a steady-state vibration | The vibration amplitude shows no increasing trend over time, and the dynamic behavior of the structure is controllable |
| When there is at least one | The system has entered the initial stage of instability | The vibration amplitude increases exponentially with the periodic iteration |
| When | The system is in a critical stable state | The vibration amplitude remains constant but is prone to instability triggered by flow field disturbances |
| Equipment Type | Capture Frequency Range | Power Density | Deep-Sea Pressure Adaptation (Maximum Water Depth) | Corrosion-Resistant Life | The Adaptation Area of the Net Box | Core Advantage |
|---|---|---|---|---|---|---|
| Surface-adaptive TENG array | 0.1–10 HZ | 0.1–0.5 mW/cm2 | 1500 m | 6 to 12 months | The curved surface and floating body of the net garment | Flexible conformal, low-frequency adaptation |
| Deep-sea compatible EMG | 0.5–50 HZ | 5–15 mW/cm2 | 2000 m | 5 years and more | Frame, anchor chain | High-power and high-voltage tolerance |
| Flexible PEH | 50–100 HZ | 0.5–12 mW/cm2 | 1000 m | 2 years and more | Local areas of the net garment and turbulent zones | High-frequency capture, flexible integration |
| Bionic multimodal integrated system | 0.1–500 HZ | 2–8 mW/cm2 | 1800 m | 3 years and more | Full net box coverage | Full-band capture and strong environmental adaptability |
| Equipment Category | Specific Equipment | Power Range | Working Mode | Average Daily Power Consumption (Wh) |
|---|---|---|---|---|
| Structural monitoring sensor | Strain sensor | 5–15 μW | Intermittent sampling (once per minute) | 0.012–0.036 |
| Vibration sensor | 10–20 μW | Intermittent sampling (once per 30 s) | 0.024–0.048 | |
| Acceleration sensor | 8–12 μW | Intermittent sampling (once/2 min) | 0.0096–0.0144 | |
| Environmental monitoring sensor | Temperature sensor | 3–8 μW | Continuous monitoring (once per 10 s) | 0.0216–0.0576 |
| Salinity sensor | 15–25 μW | Intermittent sampling (once for 5 min) | 0.0432–0.072 | |
| Dissolved oxygen sensor | 30–50 μW | Continuous monitoring (once per 5 s) | 0.432–0.72 | |
| pH sensor | 20–35 μW | Intermittent sampling (once/2 min) | 0.0576–0.1008 | |
| Execution device | Automatic feeding machine | 10–30 W | Intermittent work (three times a day, 10 min each time) | 5–15 |
| Underwater camera | 50–100 mW | Intermittent shooting (1 h each day) | 0.05–0.1 | |
| Data transmission system | Short-range wireless transmission module | 50–100 mW | Intermittent transmission (once per 10 min) | 0.072–0.144 |
| Long-range wireless transmission module | 1–5 W | Intermittent transmission (once per hour) | 0.04–0.2 | |
| Auxiliary system | Water quality regulating pump | 5–15 W | Intermittent work (twice a day, 30 min each time) | 5–15 |
| Biological cleaning device | 8–20 W | Intermittent work (once a day, 20 min each time) | 2.67–6.67 |
| Dimensions | Surface-Adaptive TENG Array | Underwater Solar Energy | Electromagnetic EMG |
|---|---|---|---|
| Power density | 0.1–0.5 mW/cm2 | <0.01 mW/cm2 | 5–15 mW/cm2 |
| Adaptation frequency | 0.1–10 Hz (low) | The deep sea is ineffective | 0.5–50 Hz (medium to high) |
| Environmental tolerance | 1500 m water pressure, corrosion-resistant for 6 to 12 months | Easy to adhere, with a 50% reduction in effectiveness in March | 2000 m water pressure, corrosion resistance for over 5 years |
| Conversion efficiency | 15–20% (low frequency) | <1% (deep sea) | 40–50% (mid and high frequencies) |
| Adaptability | Flexible mesh fabric | It takes up space and is not usable in the deep sea | A fixed frame is required |
| Unit cost | 0.02 dollar/Wh | 0.8 dollar/Wh | 0.08 dollar/Wh |
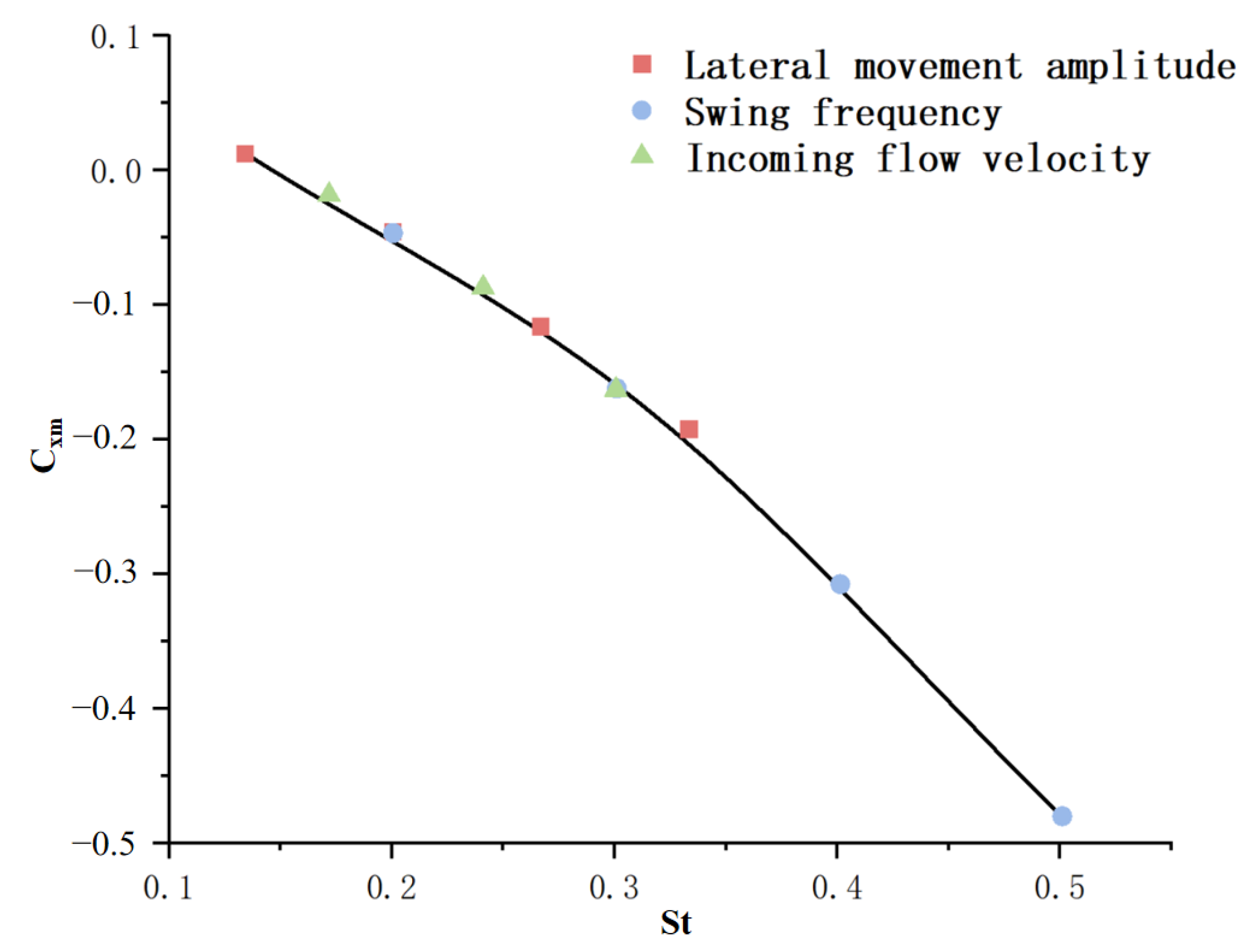
| Different Incoming Flow Velocity Operating Conditions | Operating Conditions with Different Swing Frequencies | Working Conditions with Different Lateral Movement Amplitudes | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Serial Number | V/ (m·s−1) | A/C0 | f/Hz | St | Serial Number | V/ (m·s−1) | A/C0 | f/Hz | St | Serial Number | V/ (m·s−1) | A/C0 | f/Hz | St |
| 1 | 0.8 | 0.6 | 0.5 | 0.30 | 5 | 1.2 | 0.6 | 0.25 | 0.10 | 9 | 1.2 | 0.4 | 0.5 | 0.13 |
| 2 | 1.0 | 0.6 | 0.5 | 0.24 | 6 | 1.2 | 0.6 | 0.5 | 0.20 | 10 | 1.2 | 0.6 | 0.5 | 0.20 |
| 3 | 1.2 | 0.6 | 0.5 | 0.20 | 7 | 1.2 | 0.6 | 0.75 | 0.30 | 11 | 1.2 | 0.8 | 0.5 | 0.27 |
| 4 | 1.4 | 0.6 | 0.5 | 0.17 | 8 | 1.2 | 0.6 | 1 | 0.40 | 12 | 1.2 | 1 | 0.5 | 0.33 |
| Grid Scheme | Core Domain Size | Total Resistance (N) | Internal Flow Velocity (m/s) | Fine Grid Error |
|---|---|---|---|---|
| Coarse grid | 5 cm | 185 | 0.28 | 12.3% |
| Middle grid | 3 cm | 205 | 0.32 | 4.7% |
| Fine grid | 1 cm | 215 | 0.33 | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Zeng, S.; Yang, K.; Zhang, D.; Zhang, Y. From Multi-Field Coupling Behaviors to Self-Powered Monitoring: Triboelectric Nanogenerator Arrays for Deep-Sea Large-Scale Cages. J. Mar. Sci. Eng. 2025, 13, 2042. https://doi.org/10.3390/jmse13112042
Yang K, Zeng S, Yang K, Zhang D, Zhang Y. From Multi-Field Coupling Behaviors to Self-Powered Monitoring: Triboelectric Nanogenerator Arrays for Deep-Sea Large-Scale Cages. Journal of Marine Science and Engineering. 2025; 13(11):2042. https://doi.org/10.3390/jmse13112042
Chicago/Turabian StyleYang, Kefan, Shengqing Zeng, Keqi Yang, Dapeng Zhang, and Yi Zhang. 2025. "From Multi-Field Coupling Behaviors to Self-Powered Monitoring: Triboelectric Nanogenerator Arrays for Deep-Sea Large-Scale Cages" Journal of Marine Science and Engineering 13, no. 11: 2042. https://doi.org/10.3390/jmse13112042
APA StyleYang, K., Zeng, S., Yang, K., Zhang, D., & Zhang, Y. (2025). From Multi-Field Coupling Behaviors to Self-Powered Monitoring: Triboelectric Nanogenerator Arrays for Deep-Sea Large-Scale Cages. Journal of Marine Science and Engineering, 13(11), 2042. https://doi.org/10.3390/jmse13112042







