Calculating the Sediment Flux in Hydrometric Data-Scarce Small Island Coastal Watersheds
Abstract
1. Introduction
2. Materials and Methods
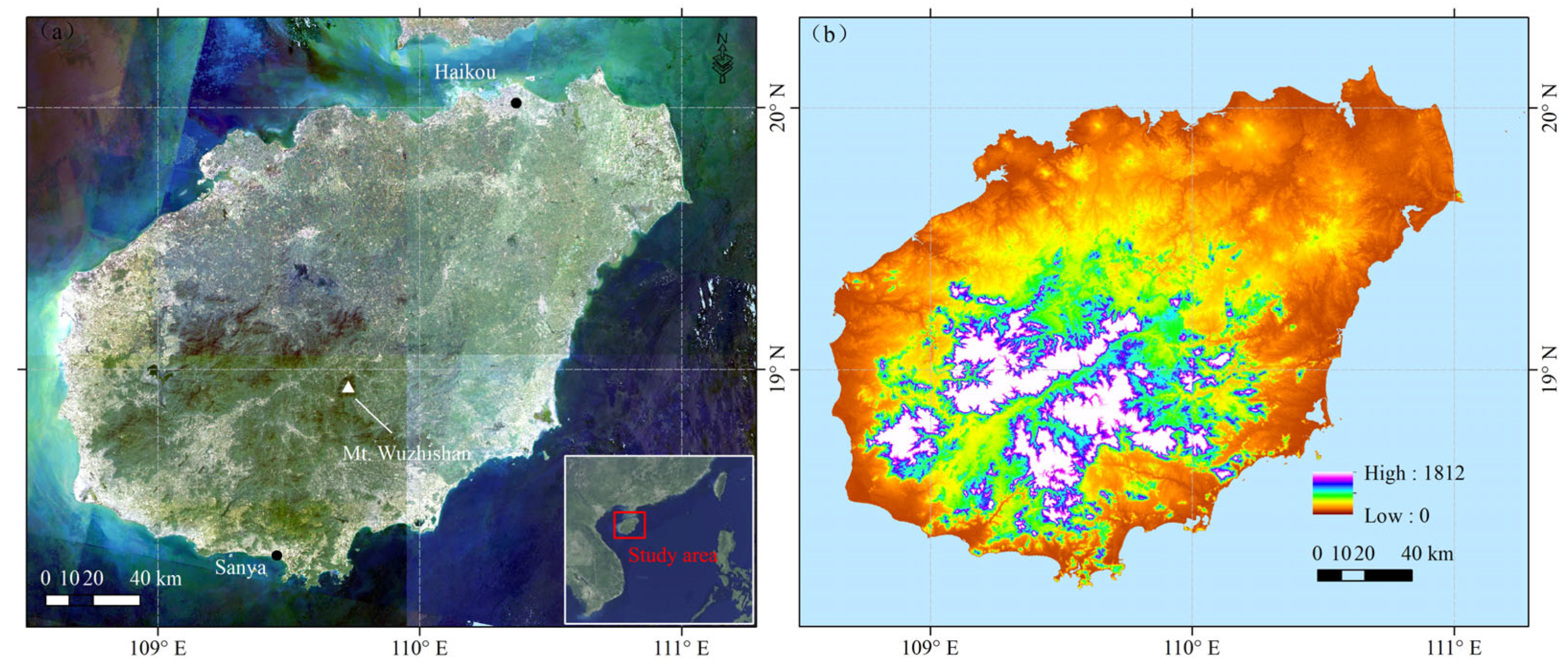
2.1. Study Area Description
2.2. Data Sources and Preparation
2.3. Calculation Methods
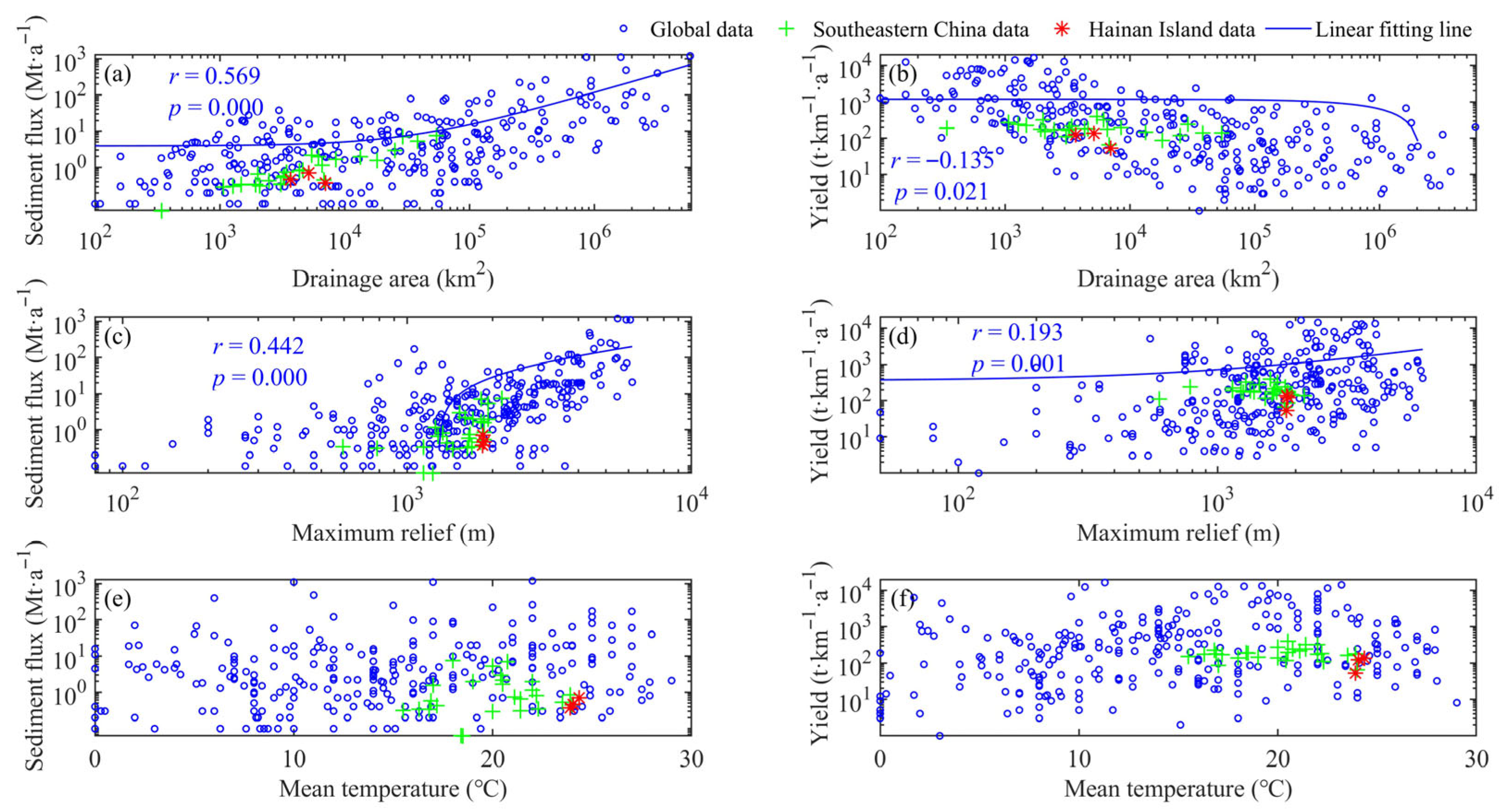
3. Results
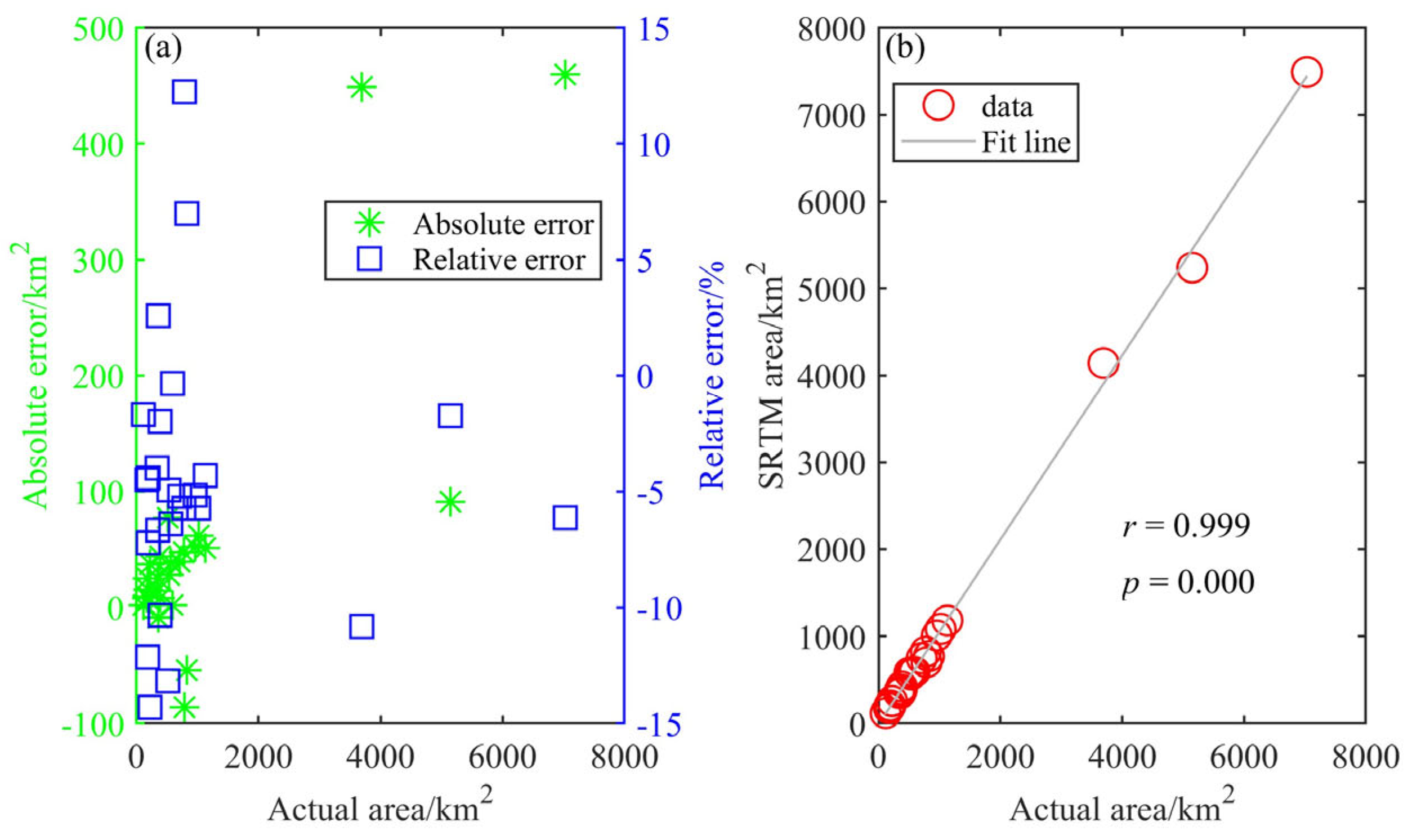
3.1. Validation of SRTM Extraction Accuracy
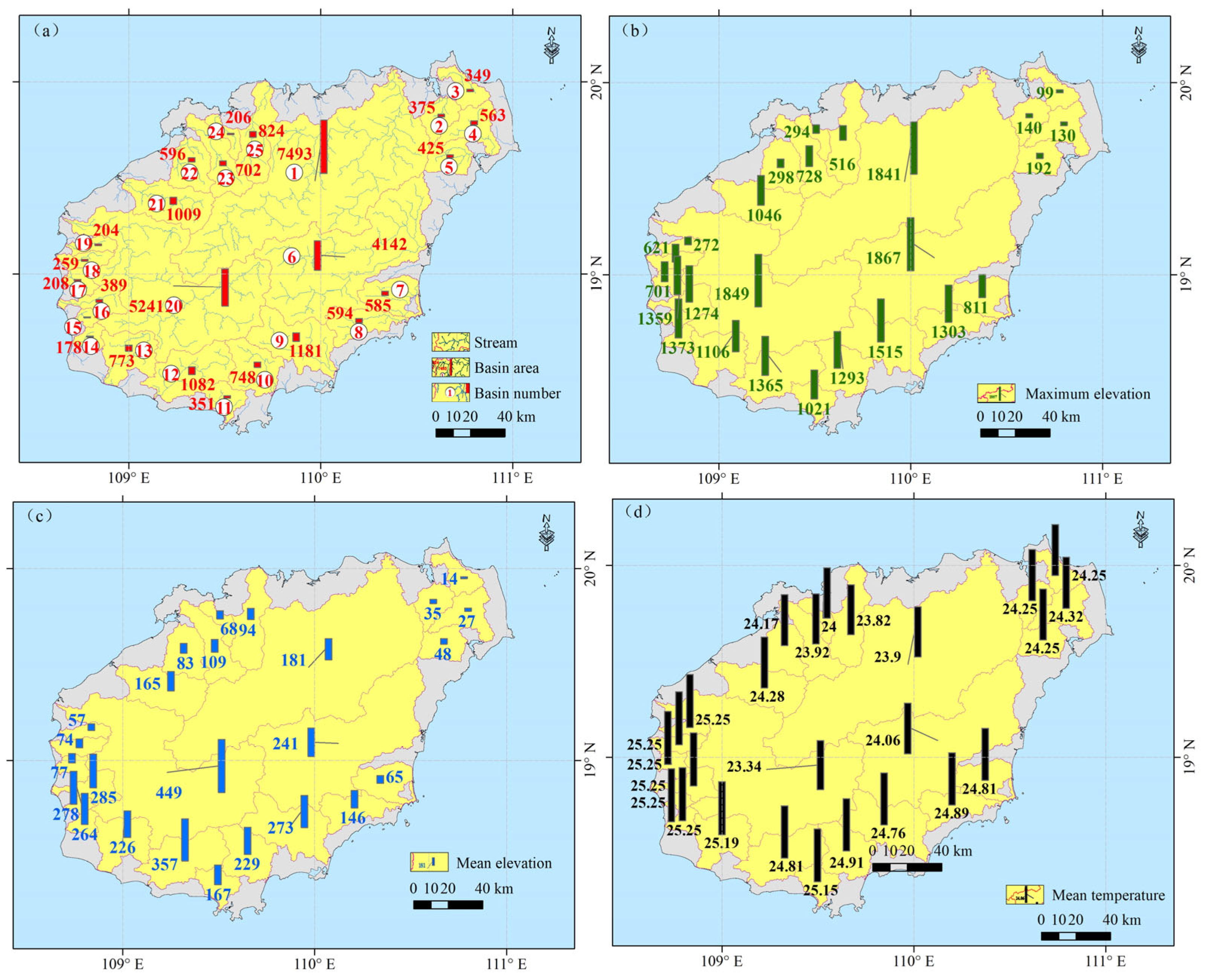
3.2. Characteristics of River Parameters
3.3. Validation of Qs Calculation Accuracy for Typical Rivers
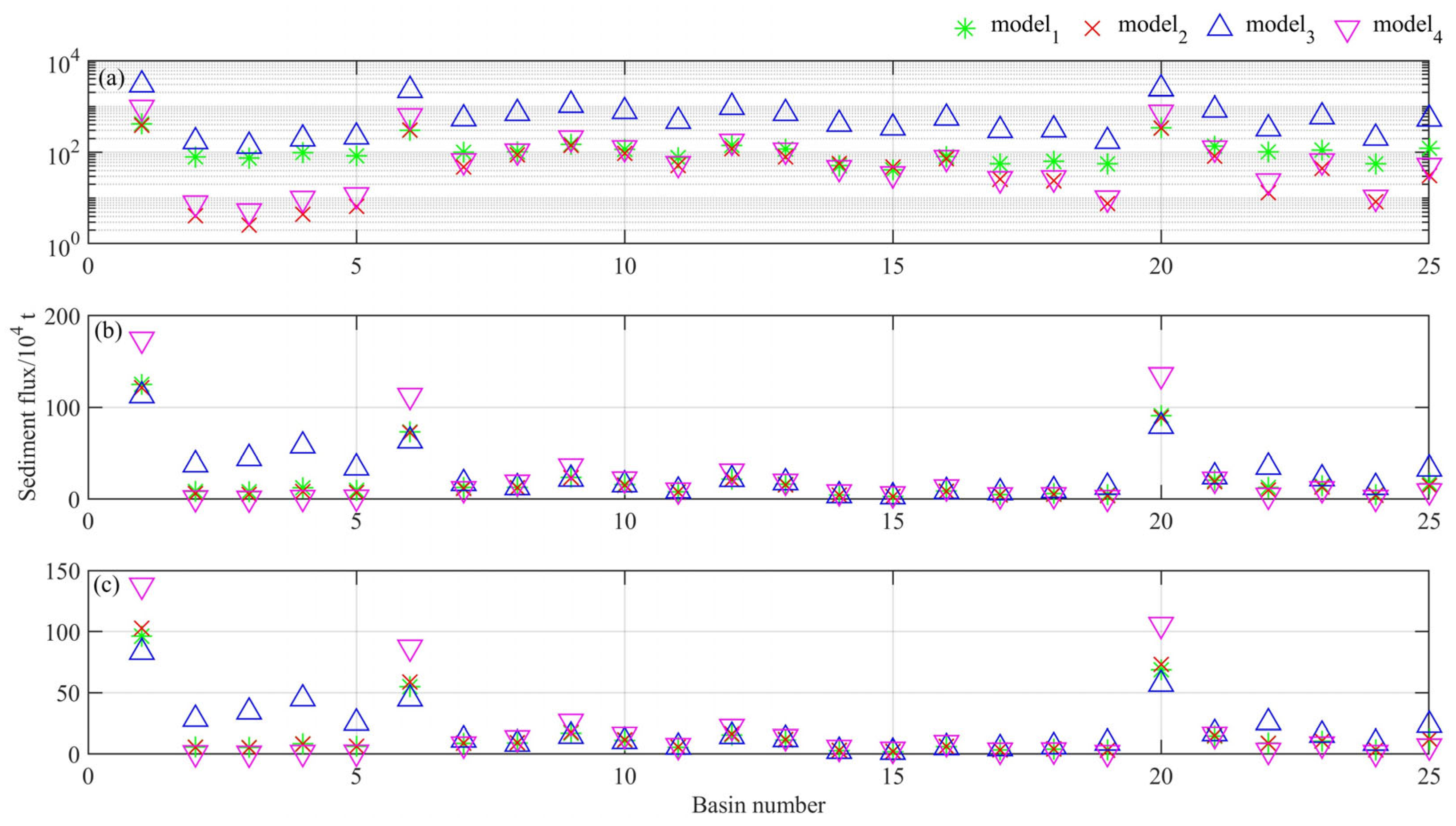
3.4. Sediment Flux
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, G.C.; Gao, S.; Wang, Y.P.; Li, C.Y. Sediment flux from the Zhoushan Archipelago, eastern China. J. Geogr. Sci. 2018, 28, 387–399. [Google Scholar] [CrossRef]
- Jia, J.J.; Gao, J.H.; Cai, T.L.; Li, Y.; Yang, Y.; Wang, Y.P.; Xia, X.M.; Li, J.; Wang, A.J.; Gao, S. Sediment accumulation and retention of the Changjiang (Yangtze River) subaqueous delta and its distal muds over the last century. Mar. Geol. 2018, 401, 2–16. [Google Scholar] [CrossRef]
- Bianchi, T.S.; Allison, M.A. Large-river delta-front estuaries as natural “recorders” of global environmental change. Proc. Natl. Acad. Sci. USA 2009, 106, 8085–8092. [Google Scholar] [CrossRef]
- Gao, S.; Collins, M.B. Holocene sedimentary systems on continental shelves. Mar. Geol. 2014, 352, 268–294. [Google Scholar] [CrossRef]
- Day, J.W.; Agboola, J.; Chen, Z.Y.; D’Elia, C.; Forbes, D.L.; Giosan, L.; Kemp, P.; Kuenzer, C.; Lane, R.; Ramachandran, R.; et al. Approaches to defining deltaic sustainability in the 21st century. Estuar. Coast. Shelf Sci. 2016, 183, 275–291. [Google Scholar] [CrossRef]
- Milliman, J.D.; Farnsworth, K.L. River Discharge to the Coastal Ocean: A Global Synthesis; Cambridge University Press: Cambridge, UK, 2013; pp. 1–20. [Google Scholar]
- Guo, L.C.; Su, N.; Townend, I.; Wang, Z.B.; Zhu, C.Y.; Wang, X.Y.; Zhang, Y.N.; He, Q. From the headwater to the delta: A synthesis of the basin-scale sediment load regime in the Changjiang River. Earth-Sci. Rev. 2019, 197, 102900. [Google Scholar] [CrossRef]
- Milliman, J.D.; Syvitski, J.P.M. Geomorphic/tectonic control of sediment discharge to the ocean: The importance of small mountainous rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Ahnert, F. Functional relationships between denudation, relief, and uplift in large, mid-latitude drainage basins. Am. J. Sci. 1970, 268, 243–263. [Google Scholar] [CrossRef]
- McLennan, S.M. Weathering and global denudation. J. Geol. 1993, 101, 295–303. [Google Scholar] [CrossRef]
- Wang, Y.P.; Pan, S.M.; Wang, H.V.; Gao, J.H.; Yang, Y.; Wang, A.J.; Li, Z.H.; Wu, Z. Measurements and analysis of water discharges and suspended sediment fluxes in Chinajiang Estuary. Acta Geogr. Sin. 2006, 61, 35–46. (In Chinese) [Google Scholar] [CrossRef]
- Holeman, J.N. The sediment yield of major rivers of the world. Water Resour. Res. 1968, 4, 737–747. [Google Scholar] [CrossRef]
- Milliman, J.D.; Meade, R.H. World-wide delivery of river sediment to the oceans. J. Geol. 1983, 91, 1–21. [Google Scholar] [CrossRef]
- Li, G.C.; Zhou, L.; Qi, Y.L.; Gao, S. Threshold sediment flux for the formation of river deltas in Hainan Island, southern China. J. Geogr. Sci. 2019, 29, 146–160. [Google Scholar] [CrossRef]
- Molliex, S.; Kettner, A.J.; Laurent, D.; Droz, L.; Marsset, T.; Laraque, A.; Rabineau, M.; N’Kaya, G.D. Simulating sediment supply from the Congo watershed over the last 155 ka. Quat. Sci. Rev. 2019, 203, 38–55. [Google Scholar] [CrossRef]
- Mulder, T.; Syvitski, J.P.M. Climatic and morphologic relationships of rivers: Implications of sea-level fluctuations on river loads. J. Geol. 1996, 104, 509–523. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Peckham, S.D.; Hilberman, R.; Mulder, T. Predicting the terrestrial flux of sediment to the global ocean: A planetary perspective. Sediment. Geol. 2003, 162, 5–24. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Milliman, J.D. Geology, geography, and humans battle for dominance over the delivery of fluvial sediment to the coastal ocean. J. Geol. 2007, 115, 509246. [Google Scholar] [CrossRef]
- Li, G.C.; Xia, Q.; Fu, D.Y.; Zeng, C.H.; Li, Z.Q.; Gao, S. Calculating the sediment flux of the small coastal watersheds: A modification of global equations. Acta Oceanol. Sin. 2021, 40, 147–154. [Google Scholar] [CrossRef]
- Milliman, J.D.; Farnsworth, K.L.; Albertin, C.S. Flux and fate of fluvial sediments leaving large islands in the East Indies. J. Sea Res. 1999, 41, 97–107. [Google Scholar] [CrossRef]
- Dadson, S.J.; Hovius, N.; Chen, H.; Dade, W.B.; Hsieh, M.L.; Willett, S.D.; Hu, J.C.; Horng, M.J.; Chen, M.C.; Stark, C.P.; et al. Links between erosion, runoff variability and seismicity in the Taiwan orogen. Nature 2003, 426, 648–651. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L.F. The volcanic coast in the area of northwest Hainan Island. Acta Geogr. Sin. 1990, 50, 321–330. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Peter, M.I.; Zhu, D.K.; Zhang, Y.Z.; Tang, W.W. Coastal plain evolution in southern Hainan Island, China. Chin. Sci. Bull. 2001, 46, 90–96. [Google Scholar] [CrossRef]
- Wu, S.A.; Xing, C.Y.; Zhu, J.J. Analysis of Climate characteristics in Hainan Island. J. Trop. Biol. 2022, 13, 315–323. (In Chinese) [Google Scholar] [CrossRef]
- Yao, L.P.; Wang, X.; Zhang, J.H.; Yao, F.M. Analysis of spatio-temporal variation and driving forces of leaf area index in Hainan Island over the last 20 years based on MODIS data. Chin. J. Eco-Agric. 2024, 32, 1719–1930. (In Chinese) [Google Scholar] [CrossRef]
- Wang, W.J.; Jin, Z.M.; Bao, Q.S. Characteristic of natural conditions and the construction of ports in the coastal areas of Hainan Island. Trop. Geogr. 1983, 3, 8–13. (In Chinese) [Google Scholar]
- Yang, Z.H.; Jia, J.J.; Wang, X.K.; Gao, J.H. Characteristics and variations of water and sediment fluxes into the sea of the top three rivers of Hainan in recent 50 years. Mar. Sci. Bull. 2013, 32, 92–99. (In Chinese) [Google Scholar] [CrossRef]
- Nienhuis, J.H.; Ashton, A.D.; Giosan, L. What makes a delta wave-dominated? Geology 2015, 43, 511–514. [Google Scholar] [CrossRef]
- Gao, S.; Zhou, L.; Li, G.C.; Wang, D.D.; Yang, Y.; Dai, C.; Han, Z.C.; Wang, H.; Tu, J.Y.; Yang, B.M. Processes and sedimentary records for Holocene coastal Environmental changes, Hainan Island: An overview. Quat. Sci. 2016, 36, 1–17. (In Chinese) [Google Scholar] [CrossRef]
- Li, L.B. Analysis of the trend of sediment changes in major rivers in Hainan Island. In Proceedings of the 3rd Youth Science and Technology Forum of the Chinese Water Conservancy Society, Chengdu, China, 11–13 October 2007; pp. 280–284. [Google Scholar]

| Regression Coefficient | Global Equation | Pristine-Modified Equation | Disturbed-Modified Equation |
|---|---|---|---|
| a | 65.00 | 102.48 | 95.67 |
| b | 0.56 | 0.90 | 0.94 |
| c | 0.41 | 0.88 | 0.94 |
| d | 1.28 | 0.14 | 0.04 |
| f | −3.68 | −2.28 | −2.26 |
| g | 0.45 | 0.95 | 1.01 |
| h | 0.57 | −0.68 | −0.76 |
| i | −0.09 | −0.02 | −0.03 |
| j | 0.08 | 0.04 | 0.05 |
| k | 0.80 | 0.97 | 0.95 |
| l | 0.31 | 0.82 | 1.08 |
| m | 0.50 | −0.03 | −0.22 |
| Equation | River | Observation (104 t/a) | Model1 | Model2 | Model3 | Model4 | Model Averaging | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Result (104 t/a) | RE | Result (104 t/a) | RE | Result (104 t/a) | RE | Result (104 t/a) | RE | Result (104 t/a) | RE | |||
| Global equation | Nandu | 37.30 | 419.49 | 10.25 | 385.65 | 9.34 | 2951.53 | 78.13 | 954.46 | 24.59 | 1177.78 | 30.58 |
| Changhua | 69.88 | 300.99 | 3.31 | 307.92 | 3.41 | 2245.68 | 31.14 | 625.47 | 7.95 | 870.01 | 11.45 | |
| Wanquan | 45.33 | 343.39 | 6.58 | 334.93 | 6.39 | 2420.03 | 52.39 | 747.40 | 15.49 | 961.44 | 20.21 | |
| Basin averaging | 50.84 | 354.62 | 5.98 | 342.83 | 5.74 | 2539.08 | 48.95 | 775.78 | 14.26 | 1003.08 | 18.73 | |
| Pristine-modified equation | Nandu | 44.99 | 125.26 | 1.78 | 121.65 | 1.70 | 112.84 | 1.51 | 174.14 | 2.87 | 133.48 | 1.97 |
| Changhua | 83.84 | 73.47 | −0.12 | 72.35 | −0.14 | 63.44 | −0.24 | 112.95 | 0.35 | 80.55 | −0.04 | |
| Wanquan | 52.97 | 90.81 | 0.71 | 88.87 | 0.68 | 79.40 | 0.50 | 135.52 | 1.56 | 98.65 | 0.86 | |
| Basin averaging | 60.60 | 96.51 | 0.59 | 94.29 | 0.56 | 85.23 | 0.41 | 140.87 | 1.32 | 104.23 | 0.72 | |
| Disturbed-modified equation | Nandu | 21.24 | 96.15 | 3.53 | 102.59 | 3.83 | 83.17 | 2.92 | 137.85 | 5.49 | 104.94 | 3.94 |
| Changhua | 40.70 | 55.07 | 0.35 | 58.79 | 0.44 | 45.00 | 0.11 | 87.28 | 1.14 | 61.54 | 0.51 | |
| Wanquan | 30.04 | 68.71 | 1.29 | 73.32 | 1.44 | 57.01 | 0.90 | 105.73 | 2.52 | 76.19 | 1.54 | |
| Basin averaging | 30.66 | 73.31 | 1.39 | 78.23 | 1.55 | 61.73 | 1.01 | 110.29 | 2.60 | 80.89 | 1.64 | |
| Calculation Model | Mean Qs | Standard Deviation | 95% Confidence Interval | |
|---|---|---|---|---|
| Model1 | Global equation | 2.77 | 0.97 | [0.81, 4.14] |
| Pristine-modified equation | 0.69 | 0.34 | [0.09, 1.23] | |
| Disturbed-modified equation | 0.51 | 0.27 | [0.06, 0.94] | |
| Model2 | Global equation | 1.30 | 0.91 | [0.09, 3.26] |
| Pristine-modified equation | 0.59 | 0.30 | [0.08, 1.12] | |
| Disturbed-modified equation | 0.52 | 0.28 | [0.06, 0.98] | |
| Model3 | Global equation | 13.22 | 6.06 | [3.34, 25.04] |
| Pristine-modified equation | 1.19 | 1.03 | [0.10, 4.16] | |
| Disturbed-modified equation | 0.96 | 0.96 | [0.06, 3.85] | |
| Model4 | Global equation | 0.96 | 0.62 | [0.11, 2.29] |
| Pristine-modified equation | 0.55 | 0.40 | [0.05, 1.45] | |
| Disturbed-modified equation | 0.42 | 0.31 | [0.03, 1.14] | |
| Calculation Equation | Variables | Qs (×104 t/a) | ||||
|---|---|---|---|---|---|---|
| Model1 | Model2 | Model3 | Model4 | Model Averaging | ||
| Global Equation | Min | 41.23 | 2.60 | 135.90 | 5.25 | 54.77 |
| Max | 419.49 | 385.65 | 2951.53 | 954.46 | 1177.78 | |
| Mean | 123.12 | 83.23 | 726.67 | 147.73 | 270.19 | |
| SD | 91.70 | 103.25 | 722.00 | 242.20 | 288.63 | |
| Total | 3077.94 | 2080.72 | 18,166.74 | 3693.28 | 6754.67 | |
| Pristine-modified equation | Min | 3.01 | 3.04 | 2.64 | 0.91 | 3.60 |
| Max | 125.26 | 121.65 | 112.84 | 174.14 | 133.48 | |
| Mean | 21.64 | 20.31 | 28.72 | 26.46 | 24.28 | |
| SD | 29.16 | 28.75 | 25.60 | 44.10 | 31.06 | |
| Total | 541.07 | 507.82 | 717.92 | 661.51 | 607.08 | |
| Disturbed-modified equation | Min | 1.96 | 2.06 | 1.53 | 0.64 | 2.34 |
| Max | 96.15 | 102.59 | 83.17 | 137.85 | 104.94 | |
| Mean | 15.78 | 16.56 | 20.53 | 20.09 | 18.24 | |
| Std. | 22.41 | 24.01 | 19.16 | 34.73 | 24.37 | |
| Total | 394.59 | 413.96 | 513.24 | 502.29 | 456.02 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Huang, L.; Deng, L.; Tong, C. Calculating the Sediment Flux in Hydrometric Data-Scarce Small Island Coastal Watersheds. J. Mar. Sci. Eng. 2025, 13, 2039. https://doi.org/10.3390/jmse13112039
Li G, Huang L, Deng L, Tong C. Calculating the Sediment Flux in Hydrometric Data-Scarce Small Island Coastal Watersheds. Journal of Marine Science and Engineering. 2025; 13(11):2039. https://doi.org/10.3390/jmse13112039
Chicago/Turabian StyleLi, Gaocong, Liping Huang, Longbo Deng, and Changliang Tong. 2025. "Calculating the Sediment Flux in Hydrometric Data-Scarce Small Island Coastal Watersheds" Journal of Marine Science and Engineering 13, no. 11: 2039. https://doi.org/10.3390/jmse13112039
APA StyleLi, G., Huang, L., Deng, L., & Tong, C. (2025). Calculating the Sediment Flux in Hydrometric Data-Scarce Small Island Coastal Watersheds. Journal of Marine Science and Engineering, 13(11), 2039. https://doi.org/10.3390/jmse13112039





