Experimental Study on Hydrodynamic Characteristics of Streamlined-Layout Double-Row Floating Breakwaters with Wing Plates

Abstract

Floating breakwater layouts require flexible adjustment to accommodate sheltered area bathymetry. However, most studies have focused solely on straight layouts and have neglected the influence of complex nearshore bathymetry and structures. This work investigates streamlined-layout double-row floating breakwaters with wing plates designed for a specific port. Wave attenuation performance, motion responses, mooring tensions, and surface wave pressures under realistic nearshore conditions are systematically evaluated through a water tank experiment. The results demonstrate that the wave attenuation performance improves as incident wave height and period decrease, with the attenuation rate increasing by 6.32~11.05%. However, both the motion responses and the uplift pressures on the head and tail modules change slightly. The maximum prototype-scale changes in the maximum amplitudes of surge, heave, and pitch are +0.0625 m, −0.488 m, and +3.8523°, respectively, and the uplift pressures on the head and tail modules exhibit maximum changes of +2.3 kPa and −5.6 kPa, respectively. Additionally, wave reflection induced by nearshore structures influences both harbor tranquility and breakwater motion response.

1. Introduction

Breakwaters are a critical component of coastal protection systems and are designed to attenuate wave energy, thereby ensuring safe and reliable operational environments for sheltered areas. Although fixed breakwaters demonstrate effective wave-attenuation performance, their construction difficulty and cost increase significantly with water depth. Moreover, natural water circulation is impeded, resulting in sediment accumulation and degradation of water quality. Over 90% of wave energy is concentrated within a depth of three times the wave height below the free surface. Compared with fixed breakwaters, floating breakwaters (FBs) are better adapted to the distribution of wave energy and offer advantages such as lower foundation bearing-capacity requirements, reduced construction cost, convenient installation and removal, and improved water circulation.

Attention has been paid to the box-type FB due to its simple geometric cross-section and stable operation in the ocean. Sutko [1] investigated the hydrodynamic performance of FBs with triangular, rectangular, and circular cross-sections. The rectangular FB had better wave attenuation performance. Drimer et al. [2] derived the analytical solution to the two-dimensional hydrodynamic problem of wave interaction with a box-type FB. Williams et al. [3] applied the 2-D potential theory to study the performance of two long FBs arranged side-by-side. Masoudi and Zeraatgar [4] used the method of separation of variables to analyze the hydrodynamic characteristics of a two-dimensional box-type FB in water of finite depth and infinite domain. Based on linear water-wave theory, Deng et al. [5] developed an analytical theory of the interaction of monochromatic waves with T-shaped FBs through the matched eigenfunction expansion method. For numerical research, Rahman et al. [6] applied the volume of fluid method to analyze the nonlinear dynamics of a box-type submerged FB subject to wave action and mooring forces. Peng et al. [7] studied the interaction of waves with a submerged box-type FB moored by inclined tension legs, using a water tank model proposed by Lee and Mizutani [8]. Ren et al. [9] developed the Smoothed Particle Hydrodynamics (SPH) method to simulate the nonlinear interaction between waves and a box-type FB. Based on the δ-SPH method, Guo et al. [10] compared the hydrodynamic performance of a box-type FB with taut, slack, and hybrid mooring systems under variable tidal ranges. Chen et al. [11] also employed the δ-SPH method to investigate the wave-attenuation performance and dynamic response of a twin FB consisting of two identical boxes with independently assembled mooring systems. He et al. [12] proposed a flexibly connected multi-float structure and demonstrated that a larger number of modules will contribute to more wave energy dissipation.

A physical experiment is a reliable method for studying the hydrodynamic characteristic of box-type FB. It can be categorized into two-dimensional wave flume and three-dimensional water tank experiments. Wave flume experiments are favored by numerous researchers due to the cost-effectiveness. Sannasiraj et al. [13] measured the motion responses and mooring forces of the FB with three mooring configurations: moored at water level; moored at the base bottom; and cross-moored at the base bottom. Huang et al. [14] compared the hydrodynamic performance of the box-type FB with and without slotted barriers. Christensen et al. [15] analyzed the damping mechanisms of three types of FBs: a pontoon, a pontoon with wing plates, and a pontoon with wing plates and porous media. They found that attaching wing plates to the FB significantly reduced the motion. Ji et al. [16] revealed that the double-row box-type FBs have better wave attenuation than the single-row ones. Liang et al. [17] compared the hydrodynamic characteristics of the box-type FB under fixed condition and three different mooring configurations. The cross mooring and parallel mooring configurations without section lying on the seabed are effective in reflecting and dissipating longer period waves. He et al. [18] investigated the hydrodynamic performance of a box-type FB with vertical plates as wave-dissipating components. The results showed that the water confined by plates increases the FB’s natural period of pitch motion towards longer waves, and thus the violent energy dissipation occurs at longer waves.

Water tank experiments are convenient for investigating the overall hydrodynamic characteristics of box-type FBs and the wave distribution. Martinelli et al. [19] compared the wave transmission loads along moorings and connectors of FBs with I-shaped and J-shaped layouts under oblique waves. Loukogeorgaki et al. [20] tested the FB consisting of an array of multiple modules that are connected with flexible connectors under perpendicular and oblique regular and irregular waves. Recently, Ji et al. [21] investigated the hydrodynamic performance of three interconnected modules, each of which was designed with wing structures and forward openings on both sides of a double-box FB. Mao et al. 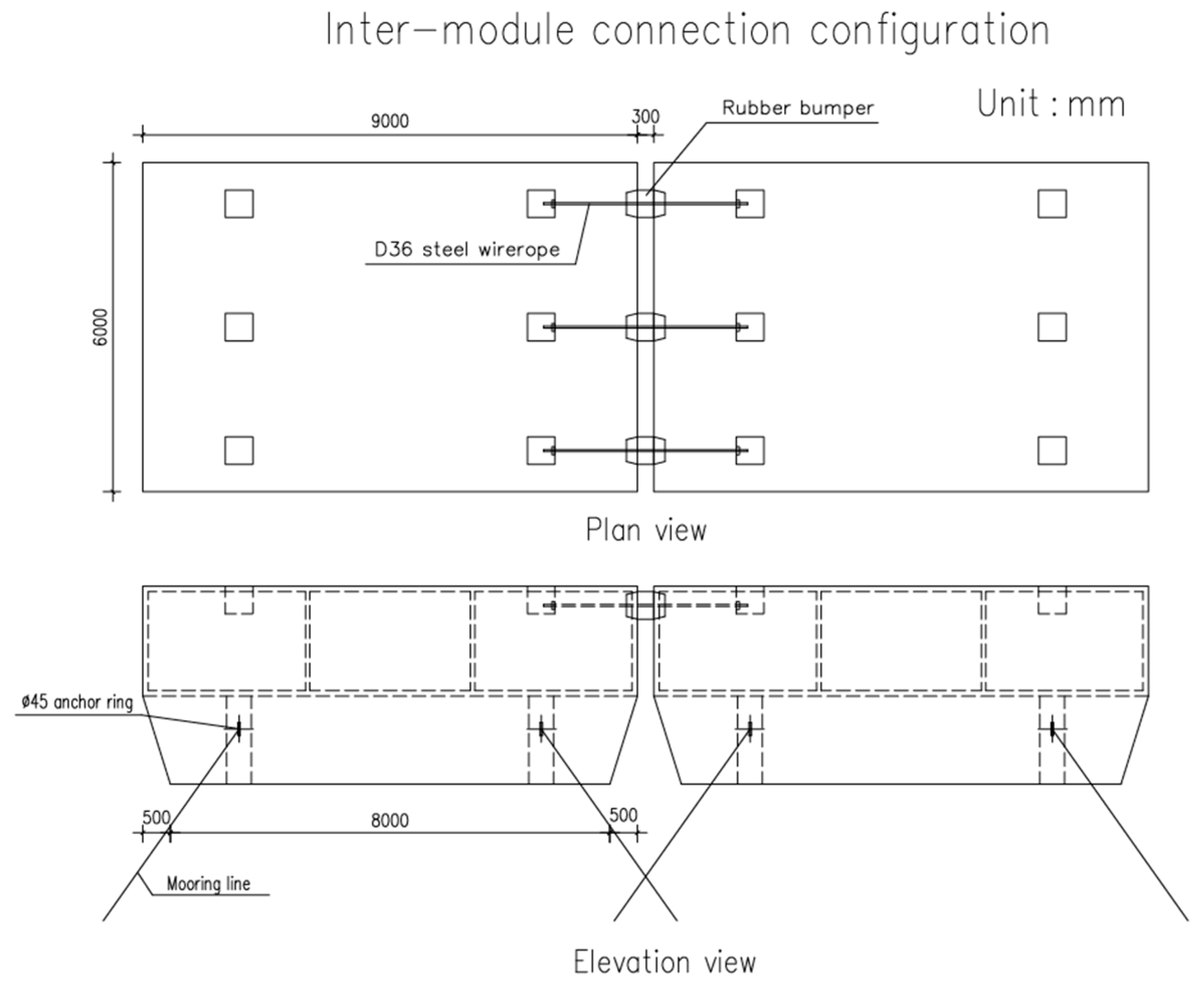[22] demonstrated that adding a wing plate can improve the wave attenuation performance of the FB, due to the increase in draft and wave-blocking area. The layout of FBs needs to be adapted to the protected area’s bathymetry. However, most studies focus only on straight layout without considering the influence of nearshore bathymetry and structures. In this work, a water tank experiment is conducted to investigate the wave attenuation performance, motion responses, mooring tensions, and surface wave pressures of streamlined-layout double-row FBs, designed for a Chinese port, under the realistic coastal environment. The examined FBs consist of winged box-type modules connected with flexible connectors.

The rest of this paper is organized as follows. Section 2 introduces the experimental setup, comprising the test facility and layout, physical model, and wave conditions. Section 3 presents the measurement results, including wave attenuation performance, motion responses, mooring tensions, and surface wave pressures of the FBs. Section 4 summarizes the main conclusions.

2. Experimental Setup

2.1. Test Facility

The experiment was conducted in the wave–current coupling tank at the Shandong Province Key Laboratory of Ocean Engineering, Ocean University of China. The tank is 60 m long, 36 m wide, and 1.5~6 m deep. It is equipped with a servo motor-driven, piston-type wavemaker at the upstream end, capable of generating both regular and irregular waves, and wave absorbers along the remaining walls, ensuring the wave reflection coefficient below 5%. The wave elevation was measured by BG08-60 capacitance-type wave gauges and a 64-channel BG2008 data acquisition system (Tianjin Research Institute for Water Transport Engineering, M.O.T., Tianjin, China). The FBs’ motion responses were recorded using a NOKOV optical 3D motion capture system (Beijing Nokov Science & Technology Co., Ltd., Beijing, China) with sub-millimeter positioning accuracy. The gravity center and the inertia moment of the FB model were calibrated by an inertia calibration rig. Mooring tensions were measured by 3 kg load cells and an 8-channel PL2-DCB2 data acquisition instrument (imc Test & Measurement GmbH, Berlin, Germany). Wave pressures on the FBs were recorded using 12 mm pressure sensors and 64-channel and 32-channel TKS-7 data acquisition systems (Tianjin Research Institute for Water Transport Engineering, M.O.T., Tianjin, China).

2.2. Physical Models and Wave Conditions

As Figure 1 illustrates, the double-row FBs designed for a Chinese port features a streamlined layout. The offshore breakwater is 150 m in length, while the nearshore one is 124 m, both with a 6 m width and separated by 30 m. The FBs comprise five types of modules (M1~M5), each featuring a box-type main structure with bottom-mounted wing plates and moored by four taut lines. Module dimensions and inter-module connection configuration are presented in Figure 2, and module weights and center-of-gravity positions are provided in

Table 1. Engineering parameters of floating-breakwater modules.

Module	Weight (kN)	Draught (m)	Gravity Center Position (m)
			X	Y	Z
1	458.43	0.893	2.776	4.501	0.757
2	933.7	1.447	3.129	4.551	1.876
3	865.4	1.337	3.124	4.394	1.899
4	888.49	1.339	3	4.5	1.911
5	1113.54	1.237	3	6.2	1.966

.

A geometric scale λ of 1:18 was chosen based on the dimensions of the water tank and the FB prototypes, and the range of available wave parameters. Consequently, the water depth d and wave height of the prototype were scaled by λ, wave period by $\sqrt{\lambda }$, as well as mass and force by λ³. Figure 3 shows the front view and top view of the FB models, which were assembled from modules M1~M5 according to the configuration in Figure 1. The models maintain similarity with the prototype in terms of geometry, weight, center of gravity, and moment of inertia. As illustrated in Figure 4, the upper segment of the mooring line model is a 0.404 m long stainless-steel chain with a linear density of 85.456 g/m, and a tensile stiffness of 4.57 × 104 N/m. The lower segment is an elastic cable weighing 0.0326 kg with a maximum load of 12.61 N. To achieve nonlinear tensile behavior, the cable was fabricated by combining two elastic components with different stiffnesses using a piecewise linear fitting method. Specifically, a 278 mm rubber band with a stiffness of 30.591 N/m and a 414 mm spring with a stiffness of 209.001 N/m were used.

Figure 5 shows the experimental layout of bathymetry and structures. Initially, the tank was divided into a 1 m × 1 m grid to position the bathymetry and structures. The experimental bathymetry was then established by filling and leveling the tank bottom to a uniform elevation of −0.167 m, followed by excavation of a trench for the floating breakwaters to −0.228 m. For localized areas with significant bathymetry undulations, control point heights were measured using leveling instruments through cross-sectional profiling, ensuring height errors remained within 1 mm. To simulate the realistic coastal environment of the port, the steep slope depicted in Figure 6 was constructed on the western and northern sides of the tank. Additionally, two pile-supported ferry terminals were constructed on the eastern side at crest elevations of 0.311 m and 0.333 m, respectively.

Given the difficulty of determining several parameters required by the original JONSWAP spectrum, the enhanced JONSWAP spectrum [23] was employed to generate unidirectional irregular waves:

$$S(f)=\beta H_s^2{T}_p^{-4}{f}^{-5}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{5}{4}}{(T_{p}f)}^{-4}\right]\cdot {\gamma }^{\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left({\displaystyle \frac{f}{f_p}}-1\right)}^2/\left(2{\sigma }^2\right)\right]},$$

(1)

where S(f) is the wave spectral density; H_s is the significant wave height; f and f_p denote the frequency and spectral peak frequency, respectively; γ = 3.3 represents the spectral peak elevation factor; β is calculated as

$$\beta ={\displaystyle \frac{0.06238(1.094-0.0195\mathrm{l}\mathrm{n}\gamma )}{0.23+0.0336\gamma -0.185{(1.9+\gamma )}^{-1}}};$$

(2)

T_p symbolizes the spectral peak period, defined by

$$T_p={\displaystyle \frac{T_s}{1-0.132{(\gamma +0.2)}^{-0.559}}},$$

(3)

with T_s standing for the significant wave period; and σ signifies the peak shape parameter, given by

$$\sigma =\left\{\begin{array}{ll}0.07,\hfill & f\le f_p;\hfill \\ 0.09,\hfill & f>f_p.\hfill \end{array}\right.$$

(4)

Table 2. Experimental wave parameters.

No.		Experiment		Prototype
	d (m)	H1% (m)	Ts (s)	d (m)	H1% (m)	Ts (s)
1	0.4483	0.1367	1.3199	8.07	2.46	5.6
2		0.1489	1.3671		2.68	5.8

presents the experimental wave parameters, which were designed based on the actual wave conditions at the specific port. H_1% represents the mean height of the highest 1% of waves identified through zero-crossing analysis and is approximately equal to 1.67H_s [24]. No. 1 and No. 2 correspond to extreme high-water-level conditions with return periods of 10 years and 50 years, respectively. Their wave spectral densities are illustrated in Figure 7. For each wave condition, a minimum of 1000 irregular waves were generated.

2.3. Test Layout

As shown in Figure 5, the offshore FB was arranged in a streamlined layout and positioned 20 m from the wavemaker. The nearshore FB was arranged in a straight layout and located 1.67 m downstream of the offshore one. Thirty-four wave gauges G1~G34 were placed in the sheltered area to monitor spatial variations in wave height. To capture the FBs’ motion responses, 1# and 17# modules, expected to experience the greatest displacement, were tracked. Their plan-view positions are illustrated in Figure 1. Load cells were installed on all eight mooring lines to record tensile loads. Mooring lines were numbered according to their fairlead orientations: 1 o’clock as Line 1, 5 o’clock as Line 2, 7 o’clock as Line 3, and 11 o’clock as Line 4. To measure the wave pressures on the FBs, multiple sensors were installed on 1# and 17# modules, as shown in Figure 8.

Prior to the trench excavation, wave parameters were calibrated by comparing the mean H_1% measured at G1 and G2 with target values.

Table 3. Wave height calibration results.

No.	H1% (m)				Relative Error
	Target Value	G1	G2	Mean Value
1	0.137	0.133	0.135	0.134	1.8%
2	0.149	0.149	0.152	0.151	1.1%

presents the relative errors between the measured and target results, all within 3%. To ensure data reliability, each wave condition was replicated three times, taking the mean of three consistent measurements as the experimental result.

3. Measurement Results

3.1. Wave Attenuation Performance

The measured H_1% at G1~G34 under No. 1 and No. 2 conditions are given in

Table 4. H_1% measured by wave gauges under No. 1 condition.

Wave-Gauge Number	Experimental Result (m)	Prototype-Scale Result (m)	Wave-Gauge Number	Experimental Result (m)	Prototype-Scale Result (m)
G1	0.1356	2.44	G18	0.1411	2.54
G2	0.1367	2.46	G19	0.1417	2.55
G3	0.1656	2.98	G20	0.1406	2.53
G4	0.1733	3.12	G21	0.1283	2.31
G5	0.1600	2.88	G22	0.1250	2.25
G6	0.1789	3.22	G23	0.1217	2.19
G7	0.1406	2.53	G24	0.1394	2.51
G8	0.1544	2.78	G25	0.1183	2.13
G9	0.1739	3.13	G26	0.1067	1.92
G10	0.1600	2.88	G27	0.1078	1.94
G11	0.1494	2.69	G28	0.0983	1.77
G12	0.1183	2.13	G29	0.0972	1.75
G13	0.1450	2.61	G30	0.1000	1.80
G14	0.1456	2.62	G31	0.1061	1.91
G15	0.1461	2.63	G32	0.1044	1.88
G16	0.1433	2.58	G33	0.1033	1.86
G17	0.1433	2.58	G34	0.0956	1.72

and

Table 5. H_1% measured by wave gauges under No. 2 condition.

Wave-Gauge Number	Experimental Result (m)	Prototype-Scale Result (m)	Wave-Gauge Number	Experimental Result (m)	Prototype-Scale Result (m)
G1	0.1489	2.68	G18	0.1483	2.67
G2	0.1483	2.67	G19	0.1439	2.59
G3	0.1711	3.08	G20	0.1439	2.59
G4	0.1844	3.32	G21	0.1372	2.47
G5	0.1794	3.23	G22	0.1439	2.59
G6	0.1839	3.31	G23	0.1422	2.56
G7	0.1583	2.85	G24	0.1650	2.97
G8	0.1689	3.04	G25	0.1217	2.19
G9	0.1750	3.15	G26	0.1094	1.97
G10	0.1606	2.89	G27	0.1250	2.25
G11	0.1494	2.69	G28	0.1044	1.88
G12	0.1406	2.53	G29	0.1028	1.85
G13	0.1433	2.58	G30	0.1033	1.86
G14	0.1972	3.55	G31	0.1222	2.20
G15	0.1606	2.89	G32	0.1239	2.23
G16	0.1450	2.61	G33	0.1250	2.25
G17	0.1506	2.71	G34	0.1206	2.17

, respectively. Under No. 1 condition, the prototype-scale H_1% at G31~G34 ranges from 1.72 m~1.91 m, corresponding to wave-height attenuation of 22.36~30.08%. Under No. 2 condition, the prototype-scale H_1% at G31~G34 ranges from 2.17 m~2.25 m, corresponding to wave-height attenuation of 16.04~19.03%. To quantitatively assess the FBs’ wave attenuation performance, the transmission coefficient is calculated:

$$K_t=H_t/H_i,$$

(5)

where H_t denotes the transmitted wave height, calculated as the mean H_1% at G32 and G33, which are located one wavelength behind the double-row FBs; H_i represents the incident wave height, taken as the mean H_1% at G6~G8. The resulting K_t values are 0.6577 and 0.7304 under No. 1 and No. 2 conditions, respectively. Comparison of H_1% values at G25~G34 reveals that G31~G34, located near the shoreline, are significantly affected by reflected waves. Moreover, as the incident wave height and period increase, wave reflection from the rear structures intensifies. Thus, H_1% values at G31~G34 are higher than those at G25~G30 under No. 2 condition.

3.2. Motion Response

Figure 9 and Figure 10 present the time histories of prototype-scale motion responses of 1# and 17# modules under No. 1 and No. 2 conditions. The corresponding maximum response amplitudes of the two modules are shown in

Table 6. Maximum amplitudes of prototype-scale motion responses of 1# and 17# modules under No. 1 condition.

Motion Type	Module Number	Maximum Negative Response	Maximum Positive Response
Surge (m)	1	−0.6222	0.8746
	17	−0.8008	0.6186
Heave (m)	1	−0.8755	0.8952
	17	−1.2576	1.1935
Pitch (°)	1	−9.2534	11.1246
	17	−10.8499	10.2674

and

Table 7. Maximum amplitudes of prototype-scale motion responses of 1# and 17# modules under No. 2 condition.

Motion Type	Module Number	Maximum Negative Response	Maximum Positive Response
Surge (m)	1	−0.6630	0.8929
	17	−0.8082	0.6811
Heave (m)	1	−0.9393	0.8252
	17	−1.7456	1.2333
Pitch (°)	1	−10.5101	9.6666
	17	−10.8437	14.1197

. As wave height and period increase, the maximum amplitudes of the FBs’ motion responses change slightly. The maximum prototype-scale changes in surge, heave, and pitch amplitudes are +0.0625 m, −0.488 m, and +3.8523°, respectively. A comparison of the surge motions reveals that the overall response and the positive-direction amplitude of the 1# module are greater, while 17# module exhibits a larger negative-direction amplitude. This is because 17# module, sheltered by other modules, experiences reduced incident wave forces. However, 17# module approaches the steep slope and is thus significantly affected by reflected wave forces. For heave motion, 17# module exhibits greater overall responses and motion amplitudes in both positive and negative directions. For pitch motion, 1# and 17# modules show comparable responses, but the latter is more sensitive to wave parameter variations.

3.3. Mooring Tension

Figure 11 plots the maximum prototype-scale tensions T_max in each line under No. 1 and No. 2 conditions. It is observed that the tensions in the mooring lines of 1# module generally exceed those of 17# module with the greatest T_max occurring in 1-2# line. Moreover, the tensions in the mooring lines of 1# module are more sensitive to wave parameter variations. This is attributed to 1# module’s seaward position and its first exposure to incident waves.

3.4. Wave Pressure

Figure 12 and Figure 13 show the maximum prototype-scale wave pressures on 1# and 17# modules under No. 1 and No. 2 conditions. The horizontal pressure on the seaward face exceeds that on the leeward face. The 17# module experiences larger horizontal pressure under No. 1 condition, whereas 1# module is subjected to the greater pressure under No. 2 condition. Although the wave overtopping-induced downward pressures on the top surfaces of both modules are nearly identical, the uplift pressure on the bottom surface of 17# module significantly exceeds that of 1# module. Additionally, the uplift pressures on the two modules remain relatively constant as wave height and period increase, with the maximum prototype-scale changes being +2.3 kPa and −5.6 kPa, respectively. However, 1# module experiences increased horizontal pressure and reduced downward pressure, whereas 17# module shows the opposite trend.

4. Conclusions

This work investigated streamlined-layout double-row FBs with wing plates designed for a specific port. Wave attenuation performance, motion responses, mooring tensions, and surface wave pressures were systematically evaluated through a water tank experiment. The main conclusions are as follows.

Under extreme high-water-level conditions with 10-year and 50-year return periods, the FBs achieve wave-height attenuation of 22.36~30.08% and 16.04~19.03%, respectively, with the transmission coefficients of 0.6577 and 0.7304. Wave reflection from nearshore structures affects harbor tranquility and intensifies significantly with increasing incident wave height and period. Therefore, coastal FB design needs to account for the effects of realistic bathymetry and structures.

As wave height and period increase, the maximum amplitudes of the FBs’ motion responses change slightly. The maximum prototype-scale changes in surge, heave, and pitch amplitudes are +0.0625 m, −0.488 m, and +3.8523°, respectively. For surge motion, the overall response and the positive-direction amplitude of the head module are greater, while the tail module exhibits a larger negative-direction amplitude. For heave motion, the tail module demonstrates greater overall responses and motion amplitudes in both positive and negative directions. For pitch motion, the head and tail modules show comparable responses, but the latter is more sensitive to wave parameter variations.

The tensions in the mooring lines of the head module generally exceed those of the tail module and are more sensitive to wave parameter variations. The horizontal wave pressure on the seaward face of the FBs exceeds that on the leeward face. Although the downward pressures on the top surfaces of the head and tail modules are nearly identical, the uplift pressure on the tail module is greater. Additionally, the uplift pressures on the two modules remain relatively constant as wave height and period increase, with the maximum prototype-scale changes being +2.3 kPa and −5.6 kPa, respectively. However, the head module experiences increased horizontal pressure and reduced downward pressure, whereas the tail module shows the opposite trend. In the future, further experiments will be conducted to investigate the relative motion between the offshore and nearshore breakwaters, the causes of the extreme values of wave heights, motion responses and mooring tensions, and the risks associated with mooring line failure.