The Effect of Wind–Wave Correlations on the Optimal Thruster Location for Offshore Vessels

Abstract

Offshore vessels are nowadays equipped with dynamic positioning systems, meaning they have additional thrusters dedicated to the station keeping of the unit. However, there is no rational criterion on the placement of these devices to increment station keeping capabilities. This is true both in case of a vessel retrofitting or for the design of a new unit. The present work proposes investigating a methodology for the optimal placement of thrusters along the hull of an offshore unit. This implies the adoption of a suitable optimisation algorithm capable of handling all the constraints of the optimisation problem. As the target is the optimal capability, the optimisation should handle multiple dynamic positioning capability calculations, meaning (in a quasi-static approach) that it is capable of solving multiple thrust allocation problems at each optimisation step. As thruster allocation is another optimisation problem, the process should handle two nested optimisations. Here, the global location problem is solved with a differential evolution algorithm, while the thrust allocation employs non-linear programming. As the capability calculations imply the adoption of a specific wind–wave correlation, the present work compares the effect of different correlations on the optimised location of the thrusters. The results presented on a reference Pipe Lay Crane Vessel highlight the differences in the final optimum as a function of the environmental modelling.

1. Introduction

The locations of the thrusters in a dynamic positioning (DP) System are often influenced by specific challenges related to the internal layout of the offshore vessel where the system is to be installed. The overall arrangement is designed to optimise the internal spaces required for the vessel’s primary operations [1], such as the drilling area on a drillship or the pipe launching line on a Pipe Lay Vessel (PLV). For converted ships, the issue of thruster placement is of secondary importance. When investigating the conversion of an existing vessel, thruster locations are drawn from the available free space created by the installation of new equipment, which often results in asymmetrical configurations [2]. Another issue is related to the size of the steerable devices [3]. Due to regulations set by the Classification Society, obtaining a specific class notation for multiple failure scenarios [4,5] necessitates the installation of more power than that required for normal vessel operations.

During the preliminary design phase of a new offshore vessel, once the final configuration of the thrusters is roughly established, it is helpful to conduct dedicated DP calculations to evaluate the current system capabilities [6,7,8,9]. Typically, the results are represented in DP capability plots [10], which illustrate the maximum sustainable wind speed for various encounter directions [11,12]. This analysis allows us to assess the true environmental limits for operations, taking into account the DP system’s capabilities [13]. It can highlight whether the power installed on board is adequate or excessive.

Since the number of devices installed on board cannot be reduced due to redundancy requirements, a focused study can be performed to enhance the overall efficiency of the DP system. In this context, a complete time-domain simulation is not recommended due to its inherent complexity. Instead, a quasi-static approach can provide a sufficiently accurate estimate of the system’s capabilities during the preliminary design stage, while also requiring a relatively short calculation time.

Currently, it is quite challenging to establish an analytical formulation for DP capability as a function of the thruster’s position and rated power. To address this, the area of the capability plot has been utilized to compare different design solutions, with larger areas indicating better performance. Designers may also choose alternative targets based on their experience, such as identifying the lowest maximum sustainable wind speed for all calculated directions.

In this case, to maximize the area of the capability plot, an optimization procedure using Differential Evolution Algorithm (DEA) has been employed [14,15]. For each generated thruster configuration, a comprehensive DP calculation has been performed to determine the final area of the capability plot, allowing for an assessment of the vessel’s overall DP capability [16].

It is well known that the shape and area of the capability plot are significantly affected by the thrust allocation algorithm used in the calculations [17]. Additionally, the calculation complexity of the most advanced methods [18] is not easily compatible with the DEA-based optimisation procedure chosen for thruster positioning. Therefore, a simpler but still optimisation-based process should be employed for solving the thrust allocation process. More specifically, a methodology based on non-linear programming [19,20] has been employed [21], capable of including features like thruster–thruster interaction [18] in the optimisation process. Such an approach is more powerful than the original optimisation process, based on simplified DP capability predictions.

Another DP calculation setting strongly influences the shape of the capability plot. This is the case of the wind–wave correlation employed for the calculations [22]. The literature provides several kinds of standard correlations [10,23,24]; however, it is also possible to use correlations specific to a given sea area [22,25].

The present study aims at addressing this second issue, analysing the impact of the selected wind-wave correlations to the optimal thruster location problem. This implies the adoption of a suitable optimisation algorithm capable of handling all the constraints of the optimisation problem. As the target is the optimal capability, the optimisation should handle multiple dynamic positioning capability calculations, meaning (in a quasi-static approach) capable of solving multiple thrust allocation problems at each optimisation step. To achieve this, the paper is organised with the following structure:

-

Section 2 provides an overview of the methods employed for DP capability predictions.

-

Section 3 reports the calculation framework for optimal thruster location.

-

Section 4 presents the reference vessel and the wind–wave correlations considered in the study.

-

Section 5 shows the results of the framework application to the reference case.

The available literature provides only one study concerning the optimal location of the thruster devices, employing a simplified methodology for the execution of DP predictions. The present work proposes enhancing the available method for thruster location optimisation by modifying the thrust allocation process of DP predictions, transitioning from a simplified method based on the pseudo-inverse matrix to an advanced algorithm employing non-linear programming. With the aid of an applied example on a reference Pipe Lane Crane Vessel (PLCV), the paper provides a comparison of the locations obtained by applying different standard and custom wind–wave correlations to define the optimal layout of the reference PLCV. This will help to verify the possible effect of different wind–wave correlations in the definition of the optimal position of thrusters on an offshore unit.

2. Dynamic Positioning Capability Predictions

The prediction of the performances of a DP system can be performed according to different methodologies, accounting for the amount of information available at different stages of the offshore unit design [26]. The available models have an increased level of complexity with the progression of the unit design; therefore, a designer could analyse DP with different tools as a function of the input data available [27].

In any case, the following are the two most relevant categories of DP predictions: quasi-static calculations [22,28] and time-domain analyses [27,29]. Time-domain analyses can also be performed with different levels of approximations, starting from simplified analyses for preliminary design phases [26,27,29] up to the complete simulation of the effective DP system mounted onboard [30]. However, even for simplified approaches, a lot of inputs are needed for the evaluation of the vessel dynamics. Such information is not always available during the early stages of design, where only few inputs concerning the main dimension and thruster sizes are present. Then, for the early stages of design, the quasi-static approach is preferable, allowing for DP performance estimation with just a few inputs.

The quasi-static approach consists in the resolution of the equilibrium of the forces and moments acting on the vessel in the horizontal plain [31]. According to the reference system of Figure 1, the equilibrium can be written in the following form:

$$\left\{\begin{array}{cc}{\sum }_{i=1}^{N_T}{F}_{x{T}_i}\hfill & =F_{x_{ext}}\hfill \\ {\sum }_{i=1}^{N_T}{F}_{y{T}_i}\hfill & =F_{y_{ext}}\hfill \\ {\sum }_{i-1}^{N_T}\left(-F_{x{T}_i}{y}_{T_i}+F_{y{T}_i}{x}_{T_i}\right)\hfill & =M_{z_{ext}}\hfill \end{array}\right.$$

(1)

where $F_{x{T}_i}$ and $F_{y{T}_i}$ are the longitudinal and later force components generated by the $N_T$ thrusters, while $x_{T_i}$ and $y_{T_i}$ are the longitudinal and lateral positions of the thruster devices, respectively. The right-hand side of system (1) indicates the external forces and moments acting on the vessel. These forces can be divided as follows:

$$\left\{\begin{array}{cc}{F}_{x_{ext}}\hfill & =F_{x_{wind}}+F_{y_{wave}}+F_{x_{curr}}+F_{x_A}+F_{x_{Add}}\hfill \\ F_{y_{ext}}\hfill & =F_{y_{wind}}+F_{y_{wave}}+F_{y_{curr}}+F_{y_A}+F_{y_{Add}}\hfill \\ M_{z_{ext}}\hfill & =M_{z_{wind}}+M_{z_{wave}}+M_{z_{curr}}+M_{z_A}+M_{z_{Add}}\hfill \end{array}\right.$$

(2)

where the subscripts _wind, _wave and _curr indicate wind, wave and current loads, respectively. These are the so-called environmental loads and are responsible for the major part of the external loads. The environmental loads are increased by an additional allowance component (identified by subscript _A) that takes into account the dynamic allowances [10,24]. Finally, the terms with subscript _Add in system (2) describe the additional loads due to the specific operation of the vessel, and can model, as an example, the pipe tension for a PLCV vessel, the drilling rig forces for a drillship or the presence of mooring lines.

System (1) has $N=N_{TT}+2N_{AT}$ unknowns and rank 3, with $N_{TT}$ being the number of tunnel thrusters and $N_{AT}$ the number of azimuth thruster devices. Therefore, except for an unrealistic case of one tunnel and one azimuth unit mounted onboard, the system admits infinite solutions (more unknowns than equations). This means that there is a need to solve the system with a dedicated thrust allocation algorithm, usually based on optimisation processes [21]. The following sections describe the method employed in this study to solve the thrust allocation process, also discussing the modelling of the external loads, i.e., the environmental one.

2.1. Thrust Allocation Algorithm

As mentioned above, system (1) admits infinite possible solutions and needs proper techniques to be solved. In this section, the algorithm employed for the thrust allocation problem resolution is briefly presented.

In general, there are simple and more sophisticated methodologies to solve the thrust allocation problem. Here, an advanced methodology is selected, based on non-linear programming techniques. The method has been chosen for solving the thrust allocation problem as it gives the right compromise between the quality of the results and the simplicity of implementation [21]. Having in mind to apply the process inside a DEA optimisation, the non-linear programming well adapts to the incorporation in a step of DEA optimisation, without requiring too much computational time. This is a step forward compared to the original optimal location solution, which was employing a pseudo-inverse matrix approach to solve the thrust allocation problem [16].

For the specific case of DP, it is relevant to have the possibility to describe the problem with non-linear functions, as, for example, the definition of the thrust constraints is a circle. Then, to avoid linearisation, it will be possible to describe these constraints with a single non-linear function. The non-linear optimisation has the following form:

$$minz=f\left(x\right)$$

(3)

subject to

$$l\le \left(\begin{array}{c}{x}_i\\ c\left(x_i\right)\end{array}\right)\le u$$

(4)

where $f\left(x\right)$ is the objective function of n variables $x_i$ and $c\left(x_i\right)$ is a vector of m constraint functions. The sole requirement for the objective function and constraints is that the functions should be continuous and differentiable at points that satisfy the bounds l and u for the given $x_i$, thus allowing the evaluation of the gradient vector $g\left(x\right)=\nabla f\left(x\right)$ and the Jacobian matrix $J\left(x\right)=\nabla c\left(x\right)$.

According to this process, the objective function can be non-linear. This allows us to consider a non-quadratic objective function, which reflects the modelling of absorbed power as a function of thrust. The function has the following form:

$$f\left(x\right)=\sum _{i=1}^{N_T}{x}_i^{{\displaystyle \frac{3}{2}}}$$

(5)

where $x_i$ is the thrust of each single device. More specifically, the optimisation resolution is adopting an extended version of the Robinson method, based on filtering and employing a trust region obtained by adopting Ritz values [32].

Adopting this kind of resolution, it is possible to adopt two different strategies for the problem definition. In fact, it is possible to write the objective function and constraints considering the thrust directly or its longitudinal and lateral components. In the first case, each thruster is defined by the thrust and the orientation; in the latter, the components are sufficient. Once the thrust and orientation are selected for describing the problem, it is possible to automatically consider the interactions between thrusters by setting the bounds on the orientations. The remaining constraints are presented by the satisfaction of the static equilibrium, meaning the satisfaction of system (1). This generates three additional equality constraints for the optimisation problem.

The thrust allocation algorithm employed in this paper has been tested and compared with other tools available on the market for DP predictions [33,34], proving the reliability of the code used for the calculations.

2.2. Environmental Loads

The principal loads acting on an offshore vessel are given by wind, waves and current. As mentioned above, it is important to estimate the magnitude of such loads by employing the most accurate method according to the available inputs [35]. There are several methodologies that allow for estimating environmental loads, starting from simple processes provided by Operator Associations and Classification Societies, up to the execution of model test experiments [33]. The self-developed code employed for the analysis is capable of handling environmental loads coming from different sources, employing the following formulations for wind, wave and current loads. For the wind, the general description of the forces and moments is as follows:

$$\left\{\begin{array}{cc}{F}_{x_{wind}}\hfill & ={\displaystyle \frac{1}{2}}{\rho }_a{C}_{x_{wind}}{A}_T{V}_w^2\hfill \\ F_{y_{wind}}\hfill & ={\displaystyle \frac{1}{2}}{\rho }_a{C}_{y_{wind}}{A}_L{V}_w^2\hfill \\ M_{z_{wind}}\hfill & ={\displaystyle \frac{1}{2}}{\rho }_a{C}_{z_{wind}}{A}_{L}L{V}_w^2\hfill \end{array}\right.$$

(6)

where ${\rho }_a$ is the air density, $A_L$ and $A_T$ are the lateral and transversal areas exposed to wind, L is the length between perpendiculars and $V_w$ is the wind speed. By employing this notation, it is possible to use the coefficients derived from different sources, like databases, similar vessels, regulations, CFD analyses or wind tunnel tests.

For the current loads, the process is similar to wind loads, adopting the following notation:

$$\left\{\begin{array}{cc}{F}_{x_{curr}}\hfill & ={\displaystyle \frac{1}{2}}\rho C_{x_{curr}}S{V}_c^2\hfill \\ F_{y_{curr}}\hfill & ={\displaystyle \frac{1}{2}}\rho C_{y_{curr}}S{V}_c^2\hfill \\ M_{z_{curr}}\hfill & ={\displaystyle \frac{1}{2}}\rho C_{z_{curr}}S{V}_c^2\hfill \end{array}\right.$$

(7)

where $\rho$ is the salt water density, S is the ship wetted surface at the reference draught and $V_c$ is the current speed. Also in this case, the coefficients can be determined with different kinds of calculations, from simple regulation indications to high-fidelity model tests.

A quite different approach should be followed for the wave load modelling. Wave loads are given by the second-order wave drift forces that may be computed by diffraction calculations or measured during model tests. Having such data, the following system can be used to calculate the wave loads:

$$\left\{\begin{array}{cc}{F}_{x_{wave}}\hfill & =\rho g{\nabla }^{{\displaystyle \frac{1}{3}}}{\int }_0^{+\infty }{C}_{x_{wave}}\left(\chi ,\omega \right)S_{\zeta }\left(\omega \right)\mathrm{d}\omega \hfill \\ F_{y_{wave}}\hfill & =\rho g{\nabla }^{{\displaystyle \frac{1}{3}}}{\int }_0^{+\infty }{C}_{y_{wave}}\left(\chi ,\omega \right)S_{\zeta }\left(\omega \right)\mathrm{d}\omega \hfill \\ M_{z_{wave}}\hfill & =\rho g{\nabla }^{{\displaystyle \frac{2}{3}}}{\int }_0^{+\infty }{C}_{z_{wave}}\left(\chi ,\omega \right)S_{\zeta }\left(\omega \right)\mathrm{d}\omega \hfill \end{array}\right.$$

(8)

where $C_i\left(\chi ,\omega \right)$ are the second-order wave drift force coefficients resulting from model tests or calculations, obtained as a function of frequency $\omega$ and encounter angle $\chi$. ∇ is the vessel displacement volume, g is the gravity acceleration and $S_{\zeta }\left(\omega \right)$ is the reference wave amplitude spectrum. As the spectrum $S_{\zeta }$, according to the multiple formulations available in the literature, is changing according to the significant wave height $H_s$ and the zero-crossing wave period $T_z$, it is possible to represent all the sea states by changing the couple ($H_s$, $T_z$). In case a more simple representation of the drift forces is selected, Equation (8) can be substituted by a direct formulation of forces and moments as a function of $H_s$ and $T_z$ (as in the case of DNV recommendations [24]).

All the environmental load coefficients should be obtained in order to be compliant with the reference system of Figure 1. In the present study, use has been made of environmental force coefficients derived from model experiments, allowing a direct application of Equations (6)–(8). According to the indications for capability plot calculations, a wind–wave correlation should be employed for determining the combinations of $V_w$, $H_s$ and $T_z$ to be employed in the calculations. Furthermore, from the environmental loads, the allowance forces could be determined in the following way:

$$\left\{\begin{array}{c}{F}_{x_A}=\left(1-C_{A_{dyn}}\right)\left(F_{x_{wind}}+F_{x_{wave}}+F_{x_{curr}}\right)\hfill \\ F_{y_A}=\left(1-C_{A_{dyn}}\right)\left(F_{y_{wind}}+F_{y_{wave}}+F_{y_{curr}}\right)\hfill \\ M_{z_A}=\left(1-C_{A_{dyn}}\right)\left(M_{z_{wind}}+M_{z_{wave}}+M_{z_{curr}}\right)\hfill \end{array}\right.$$

(9)

where $C_{A_{dyn}}$ is the allowance coefficient defined by empirical recommendations. Here, a $C_{A_{dyn}}=1.25$ has been used, as suggested by DNV guidelines [24]. A more detailed overview of the wind–wave correlations will be given in Section 4.

3. Optimal Thruster Location

Traditionally, during the design process of an offshore vessel, the DP system does not represent one of the primary constraints for the general arrangements. The thruster locations derive from the available spaces remaining after the disposal of all the devices and spaces needed for the offshore activities of the unit. Therefore, the DP system is not designed in such a way to have the maximum capability for the vessel. Such a consideration remains valid also in the case of the conversion of an old unit [1,2].

With the ongoing focus on reducing fuel consumption and emissions during operations, improving DP efficiency has become increasingly important in the design of offshore vessels. This is especially relevant when considering the specific operational profile of the unit. Finding the optimal location for thrusters involves conducting an optimization process where the variables are the positions of the thrusters along the hull’s bottom. However, it is challenging to define an objective function for these optimal locations that explicitly includes the thruster positions. In reality, the locations of the thrusters only appear in the constraints of the thrust allocation problem associated with DP. As a result, conventional gradient-based optimisation methods cannot be applied. Instead, alternative approaches such as genetic algorithms, differential evolution algorithms, or particle swarm optimisation should be considered.

The issue of determining the optimal placement of thrusters along the bottom of an offshore vessel has not been thoroughly analyzed in the existing literature. The only research available on this topic was conducted several years ago by one of the authors, who utilized a simplified algorithm for thrust allocation and selected DP capability as the objective function for the process [16]. Furthermore, the study took into account only one wind–wave correlation, derived from IMCA recommendations [10]. As mentioned, the study used a thrust allocation algorithm based on the pseudo-inverse matrix in order to calculate the thrust components extremely quickly and not direct involve an optimisation process [36].

However, the pseudo-inverse algorithm is not the best solution to investigate the capability of a DP system, as, for example, it is not capable of handling the interactions of the thrusters and is not capable of fully saturating all the available thrust [17]. To this end, the application of a resolution algorithm like non-linear programming, as described in the previous section, is a step forward in improving the process already developed in the past.

The following sections describe the objective function of the thruster location optimisation problem and the calculation framework employed to evaluate the optimal solution.

3.1. Objective Function

The objective function of the process should be related to the DP performances of the vessel. In the literature, there are two available methods to assess the performances of a DP system in an early design stage: the capability [10] and the operability [34]. In the present study, this has been selected to consider the capability as a metric for DP performances as it is the most common method used by DP operators.

The capability is the conventional way employed in the offshore industry to assess the performances of the DP system in all the stages of the design process of an offshore unit. The methodology is described by API regulations [10] and the main output of the analysis is the DP capability plot, showing at each encounter angle the maximum wind speed the DP system can counteract without losing the position. This approach can be used to perform both quasi-static and time-domain calculations. An example of a capability plot is shown in Figure 2. To determine the maximum wind speed, multiple DP calculations are conducted at each encounter angle, gradually increasing the wind speed until the limit is reached. During this process, both the significant wave height and the reference wave period change according to a specific wind–wave correlation. As a result, only a limited number of combinations of wave period and wave height are analysed in a DP capability assessment, and sometimes conditions that are not practically reliable are considered [34]. Wind and waves are expected to be collinear, acting at the same angle of encounter $\chi$. The third load, the current, is assumed to be constant and collinear with the other two loads. Since the capability plot is a diagram rather than a specific index, it is necessary to determine a suitable parameter to associate with capabilities for identifying an objective function in the location optimisation problem. More specifically, the selected parameter is the area included in the DP capability envelope $A_{CP}$. The area evaluation requires the implementation of the following function:

$$A_{CP}={\displaystyle \frac{1}{2}}{\int }_0^{2\pi }{\left[V_{w_{max}}\left(\chi \right)\right]}^2\mathrm{d}\chi$$

(10)

where $\chi$ is the heading angle and $V_{w_{max}}$ is the maximum sustainable wind speed at each encounter angle $\chi$. Formulation (10) allows for finding the thruster locations that grants the bigger area of a DP capability plot for the vessel under analysis. However, it should be noticed that the thruster locations (i.e., the unknowns of the problem) do not appear in the objective function. This matter complicates the applicability of the simple optimisation process, making necessary the employment of more sophisticated procedures, like the application of differential evolution algorithm.

Having defined the form of the objective function, it is then necessary to understand how to proceed with the optimisation process, defining the steps needed to perform the optimisation by employing a differential evolution algorithm.

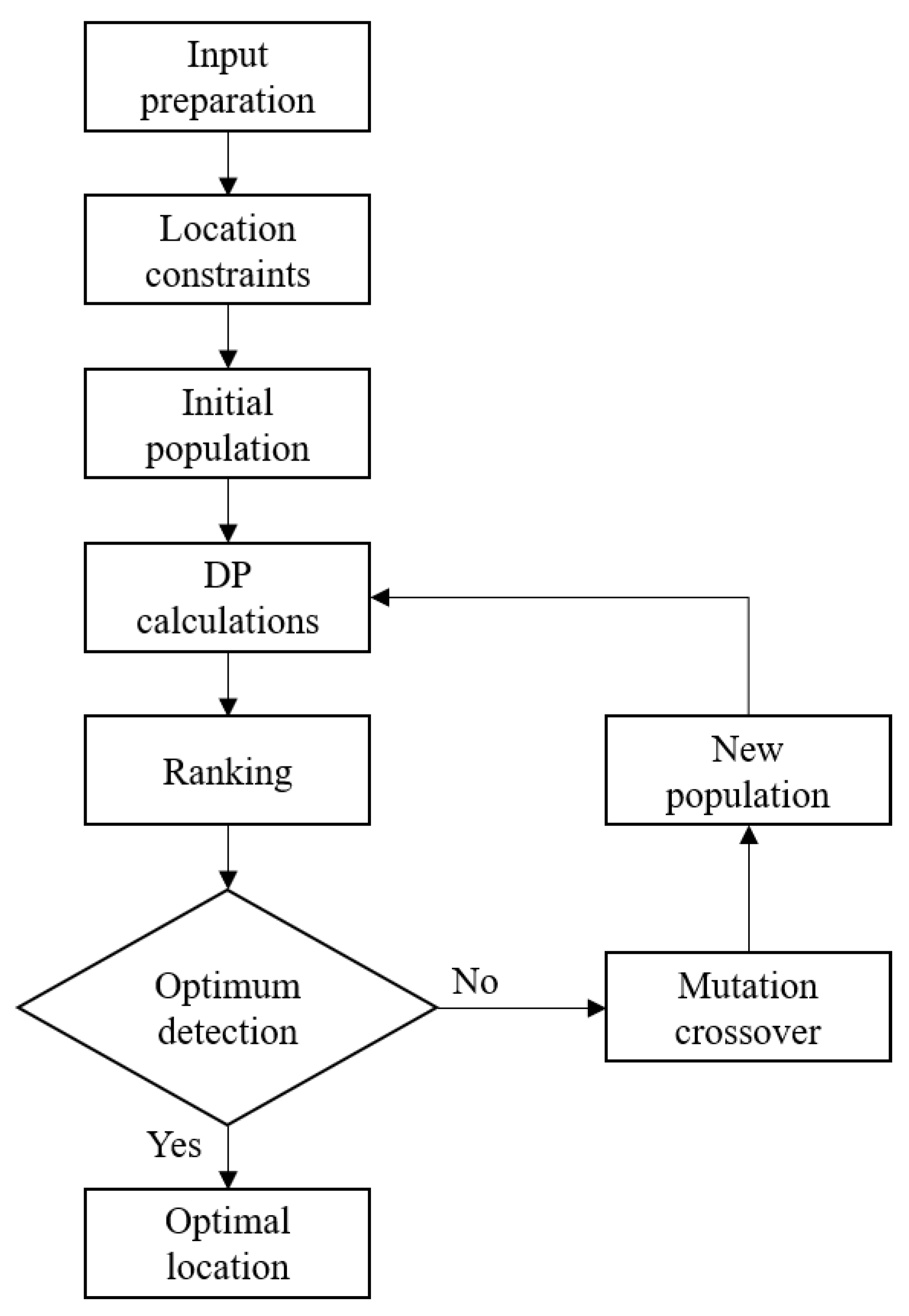
3.2. Calculation Framework

As mentioned above, the unknowns of the problem (i.e., the thruster locations) do not appear inside the objective function defined by Equation (10). However, location appears in the local equality constraints of the DP thruster allocation problem (i.e., the three equations composing system (1)), and in the calculation of the interaction angles. The global process utilises a differential evolution algorithm that, at each iteration, incorporates calls to DP calculations to assess the capability plot area $A_{CP}$. This approach leads to a series of local recursive non-linear programming optimisations for each environmental condition, which are essential for determining the overall capability.

It is then relevant to propose a calculation framework to establish the calculation steps needed to perform this nested optimisation process. The following set of recursive operations are then needed:

• Input preparation: loading the initial general particulars of the ship necessary for environmental load calculations and establishing the initial location and size of the thruster devices.
• Location constraints definition: determination of all the constraints related to the location of each thruster device, including forbidden areas and upper and lower bounds.
• Generation of the initial population: random generation of the initial population of $N_{pop}$ individuals, satisfying the location constraints.
• DP capability calculations: evaluation of the objective function $A_{CP}$ for all the generated individuals.
• Ranking: ranking of the individuals based on the evaluated $A_{CP}$ values.
• Mutation and Crossover: mutation and crossover procedure on the initial population.
• DP calculations on the new individuals: evaluation of $A_{CP}$ on the new individuals generated at step 6.
• Generation of the new population: generation of the new population composed by the best individuals of the initial population and of the mutation/crossover process.
• Iterative optimisation: execution of points from 4 to 8 until the convergence on optimal solution is reached.
• Optimal solution: identification of the optimal thruster locations.

Figure 3 shows the flowchart of the proposed framework for thruster location optimisation.

For the specific problem of optimal thruster location, the number of individuals has been set to $N_{pop}=8N_{var}$, with $N_{var}$ being the number of variables involved in the global optimisation, i.e., the thruster location coordinates in x and y directions. Then, for a offshore unit we have the following:

$$N_{var}=N_{TT}+2N_{AT}$$

(11)

This means that tunnel thruster can change only the x location (they are supposed to be located on the diametral plane), while azimuth units can change both x and y locations. The maximum number of iterations has been set to 1000, considering that calculation converged if, after 50 consecutive iterations, the objective function value of the best individual does not change more than 1 × 10³. Concerning the mutation process, a uniform mutation has been implemented with a mutation rate of 0.01. For the crossover, the following model has been used for the determination of a child c from two parents $p_1$ and $p_2$:

$$c=p_1+n·r\left(p_1-p_2\right)$$

(12)

where n is a pseudo random number and r is a crossover ratio set at 0.5 [16]. At each iteration, the crossover probability for each individual is 0.8.

The parameters chosen for the global optimisation process ensure a smooth convergence of the solution for a set of offshore vessels used to test this process. The parameters employed for the DEA optimisation process derive from previous studies on optimal thruster location performed by the authors [16,33]. The following sections describe the reference ship and environmental conditions considered in the study, presenting and analysing the obtained results.

4. The Reference Ship and Wind–Wave Correlations

To test the implemented procedure and verify the dependence of the results from the environmental conditions, a reference ship and a set of reference wind–wave correlations have been selected. The following sections describe the main particulars and the thruster layout of the reference PLCV selected, together with the environmental conditions selected for the study. More specifically, for the environmental conditions, we referred to the adoption of wind–wave correlations. Here, statutory and custom site-specific formulations are discussed.

4.1. The Reference Ship

The ship selected for the study is a Pipe Lay Crane Vessel (PLCV). The vessel is a result of one conversion of an old Ro-Ro ship in a PLCV [2]. The ship is particularly interesting because of the totally asymmetric layout of the steerable thruster devices and for the presence of a pipe line not located on the diametral plane of the ship.

Figure 4 shows the lateral view of the vessel, while

Table 1. Reference PLCV general particulars.

	Symbol		Unit
Length between perpendiculars	L	152.62	m
Length overall	$L_{OA}$	162.00	m
Length on waterline	$L_{WL}$	153.00	m
Maximum breadth	B	38.00	m
Design draught	T	5.00	m
Volume	∇	22,800	m3
Wetted surface	S	1681	m2
Lateral exposed wind area	$A_L$	2410	m2
Transversal exposed wind area	$A_T$	810	m2

reports the general particulars of the ship.

Table 2. Thruster and pipe line layout and sizing of the reference PLCV.

Thruster ID	${\mathit{x}}_{\mathit{T}}$ (m)	${\mathit{y}}_{\mathit{T}}$ (m)	D (m)	${\mathit{P}}_{\mathit{s}}$ (kW)
Thruster 1	57.0	4.2	2.4	2050
Thruster 2	52.3	−4.2	2.4	2050
Thruster 3	27.5	−15.0	2.0	1400
Thruster 4	−22.5	15.0	2.0	1400
Thruster 5	−60.0	15.0	2.4	2050
Thruster 6	−60.0	−15.0	2.0	2050
	$x_L$ (m)	$y_L$ (m)	$F_{x_L}$ (kN)	$F_{y_L}$ (kN)
Pipe line	−77.31	4.00	−490.50	0.00

shows the general layout of the six thrusters ($N_T$ = 6) with the associated size, reporting the positions $x_T$ and $y_T$, the propeller diameter D and the shaft power $P_s$. The table also reports the characteristics of the pipe line, giving the locations $x_L$ and $y_L$, and the tension forces in x and y directions ($F_{x_L}$ and $F_{y_L}$, respectively). As mentioned before, the thruster layout and the pipe line are not symmetrical with respect to the y axis. Also, the thruster sizes are not homogeneous, with for and aft thrusters having one size and the two mid thrusters another one. This layout is particularly challenging for the determination of DP capability as the thruster layout is asymmetric and the external loads are also asymmetric (due to the asymmetric pipe line location), resulting in an asymmetric capability plot for port ($\pi ,2\pi$) and starboard ($0,\pi$) encounter angles $\chi$.

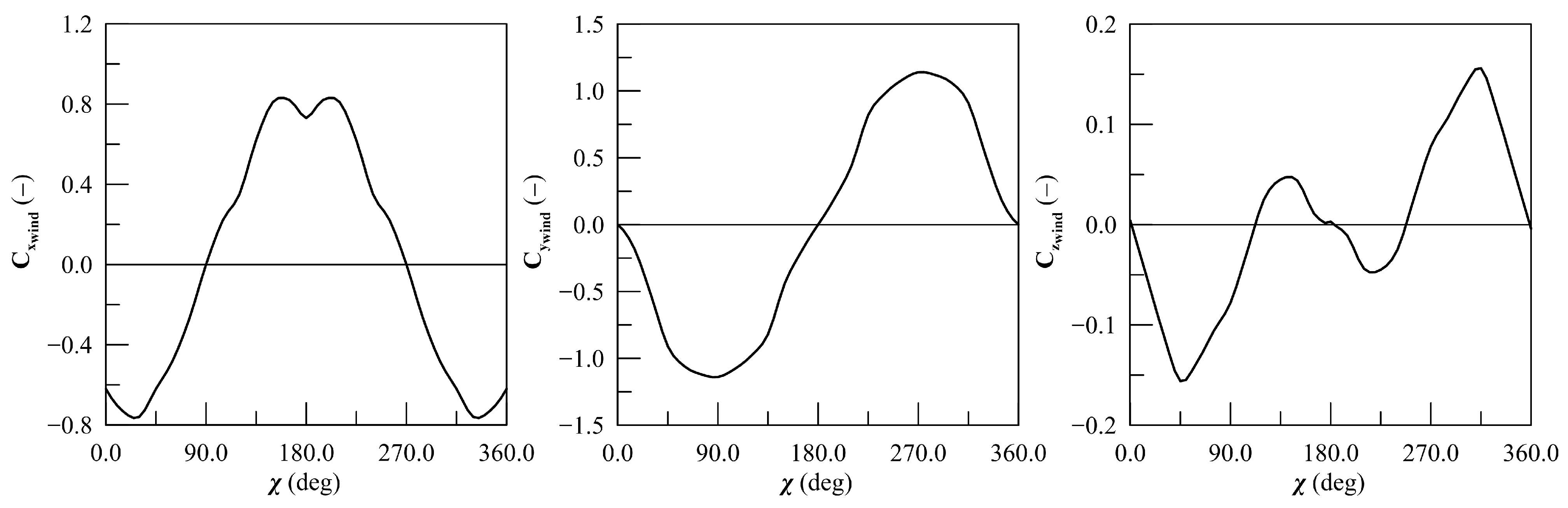
For the reference PLCV, experimental loads are available for either wind, wave or current loads. This allows for evaluating environmental loads through the direct application of Equations (6)–(8). Figure 5 shows the wind load coefficients as a function of the encounter angle $\chi$. It is possible to observe that the loads are almost symmetric between starboard and port side, highlighting no asymmetries in the PLCV superstructures. This is different in the case of current loads. Figure 6 shows the current loads as a function of the $\chi$ angle, highlighting an asymmetry between starboard and port side due to the presence of the stinger, which is located 4 m outside the diametral plane. The asymmetry is also present in the drift forces. 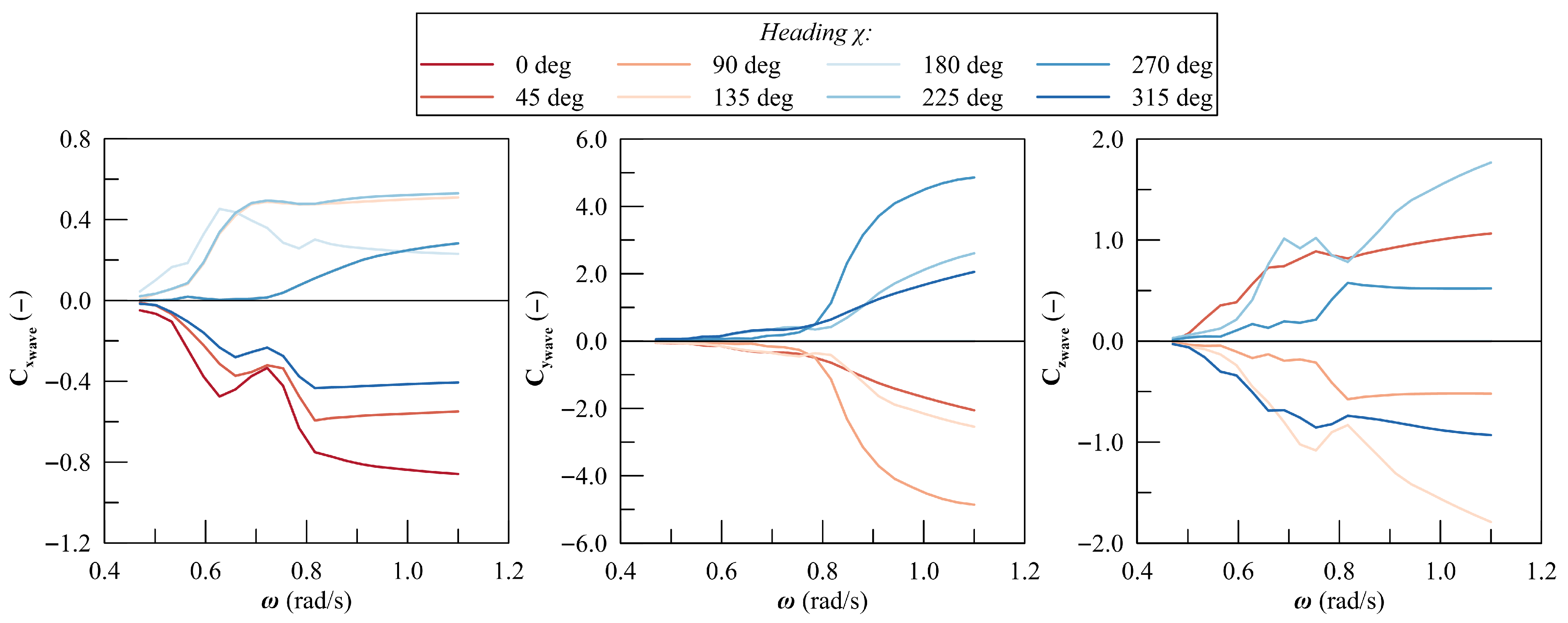Figure 7 shows the drift force coefficients at different $\chi$ angles as a function of the wave frequency $\omega$. It is also possible to observe here the small asymmetry due to the stinger location.

With these settings as the initial layout of the thrusters and inputs for environmental loads, it is possible to set up the DP capability calculation. However, prior to starting with the optimisation of thruster locations, it is necessary to discuss more in detail the combinations of wind speed and wave heights and periods to be employed in the calculation process.

4.2. Wind–Wave Correlations

The most common and straightforward method to model the combined effects of wind and waves is by using a wind–wave correlation, which provides a unique deterministic relationship between $H_s$, $T_p$, and $V_w$. Although the relationship between wave parameters and wind speed varies depending on the operating location of the vessel, classification societies [24] and operators’ associations [10] recommend adopting the reference values listed in

Table 3. Standard wind–wave correlations.

IMCA			DNV
${\mathit{V}}_{\mathit{w}}$ (m/s)	${\mathit{H}}_{\mathit{s}}$ (m)	${\mathit{T}}_{\mathit{p}}$ (s)	${\mathit{V}}_{\mathit{w}}$ (m/s)	${\mathit{H}}_{\mathit{s}}$ (m)	${\mathit{T}}_{\mathit{p}}$ (s)
0.0	0.0	–	0.0	0.0	–
2.5	1.28	5.30	1.5	0.1	3.5
5.0	1.78	6.26	3.4	0.4	4.5
7.5	2.44	7.32	5.4	0.8	5.5
10.0	3.21	8.41	7.9	1.3	6.5
12.5	4.09	9.49	10.7	2.1	7.5
15.0	5.07	10.56	13.8	3.1	8.5
17.5	6.12	11.61	17.1	4.2	9.0
20.0	7.26	12.64	20.7	5.7	10.0
22.5	8.47	13.65	24.4	7.4	10.5
25.0	9.75	14.65	28.4	9.5	11.5
27.5	11.09	15.62	32.6	12.1	12.0
30.0	12.50	16.58
32.5	13.97	17.53
35.0	15.49	18.46

.

Another approach is to derive the correlation between wind and waves using an irregular wave spectrum formulation, such as the Pierson–Moskowitz (PM) model [13], by solving the following system:

$$\left\{\begin{array}{cc}{H}_s\hfill & ={\displaystyle \frac{2}{g}}\sqrt{{\displaystyle \frac{\alpha }{\beta }}}{V}_w^2\hfill \\ T_p\hfill & =1.4049{\displaystyle \frac{2\pi }{g\sqrt[4]{\pi \beta }}}{V}_w\hfill \end{array}\right.$$

(13)

where $\alpha$ and $\beta$ for the standard PM spectrum are two constants equal to 0.0081 and 0.74, respectively.

It is also possible to determine wind–wave correlations for site-specific environmental conditions [24]. In such cases, wind–wave correlations are represented through simplified models derived from a direct comparison of the Cumulative Density Functions (CDFs) of the marginal distributions of $V_w$, $H_s$, and $T_p$. This approximation results in triplets ($V_w$-$H_s$-$T_p$) that correspond to the same occurrences identified in the CDF analysis. This approach provides a simplified characterization of a sea state, which is useful when joint statistics of environmental variables are not available.

For DP applications, using site-specific wind–wave correlations enhances environmental modeling while maintaining the same logical structure as the standard correlations previously described. This means the process of evaluating DP capability remains unchanged even when adopting site-specific wind–wave correlations for the area of interest.

In the present study, as an example, a specific sea area located in the Atlantic Ocean near Cabo Sillero is considered. For this area, named for simplicity SITE-A, joint probability distributions representative for $V_w$, $H_s$ and $T_p$ are available in the literature [25], allowing for the reproduction of a site-specific wind–wave correlation.

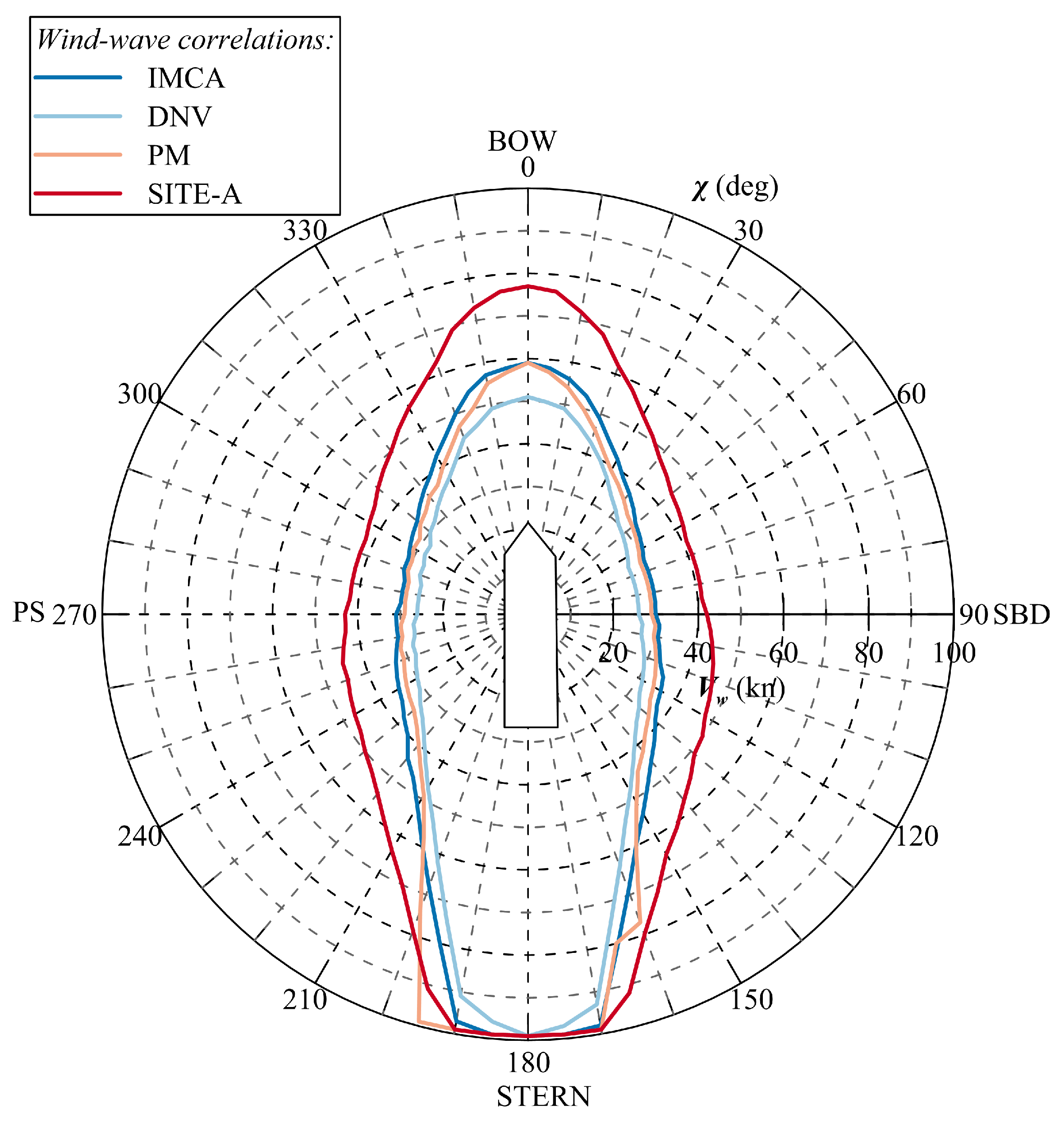
Figure 8 shows the comparison between IMCA, DNV, PM and SITE-A wind-wave correlations.

All the correlations identify alternative triplets ($H_s$-$V_w$-$T_p$) for the modelled environment. This matter, as already demonstrated [22], leads to different shapes of the capability envelop on the final DP capability plot. Then, as the capability plots are different, the research question became whether a different capability plot results in a different optimal location of the thrusters.

5. Applied Example

Having defined the calculation framework and the different kinds of inputs needed for the environmental modelling, it is possible to apply the location optimisation problem on the reference ship presented in Section 4. The calculations are performed according to the four different wind–wave correlations represented in Figure 8, meaning the IMCA, DNV, PM and SITE-A wind–wave correlations. More specifically, the tested environmental conditions represent two statutory wind–wave correlations (IMCA and DNV), a theoretic formulation (PM) and a site-specific (SITE-A) correlation.

The following sections describe the capability results for the different wind–wave correlations of the original configuration, together with the location optimisation process. Finally, the capability plots of the optimised configurations are compared with the original one. The tools employed for the dynamic positioning prediction have been verified against codes provided by classification societies, providing good agreement using the same set of inputs [33].

5.1. Capability Plots of the Original Configuration

Before starting with the thruster location optimisation problem, it is useful to check the initial DP capability of the reference vessel in its original thruster configuration, highlighting the differences between the selected wind–wave correlations.

To this end, dedicated DP calculations have been carried out on the initial thruster configuration (thruster location as per Table 2). The considered inputs for all the four environmental conditions include the pipe load, considering a concurrent current with a speed of 1.5 m/s. Calculations have been carried out with a $\chi$ step of 5 degrees, ranging from 0 to 360 degrees, in order to capture the asymmetries of the system. The DP calculations at each $\chi$ angle have been performed by constantly increasing the wind speed $V_w$ in steps of 1 knots until reaching a maximum of 100 knots. The calculation stops when the system is no longer capable of holding the position, determining the maximum sustainable wind speed $V_{w_{max}}$ necessary to determine the DP capability plot.

Figure 9 shows the differences between the DP capability plots obtained by applying the four different wind–wave correlations. From the figure, the differences among the capability plots are evident, reflecting the differences in wind–wave correlations. The DNV formulation is the most conservative wind–wave correlation, leading to the lower capability envelope in the figure. IMCA and PM formulations reproduce similar results, with the PM correlation being a little bit more conservative than the IMCA formulation. The site-specific correlation SITE-A is the less severe among the four tested correlations, resulting in a higher capability envelope in the DP capability plot.

The differences are reflected in the capability area of the generated plots, thus in the initial level of the objective function for location optimisation according to Equation (10). It is then relevant to investigate whether the different wind–wave correlations, generating different capability plots on the original thruster configuration, lead to different optimal locations during the layout optimisation process. The following section will provide the results of the four optimisation processes carried out on the reference PLCV vessel.

5.2. Optimal Thruster Locations

Having defined the different starting level of the DP capability with the different wind–wave correlations, it is possible to start with the optimisation process described in Section 3.

The DEA algorithm employed for the resolution of the optimisation process is designed to minimise the objective function. As the objective function $A_{CP}$, expressed by Equation (10), is a target to maximise, the algorithm is set to minimise $-A_{CP}$. Then, additional constraints are needed to ensure the correct placement of the thruster devices, ensuring no overlapping between the thruster and the location of the devices on the flat bottom of the ship. The first issue is addressed by imposing that the location of each thruster should be at least four diameters D away from the closest device. This avoids the overlapping and also minimises the effect of thruster–thruster interactions [16]. The second issue is solved by imposing at each generation the maximum $y_T$ as the half-breadth of the flat bottom of the sampled $x_T$ location. During the mutation and crossover procedure, in case a $y_T$ goes outside the bounds, it is saturated at the maximum $y_T$ level. Concerning the limits of the $x_T$ values, these are free to vary along the whole flat bottom of the ship. As a final remark, as Thruster 5 and Thruster 6 are the propulsive thruster units of the vessel, they are kept fixed during the optimisation process; thus, only the first two thrusters vary the position, with a total of eight unknowns. With this in mind, each population has then 64 individuals. During the optimisation process, the thruster size remains constant.

With these additional settings, together with the ones exposed in Section 3, the optimisation problem has been performed for the four different wind–wave correlations. Figure 10 shows the change in the objective function $-A_{CP}$ at each generation performed by the DEA algorithm. For all four cases, the process finished after 52 consecutive generations (meaning 3328 evaluations of the objective function), reaching in all cases the convergence of the objective function. Concerning the computational time, this varies with the $-A_{CP}$ values, ranging from a minimum of 8800 s to a maximum of 12000 s on a regular laptop with six parallel processes. Of course, the values of the $-A_{CP}$ are different among the selected wind–wave correlations, due to the different capability areas of reference, as shown for the original configuration in Figure 9. Concerning the reduction in $-A_{CP}$ achieved by the optimisation, the values are different for each wind–wave correlation. The IMCA wind–wave correlation achieves a 4.3% reduction in $-A_{CP}$. DNV correlation has a reduction of 2.2% for the objective function. The PM formulation has the best reduction performance, with a $-A_{CP}$ reduction of 6.7%. Finally, the SITE-A site-specific wind–wave correlation registers a reduction in objective function of 3.9%.

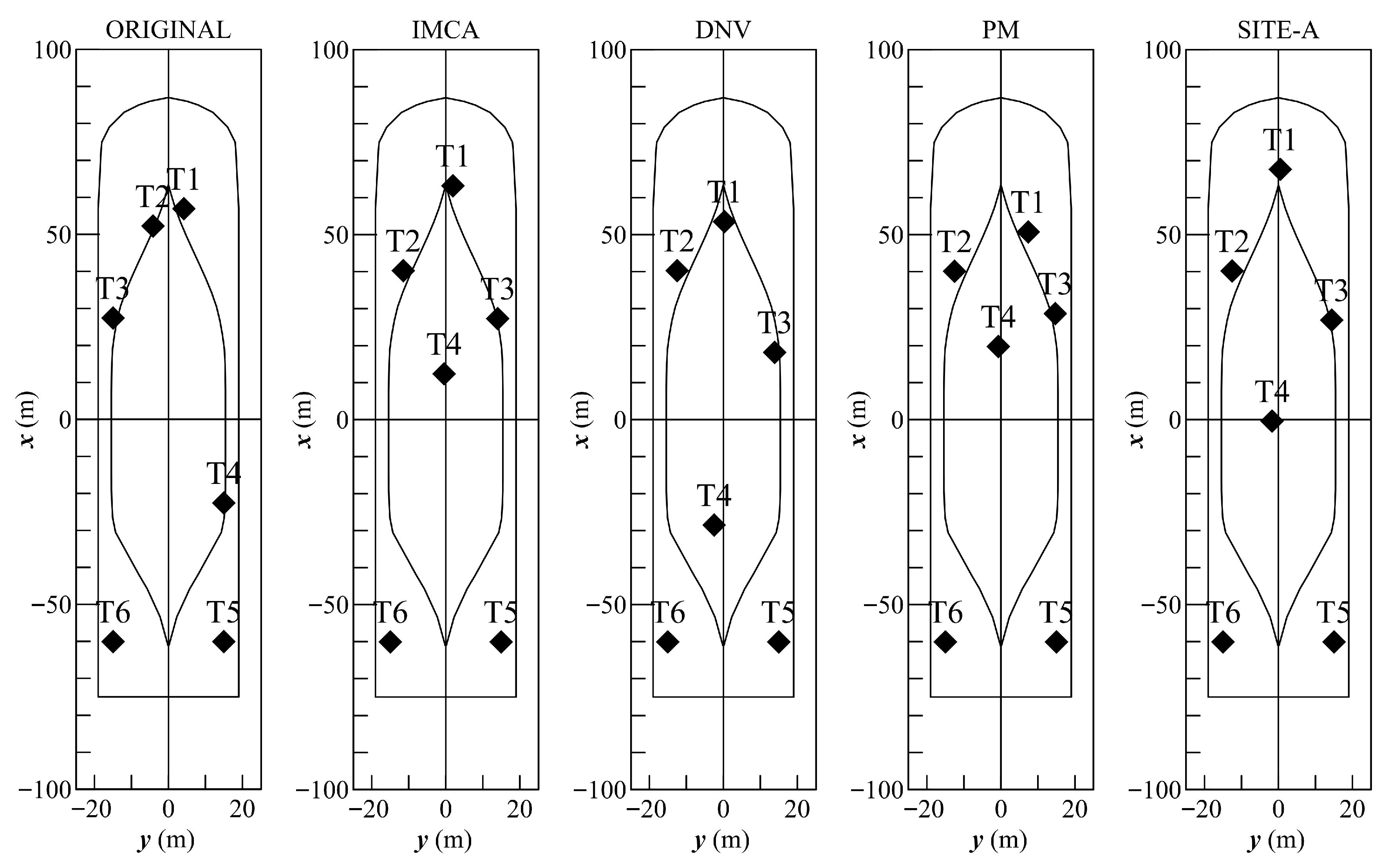
Besides the objective function evaluation, it is relevant to analyse the location results after the optimisation process. Figure 11 and

Table 4. Optimal thruster locations according to different wind–wave correlations.

	ORIGINAL		IMCA		DNV		PM		SITE-A
Thruster ID	${\mathit{x}}_{\mathit{T}}$ (m)	${\mathit{y}}_{\mathit{T}}$ (m)	${\mathit{x}}_{\mathit{T}}$ (m)	${\mathit{y}}_{\mathit{T}}$ (m)	${\mathit{x}}_{\mathit{T}}$ (m)	${\mathit{y}}_{\mathit{T}}$ (m)	${\mathit{x}}_{\mathit{T}}$ (m)	${\mathit{y}}_{\mathit{T}}$ (m)	${\mathit{x}}_{\mathit{T}}$ (m)	${\mathit{y}}_{\mathit{T}}$ (m)
Thruster 1	57.0	4.2	63.3	2.0	53.6	0.3	50.8	7.3	67.7	0.5
Thruster 2	52.3	−4.2	40.3	−11.5	40.3	−12.5	40.2	−12.6	40.2	−12.5
Thruster 3	27.5	−15.0	27.4	14.0	18.3	13.9	28.7	14.7	26.9	14.4
Thruster 4	−22.5	15.0	12.5	−0.5	−28.4	−2.5	19.9	−0.7	−0.3	−1.7
Thruster 5	−60.0	15.0	−60	15.0	−60.0	15.0	−60.0	15.0	−60.0	15.0
Thruster 6	−60.0	−15.0	−60.0	−15.0	−60.0	−15.0	60.0	−15.0	−60.0	−15.0

show the optimal thruster layout according to the four different wind–wave correlations. It is immediately recognisable that the four optimal solutions are different, highlighting the dependency of the optimum location on the wind–wave correlation. In any case, all the solutions are different from the original configuration, which is then not optimal for the reference PLCV vessel. According to the results, the adoption of the IMCA correlation led to a disposition of the thrusters with Thruster 1 (T1 in Figure 11) in the foremost position of the flat of bottom, Thruster 2 and 3 (T2 and T3 in Figure 11) shifted in x direction at disposed at the boundaries of the flat bottom and Thruster 4 (T4 in Figure 11) in the fore part of the ship close to the centreline. The adoption of DNV wind–wave correlation led to some different results, with T1 in the foremost position, T2 and T3 again shifted in x direction and located at the boundaries of the flat bottom; however, T4 is located in the aft part of the ship close to the centreline. When the PM formulation is implemented, the optimal location consists in the four thrusters forming a square in the foremost part of the flat bottom. Finally, the employment of the site-specific SITE-A wind–wave correlation gives an optimal layout similar to the one provided by IMCA, but with thruster T1 located at the foremost position of the flat bottom and T4 close to the midship.

Even though the four wind–wave correlations gave different results, some trends could be figured out for the general layout of the vessel:

• Thruster 1 position: all the four different optimisation processes locate thruster T1 in the fore part of the ship. T1 is always the foremost thruster of the DP system. As such, its location is close to the centreline, except for the configuration obtained with the PM formulation.
• Thruster 2 position: thruster T2 is always located in the fore part of the ship at port side. Thruster T2 has the same size of thruster T1, which is higher compared to thruster T3 and T4. As such, the optimal layout always locates thruster T2 forward of thruster T3, trying to increase the maximum moment achievable with the thrusters and counteracting the asymmetry of the pipe lane load.
• Thruster 3 position: the thruster is always located at starboard side. As mentioned above, the thruster is always behind the position of thruster T2 for the reasons already explained.
• Thruster 4 position: at any time, the fourth thruster changes the longitudinal position. However, by employing all the wind–wave correlations, the thruster is always located close to the centreline.

The above considerations are helpful for a designer to understand the optimal strategy to place the thrusters along the ship. Even though there is not a unique solution due to the differences in the wind–wave correlations, the general guidelines drawn out highlight the incorrect strategy of placement for the original thruster configuration of the reference PLCV. Of course, the final placement of thrusters should take into account some design constraints due to the internal layout of the vessel. Here, these additional constraints are not known; however, the developed framework is also capable of considering these additional issues in the global process.

5.3. Capability Plot Comparison

Besides understanding the strategy to place thrusters in an optimal position, it is also handy to visualise the improvements due to the application of an optimal thruster layout. In the previous section, the differences among the different options and the original layout were given only in terms of $A_{CP}$ reduction. However, $A_{CP}$ is just a numerical objective function, which does not represent to an end user the effective capability of the system. To this end, it is worth visualising the capability plot obtained with the original and the optimised configuration with the four different wind–wave correlations.

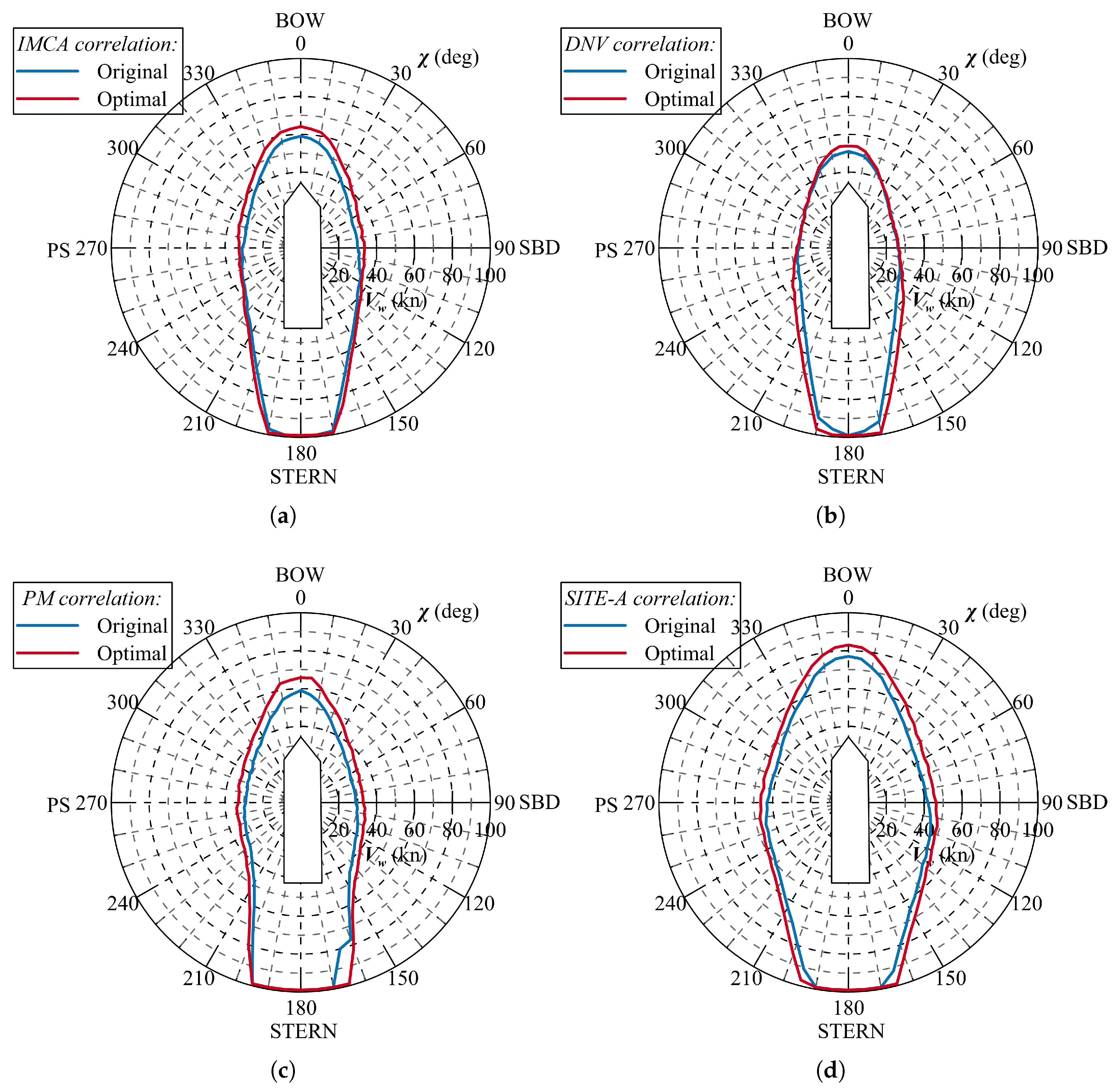
Figure 12 shows the comparisons between the DP capability plots of the original and optimised thruster layout for the reference PLCV. From the figure, it is possible to understand for which conditions there are gains due to the optimal location of thrusters. The following conclusions can be drawn:

• IMCA wind–wave correlation: according to this correlation, the main differences between original and optimised layout DP capability plots are for head-seas. In the range 0–90 deg and 270–360 deg, the optimised capability plot grants almost 5 knots of wind more than the original layout. For the remaining headings, the gain is not that much.
• DNV wind–wave correlation: according to this correlation, the gains are for head seas ranging from 0–30 degrees and 330–360 degrees. Additional gains are also for following seas, granting an average of 2.5–3.0 knots of wind more than the original configuration.
• PM wind-wave correlation: according to this wind–wave correlation, the differences are on the whole set of headings; an average of 5 knots of additional wind capability is achieved along the whole heading set.
• SITE-A wind–wave correlation: also according to this site-specific wind–wave correlation, the gains are on the whole set of headings. An average gain of 3–4 knots can be registered for all the considered headings in the analysis.

The above considerations are helpful in visualising the effective gains in capability obtained with the optimised configuration. However, the capability cannot be represented with a unique significant number. In fact, it is not possible to associate to a capability plot a workability index quantifying the operability of the system with the associated downtime period. Therefore, the present results can give an indication to designers and end users of a potential increase in the maximum sustainable wind speed at some encounter angles. For an effective determination of the downtime period of the system, a different approach should be followed [21,34].

6. Conclusions

The present work presents a framework for optimal thruster layout determination, investigating the effect of different options for the environmental modelling that a designer or end user can choose in a quasi-static capability analysis of a DP system. More specifically, the work considers four different wind–wave correlations representative of statutory (IMCA and DNV) correlations, theoretic formulation (PM) or site-specific correlations (SITE-A). The proposed calculation framework is based on a Differential Evolution Algorithm (DEA) capable of performing global optimisation, drawing on the DP thrust allocation routine (based on non-linear optimisation) to evaluate the DP capability plot. The process aims to maximise the DP capability plot area, using multiple constraints to ensure a reliable placement of the thruster units.

A preliminary analysis on the original configuration of the reference PLCV highlighted some differences among the DP capability plots generated with the different wind–wave correlations. Such a matter highlighted the possibility of having different results after the optimisation process. The results of the framework application confirm this observation, resulting in four different thruster layouts, one per each wind–wave correlation analysed. Even though the correlations are different, the process highlights some general trends concerning the placement of the thrusters, giving some useful guidelines to the designers on how to place thrusters, regardless of the adopted wind–wave correlation. Of course, the final decision should also take into account internal layout constraints not considered in the optimisation, that can be, in any case, included and solved by the present calculation framework. In any case, the general trends highlighted by the study may suggest that designers group the thrusters devoted only to DP duties and position them in the fore part of the vessel, leaving the propulsive thrusters only in the aft part of the ship. Such considerations are valid regardless of the wind–wave correlation employed for the study. The reported analysis is valid for the vessel considered for the analysis. The application of the process to another offshore unit may lead to different considerations due to the different loads acting on the specific units. Nonetheless, the application of the framework highlights that, except for the case of DNV correlation, the effect of the wind–wave correlation does not affect the optimal location of thruster that much.

In conclusion, the present study highlights the feasibility of studying the optimal location of thrusters on an offshore vessel by considering an advanced optimisation methodology for both the thruster location problem and the capability predictions. The applied example provides evidence of the capability benefits of employing an optimised solution for the thruster location instead of the original one. The adoption of different wind–wave correlations influences the final result in terms of capability; however, the general trends in terms of optimal location are similar, except for the DNV correlation regarding the placement of thruster T4. Therefore, the general framework can be applied, taking care of the wind–wave correlation for the capability calculations.

As a final remark, the process considers capability as the objective function of the optimisation process. However, the capability, even though it is widely used by designers and operators for DP analyses, cannot measure the effective operability of the system. To this end, the operability of the DP has to be used in the optimisation process, something that should be studied in the future. In any case, the findings of the paper and the presented framework are useful in guiding designers in the rationale of placing thrusters on an offshore unit.