Structural Response Research for a Submarine Power Cable with Corrosion-Damaged Tensile Armor Layers Under Pure Tension

Abstract

Submarine power cables (SPCs), as critical infrastructure for offshore wind farms, are the primary conduits for transmitting electricity from turbines to the grid. Actions such as seabed friction can cause damage to the submarine power cable’s outer sheath, accelerating the penetration of seawater corrosion media. This subsequently leads to corrosion fatigue or excessive loading in the tensile armor layer, which seriously threatens the long-term operational reliability of SPCs and the security of energy transmission. Based on homogenization theory and periodic boundary conditions, a repetitive unit cell (RUC) ABAQUS finite element model for a single-core submarine power cable (SPC) was established in this paper. And the mechanical response of the single-core SPC with the corroded tensile armor layers under tensile loading condition were systematically investigated. By comparing with a full-scale model, the feasibility and accuracy of the cable RUC damaged model proposed in this paper were effectively verified. It was found that the RUC damaged model exhibits significant stress concentration phenomena due to localized corrosion damage in the tensile armor layers, with its maximum von Mises stress being considerably higher than that of the RUC intact model; the elastic tensile stiffness of the SPC continuously decreases with increasing corrosion damage depth, but the magnitude of this reduction is small. This is because the corroded region is relatively small compared to the entire cable model dimension. This research reveals the potential impact of localized corrosion on the mechanical performance of the tensile armor layer, which can hold significant engineering importance for assessing the remaining load-bearing capacity of in-service SPCs and ensuring the reliability of subsea energy transmission corridors.

1. Introduction

As critical infrastructure for offshore wind farms, submarine power cables (SPCs) serve as primary energy transmission conduits delivering electricity from wind turbines to the power grid. As illustrated in Figure 1, these cables feature complex multilayered structures comprising the conductor layer, insulation layer, aluminum sheath, shielding layer, armor layer, and outer sheath [1]. Among them, the armor layer is composed of multiple metal components arranged in a spiral pattern. During service, submarine power cables will endure harsh marine conditions including mechanical stresses (e.g., anchoring and fishing operations), environmental degradation (salt spray and hydrostatic pressure), and thermochemical loads (thermal cycling and chemical corrosion). Under extreme operational scenarios such as trawling, anchor impact, strong currents, and corrosive damage, SPCs will exhibit progressive structural deterioration [2,3].

Recent years have witnessed growing scholarly focus on the mechanical behavior research of submarine power cables. Early SPC models typically established numerical models with relatively long lengths by using solid elements for meshing, which often demands substantial computational resources [4]. Lu et al. [5] developed a 3D finite element model (FEM) of umbilical cable under tensile loading via ANSYS (version 16.0) software, validating numerical results against experimental and theoretical analyses with strong agreement. Chang et al. [6] constructed a 1 m SPC model in ANSYS (version 16.0) to investigate its mechanical performance under coupled tension, torsion, and compressive loads. This model adopted quadrilateral and triangular meshes to balance computational efficiency and accuracy, albeit with compromised precision. Fang et al. [7] established an analytical model incorporating contact behavior and geometric deformation to predict tensile stiffness and torsional stiffness of the SPC, verifying predictions against a 1 m ABAQUS (version 2021) full-scale cable model. Ehlers et al. [8] created ANSYS (version 17.0) models for direct current (DC) single-core and alternating current (AC) three-core cables, achieving alignment between numerical and full-scale experimental ultimate strengths. Huang et al. [9] integrated OrcaFlex (version 10.0) and ABAQUS (version 2021) by inputting curvature and axial tension from OrcaFlex simulations as boundary conditions in ABAQUS. The ABAQUS model simulated mechanical responses under combined tension-bending loads, with monitoring data comparison confirming reliability.

Like submarine power cables, flexible pipes also constitute multi-layer structures containing numerous helical components. Extensive research has been conducted on the mechanical behavior of flexible pipes [10,11,12,13,14,15,16,17]. Within these studies, novel techniques have been developed and implemented, such as the RUC FEM based on periodic boundary conditions and homogenization theory. This approach can reduce the model length by leveraging structural/loading periodicity through periodic boundary conditions while assuming homogenized helical wires in the armor layer, thereby significantly enhancing computational efficiency [17,18]. Consequently, researchers have applied RUC technology to SPC modeling with further integration of beam–surface coupling techniques. This methodology employs beam elements to simulate the cable helical structures. It couples these beam elements with surface elements to capture contact interactions, thereby preserving computational resources. Ménard and Cartraud [19] established a 234.2 mm-long three-core SPC mechanical model using RUC technology and beam–surface coupling technique, applying periodic boundary conditions to resolve its nonlinear bending behavior. Subsequently, Fang et al. [20] combined RUC technology with beam–surface coupling technique to construct a 20 mm-long bending model of single-core SPC, with validation against full-scale numerical models and four-point bending tests confirming model accuracy. Comparative analysis demonstrates that the RUC model offers a significant reduction in simulation time, requiring only about 30% of the computational time of the full-scale model.

Offshore wind farms require a minimum burial depth of 0.6 m for submarine power cables [21,22,23]. Once installed, these cables are continuously subjected to the harsh marine environment. This environment imposes a combination of temperature fluctuations, significant hydrostatic pressure, and corrosive conditions that directly threaten the cable’s integrity. A primary agent of this degradation is seawater, whose salinity generally increases with depth. This saline solution is highly corrosive and progressively damages cable components. The corrosion process is not uniform and can lead to localized corrosion, particularly in the tensile armor layer. The armor layer, often made of steel, is designed to provide mechanical strength but is susceptible to electrochemical reactions in seawater. This damage can lead to a reduction in the cable’s service life and poses a significant threat to the overall reliability of the power grid it supports. Jiang et al. [24] demonstrated that the alternating current is induced in cable armor layers through electromagnetic induction. This induced AC at electrolyte–metal interfaces accelerates the armor corrosion, thereby promoting cable failures. While significant industry research exists on cable corrosion mechanisms, studies examining mechanical responses of corroded cables remain scarce.

Similar research has been conducted in the flexible pipe domain [14,15,25,26]. When tensile armor layers become exposed to seawater due to outer sheath damage, corrosion-induced fatigue or overload may occur, ultimately leading to armor wire rupture [27,28]. Consequently, de Sousa et al. [14] investigated the influence of the number of broken armor wires on the tensile stiffness of flexible pipes. Their study considered both pure tension and combined tension–torsion loading conditions. To simulate wire breakage, they deactivated selected elements of the inner and outer tensile armor wires in ANSYS (version 17.0). This study found that the tensile stiffness of the flexible pipe decreases as the number of broken tensile armor wires increases. Similarly, Ren et al. [25] employed the model change technique in ABAQUS (version 2018) to simulate damaged tensile armor wires, investigating their influence on the stress distribution of the remaining intact wires. Zhu et al. [26] demonstrated that inner-layer tensile armor wires bear greater loads than outer-layer tensile armor wires during tension. Consequently, the damage to the inner-layer tensile armor layer will cause more significant tensile stiffness reduction. These conclusions were validated by Lei et al. [29], who additionally identified that inner-layer tensile armor wire fractures trigger torsional buckling. However, existing studies that directly simulate the fracture of tensile armor layers often overlook the impact of localized corrosion conditions. To accurately capture the stress concentration phenomenon induced by such localized corrosion, the beam–surface coupling technology proves insufficient. Instead, it is necessary to develop a tensile armor layer model utilizing solid elements, which allows for detailed numerical analysis of regions with corrosion defects.

In summary, considerable progress has been made in the study of the mechanical performance of flexible pipes with corroded tensile armor layers. However, these numerical models are generally time-consuming, and existing research has not considered the local corrosion damage of the armor layer. Moreover, the study on the mechanical performance of submarine power cables with a local-corroded tensile armor layer has not yet been conducted. Therefore, an ABAQUS (version 2021) finite element model of the SPC with the tensile armor layer local-corroded under tensile loading conditions was established by the RUC technique in this paper. Then, the tension–strain curves obtained from the single-core cable RUC damaged model, RUC intact model, full-scale damaged model, and full-scale intact model were well compared. Additionally, a sensitivity analysis was performed on the corrosion-damaged depth of the tensile armor layer. This analysis aimed to systematically assess how varying corrosion depths affect the mechanical response of the SPC. Specifically, it addressed cases in which the tensile armor layer is locally corroded and subjected to tensile loading.

2. Homogenization Theory and Periodic Boundary Conditions

Homogenization theory is a multiscale analysis method that derives macroscopic equivalent properties from the representative behavior of the microstructure. This method is essentially based on the formulation of boundary value problems at the microscale to determine the local governing behavior at the macroscale [30]. Li et al. [31] developed a representative volume element (RVE) model with dashpot-enhanced periodic boundary conditions for a three-core SPC, also known as a “RUC model”. In the past, homogenization theory has been used to conduct the analysis of periodic beam-like structures [32,33,34]; however, these studies did not consider contact nonlinearities. Since submarine power cables involve complex contact nonlinearities, the applicability of this method is questionable when extending it to structures containing multiple contact interaction components. It was not until later that Ménard and Cartraud [35], as well as Saadat and Durville [36], demonstrated the feasibility of extending the classical homogenization framework to periodic structures with nonlinear contact. Submarine power cables can be regarded as slender beam-like structures. By applying periodic boundary conditions to submarine power cables, boundary effects can be minimized as much as possible, and computational efficiency can be improved by reducing model length. The periodic length l of the cable RUC model can be obtained by the following formula:

$$l={\displaystyle \frac{p}{n}}={\displaystyle \frac{2\pi R_h}{ntan\left(\alpha \right)}},$$

(1)

where p is the pitch of the helical armor layer; n is the number of helical armor wires; R_h denotes the mean radius of the layer; and α is the lay angle. When the cable is composed of multiple helical layers, its periodic length can be determined jointly by the common pitch among the helical layers j and the number of components n_j in each layer j.

$$l=k_j{\displaystyle \frac{p_j}{n_j}}=k_{j+1}{\displaystyle \frac{p_{j+1}}{n_{j+1}}}=\cdots =k_m{\displaystyle \frac{p_m}{n_m}},$$

(2)

where $k_j\in \mathbb{N}$ and m represents the number of helical layers.

Homogenization is a multi-scale analysis approach for both microscopic and macroscopic problems. In this paper, the microscopic scale is a RUC model with a periodic length l. The solution to the microscopic problem establishes the relationship between local strain/stress states and macroscopic strains. As illustrated in Figure 2, the macroscopic strain components $E^E$ (axial elongation), $E^{F_1}$ and $E^{F_2}$ (curvature), and $E^T$ (torsion rate) are defined in [19]. Within the microscopic formulation defined on the periodic domain, the displacement field exhibits l-periodicity in variable $y_3$, while the strain and stress fields are derived from the macroscopic strains as specified in [32].

The periodic homogenization problem is addressed numerically using the finite element method with periodic boundary constraints. These constraints, parametrized by the macroscopic strains in Figure 2, impose linear relations between each degree of freedom of two opposite nodes belonging to the boundary ∂Y⁺ and ∂Y⁻. The translational DOFs, denoted as $U_i^{+}$ and $U_i^{-}$ at these boundaries are governed by the linear system defined in the following equations [19,32]:

$$U_1^{+}-U_1^{-}=l\left({\overline{y}}_3{E}^{F_1}-y_2{E}^T\right),$$

(3)

$$U_2^{+}-U_2^{-}=l\left({\overline{y}}_3{E}^{F_2}+y_1{E}^T\right),$$

(4)

$$U_3^{+}-U_3^{-}=l\left(E^E-y_{\alpha }{E}^{F_{\alpha }}\right),\hspace{1em}\hspace{1em}\hspace{1em}\alpha =\left[1,2\right],$$

(5)

with ${\overline{y}}_3={\displaystyle \frac{1}{2}}\left(y_3^{+}+y_3^{-}\right)$ and $y_{\alpha }=y_{\alpha }^{+}=y_{\alpha }^{-}$.

For beams, three equations are added for the rotational degrees of freedom of the boundaries, denoted as ${\theta }_i^{+}$ and ${\theta }_i^{-}$:

$${\theta }_1^{+}-{\theta }_1^{-}=l{E}^{F_1},$$

(6)

$${\theta }_2^{+}-{\theta }_2^{-}=l{E}^{F_2},$$

(7)

$${\theta }_3^{+}-{\theta }_3^{-}=l{E}^T.$$

(8)

The finite element problem can be written as

$$\left[K\right]\left\{\begin{array}{c}\left\{U\right\}\\ \left\{\begin{array}{c}{E}^E\\ E^{F_1}\\ E^{F_2}\\ E^T\end{array}\right\}\end{array}\right\}=\left\{\begin{array}{c}\left\{0\right\}\\ l\left\{\begin{array}{c}N\\ M_1\\ M_2\\ M_3\end{array}\right\}\end{array}\right\},$$

(9)

where [K] is the stiffness matrix. The load case is defined by the corresponding macroscopic strain values. The axial force (N) and macroscopic moments (M₁, M₂, M₃) are derived from the right-hand side of Equation (9). Since only pure tension is applied in this study, the values of the macroscopic moments are all set to zero. It is worth noting that the microscopic problem involving the application of macroscopic deformation is solved using the finite element method with specific periodic boundary conditions. Its solution is defined up to rigid body displacements. For such problems, there are two solutions available: one involves applying kinematic conditions [37], and the other is to solve it via an explicit integration scheme [38]. To simplify computations, Ménard and Fabien [35] introduced a viscous damping coefficient to dissipate the rigid body displacements. However, this viscous damping coefficient needs to be evaluated throughout the simulation to ensure the ratio of damping energy to total energy remains below 5%. This guarantees that its influence on the final solution is negligible. An alternative method to eliminate rigid body displacements was proposed by Fang et al. [39]. In this method, the outer sheath of the cable at both ends is coupled to a reference point at the center of its cross-section, while periodic boundary conditions are applied to the components of the remaining layers. The present study adopts the method proposed by Fang et al. [39], and the specific setup will be demonstrated within the finite element model.

3. RUC Finite Element Model

To achieve efficient numerical simulation by reducing modeling length, a single-core cable RUC ABAQUS finite element model is constructed based on periodic boundary conditions (Figure 3). Based on numerical simulation, the mechanical response of the SPC with the tensile armor layer local-corroded under tensile loading condition is investigated. Initial defects in submarine power cables originate from the outer sheath. Damage to this sheath will expose the contacting tensile armor layer to seawater, leading to corrosion. Consequently, the proposed model takes into account that the corrosion area occurs on the outer surface of the outermost tensile armor layer.

3.1. Finite Element Modeling

This paper conducts modeling research based on the single-core cable model [7]. The types and structural dimensions of each layer of materials for the submarine cable are detailed in

Table 1. SPC structure dimensions.

Item	Component	Thickness (mm)	Radius (mm)
Layer I	Conductor	-	23.55
Layer II	Insulation	21.05	44.6
Layer III	Lead sheath	3.3	47.9
Layer IV	PE sheath	3.6	51.5
Layer V	Armor layer	3	54.5
Layer VI	Bedding	0.5	55
Layer VII	Armor layer	3	58
Layer VIII	Outer sheath	6	64

. The helical armor wires in Layer V and Layer VII feature rectangular cross-sections measuring 6 mm (width) × 3 mm (thickness). These layers contain 52 and 56 helical wires, respectively, with winding angles of 12.7° (Layer V) and −10.5° (Layer VII). The constitutive relation that accurately describes the material’s stress–strain relationship is essential for the calculations [40]. The elastic moduli and Poisson ratios of each material layer are provided in

Table 2. SPC material properties.

Item	Elastic Modulus (MPa)	Material Type	Poisson Ratio
Layer I	1.2 × 105	Copper	0.34
Layer II	350	XLPE	0.40
Layer III	12,000	Lead	0.43
Layer IV	600	PE	0.46
Layer V	2 × 105	Steel	0.30
Layer VI	780	HDPE	0.46
Layer VII	2 × 105	Steel	0.30
Layer VIII	780	HDPE	0.46

. In addition, the constitutive models for these materials are referenced from [3,41,42], with the specific constitutive model for metallic materials detailed in Figure 4a and that for polyethylene (PE)-type materials illustrated in Figure 4b.

The length of the proposed RUC model constructed in this study is determined according to Equation (2), yielding a value of 210 mm. The single-core SPC model incorporates multiple helical armor layers, introducing significant geometric nonlinearity and contact nonlinearity. Due to complex contact nonlinearities, the numerical model would encounter significant convergence difficulties if analyzed using a static approach. Consequently, a dynamic implicit approach is employed for a numerical solution. Compared to the excessive computational demands of the dynamic explicit method and the strict convergence requirements of the static general solution, the dynamic implicit approach can provide balanced computational efficiency while maintaining solution stability. However, since the dynamic implicit algorithm is adopted, the ratio of kinetic energy (ALLKE) to strain energy (ALLSE) must be controlled below 5% to prevent excessive inertial effects from compromising result accuracy.

3.2. Interaction and Boundary Condition Setting

Due to numerous helical steel strips and other multi-layer structures contained in submarine cables, the contact problem is very complex that it frequently causes convergence difficulties. The discretization solution for contacts depends on the contact surface width between adjacent layers, with two armor layers contacting the PE sheath, bedding, and outer sheath, respectively. Given the rectangular cross-sections of helical layers, surface-to-surface contact discretization is employed throughout the model. For the sliding settings between cable components, the small sliding formulation is universally adopted. The calculation of the contact relationship is performed only once per iteration, thereby enhancing the calculation efficiency [43]. In addition, the definition of the contact property is also very important. In the tangential behavior of the contact property, the Lagrange multiplier method and the penalty method are widely used. However, compared with the former, the penalty method does not increase the additional degrees of freedom of the system [7], and is more conducive to a numerical solution. Therefore, the penalty method is adopted to simulate tangential behavior in this study, and the friction coefficient is defined as 0.3 [39]. Furthermore, the “hard contact” setting is adopted for the normal behavior, and separation is allowed after the contact.

The boundary conditions of the proposed RUC model are shown in Figure 5. The outer sheath of the outermost layer is fully coupled with the reference points at the center of both sides of the cable (RP1 and RP2) to eliminate rigid body motion. Periodic boundary conditions are applied to the other layers via a written subroutine. The boundary condition at the right reference point RP2 is set as fully fixed (all six degrees of freedom constrained); at the left reference point RP1, a tensile load of T = 500 kN is applied while releasing the degrees of freedom in the U3 and UR3 directions, with the other degrees of freedom constrained.

3.3. Mesh Generation and Element Type

Mesh division is crucial for the convergence of the FEM and the accuracy of the results. To better simulate the deformation and stress distribution of each layer, the components of each layer in the RUC model are all simulated numerically using the C3D8R element. The radial and circumferential mesh divisions are relatively fine, while the axial mesh division is coarser to reduce the total number of elements. In addition, mesh refinement is carried out near the corrosion region of the outer armor layer in Layer VII. When adopting C3D8R elements to conduct the simulation, attention must be paid to hourglass control. Additionally, during subsequent result verification, the ratio of strain energy to internal energy should be kept within 5%.

As displayed in Figure 6, to verify the feasibility and accuracy of the proposed RUC model of the SPC with the tensile armor layer local-corroded under tensile loading conditions, three finite element models are constructed for comparative study: (1) a RUC intact model (length 210 mm); (2) a full-scale damaged model (length 1000 mm); (3) a full-scale intact model (length 1000 mm).

Herein, the full-scale model takes into account that the boundary conditions at both ends of the submarine cable model may have a certain impact on the local stress of each layer of the cable structure. The length of the full-scale cable model is selected to be approximately 10 times the outer diameter of the cable, and the homogenization theory and periodic boundary conditions adopted by the RUC model are not used in the full-scale model. All four models use C3D8R solid elements. The boundary conditions of the right reference point RP2 in the two full-scale models are fully fixed (all six degrees of freedom constrained), and all the points on the right-side cross-section are coupled to RP2. All points on the left-side cross-section are coupled to the left reference point RP1, where a tensile load of 500 kN is applied. At the same time, the degrees of freedom in the U3 and UR3 directions are released, while the other degrees of freedom are restricted. In this study, a rectangular cuboid of 2 mm³ was partitioned on the outer surface of the seventh layer’s armor layer to simulate the corrosion region, as shown in Figure 6. The corrosion region is in the middle of the armoring layer. The dimensions of the rectangular corrosion region are 2 mm × 2 mm × 0.5 mm. It should be noted that corrosion damage in this study’s numerical model is represented as an idealized rectangular cuboid for meshing convenience. In actual marine environments, corrosion typically exhibits semi-ellipsoidal or irregular geometries with sharper corners, potentially resulting in significantly higher stress concentration levels than those calculated in this research.

Mesh convergence studies constitute an essential foundation for reliable finite element analysis, necessitating mandatory mesh sensitivity analysis. Accordingly, this research discretized the tensile armor layer (Layer VII) with four element sizes (0.5 mm, 1 mm, 1.5 mm, and 2 mm), comparatively analyzing the maximum Mises stresses in the corrosion-damaged region and the cable’s tensile stiffness under pure tensile loading to validate mesh accuracy. Figure 7, respectively, shows the variation in the maximum Mises stress at the corrosion damage location and the tensile stiffness of the submarine cable with four different element sizes. As can be seen from the figure, the maximum Mises stress deviation at the corrosion damage site under different element mesh sizes is not significant, with the maximum value and the minimum value differing by approximately 3%, while the tensile stiffness of the submarine cable under different element mesh sizes is basically consistent, with the maximum value and the minimum value differing by less than 1%. Therefore, to ensure calculation accuracy and balance calculation efficiency, the element mesh size is set at 0.5 mm.

4. Results and Discussions

In this section, the tension–strain curves obtained from the single-core cable RUC damaged model, RUC intact model, full-scale damaged model, and full-scale intact model were compared to carry out verification and discussion. To systematically investigate how different corrosion depths affect the mechanical response of the SPC, a sensitivity analysis was conducted on the corrosion-damaged depth of the tensile armor layer. This study specifically considered cases where the tensile armor layer is locally corroded and subjected to tensile loading.

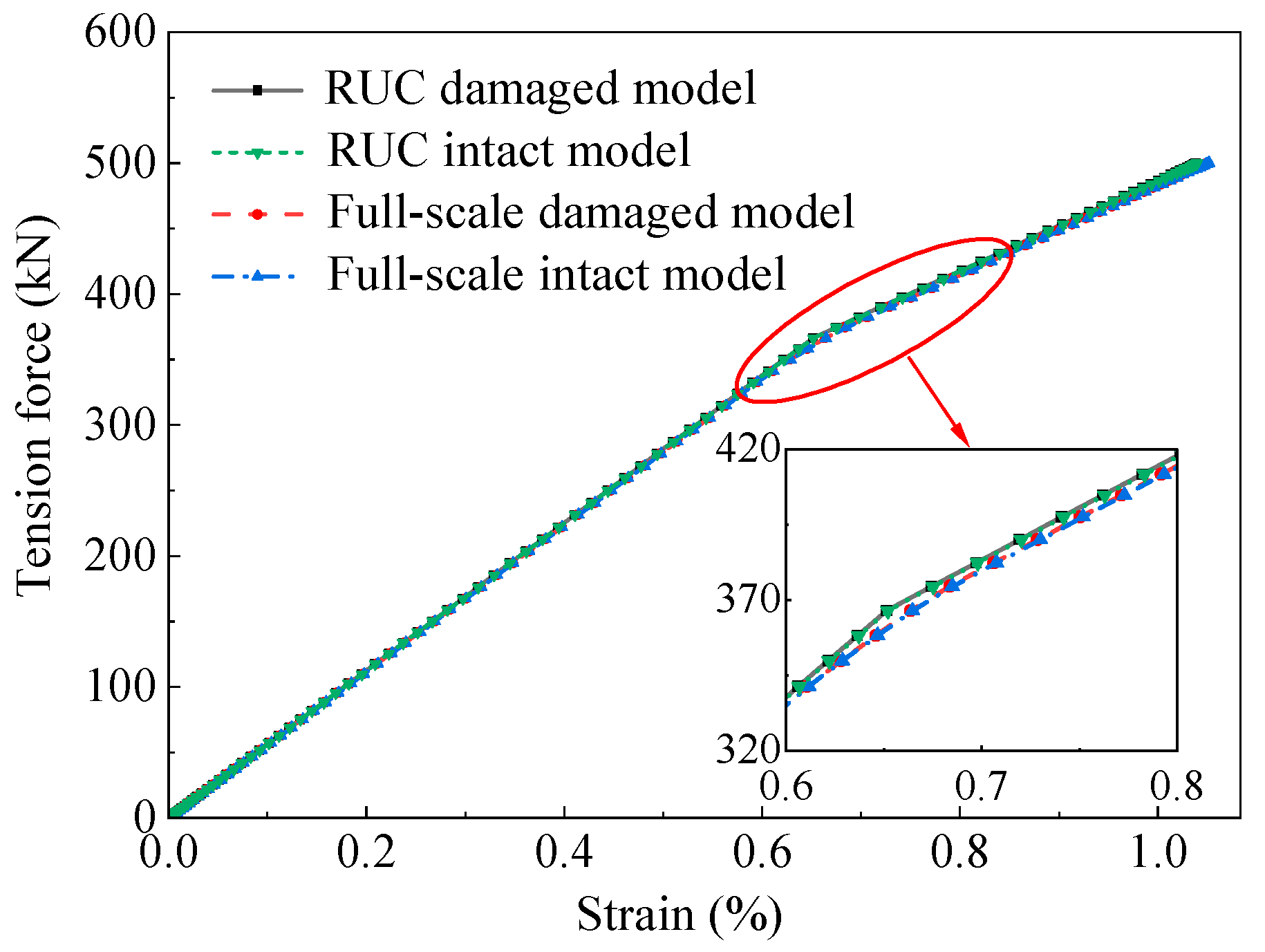
4.1. RUC Model Verification

Figure 8 exhibits the tension–strain curves for the single-core submarine power cable under a 500 kN axial tensile load with four finite element models (i.e., RUC damaged model, RUC intact model, full-scale damaged model, and full-scale intact model). It can be found that the tensile stiffness of the SPC remains constant during the linear elastic stage of the material. The corresponding elastic tensile stiffness of the single-core cable in the linear elastic stage can be obtained as 5.63 × 10⁸ N (RUC damaged model), 5.63 × 10⁸ N (RUC intact model), 5.59 × 10⁸ N (full-scale damaged model), and 5.58 × 10⁸ N (full-scale intact model), respectively. Upon partial material yielding, the tensile stiffness undergoes progressive degradation. Notably, the RUC damaged/intact tension–strain curves demonstrate negligible deviation, as do the full-scale damaged/intact pairs. This implies that localized tensile armor layer corrosion exerts minimal influence on the tensile stiffness of the whole cable in the proposed model. The RUC intact model under the tensile loading for three-core submarine cables showed better agreement with experimental results than the full-scale model [39]. Furthermore, inter-model comparisons reveal stiffness discrepancies of merely 0.896% (RUC intact model vs. full-scale intact model) and 0.716% (RUC damaged model vs. full-scale damaged model), with significant variances emerging predominantly in the plastic phase. These findings robustly validate the feasibility and accuracy of the proposed RUC damaged model.

To conserve computational resources, the full-scale model employed 20 axial grid elements for all layers except the tensile armor layer with corrosion zones, resulting in a 376% increase in axial grid size compared to the RUC model. As a result, numerical simulations on a computer with a 6-core CPU yielded the following: (1) RUC damaged model: 348,904 elements, computation time: 13.12 h; (2) RUC intact model: 116,840 elements, computation time 6.22 h; (3) full-scale damaged model: 348,904 elements, computation time: 13.15 h; (4) full-scale intact model: 116,840 elements, computation time: 6.7 h. If the full-scale model employed the same axial grid size for all layers, the number of grid elements in the full-scale model will increase to about five times the original amount. This will result in the full-scale model requiring a longer amount of time for computation. Hence, RUC technology can significantly enhance computational efficiency by implementing periodic boundary conditions to reduce modeling length, which is also verified by Fang et al. [39].

Since all models in this study employ C3D8R elements for numerical simulation, it is essential to ensure the negligible influence of hourglass effects in reduced-integration elements. This requires the ratio of artificial strain energy (ALLAE) to internal energy (ALLIE) not to exceed 5%. Furthermore, given the adoption of quasi-static simulation in the finite element models, the ratio of kinetic energy (ALLKE) to strain energy (ALLSE) must remain sufficiently low, specifically controlled within 5% to guarantee result validity [44]. The energy dissipation diagrams of the RUC damaged/intact models and full-scale damaged/intact models for the whole numerical simulation process are presented in Figure 9. Computational results demonstrate that (1) the ALLAE/ALLIE ratios for all models are significantly below 5%, effectively preventing significant hourglass effects; (2) the ALLKE/ALLSE ratios are consistently under 5%, thereby minimizing dynamic effects in quasi-static simulations.

4.2. Results and Analyses

Figure 10 illustrates the cross-sectional Mises stress nephograms of the RUC damaged model and RUC intact model under pure tensile loading. It can be observed that the tensile load is primarily shouldered by the tensile armor layers in the fifth and seventh layers, as well as the conductor layer in the first layer. This is because the material elastic moduli of these in the tensile armor layers and conductor layer are significantly higher than those in the other layers. Furthermore, the elastic modulus of the tensile armor layers (2 × 10⁵ MPa) is greater than that of the conductor layer (1.2 × 10⁵ MPa). Consequently, under the same tensile deformation, the Mises stress experienced by the tensile armor layers is the most pronounced. The maximum Mises stress in the RUC damaged model is 243.7 MPa, while that in the RUC intact model is only 196.7 MPa. The maximum Mises stress in the RUC damaged model is 23.89% larger than that in the RUC intact model.

To eliminate the influence of boundary effects on the numerical simulation of the RUC finite element model, an intermediate segment (126 mm axial length) of Layer VII (tensile armor layer) is extracted for analysis. As displayed in Figure 11, the Mises stress distribution in the RUC intact model is highly uniform, with a maximum Mises stress of 198.6 MPa and a minimum of 192.0 MPa, resulting in a difference in only 6.6 MPa. In contrast, the RUC damaged model exhibits significant stress concentration, with a maximum-to-minimum Mises stress difference reaching 152.3 MPa. The stress concentration phenomenon is closely related to the geometric shape of the cable structure. Defects caused by localized corrosion can lead to abrupt changes in the structural profile of the cable, thereby significantly exacerbating the stress concentration effect.

Therefore, pronounced stress concentration occurs in the corrosion damage region on the outer surface of Layer VII (tensile armor layer), peaking at approximately 243.7 MPa (Figure 11a). The tensile armor layer remains in a linear elastic state and is always in a safe condition. Along the axial direction, the stress gradient suddenly changes to around 91 MPa at the two edges of the corrosion damage region, and then gradually increases along the axial direction at the edges. Circumferentially, the Mises stress decreases symmetrically from the damage center toward both sides, though with a gentler gradient compared to the axial direction. Additionally, non-uniform stress distribution is observed on the circumferential inner surface of the corrosion damage region. Its profile resembles that of the outer surface, exhibiting a “wider at the edges, narrower at the center” pattern (Figure 12).

An arbitrary helical strip from Layer VII (tensile armor layer) is selected. As illustrated in Figure 13a, Mises stresses along 13 paths within the axial refined mesh zone (12 mm axial length) for the external surface of Layer VII (tensile armor layer) are extracted. Taking the center of the corrosion damage region as the origin, the Mises stress distribution on the outer surface of the tensile armor layer is plotted in Figure 13b (the results have been flattened for presentation). It can be seen that the Mises stresses across the 13 paths exhibit minimal differences at both ends of the refined mesh zone. However, stress gradients intensify significantly approaching the corrosion damage region. Particularly for the five paths traversing the damage region (Path 5–Path 9), the stress gradients substantially exceed those of other paths. This is primarily due to the corrosion defects, which have resulted in significant geometric discontinuity in this region.

Figure 14 illustrates the distribution of plastic strain in both the RUC damaged model and the RUC intact model for a single-core submarine power cable (SPC) subjected to an axial tensile load of 500 kN. Observation reveals that neither of the two tensile armor layers in either the RUC damaged model or the RUC intact model undergoes plastic yielding, even in regions with significant stress concentration induced by corrosion defects. This indicates that, under the specified loading condition (e.g., a 500 kN axial tensile load), the tensile armor layers remain within their linear elastic deformation range. In contrast, plastic deformation is confined to the conductor layer (Layer I) and the lead sheath layer (Layer III). The plastic strain distribution of the RUC damaged model is nearly identical to that of the RUC intact model. Consequently, the subsequent detailed analysis focuses specifically on the plastic behavior of the RUC damaged model.

When the tensile load reaches 265 kN, plastic deformation first initiates at the cross-sections located at the two ends of the lead sheath layer (Layer III), specifically in the 0°, 90°, 180°, and 270° circumferential regions. As the tensile load increases to approximately 300~315 kN, the plastic zone within the lead sheath layer expands progressively. This expansion occurs in a radial direction, propagating from the outer surface of the layer towards its interior. When the load reaches 320 kN, plastic deformation begins to manifest in the middle section of the conductor layer (Layer I). Subsequently, with further increase in load, the plastic zone in the conductor layer also expands radially from the outside towards the inside. At a tensile load of approximately 420 kN, both the conductor layer and the lead sheath layer have completely yielded, entering a fully plastic state.

The bedding layer (Layer VI), situated between the fifth and seventh helix tensile armor layers, experiences complex stress conditions. Figure 15 displays the CPRESS (contact pressure) cloud diagrams of the mid-segment (126 mm axial length) of the bedding layer for both the RUC damaged model and the RUC intact model. It is observed that the CPRESS on the inner surface of the bedding layer universally exceeds that on the outer surface in both models, exhibiting a helical distribution pattern. Specifically, the maximum CPRESS in the RUC intact model reaches 0.9260 MPa, exceeding the 0.6914 MPa in the RUC damaged model.

To conduct an in-depth investigation of the impact of corrosion damage on the internal contact pressure of cables, 3D and 2D CPRESS distributions on the outer surface of the mid-segment (126 mm axial length) of the bedding layer are extracted along the axial direction from both the RUC damaged model and the RUC intact model, as shown in Figure 16. In the 2D views (Figure 16b,d), the CPRESS distributions for both the RUC damaged model and the RUC intact model display clear helical band patterns. Furthermore, the contact pressure in the bedding layer adjacent to the corrosion damage region (near the axial coordinate of 105 mm) is markedly lower than that in other regions.

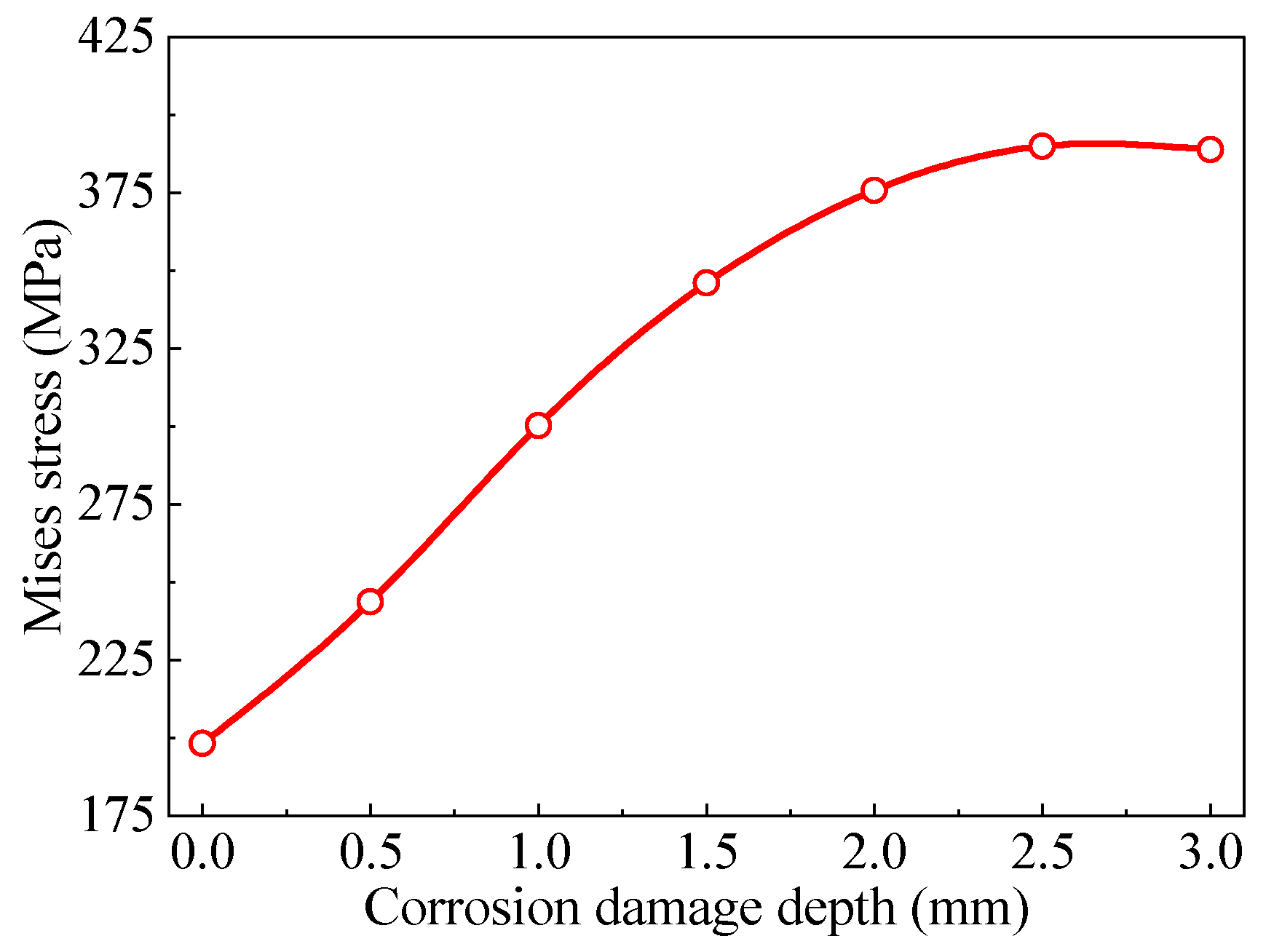
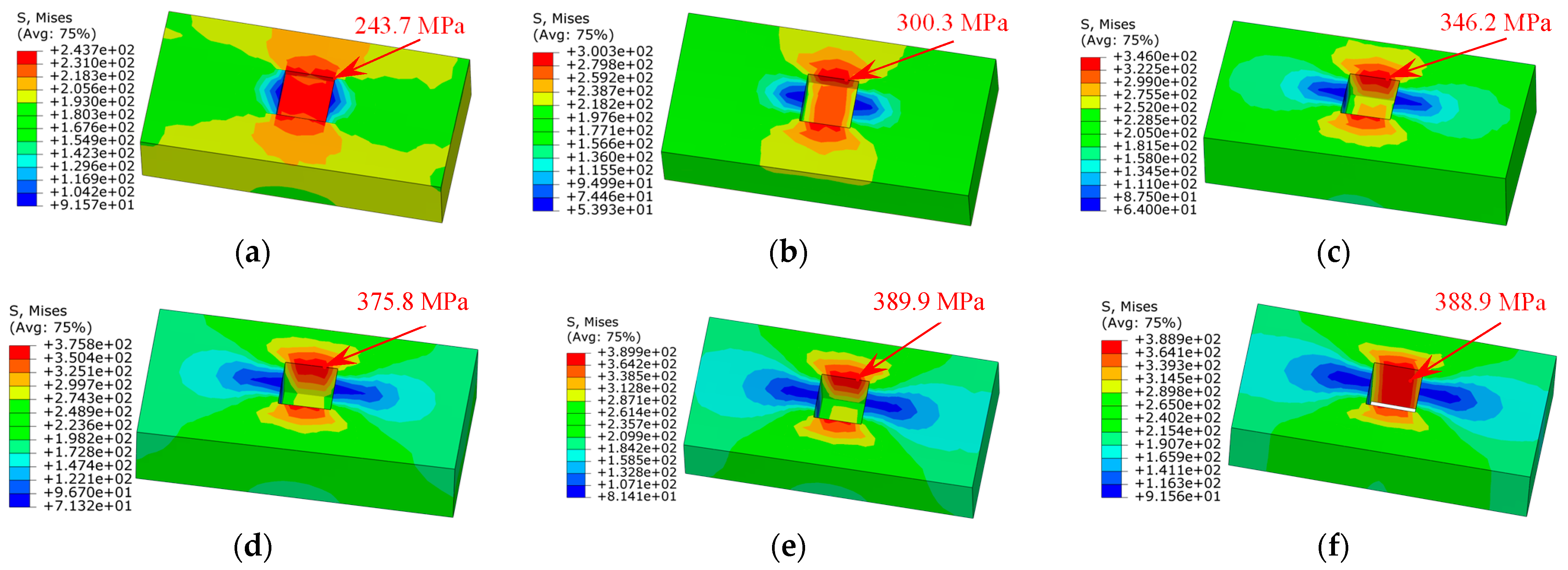
4.3. Effect of Corrosion Damage Depth

To investigate the influence of corrosion damage depth for the tensile armor layer (Layer VII) on the mechanical response of the submarine power cable under tensile loading conditions, RUC models with varying corrosion damage depths for the tensile armor layer (length × width × depth: 2 mm × 2 mm × 0 mm; 2 mm × 2 mm × 0.5 mm; 2 mm × 2 mm × 1 mm; 2 mm × 2 mm × 1.5 mm; 2 mm × 2 mm × 2 mm; 2 mm × 2 mm × 2.5 mm; and 2 mm × 2 mm × 3 mm) are developed. Figure 17 illustrates the maximum Mises stress variations in the cable’s tensile armor layer under seven different corrosion damage depth sizes. The results demonstrate that as the corrosion damage depth increases from 0 mm to 2.5 mm, the maximum Mises stress rises progressively from 198.2 MPa to 389.9 MPa. However, when the corrosion damage depth reaches 3 mm (i.e., through-thickness penetration of the armor layer), the maximum Mises stress exhibits a slight reduction to 388.9 MPa despite the increased damage severity.

This phenomenon occurs because when the corrosion damage does not fully penetrate the tensile armor layer, the Mises stress distribution along the depth direction within the corrosion region is highly non-uniform, with the maximum Mises stress arising at the edge where the outer surface intersects the corrosion damage (Figure 18). Conversely, when the corrosion damage penetrates entirely through the tensile armor layer, the Mises stress distribution along the depth direction becomes relatively uniform, and the maximum Mises stress shifts to the mid-thickness region of the corrosion region. Consequently, this redistribution results in a slightly lower maximum Mises stress compared to the 2.5 mm-depth case (388.9 MPa vs. 389.9 MPa), as visually confirmed in Figure 18. This phenomenon may be due to stress redistribution. Additionally, when the corrosion damage fully penetrates the tensile armor layer, the Mises stress distributions on the outer and inner surfaces near the corrosion damage region exhibit near symmetry (Figure 19).

Figure 20 illustrates the evolution of the elastic tensile stiffness of the submarine power cable, derived from the RUC damaged model, across seven different corrosion damage depths. The results indicate that the elastic tensile stiffness of the SPC progressively decreases with increasing corrosion damage depth. As the corrosion damage depth rises from 0 mm to 3.0 mm, the elastic tensile stiffness declines from 5.63 × 10⁸ N to 5.61 × 10⁸ N, representing a reduction in merely 0.36%. This demonstrates that corrosion damage depth has little significant effect on the degradation of the cable’s tensile stiffness. The primary reason for this limited effect is that the localized corrosion damage area remains small relative to the total dimensions of the cable model. However, it is anticipated that, should the corrosion area expand significantly—for instance, due to broader environmental degradation or progressive material loss—the consequent reduction in the tensile stiffness would become considerably more pronounced.

5. Conclusions

This paper employs RUC technology to establish a finite element model of a submarine power cable with corrosion-damaged tensile armor layers, investigating the mechanical response under tensile loading conditions. By comparing tension–strain curves obtained from a single-core cable RUC damaged model, RUC intact model, full-scale damaged model, and full-scale intact model, the RUC intact model exhibits a tensile stiffness error of 0.896% against the full-scale intact model, while the RUC damaged model shows a 0.716% error compared to the full-scale damaged model, with primary deviations occurring during the plastic phase. It can effectively validate the feasibility and accuracy of the proposed cable RUC damaged model and the computational efficiency of RUC model through reducing the model length. Additionally, a sensitivity analysis for the corrosion damage depth of the tensile armor layer in the SPC is carried out. The following conclusions can be drawn:

(1)

Tensile load is primarily carried by the two tensile armor layers and the conductor layer for the single-core submarine power cable.

(2)

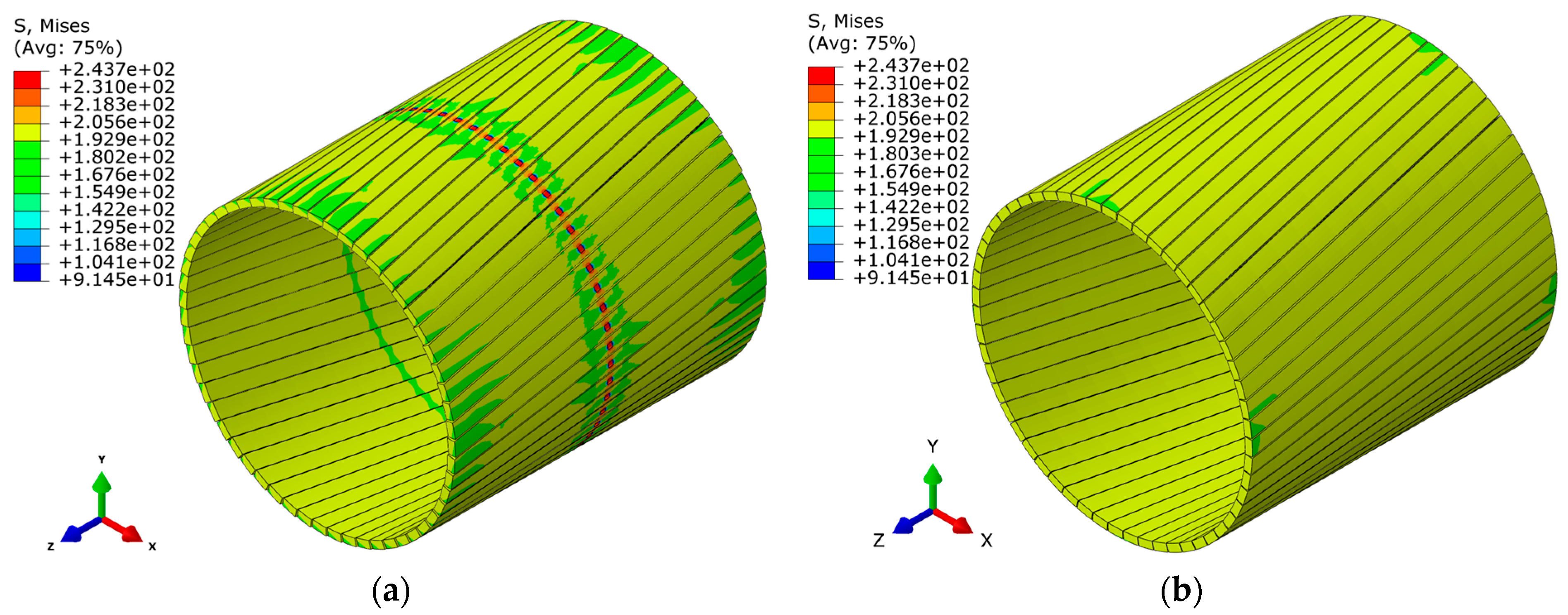
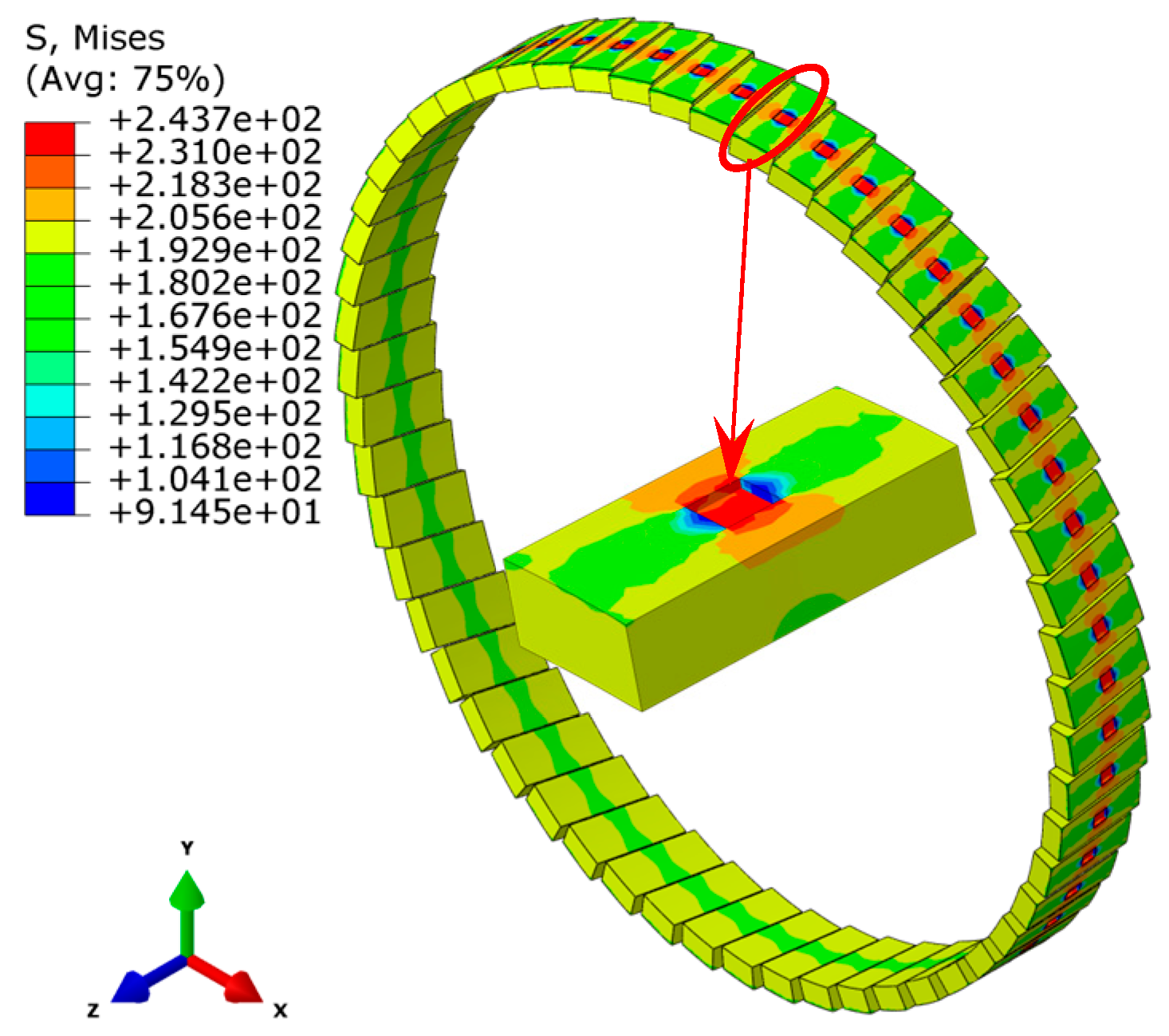
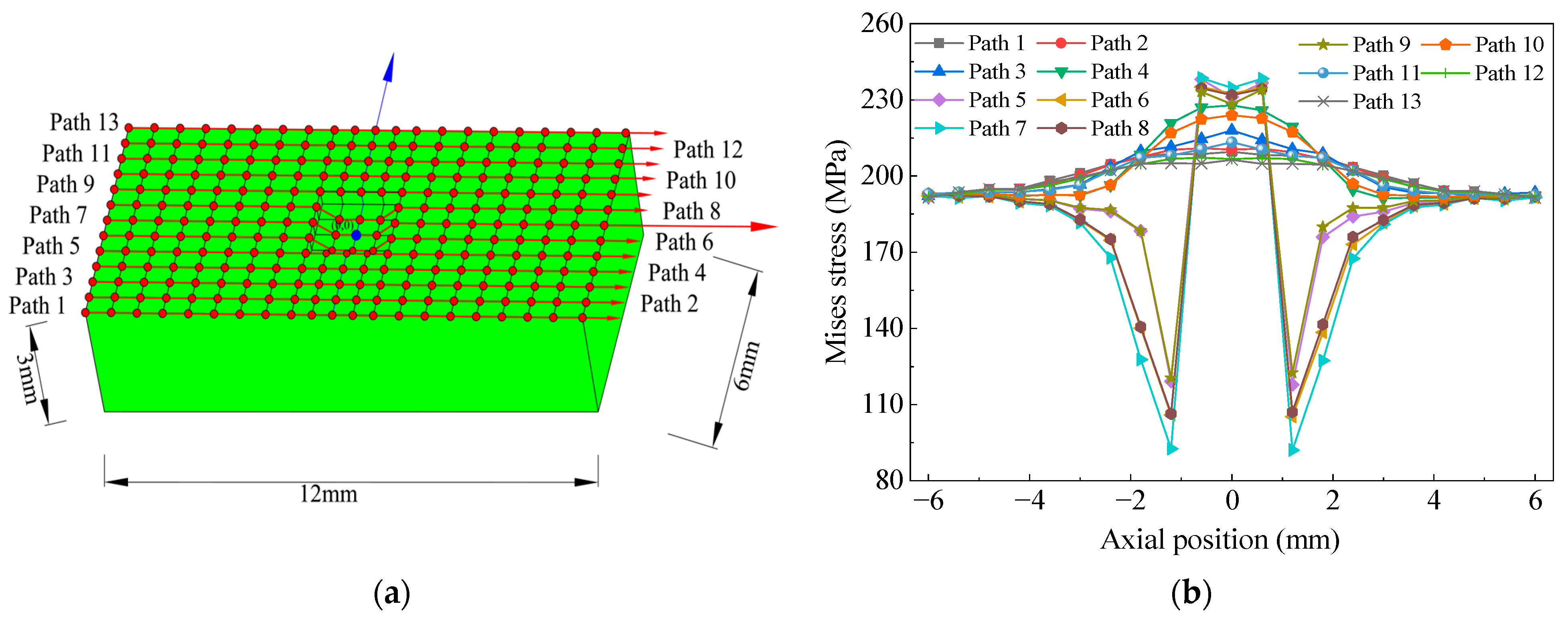
Pronounced stress concentration occurs in the corrosion damage region on the outer surface of Layer VII (tensile armor layer). Moreover, in this region, there is a relatively large Mises stress gradient along the cable axial direction. The closer to the corrosion damage region, the greater the Mises stress gradient.

(3)

Under the action of a 500 kN tensile load, only the conductor layer (Layer I) and lead sheath layer (Layer III) enter the plastic stage. The plastic strain expands radially from the outside to the inside as the tensile load increases.

(4)

For non-penetrating corrosion damage, the maximum Mises stress of the tensile armor layer caused by stress concentration increases with the corrosion damage depth. The tensile stiffness of the SPC decreases as the corrosion damage depth increases, but the decrease is very small, because the corrosion damage area is relatively small compared to the entire cable model dimension.

(5)

When the corrosion damage fully penetrates the tensile armor layer, the maximum Mises stress exhibits a slight reduction to 388.9 MPa despite the increased damage severity, which may be due to stress redistribution.