CFD-Based Estimation of Ship Waves in Shallow Waters
Abstract
1. Introduction
2. Ship Wave Theory
2.1. Fundamental Theory of Ship Waves
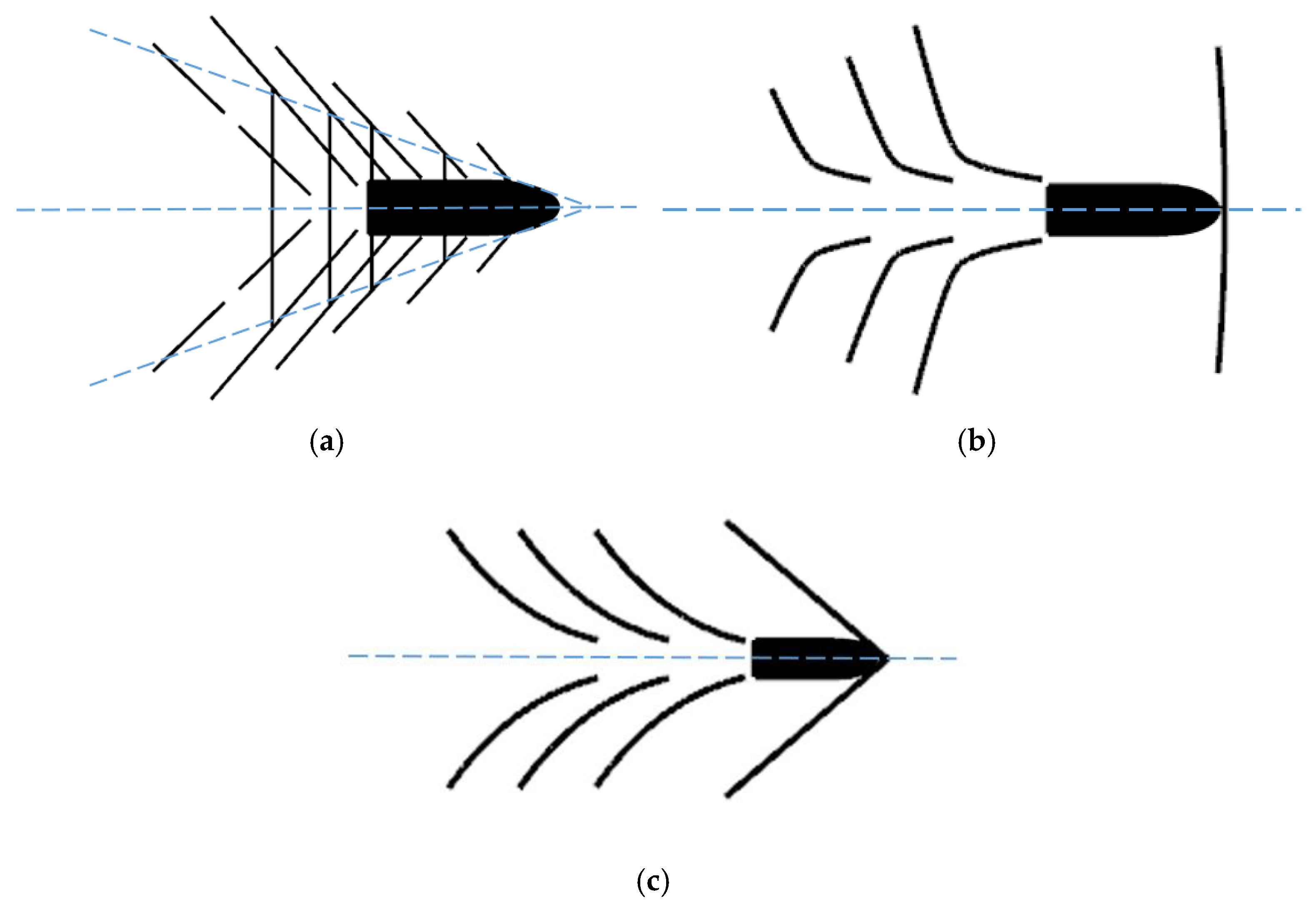
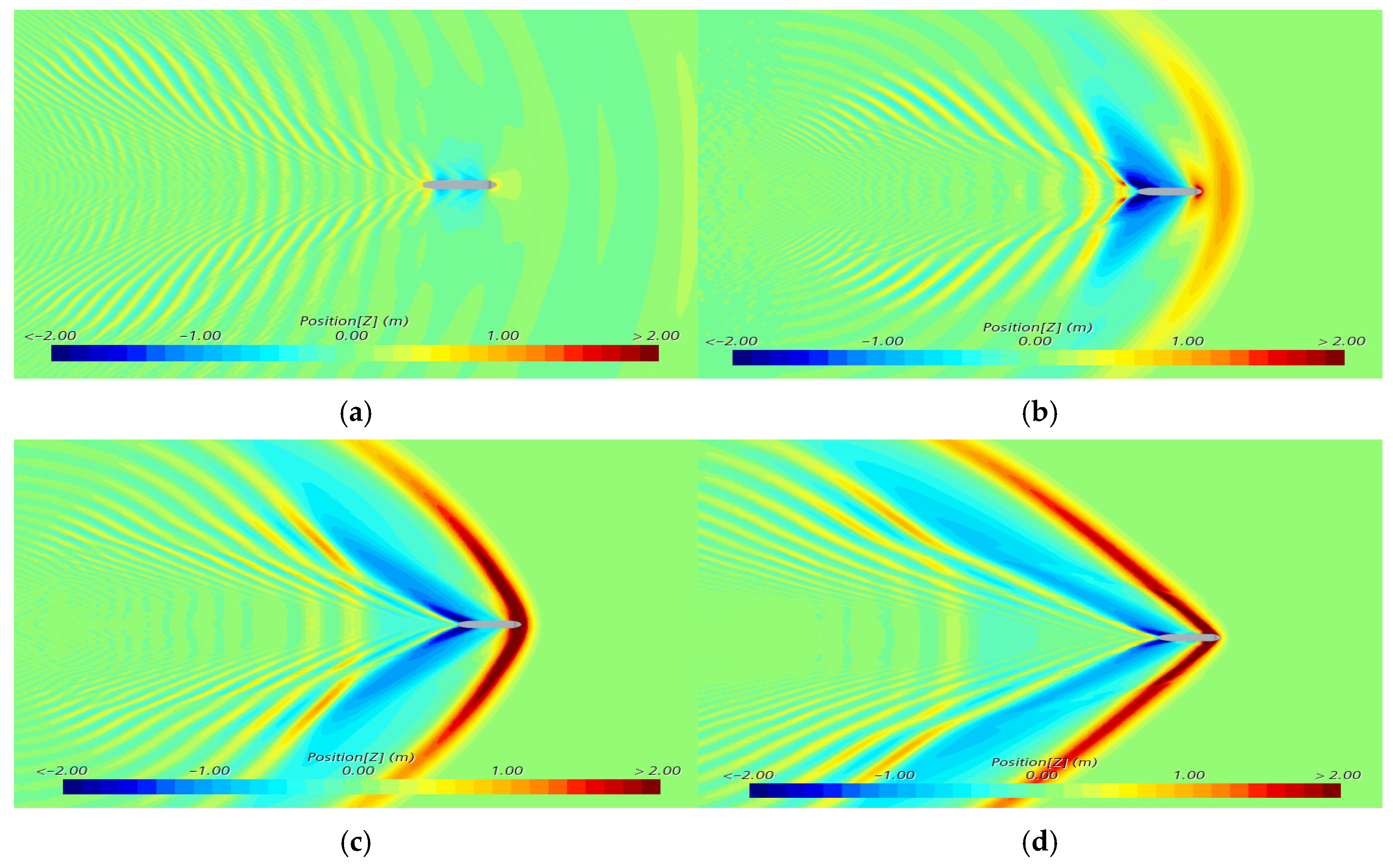
2.2. Ship Wave Patterns
3. Numerical Modeling and Validation
3.1. Fundamental Equations for Shallow Water
3.1.1. Governing Equations
3.1.2. Turbulence Equations
3.2. VOF Model and Discretization Method Selection
3.3. Validation of Numerical Methods
3.3.1. Computational Model and Domain
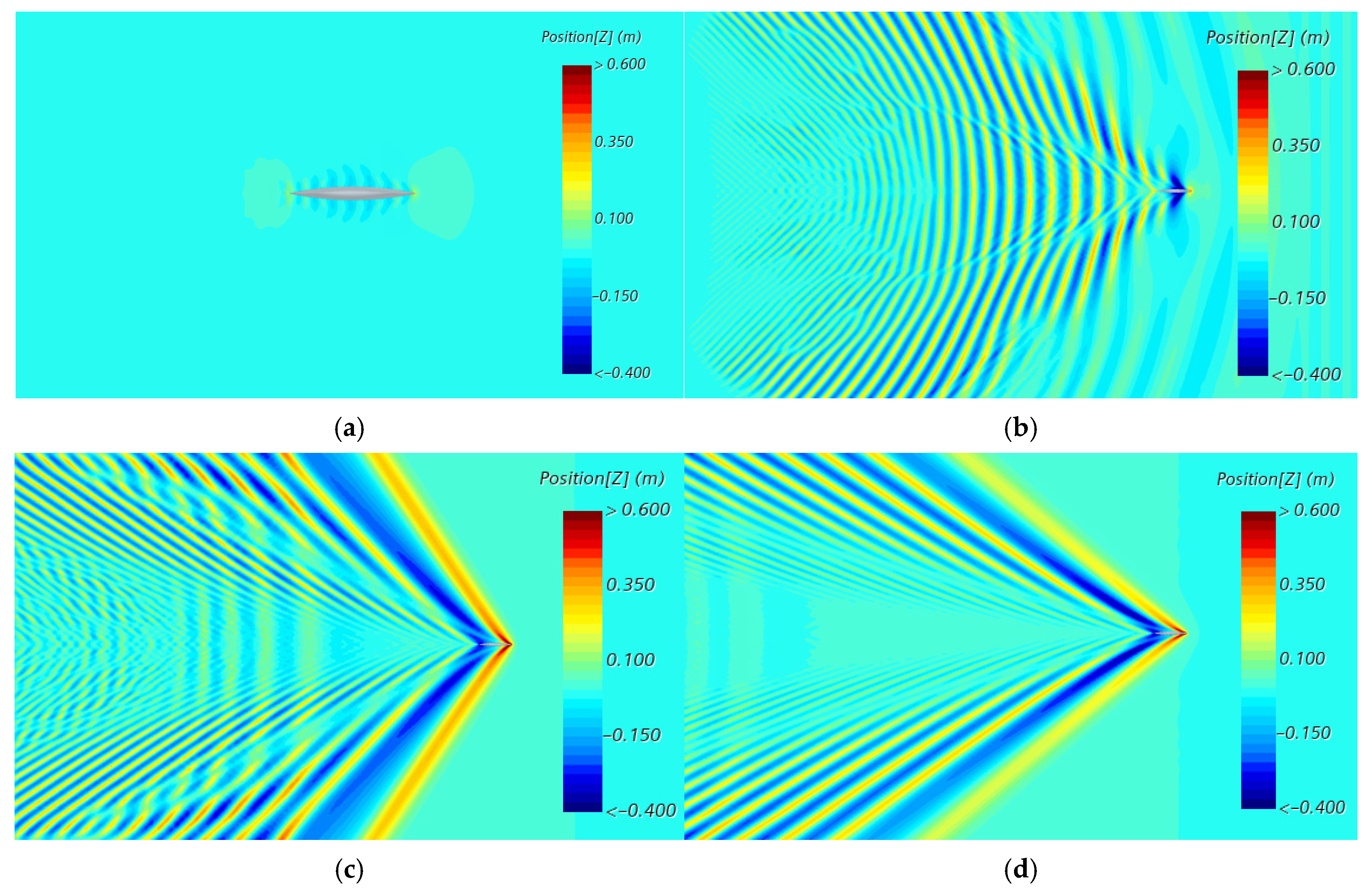
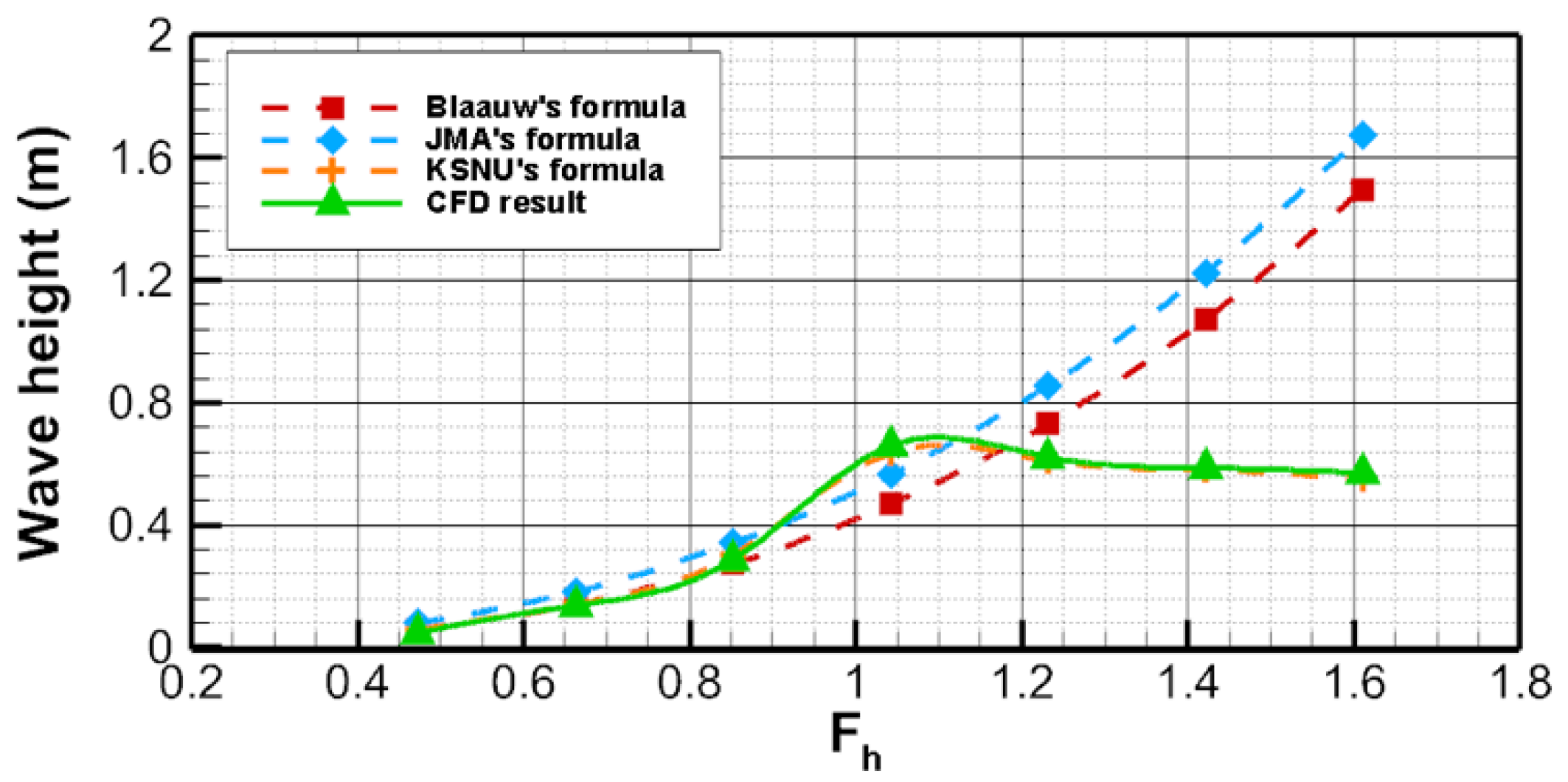
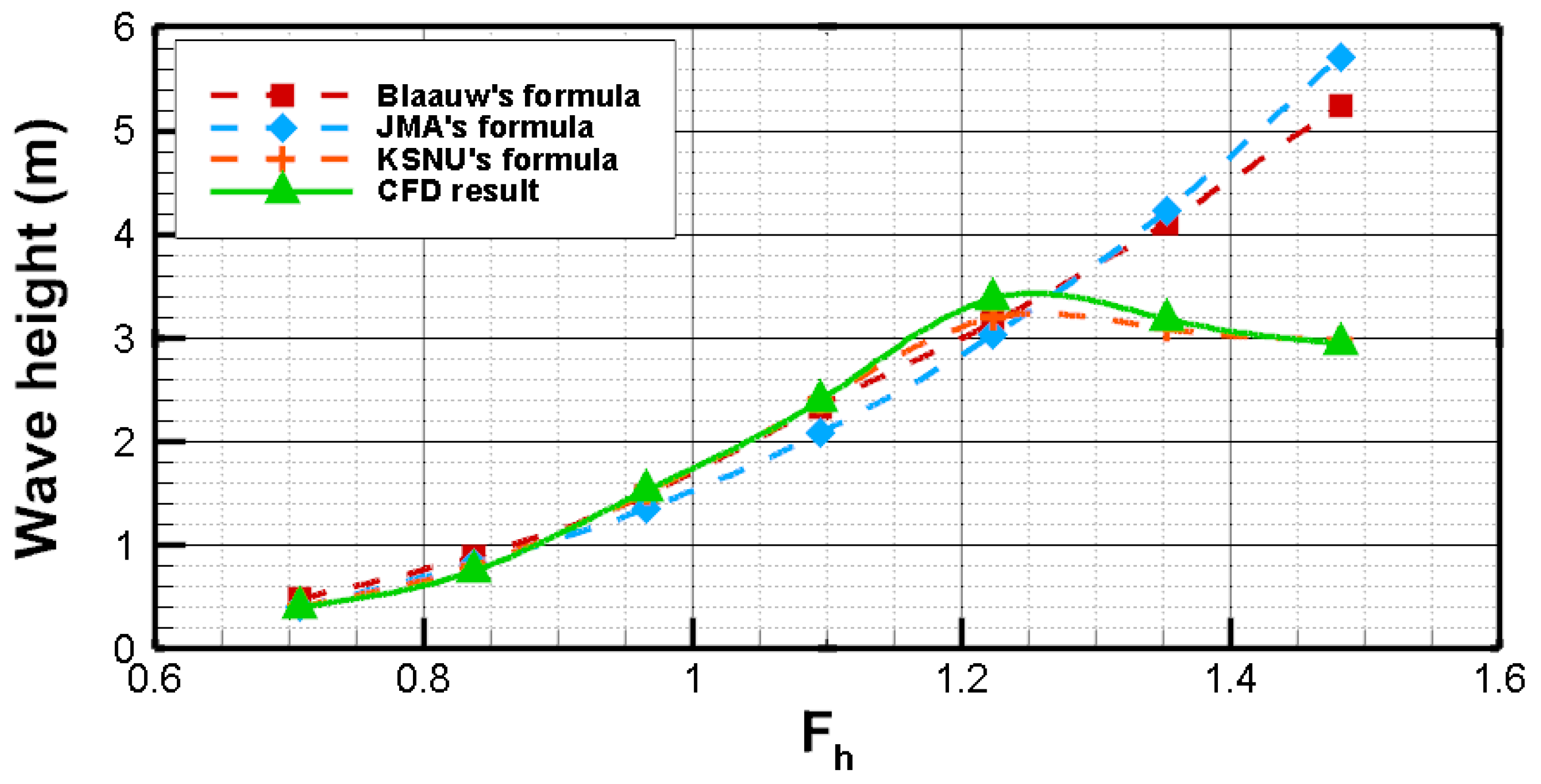
3.3.2. Theoretical Validation of Wave Angle and Height in Shallow Water
4. Numerical Simulation of Ship Waves in Shallow Waters
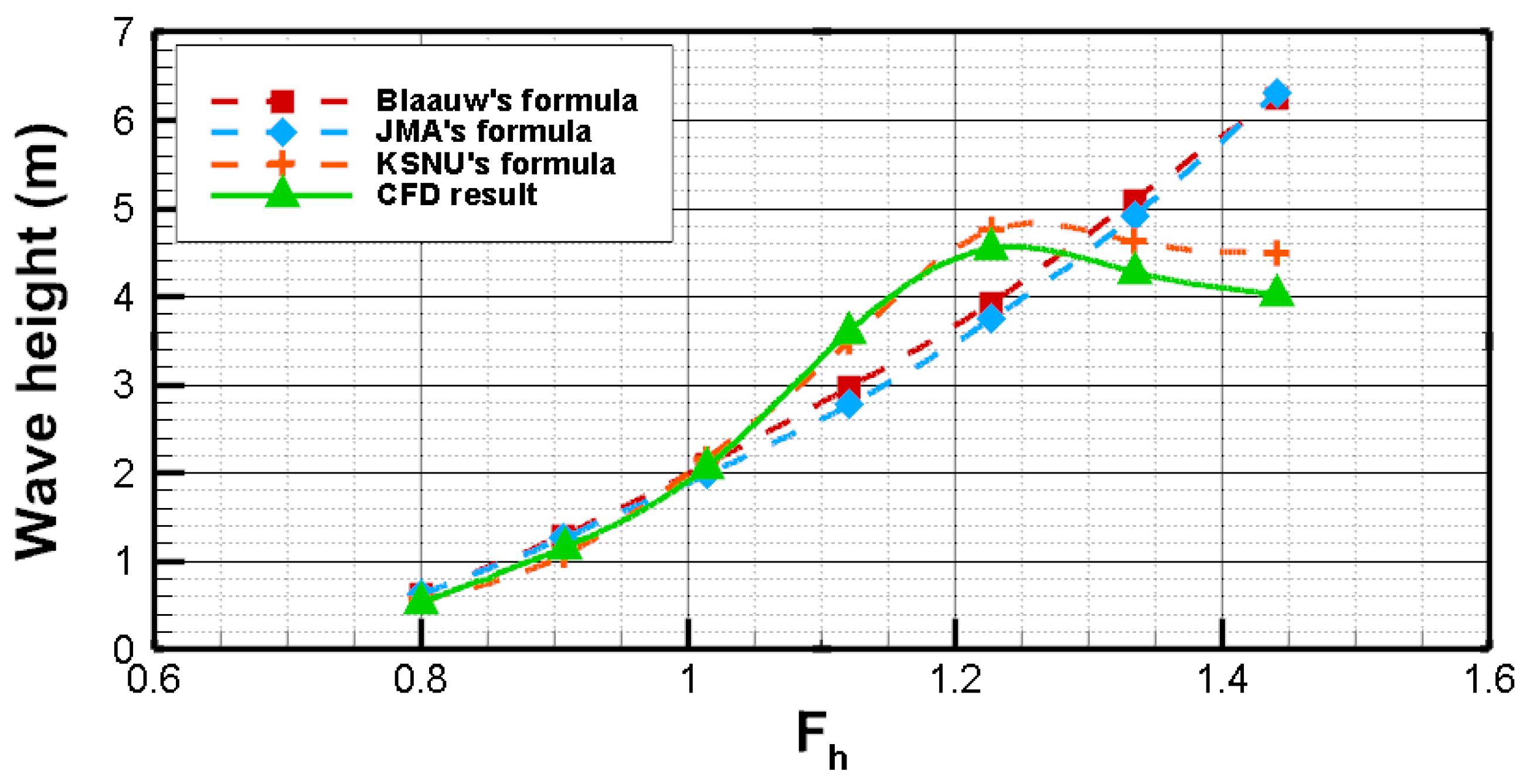
4.1. Ship Waves for 2000-Ton Class Vessel
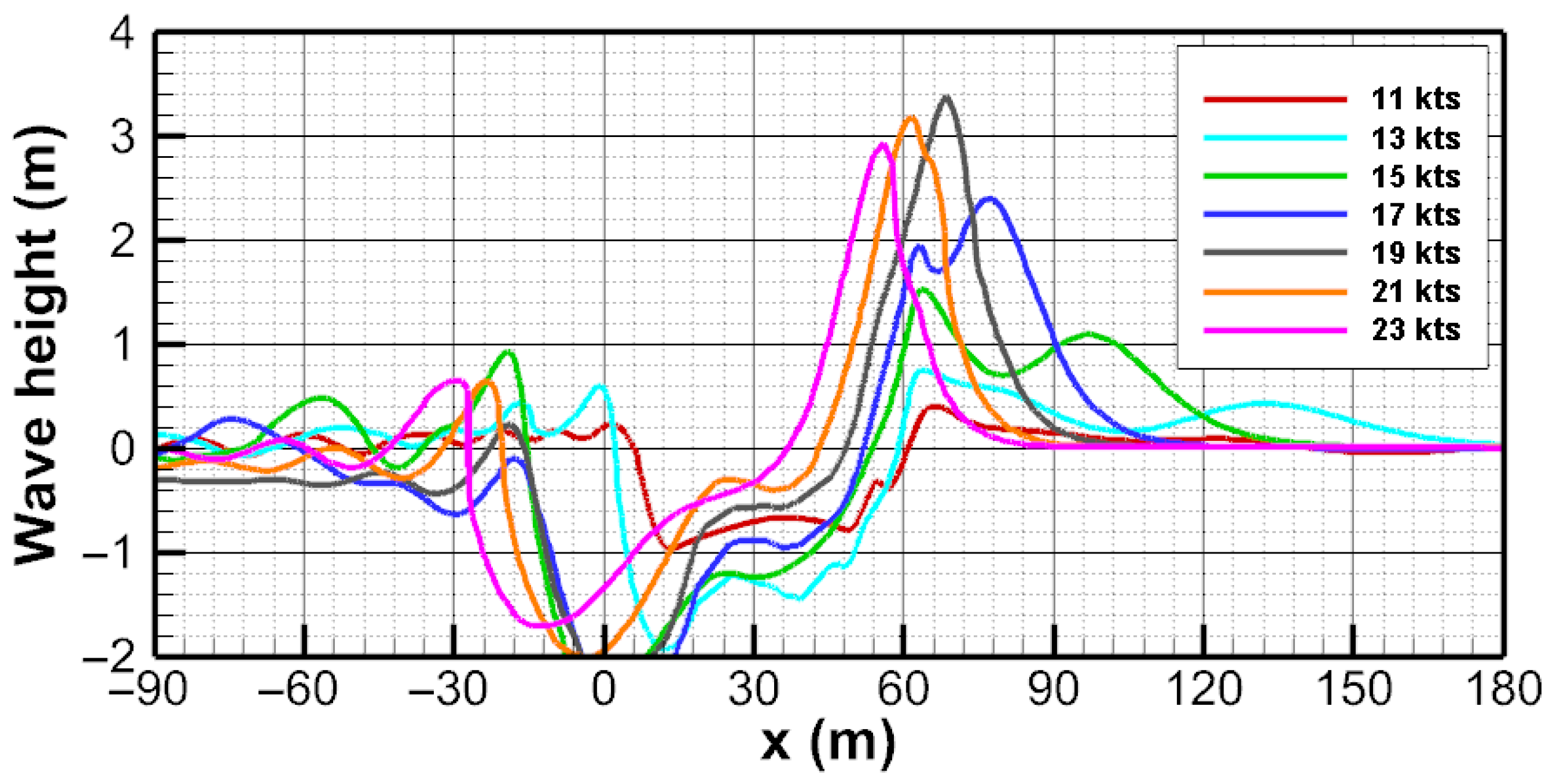
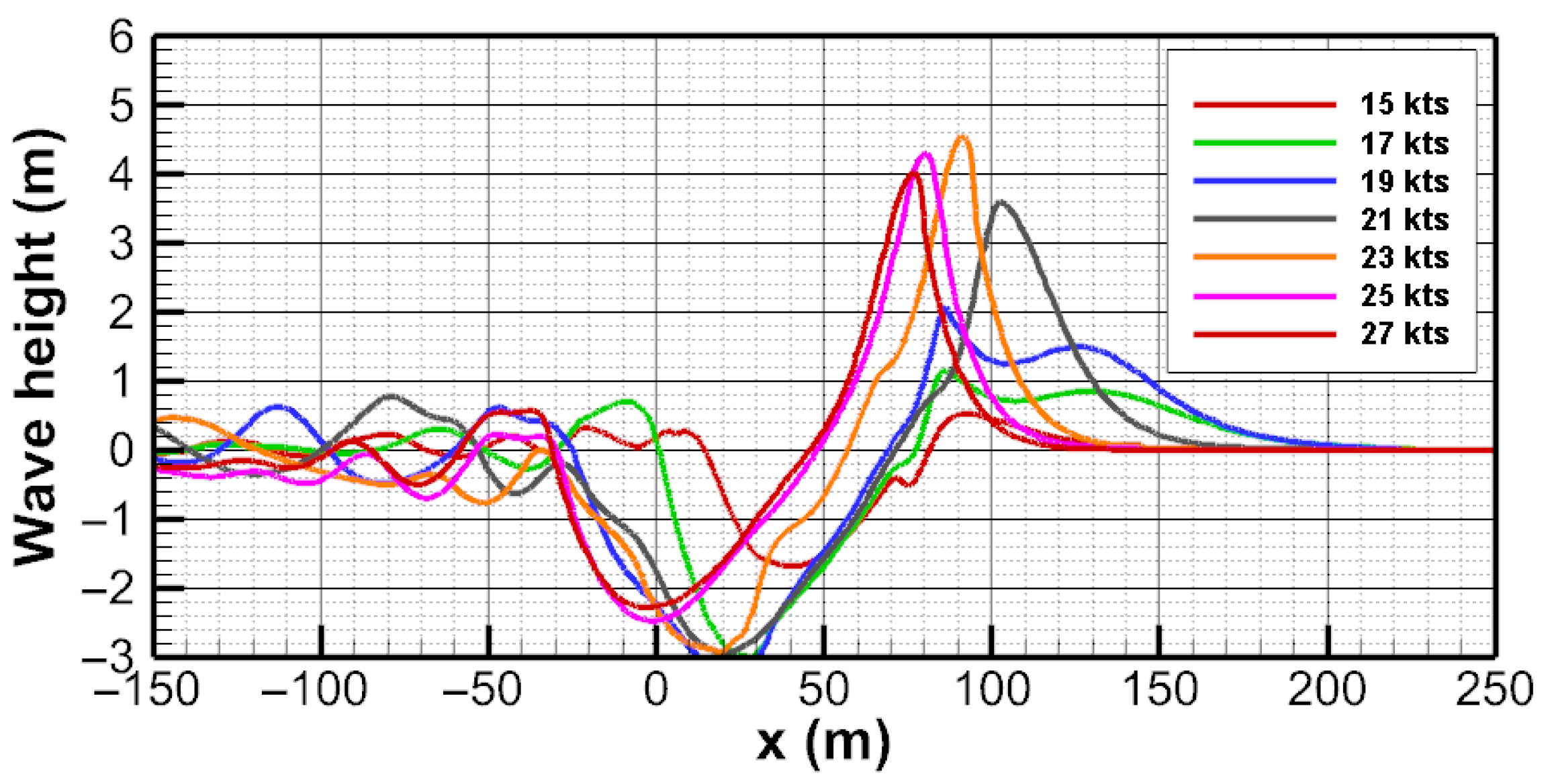
4.2. Ship Waves for 6000-Ton Class Vessel
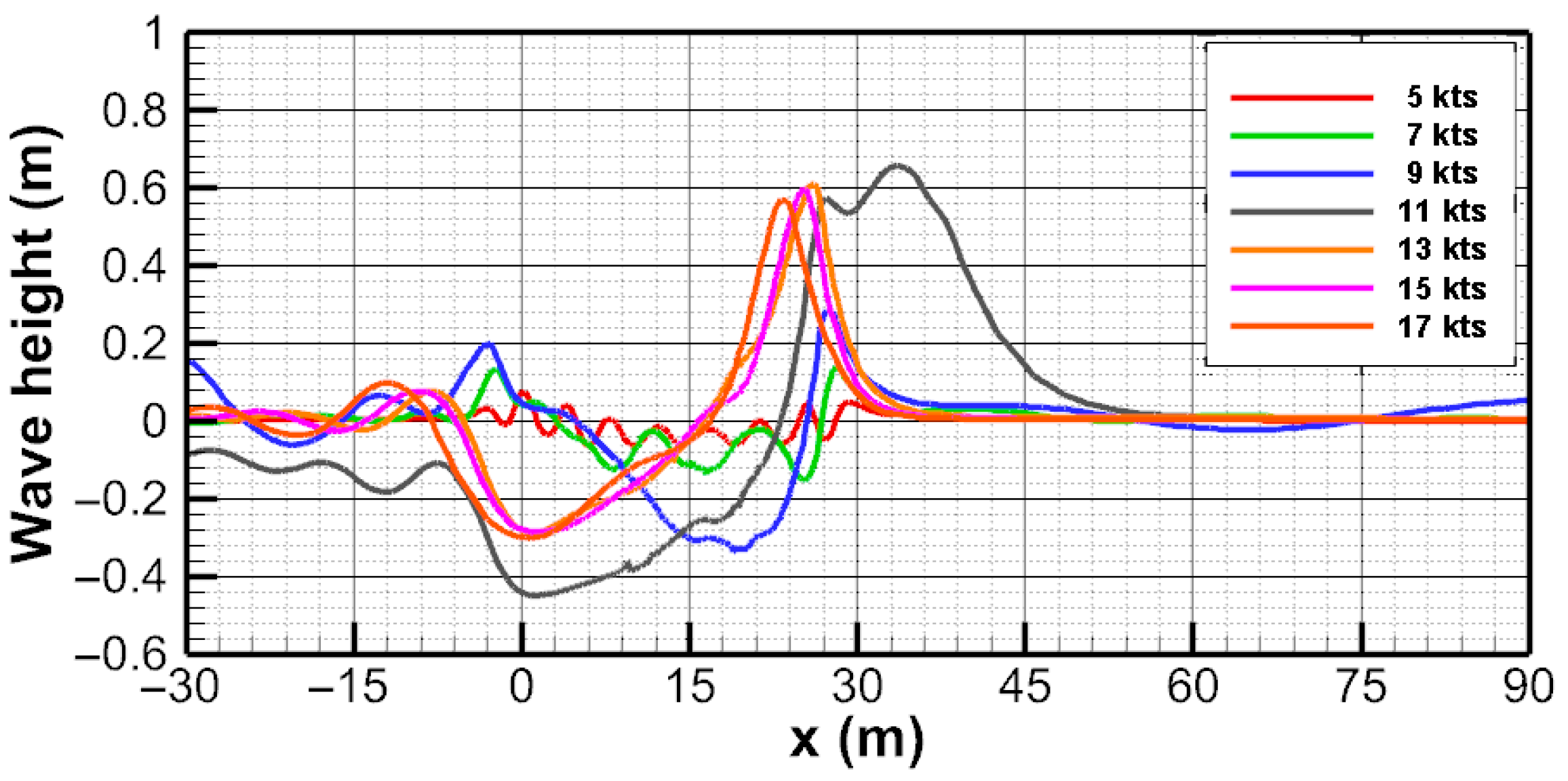
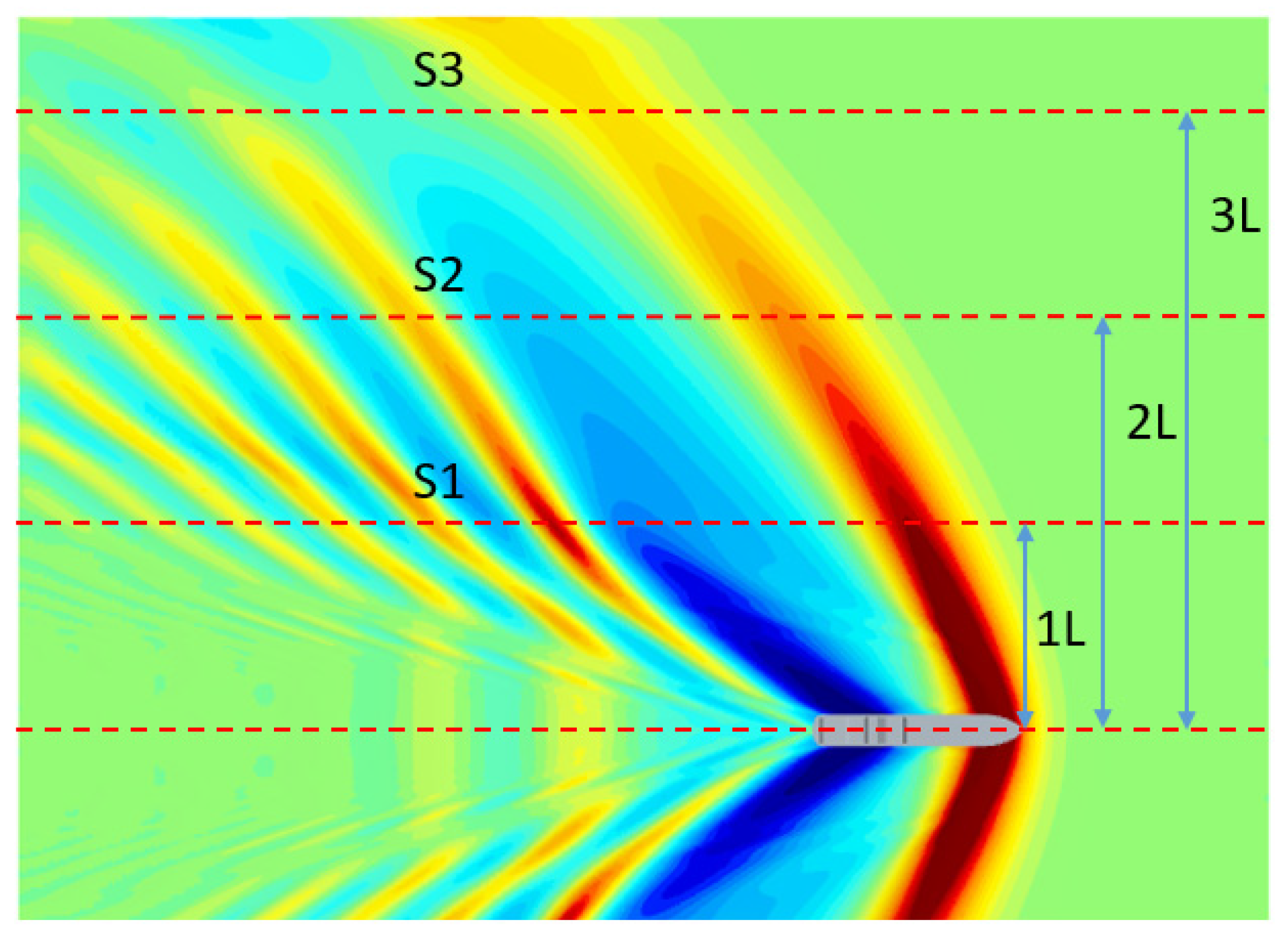
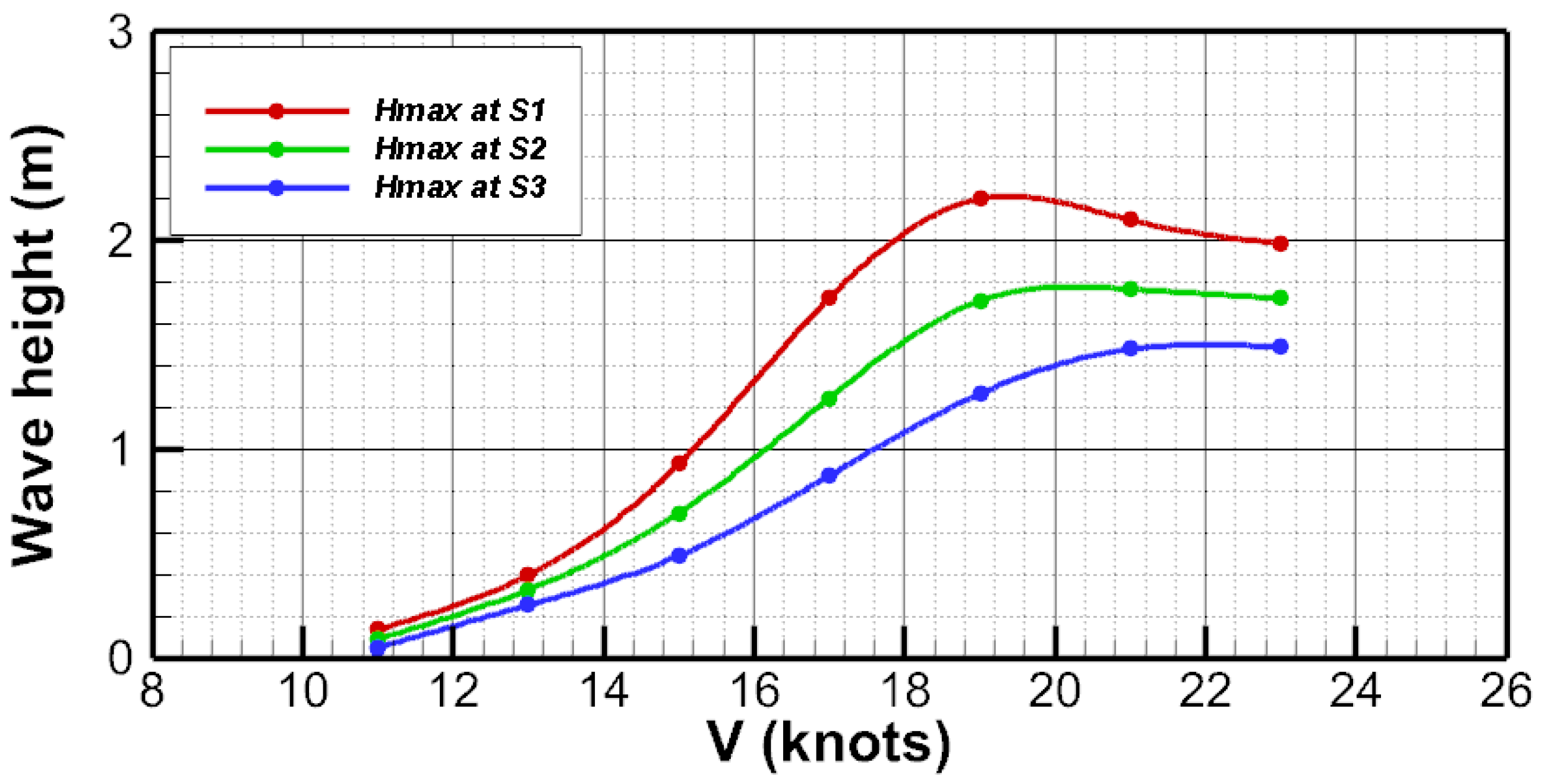
4.3. Wave Height Attenuation Analysis
5. Conclusions
- (1)
- Near the critical depth-based Froude number ( ≈ 1.0), ship waves reach their maximum height, exhibiting a pronounced nonlinear surge in the transcritical regime.
- (2)
- The CFD results for a Wigley hull show strong agreement with the proposed correction formulas, verifying their reliability for predicting wave heights in transcritical and supercritical regimes.
- (3)
- Comparative analysis of 2000-ton and 6000-ton vessels under identical depth-to-draft ratios revealed that larger vessels generate higher peak wave heights, but the presence of a bulbous bow significantly influences attenuation characteristics.
- (4)
- Lateral attenuation of ship waves was confirmed, with rapid decay near the hull and slower attenuation farther away, underscoring the importance of vessel separation in navigation safety.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ravens, T.M.; Thomas, R.C. Ship wave-induced sedimentation of a tidal creek in Galveston Bay. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 21–29. [Google Scholar] [CrossRef]
- Sun, X.; Cai, M.; Wang, J.; Liu, C. Numerical simulation of the Kelvin wake patterns. Appl. Sci. 2022, 12, 6265. [Google Scholar] [CrossRef]
- Thomson, W. On ship waves. Inst. Mech. Eng. 1887, 38, 409–434. [Google Scholar] [CrossRef]
- Havelock, T.H. The propagation of groups of waves in dispersive media, with application to waves on water produced by a travelling disturbance. Proc. R. Soc. Lond. A Math. Phys. Sci. 1908, 81, 398–430. [Google Scholar]
- Hogner, E. Contributions to the theory of ship waves. Ark. Mat. Astron. Fys. 1925, 17, 1–68. [Google Scholar]
- Wehausen, J.V.; Laitone, E.V. Surface Waves. In Encyclopedia of Physics; Springer: Berlin, Germany, 1960; Volume IX, pp. 446–778. [Google Scholar]
- Ursell, F. On Kelvin’s ship-wave pattern. J. Fluid Mech. 1960, 8, 418–431. [Google Scholar] [CrossRef]
- Cumberbatch, E. Effects of viscosity on ship waves. J. Fluid Mech. 1965, 23, 471–479. [Google Scholar] [CrossRef]
- Dawson, C.W. A practical computer method for solving ship-wave problems. In Proceedings of the 2nd International Conference on Numerical Ship Hydrodynamics, Washington, DC, USA, 19–21 September 1977; pp. 30–38. [Google Scholar]
- Ertekin, R.C.; Webster, W.C.; Wehausen, J.V. Waves caused by a moving disturbance in a shallow channel of finite width. J. Fluid Mech. 1986, 169, 275–292. [Google Scholar] [CrossRef]
- Kazi, S.A. Hydrodynamic modelling of vessel-induced water motion using Delft2D-Rivers. In Proceedings of the IHE, Paris, France, 5–9 October 1998. [Google Scholar]
- Wang, J.; Lee, T.S.; Shu, C. Numerical study of wave interaction generated by two ships moving parallely in shallow water. Comput. Methods Appl. Mech. Eng. 2001, 190, 2099–2110. [Google Scholar] [CrossRef]
- Davis, A.M.J.; Geer, J.F. The application of uniform-slender-body theory to the motion of two ships in shallow water. J. Fluid Mech. 1982, 114, 419–441. [Google Scholar] [CrossRef]
- Kijima, K. Manoeuvrability of ship in confined water. In Proceedings of the International Conference on Ship Manoeuvrability—Prediction and Achievement, London, UK, 29 April–1 May 1987. [Google Scholar]
- Vantorre, M.; Verzhbitskaya, E.; Laforce, E. Model test based formulations of ship-ship interaction forces. Ship Technol. Res. 2002, 49, 124–141. [Google Scholar]
- Lataire, E.; Vantorre, M.; Delefortrie, G. Captive model testing for ship to ship operations. In Proceedings of the International Conference Marine Simulation and Ship Maneuverability (MARSIM’09), Panama City, Panama, 17–20 August 2009; Panama Canal Authority: Panama City, Panama, 2009. [Google Scholar]
- Swiegers, P.B. Calculation of the Forces on a Moored Ship Due to a Passing Container Ship. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2011. [Google Scholar]
- Miller, A. Interaction forces between two ships during underway replenishment. J. Navig. 2016, 69, 1197–1214. [Google Scholar] [CrossRef]
- Mursid, O.; Oterkus, E.; Oterkus, S. Coupled ship simulation in hydrodynamics and structural dynamics induced by wave loads: A systematic literature review. J. Mar. Sci. Eng. 2025, 13, 447. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Wang, C.; Kim, H.; Park, Y. A numerical study of drift angle effect on hydrodynamic performance of a fully appended container ship in head waves. Ocean Eng. 2024, 313, 119343. [Google Scholar] [CrossRef]
- Htein, N.M.; Rahman, M.M.; Oka, M.; Okada, T. AI-based optimization techniques for hydrodynamic and structural design in ships: A review. J. Mar. Sci. Eng. 2025, 13, 1719. [Google Scholar] [CrossRef]
- Bagazinski, N.J.; Ahmed, F. ShipGen: A diffusion model for parametric ship hull generation with multiple objectives and constraints. J. Mar. Sci. Eng. 2023, 11, 2215. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, D.; Gao, L.; Miao, Q.M. CFD computation of ship motions and added resistance for a high speed trimaran in regular head waves. Int. J. Nav. Archit. Ocean Eng. 2011, 3, 105–110. [Google Scholar] [CrossRef]
- Ngoc, P.M.; Kim, B.; Yang, C. A velocity prediction program for an autonomous sailing drone. J. Adv. Mar. Eng. Technol. 2021, 45, 288–299. [Google Scholar] [CrossRef]
- Yaakob, O.; Ahmed, Y.M.; Rashid, M.F.A.; Elbatran, A.H. Determining ship resistance using computational fluid dynamics (CFD). J. Transp. Syst. Eng. 2015, 2, 20–25. [Google Scholar]
- Perez, G.; Tan, M.; Wilson, P.A. Validation and verification of hull resistance components using a commercial CFD code. In Proceedings of the 11th Numerical Towing Tank Symposium, Brest, France, 7–9 September 2008. [Google Scholar]
- Lv, X.; Wu, X.; Sun, J.; Tu, H. Trim optimization of ship by a potential-based panel method. Adv. Mech. Eng. 2013, 5, 378140. [Google Scholar] [CrossRef]
- Nam, B.W.; Park, J.Y. Numerical simulation for a passing ship and a moored barge alongside quay. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 566–582. [Google Scholar] [CrossRef]
- Duarte, H.O.; Droguett, E.L.; Martins, M.R.; Lutzhoft, M.; Pereira, P.S.; Lloyd, J. Review of practical aspects of shallow water and bank effects. Int. J. Marit. Eng. 2016, 158, 177–186. [Google Scholar] [CrossRef]
- Yan, K.; Oh, J.; Seo, D.W. Numerical Study on the Performance of Resistance various Trim Tab’s Position and Size for High-Speed Small Boat. J. Korea Acad.-Ind. Coop. Soc. 2023, 24, 206–218. [Google Scholar]
- ITTC Resistance Committee. Cooperative Experiments on Wigley Parabolic Models in Japan. In 17th ITTC Resistance Committee Report, 2nd ed.; Resistance Committee of the International Towing Tank Conference (ITTC): Varna, Bulgaria, 1983. [Google Scholar]
- Blaauw, H.G.; van der Knaap, F.C.M.; de Groot, M.T.; Pilarczyk, K.W. Design of Bank Protection of Inland Navigation Fairways; Delft Hydraulics Laboratory: Delft, The Netherlands, 1984. [Google Scholar]
- Lee, J.M. Study on the Characteristics of Ship Wave Generation Due to Ship Traffic in Busan North Port. Master’s Thesis, Pukyong National University, Busan, Republic of Korea, 2022. [Google Scholar]
- Kang, Y.S.; Kim, P.J.; Hyun, S.K.; Sung, H.K. Numerical simulation of ship-induced wave using FLOW-3D®. J. Korean Soc. Coast. Ocean Eng. 2008, 20, 255–267. [Google Scholar]
- Shin, S.H.; Jeong, D.D. Numerical prediction of ship induced wave and its propagation using nonlinear dispersive wave model. J. Navig. Port Res. 2003, 27, 527–537. [Google Scholar]
- Lee, D.S.; Kwon, K.D.; Jo, H.S. A study on the greenhouse gas emission from ships with training ship HANBADA. J. Korean Soc. Mar. Eng. 2014, 38, 240–245. [Google Scholar] [CrossRef]

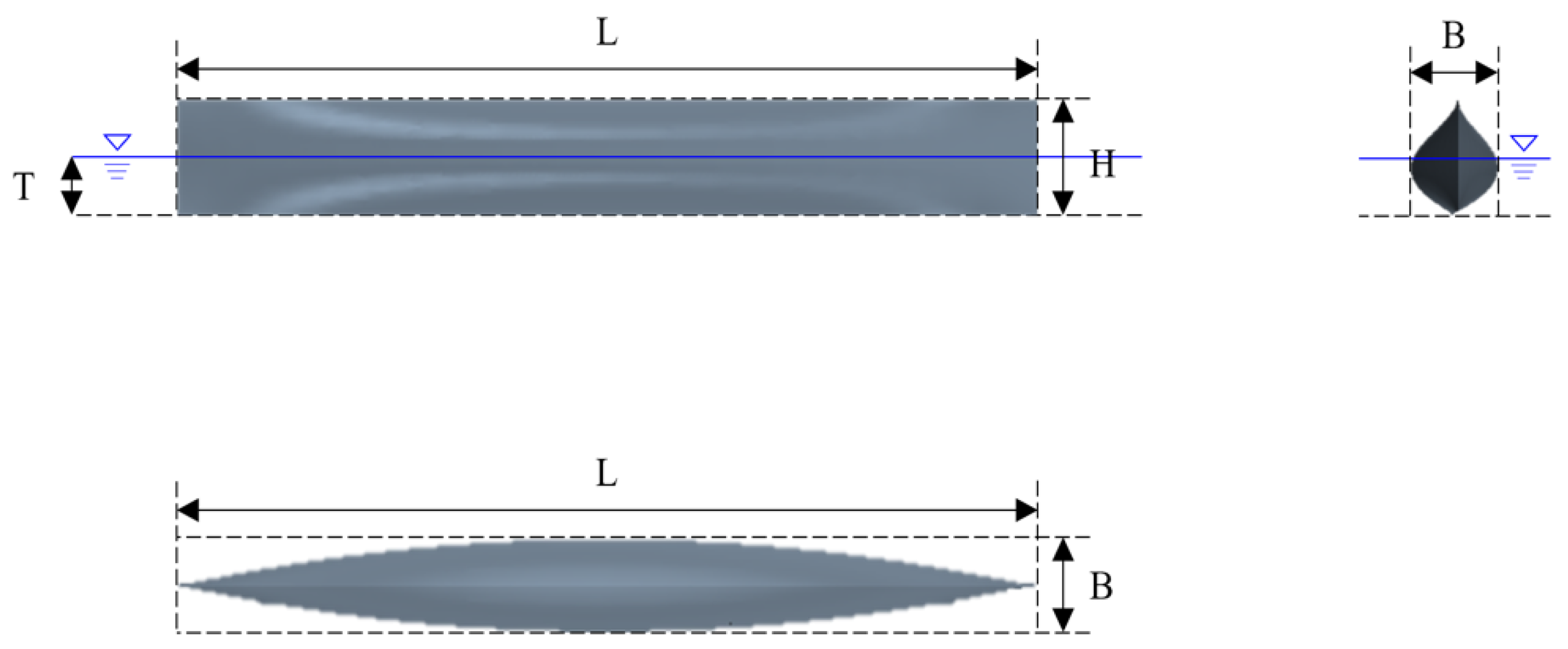



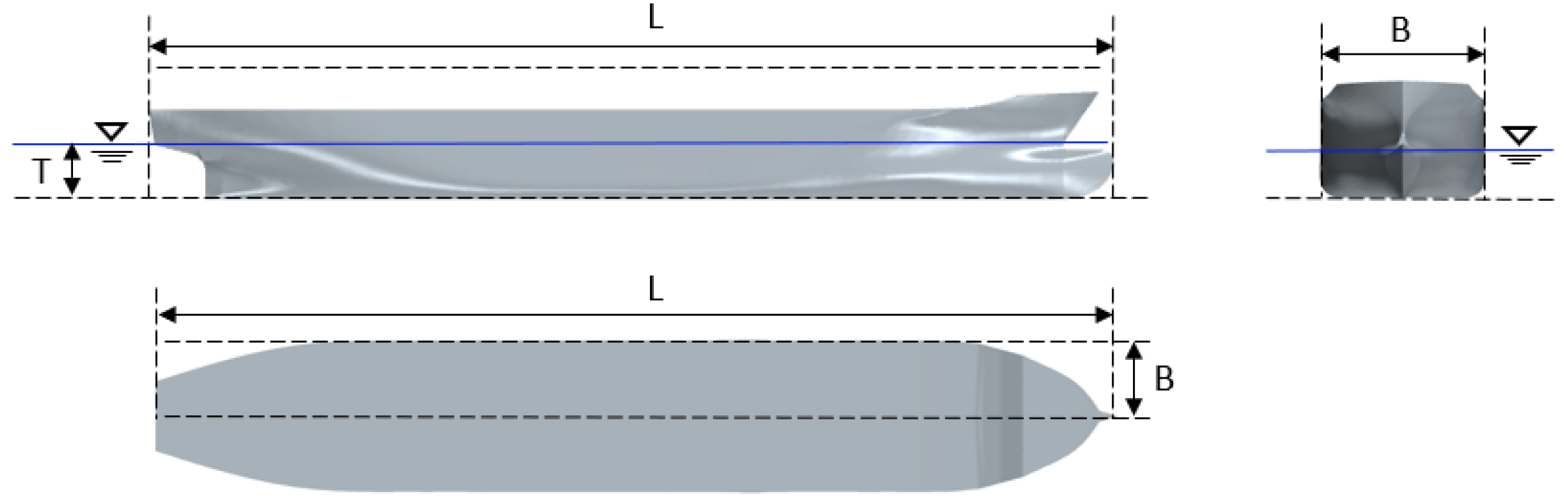

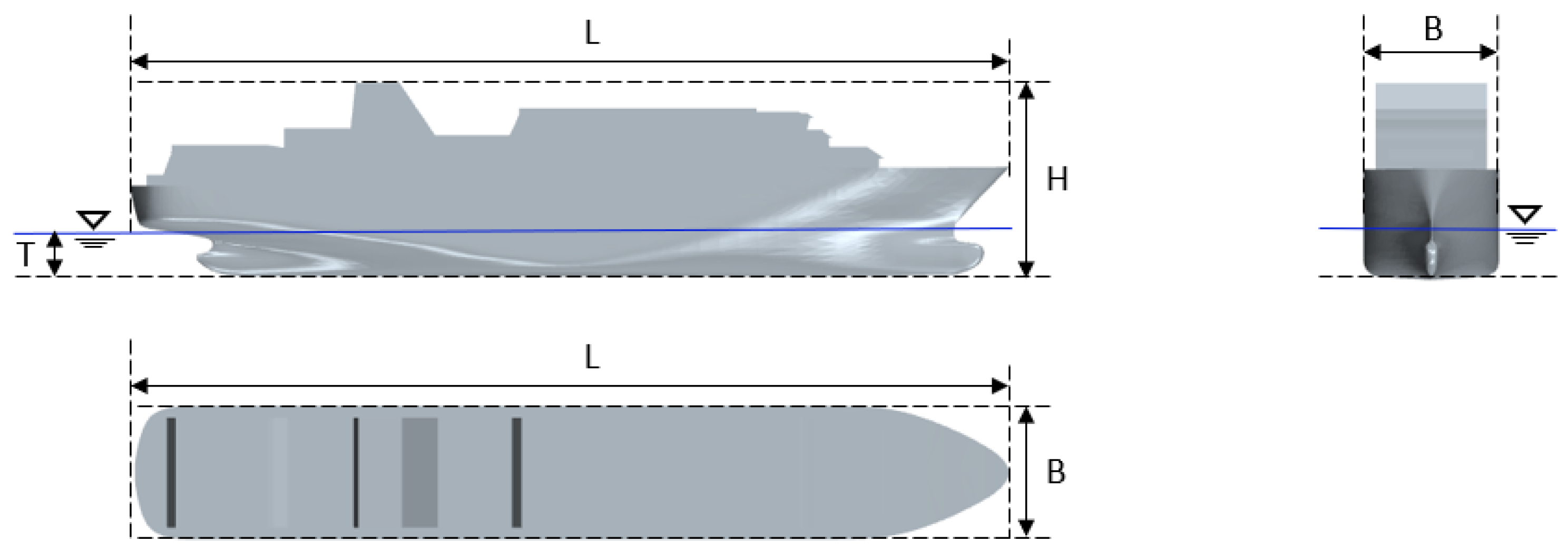



| Parameters (Symbol) | Value (Unit) |
|---|---|
| Length (L) | |
| Breadth (B) | |
| Height (H) | |
| Draft (T) | |
| Wetted surface area (Sw) | |
| ) | |
| ) |
| (kts) | (m/s) | |
|---|---|---|
| 5 | 5.425 | 0.474 |
| 7 | 0.663 | |
| 9 | 0.853 | |
| 11 | 1.042 | |
| 13 | 1.232 | |
| 15 | 1.421 | |
| 17 | 1.611 |
| Parameters (Symbol) | Value (Unit) |
|---|---|
| Length (L) | |
| Length Between Perpendicular (LBP) | |
| Breadth (B) | |
| Draft (T) | |
| ) | |
| ) |
| (kts) | (m/s) | |
|---|---|---|
| 11 | 7.983 | 0.708 |
| 13 | 0.837 | |
| 15 | 0.966 | |
| 17 | 1.095 | |
| 19 | 1.223 | |
| 21 | 1.352 | |
| 23 | 1.481 |
| Parameters (Symbol) | Value (Unit) |
|---|---|
| Length (L) | |
| Length Between Perpendicular (LBP) | |
| Breadth (B) | |
| Draft (T) | |
| ) | |
| ) |
| (kts) | (m/s) | |
|---|---|---|
| 15 | 9.635 | 0.800 |
| 17 | 0.907 | |
| 19 | 1.014 | |
| 21 | 1.120 | |
| 23 | 1.227 | |
| 25 | 1.334 | |
| 27 | 1.440 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Lee, I.; Oh, J.; Seo, D. CFD-Based Estimation of Ship Waves in Shallow Waters. J. Mar. Sci. Eng. 2025, 13, 1965. https://doi.org/10.3390/jmse13101965
Ma M, Lee I, Oh J, Seo D. CFD-Based Estimation of Ship Waves in Shallow Waters. Journal of Marine Science and Engineering. 2025; 13(10):1965. https://doi.org/10.3390/jmse13101965
Chicago/Turabian StyleMa, Mingchen, Ingoo Lee, Jungkeun Oh, and Daewon Seo. 2025. "CFD-Based Estimation of Ship Waves in Shallow Waters" Journal of Marine Science and Engineering 13, no. 10: 1965. https://doi.org/10.3390/jmse13101965
APA StyleMa, M., Lee, I., Oh, J., & Seo, D. (2025). CFD-Based Estimation of Ship Waves in Shallow Waters. Journal of Marine Science and Engineering, 13(10), 1965. https://doi.org/10.3390/jmse13101965






