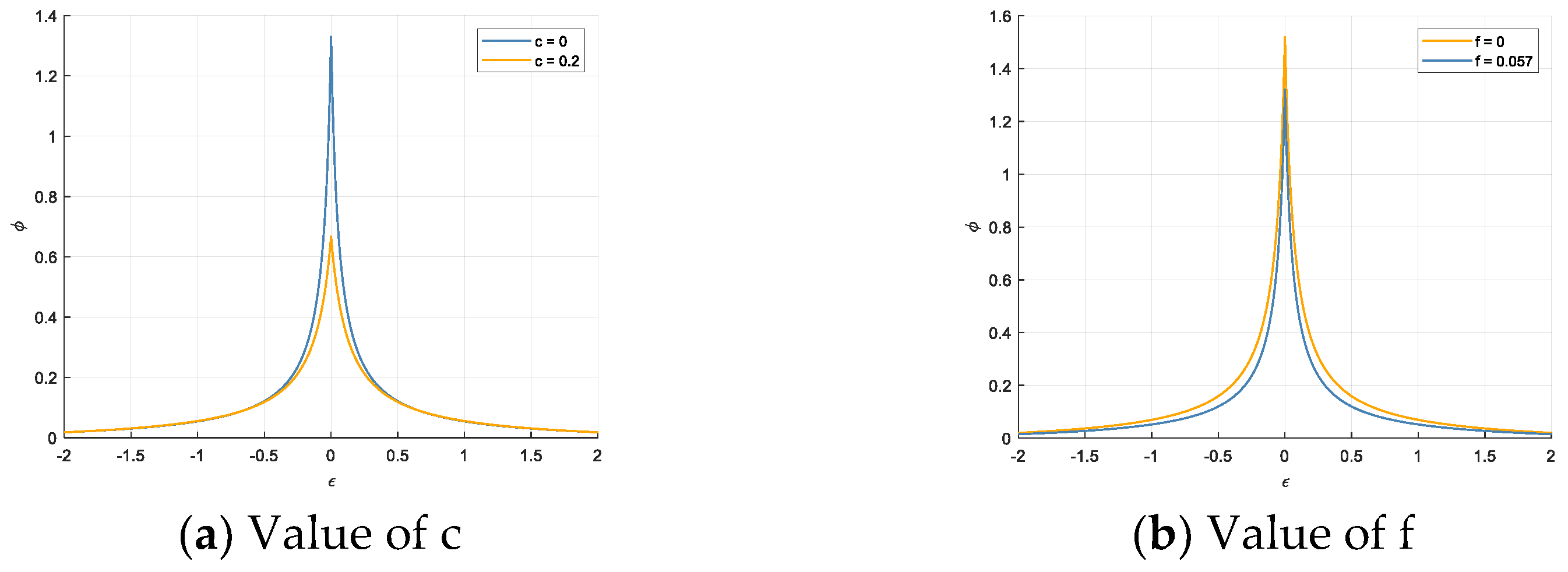Risk-Coupling Analysis and Control Mechanism of Port Dangerous Goods Transportation System

Abstract

With the integration of the global economy and the rapid development of port logistics, the port dangerous goods transportation system faces complex risk-coupling problems, and the probability of accidents keeps climbing. However, the existing research on the system risk-coupling mechanism and dynamic control mechanism is still insufficient, and there is an urgent need to construct a scientific risk analysis and control model. This study takes the port dangerous goods transportation system as the object, based on the four-factor framework of “personnel-machine-environment-management,” uses the N-K model to quantify the degree of risk coupling, analyzes the dynamic evolution mechanism of risk under the action of a single factor, and uses Dufferin’s oscillation and bifurcation response equation to reveal the interaction between the system’s internal defenses and the external influences. It is found that the coupled risk value of personnel–machine factors is the highest, and the sudden change in system state is characterized by a sudden jump and lag. The system stability can be significantly improved by enhancing internal damping control and optimizing external excitation regulation. This study provides a quantitative tool for the risk assessment of dangerous goods transportation in ports and theoretical support for the development of the “damping-excitation” synergistic control strategy, which is of great practical significance for the improvement of the port safety management system.

1. Introduction

In the context of the continuous promotion of global economic integration and the rapid development of port logistics, ports have become extremely critical hubs in the field of international trade and logistics. However, the port dangerous goods transportation system, in its complicated operation process, encounters personnel, machinery and equipment, environment, management, and other factors intertwined with each other, so that the probability of accidents continues to rise. For example, in 2015, the “8–12” Ruihai Dangerous Goods Warehouse in Tianjin Port was involved in a particularly major fire and explosion accident, resulting in the deaths of 173 people and a direct economic loss of RMB 6.866 billion. In addition, in 2020, the tanker explosion accident that occurred in the Wenling section of the Shenhai Expressway also caused extremely serious casualties and property losses; thus, the risk a coupling problem in the port hazardous materials transportation system is becoming increasingly serious, and there is an urgent need to carry out in-depth research on the risk-coupling mechanism and control mechanism and to formulate an effective risk assessment and control model. Traditional risk assessment methods struggle to effectively address highly coupled risk events due to their failure to adequately account for the complex interactions among multiple factors—personnel, machinery, environment, and management. Consequently, there is an urgent need for an innovative risk-assessment model integrating complex systems theory to enhance the safety management level of hazardous materials transportation in ports. The current research is still lacking in this aspect, and there is a lack of systematic theoretical support and practical guidance for the exploration of dynamic control mechanisms. The analysis of the risk coupling of the port dangerous goods transportation system and the study of control mechanisms have key theoretical significance and practical value, and, with the help of constructing a scientific risk analysis and control model, a quantitative tool can be provided for the management of port safety, the development of a “damping-excitation” synergistic control strategy, and the development of an effective risk assessment and control model. An incentive synergistic control strategy can be formulated to improve the stability of the system, prevent and reduce the occurrence of accidents, safeguard the safety of people and property, and promote the realization of sustainable development of port logistics.

In the Port Dangerous Goods Safety Regulations, Article 87, dangerous goods refer to explosive, flammable, poisonous, corrosive, radioactive, and other hazardous properties of substances, materials, or goods. Such substances in the port operation can easily cause personal injury or death, destruction of property, or environmental pollution, and, therefore, require special protective measures. Port dangerous goods transportation accidents involve a variety of risk factors coupled with each other to form a composite mechanism. Nowadays, the research on the risk of dangerous goods transportation has achieved certain results in the domestic and international academic fields, mainly focusing on the use of accident statistics to carry out analysis and the construction and application of risk assessment or evaluation models and other levels [1,2,3,4]. Y. Zhang et al. constructed a fuzzy comprehensive evaluation model, which is innovatively applied to risk assessment for hazardous chemical storage in power grid enterprises [5]. L. Wang et al., from the perspective of mixed traffic flows, worked on a data-driven risk assessment method that is proposed to identify high-risk collision events between automated vehicles and surrounding vehicles [6]. In the field of exploring safety issues in hazardous materials transportation, extensive statistical analysis and root-cause investigations have been conducted [7,8,9,10]. W. Yukun, L conducted qualitative analysis of hazardous materials during port trans-shipment, provided quantitative combustion calculation methods, and analyzed and evaluated the safety risks associated with hazardous materials [11]. In the field of physics, the coupling phenomenon is rigorously defined as the interconnection and influence between two or more systems or motion patterns, which can cause significant changes in the nature and state of the coupling factors. Research on risk coupling primarily focuses on areas with higher risk coefficients [12,13,14,15,16]. X. Meng employs a novel risk-coupling quantification method, combining the N-K model with Bayesian networks (BN) to analyze ship collision accidents [17]. Jianqun Guo proposed an optimization model for port emergency resource allocation based on IMOPSO and entropy-weighted TOPSIS [18]. Zengkai Liu proposed a risk-coupling analysis method based on DBN and NK models [19]. Mohsen Azimi proposed a risk-coupling analysis method based on DBN and NK models [20]. Jian Guo developed a novel risk-coupling model using AHP and N-K theory, employing the AHP-N-K model to calculate the coupling degree of risk factors. This approach further analyzed the underlying mechanisms, linking risk values and risk composition within complex marine environments [21]. The steady development of the dangerous goods transportation industry has highlighted the importance of systematic risk control, and the implementation of a series of efficient risk-control strategies can significantly reduce the probability of accidents and ensure the safe transportation of dangerous goods. At present, most of the literature focuses on risk assessment through the identification of the core risk factors of the system, and puts forward targeted risk control measures, but there is insufficient in-depth exploration of the system risk-control mechanism. Kamran Gholamizadeh et al. identified key investigation areas such as risk management, safety routes, and emergency response through bibliometric analysis and systematic review methodologies [22]. Di Kang developed a probabilistic risk analysis model for modeling risks in the transportation of dangerous goods by rail [23].

There are still difficult problems with the coupling analysis and risk control of the port dangerous goods transportation system. This paper innovates by using the “personnel-equipment-environment-management” framework to quantify the risk-coupling degree of framework, integrating the N-K model to quantify risk coupling within port hazardous cargo transportation systems. Utilizing the Dufour equation, it reveals interactions between system defenses and external influences, identifying personnel–machine coupling as the highest risk area and demonstrating system mutations exhibit abruptness and lag. The study proposes a “damping-excitation” coordinated control strategy, filling a gap in research on dynamic control mechanisms.

In this study, the N-K model is first used to model the risk coupling of the port dangerous goods transportation system and calculate the system-related coupling risk value. On this basis, the interactions and coupling effects of the four key factors of “personnel, machine, environment and management” in the port dangerous goods transportation are analyzed in depth. Secondly, single-factor coupled-risk folding mutation modeling and Dufferin oscillation modeling are carried out, focusing on the dynamic evolution of risk and related risk control of the port dangerous goods transportation system under a single influencing factor. The results of the study are of great theoretical and social significance for the safe management and efficient operation of the port dangerous goods transportation system.

2. Description

This study analyzes the risk-coupling problem in the port dangerous goods transportation system, constructs a risk analysis and management model, identifies and defines the four key factors of “personnel-equipment-environment-management” that have an impact on transportation safety, constructs a scientific index system based on the above factors, and quantifies the coupling relationship between the risk factors by using the N-K model to evaluate the overall risk of the system. The N-K model is used to quantify the coupling relationship between each risk factor and assess the overall risk of the system. With the help of Dufferin’s oscillation bifurcation response equation to analyze the dynamic impact of a single factor on the state of the system, revealing the evolution mechanism of the potential risk, the study proposes targeted risk-control strategies based on the results of the analysis to enhance the overall safety management level of the transportation of dangerous goods in ports and to provide strong support for the theoretical research and practical application of the related fields.

The causative mechanisms of risk incidents in port hazardous materials transportation systems are primarily analyzed from four aspects: personnel, equipment, environment, and management [24,25,26]. On the basis of an in-depth analysis of the causal mechanism of risky accidents in the port dangerous goods transportation system, an evaluation system for the risk factors of the system is designed and constructed, as shown in Figure 1.

This study constructs a risk analysis and management model based on the four factors of “personnel-machine-environment-management” for the research subject of the port hazardous materials transportation systems. The core tool is the N-K model, used to quantitatively describe and evaluate the coupling relationships among different risk factors. The fundamental unit count N corresponds to the total number of the four major factors and their internal sub-factors. If each sub-unit possesses multiple states, the total number of possible states is n~K, where K represents the number of interdependencies among sub-units. The states of the four risk factors—personnel, machine, environment, and management—are denoted as h, i, j, and k, respectively, satisfying h = 1…H, i = 1…I, j = 1…J, and k = 1…K. Under these state combinations, Equation (1) provides the computational framework for the coupled risk T. An increase in T indicates tighter coupling among the four factors and a greater likelihood of the system entering a high-risk state. Based on this, subsequent analysis focuses on the dynamic characteristics of single-factor and multi-factor coupling and the effectiveness of control strategies. This study utilizes 491 accident investigation reports from the MSA between 2014 and 2024 as its data foundation. The four core risk factors are discretized into multiple states, denoted by h = 1…H, i = 1…I, j = 1…J, and k = 1…K for each respective state. For each state combination (h, i, j, k), corresponding probability metrics P_h, P_i, P_j, and P_k are calculated. Subsequently, Equation (1) is used to determine the probability of coupling effects under this state combination and the distribution of coupling risk T.

3. Methodology

This study aims to develop a scientific risk analysis and control model tailored to the complexity and dynamic characteristics of port hazardous materials transportation systems. By systematically analyzing the coupling and evolution mechanisms of multi-factor risks, effective control strategies will be formulated to enhance the overall safety management level of the system and reduce accident risks. This paper classifies risks in port hazardous materials transportation systems based on the “personnel-machine-environment-management” four-factor framework, providing a clear delineation of elements for subsequent coupling analysis. Subsequently, the N-K model is introduced to quantify the interactions among different risk factors, yielding the risk-coupling value T to measure the strength of each risk coupling. Building upon this, the Duffin equation is employed to analyze the dynamic response characteristics of the risk system, focusing on characterizing the critical conditions for a system’s abrupt changes and stability under risk coupling. This provides theoretical support for constructing a “damping-excitation” coordinated control strategy.

The research methodology employs the N-K model for comprehensive risk-coupling analysis, utilizing the Dufferin equation to conduct an in-depth exploration of risk dynamics. This methodological choice aligns closely with the study’s objective: to identify critical risk factors and their combined effects through quantitative analysis, thereby achieving more precise safety assessment and control. The model’s applicability not only ensures the fulfillment of research objectives but also provides theoretical support for port safety management at the empirical level, laying a significant foundation for both academic and practical contributions.

This study employs a systematic analytical framework grounded in complex systems theory, utilizing the N-K model and the Dufour equation for risk assessment. First, through the N-K model, we quantitatively describe the coupling relationships among the four factors—personnel, machinery, environment, and management—within the port hazardous materials transportation system. Here, N represents the number of basic system units, while K denotes the degree of interdependence between units. Subsequently, the Dufour equation analyzes the system’s dynamic evolution to explore how different combinations of factors affect system stability. To ensure the model’s practical applicability, we conduct a comparative analysis of real accident data spanning several years to validate the alignment between model assumptions and actual conditions. During data processing, sensitivity analysis was employed to identify critical risk factors. Statistical methods were applied to calculate state probabilities for both single-factor and multi-factor coupling scenarios, ensuring the reliability and interpretability of results. This methodology not only provides concrete theoretical support but also enhances the credibility and scientific rigor of research conclusions through empirical data validation.

3.1. N-K Model

The N-K model was proposed by Kauffman in 1993 for the evolutionary mechanism of biological gene combinations [27], the core of which lies in two parameters: N and K. Among them, N refers to the total number of basic constituent units in the system, and if each such group member can be in n different states, then the whole system has all the possible combinations of states as n^K; K represents the number of interdependencies or interactions existing between system components; the value of K ranges from 0 to N-1, and when K reaches a certain critical point, the relationship between group elements can form a network [28,29,30].

This research concept is grounded in complex systems theory, positing that risk factors within port hazardous materials transportation systems do not exist in isolation but interact to influence the overall system state. Consequently, the N-K model and Duffen equation were selected for modeling to capture these intricate interactions, ensuring the study effectively reveals dynamic coupling mechanisms. Furthermore, this modeling approach aligns with modern scientific methods for analyzing and controlling nonlinear systems. It fully reflects and detects state changes under different intervention measures, providing a solid foundation for theoretical deduction.

In this paper, the risk-coupling analysis of the port dangerous goods transportation system is carried out by constructing the N-K model. The core function of the model lies in the comprehensive evaluation of the coupling effect between factors by quantifying the value of interaction information (T) between the risks of multiple factors, such as people, machinery and equipment, environment, and management [31,32]. When the value of T increases, it reflects a rise in the frequency of these factors coupling in a certain way, and the risk of an accident occurring in the system increases accordingly. The coupling risk T is calculated by the following formula:

$$\mathrm{T}(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{j}=1}^{\mathrm{J}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{j},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{j},\mathrm{k}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{..\mathrm{j}.}{\mathrm{P}}_{...\mathrm{k}}}}$$

(1)

where a, b, c, d denote four types of risk factors such as personnel, machine and equipment, environment, and management, respectively; h, i, j, k denote the state indexes of the four factors of personnel, machine, environment, and management, respectively, with h = 1, …, H; i = 1, …, I; j = 1, …, J; k = 1, … …, K; P_h…, P_.i.., P_…j., P_…k are denoted as the probability indexes about people, machines and equipment, environment, management, etc., in h, i, j, k states, respectively; and P_h,i,j,k are defined as the coupling effect probability.

3.1.1. Single-Factor Coupling Risk

In the safety consideration of the port dangerous goods transportation system, the risk originating from the interaction and influence of multiple risk factors within a risk factor of the system is defined as the single-factor coupled risk. This risk category involves multiple dimensions, covering various types of coupled risks arising from human factors, machinery and equipment, environmental factors, and management factors, whose T is denoted as T₁₁(a), T₁₂(b), T₁₃(c), and T₁₄(d), respectively.

3.1.2. Two-Factor Coupling Risk

In the port dangerous goods transportation system, the interaction and influence between risk factors constitute a complex risk network. When two different risk factors are intertwined, it is defined as a two-factor coupling risk. It can be mainly subdivided into the following categories: coupled risk of man and machine, coupled risk of man and environment, coupled risk of man and management, coupled risk of machine and environment, coupled risk of machine and management, and coupled risk of environment and management, whose T are denoted as T₂₁(a,b), T₂₂(a,c), T₂₃(a,d), T₂₄(b,c), T₂₅(b,d), and T₂₆(c,d), calculated as follows:

$${\mathrm{T}}_{21}(\mathrm{a},\mathrm{b})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{\mathrm{I}}{\mathrm{P}}_{\mathrm{h},\mathrm{i}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{i}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{.\mathrm{i}..}}}$$

(2)

$${\mathrm{T}}_{22}(\mathrm{a},\mathrm{c})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{j}=1}^{\mathrm{J}}{\mathrm{P}}_{\mathrm{h},\mathrm{j}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{j}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{..\mathrm{j}.}}}$$

(3)

$${\mathrm{T}}_{23}(\mathrm{a},\mathrm{d})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{h},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{k}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{...\mathrm{k}}}}$$

(4)

$${\mathrm{T}}_{24}(\mathrm{b},\mathrm{c})=\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{j}=1}^{\mathrm{J}}{\mathrm{P}}_{\mathrm{i},\mathrm{j}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{i},\mathrm{j}}}{{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{..\mathrm{j}.}}}$$

(5)

$${\mathrm{T}}_{25}(\mathrm{b},\mathrm{d})=\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{i},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{i},\mathrm{k}}}{{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{...\mathrm{k}}}}$$

(6)

$${\mathrm{T}}_{26}(\mathrm{c},\mathrm{d})=\sum _{\mathrm{j}=1}^{\mathrm{J}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{j},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{j},\mathrm{k}}}{{\mathrm{P}}_{..\mathrm{j}.}{\mathrm{P}}_{...\mathrm{k}}}}$$

(7)

3.1.3. Multi-Factor Coupling Risk

Risks arising from three or more risk factors acting together in a port DG transportation system are referred to as multi-factor coupled risks [33]. This type of risk contains several complicated interactions, such as the risk that may be triggered by the interaction between people, machines and equipment, and the environment; the coupling risk between people, machines and equipment, and management; the potential threat that people and the environment and management are intertwined with each other; and the potential risk that machines and equipment and the environment and management interact with each other, whose T are denoted as T₃₁(a,b,c), T₃₂(a,b,d), T₃₃(a,c,d), and T₃₄(b,c,d). In this system, the personnel–machine–environment–pipe coupling risk is a four-factor coupling risk, whose T is denoted as T₄(a,b,c,d). The formula for the multi-factor coupled risk T is as follows:

$${\mathrm{T}}_{31}(\mathrm{a},\mathrm{b},\mathrm{c})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{j}=1}^{\mathrm{J}}{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{j}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{j}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{..\mathrm{j}.}}}$$

(8)

$${\mathrm{T}}_{32}(\mathrm{a},\mathrm{b},\mathrm{d})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{h},\mathrm{j},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{k}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{...\mathrm{k}}}}$$

(9)

$${\mathrm{T}}_{33}(\mathrm{a},\mathrm{c},\mathrm{d})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{j}=1}^{\mathrm{J}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{h},\mathrm{j},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{j},\mathrm{k}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{..\mathrm{j}.}{\mathrm{P}}_{...\mathrm{k}}}}$$

(10)

$${\mathrm{T}}_{34}(\mathrm{b},\mathrm{c},\mathrm{d})=\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{j}=1}^{\mathrm{J}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{i},\mathrm{j},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{i},\mathrm{j},\mathrm{k}}}{{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{..\mathrm{j}.}{\mathrm{P}}_{...\mathrm{k}}}}$$

(11)

$${\mathrm{T}}_4(\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d})=\sum _{\mathrm{h}=1}^{\mathrm{H}}\sum _{\mathrm{i}=1}^{\mathrm{I}}\sum _{\mathrm{j}=1}^{\mathrm{J}}\sum _{\mathrm{k}=1}^{\mathrm{K}}{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{j},\mathrm{k}}{\log }_2{\displaystyle \frac{{\mathrm{P}}_{\mathrm{h},\mathrm{i},\mathrm{j},\mathrm{k}}}{{\mathrm{P}}_{\mathrm{h}...}{\mathrm{P}}_{.\mathrm{i}..}{\mathrm{P}}_{..\mathrm{j}.}{\mathrm{P}}_{...\mathrm{k}}}}$$

(12)

3.2. Modeling of Single-Factor Coupled-Risk Folding Mutations

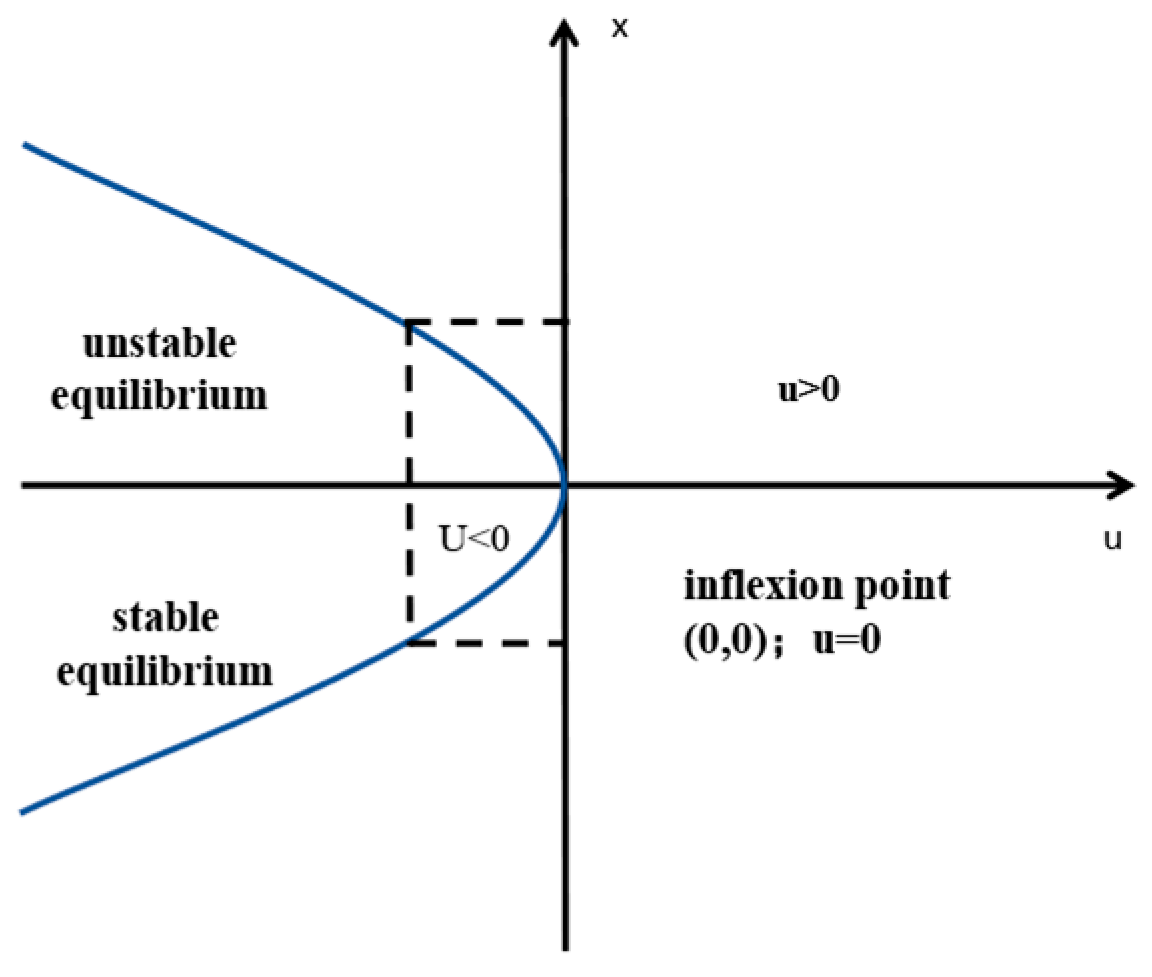
Mutation theory is a discipline that studies how continuous gradual changes can trigger mutations or leaps in nature and human society, and tries to use unified mathematical models to describe, predict, and control such mutations or leaps, taking stability theory and singularity theory as the theoretical basis, which was put forward by the French mathematician Thom in the 1960s to analyze the mutation phenomena in the process of the evolution of the system risk state. As a typical complex dynamic system, the transition from a safe state to an accident state in port hazardous materials transportation systems is not always smooth, but often exhibits distinct abrupt characteristics, which is compatible with the core idea of the folding mutation model.

The phenomenon of a sudden change in the state of a system or process under the action of a single factor is known as a single-factor folding mutation. Such sudden changes are usually due to a small change in a key factor within or outside the system that results in a significant change in the overall behavior or performance of the system. The state change in the port hazardous materials transportation system is abrupt, and its abrupt change from a safe state to an accident involves multiple states. Therefore, it is appropriate to use the mutation theory modeling. Thus, the potential function of the collapsed mutation model of the risky accident of the port dangerous goods transportation system is firstly established as follows:

$$\mathrm{V}\left(\mathrm{x}\right)={\mathrm{x}}^3+\mathrm{ux}$$

(13)

The equilibrium surface equation is obtained by taking the derivative of Equation (13):

$$3{\mathrm{x}}^3+\mathrm{u}=0$$

(14)

The singularity set equation is obtained by second-order derivation, i.e, the following:

$$6\mathrm{x}=0$$

(15)

The set of singularities S is a subset of the equilibrium surface containing the points at which the state of the system under specific conditions undergoes a mutation, and the set of singularities in the case of collapsing mutations may consist of one or more points at which the behavior of the system undergoes a discontinuous change. A folding mutation is a special type of mutation in which the output state of the system shows discontinuous changes when the system parameters are continuously changed. In this system, the folding mutation singularity set is located at the point (0,0), indicating that the folding mutation is triggered when the system state parameter reaches this point. The bifurcation set B is the mapping of the singularity set S in the control space (parameter ranges), where the bifurcation set B identifies the parameter values that cause the system to mutate. In this system, the bifurcation set B is formed by the mapping of the singularity set S along the straight line x = 0, i.e., the u = 0 position, which indicates that the control parameter u reaches 0, and the system may undergo the phenomenon of the singularity set S determining the mutation, as shown in Figure 2.

In the dynamic change in the risk state of the port dangerous goods transportation system, the positive and negative u-axis of the control space plays a key role; when u is positive, Equation (14) has no real solution, indicating that the system cannot maintain a stable state in this case. On the contrary, when u is negative, the potential function presents a very small value point and a very large value point situation. u equals zero, and the two points overlap, forming an inflection point, which signifies that the system may undergo a risky mutation. In order to more accurately describe the folding mutation on the system dynamics, define the control variable u_ij; the variable represents the ith kind of single factor in the j year caused by the port dangerous goods transportation accident probability. Based on this, derive the equilibrium surface M_ij of the folding mutation state of the i-th single-factor coupled risk system for a specific year j:

$$3{\mathrm{x}}_{\mathrm{ij}}^2+{\displaystyle \frac{{\mathrm{a}}_{\mathrm{ij}}\times {\mathrm{n}}_{\mathrm{ij}}}{\sum \mathrm{j}\sum \mathrm{i} {\mathrm{n}}_{\mathrm{ij}}}}=0,{\mathrm{a}}_{\mathrm{ij}}<0$$

(16)

where a_ij denotes a fixed negative constant representing a specific weight; n_ij records the number of accidents due to the ith single-factor coupled risk in a specific year j. Based on the derivation and data integration of Equation (16), the equilibrium surface Mi describing the system folding mutation state of the ith single-factor coupled risk can be further constructed as follows:

$$3{\mathrm{x}}_{\mathrm{i}}^2+{\displaystyle \frac{{\mathrm{a}}_{\mathrm{i}}\sum \mathrm{j}{\mathrm{n}}_{\mathrm{ij}}}{\sum \mathrm{j}\sum \mathrm{i}{\mathrm{n}}_{\mathrm{ij}}}}=0,{\mathrm{a}}_{\mathrm{i}}<0$$

(17)

Single-Factor Coupled-Risk Dufferin Shock Modeling

The Dufferin equation is a mathematical tool for describing nonlinear behavior in vibrating systems. In this study, the Dufferin equation is used to model the interaction of risk factors in a port hazmat transportation system. By considering risk factors as state variables of the system, the Dufferin equation is able to reveal the stability and dynamic evolution characteristics of the system under different conditions. When the system is affected by different internal and external factors, the solution of this equation can be used to analyze the system for oscillations and jumps. This analysis helps bring an understanding of the mechanism of risk-coupled events, especially in complex port environments, and how to intervene and regulate the dynamic behavior of the system through appropriate management strategies. This equation provides a powerful mathematical tool to characterize the dynamics of complex systems.

In the actual modeling process, we will quantitatively describe the coupling between risk factors through equations. For example, based on the N-K model, the coupled risk values under the interaction of different risk factors are calculated, and these values are further introduced into Dufferin’s equation in order to study the effect of risk coupling on the dynamic behavior of the system. Through the organic combination of theory and application, this study aims to comprehensively reveal the complexity of risk coupling in ports’ dangerous goods transportation systems and provide a solid theoretical foundation for related safety management practices. The standard type of Dufferin equation containing the cubic term is as follows:

$$\mathrm{x}+\mathrm{kx}+\mathrm{x}+\mathrm{a}{\mathrm{x}}^3=\mathrm{Fcos} \mathrm{wt}$$

(18)

Equation (18): x represents the risk posture of the dangerous goods transportation system, in which u is the system control variable; k is the internal damping coefficient of the system, reflecting the system’s own ability to defend against risks; a is the cubic term coefficient, used to quantify the complexity of the impact of the risk factors on the system; F denotes the amplitude of the system affected by the external risk factors; w represents the frequency of the impact of the external risk factors, i.e., how often different external risk factors impact the system; and t is the time parameter factors, i.e., the frequency of different external risk factors’ impacts on the system. According to Equation (18), it can be seen that the sudden change in single-factor coupled risk of the port hazmat transportation system is mainly affected by two core parameters, k and F. In this paper, the influence of time lag is eliminated by the multiscale method, which is further transformed into the bifurcation response equation without the time parameter t as follows:

$${\mathrm{k}}^2{\phi }^2+(2\phi \mathsf{\epsilon }-{\displaystyle \frac{3\mathrm{a}{\phi }^3}{4}}{)}^2={\mathrm{F}}^2$$

(19)

Equation (19): $\mathsf{\epsilon }$ is defined as the coordination parameter, which measures the proximity between the amplitude frequency of the influence of the external risk factor and the intrinsic frequency of the Dufferin oscillator of the system; x characterizes the magnitude of the amplitude of the Dufferin oscillations of the system. Using this as the basis for introducing the internal damping feedback controller $\mathsf{\sigma }=\mathsf{\rho }\cdot \mathrm{c}\cdot \mathrm{x}$, where $\mathsf{\rho }$ represents the small parameter and $\mathrm{c}$ is the control coefficient of the internal risk-defense damping of the port dangerous goods transportation system; by substituting this controller into Equation (18) and applying the multiscale method, we obtain the bifurcation response equation containing the control coefficient of the internal risk-defense damping as follows:

$${\left(\mathrm{k}-\mathrm{c}\right)}^2{\phi }^2+(2\phi \mathsf{\epsilon }-{\displaystyle \frac{3\mathrm{a}{\phi }^3}{4}}{)}^2={\mathrm{F}}^2$$

(20)

Introducing the external amplitude feedback controller $\mathsf{\sigma }=\mathsf{\rho }\cdot \mathrm{f}\cdot \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{w}\mathrm{t}$, in which $\mathsf{\rho }$ is still used as a small parameter and $\mathrm{f}$ represents the amplitude adjustment coefficients of the external influencing factors of the port hazmat transportation system; this external feedback controller is also substituted into Equation (18), and the bifurcation response equations containing the amplitude control coefficients $\mathrm{f}$ of the external influencing factors are obtained by using the multiscale method:

$${\mathrm{k}}^2{\phi }^2-{\displaystyle \frac{3\mathrm{a}{\phi }^3}{4}}={(\mathrm{F}+\mathrm{f})}^2$$

(21)

To explore the risk management of the port dangerous goods transportation system, we consider the parameters k, a, and F as fixed values and focus on the two core control elements: the damping coefficient c for internal risk defense and the modifying coefficient f for external influence amplitude; and deeply understand how these two elements affect the coordination parameter ε and the oscillation amplitude of the system, so as to improve the understanding of the risk of the port dangerous goods transportation system, and, accordingly, to implement an effective risk. In this way, the understanding of the risk of the port dangerous goods transportation system can be improved, and effective risk control strategies can be implemented.

4. Applications and Results

4.1. Case 1

This paper collects and organizes 491 maritime accident investigation reports in MSA from 2014 to 2024, and the accident types and the number of accidents occurring are detailed in

Table 1. Accident type statistics.

Type of Accident	Collisions	Fire	Fire and Explosion	Ground	Touch	Wind Damage	Sink	Other	Total
amount	237	15	33	22	56	29	83	16	491

. This paper lists the process of calculating the accident-coupled risk T and calculates the corresponding results. It is assumed that there are four major risk factors for port transportation safety, i.e., people, machinery and equipment, environment, and management. If the non-occurrence of coupling and the occurrence of coupling are represented by 0 and 1, respectively, there are 16 possible forms of risk coupling, and the number of occurrences and frequency of each risk coupling are detailed in

Table 2. Number and frequency of risk coupling.

Coupling Method	Number and Frequency
one-factor coupling	Number	n0000 = 0	n1000 = 125	n0100 = 12	n0010 = 3	n0001 = 1
	frequency	P0000 = 0	P1000 = 0.2546	P0100 = 0.0244	P0010 = 0.0061	P0001 = 0.0020
two-factor coupling	Number	n1100 = 57	n1010 = 88	n1001 = 93	n0110 = 2	n0101 = 2	n0011 = 6
	frequency	P1100 = 0.1160	P1010 = 0.1792	P1001 = 0.1894	P0110 = 0.0041	P0101 = 0.0041	P0011 = 0.0122
Multi-factor coupling	Number	n1110 = 32	n1101 = 19	n1011 = 41	n0111 = 1	n1111 = 9
	frequency	P1110 = 0.0652	P1101 = 0.0387	P1011 = 0.0835	P0111 = 0.0020	P1111 = 0.0183

.

4.1.1. Calculation of Risk-Coupling Values

To calculate the risk-coupling value, first assess the probability of occurrence of the risk-coupling event.

(1)

Single-factor coupling probability

In a coupled-risk analysis, the influence of human factors is removed, and the probability of other factors acting to cause an accident is assessed:

P_0… = P₀₀₀₀ + P₀₁₀₀ + P₀₀₁₀ + P₀₀₀₁ + P₀₁₁₀ + P₀₁₀₁ + P₀₀₁₁ + P₀₁₁₁ = 0.0549.

The same reasoning applies: P_.0.. = 0.7170, P_..0. = 0.6292, P_…0 = 0.6496, P_1… = 0.9449, P_.1.. = 0.2728, P_..1. = 0.3706, P_…1 = 0.3502.

(2)

Two-factor coupling probability

When conducting a risk-coupling analysis, the probability of an accident occurring as a result of other factors is assessed without taking into account the influence of human factors and machine and equipment factors: P_00.. = P₀₀₀₀ + P₀₀₀₁ + P₀₀₁₀ + P₀₀₁₁ = 0.0203.

The same reasoning applies: P_.00. = 0.4460, P_..00 = 0.3950, P_0.0. = 0.0305, P_0..0 = 0.0346, P_.0.0 = 0.4400, P_10.. = 0.6967, P_01.. = 0.0346, P_0.1. = 0.0244, P_0..1 = 0.0203, P_.0.1 = 0.2871, P_..01 = 0.2342, P_.10. = 0.2810, P_.1.0 = 0.2097, P_..10 = 0.2546, P_.01. = 0.1832, P_1.0. = 0.5987, P_1..0 = 0.6150, P_11.. = 0.2382, P_.11. = 0.0896, P_..11 = 0.1160, P_1.1. = 0.3462, P_.1.1 = 0.0631, P_1..1 = 0.3300.

(3)

Multi-factor coupling probability

In the risk-coupling analysis, the effects of human factors, machine and equipment factors, and environmental factors are not considered, and the probability of an accident occurring due to other factors is assessed: P_000. = P₀₀₀₀ + P₀₀₀₁ = 0.0020.

The same reasoning applies: P_00.0 = 0.0061, P _0.00 = 0.0244, P_.000 = 0.2546, P_100. = 0.4440, P_10.0 = 0.4338, P_1.00 = 0.3706, P_.100 = 0.1404, P_010. = 0.0285, P_01.0 = 0.0285, P_0.10 = 0.0102, P_.010 = 0.1853, P_.001 = 0.1914, P_0.01 = 0.0061, P_00.1 = 0.0142, P_001. = 0.0183, P_110. = 0.1547, P_11.0 = 0.1812, P_1.10 = 0.2444, P_.110 = 0.0693, P_.101 = 0.0428, P_1.01 = 0.2281, P_10.1 = 0.2729, P_101. = 0.2627, P_011. = 0.0061, P_01.1 = 0.0061, P_0.11 = 0.0142, P_.011 = 0.0957, P_.111 = 0.0203, P_1.11 = 0.1018, P_11.1 = 0.0570, P_111. = 0.0835, P₁₁₁₁ = 0.0183.

Based on Equations (1)–(12), the risk-coupling value T under the coupling effect of different risk factors can be calculated separately, as shown in

Table 3. Risk-coupling values under the coupling of different risk factors T.

Factor Coupling	The Risk-Coupling Value T	Arrange in Order
Personnel–Equipment	0.0244	4
Personnel–Environmental	0.0001	11
Personnel–Management	0.0008	8
Equipment–Environmental	0.0002	10
Equipment–Management	0.0013	7
Environmental–Management	0.0003	9
Personnel–Equipment–Environmental	0.0354	3
Personnel–Equipment–Management	0.0471	1
Personnel–Environmental–Management	0.0444	2
Equipment–Environmental–Management	0.0083	6
Personnel–Equipment-Environmental–Management	0.0158	5

.

4.1.2. Analysis of Results

In the analysis of the MSA maritime accident investigation report, the constructed N-K model and Dufferin’s equation are utilized to quantitatively analyze the risk coupling of the port hazardous materials transportation system. The model results show that the high coupling-risk events are mostly focused on the interaction between personnel and machines and equipment, which validates the assumption of the importance of personnel–machine factors in the theoretical analysis. The results of the analysis show that investments targeting personnel training and equipment maintenance can significantly improve system stability and thus reduce the probability of accidents. The validity of the model was verified by comparing it with actual accident data, i.e., the condition of the machinery and equipment is often the determining factor when accidents are caused by a single factor of operator error. This finding is an important guideline for port managers, emphasizing the need and urgency for personnel training. Based on the findings of the study, it is recommended that port management implement regular training and assessment, especially in high-risk operations, to enhance staff’s awareness of their responsibilities and professional skills. In addition, a regular maintenance mechanism for equipment should be established to ensure safety and continuity during the transportation of dangerous goods.

4.2. Case 2

According to the causes of risky accidents, MSA collects the number of port dangerous goods transportation safety accidents in 2020–2024 and calculates the corresponding probability of accidents, as shown in

Table 4. Number and probability of dangerous goods transportation accidents in ports in China, 2020–2024.

Vintage	Personnel	Equipment	Environmental	Management
2020	12/0.190	3/0.048	1/0.016	0/0
2021	5/0.079	0/0	1/0.016	0/0
2022	14/0.222	1/0.016	0/0	0/0
2023	15/0.238	0/0	0/0	1/0.016
2024	9/0.143	0/0	1/0.016	0/0

. Meanwhile, a mutation diagram is drawn to show the mutation of accidents, as shown in Figure 3. Figure 3a–d are the results of the collapsed mutation of four types of risks in the port dangerous goods transportation system of China in the period of 2020–2024; Figure 3e is the overall situation of the system facing the collapsed mutation of four types of risk factors. Figure 3a–d are the results of the collapsed mutation of four kinds of risks in the hazardous materials transportation system, namely, personnel factors, machinery and equipment, environmental factors, and management factors; Figure 3e is the overall situation of the system facing the collapsed mutation of the four kinds of risk factors.

Analysis of Data and Simulation Results

Drawing on the railroad nonlinear system and the civil aviation control nonlinear system for the coefficient setting of risk management, the horizontal and vertical coordinates are set as the coordination parameter ε and oscillation amplitude, respectively, to simulate the study of Equation (19), and the results are shown in Figure 4. Where Figure 4a,b are the simulation results of risk oscillations after the single-factor coupled risk of the port dangerous goods transportation system is subjected to changes in the amplitude of man-made external force F and the internal risk defense damping coefficient k, respectively (respectively, F = 0.11137, 0.07637, 0.04637, when taking a = 0.05; k = -0.0583 and k taking 0.0335, 0.0535, 0.0735, at which point a = −0.0583 and F = 0.11137 are taken).

The results show that when the F value is set at 0.11137, one parameter value corresponds to one oscillation amplitude along the horizontal axis, gradually increasing and decreasing, indicating that the port dangerous goods transportation system maintains stable operation, and when the coordinated parameter interval [0.0629, 0.0637] is set at [0.0629, 0.0637], one parameter value corresponds to two oscillation amplitudes, indicating that the stability of the system is threatened with the amplitude jumping and changing. At this time, the system may face a single-factor coupling-risk folding mutation and fall into an unstable state. When the F value gradually decreases, or the k value gradually increases, the range of the mutation interval of the port hazardous materials transportation system is gradually narrowed until the folding mutation no longer occurs.

Based on the results of Figure 4, the same horizontal and vertical coordinates are set as the coordination parameter and oscillation amplitude, respectively, and the simulation study of Equations (20) and (21) is carried out, and the results are shown in Figure 5 (taking k = 0.0335, a = −0.0583, and F = 0.11137). Where Figure 5a,b denote the Dufferin oscillations of the single-factor coupled risk of the port hazmat transportation system when c = 0, c = 0.02, and f = 0, f = 0.05, respectively.

Results indicate that as the c-value increases—reflecting enhanced internal risk defense capabilities and amplified damping effects—the f-value decreases. When the amplitude of external influencing factors is effectively controlled, the phenomenon of fold-over transitions in port hazardous cargo transportation systems gradually diminishes. System amplitude stabilizes, leading to improved overall stability and safety. Therefore, it is recommended to establish a comprehensive risk-management system that continuously monitors meteorological changes and equipment status, utilizing dynamic early warning mechanisms to assess potential risks. Upon detecting potential abrupt change risks, emergency response plans should be promptly activated to reduce accident likelihood. These findings further underscore the importance of foresight and adaptability in system management, providing empirical support for developing port safety management strategies.

In this study, the model was applied to analyze risk coupling within port hazardous materials transportation systems, revealing that high-coupling risk events primarily stem from personnel–machine interaction. This finding validates the theoretical hypothesis regarding the critical importance of personnel–machine factors. However, to ensure rigorous and scientific conclusions, we did not rely solely on model simulation results. Instead, we further validated the model’s effectiveness by comparing it with actual accident data.

First, the model posits that in high-coupling risk events, the interdependence between human operations and machinery constitutes a critical risk factor. To test this hypothesis, we collected and analyzed a series of real-world accident data, focusing particularly on incidents caused by a single operator error. In these cases, we found that the current state of machinery and equipment often served as the decisive factor in amplifying the event’s severity. This finding aligns with the model’s predictions, indicating that the research hypothesis possesses a sound empirical foundation.

Secondly, comparative analysis of accident data reveals greater detail, highlighting that the reliability of machinery and equipment serves as the final line of defense against human operational errors during critical procedures. Accident statistics indicate that ports equipped with highly reliable machinery experience significantly fewer accidents caused by human error compared to ports with poorly maintained equipment. This further corroborates the model’s inference regarding the importance of personnel–machine coupling, underscoring the critical role of optimizing equipment management in maintaining system stability.

Through this validation process, we not only confirmed the validity of theoretical assumptions but also provided empirical support for the model, enhancing its credibility and applicability in practical scenarios. This research offers crucial insights and data-driven foundations for developing future port security management strategies, particularly proposing actionable improvement directions for control measures targeting risks associated with human–equipment interactions.

5. Conclusions

This study systematically analyzes the risk coupling and control mechanism of the port dangerous goods transportation system, builds a risk analysis and management model based on the four major factors of “personnel-machine-environment-management,” and quantifies the coupling relationship among risk factors with the help of the N-K model, revealing the impact of the interaction of each factor on the safety of the system, among which the personnel–machine factor has the highest coupling risk value, indicating that priority attention should be given to personnel training and equipment management in risk management. The coupling risk value of personnel–machine factors is the highest, indicating that personnel training and equipment management should be prioritized in risk management. The Dufferin equation explores the dynamic control mechanism in depth, clarifies the hysteresis and sudden change in the system state under the action of a single factor, and provides theoretical support for the implementation of dynamic risk-control strategies in the future. This study verifies the validity of the proposed risk-coupling model, reveals the main causes of accidents and frequent risk factors, and provides guidance for monitoring and management in actual operation. Combined with the research results, it is recommended to develop a risk analysis system to monitor potential risks of port transportation in real time, establish a dynamic early warning mechanism to respond to possible mutation risks in time, and improve the overall safety management level of ports. This study provides scientific risk analysis tools and strategies, which have key theoretical value and practical significance, and helps the safe management and sustainable development of port transportation of dangerous goods.

At the same time, this study still has some subjective and objective limitations; the risk analysis of port dangerous goods transportation relies heavily on accurate and comprehensive data; however, empirical research is often limited by the availability and quality of data, and the collection and organization of relevant data is especially challenging after an accident; secondly, the existing research is relatively less involved in the analysis of the effectiveness of emergency response and management strategies after an accident. Implementing guidance for how to take effective measures quickly after an accident to reduce losses and protect people’s safety is a key part of risk management, and the research on this is still relatively lagging, which requires further in-depth exploration of effective emergency management models and strategies.