Ship Motion Control Methods in Confined and Curved Waterways Combining Good Seamanship
Abstract
1. Introduction
- (1)
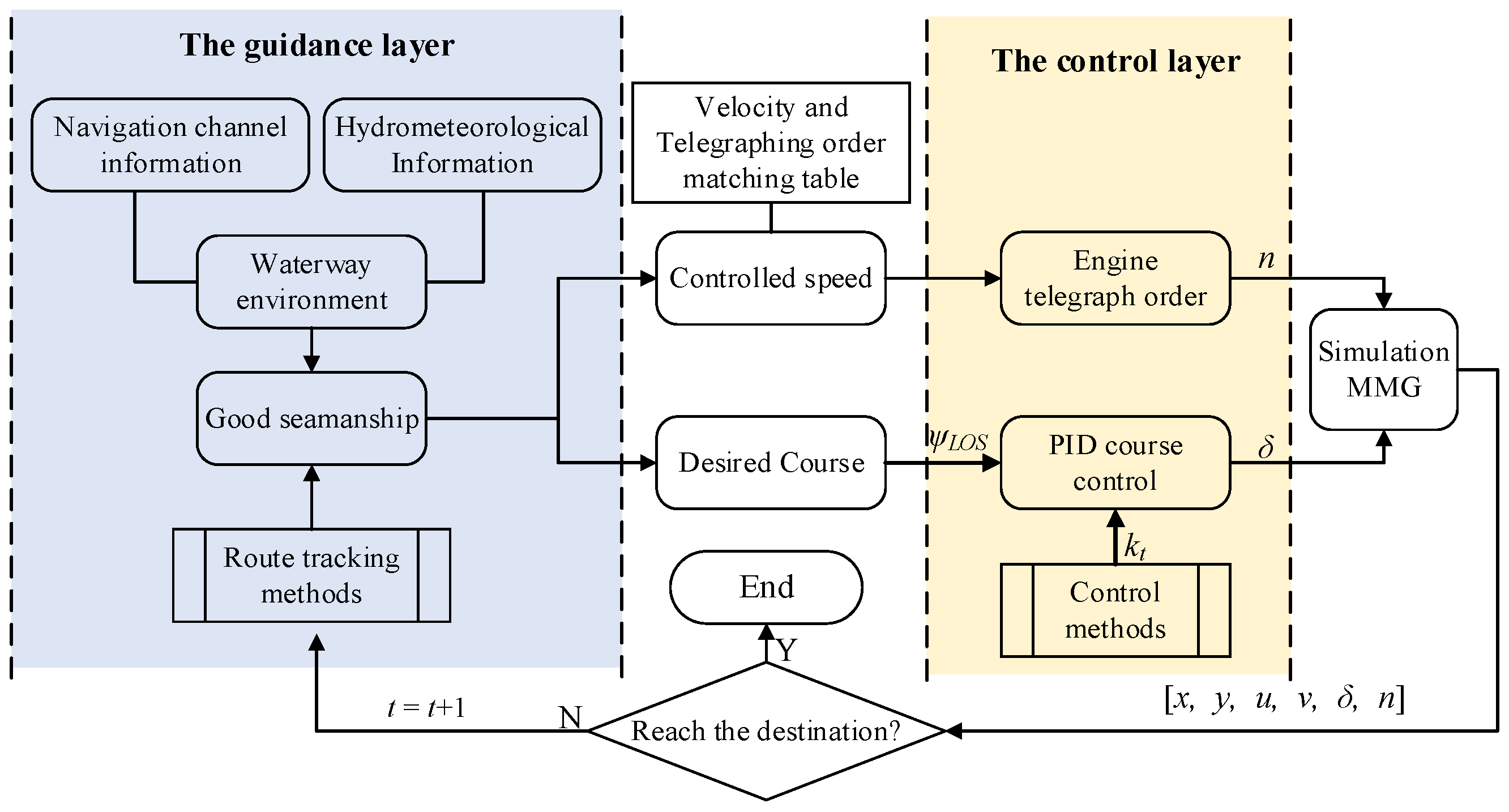
- A Hierarchical, Decoupled Control Architecture: A key contribution is the design of a two-layer framework that strategically decouples the control problem. The high-level guidance layer is responsible for strategic path generation and external disturbance rejection, while the low-level control layer adapts to internal model uncertainty, enabling robust performance across different scenarios.
- (2)
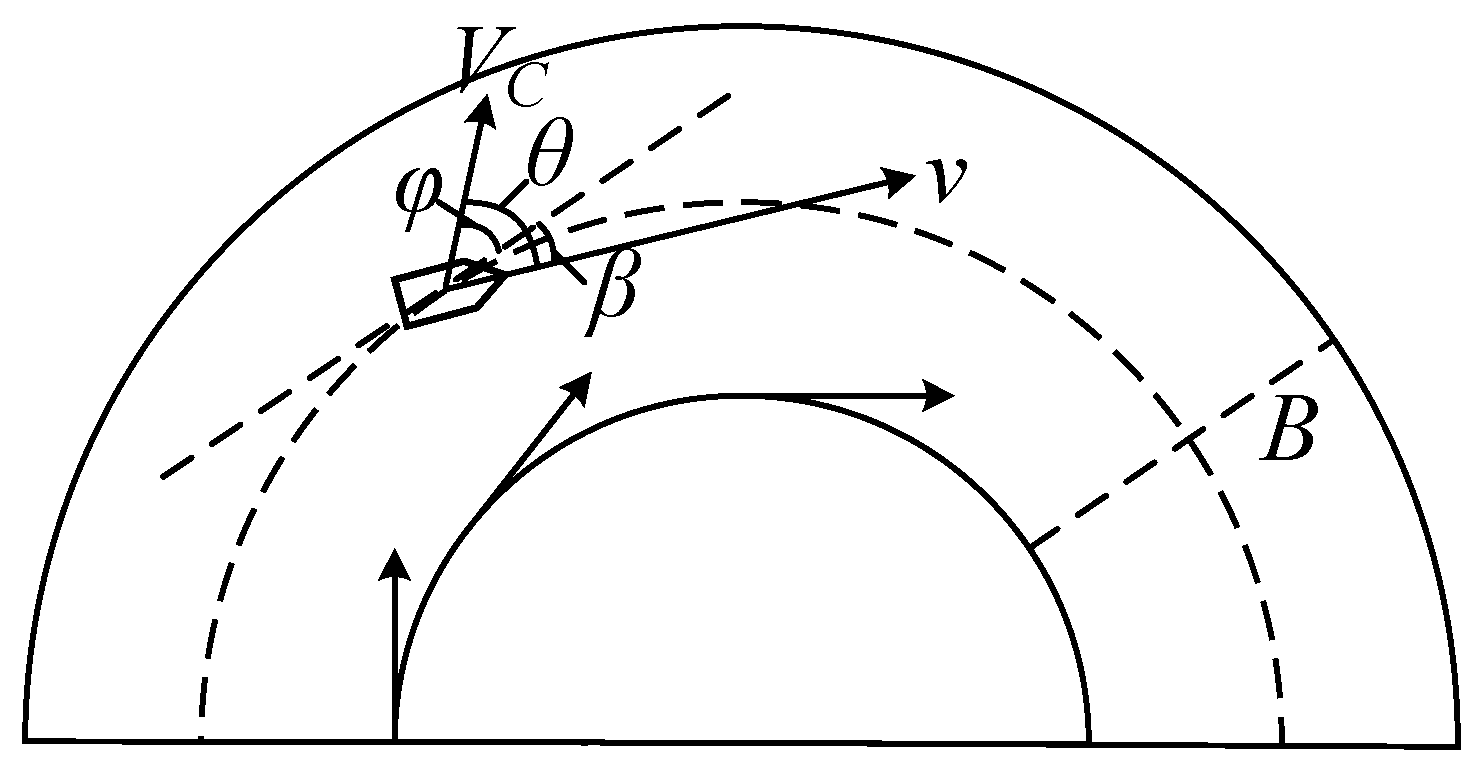
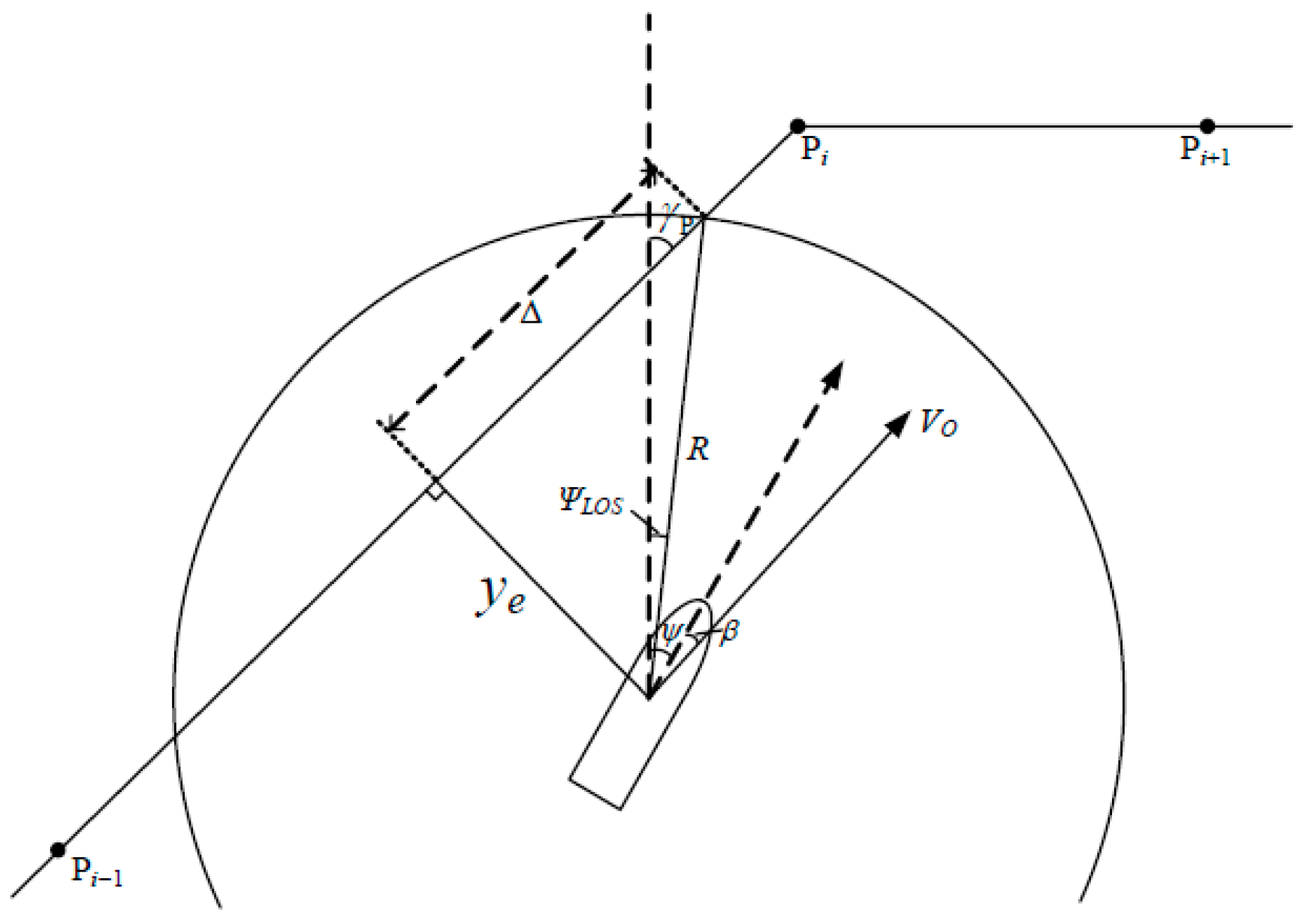
- A Context-Adaptive Guidance Rules Informed by Good Seamanship: A versatile guidance rules is proposed that moves beyond naive centerline tracking. It is designed to be context-adaptive, providing robust adaptive control for general maritime scenarios while being capable of embedding the specific inland navigational strategy of “holding high and taking low” (A navigation technique for maintaining safe clearance in restricted waters by holding elevated position while adjusting course at lower elevation) [39], for the most hazardous river bends. This ability to deploy situationally appropriate strategies, consistent with proven maritime practice, significantly enhances navigational safety. The law also incorporates an adaptive integral term to resolve the steady-state error of conventional LOS guidance.
- (3)
- Reinforcement Learning for Adaptive PID Control: At the control layer, a Double Q-learning algorithm is employed for the online, adaptive tuning of PID gains. This leverages the model-free nature of RL to enhance the controller’s adaptability to the vessel’s time-varying dynamics and model-plant mismatch, ensuring high-fidelity execution of the guidance commands.
2. Modeling of Vessel and Curved Waterways
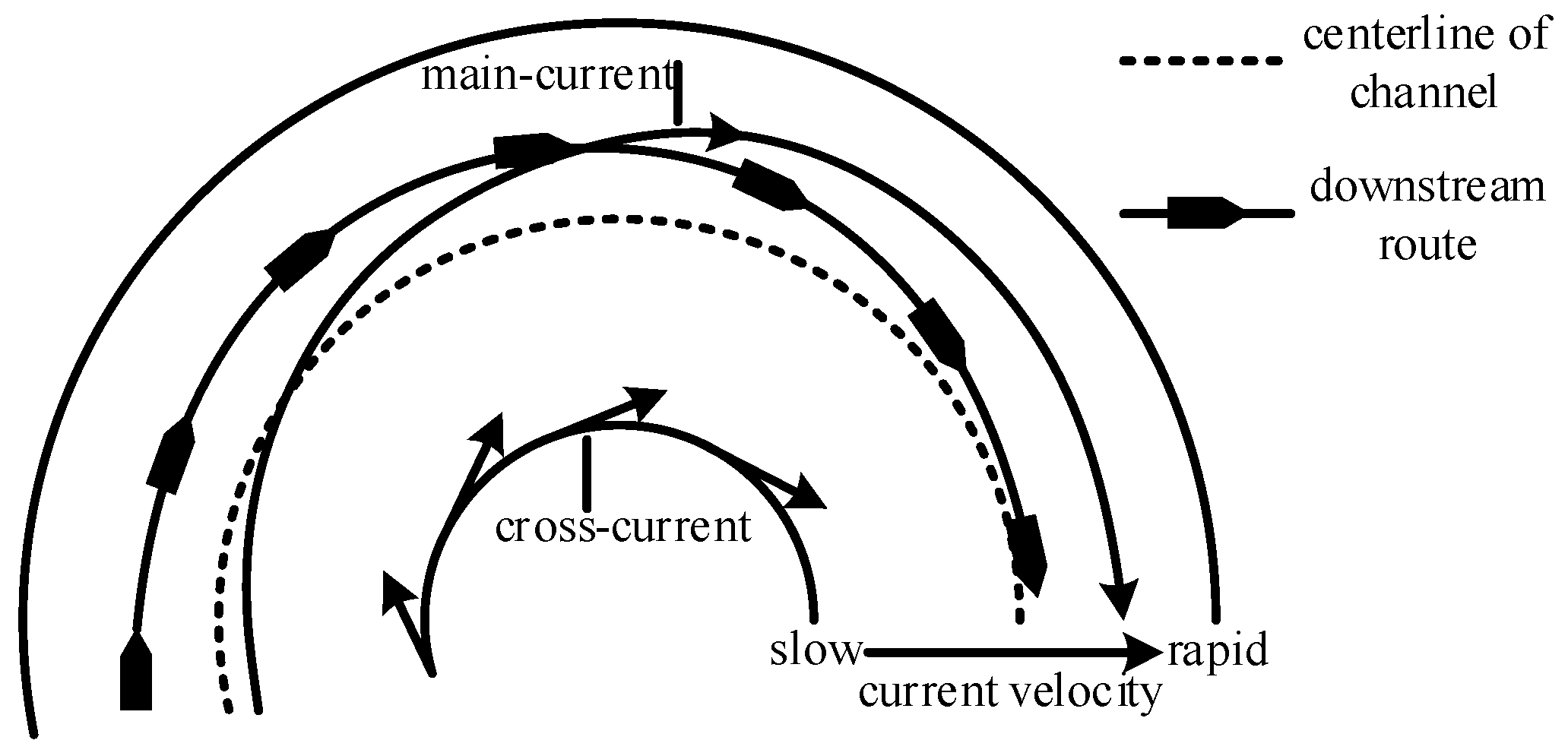
2.1. Current Pattern Modeling
2.2. Digital Modeling of Confined and Curved Waterways
2.3. Mathematical Modeling of Ship Motion
3. Ship Motion Control Methods for Confined and Curved Channels
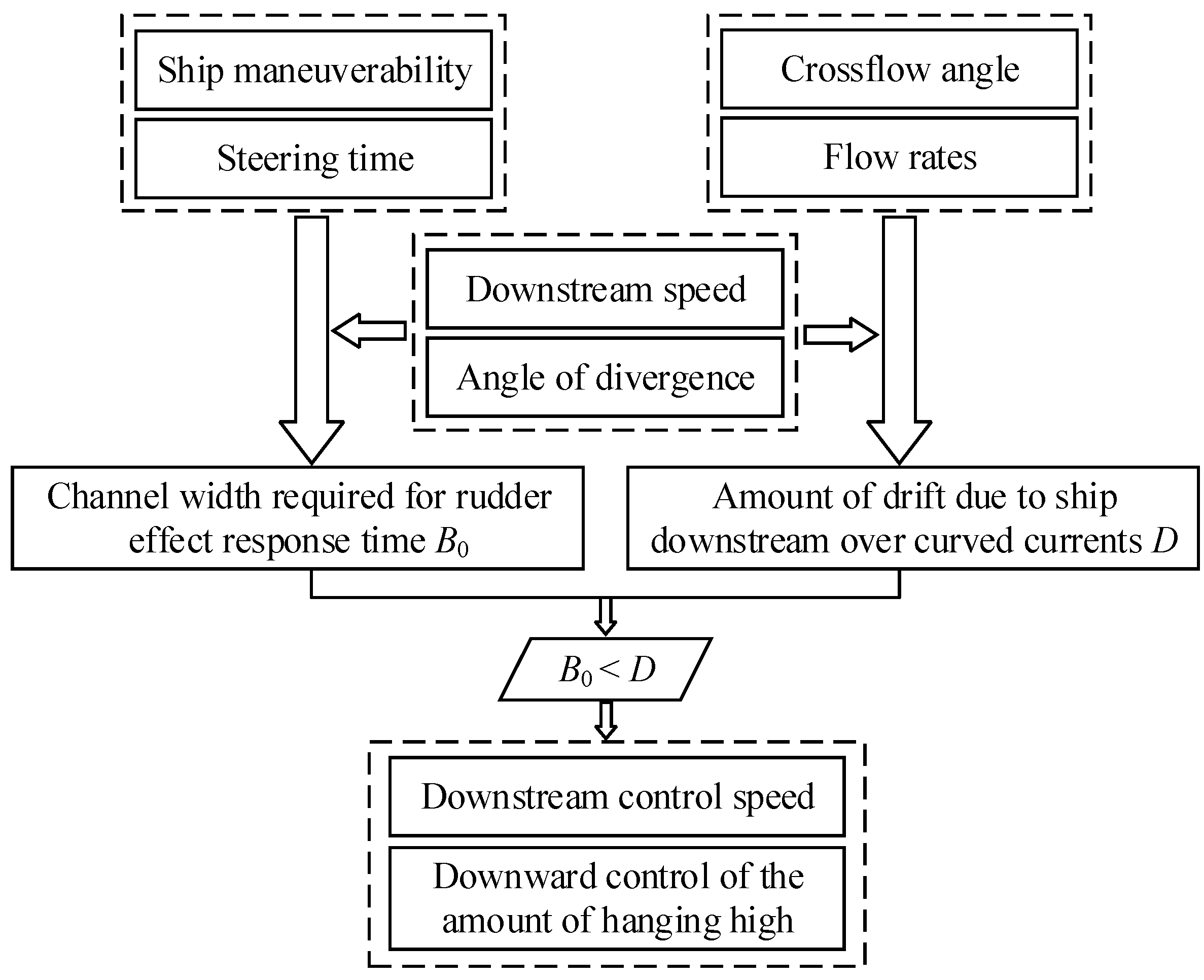
3.1. Methodology of Control Framework
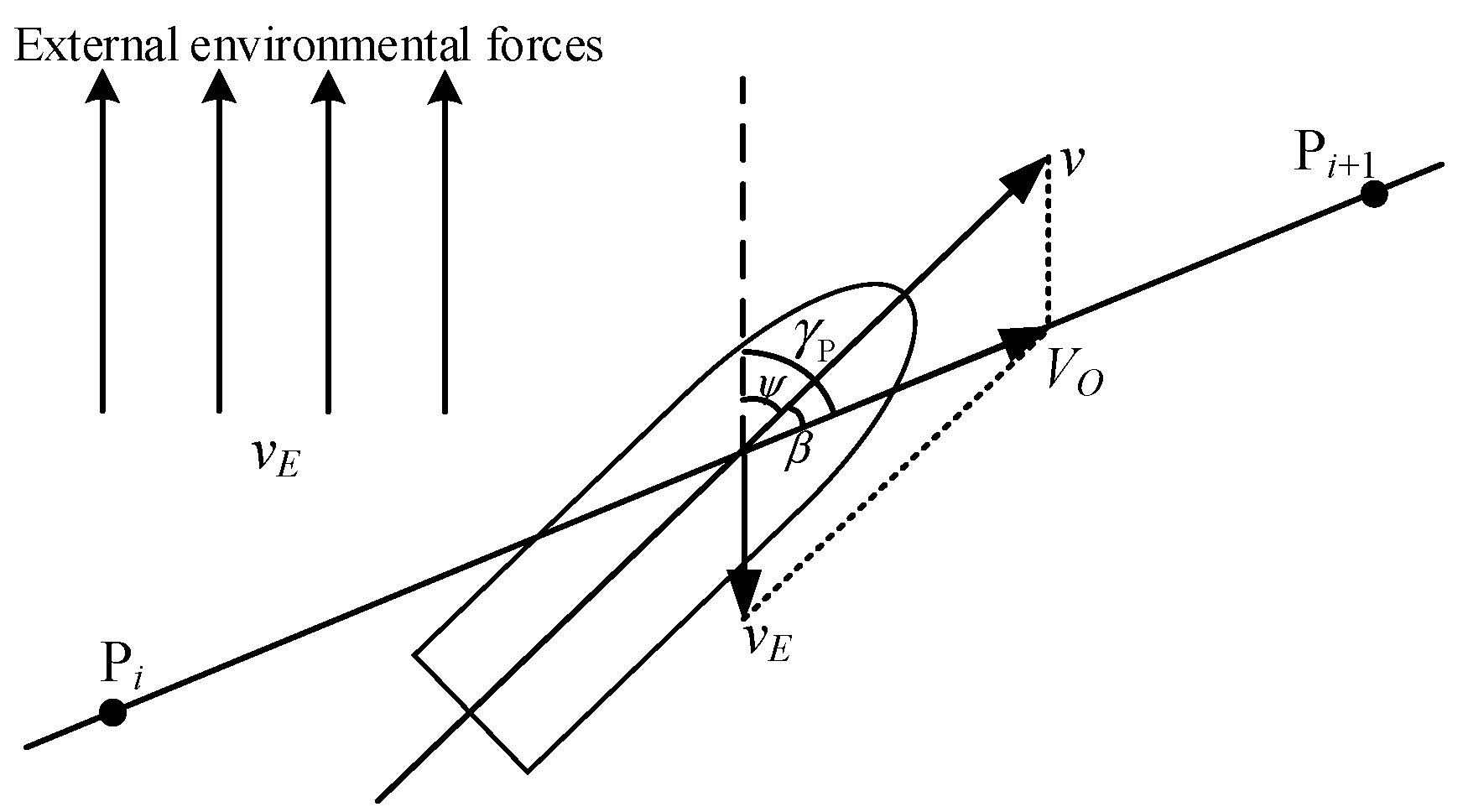
3.2. Robust and Adaptive Guidance for Route Tracking
3.3. Navigation Strategy Based on Maritime Practice
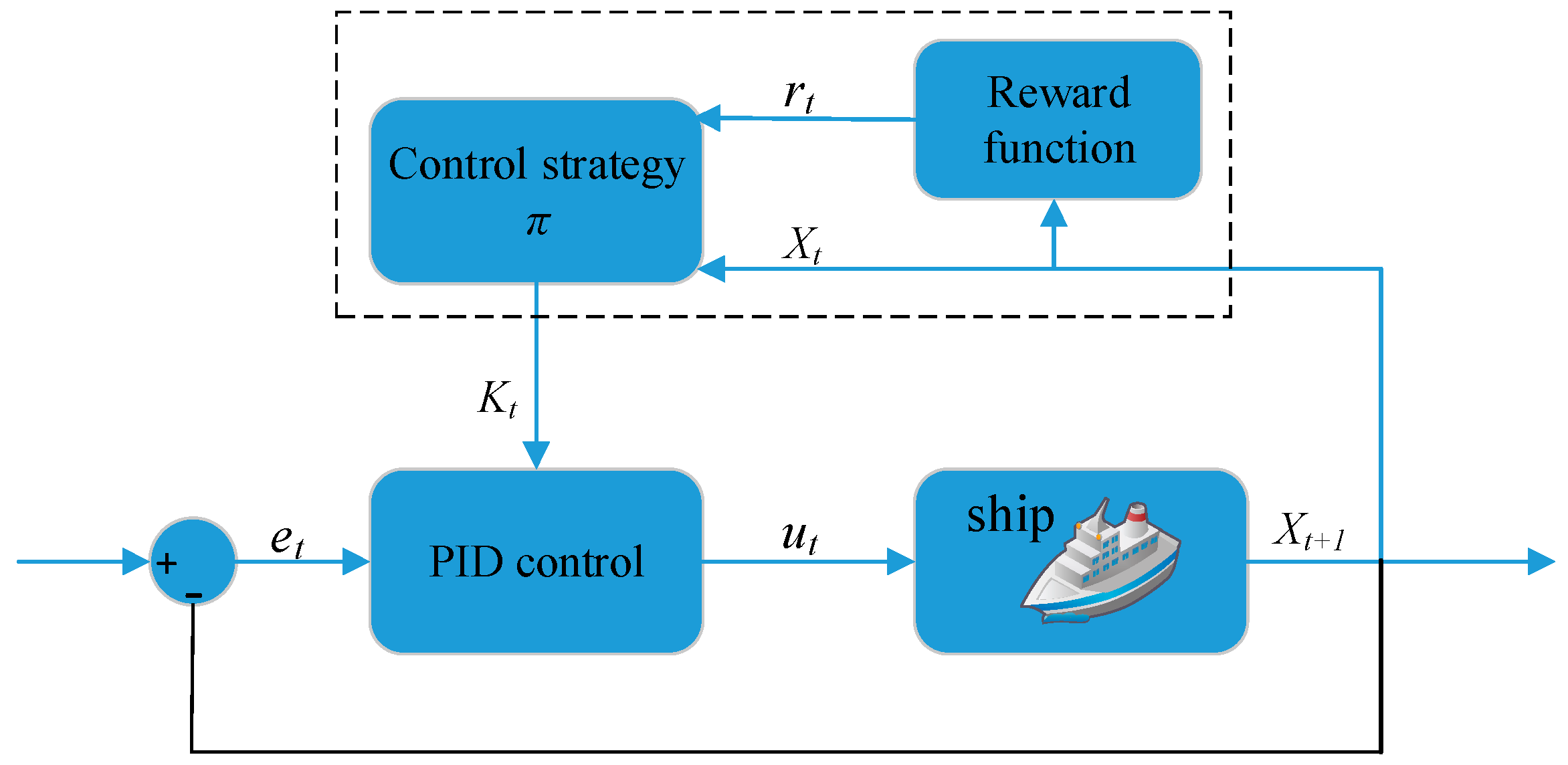
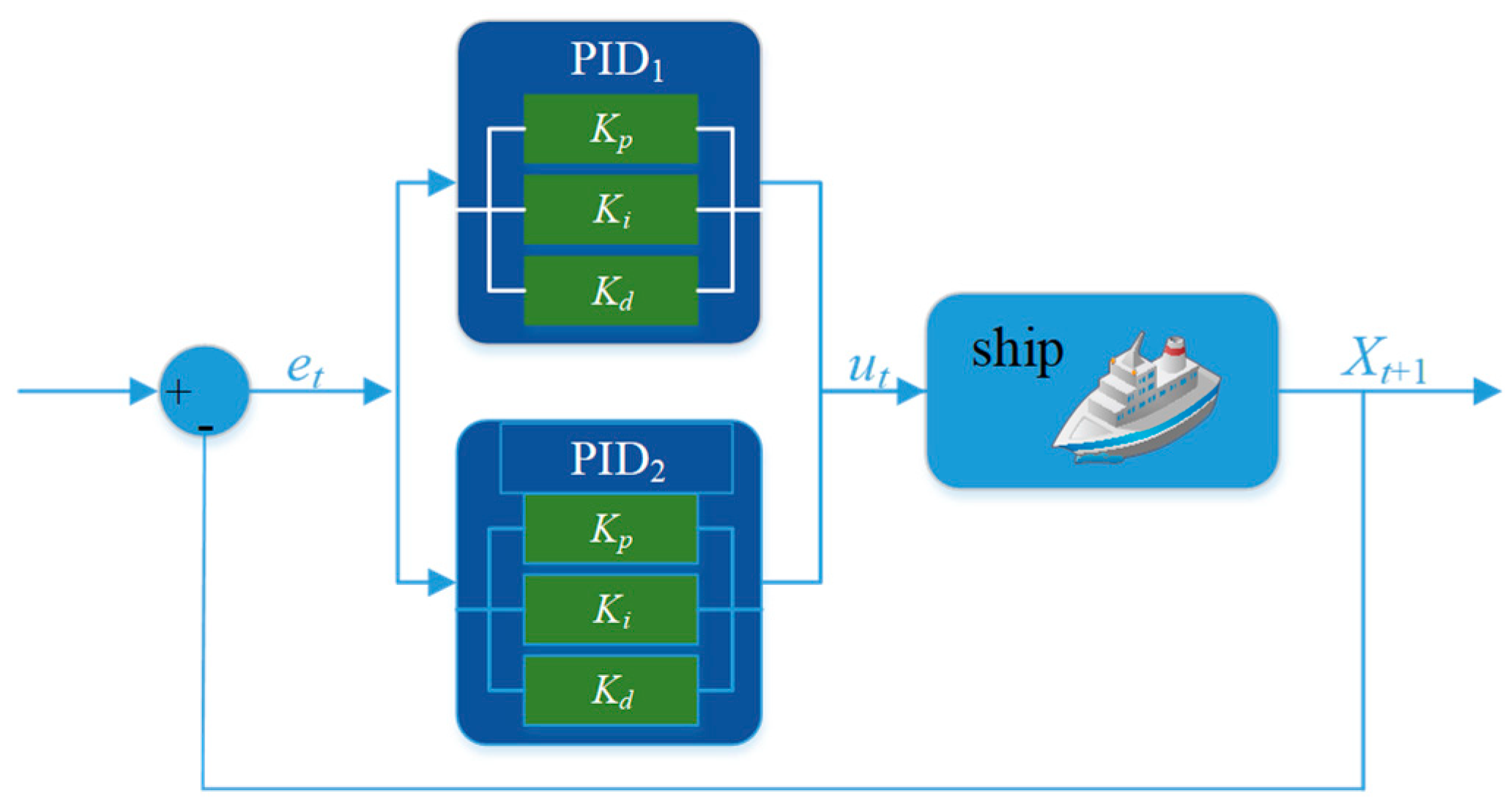
3.4. Optimal PID Control Method Based on DQ-Learning Algorithm
| Algorithm 1 PID control method for double Q-learning |
| Input: α, γ, r(-, -), ω0, K, η(-, -), n, m, N, Λ, ∆ x0: The state of the ship at the moment t0 is obtained by the ship’s sensors Initialize QA, QB, use same structure but different weights |
|
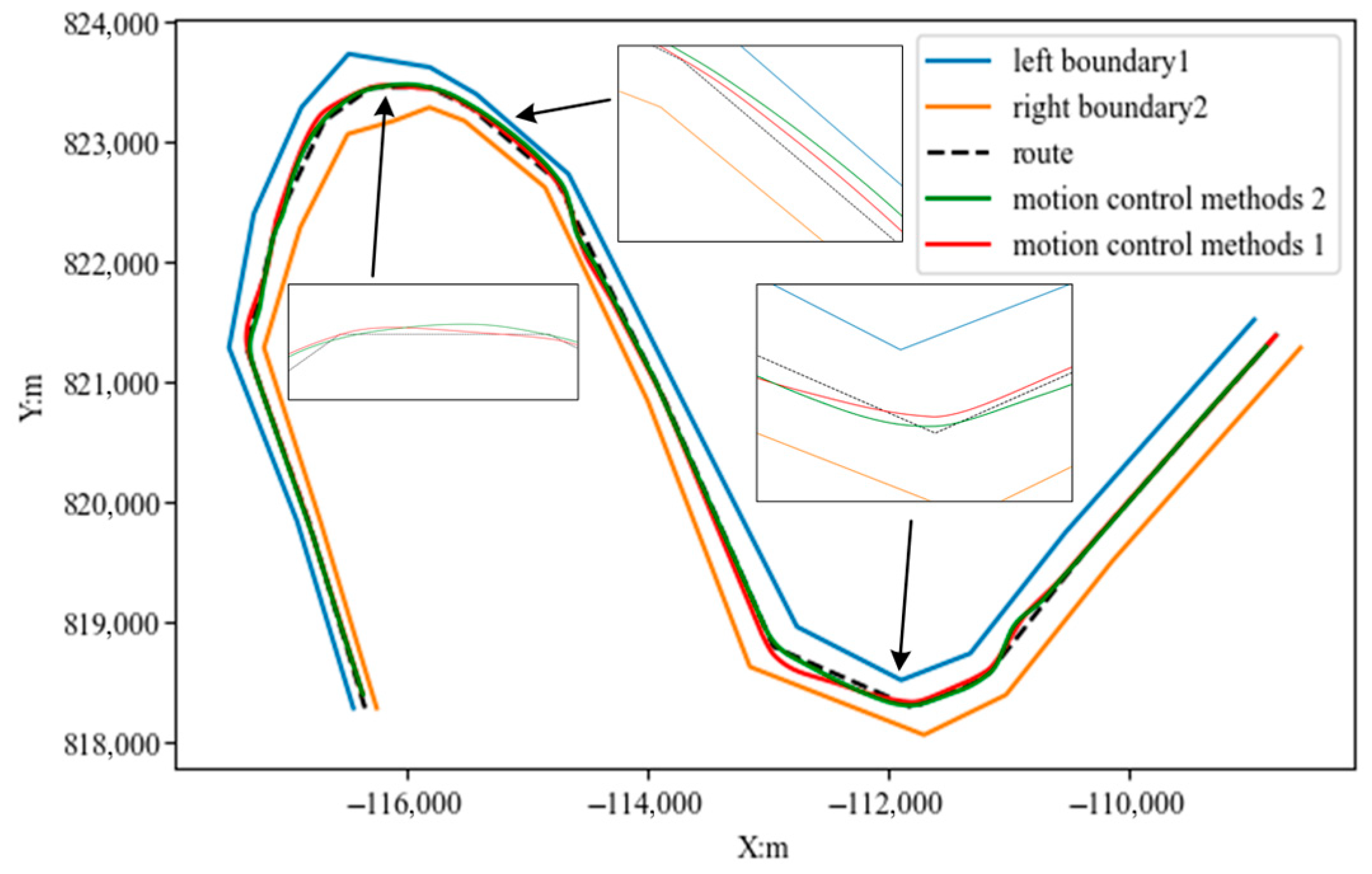
4. Experimental Validation and Performance Analysis of Motion Control
4.1. Performance in Hydrostatic Conditions
4.2. Performance Under Environmental Disturbances
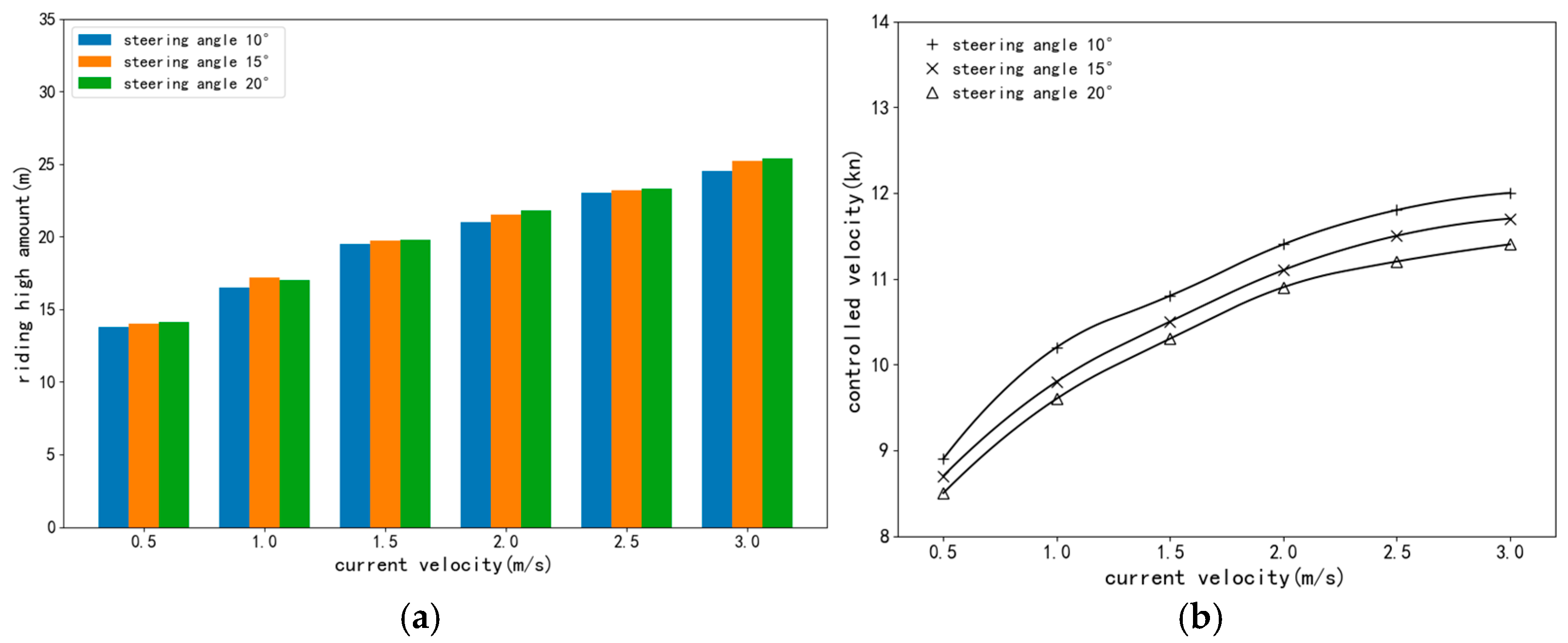
4.3. Performance Based on Both Environmental Disturbances and Maritime Practice
4.4. Discussion and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RL | Reinforce Learning |
| ENCs | Electronic Navigational Charts |
| LOS | Line-of-Sight |
| SMC | Sliding Mode Control |
| PID | Proportional-Integral-Derivative |
| ESO | Extended State Observer |
| SER | Stochastic Experience Replay |
| DQ-PID | Double Q-learning PID |
| COG | Course over Ground |
| CTE | Cross-Track Error |
| CFD | Computational Fluid Dynamics |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
References
- Wu, B.; Xu, X.; Teixeira, Â.P.; Yan, X.; Jiang, J. An Inland Waterway Traffic Complexity Evaluation Method Using Radar Sequential Images. Ocean Eng. 2025, 315, 119842. [Google Scholar] [CrossRef]
- Yang, B.; Kaidi, S.; Lefrançois, E. Numerical Investigation of the Parameters That May Seriously Impact the Ship Control Lability in Restricted Bending Channels. Ocean Eng. 2022, 266, 112735. [Google Scholar] [CrossRef]
- Moreira, L.; Fossen, T.I.; Guedes Soares, C. Path Following Control System for a Tanker Ship Model. Ocean Eng. 2007, 34, 2074–2085. [Google Scholar] [CrossRef]
- Xu, H.; Guedes Soares, C. Review of Path-Following Control Systems for Maritime Autonomous Surface Ships. J. Mar. Sci. Appl. 2023, 22, 153–171. [Google Scholar] [CrossRef]
- Wang, S.; Ma, F.; Yan, X.; Wu, P.; Liu, Y. Adaptive and Extendable Control of Unmanned Surface Vehicle Formations Using Distributed Deep Reinforcement Learning. Appl. Ocean Res. 2021, 110, 102590. [Google Scholar] [CrossRef]
- Ma, H.-J.; Yang, G.-H. Adaptive Fault Tolerant Control of Cooperative Heterogeneous Systems With Actuator Faults and Unreliable Interconnections. IEEE Trans. Autom. Control 2016, 61, 3240–3255. [Google Scholar] [CrossRef]
- You, C.; Zhang, R. Hybrid Offline-Online Design for UAV-Enabled Data Harvesting in Probabilistic LoS Channels. IEEE Trans. Wirel. Commun. 2020, 19, 3753–3768. [Google Scholar] [CrossRef]
- Faramin, M.; Goudarzi, R.H.; Maleki, A. Track-Keeping Observer-Based Robust Adaptive Control of an Unmanned Surface Vessel by Applying a 4-DOF Maneuvering Model. Ocean Eng. 2019, 183, 11–23. [Google Scholar] [CrossRef]
- Li, M.; Guo, C.; Yu, H.; Yuan, Y. Line-of-Sight-Based Global Finite-Time Stable Path Following Control of Unmanned Surface Vehicles with Actuator Saturation. ISA Trans. 2022, 125, 306–317. [Google Scholar] [CrossRef]
- Kelasidi, E.; Liljebäck, P.; Pettersen, K.Y.; Gravdahl, J.T. Integral Line-of-Sight Guidance for Path Following Control of Underwater Snake Robots: Theory and Experiments. IEEE Trans. Robot. 2017, 33, 610–628. [Google Scholar] [CrossRef]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Gravdahl, J.T.; Sørensen, A.J.; Milovanović, M.; Bruzzone, G. Integral Line-of-Sight Guidance and Control of Underactuated Marine Vehicles: Theory, Simulations, and Experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef]
- Wan, L.; Su, Y.; Zhang, H.; Shi, B.; AbouOmar, M.S. An Improved Integral Light-of-Sight Guidance Law for Path Following of Unmanned Surface Vehicles. Ocean Eng. 2020, 205, 107302. [Google Scholar] [CrossRef]
- Borhaug, E.; Pavlov, A.; Pettersen, K.Y. Integral LOS Control for Path Following of Underactuated Marine Surface Vessels in the Presence of Constant Ocean Currents. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4984–4991. [Google Scholar]
- Oh, S.-R.; Sun, J. Path Following of Underactuated Marine Surface Vessels Using Line-of-Sight Based Model Predictive Control. Ocean Eng. 2010, 37, 289–295. [Google Scholar] [CrossRef]
- Fossen, T.I.; Lekkas, A.M. Direct and Indirect Adaptive Integral Line-of-Sight Path-Following Controllers for Marine Craft Exposed to Ocean Currents. Int. J. Adapt. Control Signal Process. 2017, 31, 445–463. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-of-Sight Path Following for Dubins Paths with Adaptive Sideslip Compensation of Drift Forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z.; Wang, H. Predictor-Based LOS Guidance Law for Path Following of Underactuated Marine Surface Vehicles with Sideslip Compensation. Ocean Eng. 2016, 124, 340–348. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Peng, Z. ESO-Based Line-of-Sight Guidance Law for Path Following of Underactuated Marine Surface Vehicles with Exact Sideslip Compensation. IEEE J. Ocean. Eng. 2017, 42, 477–487. [Google Scholar] [CrossRef]
- Nie, J.; Lin, X. Improved Adaptive Integral Line-of-Sight Guidance Law and Adaptive Fuzzy Path Following Control for Underactuated MSV. ISA Trans. 2019, 94, 151–163. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, L. Path Following Control for Marine Surface Vessel with Uncertainties and Input Saturation. Neurocomputing 2016, 177, 158–167. [Google Scholar] [CrossRef]
- Wang, N.; Sun, Z.; Yin, J.; Su, S.-F.; Sharma, S. Finite-Time Observer Based Guidance and Control of Underactuated Surface Vehicles with Unknown Sideslip Angles and Disturbances. IEEE Access 2018, 6, 14059–14070. [Google Scholar] [CrossRef]
- Li, W.; Wu, C.; Lin, S.; Li, G.; Zhang, P. Active Heave Compensation of Marine Winch Based on Hybrid Neural Network Prediction and Sliding Mode Controller with a High-Gain Observer. Ocean Eng. 2025, 322, 120448. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Zhou, P.; Jia, B.; Li, R.; Xu, Y. A Saturation Adaptive Nonlinear Integral Sliding Mode Controller for Ship Permanent Magnet Propulsion Motors. J. Mar. Sci. Eng. 2025, 13, 976. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Xu, H.; Guedes Soares, C. Heterogeneous Cooperative Trajectory Tracking Control between Surface and Underwater Unmanned Vehicles. Ocean Eng. 2024, 301, 117137. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, W.; Zhang, G.; Zhang, X. Disturbance Observer-Based Adaptive Neural Control for Underactuated Surface Vehicle with Constraint of Input Saturation. Ocean Eng. 2023, 287, 115744. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. State- and Output-Feedback Robust Path-Following Controllers for Underactuated Ships Using Serret–Frenet Frame. Ocean Eng. 2004, 31, 587–613. [Google Scholar] [CrossRef]
- Ghommam, J.; Mnif, F.; Benali, A.; Derbel, N. Nonsingular Serret–Frenet Based Path Following Control for an Underactuated Surface Vessel. J. Dyn. Syst. Meas. Control 2009, 131, 21006. [Google Scholar] [CrossRef]
- Do, K.D.; Jiang, Z.P.; Pan, J. Robust Adaptive Path Following of Underactuated Ships. Automatica 2004, 40, 929–944. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Wu, D.; Yan, Y. Nonsingular Fixed-Time Terminal Sliding Mode Trajectory Tracking Control for Marine Surface Vessels with Anti-Disturbances. Ocean Eng. 2020, 217, 108158. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.; Im, N. Ship Nonlinear-Feedback Course Keeping Algorithm Based on MMG Model Driven by Bipolar Sigmoid Function for Berthing. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 525–536. [Google Scholar] [CrossRef]
- Zhu, M.; Hahn, A.; Wen, Y.-Q. Identification-Based Controller Design Using Cloud Model for Course-Keeping of Ships in Waves. Eng. Appl. Artif. Intell. 2018, 75, 22–35. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Dlabač, T.; Ćalasan, M.; Krčum, M.; Marvučić, N. PSO-Based Pid Controller Design for Ship Course-Keeping Autopilot. Brodogradnja 2019, 70, 1–15. [Google Scholar] [CrossRef]
- Bhopale, P.; Kazi, F.; Singh, N. Reinforcement Learning Based Obstacle Avoidance for Autonomous Underwater Vehicle. J. Mar. Sci. Appl. 2019, 18, 228–238. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Im, N.; Zhang, G.; Zhang, Q. Adaptive Fuzzy Tracking Control for Underactuated Surface Vessels with Unmodeled Dynamics and Input Saturation. ISA Trans. 2020, 103, 52–62. [Google Scholar] [CrossRef] [PubMed]
- Majidiyan, H.; Enshaei, H.; Howe, D. A Concise Account for Challenges of Machine Learning in Seakeeping. Procedia Comput. Sci. 2025, 253, 2849–2858. [Google Scholar] [CrossRef]
- Piao, Z.; Guo, C.; Sun, S. Research into the Automatic Berthing of Underactuated Unmanned Ships under Wind Loads Based on Experiment and Numerical Analysis. J. Mar. Sci. Eng. 2019, 7, 300. [Google Scholar] [CrossRef]
- Li, M.; Guo, C.; Yu, H. Extended State Observer-Based Integral Line-of-Sight Guidance Law for Path Following of Underactuated Unmanned Surface Vehicles with Uncertainties and Ocean Currents. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211011035. [Google Scholar] [CrossRef]
- Editorial Board of the Dictionary of Water Transport Technology. Dictionary of Water Transport Technology; China Communications Press: Beijing, China, 1986. [Google Scholar]
- Aoki, I.; Kijima, K.; Furukawa, Y.; Nakiri, Y. On the Prediction Method for Maneuverability of a Full Scale Ship. J. Japan Soc. Nav. Archit. Ocean Eng. 2006, 3, 157–165. [Google Scholar] [CrossRef]
- Tangirala, A.K. Principles of System Identification: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2014; pp. 1–845. [Google Scholar]
- Buşoniu, L.; Babuška, R.; De Schutter, B.; Ernst, D. Reinforcement Learning and Dynamic Programming Using Function Approximators; CRC Press: Boca Raton, FL, USA, 2010; pp. 1–271. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Zhang, S.; Sutton, R.S. A Deeper Look at Experience Replay. arXiv 2017, arXiv:1712.01275. [Google Scholar]




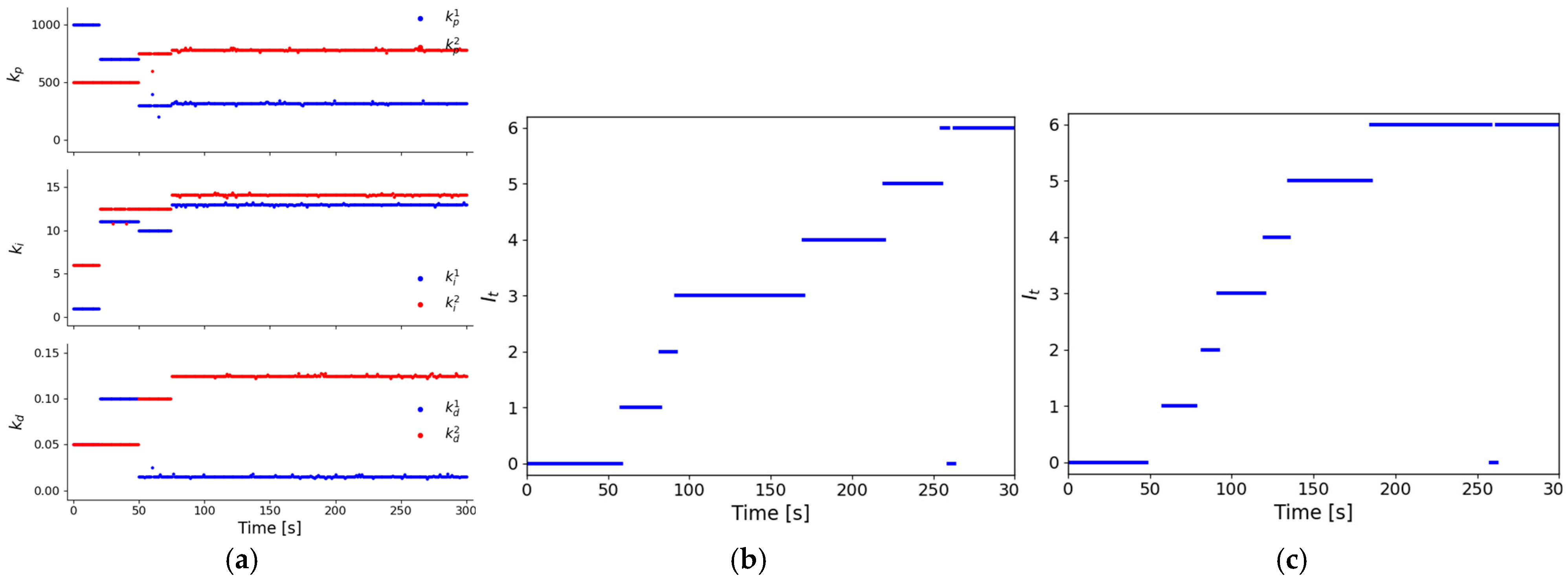
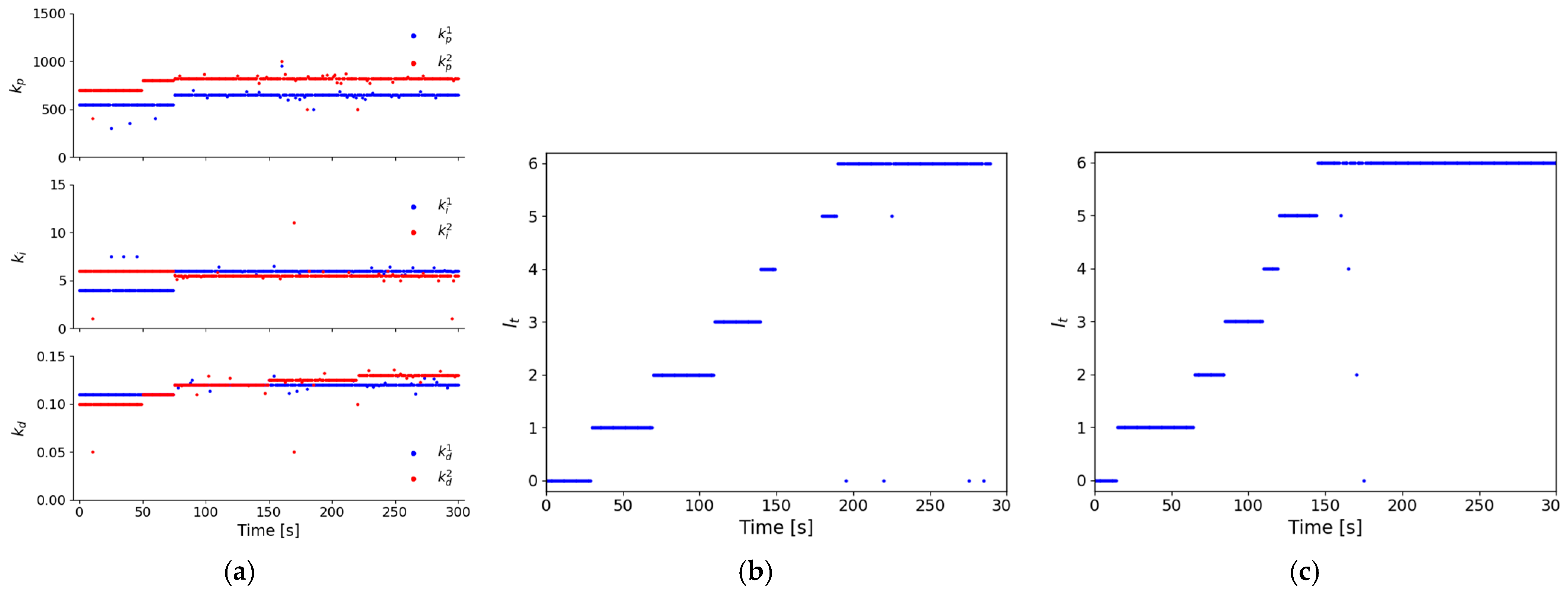
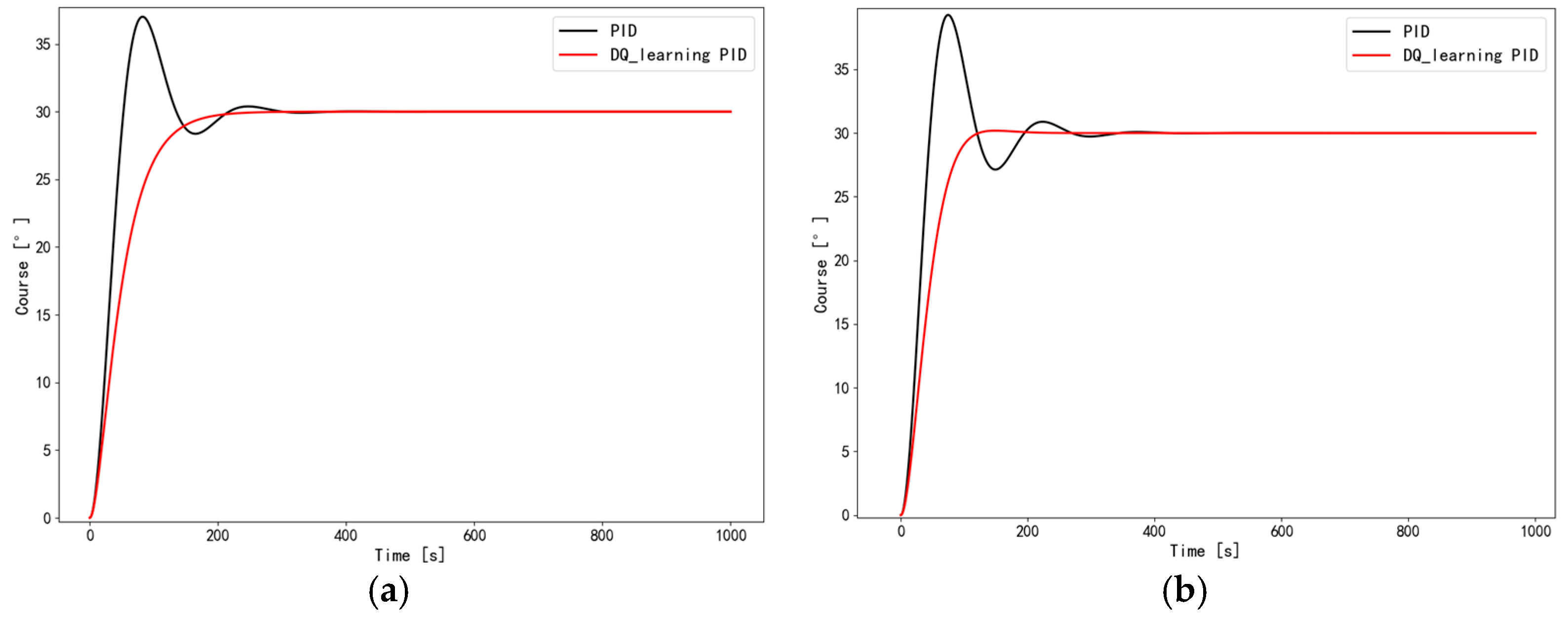
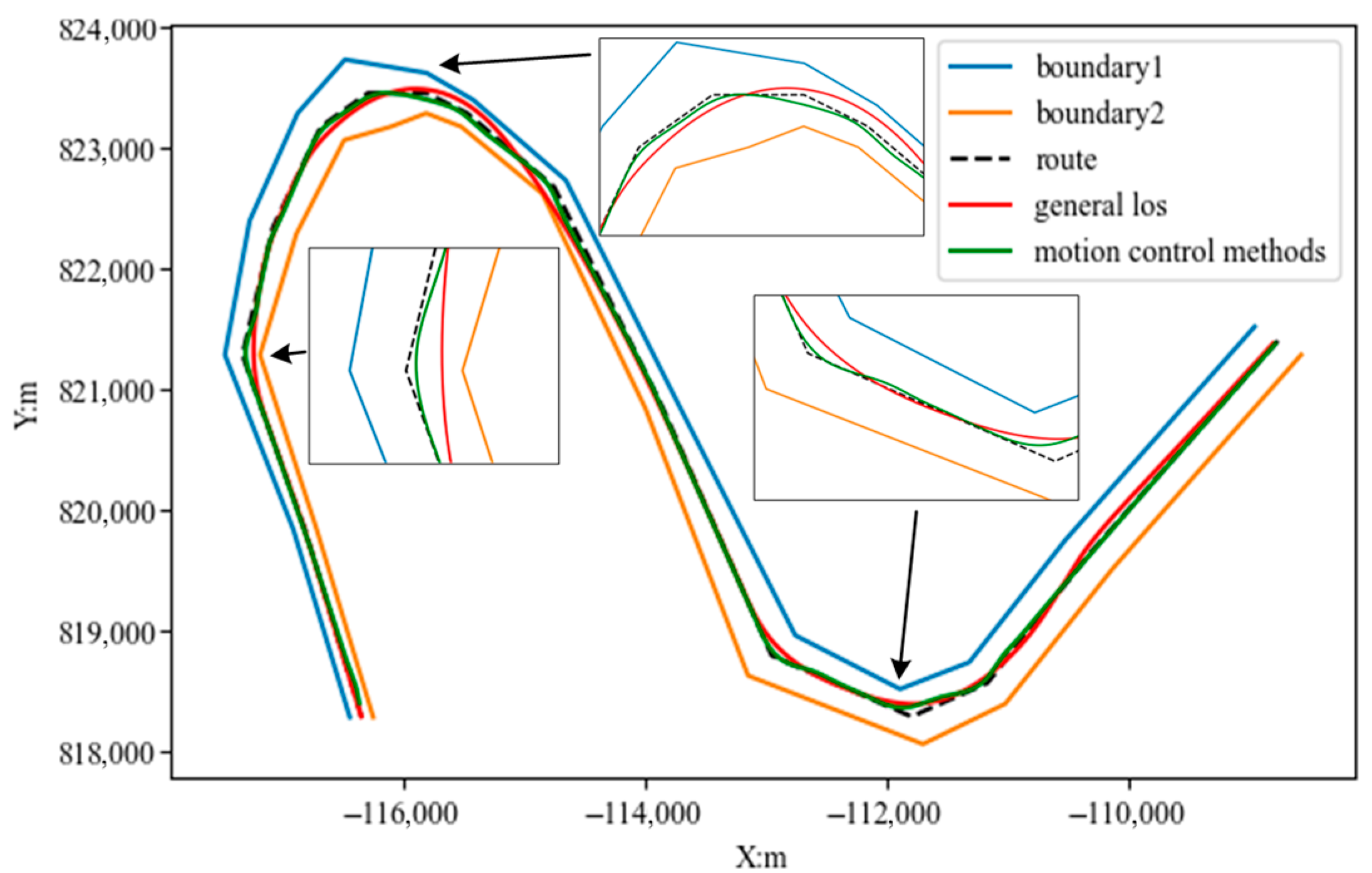
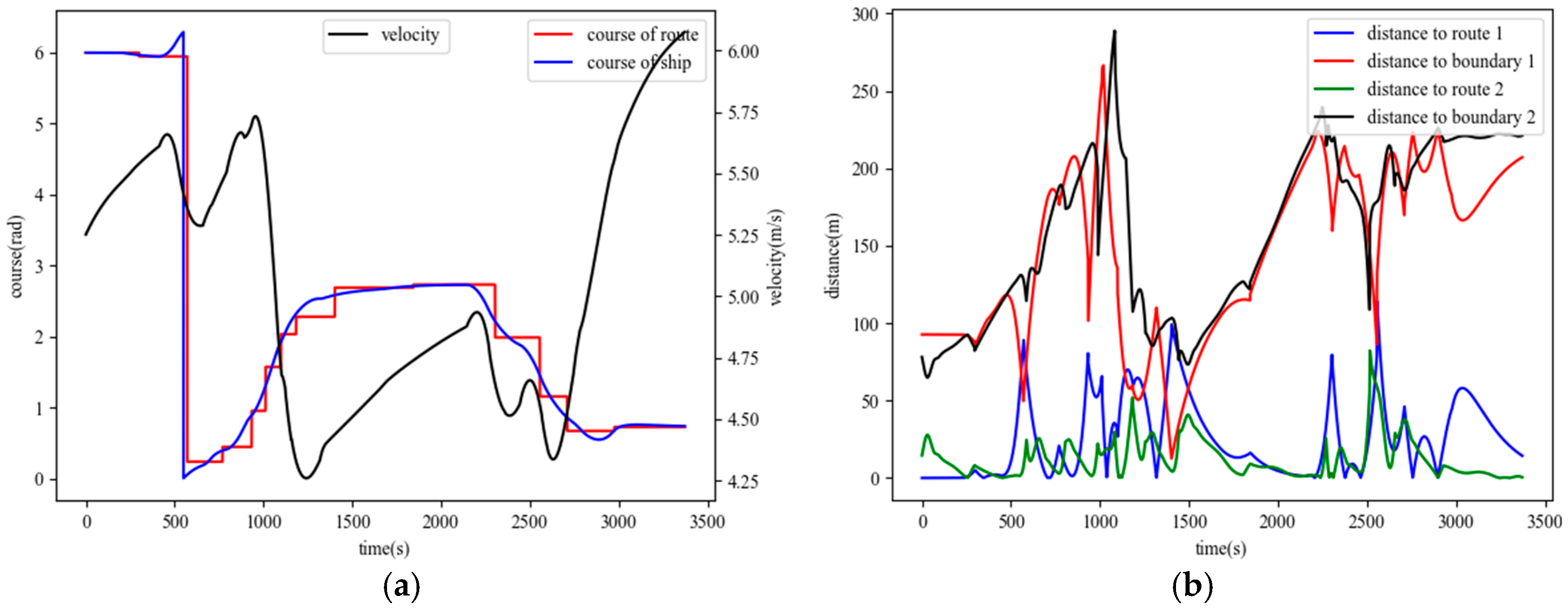
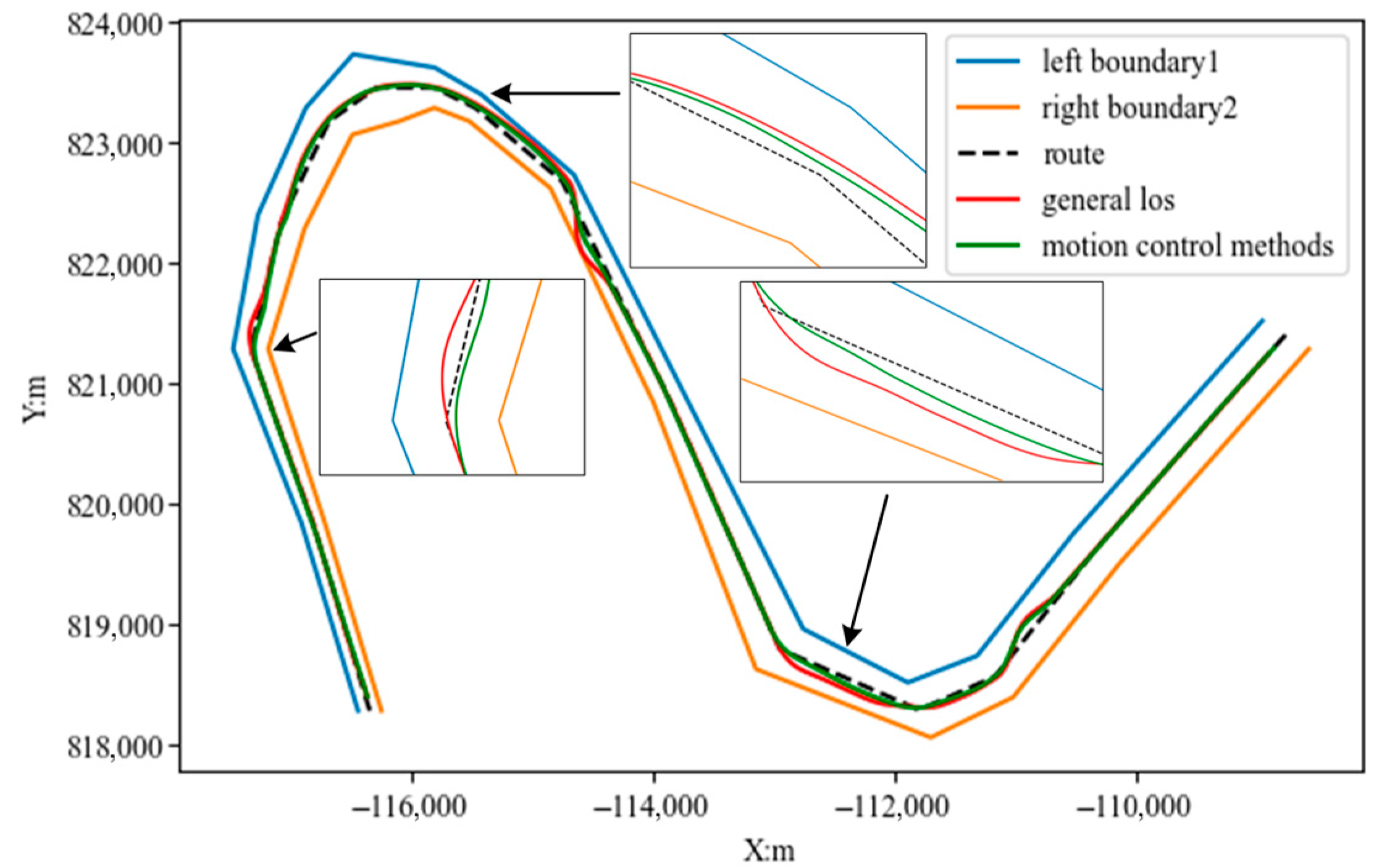
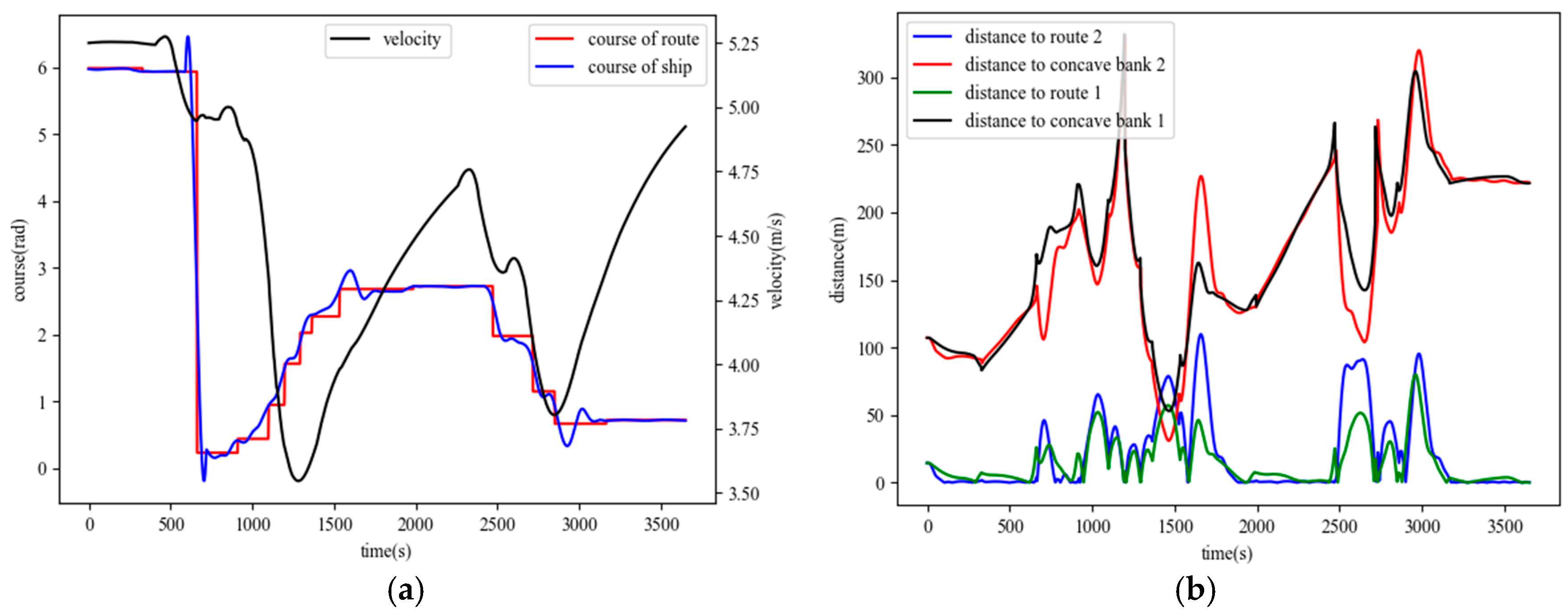


| Performance Metric | Benchmark | Proposed Method | Improvement |
|---|---|---|---|
| CTE RMSE (m) | 23.9 | 12.6 | 47.3% |
| Max CTE (m) | 114.3 | 82.2 | 28.1% |
| Heading MAE (deg) | 7.14 | 2.50 | 65.0% |
| Performance Metric | Benchmark | Proposed Method | Improvement |
|---|---|---|---|
| CTE RMSE (m) | 28.8 | 16.9 | 41.3% |
| Max CTE (m) | 109.8 | 80.1 | 27.0% |
| Heading MAE (deg) | 10.56 | 5.62 | 46.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Chen, J. Ship Motion Control Methods in Confined and Curved Waterways Combining Good Seamanship. J. Mar. Sci. Eng. 2025, 13, 1800. https://doi.org/10.3390/jmse13091800
Huang L, Chen J. Ship Motion Control Methods in Confined and Curved Waterways Combining Good Seamanship. Journal of Marine Science and Engineering. 2025; 13(9):1800. https://doi.org/10.3390/jmse13091800
Chicago/Turabian StyleHuang, Liwen, and Jiahao Chen. 2025. "Ship Motion Control Methods in Confined and Curved Waterways Combining Good Seamanship" Journal of Marine Science and Engineering 13, no. 9: 1800. https://doi.org/10.3390/jmse13091800
APA StyleHuang, L., & Chen, J. (2025). Ship Motion Control Methods in Confined and Curved Waterways Combining Good Seamanship. Journal of Marine Science and Engineering, 13(9), 1800. https://doi.org/10.3390/jmse13091800





