Design of UUV Underwater Autonomous Recovery System and Controller Based on Mooring-Type Mobile Docking Station
Abstract
1. Introduction
- A fork-pillar-type recovery system was designed for dynamic docking of UUVs. Considering the characteristics of the docking device, a segmented sit-down docking strategy was developed, consisting of two phases: a long-distance approach phase and a follow-up descent phase.
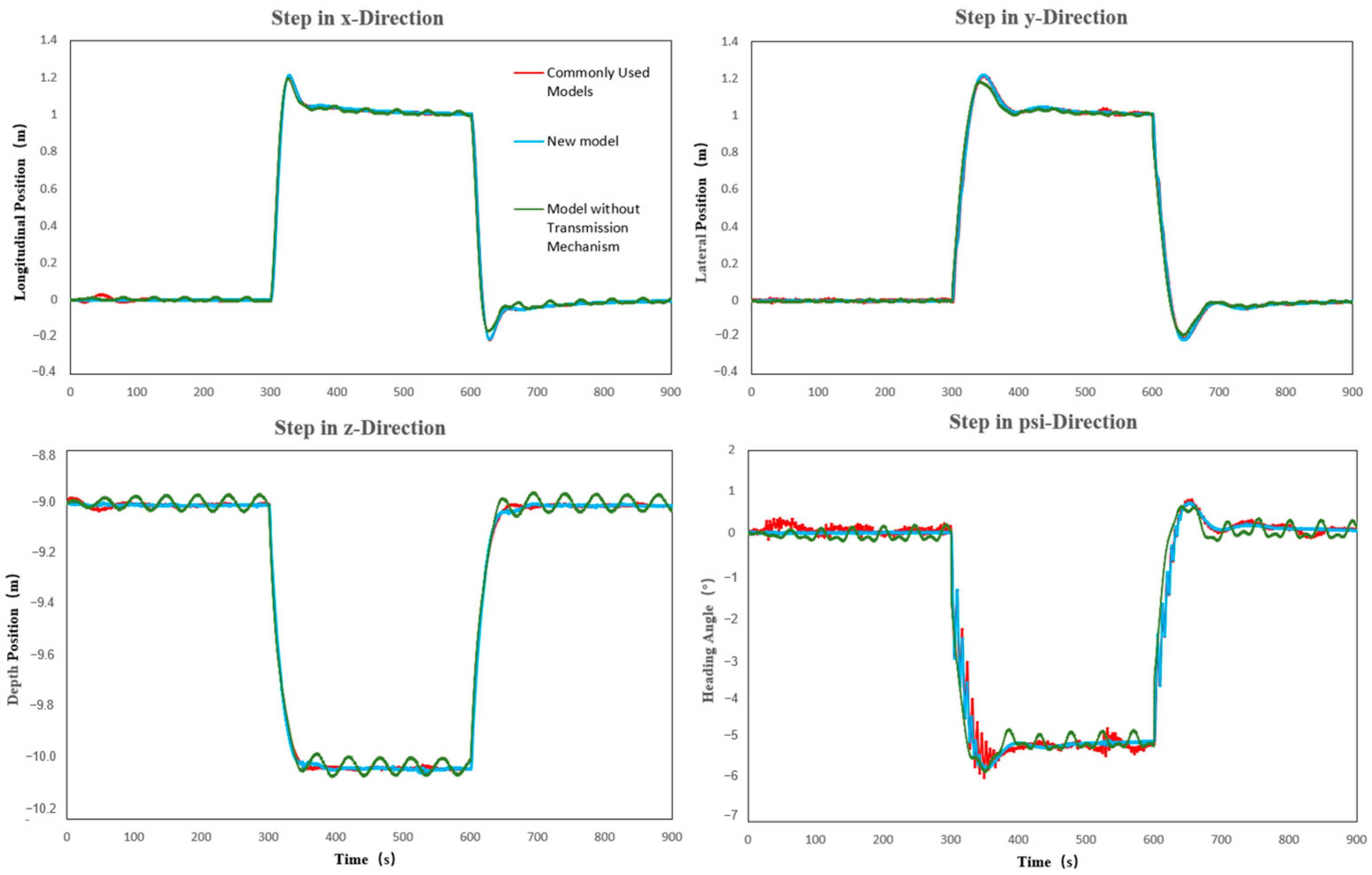
- To address the accuracy issues of the UUV model, a transfer-function-based representation was designed and incorporated into the UUV model to mitigate the transmission lag of control inputs acting on the actuators. Subsequently, a quasi-linear parameter-varying (QLPV) system was employed to characterize the nonlinear components in the dynamic model, and the function substitution method was improved, resulting in a more accurate and practical UUV model that better aligns with real-world conditions.
- For the two distinct phases of UUV segmented recovery, a variable prediction horizon step size method was adopted to enhance both the prediction accuracy and computational efficiency of the UUV model. To address the complex constraints encountered during the recovery and docking process, a model predictive controller (MPC) was designed based on the aforementioned improved UUV dynamic model. This controller significantly improves the predictive capability and control performance for future UUV behavior.
- A hardware-in-the-loop (HIL) simulation system was designed and analyzed to validate the proposed innovations. Physical experiments were also conducted on key components, which fully demonstrates the feasibility of the proposed approach.
2. Problem Statement and Preliminary Design
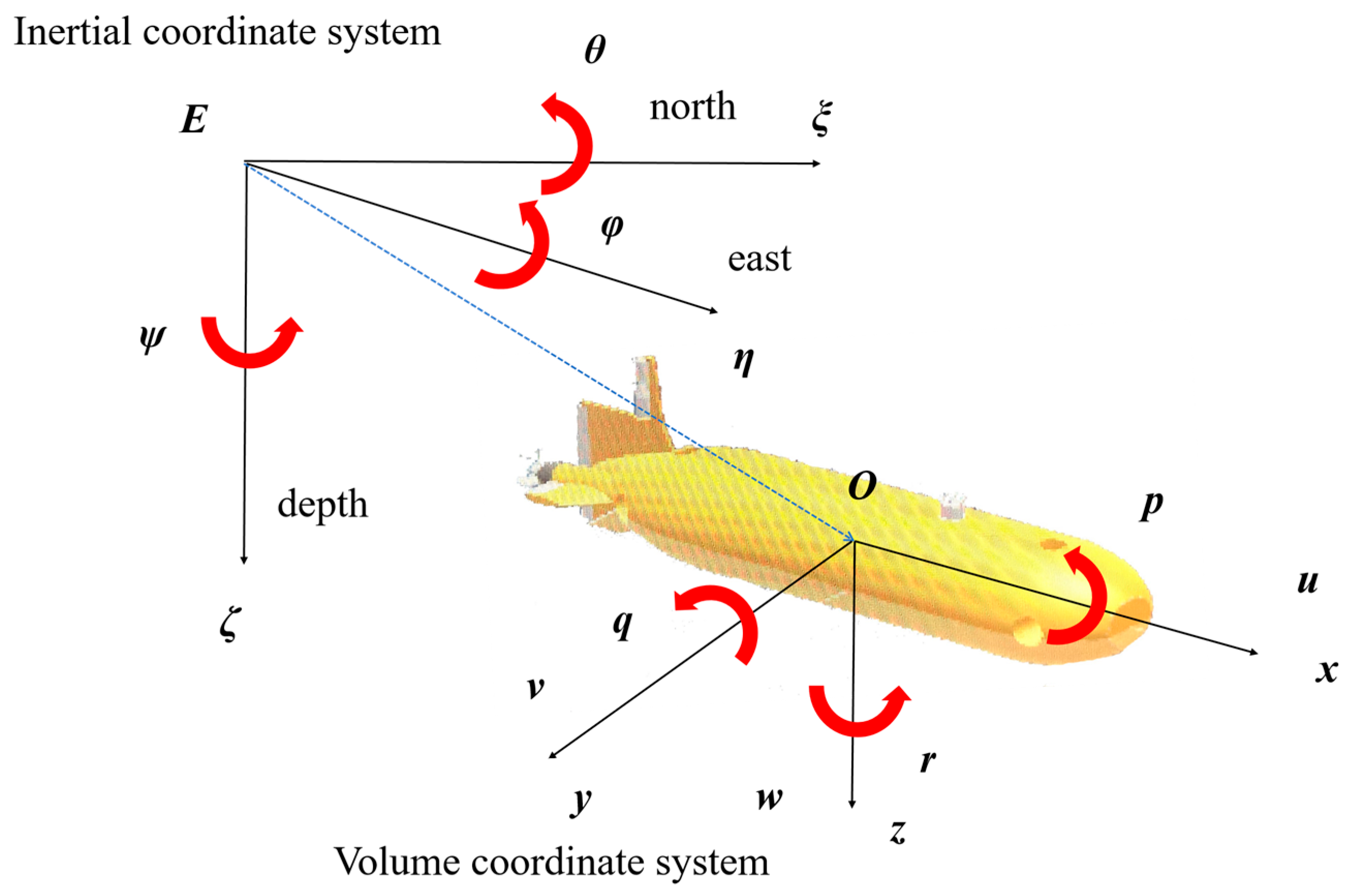
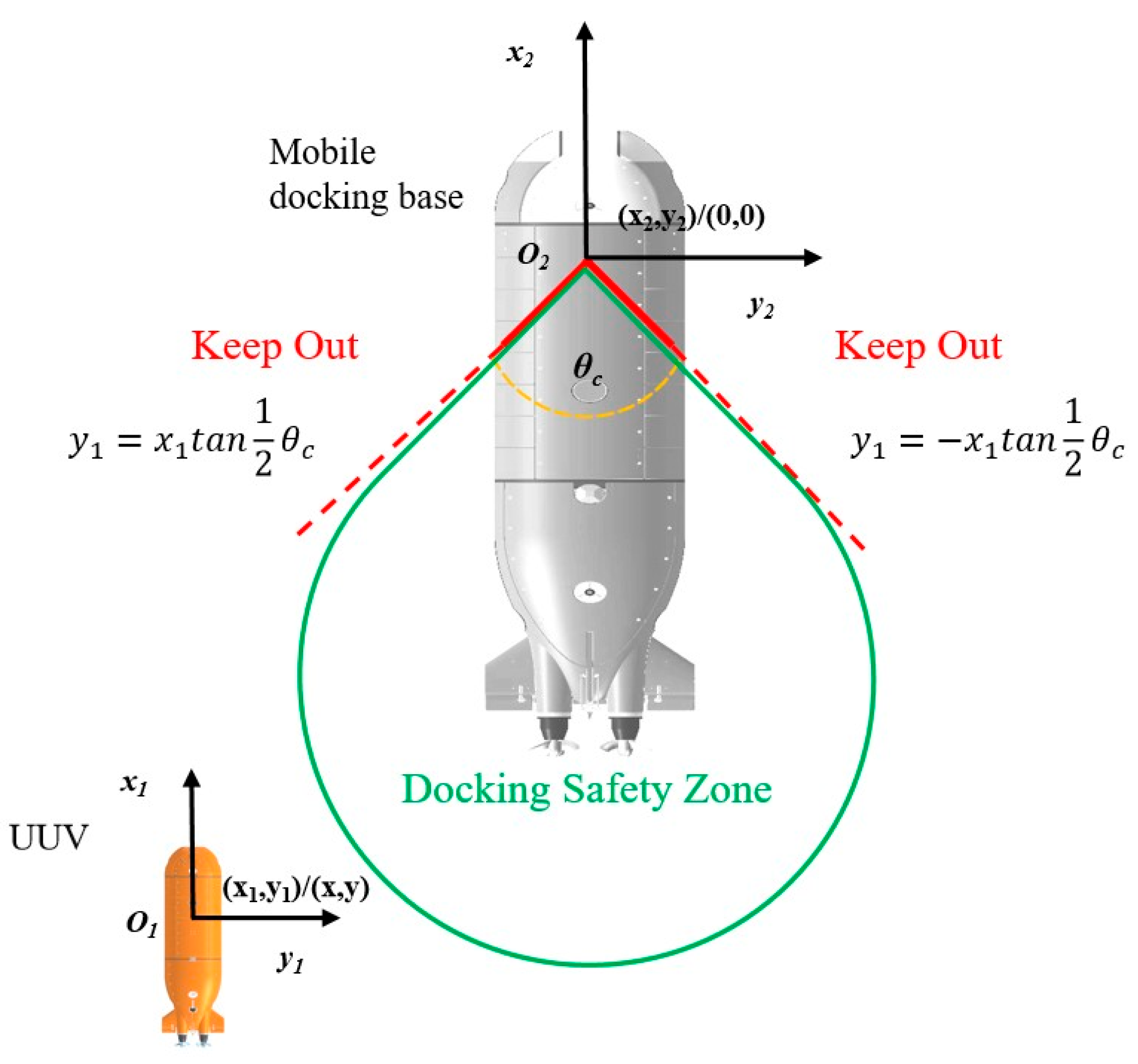
2.1. Coordinate System Formulation
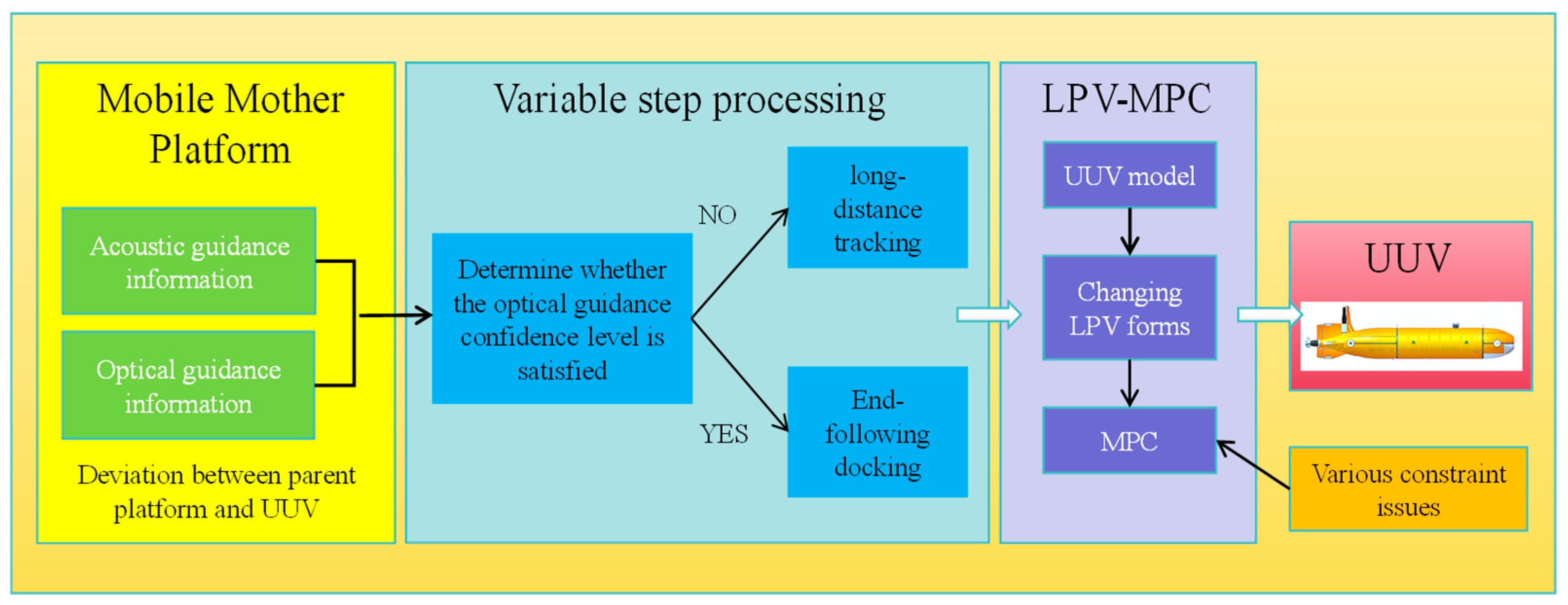
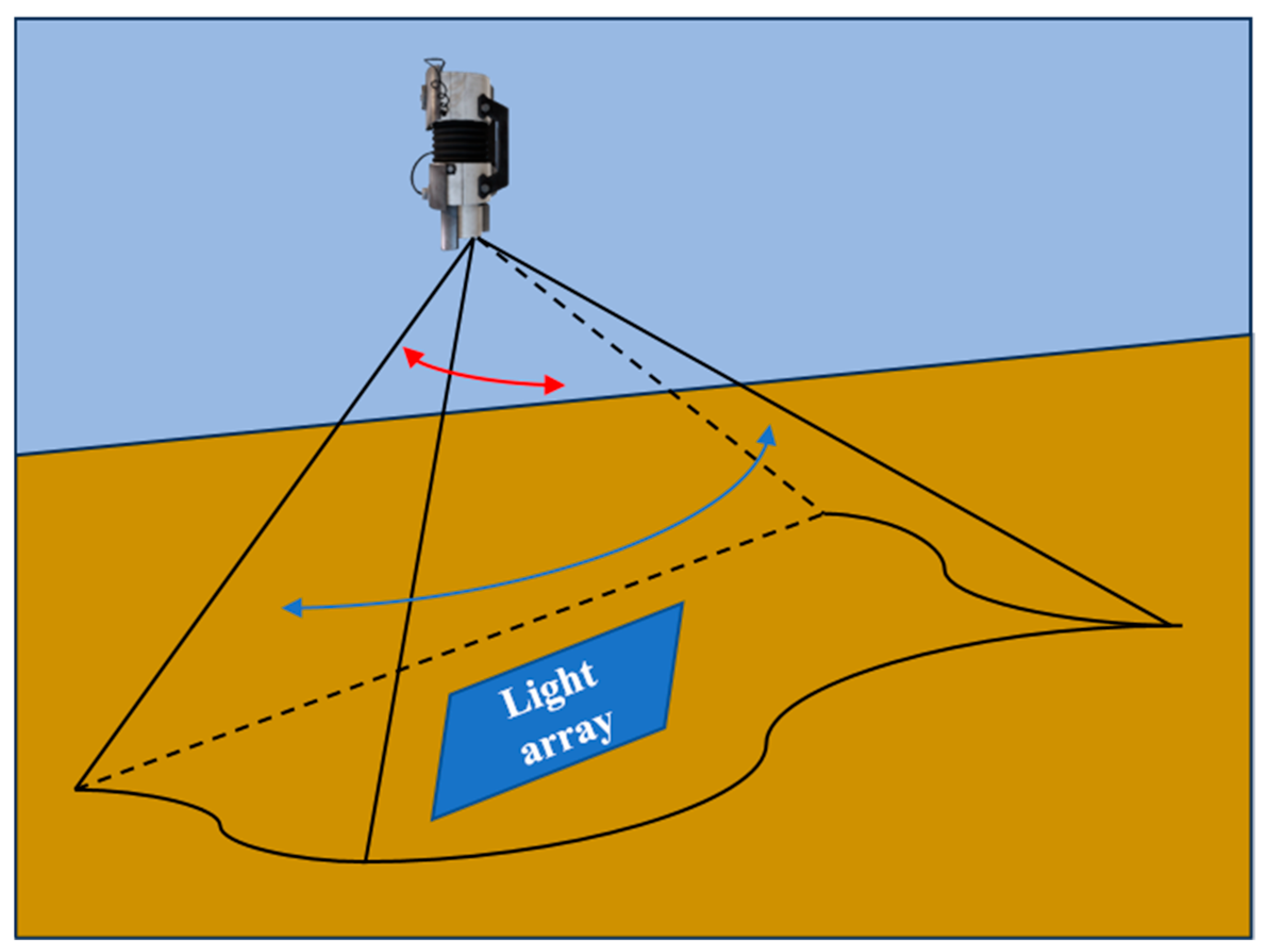
2.2. Settlement-Based Recovery Strategy and Control Framework
- Stage 1: Long-distance tracking stage
- Stage 2: Short-distance docking stage
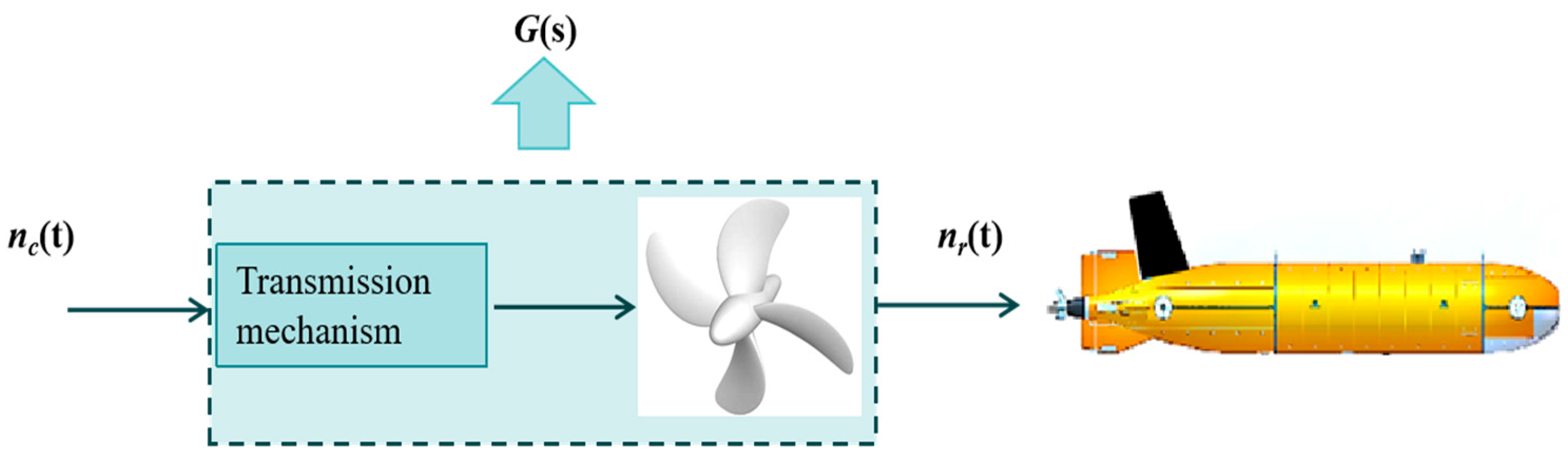
2.3. Modeling of the UUV
3. Quasi-LPV Modeling of UUV Dynamics
4. Design of a Piecewise Variable-Step-Size MPC Controller for QLPV Systems
4.1. Long-Range Tracking Phase
- (1)
- Thruster Thrust Saturation Constraint:
- (2)
- UUV Depth Constraint:
- (3)
- Mission Time Constraint:
4.2. Close-Range Docking Phase
- (1)
- Sensor observation constraints:
- (2)
- Geometric Constraints:
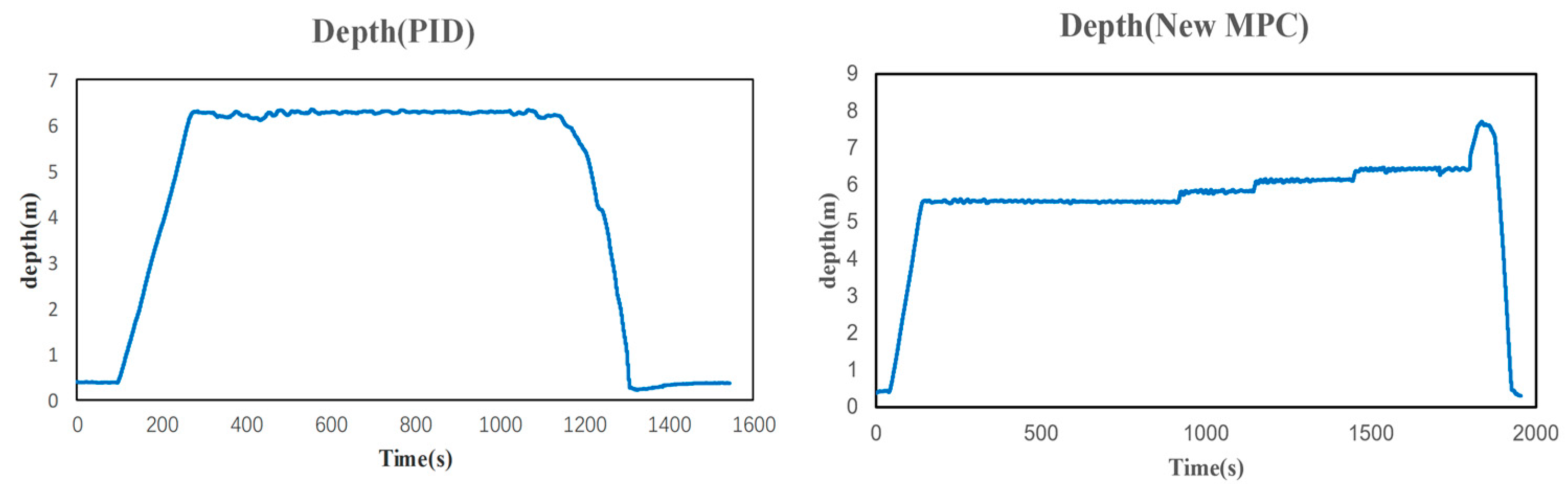
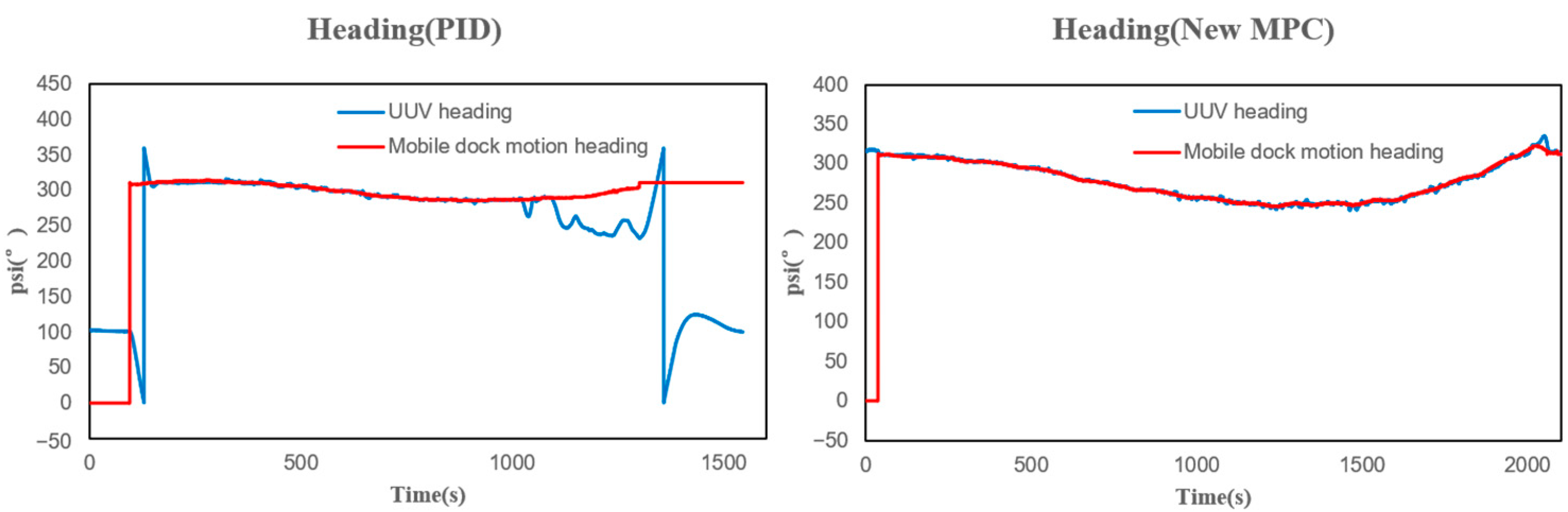
5. Simulations and Experiments
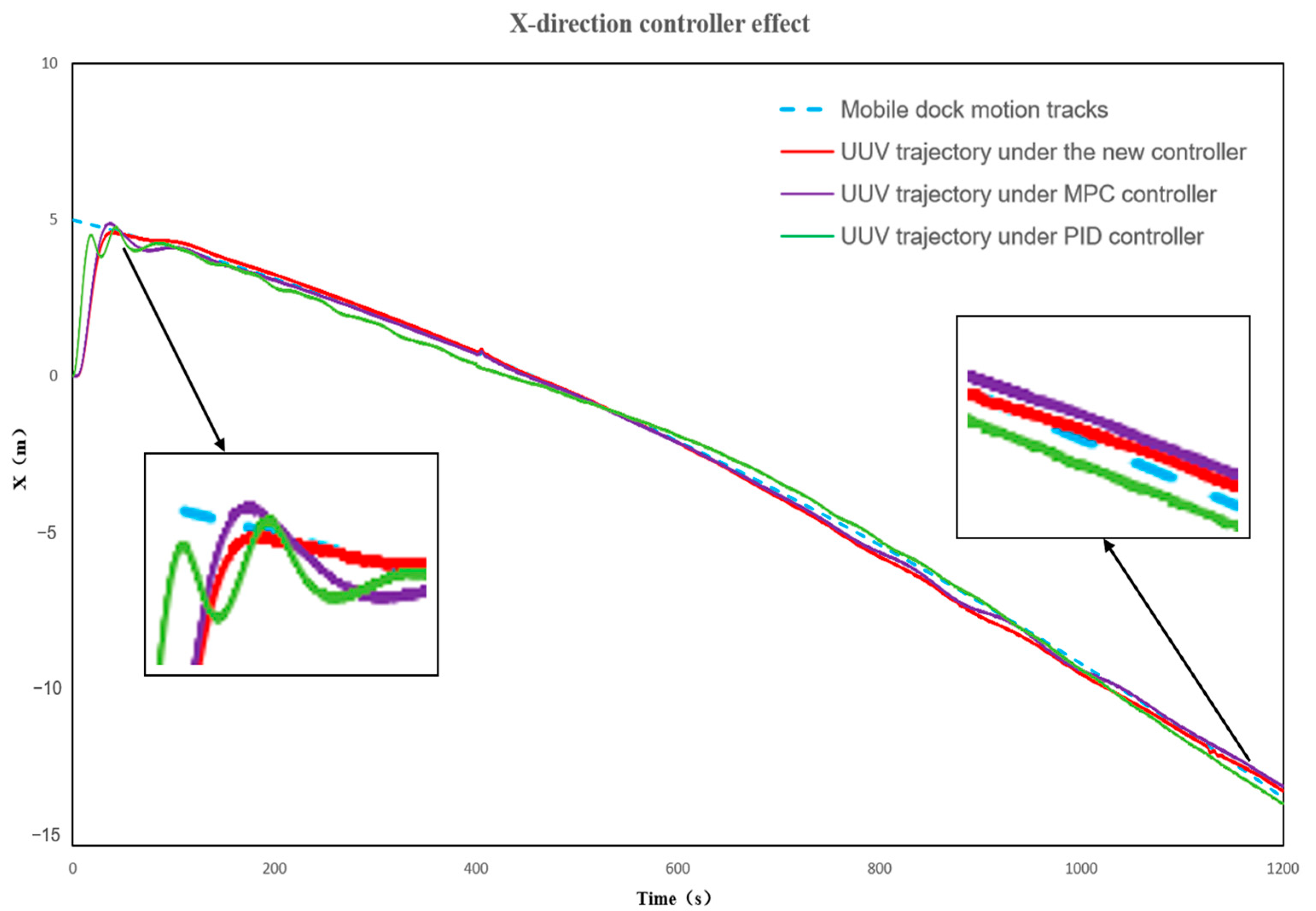
5.1. Simulation Analysis
- (1)
- Input: The deviation between the system output and the desired setpoint;
- (2)
- Core Algorithm: Proportional, integral, and derivative operations applied to the error, followed by a weighted summation of the results;
- (3)
- Output: The computed control signal.
- (1)
- Input: The current state of the system;
- (2)
- Core Algorithm: Utilizing an internal predictive model to forecast system behavior over a finite horizon, solving an optimization problem to identify a sequence of future control actions that minimize the objective function, applying only the first control action in the sequence, and repeating the entire process at the next time step (receding horizon optimization);
- (3)
- Output: The optimized control signal computed.
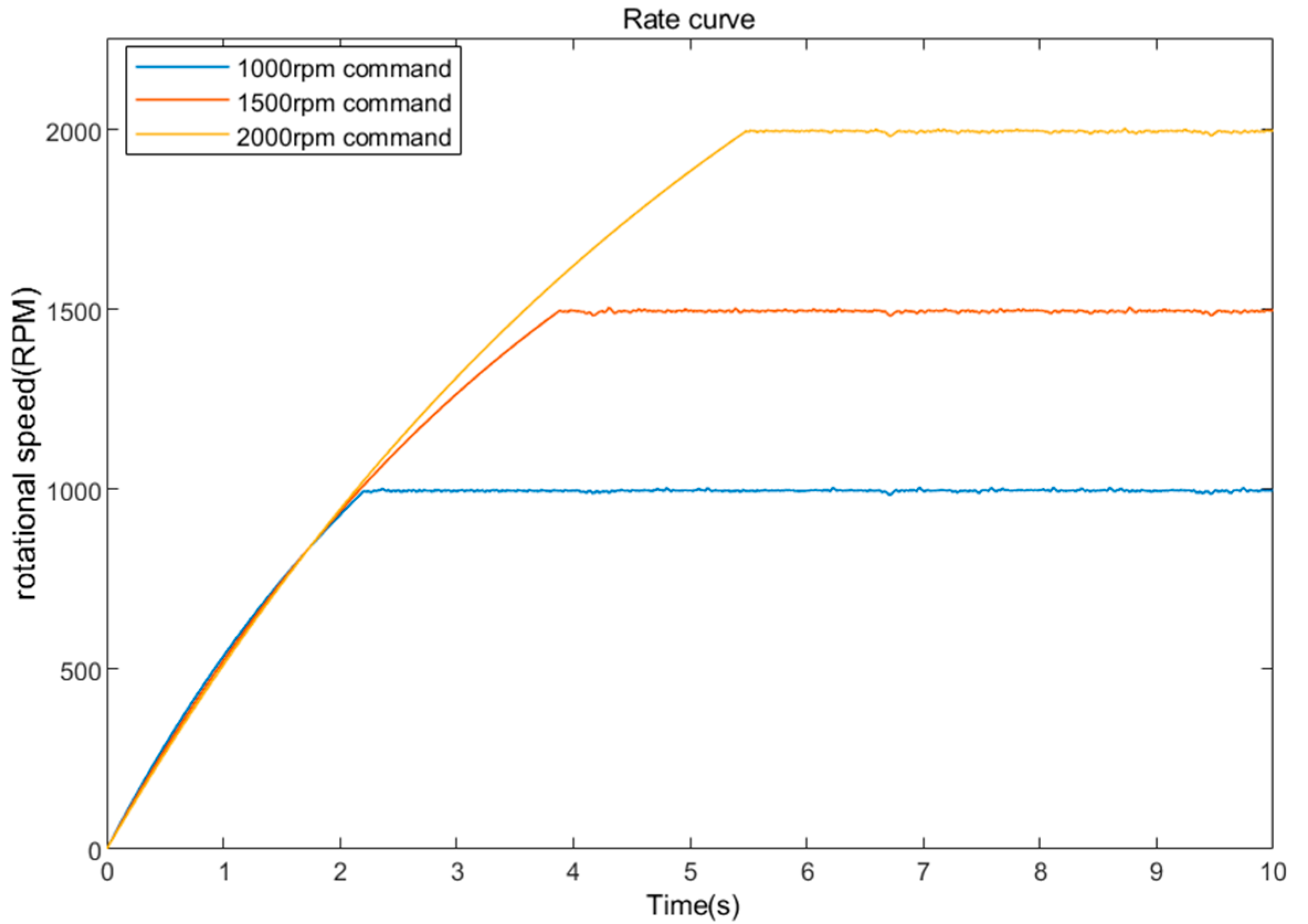
5.2. Experimental Validation
- (1)
- Inertial Navigation System (INS): A self-developed device by the university, providing the UUV’s own position and attitude information.
- (2)
- Doppler Velocity Log (DVL): Measures the UUV’s velocity relative to water, thereby supplying speed data.
- (3)
- GPS: Provides the UUV’s latitude and longitude coordinates.
- (4)
- Depth Sensor: Measures and reports the UUV’s depth.
- (5)
- Ultra-Short Baseline (USBL)/Transducer: A self-developed system by the university, which acoustically measures the target’s distance and azimuth to determine its coordinates relative to the array.
- (6)
- Optical Camera: Identifies the guidance light array, enabling calculation of the relative position and attitude deviation between the UUV and the mobile docking station.
6. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S. Determination of the legal status of maritime unmanned systems. Shanghai Leg. Stud. Collect. Anthol. Emerg. Rights Rule Law China 2021, 54, 47–56. [Google Scholar] [CrossRef]
- Miao, R.L. Research on Energy-Efficient Path Planning for Autonomous Underwater Vehicles. Master’s Thesis, Harbin Engineering University, Harbin, China, 2013. [Google Scholar]
- Xu, G. Development status and key technologies of UUV underwater docking technology. Acoust. Electron. Eng. 2019, 4, 1–5+9. [Google Scholar]
- Zhang, W.; Han, P.; Liu, Y.; Zhang, Y.; Wu, W.; Wang, Q. Design of an Improved Adaptive Slide Controller in UUV Dynamic Base Recovery. Ocean Eng. 2023, 285, 115266. [Google Scholar] [CrossRef]
- Bhat, S.; Panteli, C.; Stenius, I.; Dimarogonas, D.V. Nonlinear Model Predictive Control for Hydrobatics: Experiments with an Underactuated AUV. J. Field Robot. 2023, 40, 1840–1859. [Google Scholar] [CrossRef]
- Qi, B. Docking Control Algorithm for AUV Based on Model Predictive Control. Autom. Instrum. 2023, 38, 44–48+90. [Google Scholar] [CrossRef]
- Bian, Y.G.; Zhang, J.J.; Li, C.K.; Xu, B.; Qin, Z.; Hu, M. Distributed Model Predictive Depth and Longitudinal Velocity Control for Multiple AUVs. J. Hunan Univ. 2022, 49, 45–54. [Google Scholar]
- Yan, Z.P.; Yang, H.Y.; Zhang, W. Trajectory Tracking Control of Hexapod Robot Based on Model Prediction-Central Pattern Generator. Robot 2023, 45, 58–69. [Google Scholar]
- Zhang, Y.; Liu, X.; Luo, M.; Yang, C. MPC-Based 3-D Trajectory Tracking for an Autonomous Underwater Vehicle with Constraints in Complex Ocean Environments. Ocean Eng. 2019, 189, 106309. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, W.H.; Teng, Y.B.; Gong, P.; Tang, Y.J. Docking Control of Dynamic Base Underwater Unmanned Vehicle Based on Satisfactory Model Predictive Control Under Constraints. J. Harbin Eng. Univ. 2022, 43, 108–118. [Google Scholar]
- Huang, Y.; Hu, F.; Yu, J.C.; Qiao, J.N.; Wang, Z.Y. Research on the Navigation Control System of Lightweight Long-Range AUV Based on Model Predictive Control Algorithm. J. Ocean Technol. 2020, 39, 32–38. [Google Scholar]
- Chen, Y.H.; Wu, H.Y.; Bian, Y.G. Trajectory Tracking Algorithm of Seabed Mining Vehicle Based on Sliding Mode Predictive Control. Inf. Control 2022, 51, 119–128. [Google Scholar]
- Wang, J.; Fader, M.T.H.; Marshall, J.A. Learning-Based Model Predictive Control for Improved Mobile Robot Path Following Using Gaussian Processes and Feedback Linearization. J. Field Robot. 2023, 40, 1014–1033. [Google Scholar] [CrossRef]
- Luo, Z.G.; Zhu, B.; Zheng, J.Y.; Zheng, Z.W. Robust Distributed Model Predictive Control for Formation Tracking of Nonholonomic Vehicles. IEEE/CAA J. Autom. Sin. 2024, 11, 560–562. [Google Scholar] [CrossRef]
- Tang, C.Y.; Zhang, M.L.; Fan, S.; Xia, J.F.; Wu, L.J. Research on Vehicle Path Tracking Control Technology Based on Model Predictive Control. Agric. Equip. Veh. Eng. 2024, 62, 71–75+104. [Google Scholar]
- Shao, P.Y.; Wu, J.; Ma, S. Model and Robust Gain-Scheduled PID Control of a Bio-Inspired Morphing UAV Based on LPV Method. Asian J. Control Affil. ACPA Asian Control Profr. Assoc. 2019, 21, 1681–1705. [Google Scholar] [CrossRef]
- Yan, Y.P.; Rao, B.; Liu, Y.J.; Feng, Y.B. Trajectory Tracking Control of Quadrotor UAV Based on Nonlinear Model Prediction. J. Shenyang Ligong Univ. 2024, 43, 36–43+49. [Google Scholar]
- Wu, C.F.; Feng, L.; Sui, D.; Wang, X.M. Application of Model Predictive Control Algorithm in Aircraft Automatic Landing Control System. J. Northwest. Polytech. Univ. 2004, 22, 140–144. [Google Scholar]
- Jiang, X.; Zeng, C.; Liu, J.; Gu, Q.; Wang, Z.; Pan, H. Dynamic Modeling and Analysis on the Cable Effect of USV/UUV System Under High-Speed Condition. J. Mar. Sci. Eng. 2025, 13, 125. [Google Scholar] [CrossRef]
- Menghini, M.; Mallipeddi, S.; Marchi, D.L.; Castaldi, P. Modelling and Parameter Identification of UUV Blucy for Control Design: A Benchmark Model. Ocean Eng. 2024, 313, 119617. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Q.; Wu, W.H.; Du, X.; Zhang, Y.; Han, P. Event-trigger NMPC for 3-D Trajectory Tracking of UUV with External Disturbances. Ocean Eng. 2023, 283, 115050. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.X.; Zeng, J.; Wu, W. Distributed Event-Triggered Coordinated Control for Multi-UUV Recovery System with Time Delay. Ocean Eng. 2023, 283, 115138. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, W.H.; Li, Z.X.; Du, X.; Yan, Z. Three-Dimensional Trajectory Tracking of AUV Based on Nonsingular Terminal Sliding Mode and Active Disturbance Rejection Decoupling Control. J. Mar. Sci. Eng. 2023, 11, 959. [Google Scholar] [CrossRef]
- Shao, P.Y.; Dong, Y.; Li, J.; Qu, G. Model Predictive Control for a Bio-Inspired Morphing UAV with Folding Wings Based on LPV System. J. Xi’an Aeronaut. Univ. 2020, 38, 3–10. [Google Scholar] [CrossRef]
- Yan, F.; Xiang, B.; Hu, J.; Chen, R.; Zhang, Z.; Liu, H.; Gao, C. Lateral Control of Autonomous Light Trucks Based on an Improved LPV Model. Automot. Eng. 2024, 46, 1403–1413. [Google Scholar] [CrossRef]
- Noor, H.N.; Visser, C.C.D.; Pavel, M.D.; Quaranta, G. Development of a Quasi-Linear Parameter Varying Model for a Tiltrotor Aircraft. CEAS Aeronaut. J. 2021, 12, 879–894. [Google Scholar] [CrossRef]
- Oliveira, A.L.; Guelton, K.; Motchon, M.K.; Leite, V.J. Refining Parameter Mismatch Handling in LPV Sampled—Data Controller Design. Automatica 2025, 180, 112470. [Google Scholar] [CrossRef]
- Qin, W.W.; Zheng, Z.Q.; Liu, G.; Ma, J.J.; Li, W.Q. LPV Robust Variable Gain Control for Hypersonic Vehicles. Syst. Eng. Electron. 2011, 33, 1327–1331. [Google Scholar]
- Wu, W.H. Research on Model Predictive Control Method for AUV Recovery and Docking Under Complex Constraints. Ph.D. Thesis, Harbin Engineering University, Harbin, China, 2024. [Google Scholar] [CrossRef]
- Ni, J.; Shi, J.; Zhan, Q.; Zhang, Z.; Gu, Y. An Improved U-Net Model with Multiscale Fusion for Retinal Vessel Segmentation. Mini-Invasive Surg. 2025, 5, 679–694. [Google Scholar] [CrossRef]
- Chen, X.; Ma, F.; Wu, Y.; Han, B.; Luo, L.; Biancardo, S.A. MFMDepth: MetaFormer-Based Monocular Metric Depth Estimation for Distance Measurement in Ports. Comput. Ind. Eng. 2025, 207, 111325. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, M.; Xu, J. Robust Adaptive Sliding Mode Control of Underactuated Autonomous Underwater Vehicles with Uncertain Dynamics. Ocean Eng. 2019, 173, 802–809. [Google Scholar] [CrossRef]
- Gkesoulis, K.A.; Georgakis, P.; Karras, C.G.; Bechlioulis, C.P. Autonomous Sea Floor Coverage with Constrained Input Autonomous Underwater Vehicles: Integrated Path Planning and Control. Sensors 2025, 25, 1023. [Google Scholar] [CrossRef] [PubMed]




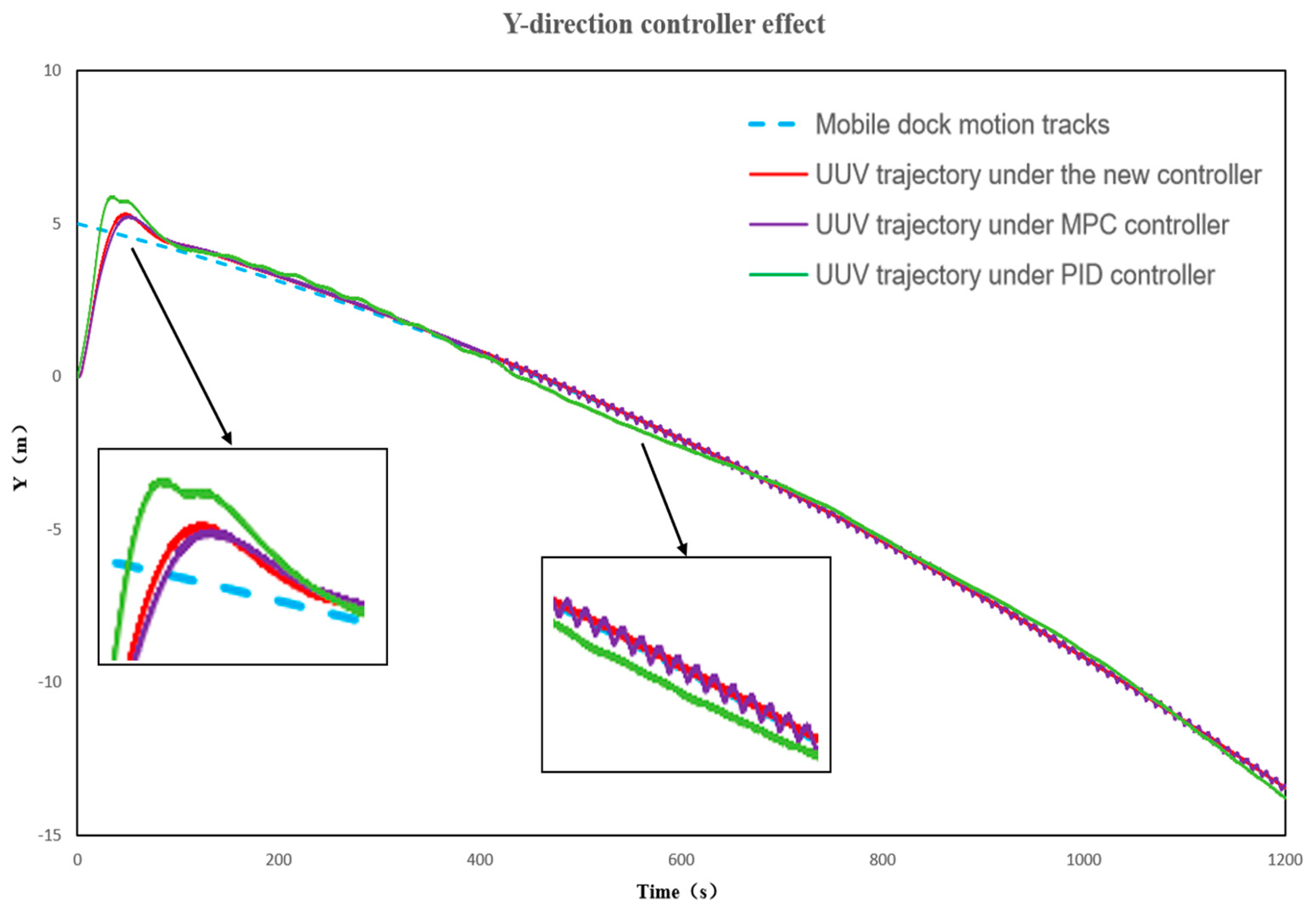
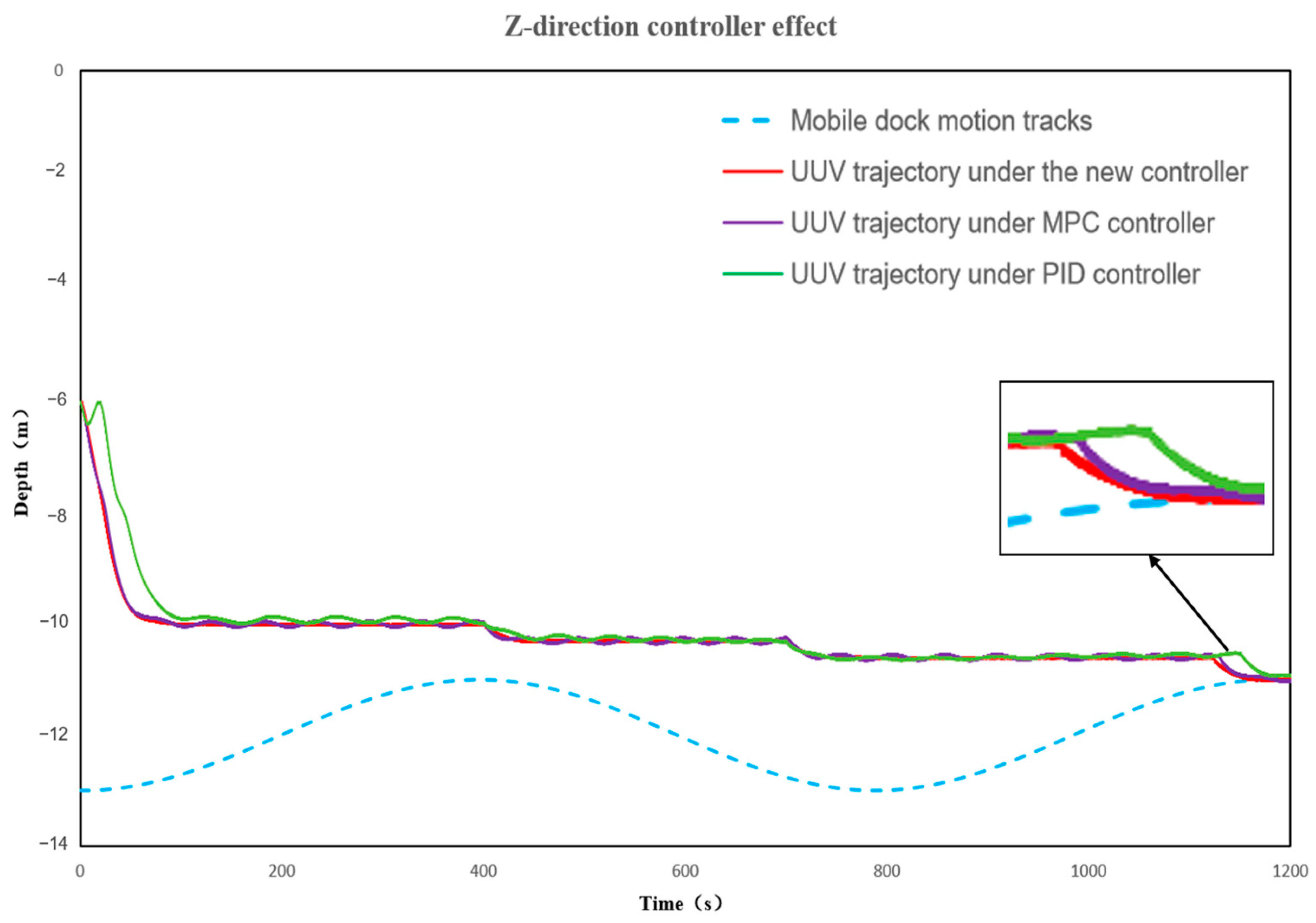

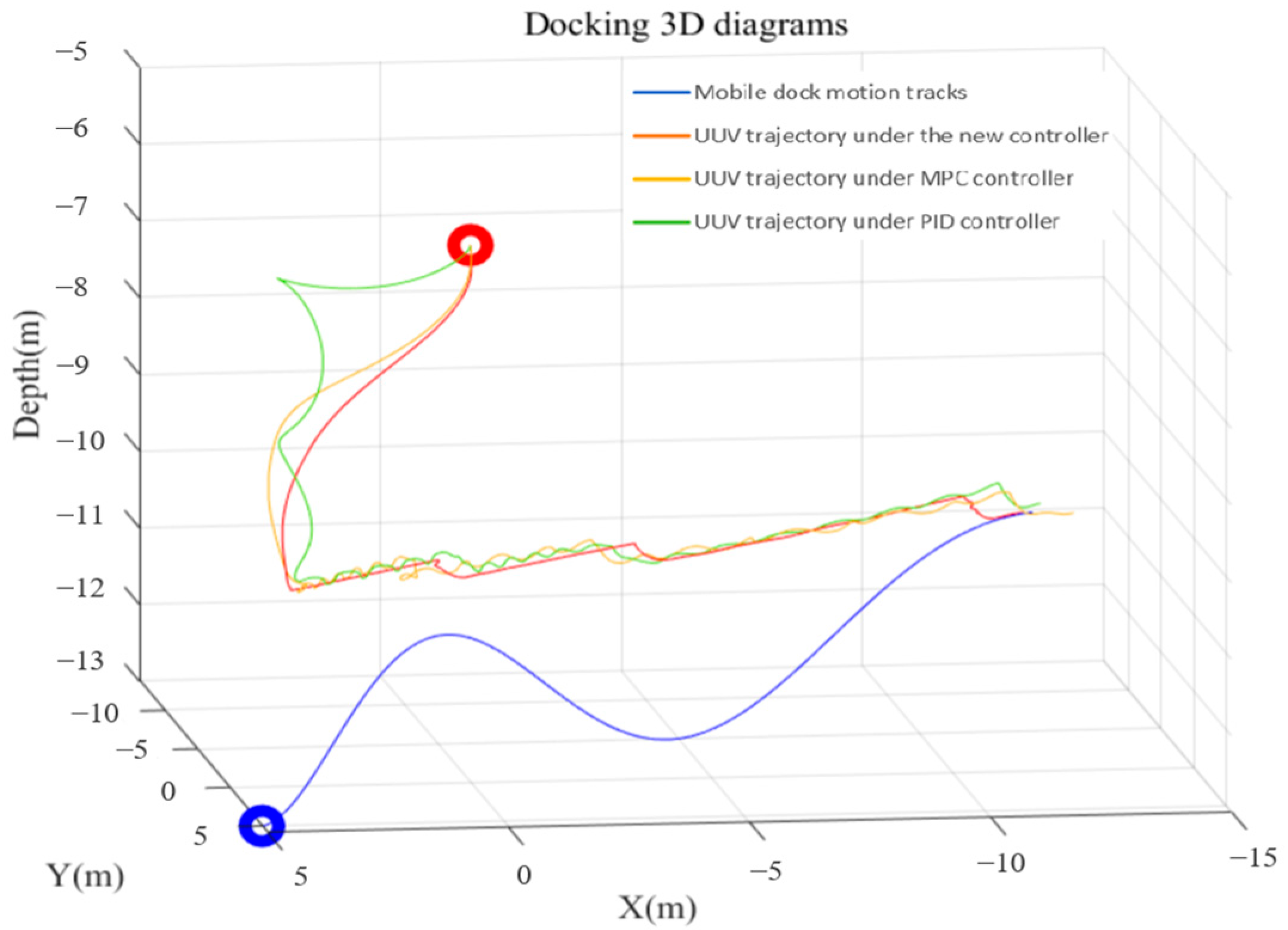



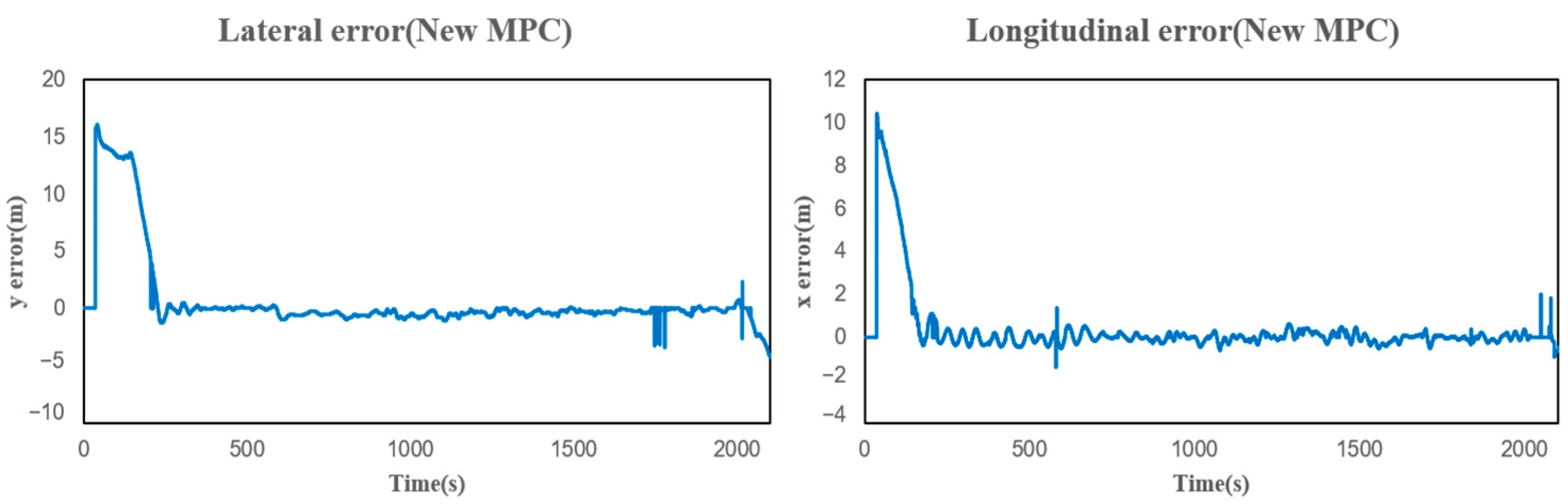


| Coefficients | UUV |
|---|---|
| 1440 | |
| 460, 1400, 1800 | |
| −217, 1, 700 | |
| −10, −80, −200 | |
| 200 | |
| 0.03 |
| Control Effects | PID | MPC | New MPC |
|---|---|---|---|
| Overshoot (Y) | 1 m | 0.42 m | 0.41 m |
| Overshoot (Psi) | 19.7° | 7.4° | 7.3° |
| Convergence Time (X) | 90 s | 50 s | 40 s |
| Convergence Time (Y) | 110 s | 84 s | 83 s |
| Convergence Time (Z) | 100 s | 60 s | 60 s |
| Convergence Time (Psi) | 150 s | 80 s | 80 s |
| Terminal Error (X) | 0.47 m | 0.33 m | 0.30 m |
| Terminal Error (Y) | 0.39 m | 0.22 m | 0.12 m |
| Terminal Error (Psi) | 2.2° | 0.4° | 0.2° |
| Docking Experiment | Ocean Current Environment | Success or Failure | Docking Experiment | Ocean Current Environment | Success or Failure |
|---|---|---|---|---|---|
| 1st | 46°, 0.40 kn | Success | 11th | 280°, 0.50 kn | Success |
| 2nd | 46°, 0.50 kn | Success | 12th | 280°, 0.60 kn | Success |
| 3rd | 46°, 0.34 kn | Success | 13th | 280°, 0.70 kn | Success |
| 4th | 316°, 0.35 kn | Success | 14th | 260°, 0.66 kn | Success |
| 5th | 45°, 0.30 kn | Success | 15th | 260°, 0.55 kn | Success |
| 6th | 45°, 0.10 kn | Success | 16th | 180°, 0.13 kn | Success |
| 7th | 60°, 0.15 kn | Success | 17th | 180°, 0.20 kn | Success |
| 8th | 100°, 0.20 kn | Success | 18th | 78°, 0.10 kn | Success |
| 9th | 100°, 0.10 kn | Success | 19th | 85°, 0.10 kn | Success |
| 10th | 280°, 0.50 kn | Failure | 20th | 265°, 0.62 kn | Success |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, P.; Zhang, W.; Wu, Q.; Shi, Y. Design of UUV Underwater Autonomous Recovery System and Controller Based on Mooring-Type Mobile Docking Station. J. Mar. Sci. Eng. 2025, 13, 1861. https://doi.org/10.3390/jmse13101861
Han P, Zhang W, Wu Q, Shi Y. Design of UUV Underwater Autonomous Recovery System and Controller Based on Mooring-Type Mobile Docking Station. Journal of Marine Science and Engineering. 2025; 13(10):1861. https://doi.org/10.3390/jmse13101861
Chicago/Turabian StyleHan, Peiyu, Wei Zhang, Qiyang Wu, and Yefan Shi. 2025. "Design of UUV Underwater Autonomous Recovery System and Controller Based on Mooring-Type Mobile Docking Station" Journal of Marine Science and Engineering 13, no. 10: 1861. https://doi.org/10.3390/jmse13101861
APA StyleHan, P., Zhang, W., Wu, Q., & Shi, Y. (2025). Design of UUV Underwater Autonomous Recovery System and Controller Based on Mooring-Type Mobile Docking Station. Journal of Marine Science and Engineering, 13(10), 1861. https://doi.org/10.3390/jmse13101861






