Calculation and Analysis of Rolling Hydrodynamic Coefficients of Free-Flooding Ship Based on CFD
Abstract
1. Introduction
2. Numerical Model and Mathematical Formula
2.1. Governing Equations
2.2. Forced Roll Numerical Model
3. Numerical Simulation and Verification of Forced Roll of Ships
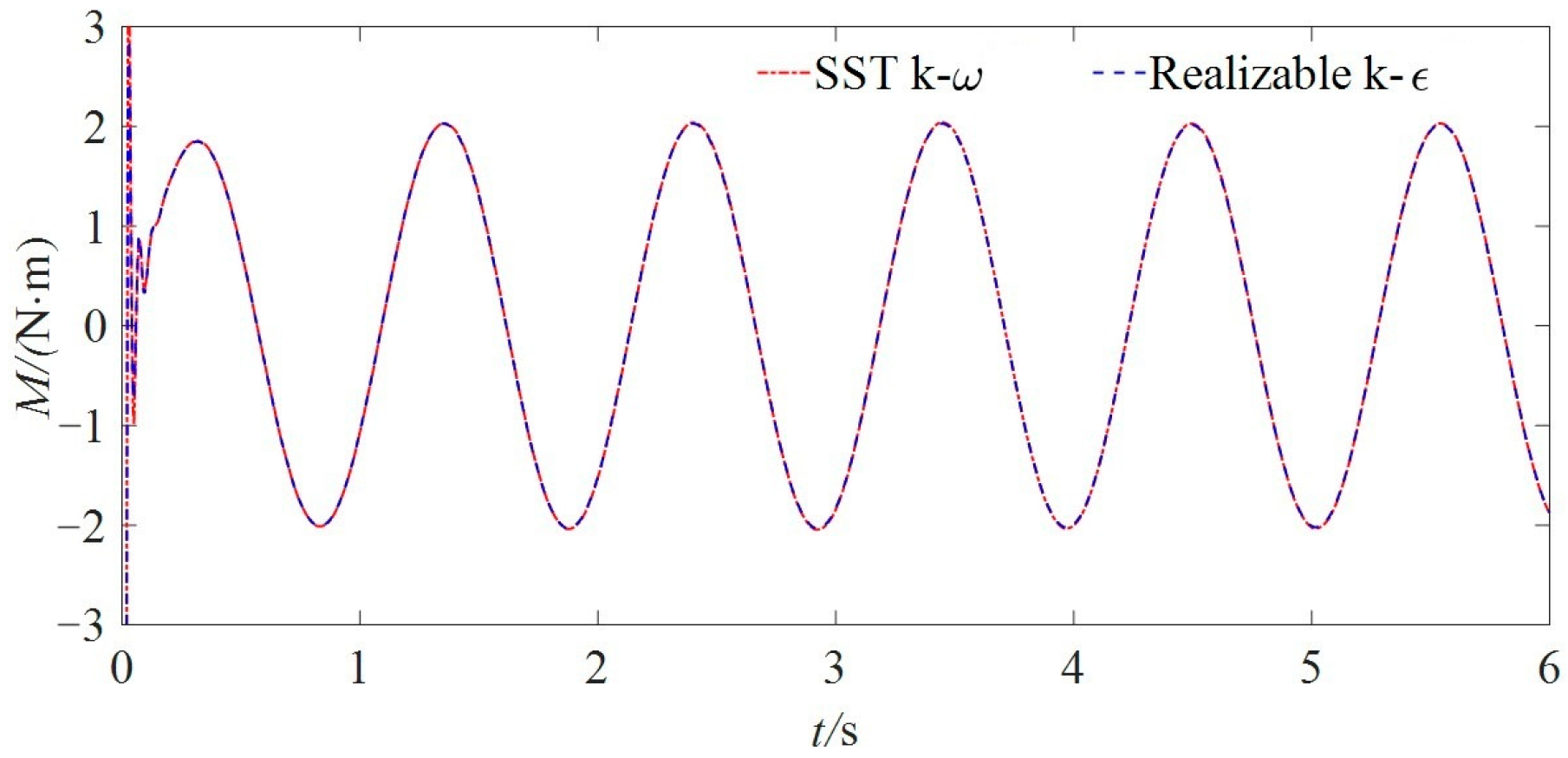
3.1. Series 60 Computing Model
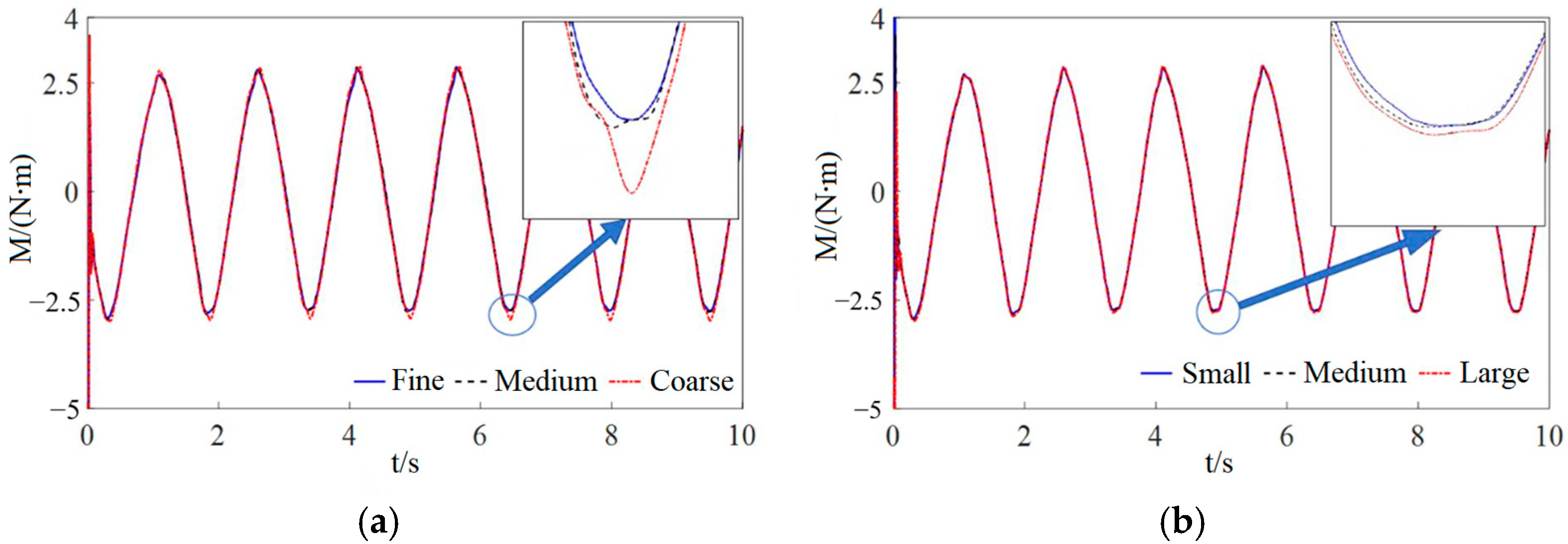
3.2. Convergence Analysis
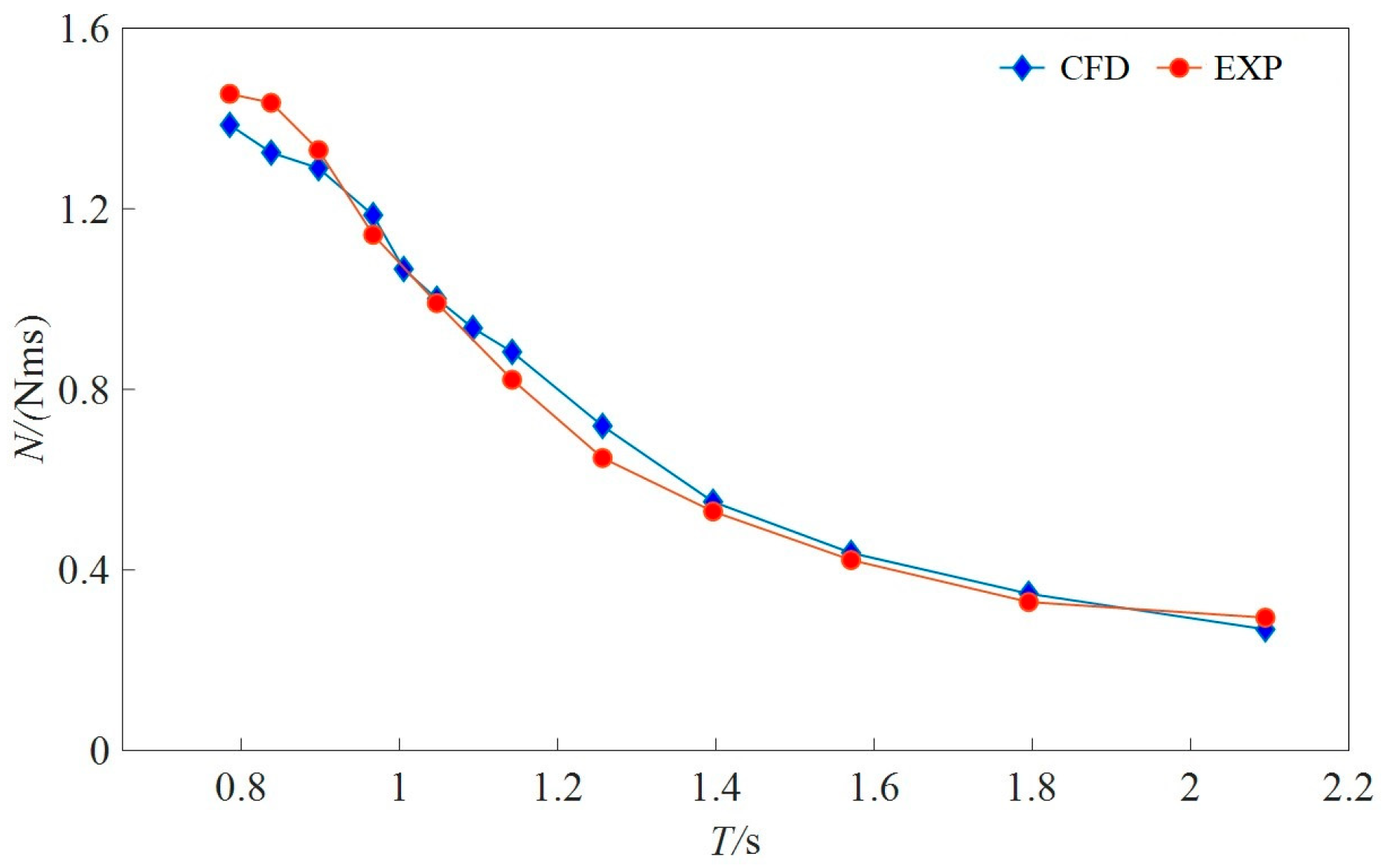
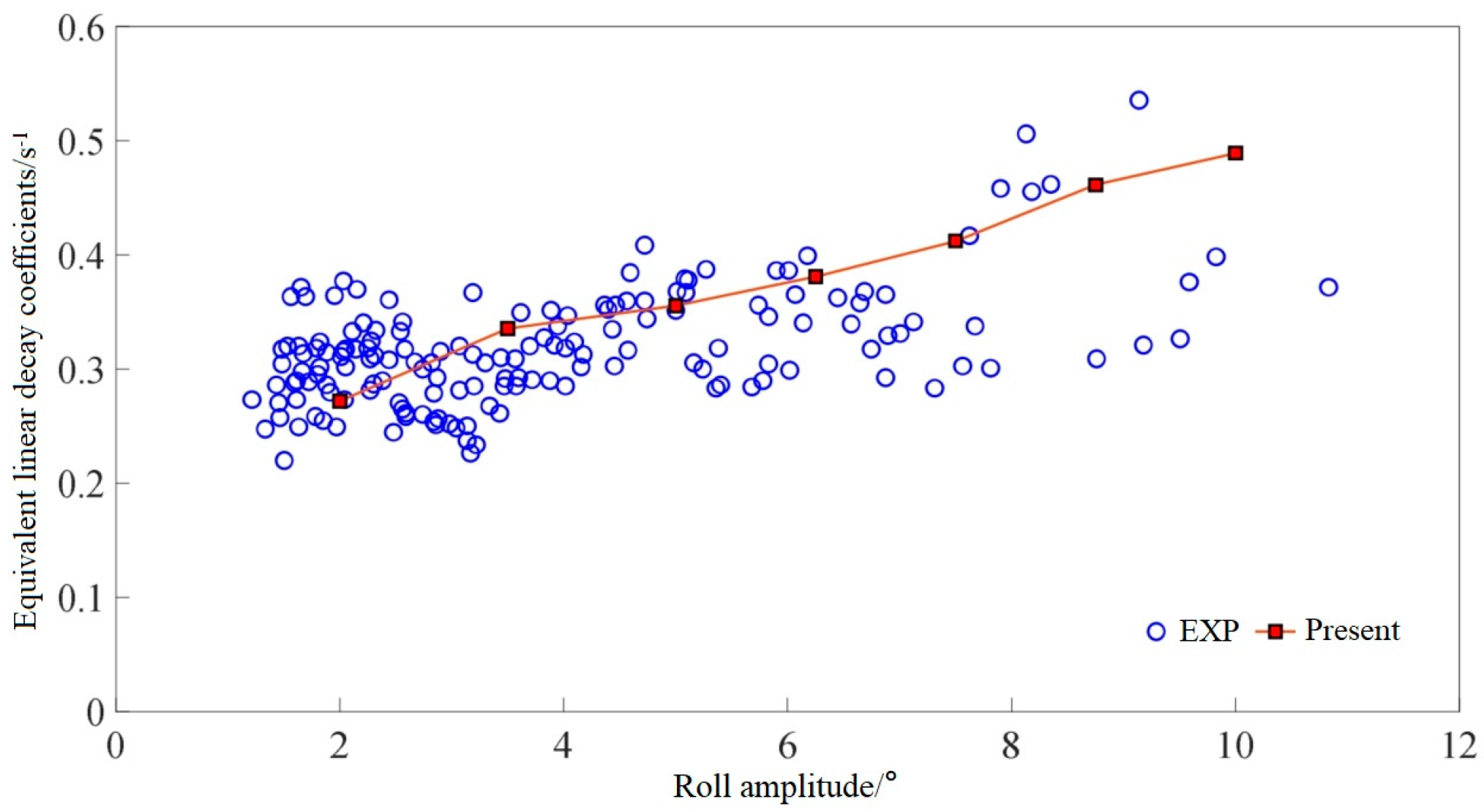
3.3. Simulation Verification of Side-Opening Ships
4. Calculation and Analysis of Hydrodynamic Roll Moment
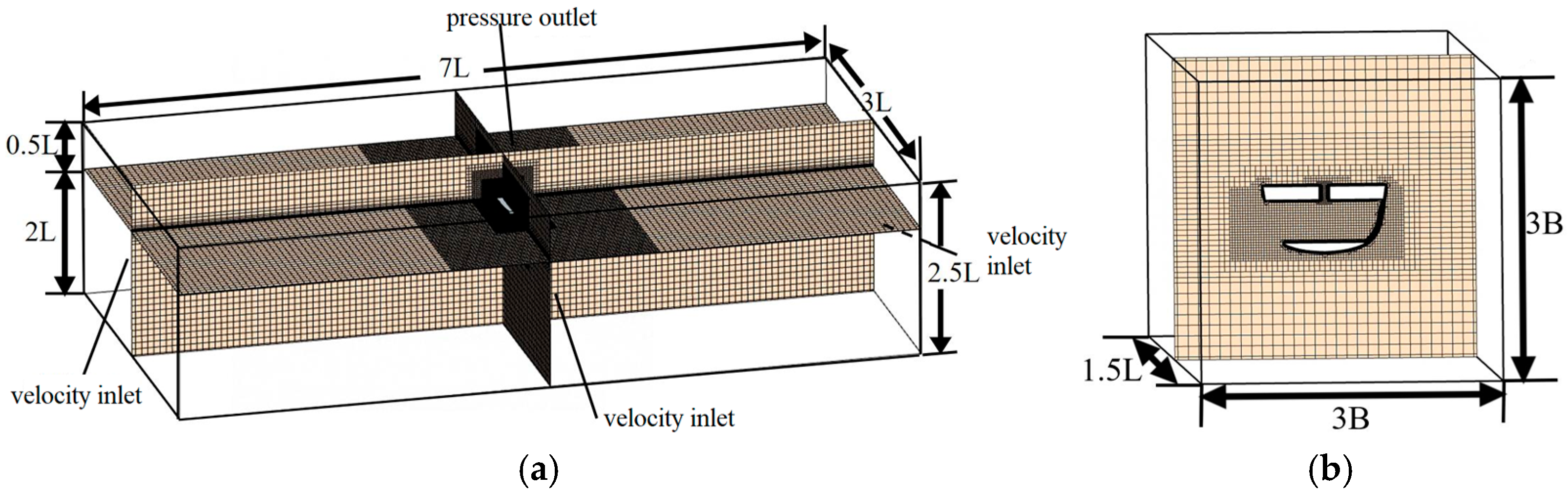
4.1. Free-Flooding Ship Model and Computational Domain Setup L
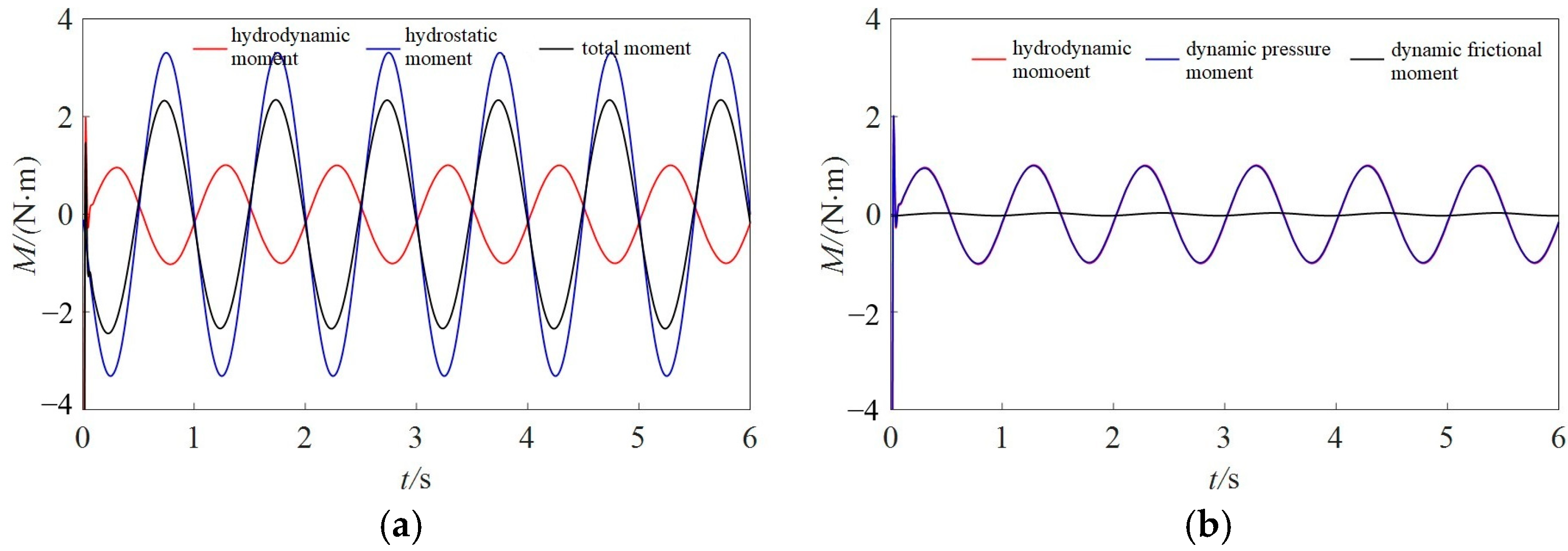
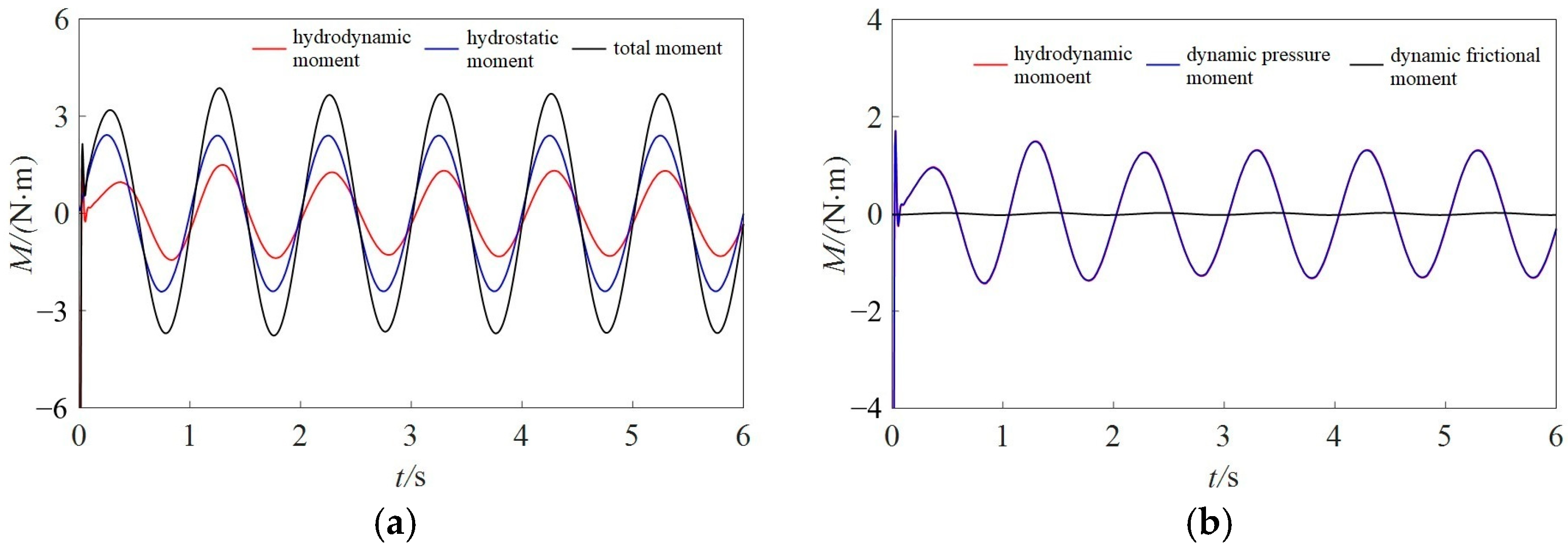
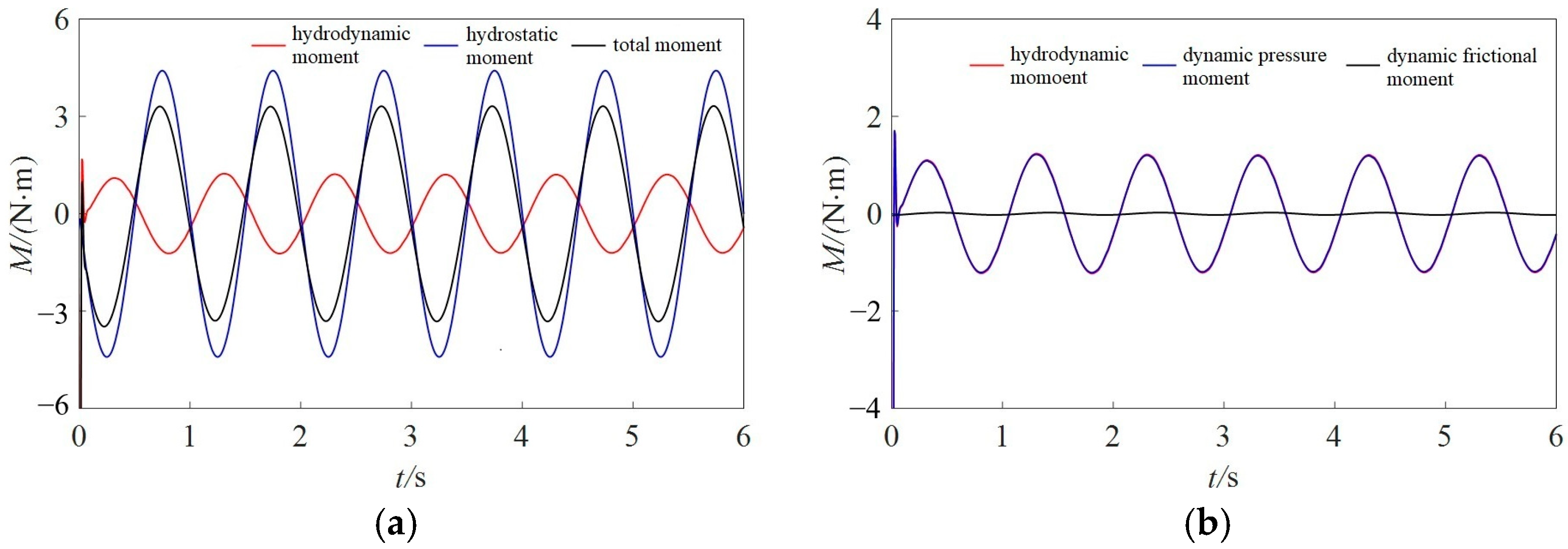
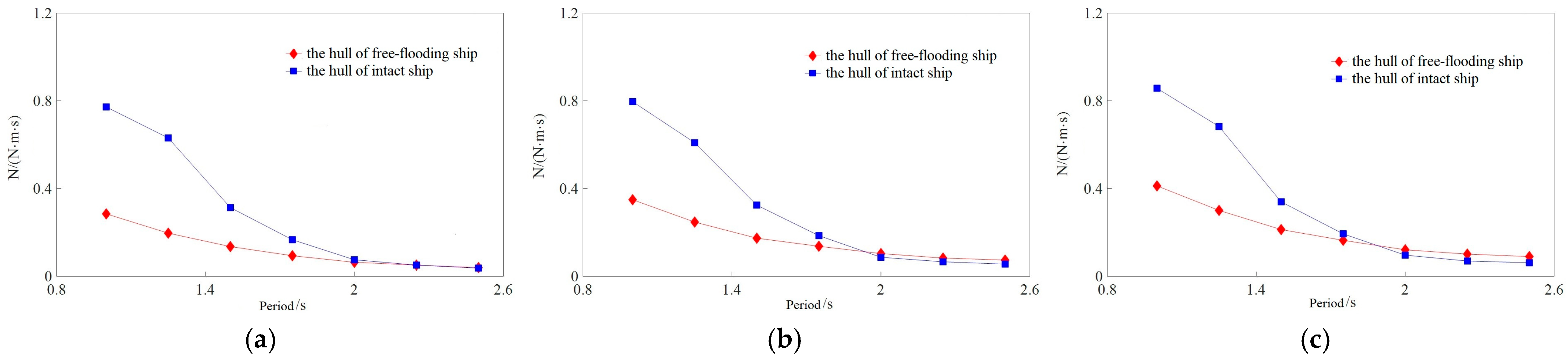
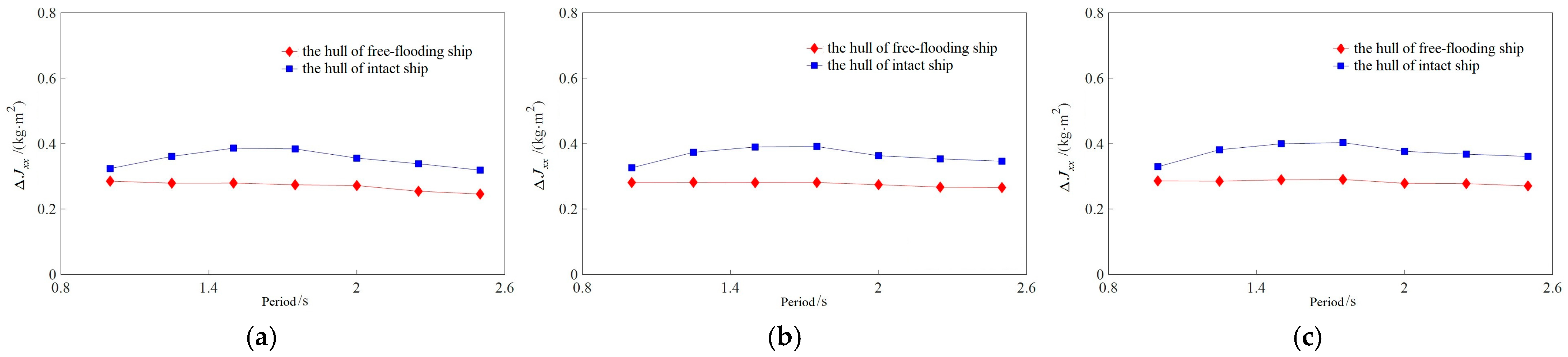
4.2. Calculation Results and Analysis of Ship Moments
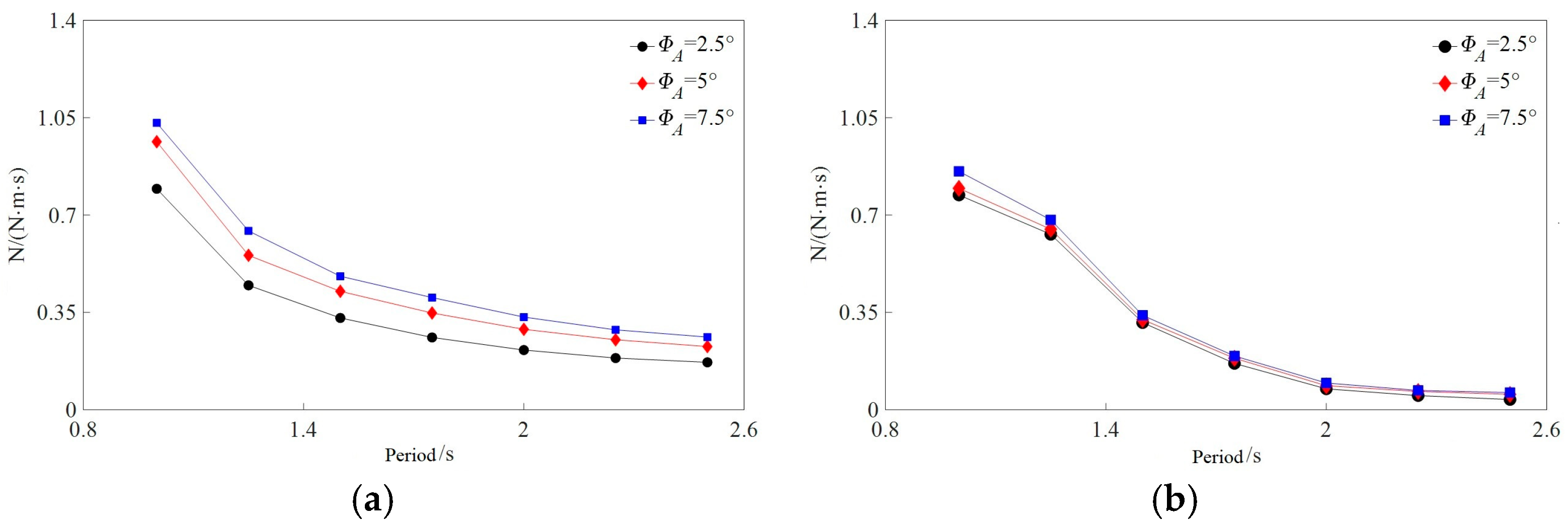
4.3. The Roll Hydrodynamic Coefficients Under Different Operating Conditions
4.4. The Influence of Ship Speed on Roll Hydrodynamic Coefficients
5. Conclusions
- (1)
- CFD-based numerical simulations can reflect the roll hydrodynamic characteristics of free-flooding ships well and predict the forced roll motion of ships considering sloshing and fluid exchange at the openings.
- (2)
- Due to the presence of opening structures, the hydrostatic moment and hydrodynamic moment of the outer hull of the free-flooding ship are reduced compared to the intact ship. For both free-flooding and intact ships, the roll damping and roll added moment of inertia decrease with increasing roll period and increase with increasing roll amplitude. The increase in roll amplitude reflects changes in angular velocity and accelerated rotation of the hull, while the increase in the added moment of inertia indicates the enhanced influence of fluid inertia on the resistance to the hull’s rotational motion. For the aquaculture ship in this paper, the roll hydrodynamic coefficients of the tank are slightly larger than those of the outer hull.
- (3)
- The research on roll hydrodynamic coefficients in this paper can provide reference and correction for the calculation of roll motion prediction of free-flooding ships using potential flow methods. Furthermore, it can be seen that side openings have a significant impact on the internal and external flow fields and roll hydrodynamic coefficients during hull rolling. Subsequent studies on the size, number, and position of openings will help improve the hydrodynamic performance of free-flooding ships.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| RANS | Reynolds-averaged Navier–Stokes |
| VOF | Volume of Fluid |
| ITTC | International Towing Tank Meeting |
References
- Ikeda, Y. A prediction method for ship roll damping. In Report of Dept of Naval Architecture Osaka Prefecture University; Osaka Prefecture University: Sakai, Japan, 1978; p. 405. [Google Scholar]
- Korpus, R.A.; Falzarano, J.M. Prediction of Viscous Ship Roll Damping by Unsteady Navier-Stokes Techniques. J. Offshore Mech. Arct. Eng. 1997, 119, 108–113. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Miu, G. Vortex patterns and roll damping on various cross sections of ships. J. China Ocean. Eng. 2000, 14, 185–192. [Google Scholar]
- Huang, H.; Guo, H.; Zhu, R.; Mu, G. Computations of ship roll damping in viscous flow. J. Ship Mech. 2008, 12, 568–573. [Google Scholar]
- Zhu, R.; Guo, H.; Miu, G.; Yu, J. A computational method for evaluation of added mass and damping of ship based on CFD theory. J. Shanghai Jiaotong Univ. 2009, 43, 198–203. [Google Scholar]
- Jaouen, F.; Koop, A.; Vaz, G. Predicting roll added mass and damping of a ship hull section using CFD. In Proceedings of the ASME 2011 30th International Conference on Ocean, Rotterdam, The Netherlands, 19–24 June 2011; Volume 7, pp. 105–115. [Google Scholar]
- Yang, C. Research and Application of Key Techniques for Ship Performance Numerical Tank. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 2014. [Google Scholar]
- Jiang, Y.; Zhu, R.; Miu, G.; Yang, C. Damping prediction of a rolling ship with bilge keel in viscous flow based on numerical simulation. Shipbuild. China 2016, 57, 1–12. [Google Scholar]
- Begovic, E.; Day, A.H.; Incecik, A. An experimental study of hull girder loads on an intact and damaged naval ship. Ocean. Eng. 2017, 133, 47–65. [Google Scholar] [CrossRef]
- Mancini, S.; Begovic, E.; Pizzirusso, D.; Day, A.H.; Incecik, A. Roll damping assessment of intact and damaged ship by CFD and EFD methods. In Proceedings of the 12th International Conference on the Stability of Ships and Ocean Vehicles, Glasgow, UK, 14–19 June 2015. [Google Scholar]
- Xu, S.; Huang, Z.; Gao, Z. On characteristics and interpolation method of roll hydrodynamic coefficients for damaged ships. Ship Boat 2022, 33, 75–81. [Google Scholar]
- Huang, Z.; Gao, Z.; Xu, S. Calculation and analysis of rolling hydrodynamic coefficients for damaged ship. Shipbuild. China 2023, 64, 151–163. [Google Scholar]
- Gao, Q.; Vassalos, D. Numerical study of damage ship hydrodynamics. Ocean. Eng. 2012, 55, 199–205. [Google Scholar] [CrossRef]
- Manderbacka, T.; Ruponen, P.; Kulovesi, J.; Matusiak, J. Model experiments of the transient response to flooding of the box shaped barge. J. Fluids Struct. 2015, 57, 127–143. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z. Coupled Motion of Tank Sloshing and Aquaculture Platform in Regular Beam Sea. Ship Eng. 2021, 43, 17–23. [Google Scholar]
- STAR-CCM+, Version 2310.0001-R8 (18.06.007-R8); Siemens Digital Industries Software: Plano, TX, USA, 2023.
- Todd, F.H. Series 60 methodical experiments with models of single-screw merchant ships. Nav. Eng. J. 2010, 76, 492. [Google Scholar]
- ITTC. Uncertainty Analysis in CFD Verification and Validation, Methodology and Procedures; ITTC: Wuxi, China, 2017; 7.5-03-01-01, Revision 03; pp. 1–13. [Google Scholar]
- Vugts, J.H. The Hydrodynamic Forces and Ship Motions in Waves; Delft University of Technology: Delft, The Netherlands, 1970. [Google Scholar]
- Begovic, E.; Mortola, G.; Incecik, A.; Day, A.H. Experimental assessment of intact and damaged ship motions in head, beam and quartering seas. Ocean. Eng. 2013, 72, 209–226. [Google Scholar]
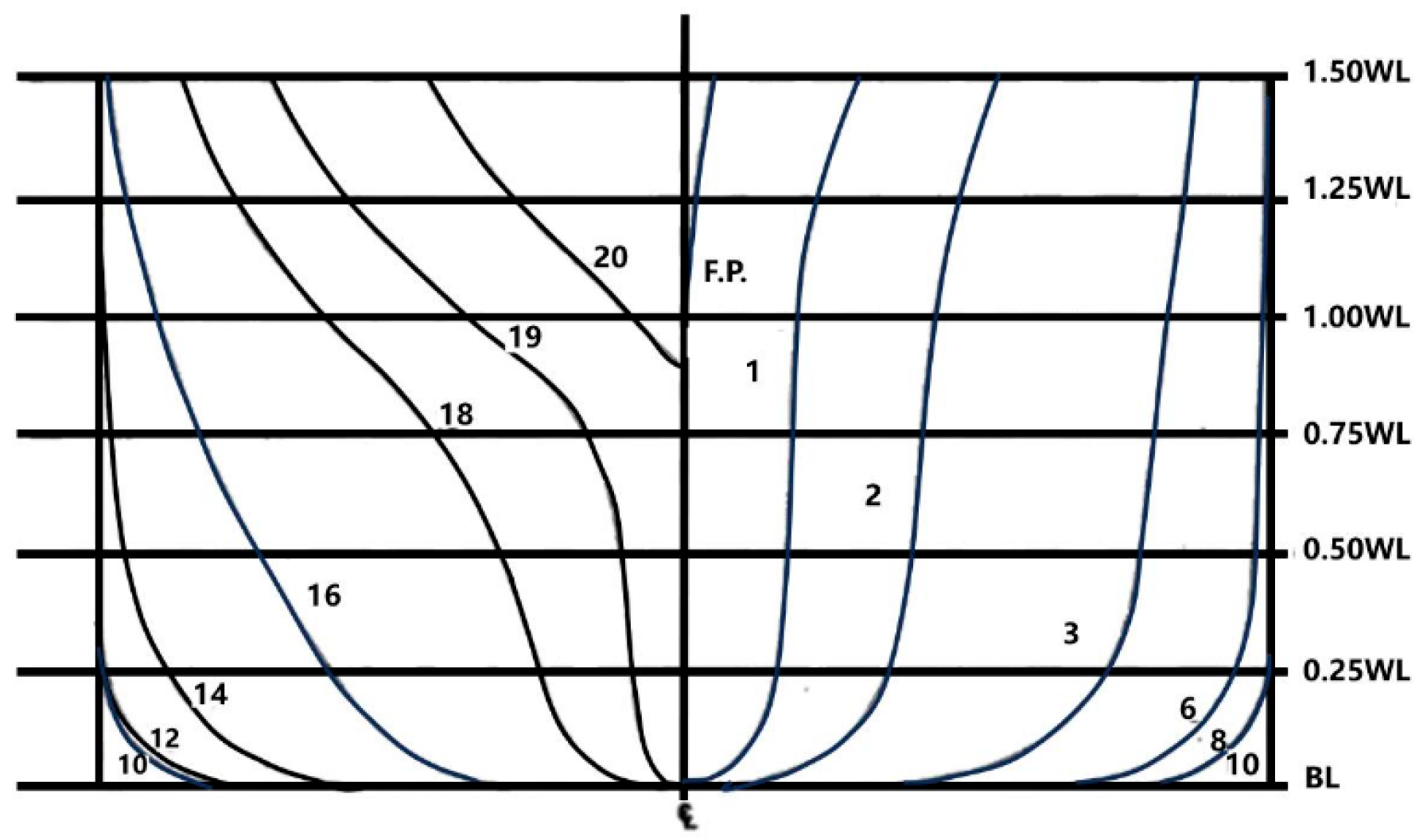
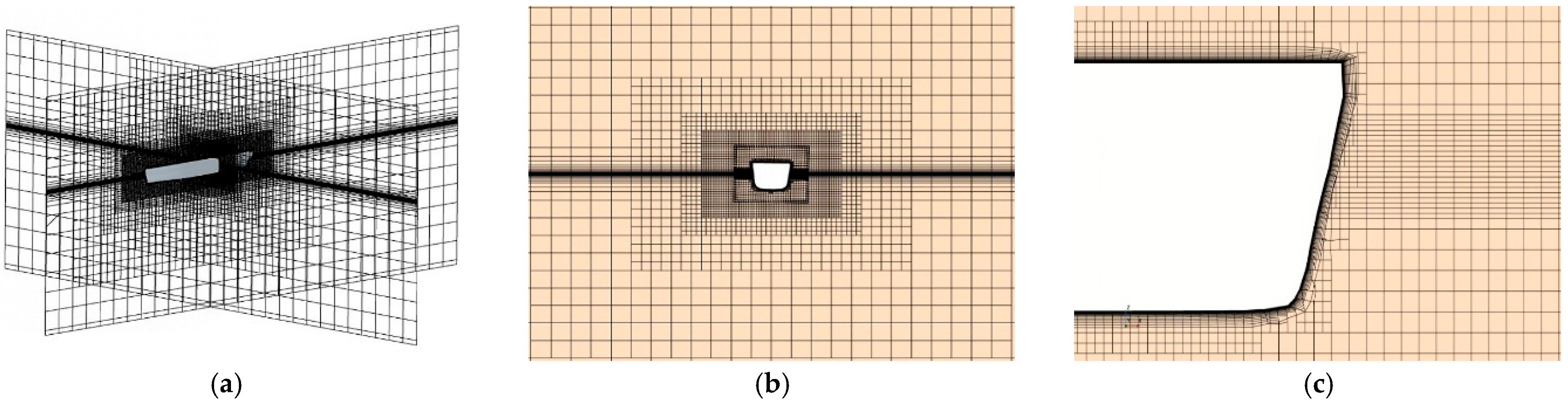

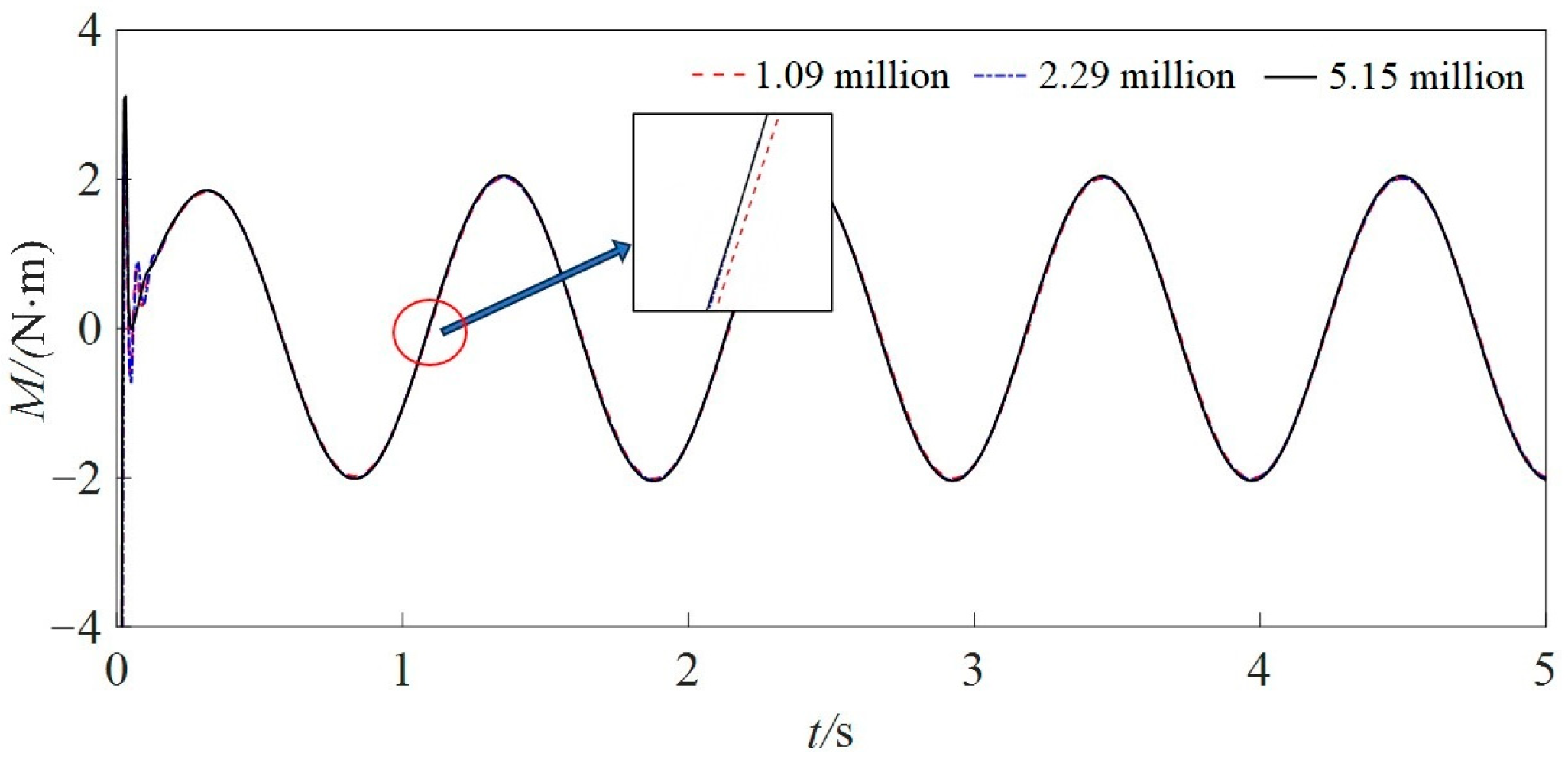
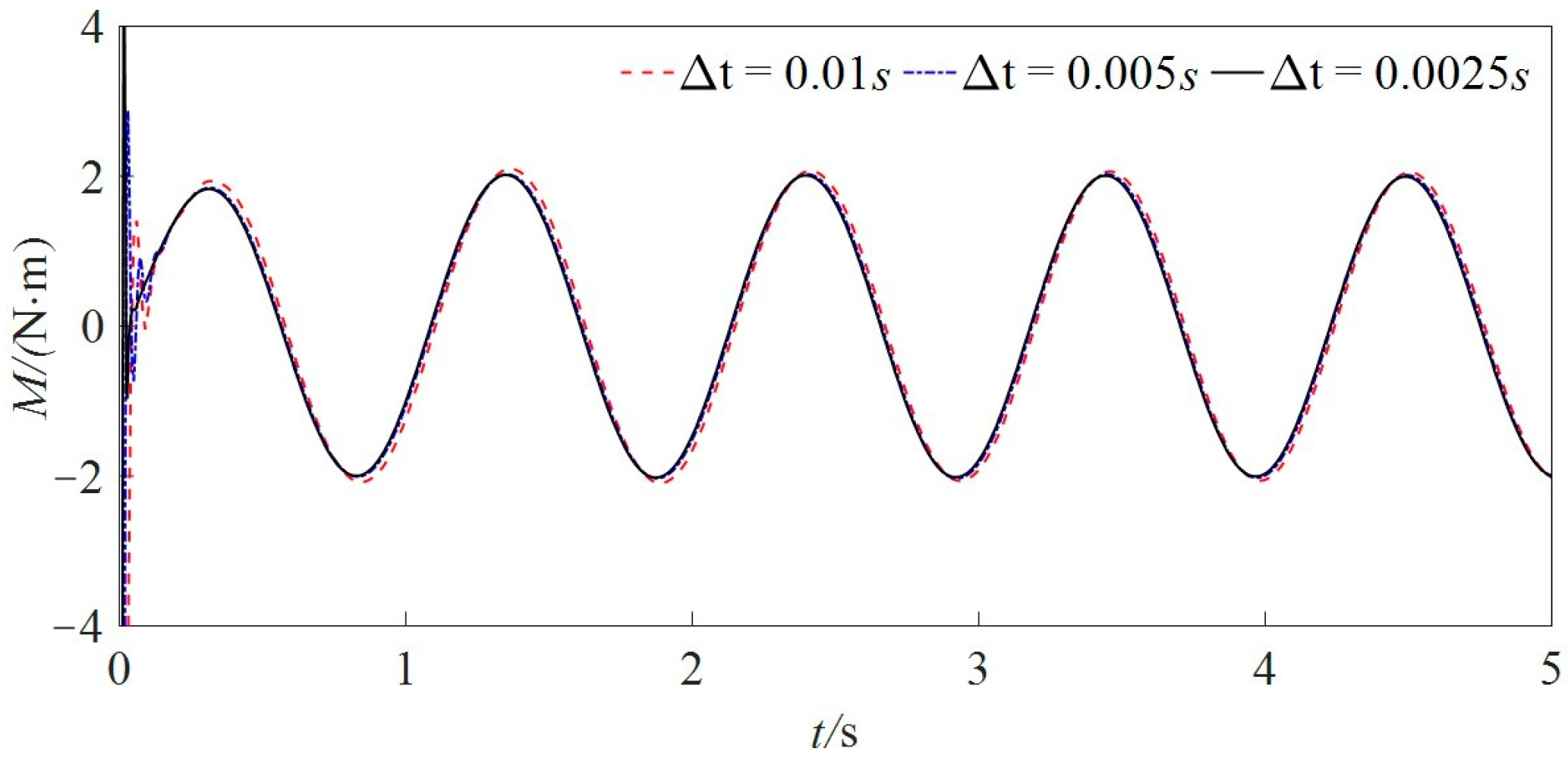







| Parameter | Full-Scale Ship | Model Ship |
|---|---|---|
| (m) | 123.962 | 3.101 |
| (m) | 121.920 | 3.048 |
| B (m) | 17.416 | 0.435 |
| T (m) | 6.968 | 0.174 |
| 0.70 | 0.70 | |
| 10,456 | 0.121 |
| Grid Type | (m) |
|---|---|
| Coarse G3 | 0.283 |
| Medium G2 | 0.200 |
| Fine G1 | 0.141 |
| Time Step Type | (s) |
|---|---|
| Large T3 | 0.01 |
| Medium T2 | 0.005 |
| Small T1 | 0.0025 |
| Scale | Lpp (m) | B (m) | D (m) | T (m) | △ (t, kg) | KG (m) | LCG (m) | Kxx (m) |
|---|---|---|---|---|---|---|---|---|
| full-scale ship | 142.2 | 19.082 | 12.47 | 6.15 | 8635 | 7.555 | 70.137 | 6.12 |
| model ship | 2.788 | 0.374 | 0.244 | 0.12 | 63.5 | 0.148 | 1.375 | 0.12 |
| Parameter | Full-Scale Ship | Model Ship |
|---|---|---|
| (m) | 98.17 | 1.963 |
| (m) | 89.95 | 1.800 |
| B (m) | 18.8 | 0.376 |
| T (m) | 8.998 | 0.18 |
| D (m) | 12.9 | 0.258 |
| △ (t) | 5363 | 0.0429 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Teng, Y.; Xu, M.; Zhu, R. Calculation and Analysis of Rolling Hydrodynamic Coefficients of Free-Flooding Ship Based on CFD. J. Mar. Sci. Eng. 2025, 13, 1857. https://doi.org/10.3390/jmse13101857
Li C, Teng Y, Xu M, Zhu R. Calculation and Analysis of Rolling Hydrodynamic Coefficients of Free-Flooding Ship Based on CFD. Journal of Marine Science and Engineering. 2025; 13(10):1857. https://doi.org/10.3390/jmse13101857
Chicago/Turabian StyleLi, Chaofan, Yuehu Teng, Min Xu, and Renchuan Zhu. 2025. "Calculation and Analysis of Rolling Hydrodynamic Coefficients of Free-Flooding Ship Based on CFD" Journal of Marine Science and Engineering 13, no. 10: 1857. https://doi.org/10.3390/jmse13101857
APA StyleLi, C., Teng, Y., Xu, M., & Zhu, R. (2025). Calculation and Analysis of Rolling Hydrodynamic Coefficients of Free-Flooding Ship Based on CFD. Journal of Marine Science and Engineering, 13(10), 1857. https://doi.org/10.3390/jmse13101857






