I-VoxICP: A Fast Point Cloud Registration Method for Unmanned Surface Vessels
Abstract
1. Introduction
- (1).
- I-VoxICP is proposed by integrating incremental sparse voxels (iVox) with singular value decomposition (SVD)-based pose estimation. Tailored for nearshore berthing scenarios, it enables robust and real-time registration of large-scale, non-uniform-density point clouds.
- (2).
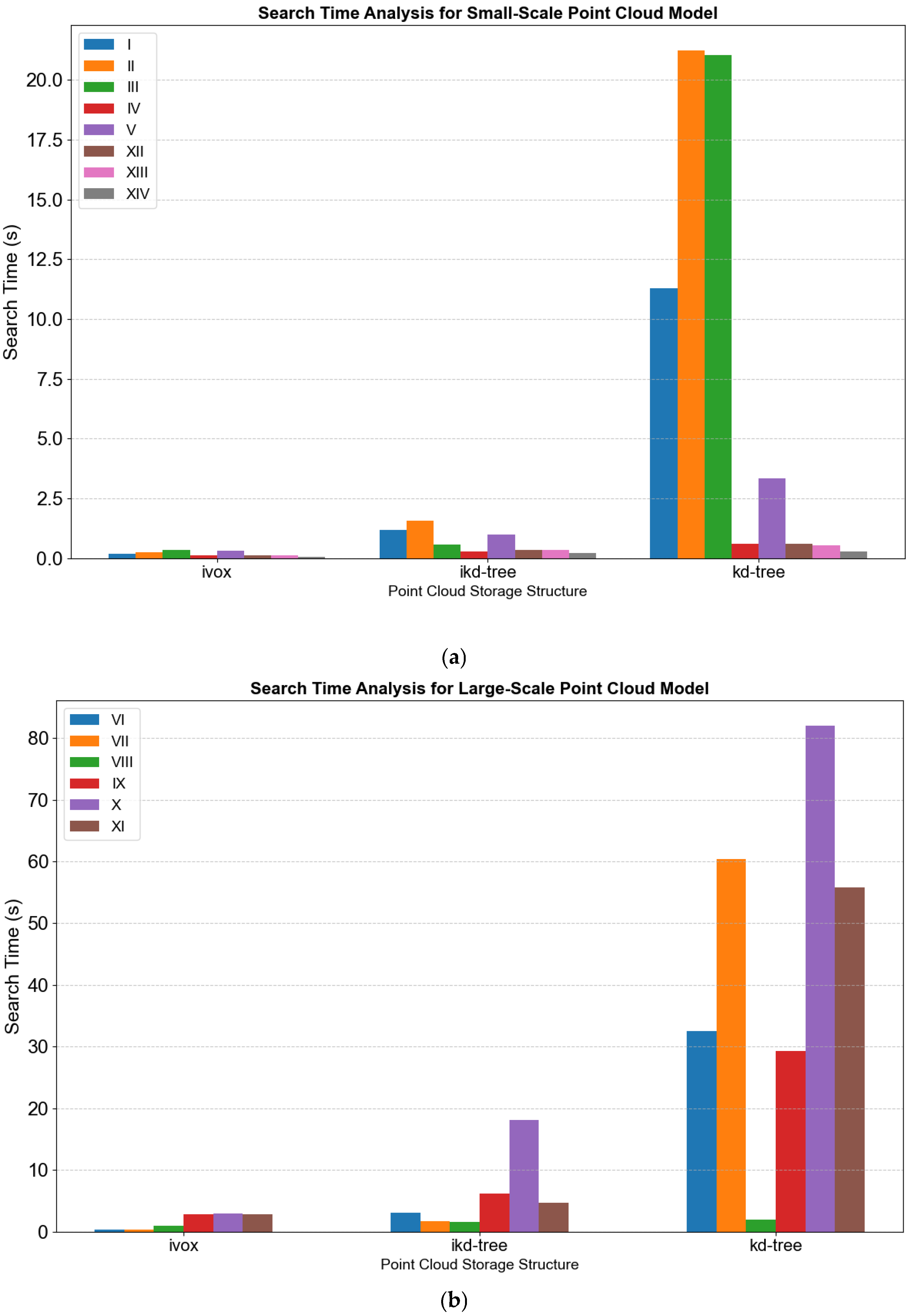
- Search efficiency is improved by almost an order of magnitude: iVox lowers average query time by 72.23% versus ikd-tree and 96.8% versus kd-tree, with a 99% reduction on some models.
- (3).
- Under noisy and partially overlapping conditions, I-VoxICP achieves lower RMSE and RMD than conventional methods, maintaining high alignment accuracy on complex structures such as ship hulls and quays. It consequently furnishes the SLAM front end with superior initial poses and effectively curbs cumulative drift.
2. Related Work
2.1. Direct Scan Matching
2.2. Integration of Point Cloud Structure and Registration
3. Point Cloud Indexing and Fine Local Position Estimation
3.1. Kd-Tree: K-Dimensional Tree
3.2. Ikd-Tree: Incremental Kd-Tree
3.3. IVox: Incremental Sparse Voxels
3.4. ICP-SVD Algorithm
- (1).
- For each point in the target point cloud, its nearest neighbors are identified in the reference point cloud to form a collection of point pairs. This step typically employs spatial indexing structures (e.g., ikd-tree, iVox) to expedite the search process.
- (2).
- The construction of a least-squares problem is then initiated to minimize the distance error between two sets of point clouds, as determined by the set of point pairs that have been identified. Specifically, the rotation matrix and translation vector are solved such that the objective function is minimized:where and are the corresponding point pairs in the target and reference point clouds, respectively.
- (3).
- The center of mass of the target and reference point clouds and must be computed.
- (4).
- By centering the original point set, the resulting de-centered point sets are and .
- (5).
- The construction of the covariance matrix is then required:
- (6).
- The singular value decomposition (SVD) of H results in the following outcome:
- (7).
- The rotation matrix is given by for and the translation vector is given by .
- (8).
- The target point cloud is to be transformed using the derived transform matrix.
- (9).
- Check whether the error satisfies the convergence condition (e.g., the error is less than a certain threshold or the maximum number of iterations is reached) and stop the iteration if it does; otherwise, return to step 2 to continue the iteration.
3.5. Improved ICP-SVD Algorithm Based on iVox
| Algorithm 1: I-VoxICP | |
| 1 | Input: |
| 2 | Source point cloud: cloud_source |
| 3 | Target point cloud: cloud_target |
| 4 | iVox: resolution (resolution), nearby type (nearby_type) |
| 5 | ICP: maximum number of iterations (max_iter), maximum matching distance (max_dist) |
| 6 | Output: |
| 7 | Transformation matrix: T |
| 8 | Registered point cloud: cloud_registered |
| 9 | RMSE: rmse |
| 10 | Voxel filter cloud_target → cloud_target_filtered |
| 11 | iVox ← Initialize iVox (resolution, nearby_type) iVox.AddPoints(cloud_target_filtered) |
| 12 | T ← Identity matrix |
| 13 | matches ← Empty list for each point p in cloud_source_transformed do closest_points ← iVox.GetClosestPoint(p, max_dist) if closest_points is not empty then matches.add((p, closest_points [0])) end if end for |
| 14 | U, Σ, V^T ← SVD(H) R ← U * V^T if det(R) < 0 then V[:,3] ← −V[:,3] R ← U * V^T end if |
| 15 | t ← mu_t − R * mu_s T ← compose(R, t) * T |
| 16 | End |
4. Experimental Results
4.1. Real-Time Performance Experiment
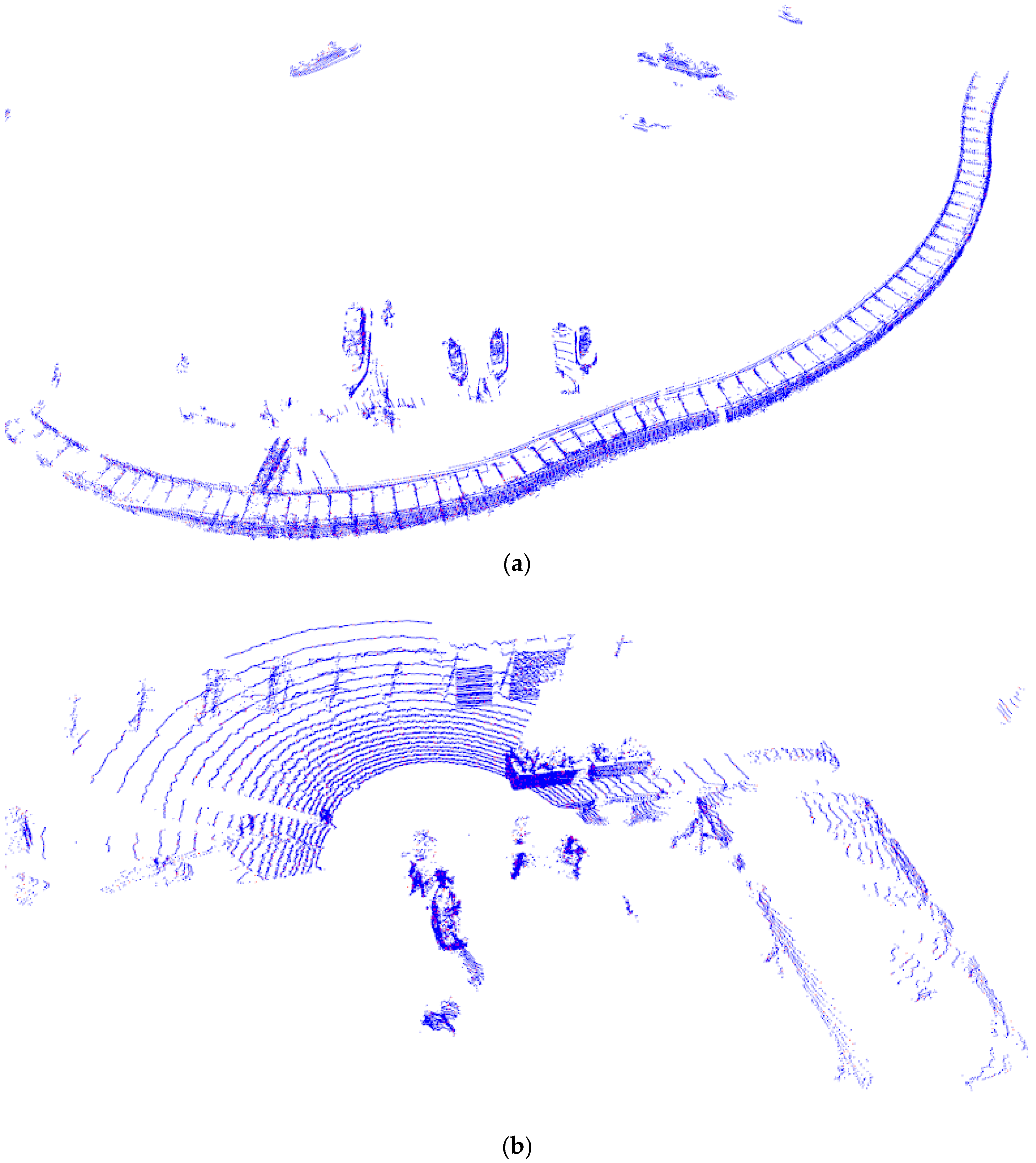
4.2. Offline Point Cloud Registration Experiment
4.3. Fine Local Pose Estimation Experiment
4.4. Registration Result Benchmarking
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, B.; He, Y.; Qian, K.; Ma, X.; Li, X. S4-SLAM: A Real-Time 3D LIDAR SLAM System for Ground/Watersurface Multi-Scene Outdoor Applications. Auton. Robot. 2021, 45, 77–98. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, M.; Meng, J.; Xiao, H.; Shi, X.; Long, Z. Semantic Map-Based Localization of USV Using LiDAR in Berthing and Departing Scene. In Proceedings of the 2023 7th International Conference on Transportation Information and Safety (ICTIS), Xi’an, China, 4–6 August 2023; pp. 583–589. [Google Scholar]
- Sawada, R.; Hirata, K. Mapping and Localization for Autonomous Ship Using LiDAR SLAM on the Sea. J. Mar. Sci. Technol. 2023, 28, 410–421. [Google Scholar] [CrossRef]
- Ponzini, F.; Zaccone, R.; Martelli, M. LiDAR Target Detection and Classification for Ship Situational Awareness: A Hybrid Learning Approach. Appl. Ocean. Res. 2025, 158, 104552. [Google Scholar] [CrossRef]
- Eustache, Y.; Seguin, C.; Pecout, A.; Foucher, A.; Laurent, J.; Heller, D. Marine Object Detection Using LiDAR on an Unmanned Surface Vehicle. IEEE Access 2025, 13, 121658–121669. [Google Scholar] [CrossRef]
- Wan, C.; Lv, X.; Mao, Z.; Wang, Z.; Li, Y.; Ni, C. Online Obstacle Detection for USV Based on Improved RANSAC Algorithm. In Proceedings of the 2023 6th International Symposium on Autonomous Systems (ISAS), Nanjing, China, 23–25 June 2023; pp. 1–6. [Google Scholar]
- Smith, R.; Self, M.; Cheeseman, P. Estimating Uncertain Spatial Relationships in Robotics. In Proceedings of the 1987 IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 March–3 April 1987; Volume 4, p. 850. [Google Scholar]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Cai, Y.; Xu, W.; Zhang, F. Ikd-Tree: An Incremental K-D Tree for Robotic Applications. arXiv 2021, arXiv:2102.10808. [Google Scholar]
- Xu, W.; Cai, Y.; He, D.; Lin, J.; Zhang, F. FAST-LIO2: Fast Direct LiDAR-Inertial Odometry. IEEE Trans. Robot. 2022, 38, 2053–2073. [Google Scholar] [CrossRef]
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-Squares Fitting of Two 3-D Point Sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 698–700. [Google Scholar] [CrossRef] [PubMed]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object Modeling by Registration of Multiple Range Images. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 3, pp. 2724–2729. [Google Scholar]
- Wang, X.; Li, Y.; Peng, Y.; Ying, S. A Coarse-to-Fine Generalized-ICP Algorithm With Trimmed Strategy. IEEE Access 2020, 8, 40692–40703. [Google Scholar] [CrossRef]
- Li, S.; Wang, J.; Liang, Z.; Su, L. Tree Point Clouds Registration Using an Improved ICP Algorithm Based on Kd-Tree. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 4545–4548. [Google Scholar]
- Caro, D.; Rodriguez, A.; Brisaboa, N.R.; Fariña, A. Compressed k D-Tree for Temporal Graphs. Knowl. Inf. Syst. 2016, 49, 553–595. [Google Scholar] [CrossRef]
- Bereczky, N.; Duch, A.; Nemeth, K.; Roura, S. Quad-Kd Trees: A General Framework for Kd Trees and Quad Trees. Theor. Comput. Sci. 2016, 616, 126–140. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Ge, G.; Jiang, Q.; Wang, Y.; Hu, L. A Hybrid Spatial Indexing Structure of Massive Point Cloud Based on Octree and 3D R*-Tree. Appl. Sci. 2021, 11, 9581. [Google Scholar] [CrossRef]
- Holanda, P.; Nerone, M.; Almeida, E.C.d.; Manegold, S. Cracking KD-Tree: The First Multidimensional Adaptive Indexing (Position Paper). In Proceedings of the 7th International Conference on Data Science, Technology and Applications, Porto, Portugal, 26 July 2018; SCITEPRESS-Science and Technology Publications, Lda.: Setubal, Portugal, 2018; pp. 393–399. [Google Scholar]
- Guan, W.; Li, W.; Ren, Y. Point Cloud Registration Based on Improved ICP Algorithm. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 1461–1465. [Google Scholar]
- Cao, Y.; Wang, H.; Zhao, W.; Duan, B.; Zhang, X.; Cheng, S. A New Method to Construct the KD Tree Based on Presorted Results. Complexity 2020, 2020, 8883945. [Google Scholar] [CrossRef]
- Hou, W.; Li, D.; Xu, C.; Zhang, H.; Li, T. An Advanced k Nearest Neighbor Classification Algorithm Based on KD-Tree. In Proceedings of the 2018 IEEE International Conference of Safety Produce Informatization (IICSPI), Chongqing, China, 10–12 December 2018; pp. 902–905. [Google Scholar]
- Ji, S.; Ren, Y.; Ji, Z.; Liu, X.; Hong, G. An Improved Method for Registration of Point Cloud. Optik 2017, 140, 451–458. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, T.; Chen, Y.; Tan, Z. A 3D Point Cloud Reconstruction Method. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Suzhou, China, 29 July–2 August 2019; pp. 1310–1315. [Google Scholar]
- Rusu, R.B.; Cousins, S. 3D Is Here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Zhang, Z.; Li, H. I-HS4PCS: Object 6D Pose Estimation Method Based on Harris3D-ikdTree Optimization. IEEE Access 2024, 12, 138018–138026. [Google Scholar] [CrossRef]
- Bai, C.; Xiao, T.; Chen, Y.; Wang, H.; Zhang, F.; Gao, X. Faster-LIO: Lightweight Tightly Coupled Lidar-Inertial Odometry Using Parallel Sparse Incremental Voxels. IEEE Robot. Autom. Lett. 2022, 7, 4861–4868. [Google Scholar] [CrossRef]
- Wang, H.; Yin, Y.; Jing, Q. Comparative Analysis of 3D LiDAR Scan-Matching Methods for State Estimation of Autonomous Surface Vessel. J. Mar. Sci. Eng. 2023, 11, 840. [Google Scholar] [CrossRef]
- Chung, D.; Kim, J.; Lee, C.; Kim, J. Pohang Canal Dataset: A Multimodal Maritime Dataset for Autonomous Navigation in Restricted Waters. Int. J. Robot. Res. 2023, 42, 1104–1114. [Google Scholar] [CrossRef]
- Guo, D.; Jing, Q.; Yin, Y.; Xu, H. sAn Efficient Laser Point Cloud Registration Method for Autonomous Surface Vehicle. J. Mar. Sci. Eng. 2025, 13, 1720. [Google Scholar] [CrossRef]


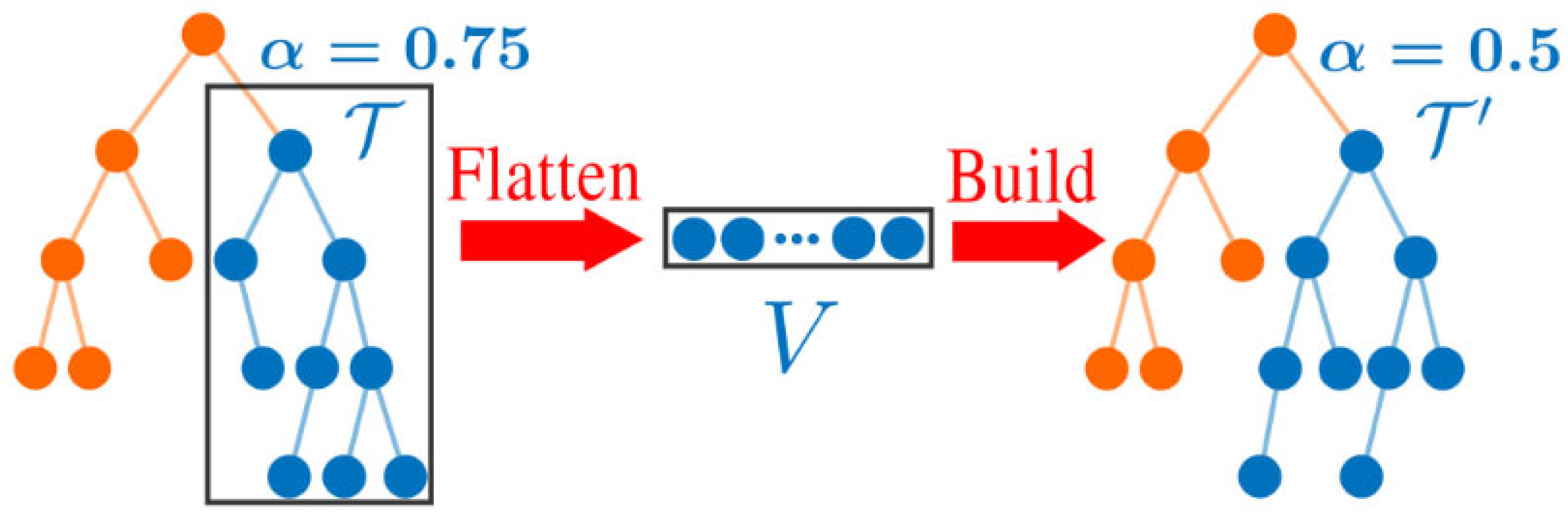









| No. | iVox Structure | Description |
|---|---|---|
| 1 | HashTable voxel_map; | Hash table storing voxel nodes, using 3D coordinates as keys. |
| 2 | List<VoxelNode> voxel_cache; | List for caching voxel nodes, possibly for quick access or lifecycle management of voxels. |
| 3 | float resolution; | The resolution of the voxel map, defining the size of each voxel. |
| 4 | float inv_resolution; | The inverse of the resolution, used for quick voxel index calculation. |
| 5 | std::size_t capacity; | The maximum capacity of the voxel map, i.e., the maximum number of voxels it can store. |
| 6 | NearbyType nearby_type; | Defines the type of voxel range considered when searching for nearest neighbors. |
| 7 | bool GetClosestPoint; | Function to find the nearest point to a given point, returning whether the operation was successful. |
| 8 | void AddPoints; | Member function to add point cloud data to the voxel map. |
| Platform | Component | Model/Version | Key Parameters |
|---|---|---|---|
| Desktop | OS | Ubuntu 20.04 LTS | 64-bit, kernel 5.4 |
| CPU | Intel i9-13900K | 5.4 GHz | |
| GPU | NVIDIA RTX 3090 | 24 GB GDDR6X | |
| RAM | DDR4-3200 | 32 GB | |
| USV | OS | Ubuntu 20.04 LTS | 64-bit, kernel 5.4 |
| CPU | ARM Cortex-A57 | 1.43 GHz | |
| GPU | NVIDIA Maxwell | 921 MHz | |
| RAM | LPDDR4 | 4 GB, 64-bit | |
| Common | Language | C++14 | —— |
| PCL | 1.10 | —— | |
| VTK | 9.1 | —— |
| Category | Dataset | LiDAR | Frequency |
|---|---|---|---|
| Self-recorded Dataset | XPD_ship | RS-Ruby-80 | 10 Hz |
| Self-recorded Dataset | Xpd_cloud | RS-Ruby-80 | 10–20 Hz |
| Public Dataset | Stanford | —— | —— |
| Public Dataset | Pohang Canal | Velodyne HDL-64E S2 | 5–20 Hz |
| LiDAR | Beam | Frequency | Resolution | HFOV |
|---|---|---|---|---|
| RS-Ruby-80 | 80 | 10–20 Hz | 0.4 m~3 m: Up to ± 5 cm | 360° |
| 3 m~200 m: Up to ± 3 cm | ||||
| R-Fans-16 | 16 | 5–20 Hz | ±2 cm | 360° |
| Velodyne HDL-64E S2 | 32 | 5–20 Hz | ±2 cm | 360° |
| Category | XPD_ship | Xpd_cloud |
|---|---|---|
| Duration (min) | 73 | 58 |
| LiDAR | RS-Ruby-80 | RS-Ruby-80 |
| Installation Height (m) | —— | 5 |
| Frame Rate (Hz) | 10 | 20 |
| Data Size (GB) | 70 | 55 |
| Weather | Sunny, light clouds | Sunny, light clouds |
| Sea Conditions | BF 1–2; waves 0.1–0.2 m | BF 1–2; waves 0.1–0.2 m |
| Data Integrity | >95% | >92% |
| Applicability | Ship | Berthing and Ship |
| Trial Site | Speed (kn) | LiDAR | Frequency (Hz) | Proc. Time (s/f) |
|---|---|---|---|---|
| A | 0.5 | R-Fans-16 | 5–20 Hz | 0.056 |
| B | 0.3 | R-Fans-16 | 5–20 Hz | 0.083 |
| A | 0.2 | RS-Ruby-80 | 10–20 Hz | 0.097 |
| B | 0.1 | RS-Ruby-80 | 10–20 Hz | 0.096 |
| Model | Num | Res | Nby_type | Cap |
|---|---|---|---|---|
| bunny | I | 5 | 6 | 300,000 |
| horse | II | 5 | 6 | 300,000 |
| XPD_ship | III | 1 | 6 | 300,000 |
| Xpd_cloud | IV | 1 | 6 | 300,000 |
| Armadillo | V | 0.5 | 6 | 300,000 |
| happy buddha | VI | 5 | 6 | 300,000 |
| China dragon | VII | 5 | 6 | 300,000 |
| manuscript | VIII | 0.2 | 6 | 300,000 |
| dragon | IX | 5 | 6 | 300,000 |
| hand | X | 5 | 6 | 300,000 |
| statuette | XI | 5 | 6 | 300,000 |
| Pohang_03_792 | XII | 0.5 | 6 | 300,000 |
| Pohang_03_794 | XIII | 0.5 | 6 | 300,000 |
| Pohang_03_802 | XIV | 0.5 | 6 | 300,000 |
| Num | Icp_n | Max_cor_dis (m) | setLeafSize (m) |
|---|---|---|---|
| I | 50 | 5 | —— |
| II | 50 | 5 | —— |
| III | 50 | 5 | —— |
| IV | 50 | 5 | [0.2f] |
| V | 50 | 5 | [1.0f] |
| VI | 50 | 5 | [0.001f] |
| VII | 50 | 5 | [0.001f] |
| VIII | 50 | 5 | [0.5f] |
| IX | 50 | 5 | [0.5f] |
| X | 50 | 5 | [0.01f] |
| XI | 50 | 5 | [1.0f] |
| XII | 50 | 5 | [0.1f] |
| XIII | 50 | 5 | [0.1f] |
| XIV | 50 | 5 | [0.2f] |
| Number | Original Size | Downsampled Size |
|---|---|---|
| I | 35,947 | 35,947 |
| II | 48,485 | 48,485 |
| III | 30,048 | 30,048 |
| IV | 144,000 | 39,919 |
| V | 172,974 | 46,228 |
| XII | 131,072 | 15,954 |
| XIII | 131,072 | 15,899 |
| XIV | 131,072 | 9703 |
| Number | Original Size | Downsampled Size |
|---|---|---|
| VI | 543,652 | 65,549 |
| VII | 437,645 | 84,972 |
| VIII | 2,155,617 | 85,026 |
| IX | 3,609,600 | 218,049 |
| X | 327,323 | 243,290 |
| XI | 4,999,996 | 277,597 |
| Kd-ICP | Ikd-ICP | I-VoxICP | ||||
|---|---|---|---|---|---|---|
| Number | RMD | RMSE | RMD | RMSE | RMD | RMSE |
| 1 | 0.0176 | 4.19 | 0.0176 | 4.19 | 0.0176 | 4.19 |
| 2 | 0.0688 | 8.29 | 0.0688 | 8.29 | 0.0688 | 8.29 |
| 3 | 137 | 370.0 | 15.1 | 123 | 1.04 | 32.3 |
| 4 | 528 | 726.0 | 42.8 | 207 | 27.9 | 167 |
| 5 | 2140 | 1460 | 77.9 | 279 | 18.9 | 180 |
| 6 | 0.0373 | 6.11 | 0.0373 | 6.11 | 0.0373 | 6.11 |
| 7 | 0.146 | 12.1 | 0.146 | 12.1 | 0.146 | 12.1 |
| 8 | 682 | 826.0 | 233 | 483 | 159 | 399 |
| 9 | 17,400 | 4170 | 844 | 919 | 682 | 891 |
| 10 | 25.8 | 161 | 13.2 | 115 | 8.7 | 70 |
| 11 | 308 | 1760 | 151 | 389 | 140 | 301 |
| 12 | 29.9 | 547 | 398 | 631 | 262 | 750 |
| 13 | 58.9 | 767 | 398 | 242 | 101 | 117 |
| 14 | 515 | 2270 | 365 | 604 | 166 | 408 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Q.; Bai, M.; Yin, Y.; Guo, D. I-VoxICP: A Fast Point Cloud Registration Method for Unmanned Surface Vessels. J. Mar. Sci. Eng. 2025, 13, 1854. https://doi.org/10.3390/jmse13101854
Jing Q, Bai M, Yin Y, Guo D. I-VoxICP: A Fast Point Cloud Registration Method for Unmanned Surface Vessels. Journal of Marine Science and Engineering. 2025; 13(10):1854. https://doi.org/10.3390/jmse13101854
Chicago/Turabian StyleJing, Qianfeng, Mingwang Bai, Yong Yin, and Dongdong Guo. 2025. "I-VoxICP: A Fast Point Cloud Registration Method for Unmanned Surface Vessels" Journal of Marine Science and Engineering 13, no. 10: 1854. https://doi.org/10.3390/jmse13101854
APA StyleJing, Q., Bai, M., Yin, Y., & Guo, D. (2025). I-VoxICP: A Fast Point Cloud Registration Method for Unmanned Surface Vessels. Journal of Marine Science and Engineering, 13(10), 1854. https://doi.org/10.3390/jmse13101854






