Coupled Vibration Response Analysis of Tension Leg Platform Tendon Under Irregular Ocean Wave Action
Abstract
1. Introduction
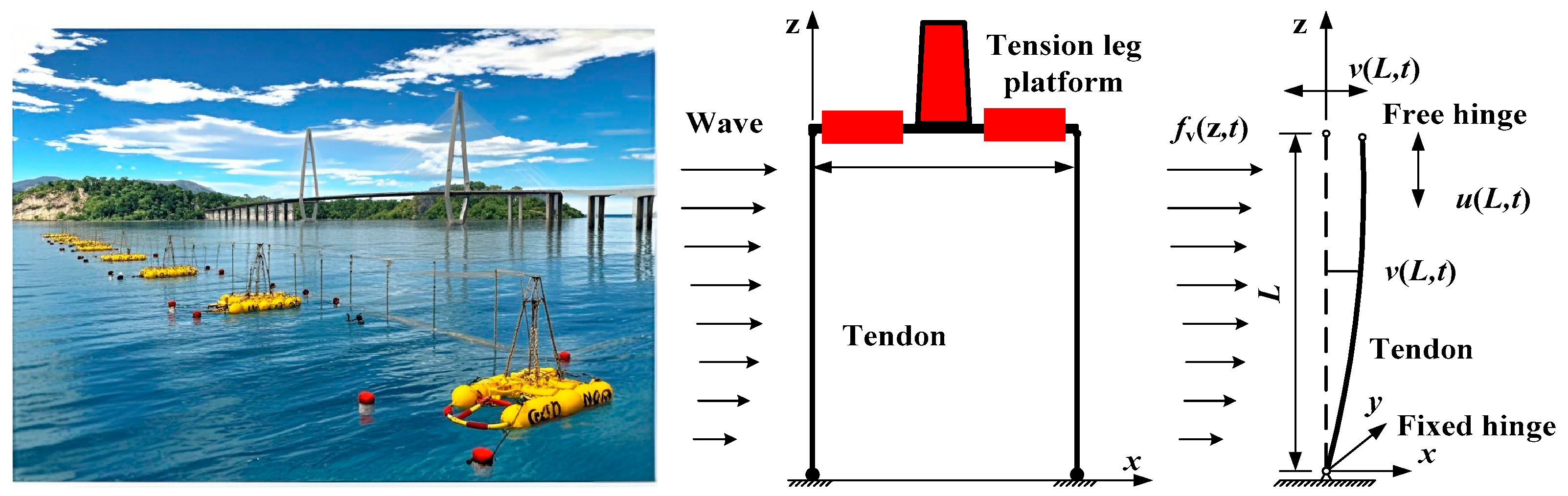
2. Structural Idealization of Tension Leg Platform Tendon Model
2.1. Governing Equations
2.2. Irregular Ocean Wave Action Calculation
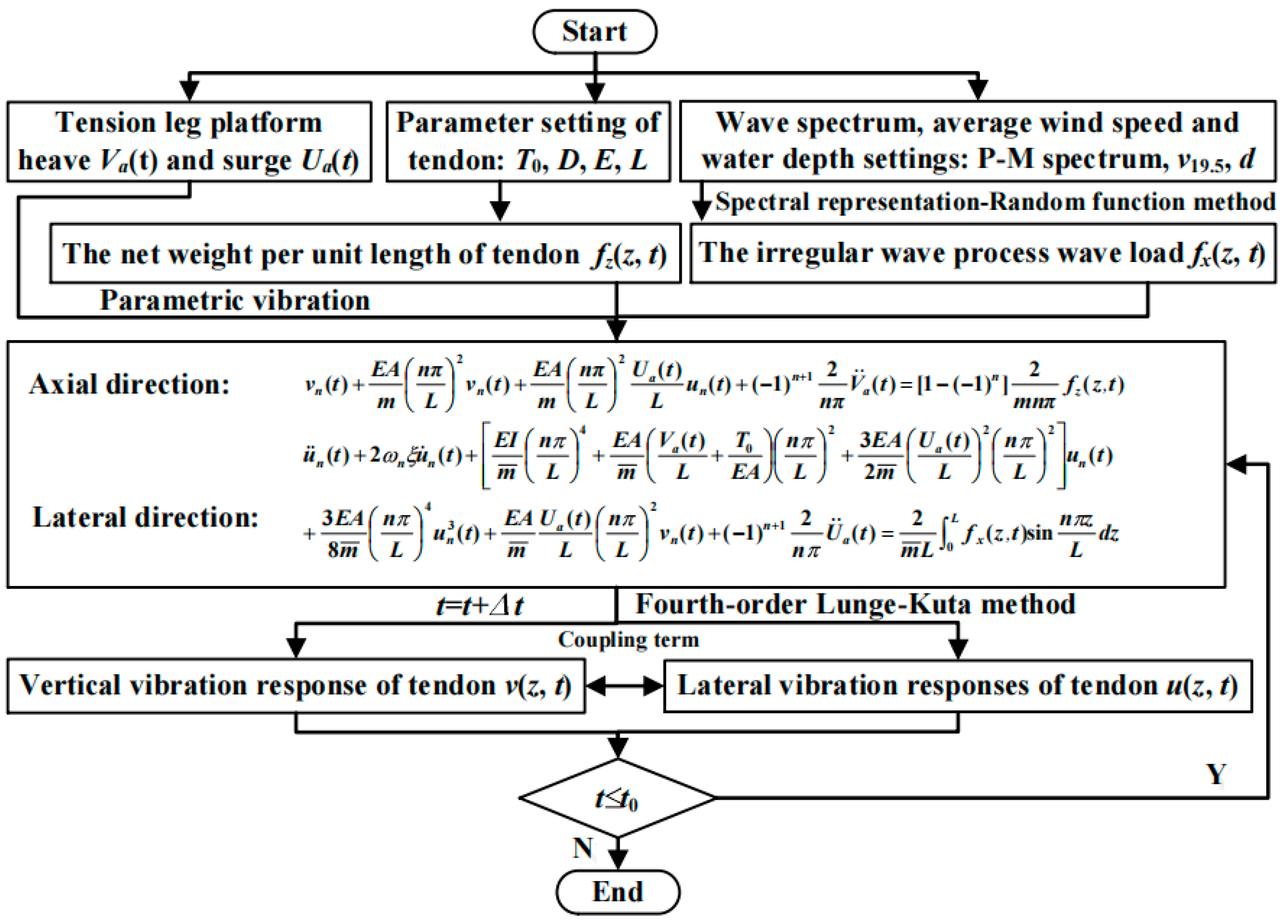
2.3. Numerical Solution Methods
3. Numerical Simulation Method and Examples
4. Results and Discussion
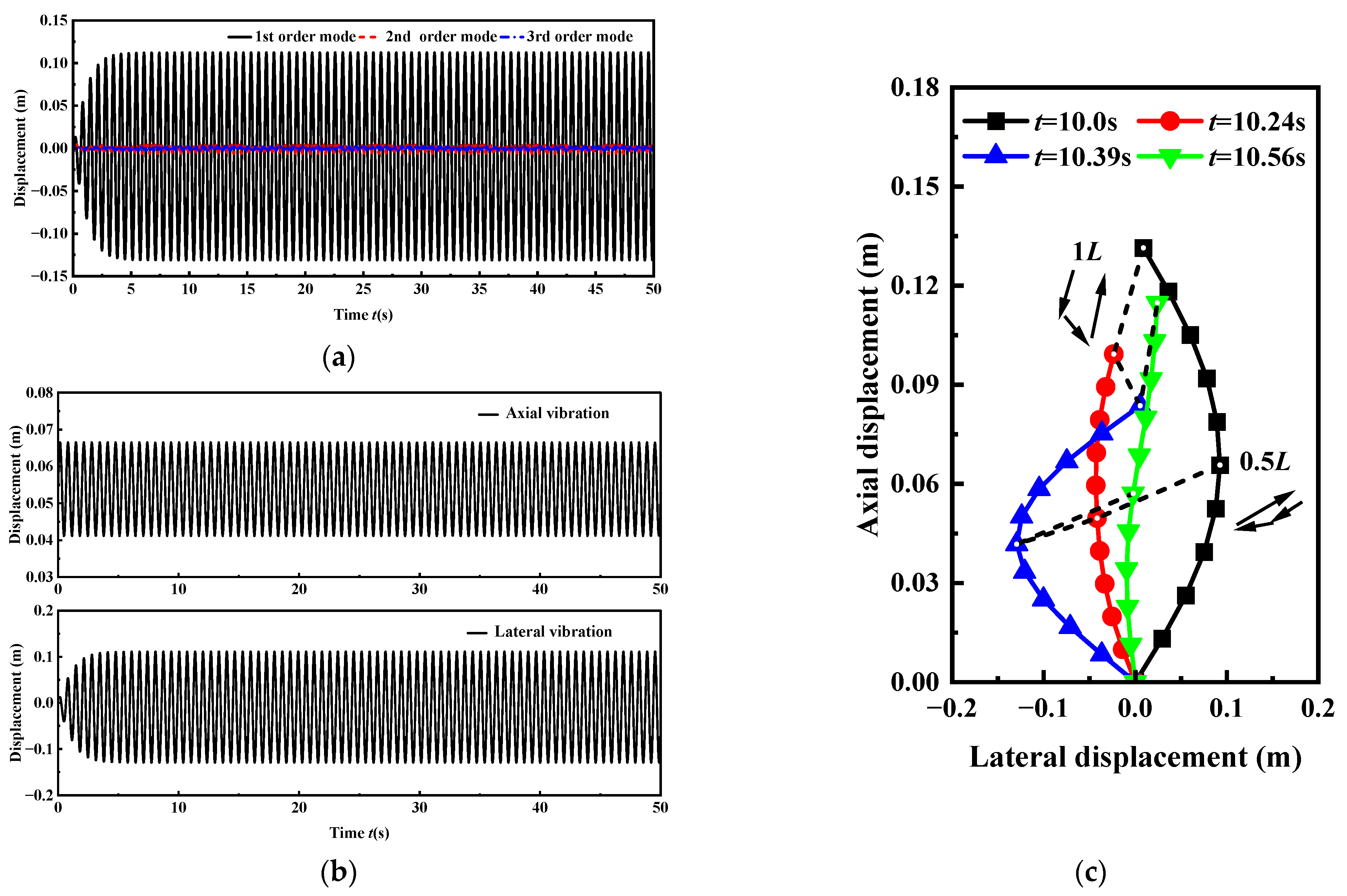
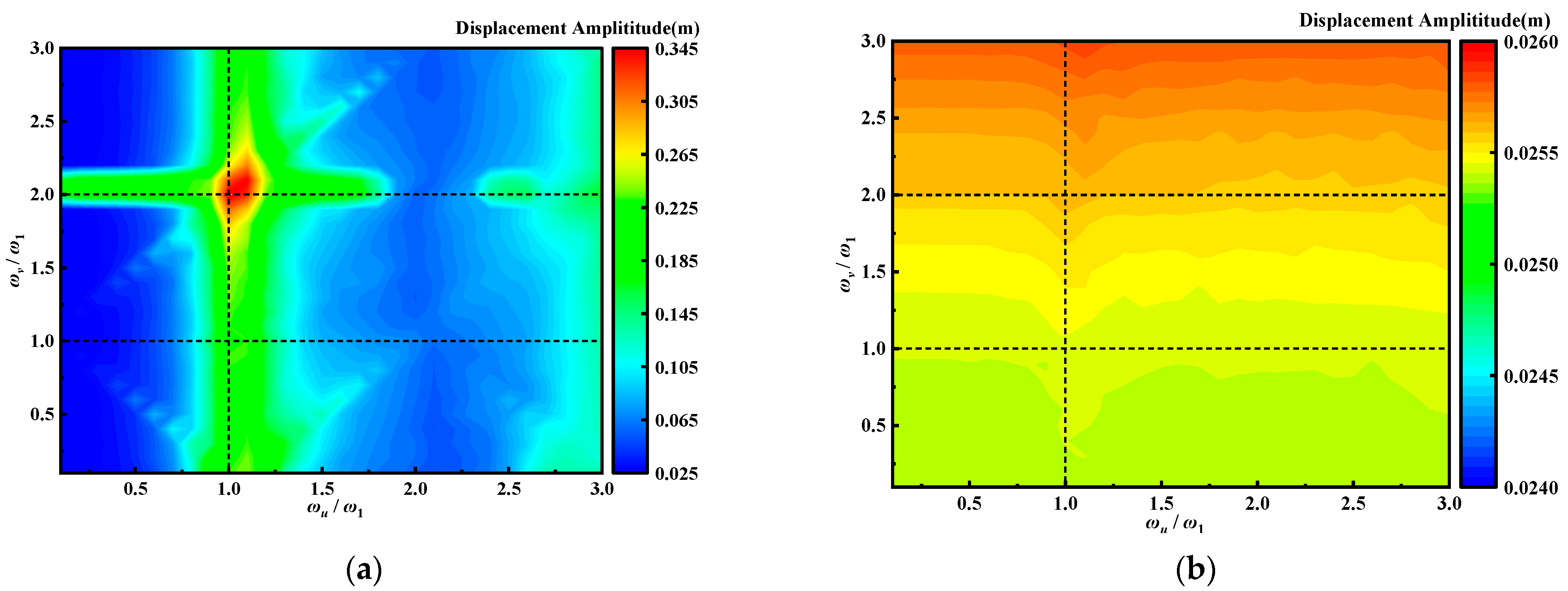
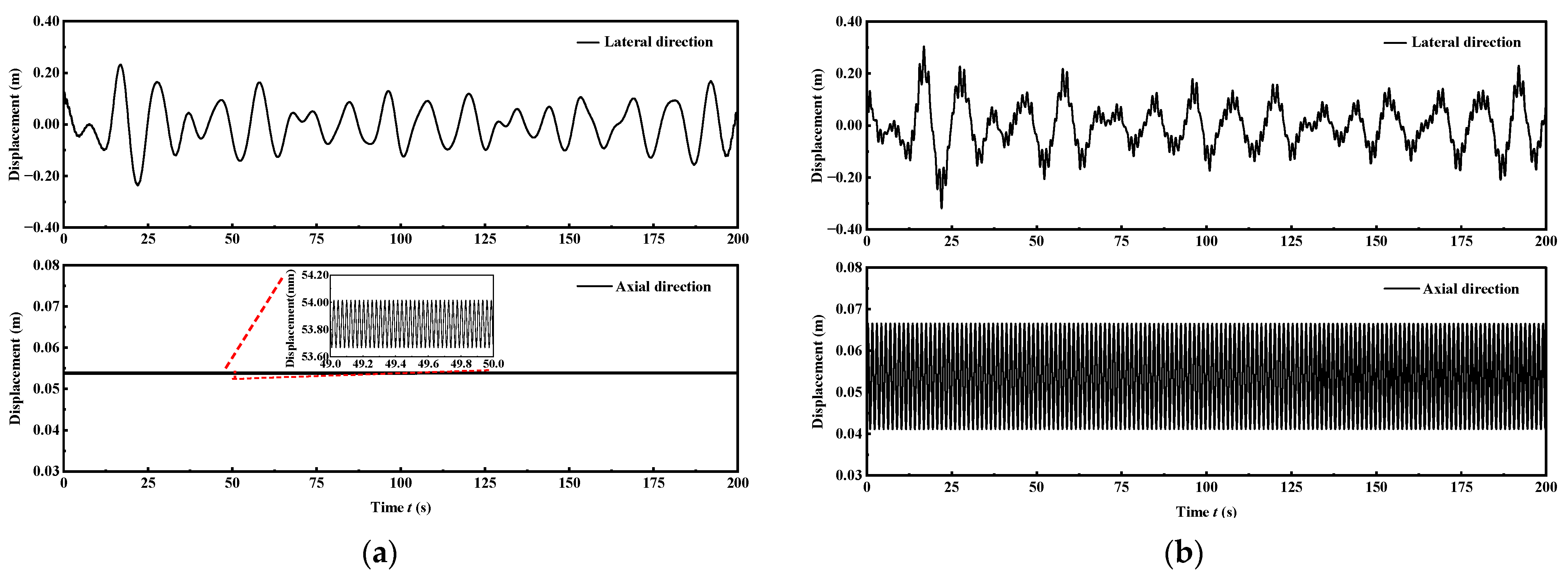
4.1. Tension Leg Platform and Tendon Coupled Vibration Analysis
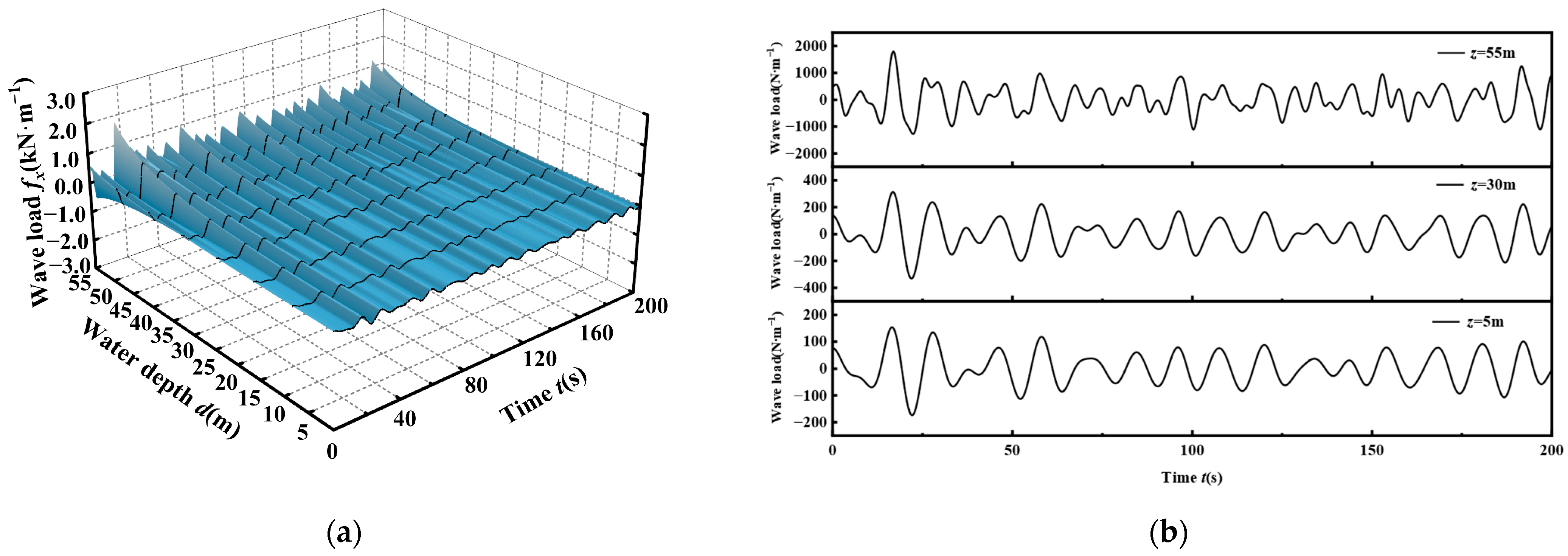
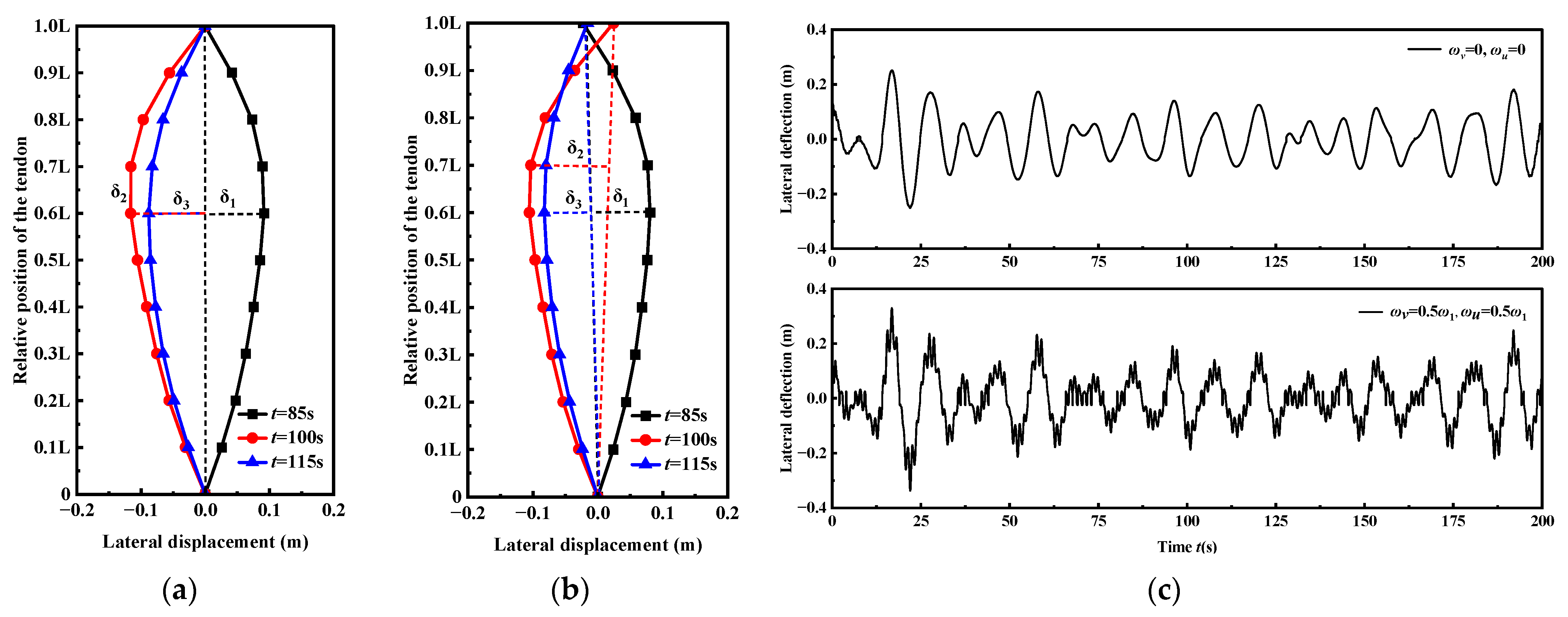
4.2. Dynamic Characteristics of the Tendon Under Irregular Wave Load
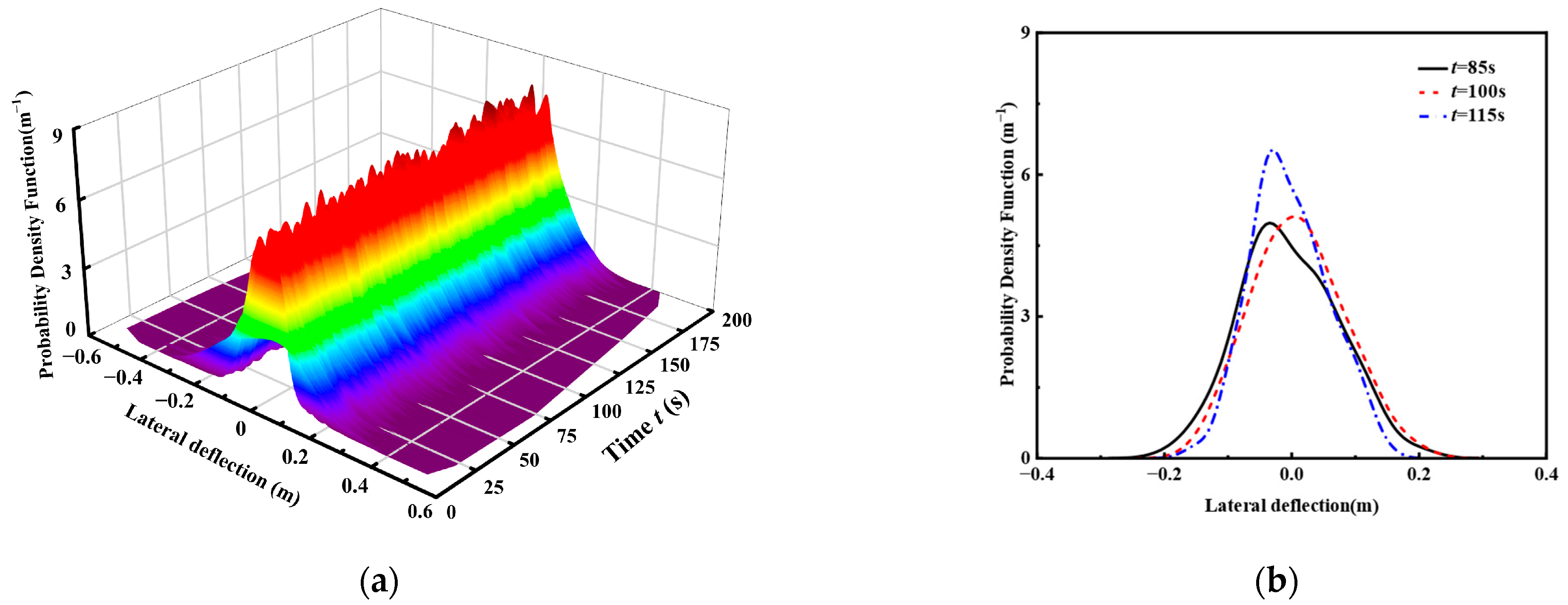
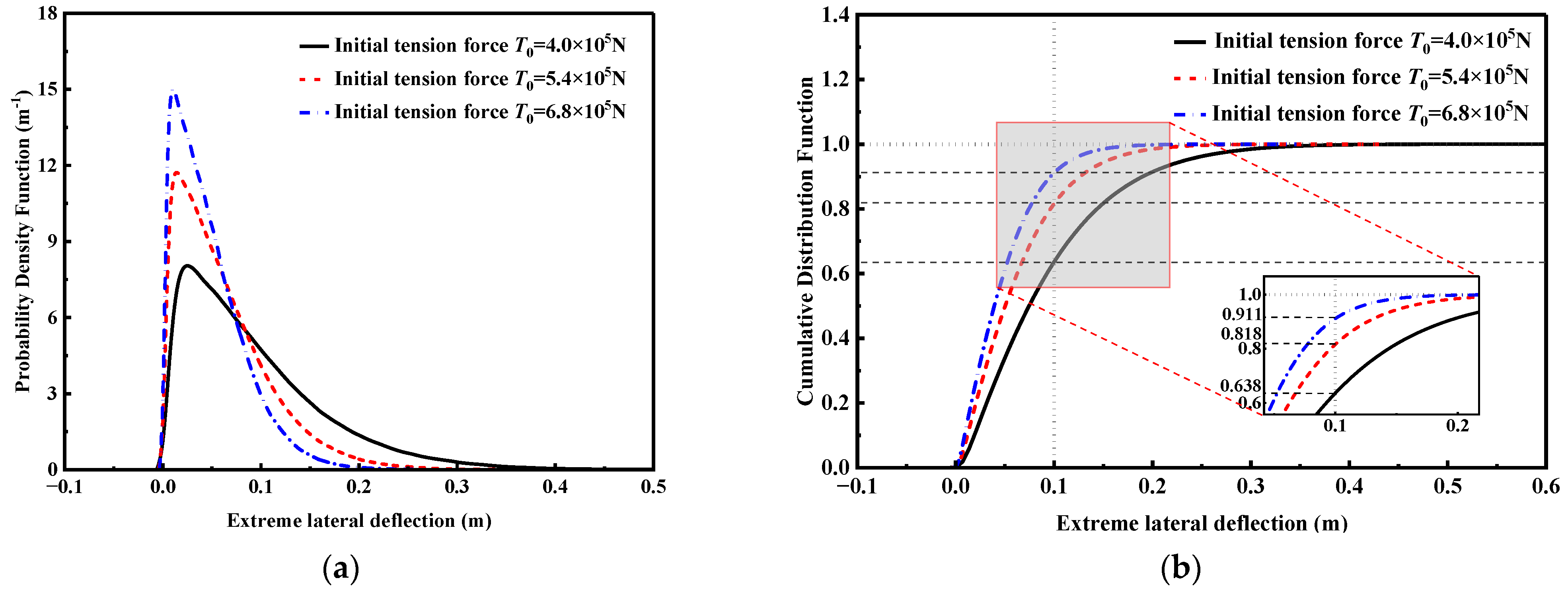
4.3. Reliability Analysis of the Tendon Under Irregular Wave Load
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Islam, A.S.; Jameel, M.; Jumaat, M.Z.; Shirazi, S.M.; Salman, F.A. Review of offshore energy in Malaysia and floating Spar platform for sustainable exploration. Renew. Sust. Energ. Rev. 2012, 16, 6268–6284. [Google Scholar] [CrossRef]
- Zhen, X.W.; Huang, Y. Parametric study on the behavior of an innovative subsurface tension leg platform in ultra-deep water. China Ocean Eng. 2017, 31, 589–597. [Google Scholar] [CrossRef]
- Manikandan, R.; Saha, N. Dynamic modelling and non-linear control of TLP supported offshore wind turbine under environmental loads. Mar. Struct. 2019, 64, 263–294. [Google Scholar] [CrossRef]
- Ren, Y.; Venugopal, V.; Shi, W. 2022. Dynamic analysis of a multi-column TLP floating offshore wind turbine with tendon failure scenarios. Ocean Eng. 2022, 245, 110472. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, T.; Zhao, Y.; Jiang, Z. Review of tension leg platform floating wind turbines: Concepts, design methods, and future development trends. Ocean Eng. 2025, 324, 120587. [Google Scholar] [CrossRef]
- Sun, S.N.; Su, Z.B.; Feng, Y.F.; Xu, X.Y. Parametric vibration analysis of submerged floating tunnel tension legs. China Ocean Eng. 2020, 34, 131–136. [Google Scholar] [CrossRef]
- Cantero, D.; Rønnquist, A.; Naess, A. Tension during parametric excitation in submerged vertical taut tethers. Appl. Ocean Res. 2017, 65, 279–289. [Google Scholar] [CrossRef]
- Hsu, W.T.; Thiagarajan, K.P.; Manuel, L. Extreme mooring tensions due to snap loads on a floating offshore wind turbine system. Mar. Struct. 2017, 55, 182–199. [Google Scholar] [CrossRef]
- He, C.; Sun, T.; Zhang, Z.; Liu, H.; Wang, C.; Wang, J. Numerical investigation on the second-order sum-frequency wave forces induced mooring fatigue of a 15 MW TLP FOWT. Ocean Eng. 2025, 322, 120463. [Google Scholar] [CrossRef]
- Wei, N.; Zhang, Z.; Xu, X.; Yao, W. Stability analysis of a TLP with inclined tension legs under different marine survival conditions. J. Mar. Sci. Eng. 2022, 10, 1058. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, A.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Zur Dtsch. Hydrogr. Z. Reihe A 1973, 12. Available online: https://pure.mpg.de/pubman/faces/ViewItemOverviewPage.jsp?itemId=item_3262854 (accessed on 2 September 2025).
- Bozzi, S.; Giassi, M.; Miquel, A.M.; Antonini, A.; Bizzozero, F.; Gruosso, G.; Archetti, R.; Passoni, G. Wave energy farm design in real wave climates: The Italian offshore. Energy 2017, 122, 378–389. [Google Scholar] [CrossRef]
- Taghipour, R.; Perez, T.; Moan, T. Hybrid frequency–time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Aggarwal, A.; Chella, M.A.; Kamath, A.; Bihs, H.; Arntsen, Ø.A. Irregular wave forces on a large vertical circular cylinder. Energy Procedia 2016, 94, 504–516. [Google Scholar] [CrossRef]
- Winsterstein, S.R. Random process simulation with the fast Hartley transform. J. Sound Vib. 1990, 137, 527–531. [Google Scholar] [CrossRef]
- Chen, J.; Sun, W.; Li, J.; Xu, J. Stochastic harmonic function representation of stochastic processes. J. Appl. Mech. 2013, 80, 011001. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Peng, Y. Random function based spectral representation of stationary and non-stationary stochastic processes. Probabilist Eng. Mech. 2016, 45, 115–126. [Google Scholar] [CrossRef]
- Jameel, M.; Oyejobi, D.O.; Siddiqui, N.A.; Ramli Sulong, N.H. Nonlinear dynamic response of tension leg platform under environmental loads. KSCE J. Civ. Eng. 2017, 21, 1022–1030. [Google Scholar] [CrossRef]
- Abaiee, M.M.; Ketabdari, M.J.; Ahmadi, A.; Ardakani, H.A. Numerical and experimental study on the dynamic behavior of a sea-star tension leg platform against regular waves. J. Appl. Mech. Tech. Phys. 2016, 57, 510–517. [Google Scholar] [CrossRef]
- Choi, Y.M.; Nam, B.W.; Hong, S.Y.; Jung, D.W.; Kim, H.J. Coupled motion analysis of a tension leg platform with a tender semi-submersible system. Ocean Eng. 2018, 156, 224–239. [Google Scholar] [CrossRef]
- Soeb, M.R.; Islam, A.S.; Jumaat, M.Z.; Huda, N.; Arzu, F. Response of nonlinear offshore spar platform under wave and current. Ocean Eng. 2017, 144, 296–304. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Q.; Liu, L.; Tang, Y. Transient response of a SPAR-type floating offshore wind turbine with fractured mooring lines. Renew. Energ. 2018, 122, 576–588. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, M.; Li, Y.; Liu, W.; Wu, H.; Cui, L.; Yan, Z.; Wang, X.; Liao, Q.; Li, M. Effects of mooring configuration on the dynamic behavior of a TLP with tendon failure. Desalin. Water Treat. 2022, 268, 215–228. [Google Scholar] [CrossRef]
- Jin, R.; Jiang, Y.; Shen, W.; Zhang, H.; Geng, B. Coupled dynamic response of a tension leg platform system under waves and flow at different heading angles: An experimental study. Appl. Ocean Res. 2021, 115, 102848. [Google Scholar] [CrossRef]
- Hmedi, M.; Uzunoglu, E.; Medina-Manuel, A.; Mas-Soler, J.; Vittori, F.; Pires, O.; Azcona, J.; Souto-Iglesias, A.; Guedes Soares, C. Experimental analysis of CENTEC-TLP self-stable platform with a 10 MW turbine. J. Mar. Sci. Eng. 2022, 10, 1910. [Google Scholar] [CrossRef]
- Gadagi, M.M.; Benaroya, H. Dynamic response of an axially loaded tendon of a tension leg platform. J. Sound Vib. 2006, 293, 38–58. [Google Scholar] [CrossRef]
- Lin, H.; Xiang, Y.; Yang, Y. Vehicle-tunnel coupled vibration analysis of submerged floating tunnel due to tether parametric excitation. Mar. Struct. 2019, 67, 102646. [Google Scholar] [CrossRef]
- Baldock, T.E.; Swan, C. Numerical calculations of large transient water waves. Appl. Ocean Res. 1994, 16, 101–112. [Google Scholar] [CrossRef]
- Borgman, L. Computation of the ocean-wave forces on inclined cylinders. Eos Trans. Amer. Geophys. Union 1958, 39, 885–888. [Google Scholar]
- Liu, Z.; Liu, Z.; Chen, D. Probability density evolution of a nonlinear concrete gravity dam subjected to nonstationary seismic ground motion. J. Eng. Mech-ASCE. 2018, 144, 04017157. [Google Scholar] [CrossRef]
- Sun, Z.; Song, Y.; Tian, Y.; Huang, G.; Zhang, N. Hydrodynamic characteristics of a flexible floating anti-collision system under beam and oblique irregular waves. Ocean Eng. 2022, 251, 111107. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, L. Simulation of stochastic ocean states by random function methods. J. Vib. Shock. 2014, 33, 1–6. (In Chinese) [Google Scholar]
- Pierson, W.J., Jr.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Lv, K.; Liu, Z. Dimension-reduction simulation for continuous random wave force field. Hydro-Sci. Eng. 2020, 5, 9–15. (In Chinese) [Google Scholar]
- Qiao, D.; Li, B.; Yan, J.; Qin, Y.; Liang, H.; Ning, D. Transient Responses Evaluation of FPSO with Different Failure Scenarios of Mooring Lines. J. Mar. Sci. Eng. 2021, 9, 103. [Google Scholar] [CrossRef]
| Object | Parameters | Value |
|---|---|---|
| Tension leg platform | Amplitude of axial vibration VL0/(m) | 0.025 |
| Amplitude of lateral vibration UL1/(m) | 0.025 | |
| Tendon | Elastic modulus E/(MPa) | 1.4 × 105 |
| Density ρ/(kg·m−3) | 7850 | |
| Diameter D/(m) | 0.5 | |
| Initial tension force T0/(N) | 5.4 × 105 | |
| Length L/(m) | 55 | |
| Wave condition | Sea depth d/(m) | 60 |
| Sea density ρw/(kg·m−3) | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Du, Y.; Luo, X.; Sun, T.; Lin, H. Coupled Vibration Response Analysis of Tension Leg Platform Tendon Under Irregular Ocean Wave Action. J. Mar. Sci. Eng. 2025, 13, 1836. https://doi.org/10.3390/jmse13101836
Wu Q, Du Y, Luo X, Sun T, Lin H. Coupled Vibration Response Analysis of Tension Leg Platform Tendon Under Irregular Ocean Wave Action. Journal of Marine Science and Engineering. 2025; 13(10):1836. https://doi.org/10.3390/jmse13101836
Chicago/Turabian StyleWu, Qiangqiang, Yinguang Du, Xiaofeng Luo, Tao Sun, and Heng Lin. 2025. "Coupled Vibration Response Analysis of Tension Leg Platform Tendon Under Irregular Ocean Wave Action" Journal of Marine Science and Engineering 13, no. 10: 1836. https://doi.org/10.3390/jmse13101836
APA StyleWu, Q., Du, Y., Luo, X., Sun, T., & Lin, H. (2025). Coupled Vibration Response Analysis of Tension Leg Platform Tendon Under Irregular Ocean Wave Action. Journal of Marine Science and Engineering, 13(10), 1836. https://doi.org/10.3390/jmse13101836





