Abstract
Due to the open underwater channels and untransparent network deployment environments, underwater acoustic networks (UANs) are more vulnerable to hostile environments. Security research is also being conducted in cryptography, including authentication based on asymmetric algorithms and key distribution based on symmetric algorithms. In recent years, the advancement of quantum computing has made anti-quantum attacks an important issue in the field of security. Algorithms such as lattice and SPHINCS+ have become a research topic of interest in the field of security. However, within the past five years, few papers have discussed security algorithms for UANs to resist quantum attacks, especially through classical algorithms. Some existing classical asymmetric and symmetric algorithms are considered to have no prospects. From the perspective of easy deployment in engineering and anti-quantum attacks, our research focuses on a comprehensive lightweight security framework for data protection, authentication, and malicious node detection through the Elliptic Curve and Hash algorithms. Our mechanism is suitable for ad hoc scenarios with limited underwater resources. Meanwhile, we have designed a multi-party bit commitment to build a security framework for the system. A management scheme is designed by combining self-certifying with the threshold sharing algorithm. All schemes are designed based on certificate-less and ad hoc features. The proposed scheme ensures that the confidentiality, integrity, and authentication of the system are well considered. Moreover, the scheme is proven to be of unconditional security and immune to channel eavesdropping. The resource and delay issues are also taken into consideration. The simulations considered multiple variables like number of nodes, attackers, and message length to calculate proper values that can increase the efficiency of this scheme. The results in terms of delay, delivery ratio, and consumption demonstrate the suitability of the proposal in terms of security, especially for malicious node detection. Meanwhile, the computational cost has also been controlled at the millisecond level.
1. Introduction
In recent years, the security issues of underwater acoustic networks (UANs) have gradually received attention from researchers. Underwater nodes are usually placed in an open underwater acoustic channel to gather information with limited resources. Therefore, UANs face many issues like greater propagation delay, limited computational power, and random node mobility, etc., which determines that research has to focus on lightweight solutions [1,2,3,4]. In addition, the CIA elements (confidentiality, integrity, availability) also require strict implementation as the core and foundation of network security prevention. Therefore, the motivation of our paper is to improve security issues by designing a lightweight secure scheme for UANs. A few key topics are clearly stated in this paper by comparing with existing works. First of all, the clear definition of application scenarios is given. Research on underwater acoustic communication has been undertaken for decades, and the most common research background is based on underwater sensor networks (UWSNs). But in fact, this background is ambiguous. The transmission methods of UWSNs do not necessarily rely solely on acoustic means. In short-distance underwater communication, both electromagnetic and optical means can serve as communication media. These two types of networks are not restricted by greater propagation delay and low bandwidth, which is a significant difference from the design of UAN schemes. Moreover, the network is self-organized, P2P, and homogeneous. A hierarchical or heterogeneous network structure should clearly consider the differences in device capabilities and propose a matching method in the algorithm statement. To the best of our knowledge, there few studies clearly explain the above topic.
Secondly, and most importantly, the anti-attack ability of the security schemes should be rigorously verified and discussed. Quantum attacks are a topic that must be addressed in the current post-quantum era. Significant progress has been made in cryptography against quantum attacks in 2022, and many underwater security studies have also been explored. As a result, there has been increasing interest in computational problems that are not known to be solved efficiently by quantum computers, which is called “quantum-safe cryptography”. Lattice cryptography has become a focus and highlight for researchers. But does traditional cryptography stand no chance entirely? The Shor algorithm [5] is the most famous algorithm in quantum attacks. Due to its emergence, the two major systems in existing cryptography, RSA and ECC algorithms, have been severely impacted. The most relevant feature of the Shor algorithm is that it can solve the problem of factoring large numbers into prime factors in polynomial time, but there is no equivalent proof that quantum attacks have the same ability to crack modular addition or hybrid operations. In addition, hash algorithms in traditional cryptography are also considered to have a certain resistance to quantum attacks. Meanwhile, there has been a large body of knowledge, experience, and hardware technology developed over the last 20 years in support of elliptic curve crypto, and so it is natural to try to continue using elliptic curves if possible. From the perspective of engineering deployment, it can also achieve the faster manufacturing of underwater devices and compatible chips. Meanwhile, the Supersingular Elliptic Curve Isogeny Cryptosystem [6], an efficient substituted technique to elliptic curve crypto, allows algorithms such as ECC or Diffie–Hellman to undergo a gradual progress in the post-quantum era. By combining other technologies such as bit commitment and multi-party computation, traditional cryptographic algorithms can be endowed with usability in the quantum age. It is worth mentioning that, even though the protocol constructed in this paper is an elliptic curve problem in a classical assumption, it does not make any restrictive assumptions about the computing power of participants and can resist quantum attacks.
Finally, guidance to engineering practicality should also be provided, such as which type of nodes to deploy and the difficulty of application on hardware chips or devices. Feasibility and availability are also important aspects of algorithm research significance.
In summary, our contributions in this paper are dedicated to clearly describe the four topics mentioned above while designing a lightweight secure scheme for UANs. Our scheme takes the self-organized and constrained resource characteristics of UANs into account, tailoring the security protection for the entire network. The main contributions of this paper are as follows:
- A certificate-less authentication scheme is designed for UANs. We propose a novel scheme based on self-certifying for node authentication, which ensures the reliability of network nodes. Dynamic crypto puzzles and Chameleon hash for nodeID generation provide an effective approach for malicious attacks;
- To identify adversaries in distributed underwater networking, a threshold-based detection scheme of malevolent nodes is introduced to realize the prevention of attacks in the process of underwater routing, which ensures that malicious nodes will not mix into the ad hoc UAN during underwater communication;
- For lightweight secure data collection in UANs, a bit commitment key framework is designed to provide comprehensive protection. We give the one-time key distribution schemes of point-to-point key to ensure data protection for UANs;
- All algorithms have been proven to be resistant to quantum attacks. Experimental simulations tested the performance of each cryptographic algorithm, which verified the rationality and low cost of our proposal. The completeness and suitability of the scheme for UANs have been well proved.
The structure of this paper is organized as follows. In Section 2, we briefly introduce the related work of our scheme. Section 3 illustrates the preliminaries and system architectural model of our proposal. The design protocol for the lightweight secure scheme is detailed in Section 4, including its working process and the related algorithms. Section 5 provides an analysis of the security of the whole scheme. The simulation results are presented and analyzed in Section 6. Finally, Section 7 offers our conclusion.
2. Related Work
Underwater security has long been a neglected research topic. With the development of other underwater communication technologies, security issues are currently gaining momentum. Meanwhile, in the past year, cryptography has made rapid progress in the field of quantum attacks, with many high-quality papers being published in explosive amounts in 2022–2024. Research on anti-quantum attacks has also begun in the field of underwater security. In general, security schemes are roughly divided into two types, detailed below.
The first type is merely based on the acoustic communication channel features, such as the number of channel taps, the relative delay spread, and the received power level. These features vary mildly over time and space, slowly enough that their distribution can be approximated as constant during the authentication process, which makes such features amenable for authentication purposes. Machine learning techniques are also widely used in this scheme to generate consistent symmetric keys for both the sender and receiver. Amedeo et al. [7] resort to physical layer key generation schemes, where the keys are generated by each user from the channel itself, by exploiting the environment as a source of randomness. They propose an adversarial auto encoder (AAE) model for advantage distillation. Similarly, [8] proposes an algorithm based on the Double Deep Q Network (D2QN) to jointly optimize the USV’s trajectory and transmit power, effectively resisting malicious underwater jamming attacks and maximizing the achievable end-to-end throughput of the system. The study in [9] proposes to learn the advantage distillation process by using a dataset of observed channels from the legitimate parties and the attacker, respectively. The proposed protocol in [10] extracts common acoustic channel features between receiving and sending nodes. Then, each party uses these features to generate his/her own secret bits via a random sequence generator. The study in [11] reverses the common digital signature solution and merely bases itself on the acoustic communication channel features. The distribution of the evaluated channel’s characteristics is leveraged by systematical measurement. The study in [12] generates secret keys dynamically based on the channel frequency response (CFR) in orthogonal frequency-division multiplexing systems, which optimizes the traditional symmetric encryption algorithm, provides higher security, and lower computational overhead. Unfortunately, the present solutions have some irreversible challenges. For the schemes of feature technology detection, the feasibility of the scheme depends on the strict time synchronization of the network nodes and the correctness of the evaluated channel’s characteristics. Machine learning cannot guarantee a 100% accurate generation of keys. It is inevitable that error eigenvalue detection will occur.
The second type applies the Cryptography Algorithm to accomplish lightweight authentication. Lattice-based public key cryptography has become a research hotspot for many cryptographers. Xu and Li et al. [13] proposed an NTRU certificate-less aggregate signature scheme for underwater acoustic communication. The pseudo-identity is generated by the polynomial fitting formula of the underwater acoustic channel, and the complete private key of the node privacy is formed with the secret value. Furthermore, [14] proposed a sky–underwater quantum key distribution scheme based on phase-matching protocol, which resulted in an asymmetric phase-matching protocol model to improve the classical phase-matching protocol.
There are also many published Elliptic Curve or Hash algorithms plans to ensure underwater security by the reduced computation sophistication, trusted encryption schemes, and resource conservation. Gupta et al. [15] introduced a lightweight certificateless signcryption system based on Hyper-elliptic Curve Cryptography (HCC). The system significantly reduces computing and communication costs, making it ideal for resource-constrained environments. But this scheme is only a measure for authentication and cannot provide comprehensive protection for the network. Krivokapic et al. [16] proposes the utilization of implicit certificates and the Hashed One-pass Menezes-QuVanstone (HOMQV) key-exchange protocol as an alternative. Goyal et al. [17] propose a reliable and secure approach by using trusted encryption schemes like HMAC and AES. Ullah et al. [18] considered an online/offline signature with a lightweight hyper-elliptic curve cryptosystem to reduce the communicational complexities for UAN communications. Du et al. [19] realized a two-way authentication between the node pair of source and destination by PKG (public key generate). However, the Shor algorithm has indicated that they would no longer be secure in the quantum era.
We provide a table to summarize the above analysis (Table 1). In summary, existing research cannot balance the ease of application and the completeness of theory. Therefore, in the proposed approach, we considered a lightweight secure scheme to support the security protection of the entire network, which ensures that the system cost and security is improved. Moreover, we have also provided an analysis and proof for the three questions (quantum attacks, system model, engineering) given in the previous section.

Table 1.
The limitations of the existing literature.
3. Preliminaries and System Model
In this section, we introduce several important concepts of our system and present the design ideas of the scheme. We first describe the preliminaries and give the system model applicable to the algorithm. A concrete mathematical discussion will be presented in the following section.
3.1. Preliminaries
- Shamir secret sharing scheme
The Shamir’s Secret Sharing Scheme (SSSS) for cryptography was introduced by Adi Shamir [20]. In the SSSS, the shares of a unique secret are distributed among users. In this secret sharing, a secret is shared between n users in a way that users combine their shares to obtain the secret. No combination of users less than t (t is termed the threshold) can decipher the secret. Therefore, not all the shares of the secret are required to recover the actual secret. This scheme is implemented with the help of a one-dimensional t-degree uniquely determined using any t points on the polynomial. A user ui’s share is given by (xi, f(xi)), where xi is a point on the X-axis and f(xi) = pt(x). In Shamir’s secret sharing scheme, generally the secret is the term a0 in the polynomial. The SSSS has information–theoretic security, which means that an attacker cannot break the cryptosystem. The attacker cannot obtain sufficient information to threaten the security even if it has unlimited computational power [21]. A Lagrange’s polynomial of degree n taking on the values f(x0), f(x1), …, f(xn) for the points x0, …, xn is given by
Note that the secret a0 in Shamir’s secret sharing scheme can be obtained as a0 = Ln(0). The ith Lagrangian coefficient [22] is Ln(0), resulting in a0 = Ln(0) = f(x0)λ0 + f(x1)λ1 + … + f(xn)λn.
- ECDLP
The security of the elliptic curve public key cryptosystem is equivalent to the solution difficulty of ECDLP (the Elliptic Curve Discrete Logarithm Problem) [23,24,25], which is the foundation of security of all elliptic curve schemes.
Definition of ECDLP: GF(q) is the finite field with q elements and E is an elliptic curve defined over GF(q). E(GF(q)) denote the group of Fq-rational points of E. Given two points P, Q in E(GF(q)) with P,Q ∈ E(GF(q)), the discrete logarithm problem is to find an integer ℓ satisfying Q = ℓP. Such an integer ℓ is unique up to module n, where n denotes the order of P in E(Fq). In particular, such an integer ℓ with 0 ≤ ℓ< n is denoted by logP(Q) (n is a huge prime). ℓ is called the P-based discrete logarithm of Q. It is easy to find point Q when ℓ and P are known.
- Chameleon hash
Definition: Anyone can perform chameleon hashing with a given public key PK, and users with sk can broadly find hash collisions, making = Ch_Hash(m). The chameleon hash function has four main algorithms [26]:
- Key generation algorithm: Given a security constant λ, the public key PK and private key sk (trapdoor) are output as the key of chameleon hash;
- Hash generation algorithm : Input the public key PK, random number r, and message m to generate a chameleon hash value h and a random number p:
- 3.
- Hash verification algorithm Input the public key PK, message m, hash value h, and a random number p. If (h, p) is the correct hash value, output 1; otherwise, output 0:
- 4.
- Hash collision algorithm ): Input the private key sk (trapdoor), message m, new message m′, hash value h, and a random number p, and output the new random number r′, resulting in
- Bit commitment
Bit commitment (BC) is an important basic protocol in cryptography, and its concept was first proposed by the 1995 Turing Award winner Blum [27]. The commitment scheme can be used to build zero-knowledge proof, verifiable secret sharing, coin throwing, and other protocols, and at the same time, form the basis of security computing, which is a research topic of interest in the field of cybersecurity [28]. A bit commitment scheme must possess the following properties:
Correctness: If both promisors honestly execute the protocol, then verifiers will correctly obtain the bit string promised during the disclosure phase.
Confidentiality: Verifiers cannot obtain bit string information before the disclosure stage.
Binding: After the commitment phase ends, promisors cannot reverse the bit string, as if they are “bound” to the bit string.
If a bit commitment protocol satisfies correctness, confidentiality, and binding, and does not make any restrictive assumptions about the attacker’s computing power, then the bit commitment protocol is unconditionally secure. Mayers, Lo, and Chau have demonstrated that bit commitment protocols under the standard model cannot be unconditionally secure, whether in classical or quantum computing environments. Their conclusion is called the Mayers–Lo–Chau (MLC) no-go theorem [29,30]. However, even if the theorem is completely correct, it does not rule out the possibility of the existence of an unconditional secure bit commitment protocol under the non-standard model. In fact, as long as the bit commitment of the constructed non-standard model does not fall into the proof framework of the MLC (such as multi-party commitments), the unconditional security bit commitment scheme is completely feasible.
3.2. System Model
As shown in Figure 1, our model is mainly composed of the following parts: Offshore data centers, Relay command ships, Buoy, and UAN nodes. The network topology type is random topology. The offshore data center is mainly responsible for the scheduling and calculation of data collected from the sensor nodes. Meanwhile, it is also the generation center of the algorithm parameters as a trusted third party. The relay command ships and buoys are in charge of preprocessing data and forwarding them toward the offshore data center, which will not be explained as the main role in the later algorithm description. They are both surface sinks. In order to improve the resistance to attack, there can be several offshore data centers and command ships. Nodes are the hardware support of the underwater acoustics networks, responsible for underwater data communication, such as mobile surveillance, marine explorations, military activity, etc. They are usually defined as an ad hoc mobile network consisting of unmanned underwater vehicles (UUVs) deployed in a three-dimensional ocean environment. This system model means that all network nodes are mobile and have a certain amount of computing power. In addition, the satellites are responsible for the positing system and wireless information transmission. The randomly moving UAN nodes need to communicate with each other, either to forward each other’s data or exchange information. The nodes may also need to send the data to offshore data centers.
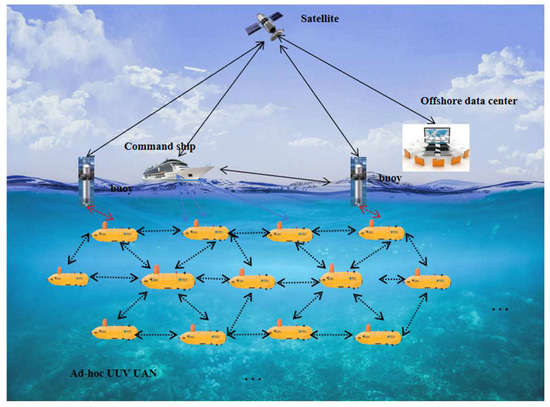
Figure 1.
System model.
3.3. Adversary Model
UANs are deployed in unattended and possible hostile underwater environments. Threats may originate from factors such as authentication errors or data thefts. Meanwhile, the UAN nodes are fully self-organized for a certain period and do not contact the ODC node frequently after deployment. All preload processes occur before the UAN nodes are placed in the underwater channel. In this section, we mainly considered several malicious adversary models with respect to the confidentiality, integrity, credibility, authentication, non-repudiation, and availability of our system.
- An adversary can passively disguise themself and eavesdrop on the communications, hardly being perceived by UAN nodes. Data theft is inevitable. Therefore, the confidentiality of underwater communications should be taken into consideration.
- Offshore data centers and command ships are tamper-resistant and no computational issues need to be considered. No adversary can impersonate an offshore data center or command ship. Meanwhile, they will not reveal the private data as a trusted third party. The algorithm can run in a trusted environment and resist various attacks [31,32].
- Nodes are half-tamper-proof. They will not reveal the private data preload in their hardware, even if captured. However, they cannot prevent the adversaries pretending to be them. Thus, a strict detection and authentication mechanism of malicious nodes is required.
- Adversaries in our model cannot capture the underwater nodes and obtain the secret from inside through hardware. It can be assumed that the hardware is equipped with a physical self-destructive protection system, and there are no adversaries other than us who can view the hardware content.
4. Lightweight Security Protocol for UAN
Our security protocols are mainly divided into the following parts: self-certified authentication scheme, threshold-based detection scheme of malevolent nodes, and a bit commitment encryption scheme. Table 2 shows the list of notations used in the formulation of our model. Without loss of generality, we describe some preconditions before presenting the improved schemes as follows:

Table 2.
Notation table.
- Each node can be a source node, a destination node, or an intermediate routing node;
- All nodes have the same initial limited energy, computing power, and other resource support. The offshore data centers are assumed to have an unlimited power supply, so the consumption of energy and computing power is not measured during the parameter preloading process;
- Before each node is deployed, security parameters will be preloaded in their cryptographic hardware, and the stored parameters will not be intentionally disclosed by nodes;
- This model is designed to resist cyber attacks, such as eavesdropping, replay, forgery, etc. The physical attacks are not considered. Parameter preloads in the underwater nodes for algorithms are assumed to be absolutely secure.
4.1. Initialization
Offshore data centers (ODCs) generate the algorithm parameters as a trusted third party. Let E(GF(q)) denote an elliptic curve over prime field GF(q) whose order is a big prime q. The base point of the elliptic curve E(GF(q)) is G.
Zp* is a multiplicative group of invertible integers modulo p. The ODC randomly generates an integer dc ∈ Zp* as its private key and computes its own public key PKc = (dc)G. Then ODC sets up the polynomial fi (x) of degree (t − 1) with fiz as the coefficient: fi(x) = dc + fi1*x + … + fiz*xz + …+ fi(t−1)*xt−1, where fiz∈Zp*, z = 1, 2, …, (t − 1). i is the sequence parameter of the polynomial. The ODC assigns nodes with the independent number Nj used for generating static IDj, as seen in Section 4.2, and security parameters Yij of the nodes as (5) and (6). (fi(IDj), Yij) are node j’s private and public keys. It is especially worth noting that both the public and private keys here are not disclosed to the public. The private key is only stored in the node’s own hardware, while the public key is stored in the neighboring nodes communicating with it directly. During the forwarding process, there will be no plain-text public and private key information directly displayed.
Meanwhile, the parameters of multi-party bit commitments are set as follows. The random numbers r in commitments can be regarded as bit strings of {0,1} uniform distribution. Then, two random points on the curve can be used to represent bits 0 and 1, respectively (denoted as P0 and P1). In order to increase eavesdropping resistance, the points corresponding to bits 0 and 1 are not limited to two random points P0 and P1, but extended to 2R(R is a sufficiently large positive integer), with multiple different random points selected from the elliptical curve. {P(0,1), P(0,2), …,P(0,R)} are denoted as bits 0 and {P(1,1+R), P(1,2+R), …, P(1,2R)} are denoted as bits 1. In particular, P(0,i) and P(1,j) are transcoded as another complex encoding. {} is the generating function. This setting makes it possible to enable cryptographic calculation and verification during communication:
In our model, multi-party bit commitments represent the interactions between nodes. There are three roles in the commitments: promisor, verifier, and variable number third party certifiers. Each node randomly generates a bit string αn with a long l as its master commitment and k short bit strings λnk of length m as its interaction commitments. Among them, the master commitments αn are stored in the node’s own security hardware and ODC, serving two purposes. The first is to serve as the data encryption key for communication with ODCs, used for instruction issuance or security parameter replacement. The second is used as an authentication parameter for detecting malicious nodes. If a node is suspected of rebelling, it verifies that third-party certifiers form a verification group, and the reliability of the node is confirmed through the verification of master commitment parameters, which are generated by the nodes. Nodes divide their master commitment into k sub-bit strings scz according to prescribed rules, and each bit string serves as a sub-commitment for authentication. Then, it generates proof fn(scz) with k certifiers by the polynomial fn(x) of degree (k−1) with fnz as the coefficient. The rules are as follows:
The interaction commitments of short bit strings λnk are used for point-to-point authentication and encryption during communication. The k sub-commitments generated by each node are distributed to k neighboring nodes, and each node defaults to storing the initial authentication commitments of neighboring nodes that it can directly interact with before deployment underwater. The sub-commitments can be changed during node interaction.
Among them, OCDs also generate the detection parameters Sij and detection parameters C1 for nodes as in Equations (9) and (10), where rs and rpk are random numbers generated by OCDs, rs, rpk∈Zp*. The specific functions of the parameters are discussed in Section 4.3 and Section 4.4.
All of the above parameters are generated before the nodes are deployed underwater and are preloaded as initial security parameters in the node’s reliable hardware. Our system algorithms are described below.
4.2. Generate Authentication ID
Due to the high propagation delay characteristics of the underwater acoustic networks, it is not suitable for nodes to authenticate with PKI or DPKI during data transmission. This will greatly increase the delay and consume unnecessary energy. Therefore, we design a self-certified identity authentication protocol to impede the Eclipse, Sybil attack, and Impersonation attack which may be initiated by adversaries. Self-certification is an effective approach for nodeID generation by using crypto puzzles. The crypto puzzles ensure that the node’s ID cannot be chosen freely, generated in large quantities, and forged [33]. The S/Kademlia [34] algorithm first mentioned this theory, and we applied and extended it, redesigning appropriate crypto puzzles based on underwater scenarios. The generation rules are as follows:
- Generate static ID: Let Gc denote a cyclic group, Gc ⊂ Zp*. A hash function H: {0, 1}* → Gc is chosen. Node static IDjs is generated from the cryptographic hash of the node’s public key, which is given by Equation (6). ⊕ is the XOR operation.
- 2.
- Generate dynamic ID: In the S/Kademlia algorithm, puzzles are calculated by adding random numbers and setting difficulty. It searches for the hash value with special value 0 in the preceding k bits. The long preceding bits will increase the attack resistance effect. In our model, puzzles are irregular parameters obtained through negotiation. Furthermore, to prevent replay and impersonation attacks, we set the hash function of the dynamic ID to a Chameleon Hash. Nodes use their own private keys to form trapdoors, which can dynamically prove their identity by finding hash collisions in a generalized way to change the verification information. The initial verification value is the random r(i)AC calculated by the receiving node according to Equation (14). Node dynamic IDjd is generated by Equation (12), HC: {0, 1}*→Gc is a Chameleon Hash.
- 3.
- Verification scheme: During identity verification, the verification node needs to export {Q1, Q2, …,Qk} and calculate r(i)′AC according to Section B. Then, it verifies the {IDjs,IDjd} as in Equation (18).
4.3. The Process of Node Security Interaction
- A initiates communication with its neighboring C: A generates its own mapping based on its own sub-commitment string λnA with C, corresponding to the set {P1, P2, …, Pk}, and calculates commitment parameters {Q1, Q2, …,Qk}:
The randomness is composed by encoding H’{P1, P2, …,Pk} is r(i)AC with the length lr. Assuming that the encoding of each elliptic curve point is v bits, then lr = vk. Node A calculates its hash value H(r(i)AC). Therefore, the initial verification information sent by node A to node C is {{Q1, Q2, …, Qk}, H(r(i)AC), [H(IDstatic), HC(IDdynamic)]}.
- 2.
- After receiving the message from A, C first verifies whether static ID of A is correct. Then, it calculates the set {P1′, P2′, …, Pk′} using the following formula, and then calculates the random number r(i)′AC based on the encoding mapping relationship of the {0,1} → {P(0,i), P(1,j)} set saved by itself, and compares its hash with the H(r(i)AC). rd is the random output of Chameleon Hash as in Equation (12).
If all the above verifications are correct, r(i)AC will be used as the symmetric key Sk for further encrypted communication. The ciphertext Csk delivers the data packet to the receiving node. The node takes the key Sk and ciphertext Csk as input, yielding the plaintext M as output, and then the data encryption is described as follows:
It should be noted that we also set hash fingerprints CID for the transmitted content during transmission to verify the integrity of the content M as in Equation (16):
4.4. Detection Malevolent Nodes
In long-distance communication, malicious nodes may mix into the self-organizing UAN during certain processes. Thus, we propose a threshold-based detection scheme to detect and prevent malevolent nodes.
The detection parameters Sij and C1 generated by ODCs are preset in the nodes before deployment. According to the rules of the Shamir algorithm, since all the nodes participating in the networking have the threshold keys Sij, the Lagrange interpolation polynomial is calculated during packet transmission:
It should be noted that the Lagrange polynomial parameters are calculated by each node on the routing path when the data packet arrives, and the calculated parameters are put into the data packet for continuous transmission. The detection key Sij is not transmitted, which can also avoid leakage. It is clear that, if there are malicious nodes in the transmission process of the routing path, the calculation of the final polynomial cannot be recovered due to the insufficient number of threshold keys. Therefore, it is necessary to choose a reasonable setting for the degree t of polynomial fi(x), so that most transmission can be calculated for malicious node detection. Meanwhile, the degree cannot be too small, which may reduce the efficiency of node detection.
If A is suspected to be an attacker, the UAN system can require A to cooperate with authentication. In the authentication stage, k certifiers send their sub-proof fn(spz) to the verifier. The verifier calculates the master commitment based on the sub-proofs of k certifiers as in Equation (22). Meanwhile, the verifier requires the promisor to encrypt a message using its master commitment as the key and decrypt. If a valid plaintext can be obtained, it proves that the promisor node is not a malicious node; otherwise, it may be a forgery attacker.
5. Correctness and Security Proof
5.1. Correctness
Correctness analysis aims to review and verify the logical and mathematic correctness of the algorithms to ensure that they can correctly and validly perform their expected security functions. The analysis is mainly from the following perspectives:
- Bit commitment: The correctness of multi-party bit commitment is provided below:
- 2.
- Chameleon Hash: We applied the scheme from [35]. The chameleon hash function is constructed based on the ECDLP. The construction process and proof are briefly described below. A detailed analysis can be found in the references.
Two secure hash functions H1: {0, 1}* × G ∈ Zp* and H2: {0, 1}* × G ∈ Zp* are used in the construction of a one-time chameleon hash function. We choose two random numbers k and y, k ∈Zp*, y ∈ Zp*, compute Y = yG, K = kG, and derive two public keys hk = (K, Y) and a trapdoor private key tk = (k, y), where the parameter in our scheme is (fi(IDj), Yij). Given the label μ, message m (), random number r ∈ Zp*(r(i)AC), X0 ← H2(μ), we then calculate ChHash(hk, m) = X0H1(m, K)G+ rY (modq).
Trapdoor collision: In the case of m≠m’, the input trapdoor tk = (k, y) outputs a value r in polynomial time such that ChHash(m, r) = ChHash(m′, r′). The process is expressed as r′ = r + y−1(X0H1(m, K) − X0H1(m′, K)(modq).
5.2. Security Analysis
Security analysis refers to the process of evaluating and verifying the security of a system. It aims to review the security mechanism of the system, analyze the strategies of the algorithms, and ensure that they respond appropriately to various threats and risks. The analysis is mainly from the following perspectives:
Theorem 1.
The above protocols are unconditionally bound and confidential, which makes them able to resist quantum attacks.
Proof.
Firstly, the above protocol does not make any restrictive assumptions on the computing power of the nodes. According to Theorem 1, the probability of a successful attack can be infinitesimal even for quantum computers with infinite computing power. Therefore, it is unconditionally bound.
For the adversaries, to invade the UAN, they must calculate the r(i)AC value through the {Q1, Q2, …, Qk} value or derive it through Hash at the initial communication since plaintext only transmits at this stage. The two well-known algorithms Shor [5] and Grover [36] are the key technologies for quantum attacks. The biggest feature of the Shor algorithm is that it can solve the problem of factoring large numbers into prime factors in polynomial time, but there is no equivalent proof that quantum attacks have the same ability to crack modular addition or mixed prime factor operations. Due to our inclusion of {dn,PKn} value into the commitment Qi value, it is not possible to determine the unknown variables Pi, dA, and simultaneously by Equation (13) alone, even if adversaries have the quantum computing of a super polynomial Turing machine.
On the other hand, most implementations of the Hash algorithm can resist the attacks from Shor. The most effective universal quantum attack on hash functions is a search technique based on Grover, which reduces the effective security of hash functions. However, the reduction is far less severe than that of the Shor algorithm, with a range between square and cubic roots. Therefore, security can be maintained by increasing message capacity and output size, and hash functions such as SHA3 have been developed.
In fact, adversaries can only obtain information about r(i)AC through random guessing, so the probability of its success is unbiased for (1/2)s. s is the length of r(i)AC and not less than 128, which can be regarded as infinitesimal. □
Theorem 2.
Identification protocols made secure against replay attacks by two identity verifications and by generating one-time session keys.
Proof.
Due to clock drift issues in UANs, it is difficult to implement the timestamp mechanism commonly used in replay attacks. Our scheme involves two dynamic authentications during the initial interaction. The sending node can take advantage of chameleon hash in dynamic ID design based on the private key trapdoors to construct new information and encrypt it to the receiving node during the second communication after the first communication is initiated. This way, the verified hash value is the same, but the content is different. Meanwhile, because only the owner of the trapdoor private key can construct the chameleon hash, replay attackers cannot complete this authentication, meaning that our scheme can be very comprehensive.
Moreover, our schemes realize encrypted transmission through preload security parameters at the first authentication, which ensures that malicious nodes in the system cannot determine the purpose of the packet. The parameters preload by the nodes and the asymmetric key algorithm constitute a challenge response mechanism to resist replay attacks. r(i)AC is a one-time session key. Even if the authenticated packet is replayed, because the malicious node does not have a symmetric key for communication, it cannot continue the next communication process and its malicious behavior. □
Impersonation attacks: Impersonation attacks typically show as routing attacks and message manipulation attacks. Routing attacks usually generate useless messages on legitimate nodes by forging identities during the routing process, thus increasing network transmission overhead and consuming node energy. Moreover, adversaries launch message manipulation attacks through interception and tampering to disrupt the entire UAN in the process of packet transmission. Strict node authentication guarantees that malicious nodes cannot impersonate legitimate nodes and replay the effective authentication message. Meanwhile, the encrypted packets prevent the interception and tampering of adversaries. According to Theorem 1, it is difficult to solve crypto puzzles when the security parameters are secret. Impersonation attacks are almost impossible in our model.
Sybil attacks: The static ID of the nodes ensures that nodeID cannot be chosen freely and a dynamic cryptopuzzle makes sure that it is complex to generate a large amount of nodeIDs. Thus, our scheme is effective against Sybil attacks.
Compromise attacks and Collusion attacks: Unlike the server nodes in the traditional network, UAN nodes are only unintelligent computing nodes. Therefore, the compromise and collusion attack here can only capture and replace the legitimate nodes, rather than instigating the node through bribery attacks. Therefore, according to the preconditions in Section IV, adversaries in our model cannot capture the underwater nodes and obtain the secret from inside through hardware. Our scheme is also effective against compromise attacks and collusion attacks.
6. Experiments and Performance
We tested the performance of each cryptographic algorithm with CentOS 7. The signature algorithm uses the SM2 algorithm, and the hash algorithm uses the SM3 algorithm. The modular exponentiation and modular multiplication algorithms used in our experiments are the same as elliptic curve scalar multiplication and point addition algorithms, respectively. The threshold algorithm is implemented based on the OpenSSL cryptographic algorithm library. Table 3 shows the performance parameters of basic cryptographic algorithms, which are the average results of running 1000 times.

Table 3.
The performance parameters of basic cryptographic algorithms.
The network simulations are built based on the OMNET++ [37] simulation platform to evaluate the performance of our model. By modeling and networking simulation, the effectiveness of the above algorithms is validated. Simulation modeling mainly includes network model, auxiliary model, channel model, and protocol model. The routing algorithm adopts the AODV (Ad Hoc On-Demand Distance Vector) routing strategy. The simulation parameters used in the proposed scheme are presented in Table 4.

Table 4.
Parameters used.
The experimental results of the algorithm performance are shown below. Firstly, we computed the computation costs of preload parameter generation at the initial stage, as shown in Figure 2.
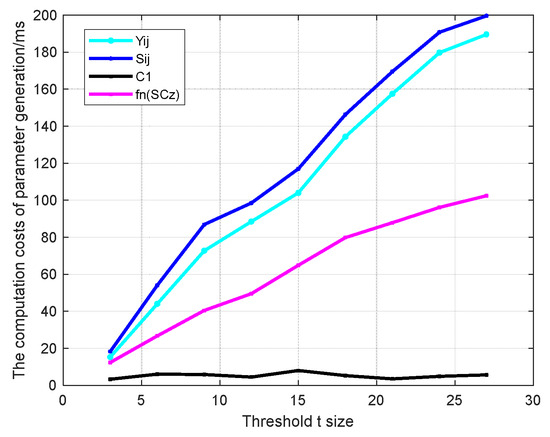
Figure 2.
The computation costs of parameter generation.
Then, the time costs of authentication are graphically compared, as seen below in Figure 3. We calculated the time it took for two nodes to fully establish secure communication and provided the time for node A to generate verification parameters and for node C to verify the parameters, respectively. This includes the costs of self-certifying security verification, including identification, bit commitment reveal, and puzzle calculation, as shown in Equations (13)–(18). Here, the Y-axis is for the entire generation or verification time, without separating each parameter as Qk or r(i)AC. Due to the fact that all these parameter calculations are on the same time scale, it is not very pertinent to count them separately. It should be noted that the time required to establish a connection here only refers to the time spent on security verification, and it does not include the delay of underwater communication. As can be seen, our plan verification time is at the millisecond level, which is longer than the microsecond-level time of the lattice cipher method proposed in reference [13]. However, in underwater environments, compared to the minute-level communication delay between two nodes, it is already very negligible.
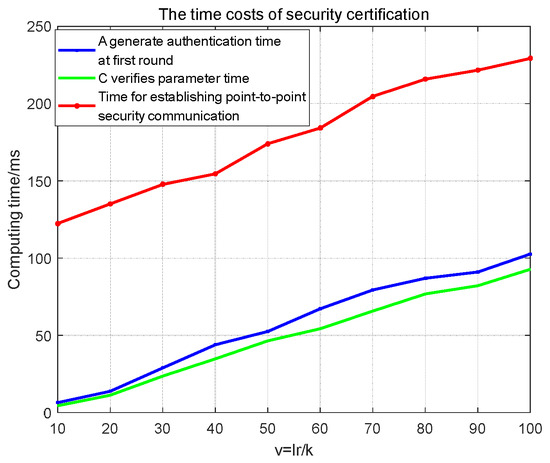
Figure 3.
The time costs of security certification.
Referring to [35], 30 samples are selected as input, and the length range of the samples is between 128 byte and 1024 byte. A total of 30 experiments of the hash generation algorithm and 30 experiments of the hash collision algorithm are conducted for the CH-ECDLP algorithm as the message length increases. In order to ensure the accuracy of the experiments, ten experiments are conducted with the same input, and finally the average of the computing time of the ten experiments is taken as the final computing time of this input. The experimental results of the hash operation time of the two schemes are shown in Figure 4 to display the time cost for generating the second verification.
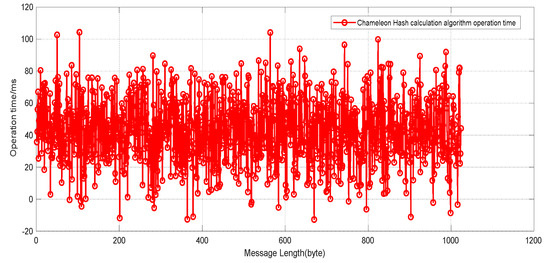
Figure 4.
The operation time of Chameleon Hash.
Figure 5, Figure 6 and Figure 7 show the performance metrics considered for comparison: average end-to-end delay, average data delivery ratio, average energy consumption. The main attacks tested are those wherein malicious nodes disguise themselves and interfere with normal routing forwarding, increasing latency. The system uses the above algorithm to identify and eliminate the average latency change in malicious nodes completing routing. We increase the number of attackers from 1 to 10 to test the basic parameters of our system for illustrating the effectiveness of the algorithm, which shows the efficiency of the system in detecting attackers and rebuilding secure and stable communication. Meanwhile, the settings about the degree t of polynomial fi(x) are also considered as variable parameters to calculate proper values of node detection.
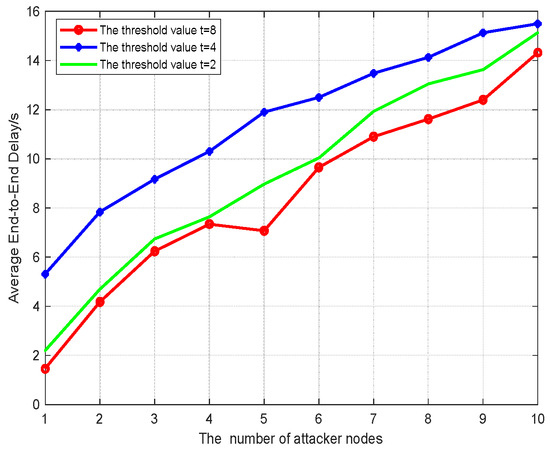
Figure 5.
The average end-to-end delay when the number of attack nodes is 10.
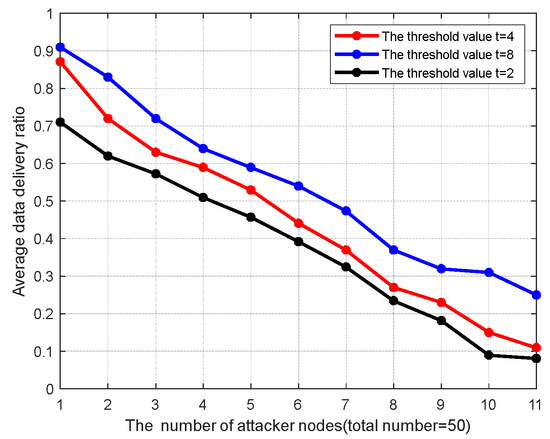
Figure 6.
The average data delivery ratio.
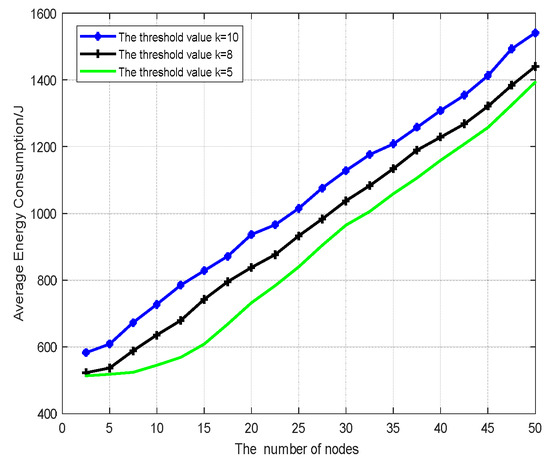
Figure 7.
The average energy consumption when the number of attack nodes is 10.
Average end-to-end delay refers to the average time consumed by data packets from source to the destination, which includes the packet routing process and the calculation time of the cryptographic algorithm. Average data delivery ratio represents the ratio of data packages successfully received. As can be seen from Figure 5, the average latency increases with the number of attackers. The proposed scheme ensures that, once a malicious node is detected, the data transmission will be interrupted and re-transmitted immediately, and the source node and destination node will be required to find the routing path again through the ADOV routing algorithm. This process will greatly increase the data transmission delay.
Meanwhile, due to the fact that the threshold t decides the detection probabilities for malicious nodes, the retransmission times are unspecific. Small thresholds (t < k, k is the average routing hops) only detect the first few hop routing nodes, and the probability of detecting malicious nodes is low, so the number of retransmissions is small. At this time, although the delay is relatively small, the robustness and data transmission rate are relatively poor.
Average energy consumption is defined as the total amount of energy consumed by all the nodes during data packets transmission in the communication when attackers exist. Figure 7 shows the energy consumption for the proposed techniques.
7. Conclusions
The security problem of UANs has become increasingly prominent. This paper designs and optimizes a lightweight security scheme according to the characteristics of UANs. Our proposal focuses on solutions for authentication, data protection, and malicious node inspection, which support the security protection in the entire network. Finally, we compared our approach with the current state of the art in the existing research, and Table 5 shows the comparison results. It can be seen that our scheme has a delay that is a magnitude larger than lattice cryptography, but it is not affected in high-latency underwater environments. Meanwhile, although our scheme is entirely based on classical computing environments, it does not require any restrictive assumptions on the computing power of protocol participants, which makes it able to resist quantum attacks and have unconditional security. In engineering practice and application scenarios, our solution also has significant advantages. The simulation results also prove the robustness and effectiveness of the scheme.

Table 5.
Comparison with existing solutions.
Author Contributions
Conceptualization, J.S.; Methodology, J.S.; Software, J.S.; Validation, J.S.; Investigation, J.S., Z.Z. and W.Z.; Resources, G.Q.; Data curation, J.W. and G.Q.; Writing—original draft, J.S.; Writing—review & editing, Z.Z., X.Q., W.Z. and D.Z.; Supervision, J.W. and G.Q.; Project administration, J.W.; Funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant No. 61901134.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Y.; Xiao, Y.; Li, T. A Survey of Autonomous Underwater Vehicle Formation: Performance, Formation Control, and Communication Capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Zhu, R.; Boukerche, A.; Long, L.; Yang, Q. Design Guidelines on Trust Management for Underwater Wireless Sensor Networks. IEEE Commun. Surv. Tutor. 2024, 1. [Google Scholar] [CrossRef]
- Wu, J.; Qi, X.; Guo, K.; Zhou, J.; Zhang, Y. Orthogonal Frequency Division Multiplexing Underwater Acoustic Communication System with Environmental Cognition Ability. Secur. Commun. Netw. 2021, 2021, 1640072. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, J.; Qi, X.; Qiao, G.; Zhang, W.; Zhang, C.; Guo, K. Design of a Broadband Cavity Baffle Bender Transducer. J. Mar. Sci. Eng. 2022, 10, 680. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Galbraith, S.D.; Vercauteren, F. Computational problems in supersingular elliptic curve isogenies. Quantum Inf. Process. 2018, 17, 265. [Google Scholar] [CrossRef]
- Giuliani, A.; Ardizzon, F.; Tomasin, S. ML-Based Advantage Distillation for Key Agreement in Underwater Acoustic Channels. In Proceedings of the 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 28 May–1 June 2023; pp. 703–708. [Google Scholar]
- Zhang, H.; Wu, L.; Zhi, Y.; Yang, C.; Cao, X.; Zhang, J.; Li, H. Throughput Maximization for USV-Enabled Underwater Wireless Networks Under Jamming Attack. IEEE Sens. J. 2023, 1. [Google Scholar] [CrossRef]
- Ardizzon, F.; Giuliani, A.; Laurenti, N.; Tomasin, S. Adversarial Learning for Advantage Distillation in Secret Key Agreement Over UWAC. In Proceedings of the 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 28 May–1 June 2023; pp. 715–720. [Google Scholar]
- Diamant, R.; Tomasin, S.; Ardizzon, F.; Eccher, D.; Casari, P. Secret Key Generation from Route Propagation Delays for Underwater Acoustic Networks. IEEE Trans. Inf. Forensics Secur. 2023, 18, 3318–3333. [Google Scholar] [CrossRef]
- Diamant, R.; Casari, P.; Tomasin, S. Cooperative Authentication in Underwater Acoustic Sensor Networks. IEEE Trans. Wirel. Commun. 2018, 18, 954–968. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, S.; Shi, Z.; Lai, L. Channel Frequency Response-Based Secret Key Generation in Underwater Acoustic Systems. IEEE Trans. Wirel. Commun. 2016, 15, 5875–5888. [Google Scholar] [CrossRef]
- Xu, M.; Li, C. An NTRU-Based Certificateless Aggregate Signature Scheme for Underwater Acoustic Communication. IEEE Internet Things J. 2023, 11, 10031–10039. [Google Scholar] [CrossRef]
- Bao, X.; Li, J.; Zhou, J. Feasibility Study of Sky-Underwater QKD Based on Asymmetric Channel. In Proceedings of the 2023 3rd International Conference on Intelligent Communications and Computing (ICC), Nanchang, China, 24–26 November 2023; pp. 132–135. [Google Scholar]
- Gupta, M.; Gera, P.; Mishra, B. A Lightweight Certificateless Signcryption Scheme based on HCC for securing Underwater Wireless Sensor Networks (UWSNs). In Proceedings of the 2023 16th International Conference on Security of Information and Networks (SIN), Jaipur, India, 20–21 November 2023; pp. 1–8. [Google Scholar]
- Krivokapic, B.; Tomovic, S.; Radusinovic, I. Authenticated Key Exchange in Underwater Acoustic Sensor Networks based on Implicit Certificates: Performance Analysis. In Proceedings of the 2023 27th International Conference on Information Technology (IT), Zabljak, Montenegro, 15–18 February 2023; pp. 1–4. [Google Scholar]
- Goyal, N.; Dave, M.; Verma, A.K. SAPDA: Secure Authentication with Protected Data Aggregation Scheme for Improving QoS in Scalable and Survivable UANs. Wireless Pers. Commun. 2020, 113, 1–15. [Google Scholar] [CrossRef]
- Ullah, S.S.; Hussain, S.; Uddin, M.; Alroobaea, R.; Iqbal, J.; Baqasah, A.M.; Abdelhaq, M.; Alsaqour, R. A Computationally Efficient Online/Offline Signature Scheme for Underwater Wireless Sensor Networks. Sensors 2022, 22, 5150. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Peng, C.; Li, K. A secure routing scheme for underwater acoustic networks. Int. J. Distrib. Sens. Netw. 2017, 13, 1550147717713643. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Ebri, N.A.; Baek, J.; Yeun, C.Y. Study on Secret Sharing Schemes (SSS) and their applications. In Proceedings of the 2011 International Conference for Internet Technology and Secured Transactions, Abu Dhabi, United Arab Emirates, 11–14 December 2011; pp. 40–45. [Google Scholar]
- Misra, S.; Tourani, R.; Natividad, F.; Mick, T.; Majd, N.E.; Huang, H. AccConF: An Access Control Framework for Leveraging In-Network Cached Data in the ICN-Enabled Wireless Edge. IEEE Trans. Dependable Secur. Comput. 2017, 16, 5–17. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Wu, Y.; Zhang, Q. An ECDLP-Based Randomized Key RFID Authentication Protocol. In Proceedings of the 2011 International Conference on Network Computing and Information Security, Guilin, China, 14–15 May 2011; pp. 146–149. [Google Scholar]
- Sadkhan, S.B. Development of Solving the ECDLP. In Proceedings of the 2021 7th International Engineering Conference “Research & Innovation amid Global Pandemic” (IEC), Erbil, Iraq, 24–25 February 2021; pp. 206–210. [Google Scholar]
- Sandeep, D.N.; Kumar, V. Review on Clustering, Coverage and Connectivity in Underwater Wireless Sensor Networks: A Communication Techniques Perspective. IEEE Access 2017, 5, 11176–11199. [Google Scholar] [CrossRef]
- Choi, J.; Jung, S. A handover authentication using credentials based on chameleon hashing. IEEE Commun. Lett. 2009, 14, 54–56. [Google Scholar] [CrossRef]
- Blum, M. Coin flipping by telephone a protocol for solving impossible problems. ACM SIGACT News 1983, 15, 23–27. [Google Scholar] [CrossRef]
- Lemus, M.; Yadav, P.; Mateus, P.; Paunkovic, N.; Souto, A. On minimal assumptions to obtain a universally composable quantum bit commitment. In Proceedings of the 2019 21st International Conference on Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019; pp. 1–4. [Google Scholar]
- Mayers, D. Unconditionally secure quantum bit commitment is impossible. Phys. Rev. Lett. 1997, 78, 3414. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Is quantum bit commitment really possible? Phys. Rev. Lett. 1997, 78, 3410. [Google Scholar] [CrossRef]
- Rojas, C.A.; Devesa, A.; Cabrera, H.; Reis, G.M.; Bobadilla, L.; Smith, R.N. Privacy-Preserving Multi-Agent Marine Data Collection via Differential Privacy. In Proceedings of the OCEANS 2023—MTS/IEEE U.S. Gulf Coast, Biloxi, MS, USA, 25–28 September 2023. [Google Scholar]
- Zhou, Z.; Gupta, B.B.; Gaurav, A.; Li, Y.; Lytras, M.D.; Nedjah, N. An Efficient and Secure Identity-Based Signature System for Underwater Green Transport System. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16161–16169. [Google Scholar] [CrossRef]
- Baumgart, I.; Mies, S. S/Kademlia: A practicable approach towards secure key-based routing. In Proceedings of the 2007 International Conference on Parallel and Distributed Systems, Hsinchu, Taiwan, 5–7 December 2007; pp. 1–8. [Google Scholar]
- Koponen, T.; Chawla, M.; Chun, B.G.; Ermolinskiy, A.; Kim, K.H.; Shenker, S.; Stoica, I. A Data-oriented (and beyond) Network Architecture. In Proceedings of the 2007 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Kyoto, Japan, 27–31 August 2007; Volume 37, p. 181. [Google Scholar]
- Qiao, Y.; Zheng, M.; Yang, J. Implementation of one-time editable blockchain chameleon hash function construction scheme. In Proceedings of the 2022 IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Wuhan, China, 9–11 December 2022; pp. 851–856. [Google Scholar]
- Grover, L. A fast quantum mechanical algorithm for database search. In Proceedings of the 28th ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- OMNeT++ User Manual [EB/OL]. Available online: http://www.omnetpp.org (accessed on 1 September 2022).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
