1. Introduction
The Fluid–Structure Interaction (FSI) is the most prevalent physical phenomenon in various engineering applications. Some of the applications, such as the interaction between waves and vegetation in coastal wetlands and wave–ice interactions in the Arctic environment [
1], are crucial in mitigating coastal flooding [
2]. FSI plays a pivotal role in the refinement of structural designs for optimal performance under fluid loads, ensuring both efficiency and reliability [
3], e.g., the construction of offshore installations and the design of windmills and ships. Identifying FSI-related issues early allows cost-effective design changes, reducing the need for any modifications during manufacturing or operation [
4]. Similarly, FSI affects the hydrodynamic performance of propellers, e.g., [
5,
6]. The damping represents energy dissipation within vibration cycles and emerges as a key factor in resonance phenomena, impacting harmonic vibration amplitudes and the count of noteworthy vibrations in time-dependent scenarios. In most cases, the role of damping can be negligible in slightly damped vibrations. However, in the natural frequencies, their influence becomes pronounced, especially in near-resonant conditions, where excitation is balanced solely through damping. Damping in the structure is generally low, except when near resonance and the vibration cycle maintains a substantial level of independence [
7].
However, simulating FSI effectively is complex, requiring certain assumptions in both structural and fluid simulations. In most of the Computational Fluid Dynamics (CFD) simulations, the consideration of elastic deformation at the boundaries is ignored [
8]. Similarly, in most of the structural simulations, a constant pressure is considered at the interior and exterior boundaries. Paik et al. [
9] presented methods for coupling the CFD solver with rigid and elastic models of a ship hull to compute structural loads. One-way and two-way coupling approaches were used when considering the ship as elastic. In one-way coupling, forces from CFD were used for structural loads analysis, but deformations were not feedback to CFD. In two-way coupling, hull deformations influenced the CFD solution. A URANS/DES overset solver with the modal superposition method is used for the analysis. The gluing method was applied to transfer forces and deformations between non-matching CFD and structural grids [
9].
Different varieties of approaches have been formulated to tackle the intricacies of one-way and two-way coupling of the FSI. A prominent approach involves fully coupled (monolithic) methods that integrate structural and flow calculations in a single solver [
10,
11]. Conventional CFD solvers predominantly use an Eulerian-based approach. However, such coupling of structural formulations, which mostly use Lagrangian-based approaches, leads to a stiffer computation for the structural component compared to the fluid component. Moreover, employing a unified scheme for extensive scenarios becomes computationally intensive [
12].
Grid-based partitioned methods offer a more feasible alternative to monolithic methods by tackling both the flow and structural formulation on two different meshes using distinct solvers [
13]. These methods necessitate the establishment of a communication protocol at the interface between grids to appropriately transfer fluid loads to the structural mesh and, conversely, to map the deformation onto the fluid mesh. In mesh-based solvers, effective adjustment of the fluid mesh boundaries requires precise manipulation of adjacent mesh nodes to prevent mesh entanglement or deformation [
14,
15]. Recent advances have demonstrated the successful application of partitioned methods, such as coupling thin-walled girder theory with potential flow theory [
16,
17] and linking modal structure solvers with RANS-VOF solvers, Boundary-Integral Equation Methods [
18]. Solid4Foam with the finite volume library is provided by OpenFOAM [
19,
20].
The meshless-based partitioned method offers several advantages, especially in scenarios that involve free surfaces, violent flow, complex models, and large deformations [
21]. In this approach, the need for re-meshing of the model after deformation is effectively avoided. FSI is achieved by coupling the Smooth Particle Hydrodynamics (SPH) with different structural solvers such as the Finite Element Method (FEM) [
22,
23,
24] and Discrete Element Method (DEM) [
25,
26,
27] to compute the structural deformation. However, transferring the information is not easy, as it is necessary to resolve the interfacial energy balance [
28]. Solving the structural deformation is computationally expensive but less so than the monolithic method.
In recent days, the Mode Superposition method has been used to solve structural deformation, and it is the most robust, fast, and computationally inexpensive method. Debrabandere et al. (2012) presented a new reduced-order modeling approach for FSI simulations. The method uses modal analysis to represent structural dynamics, solving the modal equations within the computational fluid dynamics solver using a complementary function and a particular integral method. Results for simple test cases compare well with full-order models and experiments. FSI predictions for realistic turbomachinery configurations demonstrate the potential of the method for efficient aeroelastic analysis of flexible structures [
29]. Sun et al. (2019) presented the Moving Particle Semi-implicit (MPS) with the mode superposition method to simulate violent hydroelastic issues [
30]. Corrado et al. (2020) validated the two-way coupling between CFD and FEM solvers and a more efficient modal superposition approach with the help of the HIRENASD test case [
31]. Modal superposition is a useful technique for evaluating structures that are subjected to dynamic loads due to its computational efficiency and simplicity. However, when dealing with large structural deformations, the accuracy of this method tends to decrease. This is because modal superposition assumes linear behavior and uncoupled modes, which may not hold true in scenarios involving significant nonlinearity or mode coupling. Despite these limitations, modal superposition remains a widely used and valuable tool, especially when applied within its valid range [
29,
30,
31]. Weak coupling in FSI offers simplicity and ease of implementation, making it suitable for scenarios with transient events. However, its limitations include stability issues necessitating small time steps, which can lead to computational inefficiency, and potential accuracy trade-offs compared to implicit methods, especially in large-scale simulations where the fluid and structural solvers use time steps of different magnitudes [
32]. The convenience of using modes superposition is that the structural solver adds insignificant computational cost [
17,
29] and therefore, can adjust to the flow solver requirements.
The aim of this study is to develop a model for Fluid–Structure Interaction (FSI) by combining the Mode Superposition method and the Lagrangian Differencing Dynamics (LDD) method in two-way partitioned weak coupling or explicit coupling. In terms of computational efficiency, the LDD method is advantageous compared to most popular meshless approaches, such as Smoothed Particle Hydrodynamics (SPH), Moving Particle Semi-implicit (MPS), finite point set method, and finite point method [
33,
34,
35]. The LDD method achieves large time steps with lower computational costs while maintaining second-order accuracy. It is well-suited for complex transient problems since it has the advantage of directly working on the meshes [
8,
16,
17,
36]. Using the mode superposition method with LDD, structural deformation is calculated for the fluid load using precalculated mode shapes and natural frequencies from the modal analysis. This approach leads to stable, robust, and computationally efficient FSI simulations. The method enables fluid-induced structural deformation to be weakly coupled into the flow solver. The deformation is obtained by using direct integration. The flow particles and vertices of the structure are advected in Lagrangian coordinates. This results in Lagrangian–Lagrangian coupling in space, while there is weak or explicit coupling in time. This ensures a more accurate representation of the interaction between fluid and structure in ship and offshore hydrodynamics. The efficiency of the LDD and Mode Superposition methods, operating directly on surface meshes, may lead to practical and effective ship and offshore hydrodynamic simulations.
This paper discusses fluid–structure interaction (FSI) modeling using the two-way weak coupling approach. Specifically, this paper details the governing equation of the LDD method and the mode superposition technique in
Section 2. The methodology of implementing two-way coupling of FSI is then explained in
Section 3. In
Section 4, various benchmark cases are presented that are then validated and verified with modal coupling results. Finally, concluding remarks and a summary of the findings are given in
Section 5.
3. Methodology
In this paper, vibration modes are expressed using natural frequencies and mass-normalized mode shapes, as detailed in
Section 2.2. Equations (
10)–(
15) encloses the force vector and the structural deformation of the system. The equation of motion for a single mode (Equation (
15)) is directly integrated in time within the fluid flow solver using the CFPI method, resulting in the generalized displacement, denoted
. The same process is repeated for all modes at each time step of the simulation. Then, the global deformation of the structure is finally obtained using Equation (
12), incorporating the calculated generalized displacement. Thereby ensuring that updated structural shape influences the flow calculations resulting in updated flow pressure and velocity fields [
29]. Natural frequencies and corresponding modal vectors are determined externally before commencing the CFD, either by analytical methods or by using external modal solvers.
The workflow of the fluid–structure solver is depicted in
Figure 1. The below steps are introduced to establish a two-way coupling of the fluid–structure interaction.
Calculate the mass-normalized mode shapes and corresponding natural frequencies, denoted as .
Define the initial and boundary conditions for the simulation, including the initial displacement of the structural system if any.
Create Radial Basis Function (RBF) connections between fluid mesh and structural mesh to transfer the mode shape information if the structural mesh is not the same as the fluid mesh [
40].
At every time step of the simulation :
- (a)
Compute the forces exerted on the structural mesh due to fluid force.
- (b)
Solve equation of motion (
15) for each mode shapes and natural frequencies
- (c)
Determine the overall deformation vector using Equation (
12) and apply the resulting deformation to the mesh.
- (d)
Solve the fluid equations for time , taking into account of structural deformation.
The coupling scheme based on the mode superposition method is formulated by solving the equation of motion with imposed loads by using mode shapes and natural frequencies which are determined from the modal analysis in the pre-calculation stage (step 1). This modal coupling is integrated into the LDD method, which takes initial and boundary conditions (step 2) from simulation input. This step is needed only in situations where the fluid mesh vertices do not overlap with structural vertices. In such a case, an interpolation is needed to compute the mode shape for the fluid mesh, based on the structural mesh (step 3). The displacement resulting from fluid forces (step 4a) is calculated within the modal coupling algorithm using CFPI method (step 4b). This deformation is applied on the mesh to account for geometric changes for the fluid solver (step 4c), consequently calculating the updated flow pressure and velocity fields using updated mesh (step 4d).
5. Conclusions
The modal-coupling solver has been seamlessly integrated into the Lagrangian Differencing Dynamics (LDD) solver. The numerical experimentation has shown that it enables effective two-way weak coupling of the fluid–structure interaction. The effectiveness of the Modal Coupling approach is attributed to its utilization of the mode superposition method. While the proposed bidirectional coupling is explicit in time, the insignificant cost of computing the structural deformation by using the mode superposition method allows the weak coupling to remain stable for time-steps that are required by the flow solver.
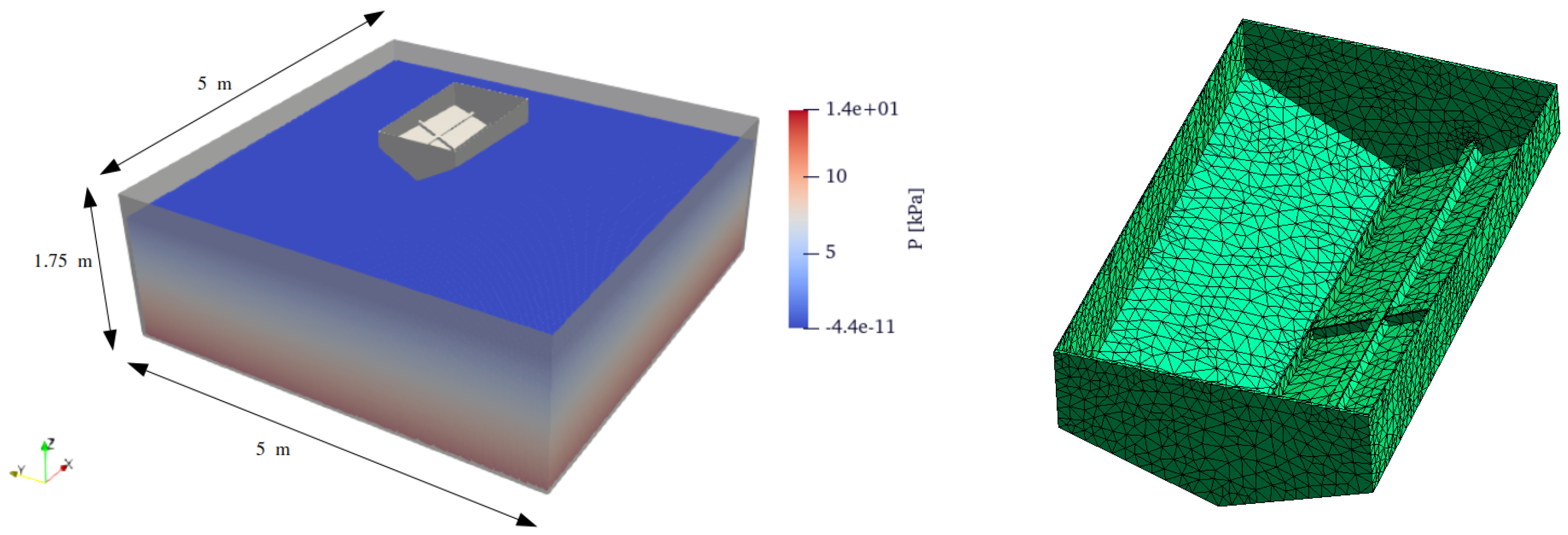
The verification and validation of the bidirectional fluid–structure interaction are successfully demonstrated through seven numerical experiments. The benchmark cases included both slowly and quickly deforming structures, and single or oscillatory fluid loads. The benchmark cases resembled swaying and rotating sloshing experiments (with and without flexible baffles), dam break experiments (with an elastic gate or obstacles) and water-entry experiment (slamming loads applied to a stiffened structure). The comparison between the numerically obtained results and the available experimental data demonstrated the ability of the proposed coupling method to capture complex interactions between fluids and structures.
The efficiency of the modal-coupling solver is accomplished by small computational cost of deforming the structure, by its flexibility to accommodate to the flow solver time-steps, and by using the Lagrangian LDD method to obtain accurate pressure loads. While this allows straightforward and efficient Lagrangian–Lagrangian coupling during the simulation, the engineering advantage is that there is no need for meshing or preparing the coupling interface, since the flow solver operates directly on surface meshes shared by the structural solver.
The above features of the proposed coupling method show practicality and applicability in future ship and offshore hydrodynamic simulations. The implementation process of the coupling scheme substantiates the tool’s capability to facilitate the effortless coupling of diverse solvers, all without necessitating changes to solver algorithms or input files. The incorporation of the energy equation into the framework is planned in future work. This expansion aims to explore the influence of energy on the fluid–structure interaction, thereby broadening the scope and insights of the analysis.